. Podemos afirmar: Dom f. c) f es creciente en un entorno de x 0. = y(t) 9.- Sean las ecuaciones paramétricas de una curva plana.
|
|
|
- José Ramón Cano Herrera
- hace 5 años
- Vistas:
Transcripción
1 1.- Sea una función coninua y = f() al que el dominio de f() =[a,b], enonces: a) El máimo absoluo de f() se alcanza en uno de los valores ales que f ()=0. b) No iene porque ener máimo absoluo. c) El máimo absoluo es el máimo de {f(a), f(b), máimos relaivos}..- Si f() es una función cuaro veces derivable en a, y verifica f (a) = f (a) = 0, f (a) > 0. Enonces a) f iene un mínimo en a. b) f iene un máimo en a. c) Ninguna de las dos aneriores..- Sea y= f() una función coninua al que en un enorno de =a iene un único mínimo relaivo en dicho puno =a. Podemos afirmar: a) f (a)=0. b) No eise f (a). c) A la izquierda de a la función es decreciene y a la derecha de a es creciene. 4.- Si f (c)=f (c)=0, enonces: a) En c hay un eremo relaivo. b) En c hay un puno de infleión. c) No podemos afirmar nada acerca de la eisencia ni de valores eremos ni de punos de infleión. 5.- Si y = f() iene un máimo en (c,f(c)), enonces: a) En un enorno de c, la función f es convea. b) Si f es coninua en c, f es convea en un enorno de c. c) Si f es derivable hasa el orden n mayor o igual que dos enonces f es convea en un enorno de c. 6.- Sea P n () un polinomio de grado n. Se verifica: a) No iene asínoas. b) Puede ener asínoas horizonales, pero no vericales. c) Puede ener asínoas vericales, pero, no horizonales. 7.- Sea y=f() una función acoada en odo R. Se puede asegurar que: a) f iene alguna asínoa horizonal. b) f no iene asínoas vericales. c) f es siempre posiiva. 8.- Sea y = f() una función coninua que presena un máimo relaivo en el puno ( 0,f ( 0)). Podemos afirmar: a) ( ) = 0 ó bien no eise f ( ). f 0 0 b) f( 0 ) f () Dom f. c) f es creciene en un enorno de Sean las ecuaciones paraméricas de una curva plana. Supongamos que lim ( lim y( = +. Podemos afirmar que: = ) 0 0 a) La curva posee una asínoa oblicua. b) La curva posee una asínoa horizonal. y( c) Si lim = +, la curva no posee una asínoa oblicua para 0. 0 ( 10.- En una curva plana se verifica que: Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 15
2 a) Un puno singular es siempre un puno críico. b) Un puno críico es siempre un puno singular. c) No se puede afirmar ni a) ni b) En un puno singular de la curva a) las derivadas de y de y se hacen infinias. b) las derivadas de y de y se anulan. c) no podemos afirmar ni a) ni b). 1.- Si son unas ecuaciones paraméricas de una curva plana y para = 0 se verifica que lím ( lím y( =, podemos afirmar que = ) 0 0 a) La curva iene asínoa oblicua. b) La curva no iene una asínoa oblicua. c) Falan cálculos para decidir si iene una asínoa oblicua o no. 1.- La gráfica corresponde a la curva: a) r = sen(ө). b) r = cosө. c) r = 1+cosӨ Si y = f () es una función real de variable real, se verifica: a) f() coninua f() derivable f() diferenciable. b) f() diferenciable f() derivable f() coninua. c) f() derivable f() coninua f() diferenciable Sean las ecuaciones paraméricas de una curva plana. Supongamos que y( lím ( = lím y( =, y lím = a R. Podemos afirmar que: ( a) La curva posee una asínoa horizonal. b) La curva posee una asínoa verical. c) La curva puede ener una asínoa oblicua de pendiene a Sean las ecuaciones paraméricas de una curva plana. Si lím ( = ± 0 lím y( = ±, enonces: 0 y( a) Si lím = 0, la reca y=0 es asínoa horizonal. 0 ( y( b) Si lím =, la reca =0 es asínoa verical. 0 (, y Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 16
3 y( c) Si lím = m 0 y m ±, puede eisir asínoa oblicua. 0 ( 17.- Sea f () = g(), siendo g() una función derivable R. Enonces: a) f() es derivable R. b) f() es coninua R. a) f() es coninua y derivable R La función f () = 1, verifica: a) La reca angene en =1 es y 0 = f '(1)( 1). b) La reca angene en =1 es =1. c) No eise reca angene en = Si una función f es coninua en [a,b], enonces: a) f iene un máimo y un mínimo relaivos en (a,b). b) f alcanza sus valores máimo y mínimo absoluos en [a,b]. c) f no puede esar acoada [a,b]. ln 0.- Si f :( 0, ) R es derivable y f '() = ( 0, ), enonces: 1+ a) f (1) f (), ( 0, ) b) f iene en =1 un máimo relaivo. c) Ninguna de las dos aneriores son cieras. = dy 1.- Si enonces es: = e d a) e + e e + e b) ( ) e + e c).- Sea f una función derivable en R, enonces la derivada de g()=f( ) es: a) f '( ) b) f '( ) c) f '().- Sea f () = 1, enonces en =1, se verifica: a) f es derivable pero no es coninua. b) f es coninua pero no es derivable. c) f no esá definida. 4.- Sea y=ln(+1), enonces: a) y' = + 1 b) y' = ( + 1) c) y' = Sea y=f() una función derivable en el inervalo (-,) y al que f (0)=0 y f es cóncava en (-,), enonces: Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 17
4 a) f presena en =0 un máimo. b) f presena en =0 un mínimo. c) f presena en =0 un puno de infleión. 6.- Si [ a,b] R,f :[ a,b] R es coninua y signo f(a) signo f(b), enonces: a) Eise un único valor c (a,b) al que f(c)=0 b) Eise al menos un valor c (a,b) al que f(c)=0 a) No eise ningún valor c (a,b) al que f(c)=0 7.- Sea f : [a,b] ---> R a) f coninua => f derivable. b) f derivable => f coninua. c) f coninua <=> f derivable. 8.- Dada la función f : R R definida por f() = e + -1, eise c (0,) al que: a) f (c) =0 b) f (c) = (+e )/ c) f (c) = Dada f () = 1, se verifica que f: a) Alcanza su mínimo absoluo en = 1 y = -1. b) No iene mínimos ya que no es derivable. c) Es derivable en odo R pero no iene eremos relaivos. 0.- La gráfica corresponde a la curva: a) y =. ( + 1) b) y =. + 1 ( ) c) y = Sea y = f() una función coninua que iene un puno de infleión en (c,f(c)), se verifica: a) En =c, f no puede ener ni máimo ni mínimo relaivo. b) Si f admie derivada segunda en un enorno de c, f cambia de signo a izquierda y derecha de c. c) Si f admie derivada ercera en un enorno de c, f '''(c) 0..- Sea la gráfica de una curva y = f() epresada por sus ecuaciones paraméricas, y. a) ( = sen ( = cos Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 18
5 ( = sen b) ( = cos ( = sen c). ( = cos.- Sea la gráfica de una curva y = f() epresada por sus ecuaciones paraméricas, y. Enonces: a) y (>0 y (<0 para odo Dom(f ). b) y (<0 y (>0 para odo Dom(f ). c) y (<0 y (<0, ó bien y (>0 y (>0 para odo Dom(f ). () = sen 4.- La curva es periódica de periodo () y = cos a) π b) 6 π c) 1 π 5.- Sean las ecuaciones paraméricas de una curva plana. Supongamos que ( = (, y(- = -y(. Podemos afirmar que la curva es simérica respeco de: a) El eje de abscisas. b) El eje de ordenadas. c) El origen. 6.- La función derivada de la función f () = sh. ch a) ch sh b) ch + sh c) ch + sh 7.- Sea y=f() una función derivable en R al que f(0)=f(1)=f(). Se verifica: a) La derivada f () se anula al menos en dos punos en (0,). b) La derivada f () se anula únicamene en dos punos en (0,). c) La derivada f () no iene porqué anularse en el inervalo (0,). 8.- Se verifica: a) ch sh = 1 b) ch + sh = 1 c) sh ch = Si son las ecuaciones paraméricas de una curva plana y para lim ( = 0 y lim y( =, podemos afirmar que : a) El eje X es una asínoa de la curva. b) El eje Y es una asínoa de la curva. c) Ninguna de las aneriores Sea f()=ch(). Enonces:, se verifica Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 19
6 a) f ()=sh(). e + e b) f () =. c) f () = ch sh = () 41.- Si la curva iene a la reca r = como asínoa, podemos afirmar que: = y() a) El campo de variación de no es R (la reca real). b) La curva no cora a la reca r. c) Si la curva represena a una función y = f (), enonces f no es acoada. = cos( 4.- La curva verifica: y = g a) Es periódica de período π. b) Es periódica de período π. c) No es periódica. 4.- Sea la curva plana de ecuaciones al que (+)=( e y(+6)=y( R. Enonces se verifica: a) La curva es periódica de período 6. b) La curva es periódica de período. c) La curva no es periódica, pues ( e y( ienen disino período Dada la curva de ecuación, [,], se verifica: a) No puede ener asínoas. b) La curva iene longiud finia pues varía en un inervalo finio. c) Ninguna de las aneriores. ( = sen() 45.- La curva verifica: y( = cos a) Su gráfica es simérica respeco del eje OY b) Es periódica de periodo π c) Tiene alguna asínoa =ϕ( ϕ ( = ϕ( 46.- La curva verifica que para odo R. Enonces se verifica: =ψ ( ψ ( = ψ ( a) La curva iene una gráfica simérica respeco del eje OY. b) La curva iene una gráfica simérica respeco del eje OX. c) La curva iene una gráfica simérica respeco del origen Dada la curva en coordenadas polares r=r(α), es simérica respeco del polo si: a) r( α+π ) = r( α ) b) r( π α ) = r( α ) c) r( α ) = r( α ) Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 0
7 48.- Sean las ecuaciones paraméricas de una curva plana. Supongamos que lím ( = lím y( =±. Es posible que cuando iende a 0 la curva enga: 0 0 a) una asínoa verical. b) una asínoa horizonal. c) una asínoa oblicua La gráfica siguiene corresponde a una curva de ecuaciones paraméricas: ( = 1 a) 1+ y( = ( = 1 b) 1+ y( = ( = 1 c). 1+ y( = 50.- Dada la curva en coordenadas polares r =sen(α), su gráfica es: a) b) Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 1
8 c) = - sen 51.- La curva = 1 - cos verifica: a) Es periódica de período π. b) Es periódica de período 4π. c) No es periódica. 5.- La curva de ecuaciones paraméricas a) T = π. b) T= π. c) T= 6π. = sen es periódica de periodo: y= g 5.- La función f()=g es: a) Periódica de periodo π y simérica respeco del eje OX. b) Periódica de periodo π y simérica respeco del origen. c) Periódica de periodo π y simérica respeco del eje OY La curva de la figura iene: a) cuaro punos críicos. b) dos punos críicos. c) ningún puno críico. Unidad Docene de Maemáicas de la E.T.S.I.T.G.C.
9 55.- Sean las ecuaciones paraméricas de una curva plana. Si lím y( = ±, se puede 0 afirmar: a) La curva iene una asínoa verical cuando 0. b) Si lím ( = enonces = es una asínoa verical de la curva. 0 c) Si lím ( = enonces la curva iene una asínoa oblicua. 0 = sen 56.- Dada la curva plana, la derivada de y respeco de en el puno (0,0) es: = sen( a) dy d = b) dy d = c) dy 1 d = 57- Dada la curva plana simérica respeco de: a) El eje de ordenadas. b) El eje de abscisas. c) El origen.. Si se verifica ( = ( podemos afirmar que la curva es ( 58.- Si una curva dada por sus ecuaciones paraméricas cumple que (-=( e y(-=y(. Se puede asegurar que la curva es simérica respeco de: a) eje OX b) eje OY c) Origen de coordenadas 59.- Dada la curva en paraméricas: a) π b) π c) π Dada la curva en paraméricas: [ ) es: a) y = b) y =. 7 c) y = para 0. 7 ( = sen(4. El periodo de esa curva es: ( = cos( ( =, 0, ( =. Una ecuación en eplícias de la curva Unidad Docene de Maemáicas de la E.T.S.I.T.G.C.
10 61.- Si una función f() es coninua en un inervalo cerrado [a,b] y oma valores de disinos signo en los eremos del inervalo, enonces: a) La función f() es derivable en [a,b]. c a,b. b) La función oma el valor f()=0 en un ciero puno ( ) c) La función es monóona creciene o decreciene en [a,b]. senα+ cosα 6.- La curva r = es simérica: senα a) respeco del polo. b) respeco del eje polar. c) no iene simerías. + e si >0 6.- La función f() = 1-( +1 ) si 0 a) Tiene asínoa horizonal hacia +. b) Tiene asínoa horizonal hacia -. c) Tiene asínoa verical en = Si la gráfica de una curva plana es simérica respeco al eje de abscisas OX, puede afirmarse que: ( a) ( = y( ( = ( b) ( c) Ninguna de las dos aneriores, pues la simería puede deberse a oros moivos. ( = 65.- La curva verifica y( = a) Tiene punos singulares. b) Tiene punos críicos, pero no iene punos singulares. c) Tiene una gráfica acoada. e - e 66.- La función senh() = es: a) Simérica respeco el origen. b) Simérica respeco el eje OX. c) Simérica respeco el eje OY. = 67.- Sean las ecuaciones paraméricas de una curva plana. Podemos afirmar que la curva es = simérica respeco de: a) El eje de abscisas. b) El eje de ordenadas. c) El origen El dominio de la función h() es: a) Todos los números reales (R). b) [-1,1] Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 4
11 c) Reales posiivos. ( = sen 69.- La curva es periódica de período: y( = cos a) π b) 6π c) 1π 70.- Dada la curva en coordenadas polares r=r(α), es simérica respeco al eje polar si: a) r( α+π ) = r( α ) b) r( π α ) = r( α ) c) r( α ) = r( α ) 71.- Sean [(,y(]las ecuaciones paraméricas de una curva dada. Si se verifica que ( 0 )=0, y ( 0 )=0, enonces: a) En el puno [( 0 ), y( 0 )] la curva no esá definida. b) En el puno [( 0 ), y( 0 )] la curva presena una asínoa. c) En el puno [( 0 ), y( 0 )] la curva presena un puno singular. ( = sen ( 7.- Dada la curva, se verifica que: y( = cos ( a) Es simérica respeco de OY. b) Es periódica de periodo π. c) Es periódica de periodo π El campo de variación para la variable de la curva,, es: a) R b) R-{0,-1,1} c) R-{-1,} 74.- Si una curva ( (, y( ), I : lím ( = a 0 a) iene una asínoa verical = a, enonces eise 0 I al que lím y( = 0 lím ( = b 0 b) iene una asínoa horizonal y = b, enonces eise 0 I al que lím y( = 0 lím ( = a 0 c) iene una asínoa oblicua y=a +b, enonces eise 0 I al que lím y( = b Si la función f() es coninua en [a,b], enonces: a) La función f() es derivable en [a,b] b) La función f() es inegrable en [a,b] c) La función f() no es acoada en [a,b] Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 5
12 76.- Sea la curva dada por las ecuaciones paraméricas P ( ), y( )) ( 0 0 = ( = y( para I. Si en el puno con 0 I se verifica que ( ) = 0, y'( ), enonces podemos afirmar que: ' 0 0 = a) La reca angene a la curva en P es una reca verical. dy b) En P la derivada vale 0. d c) Ese dao no es relevane para describir la curva Si una función y = f() es coninua en R y la reca y = 5 es una asínoa horizonal cuando ±, enonces podemos afirmar que: a) 5 es una coa, o bien superior o bien inferior de los valores de la función. b) La curva esá acoada superior e inferiormene pero no podemos inferir el valor de posibles coas de la función. c) Ese dao no apora ninguna información sobre si la curva esá o no acoada. Unidad Docene de Maemáicas de la E.T.S.I.T.G.C. 6
EXAMEN DE MATEMÁTICAS I (Primer Parcial) 11 de febrero de 2009
 EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
El sistema es incompatible. b) El sistema es compatible determinado. Lo resolvemos por la regla de Cramer.
 Prueba de Acceso a la Universidad. JUNIO 0. Maemáicas II. El alumno debe responder a una de las dos opciones propuesas, A o B. En cada preguna se señala la punuación máima. OPCIÓN A a y z A. Sean a un
Prueba de Acceso a la Universidad. JUNIO 0. Maemáicas II. El alumno debe responder a una de las dos opciones propuesas, A o B. En cada preguna se señala la punuación máima. OPCIÓN A a y z A. Sean a un
EXAMEN DE MATEMÁTICAS I 8 de febrero de 2006
 EXAMEN DE MATEMÁTICAS I 8 de febrero de 006 MATEMÁTICAS I Eamen del º PARCIAL 8 de febrero de 006 Sólo una respuesa a cada cuesión es correca. Respuesa correca: 0. punos. Respuesa incorreca: -0. punos
EXAMEN DE MATEMÁTICAS I 8 de febrero de 006 MATEMÁTICAS I Eamen del º PARCIAL 8 de febrero de 006 Sólo una respuesa a cada cuesión es correca. Respuesa correca: 0. punos. Respuesa incorreca: -0. punos
GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA
 GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA Una curva C se dice definida paraméricamene por medio de un parámero, si las coordenadas afines de sus punos M se expresan en función de ese parámero, cuando varía
GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA Una curva C se dice definida paraméricamene por medio de un parámero, si las coordenadas afines de sus punos M se expresan en función de ese parámero, cuando varía
REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA
 Represenación de curvas planas dadas en forma paramérica REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA PLANTEAMIENTO DEL PROBLEMA Sean x e y dos funciones reales de variable real, de dominios
Represenación de curvas planas dadas en forma paramérica REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA PLANTEAMIENTO DEL PROBLEMA Sean x e y dos funciones reales de variable real, de dominios
1 a 1 a 1. 0 a 1 a a 0. 0 a 1 a 1 a a 1 a 1 a 1 a 1 a a 1 a 1 a 1 a 1. a 1 a 1 a 1 a 1 0 a 1, a 1
 Pruebas de Apiud para el Acceso a la Universidad. JUNIO 1998. Maemáicas II. OPCIÓN A 1. Discuir el sisema a z solución del mismo cuando a = [1 puno] (a 1) y a z 1 (a 1) y (a 1) z según sea el valor del
Pruebas de Apiud para el Acceso a la Universidad. JUNIO 1998. Maemáicas II. OPCIÓN A 1. Discuir el sisema a z solución del mismo cuando a = [1 puno] (a 1) y a z 1 (a 1) y (a 1) z según sea el valor del
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO 2011 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho
 IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
Unidad 9 Funciones exponenciales, logarítmicas y trigonométricas
 Unidad 9 Funciones eponenciales, logarímicas y rigonoméricas PÁGINA 177 SOLUCIONES 1. En cada uno de los res casos: a) Domf = Imf = Esricamene creciene en odo su dominio. No acoada. Simérica respeco al
Unidad 9 Funciones eponenciales, logarímicas y rigonoméricas PÁGINA 177 SOLUCIONES 1. En cada uno de los res casos: a) Domf = Imf = Esricamene creciene en odo su dominio. No acoada. Simérica respeco al
INTEGRALES Prueba de Evaluación Continua Grupo A1 10-XI Enunciar y demostrar el Teorema Fundamental del Cálculo Integral.
 INTEGRALES Pruea de Evaluación Coninua Grupo A -XI-.- Enunciar y demosrar el Teorema Fundamenal del Cálculo Inegral. Ver eoría de la maeria..- Calcular las derivadas de las siguienes funciones: a) F()
INTEGRALES Pruea de Evaluación Coninua Grupo A -XI-.- Enunciar y demosrar el Teorema Fundamenal del Cálculo Inegral. Ver eoría de la maeria..- Calcular las derivadas de las siguienes funciones: a) F()
a) en [0, 2] ; b) en [-1, 1]
![a) en [0, 2] ; b) en [-1, 1] a) en [0, 2] ; b) en [-1, 1]](/thumbs/80/82443407.jpg) UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO FACULTAD DE CIENCIAS NATURALES CATEDRA: Maemáica I CURSO: 04 TRABAJO PRACTICO Nº -Tercera Pare Pare III. Aplicaciones de la derivada TEOREMA DE ROLLE
UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO FACULTAD DE CIENCIAS NATURALES CATEDRA: Maemáica I CURSO: 04 TRABAJO PRACTICO Nº -Tercera Pare Pare III. Aplicaciones de la derivada TEOREMA DE ROLLE
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 I.E.S. CASTELAR BADAJOZ A. Menguiano PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE - 8 (RESUELTOS por Anonio Menguiano) MATEMÁTICAS II Tiempo máimo: horas minuos Se valorará la corrección
I.E.S. CASTELAR BADAJOZ A. Menguiano PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE - 8 (RESUELTOS por Anonio Menguiano) MATEMÁTICAS II Tiempo máimo: horas minuos Se valorará la corrección
Técnicas cualitativas para las Ecuaciones diferenciales de primer orden: Campos de pendientes y ĺıneas de fase. Campos de pendientes
 Lección 5 Técnicas cualiaivas para las Ecuaciones diferenciales de primer orden: Campos de pendienes y ĺıneas de fase Campos de pendienes () solución de = f (, ) pendiene de la reca angene a la gráfica
Lección 5 Técnicas cualiaivas para las Ecuaciones diferenciales de primer orden: Campos de pendienes y ĺıneas de fase Campos de pendienes () solución de = f (, ) pendiene de la reca angene a la gráfica
Representación gráfica de curvas en forma paramétrica x a(t sent) 1.- Representar la curva dada por
 Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
45 EJERCICIOS de INTEGRAL DEFINIDA 2º BACH. ( )
 5 EJERCICIOS de INTEGRAL DEFINIDA º BACH. Inegral definida:. Enunciar la regla de Barrow. Calcular:. Calcular:. (S) Calcular: d (Soluc: ) a + b a ( ) a + b d Soluc : b d (Soluc: 5/). Calcular: 5. Calcular:
5 EJERCICIOS de INTEGRAL DEFINIDA º BACH. Inegral definida:. Enunciar la regla de Barrow. Calcular:. Calcular:. (S) Calcular: d (Soluc: ) a + b a ( ) a + b d Soluc : b d (Soluc: 5/). Calcular: 5. Calcular:
TEMA: FUNCIONES: Cuadrantes 3 er cuadrante, x 0, 4º cuadrante, x 0,
 TEMA: FUNCIONES: ÍNDICE:. Inroducción.. Dominio y recorrido.. Gráficas de funciones elemenales. Funciones definidas a rozos. 4. Coninuidad.. Crecimieno y decrecimieno, máimos y mínimos. 6. Concavidad y
TEMA: FUNCIONES: ÍNDICE:. Inroducción.. Dominio y recorrido.. Gráficas de funciones elemenales. Funciones definidas a rozos. 4. Coninuidad.. Crecimieno y decrecimieno, máimos y mínimos. 6. Concavidad y
MATEMÁTICAS II. x x x d) ( ) b) Como el grado del numerador y del denominador son iguales, hay que empezar por hacer la división.
 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio Calcula la siguienes inegrales a) d b) d c) 6 d d) 3 d e) d 9 e a) Haciendo el cambio de variable d d. d d d
Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio Calcula la siguienes inegrales a) d b) d c) 6 d d) 3 d e) d 9 e a) Haciendo el cambio de variable d d. d d d
ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1
 ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1 A) Hallar la pendiene de la reca secane a la parábola y + 8,cuyas abscisas de los punos de inersección son 1 y 4 f ( ) f ( a) B) Dada la siguiene epresión
ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1 A) Hallar la pendiene de la reca secane a la parábola y + 8,cuyas abscisas de los punos de inersección son 1 y 4 f ( ) f ( a) B) Dada la siguiene epresión
TRABAJO PRÁCTICO N 3: Derivadas - Diferencial
 TRABAJO PRÁCTICO N : Derivadas - Diferencial ) Definición de derivada en un puno: La derivada de la función f es aquella función, denoada por f ', al que su valor en un número del dominio de f esá dado
TRABAJO PRÁCTICO N : Derivadas - Diferencial ) Definición de derivada en un puno: La derivada de la función f es aquella función, denoada por f ', al que su valor en un número del dominio de f esá dado
De las siguientes funciones decir cuál de ellas son funciones, y en ese caso indica el dominio y el recorrido.
 EJERCICIOS FUNCIONES 4º OPCIÓN B 1 De las siguienes funciones decir cuál de ellas son funciones, en ese caso indica el dominio el recorrido. a) b) c) Aplicando el es de la línea verical se observa que
EJERCICIOS FUNCIONES 4º OPCIÓN B 1 De las siguienes funciones decir cuál de ellas son funciones, en ese caso indica el dominio el recorrido. a) b) c) Aplicando el es de la línea verical se observa que
DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =
![DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función = DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =](/thumbs/52/30419199.jpg) DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
Funciones en explícitas
 Funciones en eplícitas.- Sea la función f() e, se pide:. Dominio.. Signo de f() en función de.. Asíntotas. 4. Crecimiento y decrecimiento. Máimos y mínimos relativos. 5. Concavidad y conveidad. Puntos
Funciones en eplícitas.- Sea la función f() e, se pide:. Dominio.. Signo de f() en función de.. Asíntotas. 4. Crecimiento y decrecimiento. Máimos y mínimos relativos. 5. Concavidad y conveidad. Puntos
Examen de Matemáticas II 2º de Bachillerato
 º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
a) p = ½. b) p = 0. c) Ninguna de las anteriores. Solución: Para que sea continua en x = 0 debe cumplirse que lím
 Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
Matemáticas Empresariales I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES si 0. La función f ( ) sen es continua en = 0 si: p si 0 a) p = ½. b) p = 0. Para que sea continua en = 0 debe cumplirse que
APLICACIONES DE LAS DERIVADAS 2º Bachillerato
 APLICACIONES DE LAS DERIVADAS º Bachillerato RECTA TANGENTE A UNA CURVA EN UN PUNTO. Si f es derivable en el punto, la ecuación de la recta tangente a f en el punto es: y = f + f ' Si f es derivable en
APLICACIONES DE LAS DERIVADAS º Bachillerato RECTA TANGENTE A UNA CURVA EN UN PUNTO. Si f es derivable en el punto, la ecuación de la recta tangente a f en el punto es: y = f + f ' Si f es derivable en
(a-3)x+(a-2)y+2z=-1 (2a-6)x+(3a-6)y+5z=-1 (3-a)x+(a-2)z=a 2-4a+5. a-3. a 2-4a a 2-4a+3
 EXTRAORDINARIO DE 8. PROBLEMA A. Esudia el siguiene sisema de ecuaciones lineales dependiene del parámero real a y resuélvelo en los casos en que es compaible: Aplicamos el méodo de Gauss: a-3 (a-3) 3-a
EXTRAORDINARIO DE 8. PROBLEMA A. Esudia el siguiene sisema de ecuaciones lineales dependiene del parámero real a y resuélvelo en los casos en que es compaible: Aplicamos el méodo de Gauss: a-3 (a-3) 3-a
1. Derivadas de funciones de una variable. Recta tangente.
 1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
Geometría del espacio
 Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
Examen Final de Ecuaciones Diferenciales Septiembre 2007
 Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
MODELO JUNIO 2005 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 Modelo de eamen Junio MODELO JUNIO MTEMÁTICS PLICDS LS CIENCIS SOCILES II OPCIÓN. (Punuación máima: punos) Se dice que una mari cuadrada es orogonal si T I: Noa: La noación T significa mari ranspuesa de.
Modelo de eamen Junio MODELO JUNIO MTEMÁTICS PLICDS LS CIENCIS SOCILES II OPCIÓN. (Punuación máima: punos) Se dice que una mari cuadrada es orogonal si T I: Noa: La noación T significa mari ranspuesa de.
C cos x sen x 0 x sen x x cos x x sen x cos x x C 1 x 0. Calculamos la matriz adjunta de C: sen x 0 cox 0 cos x sen x. sen x x 1 x 1 sen x
 Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
Ecuaciones de primer orden
 Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
Cálculo Diferencial e Integral - Funciones trascendentales. Prof. Farith J. Briceño N.
 Cálculo Diferencial e Inegral - Funciones rascenenales. Prof. Farih J. Briceño N. Objeivos a cubrir Función logarimo y eponencial. Propieaes. Derivaa e inegración. Cóigo : MAT-CDI.5 Ejercicios resuelos
Cálculo Diferencial e Inegral - Funciones rascenenales. Prof. Farih J. Briceño N. Objeivos a cubrir Función logarimo y eponencial. Propieaes. Derivaa e inegración. Cóigo : MAT-CDI.5 Ejercicios resuelos
Trabajo Práctico N 0: Curvas planas-ecuaciones paramétricas y Coordenadas polares
 Trabajo Prácico N 0: Curvas planas-ecuaciones paraméricas y Coordenadas polares Curvas planas y ecuaciones paraméricas Hasa ahora hemos represenado una gráfica por medio de una sola ecuación que coniene
Trabajo Prácico N 0: Curvas planas-ecuaciones paraméricas y Coordenadas polares Curvas planas y ecuaciones paraméricas Hasa ahora hemos represenado una gráfica por medio de una sola ecuación que coniene
U.P.R. Departamento de Ciencias Matemáticas RUM MATE 3031 Examen Final 3 de diciembre de 2007
 U.P.R. Dearameno de Ciencias Maemáicas RUM MATE 33 Eamen Final 3 de diciembre de 7 Nombre: Profesor: Sección: Insrucciones: Lea cada reguna minuciosamene y muesre odo su rabajo. Esá rohibido coiar, consular
U.P.R. Dearameno de Ciencias Maemáicas RUM MATE 33 Eamen Final 3 de diciembre de 7 Nombre: Profesor: Sección: Insrucciones: Lea cada reguna minuciosamene y muesre odo su rabajo. Esá rohibido coiar, consular
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE)
 UNIVERSIDDES PÚLICS DE L COUNIDD DE DRID PRUET DE CCESO ESTUDIOS UNIVERSITRIOS (LOGSE) Curso 8-9 (Sepiebre) TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN El aluno conesará a los cuaro ejercicios de
UNIVERSIDDES PÚLICS DE L COUNIDD DE DRID PRUET DE CCESO ESTUDIOS UNIVERSITRIOS (LOGSE) Curso 8-9 (Sepiebre) TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN El aluno conesará a los cuaro ejercicios de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE)
 UNIVERSIDADES PÚBLICAS DE LA COUNIDAD DE ADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 8-9 (Sepiebre) ATERIA: ATEÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El aluno conesará a los
UNIVERSIDADES PÚBLICAS DE LA COUNIDAD DE ADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 8-9 (Sepiebre) ATERIA: ATEÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El aluno conesará a los
CUESTIONES RESUELTAS 2. FUNCIONES REALES DE VARIABLE REAL FUNDAMENTOS DE MATEMÁTICAS. 1º GRADO GESTIÓN AERONAÚTICA CURSO
 CUESTIONES RESUELTAS. FUNCIONES REALES DE VARIABLE REAL FUNDAMENTOS DE MATEMÁTICAS. º GRADO GESTIÓN AERONAÚTICA CURSO 0-0. CONCEPTOS DE DOMINIO, RECORRIDO Y GRÁFICA e. Sea f() definida por: f ( ) Entonces
CUESTIONES RESUELTAS. FUNCIONES REALES DE VARIABLE REAL FUNDAMENTOS DE MATEMÁTICAS. º GRADO GESTIÓN AERONAÚTICA CURSO 0-0. CONCEPTOS DE DOMINIO, RECORRIDO Y GRÁFICA e. Sea f() definida por: f ( ) Entonces
CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES 2.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS
 CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS Hasa ahora conocemos la represenación de una grafica mediane una ecuación con dos variables. En ese
CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS Hasa ahora conocemos la represenación de una grafica mediane una ecuación con dos variables. En ese
Opción A Ejercicio 1.-
 Soluciones modelo (Sepiembre de 009) Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f( ) -+. Deermina la asínoa de la gráfica Evidenemene, la función no iene asínoas vericales,
Soluciones modelo (Sepiembre de 009) Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f( ) -+. Deermina la asínoa de la gráfica Evidenemene, la función no iene asínoas vericales,
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA APELLIDOS:
 DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL APELLIDOS: NOMBRE: D.N.I. CUESTIONARIO DE RESPUESTA MÚLTIPLE (5%) (Cada respuesta incorrecta resta, puntos)
Figura 1. Coordenadas de un punto
 1 Tema 1. Sección 1. Diagramas espacio-iempo. Manuel Guiérrez. Deparameno de Álgebra, Geomería y Topología. Universidad de Málaga. 2971-Málaga. Spain. Marzo de 21. En la mecánica es usual incluir en los
1 Tema 1. Sección 1. Diagramas espacio-iempo. Manuel Guiérrez. Deparameno de Álgebra, Geomería y Topología. Universidad de Málaga. 2971-Málaga. Spain. Marzo de 21. En la mecánica es usual incluir en los
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. En las siguientes funciones estudia las características: dominio, los puntos de corte con los ejes, las simetrías, la periodicidad, las asíntotas, la monotonía,
RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. En las siguientes funciones estudia las características: dominio, los puntos de corte con los ejes, las simetrías, la periodicidad, las asíntotas, la monotonía,
Límites y Continuidad de funciones de dos variables
 Límites y Continuidad de funciones de dos variables 1.- Si en un cierto punto ( a, b) R existe el lim f = L R a,b, entonces: f es continua en (a, b). b) Existen los límites reiterados de f en (a, b) y
Límites y Continuidad de funciones de dos variables 1.- Si en un cierto punto ( a, b) R existe el lim f = L R a,b, entonces: f es continua en (a, b). b) Existen los límites reiterados de f en (a, b) y
MATEMATICA PARA MEDICINA
 MATEMATICA PARA MEDICINA CAPITULO II: NOCIONES DE CALCULO DIFERENCIAL... Concepo inuiivo de límie y el concepo de derivada en un puno. Considere la siguiene epresión: n, siendo n un número naural, es decir,
MATEMATICA PARA MEDICINA CAPITULO II: NOCIONES DE CALCULO DIFERENCIAL... Concepo inuiivo de límie y el concepo de derivada en un puno. Considere la siguiene epresión: n, siendo n un número naural, es decir,
5. Planos y rectas en el espacio
 5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
Autoevaluación Cálculo Integral. sen(x) dx (i) cos(x)
 Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
ejerciciosyexamenes.com
 ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
Gráficas de curvas trigonométricas
 Capíulo 4 Gráficas de curvas rigonoméricas La definición de las razones rigonoméricas, como funciones del ángulo, lleva implicado el esudio de las funciones rigonoméricas desde el puno de visa de las funciones
Capíulo 4 Gráficas de curvas rigonoméricas La definición de las razones rigonoméricas, como funciones del ángulo, lleva implicado el esudio de las funciones rigonoméricas desde el puno de visa de las funciones
Problemas resueltos funciones de una variable. Continuidad. Matemáticas I. La función es continua en { 3} La función es continua en (, 1) ( 1, )
 Problemas resueltos funciones de una variable. Continuidad. Matemáticas I. 1.-Estudiar la continuidad de las siguientes funciones: + f( ) = f( ) = f( ) = 1 + + 1 1 + 1 f( ) = log 1 f( ) = + 1 f ( ) 6 La
Problemas resueltos funciones de una variable. Continuidad. Matemáticas I. 1.-Estudiar la continuidad de las siguientes funciones: + f( ) = f( ) = f( ) = 1 + + 1 1 + 1 f( ) = log 1 f( ) = + 1 f ( ) 6 La
Cálculo Integral. dt, entonces: a) f no es integrable en 11. , pues no es continua. c) f es integrable en Dada f integrable en ab
 .- Se F () ( ) d, enonces: cos Cálculo Inegrl ) F'() -(cos ) sen b) F'() cos c) F'() cos si.- Se f( ) - < si enonces: ) f no es inegrble en, pues no es coninu. b) f es inegrble en, y f( ) d. c) f es inegrble
.- Se F () ( ) d, enonces: cos Cálculo Inegrl ) F'() -(cos ) sen b) F'() cos c) F'() cos si.- Se f( ) - < si enonces: ) f no es inegrble en, pues no es coninu. b) f es inegrble en, y f( ) d. c) f es inegrble
prepara TU SElECTIVIDAD
 prepara TU SElECTIVIDAD Se considera la función f ( ) = ( + a) e a siendo a un parámero real. a) Razone a qué es igual el dominio de f ( ). b) Deermine el valor de a para que la gráfica de f() pase por
prepara TU SElECTIVIDAD Se considera la función f ( ) = ( + a) e a siendo a un parámero real. a) Razone a qué es igual el dominio de f ( ). b) Deermine el valor de a para que la gráfica de f() pase por
FÍSICA Y QUÍMICA 1º BACHILLERATO
 FÍSICA Y QUÍMICA 1º BACHILLERATO BLOQUE I: MECÁNICA Unidad 1: Cinemáica 1. INTRODUCCIÓN (pp. 8-3) 1.1. Definición de movimieno. Relaividad del movimieno Un cuerpo esá en movimieno cuando cambia de posición
FÍSICA Y QUÍMICA 1º BACHILLERATO BLOQUE I: MECÁNICA Unidad 1: Cinemáica 1. INTRODUCCIÓN (pp. 8-3) 1.1. Definición de movimieno. Relaividad del movimieno Un cuerpo esá en movimieno cuando cambia de posición
ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN 2013
 GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
EXAMEN DE DIAGNÓSTICO PARA LA UNIDAD 1. Instrucciones. Selecciona la opción correcta en cada uno de los reactivos.
 EXAMEN DE DIAGNÓSTICO PARA LA UNIDAD 1 Insrucciones. Selecciona la opción correca en cada uno de los reacivos. 1. La relación de una variable independiene a una variable dependiene es una función cuando
EXAMEN DE DIAGNÓSTICO PARA LA UNIDAD 1 Insrucciones. Selecciona la opción correca en cada uno de los reacivos. 1. La relación de una variable independiene a una variable dependiene es una función cuando
2) (1p) Demuestra que la derivada de y=ln x es y'=1/x.
 CURSO 00-0 6 de noviembre de 00. ) (p) Define función derivada. ) (p) Demuestra que la derivada de yln es y'/. 3) (p) Enuncia el criterio de la derivada segunda para el estudio de la curvatura y los puntos
CURSO 00-0 6 de noviembre de 00. ) (p) Define función derivada. ) (p) Demuestra que la derivada de yln es y'/. 3) (p) Enuncia el criterio de la derivada segunda para el estudio de la curvatura y los puntos
FUNCIONES DE UNA VARIABLE
 FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
FUNCIONES DE UNA VARIABLE 1- Definiciones 2- Algunas funciones reales 3- Ecuaciones de curvas planas en coordenadas cartesianas 4- Coordenadas polares 5- Coordenadas paramétricas 6- Funciones hiperbólicas
ω ω ω y '' + 3 y ' y = 0 en la que al resolver se debe obtener la función y. dx = + d y y+ m = mg k dt d y dy dx dx = x y z d y dy u u x t t
 E.D.O para Ingenieros CAPITULO INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES Las ecuaciones diferenciales son ecuaciones en las que conienen derivadas, Por ejemplo: '' + ' = en la que al resolver se debe
E.D.O para Ingenieros CAPITULO INTRODUCCIÓN A LAS ECUACIONES DIFERENCIALES Las ecuaciones diferenciales son ecuaciones en las que conienen derivadas, Por ejemplo: '' + ' = en la que al resolver se debe
INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx
![INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx INTEGRAL DEFINIDA. senx. sen PROBLEMAS. 1º-Calcular las siguientes integrales definidas: E[x]dx](/thumbs/56/39119384.jpg) INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
INTEGRAL DEFINIDA. PROBLEMAS. º-Calcular las siguientes integrales definidas: π sen. ln(+ )d. d. + sen - cos -π +. d.5 -) - ( - d.6 E[]d -.7 E[] d.8 cos d - º-Calcular el área limitada por las gráficas
TEMA: ESTUDIO LOCAL DE FUNCIONES DERIVABLES
 TEMA: ESTUDIO LOCAL DE FUNCIONES DERIVABLES 1 DOMINIO DE DEFINICIÓN DE UNA FUNCIÓN El dominio de una función está formado por aquellos valores de (números reales) para los que se puede calcular f(). PUNTOS
TEMA: ESTUDIO LOCAL DE FUNCIONES DERIVABLES 1 DOMINIO DE DEFINICIÓN DE UNA FUNCIÓN El dominio de una función está formado por aquellos valores de (números reales) para los que se puede calcular f(). PUNTOS
Matemáticas aplicadas a las CC.SS. II
 Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
L A D E R I V A D A. C Á L C U L O Y A P L I C A C I O N E S
 L A D E R I V A D A. C Á L C U L O Y A P L I C A C I O N E S 1. T A S A D E V A R I A C I Ó N M E D I A Definimos la variación media de una función f en un intervalo [, + ], y la designamos por t m o TVM[,
L A D E R I V A D A. C Á L C U L O Y A P L I C A C I O N E S 1. T A S A D E V A R I A C I Ó N M E D I A Definimos la variación media de una función f en un intervalo [, + ], y la designamos por t m o TVM[,
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-V--00-208 CURSO: Maemáica Inermedia CÓDIGO DEL CURSO: 07 SEMESTRE: Primer Semesre JORNADA: Vesperina
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-V--00-208 CURSO: Maemáica Inermedia CÓDIGO DEL CURSO: 07 SEMESTRE: Primer Semesre JORNADA: Vesperina
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
Aplicaciones de la derivada
 Aplicaciones de la derivada º) Calcula los máimos y mínimos de la función f() = Máimo en P( 6, ) ; Mínimo en Q(0, 0) º) Determina el parámetro c para que la función f() = + + c tenga un mínimo igual a
Aplicaciones de la derivada º) Calcula los máimos y mínimos de la función f() = Máimo en P( 6, ) ; Mínimo en Q(0, 0) º) Determina el parámetro c para que la función f() = + + c tenga un mínimo igual a
Unidad 5 Geometría afín en el espacio
 Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
MATEMÁTICAS II TEMA 5 Ecuaciones de rectas y planos en el espacio. Posiciones relativas Problemas propuestos
 Geomería del espacio ecuaciones de recas planos; posiciones relaivas MATEMÁTICAS II TEMA Ecuaciones de recas planos en el espacio. Posiciones relaivas Problemas propuesos Ecuaciones de recas planos. Halla,
Geomería del espacio ecuaciones de recas planos; posiciones relaivas MATEMÁTICAS II TEMA Ecuaciones de recas planos en el espacio. Posiciones relaivas Problemas propuesos Ecuaciones de recas planos. Halla,
Unidad 8 Representación gráfica de funciones
 Unidad 8 Representación gráfica de funciones PÁGINA 187 SOLUCIONES 1. Las funciones quedan: a) f( ) = 8 Dominio: Dom f =R Puntos de corte con el eje OX: Puntos de corte con el eje OY Simetrías: f( ) =
Unidad 8 Representación gráfica de funciones PÁGINA 187 SOLUCIONES 1. Las funciones quedan: a) f( ) = 8 Dominio: Dom f =R Puntos de corte con el eje OX: Puntos de corte con el eje OY Simetrías: f( ) =
Soluciones problemas 1. Ecuaciones I (C). 08/09
 Soluciones problemas Ecuaciones I (C) 8/9 a) = (+ cos ) Bernouilli: z = z = z + ( + cos ) = Ce ++sen +cos = homogénea: z = z + z = z z, dz z( z) = d + C = C +C = C + ; o Bernouilli: z = z = z + z = C+
Soluciones problemas Ecuaciones I (C) 8/9 a) = (+ cos ) Bernouilli: z = z = z + ( + cos ) = Ce ++sen +cos = homogénea: z = z + z = z z, dz z( z) = d + C = C +C = C + ; o Bernouilli: z = z = z + z = C+
Criterio 1: Sea f una función derivable en (a,b). f es estrictamente creciente en el intervalo abierto (a, b) si f es positiva en dicho intervalo.
 UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
x t, x t, x dx dt sustituyendo e integrando, obtenemos: 3
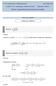 E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.4. APLICACIONES DE LA DERIVABILIDAD
 TEMA. FUNCIONES REALES DE VARIABLE REAL.4. APLICACIONES DE LA DERIVABILIDAD .4. APLICACIONES DE LA DERIVABILIDAD.4.1. Intervalos de crecimiento y decrecimiento.4.. Etremos locales de una función.4.3. Intervalos
TEMA. FUNCIONES REALES DE VARIABLE REAL.4. APLICACIONES DE LA DERIVABILIDAD .4. APLICACIONES DE LA DERIVABILIDAD.4.1. Intervalos de crecimiento y decrecimiento.4.. Etremos locales de una función.4.3. Intervalos
CAPITULO 2: Movimiento en una dirección [S.Z.F.Y. 2]
![CAPITULO 2: Movimiento en una dirección [S.Z.F.Y. 2] CAPITULO 2: Movimiento en una dirección [S.Z.F.Y. 2]](/thumbs/87/96684426.jpg) UNIVERSIDAD TECNOLÓGICA NACIONAL Faculad Regional Rosario UDB Física Cáedra FÍSICA I CAPITULO : Movimieno en una dirección [S.Z.F.Y. ] Cinemáica: La Cinemáica se ocupa de describir los movimienos de los
UNIVERSIDAD TECNOLÓGICA NACIONAL Faculad Regional Rosario UDB Física Cáedra FÍSICA I CAPITULO : Movimieno en una dirección [S.Z.F.Y. ] Cinemáica: La Cinemáica se ocupa de describir los movimienos de los
Límites y Continuidad de funciones de dos variables
 Límites Continuidad de funciones de dos variables 1.- Si en un cierto punto a, b R existe el lim f x, L R, entonces: x, a, b a) f es continua en (a, b). b) Existen los límites reiterados de f en (a, b)
Límites Continuidad de funciones de dos variables 1.- Si en un cierto punto a, b R existe el lim f x, L R, entonces: x, a, b a) f es continua en (a, b). b) Existen los límites reiterados de f en (a, b)
Lección 3. Curvas. 4. Curvas parametrizadas: ejemplos.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. 4. Curvas paramerizadas: ejemplos. La descripción más direca y flexible de una curva es una represenación paramérica. En lugar de considerar una de las coordenadas
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. 4. Curvas paramerizadas: ejemplos. La descripción más direca y flexible de una curva es una represenación paramérica. En lugar de considerar una de las coordenadas
Parte II. DERIVADAS. APLICACIONES.
 Parte II. DERIVADAS. APLICACIONES. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. f ( a + h ) f ( a ) Se dice que f es derivable en = a si eiste el límite lim. Este número se denomina derivada
Parte II. DERIVADAS. APLICACIONES. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. f ( a + h ) f ( a ) Se dice que f es derivable en = a si eiste el límite lim. Este número se denomina derivada
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. f : R R
 TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
TEMA 3: CONTINUIDAD Y DERIVABILIDAD DE FUNCIONES REALES DE UNA VARIABLE REAL. Concepto de función. Definición Se llama función (real de variable real) a toda aplicación f : R R f() que a cada número le
a) Dar la definición de dominio y rango de una función. b) Explicar cada una de las siguientes funciones y dar tres ejemplos de cada una.
 UNIVERSIDAD DE LONDRES PREPARATORIA GUIA DE MATEMÁTICAS VI Áreas I-II Plan : 9 Clave maeria : 00 Clave UNAM : Unidad I. Funciones Objeivos Que el alumno idenifique disinos ipos de funciones, esablezca
UNIVERSIDAD DE LONDRES PREPARATORIA GUIA DE MATEMÁTICAS VI Áreas I-II Plan : 9 Clave maeria : 00 Clave UNAM : Unidad I. Funciones Objeivos Que el alumno idenifique disinos ipos de funciones, esablezca
Unidad 6 Derivadas PÁGINA 135 SOLUCIONES. 1. La solución en cada caso es: = lím. lím. = h. 2. Queda: La recta debe tener una forma: y = x + b 5
 Unidad 6 Derivadas PÁGINA 15 SOLUCIONES 1. La solución en cada caso es: f ( ) f () ( ) 5 17 1 a) lím lím lím lím (1 ) 1 0 0 0 0 b) g ( ) g ( ) ( ) 1 1 lím lím lím 0 ( 1 1) 1. Queda: 1 La reca debe ener
Unidad 6 Derivadas PÁGINA 15 SOLUCIONES 1. La solución en cada caso es: f ( ) f () ( ) 5 17 1 a) lím lím lím lím (1 ) 1 0 0 0 0 b) g ( ) g ( ) ( ) 1 1 lím lím lím 0 ( 1 1) 1. Queda: 1 La reca debe ener
Apellidos: Nombre: Curso: 1º Grupo: C Día: 2- III- 16 CURSO
 EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
EXAMEN DE MATEMÁTICAS GRÁFICAS E INTEGRALES Apellidos: Nombre: Curso: º Grupo: C Día: - III- 6 CURSO 05-6. [ punto] Estudia si las siguientes funciones presentan simetría par (respecto del eje de ordenadas)
Solución y criterios de corrección. Examen de mayores de 25 años. 2012. Matemáticas aplicadas a las ciencias sociales.
 Solución y crierios de corrección. Examen de mayores de años.. Maemáicas aplicadas a las ciencias sociales. BLOQUE A En un cenro de ocio hay salas de cine: A, B y. A una deerminada sesión han acudido personas.
Solución y crierios de corrección. Examen de mayores de años.. Maemáicas aplicadas a las ciencias sociales. BLOQUE A En un cenro de ocio hay salas de cine: A, B y. A una deerminada sesión han acudido personas.
Aplicaciones de las derivadas
 Aplicaciones de las derivadas. Recta tangente a una curva en un punto La pendiente de la recta tangente a la gráfica de la función f() en el punto ( 0, f( 0 )) viene dada por f ( 0 ) siempre que la función
Aplicaciones de las derivadas. Recta tangente a una curva en un punto La pendiente de la recta tangente a la gráfica de la función f() en el punto ( 0, f( 0 )) viene dada por f ( 0 ) siempre que la función
Actividades de recuperación
 Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
SERIE DE ECUACIONES DIFERENCIALES
 SERIE DE ECUACIONES DIFERENCIALES PROFESOR: PEDRO RAMÍREZ MANNY TEMA ) Clasifique cada una de las ecuaciones diferenciales siguienes indicando orden (O), grado (G) y si es lineal (L) o no (NL). a) ( y)
SERIE DE ECUACIONES DIFERENCIALES PROFESOR: PEDRO RAMÍREZ MANNY TEMA ) Clasifique cada una de las ecuaciones diferenciales siguienes indicando orden (O), grado (G) y si es lineal (L) o no (NL). a) ( y)
Unidad 13 Representación gráfica de funciones
 1 Unidad 13 Representación gráfica de funciones PÁGINA 315 SOLUCIONES 1. Las funciones son: a) f 8 ) ( = Dominio: = f Dom Puntos de corte con el eje OX: = = (4,0) (0,0) 0 8 Q P y y Puntos de corte con
1 Unidad 13 Representación gráfica de funciones PÁGINA 315 SOLUCIONES 1. Las funciones son: a) f 8 ) ( = Dominio: = f Dom Puntos de corte con el eje OX: = = (4,0) (0,0) 0 8 Q P y y Puntos de corte con
( ) ( 15 50) 0
 PRUE DE CCESO L UNIVERSIDD JUNIO 7 OPCION ) Deermina dos números reales posiivos sabiendo que su suma es y que el produco de sus cuadrados es máximo. Sean x e y los números reales que suman y P x y odos
PRUE DE CCESO L UNIVERSIDD JUNIO 7 OPCION ) Deermina dos números reales posiivos sabiendo que su suma es y que el produco de sus cuadrados es máximo. Sean x e y los números reales que suman y P x y odos
TEMA 2: CINETICA DE LA TRASLACIÓN
 TEMA 2: CINETICA DE LA TRASLACIÓN 1.1. Inroducción. Para ener caracerizado un movimieno mecánico cualquiera, hay que esablecer primero respeco a que cuerpo (s) se va a considerar dicho movimieno. Ese cuerpo
TEMA 2: CINETICA DE LA TRASLACIÓN 1.1. Inroducción. Para ener caracerizado un movimieno mecánico cualquiera, hay que esablecer primero respeco a que cuerpo (s) se va a considerar dicho movimieno. Ese cuerpo
I.- Representación gráfica de una función polinómica
 Los campos a considerar en el estudio de una representación gráfica son; Dominio de la función Continuidad y derivabilidad Simetrías Periodicidad Asíntotas Verticales Horizontales Oblicuas Posición de
Los campos a considerar en el estudio de una representación gráfica son; Dominio de la función Continuidad y derivabilidad Simetrías Periodicidad Asíntotas Verticales Horizontales Oblicuas Posición de
Lección 13 Introducción a los sistemas no lineales de ecuaciones diferenciales
 Lección Inroducción a los sisemas no lineales de ecuaciones diferenciales Un modelo de Gierer-Meinhard para ecuaciones de ipo Acivador-Inhibidor Modelo G-M: con = [A], = [B]. k = k = k = k 4 = A B A +
Lección Inroducción a los sisemas no lineales de ecuaciones diferenciales Un modelo de Gierer-Meinhard para ecuaciones de ipo Acivador-Inhibidor Modelo G-M: con = [A], = [B]. k = k = k = k 4 = A B A +
MATEMÁTICAS II. ANDALUCÍA Pruebas de acceso a la Universidad SOLUCIONES 1. (2001-1A-3) Tienen inversa las matrices A y D.
 MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
5 GUÍA PARA REALIZAR ESTUDIO DE FUNCIÓN
 5 GUÍA PARA REALIZAR ESTUDIO DE UNCIÓN ) Determinar el Dominio de la función. ) Hallar, si eisten, las Intersecciones con los Ejes de Coordenadas Signo. ( Int. con eje y, hacer = Int. con eje, hacer y
5 GUÍA PARA REALIZAR ESTUDIO DE UNCIÓN ) Determinar el Dominio de la función. ) Hallar, si eisten, las Intersecciones con los Ejes de Coordenadas Signo. ( Int. con eje y, hacer = Int. con eje, hacer y
1 Consideramos la gráfica siguiente:
 Conderamos la gráfica guiente: Determina, a la vista de la gráfica, el dominio de definición, metrías, el recorrido, la eistencia de asíntotas, los intervalos de crecimiento y decrecimiento. Justifica,
Conderamos la gráfica guiente: Determina, a la vista de la gráfica, el dominio de definición, metrías, el recorrido, la eistencia de asíntotas, los intervalos de crecimiento y decrecimiento. Justifica,
CAPITULO 7.FUNCIONES DE VARIAS VARIABLES Campo de definición de una función de varias variables.
 CAPITULO 7.FUNCIONES DE VARIAS VARIABLES Deinición Sean E F dos conjunos inios o ininios de cualquier nauralea. Una aplicaron del conjuno E en el conjuno F es una le o proceso mediane el cual se hace corresponder
CAPITULO 7.FUNCIONES DE VARIAS VARIABLES Deinición Sean E F dos conjunos inios o ininios de cualquier nauralea. Una aplicaron del conjuno E en el conjuno F es una le o proceso mediane el cual se hace corresponder
March 2, 2009 CAPÍTULO 3: DERIVADAS PARCIALES Y DIFERENCIACIÓN
 March 2, 2009 1. Derivadas Parciales y Funciones Diferenciables En ese capíulo, D denoa un subconjuno abiero de R n. Definición 1.1. Consideremos una función f : D R y sea p D, i = 1,, n. Definimos la
March 2, 2009 1. Derivadas Parciales y Funciones Diferenciables En ese capíulo, D denoa un subconjuno abiero de R n. Definición 1.1. Consideremos una función f : D R y sea p D, i = 1,, n. Definimos la
