BLOQUE 3.2 ONDAS. Se puede transferir energía a un cuerpo distante mediante otro cuerpo portador: por ejemplo, la bola que
|
|
|
- Miguel Mendoza Juárez
- hace 9 años
- Vistas:
Transcripción
1 BLOQUE 3. ONDAS La mayor parte de la información que recibimos nos llega en forma de algún tipo de onda. El sonido, la luz, las señales que reciben nuestros aparatos de radio y televisores son ejemplos de ondas. - QUÉ ES UNA ONDA? Se puede transferir energía a un cuerpo distante mediante otro cuerpo portador: por ejemplo, la bola que golpea a unos bolos que se encuentran en reposo. Pero también es posible transferirla de otra manera: una piedra cae a un estanque y, al cabo de un rato, un objeto que flota a cierta distancia comienza a moverse oscilando de arriba a abajo. Aquí no ha sido necesario que la piedra golpee directamente al objeto y, sin embargo, se ha transferido igualmente energía. Cuando los indios pegaban la oreja al suelo para adivinar la proximidad de una manada de búfalos, lo que pretendían era percibir la transmisión de las vibraciones a través del suelo. Distinguimos así dos tipos de movimientos: el movimiento vibratorio del suelo golpeado por los búfalos y el movimiento de transmisión de la energía de las vibraciones a larga distancia. Este segundo movimiento, en el que no se propaga materia, es el que conocemos como movimiento ondulatorio o de propagación de la onda. Para que haya transferencia de energía mediante una onda, tiene que haber una fuente que origine una perturbación (la piedra que golpea el agua, el búfalo que pisa el suelo). Por tanto: Una onda representa el movimiento de propagación de una perturbación (vibración) de un punto a otro sin que exista transporte neto de materia. Aunque hemos hablamos reiteradamente de la presencia de un medio para la propagación de la perturbación., existen ondas que pueden transmitirse por el vacío, sin necesidad de medio o soporte material. Así, cabe distinguir dos tipos de ondas:.ondas MECÁNICAS: Son aquellas que necesitan de un medio material para propagarse. Un ejemplo típico es la propagación del desplazamiento vertical de los elementos de una cuerda. Si tenemos una cuerda sujeta de uno de sus extremos y sobre el otro realizamos un movimiento vertical hacia arriba y hacia abajo, observaremos como el desplazamiento vertical se propaga a otros elementos de la cuerda alejados del extremo, también el movimiento de un corcho que flota en un estanque de agua al tirar una piedra en otro punto del
2 estanque y también las ondas sonoras. ONDAS ELECTROMAGNÉTICAS: Son aquellas que no requieren un medio material para propagarse y pueden transmitirse en el vacío. Son ejemplos las ondas de radio, las microondas, la luz visible, etc...así, por ejemplo, los electrones de una antena transmisora de una estación de radio que emite a 960 khz en la banda de AM vibran veces cada segundo Ahora bien, QUÉ QUEREMOS DECIR AL HABLAR DE PROPAGACIÓN DE UNA PERTURBACIÓN? QUÉ ES REALMENTE LO QUE TRANSMITE UNA ONDA? En una onda se propaga energía. Así, en las ondas mecánicas se propaga energía mecánica, y en las electromagnéticas, energía electromagnética. La fuente de toda onda es un objeto o partícula que vibra (onda mecánica) o una partícula con carga que vibra (onda electromagnética). La frecuencia de la fuente vibratoria y la frecuencia de la onda que la misma produce son iguales En ningún momento se produce transferencia de materia. A lo largo de este tema nos centraremos en el estudio de las ondas mecánicas principalmente.- TIPOS DE ONDAS Además de la diferencia ya mencionada entre ondas mecánicas y electromagnéticas, podemos clasificarlas en función de otros tres criterios que pasamos a ver a continuación:.-según LA EXTENSIÓN DEL MEDIO EN EL QUE SE PROPAGAN: Diferenciamos entre ONDAS ESTACIONARIAS si el medio está acotado (resultan de la combinación de la onda y su reflejada), como por ejemplo la onda que se produce al tañer una cuerda de guitarra y ONDAS PROGRESIVAS si el medio de propagación es ilimitado..-según LA COINCIDENCIA O NO ENTRE LA DIRECCIÓN DE OSCILACIÓN DE LA PROPIEDAD PERTURBADA Y LA DE PROPAGACIÓN DE LA ONDA: ONDAS TRANSVERSALES, en las que la propagación tiene dirección perpendicular a la vibración de las partículas, (ondas obtenidas en una cuerda, olas en medio acuático, etc..). Y ONDAS LONGITUDINALES en las que la propagación tiene una dirección paralela a la dirección de la vibración de las partículas (por ejemplo, las ondas sonoras formadas por compresiones y expansiones del aire, o una onda longitudinal en un resorte).
3 3.-SEGÚN EL NÚMERO DE DIMENSIONES EN QUE SE PROPAGA LA ONDA: ONDAS MONODIMENSIONALES : se propagan un una sola dimensión, como las ondas de un muelle ONDAS BIDIMENSIONALES : se propagan en cualquier dirección de un plano, como las ondas en un estanque ONDAS TRIDIMENSIONALES :si se propagan en las 3 dimensiones del espacio, como es el caso del sonido 3.-ONDAS Cuando la perturbación que se propaga está producida por un oscilador armónico, es decir, por un cuerpo que presenta un M.A.S, decimos que dicha perturbación se propaga en forma de ONDA ARMÓNICA. Un ejemplo es la que se transmitiría a través de una cuerda unida a un oscilador armónico como el de la figura. Este tipo de ondas se caracterizan además porque la función de onda que las describe es una función sinusoidal (seno o coseno) de x (dirección de propagación) y t (tiempo). Su estudio es de gran utilidad porque muchas de las ondas ordinarias de la naturaleza pueden considerarse como una composición de diversas ondas armónicas. Por tanto, aunque rara vez encontramos ondas perfectamente armónicas se trata de una buena aproximación. Presentan una serie de parámetros constantes que las caracterizan y que aparecen implícitamente en la ecuación o función de onda que las representa, tal y como veremos más adelante. 3.. ECUACIÓN DE PROPAGACIÓN DE UNA ONDA ARMÓNICA Vamos a considerar una onda armónica que se propaga en una única dirección del espacio. Por tanto, la ecuación que la representa deberá ser una función que indique la propagación de la perturbación inicial (de un M.A.S) en la dirección del espacio considerada. Describir matemáticamente el movimiento ondulatorio, requiere encontrar una ecuación que nos permita conocer, en cada punto, el valor de la perturbación introducida. Esto supone admitir que cada punto describe un M.A.S; por lo que nos interesa poder determinar el estado de perturbación que tendrá cada punto P situado alrededor del foco de perturbación en cualquier instante La expresión matemática que representa la propagación de una onda será una función seno o coseno de la coordenada de la dirección de avance y del tiempo. Para encontrarla, vamos a considerar el caso de una onda armónica producida en una cuerda y que se propaga a una velocidad v. La perturbación tardará en llegar a P un tiempo x t = v que dependerá de la 3
4 velocidad de propagación (v) y de la distancia al punto P (x) Lo que sí sabemos es que si el foco tiene una perturbación de tipo M.A.S, el punto P acabará teniendo la misma perturbación M.A.S sólo que t segundos más tarde. Para un punto P, tendremos que su estado de vibración, instante ( t-t ). Esto es: ψ ( t) =ψ ( t t ). P O ψ P será idéntico al estado que tenía el foco en el Ya que estamos suponiendo que la velocidad que se propaga es de tipo MAS, tendremos: ψ ( t) = ψ ( t t ) P ψ ( t) = A sen P O [ ( )] x ω t t = A sen ω t La ecuación de la onda será: x ( x t ) = A sen ω t v ψ, v Si la perturbación se desplazara en el sentido negativo de las x, el razonamiento sería el mismo pero la x expresión final, sería: ψ ( x, t ) = A sen ω t + v 3.. PARÁMETROS CONSTANTES DE UNA ONDA ARMÓNICA x ( x t ) = A sen ω t ± v ψ, Las expresiones anteriores constituyen la ECUACIÓN DE ONDA ARMÓNICA también llamada función de onda. En ella aparece explícitamente su dependencia respecto de las variables posición y tiempo; y por lo tanto proporciona toda la información sobre el estado de perturbación del medio en cualquier punto y en cualquier instante. Puesto que la función seno es una función periódica, la función de onda, al depender de las variables espacio (x) y tiempo (t), será doblemente periódica. Podemos definir una serie de parámetros que permanecen constantes durante su propagación:. Longitud de onda(λ) : Es la distancia entre dos puntos consecutivos que se encuentran en idéntico estado de perturbación (suele decirse entre dos puntos consecutivos de idéntica fase). Período(T): Es el tiempo que tarda un punto cualquiera en repetir un determinado estado de perturbación u oscilación 3. Frecuencia (f): Es el número de veces que un determinado punto 4
5 repite cierto estado de perturbación u oscilación por unidad de tiempo. La frecuencia es la magnitud inversa del tiempo f = T 4. Velocidad de propagación (v):es la distancia que recorre la onda en la unidad de tiempo. Considerando los parámetros que hemos definido hasta el momento podemos escribir: λ v = T 5. Número de onda (K): Se define como el número de longitudes de onda que hay en una distancia. Es decir: K = π λ Considerando todos estos parámetros; encontramos otras expresiones para la ecuación de onda: x t x ψ ( x, t ) = A sen ω t ψ ( x t ) = A sen π v T λ ψ, ( x, t ) = A sen ( ω t K x) OTRAS FORMAS DE ESCRIBIR LA ECUACIÓN DE UNA ONDA ARMÓNICA Es muy frecuente encontrar la ecuación de una onda armónica escrita de diversas maneras: Con la función seno: ( x t ) = A sen ( K x ± ω t) ψ, ψ ( x, t ) = A sen ( ω t ± K x) Hay que considerar que: sen( a b) = sen( b a) o sen ( a b) = sen( b a ± π ) Con la función coseno: ψ ψ ( x, t ) = A cos ( K x ± ω t) ( x, t ) = A cos ( ω t ± K x) En este caso consideramos que: cos ( a b) = cos( b a) IMPORTANTE: las ecuaciones que utilizan el signo negativo representan una onda armónica que se desplaza hacia la derecha, mientras que aquellas con signo positivo indican que se desplaza hacia la izquierda 4. CÓMO SE PROPAGA UNA ONDA? PRINCIPIO DE HUYGENS La descripción de las características de la propagación de una onda puede hacerse de una forma sencilla considerando el principio propuesto por el físico y astrónomo holandés Christian Huygens: cada uno de los puntos de un frente de ondas puede ser considerado como un foco emisor de ondas secundarias que avanzan en el 5
6 sentido de la perturbación y cuya envolvente constituye un nuevo frente de ondas,entendiendo por frente de onda la superficie que une todos los puntos del medio alcanzados por el movimiento ondulatorio en el mismo instante. La aplicación de este principio permite explicar el comportamiento de una onda en diversas situaciones como la reflexión, refracción y difracción 5.-EFECTO DOPLER Seguramente habrás notado alguna vez cómo cambia el sonido de la sirena de una ambulancia o de un coche de bomberos. Cuando se aproxima a nosotros es más agudo, mientras que se hace más grave a medida que se aleja. Se conoce como efecto Dopler el fenómeno debido al movimiento relativo de la fuente sonora y el observador por el que cambia la frecuencia que se percibe de un sonido. Pero, por qué sucede esto? Veamos los casos más habituales: a. Observador en movimiento y foco en reposo Si el observador se desplaza respecto de un foco en reposo con una velocidad radial v 0. Los frentes de ondas mantendrán su geometría puesto que el foco está en reposo pero sin embargo el número de frentes que llegan al observador en la unidad de tiempo variarán, dependiendo de si el observador se acerca o se aleja. Si se aproxima al foco será mayor y si de aleja de él sera menor. La frecuencia f percibida por el observador será: v o = velocidad del observador v = velocidad del sonido Si el observador se acerca, la velocidad con que llegan los frentes de onda será mayor (+) y el sonido más agudo. Si el observador se aleja de la fuente, la velocidad será menor (-) y el sonido más grave. b. Observador en reposo y foco en movimiento La situación es distinta ya que debido al movimiento de la fuente los frentes de onda alteran su geometría, perdiendo su concentricidad. Estos frentes estarán más juntos en el sentido de avance del foco y más separados en el contrario lo cual supone para el observador una variación de la frecuencia del sonido. Si la fuente se mueve con una velocidad v f y v es la velocidad del sonido: 6
7 La frecuencia que percibe un observador cuando la fuente se aleja de él es menor (sonido más grave) La frecuencia que percibe un observador cuando la fuente se acerca es mayor (más agudo) ι La policía usa el efecto Dopler de las ondas de radar para determinar la rapidez de los coches en la carretera. El sistema emite estas ondas y las hace rebotar sobre un coche en movimiento, comparando la frecuencia de las ondas emitidas y las de las ondas reflejadas se determina la velocidad del coche. ι La luz también está sujeta al efecto Dopler. Cuando una fuente de luz se aproxima, aumenta la frecuencia medida y si se aleja disminuye. 6.- RESONANCIA Cuando alguien deja caer una llave sobre un piso produce un sonido característico y no es probable que confundamos este ruido con el de una pelota que golpea contra el mismo suelo. Esto se debe a que los objetos vibran de forma distinta cuando se golpean. Todo objeto hecho de un material elástico vibra cuando es perturbado con una FRECUENCIA ESPECIAL PROPIA, conocida como FRECUENCIA NATURAL del objeto. Cuando la frecuencia de las vibraciones forzadas de un objeto coincide con la frecuencia natural del mismo, se provoca un aumento impresionante de la amplitud conocido como RESONANCIA. Una experiencia frecuente que ilustra la resonancia es un columpio. Cuando lo empujamos al ritmo de su frecuencia natural, aumentan las oscilaciones. Más importante que la fuerza con la que se impulse es su sincronización. Hasta con impulsos pequeños, con el ritmo adecuado, producen grandes amplitudes. En 83 una tropa cruzaba un puente cerca de Manchester y, por accidente hicieron que se derrumbara el puente al marchar al ritmo de la frecuencia natural del mismo. Desde entonces se acostumbra a ordenar romper filas al cruzar los puentes, para evitar la resonancia. En 940 en el estado de Washington, la resonancia generada por el viento aumentó continuamente la amplitud de la vibración hasta que 7
8 el puente se vino abajo. 7.-SUPERPOSICIÓN DE ONDAS. INTERFERENCIAS PRINCIPIO DE SUPERPOSICIÓN Se comprueba experimentalmente que, cuando se cruzan dos ondas, por ejemplo, en la superficie tranquila del agua, cada una conserva después de cruzarse la misma forma. Cuando dos ondas se superponen se cumple el principio de superposición: el movimiento resultante en un punto y en un instante dados, producido por ondas viajeras que se desplazan por el mismo medio, es la suma de los desplazamientos que hubiera tenido cada onda de haberse propagado aisladamente y se expresa y=y +y. Entre los fenómenos físicos en que interviene el principio de superposición tenemos las interferencias de las que vamos a hablar a continuación. 7.. INTERFERENCIAS La interferencia de dos ondas se observa claramente en el agua. En la figura anterior de la derecha se muestra el patrón de interferencia que se crea cuando dos cuerpos que vibran tocan la superficie del agua. Las regiones que se encuentran más oscuras y claras son zonas en las que las crestas de una onda se superponen con las crestas de la otra en el primer caso o que los valles de una se superponen con los valles de otra en el segundo. En estas regiones las ondas llegan acompasadas, y decimos que están en fase. Las zonas grises se corresponden con regiones donde la cresta de una de ellas se superpone con el valle de la otra. Decimos que las ondas están desacompasadas y fuera de fase.. Dos ondas pueden combinar sus efectos en un punto reforzándose o debilitándose.. Cuando la cresta de una onda se superpone con la cresta de la otra, los efectos individuales se suman. El resultado es una onda de mayor amplitud (interferencia constructiva) 3. Cuando la cresta de una se superpone al valle de otra los efectos individuales se reducen (interferencia destructiva) 8
9 INTERFERENCIA DE DOS ONDAS DE IGUAL FRECUENCIA,AMPLITUD Y NÚMERO DE ONDAS er caso Consideraremos el caso más sencillo. Interferencia de dos ondas de igual frecuencia, amplitud y número de ondas que se encuentren viajando en igual dirección y con distinta fase. En un punto en el que ambas perturbaciones coincidan: º caso Cuando tenemos ondas idénticas que proceden de fuentes emisoras diferentes, la diferencia de fase en aquellos puntos en los que interfieren se deberá a la diferencia entre las distancias que hay de cada una de ellas al punto en cuestión. Gráficamente observamos: 9
10 7.. ONDAS ESTACIONARIAS Una onda estacionaria surge de la interferencia de dos ondas idénticas que se propagan en el mismo tiempo en sentidos opuestos. Si tenemos una cuerda fija en sus dos extremos y se hace vibrar uno de ellos, se crea un tren de ondas que se refleja en el otro extremo. Un ejemplo característico es la onda que surge al tañer una cuerda de guitarra o la onda que se genera en el interior de un horno microondas. Los vientres son los puntos que oscilan con amplitud máxima y los nodos los que oscilan con amplitud mínima. Aplicando el principio de superposición: Si las ondas que se superponen están expresadas en función de la función coseno, la expresión de la onda será: 0
11 y ( K x) cos( t) = A cos ω 8.-ENERGÍA TRANSMITIDA POR LAS ONDAS ARMÓNICAS Toda partícula de masa m afectada de una onda armónica vibra alrededor de su posición de equilibrio según un MAS y posee energía onda. Si además consideramos que E m = K A. Por lo tanto, éste será el valor de la energía que propaga la K ω m obtenemos: = E m = m 4 π f Definimos la intensidad (I) de onda en un punto como la energía que atraviesa por unidad de tiempo, una superficie unidad colocada en dicho punto, perpendicular a la dirección de propagación. En el S.I. su unidad A es de wat/m.por lo tanto Intensidad α Energía α A A. ONDAS ARMÓNICAS UNIDIMENSIONALES Supongamos una onda transversal unidimensional generada por un MAS producido en el foco emisor. Si el medio es perfectamente elástico, en cualquier punto de la cuerda ( m ) alcanzado por la onda se cumplirá que: E m = m π f A Considerando que µ ( lineal de masa) densidad µ = masa longitud E = µ π x A f Si no se disipa energía en el medio de transmisión de la onda unidimensional, su amplitud permanece constante. En caso contrario, la amplitud de la onda resultaría amortiguada tal y como se observa su amplitud disminuye B. ATENUACIÓN Y ABSORCIÓN (ONDAS BIDIMENSIONALES Y TRIDIMENSIONALES) La amortiguación de una onda puede producirse de dos formas; absorción y atenuación. La onda, a medida que se aleja del foco emisor, se va amortiguando. La amplitud disminuye y por tanto, las partículas vibran con menos energía. Esto se debe a que la misma energía se reparte, en cada frente de onda, entre mayor número de partículas. Este fenómeno recibe el nombre de atenuación. Tiene lugar en ondas bidimensionales y tridimensionales. Al alejarnos del foco, el radio aumenta y disminuye la amplitud En una onda bidimensional (frente de onda circular).al alejarnos del foco la misma Energía se Τ ι repartirá entre más partículas (circunferencia más grande). Luego E = µ π r ω A Iα r En una onda tridimensional (frente de onda esférico): Iα Aα r r. Donde ρ = masa volumen Aα r E. Donde µ = = ρ 4 π r ω masa longitud En los medios reales, la onda también se amortigua por pérdida de energía debido a rozamientos, A
12 viscosidad, etc. En este caso se dice que la onda se amortigua por absorción 9- EL SONIDO (UN EJEMPLO DE ONDA LONGITUDINAL) Cuando se golpea un cuerpo, se habla o se pulsa un instrumento musical, se produce un efecto psicofisiológico llamado sonido, pero, en qué consiste? Las vibraciones del foco emisor se propagan a las partículas del medio en el que se encuentra, y estas las transmiten de unas a otras y también a las de otros medios que estén en contacto. Se ha producido una onda longitudinal que se propaga mediante compresiones y expansiones del aire que, si llega a la membrana del tímpano, la hará vibrar, transmitiendo esta energía al interior de este órgano. INTENSIDAD SONORA -ATENUACIÓN El frente de ondas de las ondas sonoras es esférico, por tanto, la intensidad de la onda sonora es inversamente proporcional a la distancia al cuadrado, entre el foco y el receptor Iα Aα r r. Lo cual quiere decir que la amplitud del movimiento ondulatorio disminuye con la distancia. ATENUACIÓN DE LAS ONDAS -ABSORCIÓN La onda sonora hace vibrar las partículas del medio material por donde se propaga. Estas vibraciones dan lugar a rozamientos en los que se produce una disipación de la energía en forma de calor. Por tanto, el medio absorbe energía que, naturalmente, perderá el movimiento ondulatorio, con la consiguiente disminución de la intensidad. Si I O es el valor inicial de la intensidad sonora e I es el valor final que tiene después de haber recorrido una distancia x, la relación entre estos valores viene dada por una función exponencial: I = I O e α x ( Ley de Beer) Donde α se denomina coeficiente de absorción, que depende de la naturaleza del medio absorbente. 3-NIVEL DE INTENSIDAD SONORA La sensación sonora en el oído humano depende de la frecuencia del sonido percibido y los límites de audición están comprendidos, por término medio, entre los 0 Hz, de los sonidos más graves, y los 0000Hz, de los sonidos más agudos. Por otra parte, el intervalo de intensidades que puede percibir una persona oscila entre un valor mínimo, llamado intensidad umbral (I O ) que es de alrededor de 0 - W/m, hasta un valor de aproximadamente W/m, que constituye el umbral del dolor. Normalmente se utiliza una escala más sencilla, definiendo una nueva magnitud llamada nivel de intensidad sonora (β): β = 0 log I I O Hay que observar que (β) es una magnitud sin dimensiones, aunque, no obstante, la unidad que la mide se llama decibelio (db). para I I db para I W = O = 0 β O = 0 log = 0 = β = 0 log0 = 0 db m
13 EJERCICIOS. Una onda transversal de la forma: y=a sen (Kx- ωt) tiene una frecuencia de 50 Hz y se desplaza con una velocidad de 0,3 m/s. En el instante inicial la velocidad de la partícula situada en el origen tiene un valor de 4 m/s. Se pide: a) Indicar el sentido de propagación de la onda a lo largo del eje x b) Calcular la amplitud, el número de onda y la frecuencia angular (ω). Una onda armónica cuya frecuencia es de 50 Hz, se propaga en la dirección positiva del eje x. Sabiendo que la diferencia de fase, en un instante dado, para dos puntos separados 0cm, es de π radianes, determinar: a. El periodo, longitud de onda y velocidad de propagación de la onda. b. En un punto dado, qué diferencia de fase existe entre los desplazamientos que tienen lugar en instantes separados por un intervalo de 0,0s? 3. La ecuación de una onda transversal en una cuerda es: y = 6 sen π ( 0, 80t, 5 x ) donde x, y se expresan en cm y t en segundos. Determinar: a. La velocidad de la onda b. La v max y a max de oscilación en un punto cualquiera de la cuerda c. La distancia que separa dos puntos de la cuerda que oscilan en oposición de fase 4. Una onda avanza con una velocidad de 3 m/s. La amplitud vale,3cm y la frecuencia 60Hz. Suponiendo que en el origen y en el instante inicial la elongación fuera máxima, se pregunta. a. La longitud de onda del movimiento b. La elongación, la velocidad y aceleración de un punto que dista del origen 5,m para t=,6s 5. Dos fuentes sonoras emiten ondas armónicas planas no amortiguadas de igual amplitud y frecuencia. Si la frecuencia es de 000 Hz y la velocidad de propagación es de 340 m/s, determinar la diferencia de fase en un punto medio de propagación situado a 8m de una fuente y a 5m de la otra fuente sonora. Razonar si se producirá interferencia constructiva o destructiva en dicho punto. (Junio 000) 6. Una onda armónica plana que se propaga en el sentido positivo del eje OX, tiene un periodo de 0,s. En un instante, la diferencia de fase entre dos puntos separados una distancia de 60 cm es igual a π radianes. Se pide determinar: a. Longitud de onda y velocidad de propagación de la onda b. Diferencia de fase entre dos estados de perturbación de un mismo punto que tienen lugar en dos instantes separados por un intervalo de tiempo de segundos (Junio 000) 7. Explicar en qué consiste el efecto Dopler aplicado a ondas sonoras. (Septiembre 000 y Junio 00) 8. La ecuación de una onda que se propaga por una cuerda es y=8senπ(00t-8x), donde x e y se miden en cm y t en s. Calcular el tiempo que tardará la onda en recorrer una distancia de 5m (Junio 00) 9. Explicar la diferencia entre ondas longitudinales y ondas transversales. Proponer un ejemplo de cada una de ellas. (Junio 00) 0. Dada la función de onda, y=6senπ(5t-0,x)cm, donde x está expresada en cm y t en s, determinar: a. La longitud de onda, el período, la frecuencia y el número de onda b. La velocidad de propagación y la de vibración del punto situado en x=0cm en el instante t=s c. Indica el sentido de propagación de la onda y expresa la ecuación de otra onda idéntica a la anterior pero propagándose en sentido contrario (Septiembre 00) 3
14 . A lo largo de un resorte se produce una onda longitudinal con la ayuda de un vibrador de 50 Hz de frecuencia. Si la distancia entre dos compresiones sucesivas en el muelle es de 6 cm. Determinar: a. La velocidad de la onda b. Supuesta la onda armónica y que se propaga en el sentido positivo del eje OY, escribe su ecuación, suponiendo que en t=0 el foco se encuentra en la posición de máxima elongación y positiva, con una amplitud de 5 cm (Septiembre 00). Describe, en función de la diferencia de fase, que ocurre cuando se superponen dos ondas progresivas armónicas de la misma amplitud y frecuencia. (Junio 00) 3. De una onda armónica se conoce la pulsación ω=00s -, y el número de ondas K=50m -. Determina la velocidad, la frecuencia y el período de la onda. (Septiembre00) 4. El extremo de una cuerda situada sobre el eje OX, oscila con un movimiento armónico simple con una amplitud de 5 cm y una frecuencia de 34 Hz. Esta oscilación se propaga, en el sentido positivo del eje OX, con una velocidad de 5m/s. Si en el instante inicial la elongación del extremo de la cuerda es nula, escribe la ecuación que represente la onda generada en la cuerda. Cuál será la elongación del extremo de la cuerda en el instante t=0,s? (Septiembre 00) 5. Una onda armónica transversal progresiva tiene una amplitud de 3cm, una longitud de onda de 0cm y se propaga con velocidad 5 m/s. Sabiendo que en t=os la elongación en el origen es de 3cm, se pide: a. Ecuación de la onda b. Velocidad transversal de un punto situado a 40cm del foco en el instante t=s c. Diferencia de fase entre dos puntos separados 5 cm, en un instante dado (Septiembre003) 6. Dos fuentes sonoras iguales, A y B, emiten en fase ondas armónicas planas de igual amplitud y frecuencia, que se propagan a lo largo del eje OX: a. Calcula la frecuencia mínima del sonido que deben emitir las fuentes para que en un punto C situado a 7 m de la fuente A y a m de la fuente b, la amplitud del sonido sea máxima b. Si las fuentes emiten sonido de 530Hz, calcula la diferencia de fase en el punto C, Cómo será la amplitud del sonido en este punto? Dato: velocidad de propagación del sonido=340m/s (Septiembre 003) 7. Explica mediante algún ejemplo, el transporte de energía en una onda. Existe transporte efectivo de masa? (Junio 004) 8. Qué son las ondas estacionarias? Explica en qué consiste este fenómeno, menciona sus características más destacables y pon un ejemplo (Junio 004) 9. Una onda acústica se propaga en el aire. Explica la diferencia entre la velocidad de una partícula del aire que transmite dicha onda y la velocidad de la onda. (Septiembre004) 0. La amplitud de una onda que se desplaza en la dirección positiva del eje x es 0 cm, su frecuencia es,5 Hz y tiene una longitud de onda de 0 m. Escribe la ecuación que describe su movimiento.(junio 006) 4
15 . Una onda en una cuerda viene dada por: y( x, t) = 0, sen ( π t ) cos( 00) m en donde x está comprendida entre 0 y 6 m. Calcula.: a) La longitud de onda y la frecuencia angular de la onda, b) El número total de nodos (incluidos los extremos),c)la velocidad de propagación de las ondas en la cuerda. πx. Una onda vibra de acuerdo con la ecuación: y = 5sen ( ) cos( 40π t ) donde x se expresa en cm y t 3 en segundos. Se pide: a) Amplitud y velocidad de las ondas cuya superposición de lugar a esa vibración, b) La distancia entre dos nodos consecutivos c) La velocidad de un punto de la cuerda en x=,5 cm cuando t=9s 3. En la figura que sigue se representa una onda transversal que viaja en la dirección positiva del eje de abscisas. Sabiendo que la velocidad de propagación es v=4m/s: a. Escribe la ecuación que representa el movimiento de la onda. b. Determina la velocidad de vibración del punto situado en x=4 m, así como su valor máximo 4. Las gráficas que siguen muestran el movimiento de una onda. La primera representa y frente al tiempo, en una determinada posición x. La segunda muestra y frente a la posición x en un instante de tiempo determinado, t. a. Qué representan las letras A, B, C, D que se observan en las gráficas? b. Calcula la velocidad de propagación de la onda? c. Escribe la ecuación de propagación de la onda sabiendo que se trata de una onda transversal que se propaga en la dirección OX 5. Dos focos en concordancia de fase emiten ondas de 4 cm de longitud de onda. Decir si hay refuerzo o debilitamiento en puntos situados: a) a 8 cm de cada foco; b) a 0 cm de uno y 6 cm de otro; c) a cm de uno y 0 cm del otro. 6. Se propagan en un medio dos ondas de las mismas características en la misma dirección y sentido. La diferencia de fase entre las ondas es de 3/4 rad y la amplitud de las mismas es de 5 mm. Cuál es la amplitud de las ondas resultantes? 7. Dos ondas que tienen la misma frecuencia, longitud de onda y amplitud, se están moviendo en la misma dirección y sentido. Si difieren en fase en 90º y cada una tiene una amplitud de 0,05 m, hallar la amplitud de la onda resultante 8. La ecuación de una onda tiene la expresión y( x, t) = A sen( π bt c x) a. Qué representan los coeficientes b y c? Cuáles son sus unidades en el S.I? 5
16 b. Qué interpretación tendría que el signo de dentro del paréntesis fuera positivo en lugar de negativo? (Junio007) 9. Una onda armónica viaja a 30 m/s en la dirección positiva del eje x con una amplitud de 0,5m y una longitud de onda de 0,6 m. Escribir la ecuación del movimiento, como una función del tiempo, para un punto al que le llega la perturbación y está situado en x=0,8m (Junio007) 30. Una onda de frecuencia 40 Hz se propaga a lo largo del eje x en el sentido de las x crecientes. En un π rad. cierto instante temporal, la diferencia de fase entre dos puntos separados entre sí 5 cm es ( ) a. Qué valor tiene la longitud de onda? Cuál es la velocidad de propagación de la onda? b. Escribe la función de onda sabiendo que la amplitud es mm. (Septiembre 007) 6 6
PROBLEMAS M.A.S. Y ONDAS
 PROBLEMAS M.A.S. Y ONDAS 1) Una masa de 50 g unida a un resorte realiza, en el eje X, un M.A.S. descrito por la ecuación, expresada en unidades del SI. Establece su posición inicial y estudia el sentido
PROBLEMAS M.A.S. Y ONDAS 1) Una masa de 50 g unida a un resorte realiza, en el eje X, un M.A.S. descrito por la ecuación, expresada en unidades del SI. Establece su posición inicial y estudia el sentido
M.A.S. Y MOV ONDULATORIO FCA 07 ANDALUCÍA
 . La ecuación de una onda armónica que se propaga por una cuerda es: y (x, t) = 0,08 cos (6 t - 0 x) (S.I.) a) Determine el sentido de propagación de la onda, su amplitud, periodo, longitud de onda y velocidad
. La ecuación de una onda armónica que se propaga por una cuerda es: y (x, t) = 0,08 cos (6 t - 0 x) (S.I.) a) Determine el sentido de propagación de la onda, su amplitud, periodo, longitud de onda y velocidad
2. Propiedades de una onda. Información importante. 1. Ondas. Preuniversitario Solidario
 2. Propiedades de una onda 1. Ondas Información importante. Aprendizajes esperados: Es guía constituye una herramienta que usted debe manejar para poder comprender los conceptos de: Clasificación de ondas
2. Propiedades de una onda 1. Ondas Información importante. Aprendizajes esperados: Es guía constituye una herramienta que usted debe manejar para poder comprender los conceptos de: Clasificación de ondas
Capítulo 14. El sonido
 Capítulo 14 El sonido 1 Ondas sonoras Las ondas sonoras consisten en el movimiento oscilatorio longitudinal de las partículas de un medio. Su velocidad de transmisión es: v = B ρ en donde ρ es la densidad
Capítulo 14 El sonido 1 Ondas sonoras Las ondas sonoras consisten en el movimiento oscilatorio longitudinal de las partículas de un medio. Su velocidad de transmisión es: v = B ρ en donde ρ es la densidad
FS-12 GUÍA CURSOS ANUALES. Ciencias Plan Común. Física 2009. Ondas
 FS-12 Ciencias Plan Común Física 2009 Ondas Introducción: La presente guía tiene por objetivo proporcionarte distintas instancias didácticas relacionadas con el proceso de aprendizaje-enseñanza. Como cualquier
FS-12 Ciencias Plan Común Física 2009 Ondas Introducción: La presente guía tiene por objetivo proporcionarte distintas instancias didácticas relacionadas con el proceso de aprendizaje-enseñanza. Como cualquier
Capítulo 15. Ultrasonidos
 Capítulo 15 Ultrasonidos 1 Efecto Doppler El efecto Doppler consiste en el cambio de frecuencia que experimenta una onda cuando el emisor o el receptor se mueven con respecto al medio de propagación. La
Capítulo 15 Ultrasonidos 1 Efecto Doppler El efecto Doppler consiste en el cambio de frecuencia que experimenta una onda cuando el emisor o el receptor se mueven con respecto al medio de propagación. La
Movimiento oscilatorio
 Capítulo 13 Ondas 1 Movimiento oscilatorio El movimiento armónico simple ocurre cuando la fuerza recuperadora es proporcional al desplazamiento con respecto del equilibrio x: F = kx k se denomina constante
Capítulo 13 Ondas 1 Movimiento oscilatorio El movimiento armónico simple ocurre cuando la fuerza recuperadora es proporcional al desplazamiento con respecto del equilibrio x: F = kx k se denomina constante
MOVIMIENTO ONDULATORIO
 1 Apunte N o 1 Pág. 1 a 7 INTRODUCCION MOVIMIENTO ONDULATORIO Proceso por el que se propaga energía de un lugar a otro sin transferencia de materia, mediante ondas mecánicas o electromagnéticas. En cualquier
1 Apunte N o 1 Pág. 1 a 7 INTRODUCCION MOVIMIENTO ONDULATORIO Proceso por el que se propaga energía de un lugar a otro sin transferencia de materia, mediante ondas mecánicas o electromagnéticas. En cualquier
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B y C, FÍSICA
 PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B y C, FÍSICA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: Lee atentamente
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B y C, FÍSICA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: Lee atentamente
MOVIMIENTO ONDULATORIO
 MOVIMIENTO ONDULATORIO Proceso por el que se propaga energía de un lugar a otro sin transferencia de materia, mediante ondas mecánicas o electromagnéticas. En cualquier punto de la trayectoria de propagación
MOVIMIENTO ONDULATORIO Proceso por el que se propaga energía de un lugar a otro sin transferencia de materia, mediante ondas mecánicas o electromagnéticas. En cualquier punto de la trayectoria de propagación
VIBRACIONES Y ONDAS. Cuestiones
 VIBRACIONES Y ONDAS Cuestiones 1 La aceleración del movimiento de una partícula viene expresada por la relación: a = ky, siendo y el desplazamiento respecto a la posición de equilibrio y k una constante.
VIBRACIONES Y ONDAS Cuestiones 1 La aceleración del movimiento de una partícula viene expresada por la relación: a = ky, siendo y el desplazamiento respecto a la posición de equilibrio y k una constante.
FÍSICA 2º BACHILLERATO EL OSCILADOR ARMÓNICO. PROBLEMAS RESUELTOS
 FÍSICA º BACHILLERATO EL OSCILADOR ARMÓNICO. PROBLEMAS RESUELTOS TIMONMATE 1. Las características conocidas de una partícula que vibra armónicamente son la amplitud, A= 10 cm, y la frecuencia, f= 50 Hz.
FÍSICA º BACHILLERATO EL OSCILADOR ARMÓNICO. PROBLEMAS RESUELTOS TIMONMATE 1. Las características conocidas de una partícula que vibra armónicamente son la amplitud, A= 10 cm, y la frecuencia, f= 50 Hz.
No hay resorte que oscile cien años...
 No hay resorte que oscile cien años... María Paula Coluccio y Patricia Picardo Laboratorio I de Física para Biólogos y Geólogos Depto. de Física, FCEyN, UBA - 1999 Resumen: En el presente trabajo nos proponemos
No hay resorte que oscile cien años... María Paula Coluccio y Patricia Picardo Laboratorio I de Física para Biólogos y Geólogos Depto. de Física, FCEyN, UBA - 1999 Resumen: En el presente trabajo nos proponemos
física física conceptual aplicada MétodoIDEA Ondas Entre la y la 4º de eso Félix A. Gutiérrez Múzquiz
 Entre la la física física conceptual aplicada MétodoIDEA Ondas 4º de eso Féli A. Gutiérrez Múzquiz Contenidos 1. CARACTERÍSTICAS DE LAS O DAS 2. I TERFERE CIAS...... 3 6 3. O DAS ESTACIO ARIAS.. 2 1. CARACTERÍSTICAS
Entre la la física física conceptual aplicada MétodoIDEA Ondas 4º de eso Féli A. Gutiérrez Múzquiz Contenidos 1. CARACTERÍSTICAS DE LAS O DAS 2. I TERFERE CIAS...... 3 6 3. O DAS ESTACIO ARIAS.. 2 1. CARACTERÍSTICAS
Unidad III Sonido. Como las vibraciones se producen en la misma dirección en la que se propaga el sonido, se trata de una onda longitudinal.
 Unidad III Sonido Unidad III - Sonido 3 Sonido Te haz preguntado qué es el sonido? Sonido: (en física) es cualquier fenómeno que involucre la propagación en forma de ondas elásticas (sean audibles o no),
Unidad III Sonido Unidad III - Sonido 3 Sonido Te haz preguntado qué es el sonido? Sonido: (en física) es cualquier fenómeno que involucre la propagación en forma de ondas elásticas (sean audibles o no),
2001 J Opción 2 5. Qué se entiende por difracción y en qué condiciones se produce?. ( 1 punto)
 Página 1 1999 J 1. Al pulsar una cuerda de guitarra, inicialmente en reposo, ésta vibra de tal modo que cada uno de sus puntos comienza a moverse en torno a su posición inicial según la dirección perpendicular
Página 1 1999 J 1. Al pulsar una cuerda de guitarra, inicialmente en reposo, ésta vibra de tal modo que cada uno de sus puntos comienza a moverse en torno a su posición inicial según la dirección perpendicular
Mira el Sonido. Mira el Sonido
 O N D A S Mira el Sonido Mira el Sonido O N D A S Llamamos sonido a la sensación producida en nuestro oído cuando llegan las ondas emitidas por un cuerpo que vibra en un intervalo de frecuencias determinado,
O N D A S Mira el Sonido Mira el Sonido O N D A S Llamamos sonido a la sensación producida en nuestro oído cuando llegan las ondas emitidas por un cuerpo que vibra en un intervalo de frecuencias determinado,
Física P.A.U. VIBRACIONES Y ONDAS 1 VIBRACIONES Y ONDAS
 Física P.A.U. VIBRACIONES Y ONDAS 1 VIBRACIONES Y ONDAS PROBLEMAS M.A.S. 1. De un resorte elástico de constante k = 500 N m -1 cuelga una masa puntual de 5 kg. Estando el conjunto en equilibrio, se desplaza
Física P.A.U. VIBRACIONES Y ONDAS 1 VIBRACIONES Y ONDAS PROBLEMAS M.A.S. 1. De un resorte elástico de constante k = 500 N m -1 cuelga una masa puntual de 5 kg. Estando el conjunto en equilibrio, se desplaza
PROBLEMAS DE ONDAS. EFECTO DOPPLER. Autor: José Antonio Diego Vives. Documento bajo licencia Creative Commons (BY-SA)
 PROBLEMAS DE ONDAS. EFECTO DOPPLER Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons (BY-SA) Problema 1 Una sirena que emite un sonido de = 1000 Hz se mueve alejándose de un observador
PROBLEMAS DE ONDAS. EFECTO DOPPLER Autor: José Antonio Diego Vives Documento bajo licencia Creative Commons (BY-SA) Problema 1 Una sirena que emite un sonido de = 1000 Hz se mueve alejándose de un observador
Problemas. Las ondas de desplazamiento y de presión asociadas a una onda sonora vienen dadas por la ecuación
 Problemas. A una frecuencia de 4 Hz, el sonido más débil que se puede escuchar corresponde a una amplitud de presión de 8x -5 Nm -. Encontrar la correspondiente amplitud de desplazamiento. (Densidad del
Problemas. A una frecuencia de 4 Hz, el sonido más débil que se puede escuchar corresponde a una amplitud de presión de 8x -5 Nm -. Encontrar la correspondiente amplitud de desplazamiento. (Densidad del
Problemas Resueltos Primera Parte
 IES Rey Fernando VI San Fernando de Henares Departamento de Física y Química Problemas Resueltos Primera Parte Movimiento Armónico Simple Movimiento Ondulatorio El Sonido Profesor : Jesús Millán Crespo
IES Rey Fernando VI San Fernando de Henares Departamento de Física y Química Problemas Resueltos Primera Parte Movimiento Armónico Simple Movimiento Ondulatorio El Sonido Profesor : Jesús Millán Crespo
Ideas básicas sobre movimiento
 Ideas básicas sobre movimiento Todos conocemos por experiencia qué es el movimiento. En nuestra vida cotidiana, observamos y realizamos infinidad de movimientos. El desplazamiento de los coches, el caminar
Ideas básicas sobre movimiento Todos conocemos por experiencia qué es el movimiento. En nuestra vida cotidiana, observamos y realizamos infinidad de movimientos. El desplazamiento de los coches, el caminar
I.E.S. Sierra de Mijas Curso 2014-15 PROBLEMAS DE SELECTIVIDAD DEL TEMA 4: ÓPTICA
 PROBLEMAS DE SELECTIVIDAD DEL TEMA 4: ÓPTICA Selectividad Andalucía 2001: 1. a) Indique qué se entiende por foco y por distancia focal de un espejo. Qué es una imagen virtual? b) Con ayuda de un diagrama
PROBLEMAS DE SELECTIVIDAD DEL TEMA 4: ÓPTICA Selectividad Andalucía 2001: 1. a) Indique qué se entiende por foco y por distancia focal de un espejo. Qué es una imagen virtual? b) Con ayuda de un diagrama
12/06/2011 ONDAS SONORAS DEFINICION DE SONIDO. Para que existan las ondas sonoras deben existir perturbaciones o vibraciones en algún medio.
 ONDAS SONORAS DEFINICION DE SONIDO Para que existan las ondas sonoras deben existir perturbaciones o vibraciones en algún medio. 1 En los fluidos (líquidos y gases) las ondas generadas son longitudinales
ONDAS SONORAS DEFINICION DE SONIDO Para que existan las ondas sonoras deben existir perturbaciones o vibraciones en algún medio. 1 En los fluidos (líquidos y gases) las ondas generadas son longitudinales
Las ecuaciones que nos dan la posición (x) de la partícula en función del tiempo son las siguientes: ( )
 DESARROLLO DE LA PARTE TEÓRICA DE LA UNIDAD DIDÁCTICA. 1. Cinemática del movimiento armónico simple. Dinámica del movimiento armónico simple 3. Energía del movimiento armónico simple 4. Aplicaciones: resorte
DESARROLLO DE LA PARTE TEÓRICA DE LA UNIDAD DIDÁCTICA. 1. Cinemática del movimiento armónico simple. Dinámica del movimiento armónico simple 3. Energía del movimiento armónico simple 4. Aplicaciones: resorte
Guía de Materia Características del sonido y fenómenos ondulatorios aplicados al sonido
 REFLEXIÓN Y REFRACCIÓN DEL SONIDO Imagen 1:Muestra lo que sucede con la energía cuando una onda incide sobre una superficie. Se comprueba que las ondas sonoras se reflejan en el mismo ángulo con el que
REFLEXIÓN Y REFRACCIÓN DEL SONIDO Imagen 1:Muestra lo que sucede con la energía cuando una onda incide sobre una superficie. Se comprueba que las ondas sonoras se reflejan en el mismo ángulo con el que
IES Menéndez Tolosa. La Línea de la Concepción. 1 Es posible que un cuerpo se mueva sin que exista fuerza alguna sobre él?
 IES Menéndez Tolosa. La Línea de la Concepción 1 Es posible que un cuerpo se mueva sin que exista fuerza alguna sobre él? Si. Una consecuencia del principio de la inercia es que puede haber movimiento
IES Menéndez Tolosa. La Línea de la Concepción 1 Es posible que un cuerpo se mueva sin que exista fuerza alguna sobre él? Si. Una consecuencia del principio de la inercia es que puede haber movimiento
OSCILACIONES ARMÓNICAS
 Tema 5 OSCILACIONES ARMÓNICAS 5.1. Introducción. 5.. Movimiento armónico simple (MAS). 5.3. Cinemática y dinámica del MAS. 5.4. Fuerza y energía en el MAS. 5.5. Péndulo simple. MAS y movimiento circular
Tema 5 OSCILACIONES ARMÓNICAS 5.1. Introducción. 5.. Movimiento armónico simple (MAS). 5.3. Cinemática y dinámica del MAS. 5.4. Fuerza y energía en el MAS. 5.5. Péndulo simple. MAS y movimiento circular
SOLUCIONARIO FÍSICA 2.º BACHILLERATO
 FÍSICA.º BACHILLERATO SOLUCIONARIO MADRID - BARCELONA - BUENOS AIRES - CARACAS GUATEMALA - LISBOA - MÉXICO - NUEVA YORK - PANAMÁ SAN JUAN - BOGOTÁ - SANTIAGO - SÃO PAULO AUCKLAND - HAMBURGO - LONDRES -
FÍSICA.º BACHILLERATO SOLUCIONARIO MADRID - BARCELONA - BUENOS AIRES - CARACAS GUATEMALA - LISBOA - MÉXICO - NUEVA YORK - PANAMÁ SAN JUAN - BOGOTÁ - SANTIAGO - SÃO PAULO AUCKLAND - HAMBURGO - LONDRES -
1.3. Intensidad: Escala de decibelios. Impedancia acústica. Las ondas sonoras son el ejemplo más importante de ondas longitudinales.
 1.3. Intensidad: Escala de decibelios. Impedancia acústica. Ondas sonoras Las ondas sonoras son el ejemplo más importante de ondas longitudinales. Pueden viajar a través de cualquier medio material con
1.3. Intensidad: Escala de decibelios. Impedancia acústica. Ondas sonoras Las ondas sonoras son el ejemplo más importante de ondas longitudinales. Pueden viajar a través de cualquier medio material con
2. TERMINOS BÁSICOS DE ACÚSTICA.
 2. TERMINOS BÁSICOS DE ACÚSTICA. Definición de términos y sistemas de medición del ruido. Qué es el sonido? Cuando nos referimos al sonido audible por el oído humano, lo definimos como ondas sonoras que
2. TERMINOS BÁSICOS DE ACÚSTICA. Definición de términos y sistemas de medición del ruido. Qué es el sonido? Cuando nos referimos al sonido audible por el oído humano, lo definimos como ondas sonoras que
Teoría y Cálculo de Antenas (parte 1)
 Teoría y Cálculo de Antenas (parte 1) Por Martín A. Moretón Gerente para el territorio latinoamericano AirLive-Ovislink Corp. Enero 2010 Contenido Introducción....1 Qué son las antenas?....1 Qué es el
Teoría y Cálculo de Antenas (parte 1) Por Martín A. Moretón Gerente para el territorio latinoamericano AirLive-Ovislink Corp. Enero 2010 Contenido Introducción....1 Qué son las antenas?....1 Qué es el
EL SONIDO: EXPERIENCIAS MEDIANTE OSCILOSCOPIO
 EL SONIDO: EXPERIENCIAS MEDIANTE OSCILOSCOPIO AUTORÍA MARÍA DEL CARMEN HERRERA GÓMEZ TEMÁTICA EL SONIDO ETAPA BACHILLERATO Resumen Llevaremos a cabo una serie de experiencias, encaminadas a poner en práctica
EL SONIDO: EXPERIENCIAS MEDIANTE OSCILOSCOPIO AUTORÍA MARÍA DEL CARMEN HERRERA GÓMEZ TEMÁTICA EL SONIDO ETAPA BACHILLERATO Resumen Llevaremos a cabo una serie de experiencias, encaminadas a poner en práctica
Ilustración: Wikipedia
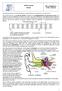 Ondas sonoras Sonido ES La Magdalena. Avilés. Asturias Cuando algo vibra en el aire esta vibración se transmite al aire originando una onda sonora. Una onda sonora es una onda de presión motivada por el
Ondas sonoras Sonido ES La Magdalena. Avilés. Asturias Cuando algo vibra en el aire esta vibración se transmite al aire originando una onda sonora. Una onda sonora es una onda de presión motivada por el
CORRIENTE ALTERNA. Fig.1 : Corriente continua
 CORRIENTE ALTERNA Hasta ahora se ha considerado que la corriente eléctrica se desplaza desde el polo positivo del generador al negativo (la corriente electrónica o real lo hace al revés: los electrones
CORRIENTE ALTERNA Hasta ahora se ha considerado que la corriente eléctrica se desplaza desde el polo positivo del generador al negativo (la corriente electrónica o real lo hace al revés: los electrones
ENSAYO DE PRUEBA SONIDO 4º MEDIO 2009 PROF.: EUGENIO CONTRERAS Z.
 VITTORIO MONTIGLIO Fondata nel 1891 DEPTO. DE MATEMATICA Y FISICA 1.) Además de sonidos, se habla de infrasonidos y ultrasonidos. En comparación con los sonidos que habitualmente percibimos, los ultrasonidos
VITTORIO MONTIGLIO Fondata nel 1891 DEPTO. DE MATEMATICA Y FISICA 1.) Además de sonidos, se habla de infrasonidos y ultrasonidos. En comparación con los sonidos que habitualmente percibimos, los ultrasonidos
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen: O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen: O también denominado Punto de aplicación. Es el punto exacto sobre
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
A continuación voy a colocar las fuerzas que intervienen en nuestro problema.
 ísica EL PLANO INCLINADO Supongamos que tenemos un plano inclinado. Sobre él colocamos un cubo, de manera que se deslice sobre la superficie hasta llegar al plano horizontal. Vamos a suponer que tenemos
ísica EL PLANO INCLINADO Supongamos que tenemos un plano inclinado. Sobre él colocamos un cubo, de manera que se deslice sobre la superficie hasta llegar al plano horizontal. Vamos a suponer que tenemos
ENERGÍA (II) FUERZAS CONSERVATIVAS
 NRGÍA (II) URZAS CONSRVATIVAS IS La Magdalena. Avilés. Asturias Cuando elevamos un cuerpo una altura h, la fuerza realiza trabajo positivo (comunica energía cinética al cuerpo). No podríamos aplicar la
NRGÍA (II) URZAS CONSRVATIVAS IS La Magdalena. Avilés. Asturias Cuando elevamos un cuerpo una altura h, la fuerza realiza trabajo positivo (comunica energía cinética al cuerpo). No podríamos aplicar la
EJERCICIOS RESUELTOS DE MOVIMIENTO ONDIULATORIO. LA LUZ (ONDAS ) 4º E.S.O.
 EJERCICIOS RESUELTOS DE MOVIMIENTO ONDIULATORIO. LA LUZ (ONDAS ) 4º E.S.O. La finalidad de este trabajo implica tres pasos: a) Leer el enunciado e intentar resolver el problema sin mirar la solución. b)
EJERCICIOS RESUELTOS DE MOVIMIENTO ONDIULATORIO. LA LUZ (ONDAS ) 4º E.S.O. La finalidad de este trabajo implica tres pasos: a) Leer el enunciado e intentar resolver el problema sin mirar la solución. b)
(b) v constante, por lo que la bola posee una aceleración normal hacia el centro de curvatura.
 Cuestiones 1. Una bola pequeña rueda en el interior de un recipiente cónico de eje vertical y semiángulo α en el vértice A qué altura h sobre el vértice se encontrará la bolita en órbita estable con una
Cuestiones 1. Una bola pequeña rueda en el interior de un recipiente cónico de eje vertical y semiángulo α en el vértice A qué altura h sobre el vértice se encontrará la bolita en órbita estable con una
[c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?.
![[c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?. [c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?.](/thumbs/15/62431.jpg) Actividad 1 La figura representa un péndulo horizontal de resorte. La masa del bloque vale M y la constante elástica del resorte K. No hay rozamientos. Inicialmente el muelle está sin deformar. [a] Si
Actividad 1 La figura representa un péndulo horizontal de resorte. La masa del bloque vale M y la constante elástica del resorte K. No hay rozamientos. Inicialmente el muelle está sin deformar. [a] Si
Práctica 4. Interferencias por división de amplitud
 Interferencias por división de amplitud 1 Práctica 4. Interferencias por división de amplitud 1.- OBJETIVOS - Estudiar una de las propiedades ondulatorias de la luz, la interferencia. - Aplicar los conocimientos
Interferencias por división de amplitud 1 Práctica 4. Interferencias por división de amplitud 1.- OBJETIVOS - Estudiar una de las propiedades ondulatorias de la luz, la interferencia. - Aplicar los conocimientos
Movimiento Armónico Simple
 Movimiento Armónico Simple Introducción al Movimiento Armónico Simple En esta página se pretende que el alumno observe la representación del Movimiento Armónico Simple (en lo que sigue M.A.S.), identificando
Movimiento Armónico Simple Introducción al Movimiento Armónico Simple En esta página se pretende que el alumno observe la representación del Movimiento Armónico Simple (en lo que sigue M.A.S.), identificando
Nombre: curso: TEMA 4: EL SONIDO
 Nombre: curso: TEMA 4: EL SONIDO 1.- CÓMO SE PRODUCE EL SONIDO En estas dos imágenes observamos cómo se produce el sonido. Cuando hacemos vibrar u oscilar la regla o la goma producimos sonido. El sonido
Nombre: curso: TEMA 4: EL SONIDO 1.- CÓMO SE PRODUCE EL SONIDO En estas dos imágenes observamos cómo se produce el sonido. Cuando hacemos vibrar u oscilar la regla o la goma producimos sonido. El sonido
FISICA Y QUÍMICA 4º ESO 1.- TRABAJO MECÁNICO.
 1.- TRABAJO MECÁNICO. Si a alguien que sostiene un objeto sin moverse le preguntas si hace trabajo, probablemente te responderá que sí. Sin embargo, desde el punto de vista de la Física, no realiza trabajo;
1.- TRABAJO MECÁNICO. Si a alguien que sostiene un objeto sin moverse le preguntas si hace trabajo, probablemente te responderá que sí. Sin embargo, desde el punto de vista de la Física, no realiza trabajo;
Av. Albarellos 2662 1º piso CABA - Argentina (C1419FSQ)
 ELECTROACUSTICA Electroacústica básica y refuerzo sonoro. Qué es el sonido? El sonido es una variación de la presión de aire con el tiempo, que se propaga en un medio elástico como el aire. Comparado a
ELECTROACUSTICA Electroacústica básica y refuerzo sonoro. Qué es el sonido? El sonido es una variación de la presión de aire con el tiempo, que se propaga en un medio elástico como el aire. Comparado a
La energía de las ondas
 7 La energía de las ondas 1. Propagación y clasificación de las ondas 102 2. Magnitudes características de las ondas 104 3. Algunos fenómenos ondulatorios 106 4. El sonido 108 5. La luz. Reflexión de la
7 La energía de las ondas 1. Propagación y clasificación de las ondas 102 2. Magnitudes características de las ondas 104 3. Algunos fenómenos ondulatorios 106 4. El sonido 108 5. La luz. Reflexión de la
INTERFERENCIA Y REFLEXIÓN CON ONDAS DE ULTRASONIDOS. Esta práctica pretende alcanzar dos objetivos fundamentales:
 INTERFERENCIA Y REFLEXIÓN CON ONDAS DE ULTRASONIDOS 1.- OBJETIVOS Esta práctica pretende alcanzar dos objetivos fundamentales: a) El manejo de una serie de instrumentos básicos como el osciloscopio y el
INTERFERENCIA Y REFLEXIÓN CON ONDAS DE ULTRASONIDOS 1.- OBJETIVOS Esta práctica pretende alcanzar dos objetivos fundamentales: a) El manejo de una serie de instrumentos básicos como el osciloscopio y el
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 FUNCIONES CONOCIDAS. FUNCIONES LINEALES. Se llaman funciones lineales a aquellas que se representan mediante rectas. Su epresión en forma eplícita es y f ( ) a b. En sentido más estricto, se llaman funciones
FUNCIONES CONOCIDAS. FUNCIONES LINEALES. Se llaman funciones lineales a aquellas que se representan mediante rectas. Su epresión en forma eplícita es y f ( ) a b. En sentido más estricto, se llaman funciones
UD1. EL SONIDO. La velocidad del sonido depende del medio y de la temperatura. Para el aire y a temperatura ambiente es de 344 m/s.
 UD1. EL SONIDO 1. El Sonido El Sonido es una vibración mecánica que se propaga por un medio material elástico y que es producido por el aporte de una energía mecánica al medio. Es una perturbación del
UD1. EL SONIDO 1. El Sonido El Sonido es una vibración mecánica que se propaga por un medio material elástico y que es producido por el aporte de una energía mecánica al medio. Es una perturbación del
ONDAS SONORAS, SONIDO. Capitulo 17 Serway
 ONDAS SONORAS, SONIDO Capitulo 17 Serway ONDAS SONORAS Las ondas sonoras viajan a través de cualquier medio material con una rapidez que depende de las propiedades del medio. A medida que las ondas sonoras
ONDAS SONORAS, SONIDO Capitulo 17 Serway ONDAS SONORAS Las ondas sonoras viajan a través de cualquier medio material con una rapidez que depende de las propiedades del medio. A medida que las ondas sonoras
LEYES DE CONSERVACIÓN: ENERGÍA Y MOMENTO
 LEYES DE CONSERVACIÓN: ENERGÍA Y MOMENTO 1. Trabajo mecánico y energía. El trabajo, tal y como se define físicamente, es una magnitud diferente de lo que se entiende sensorialmente por trabajo. Trabajo
LEYES DE CONSERVACIÓN: ENERGÍA Y MOMENTO 1. Trabajo mecánico y energía. El trabajo, tal y como se define físicamente, es una magnitud diferente de lo que se entiende sensorialmente por trabajo. Trabajo
Potencial eléctrico. du = - F dl
 Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
PROBLEMAS RESUELTOS SOBRE MOVIMIENTO ARMÓNICO SIMPLE
 PROBLEMAS RESUELTOS SOBRE MOVIMIENTO ARMÓNICO SIMPLE ) La ecuación de un M.A.S. es x(t) cos 0t,, en la que x es la elongación en cm y t en s. Cuáles son la amplitud, la frecuencia y el período de este
PROBLEMAS RESUELTOS SOBRE MOVIMIENTO ARMÓNICO SIMPLE ) La ecuación de un M.A.S. es x(t) cos 0t,, en la que x es la elongación en cm y t en s. Cuáles son la amplitud, la frecuencia y el período de este
EJERCICIOS RESUELTOS 1º DE BACHILLERATO (Hnos. Machado): EJERCICIOS DE REFUERZO 1º EVALUACIÓN (Cinemática) Por Álvaro Téllez Róbalo
 EJERCICIOS RESUELTOS 1º DE BACHILLERATO (Hnos. Machado): EJERCICIOS DE REFUERZO 1º EVALUACIÓN (Cinemática) Por Álvaro Téllez Róbalo 1. El vector posición de un punto, en función del tiempo, viene dado
EJERCICIOS RESUELTOS 1º DE BACHILLERATO (Hnos. Machado): EJERCICIOS DE REFUERZO 1º EVALUACIÓN (Cinemática) Por Álvaro Téllez Róbalo 1. El vector posición de un punto, en función del tiempo, viene dado
Solución: a) En un periodo de revolución, el satélite barre el área correspondiente al círculo encerrado por la órbita, r 2. R T r
 1 PAU Física, junio 2011 OPCIÓN A Cuestión 1.- Un satélite que gira con la misma velocidad angular que la Tierra (geoestacionario) de masa m = 5 10 3 kg, describe una órbita circular de radio r = 3,6 10
1 PAU Física, junio 2011 OPCIÓN A Cuestión 1.- Un satélite que gira con la misma velocidad angular que la Tierra (geoestacionario) de masa m = 5 10 3 kg, describe una órbita circular de radio r = 3,6 10
PARÁBOLA. 1) para la parte positiva: 2) para la parte negativa: 3) para la parte positiva: 4) para la parte negativa:
 Página 90 5 LA PARÁBOLA 5.1 DEFINICIONES La parábola es el lugar geométrico 4 de todos los puntos cuyas distancias a una recta fija, llamada, y a un punto fijo, llamado foco, son iguales entre sí. Hay
Página 90 5 LA PARÁBOLA 5.1 DEFINICIONES La parábola es el lugar geométrico 4 de todos los puntos cuyas distancias a una recta fija, llamada, y a un punto fijo, llamado foco, son iguales entre sí. Hay
FUNDAMENTOS FÍSICOS DE LA RADIOASTRONOMÍA. CAPÍTULO 1. Propiedades de la radiación electromagnética
 Página principal El proyecto y sus objetivos Cómo participar Cursos de radioastronomía Material Novedades FUNDAMENTOS FÍSICOS DE LA RADIOASTRONOMÍA Índice Introducción Capítulo 1 Capítulo 2 Capítulo 3
Página principal El proyecto y sus objetivos Cómo participar Cursos de radioastronomía Material Novedades FUNDAMENTOS FÍSICOS DE LA RADIOASTRONOMÍA Índice Introducción Capítulo 1 Capítulo 2 Capítulo 3
CASTILLA LA MANCHA / JUNIO 03. LOGSE / FÍSICA / EXAMEN COMPLETO
 OPCIÓN A CASTILLA LA MANCHA / JUNIO 03. LOGSE / FÍSICA / EXAMEN PROBLEMAS: El alumno deberá contestar a una de las dos opciones propuestas A o B. Los problemas puntúan 3 puntos cada uno y las cuestiones
OPCIÓN A CASTILLA LA MANCHA / JUNIO 03. LOGSE / FÍSICA / EXAMEN PROBLEMAS: El alumno deberá contestar a una de las dos opciones propuestas A o B. Los problemas puntúan 3 puntos cada uno y las cuestiones
Profr. Efraín Soto Apolinar. La función lineal. y = a 0 + a 1 x. y = m x + b
 La función lineal Una función polinomial de grado uno tiene la forma: y = a 0 + a 1 x El semestre pasado estudiamos la ecuación de la recta. y = m x + b En la notación de funciones polinomiales, el coeficiente
La función lineal Una función polinomial de grado uno tiene la forma: y = a 0 + a 1 x El semestre pasado estudiamos la ecuación de la recta. y = m x + b En la notación de funciones polinomiales, el coeficiente
Artes musicales Primer año medio 2008 Música y sonido: el medio ambiente sonoro
 1 Definición de música Qué es la música? La música es un arte que, al igual que otras artes, es un medio de expresión, y por lo tanto de comunicación entre los hombres. Utiliza elementos físicos como son
1 Definición de música Qué es la música? La música es un arte que, al igual que otras artes, es un medio de expresión, y por lo tanto de comunicación entre los hombres. Utiliza elementos físicos como son
Ejercicios de FÍSICA DE 2º DE BACHILLERATO
 Movimiento Armónico Simple, Ondas, Sonido Ejercicios de FÍSICA DE 2º DE BACHILLERATO INDICE 1 ONDAS... 2 1.1 MOVIMIENTO ARMÓNICO... 2 1.2 MOVIMIENTO ONDULATORIO... 5 1.3 EL SONIDO... 10 2 INTERACCIÓN GRAVITATORIA...
Movimiento Armónico Simple, Ondas, Sonido Ejercicios de FÍSICA DE 2º DE BACHILLERATO INDICE 1 ONDAS... 2 1.1 MOVIMIENTO ARMÓNICO... 2 1.2 MOVIMIENTO ONDULATORIO... 5 1.3 EL SONIDO... 10 2 INTERACCIÓN GRAVITATORIA...
La magnitud vectorial mas simple es el desplazamiento (cambio de posición de un punto a otro de una partícula o de un cuerpo)
 Existen ciertas magnitudes que quedan perfectamente determinadas cuando se conoce el nombre de una unidad y el numero de veces que se ha tomado.estas unidades se llaman escalares (tiempo, volumen, longitud,
Existen ciertas magnitudes que quedan perfectamente determinadas cuando se conoce el nombre de una unidad y el numero de veces que se ha tomado.estas unidades se llaman escalares (tiempo, volumen, longitud,
La Física del Sonido
 La Física del Sonido Qué produce el sonido? El sonido se produce cuando algo vibra. La vibración perturba el aire a su alrededor Esto causa cambios en la presión. Estos cambios de presión se propagan constituyendo
La Física del Sonido Qué produce el sonido? El sonido se produce cuando algo vibra. La vibración perturba el aire a su alrededor Esto causa cambios en la presión. Estos cambios de presión se propagan constituyendo
ESTATICA: TIPOS DE MAGNITUDES: CARACTERÍSTICAS DE UN VECTOR. Rama de la física que estudia el equilibrio de los cuerpos.
 ESTATICA: Rama de la física que estudia el equilibrio de los cuerpos. TIPOS DE MAGNITUDES: MAGNITUD ESCALAR: Es una cantidad física que se especifica por un número y una unidad. Ejemplos: La temperatura
ESTATICA: Rama de la física que estudia el equilibrio de los cuerpos. TIPOS DE MAGNITUDES: MAGNITUD ESCALAR: Es una cantidad física que se especifica por un número y una unidad. Ejemplos: La temperatura
Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1
 Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1 TEMA 4 - FUNCIONES ELEMENTALES 4.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : Una función real de variable real es una aplicación de un subconjunto
Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1 TEMA 4 - FUNCIONES ELEMENTALES 4.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : Una función real de variable real es una aplicación de un subconjunto
Departamento de Física y Química
 1 PAU Física, junio 2010. Fase general OPCION A Cuestión 1.- Enuncie la 2 a ley de Kepler. Explique en qué posiciones de la órbita elíptica la velocidad del planeta es máxima y dónde es mínima. Enuncie
1 PAU Física, junio 2010. Fase general OPCION A Cuestión 1.- Enuncie la 2 a ley de Kepler. Explique en qué posiciones de la órbita elíptica la velocidad del planeta es máxima y dónde es mínima. Enuncie
6. VECTORES Y COORDENADAS
 6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
Ejercicios de cinemática
 Ejercicios de cinemática 1.- Un ciclista recorre 32,4 km. en una hora. Calcula su rapidez media en m/s. (9 m/s) 2.- La distancia entre dos pueblos es de 12 km. Un ciclista viaja de uno a otro a una rapidez
Ejercicios de cinemática 1.- Un ciclista recorre 32,4 km. en una hora. Calcula su rapidez media en m/s. (9 m/s) 2.- La distancia entre dos pueblos es de 12 km. Un ciclista viaja de uno a otro a una rapidez
Solución: a) M = masa del planeta, m = masa del satélite, r = radio de la órbita.
 1 PAU Física, junio 2010. Fase específica OPCIÓN A Cuestión 1.- Deduzca la expresión de la energía cinética de un satélite en órbita circular alrededor de un planeta en función del radio de la órbita y
1 PAU Física, junio 2010. Fase específica OPCIÓN A Cuestión 1.- Deduzca la expresión de la energía cinética de un satélite en órbita circular alrededor de un planeta en función del radio de la órbita y
Tema 6. Movimiento ondulatorio
 Física y Química 4º ESO Movimiento ondulatorio Tema 6. Movimiento ondulatorio Movimiento ondulatorio Tipos de ondas Elementos de una onda El sonido. Audición Cualidades del sonido La luz Reflexión Refracción
Física y Química 4º ESO Movimiento ondulatorio Tema 6. Movimiento ondulatorio Movimiento ondulatorio Tipos de ondas Elementos de una onda El sonido. Audición Cualidades del sonido La luz Reflexión Refracción
Hay tres categorías de ondas mecánicas:
 LAS ONDAS SONORAS en un medio material como el aire, el agua o el acero son ONDAS DE COMPRESIÓN Cuando las compresiones y rarefacciones de las ondas inciden sobre el tímpano del oído, dan como resultado
LAS ONDAS SONORAS en un medio material como el aire, el agua o el acero son ONDAS DE COMPRESIÓN Cuando las compresiones y rarefacciones de las ondas inciden sobre el tímpano del oído, dan como resultado
Qué es una fuerza? Cómo se relaciona con el movimiento?
 Qué es una fuerza? Cómo se relaciona con el movimiento? Prof. Bartolomé Yankovic Nola, 2012 1 Cuando pateamos una pelota o empujamos una mesa, podemos afirmar que se está ejerciendo o se ha ejercido una
Qué es una fuerza? Cómo se relaciona con el movimiento? Prof. Bartolomé Yankovic Nola, 2012 1 Cuando pateamos una pelota o empujamos una mesa, podemos afirmar que se está ejerciendo o se ha ejercido una
INSTITUCION EDUCATIVA SAN JORGE MONTELIBANO
 INSTITUCION EDUCATIVA SAN JORGE MONTELIBANO GUAS DE ESTUDIO PARA LOS GRADOS: 10º AREA: FISICA PROFESOR: DALTON MORALES TEMA DE LA FISICA A TRATAR: ONDAS La naturaleza que nos rodea la percibimos a través
INSTITUCION EDUCATIVA SAN JORGE MONTELIBANO GUAS DE ESTUDIO PARA LOS GRADOS: 10º AREA: FISICA PROFESOR: DALTON MORALES TEMA DE LA FISICA A TRATAR: ONDAS La naturaleza que nos rodea la percibimos a través
TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS
 TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. CONCEPTO DE TRABAJO: A) Trabajo de una fuerza constante Todos sabemos que cuesta trabajo tirar de un sofá pesado, levantar una pila de libros
TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. CONCEPTO DE TRABAJO: A) Trabajo de una fuerza constante Todos sabemos que cuesta trabajo tirar de un sofá pesado, levantar una pila de libros
ANÁLISIS DEL ESTADO DE POLARIACIÓN
 SESIÓN 5: ANÁLISIS DEL ESTADO DE POLARIACIÓN TRABAJO PREVIO CONCEPTOS FUNDAMENTALES Luz natural Luz con el vector eléctrico vibrando en todas las direcciones del plano perpendicular a la dirección de propagación.
SESIÓN 5: ANÁLISIS DEL ESTADO DE POLARIACIÓN TRABAJO PREVIO CONCEPTOS FUNDAMENTALES Luz natural Luz con el vector eléctrico vibrando en todas las direcciones del plano perpendicular a la dirección de propagación.
Opción A. Ejercicio 1. Respuesta. E p = 1 2 mv 2. v max = 80 = 8, 9( m s ).
 Opción A. Ejercicio 1 Una masa m unida a un muelle realiza un movimiento armónico simple. La figura representa su energía potencial en función de la elongación x. (1 punto) [a] Represente la energía cinética
Opción A. Ejercicio 1 Una masa m unida a un muelle realiza un movimiento armónico simple. La figura representa su energía potencial en función de la elongación x. (1 punto) [a] Represente la energía cinética
2. MOVIMIENTOS ONDULATORIOS. ONDAS MECÁNICAS.
 Vibraciones y ondas 12 2. MOVIMIENTOS ONDULATORIOS. ONDAS MECÁNICAS. Desarrollamos la unidad de acuerdo con el siguiente hilo conductor: 1. Qué es un movimiento ondulatorio? Qué es una onda? 2. Cómo clasificar
Vibraciones y ondas 12 2. MOVIMIENTOS ONDULATORIOS. ONDAS MECÁNICAS. Desarrollamos la unidad de acuerdo con el siguiente hilo conductor: 1. Qué es un movimiento ondulatorio? Qué es una onda? 2. Cómo clasificar
MCBtec Mas información en
 MCBtec Mas información en www.mcbtec.com INTRODUCCIÓN A LA SIMULACION POR ORDENADOR Indice: Objetivo de este texto. Simulación por ordenador. Dinámica y simulación. Ejemplo disparo de un proyectil. Ejemplo
MCBtec Mas información en www.mcbtec.com INTRODUCCIÓN A LA SIMULACION POR ORDENADOR Indice: Objetivo de este texto. Simulación por ordenador. Dinámica y simulación. Ejemplo disparo de un proyectil. Ejemplo
EL SONIDO Y LAS ONDAS
 EL SONIDO Y LAS ONDAS Una onda es una perturbación que avanza o que se propaga en un medio material o incluso en el vacío. A pesar de la naturaleza diversa de las perturbaciones que pueden originarlas,
EL SONIDO Y LAS ONDAS Una onda es una perturbación que avanza o que se propaga en un medio material o incluso en el vacío. A pesar de la naturaleza diversa de las perturbaciones que pueden originarlas,
Problemas de Física 1 o Bachillerato
 Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Funciones más usuales 1
 Funciones más usuales 1 1. La función constante Funciones más usuales La función constante Consideremos la función más sencilla, por ejemplo. La imagen de cualquier número es siempre 2. Si hacemos una
Funciones más usuales 1 1. La función constante Funciones más usuales La función constante Consideremos la función más sencilla, por ejemplo. La imagen de cualquier número es siempre 2. Si hacemos una
Examen de Selectividad de Física. Septiembre 2009. Soluciones
 Examen de electividad de Física. eptiembre 2009. oluciones Primera parte Cuestión 1.- Razone si son verdaderas o falsas las siguientes afirmaciones: El valor de la velocidad de escape de un objeto lanzado
Examen de electividad de Física. eptiembre 2009. oluciones Primera parte Cuestión 1.- Razone si son verdaderas o falsas las siguientes afirmaciones: El valor de la velocidad de escape de un objeto lanzado
1.- Explica por qué los cuerpos cargados con cargas de distinto signo se atraen, mientras que si las cargas son del mismo signo, se repelen.
 Física 2º de Bachillerato. Problemas de Campo Eléctrico. 1.- Explica por qué los cuerpos cargados con cargas de distinto signo se atraen, mientras que si las cargas son del mismo signo, se repelen. 2.-
Física 2º de Bachillerato. Problemas de Campo Eléctrico. 1.- Explica por qué los cuerpos cargados con cargas de distinto signo se atraen, mientras que si las cargas son del mismo signo, se repelen. 2.-
Olimpiadas de Física Córdoba 2010
 2 2013 E n el interior encontrarás las pruebas que componen esta fase local de las olimpiadas de Física 2013. Están separadas en tres bloques. Uno relativo a dinámica y campo gravitatorio (obligatorio)
2 2013 E n el interior encontrarás las pruebas que componen esta fase local de las olimpiadas de Física 2013. Están separadas en tres bloques. Uno relativo a dinámica y campo gravitatorio (obligatorio)
Máster Universitario en Profesorado
 Máster Universitario en Profesorado Complementos para la formación disciplinar en Tecnología y procesos industriales Aspectos básicos de la Tecnología Eléctrica Contenido (II) SEGUNDA PARTE: corriente
Máster Universitario en Profesorado Complementos para la formación disciplinar en Tecnología y procesos industriales Aspectos básicos de la Tecnología Eléctrica Contenido (II) SEGUNDA PARTE: corriente
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
FUNCIONES CUADRÁTICAS Y RACIONALES
 www.matesronda.net José A. Jiménez Nieto FUNCIONES CUADRÁTICAS Y RACIONALES 1. FUNCIONES CUADRÁTICAS. Representemos, en función de la longitud de la base (), el área (y) de todos los rectángulos de perímetro
www.matesronda.net José A. Jiménez Nieto FUNCIONES CUADRÁTICAS Y RACIONALES 1. FUNCIONES CUADRÁTICAS. Representemos, en función de la longitud de la base (), el área (y) de todos los rectángulos de perímetro
Conocimiento del medio 6.º > Unidad 5 > La luz y el sonido. 1. Señala los dibujos que muestran fuentes luminosas y contesta la pregunta.
 Conocimiento del medio 6.º > Unidad 5 > La luz y el sonido _ Alumno/a: Curso: Fecha: 1. Señala los dibujos que muestran fuentes luminosas y contesta la pregunta. a. Por qué puede decirse que el fuego es
Conocimiento del medio 6.º > Unidad 5 > La luz y el sonido _ Alumno/a: Curso: Fecha: 1. Señala los dibujos que muestran fuentes luminosas y contesta la pregunta. a. Por qué puede decirse que el fuego es
Física P.A.U. VIBRACIONES Y ONDAS 1 VIBRACIONES Y ONDAS
 Física P.A.U. VIBRACIONES Y ONDAS 1 VIBRACIONES Y ONDAS INTRODUCCIÓN MÉTODO 1. En general: Se dibujan las fuerzas que actúan sobre el sistema. Se calcula la resultante por el principio de superposición.
Física P.A.U. VIBRACIONES Y ONDAS 1 VIBRACIONES Y ONDAS INTRODUCCIÓN MÉTODO 1. En general: Se dibujan las fuerzas que actúan sobre el sistema. Se calcula la resultante por el principio de superposición.
Capítulo V Resultados y conclusiones
 Capítulo V Resultados y conclusiones Nadav Levanon, autor del libro Radar Principles dijo: el estudio de los radares no solo una aplicación práctica, pero también una disciplina científica madura con fundamentos
Capítulo V Resultados y conclusiones Nadav Levanon, autor del libro Radar Principles dijo: el estudio de los radares no solo una aplicación práctica, pero también una disciplina científica madura con fundamentos
TEMA I.7. Ondas en Tres Dimensiones. Dr. Juan Pablo Torres-Papaqui
 TEMA I.7 Ondas en Tres Dimensiones Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus
TEMA I.7 Ondas en Tres Dimensiones Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus
Física de los Procesos Biológicos Curso 2005/6
 Bibliografía: ísica, Kane, Tema 8 ísica de los Procesos Biológicos Curso 2005/6 Grupo 3 TEMA 2 BIOMECÁNICA 2.1 SÓIDO DEORMABE Parte 1 Introducción Vamos a estudiar como los materiales se deforman debido
Bibliografía: ísica, Kane, Tema 8 ísica de los Procesos Biológicos Curso 2005/6 Grupo 3 TEMA 2 BIOMECÁNICA 2.1 SÓIDO DEORMABE Parte 1 Introducción Vamos a estudiar como los materiales se deforman debido
SINTESIS INFORMATICA MUSICAL DISTINGUIR: "sonido real" de uno digital o análogo sonidos, naturales humanos tecnologícos.
 SINTESIS INFORMATICA MUSICAL DISTINGUIR: "sonido real" de uno digital o análogo sonidos, naturales humanos tecnologícos. Hay una gran energía desplegada en un sonido fuerte;tensión en un sonido agudo y
SINTESIS INFORMATICA MUSICAL DISTINGUIR: "sonido real" de uno digital o análogo sonidos, naturales humanos tecnologícos. Hay una gran energía desplegada en un sonido fuerte;tensión en un sonido agudo y
FUNCIONES DE PROPORCIONALIDAD
 UNIDAD 2 PROPORCIONALIDAD. FUNCIONES DE PROPORCIONALIDAD 1.- INTRODUCCIÓN Continuamente hacemos uso de las magnitudes físicas cuando nos referimos a diversas situaciones como medida de distancias (longitud),
UNIDAD 2 PROPORCIONALIDAD. FUNCIONES DE PROPORCIONALIDAD 1.- INTRODUCCIÓN Continuamente hacemos uso de las magnitudes físicas cuando nos referimos a diversas situaciones como medida de distancias (longitud),
= 10 sin 2π (500 t 0,5 x)
 UNIDD ctividades de final de unidad Ejercicios básicos. La frecuencia del sonido que se obtiene con un diapasón es 440 Hz. Si la velocidad del sonido en el aire es 40 m s, calcula la longitud de onda correspondiente
UNIDD ctividades de final de unidad Ejercicios básicos. La frecuencia del sonido que se obtiene con un diapasón es 440 Hz. Si la velocidad del sonido en el aire es 40 m s, calcula la longitud de onda correspondiente
Circuito RC, Respuesta a la frecuencia.
 Circuito RC, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (13368) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se armó un
Circuito RC, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (13368) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se armó un
