Modelado de sistemas de inyección de combustible
|
|
|
- José Peña Ríos
- hace 8 años
- Vistas:
Transcripción
1 odlado d sistas d inyión d obustibl Krishna K. Busawon* David A. Díaz Roro* Rsun El rinial roósito d st artíulo s dar a onor un nuvo odlo ara sistas d inyión d obustibl. El odlo inorora los ftos d intrabio d alor ntr zlas d gas y otras arts físias dl sista. En st odlo, los últils d adisión y salida son vistos oo dos rators introntados a través d los uals fluyn gass a distintas traturas. El odlo rousto ud ostriornt utilizars ara disutir algunos roblas nontrados n l ontrol y stiaión d arátros d los sistas autootors. 1. INRODUCCIÓN Durant las dos déadas asadas, l odlado dináio d otors ha sido objto d intnsa invstigaión. Esto s dbido a varias lgislaions sobr isión d gass y rgulaions sobr onoía d obustibls, lo qu ha rqurido olítias d ontrol d otors ás oljas. Es bin sabido qu la rlaión Air/Cobustibl (A/F or sus siglas n inglés, la igniión y l ontrol d rirulaión d gass d obustión, aftan d anra dirta las isions y la onoía d obustibl n los autootors, a st rsto, un odlado aduado d la dináia dl últil d adisión s d artiular iortania. Un odlado uidadoso d la dináia d los últils qu oinida on los divrsos fnónos involurados dntro d stos, tals oo l fnóno aústio, aratrizado or la gotría d la boquilla y l torizado d la válvula, noralnt srán dados n térinos d arátros distribuidos d la rrsntaión dl sista. Sin bargo, ésta rrsntaión no ud sr utilizada on roósitos d ontrol n tio ral. Consuntnt, una búsquda ara odlos sils bajo hiótsis razonabls ha sido la labor d varios trabajos (véas 1,2,3,4,5. La ayoría d * stos trabajos solant onsidran la uaión d rsión-stado n los últils d salida y ntrada y iniizan sus abios d tratura. Esto s dbido a qu n gnral, la transfrnia d alor n l últil d adisión s onsidra quña ara asi todos los odos orativos. Adás, los tios d abio d rsión rlativa n l últil son uho ás largos qu los tios d abio d tratura rlativa. Sin bargo, n irtos asos, sialnt durant las ondiions d arranqu y uando la rirulaión d gass s onsidrada, los ftos d tratura n los últils no son nsariant dsriabls. En st artíulo, s dará un odlo global d las traturas y rsions n los últils ara un sista d inyión d obustibl uando la rirulaión d gass s * Dotorado n Ingniría Elétria, Ara d Control y Robótia, d la FIE - UANL. 6 Ingnirías, ayo-agosto 1999, ol. II, No.4
2 Krishna K. Busawon, David A. Díaz Roro onsidrada. Los últils d adisión y salida son vistos oo dos rators introntados a través d los uals fluyn gass a distintas traturas. El odlo s obtin al alular los balans d asas y nrgía n los rators bajo suosiions usuals d gass idals y rsión-tratura unifors. S ustra qu uando la tratura dl gas d obustión, la tratura dl últil y la tratura abint son iguals, la uaión lásia d rsión n los últils lada n varios trabajos (vér 2, 3, 5 s obtnida. Est artíulo s strutura d la siguint anra: En la siguint sión, s dará un odlo gnral d uaions d rsión y tratura ara los últils d adisión y salida. Dsués algunas silifiaions son hhas on l roósito d drivar un odlo razonabl ara ontrol y obsrvaión. 2. ODELADO DEL ÚLIPLE DE ADISIÓN El roósito d sta sión s dar una rlaión dináia d la rsión y tratura d los últils d adisión y salida sin onsidrar las dináias dl roso d obustión dntro d los istons. Podos onsidrar los últils d adisión y salida oo dos rators sarados n los uals fluyn gass a distintas traturas. El odlo s driva d la siguint rrsntaión squátia, n la ual: P,,, rrsntan la rsión, tratura y volun dl últil d adisión rstivant. P,,, rrsntan la rsión, tratura y volun dl últil d salida.,, asas d gass n los últils d adisión y salida., razón d flujo ásio d r ingrsando al últil d adisión (razón d flujo n la garganta. o, razón d flujo ásio d gas abandonando l últil d adisión (razón d flujo dl otor., razón d flujo ásio d gas d obustión qu ntra al últil d adisión., razón d flujo ásio d gas ntrando al últil d salida. Ingnirías, ayo-agosto vol. II, No.4 7
3 odlado d sistas d inyión d obustibl in, razón d flujo ásio d gas d obustión ntrando a la válvula d rirulaión(egr. out, razón d flujo ásio d gas d obustión abandonando al últil d salida. h, ho, h, h, hin, hout, h, h, ntalías asoiadas a los rstivos flujos d gass. 3. BALANCE DE ASA Y ENERGÍA EN EL ÚLIPLE DE ADISIÓN Balan d nrgía: h h o ho d ( h (1 Dond rrsnta las érdidas d alor n las ards dl últil d adisión. Balan d asa: o d Cobinando abas uaions obtnos: ( h h ( h h o ( ho h Asuios lo siguint: i Los gass son idals: dh ( (2 dh ii La zla s rfta y unifor: h h; h h h. o out in iii La zla tin un alor sífio global y s indndint d la tratura. La obinaión d lo asuido n i y iii ilia qu dh. Por lo tanto, ( h h ( y h h. Rsultando: ( ( La funión ( ( oo k( (3 ud sr odlada vntualnt, dond k s una onstant qu dnd d la ondutividad téria d las ards dl últil d adisión. 4. BALANCE DE ENERGÍA Y ASA EN EL ÚLIPLE DE SALIDA Balan d nrgía: d h in hin out hout ( h (4 Dond rrsnta las érdidas d alor d las ards dl últil d salida haia l dio xtrior. Balan d asa: d ín out (5 Cobinando las uaions (4 y (5 obtnos: dh ( h h in( hin h out( hout h Utilizando las suosiions itadas obtnos: 8 Ingnirías, ayo-agosto 1999, ol. II, No.4
4 Krishna K. Busawon, David A. Díaz Roro ( h h ( Por lo tanto, ( oo k ( (6 Coo ants ud odlars, dond k dnd d la ondutividad téria d las ards dl últil d salida. 5. UN ODELO SIPLIFICADO PARA CONROL En sta sión utilizaros las antriors uaions ara drivar un odlo on roósitos d ontrol y obsrvaión, haindo unas uantas hiótsis ás. Estas hiótsis son otivadas or ralidads rátias. Por lo asuido n (i, P r, dond r s la onstant dl gas. Por lo tanto, r r r d r ( ( o D una anra siilar, r P r y r r r d (7 ( in out abién tnos: (8. y, En sua tnos: ( ( ( r o r in ( ( ( Ahora, si asuios qu: out (9 (10 iv Las érdidas d alor a través d las ards s dsriabl, d anra qu 0. v La tratura d la zla d gass qu abandona los istons s igual a la tratura dl gas d sa, i... Entons obtnos: Ingnirías, ayo-agosto vol. II, No.4 9
5 odlado d sistas d inyión d obustibl r r P r 0 NOAS: o ( r ( in out P (11 (12 (13 (14 1 Lo asuido n iv y v tin un otivo rátio. D hho, si l valor dio d, d la zla d gass y la ondutividad téria son onoidas, s ud lograr un odlo ás xato. abién s intrsant notar qu l roso d obustión s toado n unta n l odlo or dio d la tratura. Por lo tanto la xatitud dl odlo ud sr jorada idindo la tratura, ro sto ilia la utilizaión d otro snsor. Esto s básiant una rstriión a lo asuido n v. 2 Es laro qu uando, obtnos la uaión lásia d rsión n los últils, utilizada n varios trabajos (véas g. 2,3,4,5. Es bin sabido qu n la oraión n ondiions d roso, la rirulaión d gass no s onsidra. En st aso, un análisis ás rano d la uaión (12 ustra qu la tratura dl últil tind a la tratura abint n ondiions d stado staionario. En tal aso la hiótsis d qu la tratura s unifor a través d todo l otor s uy razonabl. Sin bargo, uando la rirulaión d gass s onsidrada, sta últia suosiión no srá nsariant vrdadra. AGRADECIIENOS Agrados al Profsor Christian Jallut dl dartanto d Control Autoátio d la Univrsidad Claud Brnard Lyon I or la gran antidad d harlas uy útils intrsants al rsto. REFERENCIAS 1. Chaurlia,., Bidan, P., and Bovri, S., Control-orintd sark ngin odl, Control Eng. Prati, No. 3, , Crossly, P.R., and Cook, J. A., A nonlinar ngin odl for drivtrn syst dvlont, IEEE Intrnational Confrn Control 91, Confrn ubliation No. 332, ol. 2, Edinburgh, U.K., Dobnr, D. J., An ngin odl for dynai ngin ontrol dvlont, ASE Par No. WA- 11:15, Hndriks, E. and Sornson, S. C., an valu odling of Sark Ignition Engins, SAE hnial Par No , Powll B.K. A dynai odl for autootiv ngin ontrol analysis, Pro. of th 18th IEEE CDC, Florida, Ingnirías, ayo-agosto 1999, ol. II, No.4
MOVIMIENTO VIBRATORIO Y VELOCIDAD TÉRMICA DE LOS ELECTRONES
MOVIMINO VIRAORIO Y VLOCIDAD ÉRMICA D LOS LCRONS M. Lópz-Garía Obsrando dsd l undo arosópio l oiinto d una partíula y spífiant l d un ltrón, podríaos onluir qu tin un oiinto rtilíno o uro y qu la traytoria
MECÁNICA CUÁNTICA - RESUMEN
I..S BATRIZ D SUABIA Dto. Físia y Quíia MCÁNICA CUÁNTICA - RSUMN. La iótsis d Plank. n l año 9 Plank introdujo una nua iótsis ara tratar d xliar la radiaión itida or los uros alints. Sgún él al igual la
El Verdadero Cálculo de la Devaluación
El vrdadro alulo d la Dvaluaión El Vrdadro Cálulo d la Dvaluaión Riardo Botro G. rbgstoks@hotmail.om Casi a diario nontramos n la prnsa onómia inormaión omo sta El día d ayr la tasa rprsntativa dl mrado
UNIDAD 5 REGIMEN LIBRE
UNIDAD 5 REGIMEN LIBRE Capítulo ENERGIA EPECIFICA ECCIÓN : ENERGIA EPECÍFICA En l apitulo antrior hos xpusto la uaión d la nrgía, n la qu l prir suando z g s z ota d la solra, varial purant onstrutiva
FÍSICA II. Guía De Problemas Nº4:
Univrsidad Nacional dl Nordst Facultad d Ingniría Dpartanto d Físico-Quíica/Cátdra Física II FÍSIC II Guía D roblas Nº4: rir rincipio d la Trodináica 1 ROBLEMS RESUELTOS 1- S dsa calcular l trabajo ralizado
PROBLEMAS DE CALOR Intercambio de calor
PROBLEMAS DE CALOR Intrcabio d calor En los problas d calor, considraos un sista ADIABÁTICO, no xist intrcabio d calor con l xtrior. Y, por lo tanto, la nrgía quda íntgrant n l sista 1 Probla.- Calcular
Tabla de contenido. Página
Tabla d contnido Página Ecuacions difrncials no hoogénas Solución d una cuación difrncial no hoogéna con coficints constants Método d variación d arátros Rsun Bibliografía rcondada 4 No 4 Autovaluación
Apéndice: Propagación de ondas electromagnéticas
Apéndic: Propagación d ondas lctroagnéticas Propagación d ondas lctroagnéticas n l studio d la propagación d las ondas lctroagnéticas, las lys d Maxwll ocupan un lugar priordial para ustificar dicha propagación.
1. CICLOS DE LOS SISTEMAS DE POTENCIA 1.1 CICLOS DE POTENCIA A VAPOR
ERMODINÁMICA II INRODUCCIÓN. CICLO DE LO IEMA DE POENCIA Dsd l unto d vista d la tnología, un unto iotant d la ingniía s oyta sistas qu alin las onvsions dsadas nt los difnts tios d ngías. En la snt unidad
4. MATERIALES Y MÉTODOS.
4. MATERIALES Y MÉTODOS. 4. Matrials. 4.. Softwar Microsoft Visual Basic 6.0 Matlab Vrsión 6.0.0.88 Rlas. Microsoft Offic Excl 003 4.. Equipo d Cóputo. Coputadora Microsoft Windows X rofsional Vrsión 00
1.2 Funciones de potencial vector magnético y eléctrico escalar
. uncions d potncial vctor agnético y léctrico scalar En l análisis d problas d radiación s coún spcificar las funts y dspués ncontrarlas los capos radiados por las funts. En la práctica n l procdiinto
Capítulo III. El sistema eléctrico del automóvil. En el capítulo anterior se analizaron algunos convertidores de energía eléctrica trifásica.
3.1 Introducción Capítulo III En l capítulo antrior s analizaron algunos convrtidors d nrgía léctrica trifásica. Estos circuitos prsntan bajo factor d potncia, lo cual va n contra d los objtivos d la prsnt
Modelo 3 Opción A. , + ) Decreciente: (0, )) = ( , f(
Modlo Opción A Ejrcicio º Sa f : (, ) R la función dfinida por f() Ln() (Ln dnota la función logarito npriano). (a) [ 5 puntos] Dtrina los intrvalos d crciinto d dcrciinto los tros rlativos d f (puntos
SOBRE EL CAMPO GRAVITATORIO
OBRE EL CAMPO GRAVITATORIO CARLO CHINEA 999 OBRE EL CAMPO GRAVITATORIO El ao gaitatoio: Dfinios l ao o su uadiotnial y o la dnsidad d aión n aío Un ao gaitatoio s dfin o la ondiión d qu l uadiotnial in
SOFTWARE PARA EL DISEÑO DE ENGRANAJES CÓNICOS Y SELECCIÓN DE COJINETES DE RODAMIENTOS DE BOLAS EMPLEANDO VISUAL BASIC 6.0.
SOFTWARE PARA EL DISEÑO DE ENGRANAJES CÓNICOS Y SELECCIÓN DE COJINETES DE RODAMIENTOS DE BOLAS EMPLEANDO VISUAL BASIC 6.0. Ing. Oscar Frnándz Frnándz, Msc. Bárbaro Pña Rodriguz. Univrsidad d Matanzas Cailo
Aplicaciones de la distribución weibull en ingeniería
COLMEME UAN Aplicacions d la distribución wibull n ingniría Raqul Salazar Morno 1 Abraham Rojano Aguilar 2 Esthr Figuroa Hrnándz Francisco Pérz Soto 1. INTRODUCCIÓN la salud n la vida d una prsona. La
Informe meteorológico
Infor torológico Estación torológica d Alcalá d la Slva Año 3 Junio 2015 Nú. 43 Junio fu ligrant cálido y uy húdo. El s d junio d 2015 ha sido ligrant ás cálido d lo noral, con una tratura dia alrddor
Complementos de Física -Ingeniería Informática- Boletín 3. Semiconductores intrínsecos
Coltos d ísia -Igiría Iforátia- oltí Siodutors itrísos 1. A ua barra d G d 10 d logitud y d sió s l alia ua d.d.. d 10 V tr sus xtros. Sabido qu i =,6 10 19 -, = 0,9 /V s y = 0,18 /V s, dtrís: a) la rsistiidad
TEOREMAS DEL VALOR MEDIO., entonces existe algún punto c (a, b) tal que f ( c)
TEOREMAS DEL VALOR MEDIO Torma d Roll Si f () s continua n [a, b] y drivabl n (a, b), y si f (, ntoncs ist algún punto c (a, b) tal qu Intrprtación gométrica: ist un punto al mnos d s intrvalo, n l qu
TEMA 1. INTERCAMBIADORES DE CALOR
Fórulas de Interabiadores TEMA INTERCAMBIAORES E CALOR Resistenia téria de onduión para pared plana: Resistenia téria de onveión: R t onv A Coefiie global de transferenia de alor U: R tot R t ond L ka
Dinámica relativista - Efecto Compton
Dinámia rlativista - Efto Compton Niolás Di Fiori Fdrio Foiri Matías Rodríguz niolasdf@fibrtl.om.ar, fdfoiri@hotmail.om, srv@labs.df.uba.ar Laboratorio 5 FCEyN UBA, Otubr d S analizó l fto Compton produido
RADIO CRÍTICO DE AISLACIÓN
DIO CÍTICO DE ISCIÓN En sta clas s studiará la transfrncia d calor n una tubría d radio xtrno (0,0 ft), rcubirta con un aislant d spsor (0,039 ft), qu transporta un vapor saturado a (80 F). El sistma cañría
ANÁLISIS DE LOS REGISTROS DE OBSERVACIÓN. 1. MOAL. I. ESCUELA GRANDE.
ANÁLISIS DE LOS REGISTROS DE OBSERVACIÓN. 1. MOAL. I. ESCUELA GRANDE. El mastro impart la matria d Física y al iniciar un tma rscata los sabrs prvios d los alumnos sobr l tma, como s mustra a continuación:
Reporte Nº: 05 Fecha: JULIO 2012. ANÁLISIS DE SITUACIÓN MIGRATORIA DE EXTRANJEROS DE NACIONALIDAD HAITIANA 1. DESCRIPCIÓN DEL REPORTE
Rport Nº: 05 Fcha: JULIO 2012. ANÁLISIS DE SITUACIÓN MIGRATORIA DE EXTRANJEROS DE NACIONALIDAD HAITIANA 1. DESCRIPCIÓN DEL REPORTE El prsnt inform tin como objtivo spcífico stablcr los movimintos migratorios
Julio A. Santaella Banco de México Mercados Financieros y Curvas de Rendimiento CEMLA y CMCA San José, 25 de Septiembre de 2008
Julio A. Santalla Banco d México Mrcados Financiros y Curvas d Rndiinto CEMLA y CMCA San José, 5 d Sptibr d 008 o Las curvas d rndiinto son uy iportants para divrsos propósitos: a. Para xtracción d tasas
VI. JUSTICIA. i. - JUSTICIA CRIMINAL.
VI. JUSTICIA. i. - JUSTICIA CRIMINAL. Utilizando la d la Administración d Justicia n l o años di 883, i 884 y i 885, publicada por l Ministrio d Graci a minto d lo prvnido n cl Ral dcrto d 18 d marzo d
UTN Bs. As - TERMODINAMICA TECNICA UNIDAD 10 TOBERAS Y DIFUSORES
UNIDAD 0 TOBERAS Y DIFUSORES S dnomina tobra a un onduto qu orinta a una na fluida, mintras s rodu n lla una onrsión d nrgía dl fluido (ntalía), n nrgía inétia Es dir qu a lo largo d una tobra la loidad
CAMPO MAGNÉTICO FCA 08 ANDALUCÍA
1. a) Exliqu las xrincias d Örstd y cont cóo las cargas n oviinto originan caos agnéticos. b) En qué casos un cao agnético no jrc ninguna furza sobr una artícula cargada? Razon la rsusta.. Dos conductors
1. CICLOS DE LOS SISTEMAS DE POTENCIA 1.1 CICLOS DE POTENCIA A VAPOR
INRODUCCIÓN. CICLO DE LO IEMA DE POENCIA Dsd l punto d vista d la tcnología, un punto iportant d la ingniría s proyctar sistas qu ralicn las convrsions dsadas ntr los difrnts tipos d nrgías. En la prsnt
PAU Movimiento Vibratorio Ejercicios resueltos
PU Moviiento Vibratorio jeriios resueltos 99-009 PU CyL S995 ley Hooke alitud y freuenia Colgado de un soorte hay un resorte de onste = 0 N/ del que uelga una asa de kg. n estas irunsias y en equilibrio,
2ª PRUEBA 24 de febrero de 2017
ª PRUEB 4 d fbrro d 017 Pruba xprintal. Mdida d la rlación carga/asa dl lctrón En 1897, J. J. Thopson utilizó un dispositivo xprintal parcido al d la figura 1 para dtrinar por prira vz la rlación ntr la
Unidad 2 : Ecuaciones Diferenciales Lineales de Orden Superior
Unidad : Euaions Difrnials Linals d Ordn Surior Ta.a : Método d Cofiints Indtrinados En sta sión studiaros uno d los dos étodos ara rsolvr EDL No- Hooénas d ordn aor o iual a dos. Ezaros on las EDLNH d
4 M. a) La(s) ecuación(es) diferencial(es) del movimiento del sistema a partir de las ecuaciones de movimiento lineal y angular.
Un si-disco unifor d radio asa, ruda sin dslizar sor una suprfici orizontal. Una partícula d asa s ncuntra conctada al disco n su iso plano, por dos varillas rígidas, d asa dprcial, coo s ustra n la figura.
Selección adversa. El principal no conoce el tipo del agente modelo sencillo:
icroconoía : Scción arsa rofsora: sthr Hak Scción arsa rincia no conoc tio agnt oo sncio: rincia ntra ant risgo hay 2 tios agnt: bno y ao a roorción agnts tio s tin tiia U tin tiia Uk con k>1 ago srao
ρ = γ = Z Y Problema PTC
Probla PTC-18 Dibujar l spctro d aplitud d un cabl con pérdidas n circuito abirto, dtrinando los valors y frcuncias d los valors áxios y ínios. Solución PTC-18 Sabos qu la función d transfrncia d un cabl
EJERCICIOS DE REPASO PARA SELECTIVIDAD: ANÁLISIS
EJERCICIOS DE REPSO PR SELECTIVIDD: NÁLISIS Ejrcicio. San f : R R y g : R R las funcions dfinidas por f( = -( + + a + b y g( = c S sab qu las gráficas d f y g s cortan n l punto (, y tinn n s punto la
2. - FLUJO LAMINAR. Fig. 36
. - FLUJO LAMINAR 3.. - Viscosidad. Proidad d un fluido u controla su vlocidad d dforación. Si colocaos un trozo d asfalto sobr una sa forando un volun, oco a oco s dforara hasta alanars, dorando un tio
Inform d Gass Efcto Invrnadro Página 1 d 9 1. INDICE 1. INDICE. 3 3. CUANTIFICACIÓN DE EMISIONES DE GEIS 3 4. LÍMITES OPERATIVOS Y EXCLUSIONES 5 5. AÑO BASE 6 6. METODOLOGÍA DE CUANTIFICACIÓN 6 7. INCERTIDUMBRE
Introducción. Incluye dentro de las potenciales variaciones al
Rsun Ejcutivo 1 Introducción El Artículo 17 d la Ly 26682 stablc qu la Autoridad d Aplicación autorizará l aunto d las cuotas cuando l iso sté fundado n variacions d la structura d costos y razonabl cálculo
DESALINIZADOR SOLAR DE MÚLTIPLES EFECTOS A ALTA TEMPERATURA: DISEÑO, MODELACIÓN Y SIMULACIÓN
FACULAD DE INGENIERÍA, U..A. (CHILE), VOL N, 00,. 5- DESALINIZADOR SOLAR DE MÚLIPLES EFECOS A ALA EMPERAURA: DISEÑO, MODELACIÓN Y SIMULACIÓN Eduardo Gálvz Soto Pdro Roth Urban Klmns Shwarzr Ribido l 09
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
III. FUNCIONES EXPONENCIALES Y LOGARÍTMICAS.. FUNCIÓN EXPONENCIAL n Hmos stado manjando n st trabajo prsions dl tipo n dond s una variabl llamada bas n una constant llamada ponnt, si intrcambiamos d lugar
Olimpiadas. Internacionales
rblas d Las Oliiadas Intrnainals D Físia Jsé Luis Hrnándz érz gustín Lzan radill Madrid 008 Jsé Luis Hrnándz érz, gustín Lzan radill, Madrid 008 0ª OLIMID INTRNCIONL D FÍSIC. OLONI. 989.-Ds líquids y sn
TEMA 14. ESTRUCTURA DEL ESTADO SOLIDO Y MOVIMIENTO ELECTRONICO
TEMA 14. ESTRUCTURA DEL ESTADO SOLIDO Y MOVIMIENTO ELECTRONICO 14.1.- ESTRUCTURA DEL ESTADO SOLIDO Coo s sab la atria s prsnta n trs stado: gass, líquidos y sólidos. Los conductors y siconductors son sólidos
Ecuación para cirquitones en líneas de transmisión con carga eléctrica discreta. K. J. Candía
Ecuación para cirquitons n ínas d transmisión con carga éctrica discrta. K. J. Candía Dpartamnto d Ectrónica, Univrsidad d Tarapacá, Arica, Chi Emai: kchandia@uta.c Rsumn En sta Chara s mustra un mcanismo
Ejercicios resueltos Distribuciones discretas y continuas
ROBABILIDAD ESADÍSICA (Espcialidads: Civil-Eléctrica-Mcánica-Química) Ejrcicios rsultos Distribucions discrtas y continuas ) La rsistncia a la comprsión d una mustra d cmnto s una variabl alatoria qu s
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos OPCIÓN A
IES CASTELAR BADAJOZ PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO - (RESUELTOS por Antonio nguiano) ATEÁTICAS II Timpo máimo: horas minutos Contsta d manra clara raonada una d las dos opcions
Facultad de Ciencias Exactas Y Naturales FRECUENCIAS DE VIBRACIÓN DE UNA BARRA CON ÁREA SECCIONAL COSENO
Revista NOOS Volumen (3) Pág 4 8 Derehos Reservados Faultad de Cienias Exatas Y Naturales FRECUENCIAS DE VIBRACIÓN DE UNA BARRA CON ÁREA SECCIONAL COSENO Carlos Daniel Aosta Medina Ingrid Milena Cholo
9 TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO
9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
ANÁLISIS DEL AMPLIFICADOR EN EMISOR COMÚN
ANÁLISIS DL AMPLIFIADO N MISO OMÚN Jsús Pizarro Pláz. INTODUIÓN... 2. ANÁLISIS N ONTINUA... 2 3. TA D AGA N ALTNA... 3 4. IUITO QUIALNT D ALTNA... 4 5. FUNIONAMINTO... 7 NOTAS... 8. INTODUIÓN l amplificador
El área del rectángulo será A = p q, donde p 0,2 es variable y q depende de p. ( ) ( ) ( )
Cálculo difrncial. Matmáticas II Curso 03/4 Opción A Ejrcicio. Sa la parábola (Puntuación máima: puntos) y 4 4 y un punto ( p, q ) sobr lla con 0 p. Formamos un rctángulo d lados parallos a los js con
Onda Exclusiva. Promo Kit de Publicidad
Promo Kit de Publicidad Onda Exclusiva Anunciarte en Onda Exclusiva nunca ha sido tan facil como ahora. Al ser un portal lider en las comunicaciones cristianas, queremos ayudarte a que tu ministerio, empresa,
EL TRANSISTOR BIPOLAR DE UNIÓN E B C. Nnr Iinv <0 (ACTIVA) >0, V BC
L O POL UÓ M strutura: M íolos: (P (PP M sró d la strutura dal (doado d as ostat r aso ás hatual: >, < ( M xso d ortadors ortaros la as: yó d ltros dsd l sor Y dfusó roaó x L ( x L τ s s dsra la roaó '
REPRESENTACION GRAFICA.
REPRESENTACION GRAFICA. Calcular puntos notabls así como intrvalos d monotonía y curvatura d: ² - = 0 ; ² = ; = son los valors d qu anulan l dnominador D = R- y () = 0 ; - 4 = 0 ; = 0 posibl ma, min Monotonia:
9 TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO
9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
TEMAS 3-6: EJERCICIOS ADICIONALES
TEMAS 3-6: EJERCICIOS ADICIONALES Asignatura: Economía y Mdio Ambint Titulación: Grado n cincias ambintals Curso: 2º Smstr: 1º Curso 2010-2011 Profsora: Inmaculada C. Álvarz Ayuso Inmaculada.alvarz@uam.s
DETERMINACION ANALITICA DE LA MORFOLOGIA DE LOS DIENTES DEL ENGRANE BIPARAMÉTRICO
Rvista Ibroamriana d Ingniría Mánia. Vol. 11, N.º 3, pp. 39-51, 007 DETERMINACION ANALITICA DE LA MORFOLOGIA DE LOS DIENTES DEL ENGRANE BIPARAMÉTRICO BORIS F. VORONIN, JESÚS A. ÁLVAREZ SÁNCHEZ, JOSÉ ANTONIO
LÍMITES DE FUNCIONES.
LÍMITES DE FUNCIONES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. Sa y una unción ral d variabl ral. D una manra intuitiva y oco rcisa, dirmos qu l it d s L, cuando s aroima a, si ocurr qu cuanto más róimo sté
Tema 2: Elección bajo incertidumbre
Tema : Eleión bajo inertidumbre Ref: Capítulo Varian Autor: Joel Sandonís Versión:..0 Javier López Departamento de Fundamentos del Análisis Eonómio Universidad de Aliante Miroeonomía Intermedia Introduión
Última modificación: www.coimbraweb.com
TRANSMISIÓN D MODULACIÓN D LITUD Conenido 1.- en el doinio del iepo..- en el doinio de la freuenia. 3.- Anho de banda de la señal. 4.- Disribuión ib ió de poenia de la señal. 5.- Tipos de ransisión. Objeio.-
+ I r@, r e + G [2] r IS normal r IS con expectativas. Cuadro 12.1 Función IS con expectativas
![+ I r@, r e + G [2] r IS normal r IS con expectativas. Cuadro 12.1 Función IS con expectativas](/thumbs/29/13766495.jpg "+ I r@, r e + G [2] r IS normal r IS con expectativas. Cuadro 12.1 Función IS con expectativas")
XII Exptativas n Maroonomía 49. El modlo IS-LM y las xptativas 49.1 Cómo amia la funión IS n prsnia d xptativas Sa un modlo onvnional: ` a = C +,T @ + I r@ + G [1] Dond l onsumo dpnd d la rnta ruta ()
FINANZAS DINÁMICAS Y OPCIONES REALES PARA EVALUAR COMPAÑÍAS START-UP DEL SECTOR BIOECONOMÍA. M. C. L I Z B E T H C O B I Á N
FINANZAS DINÁMICAS Y OPCIONES REALES PARA EVALUAR COMPAÑÍAS START-UP DEL SECTOR BIOECONOMÍA. M. C. L I Z B E T H C O B I Á N Los modelos que se desarrollaban para la valoración de proyectos de inversión
Problemas Resueltos. el radio de la órbita circular, y la energía tiene el valor GMm 2 = a GM. 0. Es decir, 2 T 4π. GMm
Problmas sultos.0 Un satélit dscrib una órbita circular n torno a la Tirra. Si s cambia d rpnt la dircción d su vlocidad, pro no su módulo, studiar l cambio n su órbita y n su príodo. Al cambiar sólo la
Reacciones en disolución. Efecto del disolvente en la constante de velocidad
3/05/06 Raions n disoluión Efto dl disolvnt n la onstant d vloidad El orign dl fto pud dbrs a: Distinto grado d solvataión Modifiaión dl manismo d raión Distinta onstant dilétria Enuntros En disoluión
Ángulo de desfase en un circuito RC Fundamento
Ángulo de desfase en un iruito RC Fundaento En un iruito de orriente alterna, están situados en serie una resistenia variable R V y un ondensador. Debido a que las aídas de tensión en ada eleento no están
Universidad Nacional de Ingeniería P.A Facultad de Ingeniería Mecánica 21/07/15 DACIBAHCC EXAMEN SUSTITUTORIO DE METODOS NUMERICOS (MB536)
Unirsidad aional d Ingniría P.A. 05- Faultad d Ingniría Mánia /07/5 Probla EXAME SUSTITUTORIO DE METODOS UMERICOS (MB536) SOLO SE PERMITE EL USO DE UA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMETE
FÍSICA GENERAL I. Leyes de Newton. 1 Cuáles de los siguientes objetos están en equilibrio?
FÍSICA GENERAL I Ls d Nwton Cuáls d los siguints objtos stán n quilibrio? Un globo d hlio qu s ntin n l ir sin sndr ni dsndr b Un bol lnzd hi rrib undo s nuntr n su punto ás lto Un j qu s dsliz sin friión
Solución: Para que sea continua deben coincidir los límites laterales con su valor de definición en dicho punto x = 2. b 1 + b
Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
3. ESTADOS FINANCIEROS PROFORMA
3. ESTADOS FINANCIEROS PROFORMA 3.1 Concepto Los estados financieros pro forma son las proyecciones financieras del proyecto de inversión que se elaboran para la vida útil estimada o también llamado horizonte
COMPUTACIÓN. Práctica nº 2
Matmáticas Computación COMPUTACIÓN Práctica nº NÚMEROS REALES Eistn algunos númros irracionals prdfinidos n Maima como son l númro π l númro qu s corrspondn con los símbolos %pi % rspctivamnt. Otros númros
UNIVERSIDAD DEL FÚTBOL Y CIENCIAS DEL DEPORTE MODELO ACADÉMICO DEPORTIVO ALTO RENDIMIENTO TUZO
PROCEDIMIENTO DE CAPTACION Y ASIGNACION NIVEL SECUNDARIA ART, Clav: Página 1 d 7 1. Objtivo Asgurar qu: la captación, otorgaminto y asignación d bcas Académicas a los Estudiants d La Univrsidad dl Fútbol
IES SALVADOR SERRANO: Dto. de Matemáticas. Curso 2 009 / 10 Relación de Ejercicios: Cálculo de Probabilidades Modelos 2 008 y 2 009
IES SALVADOR SERRANO: Dto. de Matemátias. Relaión de Ejeriios: Cálulo de Probabilidades Modelos 2 008 y 2 009 EJERCICIO 1: Lena y Adrián son afiionados al tiro on aro. Lena da en el blano on probabilidad
Un cortadito, por favor!
Introduión a las Cienias Experientales Carrera de Cienias Eonóias Otoño 2001 Un ortadito, por favor! Sherzo sobre la ley de enfriaiento de Newton Martín M. Saravia, Carlos Tahi y Diego Vogelbau saravia@latinsurf.o
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 QUÍMICA TEMA 5: EQUILIBRIO QUÍMICO
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 QUÍMICA TEMA 5: EQUILIBRIO QUÍMICO Junio, Ejeriio 3, Oión B Junio, Ejeriio 6, Oión B Reserva 1, Ejeriio 3, Oión A Reserva 1, Ejeriio 5, Oión B Reserva, Ejeriio
2. MÉTODO DE COEFICIENTES INDETERMINADOS.
. MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint
Tema 2 La oferta, la demanda y el mercado
Ejrcicios rsultos d ntroducción a la Toría Económica Carmn olors Álvarz Alblo Migul Bcrra omínguz Rosa María Cácrs Alvarado María dl Pilar Osorno dl Rosal Olga María Rodríguz Rodríguz Tma 2 La ofrta, la
Máquinas asincrónicas
Electricidad básica ENTREGA 1 Máquinas asincrónicas Elaborado por Joel S.Faneite Ross Consideraciones generales sobre la áquina asincrónica En artículos anteriores, se ha considerado la áquina de C.C que
ENERGÍA (II) FUERZAS CONSERVATIVAS
NRGÍA (II) URZAS CONSRVATIVAS IS La Magdalena. Avilés. Asturias Cuando elevaos un cuerpo una altura h, la fuerza realiza trabajo positivo (counica energía cinética al cuerpo). No podríaos aplicar la definición
I.E.S. Al-Ándalus. Arahal. Sevilla. Dpto. Física y Química. Selectividad Andalucía. Física. Junio
I.E.S. Al-Ándalus. Araal. Svilla. Dto. Físia y Quíia. Sltividad Andaluía. Físia. unio 6-8 4. Al iluinar la surii d un tal on luz d longitud d onda 8 n, la isión d otoltrons sa ara un otnial d rnado d 1,3
Informe meteorológico
Infor torológico Estación torológica d Alcalá d la Slva Año 3 Abril 2015 Nú. 41 Abril fu uy cálido históricant sco. El s d abril d 2015 ha sido uy cálido, hasta l unto d habrs situado coo l sgundo ás cálido
Representación esquemática de un sistema con tres fases
6 APLICACIONES 6.1 Sistma con varias fass Una vz consguido l modlo para simular una mmbrana, s planta su uso para simular procsos con más d una. Uno d stos procsos podría sr un sistma con varias fass.
OPCIÓN A. MATEMÁTICAS 2º BACHILLERATO B Lo contrario de vivir es no arriesgarse. Fito y los Fitipaldis
MATEMÁTICAS º BACHILLERATO B --5 Lo contrario d vivir s no arrisgars Análisis Fito y los Fitipaldis OPCIÓN A.- a) S dsa construir un parallpípdo rctangular d 9 dm d volumn y tal qu un lado d la bas sa
Tema 1. Termodinámica Estadística. Problemas
ma. rmodinámica Estadística Problmas jrcicios E.- S tin un sistma formado por partículas iguals, con 6 nivls nrgéticos no dgnrados. a) Calcular l númro acto d microstados (M) n los trs casos siguints:
Problemas Tema 1 Solución a problemas de Repaso de 1ºBachillerato - Hoja 07 - Problemas 2, 4, 5
página 1/7 Problmas Tma 1 Solución a problmas d Rpaso d 1ºBachillrato - Hoja 07 - Problmas 2, 4, 5 Hoja 7. Problma 2 Rsulto por Luis Sola Ruiz (sptimbr 2014) 1. Los vértics d un triángulo son A( 2, 1),
La distribución canónica y la aproximación clásica. Espacio de fases clásico. Distribución de velocidades de Maxwell. Aplicaciones de la distribución
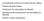La distibució caóica y la aoiació clásica. Esacio d fass clásico. Distibució d locidads d Mawll. Alicacios d la distibució d locidads d Mawll. Efusió y hacs olculas La distibució caóica sgú la aoiació
ARTÍCULOS NIIF 5 ACTIVOS NO CORRIENTES MANTENIDOS PARA LA VENTA Y OPERACIONES DISCONTINUAS. Por C.P.C. GERARDO QUEZADA* gerardoquezada@bdomexico.
ARTÍCULOS www.bdomexico.com 16 de Mayo de 2011 NIIF 5 ACTIVOS NO CORRIENTES MANTENIDOS PARA LA VENTA Y OPERACIONES DISCONTINUAS Por C.P.C. GERARDO QUEZADA* gerardoquezada@bdomexico.com Cuántas veces nos
Para aprender Termodinámica resolviendo problemas
GASES REAES. Fator de ompresibilidad. El fator de ompresibilidad se define omo ( ) ( ) ( ) z = real = real y es funión de la presión, la temperatura y la naturaleza de ada gas. Euaión de van der Waals.
Barómetro Sectorial Clima de Negocios. Unidad de Información Estratégica del Consejo Nacional de Competitividad
Barómetro Sectorial Clima de Negocios Unidad de Información Estratégica del Consejo Nacional de Competitividad Introducción Junto con la globalización y la constante demonstración de la importancia del
EJERCICIOS RESUELTOS TEMA 1: PARTE 3
Ejrcicios rsultos Tma part III): Límits d uncions º BCN EJERCICIOS RESUELTOS TEMA : PARTE 3 LÍMITES DE FUNCIONES. CONTINUIDAD Ejrcicios rsultos Tma part III): Límits d uncions º BCN ) Dada la guint unción:
Serie 11. Sistemas de control más elaborados
Serie Sistemas de ontrol más elaborados Sistemas de ontrol más elaborados Se utilizan uando los lazos de ontrol onvenionales no son sufiientemente apropiados, debido a difiultades omo proesos on grandes
Análisis información estadística de cooperativas de ahorro y crédito al 30 de septiembre de 2015. Total de Cooperativas al 30 de septiembre de 2015
Análisis información estadística de cooperativas de ahorro y crédito Al 30 de septiembre de 2015 en Puerto Rico operan cooperativas de ahorro y crédito (CAC) aseguradas y reguladas por la Corporación (COSSEC),
ECONOMÍA DE FIESTAS ESTUDIOS DE LA ACTIVIDAD COMERCIAL EN LA FERIA DE LAS ALASITAS EDICIÓN: de mayo del 2014
ECONOMÍA EDICIÓN: 02 16 d mayo dl 2014 LA ACTIVIDAD COMERCIAL EN LA FERIA LAS ALASITAS - 2014 PRODUCCIÓN: Cntro d Estudios Económicos 07 fbrro dl 2014 ESTUDIO LA ACTIVIDAD COMERCIAL EN LA FERIA LAS ALASITAS
LETRA DE CATEGORÍA: F VAGÓN DESCUBIERTO DE BORDES ALTOS
LETRA DE CATEGORÍA: F VAGÓN DESCUBIERTO DE BORDES ALTOS Vagón d rrnia Ltras índi a on bogis part suprior ( a ) part inrior ( a ) on 3 unidads on 4 ó más unidads (xlusivamnt a través dl túnl) (xlusivamnt
Definición de derivada
Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
Unidad 18. Clasificación según el momento en que se determinan los costos.
Unidad 18 Clasificación según el momento en que se determinan los costos. Desde este punto de vista, los costos de producción pueden determinarse con posterioridad a la conclusión del periodo de costos,
La ecuación diferencial ordinaria lineal de primer y segundo orden
La uaión ifrnial orinaria linal rimr sguno orn José Graro Dionisio Romro Jiménz Aamia Mamáias l Daramno Ingniría n Comuniaions Elrónia Esula Surior Ingniría Mánia Eléria IPN Méxio Rsumn. En s rabajo s
2ħ [ x2 2axe i ωt + a2
En 96 Schrödingr ncontró la siguint solución xacta d su cuación (dpndint dl tipo) para un oscilador arónico: Ψ( x, t)=( ω π ħ ) 4 xp{ ω ħ [ x ax i ωt + a (+ i ωt )+ i ħ t } dond s la asa d la particula,
Capítulo 5 Modelo constitutivo no lineal anisótropo continuo para composites 5.1. Introducción
Caítulo 5 Modlo onstitutivo no linal anisótroo ontinuo ara oosits 5.. Introduión Los atrials oustos rsntan uha oljidad uando s intnta aroxiar su oortainto ral. Los oosits son atrials htrogénos d uy divrsas
CIRCULAR CON ANIMALES
RULR N NML DUÓN VL R RN DUL DRÓN GNRL D RÁF MNR DL NRR Dibujos: lberto Fernández Ángel vejero Beatriz Martín allejo sesora de Matemáticas M. a armen Rodríguez Fernández sesora de Lengua Dirigido por: erfecto
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
Introducción. ( Por favor, lea cuidadosamente!) por el Dr. David A. Wood. Operación Id
Introducción ( Por favor, lea cuidadosamente!) por el Dr. David A. Wood Felicitaciones por su decisión de empezar las sesiones de entrenamiento más importantes en la vida Cristiana - la de aprender a ganar