LABORATORIO DE MECÁNICA LEY DE HOOKE
|
|
|
- María Rosario Vargas Montero
- hace 8 años
- Vistas:
Transcripción
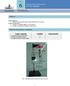
1 No 6 LABORATORIO DE MECÁNICA LEY DE HOOKE DEPARTAMENTO DE FÍSICA Y GEOLOGÍA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo General: Estudiar experimentalmente el comportamiento de los resortes. Objetivos Específicos: Calcular la constante elástica k de el resorte Verificar la existencia de fuerzas recuperadoras. Esquema del laboratorio y materiales Equipo requerido Cantidad Observaciones Un soporte para la ley de hooke. 1 Resortes de distintas durezas 2 Un juego de masas ente 5g y 500g. 1 Fig 1. Montaje experimental de la ley de Hooke 1
2 Marco teórico y Cuestionario Un cuerpo se denomina elástico si al actuar una fuerza sobre el sufre una deformación de tal manera que al cesar la fuerza recupera su forma original. Cuando una fuerza externa actúa sobre un material causa un esfuerzo o tensión en el interior del material que provoca la deformación del mismo. En muchos materiales, ente ellos los metales y minerales, la deformación es directamente proporcional al esfuerzo. Esta relación se conoce como la ley de hooke, que fue el primero en expresarla. No obstante si la fuerza externa supera un determinado valor, el material puede quedar deformado permanentemente, y la ley de hooke ya no es válida. El máximo esfuerzo que un material puede soportar antes de quedar permanentemente deformado se denomina limite de elasticidad. La relación entre el esfuerzo y la deformación, denominada módulo de elasticidad, así como el límite de elasticidad, están determinados por la estructura molecular del material. La distancia entre las moléculas de un material no sometido a esfuerzo depende de un equilibrio entre las fuerzas moleculares de atracción y repulsión. Cuando se aplica una fuerza externa que crea una tensión en el interior del material, las distancias moleculares cambian y el material se deforma. Si las moléculas están firmemente unidas entre sí, la deformación no será muy grande incluso con un esfuerzo elevado. En cambio si las moléculas están poco unidas, una tensión relativamente pequeña causara una deformación grande. Por debajo del límite de elasticidad, cuando se deja de aplicar la fuerza, las moléculas vuelven a su posición de equilibrio y el material elástico recupera su forma original. Más allá del límite de elasticidad, la fuerza aplicada separa tanto las moléculas que no pueden volver a su posición de partida y el material queda permanentemente deformado o se rompe. Para un resorte sencillo, se determina la constante de elasticidad como la fuerza necesaria para estirarlo en una unidad de longitud, tal como se observa en la Fig. 2a y Fig. 2b, es decir. En el sistema MKS, la constante se expresa en N/m. Fig. 2. a. Resorte en su longitud inicial y b. Resorte estirado en su longitud. 2
3 Si tenemos dos resortes los podemos combinar para formar un sistema de resortes en serie (figura 3a) y un sistema de resortes en paralelo (figura 3b). Fig. 3. a. Sistema de resortes en paralelo y b. Sistema de resortes en serie. Si calibramos estos sistemas, es decir, si medimos la constante de elasticidad resultante sistema,podremos verificar que para resortes en serie se cumple que, de cada para resortes en paralelo se cumple que, donde y son las constantes de Elasticidad de cada uno de los resortes del sistema y es la constante resultante del montaje en serie ó en paralelo. Resortes en serie: De acuerdo con el diagrama de cuerpo libre de cada uno de los resortes en la figura 4 d).se ha despreciado el peso de los resortes: además, por ley de acción y reacción (tercera ley de Newton), y por tanto, 3
4 De la figura 4.c. podemos concluir que la deformación resultante experimental del sistema en serie es: De manera que: Cada resorte y el sistema total cumplen la ley de Hooke, por lo que la relación anterior la podremos escribir, como,, obtenemos, Fig. 4. a. Montaje de resortes en serie y diagramas de cuerpo libre de los resortes. 4
5 Resortes en paralelo: Fig. 5. a. Montaje de resortes en paralelo y diagramas de cuerpo libre de los resortes. De la figura 5 b. podemos concluir que la deformación resultante experimental del sistema en paralelo es: Δx 1 = Δx 2 = Δx paralelo. De manera que: De acuerdo con el diagrama de cuerpo libre de cada uno de los resortes en la figura 5 c. en donde se ha despreciado el peso de los resortes, se obtiene que: F 1 + F 2 = P F ep = P Por tanto, Y como: F 1 + F 2 = F ep F 1 = k 1 Δx 1 = k 1 Δx F 2 = k 2 Δx 2 = k 2 Δx F ep = k es Δx ep = k ep Δx Entonces obtenemos: k 1 Δx + k 2 Δx = k ep Δx k ep = k 1 + k 2 5
6 Procedimiento Montaje I. Cálculo de la constante de elasticidad k. 1. Realice el montaje de la figura 1. Para ello cuelgue un resorte del brazo horizontal del soporte. 2. Mida la longitud inicial del resorte con ayuda de la escala métrica y regístrelo en la tabla de datos 1 como. 3. Cuelgue del extremo inferior del resorte una masa. Registre este valor en la tabla de datos 1. como. Mida la longitud final del resorte y regístrelo en la tabla 1. como 4. Varíe el valor de la masa colgante cuatro veces y registre estos valores en la tabla de datos 1. como. También mida la longitud final del resorte en cada caso y regístrelos en la tabla de datos 1 como. 5. Cambie el resorte por otro de diferente dureza. Repita los pasos 1, 2,3, y 4. Registre estos datos en la tabla de datos 2. Montaje II. Sistemas de resortes en serie y en paralelo. 1. Coloque los resortes 1 y 2 en serie según la figura 3.b. Y repita los pasos 2,3 y 4. Registre estos datos en la tabla de datos Coloque los resortes en paralelo según la figura 3.a. Y repita los pasos 2,3 y 4. Registre estos datos en la tabla de datos 4. Análisis de datos Montaje I. Cálculo de la constante de elasticidad k. 1. Encuentre la fuerza aplicada al resorte como para cada masa colgante... Registre estos datos en la tabla de datos 1. como,. 2. Grafique sobre una hoja de papel milimetrado, la fuerza aplicada en función del alargamiento para el resorte 1. Encuentre gráficamente la pendiente de la grafica encontrada. Tabla 1. Datos para el resorte 1. Masa colgante m (g) Fuerza Aplicada F=mg (dinas) Longitud inicial del resorte (cm) Longitud final del resorte Alargamiento del resorte (cm) = Constante de Elasticidad del resorte 1. = 6
7 3. Promedie los valores de el alargamiento de cada resorte y su respectiva incertidumbre. Encuentre la constante de elasticidad del resorte con la ecuación experimentalmente. Registrelo en la tabla de datos. 4. Repita los pasos 1 y 3 del análisis de datos anterior para el segundo resorte. Regístre estos datos en la tabla de datos 2. Tabla 2. Datos para el resorte 2. Masa colgante m (g) Fuerza Aplicada F=mg (dinas) Longitud inicial del resorte (cm) Longitud final del resorte Alargamiento del resorte (cm) = Constante de Elasticidad del resorte 2. = Montaje II. Sistemas de resortes en serie y en paralelo. 5. Repita los pasos 1 para los casos de resortes en serie. 6. Encuentre la constante resultante del sistema en serie experimentalmente con ayuda de las ecuaciones para este sistema. Tabla 3. Datos para el los resorte 1 y 2 en serie. Masa colgante m (g) Fuerza Aplicada F=mg (dinas) Alargamiento del resorte 1 Alargamiento del resorte 2 = Constante de Elasticidad del sistema en serie. = 7
8 7. Repita los pasos 1 para los casos de resortes en paralelo. 8. Encuentre la constante resultante del sistema en serie experimentalmente con ayuda de las ecuaciones para este sistema. Tabla 4. Datos para el los resorte 1 y 2 en paralelo. Masa colgante m (g) Fuerza Aplicada F=mg (dinas) Alargamiento del resorte 1 Alargamiento del resorte 2 = Constante de Elasticidad del sistema en paralelo. = Preguntas de control 1. Que representa la pendiente de cada una de las graficas de F Vs para cada resorte? 2. Compare la equivalencia del resultado con los valores experimentales obtenidos y el resultado a partir de la siguiente expresión para el sistema en serie: 3. Compare la equivalencia del resultado con los valores experimentales obtenidos y el resultado a partir de la siguiente expresión para el sistema en paralelo: kep = k1 + k2 4. Para las configuraciones en serie y en paralelo, determinar: a. Cuál de las dos configuracones soporta una fuerza mayor? b. Cuál de los dos se alarga más? Conclusiones y observaciones En este espacio el estudiante debe anotar las conclusiones de lo observado en la práctica, de manera sencilla y coherente. 8
9 9
porque la CALIDAD es nuestro compromiso
 PRÁCTICA 9 LEY DE HOOKE 1. NORMAS DE SEGURIDAD El encargado de laboratorio y el docente de la asignatura antes de comenzar a desarrollar cada práctica indicaran las normas de seguridad y recomendaciones
PRÁCTICA 9 LEY DE HOOKE 1. NORMAS DE SEGURIDAD El encargado de laboratorio y el docente de la asignatura antes de comenzar a desarrollar cada práctica indicaran las normas de seguridad y recomendaciones
LABORATORIO DE MECANICA LEY DE HOOKE
 No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
Estudiar experimentalmente el comportamiento de resortes y bandas elásticas.
 No 6 LABORATORIO DE FISICA PARA LAS CIENCIAS DE LA VIDA DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Estudiar experimentalmente el comportamiento de
No 6 LABORATORIO DE FISICA PARA LAS CIENCIAS DE LA VIDA DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Estudiar experimentalmente el comportamiento de
LABORATORIO 7: LEY DE HOOKE. Calcular la constante de elasticidad de un resorte y determinar el límite de elasticidad.
 UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BASICA LABORATORIO DE FISICA ASIGNATURA: FISICA TECNICA I. OBJETIVO GENERAL LABORATORIO 7: LEY DE HOOKE Calcular la constante de elasticidad de un resorte
UNIVERSIDAD DON BOSCO DEPARTAMENTO DE CIENCIAS BASICA LABORATORIO DE FISICA ASIGNATURA: FISICA TECNICA I. OBJETIVO GENERAL LABORATORIO 7: LEY DE HOOKE Calcular la constante de elasticidad de un resorte
Estudio estático y dinámico de un muelle
 PRÁCTICA Nº 2 Estudio estático y dinámico de un muelle Objetivo general.- Determinar la constante elástica de un muelle. A.- Estudio Estático A.1.- Objetivo.- Calcular la constante K de un muelle mediante
PRÁCTICA Nº 2 Estudio estático y dinámico de un muelle Objetivo general.- Determinar la constante elástica de un muelle. A.- Estudio Estático A.1.- Objetivo.- Calcular la constante K de un muelle mediante
LABORATORIO DE MECANICA LEY DE HOOKE
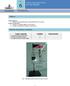 No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
No 6 LABORATORIO DE MECANICA LEY DE HOOKE DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo general: Estudiar experimentalmente el comportamiento
LAS FUERZAS Y SU MEDICIÓN : LEY DE HOOKE
 LAS FUERZAS Y SU MEDICIÓN : LEY DE HOOKE SANGER, Agustina Escuela de Enseñanza Media N 221 "Malvinas Argentinas", Villa Eloisa, Santa Fe Profesor guía: MOSCA, Sandra Mabel INTRODUCCIÓN Para poder desarrollar
LAS FUERZAS Y SU MEDICIÓN : LEY DE HOOKE SANGER, Agustina Escuela de Enseñanza Media N 221 "Malvinas Argentinas", Villa Eloisa, Santa Fe Profesor guía: MOSCA, Sandra Mabel INTRODUCCIÓN Para poder desarrollar
ELASTICIDAD. Determinar experimentalmente el módulo de elasticidad de un material usando una viga.
 ELASTICIDAD OBJETIVOS Observar el fenómeno de deformación de una viga provocado al actuar sobre ella un esfuerzo normal y un momento flector Relacionar los criterios básicos para determinar el material,
ELASTICIDAD OBJETIVOS Observar el fenómeno de deformación de una viga provocado al actuar sobre ella un esfuerzo normal y un momento flector Relacionar los criterios básicos para determinar el material,
LABORATORIO Nº 2 LEY DE HOOKE Y CAMBIOS DE ENERGÍA POTENCIAL
 LABORATORIO Nº 2 LEY DE HOOKE Y CAMBIOS DE ENERGÍA POTENCIAL I. LOGROS Calcular experimentalmente el valor de la constante de elasticidad de un resorte empleando la ley de Hooke. Analizar los cambios de
LABORATORIO Nº 2 LEY DE HOOKE Y CAMBIOS DE ENERGÍA POTENCIAL I. LOGROS Calcular experimentalmente el valor de la constante de elasticidad de un resorte empleando la ley de Hooke. Analizar los cambios de
ENERGIA POTENCIAL: ELÁSTICA Y GRAVITATORIA
 LABORATORIO DE FÍSICA GENERAL 0ª Edición ENERGIA POTENCIAL: ELÁSTICA Y GRAVITATORIA EXPERIENCIA N 05 Robert Hooke (Freshwater, Inglaterra, 635 - Londres, 703) Físico y astrónomo inglés. En 655 Robert Hooke
LABORATORIO DE FÍSICA GENERAL 0ª Edición ENERGIA POTENCIAL: ELÁSTICA Y GRAVITATORIA EXPERIENCIA N 05 Robert Hooke (Freshwater, Inglaterra, 635 - Londres, 703) Físico y astrónomo inglés. En 655 Robert Hooke
Resortes y fuerzas. Analiza la siguiente situación. Ley de Hooke. 2do Medio > Física Ley de Hooke. Qué aprenderé?
 2do Medio > Física Ley de Hooke Resortes y fuerzas Analiza la siguiente situación Aníbal trabaja en una fábrica de entretenimientos electrónicos. Es el encargado de diseñar algunas de las máquinas que
2do Medio > Física Ley de Hooke Resortes y fuerzas Analiza la siguiente situación Aníbal trabaja en una fábrica de entretenimientos electrónicos. Es el encargado de diseñar algunas de las máquinas que
MANUAL DE LABORATORIO DE FÍSICA GENERAL 9ª Edición EXPERIENCIA N 05
 ENERGIA POTENCIAL: ELÁSTICA Y GRAVITATORIA EXPERIENCIA N 05 Robert Hooke (Freshwater, Inglaterra, 635 - Londres, 703) Físico y astrónomo inglés. En 655 Robert Hooke colaboró con Robert Boyle en la construcción
ENERGIA POTENCIAL: ELÁSTICA Y GRAVITATORIA EXPERIENCIA N 05 Robert Hooke (Freshwater, Inglaterra, 635 - Londres, 703) Físico y astrónomo inglés. En 655 Robert Hooke colaboró con Robert Boyle en la construcción
LABORATORIO DE MECANICA FUERZA CENTRÍPETA
 8 LABORATORIO DE MECANICA FUERZA CENTRÍPETA DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Comprobar experimentalmente la relación entre la fuerza centrípeta
8 LABORATORIO DE MECANICA FUERZA CENTRÍPETA DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Comprobar experimentalmente la relación entre la fuerza centrípeta
Física de los Procesos Biológicos Curso 2005/6
 Bibliografía: ísica, Kane, Tema 8 ísica de los Procesos Biológicos Curso 2005/6 Grupo 3 TEMA 2 BIOMECÁNICA 2.1 SÓIDO DEORMABE Parte 1 Introducción Vamos a estudiar como los materiales se deforman debido
Bibliografía: ísica, Kane, Tema 8 ísica de los Procesos Biológicos Curso 2005/6 Grupo 3 TEMA 2 BIOMECÁNICA 2.1 SÓIDO DEORMABE Parte 1 Introducción Vamos a estudiar como los materiales se deforman debido
OBJETIVO MATERIAL. 1 resorte, 1 soporte, 1 regla de un metro, 1 gancho, 5 pesas ranuradas de 20 gf, 2 pesas de 50 gf y 4 balanzas TEORÍA
 OBJETIVO Comprobar experimentalmente la ley de Hooke y examinar la ley de conservación de energía en un proceso de interacción entre un resorte que se ha estirado y una masa suspendida del resorte a cierta
OBJETIVO Comprobar experimentalmente la ley de Hooke y examinar la ley de conservación de energía en un proceso de interacción entre un resorte que se ha estirado y una masa suspendida del resorte a cierta
Experimento 9 LEY DE HOOKE Y MOVIMIENTO ARMÓNICO SIMPLE. Objetivos. Teoría
 Experimento 9 LEY DE HOOKE Y MOVIMIENTO ARMÓNICO SIMPLE Objetivos 1. Verificar la ley de Hooke, 2. Medir la constante k de un resorte, y 3. Medir el período de oscilación de un sistema masa-resorte y compararlo
Experimento 9 LEY DE HOOKE Y MOVIMIENTO ARMÓNICO SIMPLE Objetivos 1. Verificar la ley de Hooke, 2. Medir la constante k de un resorte, y 3. Medir el período de oscilación de un sistema masa-resorte y compararlo
No hay resorte que oscile cien años...
 No hay resorte que oscile cien años... María Paula Coluccio y Patricia Picardo Laboratorio I de Física para Biólogos y Geólogos Depto. de Física, FCEyN, UBA - 1999 Resumen: En el presente trabajo nos proponemos
No hay resorte que oscile cien años... María Paula Coluccio y Patricia Picardo Laboratorio I de Física para Biólogos y Geólogos Depto. de Física, FCEyN, UBA - 1999 Resumen: En el presente trabajo nos proponemos
EL PÉNDULO SIMPLE: DETERMINACIÓN DE LA ACELERACIÓN DE LA GRAVEDAD (A) FUNDAMENTO
 EL PÉNDULO SIMPLE: DETERMINACIÓN DE LA ACELERACIÓN DE LA GRAVEDAD (A) FUNDAMENTO Se denomina péndulo simple (o péndulo matemático) a un punto material suspendido de un hilo inextensible y sin peso, que
EL PÉNDULO SIMPLE: DETERMINACIÓN DE LA ACELERACIÓN DE LA GRAVEDAD (A) FUNDAMENTO Se denomina péndulo simple (o péndulo matemático) a un punto material suspendido de un hilo inextensible y sin peso, que
Equipo requerido Cantidad Observaciones Mesa de fuerzas 1 Poleas 3 Anillo de Plástico 1 Portapesa + hilo 3 Juego de Masas 1
 DEPARTAMENTO DE FISICA Y GEOLOGIA No 1 UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo General Encontrar la fuerza resultante de dos vectores por descomposición y por graficación.
DEPARTAMENTO DE FISICA Y GEOLOGIA No 1 UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo General Encontrar la fuerza resultante de dos vectores por descomposición y por graficación.
LEY DE HOOKE: CONSTANTE DE RECUPERACIÓN DE UN CUERPO ELÁSTICO.
 LEY DE HOOKE: CONSTANTE DE RECUPERACIÓN DE UN CUERPO ELÁSTICO. Para la realización de esta práctica el alumno deberá venir al laboratorio provisto con hojas de papel milimetrado Objetivo: Estudiar la ley
LEY DE HOOKE: CONSTANTE DE RECUPERACIÓN DE UN CUERPO ELÁSTICO. Para la realización de esta práctica el alumno deberá venir al laboratorio provisto con hojas de papel milimetrado Objetivo: Estudiar la ley
Instrumentación y Ley de OHM
 Instrumentación y Ley de OHM A) INSTRUMENTACIÓN 1. OBJETIVOS. 1. Conocer el manejo de instrumentos y materiales de uso corriente en los experimentos de electricidad y magnetismo. 2. Conocer el área de
Instrumentación y Ley de OHM A) INSTRUMENTACIÓN 1. OBJETIVOS. 1. Conocer el manejo de instrumentos y materiales de uso corriente en los experimentos de electricidad y magnetismo. 2. Conocer el área de
FÍSICA Y QUÍMICA - 4º ESO LAS FUERZAS PRINCIPIOS FUNDAMENTALES DE LA DINÁMICA (LEYES DE NEWTON) INERCIA
 PRINCIPIOS FUNDAMENTALES DE LA DINÁMICA (LEYES DE NEWTON) INERCIA 1. Todo cuerpo tiene tendencia a permanecer en su estado de movimiento. Esta tendencia recibe el nombre de inercia. 2. La masa es una medida
PRINCIPIOS FUNDAMENTALES DE LA DINÁMICA (LEYES DE NEWTON) INERCIA 1. Todo cuerpo tiene tendencia a permanecer en su estado de movimiento. Esta tendencia recibe el nombre de inercia. 2. La masa es una medida
La Función lineal en la demostración de la ley de Hooke
 La Función lineal en la demostración de la ley de Hooke María del Socorro Valero, Ma. Guadalupe Barba Sandoval, Ma. Paulina Ventura Regalado Tecnología: TI Nspire CX y TI Nspire Lab Cradle de Texas Instruments
La Función lineal en la demostración de la ley de Hooke María del Socorro Valero, Ma. Guadalupe Barba Sandoval, Ma. Paulina Ventura Regalado Tecnología: TI Nspire CX y TI Nspire Lab Cradle de Texas Instruments
ENSAYOS MECÁNICOS II: TRACCIÓN
 1. INTRODUCCIÓN. El ensayo a tracción es la forma básica de obtener información sobre el comportamiento mecánico de los materiales. Mediante una máquina de ensayos se deforma una muestra o probeta del
1. INTRODUCCIÓN. El ensayo a tracción es la forma básica de obtener información sobre el comportamiento mecánico de los materiales. Mediante una máquina de ensayos se deforma una muestra o probeta del
EXPERIENCIA DIDÁCTICA DE FÍSICA PARA DETERMINAR LA CONSTANTE ELÁSTICA DE UN MUELLE
 EXPERIENCIA DIDÁCTICA DE FÍSICA PARA DETERMINAR LA CONSTANTE ELÁSTICA DE UN MUELLE AUTORÍA MARÍA FRANCISCA OJEDA EGEA TEMÁTICA EXPERIMENTO FÍSICA Y QUÍMICA, APLICACIÓN MÉTODO CIENTÍFICO ETAPA EDUCACIÓN
EXPERIENCIA DIDÁCTICA DE FÍSICA PARA DETERMINAR LA CONSTANTE ELÁSTICA DE UN MUELLE AUTORÍA MARÍA FRANCISCA OJEDA EGEA TEMÁTICA EXPERIMENTO FÍSICA Y QUÍMICA, APLICACIÓN MÉTODO CIENTÍFICO ETAPA EDUCACIÓN
Diseño y Construcción de un Generador de Van de Graaff
 Diseño y Construcción de un Generador de Van de Graaff ASIGNATURA: Física Electromagnética TEMA DEL PROYECTO: Electrostática OBJETIVOS Afianzar los conceptos de la fuerza eléctrica a nivel de la interacción
Diseño y Construcción de un Generador de Van de Graaff ASIGNATURA: Física Electromagnética TEMA DEL PROYECTO: Electrostática OBJETIVOS Afianzar los conceptos de la fuerza eléctrica a nivel de la interacción
MEDIDA DEL MÓDULO DE YOUNG DE UNA BARRA
 PRÁCTICA MDIDA DL MÓDULO D YOUNG D UNA BARRA INTRODUCCIÓN La Ley de Hooke gobierna el comportamiento elástico lineal de un material y afirma que existe proporcionalidad entre los esfuerzos aplicados (σ)
PRÁCTICA MDIDA DL MÓDULO D YOUNG D UNA BARRA INTRODUCCIÓN La Ley de Hooke gobierna el comportamiento elástico lineal de un material y afirma que existe proporcionalidad entre los esfuerzos aplicados (σ)
La forma algebraica de la ecuación producto cruz es más complicada que la del producto escalar. Para dos vectores 3D y,
 Materia: Matemática de 5to Tema: Producto Cruz Marco Teórico Mientras que un producto escalar de dos vectores produce un valor escalar; el producto cruz de los mismos dos vectores produce una cantidad
Materia: Matemática de 5to Tema: Producto Cruz Marco Teórico Mientras que un producto escalar de dos vectores produce un valor escalar; el producto cruz de los mismos dos vectores produce una cantidad
Conservación de la Energía
 Conservación de la Energía Objetivo Estudiar empíricamente la conservación de la Energía Mecánica realizando experimentos de conversión de Energía Potencial de un resorte en Energía Cinética de masas en
Conservación de la Energía Objetivo Estudiar empíricamente la conservación de la Energía Mecánica realizando experimentos de conversión de Energía Potencial de un resorte en Energía Cinética de masas en
T R A C C I Ó N periodo de proporcionalidad o elástico. limite elástico o aparente o superior de fluencia.
 T R A C C I Ó N Un cuerpo se encuentra sometido a tracción simple cuando sobre sus secciones transversales se le aplican cargas normales uniformemente repartidas y de modo de tender a producir su alargamiento.
T R A C C I Ó N Un cuerpo se encuentra sometido a tracción simple cuando sobre sus secciones transversales se le aplican cargas normales uniformemente repartidas y de modo de tender a producir su alargamiento.
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS
 CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 2.- RESISTENCIA DE MATERIALES. TRACCION. 1.1.- Resistencia de materiales. Objeto. La mecánica desde el punto de vista Físico
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 2.- RESISTENCIA DE MATERIALES. TRACCION. 1.1.- Resistencia de materiales. Objeto. La mecánica desde el punto de vista Físico
Las ecuaciones que nos dan la posición (x) de la partícula en función del tiempo son las siguientes: ( )
 DESARROLLO DE LA PARTE TEÓRICA DE LA UNIDAD DIDÁCTICA. 1. Cinemática del movimiento armónico simple. Dinámica del movimiento armónico simple 3. Energía del movimiento armónico simple 4. Aplicaciones: resorte
DESARROLLO DE LA PARTE TEÓRICA DE LA UNIDAD DIDÁCTICA. 1. Cinemática del movimiento armónico simple. Dinámica del movimiento armónico simple 3. Energía del movimiento armónico simple 4. Aplicaciones: resorte
LABORATORIO DE MECÁNICA LEY DE HOOKE
 No 6 LABORATORIO DE MECÁNICA DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos 1. Estudiar la relación que existe entre el alargamiento de un resorte y la
No 6 LABORATORIO DE MECÁNICA DEPARTAMENTO DE FISICA Y GEOLOGIA UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos 1. Estudiar la relación que existe entre el alargamiento de un resorte y la
FÍSICA 2º BACHILLERATO EL OSCILADOR ARMÓNICO. PROBLEMAS RESUELTOS
 FÍSICA º BACHILLERATO EL OSCILADOR ARMÓNICO. PROBLEMAS RESUELTOS TIMONMATE 1. Las características conocidas de una partícula que vibra armónicamente son la amplitud, A= 10 cm, y la frecuencia, f= 50 Hz.
FÍSICA º BACHILLERATO EL OSCILADOR ARMÓNICO. PROBLEMAS RESUELTOS TIMONMATE 1. Las características conocidas de una partícula que vibra armónicamente son la amplitud, A= 10 cm, y la frecuencia, f= 50 Hz.
Circuito RC, Respuesta a la frecuencia.
 Circuito RC, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (13368) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se armó un
Circuito RC, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (13368) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se armó un
CAMBIO DE LA ENERGÍA POTENCIAL
 CAMBIO DE LA ENERGÍA POTENCIAL Eperiencia N 9 Enería potencial: enería asociada con la posición de la partícula en un campo ravitacional. I. OBJETIVO. Investiar los cambios de enería potencial elástica
CAMBIO DE LA ENERGÍA POTENCIAL Eperiencia N 9 Enería potencial: enería asociada con la posición de la partícula en un campo ravitacional. I. OBJETIVO. Investiar los cambios de enería potencial elástica
Líneas Equipotenciales
 Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
Segunda Ley de Newton
 Segunda Ley de Newton Laboratorio de Mecánica y fluidos Objetivos El alumno entenderá la relación entre las fuerzas de la naturaleza y el movimiento. El estudiante encontrará la relación entre las fuerzas
Segunda Ley de Newton Laboratorio de Mecánica y fluidos Objetivos El alumno entenderá la relación entre las fuerzas de la naturaleza y el movimiento. El estudiante encontrará la relación entre las fuerzas
Informe 1: Ensayos de Tracción Ciencias de los Materiales CM3201
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ciencia de los Materiales Informe 1: Ensayos de Tracción Ciencias de los Materiales CM3201 Alumno: Pablo J. Cabello H. Grupo:
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ciencia de los Materiales Informe 1: Ensayos de Tracción Ciencias de los Materiales CM3201 Alumno: Pablo J. Cabello H. Grupo:
UNIVERSIDAD DEL VALLE INGENIERIA ELECTRONICA
 UNIVERSIDAD DEL VALLE INGENIERIA ELECTRONICA INSTRUMENTOS DE MEDICION INFORME DE LABORATORIO Presentado por: Andrés González - 0329032 Andrea Herrera - 0327121 Hans Haeusler - 0332903 Rafael Triviño -
UNIVERSIDAD DEL VALLE INGENIERIA ELECTRONICA INSTRUMENTOS DE MEDICION INFORME DE LABORATORIO Presentado por: Andrés González - 0329032 Andrea Herrera - 0327121 Hans Haeusler - 0332903 Rafael Triviño -
Fallo estructural del concreto en diagramas de dominio
 Fallo estructural del concreto en diagramas de dominio (Parte II) Eduardo de J. Vidaud Quintana Ingeniero Civil/Maestría en Ingeniería. Su correo electrónico es: evidaud@mail.imcyc.com Ingrid N. Vidaud
Fallo estructural del concreto en diagramas de dominio (Parte II) Eduardo de J. Vidaud Quintana Ingeniero Civil/Maestría en Ingeniería. Su correo electrónico es: evidaud@mail.imcyc.com Ingrid N. Vidaud
Circuito RL, Respuesta a la frecuencia.
 Circuito RL, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se estudia
Circuito RL, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se estudia
Péndulo simple. Curso 2010/11. Comprobar los factores que determinan el periodo de un péndulo simple.
 Prácticas de laboratorio de Física I 1 Objetivos Péndulo simple Curso 2010/11 Comprobar los factores que determinan el periodo de un péndulo simple. Determinar la aceleración de la gravedad a través del
Prácticas de laboratorio de Física I 1 Objetivos Péndulo simple Curso 2010/11 Comprobar los factores que determinan el periodo de un péndulo simple. Determinar la aceleración de la gravedad a través del
Equipo requerido Cantidad Observaciones Mesa de fuerzas 1 Poleas 3 Anillo de Plástico 1 Portapesa + hilo 3 Juego de Masas 1
 DEPARTAMENTO DE FISICA Y GEOLOGIA No 1 UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo General Encontrar la fuerza resultante de dos vectores por descomposición y por graficación.
DEPARTAMENTO DE FISICA Y GEOLOGIA No 1 UNIVERSIDAD DE PAMPLONA FACULTAD DE CIENCIAS BÁSICAS Objetivos Objetivo General Encontrar la fuerza resultante de dos vectores por descomposición y por graficación.
CAPÍTULO 2 COLUMNAS CORTAS BAJO CARGA AXIAL SIMPLE
 CAPÍTULO 2 COLUMNAS CORTAS BAJO CARGA AXIAL SIMPLE 2.1 Comportamiento, modos de falla y resistencia de elementos sujetos a compresión axial En este capítulo se presentan los procedimientos necesarios para
CAPÍTULO 2 COLUMNAS CORTAS BAJO CARGA AXIAL SIMPLE 2.1 Comportamiento, modos de falla y resistencia de elementos sujetos a compresión axial En este capítulo se presentan los procedimientos necesarios para
Agentes para la conservación de la energía mecánica
 Agentes para la conservación de la energía mecánica Para levantar un cuerpo verticalmente a velocidad constante, es necesario que algún agente externo realice trabajo y hemos demostrado que este trabajo
Agentes para la conservación de la energía mecánica Para levantar un cuerpo verticalmente a velocidad constante, es necesario que algún agente externo realice trabajo y hemos demostrado que este trabajo
Mecánica Racional 20 TEMA 3: Método de Trabajo y Energía.
 INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
ENSAYO DE TRACCIÓN UNIVERSAL
 BLOQUE II.- Práctica II.-Ensayo de Tracción, pag 1 PRACTICA II: ENSAYO DE TRACCIÓN UNIVERSAL OBJETIVOS: El objetivo del ensayo de tracción es determinar aspectos importantes de la resistencia y alargamiento
BLOQUE II.- Práctica II.-Ensayo de Tracción, pag 1 PRACTICA II: ENSAYO DE TRACCIÓN UNIVERSAL OBJETIVOS: El objetivo del ensayo de tracción es determinar aspectos importantes de la resistencia y alargamiento
Determinación del equivalente eléctrico del calor
 Determinación del equivalente eléctrico del calor Julieta Romani Paula Quiroga María G. Larreguy y María Paz Frigerio julietaromani@hotmail.com comquir@ciudad.com.ar merigl@yahoo.com.ar mapaz@vlb.com.ar
Determinación del equivalente eléctrico del calor Julieta Romani Paula Quiroga María G. Larreguy y María Paz Frigerio julietaromani@hotmail.com comquir@ciudad.com.ar merigl@yahoo.com.ar mapaz@vlb.com.ar
FRICCIÓN TRABAJO Y POTENCIA.
 INSTITUTO POLITÉCNICO NACIONAL CECyT N 13 RICARDO FLORES MAGÓN LABORATORIO DE FÍSICA II PRÁCTICA No. 10 FRICCIÓN TRABAJO Y POTENCIA. NOMBRE. GRUPO. No. BOLETA. FECHA. EQUIPO No. ASISTENCIA. BATA. REPORTE.
INSTITUTO POLITÉCNICO NACIONAL CECyT N 13 RICARDO FLORES MAGÓN LABORATORIO DE FÍSICA II PRÁCTICA No. 10 FRICCIÓN TRABAJO Y POTENCIA. NOMBRE. GRUPO. No. BOLETA. FECHA. EQUIPO No. ASISTENCIA. BATA. REPORTE.
FORMACIÓN DE IMÁGENES CON LENTES
 Laboratorio de Física de Procesos Biológicos FORMACIÓN DE IMÁGENES CON LENTES Fecha: 19/12/2005 1. Objetivo de la práctica Estudio de la posición y el tamaño de la imagen de un objeto formada por una lente
Laboratorio de Física de Procesos Biológicos FORMACIÓN DE IMÁGENES CON LENTES Fecha: 19/12/2005 1. Objetivo de la práctica Estudio de la posición y el tamaño de la imagen de un objeto formada por una lente
FISICA I Escuela Politécnica de Ingeniería de Minas y Energía AJUSTE POR MÍNIMOS CUADRADOS
 AJUSTE POR MÍNIMOS CUADRADOS Existen numerosas leyes físicas en las que se sabe de antemano que dos magnitudes x e y se relacionan a través de una ecuación lineal y = ax + b donde las constantes b (ordenada
AJUSTE POR MÍNIMOS CUADRADOS Existen numerosas leyes físicas en las que se sabe de antemano que dos magnitudes x e y se relacionan a través de una ecuación lineal y = ax + b donde las constantes b (ordenada
Solubilidad. y se representa por.
 Solubilidad Solubilidad. La solubilidad mide la cantidad máxima de soluto capaz de disolverse en una cantidad definida de disolvente, a una temperatura determinada, y formar un sistema estable que se denomina
Solubilidad Solubilidad. La solubilidad mide la cantidad máxima de soluto capaz de disolverse en una cantidad definida de disolvente, a una temperatura determinada, y formar un sistema estable que se denomina
Tema 3. Medidas de tendencia central. 3.1. Introducción. Contenido
 Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Integrantes: 2. Introducción
 Facultad de Ciencias Departamento de Física Fundamentos de Electricidad y Magnetismo Laboratorio N 7 Campo Magnético Ovidio Almanza Noviembre 28 de 2011 Integrantes: Diana Milena Ramírez Gutiérrez Cod.
Facultad de Ciencias Departamento de Física Fundamentos de Electricidad y Magnetismo Laboratorio N 7 Campo Magnético Ovidio Almanza Noviembre 28 de 2011 Integrantes: Diana Milena Ramírez Gutiérrez Cod.
1 Estática Básica Prohibida su reproducción sin autorización. CONCEPTOS DE FISICA MECANICA. Conceptos de Física Mecánica
 1 CONCEPTOS DE FISICA MECANICA Introducción La parte de la física mecánica se puede dividir en tres grandes ramas de acuerdo a lo que estudia cada una de ellas. Así, podemos clasificarlas según lo siguiente:
1 CONCEPTOS DE FISICA MECANICA Introducción La parte de la física mecánica se puede dividir en tres grandes ramas de acuerdo a lo que estudia cada una de ellas. Así, podemos clasificarlas según lo siguiente:
2. Dado el campo de fuerzas F x, Solución: W = 6 J
 UNIVERSIDD DE OVIEDO Escuela Politécnica de Ingeniería de Gijón Curso 013-4 1. Dos objetos, uno con masa doble que el otro, cuelgan de los extremos de la cuerda de una polea fija de masa despreciable y
UNIVERSIDD DE OVIEDO Escuela Politécnica de Ingeniería de Gijón Curso 013-4 1. Dos objetos, uno con masa doble que el otro, cuelgan de los extremos de la cuerda de una polea fija de masa despreciable y
TRANSDUCTORES CAPACITIVOS
 CLASE 10 -- TRANSDUCTORES CAPACITIVOS Un capacitor o condensador consiste en dos superficies conductivas separadas por un material dieléctrico, el cual puede ser un sólido, líquido, gas o vacío. La capacitancia
CLASE 10 -- TRANSDUCTORES CAPACITIVOS Un capacitor o condensador consiste en dos superficies conductivas separadas por un material dieléctrico, el cual puede ser un sólido, líquido, gas o vacío. La capacitancia
Actividad V.53 Transiciones de fases Calor latente de transformación
 Actividad V.53 Transiciones de fases Calor latente de transformación Objetivo Estudio de transiciones de fase líquido vapor y sólido líquido. Medición de los calores latentes de evaporación y de fusión
Actividad V.53 Transiciones de fases Calor latente de transformación Objetivo Estudio de transiciones de fase líquido vapor y sólido líquido. Medición de los calores latentes de evaporación y de fusión
PRACTICA 2: ENSAYO DE CORTE DIRECTO EN ARENA DENSA Y SUELTA.
 PRACTICA 2: ENSAYO DE CORTE DIRECTO EN ARENA DENSA Y SUELTA. 1.- Introducción. En el aparato de corte directo se intenta conseguir la rotura de una muestra según un plano predeterminado, con el fin de
PRACTICA 2: ENSAYO DE CORTE DIRECTO EN ARENA DENSA Y SUELTA. 1.- Introducción. En el aparato de corte directo se intenta conseguir la rotura de una muestra según un plano predeterminado, con el fin de
Prueba experimental (15 puntos)
 Prueba experimental (5 puntos) Determinación de la distancia focal f de una lente y del índice de refracción n del vidrio del que está hecha Desde que se inventaron las lentes hace ya cinco siglos, han
Prueba experimental (5 puntos) Determinación de la distancia focal f de una lente y del índice de refracción n del vidrio del que está hecha Desde que se inventaron las lentes hace ya cinco siglos, han
PRÁCTICA NÚMERO 8 EL POLARÍMETRO Y LA ACTIVIDAD ÓPTICA
 PRÁCTICA NÚMERO 8 EL POLARÍMETRO Y LA ACTIVIDAD ÓPTICA I. Objetivos. 1. Estudiar el efecto que tienen ciertas sustancias sobre la luz polarizada. 2. Encontrar la gráfica y ecuación de la concentración
PRÁCTICA NÚMERO 8 EL POLARÍMETRO Y LA ACTIVIDAD ÓPTICA I. Objetivos. 1. Estudiar el efecto que tienen ciertas sustancias sobre la luz polarizada. 2. Encontrar la gráfica y ecuación de la concentración
Incertidumbre y errores en mediciones experimentales
 UNIVERSIDAD SAN CARLOS DE GUATEMALA FACULTAD DE ODONTOLOGÍA ÁREA BÁSICA CURSO FÍSICAMATEMÁTICA Incertidumbre y errores en mediciones experimentales Documento de apoyo a la docencia Elaborado por: Ing.
UNIVERSIDAD SAN CARLOS DE GUATEMALA FACULTAD DE ODONTOLOGÍA ÁREA BÁSICA CURSO FÍSICAMATEMÁTICA Incertidumbre y errores en mediciones experimentales Documento de apoyo a la docencia Elaborado por: Ing.
TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d.
![TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d. TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d.](/thumbs/31/15114944.jpg) C U R S O: FÍSICA COMÚN MATERIAL: FC-09 TRABAJO Y ENERGÍA La energía desempeña un papel muy importante en el mundo actual, por lo cual se justifica que la conozcamos mejor. Iniciamos nuestro estudio presentando
C U R S O: FÍSICA COMÚN MATERIAL: FC-09 TRABAJO Y ENERGÍA La energía desempeña un papel muy importante en el mundo actual, por lo cual se justifica que la conozcamos mejor. Iniciamos nuestro estudio presentando
UNIVERSIDAD LIBRE FACULTAD DE INGENIERÍA DEPARTAMENTO DE CIENCIAS BÁSICAS GUÍA DE TRABAJO DE LABORATORIO DE FÍSICA MECÁNICA PRÁCTICA N 4A
 UNIVERSIDAD LIBRE FACULTAD DE INGENIERÍA DEPARTAMENTO DE CIENCIAS BÁSICAS GUÍA DE TRABAJO DE LABORATORIO DE FÍSICA MECÁNICA PRÁCTICA N 4A TEMA: MOVIMIENTO PARABOLICO CON DIFERENTES ANGULOS DE LANZAMIENTO.
UNIVERSIDAD LIBRE FACULTAD DE INGENIERÍA DEPARTAMENTO DE CIENCIAS BÁSICAS GUÍA DE TRABAJO DE LABORATORIO DE FÍSICA MECÁNICA PRÁCTICA N 4A TEMA: MOVIMIENTO PARABOLICO CON DIFERENTES ANGULOS DE LANZAMIENTO.
INTRODUCCIÓN: LA FÍSICA Y SU LENGUAJE, LAS MATEMÁTICAS
 INTRODUCCIÓN: LA FÍSICA Y SU LENGUAJE, LAS MATEMÁTICAS La física es la más fundamental de las ciencias que tratan de estudiar la naturaleza. Esta ciencia estudia aspectos tan básicos como el movimiento,
INTRODUCCIÓN: LA FÍSICA Y SU LENGUAJE, LAS MATEMÁTICAS La física es la más fundamental de las ciencias que tratan de estudiar la naturaleza. Esta ciencia estudia aspectos tan básicos como el movimiento,
PLANIFICACIÓN DE SESIÓN DE APRENDIZAJE. independiente, dependiente e pueden ser. intervinientes, que responden al investigadas por la
 PLANIFICACIÓN DE SESIÓN DE APRENDIZAJE GRADO UNIDAD SESIÓN HORAS QUINTO IV 1/9 3 TÍTULO DE LA SESIÓN Trabajo mecánico APRENDIZAJES ESPERADOS COMPETENCIAS CAPACIDADES INDICADORES Indaga, mediante Problematiza
PLANIFICACIÓN DE SESIÓN DE APRENDIZAJE GRADO UNIDAD SESIÓN HORAS QUINTO IV 1/9 3 TÍTULO DE LA SESIÓN Trabajo mecánico APRENDIZAJES ESPERADOS COMPETENCIAS CAPACIDADES INDICADORES Indaga, mediante Problematiza
ENERGÍA (II) FUERZAS CONSERVATIVAS
 NRGÍA (II) URZAS CONSRVATIVAS IS La Magdalena. Avilés. Asturias Cuando elevamos un cuerpo una altura h, la fuerza realiza trabajo positivo (comunica energía cinética al cuerpo). No podríamos aplicar la
NRGÍA (II) URZAS CONSRVATIVAS IS La Magdalena. Avilés. Asturias Cuando elevamos un cuerpo una altura h, la fuerza realiza trabajo positivo (comunica energía cinética al cuerpo). No podríamos aplicar la
PROBLEMAS M.A.S. Y ONDAS
 PROBLEMAS M.A.S. Y ONDAS 1) Una masa de 50 g unida a un resorte realiza, en el eje X, un M.A.S. descrito por la ecuación, expresada en unidades del SI. Establece su posición inicial y estudia el sentido
PROBLEMAS M.A.S. Y ONDAS 1) Una masa de 50 g unida a un resorte realiza, en el eje X, un M.A.S. descrito por la ecuación, expresada en unidades del SI. Establece su posición inicial y estudia el sentido
ECUACION DE DEMANDA. El siguiente ejemplo ilustra como se puede estimar la ecuación de demanda cuando se supone que es lineal.
 ECUACION DE DEMANDA La ecuación de demanda es una ecuación que expresa la relación que existe entre q y p, donde q es la cantidad de artículos que los consumidores están dispuestos a comprar a un precio
ECUACION DE DEMANDA La ecuación de demanda es una ecuación que expresa la relación que existe entre q y p, donde q es la cantidad de artículos que los consumidores están dispuestos a comprar a un precio
Ejemplo 2. Velocidad de arrastre en un alambre de cobre
 Ejemplo 1 Cual es la velocidad de desplazamiento de los electrones en un alambre de cobre típico de radio 0,815mm que transporta una corriente de 1 A? Si admitimos que existe un electrón libre por átomo
Ejemplo 1 Cual es la velocidad de desplazamiento de los electrones en un alambre de cobre típico de radio 0,815mm que transporta una corriente de 1 A? Si admitimos que existe un electrón libre por átomo
Capítulo 5 Oscilaciones
 Capítulo 5 Oscilaciones 9 Problemas de selección - página 77 (soluciones en la página 120) 6 Problemas de desarrollo - página 82 (soluciones en la página 121) 75 5.A PROBLEMAS DE SELECCIÓN Sección 5.A
Capítulo 5 Oscilaciones 9 Problemas de selección - página 77 (soluciones en la página 120) 6 Problemas de desarrollo - página 82 (soluciones en la página 121) 75 5.A PROBLEMAS DE SELECCIÓN Sección 5.A
Problemas de Física 1 o Bachillerato
 Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Problemas de Física o Bachillerato Principio de conservación de la energía mecánica. Desde una altura h dejamos caer un cuerpo. Hallar en qué punto de su recorrido se cumple E c = 4 E p 2. Desde la parte
Universidad de Pamplona Sede Villa del Rosario LABORATORIO DE MECÁNICA CUESTIONARIO GUIA PARA LAS PRÁCTICAS DE LABORATORIO DE MECÁNICA
 Universidad de Pamplona Sede Villa del Rosario LABORATORIO DE MECÁNICA CUESTIONARIO GUIA PARA LAS PRÁCTICAS DE LABORATORIO DE MECÁNICA El cuestionario correspondiente a cada práctica de laboratorio debe
Universidad de Pamplona Sede Villa del Rosario LABORATORIO DE MECÁNICA CUESTIONARIO GUIA PARA LAS PRÁCTICAS DE LABORATORIO DE MECÁNICA El cuestionario correspondiente a cada práctica de laboratorio debe
INFORME. Prestaciones del nuevo neopreno de baja compresión de Cressi respecto al Yamamoto 45
 INFORME Low Compression Yamamoto 45 Prestaciones del nuevo neopreno de baja compresión de Cressi respecto al Yamamoto 45 Realizado por J. Errondosoro Mondragón, 16 de agosto de 2006 Informe CS060816 (neopreno).doc
INFORME Low Compression Yamamoto 45 Prestaciones del nuevo neopreno de baja compresión de Cressi respecto al Yamamoto 45 Realizado por J. Errondosoro Mondragón, 16 de agosto de 2006 Informe CS060816 (neopreno).doc
1. Resolver el sistema de dos ecuaciones con dos incógnitas AX = B, donde 1 0,999 1,999 A = 1,999 . 0,999 1 1 0,999 A = . 0,999 1. AX = αo 1 + βo 2.
 Instituto de Matemática y Estadística Prof Ing Rafael Laguardia Facultad de Ingeniería Universidad de la República C1 y GAL1 anuales 2009 Trabajo: número de condición y SVD El objetivo de este trabajo
Instituto de Matemática y Estadística Prof Ing Rafael Laguardia Facultad de Ingeniería Universidad de la República C1 y GAL1 anuales 2009 Trabajo: número de condición y SVD El objetivo de este trabajo
SISTEMAS MECÁNICOS Septiembre 2001
 SISTEMAS MECÁNICOS Septiembre 2001 Dos resortes helicoidales de compresión, ambos de hilo del mismo acero y diámetro del alambre d=1,5 cm y 7 espiras cada uno, escuadradas y rectificadas, tiene la misma
SISTEMAS MECÁNICOS Septiembre 2001 Dos resortes helicoidales de compresión, ambos de hilo del mismo acero y diámetro del alambre d=1,5 cm y 7 espiras cada uno, escuadradas y rectificadas, tiene la misma
Introducción a la Firma Electrónica en MIDAS
 Introducción a la Firma Electrónica en MIDAS Firma Digital Introducción. El Módulo para la Integración de Documentos y Acceso a los Sistemas(MIDAS) emplea la firma digital como método de aseguramiento
Introducción a la Firma Electrónica en MIDAS Firma Digital Introducción. El Módulo para la Integración de Documentos y Acceso a los Sistemas(MIDAS) emplea la firma digital como método de aseguramiento
amax=aω 2 ; β=10logi/io; ω=2πf;t=1/f; κ=1/λ; τ=ln2/λ; P=1/f (m);e p= gdr; N=Noe λt ; 1/f =1/s +1/s; Fc=mv 2 /r; y(x,t)=asen(ωt±kx); W=qΔV; F=qvxB;
 E=hf;p=mv;F=dp/dt;I=Q/t;Ec=mv 2 /2; TEMA 5: VIBRACIONES Y ONDAS F=KQq/r 2 ;L=rxp;x=Asen(ωt+φo);v=λf c 2 =1/εoµo;A=πr 2 ;T 2 =4π 2 /GMr 3 ;F=ma; L=dM/dtiopasdfghjklzxcvbvv=dr/dt; M=rxF;sspmoqqqqqqqqqqqp=h/λ;
E=hf;p=mv;F=dp/dt;I=Q/t;Ec=mv 2 /2; TEMA 5: VIBRACIONES Y ONDAS F=KQq/r 2 ;L=rxp;x=Asen(ωt+φo);v=λf c 2 =1/εoµo;A=πr 2 ;T 2 =4π 2 /GMr 3 ;F=ma; L=dM/dtiopasdfghjklzxcvbvv=dr/dt; M=rxF;sspmoqqqqqqqqqqqp=h/λ;
1. ACTIVIDAD ACADÉMICA MEDIDA DE CAUDALES Y DE PRESIONES
 1. ACTIVIDAD ACADÉMICA MEDIDA DE CAUDALES Y DE PRESIONES 1.1. Introducción 1.2. Descripción de la instalación fluidomecánica 1.3. Descripción de la actividad práctica propuesta Profesor: Inmaculada Pulido
1. ACTIVIDAD ACADÉMICA MEDIDA DE CAUDALES Y DE PRESIONES 1.1. Introducción 1.2. Descripción de la instalación fluidomecánica 1.3. Descripción de la actividad práctica propuesta Profesor: Inmaculada Pulido
[c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?.
![[c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?. [c] Qué energía mecánica posee el sistema muelle-masa? Y si la masa fuese 2 y la constante 2K?.](/thumbs/15/62431.jpg) Actividad 1 La figura representa un péndulo horizontal de resorte. La masa del bloque vale M y la constante elástica del resorte K. No hay rozamientos. Inicialmente el muelle está sin deformar. [a] Si
Actividad 1 La figura representa un péndulo horizontal de resorte. La masa del bloque vale M y la constante elástica del resorte K. No hay rozamientos. Inicialmente el muelle está sin deformar. [a] Si
Medias Móviles: Señales para invertir en la Bolsa
 www.gacetafinanciera.com Medias Móviles: Señales para invertir en la Bolsa Juan P López..www.futuros.com Las medias móviles continúan siendo una herramienta básica en lo que se refiere a determinar tendencias
www.gacetafinanciera.com Medias Móviles: Señales para invertir en la Bolsa Juan P López..www.futuros.com Las medias móviles continúan siendo una herramienta básica en lo que se refiere a determinar tendencias
FÍSICA Y QUÍMICA 4º ESO Ejercicios: Fuerzas
 1(10) Ejercicio nº 1 Durante cuánto tiempo ha actuado una fuerza de 20 N sobre un cuerpo de masa 25 Kg si le ha comunicado una velocidad de 90 Km/h? Ejercicio nº 2 Un coche de 1000 Kg aumenta su velocidad
1(10) Ejercicio nº 1 Durante cuánto tiempo ha actuado una fuerza de 20 N sobre un cuerpo de masa 25 Kg si le ha comunicado una velocidad de 90 Km/h? Ejercicio nº 2 Un coche de 1000 Kg aumenta su velocidad
EXPERIMENTOS Nos. 3 y 4 FENÓMENOS ELECTROSTÁTICOS
 EXPERIMENTO 1: Electrostática EXPERIMENTOS Nos. 3 y 4 FENÓMENOS ELECTROSTÁTICOS Objetivos Obtener cargas de distinto signo mediante varios métodos y sus características Uso del electroscopio como detector
EXPERIMENTO 1: Electrostática EXPERIMENTOS Nos. 3 y 4 FENÓMENOS ELECTROSTÁTICOS Objetivos Obtener cargas de distinto signo mediante varios métodos y sus características Uso del electroscopio como detector
ESTADÍSTICA SEMANA 4
 ESTADÍSTICA SEMANA 4 ÍNDICE MEDIDAS DE DISPERSIÓN... 3 APRENDIZAJES ESPERADOS... 3 DEfinición de Medida de dispersión... 3 Rango o Recorrido... 3 Varianza Muestral (S 2 )... 3 CÁLCULO DE LA VARIANZA...
ESTADÍSTICA SEMANA 4 ÍNDICE MEDIDAS DE DISPERSIÓN... 3 APRENDIZAJES ESPERADOS... 3 DEfinición de Medida de dispersión... 3 Rango o Recorrido... 3 Varianza Muestral (S 2 )... 3 CÁLCULO DE LA VARIANZA...
Funciones lineales. Objetivos. Antes de empezar. 1.Función de proporcionalidad directa pág. 170 Definición Representación gráfica
 10 Funciones lineales Objetivos En esta quincena aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
10 Funciones lineales Objetivos En esta quincena aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
P9: ENSAYO DE VACÍO Y CORTOCIRCUITO DEL TRANSFORMADOR MONOFÁSICO FUNDAMENTOS DE TECNOLOGÍA ELÉCTRICA
 ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
Anexo 4 Prueba de Cleaver La técnica y su fundamento teórico Cleaver encontró 13 factores críticos de puestos, que determinan la evaluación de una
 Anexo 4 Prueba de Cleaver La técnica y su fundamento teórico Cleaver encontró 13 factores críticos de puestos, que determinan la evaluación de una persona, básicamente en la selección de personal y que
Anexo 4 Prueba de Cleaver La técnica y su fundamento teórico Cleaver encontró 13 factores críticos de puestos, que determinan la evaluación de una persona, básicamente en la selección de personal y que
QUÉ ES UN NÚMERO DECIMAL?
 QUÉ ES UN NÚMERO DECIMAL? Un número decimal representa un número que no es entero, es decir, los números decimales se utilizan para representar a los números que se encuentran entre un número entero y
QUÉ ES UN NÚMERO DECIMAL? Un número decimal representa un número que no es entero, es decir, los números decimales se utilizan para representar a los números que se encuentran entre un número entero y
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 2012 Problemas (Dos puntos por problema).
 Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 01 Problemas (Dos puntos por problema). Problema 1 (Primer parcial): Suponga que trabaja para una gran compañía de transporte y que
Examen de Física-1, 1 Ingeniería Química Examen final. Septiembre de 01 Problemas (Dos puntos por problema). Problema 1 (Primer parcial): Suponga que trabaja para una gran compañía de transporte y que
EXPERIMENTOS PARA ESTUDIAR PROPIEDADES MECÁNICAS DE MATERIALES. Dirigida a docentes de las áreas Ciencia y Tecnología. Dra.
 EXPERIMENTOS PARA ESTUDIAR PROPIEDADES MECÁNICAS DE MATERIALES Dirigida a docentes de las áreas Ciencia y Tecnología Dra. Alicia Sarce INSTITUTO SABATO Universidad Nacional de General San Martín-Comisión
EXPERIMENTOS PARA ESTUDIAR PROPIEDADES MECÁNICAS DE MATERIALES Dirigida a docentes de las áreas Ciencia y Tecnología Dra. Alicia Sarce INSTITUTO SABATO Universidad Nacional de General San Martín-Comisión
INDICADOR : CONSUMO DE ÁCIDO.
 INDICADOR : CONSUMO DE ÁCIDO. Las empresas de recubrimientos metálicos utilizan ácidos para realizar el decapaje de las piezas. Este indicador pretende mostrar la tendencia en el consumo de estas sustancias.
INDICADOR : CONSUMO DE ÁCIDO. Las empresas de recubrimientos metálicos utilizan ácidos para realizar el decapaje de las piezas. Este indicador pretende mostrar la tendencia en el consumo de estas sustancias.
1.2 Algoritmo. Proceso de solución de un problema. Resolviendo problemas con la computadora. Programación
 Universidad Autónoma de Baja California Facultad de Ingeniería Mexicali Programación Unidad I - Metodología para la solución de s 1.2 Algoritmo 1. Definición de 2. Características de un 3. Pruebas de escritorio
Universidad Autónoma de Baja California Facultad de Ingeniería Mexicali Programación Unidad I - Metodología para la solución de s 1.2 Algoritmo 1. Definición de 2. Características de un 3. Pruebas de escritorio
ESTADOS DE AGREGACIÓN DE LA MATERIA
 ESADOS DE AGREGACIÓN DE LA MAERIA. Propiedades generales de la materia La materia es todo aquello que tiene masa y volumen. La masa se define como la cantidad de materia de un cuerpo. Se mide en kg. El
ESADOS DE AGREGACIÓN DE LA MAERIA. Propiedades generales de la materia La materia es todo aquello que tiene masa y volumen. La masa se define como la cantidad de materia de un cuerpo. Se mide en kg. El
BALANZA BARTOLO PAREDES ROBERTO
 BALANZA Es un instrumento que mide la masa de una sustancia o cuerpo, utilizando como medio de comparación la fuerza de la gravedad que actúa sobre dicha masa. Se debe tener en cuenta que el peso es la
BALANZA Es un instrumento que mide la masa de una sustancia o cuerpo, utilizando como medio de comparación la fuerza de la gravedad que actúa sobre dicha masa. Se debe tener en cuenta que el peso es la
Capítulo V APLICACIONES DE LAS FUNCIONES A LA ADMINISTRACIÓN
 Capítulo V APLICACIOES DE LAS FUCIOES A LA ADMIISTRACIÓ 5.1 ITRODUCCIÓ: Muchos problemas relacionados con la administración, la economía y las ciencias afines, además de la vida real, requieren la utilización
Capítulo V APLICACIOES DE LAS FUCIOES A LA ADMIISTRACIÓ 5.1 ITRODUCCIÓ: Muchos problemas relacionados con la administración, la economía y las ciencias afines, además de la vida real, requieren la utilización
Tema 8 Propiedades Mecánicas: curva Esfuerzo Deformación Unitaria.
 Tema 8 Propiedades Mecánicas: curva Esfuerzo Deformación Unitaria. Las propiedades mecánicas describen como se comporta un material cuando se le aplican fuerzas externas. Para propósitos de análisis, las
Tema 8 Propiedades Mecánicas: curva Esfuerzo Deformación Unitaria. Las propiedades mecánicas describen como se comporta un material cuando se le aplican fuerzas externas. Para propósitos de análisis, las
