CAPITULO 4. LA FORMA EN PLANTA DE LAS PLAYAS.
|
|
|
- Inés Roldán Quiroga
- hace 8 años
- Vistas:
Transcripción
1 CAPITULO INTRODUCCIÓN: MODELOS DE EVOLUCIÓN Y MODELOS DE EQUILIBRIO. El objetivo de los modelos de forma en planta de playas es la predicción de la misma, conocidos las condiciones de contorno y las características del oleaje y de los sedimentos. La separación entre modelos de evolución y modelos de equilibrios estriba en la escala de tiempos sobre la que se realiza la predicción. Los modelos de evolución, pretenden determinar el cambio de la línea de costa en la escala de los estados de mar, es decir, horas, mientras que los modelos de equilibrio determinan la forma en planta de equilibrio media en escalas de tiempo del orden meses o estaciones. En los siguientes apartados se analizará el modelo de evolución de una línea, y el modelo de forma en planta de equilibrio de González (1996). En ambos la playa se esquematiza por una línea batimétrica, en nuestro caso, la línea de pleamar MODELOS PREDICTIVOS PARA EL CAMBIO DE LA LÍNEA DE COSTA Un modelo de línea de costa es un modelo de predicción numérica basado en la ecuación de continuidad del sedimento y en una ecuación para el transporte longitudinal de sedimentos. Se denomina también Teoría de Una Línea (One Line Theory, OLT) para la predicción de la línea de costa, donde "Una Línea" se refiere a la línea de costa. El movimiento de sedimentos causado por el oleaje puede ser clasificado en dos tipos, según su dirección: Transporte longitudinal, a lo largo de la línea de costa, y transporte transversal, perpendicular a ella. Salvo en determinados casos como puede ser la caída del sedimento en cañones submarinos, o el transporte de sedimento hacia tierra por el viento, a largo plazo, el transporte transversal está confinado en una franja de costa. Esta franja esta limitada entre la línea de máximo ascenso en el período invernal (cuando la playa se encuentra en estado disipativo) y la zona donde el oleaje ya no es capaz de poner en movimiento el sedimento. Para predicciones a largo plazo, la mayor parte de la información del cambio de la línea de costa viene dada por el transporte longitudinal de sedimentos. Ya que las ecuaciones del transporte longitudinal de sedimentos dependen de las características del oleaje, en el modelo de línea de costa será necesario determinar las variaciones longitudinales de aquél mediante modelos de refracción-difracción. El cambio de línea de costa que se produce en un intervalo de tiempo, podrá ser calculado a partir de las diferencias en el caudal de transporte longitudinal, suponiendo que el perfil de la playa se mueve paralelamente a si mismo. En el caso de que se produzcan pérdidas o aportaciones puntuales de sedimento, podrán ser 1
2 tenidas en cuenta igualmente en el modelo. En el modelo mas general, será necesario tener en cuenta la interacción entre el modelo de oleaje y el de línea de costa, pues aquél modifica las características del oleaje a medida que cambia la línea de costa. El modelo de línea de costa sólo debe ser utilizado para la predicción espacial a media y gran escala. Es especialmente adecuado para determinar el efecto de espigones, diques exentos, aportaciones puntuales de sedimento (deltas), etc. Este modelo no puede describir la formación del perfil de playa ni determinar por lo tanto los cambios estacionales del perfil, erosiones por muros de protección y otros cambios que involucren transporte transversal de sedimentos. Asimismo, no determinará las formas de media (megacusps o cusps) escala, al no quedar definidas por las ecuaciones del transporte longitudinal. El modelo OLT fue desarrollado originalmente por Pernald-Considere (1956), para examinar el cambio de la línea de costa debido a un espigón. Supuso que el caudal de transporte longitudinal era proporcional al ángulo de incidencia del oleaje. Los resultados se ajustaron bien con los de ensayos de laboratorio. Bakker (1968) y Bakker, Klein, Breteler y Roos (1970) ampliaron el modelo a dos líneas (Two Line Theory, TLT), para describir los movimientos transversales de la batimetría. El cambio de la playa se expresa en el TLT mediante dos líneas; una de ellas representa el movimiento de las batimétricas en la zona de rompientes y la otra el cambio de las mismas mar adentro de la zona de rotura. El transporte transversal de sedimentos se da como una función de la distancia entre las dos líneas, de manera que el sedimento se mueve hacia el mar en una playa de talud muy pendiente y hacia tierra en playas de taludes suaves. El procedimiento para la aplicación de los modelos de cambio de línea de costa se puede resumir de la manera siguiente, ver diagrama 1: 1º Recopilación y análisis de los datos disponibles de oleaje (series de estados de mar) y perfil de playa. 2º Condiciones de contorno. 3º Propagación del oleaje: altura de ola y dirección en el punto de rotura a lo largo de la línea de costa, utilizando un modelo de refracción- difracción. 4º Cálculo del caudal de transporte longitudinal de sedimentos a lo largo de la línea de costa, utilizando alguna de las formulaciones existentes. 5º Cálculo del cambio de la línea de costa mediante la ecuación de la conservación del sedimento. Calculada la nueva línea de costa, se vuelve a empezar en el punto 2º, dándose por terminada la iteración cuando se terminan las series de estados de mar o se alcanza un equilibrio o una determinada posición de la línea de costa. 2
3 N ESTADOS DE MAR, Hsi, Tsi BATIMETRÍA DATOS SEDIMENTO: ρ s, D n50, n DATOS DEL PERFIL PROFUNDIDAD DE CORTE ESTADO DE MAR E, DURACIÓN D MODELO DE PROPAGACIÓN DE OLEAJE MODELO DE TRANSPORTE DE SEDIMENTOS PASO DE TIEMPO DEL MODELO DE UNA LINEA, T MODIFICACIÓN DE LA LÍNEA DE COSTA T = D? NO SI E=N? SI FIN Diagrama 1. Diagrama de flujo del modelo de una línea 3
4 4.3. MODELOS DE EQUILIBRIO PARA LA LÍNEA DE COSTA Introducción. Los modelos de evolución de la forma en planta de playas como es el caso del de una línea descrito en los apartados anteriores, permiten determinar el cambio de la línea de costa en escalas de tiempo del orden de los estados de mar. Debido a esta capacidad, estos modelos son adecuados para la determinación de cambios rápidos en las playas, provocados por modificaciones de las condiciones de contorno, como puede ser, una realimentación o la construcción de diques y espigones. Una vez que la playa a sufrido los cambios impuestos por las nuevas condiciones de contorno, su evolución posterior en planta, debida a los cambios del oleaje son, en general de pequeña magnitud. Se dice entonces que la playa a alcanzado una situación de equilibrio en planta. Aunque siempre se puede utilizar un modelo de una línea para determinar la situación de equilibrio de una playa, es mucho más rápido la utilización de modelos semiempíricos de equilibrio, que permiten determinar la citada forma en planta de equilibrio a partir de las condiciones de contorno y de las características medias del oleaje. Estos modelos de equilibrio en planta asumen que el transporte neto longitudinal en cada sección de la playa es nulo, por lo que sólo son válidos para playas encajadas. En playas con desequilibrio dinámico, como es el caso de los puntales en las desembocaduras, estos modelos no pueden ser aplicados. Los modelos de forma en planta de equilibrio se aplican en escalas de tiempo de largo plazo (estaciones o años) y gran escala (forma en planta general) y se basan en la parametrización de la forma en planta de la playa según una determinada curva, cuyas características dependen de las condiciones de contorno y del oleaje medio que aborda la playa. Al indicar que se aplica a playas encajadas, se asume que no existen entradas ni salidas de sedimento fuera del sistema limitado por la costa y la profundidad de corte. Estos modelos son de tipo empírico y simples de aplicación Historia y tipos de modelos. En la bibliografía existe un extensa gama de modelos para la definición de la forma en planta de equilibrio de las playas. Hasta la propuesta de González (1995), las curvas propuesta para la forma en planta de equilibrio eran capaces de ajustar las formas de planta observadas en playas existentes, pero carecían de capacidad de predicción, es decir no permitían definir la forma en planta futura de una playa tras una determinada actuación. Como puede observarse en la tabla 2, los modelos propuestos se basan en elipses, espirales logarítmicas y parábolas. De entre los modelos propuestos, el de parábolas de Hsu y Evans (1989) es el que mejor permite el ajuste de la forma en planta de las playas. El único autor que propone una metodología de predicción de la forma en planta de playas es González (1995), 4
5 basada en el modelo parabólico de Hsu y Evans. Autores Años Características Mashima 1961 Elipses Yasso 1965 Espirales logarítmicas Vichetpan Ho Silvester Espirales logarítmicas. Relaciones geometría oleaje. Problema: definición del centro de la espiral. Hsu 1987 Demuestra que las espirales logarítmicas no son adecuadas. Propone un modelo parabólico. Hsu y Evans 1989 Modelo parabólico dependiente de la oblicuidad del oleaje. Demuestra su buen ajuste a playas naturales. Hsu, Silvester 1990 Aplican el modelo parabólico a tómbolos con incidencia normal. Mc Cormick 1993 Estudia los salientes y tómbolos formados por diques exentos. Estudia la influencia del peralte del oleaje, pendiente de la playa y ángulo de incidencia. Propone un modelo elíptico. Tan y Chiew 1994 Mediante ensayos validan el modelo de Hsu y Evans. Como variable principal proponen el ángulo de incidencia del oleaje González 1995 Propone una metodología para el diseño de la forma en planta de equilibrio de nuevas playas, basada en el modelo parabólico de Hsu y Evans. Tabla 2. Características de los modelos de forma en planta de equilibrio Modelo para la predicción de la forma en planta de equilibrio. La forma en planta de una playa viene condicionada, principalmente, por el sistema de corrientes asociado a la rotura del oleaje, por el sedimento existente (cantidad y tamaño) y por los contornos o geometría donde ha de encajarse la playa. Las corrientes longitudinales son de especial importancia para la forma de equilibrio de la planta de la playa, dado su importancia en el transporte de sedimentos. Bajo la hipótesis de que la playa alcanza un estado de equilibrio estático cuando las corrientes longitudinales se anulan en todos los puntos de la playa, González (1995) llega a la siguiente ecuación diferencial para la línea de costa: xs = xb + K2 Hb donde la forma en planta de la costa de equilibrio, x s, se define por la forma en planta de la curva de rotura del oleaje, x b mas una cantidad proporcional al gradiente longitudinal de la altura de ola en rotura. Cuando un oleaje incide en una barrera o dique, ver figura 1, se presentan efectos de refracción y difracción detrás del mismo, quedando definidas tres regiones desde el punto de vista del oleaje: región 1, donde no existe efecto del dique sobre el oleaje y los gradientes de 5
6 altura de ola en rotura son nulos, región 2, donde los frentes no se ven modificados en su dirección de propagación, pero la difracción en el dique crea un gradiente longitudinal de altura de ola y región 3, donde la refracción y la difracción se combinan para alterar tanto la dirección de propagación de los frentes como para alterar la altura de ola en rotura. El punto P o de la figura 1, corresponde al límite entre las regiones 1 y 2. En la región 1, la línea de costa coincide con la curva en planta del oleaje en rotura, x s = x b. Figura 1. Esquema general de una playa encajada en equilibrio estático. Al aplicar el modelo parabólico de Hsu y Evans (1989) a las playas del litoral español, González (1995) comprobó que dicho modelo parabólico sólo era aplicable a las regiones 2 y 3, es decir, en las zonas donde el dique altera el oleaje que alcanza la playa. El punto P 0 define pues el inicio de la zona donde es aplicable el modelo parabólico. Para poder definir tal punto, es necesario determinar el ángulo α min y la distancia Y a la cual se encuentra la playa. Para la determinación del α min en playas reales, González recopiló información de playas de la costa española (Atlántica y Mediterránea) en situación de equilibrio, y en las cuales existiera las tres regiones anteriormente citadas. Para la adimensionalización de la distancia Y, se utilizó la longitud de onda media (entre la profundidad del punto de difracción y la costa), L, correspondiente al periodo T z12, que se obtiene a partir de la relación dada por la ROM 03-91entr la altura de ola H s12 en temporales y el periodo. La expresión de mejor ajuste para α min es: 1/ β r β r Y min arctan L α = ; con β r = 2.13 ( 1) Y / L 6
7 Metodología propuesta por González (1995) para la forma en planta de equilibrio. Como se ha indicado, González propone la utilización de la parábola de Hsu y Evans (1989), dada por la expresión: R R 0 = C 0 + C 1 β + C θ 2 β θ 2 para la forma en planta de la playa afectada por la difracción refracción. Los coeficientes C i, fueron dados por Silvestre y Hsu (1993) y se obtienen de la tabla 3. La definición para R, β=90- α min y θ se indica en la figura 2. La metodología propuesta por González para la definición de la forma en planta de equilibrio es la siguiente (ver figura 2). 1- Determinar la orientación del flujo medio de energía en el punto de difracción. 2- Definir dentro de la zona afectada por la difracción, un punto, P c, de la línea de costa. Dicho punto puede ser una imposición a priori (por ejemplo por una condición de anchura de playa), o puede ser consecuencia de una condición de contorno, por ejemplo, el máximo avance que puede tener la línea de costa en el apoyo contra un espigón, en cuyo caso será necesario inscribir el perfil. 3- Determinar, aproximadamente, la distancia, Y, entre el punto de difracción y la proyección, en la dirección del flujo medio de energía, de la futura línea de costa no afectada por la zona de difracción. 7
8 β Figura 34. Ajuste del α min para varias playas españolas. θ = Tabla 3. Coeficientes C 0, C 1 y C 2 en función de β y valores de R/R 0 en función del ángulo 8
9 Rc Frente de onda del flujo medio de energía Y b q c Ro amin Playa paralela al frente Pc Figura 2. Definición de las variables para la determinación de la forma en planta de equilibrio. 4- Calcular la longitud de onda media, L, asociada al período T s12 y a la profundidad media existente entre el punto de difracción y la futura línea de costa, en el límite de difracción. El período T s12 es el correspondiente a la H s12 a través de la relación dada por la ROM para temporales. 5- Calcular el α min, correspondiente al Y/L, utilizando la figura 2 o la expresión (23). Calcular β = 90 -α min y los coeficientes C 1, C 2 y C 3 de la parábola de Silvester y Hsu (1993) (Tabla 3). 6- Calcular el R c y el θ c correspondiente al punto P c. 7- Aplicar la ecuación de la parábola de Silvester y Hsu al punto P c. Despejar el valor de R 0 : R 0 = C 0 c R c β + C1 + C θ 2 β θc 2 8- Dibujar el resto de la línea de costa, utilizando la parábola de Silvester y Hsu, entre θ = β y la estructura que provoca la difracción. 9
10 Ejemplos de aplicación. La metodología descrita en el apartado anterior se ha aplicado a varias playas del Cantábrico y Mediterráneo, tanto para la línea de costa en pleamar como para la de bajamar, obteniéndose muy buenos resultados. Figura 3. Forma en planta de equilibrio de la playa de la ensenada de Urdiales, Cantabria. Playa de Urdiales (Cantabria). La playa de la ensenada de Urdiales es una playa construida mediante la realimentación con arenas de cantera del fondo de la ensenada rocosa de Urdiales. En la figura 3 se compara la forma en planta obtenida mediante la metodología anterior con la forma en planta de equilibrio final. Como puede verse, la zona central de la playa responde a un punto de difracción externo, mientras que los extremos Noroeste y Sureste responden a puntos de difracción mas cercanos, correspondientes a salientes del interior de la ensenada. Playas del Sardinero (Cantabria). Las playas del Sardinero, en Santander, son playas naturales, cuya forma en planta está determinada por la difracción e Cabo Menor. En la figura 4 se ha dibujado la forma en planta correspondiente. Como puede verse en la figura, el método predice la forma en planta de la playa del Camello, situada en el extremo Sureste de la playa. Esta playa no es natural, sino que se obtuvo realimentando con arenas de dragado la ensenada rocosa. 10
11 Figura 4. Forma en planta de equilibrio de las playas del Sardinero, Cantabria. Playa de la Salvé de Laredo (Cantabria). La playa de la Salvé de Laredo es un extenso puntal arenoso generado en la desembocadura del río Asón, al abrigo del monte Buciero. En su extremo Noroeste, la playa queda interrumpida por la bocana de las marismas de Santoña. En dicha bocana, los flujos y reflujos de la marea mantienen abierta una canal con profundidades del orden de los 10 m en bajamar. En el lado del mar de la bocana, los sedimentos transportados en el reflujo generan el extenso bajo de San Carlos, con profundidades en bajamar inferiores a los 4 m. Este bajo se extiende hasta la playa, generando un saliente en la misma. Desde el bajo hasta el puntal, la playa esta en equilibrio dinámico, es decir con transporte neto no nulo, con dirección del transporte hacia el puntal. El sedimento en esta zona cierra un ciclo bajo puntal bajo, en equilibrio dinámico. La parte Este de la playa, en las proximidades del puerto de Laredo, tiene su forma en planta determinada por la difracción producida por los diques del puerto. En la figura 5 se ha dibujado la forma en planta de equilibrio correspondiente a un punto de difracción situado en los acantilados del Buciero. Como puede verse, solo la zona central y este de la playa siguen la forma en planta de equilibrio, pues la zona Noroeste desde el saliente del bajo de San Carlos hasta el Puntal, son zonas en desequilibrio dinámico, debido al flujo mareal. En este extremo de la playa no es aplicable el modelo propuesto, en el que se asume equilibrio estático del transporte. 11
12 Figura 5. Forma en planta de equilibrio de la playa de la Salvé, en Cantabria. Playa del Puntal de Santander. La playa del Puntal de Santander es una flecha situada en la entrada de la bahía de Santander. Su extremo Oeste está controlado por la difracción desde la península de la Magdalena, mientras que su extremo Este lo controla la difracción provocada por la isla de Santamarina. En este caso, al contrario que en el puntal de Laredo, los continuos dragados de mantenimiento de la canal de navegación han eliminado el bajo de la Quebrantas, existente antiguamente en la zona de expansión del reflujo de marea. Estas actividades de dragado se manifiestan claramente al dibujar la forma en planta de equilibrio, figura 6, que muestra como el extremo Oeste está completamente desequilibrado (o en equilibrio dinámico). En esta zona, el transporte neto no es nulo, existiendo un bucle Puntal dragado playa (el sedimento se retorna a la playa). 12
13 Figura 6. Forma en planta de equilibrio del Puntal de Santander, Cantabria Predicción de la forma en planta de equilibrio debida a diques exentos. Los diques exentos, impermeables y paralelos a la línea de costa, reducen efectivamente la cantidad de energía del oleaje incidente y se utilizan con profusión para modificar la forma de la línea de costa. Uno de los problemas mas importantes en el diseño de estas estructuras es la predicción de la respuesta de la citada línea de costa. González (1996), propuso extender la metodología anteriormente propuesta al estudio de la forma en planta de equilibrio generada por estas estructuras, para el caso de incidencia normal del oleaje, parametrizando las soluciones obtenidas, que se representan en una serie de gráficas. En el caso de incidencia oblicua, la metodología se puede aplicar igualmente, aunque no esta parametrizada la respuesta. Para el caso de incidencia normal, la respuesta de la playa, figuras 7 a-c puede definirse por tres tipos distintos: Tómbolo, figura 7a: Las parábolas correspondientes a cada punto de difracción no se cortan y alcanzan el dique, que de esta manera queda unido a la playa. Saliente, figura 7b: En este caso, las parábolas correspondientes a cada punto de difracción se cortan una vez, provocando un saliente en la playa. 13
14 Doble saliente, figura 7c: Las parábolas se cortan en dos puntos, generando un saliente en la playa y otro en el dique. a b c Figura 7. Parametrización de las formas de playa generadas por un dique exento: a) Tómbolo, b) saliente y c) doble saliente. En la figura 7. se definen las características geométricas de las formas generadas. En el eje horizontal se dibuja la distancia adimensional desde el dique hasta la costa original, Y/L y en el eje vertical se dispone la semianchura adimensional del dique, B/L. Según donde se encuentren las coordenadas Y/L y B/L, tendremos tómbolo, doble saliente o saliente. En el caso de coordenadas en la zona de tómbolo, el gráfico suministra la semianchura adimensional de la playa en el dique, B K /B y la semianchura del tómbolo en la playa, B 1 /L. En el caso de coordenadas en la zona de doble saliente, el gráfico 8 suministra la altura adimensional del saliente en la costa, Y 1 /Y y la semianchura del saliente en la costa, B 1 /L. Obtenidos estos valores, la gráfica permite determinar la altura del saliente en el dique, Y 2 /Y y la semianchura del saliente en el dique, B k /B. En el caso de coordenadas en la zona de saliente, la gráfica 9 permite determinar la semianchura del saliente en la costa, B 1 /L y la altura del mismo, Y 0 /Y. 14
15 Figura 8. Diagrama para la determinación de las características geométricas de tómbolos, dobles salientes y salientes. 15
16 BK/B Figura 9. Diagrama para la determinación de las características geométricas de dobles salientes. 16
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
Potencial eléctrico. du = - F dl
 Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
0.01 0.4 4. Operando sobre esta relación, se obtiene
 ORGANIZACIÓN INDUSTRIAL (16691-ECO) TEMA 1: LA COMPETENCIA PERFECTA EN UN MARCO DE EQUILIBRIO PARCIAL 1.1 ANÁLISIS DE LA ESTÁTICA COMPARATIVA DE UN MERCADO COMPETITIVO SOLUCIÓN A LOS PROBLEMAS PROPUESTOS
ORGANIZACIÓN INDUSTRIAL (16691-ECO) TEMA 1: LA COMPETENCIA PERFECTA EN UN MARCO DE EQUILIBRIO PARCIAL 1.1 ANÁLISIS DE LA ESTÁTICA COMPARATIVA DE UN MERCADO COMPETITIVO SOLUCIÓN A LOS PROBLEMAS PROPUESTOS
PRISMA OBLICUO > REPRESENTACIÓN Y DESARROLLO POR EL MÉTODO DE LA SECCIÓN NORMAL
 1. CARACTERÍSTICAS GENERALES DEL PRISMA OBLICUO Desde el punto de vista de la representación en SISTEMA DIÉDRICO, el prisma oblicuo presenta dos características importantes que lo diferencian del prisma
1. CARACTERÍSTICAS GENERALES DEL PRISMA OBLICUO Desde el punto de vista de la representación en SISTEMA DIÉDRICO, el prisma oblicuo presenta dos características importantes que lo diferencian del prisma
1.1 Probetas de sección cuadrada
 ANEXOS En este apartado se muestran todas las gráficas de todos los ensayos realizados en cada uno de los planos. 1.1 Probetas de sección cuadrada Con este tipo de ensayos se pretende estudiar si los resultados
ANEXOS En este apartado se muestran todas las gráficas de todos los ensayos realizados en cada uno de los planos. 1.1 Probetas de sección cuadrada Con este tipo de ensayos se pretende estudiar si los resultados
Resolución de problemas. Temas: VOR e ILS
 Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES
 CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
Dinamica de Fluidos: Principio de Bernoulli. Aplicaciones
 Dinamica de Fluidos: Principio de Bernoulli. Aplicaciones Cuando un fluido está en movimiento, el flujo se puede clasificar en dos tipos: a) Flujo estacionario o laminar si cada partícula de fluido sigue
Dinamica de Fluidos: Principio de Bernoulli. Aplicaciones Cuando un fluido está en movimiento, el flujo se puede clasificar en dos tipos: a) Flujo estacionario o laminar si cada partícula de fluido sigue
35 Facultad de Ciencias Universidad de Los Andes Mérida-Venezuela. Potencial Eléctrico
 q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
4. LA ENERGÍA POTENCIAL
 4. LA ENERGÍA POTENCIAL La energía potencial en un punto es una magnitud escalar que indica el trabajo realizado por las fuerzas de campo para traer la carga desde el infinito hasta ese punto. Es función
4. LA ENERGÍA POTENCIAL La energía potencial en un punto es una magnitud escalar que indica el trabajo realizado por las fuerzas de campo para traer la carga desde el infinito hasta ese punto. Es función
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
EL PUERTO DE AGUETE Y LA PLAYA
 NOTA INFORMATIVA Aguete, 27 enero 2014. EL PUERTO DE AGUETE Y LA PLAYA El Real Club de Mar de Aguete es una sociedad Marinense sin ánimo de lucro, que lleva 40 años en la ensenada de Aguete y cuenta como
NOTA INFORMATIVA Aguete, 27 enero 2014. EL PUERTO DE AGUETE Y LA PLAYA El Real Club de Mar de Aguete es una sociedad Marinense sin ánimo de lucro, que lleva 40 años en la ensenada de Aguete y cuenta como
Estudio de las fuerzas actuantes en la interacción de un disco en rotación con un campo magnético estacionario.
 Estudio de las fuerzas actuantes en la interacción de un disco en rotación con un campo magnético estacionario. Sebastián Arroyo, Tomas Riccardi (Marzo 2011) Se estudió el fenómeno de interacción magnética
Estudio de las fuerzas actuantes en la interacción de un disco en rotación con un campo magnético estacionario. Sebastián Arroyo, Tomas Riccardi (Marzo 2011) Se estudió el fenómeno de interacción magnética
Nombre:..Curso:.. GUIA DE TRABAJO Y POTENCIA MECANICA. Un niño traslada una caja desde el punto A al punto B recorriendo 4 m (fig.
 Nombre:..Curso:.. GUIA DE TRABAJO Y POTENCIA MECANICA Trabajo realizado por una fuerza. Un niño traslada una caja desde el punto A al punto B recorriendo 4 m (fig. N 1), fig N 1 Desde el punto de vista
Nombre:..Curso:.. GUIA DE TRABAJO Y POTENCIA MECANICA Trabajo realizado por una fuerza. Un niño traslada una caja desde el punto A al punto B recorriendo 4 m (fig. N 1), fig N 1 Desde el punto de vista
Comparaciones de pobreza y desigualdad
 Comparaciones de pobreza y desigualdad El problema de la pobreza en una sociedad puede ser evaluado desde tres perspectivas complementarias entre sí : Las medidas de incidencia. Informan acerca de la extensión
Comparaciones de pobreza y desigualdad El problema de la pobreza en una sociedad puede ser evaluado desde tres perspectivas complementarias entre sí : Las medidas de incidencia. Informan acerca de la extensión
WAVENERGY La energía del Océano
 WAVENERGY La energía a del Océano La energía a del Océano - Introducción La energía a de los océanos se presenta con una gran perspectiva de futuro, ya que el recurso de los mares es el menos explotado
WAVENERGY La energía a del Océano La energía a del Océano - Introducción La energía a de los océanos se presenta con una gran perspectiva de futuro, ya que el recurso de los mares es el menos explotado
ASPECTOS GENERALES PARA LA SOLUCIÓN DE PROBLEMAS RELACIONADOS CON LA CONDUCCIÓN TRANSITORIA.
 CONDUCCIÓN TRANSITORIA Aquí encontrarás Los métodos gráficos y el análisis teórico necesario para resolver problemas relacionados con la transferencia de calor por conducción en estado transitorio a través
CONDUCCIÓN TRANSITORIA Aquí encontrarás Los métodos gráficos y el análisis teórico necesario para resolver problemas relacionados con la transferencia de calor por conducción en estado transitorio a través
Informe técnico S-23/2012
 Informe técnico S-23/2012 Investigación del accidente del pesquero SIEMPRE DIABLILLO, en la ría de San Martín de la Arena (Cantabria), el 21 de abril de 2011 ADVERTENCIA Este informe ha sido elaborado
Informe técnico S-23/2012 Investigación del accidente del pesquero SIEMPRE DIABLILLO, en la ría de San Martín de la Arena (Cantabria), el 21 de abril de 2011 ADVERTENCIA Este informe ha sido elaborado
ENSAYOS MECÁNICOS II: TRACCIÓN
 1. INTRODUCCIÓN. El ensayo a tracción es la forma básica de obtener información sobre el comportamiento mecánico de los materiales. Mediante una máquina de ensayos se deforma una muestra o probeta del
1. INTRODUCCIÓN. El ensayo a tracción es la forma básica de obtener información sobre el comportamiento mecánico de los materiales. Mediante una máquina de ensayos se deforma una muestra o probeta del
1 Estática Básica Prohibida su reproducción sin autorización. CONCEPTOS DE FISICA MECANICA. Conceptos de Física Mecánica
 1 CONCEPTOS DE FISICA MECANICA Introducción La parte de la física mecánica se puede dividir en tres grandes ramas de acuerdo a lo que estudia cada una de ellas. Así, podemos clasificarlas según lo siguiente:
1 CONCEPTOS DE FISICA MECANICA Introducción La parte de la física mecánica se puede dividir en tres grandes ramas de acuerdo a lo que estudia cada una de ellas. Así, podemos clasificarlas según lo siguiente:
METODOLOGÍA DE LA OPERACIÓN ESTADÍSTICA DE MOVIMIENTOS MIGRATORIOS
 METODOLOGÍA DE LA OPERACIÓN ESTADÍSTICA DE MOVIMIENTOS MIGRATORIOS 1. Introducción Las migraciones son un componente fundamental en la dinámica de los procesos de cambio de la población, de su crecimiento
METODOLOGÍA DE LA OPERACIÓN ESTADÍSTICA DE MOVIMIENTOS MIGRATORIOS 1. Introducción Las migraciones son un componente fundamental en la dinámica de los procesos de cambio de la población, de su crecimiento
UNIVERSIDAD DE CANTABRIA TESIS DOCTORAL
 UNIVERSIDAD DE CANTABRIA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS TESIS DOCTORAL Desarrollo de una metodología para el estudio de la morfología de playas basado en mapas auto-organizativos
UNIVERSIDAD DE CANTABRIA ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS TESIS DOCTORAL Desarrollo de una metodología para el estudio de la morfología de playas basado en mapas auto-organizativos
Vectores no colineales.
 Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
www.fundibeq.org Es de aplicación a aquellos estudios o situaciones en que es necesario priorizar entre un conjunto de elementos.
 GRAÁFICOS DE GESTIÓON (LINEALES, BARRAS Y TARTAS) 1.- INTRODUCCIÓN Este documento introduce los Gráficos de Gestión de uso más común y de mayor utilidad: Gráficos Lineales, Gráficos de Barras y Gráficos
GRAÁFICOS DE GESTIÓON (LINEALES, BARRAS Y TARTAS) 1.- INTRODUCCIÓN Este documento introduce los Gráficos de Gestión de uso más común y de mayor utilidad: Gráficos Lineales, Gráficos de Barras y Gráficos
Resistencia de Materiales
 Tema 5 - Deflexión en Vigas Resistencia de Materiales Tema 5 Deflexión en vigas Sección 1 - Ecuación diferencial de la elástica Ecuación diferencial de la elástica Para comenzar este tema se debe recordar
Tema 5 - Deflexión en Vigas Resistencia de Materiales Tema 5 Deflexión en vigas Sección 1 - Ecuación diferencial de la elástica Ecuación diferencial de la elástica Para comenzar este tema se debe recordar
d s = 2 Experimento 3
 Experimento 3 ANÁLISIS DEL MOVIMIENTO EN UNA DIMENSIÓN Objetivos 1. Establecer la relación entre la posición y la velocidad de un cuerpo en movimiento 2. Calcular la velocidad como el cambio de posición
Experimento 3 ANÁLISIS DEL MOVIMIENTO EN UNA DIMENSIÓN Objetivos 1. Establecer la relación entre la posición y la velocidad de un cuerpo en movimiento 2. Calcular la velocidad como el cambio de posición
UNIDAD 6 Fotogrametría
 UNIDAD 6 Fotogrametría La fotogrametría es la técnica de obtener mediciones reales de un objeto por medio de la fotografía, tanto aérea como terrestre Las fotografías se las realiza con una cámara métrica
UNIDAD 6 Fotogrametría La fotogrametría es la técnica de obtener mediciones reales de un objeto por medio de la fotografía, tanto aérea como terrestre Las fotografías se las realiza con una cámara métrica
Geometría Tridimensional
 Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
FISICA Y QUÍMICA 4º ESO 1.- TRABAJO MECÁNICO.
 1.- TRABAJO MECÁNICO. Si a alguien que sostiene un objeto sin moverse le preguntas si hace trabajo, probablemente te responderá que sí. Sin embargo, desde el punto de vista de la Física, no realiza trabajo;
1.- TRABAJO MECÁNICO. Si a alguien que sostiene un objeto sin moverse le preguntas si hace trabajo, probablemente te responderá que sí. Sin embargo, desde el punto de vista de la Física, no realiza trabajo;
Mecánica Racional 20 TEMA 3: Método de Trabajo y Energía.
 INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
INTRODUCCIÓN. Mecánica Racional 20 Este método es útil y ventajoso porque analiza las fuerzas, velocidad, masa y posición de una partícula sin necesidad de considerar las aceleraciones y además simplifica
1. Magnitudes vectoriales
 FUNDACIÓN INSTITUTO A DISTANCIA EDUARDO CABALLERO CALDERON Espacio Académico: Física Docente: Mónica Bibiana Velasco Borda mbvelascob@uqvirtual.edu.co CICLO: V INICADORES DE LOGRO VECTORES 1. Adquiere
FUNDACIÓN INSTITUTO A DISTANCIA EDUARDO CABALLERO CALDERON Espacio Académico: Física Docente: Mónica Bibiana Velasco Borda mbvelascob@uqvirtual.edu.co CICLO: V INICADORES DE LOGRO VECTORES 1. Adquiere
Fundamentos de Energía Solar Térmica
 Fundamentos de Energía Solar Térmica SOLARIMETRÍA Emiliano Sierra CI 4230513-5 Nov. 2010 OBJETIVO Estimar la irradiación global en plano inclinado a partir de medidas de irradiación en plano horizontal
Fundamentos de Energía Solar Térmica SOLARIMETRÍA Emiliano Sierra CI 4230513-5 Nov. 2010 OBJETIVO Estimar la irradiación global en plano inclinado a partir de medidas de irradiación en plano horizontal
ESTÁTICA 2. VECTORES. Figura tomada de http://www.juntadeandalucia.es/averroes/~04001205/fisiqui/imagenes/vectores/473396841_e1de1dd225_o.
 ESTÁTICA Sesión 2 2 VECTORES 2.1. Escalares y vectores 2.2. Cómo operar con vectores 2.2.1. Suma vectorial 2.2.2. Producto de un escalar y un vector 2.2.3. Resta vectorial 2.2.4. Vectores unitarios 2.2.5.
ESTÁTICA Sesión 2 2 VECTORES 2.1. Escalares y vectores 2.2. Cómo operar con vectores 2.2.1. Suma vectorial 2.2.2. Producto de un escalar y un vector 2.2.3. Resta vectorial 2.2.4. Vectores unitarios 2.2.5.
EL MAPA TOPOGRÁFICO curva de nivel
 EL MAPA TOPOGRÁFICO El mapa topográfico es una representación de la superficie terrestre mediante curvas de nivel que tiene como finalidad mostrar las variaciones del relieve de la Tierra. Además de las
EL MAPA TOPOGRÁFICO El mapa topográfico es una representación de la superficie terrestre mediante curvas de nivel que tiene como finalidad mostrar las variaciones del relieve de la Tierra. Además de las
Movilidad habitual y espacios de vida en España. Una aproximación a partir del censo de 2001
 Movilidad habitual y espacios de vida en España. Una aproximación a partir del censo de 2001 Centre d Estudis Demogràfics (Universitat Autònoma de Barcelona) Dirección de la investigación: Marc Ajenjo
Movilidad habitual y espacios de vida en España. Una aproximación a partir del censo de 2001 Centre d Estudis Demogràfics (Universitat Autònoma de Barcelona) Dirección de la investigación: Marc Ajenjo
SISTEMA DIÉDRICO PARA INGENIEROS. David Peribáñez Martínez DEMO
 SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez Valderrebollo 20, 1 A 28031 MADRID 1ª Edición Ninguna parte de esta publicación, incluido
SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez SISTEMA DIÉDRICO PARA INGENIEROS David Peribáñez Martínez Valderrebollo 20, 1 A 28031 MADRID 1ª Edición Ninguna parte de esta publicación, incluido
OPTIMIZACIÓN DEL AISLAMIENTO ACÚSTICO A RUIDO AÉREO EN SISTEMAS DE DOBLE PARED DE YESO LAMINADO Y LANA DE ROCA.
 OPTIMIZACIÓN DEL AISLAMIENTO ACÚSTICO A RUIDO AÉREO EN SISTEMAS DE DOBLE PARED DE YESO LAMINADO Y LANA DE ROCA. José Carlos Aguilar ROCKWOOL PENINSULAR S.A. C/Bruc, nº 50-3ª, 08010 Barcelona; tel: 93.318.9028;
OPTIMIZACIÓN DEL AISLAMIENTO ACÚSTICO A RUIDO AÉREO EN SISTEMAS DE DOBLE PARED DE YESO LAMINADO Y LANA DE ROCA. José Carlos Aguilar ROCKWOOL PENINSULAR S.A. C/Bruc, nº 50-3ª, 08010 Barcelona; tel: 93.318.9028;
Glosario del itinerario II
 Glosario del itinerario II Altura del punto de vista: (Véase Altura) Altura o altura del punto de vista: Distancia a la que se sitúa el punto de vista con respecto al suelo o plano geometral (véase). Arco
Glosario del itinerario II Altura del punto de vista: (Véase Altura) Altura o altura del punto de vista: Distancia a la que se sitúa el punto de vista con respecto al suelo o plano geometral (véase). Arco
MICRÓFONOS. Conceptos básicos
 MICRÓFONOS Conceptos básicos Un micrófono es un dispositivo capaz de convertir la energía acústica en energía eléctrica. El valor de la tensión de la energía eléctrica es proporcional a la presión ejercida
MICRÓFONOS Conceptos básicos Un micrófono es un dispositivo capaz de convertir la energía acústica en energía eléctrica. El valor de la tensión de la energía eléctrica es proporcional a la presión ejercida
Unidad: Representación gráfica del movimiento
 Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
ELASTICIDAD. Determinar experimentalmente el módulo de elasticidad de un material usando una viga.
 ELASTICIDAD OBJETIVOS Observar el fenómeno de deformación de una viga provocado al actuar sobre ella un esfuerzo normal y un momento flector Relacionar los criterios básicos para determinar el material,
ELASTICIDAD OBJETIVOS Observar el fenómeno de deformación de una viga provocado al actuar sobre ella un esfuerzo normal y un momento flector Relacionar los criterios básicos para determinar el material,
5. METODOLOGÍA. OBTENCIÓN DE DATOS
 5. 48 5.1. INTRODUCCIÓN AL ANÁLISIS Y OBTENCIÓN DE DATOS Los datos obtenidos de los ensayos del proyecto VOWS fueron almacenados como archivos binarios. Mediante el programa EXTRACT.FOR se obtuvo los datos
5. 48 5.1. INTRODUCCIÓN AL ANÁLISIS Y OBTENCIÓN DE DATOS Los datos obtenidos de los ensayos del proyecto VOWS fueron almacenados como archivos binarios. Mediante el programa EXTRACT.FOR se obtuvo los datos
P9: ENSAYO DE VACÍO Y CORTOCIRCUITO DEL TRANSFORMADOR MONOFÁSICO FUNDAMENTOS DE TECNOLOGÍA ELÉCTRICA
 ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
MECANICA CLASICA Segundo cuatrimestre de 2007. Cinemática y dinámica del cuerpo rígido, ángulos de Euler, Ecuaciones de Euler.
 MECANICA CLASICA Segundo cuatrimestre de 2007. Cinemática y dinámica del cuerpo rígido, ángulos de Euler, Ecuaciones de Euler. Problema 1: Analizar los siguientes puntos. a) Mostrar que la velocidad angular
MECANICA CLASICA Segundo cuatrimestre de 2007. Cinemática y dinámica del cuerpo rígido, ángulos de Euler, Ecuaciones de Euler. Problema 1: Analizar los siguientes puntos. a) Mostrar que la velocidad angular
Medición de la aceleración de la gravedad mediante plano inclinado
 Medición de la aceleración de la gravedad mediante plano inclinado Lopez, Johanna Giselle (gyf_lola@hotmail.com) Martinez Roldan, Antu (antucolomenos@hotmail.com) Viglezzi, Ramiro (ramiro.viglezzi@gmail.com)
Medición de la aceleración de la gravedad mediante plano inclinado Lopez, Johanna Giselle (gyf_lola@hotmail.com) Martinez Roldan, Antu (antucolomenos@hotmail.com) Viglezzi, Ramiro (ramiro.viglezzi@gmail.com)
Definir columnas de estilo periodístico
 Columnas de texto estilo periodístico Trabajar con columnas de texto Word posee una herramienta denominada columnas estilo periodístico la cual permite organizar el texto de un documento en dos o más columnas
Columnas de texto estilo periodístico Trabajar con columnas de texto Word posee una herramienta denominada columnas estilo periodístico la cual permite organizar el texto de un documento en dos o más columnas
La variabilidad interanual de las precipitaciones y las condiciones de sequía en la provincia de Tucumán (R. Argentina)
 La variabilidad interanual de las precipitaciones y las condiciones de sequía en la provincia de Tucumán (R. Argentina) César M. Lamelas*, Jorge D. Forciniti** y Lorena Soulé Gómez*** La variabilidad temporal
La variabilidad interanual de las precipitaciones y las condiciones de sequía en la provincia de Tucumán (R. Argentina) César M. Lamelas*, Jorge D. Forciniti** y Lorena Soulé Gómez*** La variabilidad temporal
APLICACIÓN DE HERRAMIENTAS INFORMÁTICAS AL ENTORNO
 CAPÍTULO 9 APLICACIÓN DE HERRAMIENTAS INFORMÁTICAS AL ENTORNO 9. APLICACIÓN DE HERRAMIENTAS INFORMÁTICAS AL ENTORNO Para profundizar en el conocimiento del medio es necesario el desarrollo de herramientas
CAPÍTULO 9 APLICACIÓN DE HERRAMIENTAS INFORMÁTICAS AL ENTORNO 9. APLICACIÓN DE HERRAMIENTAS INFORMÁTICAS AL ENTORNO Para profundizar en el conocimiento del medio es necesario el desarrollo de herramientas
5.3 Esfuerzos y deformaciones producidos por flexión. Puente grúa. 5.3.1 Flexión pura
 5.3 Esfuerzos y deformaciones producidos por flexión Puente grúa 5.3.1 Flexión pura Para cierta disposición de cargas, algunos tramos de los elementos que las soportan están sometidos exclusivamente a
5.3 Esfuerzos y deformaciones producidos por flexión Puente grúa 5.3.1 Flexión pura Para cierta disposición de cargas, algunos tramos de los elementos que las soportan están sometidos exclusivamente a
Control de procesos. Introducción
 Control de procesos Introducción El objeto de todo proceso industrial será la obtención de un producto final, de unas características determinadas de forma que cumpla con las especificaciones y niveles
Control de procesos Introducción El objeto de todo proceso industrial será la obtención de un producto final, de unas características determinadas de forma que cumpla con las especificaciones y niveles
REGENERACIÓN DE LA PLAYA DE SAN LORENZO, T.M. DE GIJÓN MEMORIA ÍNDICE 7. ESTUDIO DE GESTIÓN DE RESIDUOS DE CONSTRUCCIÓN Y DEMOLICIÓN...
 MEMORIA REGENERACIÓN DE LA PLAYA DE SAN LORENZO, T.M. DE GIJÓN MEMORIA ÍNDICE 1. INTRODUCCIÓN Y ANTECEDENTES... 1 2. MEDIO FÍSICO... 3 2.1. MORFOLOGÍA DE LA PLAYA DE SAN LORENZO... 3 2.2. CARACTERÍSTICAS
MEMORIA REGENERACIÓN DE LA PLAYA DE SAN LORENZO, T.M. DE GIJÓN MEMORIA ÍNDICE 1. INTRODUCCIÓN Y ANTECEDENTES... 1 2. MEDIO FÍSICO... 3 2.1. MORFOLOGÍA DE LA PLAYA DE SAN LORENZO... 3 2.2. CARACTERÍSTICAS
5. Tensión superficial
 5. Tensión superficial Este concepto es de suma importancia para el propósito de la presente tesis, ya que como se mencionó anteriormente es una de las variables de respuesta para la correlación buscada.
5. Tensión superficial Este concepto es de suma importancia para el propósito de la presente tesis, ya que como se mencionó anteriormente es una de las variables de respuesta para la correlación buscada.
Beatriz Galán Luque Natividad Adamuz-Povedano Universidad de Córdoba
 Épsilon - Revista de Educación Matemática 2012, Vol. 29(1), nº 80, pp. 75-81 Actividades sobre el tamaño de la Luna y su distancia a la Tierra Beatriz Galán Luque Natividad Adamuz-Povedano Universidad
Épsilon - Revista de Educación Matemática 2012, Vol. 29(1), nº 80, pp. 75-81 Actividades sobre el tamaño de la Luna y su distancia a la Tierra Beatriz Galán Luque Natividad Adamuz-Povedano Universidad
Código/Título de la Unidad Didáctica: MATEMÁTICAS BASICAS APLICADAS EN EL MECANIZADO. Actividad nº/título: REGLA DE TRES y SISTEMAS DE COORDENADAS
 Código/Título de la Unidad Didáctica: MATEMÁTICAS BASICAS APLICADAS EN EL MECANIZADO Actividad nº/título: REGLA DE TRES y SISTEMAS DE COORDENADAS Introducción a la actividad Material Didáctico: Tiempo:
Código/Título de la Unidad Didáctica: MATEMÁTICAS BASICAS APLICADAS EN EL MECANIZADO Actividad nº/título: REGLA DE TRES y SISTEMAS DE COORDENADAS Introducción a la actividad Material Didáctico: Tiempo:
Los filtros capacitivos (condensadores) conectados a tierra de los receptores electrónicos existentes en las instalaciones.
 Una de las causas más habituales de disparos intempestivos de diferenciales en instalaciones de baja tensión es el coloquialmente denominado disparo por simpatía. Estos disparos consisten en la apertura
Una de las causas más habituales de disparos intempestivos de diferenciales en instalaciones de baja tensión es el coloquialmente denominado disparo por simpatía. Estos disparos consisten en la apertura
REVISION Y CONTROL DEL FUNCIONAMIENTO DE LOS HORNOS DE CURADO TEXTIL
 REVISION Y CONTROL DEL FUNCIONAMIENTO DE LOS HORNOS DE CURADO TEXTIL Las tintas de plastisol curan cuando se les somete a una temperatura durante cierto tiempo; hablando en términos analíticos, podemos
REVISION Y CONTROL DEL FUNCIONAMIENTO DE LOS HORNOS DE CURADO TEXTIL Las tintas de plastisol curan cuando se les somete a una temperatura durante cierto tiempo; hablando en términos analíticos, podemos
TEMA 1: REPRESENTACIÓN GRÁFICA. 0.- MANEJO DE ESCUADRA Y CARTABON (Repaso 1º ESO)
 TEMA 1: REPRESENTACIÓN GRÁFICA 0.- MANEJO DE ESCUADRA Y CARTABON (Repaso 1º ESO) Son dos instrumentos de plástico transparente que se suelen usar de forma conjunta. La escuadra tiene forma de triángulo
TEMA 1: REPRESENTACIÓN GRÁFICA 0.- MANEJO DE ESCUADRA Y CARTABON (Repaso 1º ESO) Son dos instrumentos de plástico transparente que se suelen usar de forma conjunta. La escuadra tiene forma de triángulo
Fundamentos del trazado electrocardiográfico
 Clase 14 Fundamentos del trazado electrocardiográfico Los fenómenos de despolarización y repolarización que se registran en un electrocardiograma se representan a través de flechas llamadas vectores. Estos
Clase 14 Fundamentos del trazado electrocardiográfico Los fenómenos de despolarización y repolarización que se registran en un electrocardiograma se representan a través de flechas llamadas vectores. Estos
Política de Gestión Integral de Riesgos Compañía Sud Americana de Vapores S.A.
 de Riesgos Compañía Sud Americana de Vapores S.A. Elaborado Por Revisado Por Aprobado por Nombre Cargo Fecha Claudio Salgado Comité de Directores Contralor Comité de Directores Diciembre 2015 21 de diciembre
de Riesgos Compañía Sud Americana de Vapores S.A. Elaborado Por Revisado Por Aprobado por Nombre Cargo Fecha Claudio Salgado Comité de Directores Contralor Comité de Directores Diciembre 2015 21 de diciembre
Líneas Equipotenciales
 Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
Geometría orbital, cambio climático y Astrocronología
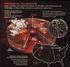 Geometría orbital, cambio climático y Astrocronología Francisco Sierro Sánchez Dpto. de Geología (Paleontología) Universidad de Salamanca. Sierro@usal.es Capítulo 5 Página - 1- Vivir en la Tierra es caro,
Geometría orbital, cambio climático y Astrocronología Francisco Sierro Sánchez Dpto. de Geología (Paleontología) Universidad de Salamanca. Sierro@usal.es Capítulo 5 Página - 1- Vivir en la Tierra es caro,
Análisis y cuantificación del Riesgo
 Análisis y cuantificación del Riesgo 1 Qué es el análisis del Riesgo? 2. Métodos M de Análisis de riesgos 3. Método M de Montecarlo 4. Modelo de Análisis de Riesgos 5. Qué pasos de deben seguir para el
Análisis y cuantificación del Riesgo 1 Qué es el análisis del Riesgo? 2. Métodos M de Análisis de riesgos 3. Método M de Montecarlo 4. Modelo de Análisis de Riesgos 5. Qué pasos de deben seguir para el
Prensas troqueladoras mecánicas actuadas mediante un servo motor. Por Dennis Boerger, Gerente de Producto: AIDA-America Corporation
 Prensas troqueladoras mecánicas actuadas mediante un servo motor. Por Dennis Boerger, Gerente de Producto: AIDA-America Corporation Por muchos años, los usuarios de prensas mecánicas han tomado como un
Prensas troqueladoras mecánicas actuadas mediante un servo motor. Por Dennis Boerger, Gerente de Producto: AIDA-America Corporation Por muchos años, los usuarios de prensas mecánicas han tomado como un
El Sistema de Actualización Dinámica del Mapa Acústico de Madrid
 paper ID: A085 /p.1 El Sistema de Actualización Dinámica del Mapa Acústico de Madrid P. Perera a & J.S. Santiago b a Bauman Consultoría Técnica, c/ Santa Isabel 19, Pozuelo de Alarcón, 28224 Madrid, placidop@telefonica.net
paper ID: A085 /p.1 El Sistema de Actualización Dinámica del Mapa Acústico de Madrid P. Perera a & J.S. Santiago b a Bauman Consultoría Técnica, c/ Santa Isabel 19, Pozuelo de Alarcón, 28224 Madrid, placidop@telefonica.net
DISEÑO DE INDICADORES DE DESIGUALDAD SOCIAL EN LAS CIUDADES.-
 DISEÑO DE INDICADORES DE DESIGUALDAD SOCIAL EN LAS CIUDADES.- 1. Introducción. El presente documento es el referente metodológico para la selección inicial de los barrios deprimidos. Se recoge una propuesta
DISEÑO DE INDICADORES DE DESIGUALDAD SOCIAL EN LAS CIUDADES.- 1. Introducción. El presente documento es el referente metodológico para la selección inicial de los barrios deprimidos. Se recoge una propuesta
MUSEO DE SAN ISIDRO. MADRID, 1989.
 Control gráfico de formas y superficies de transición Torre de San Isidro MUSEO DE SAN ISIDRO. MADRID, 1989. Francisco Alonso. Proyecto no construido. 249 Torre de San Isidro Control gráfico de formas
Control gráfico de formas y superficies de transición Torre de San Isidro MUSEO DE SAN ISIDRO. MADRID, 1989. Francisco Alonso. Proyecto no construido. 249 Torre de San Isidro Control gráfico de formas
MOVIMIENTO ABSOLUTO Y MOVIMIENTO RELATIVO
 BOLILLA 5 MOVIMIENTO ABSOLUTO Y MOVIMIENTO RELATIVO Sistemas de referencia Inerciales y No-inerciales En la bolilla anterior vimos que las leyes de Newton se cumplían en marcos de referencia inercial.
BOLILLA 5 MOVIMIENTO ABSOLUTO Y MOVIMIENTO RELATIVO Sistemas de referencia Inerciales y No-inerciales En la bolilla anterior vimos que las leyes de Newton se cumplían en marcos de referencia inercial.
Representación de un Vector
 VECTORES Vectores Los vectores se caracterizan por tener una magnitud, expresable por un número real, una dirección y un sentido. Un ejemplo de vectores son los desplazamientos. Otro ejemplo de vectores
VECTORES Vectores Los vectores se caracterizan por tener una magnitud, expresable por un número real, una dirección y un sentido. Un ejemplo de vectores son los desplazamientos. Otro ejemplo de vectores
Nivelación de Matemática MTHA UNLP 1. Vectores
 Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
REGENERACIÓN DE LA PLAYA DE LA ZURRIÓLA SAN SEBASTIAN (GUIPÚZCOA)
 PROYECTOS Y CONSTRUCCIÓN DE PLAYAS ARTIFICIALES Y REGENERACIÓN DE PLAYAS V. Experiencias Recientes. MOPTMA. REGENERACIÓN DE LA PLAYA DE LA ZURRIÓLA SAN SEBASTIAN (GUIPÚZCOA) Gregorio Gómez-Pina*, Galo
PROYECTOS Y CONSTRUCCIÓN DE PLAYAS ARTIFICIALES Y REGENERACIÓN DE PLAYAS V. Experiencias Recientes. MOPTMA. REGENERACIÓN DE LA PLAYA DE LA ZURRIÓLA SAN SEBASTIAN (GUIPÚZCOA) Gregorio Gómez-Pina*, Galo
nom web Manual: Cierre de Ejercicio
 Manual: Cierre de Ejercicio Sumario Prólogo... 2 Esquema del proceso a seguir... 3 1. Entrada de Incidencias del mes de diciembre... 4 1.1.- Entrada de variables en la Paga Mensual y Paga Extra...4 1.2.-
Manual: Cierre de Ejercicio Sumario Prólogo... 2 Esquema del proceso a seguir... 3 1. Entrada de Incidencias del mes de diciembre... 4 1.1.- Entrada de variables en la Paga Mensual y Paga Extra...4 1.2.-
Fuerza Cortante y Momento Flector
 TEMA VI Fuerza Cortante y Momento Flector Mecánica Racional 10 Profesora: Nayive Jaramillo S. Contenido Vigas. Pórticos. Fuerza Cortante (V). Momento Flector (M). Convenio de signos. Diagramas de fuerza
TEMA VI Fuerza Cortante y Momento Flector Mecánica Racional 10 Profesora: Nayive Jaramillo S. Contenido Vigas. Pórticos. Fuerza Cortante (V). Momento Flector (M). Convenio de signos. Diagramas de fuerza
TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS
 TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. CONCEPTO DE TRABAJO: A) Trabajo de una fuerza constante Todos sabemos que cuesta trabajo tirar de un sofá pesado, levantar una pila de libros
TRABAJO Y ENERGÍA; FUERZAS CONSERVATIVAS Y NO CONSERVATIVAS 1. CONCEPTO DE TRABAJO: A) Trabajo de una fuerza constante Todos sabemos que cuesta trabajo tirar de un sofá pesado, levantar una pila de libros
III. 9. Procesos de relajación. Efecto Nuclear Overhauser.
 9 Procesos de relajación Efecto uclear Overhauser En el modelo vectorial estudiamos los procesos de relajación longitudinal y transversal como procesos de evolución de la magnetización después de la excitación
9 Procesos de relajación Efecto uclear Overhauser En el modelo vectorial estudiamos los procesos de relajación longitudinal y transversal como procesos de evolución de la magnetización después de la excitación
TEMA 2. CIRCUITOS ELÉCTRICOS.
 TEMA 2. CIRCUITOS ELÉCTRICOS. 1. INTRODUCCIÓN. A lo largo del presente tema vamos a estudiar los circuitos eléctricos, para lo cual es necesario recordar una serie de conceptos previos tales como la estructura
TEMA 2. CIRCUITOS ELÉCTRICOS. 1. INTRODUCCIÓN. A lo largo del presente tema vamos a estudiar los circuitos eléctricos, para lo cual es necesario recordar una serie de conceptos previos tales como la estructura
6. VECTORES Y COORDENADAS
 6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
El proyecto Eratóstenes. Guía para el estudiante.
 El proyecto Eratóstenes. Guía para el estudiante. En esta actividad vas a trabajar en colaboración con estudiantes de otra escuela para medir el radio de la Tierra. Vas a usar los mismos métodos y principios
El proyecto Eratóstenes. Guía para el estudiante. En esta actividad vas a trabajar en colaboración con estudiantes de otra escuela para medir el radio de la Tierra. Vas a usar los mismos métodos y principios
INTERACCIÓN DE UNA CIMENTACIÓN PROFUNDA CON LA ESTRUCTURA
 INTERACCIÓN DE UNA CIMENTACIÓN PROFUNDA CON LA ESTRUCTURA Fernando MUZÁS LABAD, Doctor Ingeniero de Caminos Canales y Puertos Profesor Titular de Mecánica del Suelo ETSAM RESUMEN En el presente artículo
INTERACCIÓN DE UNA CIMENTACIÓN PROFUNDA CON LA ESTRUCTURA Fernando MUZÁS LABAD, Doctor Ingeniero de Caminos Canales y Puertos Profesor Titular de Mecánica del Suelo ETSAM RESUMEN En el presente artículo
2. Seleccionamos Ventana > Propiedades y, a continuación, el color para el trazo, el grosor de la línea y el estilo en el inspector de propiedades.
 TEMA 2: HERRAMIENTAS DE DIBUJO Y PINTURA 1. Herramienta Lápiz Para dibujar líneas y formas, se utiliza la herramienta Lápiz de manera muy similar a como se emplea un lápiz para realizar un dibujo. Para
TEMA 2: HERRAMIENTAS DE DIBUJO Y PINTURA 1. Herramienta Lápiz Para dibujar líneas y formas, se utiliza la herramienta Lápiz de manera muy similar a como se emplea un lápiz para realizar un dibujo. Para
CONSTRUCCIÓN GEOMÉTRICA DE CUBIERTAS. Geometrical roof construction
 JOSÉ ANTONIO GONZÁLEZ CASARES CONSTRUCCIÓN GEOMÉTRICA DE CUBIERTAS Geometrical roof construction INTRODUCCIÓN La resolución de cubiertas (fundamentalmente inclinadas) no debería de plantear mayor dificultad
JOSÉ ANTONIO GONZÁLEZ CASARES CONSTRUCCIÓN GEOMÉTRICA DE CUBIERTAS Geometrical roof construction INTRODUCCIÓN La resolución de cubiertas (fundamentalmente inclinadas) no debería de plantear mayor dificultad
CAPITULO 3 LA TEMPERATURA
 CAPITULO 3 LA TEMPERATURA 1. CONCEPTO: La temperatura de un cuerpo indica en qué dirección se desplazará el calor al poner en contacto dos cuerpos que se encuentran a temperaturas distintas, ya que éste
CAPITULO 3 LA TEMPERATURA 1. CONCEPTO: La temperatura de un cuerpo indica en qué dirección se desplazará el calor al poner en contacto dos cuerpos que se encuentran a temperaturas distintas, ya que éste
Qué quiere decir Nuestro Entorno?
 Qué quiere decir Nuestro Entorno? En todo momento estamos rodeados de paisajes. Todo lo que nos envuelve se presenta ante nosotros formando imágenes instantáneas en permanente cambio. Valoramos nuestro
Qué quiere decir Nuestro Entorno? En todo momento estamos rodeados de paisajes. Todo lo que nos envuelve se presenta ante nosotros formando imágenes instantáneas en permanente cambio. Valoramos nuestro
Ing. Benoît FROMENT MODULO 4 4.2 FOTOGRAFIAS AEREAS
 4.2 FOTOGRAFIAS AEREAS 1 - DESARROLLO DE LA FOTOGRAFIA AEREA El hombre, para enfrentar los problemas que le plantea la organización y el desarrollo del medio que habita, se ha visto obligado a crear novedosas
4.2 FOTOGRAFIAS AEREAS 1 - DESARROLLO DE LA FOTOGRAFIA AEREA El hombre, para enfrentar los problemas que le plantea la organización y el desarrollo del medio que habita, se ha visto obligado a crear novedosas
8º Estudio sobre el secretariado en España El perfil
 8º Estudio sobre el secretariado en España El perfil Cuántos años de experiencia tienen las secretarias en España? Más del 80% de las personas encuestadas tienen una experiencia de más de 10 años, y de
8º Estudio sobre el secretariado en España El perfil Cuántos años de experiencia tienen las secretarias en España? Más del 80% de las personas encuestadas tienen una experiencia de más de 10 años, y de
GEOMETRÍA DESCRIPTIVA SISTEMAS DE PROYECCIÓN
 GEOMETRÍA DESCRIPTIVA La Geometría Descriptiva es la ciencia de representación gráfica, sobre superficies bidimensionales, de los problemas del espacio donde intervengan, puntos, líneas y planos. La Geometría
GEOMETRÍA DESCRIPTIVA La Geometría Descriptiva es la ciencia de representación gráfica, sobre superficies bidimensionales, de los problemas del espacio donde intervengan, puntos, líneas y planos. La Geometría
Ingeniería Gráfica Aplicada
 Acotación Ingeniería Gráfica Aplicada Curso 2010-11 Manuel I. Bahamonde García Índice Acotación 1. Principios generales de acotación 2. Método de acotación 3. Acotación de círculos, radios, arcos, cuadrados
Acotación Ingeniería Gráfica Aplicada Curso 2010-11 Manuel I. Bahamonde García Índice Acotación 1. Principios generales de acotación 2. Método de acotación 3. Acotación de círculos, radios, arcos, cuadrados
SISTEMA DE LIMPIEZA POR VACÍO
 SISTEMA DE LIMPIEZA POR VACÍO MODELO MF PARA TANQUES RECTANGULARES Catálogo 48.1.1 Limpieza automática Adecuado incluso para grandes longitudes Mantenimiento sin riesgos Uno de los problemas que presentan
SISTEMA DE LIMPIEZA POR VACÍO MODELO MF PARA TANQUES RECTANGULARES Catálogo 48.1.1 Limpieza automática Adecuado incluso para grandes longitudes Mantenimiento sin riesgos Uno de los problemas que presentan
MOMENTO ANGULAR Y TORCAS COMO VECTORES
 MOMENTO ANGULAR Y TORCAS COMO VECTORES OBJETIVOS: Identificar la torca y el momento angular como magnitudes vectoriales. Examinar las propiedades matemáticas del producto cruz y algunas aplicaciones. Describir
MOMENTO ANGULAR Y TORCAS COMO VECTORES OBJETIVOS: Identificar la torca y el momento angular como magnitudes vectoriales. Examinar las propiedades matemáticas del producto cruz y algunas aplicaciones. Describir
Aproximación local. Plano tangente. Derivadas parciales.
 Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 004-005 Aproximación local. Plano tangente. Derivadas parciales. 1. Plano tangente 1.1. El problema de la aproximación
Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 004-005 Aproximación local. Plano tangente. Derivadas parciales. 1. Plano tangente 1.1. El problema de la aproximación
Trabajo, fuerzas conservativas. Energia.
 Trabajo, fuerzas conservativas. Energia. TRABAJO REALIZADO POR UNA FUERZA CONSTANTE. Si la fuerza F que actúa sobre una partícula constante (en magnitud y dirección) el movimiento se realiza en línea recta
Trabajo, fuerzas conservativas. Energia. TRABAJO REALIZADO POR UNA FUERZA CONSTANTE. Si la fuerza F que actúa sobre una partícula constante (en magnitud y dirección) el movimiento se realiza en línea recta
AutoSope. Alejandro Langton Gimeno Boal 1. INTRODUCCION A AUTOSLOPE
 1. INTRODUCCION A AUTOSLOPE SLOPE/W es el principal software de CAD empleado para calcular factores de seguridad en estabilidad de taludes por métodos finitos. Puede ser usado para analizar prácticamente
1. INTRODUCCION A AUTOSLOPE SLOPE/W es el principal software de CAD empleado para calcular factores de seguridad en estabilidad de taludes por métodos finitos. Puede ser usado para analizar prácticamente
Introducción al diseño híbrido con ZW3D
 Introducción al diseño híbrido con ZW3D Con este tutorial podrá aprender el diseño 3D con un programa CAD 3D híbrido de modelado de sólidos y superficies combinadas. El objetivo es dibujar un grifo en
Introducción al diseño híbrido con ZW3D Con este tutorial podrá aprender el diseño 3D con un programa CAD 3D híbrido de modelado de sólidos y superficies combinadas. El objetivo es dibujar un grifo en
7. MODELADO EN DINAMICA DE SISTEMAS
 7. MODELADO EN DINAMICA DE SISTEMAS 7.1. Dinámica de Sistemas El origen de la dinámica de sistemas se encuentra ligado al desarrollo de una aplicación para analizar los pedidos de una empresa fabricante
7. MODELADO EN DINAMICA DE SISTEMAS 7.1. Dinámica de Sistemas El origen de la dinámica de sistemas se encuentra ligado al desarrollo de una aplicación para analizar los pedidos de una empresa fabricante
Generador Solar de Energía Eléctrica a 200W CAPÍTULO V. Planteamiento del problema, parámetros y diseño fotovoltaico
 CAPÍTULO V Planteamiento del problema, parámetros y diseño fotovoltaico 5.1 Objetivo general El objetivo general de esta tesis es generar energía eléctrica por medio de la luz solar, con la finalidad de
CAPÍTULO V Planteamiento del problema, parámetros y diseño fotovoltaico 5.1 Objetivo general El objetivo general de esta tesis es generar energía eléctrica por medio de la luz solar, con la finalidad de
MODELOS DE MORFODINÁMICA DE PLAYAS.
 PROYECTOS Y CONSTRUCCIÓN DE PLAYAS ARTIFICIALES Y REGENERACIÓN DE PLAYAS ll. Fundamentos MODELOS DE MORFODINÁMICA DE PLAYAS. César Vidal, Miguel A. Losada, Raúl Medina e íñigo Losada. Grupo de Ingeniería
PROYECTOS Y CONSTRUCCIÓN DE PLAYAS ARTIFICIALES Y REGENERACIÓN DE PLAYAS ll. Fundamentos MODELOS DE MORFODINÁMICA DE PLAYAS. César Vidal, Miguel A. Losada, Raúl Medina e íñigo Losada. Grupo de Ingeniería
ENERGÍA ELÉCTRICA. Central Eólica
 ENERGÍA ELÉCTRICA. Central Eólica La energía eólica es la energía obtenida por el viento, es decir, la energía cinética obtenida por las corrientes de aire y transformada en energía eléctrica mediante
ENERGÍA ELÉCTRICA. Central Eólica La energía eólica es la energía obtenida por el viento, es decir, la energía cinética obtenida por las corrientes de aire y transformada en energía eléctrica mediante
FASES DEL PROCESO DE RESOLUCIÓN DE PROBLEMAS
 FASES DEL PROCESO DE RESOLUCIÓN DE PROBLEMAS Varios autores han tratado de identificar y describir las distintas fases en el proceso de resolución de problemas. Polya (1945), en su modelo descriptivo,
FASES DEL PROCESO DE RESOLUCIÓN DE PROBLEMAS Varios autores han tratado de identificar y describir las distintas fases en el proceso de resolución de problemas. Polya (1945), en su modelo descriptivo,
Estudio experimental de la influencia del estrato rocoso en la forma del foso de erosión producida por jet en salto de esquí.
 1. Introducción. Este capítulo trata sobre los sistemas de medición que hemos utilizado en la realización de los ensayos. Se han incluido todos los sistemas de medida utilizados, aquellos que han funcionado
1. Introducción. Este capítulo trata sobre los sistemas de medición que hemos utilizado en la realización de los ensayos. Se han incluido todos los sistemas de medida utilizados, aquellos que han funcionado
