Figura 5.1 a: Acimut de una dirección de mira
|
|
|
- Rodrigo Araya Fidalgo
- hace 8 años
- Vistas:
Transcripción
1 Tema N 5 Determinación del Acimut de una dirección 5.1- Acimut de una dirección El acimut de una línea cualquiera es el ángulo que forma el meridiano del lugar con el plano vertical que contiene dicha línea, [Figura 5.1a]. Si consideramos las proyecciones de los planos verticales sobre el horizonte astronómico del observador, definimos al acimut de una línea o dirección como el ángulo horizontal que forma el plano del meridiano (o la línea meridiana Norte Sur) y el plano vertical que contiene a la línea de una dirección considerada. La dirección considerada puede materializarse mediante una mira. Figura 5.1 a: Acimut de una dirección de mira El objeto elegido como mira debe ser fijo, lejano y muy puntual. Por lo general se toma el foco o la punta de alguna antena que sea visible a la noche. Si estamos en el campo y no se cuenta con nada, deberemos materializar la mira nosotros mismos.
2 Sea el punto O la posición de un observador con coordenadas latitud y longitud conocidas, [Figura 5.1b], se definen sobre el plano horizontal los siguientes elementos: Figura 5.1b: Acimut de la Mira AM Mira dirección hacia un objeto fijo alejado. S dirección de un astro cualquiera. Lo origen de las lecturas horizontales del instrumento (valor de cero grados en el círculo graduado). AM acimut de la mira. Dirección que deseamos conocer. A acimut calculado a través de las observaciones del astro S. Ls ángulo horizontal medido del astro S. LM ángulo horizontal medido a la mira. De la [Figura 5.1b] puede deducirse la siguiente expresión: AM A LM Ls AM A + (LM Ls) (1) Analizando la ecuación (1) notamos que el problema consiste en hallar el acimut de cálculo A del astro observado. Para obtener A, trabajamos sobre el triángulo de posición, [Figura 5.1c]:
3 Aplicando el teorema del coseno: cos (90 - δ) cos (90 - ϕ) cos Z + + sen (90 - ϕ) sen Z cos (π - A) sen δ sen ϕ cos Z + cos ϕ sen Z (-cos A) Figura 5.1c: Triángulo de posición sen δ sen ϕ cos Z cos ϕ sen Z cos A Finalmente: cos A sen ϕ cos Z - sen δ (2) cos ϕ sen Z En la expresión (2) tenemos que ϕ es la latitud del lugar de observación (se supone conocida al menos aproximadamente), δ es la declinación del astro extraída de un catálogo o efemérides, interpolada para la fecha y hora de observación y, Z es la distancia cenital medida con el instrumento (corregida por refracción y paralaje). Como vemos, podemos conocer A midiendo solamente distancias cenitales. Con el valor calculado de A lo introducimos en la ecuación (1) para obtener el acimut de la mira AM buscado. Resumiendo, a través de la observación de un astro podemos calcular el acimut de una dirección cualquiera (AM). Este valor nos servirá para materializar la dirección de la línea meridiana en el punto de estacionamiento y, por lo tanto, conocer la posición del punto Sur, origen del sistema de coordenadas Horizontal Acimut de una dirección por medio de observaciones del Sol. No siendo el Sol un elemento puntual (ocupa aproximadamente medio grado), se deberá observar en forma doble tangenteando sus bordes con los hilos vertical y horizontal de la cruz de retículo instrumental, [Figura 5.2a].
4 Figura 5.2 a: Bisección del Sol en dos cuadrantes simétricos Es evidente que con una sola observación podríamos hacer el cálculo, corrigiendo las lecturas vertical y horizontal por el semi-diámetro del Sol (extraído de las efemérides). Pero logramos mejor precisión y nos aseguramos bisectar el centro del Sol realizando un par de mediciones en cuadrantes simétricos. Tomando los promedios hallaremos las lecturas reducidas al centro del astro y como si éste hubiese sido medido en el instante intermedio entre las dos posiciones. Las observaciones en los cuadrantes deben realizarse en el menor tiempo posible a fin de minimizar errores. En la práctica se efectúan lecturas de varios pares de observaciones en las dos posiciones del instrumento (círculo izquierdo I y círculo derecho II) Operaciones Prácticas La sucesión de operaciones para llevar a cabo las prácticas de las observaciones solares, utilizando un teodolito topográfico o astronómico provisto de un filtro solar es la siguiente: (1) Materialización del topocentro con una estaca. Estacionamiento y nivelación del instrumento. (2) Determinación del error de índice (ε) instrumental. Para ello se bisecta un punto alejado cercano al horizonte en las dos posiciones del teodolito. La suma de ambas lecturas verticales debería dar 360º pero, como el aparato no está libre de este error,
5 la diferencia en más o en menos corresponderá al doble del error. El error de índice deberá sumarse con su signo a cada lectura vertical que se realice. (3) Se elige una mira en un punto alejado para evitar errores de paralaje y se realiza la lectura horizontal de la misma en primera posición (o círculo izquierdo). (4) Bisección del Sol tangenteando los hilos. Se toma la hora al minuto para interpolar la declinación. Se hacen las lecturas vertical y horizontal completando al menos tres parejas. (5) Se finaliza la serie bisectando nuevamente la mira para leer su ángulo vertical. (6) Se gira el instrumento en posición II (vuelta de campana) y se repite la sucesión anterior. (7) Se completa la planilla de observación promediando las lecturas horizontales y verticales de cada pareja y se promedian las lecturas horizontales de mira para cada posición. (8) Se toma la presión y la temperatura Planilla de Observación La siguiente tabla es un ejemplo de una planilla con las observaciones realizadas en campaña.
6 La declinación del Sol debe emplearse en la fórmula (2) interpolada para el día y la hora promedio de la observación Cálculo de la Distancia Cenital La distancia cenital leída, que denotaremos con Z, es la lectura vertical leída (Lv) compensada por el error de índice (ε): Z Lv ± ε. A partir de esta medida leída, podemos calcular la distancia cenital verdadera (Z), afectándola de las siguientes correcciones: Z Z + Ro - p (3) donde: Z es la distancia cenital leída. Ro es la refracción. Se calcula como Ro Rn (1+A) (1+B), donde a su vez Rn es la refracción normal (Rn 60.4 tg Z ), A es un coeficiente en función de la temperatura y B es un coeficiente en función de la presión atmosférica en mm de Hg. p es la paralaje anual del Sol. Se calcula como p po sen Z, donde po es la paralaje normal y vale 8.8 Los valores de A y B tabulados son los siguientes : t C A Presión B La planilla de cálculo a continuación nos permite organizar la reducción de las observaciones.
7 Promedios Promedio 1 (Pareja 1 + Pareja 6) / 2 Promedio 2 (Pareja 2 + Pareja 5) / 2 Promedio 3 (Pareja 3 + Pareja 4) / 2 Promedio final (Promedio 1 + Promedio 2 + Promedio 3) / 3
8 Residuos V 1 Promedio final Promedio 1 V 2 Promedio final Promedio 2 V 3 Promedio final Promedio 3 Error Cuadrático Medio dónde: n es el número de parejas. ε cm 2 ΣVi n ( n 1) 5.3- Acimut de una dirección por medio de observaciones de estrellas. Cuando el astro utilizado es una estrella, la observación se simplifica notablemente por ser éstas un punto y facilitar en consecuencia su bisección. Para el cálculo, no se tiene en cuenta la corrección por paralaje anual ya que, a diferencia del Sol, se desprecia por tomar un valor muy pequeño. Pero la observación con estrellas implica la confección previa de un programa de estrellas que contenga los elementos de calaje para poder así ubicarlas en la esfera celeste. Además, las observaciones se complican por el hecho de trabajar en horario nocturno y tener que dar vuelta campana del teodolito con el consiguiente peligro de perder la estrella Condiciones más favorables para la observación Para la determinación del acimut de una dirección mediante observaciones con estrellas, encontraremos la posición en la esfera celeste para la cual los valores de latitud (ϕ) adoptada y la distancia cenital (Z) leída, influyan lo menos posible con sus errores. Vamos a calcular entonces la influencia de dichos errores en la determinación del acimut (A). Del triángulo de posición, [Figura 5.1c], podemos deducir la siguiente expresión: sen δ senϕ cos Z sen Z cos ϕ cos A (4)
9 Diferenciando la ecuación (4) respecto a ϕ, Z y A, y haciendo constar que podemos considerar que δ constante debido a que el valor extraído del catálogo tiene un error muy insignificante a los valores que establecemos para la latitud o la distancia cenital, es decir que dδ 0. 0 (cos ϕ cos Z + sen Z senϕ cos A) dϕ + ( senϕ ( sen Z) cos Z cos ϕ cos A) dz + + ( sen Z cos ϕ sen A) da 0 (cos ϕ cos Z + sen Z senϕ cos A) dϕ ( sen ϕ sen Z cos Z cos ϕ cos A) dz + + ( sen Z cos ϕ sen A) da sen Z cos ϕ sen A da ( sen ϕ sen Z + cos Z cos ϕ cos A) dz (cos ϕ cos Z + sen Z sen ϕ cos A) dϕ (5) + Sea el conocido triángulo de posición, [Figura 5.3a], aplicando el teorema de los cinco elementos al lado 90-δ tenemos: Figura 5.3 a: Triángulo de posición cos δ cos H cos ϕ cos Z + sen Z sen ϕ cos A (6) sen ( 90 δ ) cosq sen Z cos (90 ϕ) sen (90 ϕ) cos Z cos ( π A) cos δ cos Q sen Z senϕ + cos ϕ cos Z cos A (7)
10 Del teorema del seno: sen (90 ϕ) sen Q sen (90 δ ) sen ( π A) sen A cos ϕ cos δ sen Q (8) Reemplazando (6), (7) y (8) en (5) obtenemos: sen Z cos δ sen Q da cos δ cos Q dz cos δ cos H dϕ da cos δ cos Q dz sen Z cos δ sen Q cos δ cos H dϕ sen Z cos δ sen Q da dz cos H dϕ (9) sen Z tg Q sen Z sen Q Para que la influencia de los errores cometidos en ϕ y Z sean mínimos, debemos buscar que el da sea lo más chico que se pueda. Para que esto último suceda, tenemos que hacer pequeñas las fracciones que constituyen el segundo miembro de la ecuación diferencial (9). Entonces, es necesario que sus denominadores sean lo más grande posible. Prescindiendo de las consideraciones que podemos hacer respecto al ángulo horario H y la distancia cenital Z, los dos denominadores serán máximos cuando el ángulo paraláctico Q 90º, en cuyo caso la tg Q y el sen Q 1. Es decir que para la determinación del acimut A es conveniente hacer las observaciones en el momento en que el ángulo paraláctico vale 90º, o sea en máxima elongación. Los elementos de calaje que nos permitirán ubicar las estrellas a observar deberán elegirse de acuerdo a la condición de máxima elongación vista en el Tema correspondiente: tg ϕ sen ϕ cos δ cos H, cos Z, sen A tg δ sen δ cos ϕ
11 En la práctica conviene observar estrellas a uno y otro lado del meridiano del lugar. Vale decir, al este y al oeste del meridiano Selección de estrellas Para conocer la ascensión recta (α) de las estrellas que se encuentren elongando, partimos de la fórmula del tiempo sidéreo θl α + H. Considerando las posiciones al este y al oeste con los signos correspondientes tendremos: θl α + H (para estrellas al oeste), θl α - H (para estrellas al este). A partir de la elección de una hora (HOA) del comienzo de las observaciones, la transformo en tiempo sidéreo (θl). Como cos H tg ϕ/tg δ y la declinación debe ser grande para que la estrella sea circunpolar (δ -60º), considerando además que para nuestra localización geográfica la latitud ϕ -31º 30, entonces: cos H tg -31º/tg -60º 4 h 30 m. Por lo tanto, será muy conveniente tomar valores para el ángulo horario H entre 4 h y 4 h 30 m. Finalmente, para estrellas al oeste del meridiano será α w θl 4 h y para estrellas al este del meridiano será α E θl + 4 h. Para calcular los elementos de calaje basta trabajar con los ángulos al minuto. Una vez estacionado el teodolito, nivelado y calculado su error de índice, se reproduce en el círculo vertical el Z de calaje y en el círculo horizontal el A de calaje. Por último, esperamos la hora de pasaje de la estrella. Si los elementos de calaje están bien calculados, las estrellas entrarán en el campo de visión del ocular, no necesariamente por el centro. Con el movimiento fino horizontal deberé llevar el hilo vertical coincidente con la estrella. Para colocar el calaje A, el cero del instrumento debe estar en el sur, es decir que el teodolito debe tener la dirección de la línea meridiana previamente determinada con algunos minutos de arco de error. Esto último debe haberse logrado con un acimut con Sol. El acimut por estrellas es mucho más preciso que el logrado con determinaciones del Sol o cualquier otro método.
12 Planilla de Observación La siguiente tabla es un ejemplo de una planilla con las observaciones realizadas en campaña. La planilla de cálculo es la misma que para el acimut con Sol, pero en este caso sin considerar la paralaje (Z Z + Ro). Una vez obtenidos los seis valores de acimutes de la mira, se promedian y se determina el error cuadrático medio de la misma manera que con las observaciones con Sol.
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
Cálculo de altura de formación de auroras.
 Cálculo de altura de formación de auroras. Andrea Polo Padilla E X P E D I C I Ó N S H E L I O S C A R L A M E N D O Z A R U T A D E L A S E S T R E L L A S 2 0 1 5 I E S L u c a s M a r t í n E s p i
Cálculo de altura de formación de auroras. Andrea Polo Padilla E X P E D I C I Ó N S H E L I O S C A R L A M E N D O Z A R U T A D E L A S E S T R E L L A S 2 0 1 5 I E S L u c a s M a r t í n E s p i
Resolución de problemas. Temas: VOR e ILS
 Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
LA ESFERA CELESTE. Atlas sosteniendo la esfera celeste
 LA ESFERA CELESTE. Atlas sosteniendo la esfera celeste Introducción: A simple vista, el cielo parece una inmensa cúpula que nos cubre. Durante el día se presenta de color azul con el Sol y en ciertas ocasiones
LA ESFERA CELESTE. Atlas sosteniendo la esfera celeste Introducción: A simple vista, el cielo parece una inmensa cúpula que nos cubre. Durante el día se presenta de color azul con el Sol y en ciertas ocasiones
Tema 07. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Teóricas de Análisis Matemático (28) - Práctica 4 - Límite de funciones. 1. Límites en el infinito - Asíntotas horizontales
 Práctica 4 - Parte Límite de funciones En lo que sigue, veremos cómo la noción de límite introducida para sucesiones se etiende al caso de funciones reales. Esto nos permitirá estudiar el comportamiento
Práctica 4 - Parte Límite de funciones En lo que sigue, veremos cómo la noción de límite introducida para sucesiones se etiende al caso de funciones reales. Esto nos permitirá estudiar el comportamiento
TIEMPO -DÍAS -HORAS CONCEPTO GENERAL DEL TIEMPO
 TIEMPO -DÍAS -HORAS CONCEPTO GENERAL DEL TIEMPO Para medir el tiempo se necesita un fenómeno periódico, que se repita continuamente y con la misma fase, lo que sucede con fenómenos astronómicos basado
TIEMPO -DÍAS -HORAS CONCEPTO GENERAL DEL TIEMPO Para medir el tiempo se necesita un fenómeno periódico, que se repita continuamente y con la misma fase, lo que sucede con fenómenos astronómicos basado
1 Estática Básica Prohibida su reproducción sin autorización. CONCEPTOS DE FISICA MECANICA. Conceptos de Física Mecánica
 1 CONCEPTOS DE FISICA MECANICA Introducción La parte de la física mecánica se puede dividir en tres grandes ramas de acuerdo a lo que estudia cada una de ellas. Así, podemos clasificarlas según lo siguiente:
1 CONCEPTOS DE FISICA MECANICA Introducción La parte de la física mecánica se puede dividir en tres grandes ramas de acuerdo a lo que estudia cada una de ellas. Así, podemos clasificarlas según lo siguiente:
MOVIMIENTO ABSOLUTO Y MOVIMIENTO RELATIVO
 BOLILLA 5 MOVIMIENTO ABSOLUTO Y MOVIMIENTO RELATIVO Sistemas de referencia Inerciales y No-inerciales En la bolilla anterior vimos que las leyes de Newton se cumplían en marcos de referencia inercial.
BOLILLA 5 MOVIMIENTO ABSOLUTO Y MOVIMIENTO RELATIVO Sistemas de referencia Inerciales y No-inerciales En la bolilla anterior vimos que las leyes de Newton se cumplían en marcos de referencia inercial.
ESTÁTICA 2. VECTORES. Figura tomada de http://www.juntadeandalucia.es/averroes/~04001205/fisiqui/imagenes/vectores/473396841_e1de1dd225_o.
 ESTÁTICA Sesión 2 2 VECTORES 2.1. Escalares y vectores 2.2. Cómo operar con vectores 2.2.1. Suma vectorial 2.2.2. Producto de un escalar y un vector 2.2.3. Resta vectorial 2.2.4. Vectores unitarios 2.2.5.
ESTÁTICA Sesión 2 2 VECTORES 2.1. Escalares y vectores 2.2. Cómo operar con vectores 2.2.1. Suma vectorial 2.2.2. Producto de un escalar y un vector 2.2.3. Resta vectorial 2.2.4. Vectores unitarios 2.2.5.
35 Facultad de Ciencias Universidad de Los Andes Mérida-Venezuela. Potencial Eléctrico
 q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
ESTATICA. Componentes ortogonales de una fuerza. Seminario Universitario Física
 ESTATICA Es la parte de la física que estudia las fuerzas en equilibrio. Si sobre un cuerpo no actúan fuerzas o actúan varias fuerzas cuya resultante es cero, decimos que el cuerpo está en equilibrio.
ESTATICA Es la parte de la física que estudia las fuerzas en equilibrio. Si sobre un cuerpo no actúan fuerzas o actúan varias fuerzas cuya resultante es cero, decimos que el cuerpo está en equilibrio.
MEDICION DE LA DISTANCIA ANGULAR EN ESTRELLAS DOBLES VISUALES UN PROCEDIMIENTO TRIGONOMÉTRICO
 MEDICION DE LA DISTANCIA ANGULAR EN ESTRELLAS DOBLES VISUALES UN SOBRE LA MEDIDA DEL ARCO DE SEPARACIÓN DE DOS ESTRELLAS BINARIAS Cuando se trata de medir el arco comprendido entre la posición en la bóveda
MEDICION DE LA DISTANCIA ANGULAR EN ESTRELLAS DOBLES VISUALES UN SOBRE LA MEDIDA DEL ARCO DE SEPARACIÓN DE DOS ESTRELLAS BINARIAS Cuando se trata de medir el arco comprendido entre la posición en la bóveda
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
A S T R O N O M Í A T e l u u rr ii oo
 A S T R O N O M Í A Telurio Telurio A S T R O N O M Í A Se trata de un módulo de gran utilidad para estudiar los movimientos relativos de los tres astros que protagonizan nuestra vida diaria: el Sol, la
A S T R O N O M Í A Telurio Telurio A S T R O N O M Í A Se trata de un módulo de gran utilidad para estudiar los movimientos relativos de los tres astros que protagonizan nuestra vida diaria: el Sol, la
Nivelación de Matemática MTHA UNLP 1. Vectores
 Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
Tema 7. Límites y continuidad de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Sistemas de coordenadas en la esfera celeste
 astronomia.org Documentación Sistemas de coordenadas en la esfera celeste Carlos Amengual Barcelona, 1989 Revisado febrero 2010 Este documento se encuentra en la dirección http://astronomia.org/doc/esfcel.pdf
astronomia.org Documentación Sistemas de coordenadas en la esfera celeste Carlos Amengual Barcelona, 1989 Revisado febrero 2010 Este documento se encuentra en la dirección http://astronomia.org/doc/esfcel.pdf
LA TIERRA PARALELA DEL MEDIO MUNDO CERCA DE QUITO
 NETWORK FOR ASTRONOMY SCHOOL EDUCATION LA TIERRA PARALELA DEL MEDIO MUNDO CERCA DE QUITO Carme Alemany, Rosa M. Ros NASE Introducción Cerca de Quito esta la Mitad del Mundo cuya latitud es 0º 0 0. En este
NETWORK FOR ASTRONOMY SCHOOL EDUCATION LA TIERRA PARALELA DEL MEDIO MUNDO CERCA DE QUITO Carme Alemany, Rosa M. Ros NASE Introducción Cerca de Quito esta la Mitad del Mundo cuya latitud es 0º 0 0. En este
b) Para encontrar los intervalos de crecimiento y decrecimiento, hay que derivar la función. Como que se trata de un cociente, aplicamos la fórmula:
 1. Dada la función f(x) = : a) Encontrar el dominio, las AH y las AV. b) Intervalos de crecimiento, decrecimiento, máximos y mínimos relativos. c) Primitiva que cumpla que F(0) = 0. a) Para encontrar el
1. Dada la función f(x) = : a) Encontrar el dominio, las AH y las AV. b) Intervalos de crecimiento, decrecimiento, máximos y mínimos relativos. c) Primitiva que cumpla que F(0) = 0. a) Para encontrar el
COORDENADAS CURVILINEAS
 CAPITULO V CALCULO II COORDENADAS CURVILINEAS Un sistema de coordenadas es un conjunto de valores que permiten definir unívocamente la posición de cualquier punto de un espacio geométrico respecto de un
CAPITULO V CALCULO II COORDENADAS CURVILINEAS Un sistema de coordenadas es un conjunto de valores que permiten definir unívocamente la posición de cualquier punto de un espacio geométrico respecto de un
LA FORMA DE LA TIERRA
 La Tierra Aprendemos también cosas sobre la Tierra mirando a la Luna y a las estrellas Por qué los griegos antiguos ya sabían que la Tierra era redonda? Qué movimientos presenta la Tierra? Por qué hay
La Tierra Aprendemos también cosas sobre la Tierra mirando a la Luna y a las estrellas Por qué los griegos antiguos ya sabían que la Tierra era redonda? Qué movimientos presenta la Tierra? Por qué hay
Ejercicios de Trigonometría
 Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
Ejercicios de Trigonometría 1) Indica la medida de estos ángulos en radianes: a) 0º b) 45º c) 60º d) 120º Recuerda que 360º son 2π radianes, con lo que para hacer la conversión realizaremos una simple
TEORÍA TEMA 9. 2. Definición de ESFUERZOS CARACTERÍSTICOS ( Mf.; Q; N)
 1. Definición de Viga de alma llena TEORÍA TEMA 9 2. Definición de ESFUERZOS CARACTERÍSTICOS ( Mf.; Q; N) 3. Determinación de los esfuerzos característicos i. Concepto de Polígonos de Presiones ii. Caso
1. Definición de Viga de alma llena TEORÍA TEMA 9 2. Definición de ESFUERZOS CARACTERÍSTICOS ( Mf.; Q; N) 3. Determinación de los esfuerzos característicos i. Concepto de Polígonos de Presiones ii. Caso
Vectores no colineales.
 Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
EJERCICIOS PROPUESTOS. 3 rad x x 2. 4 rad d) 2 rad
 TRIGONOMETRÍA EJERCICIOS PROPUESTOS.. Indica la medida de estos ángulos en radianes. a) º c) º b) º d) º a) º rad c) rad º rad b) rad º rad d) rad rad º º Epresa en grados los siguientes ángulos. a) rad
TRIGONOMETRÍA EJERCICIOS PROPUESTOS.. Indica la medida de estos ángulos en radianes. a) º c) º b) º d) º a) º rad c) rad º rad b) rad º rad d) rad rad º º Epresa en grados los siguientes ángulos. a) rad
RELOJES DE SOL. 1. Movimiento diurno del Sol. 2. Variaciones anuales del movimiento del Sol
 1. Movimiento diurno del Sol RELOJES DE SOL Sin necesidad de utilizar instrumento alguno, todo el mundo sabe que el Sol, por la mañana sale por algún lugar hacia el Este, que hacia el mediodía está en
1. Movimiento diurno del Sol RELOJES DE SOL Sin necesidad de utilizar instrumento alguno, todo el mundo sabe que el Sol, por la mañana sale por algún lugar hacia el Este, que hacia el mediodía está en
Líneas Equipotenciales
 Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
El proyecto Eratóstenes. Guía para el estudiante.
 El proyecto Eratóstenes. Guía para el estudiante. En esta actividad vas a trabajar en colaboración con estudiantes de otra escuela para medir el radio de la Tierra. Vas a usar los mismos métodos y principios
El proyecto Eratóstenes. Guía para el estudiante. En esta actividad vas a trabajar en colaboración con estudiantes de otra escuela para medir el radio de la Tierra. Vas a usar los mismos métodos y principios
La ventana de Microsoft Excel
 Actividad N 1 Conceptos básicos de Planilla de Cálculo La ventana del Microsoft Excel y sus partes. Movimiento del cursor. Tipos de datos. Metodología de trabajo con planillas. La ventana de Microsoft
Actividad N 1 Conceptos básicos de Planilla de Cálculo La ventana del Microsoft Excel y sus partes. Movimiento del cursor. Tipos de datos. Metodología de trabajo con planillas. La ventana de Microsoft
Determinación del acimut por observación al Sol
 Astronomía Geodésica Práctica Número 3 Determinación del acimut por observación al Sol ADVERTENCIA DE SEGURIDAD: en esta práctica nunca miréis al Sol directamente con el teodolito!!! 1 Objetivos En la
Astronomía Geodésica Práctica Número 3 Determinación del acimut por observación al Sol ADVERTENCIA DE SEGURIDAD: en esta práctica nunca miréis al Sol directamente con el teodolito!!! 1 Objetivos En la
Transformación de coordenadas
 Anexo A Transformación de coordenadas Para realizar las transformaciones entre sistemas de coordenadas astronómicos, se utilizarán giros en el espacio, ya que todos los sistemas se suponen con el mismo
Anexo A Transformación de coordenadas Para realizar las transformaciones entre sistemas de coordenadas astronómicos, se utilizarán giros en el espacio, ya que todos los sistemas se suponen con el mismo
UNIDAD 6 PARA ENTENDER MEJOR LOS MAPAS
 UNIDAD 6 PARA ENTENDER MEJOR LOS MAPAS Interpretar y utilizar recursos y simbología utilizados en la asignatura de estudios sociales. Analizar con espíritu reflexivo y crítico las informaciones que se
UNIDAD 6 PARA ENTENDER MEJOR LOS MAPAS Interpretar y utilizar recursos y simbología utilizados en la asignatura de estudios sociales. Analizar con espíritu reflexivo y crítico las informaciones que se
Funciones y sus gráficas
 Funciones y sus gráficas El concepto de función es de suma importancia en la matemática moderna, debido a esto vamos a estudiar este tema de una manera un poco detallada. Dos conjuntos de números, por
Funciones y sus gráficas El concepto de función es de suma importancia en la matemática moderna, debido a esto vamos a estudiar este tema de una manera un poco detallada. Dos conjuntos de números, por
Tema 2 Límites de Funciones
 Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
Teclado sobre una PDA para Personas con Parálisis Cerebral
 Manual de Usuario - 1 - - 2 - Teclado sobre una PDA para Personas con Parálisis Cerebral Capítulo 1. MANUAL DE USUARIO 12.1 Descripción de la aplicación Este programa le permitirá llevar a cabo las siguientes
Manual de Usuario - 1 - - 2 - Teclado sobre una PDA para Personas con Parálisis Cerebral Capítulo 1. MANUAL DE USUARIO 12.1 Descripción de la aplicación Este programa le permitirá llevar a cabo las siguientes
SISTEMA DE PLANOS ACOTADOS APUNTES REALIZADOS POR ANTONIO CUESTA
 SISTEMA DE LANOS ACOTADOS AUNTES REALIZADOS OR ANTONIO CUESTA El sistema de lanos Acotados o Sistema Acotado constituye, al igual que el Sistema Diédrico, un sistema de representación reversible en el
SISTEMA DE LANOS ACOTADOS AUNTES REALIZADOS OR ANTONIO CUESTA El sistema de lanos Acotados o Sistema Acotado constituye, al igual que el Sistema Diédrico, un sistema de representación reversible en el
JOSÉ PERAZA, FÍSICA 2 JOSÉ PERAZA, FÍSICA 2 JOSÉ PERAZA, FÍSICA 2 Energía Potencial eléctrica
 Energía Potencial eléctrica Si movemos la carga q2 respecto a la carga q1 Recordemos que la diferencia en la energía tenemos que: potencial U cuando una partícula se mueve entre dos puntos a y b bajo la
Energía Potencial eléctrica Si movemos la carga q2 respecto a la carga q1 Recordemos que la diferencia en la energía tenemos que: potencial U cuando una partícula se mueve entre dos puntos a y b bajo la
CALCULO CAPITULO 1 1.6 ASINTOTAS VERTICALES Y HORIZONTALES
 1.6 ASINTOTAS VERTICALES Y HORIZONTALES 1.6.1.- Definición. Una asíntota es una recta que se encuentra asociada a la gráfica de algunas curvas y que se comporta como un límite gráfico hacia la cual la
1.6 ASINTOTAS VERTICALES Y HORIZONTALES 1.6.1.- Definición. Una asíntota es una recta que se encuentra asociada a la gráfica de algunas curvas y que se comporta como un límite gráfico hacia la cual la
A RG. Giro de un punto A respecto del eje vertical, e. Giro de un punto A respecto del eje de punta, e.
 Giro de un punto A respecto del eje vertical, e. A''' A''' 2 e A'' 60 El giro es otro de los procedimietos utilizados en diédrico para resolver construcciones. Aquí vamos a ver solo uno de sus aspectos:
Giro de un punto A respecto del eje vertical, e. A''' A''' 2 e A'' 60 El giro es otro de los procedimietos utilizados en diédrico para resolver construcciones. Aquí vamos a ver solo uno de sus aspectos:
TALLER DE ASTRONOMIA
 TALLER DE ASTRONOMIA Es necesario levantar al cielo los ojos para poder ver la tierra Francisco José de Caldas Desde la antigüedad el hombre ha construido monumentos y observatorios astronómicos para seguir
TALLER DE ASTRONOMIA Es necesario levantar al cielo los ojos para poder ver la tierra Francisco José de Caldas Desde la antigüedad el hombre ha construido monumentos y observatorios astronómicos para seguir
Covarianza y coeficiente de correlación
 Covarianza y coeficiente de correlación Cuando analizábamos las variables unidimensionales considerábamos, entre otras medidas importantes, la media y la varianza. Ahora hemos visto que estas medidas también
Covarianza y coeficiente de correlación Cuando analizábamos las variables unidimensionales considerábamos, entre otras medidas importantes, la media y la varianza. Ahora hemos visto que estas medidas también
GEOMETRÍA DESCRIPTIVA SISTEMAS DE PROYECCIÓN
 GEOMETRÍA DESCRIPTIVA La Geometría Descriptiva es la ciencia de representación gráfica, sobre superficies bidimensionales, de los problemas del espacio donde intervengan, puntos, líneas y planos. La Geometría
GEOMETRÍA DESCRIPTIVA La Geometría Descriptiva es la ciencia de representación gráfica, sobre superficies bidimensionales, de los problemas del espacio donde intervengan, puntos, líneas y planos. La Geometría
10 Anexo A: Aspectos Básicos de la Radiación Solar
 10 Anexo A: Aspectos Básicos de la Radiación Solar 10.1 Relaciones astronómicas Tierra-Sol La literatura solar contiene una gran variedad de sistemas, métodos y ecuaciones para establecer las relaciones
10 Anexo A: Aspectos Básicos de la Radiación Solar 10.1 Relaciones astronómicas Tierra-Sol La literatura solar contiene una gran variedad de sistemas, métodos y ecuaciones para establecer las relaciones
Equivalencias con el programa oficial de la asignatura de Topografía del Grado en Ingeniería Agronómica
 Equivalencias con el programa oficial de la asignatura de Topografía del Grado en Ingeniería Agronómica Bloque 1: CONCEPTOS BÁSICOS Tema 1: Generalidades Tema 2: Estudio de los errores en Topografía Bloque
Equivalencias con el programa oficial de la asignatura de Topografía del Grado en Ingeniería Agronómica Bloque 1: CONCEPTOS BÁSICOS Tema 1: Generalidades Tema 2: Estudio de los errores en Topografía Bloque
5.3 Esfuerzos y deformaciones producidos por flexión. Puente grúa. 5.3.1 Flexión pura
 5.3 Esfuerzos y deformaciones producidos por flexión Puente grúa 5.3.1 Flexión pura Para cierta disposición de cargas, algunos tramos de los elementos que las soportan están sometidos exclusivamente a
5.3 Esfuerzos y deformaciones producidos por flexión Puente grúa 5.3.1 Flexión pura Para cierta disposición de cargas, algunos tramos de los elementos que las soportan están sometidos exclusivamente a
GEOMETRÍA 1.- INTRODUCCIÓN:
 GEOMETRÍA 1.- INTRODUCCIÓN: Etimológicamente hablando, la palabra Geometría procede del griego y significa Medida de la Tierra. La Geometría es la parte de las Matemáticas que estudia las idealizaciones
GEOMETRÍA 1.- INTRODUCCIÓN: Etimológicamente hablando, la palabra Geometría procede del griego y significa Medida de la Tierra. La Geometría es la parte de las Matemáticas que estudia las idealizaciones
Operaciones con polinomios
 Operaciones con polinomios Los polinomios son una generalización de nuestro sistema de numeración. Cuando escribimos un número, por ejemplo, 2 354, queremos decir: 2 354 = 2 000 + 300 + 50 + 4 = 2)1 000)
Operaciones con polinomios Los polinomios son una generalización de nuestro sistema de numeración. Cuando escribimos un número, por ejemplo, 2 354, queremos decir: 2 354 = 2 000 + 300 + 50 + 4 = 2)1 000)
Los números racionales
 Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Los polinomios. Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x
 Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Clase de apoyo de matemáticas Ángulos Escuela 765 Lago Puelo Provincia de Chubut
 Clase de apoyo de matemáticas Ángulos Escuela 765 Lago Puelo Provincia de Chubut Este texto intenta ser un complemento de las clases de apoyo de matemáticas que se están realizando en la escuela 765 de
Clase de apoyo de matemáticas Ángulos Escuela 765 Lago Puelo Provincia de Chubut Este texto intenta ser un complemento de las clases de apoyo de matemáticas que se están realizando en la escuela 765 de
Cálculo del radio de la Tierra. Método de Eratóstenes ( Siglo III a.c.)
 Cálculo del radio de la Tierra. Método de Eratóstenes ( Siglo III a.c.) Introducción histórica El griego Eratóstenes vivió en Alejandría entre los años 276 a. C. y 194 a. C. Era un conocido matemático,
Cálculo del radio de la Tierra. Método de Eratóstenes ( Siglo III a.c.) Introducción histórica El griego Eratóstenes vivió en Alejandría entre los años 276 a. C. y 194 a. C. Era un conocido matemático,
LÍMITES Y CONTINUIDAD DE FUNCIONES
 Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
1. Dominio, simetría, puntos de corte y periodicidad
 Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
(a) El triángulo dado se descompone en tres segmentos de recta que parametrizamos de la siguiente forma: (0 t 1); y = 0. { x = 1 t y = t. (0 t 1).
 INTEGRALES DE LÍNEA. 15. alcular las siguientes integrales: (a) (x + y) ds donde es el borde del triángulo con vértices (, ), (1, ), (, 1). (b) x + y ds donde es la circunferencia x + y ax (a > ). (a)
INTEGRALES DE LÍNEA. 15. alcular las siguientes integrales: (a) (x + y) ds donde es el borde del triángulo con vértices (, ), (1, ), (, 1). (b) x + y ds donde es la circunferencia x + y ax (a > ). (a)
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen: O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen: O también denominado Punto de aplicación. Es el punto exacto sobre
Unidad 5 Estudio gráfico de funciones
 Unidad 5 Estudio gráfico de funciones PÁGINA 84 SOLUCIONES Representar puntos en un eje de coordenadas. 43 Evaluar un polinomio. a) P(-1) = 1 + + 1 1 = 3 b) P(0) = -1 c) P(-) = 8 + 8 + 1 = 17 d) P(1) =
Unidad 5 Estudio gráfico de funciones PÁGINA 84 SOLUCIONES Representar puntos en un eje de coordenadas. 43 Evaluar un polinomio. a) P(-1) = 1 + + 1 1 = 3 b) P(0) = -1 c) P(-) = 8 + 8 + 1 = 17 d) P(1) =
PRISMA OBLICUO > REPRESENTACIÓN Y DESARROLLO POR EL MÉTODO DE LA SECCIÓN NORMAL
 1. CARACTERÍSTICAS GENERALES DEL PRISMA OBLICUO Desde el punto de vista de la representación en SISTEMA DIÉDRICO, el prisma oblicuo presenta dos características importantes que lo diferencian del prisma
1. CARACTERÍSTICAS GENERALES DEL PRISMA OBLICUO Desde el punto de vista de la representación en SISTEMA DIÉDRICO, el prisma oblicuo presenta dos características importantes que lo diferencian del prisma
Colegio Alexander von Humboldt - Lima. Tema: La enseñanza de la matemática está en un proceso de cambio
 Refo 07 2004 15 al 19 de noviembre 2004 Colegio Alexander von Humboldt - Lima Tema: La enseñanza de la matemática está en un proceso de cambio La enseñanza de la matemática debe tener dos objetivos principales:
Refo 07 2004 15 al 19 de noviembre 2004 Colegio Alexander von Humboldt - Lima Tema: La enseñanza de la matemática está en un proceso de cambio La enseñanza de la matemática debe tener dos objetivos principales:
Guía 1: Sistemas de referencia y coordenadas ArcGIS 10 o ArcGis 10.1
 Guía 1: Sistemas de referencia y coordenadas ArcGIS 10 o ArcGis 10.1 La localización de los lugares en la superficie terrestre y su representación sobre un plano requieren de dos procesos distintos: en
Guía 1: Sistemas de referencia y coordenadas ArcGIS 10 o ArcGis 10.1 La localización de los lugares en la superficie terrestre y su representación sobre un plano requieren de dos procesos distintos: en
Geometría Tridimensional
 Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice
 Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Para cada cada valor de la función original lo multiplicas por 3 lo recorres 45 a la derecha y lo subes 5 unidades.
 3.5 Gráficas de las funciones: f(x) = a sen (bx + c) + d f(x) = a cos (bx + c) + d f(x) = a tan (bx + c) + d en donde a, b, c, y d son números reales En la sección 3.4 ya realizamos algunos ejemplos en
3.5 Gráficas de las funciones: f(x) = a sen (bx + c) + d f(x) = a cos (bx + c) + d f(x) = a tan (bx + c) + d en donde a, b, c, y d son números reales En la sección 3.4 ya realizamos algunos ejemplos en
Construimos un CUADRANTE y aprendemos a utilizarlo.
 Construimos un CUADRANTE y aprendemos a utilizarlo. El cuadrante es un sencillo instrumento que sirve para medir, generalmente, ángulos de elevación. Fue utilizado, sobretodo, en los comienzos de la navegación
Construimos un CUADRANTE y aprendemos a utilizarlo. El cuadrante es un sencillo instrumento que sirve para medir, generalmente, ángulos de elevación. Fue utilizado, sobretodo, en los comienzos de la navegación
Las razones financieras ayudan a determinar las relaciones existentes entre diferentes rubros de los estados financieros
 Razones financieras Uno de los métodos más útiles y más comunes dentro del análisis financiero es el conocido como método de razones financieras, también conocido como método de razones simples. Este método
Razones financieras Uno de los métodos más útiles y más comunes dentro del análisis financiero es el conocido como método de razones financieras, también conocido como método de razones simples. Este método
Programa Tracker : Cómo generar Vectores y sumarlos
 Programa Tracker : Cómo generar Vectores y sumarlos Esta guía explica cómo usar vectores, la posibilidad de sumarlos, presentar los resultados directamente en pantalla y compararlos de forma gráfica y
Programa Tracker : Cómo generar Vectores y sumarlos Esta guía explica cómo usar vectores, la posibilidad de sumarlos, presentar los resultados directamente en pantalla y compararlos de forma gráfica y
Funciones de varias variables
 Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Funciones de varias variables Derivadas parciales. El concepto de función derivable no se puede extender de una forma sencilla para funciones de varias variables. Aquí se emplea el concepto de diferencial
Potencial eléctrico. du = - F dl
 Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
Biblioteca Virtual Ejercicios Resueltos
 EJERCICIO 13 13 V a l o r n u m é r i c o Valor numérico de expresiones compuestas P r o c e d i m i e n t o 1. Se reemplaza cada letra por su valor numérico 2. Se efectúan las operaciones indicadas Hallar
EJERCICIO 13 13 V a l o r n u m é r i c o Valor numérico de expresiones compuestas P r o c e d i m i e n t o 1. Se reemplaza cada letra por su valor numérico 2. Se efectúan las operaciones indicadas Hallar
LÍMITES DE FUNCIONES Y DE SUCESIONES
 LÍMITES DE FUNCIONES Y DE SUCESIONES Índice: 1.Funciones reales de variable real-------------------------------------------------------------- 1 2. Límite finito de una función en un punto.---------------------------------------------------
LÍMITES DE FUNCIONES Y DE SUCESIONES Índice: 1.Funciones reales de variable real-------------------------------------------------------------- 1 2. Límite finito de una función en un punto.---------------------------------------------------
Profr. Efraín Soto Apolinar. Factorización
 Factorización La factorización es la otra parte de la historia de los productos notables. Esto es, ambas cosas se refieren a las mismas fórmulas, pero en los productos notables se nos daba una operación
Factorización La factorización es la otra parte de la historia de los productos notables. Esto es, ambas cosas se refieren a las mismas fórmulas, pero en los productos notables se nos daba una operación
SISTEMAS DE COORDENADAS SISTEMA COORDENADO UNIDIMENSIONAL
 SISTEMAS DE COORDENADAS En la vida diaria, nos encontramos con el problema de ordenar algunos objetos; de tal manera que es necesario agruparlos, identificarlos, seleccionarlos, estereotiparlos, etc.,
SISTEMAS DE COORDENADAS En la vida diaria, nos encontramos con el problema de ordenar algunos objetos; de tal manera que es necesario agruparlos, identificarlos, seleccionarlos, estereotiparlos, etc.,
Fórmulas y funciones
 Fórmulas y funciones Uso de fórmulas Las fórmulas son el corazón y el alma de la hoja de cálculo. Si no las necesitáramos sería lo mismo que trabajáramos en un procesador de textos. Excel 2007 ofrece un
Fórmulas y funciones Uso de fórmulas Las fórmulas son el corazón y el alma de la hoja de cálculo. Si no las necesitáramos sería lo mismo que trabajáramos en un procesador de textos. Excel 2007 ofrece un
DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN DE UN TRANSFORMADOR DE POTENCIA
 PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN DE UN TRANSFORMADOR DE POTENCIA Departamento de Ingeniería Eléctrica E.T.S.I.I. Página 1 de 14 PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN
PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN DE UN TRANSFORMADOR DE POTENCIA Departamento de Ingeniería Eléctrica E.T.S.I.I. Página 1 de 14 PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN
VECTORES: VOCABULARIO 1. Abscisa de un punto. 2. Ordenada de un punto. 3. Concepto de vector. 4. Coordenadas o componentes de un vector. 5.
 VECTORES: VOCABULARIO 1. Abscisa de un punto. 2. Ordenada de un punto. 3. Concepto de vector. 4. Coordenadas o componentes de un vector. 5. Elementos de un vector. 6. Concepto de origen de un vector. 7.
VECTORES: VOCABULARIO 1. Abscisa de un punto. 2. Ordenada de un punto. 3. Concepto de vector. 4. Coordenadas o componentes de un vector. 5. Elementos de un vector. 6. Concepto de origen de un vector. 7.
Interpolación polinómica
 9 9. 5 9. Interpolación de Lagrange 54 9. Polinomio de Talor 57 9. Dados dos puntos del plano (, ), (, ), sabemos que ha una recta que pasa por ellos. Dicha recta es la gráfica de un polinomio de grado,
9 9. 5 9. Interpolación de Lagrange 54 9. Polinomio de Talor 57 9. Dados dos puntos del plano (, ), (, ), sabemos que ha una recta que pasa por ellos. Dicha recta es la gráfica de un polinomio de grado,
LÍMITES DE FUNCIONES. CONTINUIDAD
 LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
1-Comportamiento de una función alrededor de un punto:
 Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Curso sobre el Sistema Solar: Lección nro. 1
 Curso sobre el Sistema Solar: Lección nro. 1 Que es el Sistema Solar? a1) Aspecto del Firmamento: Idea General. Comenzaremos por considerar lo que es posible conocer del Sistema Solar sin la ayuda de ningún
Curso sobre el Sistema Solar: Lección nro. 1 Que es el Sistema Solar? a1) Aspecto del Firmamento: Idea General. Comenzaremos por considerar lo que es posible conocer del Sistema Solar sin la ayuda de ningún
TEMA 8: LÍMITES DE FUNCIONES. CONTINUIDAD
 TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
Practica No. 02 LEVANTAMIENTO TOPOGRÁFICO DE UN TERRENO CON WINCHA Y JALÓNES AGRIMENSURA
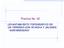 Practica No. 02 LEVANTAMIENTO TOPOGRÁFICO DE UN TERRENO CON WINCHA Y JALÓNES AGRIMENSURA C D B A Canal de riego Parcela de Cultivo Objetivo: Realizar el levantamiento de una pequeña parcela usando instrumentos
Practica No. 02 LEVANTAMIENTO TOPOGRÁFICO DE UN TERRENO CON WINCHA Y JALÓNES AGRIMENSURA C D B A Canal de riego Parcela de Cultivo Objetivo: Realizar el levantamiento de una pequeña parcela usando instrumentos
Unidad: Representación gráfica del movimiento
 Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Programa para el Mejoramiento de la Enseñanza de la Matemática en ANEP Proyecto: Análisis, Reflexión y Producción. Fracciones
 Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Lección 4: Suma y resta de números racionales
 GUÍA DE MATEMÁTICAS II Lección : Suma y resta de números racionales En esta lección recordaremos cómo sumar y restar números racionales. Como los racionales pueden estar representados como fracción o decimal,
GUÍA DE MATEMÁTICAS II Lección : Suma y resta de números racionales En esta lección recordaremos cómo sumar y restar números racionales. Como los racionales pueden estar representados como fracción o decimal,
APLICABILIDAD DE LA TRIGONOMETRÍA: MIDIENDO ALTURAS
 APLICABILIDAD DE LA TRIGONOMETRÍA: MIDIENDO ALTURAS AUTORIA NOEMI MÍNGUEZ LOPERA TEMÁTICA TRIGONOMETRÍA ETAPA 3º Y 4º DE ESO Resumen En este artículo vemos una de las aplicaciones de la tosca geometría
APLICABILIDAD DE LA TRIGONOMETRÍA: MIDIENDO ALTURAS AUTORIA NOEMI MÍNGUEZ LOPERA TEMÁTICA TRIGONOMETRÍA ETAPA 3º Y 4º DE ESO Resumen En este artículo vemos una de las aplicaciones de la tosca geometría
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Soluciones a los problemas Olimpiada de Matemáticas Fase local Extremadura Enero de 2015
 Olimpiada atemática Española RSE Soluciones a los problemas Olimpiada de atemáticas Fase local Extremadura Enero de 2015 1. lrededor de una mesa circular están sentadas seis personas. ada una lleva un
Olimpiada atemática Española RSE Soluciones a los problemas Olimpiada de atemáticas Fase local Extremadura Enero de 2015 1. lrededor de una mesa circular están sentadas seis personas. ada una lleva un
FUNCIONES CUADRÁTICAS Y RACIONALES
 www.matesronda.net José A. Jiménez Nieto FUNCIONES CUADRÁTICAS Y RACIONALES 1. FUNCIONES CUADRÁTICAS. Representemos, en función de la longitud de la base (), el área (y) de todos los rectángulos de perímetro
www.matesronda.net José A. Jiménez Nieto FUNCIONES CUADRÁTICAS Y RACIONALES 1. FUNCIONES CUADRÁTICAS. Representemos, en función de la longitud de la base (), el área (y) de todos los rectángulos de perímetro
INTRODUCCIÓN A VECTORES Y MAGNITUDES
 C U R S O: FÍSIC Mención MTERIL: FM-01 INTRODUCCIÓN VECTORES Y MGNITUDES La Física tiene por objetivo describir los fenómenos que ocurren en la naturaleza, a través de relaciones entre magnitudes físicas.
C U R S O: FÍSIC Mención MTERIL: FM-01 INTRODUCCIÓN VECTORES Y MGNITUDES La Física tiene por objetivo describir los fenómenos que ocurren en la naturaleza, a través de relaciones entre magnitudes físicas.
NÚMEROS NATURALES Y NÚMEROS ENTEROS
 NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
VII INTEGRALES TRIGONOMÉTRICAS
 VII INTEGRALES TRIGONOMÉTRICAS Diez fórmulas más habrán de agregarse al formulario actual de integrales del estudiante. Son seis correspondientes a las seis funciones trigonométricas seno, coseno, tangente,
VII INTEGRALES TRIGONOMÉTRICAS Diez fórmulas más habrán de agregarse al formulario actual de integrales del estudiante. Son seis correspondientes a las seis funciones trigonométricas seno, coseno, tangente,
MICROECONOMÍA II PRÁCTICA TEMA III: MONOPOLIO
 MICROECONOMÍA II PRÁCTICA TEMA III: MONOPOLIO EJERCICIO 1 Primero analizamos el equilibrio bajo el monopolio. El monopolista escoge la cantidad que maximiza sus beneficios; en particular, escoge la cantidad
MICROECONOMÍA II PRÁCTICA TEMA III: MONOPOLIO EJERCICIO 1 Primero analizamos el equilibrio bajo el monopolio. El monopolista escoge la cantidad que maximiza sus beneficios; en particular, escoge la cantidad
FUNDAMENTOS FÍSICOS DE LA RADIOASTRONOMÍA. CAPÍTULO 1. Propiedades de la radiación electromagnética
 Página principal El proyecto y sus objetivos Cómo participar Cursos de radioastronomía Material Novedades FUNDAMENTOS FÍSICOS DE LA RADIOASTRONOMÍA Índice Introducción Capítulo 1 Capítulo 2 Capítulo 3
Página principal El proyecto y sus objetivos Cómo participar Cursos de radioastronomía Material Novedades FUNDAMENTOS FÍSICOS DE LA RADIOASTRONOMÍA Índice Introducción Capítulo 1 Capítulo 2 Capítulo 3
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Código/Título de la Unidad Didáctica: MATEMÁTICAS BASICAS APLICADAS EN EL MECANIZADO. Actividad nº/título: REGLA DE TRES y SISTEMAS DE COORDENADAS
 Código/Título de la Unidad Didáctica: MATEMÁTICAS BASICAS APLICADAS EN EL MECANIZADO Actividad nº/título: REGLA DE TRES y SISTEMAS DE COORDENADAS Introducción a la actividad Material Didáctico: Tiempo:
Código/Título de la Unidad Didáctica: MATEMÁTICAS BASICAS APLICADAS EN EL MECANIZADO Actividad nº/título: REGLA DE TRES y SISTEMAS DE COORDENADAS Introducción a la actividad Material Didáctico: Tiempo:
1.- Explica por qué los cuerpos cargados con cargas de distinto signo se atraen, mientras que si las cargas son del mismo signo, se repelen.
 Física 2º de Bachillerato. Problemas de Campo Eléctrico. 1.- Explica por qué los cuerpos cargados con cargas de distinto signo se atraen, mientras que si las cargas son del mismo signo, se repelen. 2.-
Física 2º de Bachillerato. Problemas de Campo Eléctrico. 1.- Explica por qué los cuerpos cargados con cargas de distinto signo se atraen, mientras que si las cargas son del mismo signo, se repelen. 2.-
Tema 2. Espacios Vectoriales. 2.1. Introducción
 Tema 2 Espacios Vectoriales 2.1. Introducción Estamos habituados en diferentes cursos a trabajar con el concepto de vector. Concretamente sabemos que un vector es un segmento orientado caracterizado por
Tema 2 Espacios Vectoriales 2.1. Introducción Estamos habituados en diferentes cursos a trabajar con el concepto de vector. Concretamente sabemos que un vector es un segmento orientado caracterizado por
Anexo I. La visión. El proceso de la visión. 1. Introducción. 2. La visión
 Anexo I. La visión El proceso de la visión 1. Introducción El ojo humano ha sufrido grandes modificaciones a través de los tiempos como consecuencia de las diferentes formas de vida, desde cuando se usaba
Anexo I. La visión El proceso de la visión 1. Introducción El ojo humano ha sufrido grandes modificaciones a través de los tiempos como consecuencia de las diferentes formas de vida, desde cuando se usaba
