AISLANTES Y CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS
|
|
|
- Belén Páez Ríos
- hace 8 años
- Vistas:
Transcripción
1 UNIVERSIDAD DE CANTABRIA DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA AISLANTES Y CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS Mguel Angel Rodríguez Pozueta
2 AISLANTES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS MATERIALES AISLANTES Aslante eléctrco o deléctrco es aquel materal que tene una conductvdad eléctrca tan baa que se puede desprecar la corrente que pasa por él. Esta pequeñísma corrente que pasa a través de un aslante se denomna corrente de fuga. El vacío es el únco aslante perfecto ya que tene conductanca nula y por él no crculan correntes de fuga. Los demás materales aslantes son deléctrcos mperfectos, con conductanca no nula pero tan pequeña que sus correntes de fuga son desprecables. Los aslantes se utlzan en las máqunas eléctrcas para asegurar el aslamento eléctrco entre los conductores y entre éstos y las pezas metálcas y la carcasa. Estos materales suelen ser la parte más delcada de una máquna eléctrca debdo a su sensbldad a las solctacones térmcas, mecáncas y deléctrcas. A la hora de elegr un aslante para una aplcacón dada hay que consderar un conunto de propedades que debe cumplr y que se pueden clasfcar en: Propedades eléctrcas Propedades mecáncas Propedades físco-químcas Evdentemente, las propedades eléctrcas son las más mportantes, pero no hay que olvdar las demás. De las propedades no eléctrcas, una de las más mportantes es la máxma temperatura que puede soportar un aslante sn que sus propedades eléctrcas se vean afectadas. RESISTENCIA DE AISLAMIENTO La resstenca de aslamento de un deléctrco es la resstenca que opone al paso de la corrente eléctrca, medda en la dreccón en que se tene que asegurar el aslamento. La corrente de fuga de un aslante sgue dos camnos: uno sobre la superfce y otro a través del nteror del materal. La resstenca de aslamento que presenta el materal se debe al efecto de estos dos camnos en paralelo. La resstvdad de aslamento superfcal se mde en MΩ y es debda a la resstenca que ofrece la superfce del materal al paso de la corrente cuando se aplca tensón entre dos puntos de dcha superfce (Fg. a). Evdentemente esta magntud está muy afectada por el estado de lmpeza de la superfce. La sucedad (grasa, polvo, etc.) depostada sobre la superfce de un deléctrco reduce la resstvdad de aslamento superfcal. Por esta razón, las pezas aslantes hay que construrlas lsas y puldas. Según la norma UNE 2303 la resstvdad superfcal es gual a la resstenca superfcal que presenta una superfce cuadrada y es ndependente del tamaño de este cuadrado. Para obtener esta resstvdad se utlza el montae de la Fg. a donde se mde la resstenca entre los electrodos (por eemplo, usando una fuente de tensón contnua, mdendo la corrente que aparece y aplcando la ley de Ohm) y la resstvdad se calcula multplcando esta resstenca por el perímetro de un electrodo y dvdéndola por la dstanca entre los electrodos. M.A.R. Pozueta --
3 La resstvdad de aslamento transversal o volumétrca se mde en MΩcm 2 /cm y es debda a la resstenca que ofrece el deléctrco a ser atravesado por una corrente cuando se aplca tensón entre dos de sus caras (Fg. b). Esta magntud no tene un valor constante para un msmo materal, ya que le afectan la temperatura, la humedad, el espesor de la peza, el enveecmento del materal, etc. Es obvo que se debe procurar que la resstenca de aslamento de un materal aslante sea lo más alta posble. RIGIDEZ DIELÉCTRICA (a) (b) Fg. : Resstenca de aslamento superfcal (a) y transversal (b). (: Materal aslante; 2: Electrodo) Cuando se aplca tensón eléctrca moderada entre dos caras de un aslante el campo eléctrco que aparece produce una pequeña corrente de fuga debdo a los pocos electrones lbres que tene el materal. Además, los átomos se ven sometdos fuerzas que afectan a las órbtas de sus electrones lgados. S la tensón y, por lo tanto, la ntensdad del campo eléctrco, aumentan y superan certo límte los electrones empezan a abandonar sus átomos y algunos de ellos chocan con otros átomos provocando un aumento de temperatura y la separacón de nuevos electrones. Se produce así un efecto acumulatvo denomnado descarga que provoca la pérdda permanente (perforacón del aslante) o temporal (descargas parcales) de las cualdades aslantes del materal. Se denomna rgdez deléctrca de un aslante a la ntensdad del campo eléctrco máxma que puede soportar el aslante sn que se produzca su perforacón. Es decr, cuando la ntensdad del campo eléctrco en el nteror del materal aslante supera a su rgdez deléctrca, este dea de ser aslante y se converte en conductor. Esta magntud se determna expermentalmente medante ensayos normalzados en los que se aplca una tensón entre dos electrodos colocados en caras opuestas de una muestra del aslante (como en la Fg. b). La tensón se va aumentando gradualmente hasta provocar la perforacón del aslante. La rgdez deléctrca se expresa como cocente entre la tensón de perforacón del materal y el espesor de la peza aslante y se mde en kv/mm. En el caso de que la tensón M.A.R. Pozueta -2-
4 que se aplca al aslante sea alterna hay que especfcar s se utlza su valor efcaz o el de cresta (valor máxmo). Usualmente se utlza el valor de cresta. El valor de la rgdez deléctrca depende de las condcones en las que se realza el ensayo del materal: dmensones y forma de los electrodos, espesor del aslante, duracón de la aplcacón del voltae, frecuenca, forma de la onda de tensón, condcones ambentales, etc. Tambén exste la rgdez deléctrca superfcal cuando la tensón se aplca entre dos puntos de la superfce del aslante. En este caso la rgdez deléctrca es el cocente entre la tensón de perforacón y la dstanca entre los electrodos (que se colocan de una manera smlar a la ndcada en la Fg. a). La rgdez deléctrca superfcal tambén se mde en kv/mm, pero ahora, s la tensón es alterna, se utlza su valor efcaz. Los materales aslantes sumergdos en acete tenen meor rgdez deléctrca que los que se encuentran al are. CONSTANTE DIELÉCTRICA Se puede defnr la constante deléctrca o permtvdad relatva de un aslante como el cocente de la capacdad de un condensador que tuvera como deléctrco a este materal entre la capacdad que tendría el msmo condensador s utlzara el vacío como deléctrco. Así s se tene un condensador plano cuyas placas tenen una seccón S, están separadas una dstanca y usa el vacío como deléctrco, su capacdad C0 vene dada por C0 0 S () En esta expresón 0 es la permtvdad absoluta del vacío. S este msmo condensador utlza como deléctrco un materal de constante deléctrca, su capacdad pasa a valer C, la cual vene dada por C 0 S (2) Luego, la constante deléctrca se obtene medante este cocente C (3) C 0 Consdérese ahora un condensador plano de seccón S que tene como deléctrco varas capas planas de dferentes materales aslantes (Fg. 2) con espesores, 2,, sendo la separacón entre las placas del condensador: L (4) La tensón total aplcada entre las placas del condensador es V y da lugar a las caídas de tensón V entre las dos caras del materal aslante, V2 entre las caras del materal aslante 2, V V + V + L (5) 2 M.A.R. Pozueta -3-
5 Fg. 2: Condensador plano cuyo deléctrco son varas capas paralelas de materal aslante. La ntensdad del campo eléctrco E en el nteror del aslante vale E V (6) y E m es la ntensdad del campo eléctrco meda en el condensador: E V m (7) Este condensador se lo puede suponer equvalente a colocar en sere varos condensadores parcales de la msma seccón S, cuyas placas tuveran respectvamente una separacón, 2, y cuyos deléctrcos tuveran respectvamente las constantes deléctrcas, 2, Las tensones entre las placas de cada uno de estos condensadores parcales serían, respectvamente, V, V2, y la capacdad C de uno de estos condensadores parcales vene dada por esta expresón C S (8) 0 Al tratarse de varos condensadores en sere, la capacdad C del conunto se puede obtener de (9) C C S 0 En sere todos los condensadores están recorrdos por la msma corrente, por lo cual tenen la msma carga Q. Luego: Q V C V C V V C C C C 0 0 S S V E (0) E V m En el caso de que el condensador sólo tuvera dos capas de materal aslante (materales y 2), la expresón (0) aplcada al materal se converte en: M.A.R. Pozueta -4-
6 E E m () que S sucede que el espesor del materal es mucho más pequeño que el del materal 2, se puede deducr 2 2 << 2 0 y E Em E 2 Em (2) En resumen, en un condensador plano cuyo deléctrco esté formado por dos capas de materal aslante (materales y 2), tales que el espesor del materal es bastante nferor al espesor 2 del materal 2, la expresón (2) permte obtener el campo eléctrco E en el nteror del materal aslante en funcón del campo eléctrco medo del condensador. De dcha expresón (2) se puede deducr que s la constante deléctrca 2 del materal 2 es mayor comparada con la constante deléctrca del materal sucede que (3) 2 > E > Em Por lo tanto, el aslante tene un campo eléctrco superor al medo, por lo que probablemente sea el que se encuentre más cerca de alcanzar su rgdez deléctrca y se pueda perforar. Aunque los párrafos anterores se han referdo a un condensador plano con dos capas de materal aslante, se puede generalzar y decr que en cualquer tpo de aslamento formado por varas capas de materal aslante sucede lo sguente: El materal aslante más solctado es el de menor constante deléctrca, lo cual hace que, s no tene una rgdez deléctrca aprecablemente más alta que la de los demás, este materal sea el que tenga más probabldad de llegar a perforarse prmero. Esto da lugar a la paradoa de que aumentando el espesor del meor aslante, pensando así aumentar la rgdez deléctrca del conunto, lo que se logra es provocar la perforacón del otro. En este caso toda la tensón queda aplcada al prmer aslante, que tambén puede acabar perforado. La meor dsposcón de aslantes en sere se consgue cuando se utlzan materales que tenen gual valor del producto de su constante deléctrca por su rgdez deléctrca. De lo anteror se deduce lo pelgrosas que resultan las burbuas de are que puedan quedar en el nteror de un aslante. La ntensdad del campo eléctrco en el nteror de estas burbuas es muy alto (ver las relacones (2) y (3)), lo que puede provocar descargas en ellas que pueden ser el nco de un fallo generalzado de todo el aslamento. En consecuenca es necesaro elmnar el are nteror de los aslantes, rellenando con barnz todos los posbles huecos, para lo cual se utlzan dstntos procedmentos de mpregnacón. Tambén es precso elmnar toda la humedad que puedan contener las bobnas, para lo cual estas se calentan antes de la mpregnacón durante el tempo necesaro para que la evaporacón del agua sea lo más completa posble. M.A.R. Pozueta -5-
7 La mpregnacón de los devanados se puede realzar por goteo, empleando un barnz elegdo especalmente para este fn. Otro procedmento es el de nmersón de la peza en un barnz hasta que ya no aparezcan burbuas de are en la superfce del msmo. Este es el procedmento que se suele emplear en máqunas pequeñas y medanas de baa tensón. Para máqunas de tensones más altas (200 a 5000 V) es convenente utlzar el método de mpregnacón en autoclave hacendo prmero vacío y luego nmersón en el barnz bao presón. La vscosdad del barnz debe ser la apropada para consegur la máxma penetracón. Después de la mpregnacón se efectúa un proceso de secado para elmnar el exceso de barnz y parte de los solventes. Según las característcas del barnz utlzado el secado puede realzarse de dos formas:. Secado al are en un ambente ben ventlado y lbre de polvo. 2. Secado al horno para mpedr que una parte de los solventes quede atrapada en la película del barnz y ataque el esmaltado del conductor. En las máqunas que superan los 5 kv y en transformadores de alta tensón se utlza un aslante semconductor, que tene por fnaldad proteger las bobnas contra los daños que producen los efluvos y las descargas parcales. PÉRDIDAS EN LOS AISLANTES Fg. 3: Hstéress deléctrca Cuando un aslante está sometdo a una tensón eléctrca aparece una corrente de fuga que da lugar a unas pequeñas pérddas de potenca por efecto Joule. Esto sucede tanto cuando la tensón es contnua como cuando es alterna. Cuando la tensón a la que se somete el aslante es alterna o, al menos, varable en el tempo, aparece el fenómeno de la hstéress deléctrca (Fg. 3). Este fenómeno guarda certa analogía con la conocda hstéress magnétca y es debdo a la nerca con que el desplazamento o densdad de carga D sgue las varacones de la ntensdad del campo eléctrco E. Las pérddas por hstéress deléctrca son mayores que las debdas al efecto Joule de las correntes de fuga y son las úncas que se tenen en cuenta cuando un aslante se encuentra sometdo a una tensón alterna. M.A.R. Pozueta -6-
8 Cuando se tenen dos conductores separados por un deléctrco y conectados a una tensón alterna, el conunto se comporta como un condensador y a través de él debería crcular una corrente puramente capactva; es decr, adelantada 90º con respecto a la tensón. El hecho de que exstan pérddas deléctrcas exge que se deba consumr algo de potenca actva de la fuente de tensón, lo que provoca que el desfase ϕ entre la tensón y la corrente sea lgeramente nferor a 90º (Fg. 4). De esta manera el factor de potenca cos ϕ no es nulo. Fg. 4: Ángulo de pérddas de un aslante El ángulo δ, complementaro del ángulo ϕ (Fg. 4), se denomna ángulo de pérddas. Es frecuente que se ndque el valor de la tangente de este ángulo (tg δ) entre los datos de un aslante. Dado el pequeño valor del ángulo δ (normalmente nferor a º) sucede que su tangente trgonométrca es gual al factor de potenca cos ϕ del materal aslante: δ << cos ϕ sen δ tg δ δ (4) Puesto que la energía almacenada en un aslante depende de su constante deléctrca, sus pérddas deléctrcas son proporconales al producto tg δ, el cual se denomna factor de pérddas deléctrcas. Las pérddas deléctrcas normalmente no se computan cuando se estudan las pérddas de una máquna eléctrca debdo a su pequeño valor frente a las demás pérddas: en el herro, en el cobre, mecáncas, Sn embargo, el estudo del valor de tg δ y de su varacón con el tempo permte conocer en qué estado se encuentra el aslamento de una máquna y su grado de enveecmento. Fg. 5: Crcuto equvalente de dos conductores, A y B, separados por un aslante. Un par de conductores, A y B, sometdos a una tensón eléctrca y separados por un aslante se pueden representar por el crcuto equvalente de la Fg. 5. En este crcuto, C es la capacdad del conunto, R asl es la resstenca de aslamento del aslante y la resstenca R perd permte nclur el efecto de las pérddas deléctrcas en este crcuto equvalente. M.A.R. Pozueta -7-
9 Las pérddas deléctrcas calentan el materal y aumentan su temperatura. Esto aumenta el fenómeno perudcal de la descarga y la perforacón subsguente. Se puede demostrar que exste para cada materal aslante un voltae crítco que puede aguantar. Por encma de este voltae se produce la perforacón del materal, sea cual sea su espesor. CLASE TÉRMICA DE LOS SISTEMAS DE AISLAMIENTO Según la norma UNE-EN un sstema de aslamento eléctrco es una estructura aslante que contene uno o más materales aslantes eléctrcos unto con partes conductoras asocadas y que se utlza en un dspostvo electrotécnco. En cas todas las máqunas eléctrcas la potenca que pueden sumnstrar está lmtada por la temperatura que alcanzan. Cuanto mayor es la potenca que sumnstra una máquna, mayores serán sus pérddas y, en consecuenca, el calor que se genera en ella. Este calor aumenta su temperatura y llega un momento en que esta temperatura es pelgrosa para la ntegrdad de la máquna. Normalmente los materales aslantes son los elementos más sensbles a la temperatura y, por consguente, los que lmtan la potenca que puede proporconar una máquna dada. A medda que pasa el tempo un materal aslante va enveecendo y el sstema de aslamento eléctrco va perdendo sus cualdades deléctrcas, lo cual se ve agravado s resulta sometdo a temperaturas elevadas. Es decr, los materales aslantes y los sstemas de aslamento eléctrco tenen una vda que, de forma orentatva, se puede establecer en 40 años en las máqunas grandes, 30 años en las medanas y 20 años en las pequeñas. Se han estudado y analzado los materales aslantes utlzados en las máqunas eléctrcas para averguar cuál es la máxma temperatura que pueden soportar sn pelgro de acortar su vda. Esta temperatura máxma se denomna enduranca térmca (véanse las normas UNE-EN 624 y 60085). CLASE TÉRMICA (ºC) Tabla I: Clase térmca de los sstemas de aslamento eléctrco según las normas UNE-EN 624, y ANTIGUA DESIGNACIÓN TEMPERATURA MÁXIMA (ºC) CALENTAMIENTO MÁXIMO (*) (ºC) 90 Y A E B F H N R (*) Esta columna ndca el calentamento máxmo en el supuesto que el fludo refrgerante sea are ambente a una alttud nferor a 000 metros sobre el nvel del mar M.A.R. Pozueta -8-
10 La clase térmca (UNE-EN 624, y ) de un sstema de aslamento se desgna medante el valor numérco de la temperatura de utlzacón contnua máxma recomendada medda en grados centígrados. Antguamente algunas de estas clases térmcas se desgnaban medante una letra. En la tabla I se recogen las desgnacones de las clases térmcas. La clase térmca de un sstema de aslamento eléctrco puede no estar drectamente relaconada con la enduranca térmca de uno de los materales aslantes ncludos en él. Es la combnacón de todos los elementos que consttuyen el sstema de aslamento lo que da lugar a su clase térmca. En la tercera columna de la tabla I se ndca la temperatura máxma a la que se puede someter un sstema de aslamento según su clase térmca para que su vda no se vea reducda. En la cuarta columna de esta tabla se señala el calentamento máxmo a que se lo puede someter s el fludo refrgerante es el are ambente. Se denomna calentamento a la dferenca entre la temperatura del sstema de aslamento y la del fludo de refrgeracón. La norma UNE establece que en España, para alttudes por debao de 000 m sobre el nvel del mar, se debe consderar que la temperatura del are ambente es 40ºC. Por lo tanto, la columna 4 de la tabla I -que muestra el calentamento máxmo admsble cuando el fludo refrgerante es el are ambente- se obtene restando 40ºC a los valores de la columna 3. Normalmente la temperatura de los bobnados se mde medante procedmentos que proporconan el valor medo de dcha magntud, pudendo haber puntos calentes de la máquna donde la temperatura tene un valor superor al medo. Por lo tanto, la norma UNE-EN establece que debe haber un margen de segurdad por debao de 5 a 5ºC -o ncluso mayor- según los casos, entre la temperatura que se mde por estos procedmentos y la temperatura límte ndcada en la tabla I. Los materales aslantes cuya enduranca térmca es más baa son aquellos con mayor proporcón de componentes orgáncos. Por el contraro, los aslantes que aguantan temperaturas más elevadas están formados en mayor medda por substancas norgáncas. A contnuacón se ctan algunos eemplos de los aslantes cuya enduranca térmca se corresponde con las clases térmcas de los sstemas de aslamento recogdas en la tabla I: 90ºC: Algodón, seda, papel sn mpregnacón. 05 ºC: Algodón, seda, papel mpregnados o sumergdos en acete. 20ºC: Fbras orgáncas sntétcas. Por eemplo: esmaltes de acetato de polvnlo, barnces de resnas alquídcas, 30ºC: Materales a base de poléster y polmdos aglutnados medante materales orgáncos. Por eemplo, los esmaltes de resnas de poluretano. 55ºC: Materales a base de fbra de mca, amanto y fbra de vdro aglutnados medante materales orgáncos. Por eemplo, la fbra de vdro tratada con resnas de poléster. 80ºC: Materales a base de mca, amanto y fbra de vdro aglutnados con slconas de alta establdad térmca. Por eemplo, el papel de mca aglomerado con slconas. 200ºC: Materales a base de mca, vdro, cerámca, capaces de soportar hasta 200ºC. 220ºC: Materales a base de mca, vdro, cerámca, polmdas tpo Kapton, capaces de soportar hasta 220ºC. 250ºC: Materales a base de mca, vdro, cerámca, polmdas tpo Kapton, capaces de soportar hasta 250ºC. M.A.R. Pozueta -9-
11 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS MATERIALES CONDUCTORES Los materales conductores se caracterzan por su elevada conductvdad que los permte conducr las correntes eléctrcas. La resstenca eléctrca R de un conductor se puede calcular medante la expresón sguente R l ρ (5) S En la expresón (5), l es la longtud del conductor, que usualmente se mde en metros (m) S es la seccón del conductor, que se suele medr en mm 2 ρ es la resstvdad del materal, que se suele ndcar en Ω mm 2 /m R es la resstenca, la cual se mde en Ohms (Ω). A veces se utlza la magntud nversa a la resstenca que se llama conductanca, G; cuya undad de medda es el Semens (S), tambén denomnado Mho (Ω - ): G (6) R La conductvdad σ es la nversa de la resstvdad y se mde en S m/mm 2 : σ ρ (7) Tabla II: Conductvdad a 20ºC de varos materales conductores MATERIAL CONDUCTIVIDAD σ A 20ºC (S m/mm 2 ) Cobre patrón 58 Cobre electrolítco recocdo 57 Cobre electrolítco comercal 56 Cobre electrolítco duro 56 Alumno recocdo 36 Alumno duro 35,4 Alumno nyectado para rotores 33 M.A.R. Pozueta -0-
12 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS En las máqunas eléctrcas se utlzan báscamente dos materales conductores, que son el cobre y el alumno. Para que la conductvdad de estos materales se mantenga alta deben ser de gran pureza. Los procesos de lamnacón y estrado dsmnuyen su conductvdad, por lo que deben ser sometdos segudamente a un proceso de recocdo. En la tabla II se ndcan los valores característcos de conductvdad a 20ºC para varos materales. EFECTO DE LA TEMPERATURA Al aumentar la temperatura la resstvdad del cobre y del alumno, como la de cas todos los metales, aumenta lnealmente. Por otra parte, el aumento de la temperatura tambén produce dlatacones que afectan a la longtud l y a la seccón S del conductor. De todo lo anteror se puede deducr que la resstenca de un conductor aumenta lnealmente con la temperatura. Por consguente, la resstenca Rθ de un conductor a la temperatura θ' se puede relaconar con la resstenca Rθ del msmo conductor a la temperatura θ, medante esta ley: θ [ + α ( θ' θ) ] R ' (8) Rθ θ El coefcente αθ se denomna coefcente aparente de temperatura y su valor no es constante, sno que depende de la temperatura θ a la que se refere la resstenca Rθ. Para 20ºC este coefcente vale aproxmadamente 0,0040 ºC -, tanto para el cobre como para el alumno. S se parte de una temperatura ncal de 0ºC (θ 0ºC) y se enfría el materal hasta que su resstenca se anule (Rθ 0), se observa que la temperatura T 0 (θ -T 0 ) en que la resstenca se anula vale: [ + α (( T ) 0) ] R [ ] 0 R α T0 T 0 (9) α 0 Luego, comparando la resstenca del conductor a dos temperaturas dferentes θ' y θ" se obtene que R R θ' θ" R R 0 0 [ + α0 θ' ] + α0 θ' α0 [ + α0 θ" ] + α0 θ" + θ" α 0 + θ' En resumen, se tene tambén esta otra expresón para relaconar la resstenca de un conductor a dos temperaturas dferentes, θ' y θ": Rθ ' T0 + θ' (20) R T + θ" θ" 0 M.A.R. Pozueta --
13 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS Para el cobre el valor de la constante T 0 es 235ºC. Para el alumno esta constante vale 225ºC (según la norma UNE-EN ). EFECTO PELICULAR Cuando por un conductor crcula una corrente contnua, esta corrente se reparte de forma unforme por toda la seccón S de dcho conductor (Fg. 6a). Sn embargo, cuando la corrente es alterna, esta genera campos magnétcos alternos que, a su vez, nducen f.e.m.s sobre el propo conductor. Esto hace que la corrente ya no se reparta de forma unforme por toda la seccón S, sno que se tenda a concentrar en la parte externa (Fg. 6b). Este es el efecto pelcular, tambén llamado efecto pel, efecto Kelvn o efecto skn. Fg. 6: Efecto pelcular en un conductor El efecto pelcular hace que en alterna la seccón efectva por la que realmente crcula la corrente sea nferor a S, lo que conlleva que la resstenca que presenta el conductor en corrente alterna sea superor que la que tene en corrente contnua. Exsten fórmulas que permten calcular un coefcente que relacona las resstencas en alterna y en contnua de un conductor eléctrco. Este coefcente depende de la forma y las dmensones del conductor, del materal y de la frecuenca. La reduccón de la resstenca debda al efecto pelcular se manfesta de forma más acusada cuanto mayor es la seccón S del conductor. Sn embargo, para seccones pequeñas este efecto apenas se manfesta. Por esta razón, cuando se necestan conductores de gran seccón para conducr correntes elevadas, se emplean un conunto de conductores elementales de pequeña seccón, aslados entre sí y conectados en paralelo. A efectos del bobnado este conunto de conductores elementales en paralelo se lo consdera como un únco conductor. Un eemplo de esto es la barra Roebel. Cada conductor elemental de una barra Roebel tene la forma ndcada en la Fg. 7c. Prmero se forman dos sembarras (Fgs. 7e y 7f) que se unen para formar la barra completa (Fg. 7g). Los conductores elementales se van transponendo a lo largo de la barra de forma que todos y cada uno de ellos ocupen todas las poscones posbles en la barra (Fgs. 7a y 7b). Así todos los conductores elementales se comportan gual y tenen el msmo fluo de dspersón. M.A.R. Pozueta -2-
14 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS a) b) c) d) e) f) g) Fg. 7: Barra Roebel a) y b) Los conductores elementales se van trasponendo de forma que ocupan todas las poscones posbles en la ranura. c) Conductor elemental de una barra Roebel. e) Sembarra Roebel (, 2, 3, 4, 5: Conductores elementales) f) Sembarra Roebel (, 2,3,4, 5 : Conductores elementales) g) Barra Roebel completa. (Fuente: Wkpeda: Obtenda de la patente presentada en 92) M.A.R. Pozueta -3-
15 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS PÉRDIDAS EN LOS CONDUCTORES La crculacón de una corrente, de valor efcaz I, a través de un conductor, de resstenca R, provoca la aparcón en él de unas pérddas por efecto Joule, las cuáles venen dadas por la conocda expresón: P Cu 2 R I (2) Las pérddas específcas por undad de peso del materal se obtenen así: P p Cu Cu G (22) En la expresón anteror G es el peso del conductor. El peso G del materal se puede obtener a partr de su peso específco γ y de su volumen, que es gual al producto de su longtud por su seccón ( l S): G γ ( l S) 000 (23) En la expresón anteror el factor /000 aparece porque se supone que l se mde en m, S en mm 2 y γ en kg/dm 3. El peso G, entonces, queda expresado en kg. El valor efcaz I de la corrente se puede obtener de la densdad de corrente por undad de superfce J: I J S (23) en mm 2. En esta fórmula, la corrente I se mde en A, la densdad de corrente J en A/mm 2 y la seccón S Tenendo en cuenta las relacones (5), (22), (23) y (24) se deduce que las pérddas específcas (expresadas en W/kg) se pueden calcular medante esta fórmula: p Cu γ 000 ( l S) ρ l S ρ 2 2 ( J S) 000 J γ (24) Como se acaba de demostrar las pérddas específcas en un conductor venen dadas por p Cu ρ J (25) γ donde: p Cu son las pérddas específcas meddas en W/kg ρ es la resstvdad del conductor en Ω mm 2 /m γ es el peso específco del conductor en kg/dm 3 J es la densdad de corrente, medda en A/mm 2 M.A.R. Pozueta -4-
16 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS Luego, las pérddas en un conductor valen P Cu ρ 2 pcu G 000 J G (26) γ En esta expresón el peso G se debe ndcar en kg. En consecuenca, se deduce que, para un materal conductor dado (donde el cocente ρ/γ es una constante), las pérddas por efecto Joule son proporconales al peso G del conductor y al cuadrado de la densdad de corrente J. ESCOBILLAS Medante colectores es posble conectar al exteror el crcuto eléctrco del rotor de una máquna. Exsten dos tpos de colectores: de delgas y de anllos. En ambos casos la corrente crcula a través de unas escobllas de grafto colocadas en el estator que rozan sobre el colector que gra con el rotor. Las escobllas se clasfcan en dos grandes grupos: Metálcas: compuestas por una mezcla de cobre y carbón. De carbón: compuestas solamente de carbón, sn agregados metálcos. El contacto de una escoblla con el colector presenta una resstenca que no es constante sno que depende de la densdad de corrente. Smplfcando, se puede aceptar que, en cuanto la densdad de corrente empeza a tener un certo valor, la caída de tensón entre una escoblla y el colector es práctcamente constante. Por otra parte, en corrente contnua no se comporta gual la escoblla postva que la negatva, habendo dferentes caídas de tensón en ambas. Esta es la causa de que se trabae con la caída de tensón por par de escobllas o por par de carbones 2u e. El sgno de esta caída de tensón depende del sentdo de la corrente (es sempre una caída de tensón; es decr, del msmo sgno que la dferenca de potencal que aparecería en una resstenca recorrda por la msma corrente que pasa por las escobllas). El valor de 2u e oscla entre 0,5 y 3 V. Los valores más usuales son los sguentes: En colectores de delgas: 2u e 2 V En colectores de anllos: 2u e V Por lo tanto, en una máquna de corrente contnua y, en general, en las máqunas con colector de delgas, con una ntensdad de nducdo I (que se reparte entre todos los pares de escobllas del colector) aparecen unas pérddas en el colector que se obtenen así: Pcol 2ue I (27) Esta msma expresón se puede aplcar para calcular la potenca perdda en el colector de dos anllos de una máquna síncrona. M.A.R. Pozueta -5-
17 CONDUCTORES UTILIZADOS EN LAS MÁQUINAS ELÉCTRICAS En el colector de tres anllos de un motor asíncrono trfásco, por cuyo rotor crculan unas correntes de valor efcaz I, las pérddas en el colector valen P 3 ( 2ue I),5 ( 2ue I) (28) 2 col BIBLIOGRAFÍA [] Corrales Martín, Juan. Cálculo ndustral de máqunas eléctrcas. Tomo I. Marcombo. Barcelona [2] Frale Mora, Jesús. Máqunas eléctrcas. McGraw-Hll/Interamercana de España. Madrd [3] N. L. Sacch, Jorge; Rfald, Alfredo. Cálculo y dseño de máqunas eléctrcas. Cátedra de sstemas de potenca. Facultad de ngenería. Unversdad de la Plata (Argentna). (ver el sto Web: _Intro.html). [4] Ramírez Vázquez, José. Materales electrotécncos. Coleccón Encclopeda CEAC de la Electrcdad. Edtoral CEAC. Barcelona [5] Serrano Irbarnegaray, Lus. Fundamentos de máqunas eléctrcas rotatvas. Marcombo. Barcelona [6] AENOR. Norma UNE-EN 624: Sstemas de aslamento eléctrco (SAE). Clasfcacón térmca. Dcembre [7] AENOR. Norma UNE-EN : Máqunas eléctrcas rotatvas. Parte : Característcas asgnadas y característcas de funconamento. Marzo [8] AENOR. Norma UNE-EN 60085: Aslamento eléctrco. Evaluacón y desgnacón térmca. Juno [9] WIKIPEDIA (versón alemana). [0] AENOR. Norma UNE-2303: Métodos para la medda de la resstvdad transversal y superfcal de los materales aslantes eléctrcos sóldos. Julo 983. M.A.R. Pozueta -6-
Unidad I. 1. 1. Definición de reacción de combustión. 1. 2. Clasificación de combustibles
 2 Undad I.. Defncón de reaccón de combustón La reaccón de combustón se basa en la reaccón químca exotérmca de una sustanca (o una mezcla de ellas) denomnada combustble, con el oxígeno. Como consecuenca
2 Undad I.. Defncón de reaccón de combustón La reaccón de combustón se basa en la reaccón químca exotérmca de una sustanca (o una mezcla de ellas) denomnada combustble, con el oxígeno. Como consecuenca
RESISTENCIAS EN SERIE Y LEY DE LAS MALLAS V 1 V 2 V 3 A B C
 RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
CÁLCULO VECTORIAL 1.- MAGNITUDES ESCALARES Y VECTORIALES. 2.- VECTORES. pág. 1
 CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
CÁLCL ECTRIAL 1. Magntudes escalares y vectorales.. ectores. Componentes vectorales. ectores untaros. Componentes escalares. Módulo de un vector. Cosenos drectores. 3. peracones con vectores. 3.1. Suma.
CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO
 CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO 1 ÍNDICE 1. INTRODUCCIÓN 2. EL CAMPO MAGNÉTICO 3. PRODUCCIÓN DE UN CAMPO MAGNÉTICO 4. LEY DE FARADAY 5. PRODUCCIÓN DE UNA FUERZA EN UN CONDUCTOR 6. MOVIMIENTO DE
CONCEPTOS GENERALES DEL CAMPO MAGNÉTICO 1 ÍNDICE 1. INTRODUCCIÓN 2. EL CAMPO MAGNÉTICO 3. PRODUCCIÓN DE UN CAMPO MAGNÉTICO 4. LEY DE FARADAY 5. PRODUCCIÓN DE UNA FUERZA EN UN CONDUCTOR 6. MOVIMIENTO DE
OPERACIONES ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS
 P L V S V LT R A BANCO DE ESPAÑA OPERACIONES Gestón de la Informacón ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS El proceso de ntegracón fnancera dervado de la Unón Monetara exge la
P L V S V LT R A BANCO DE ESPAÑA OPERACIONES Gestón de la Informacón ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS El proceso de ntegracón fnancera dervado de la Unón Monetara exge la
DEFINICIÓN DE INDICADORES
 DEFINICIÓN DE INDICADORES ÍNDICE 1. Notacón básca... 3 2. Indcadores de ntegracón: comerco total de benes... 4 2.1. Grado de apertura... 4 2.2. Grado de conexón... 4 2.3. Grado de conexón total... 5 2.4.
DEFINICIÓN DE INDICADORES ÍNDICE 1. Notacón básca... 3 2. Indcadores de ntegracón: comerco total de benes... 4 2.1. Grado de apertura... 4 2.2. Grado de conexón... 4 2.3. Grado de conexón total... 5 2.4.
Física I. TRABAJO y ENERGÍA MECÁNICA. Apuntes complementarios al libro de texto. Autor : Dr. Jorge O. Ratto
 ísca I Apuntes complementaros al lbro de teto TRABAJO y ENERGÍA MECÁNICA Autor : Dr. Jorge O. Ratto Estudaremos el trabajo mecánco de la sguente manera : undmensonal constante Tpo de movmento varable bdmensonal
ísca I Apuntes complementaros al lbro de teto TRABAJO y ENERGÍA MECÁNICA Autor : Dr. Jorge O. Ratto Estudaremos el trabajo mecánco de la sguente manera : undmensonal constante Tpo de movmento varable bdmensonal
Trabajo y Energía Cinética
 Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Tema 3. Estadísticos univariados: tendencia central, variabilidad, asimetría y curtosis
 Tema. Estadístcos unvarados: tendenca central, varabldad, asmetría y curtoss 1. MEDIDA DE TEDECIA CETRAL La meda artmétca La medana La moda Comparacón entre las meddas de tendenca central. MEDIDA DE VARIACIÓ
Tema. Estadístcos unvarados: tendenca central, varabldad, asmetría y curtoss 1. MEDIDA DE TEDECIA CETRAL La meda artmétca La medana La moda Comparacón entre las meddas de tendenca central. MEDIDA DE VARIACIÓ
UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II
 UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II PRACTICA 11: Crcutos no lneales elementales con el amplfcador operaconal OBJETIVO: El alumno se famlarzará con
UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II PRACTICA 11: Crcutos no lneales elementales con el amplfcador operaconal OBJETIVO: El alumno se famlarzará con
EXPERIMENTACIÓN COMERCIAL(I)
 EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
EXPERIMENTACIÓN COMERCIAL(I) En un expermento comercal el nvestgador modfca algún factor (denomnado varable explcatva o ndependente) para observar el efecto de esta modfcacón sobre otro factor (denomnado
Guía de ejercicios #1
 Unversdad Técnca Federco Santa María Departamento de Electrónca Fundamentos de Electrónca Guía de ejerccos # Ejercco Ω v (t) V 3V Ω v0 v 6 3 t[mseg] 6 Suponendo el modelo deal para los dodos, a) Dbuje
Unversdad Técnca Federco Santa María Departamento de Electrónca Fundamentos de Electrónca Guía de ejerccos # Ejercco Ω v (t) V 3V Ω v0 v 6 3 t[mseg] 6 Suponendo el modelo deal para los dodos, a) Dbuje
2.5 Especialidades en la facturación eléctrica
 2.5 Especaldades en la facturacón eléctrca Es necesaro destacar a contnuacón algunos aspectos peculares de la facturacón eléctrca según Tarfas, que tendrán su mportanca a la hora de establecer los crteros
2.5 Especaldades en la facturacón eléctrca Es necesaro destacar a contnuacón algunos aspectos peculares de la facturacón eléctrca según Tarfas, que tendrán su mportanca a la hora de establecer los crteros
Clase 25. Macroeconomía, Sexta Parte
 Introduccón a la Facultad de Cs. Físcas y Matemátcas - Unversdad de Chle Clase 25. Macroeconomía, Sexta Parte 12 de Juno, 2008 Garca Se recomenda complementar la clase con una lectura cudadosa de los capítulos
Introduccón a la Facultad de Cs. Físcas y Matemátcas - Unversdad de Chle Clase 25. Macroeconomía, Sexta Parte 12 de Juno, 2008 Garca Se recomenda complementar la clase con una lectura cudadosa de los capítulos
12-16 de Noviembre de 2012. Francisco Javier Burgos Fernández
 MEMORIA DE LA ESTANCIA CON EL GRUPO DE VISIÓN Y COLOR DEL INSTITUTO UNIVERSITARIO DE FÍSICA APLICADA A LAS CIENCIAS TECNOLÓGICAS. UNIVERSIDAD DE ALICANTE. 1-16 de Novembre de 01 Francsco Javer Burgos Fernández
MEMORIA DE LA ESTANCIA CON EL GRUPO DE VISIÓN Y COLOR DEL INSTITUTO UNIVERSITARIO DE FÍSICA APLICADA A LAS CIENCIAS TECNOLÓGICAS. UNIVERSIDAD DE ALICANTE. 1-16 de Novembre de 01 Francsco Javer Burgos Fernández
CANTIDADES VECTORIALES: VECTORES
 INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
INSTITUION EDUTIV L PRESENTION NOMRE LUMN: RE : MTEMÁTIS SIGNTUR: GEOMETRÍ DOENTE: JOSÉ IGNIO DE JESÚS FRNO RESTREPO TIPO DE GUI: ONEPTUL - EJERITION PERIODO GRDO FEH DURION 3 11 JUNIO 3 DE 2012 7 UNIDDES
TEMA 4 Amplificadores realimentados
 TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
PROBLEMAS DE ELECTRÓNICA ANALÓGICA (Diodos)
 PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
ELEMENTOS DE ELECTRICIDAD BASICA
 MODULO 1 ELEMENTOS DE ELECTRICIDAD BASICA A contnuacón se resumen algunos elementos de Electrcdad Básca que se supone son conocdos por los estudantes al ngresar a la Unversdad DESCUBRIMIENTO DE LA ELECTRICIDAD:
MODULO 1 ELEMENTOS DE ELECTRICIDAD BASICA A contnuacón se resumen algunos elementos de Electrcdad Básca que se supone son conocdos por los estudantes al ngresar a la Unversdad DESCUBRIMIENTO DE LA ELECTRICIDAD:
COMPARADOR CON AMPLIFICADOR OPERACIONAL
 COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
Leyes de tensión y de corriente
 hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
Pruebas Estadísticas de Números Pseudoaleatorios
 Pruebas Estadístcas de Números Pseudoaleatoros Prueba de meda Consste en verfcar que los números generados tengan una meda estadístcamente gual a, de esta manera, se analza la sguente hpótess: H 0 : =
Pruebas Estadístcas de Números Pseudoaleatoros Prueba de meda Consste en verfcar que los números generados tengan una meda estadístcamente gual a, de esta manera, se analza la sguente hpótess: H 0 : =
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Tema 3: Adaptadores de Señal
 Tema 3: Adaptadores de Señal Sstema GENERAL de nstrumentacón (bloques( funconales): Señal sensor Fltrado, A/D Amplfcacón Rado, nternet bus de datos Medo Sensor prmaro Transductor de entrada Adaptacón de
Tema 3: Adaptadores de Señal Sstema GENERAL de nstrumentacón (bloques( funconales): Señal sensor Fltrado, A/D Amplfcacón Rado, nternet bus de datos Medo Sensor prmaro Transductor de entrada Adaptacón de
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
Tema 1: Estadística Descriptiva Unidimensional Unidad 2: Medidas de Posición, Dispersión y de Forma
 Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Estadístca Tema 1: Estadístca Descrptva Undmensonal Undad 2: Meddas de Poscón, Dspersón y de Forma Área de Estadístca e Investgacón Operatva Lceso J. Rodríguez-Aragón Septembre 2010 Contendos...............................................................
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
PRÁCTICA 1. IDENTIFICACIÓN Y MANEJO DE MATERIAL DE LABORATORIO: PREPARACIÓN DE DISOLUCIONES Y MEDIDA DE DENSIDADES
 PRÁCTICA 1. IDENTIFICACIÓN Y MANEJO DE MATERIAL DE LABORATORIO: PREPARACIÓN DE DISOLUCIONES Y MEDIDA DE DENSIDADES OBJETIVOS ESPECÍFICOS 1) Identfcar y manejar el materal básco de laboratoro. ) Preparar
PRÁCTICA 1. IDENTIFICACIÓN Y MANEJO DE MATERIAL DE LABORATORIO: PREPARACIÓN DE DISOLUCIONES Y MEDIDA DE DENSIDADES OBJETIVOS ESPECÍFICOS 1) Identfcar y manejar el materal básco de laboratoro. ) Preparar
Disipación de energía mecánica
 Laboratoro de Mecáa. Expermento 13 Versón para el alumno Dspacón de energía mecáa Objetvo general El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Objetvos partculares
Laboratoro de Mecáa. Expermento 13 Versón para el alumno Dspacón de energía mecáa Objetvo general El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Objetvos partculares
Análisis de Regresión y Correlación
 1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
Respuesta A.C. del FET 1/14
 espuesta A.C. del FET 1/14 1. Introduccón Una ez que se ubca al transstor dentro de la zona saturada o de corrente de salda constante, se puede utlzar como amplfcador de señales. En base a un FET canal
espuesta A.C. del FET 1/14 1. Introduccón Una ez que se ubca al transstor dentro de la zona saturada o de corrente de salda constante, se puede utlzar como amplfcador de señales. En base a un FET canal
CIRCUITOS ELÉCTRICOS
 .E.S. CÁ STULO 1 CRCUTOS ELÉCTRCOS 1. COMPONENTES DE UN CRCUTO. Los circuitos eléctricos son sistemas por los que circula una corriente eléctrica. Un circuito eléctrico esta compuesto por los siguientes
.E.S. CÁ STULO 1 CRCUTOS ELÉCTRCOS 1. COMPONENTES DE UN CRCUTO. Los circuitos eléctricos son sistemas por los que circula una corriente eléctrica. Un circuito eléctrico esta compuesto por los siguientes
TEMA 6 AMPLIFICADORES OPERACIONALES
 Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6a)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 Rcardo Ramírez Facultad de Físca, Pontfca Unversdad Católca, Chle 1er. Semestre 2008 Corrente eléctrca CORRIENTE ELECTRICA Corrente eléctrca mplca carga en movmento.
Tema 7. MOTORES ELÉCTRICOS DE CORRIENTE CONTINUA
 Tema 7. MOTORES ELÉCTRICOS DE CORRIENTE CONTINUA 1. MAGNETISMO Y ELECTRICIDAD...2 Fuerza electromotriz inducida (Ley de inducción de Faraday)...2 Fuerza electromagnética (2ª Ley de Laplace)...2 2. LAS
Tema 7. MOTORES ELÉCTRICOS DE CORRIENTE CONTINUA 1. MAGNETISMO Y ELECTRICIDAD...2 Fuerza electromotriz inducida (Ley de inducción de Faraday)...2 Fuerza electromagnética (2ª Ley de Laplace)...2 2. LAS
ANÁLISIS DE ACCESIBILIDAD E INTERACCIÓN ESPECIAL:
 Geografía y Sstemas de Informacón Geográfca (GEOSIG). Revsta dgtal del Grupo de Estudos sobre Geografía y Análss Espacal con Sstemas de Informacón Geográfca (GESIG). Programa de Estudos Geográfcos (PROEG).
Geografía y Sstemas de Informacón Geográfca (GEOSIG). Revsta dgtal del Grupo de Estudos sobre Geografía y Análss Espacal con Sstemas de Informacón Geográfca (GESIG). Programa de Estudos Geográfcos (PROEG).
PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE FACULTAD DE FISICA FISICA I FIS101M. Sección 03. José Mejía López. jmejia@puc.cl
 PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE FACULTAD DE FISICA FISICA I FIS11M Seccón 3 José Mejía López jmeja@puc.cl http://www.s.puc.cl/~jmeja/docenca/s11m.html JML s11m-1 Capítulo Dnámca Trabajo y energía
PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE FACULTAD DE FISICA FISICA I FIS11M Seccón 3 José Mejía López jmeja@puc.cl http://www.s.puc.cl/~jmeja/docenca/s11m.html JML s11m-1 Capítulo Dnámca Trabajo y energía
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
TERMODINÁMICA AVANZADA
 ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
ERMODINÁMICA AANZADA Undad III: ermodnámca del Equlbro Fugacdad Fugacdad para gases, líqudos y sóldos Datos volumétrcos 9/7/ Rafael Gamero Fugacdad ropedades con varables ndependentes y ln f ' Con la dfncón
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
TEMA 10. OPERACIONES PASIVAS Y OPERACIONES ACTIVAS.
 GESTIÓN FINANCIERA. TEMA 10. OPERACIONES PASIVAS Y OPERACIONES ACTIVAS. 1.- Funconamento de las cuentas bancaras. FUNCIONAMIENTO DE LAS CUENTAS BANCARIAS. Las cuentas bancaras se dvden en tres partes:
GESTIÓN FINANCIERA. TEMA 10. OPERACIONES PASIVAS Y OPERACIONES ACTIVAS. 1.- Funconamento de las cuentas bancaras. FUNCIONAMIENTO DE LAS CUENTAS BANCARIAS. Las cuentas bancaras se dvden en tres partes:
Calorimetría - Soluciones. 1.- Cuántas calorías ceden 5 kg de cobre (c = 0,094 cal/g C) al enfriarse desde 36 o C hasta -4 C?
 Calormetría - Solucones 1.- Cuántas calorías ceden 5 kg de cobre () al enfrarse desde 3 o C hasta -4 C? m = 5 kg = 5.000 g T = 3 C T f = - 4 C = - T = - (T f T ) = - 5.000 g 0,094 cal/g C (-4 C 3 C) =
Calormetría - Solucones 1.- Cuántas calorías ceden 5 kg de cobre () al enfrarse desde 3 o C hasta -4 C? m = 5 kg = 5.000 g T = 3 C T f = - 4 C = - T = - (T f T ) = - 5.000 g 0,094 cal/g C (-4 C 3 C) =
Histogramas: Es un diagrama de barras pero los datos son siempre cuantitativos agrupados en clases o intervalos.
 ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
ESTADÍSTICA I. Recuerda: Poblacón: Es el conjunto de todos los elementos que cumplen una determnada propedad, que llamamos carácter estadístco. Los elementos de la poblacón se llaman ndvduos. Muestra:
9.1 DIELÉCTRICOS 9.1.1 QUÉ SON LOS DIELÉCTRICOS? 9.1.2 RIGIDEZ DIELÉCTRICA
 9 DIELÉCTRICOS 9.1 DIELÉCTRICOS 9.1.1 QUÉ SON LOS DIELÉCTRICOS? Los dieléctricos son materiales, generalmente no metálicos, con una alta resistividad, por lo que la circulación de corriente a través de
9 DIELÉCTRICOS 9.1 DIELÉCTRICOS 9.1.1 QUÉ SON LOS DIELÉCTRICOS? Los dieléctricos son materiales, generalmente no metálicos, con una alta resistividad, por lo que la circulación de corriente a través de
Temas de electricidad II
 Temas de electricidad II CAMBIANDO MATERIALES Ahora volvemos al circuito patrón ya usado. Tal como se indica en la figura, conecte un hilo de cobre y luego uno de níquel-cromo. Qué ocurre con el brillo
Temas de electricidad II CAMBIANDO MATERIALES Ahora volvemos al circuito patrón ya usado. Tal como se indica en la figura, conecte un hilo de cobre y luego uno de níquel-cromo. Qué ocurre con el brillo
Comparación entre distintos Criterios de decisión (VAN, TIR y PRI) Por: Pablo Lledó
 Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
Cifrado de imágenes usando autómatas celulares con memoria
 Cfrado de mágenes usando autómatas celulares con memora L. Hernández Encnas 1, A. Hernández Encnas 2, S. Hoya Whte 2, A. Martín del Rey 3, G. Rodríguez Sánchez 4 1 Insttuto de Físca Aplcada, CSIC, C/Serrano
Cfrado de mágenes usando autómatas celulares con memora L. Hernández Encnas 1, A. Hernández Encnas 2, S. Hoya Whte 2, A. Martín del Rey 3, G. Rodríguez Sánchez 4 1 Insttuto de Físca Aplcada, CSIC, C/Serrano
Tallerine: Energías Renovables. Fundamento teórico
 Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Tallerne: Energías Renovables Fundamento teórco Tallerne Energías Renovables 2 Índce 1. Introduccón 3 2. Conceptos Báscos 3 2.1. Intensdad de corrente................................. 3 2.2. Voltaje..........................................
Tabla 6.3. Frecuencia de causas de humedades en caso III: Misiones de San Francisco: etapa VI
 CAPÍTULO VI. CONCLUSIONES GENERALES En un resumen general de las principales causas de humedades, sin llegar a detalles debido a que se mencionan en el capítulo III, la siguiente tabla menciona causas
CAPÍTULO VI. CONCLUSIONES GENERALES En un resumen general de las principales causas de humedades, sin llegar a detalles debido a que se mencionan en el capítulo III, la siguiente tabla menciona causas
UNIVERSIDAD CARLOS III DE MADRID Ingeniería Informática Examen de Investigación Operativa 21 de enero de 2009
 UNIVERSIDAD CARLOS III DE MADRID Ingenería Informátca Examen de Investgacón Operatva 2 de enero de 2009 PROBLEMA. (3 puntos) En Murca, junto al río Segura, exsten tres plantas ndustrales: P, P2 y P3. Todas
UNIVERSIDAD CARLOS III DE MADRID Ingenería Informátca Examen de Investgacón Operatva 2 de enero de 2009 PROBLEMA. (3 puntos) En Murca, junto al río Segura, exsten tres plantas ndustrales: P, P2 y P3. Todas
v i CIRCUITOS ELÉCTRICOS (apuntes para el curso de Electrónica)
 IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
ELECTRICIDAD II - INDICE TEMÁTICO
 ELECTRICIDAD II - INDICE TEMÁTICO ELECTRODINÁMICA 1 ELECTRICIDAD II - INDICE TEMÁTICO...1 EFECTOS MAGNÉTICOS DE LA CORRIENTE ELÉCTRICA...2 CAMPO MAGNÉTICO...2 Cómo decrece el campo magnétco con la dstanca?:...2
ELECTRICIDAD II - INDICE TEMÁTICO ELECTRODINÁMICA 1 ELECTRICIDAD II - INDICE TEMÁTICO...1 EFECTOS MAGNÉTICOS DE LA CORRIENTE ELÉCTRICA...2 CAMPO MAGNÉTICO...2 Cómo decrece el campo magnétco con la dstanca?:...2
Una viga se encuentra sometida a Flexión Pura cuando el momento Flector es la única fuerza al interior de la sección.
 3. FLEXÓ E VGS RECTS 3.1.- Conceptos Báscos Una ga se encentra sometda a Fleón Pra cando el momento Flector es la únca fera al nteror de la seccón. Ejemplo: Una ga smplemente apoada de l L solctada por
3. FLEXÓ E VGS RECTS 3.1.- Conceptos Báscos Una ga se encentra sometda a Fleón Pra cando el momento Flector es la únca fera al nteror de la seccón. Ejemplo: Una ga smplemente apoada de l L solctada por
ELECTRODOS ESPECIALES Y PLACAS. Electrodo de Grafito Rígido ELECTRODOS DE GRAFITO RIGIDO
 ELECTRODOS ESPECIALES Y PLACAS Electrodo de Grafito Rígido ELECTRODOS DE GRAFITO RIGIDO Nuestro Proveedor, ha diseñado nuevos electrodos fabricados a partir de grafito para ser utilizados en sistemas de
ELECTRODOS ESPECIALES Y PLACAS Electrodo de Grafito Rígido ELECTRODOS DE GRAFITO RIGIDO Nuestro Proveedor, ha diseñado nuevos electrodos fabricados a partir de grafito para ser utilizados en sistemas de
Tema 11 Endurecimiento por deformación plástica en frío. Recuperación, Recristalización y Crecimiento del grano.
 Tema 11 Endurecimiento por deformación plástica en frío. Recuperación, Recristalización y Crecimiento del grano. El endurecimiento por deformación plástica en frío es el fenómeno por medio del cual un
Tema 11 Endurecimiento por deformación plástica en frío. Recuperación, Recristalización y Crecimiento del grano. El endurecimiento por deformación plástica en frío es el fenómeno por medio del cual un
El motor eléctrico. Física. Liceo integrado de zipaquira MOTOR ELECTRICO
 El motor eléctrico Física Liceo integrado de zipaquira MOTOR ELECTRICO Motores y generadores eléctricos, grupo de aparatos que se utilizan para convertir la energía mecánica en eléctrica, o a la inversa,
El motor eléctrico Física Liceo integrado de zipaquira MOTOR ELECTRICO Motores y generadores eléctricos, grupo de aparatos que se utilizan para convertir la energía mecánica en eléctrica, o a la inversa,
Gráficos de flujo de señal
 UNIVRSIDAD AUTÓNOMA D NUVO ÓN FACUTAD D INGNIRÍA MCANICA Y ÉCTRICA Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente
UNIVRSIDAD AUTÓNOMA D NUVO ÓN FACUTAD D INGNIRÍA MCANICA Y ÉCTRICA Gráfcos de flujo de señal l dagrama de bloques es útl para la representacón gráfca de sstemas de control dnámco y se utlza extensamente
CAPACIDAD DE LAS HOJAS DE CÁLCULO EN EL ANÁLISIS Y OPTIMIZACIÓN DE PROCESOS Y SISTEMAS
 CAPACIDAD DE LAS OJAS DE CÁLCULO EN EL ANÁLISIS Y OPIMIZACIÓN DE PROCESOS Y SISEMAS A. Rvas y. Gómez-Acebo Departamento de Ingenería Mecánca-Área de Ingenería érmca y de Fludos ECNUN - Escuela Superor
CAPACIDAD DE LAS OJAS DE CÁLCULO EN EL ANÁLISIS Y OPIMIZACIÓN DE PROCESOS Y SISEMAS A. Rvas y. Gómez-Acebo Departamento de Ingenería Mecánca-Área de Ingenería érmca y de Fludos ECNUN - Escuela Superor
De factores fijos. Mixto. Con interacción Sin interacción. No equilibrado. Jerarquizado
 Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Análss de la varanza con dos factores. Introduccón Hasta ahora se ha vsto el modelo de análss de la varanza con un factor que es una varable cualtatva cuyas categorías srven para clasfcar las meddas de
Circuito Monoestable
 NGENEÍA ELETÓNA ELETONA (A-0 00 rcuto Monoestable rcuto Monoestable ng. María sabel Schaon, ng. aúl Lsandro Martín Este crcuto se caracterza por presentar un únco estado estable en régmen permanente, y
NGENEÍA ELETÓNA ELETONA (A-0 00 rcuto Monoestable rcuto Monoestable ng. María sabel Schaon, ng. aúl Lsandro Martín Este crcuto se caracterza por presentar un únco estado estable en régmen permanente, y
Unidad II: Análisis de la combustión completa e incompleta. 2. 1. Aire
 4 Undad II: Análss de la combustón completa e ncompleta. 1. Are El are que se usa en las reaccones de combustón es el are atmosférco. Ya se djo en la Undad I que, debdo a que n el N n los gases nertes
4 Undad II: Análss de la combustón completa e ncompleta. 1. Are El are que se usa en las reaccones de combustón es el are atmosférco. Ya se djo en la Undad I que, debdo a que n el N n los gases nertes
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA
 CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
CÁLCULO DE INCERTIDUMBRE EN MEDIDAS FÍSICAS: MEDIDA DE UNA MASA Alca Maroto, Rcard Boqué, Jord Ru, F. Xaver Rus Departamento de Químca Analítca y Químca Orgánca Unverstat Rovra Vrgl. Pl. Imperal Tàrraco,
C I R C U L A R N 2.133
 Montevdeo, 17 de Enero de 2013 C I R C U L A R N 2.133 Ref: Insttucones de Intermedacón Fnancera - Responsabldad patrmonal neta mínma - Susttucón de la Dsposcón Transtora del art. 154 y de los arts. 158,
Montevdeo, 17 de Enero de 2013 C I R C U L A R N 2.133 Ref: Insttucones de Intermedacón Fnancera - Responsabldad patrmonal neta mínma - Susttucón de la Dsposcón Transtora del art. 154 y de los arts. 158,
ANEJO Nº 4: INSTALACIÓN ELÉCTRICA.
 ANEJO Nº 4: INSTALACIÓN ELÉCTRICA. Mejora de bodega en Valdefuentes (Cáceres 4.-INSTALACIÓN ELÉCTRICA EN BAJA TENSIÓN 4.1.-Ilumnacón. 4.1.1. Alumbrado nteror. 4.1.2. Alumbrado de emergenca 4.1.3. Alumbrado
ANEJO Nº 4: INSTALACIÓN ELÉCTRICA. Mejora de bodega en Valdefuentes (Cáceres 4.-INSTALACIÓN ELÉCTRICA EN BAJA TENSIÓN 4.1.-Ilumnacón. 4.1.1. Alumbrado nteror. 4.1.2. Alumbrado de emergenca 4.1.3. Alumbrado
1. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA. Definición del álgebra geométrica del espacio-tiempo
 EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
1.- Una empresa se plantea una inversión cuyas características financieras son:
 ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES. Departamento de Economía Aplcada (Matemátcas). Matemátcas Fnanceras. Relacón de Problemas. Rentas. 1.- Una empresa se plantea una nversón cuyas característcas
ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES. Departamento de Economía Aplcada (Matemátcas). Matemátcas Fnanceras. Relacón de Problemas. Rentas. 1.- Una empresa se plantea una nversón cuyas característcas
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
ELECTRICIDAD Secundaria
 ELECTRICIDAD Secundaria Carga eléctrica. Los átomos que constituyen la materia están formados por otras partículas todavía más pequeñas, llamadas protones, neutrones y electrones. Los protones y los electrones
ELECTRICIDAD Secundaria Carga eléctrica. Los átomos que constituyen la materia están formados por otras partículas todavía más pequeñas, llamadas protones, neutrones y electrones. Los protones y los electrones
TEMA 4 CONDENSADORES
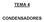 TEMA 4 CONDENSADORES CONDENSADORES Un condensador es un componente que tiene la capacidad de almacenar cargas eléctricas y suministrarlas en un momento apropiado durante un espacio de tiempo muy corto.
TEMA 4 CONDENSADORES CONDENSADORES Un condensador es un componente que tiene la capacidad de almacenar cargas eléctricas y suministrarlas en un momento apropiado durante un espacio de tiempo muy corto.
Unidad Didáctica. Transformadores Trifásicos
 Unidad Didáctica Transformadores Trifásicos Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION
Unidad Didáctica Transformadores Trifásicos Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION
Fisicoquímica CIBEX Guía de Trabajos Prácticos 2010. Trabajo Práctico N 7. - Medida de la Fuerza Electromotriz por el Método de Oposición-
 Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Cómo Reducir la Factura de Energía Eléctrica Corrigiendo el Factor de Potencia
 Cómo Reducir la Factura de Energía Eléctrica Corrigiendo el Factor de Potencia Por Ing. José Luís Ola García ( 1 ) RESUMEN El elevado consumo de la Potencia Reactiva (aumento de la necesidad de magnetizar
Cómo Reducir la Factura de Energía Eléctrica Corrigiendo el Factor de Potencia Por Ing. José Luís Ola García ( 1 ) RESUMEN El elevado consumo de la Potencia Reactiva (aumento de la necesidad de magnetizar
PROBLEMAS RESUELTOS DE MÁQUINAS DE CORRIENTE CONTINUA
 UIVERSIDAD DE CATABRIA DEARTAMETO DE IGEIERÍA ELÉCTRICA Y EERGÉTICA ROBLEMAS RESUELTOS DE MÁQUIAS DE CORRIETE COTIUA Mguel Angel Rodríguez ozueta Doctor Ingenero Industral RESETACIÓ Esta coleccón de problemas
UIVERSIDAD DE CATABRIA DEARTAMETO DE IGEIERÍA ELÉCTRICA Y EERGÉTICA ROBLEMAS RESUELTOS DE MÁQUIAS DE CORRIETE COTIUA Mguel Angel Rodríguez ozueta Doctor Ingenero Industral RESETACIÓ Esta coleccón de problemas
En la 3ª entrega de este trabajo nos centraremos en la relación entre magnitudes eléctricas, hecho que explica la famosa Ley de Ohm.
 3º parte En la 3ª entrega de este trabajo nos centraremos en la relación entre magnitudes eléctricas, hecho que explica la famosa Ley de Ohm. ELEMENTOS DEL CIRCUITO ELÉCTRICO Para poder relacionar las
3º parte En la 3ª entrega de este trabajo nos centraremos en la relación entre magnitudes eléctricas, hecho que explica la famosa Ley de Ohm. ELEMENTOS DEL CIRCUITO ELÉCTRICO Para poder relacionar las
SEMICONDUCTORES PREGUNTAS
 SEMICONDUCTORES PREGUNTAS 1. Por qué los metales conducen mejor que los semiconductores 2. Por qué la conducción de la corriente eléctrica en los metales y los semiconductores tienen distinto comportamiento
SEMICONDUCTORES PREGUNTAS 1. Por qué los metales conducen mejor que los semiconductores 2. Por qué la conducción de la corriente eléctrica en los metales y los semiconductores tienen distinto comportamiento
Explicación de las tecnologías - PowerShot SX500 IS y PowerShot SX160 IS
 Explcacón de las tecnologías - PowerShot SX500 IS y PowerShot SX160 IS EMBARGO: 21 de agosto de 2012, 15:00 (CEST) Objetvo angular de 24 mm, con zoom óptco 30x (PowerShot SX500 IS) Desarrollado usando
Explcacón de las tecnologías - PowerShot SX500 IS y PowerShot SX160 IS EMBARGO: 21 de agosto de 2012, 15:00 (CEST) Objetvo angular de 24 mm, con zoom óptco 30x (PowerShot SX500 IS) Desarrollado usando
Componentes Pasivos. CATEDRA: Mediciones Electricas I Y II. Facultad de Ciencias Exactas y Tecnología UNIVERSIDAD NACINAL DE TUCUMÁN
 Componentes Pasivos CATEDRA: Mediciones Electricas I Y II Facultad de Ciencias Exactas y Tecnología UNIVERSIDAD NACINAL DE TUCUMÁN Año 2011 Resistencias Resistencia es la oposición que presenta un conductor
Componentes Pasivos CATEDRA: Mediciones Electricas I Y II Facultad de Ciencias Exactas y Tecnología UNIVERSIDAD NACINAL DE TUCUMÁN Año 2011 Resistencias Resistencia es la oposición que presenta un conductor
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E
 PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
PRUES DE CCESO L UNVERSDD L.O.G.S.E CURSO 004-005 CONVOCTOR SEPTEMRE ELECTROTECN EL LUMNO ELEGRÁ UNO DE LOS DOS MODELOS Crteros de calfcacón.- Expresón clara y precsa dentro del lenguaje técnco y gráfco
EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL
 EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL OBJETIVO El alumno obtendrá el punto azeotrópco para el sstema acetona-cloroformo, calculará los coefcentes de actvdad de cada componente a las composcones
EQUILIBRIO LÍQUIDO VAPOR EN UN SISTEMA NO IDEAL OBJETIVO El alumno obtendrá el punto azeotrópco para el sstema acetona-cloroformo, calculará los coefcentes de actvdad de cada componente a las composcones
Conceptos y determinaciones aplicables a transformadores de intensidad
 Definiciones: Error de Calibración de un instrumento o Error de Clase: es el mayor error absoluto que acusa un instrumento en algún punto de la escala Cuando este error se expresa referido al máximo valor
Definiciones: Error de Calibración de un instrumento o Error de Clase: es el mayor error absoluto que acusa un instrumento en algún punto de la escala Cuando este error se expresa referido al máximo valor
Máquinas Eléctricas I - G862
 Máqunas Eléctrcas I - G862 Tema 5. Máqunas eléctrcas de Corrente Con7nua. roblemas resueltos Mguel Ángel Rodríguez ozueta Departamento de Ingenería Eléctrca y Energé5ca Este tema se publca bajo Lcenca:
Máqunas Eléctrcas I - G862 Tema 5. Máqunas eléctrcas de Corrente Con7nua. roblemas resueltos Mguel Ángel Rodríguez ozueta Departamento de Ingenería Eléctrca y Energé5ca Este tema se publca bajo Lcenca:
Polo positivo: mayor potencial. Polo negativo: menor potencial
 CORRIENTE ELÉCTRICA Es el flujo de carga a través de un conductor Aunque son los electrones los responsables de la corriente eléctrica, está establecido el tomar la dirección de la corriente eléctrica
CORRIENTE ELÉCTRICA Es el flujo de carga a través de un conductor Aunque son los electrones los responsables de la corriente eléctrica, está establecido el tomar la dirección de la corriente eléctrica
COMPONENTES ELEMENTALES
 Capítulo COMPONENTES ELEMENTALES.. Modelos de Componentes Una componente eléctrca se descrbe por una relacón entre sus arables termnales, la que se denomna relacón de equlbro. El oltaje y la corrente,
Capítulo COMPONENTES ELEMENTALES.. Modelos de Componentes Una componente eléctrca se descrbe por una relacón entre sus arables termnales, la que se denomna relacón de equlbro. El oltaje y la corrente,
MÁQUINAS ELECTRICAS DE C.C y C.A.. ELECTROMECANICA UNIDAD 4 Generadores de Corriente Continua. Partes de una maquina eléctrica de corriente continua.
 Página19 UNIDAD 4 Generadores de Corriente Continua. Introducción En la actualidad, la generación de C.C. se realiza mediante pilas y acumuladores o se obtiene de la conversión de C.A. a C.C. mediante
Página19 UNIDAD 4 Generadores de Corriente Continua. Introducción En la actualidad, la generación de C.C. se realiza mediante pilas y acumuladores o se obtiene de la conversión de C.A. a C.C. mediante
www.fisicaeingenieria.es
 2.- PRIMER PRINCIPIO DE LA TERMODINÁMICA. 2.1.- Experencas de Joule. Las experencas de Joule, conssteron en colocar una determnada cantdad de agua en un calorímetro y realzar un trabajo, medante paletas
2.- PRIMER PRINCIPIO DE LA TERMODINÁMICA. 2.1.- Experencas de Joule. Las experencas de Joule, conssteron en colocar una determnada cantdad de agua en un calorímetro y realzar un trabajo, medante paletas
TEMA 2. CIRCUITOS ELÉCTRICOS.
 TEMA 2. CIRCUITOS ELÉCTRICOS. 1. INTRODUCCIÓN. A lo largo del presente tema vamos a estudiar los circuitos eléctricos, para lo cual es necesario recordar una serie de conceptos previos tales como la estructura
TEMA 2. CIRCUITOS ELÉCTRICOS. 1. INTRODUCCIÓN. A lo largo del presente tema vamos a estudiar los circuitos eléctricos, para lo cual es necesario recordar una serie de conceptos previos tales como la estructura
TRANSFORMADORES EN PARALELO
 UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
DEPARTAMENTO DE INGENIERIA MECÁNICA INGENIERÍA INDUSTRIAL
 DEPARTAMENTO DE INGENIERIA MECÁNICA INGENIERÍA INDUSTRIAL DISEÑO MECÁNICO PRÁCTICA Nº 4 METROLOGÍA Y CALIDAD. CALIBRACIÓN DE UN PIE DE REY Metrología y Caldad. Calbracón de n pe de rey. INDICE 1. OBJETIVOS
DEPARTAMENTO DE INGENIERIA MECÁNICA INGENIERÍA INDUSTRIAL DISEÑO MECÁNICO PRÁCTICA Nº 4 METROLOGÍA Y CALIDAD. CALIBRACIÓN DE UN PIE DE REY Metrología y Caldad. Calbracón de n pe de rey. INDICE 1. OBJETIVOS
Investigación y Técnicas de Mercado. Previsión de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): Ajustes de Tendencia
 Investgacón y Técncas de Mercado Prevsón de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): s de Tendenca Profesor: Ramón Mahía Curso 00-003 I.- Introduccón Hasta el momento,
Investgacón y Técncas de Mercado Prevsón de Ventas TÉCNICAS CUANTITATIVAS ELEMENTALES DE PREVISIÓN UNIVARIANTE. (IV): s de Tendenca Profesor: Ramón Mahía Curso 00-003 I.- Introduccón Hasta el momento,
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
METODOS VOLTAMPEROMETRICOS
 Métodos Voltamperométrcos 2 Tema 9 METODOS VOLTAMPEROMETRICOS Los métodos voltamperométrcos ncluyen un conjunto de métodos electroanalítcos en los que la nformacón sobre el analto se obtene a partr de
Métodos Voltamperométrcos 2 Tema 9 METODOS VOLTAMPEROMETRICOS Los métodos voltamperométrcos ncluyen un conjunto de métodos electroanalítcos en los que la nformacón sobre el analto se obtene a partr de
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 2 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. La dureza Rockwell de un metal
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 2 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. La dureza Rockwell de un metal
GANTT, PERT y CPM INDICE
 GANTT, PERT y CPM INDICE 1 Antecedentes hstórcos...2 2 Conceptos báscos: actvdad y suceso...2 3 Prelacones entre actvdades...3 4 Cuadro de prelacones y matrz de encadenamento...3 5 Construccón del grafo...4
GANTT, PERT y CPM INDICE 1 Antecedentes hstórcos...2 2 Conceptos báscos: actvdad y suceso...2 3 Prelacones entre actvdades...3 4 Cuadro de prelacones y matrz de encadenamento...3 5 Construccón del grafo...4
CUADRIENIO 2011 2014
 INFORME TÉCNICO PEAJE POR USO DE INSTALACIONES DE TRANSMISIÓN ADICIONAL POR PARTE DE USUARIOS SOMETIDOS REGULACIÓN DE PRECIOS QUE SE CONECTAN DIRECTAMENTE DESDE INSTALACIONES ADICIONALES CUADRIENIO 2011
INFORME TÉCNICO PEAJE POR USO DE INSTALACIONES DE TRANSMISIÓN ADICIONAL POR PARTE DE USUARIOS SOMETIDOS REGULACIÓN DE PRECIOS QUE SE CONECTAN DIRECTAMENTE DESDE INSTALACIONES ADICIONALES CUADRIENIO 2011
Electricidad y electrónica - Diplomado
 CONOCIMIENTOS DE CONCEPTOS Y PRINCIPIOS Circuitos Eléctricos: principios, conceptos, tipos, características Unidades Básicas de los circuitos eléctricos: conceptos, tipos, características Leyes fundamentales
CONOCIMIENTOS DE CONCEPTOS Y PRINCIPIOS Circuitos Eléctricos: principios, conceptos, tipos, características Unidades Básicas de los circuitos eléctricos: conceptos, tipos, características Leyes fundamentales
OPTIMIZACIÓN DEL AISLAMIENTO ACÚSTICO A RUIDO AÉREO EN SISTEMAS DE DOBLE PARED DE YESO LAMINADO Y LANA DE ROCA.
 OPTIMIZACIÓN DEL AISLAMIENTO ACÚSTICO A RUIDO AÉREO EN SISTEMAS DE DOBLE PARED DE YESO LAMINADO Y LANA DE ROCA. José Carlos Aguilar ROCKWOOL PENINSULAR S.A. C/Bruc, nº 50-3ª, 08010 Barcelona; tel: 93.318.9028;
OPTIMIZACIÓN DEL AISLAMIENTO ACÚSTICO A RUIDO AÉREO EN SISTEMAS DE DOBLE PARED DE YESO LAMINADO Y LANA DE ROCA. José Carlos Aguilar ROCKWOOL PENINSULAR S.A. C/Bruc, nº 50-3ª, 08010 Barcelona; tel: 93.318.9028;
TEMA 5: APLICACIONES DEL EFECTO TÉRMICO
 Elementos de caldeo TEMA 5: APLICACIONES DEL EFECTO TÉRMICO Son resistencias preparadas para transformar la energía eléctrica en calor (Figura). Se utilizan para la fabricación de estufas, placas de cocina,
Elementos de caldeo TEMA 5: APLICACIONES DEL EFECTO TÉRMICO Son resistencias preparadas para transformar la energía eléctrica en calor (Figura). Se utilizan para la fabricación de estufas, placas de cocina,
