Escalamiento de las ecuaciones del flujo del agua subterránea mediante filtrado de Butterworth
|
|
|
- María Rosario Camacho Murillo
- hace 8 años
- Vistas:
Transcripción
1 Ingeniería hidráuica en México, vo. XXI, núm. 4, pp. 5-16, octubre-diciembre de 2006 Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth Ávaro A. Adama Migue Á. Meía Instituto Mexicano de Tecnoogía de Agua Roger Beckie University of British Coumbia, Canadá E fuo de agua y e transporte de soutos en medios geoógicos se desarroan en muchas escaas de ongitud (poros de orden de miímetros hasta regiones que tienen kiómetros de ongitud). Por o mismo, hay escaas demasiado pequeñas para ser resuetas mediante un modeo o para ser observadas con os aparatos convencionaes de medición. Aun cuando no es factibe desarroar modeos que resuevan todas as escaas significantes, sí es posibe desarroar modeos de a dinámica de as escaas grandes. Estos modeos de escaa grande no requieren a descripción expícita de as escaas pequeñas, pero deben incuir e efecto de as escaas pequeñas en a dinámica de as escaas grandes. La incorporación de taes efectos requiere a soución de un probema de cerradura. Por medio de uso de fitros de Butterworth se desarroa una soución exacta para e probema de cerradura para e fuo de agua en un medio poroso con gran heterogeneidad. Se incuyen pruebas numéricas que vaidan os resutados teóricos. Paabras cave: fuo en medios porosos, escaas grandes, escaas pequeñas, probema de cerradura, fitro de Butterworth. Introducción E carácter atamente heterogéneo de as propiedades de sueo genera a presencia de una mutitud de escaas de ongitud en as variabes de interés presentes en os procesos de fuo y transporte en e agua subterránea. Dado que as ecuaciones que representan estos procesos por o genera se resueven numéricamente, se debe introducir una discretización espacia. E teorema de muestreo impica que as escaas que son más pequeñas que dos veces e tamaño de a maa no pueden ser resuetas por un modeo numérico. E uso de maas extremadamente refinadas demanda cargas computacionaes excesivas. Aun si fuera posibe superar as imitaciones computacionaes, sería prácticamente imposibe obtener a información asociada con as escaas pequeñas de fuo. Por o tanto, es de interés práctico desarroar modeos de as escaas grandes que están presentes en as variabes de fuo. E proceso de transformar una ecuación que tiene todas as escaas significativas en una ecuación que gobierna e comportamiento de as escaas grandes es comúnmente conocido como escaamiento (upscaing en ingés). Las ecuaciones escaadas no deberían contener a dinámica de as escaas pequeñas expícitamente, sino soamente e efecto que as escaas pequeñas producen en a dinámica de as escaas grandes. La naturaeza de os procesos de fuo y transporte coneva que, cuando se intenta determinar este efecto, surge un probema de cerradura. E probema de escaamiento ha sido abordado por otros investigadores empeando e enfoque estocástico (e.g. Gehar, 1993). Dicho enfoque está basado en a suposición de que os procesos de fuo y transporte en aguas subterráneas poseen un comportamiento ergódico. Evidentemente, una condición necesaria para a ergodicidad es a homogeneidad estadística. Los procesos de fuo y transporte sueen no ser estadísticamente homogéneos. Por eempo, se sabe que a concentración de un souto en una puma contaminante transportada en un acuífero será estadísticamente homogénea sóo si 5
2 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth a dimensión transversa de a puma es mucho mayor que a escaa de ongitud característica de as fuctuaciones de concentración. Frecuentemente, dicha condición no se satisface en a práctica (Dagan, 1994). Por tanto, a hipótesis de ergodicidad es débi. Además, e enfoque estocástico descansa en metodoogías fenomenoógicas para a determinación de propiedades materiaes efectivas, como a conductividad, a transmisividad, e coeficiente de amacenae y a dispersividad. Dichas metodoogías se basan en consideraciones de carácter semiempírico, cuya vaidez genera es dudosa. Asimismo, e enfoque estadístico-fenomenoógico asocia escaas de ongitud características de as propiedades materiaes, taes como as respectivas ongitudes de correación, que dependen de comportamiento estadístico de dichas propiedades. E cácuo de esas ongitudes que a su vez determinan a estructura tanto de as correaciones o covariancias espaciaes como de os espectros de as propiedades materiaes requiere información que usuamente no está disponibe en a práctica, o cua dificuta a apicación de enfoque en comento. E primer autor de este artícuo y sus coaboradores han estado trabaando en e desarroo de un enfoque aterno a probema de escaamiento, que o aborda directamente, sin requerir de a hipótesis ergódica ni de modeos fenomenoógicos (Adama, 1992; Beckie et a., 1996a, Beckie et a., 1996b). Dicho enfoque se basa en e uso de fitros espaciaes y es simiar a que se usa en as simuaciones de turbuencia (Adama, 1990). En este trabao se presenta e desarroo de as ecuaciones que describen a dinámica de as escaas grandes de fuos de agua subterránea. Se introduce a famiia de fitros de Butterworth, que es utiizada en e anáisis de señaes digitaes (Stearns, 1975). En particuar, se empea e fitro de Butterworth de primer orden, que permite resover e probema de cerradura en forma exacta. Mediante a reaización de experimentos numéricos, se evaron a cabo pruebas a priori y a posteriori para vaidar a apicación de a teoría presentada a a simuación de medios porosos atamente heterogéneos. Ecuaciones de movimiento Se supone que e agua está fuyendo en un medio poroso saturado con una matriz rígida de sueo. Por tanto, en ausencia de fuentes o sumideros, e principio de conservación de masa toma a forma de a siguiente ecuación de continuidad: Q = 0 (1) donde Q representa e vector de fuo y x, e vector de posición. Si se supone que e fuo es darciano en as escaas de interés y que e medio es isotrópico, se tiene a siguiente reación constitutiva: donde = ( x) representa a conductividad hidráuica y H, a carga piezométrica. La ecuación (2) es una expresión de a céebre ey de Darcy. Combinando as ecuaciones (1) y (2) se obtiene a conocida ecuación de fuo de agua subterránea: Interacción de escaas Q H = H x = 0 x La interacción de as diferentes escaas de ongitud presentes en e agua subterránea se entiende meor en e espacio de Fourier. Por tanto, se introducirá a transformada a espacio de Fourier de una función que depende de as coordenadas espaciaes, F=F(x ), en a siguiente forma: Fk ˆ( ) = Fx ( ) exp ( ikx) d x Donde, a partir de ahora, e circunfeo representa a transformación de Fourier; e signo de integra, a integración sobre un dominio tridimensiona no acotado; k, e vector de número de onda, y dx dx 1 dx 2 dx 3. Si e dominio de interés es acotado, se supone que F y todas as variabes reevantes se extienden apropiadamente fuera de dominio. Tomando a transformada de Fourier de a ecuación (2) y empeando e teorema de a convoución, se obtiene: donde dk dk 1 dk 2 dk 3. Por tanto, todas as escaas (números de onda) presentes en interactúan con todas as escaas presentes en H para producir as escaas de Q. Esta interacción es particuarmente significativa cuando posee un espectro muy ancho, i.e., cuando e campo de conductividad es muy heterogéneo. Metodoogía de fitrado espacia ˆ i Q ( k ) = k ˆ( k ) khk ˆ( ) d ( 2π) 3 k En e marco de un método de fitrado espacia, as componentes de escaa grande (eg) de una variabe F=F(x ) son definidas por a siguiente operación de convoución (Adama, 1990 y 1992): (2) (3) (4) (5) 6 ingeniería hidráuica en méxico /octubre-diciembre de 2006
3 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth F( x ) = G( x x ) F( x ) dx (6) Q H = (13) donde, a partir de ahora, a barra superior representa a operación de fitrado dada por (6) y G es una función de fitrado que posee as siguientes propiedades: H x = 0 x (14) Gx ( ) dx = 1 ím x α DG= x 0 α (7) (8) Expresando a conductividad, e fuo y a carga en términos de sus componentes de escaa grande (eg), denotadas con sobrebarra y definidas a través de a operación de fitrado (6), y de escaa pequeña (ep), denotadas por medio de etras minúscuas, se tiene que: α ím DG= ˆ k 0 α k donde D α x y D α k representan operadores diferenciaes definidos como: D α x α = α1 α2 α (9) (10) = k (15) Q= Q q (16) H= H h (17) La substitución de as expresiones (15)-(17) en as ecuaciones (13) y (14) resuta en: D α k α = k k k α1 α2 α (11) Q H = = H h k H k h (18) α=(α 1,α 2,α 3 ) representa un muti-índice, α 1, α 2 y α 3 son enteros no negativos y Σα α 1 α 2 α 3. La propiedad (7) impica que G preserva a media y a propiedad (8) es necesaria para demostrar que a operación de fitrado conmuta con derivadas espaciaes de orden arbitrario. La impicación de a propiedad (9), así como a importancia de a operación de fitrado, se comprenden meor en e espacio de Fourier. Transformando a ecuación (6) a espacio de Fourier se obtiene: F ˆ( k ) = G ˆ( k )ˆ( F k ) La propiedad (9) impica, para α = 0, que as componentes de número de onda atas de ˆF (componentes atamente fuctuantes) son eiminadas (graduamente si Ĝ posee un soporte no acotado, o totamente si Ĝ posee un soporte acotado) a través de a operación de fitrado. E probema de cerradura y ocaización (12) Fitrando a ey de Darcy (2) y a ecuación de fuo de agua subterránea (3), y tomando en cuenta e hecho de que, gracias a a propiedad (8), a operación de fitrado conmuta con as derivadas espaciaes, se obtiene: H h k H k h = 0 x E primer término en a ecuación (18) representa a interacción eg-eg (escaa grande-escaa grande); e segundo y tercer términos, a interaccción eg-ep (escaa grande-escaa pequeña), y e cuarto, a interacción epep (escaa pequeña-escaa pequeña). E probema de cerradura se muestra caramente en a expresión (19), que representa a ecuación de agua subterránea escaada. Los términos de interacción eg-ep y ep-ep contienen variabes de escaa pequeña. Para cerrar a ecuación (19) es necesario expresar estos términos excusivamente en términos de variabes de escaas grandes. También es necesario que os términos de interacción eg-eg se expresen ocamente, debido a que, en vista de a definición de a operación de fitrado a través de a expresión (6), su naturaeza e da a a ecuación (19) un carácter integrodiferencia. Metodoogía de fitrado espacia gaussiano (19) Adama (1992) y Beckie et a. (1996a y 1996b) han empeado un fitro gaussiano que, en e espacio de Fourier, tiene a forma (véase iustración 1): ingeniería hidráuica en méxico /octubre-diciembre de
4 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth Iustración 1. Fitro gaussiano en e espacio de Fourier. Ordenada de fitro gaussiano Una expan- donde λ es e ancho de fitro y k kk sión en serie de Tayor de ĜG resuta en: 1 Substituyendo (21) en (12), empeando e resutado de (18) y usando e teorema de diferenciación de Fourier, se obtiene a siguiente expresión (Adama, 1992; Beckie et a., 1996a): Apicando a expresión (22) a a ecuación (14) se obtiene a ecuación de fuo de agua subterránea de escaa grande ocaizada: Número de onda ˆ( ) ˆ k Gk = G G ( k) = exp λ ( ) 12 / ˆ λ k λ k G G ( k) = 1 O ( 6 λ ) Q H = λ 288 = H H λ 12 O( λ ) H m m H x x = λ H λ x m m 6 (20) (21) (22) (23) H 6 O( λ ) x x x Mientras que e ancho de fitro, λ, sea mucho más pequeño que a escaa de ongitud dominante en as variabes de eg, Λ, se esperaría que os términos de O(λ 6 ) fueran despreciabes en a ecuación (23). Por tanto, una vez que esos términos se hubieren despreciado, se esperaría que a tasa de convergencia de a norma de error de a soución de a ecuación (23), H, fuera de orden sexto en λ. Es de notar también que as ecuaciones de eg contienen derivadas de ato orden. Por esta razón, cabría esperar a necesidad de condiciones de frontera adicionaes para resover as ecuaciones. Sin embargo, Beckie et a. (1996b) apicaron con éxito un método de perturbación reguar que no requiere condiciones de frontera adicionaes. Aunque Beckie et a. (1996b) obtuvieron resutados numéricos muy aentadores en a soución de as ecuaciones de escaa grande de agua subterránea, para campos de conductividad atamente heterogéneos, no se obtuvo a tasa teórica de convergencia de error que se esperaba. Esto se atribuyó a hecho de que cuando a expansión (21) se trunca, o cua es equivaente a despreciar términos proporcionaes a cierta potencia de λ en (23), a función de fitro gaussiano se aproxima mediante un poinomio en e espacio de Fourier. Este tipo de aproximaciones es muy precisa en números de onda baos, pero se degrada significativamente en números de onda atos. De hecho, por definición, e fitro gaussiano es definido-positivo, mientras que as aproximaciones poinomiaes que surgen de a expansión de Tayor no o son. Aun más, estas aproximaciones no satisfacen a propiedad (9), dado que su magnitud no tiende a cero para k. Estas observaciones evaron a buscar aternativas a a aproximación poinomia de fitro gaussiano que dieran una meor soución a probema de cerradura y ocaización de as ecuaciones de escaa grande (18) y (19). La metodoogía de fitrado de Butterworth y a soución de probema de cerradura La principa ventaa de apicar una aproximación poinomia a fitro gaussiano es que, en e espacio de Fourier, a variabe de eg, ˆ F, se expresa como e producto de un poinomio de grado par en k por a variabe primitiva ˆF. Esto permite e uso de teorema de diferenciación de Fourier cuando se invierte ta expresión. De esta manera, un término que invoucra una potencia par en k mutipicado por ˆF se convierte, después de invertiro, en una potencia par de operador apicado a F. Por tanto, una aproximación poinomia de fitro gaussiano en e espacio de Fourier permite expresar F en términos de F y de sumandos proporcionaes a potencias pares de producto λ apicados a F. Estos términos son presumibemente pequeños en comparación con F, por o que se 8 ingeniería hidráuica en méxico /octubre-diciembre de 2006
5 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth puede apicar un método basado en una substitución iterada que permite a derivación de expresiones como (22) y (23) Sin embargo, como se señaó antes, a fata de propiedades como a definición-positiva y e decaimiento en e infinito en as aproximaciones poinomiaes de fitro gaussiano motivó a os autores a encontrar un fitro aternativo que preservara as ventaas de dicho fitro, pero que no tuviera as desventaas de as aproximaciones poinomiaes. Los fitros que se proponen en este trabao son os de Butterworth, os cuaes están definidos por a siguiente expresión en e espacio de Fourier (Stearns, 1975): ˆ BN ; G ( k)= 1 η 1 k k (24) donde N es un número entero que representa e orden de fitro; k c, un número de onda de corte, y η N es un parámetro reacionado con a tasa de decaimiento de fitro, en sentido que k> kc Gˆ 2 BN, ( k) < 1/( 1 η N). Como se puede observar en (24), ĜB.N es definido-positivo. También se puede demostrar que cuanto más ato es e vaor de N, ĜB.N se aproxima más y más a un fitro idea de paso bao (Stearns, 1975). Finamente, ĜB.N también satisface as propiedades (7)-(9). Es interesante notar que e fitro propuesto corresponde a a función característica de una distribución de Lapace, con parámetro de ocaización coincidente con a media y e parámetro de escaa dado en términos de número de onda de corte. Hasta e momento se ha investigado e uso de miembro más simpe de a famiia de Butterworth, esto es, e fitro de orden uno, correspondiente a N=1. Asimismo, se eigió a siguiente opción para os parámetros de fitro: η 1 k c De esta manera, substituyendo (25) en (24), con N=1, se obtiene a siguiente expresión para a función de fitro a ser apicada de aquí en adeante (iustración 2): La razón para eegir a opción (25) es que a expresión que resuta para e fitro, (26), se puede considerar como a aproximación de Padé (0,2) de fitro gaussiano (20). No obstante, a partir de este momento, a expresión (26) debe ser vista como una redefinición de a función de fitrado y no como una aproximación. 2 N 2 2 c λ = 24 2N ˆ( ) ˆ 1 Gk = GB, ( k) = λ k (25) (26) Iustración 2. Fitro de Butterworth en e espacio de Fourier. Ordenada de fitro de Butterworth Número de onda Substituyendo a expresión (26) en a ecuación (12), y resoviendo para ˆF resuta: Invirtiendo (27) se obtiene: ˆ ˆ λ 2 k 2 ˆ F = F F 24 F = F λ 2 2 F 24 (27) (28) Como se puede observar, e uso de un fitro de Butterworth permite derivar un resutado más conveniente que e que se obtiene apicando e fitro gaussiano. En efecto, (28) expresa en forma exacta una variabe primitiva en términos de a variabe de eg y su apaciano. Empeando (28) para a conductividad hidráuica y e gradiente de a carga se tiene: = H = H λ λ 2 3 H 24 (29) (30) ingeniería hidráuica en méxico /octubre-diciembre de
6 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth Substituyendo (29) y (30) en (13) resuta: 2 2 H H Q = 2 3 λ λ (31) H 2 2 λ H 12 λ H λ H m m m m Substituyendo ahora (31) en a ecuación de continuidad de eg, Q / =0 resuta: λ H λ H 24 x x 24 = 0 (32) λ H H 288 x xm xm x x x xm xm x 6 6 λ H x x xm xm xn xn x La expresión (32) representa a ecuación de fuo de agua subterránea de eg, a cua se ha cerrado exactamente. Sin embargo, (32) no es oca, dado que a barra superior representa a operación de convoución. Por tanto, dicha ecuación posee un carácter integrodiferencia. La ecuación (28) se puede resover para F expresándoa como a suma de F y un residuo de O(λ 2 ). Con base en esta observación se puede reaizar e producto en (31) y (32), y os cuatro términos fitrados que resutan se pueden expresar en términos de su contraparte no fitrada más un residuo de O(λ 2 ). La operación se puede repetir una y otra vez, o que genera un procedimiento de substitución iterada. Su apicación a (31) y (32) da como resutado respectivo as siguientes expresiones de eg para a ey de Darcy y a ecuación de agua subterránea, que son ocaizadas (hasta os términos de O(λ 4 )), cerradas y exactas: Q H = 2 2 λ 12 H λ H λ H m m m m λ H H 288 x xm xm x x x xm xm x 6 6 λ H x x xm xm xn xn x H H m m n n n n H m m n n (33) Soución de as ecuaciones de escaa grande de agua subterránea La ecuación de escaa grande de agua subterránea (34) invoucra derivadas de ato orden, o que en estricto sentido impicaría contar con condiciones de frontera adicionaes, cuya determinación constituye en sí misma un probema abierto y compeo. Es posibe evitar requerir estas nuevas condiciones de frontera si se empea a estrategia de perturbaciones propuesta por Beckie et a. (1996b) y Adama et a. (1998). Para e efecto, se supondrá que as variabes de interés presentes en as ecuaciones (33) y (34) escaan de siguiente modo: H x = = HH H H m m n n n n H = 0 x x x m m n n =Λ x (35) (36) (37) Q H (38) = Q Λ donde as variabes con tide representan escaas características y as denotadas con asterisco son adimensionaes, y se supone que son de O(1). Asimismo, se supondrá que e ancho de fitro, λ, satisface a siguiente reación: λ ε << 1 Λ (34) (39) 10 ingeniería hidráuica en méxico /octubre-diciembre de 2006
7 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth donde Λ representa a escaa de ongitud dominante de as variabes de eg. Substituyendo (35)-(38) en (33) y (34) se obtiene: Q 2 2 H ε H = ε H ε La forma de a ecuación de agua subterránea de eg (41) sugiere expandir a carga adimensiona de eg, H, en una serie perturbatoria, como sigue: donde H0, H0 ε H1 y H1 ε H1 ε H, respectivamente, representan as souciones adimensionaes aproximadas de orden cero, uno y dos a a ecuación de agua subterránea de eg (41). Evidentemente, a expresión dimensiona correspondiente a a serie (42) es 2 4 Hx ( ) = H0 ( x) ε H1( x) ε H2 ( x)..., donde Hn = HH n, ( n= 0, 1, 2,...). Substituyendo a ecuación (42) en a ecuación (41) y suponiendo que a iguadad resutante se cumpa como identidad para ε 2 arbitrariamente pequeño, se obtiene a sucesión de ecuaciones presentada a continuación. Para a soución de orden cero: Para a corrección de orden uno: (40) H 6 O( ε ) m m m m 2 2 H ε H 12 ε H ε ε 288 H m m m m H (41) H 6 O( ε ) x x x x m m m m H ( x ) = H ( x ) ε H ( x ) ε H ( x ) O( ε ) H1 0 H = 0 2 H0 1 = 12 (42) (43) (44) Para a corrección de orden dos: H2 = x H H H0 m m m m x 4 H0 3 2 H0 m m m m Las versiones dimensionaes de as ecuaciones (43), (44) y (45) son, respectivamente: H H 1 Λ = Como se puede apreciar, as ecuaciones (44) y (45) o sus contrapartes dimensionaes, (47) y (48) son forzadas por términos no homogéneos que contienen información de orden más bao. Dichos términos se conocen si as ecuaciones se resueven en forma secuencia. La ventaa de este procedimiento es que sóo se tiene que resover a ecuación de fuo estándar, homogénea para a soución de orden cero y no homogénea para as correcciones de orden superior. En vista de a naturaeza de a serie de perturbaciones de (42), a soución de orden cero H 0 (o su contraparte dimensiona, H 0 ) satisface as mismas condiciones de frontera de Dirchet, Neumann o Robin que H (o su contraparte dimensiona, H), y as sucesivas correcciones, H 1, H 2,... (o sus contrapartes dimensionaes, H 1, H 2,...), versiones homogéneas de a mismas condiciones de frontera = 0 H0 2 2 = H Λ H1 x Λ H0 Λ H m m m m H Λ H0 m m m m (45) (46) (47) (48) ingeniería hidráuica en méxico /octubre-diciembre de
8 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth Vaidación Prueba a priori E obetivo de esta prueba es examinar a precisión de as expansiones de eg mediante variabes fitradas exactas que se conocen a priori. Se investiga, asimismo, a tasa de convergencia asintótica de as aproximaciones en un pequeño parámetro que caracteriza as escaas significativas de probema. La teoría predice que as expansiones deberían ser asintóticas en potencias pares de parámetro pequeño ε, definido como a reación de ancho de fitro, λ, respecto de a escaa de a ongitud dominante de as escaas fitradas, Λ. Tanto as pruebas a priori como as a posteriori (que se describirán posteriormente) se reaizaron en un dominio bidimensiona Ω = [0,L] x [0,L], L=512, con condiciones de fronteras de carga constante en dos ados opuestos (H = 1 en un ado y H = 0 en e otro ado) y de fuo nuo (H/ = 0) en os otros dos ados. Como primer paso se generó un campo primitivo atamente heterogéneo de conductividades (con varianza de n, σ 2 In = 6.3), especificando e espectro mostrado en a iustración 3 y empeando un método rápido de transformada de Fourier (Fenton, 1990). En a iustración 4 se muestra e campo de conductividades resutante que, como se puede apreciar, posee una variabiidad de cinco a seis órdenes de magnitud. Iustración 3. Espectro de energía de campo de conductividades primitivo. Energía 1.0E02 1.0E01 1.0E00 1.0E E E E E E00 Frecuencia adimensiona Iustración 4. Campo de conductividades expresado como og La escaa de ongitud dominante de campo de conductividad, Λ, se determinó a partir de espectro de energía. Esta escaa se estimó como a escaa de ongitud asociada con e número de onda que corresponde a máximo oca más sobresaiente de espectro de energía. En este caso, como se puede observar en a iustración 3, dicho máximo corresponde a una frecuencia adimensiona f =, donde, como se comenta posterior- x Λ 001. mente, x = 1, por o que se estimó que Λ 100. Empeando e campo de conductividades mostrado en a iustración 4, se resovió a ecuación primitiva de fuo de agua subterránea (3). Para ta efecto, se empeó e método de voumen finito, con intervaos de discretización x = y = 1. La magnitud apropiada de estos intervaos se determinó por división sucesiva de una magnitud inicia entre dos, hasta que no hubo cambios apreciabes en os resutados obtenidos para a variabe dependiente H. De este modo se obtuvo un campo de cargas primitivo y un campo de fuo primitivo. Dichos campos se fitraron numéricamente, empeando un ancho de fitro λ = 20 x, generando así una soución de eg exacta. Para fitrar os campos, os datos se transforman primeramente de espacio físico a espacio de Fourier, utiizando un agoritmo de transformada rápida de Fourier. Por e teorema de convoución, a integra de convoución que define a operación de fitrado espacia en e espacio físico se puede cacuar en e espacio de Fourier mutipicando a transformada de Fourier de os campos primitivos por a transformada de Fourier de fitro (Bracewe, 1965), y posteriormente invirtiendo e resutado mediante e uso de un agoritmo de transformada rápida de Fourier inversa. 12 ingeniería hidráuica en méxico /octubre-diciembre de 2006
9 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth Iustración 5. Fuo exacto y fuo aproximado de orden cero Q x (L/2, y), λ = 20 x. Iustración 6. Fuo exacto y fuo aproximado de orden dos Q x (L/2, y), λ = 20 x. 1.8E E E E E-02 Exacto Cero 1.2E-02 Exacto Dos Q x 1.2E E E E E E E Y Q x 1.0E E E E E E Y La ecuación (33) se empeó como a base de a prueba a priori. Usando os vaores exactos de campo de conductividades de eg, y H, se construyeron varias aproximaciones a Q x, Q y usando versiones truncadas de a expresión (33). De esta manera, una aproximación de orden cero se obtuvo despreciando os términos de orden O(λ 2 ) y más ato; una aproximación de primer orden, despreciando os términos O(λ 4 ) y más ato, y una aproximación de segundo orden, despreciando os términos de O(λ 6 ). La iustración 5 muestra a comparación de un corte de vaor exacto contra e vaor aproximado de orden cero, de Q x a o argo de a ínea x = L/2. Como se puede observar, as dos souciones difieren significativamente en agunas partes de dominio. Por otra parte, a iustración 6 muestra a comparación de un corte de vaor exacto contra e vaor aproximado de segundo orden. En este caso, a concordancia entre a soución exacta y a aproximación es exceente. La norma 2 de error, definida como a raíz cuadrada de a suma de os cuadrados de as diferencias entre a soución aproximada y a exacta, se obtuvo para diferentes vaores de ε. Las tasas de convergencia observadas se muestran en a iustración 7. Las pendientes de estas íneas corresponden a as tasas de convergencia teóricamente esperadas de as aproximaciones, esto es, os errores son proporcionaes a ε 2, ε 4, y ε 6, para as aproximaciones de orden cero, uno y dos, respectivamente. Iustración 7. Tasa de convergencia cacuada de a norma 2 de error, para as aproximaciones de orden cero, uno y dos. Norma de error L E-05 1E-06 1E-07 1E Epsion 0.1 Prueba a posteriori Orden cero Pendiente 2 Orden uno Pendiente 4 Orden dos Pendiente 6 En esta prueba se resueven as ecuaciones de escaa grande empeando directamente e campo de conductividades de escaa grande. A apicar a teoría propuesta a a práctica, as ecuaciones se utiizarían a posteriori. La ecuación de agua subterránea de eg (34) se resueve apicando e método de perturbaciones descrito ante- ingeniería hidráuica en méxico /octubre-diciembre de
10 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth riormente y un método de voumen finito. De esta manera se obtienen as aproximaciones de orden cero, uno y dos. En a iustración 8 se muestran e fuo fitrado exacto y e aproximado de orden cero a o argo de una sección Iustración 8. Fuo exacto y fuo aproximado de orden cero Q x (L/2, y), con ε = 0.2. Q x Iustración 9. Fuo exacto y fuo aproximado de orden dos Q x (L/2, y), con ε = 0.2. Q x 1.8E E E E E E E E E E E E E E E E E E-03 Exacto Cero 0.0E Y Exacto Dos 0.0E Y Iustración 10. Tasa de convergencia de a norma 2 de error teórica (ínea discontinua) y a cacuada (ínea continua). Norma de error 1.E00 1.E-01 1.E-02 1.E-03 1.E-04 1.E-05 1.E-06 1.E Epsion ocaizada en x = L/2. Como se puede observar, a aproximación de orden cero se desvía considerabemente de a soución exacta. En a iustración 9 se muestran e fuo fitrado exacto y e aproximado de segundo orden a o argo de una sección ocaizada en x=l/2. Los resutados son muy aentadores, ya que a aproximación de orden dos es prácticamente igua a a soución exacta. La norma 2 de error se obtuvo para diferentes vaores de ε. De acuerdo con os argumentos teóricos que se presentaron anteriormente, se espera una tasa de convergencia de orden sexto para a soución de orden dos. En a iustración 10 se muestra a tasa de convergencia observada, que confirma a expectativa teórica. Concusiones y recomendaciones Error Pendiente = 6 En este trabao se presenta una metodoogía de modeación que utiiza as componentes de escaa grande. Esta metodoogía difiere de os métodos convencionaes en e requerimiento de os datos. Mientras que otras teorías, por o genera requieren información estadística acerca de as propiedades de submaa de sistema, e método propuesto sóo utiiza información de as propiedades de as escaas grandes de sistema, a cua es mucho más fáci de obtener. La principa aportación de este trabao es a soución exacta de probema de cerradura cuando se estudia a dinámica de as escaas grandes en fuos en medios porosos atamente heterogéneos. La teoría desarroada se basa en e uso de fitros de Butterworth y a derivación de ecuaciones para a dinámica de as escaas grandes, as cuaes se resueven por medio de un esquema perturbatorio que permite eudir e probema de especificar condi- 14 ingeniería hidráuica en méxico /octubre-diciembre de 2006
11 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth ciones de frontera adicionaes, ya que as ecuaciones que gobiernan e comportamiento de as escaas grandes contienen derivadas espaciaes de ato orden. Este trabao constituye e primer paso en a evauación de a metodoogía de escaas grandes para modear as escaas resuetas de fuo de agua subterránea. Las pruebas numéricas que se reaizaron para vaidar a teoría muestran resutados muy prometedores. En este trabao únicamente se utiizaron fitros isotrópicos. Este tipo de fitros es adecuado para a mayoría de os sistemas horizontaes bidimensionaes. Sin embargo, si se va a modear una sección vertica, sería más apropiado usar fitros anisotrópicos. En este caso se usa un ancho de fitro pequeño en a dirección vertica, donde as características de medio poroso cambian rápidamente con a posición. En a dirección horizonta se utiizarían anchos de fitro más grandes. Adama (1993) presenta agunas ideas que se pueden utiizar para reaizar este anáisis. Referencias Recibido: 24/05/2005 Aprobado: 30/03/2006 ALDAMA, A. Fitering techniques for turbuent fow simuation. Berín: Springer-Verag, 1990, 397 pp. ALDAMA, A. A subgrid scae theory for physica processes with quadratic noninearities: An a priori test for Burgers fow. Proc. IX Int. Conf. Comp. Meth. Water Res. Vo. 2. Southampton: Comp. Mech. Pubications, 1992, pp ALDAMA, A. Leonard and cross terms approximations in the anisotropicay fitered equations of motion, en Gaperin, B. y S. Orszag, Large Eddy Simuation of Compex Engineering on Geophysica Fows. New York: Cambridge University Press, ALDAMA, A., BECIE, R. y MEJÍA, M. A new approach for scaing-up fow and transport processes based on the use of Butterworth fiters. Proc. XII Int. Conf. Comp. Meth. Water Res. Vo. 1. Southampton: Comp. Mech. Pubications, 1998, pp BECIE, R., ALDAMA, A. y WOOD, E. Modeing the arge-scae dynamics of saturated groundwater fow using spatia-fitering theory: 1. Theoretica deveopment. Water Resources Res. Vo. 22, 1996a, pp BECIE, R., ALDAMA, A. y WOOD, E. Modeing the arge-scae dynamics of saturated groundwater fow using spatia-fitering theory: 2. Numerica evauation. Water Resources Res. Vo. 22, 1996b, pp BRACEWELL, R. In the Fourier transform and its appications. Eectrica and eectronic engineering series, New York: McGraw-Hi, DAGAN, G. Upscaing of dispersion coefficients in transport through heterogeneous porous media. Computationa Methods in Water Resources, 1994, pp FENTON, G.A. Simuation and anaysis of random fieds. Tesis de doctorado. Princeton, N.J.: Dep. of Civi Eng. and Oper. Res., Universidad de Princeton, GELHAR, L. Stochastic subsurface hydroogy. New Jersey: Prentice-Ha, STEARNS, S. Digita signa anaysis. Rochee Park: Hayden, 1975, 280 pp. ingeniería hidráuica en méxico /octubre-diciembre de
12 Adama, A.A. et a., Escaamiento de as ecuaciones de fuo de agua subterránea mediante fitrado de Butterworth Abstract ALDAMA, A.A., MEJÍA, M.A. & BECIE, R. Scaing-up of groundwater fow equations via Butterworth fitering. Hydrauic engineering in Mexico (in Spanish). Vo. XXI, no. 4, October-December, 2006, pp Water fow and soute transport in porous media evove over many different ength scaes. The numerica simuation of the dynamics of a scaes woud require excessivey arge computationa resources. Whereas it may never be possibe to deveop modes to resove a significant scaes, it may be feasibe to deveop modes of the arge scae dynamics. These arge scae modes woud not require the expicit description of the sma scaes, but shoud incude the effect of the sma scaes on the arge scae dynamics. The incorporation of such effects requires the soution of a probem of cosure. Through the use of Butterworth fiters, an exact soution of the cosure probem for highy heterogeneous groundwater fow is deveoped. Numerica tests that vaidate the theoretica resuts are incuded. eywords: fow in porous media, arge scaes, sma scaes, probem of cosure, Butterworth fiters. Dirección instituciona de os autores: Dr. Ávaro A. Adama Dr. Migue A. Meía Instituto Mexicano de Tecnoogía de Agua, Paseo Cuauhnáhuac 8532, Progreso, Jiutepec, Moreos, México, C.P , teéfono: (52) (777) , director@taoc.imta.mx, mameia@taoc.imta.mx Dr. Roger Beckie Department of Earth and Ocean Sciences, University of British Coumbia, 6339 Stores Road, Vancouver, B.C. V6T 1Z A Canada, rbeckie@geoogy.ubc.ca 16 ingeniería hidráuica en méxico /octubre-diciembre de 2006
Vibración y rotación en mecánica cuántica
 Vibración y rotación en mecánica cuántica Antonio M. Márquez Departamento de Química Física Universidad de Sevia Curso 14-15 Probema 1 Una moécua de 1 H 17 I en fase gaseosa, cuya ongitud de enace es 16.9
Vibración y rotación en mecánica cuántica Antonio M. Márquez Departamento de Química Física Universidad de Sevia Curso 14-15 Probema 1 Una moécua de 1 H 17 I en fase gaseosa, cuya ongitud de enace es 16.9
2.1 Sistemas discretos en tiempo. 2.1.1 Sistemas lineales. 2.1.2 Sistemas invariantes en tiempo
 2.1 stemas discretos en tiempo Un sistema discreto en el tiempo se define matemáticamente como la transformación o el operador que traza una secuencia de entrada con valores x[n], en una secuencia de salida
2.1 stemas discretos en tiempo Un sistema discreto en el tiempo se define matemáticamente como la transformación o el operador que traza una secuencia de entrada con valores x[n], en una secuencia de salida
35 Facultad de Ciencias Universidad de Los Andes Mérida-Venezuela. Potencial Eléctrico
 q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
Flexión termoelást ica de placas ortdtropas
 Vo. 15, 1, 135-145 (1999) Revista Internaciona de Méto os Numéricos para Cácuo y Diseño en Ingeniería r Fexión termoeást ica de pacas ortdtropas Caros A. Rossit y Patricio A.A. Laura Departamento de Ingeniería
Vo. 15, 1, 135-145 (1999) Revista Internaciona de Méto os Numéricos para Cácuo y Diseño en Ingeniería r Fexión termoeást ica de pacas ortdtropas Caros A. Rossit y Patricio A.A. Laura Departamento de Ingeniería
Tema 07. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Programa para el Mejoramiento de la Enseñanza de la Matemática en ANEP Proyecto: Análisis, Reflexión y Producción. Fracciones
 Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
Fracciones. Las fracciones y los números Racionales Las fracciones se utilizan cotidianamente en contextos relacionados con la medida, el reparto o como forma de relacionar dos cantidades. Tenemos entonces
2.2 Transformada de Laplace y Transformada. 2.2.1 Definiciones. 2.2.1.1 Transformada de Laplace
 2.2 Transformada de Laplace y Transformada 2.2.1 Definiciones 2.2.1.1 Transformada de Laplace Dada una función de los reales en los reales, Existe una función denominada Transformada de Laplace que toma
2.2 Transformada de Laplace y Transformada 2.2.1 Definiciones 2.2.1.1 Transformada de Laplace Dada una función de los reales en los reales, Existe una función denominada Transformada de Laplace que toma
T.1 CONVERGENCIA Y TEOREMAS LÍMITE
 T.1 CONVERGENCIA Y TEOREMAS LÍMITE 1. CONVERGENCIA DE SUCESIONES DE VARIABLES ALEATORIA CONVERGENCIA CASI-SEGURA CONVERGENCIA EN PROBABILIDAD CONVERGENCIA EN MEDIA CUADRÁTICA CONVERGENCIA EN LEY ( O DISTRIBUCIÓN)
T.1 CONVERGENCIA Y TEOREMAS LÍMITE 1. CONVERGENCIA DE SUCESIONES DE VARIABLES ALEATORIA CONVERGENCIA CASI-SEGURA CONVERGENCIA EN PROBABILIDAD CONVERGENCIA EN MEDIA CUADRÁTICA CONVERGENCIA EN LEY ( O DISTRIBUCIÓN)
NÚMEROS NATURALES Y NÚMEROS ENTEROS
 NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
NÚMEROS NATURALES Y NÚMEROS ENTEROS Los números naturales surgen como respuesta a la necesidad de nuestros antepasados de contar los elementos de un conjunto (por ejemplo los animales de un rebaño) y de
ECUACIÓN QUE OBTIENE CON BUENA APROXIMACIÓN LA SUMA DE LOS PRIMEROS ENTEROS A CUALQUIER POTENCIA ENTERA POSITIVA
 DESDE LA ACADEMIA ECUACIÓN QUE OBTIENE CON BUENA APROXIMACIÓN LA SUMA DE LOS PRIMEROS ENTEROS A CUALQUIER POTENCIA ENTERA POSITIVA LUIS MANUEL MONTAÑO ZETINA* En este trabajo se presenta un análisis numérico
DESDE LA ACADEMIA ECUACIÓN QUE OBTIENE CON BUENA APROXIMACIÓN LA SUMA DE LOS PRIMEROS ENTEROS A CUALQUIER POTENCIA ENTERA POSITIVA LUIS MANUEL MONTAÑO ZETINA* En este trabajo se presenta un análisis numérico
PRÁCTICA N 2 SISTEMAS DE NUMERACIÓN
 PRÁCTICA N 2 SISTEMAS DE NUMERACIÓN Ejercicio 1. Diseñar una planilla EXCEL que tome como dato de entrada un número entero y devuelva la representación en base 2. Testearla con los números 23, 245, 673,
PRÁCTICA N 2 SISTEMAS DE NUMERACIÓN Ejercicio 1. Diseñar una planilla EXCEL que tome como dato de entrada un número entero y devuelva la representación en base 2. Testearla con los números 23, 245, 673,
Unidad 5 Utilización de Excel para la solución de problemas de programación lineal
 Unidad 5 Utilización de Excel para la solución de problemas de programación lineal La solución del modelo de programación lineal (pl) es una adaptación de los métodos matriciales ya que el modelo tiene
Unidad 5 Utilización de Excel para la solución de problemas de programación lineal La solución del modelo de programación lineal (pl) es una adaptación de los métodos matriciales ya que el modelo tiene
2.5 Linealización de sistemas dinámicos no lineales
 25 Linealización de sistemas dinámicos no lineales En las secciones anteriores hemos visto como representar los sistemas lineales En esta sección se estudia una manera de obtener una aproximación lineal
25 Linealización de sistemas dinámicos no lineales En las secciones anteriores hemos visto como representar los sistemas lineales En esta sección se estudia una manera de obtener una aproximación lineal
2. MATERIALES 2.1. ENSAYO DE TRACCIÓN
 DTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES 24 V. BADIOLA 2. MATERIALES 2.1. ENSAYO DE TRACCIÓN En e ensayo de tracción a una probeta se e apica una carga uniaxia. En cada instante se mide a carga
DTO. INGENIERÍA MECÁNICA, ENERGÉTICA Y DE MATERIALES 24 V. BADIOLA 2. MATERIALES 2.1. ENSAYO DE TRACCIÓN En e ensayo de tracción a una probeta se e apica una carga uniaxia. En cada instante se mide a carga
Teoría del Juego - Juegos Combinatoriales Imparciales
 Teoría del Juego - Juegos Combinatoriales Imparciales Carlos Gámez Taller de Resolución de Problemas Escuela de Matemática Universidad de El Salvador Estudio de Casos Esquema Introducción Juegos de Agarrar
Teoría del Juego - Juegos Combinatoriales Imparciales Carlos Gámez Taller de Resolución de Problemas Escuela de Matemática Universidad de El Salvador Estudio de Casos Esquema Introducción Juegos de Agarrar
EL PÉNDULO SIMPLE. Laboratorio de Física General Primer Curso (Mecánica) 1. Objetivo de la práctica. 2. Material. Fecha: 07/02/05
 Laboratorio de Física Genera Primer Curso (Mecánica) EL PÉNDULO SIMPLE Fecha: 07/02/05 1. Objetivo de a práctica Estudio de pénduo simpe. Medida de a aceeración de a gravedad, g. 2. Materia Pénduo simpe
Laboratorio de Física Genera Primer Curso (Mecánica) EL PÉNDULO SIMPLE Fecha: 07/02/05 1. Objetivo de a práctica Estudio de pénduo simpe. Medida de a aceeración de a gravedad, g. 2. Materia Pénduo simpe
Objetivos: Al inalizar la unidad, el alumno:
 Unidad 7 transformaciones lineales Objetivos: Al inalizar la unidad, el alumno: Comprenderá los conceptos de dominio e imagen de una transformación. Distinguirá cuándo una transformación es lineal. Encontrará
Unidad 7 transformaciones lineales Objetivos: Al inalizar la unidad, el alumno: Comprenderá los conceptos de dominio e imagen de una transformación. Distinguirá cuándo una transformación es lineal. Encontrará
_ Antología de Física I. Unidad II Vectores. Elaboró: Ing. Víctor H. Alcalá-Octaviano
 24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
24 Unidad II Vectores 2.1 Magnitudes escalares y vectoriales Unidad II. VECTORES Para muchas magnitudes físicas basta con indicar su valor para que estén perfectamente definidas y estas son las denominadas
VI-104 - ANÁLISIS DE LA ESTRUCTURA DE VARIABLES AMBIENTALES CON MIRAS A LA GENERACIÓN SINTÉICA DE DATOS
 VI-104 - ANÁLISIS DE LA ESTRUCTURA DE VARIABLES AMBIENTALES CON MIRAS A LA GENERACIÓN SINTÉICA DE DATOS Edilberto Guevara Pérez (1) Prof. Dr. Ing., Escuela de Ingenaría Civil, Director de Estudios para
VI-104 - ANÁLISIS DE LA ESTRUCTURA DE VARIABLES AMBIENTALES CON MIRAS A LA GENERACIÓN SINTÉICA DE DATOS Edilberto Guevara Pérez (1) Prof. Dr. Ing., Escuela de Ingenaría Civil, Director de Estudios para
MATEMÁTICAS 3º CURSO DE ESO INFORMACIÓN PARA LOS ALUMNOS
 I.E.S. Dr. FLEMING (OVIEDO) DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS 3º CURSO DE ESO INFORMACIÓN PARA LOS ALUMNOS Estas hojas son un resumen de la Programación Didáctica que está a disposición de los alumnos
I.E.S. Dr. FLEMING (OVIEDO) DEPARTAMENTO DE MATEMÁTICAS MATEMÁTICAS 3º CURSO DE ESO INFORMACIÓN PARA LOS ALUMNOS Estas hojas son un resumen de la Programación Didáctica que está a disposición de los alumnos
Física Contemporánea, Grupo: 8104 Tarea # 4, Fecha de entrega: viernes 18 de septiembre de 2015 Nombre:
 Física Contemporánea, Grupo: 8104 Tarea # 4, Fecha de entrega: viernes 18 de septiembre de 015 Nombre: Lee con atención as siguientes notas sobre e movimiento en un campo centra y reaiza os ejercicios
Física Contemporánea, Grupo: 8104 Tarea # 4, Fecha de entrega: viernes 18 de septiembre de 015 Nombre: Lee con atención as siguientes notas sobre e movimiento en un campo centra y reaiza os ejercicios
JOSE VICENTE CONTRERAS JULIO CALCULO INTEGRAL LA ANTIDERIVADA
 CALCULO INTEGRAL LA ANTIDERIVADA Así como las operaciones matemáticas de la adición, la multiplicación y la potenciación tienen sus inversas en la sustracción, la división y la radicación, la diferenciación
CALCULO INTEGRAL LA ANTIDERIVADA Así como las operaciones matemáticas de la adición, la multiplicación y la potenciación tienen sus inversas en la sustracción, la división y la radicación, la diferenciación
UNIDAD I NÚMEROS REALES
 UNIDAD I NÚMEROS REALES Los números que se utilizan en el álgebra son los números reales. Hay un número real en cada punto de la recta numérica. Los números reales se dividen en números racionales y números
UNIDAD I NÚMEROS REALES Los números que se utilizan en el álgebra son los números reales. Hay un número real en cada punto de la recta numérica. Los números reales se dividen en números racionales y números
Curso: Arquitectura Empresarial basado en TOGAF
 Metodología para desarrollo de Arquitecturas (ADM) El ADM TOGAF es el resultado de las contribuciones continuas de un gran número de practicantes de arquitectura. Este describe un método para el desarrollo
Metodología para desarrollo de Arquitecturas (ADM) El ADM TOGAF es el resultado de las contribuciones continuas de un gran número de practicantes de arquitectura. Este describe un método para el desarrollo
Solución del examen de Variable Compleja y Transformadas I. T. I. Electrónica y Electricidad 29 de enero de 2004
 Solución del examen de Variable Compleja y Transformadas I. T. I. Electrónica y Electricidad 29 de enero de 2004. Estudia si existe alguna función de variable compleja f() entera cuya parte real sea x
Solución del examen de Variable Compleja y Transformadas I. T. I. Electrónica y Electricidad 29 de enero de 2004. Estudia si existe alguna función de variable compleja f() entera cuya parte real sea x
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
Aire ambiente: No se recogieron muestras en esta comunidad.
 Ejercicio en grupo: A) Introducción En este ejercicio, los participantes calcularán e interpretarán la exposición a arsénico de los residentes de una comunidad rural en una región que tiene, de forma natural,
Ejercicio en grupo: A) Introducción En este ejercicio, los participantes calcularán e interpretarán la exposición a arsénico de los residentes de una comunidad rural en una región que tiene, de forma natural,
Universidad Católica del Maule. Fundamentos de Computación Especificación de tipos de datos ESPECIFICACIÓN ALGEBRAICA DE TIPOS DE DATOS
 Especificación algebraica ESPECIFICACIÓN ALGEBRAICA DE TIPOS DE DATOS Un tipo abstracto de datos se determina por las operaciones asociadas, incluyendo constantes que se consideran como operaciones sin
Especificación algebraica ESPECIFICACIÓN ALGEBRAICA DE TIPOS DE DATOS Un tipo abstracto de datos se determina por las operaciones asociadas, incluyendo constantes que se consideran como operaciones sin
Tema : ELECTRÓNICA DIGITAL
 (La Herradura Granada) Departamento de TECNOLOGÍA Tema : ELECTRÓNICA DIGITAL.- Introducción. 2.- Representación de operadores lógicos. 3.- Álgebra de Boole. 3..- Operadores básicos. 3.2.- Función lógica
(La Herradura Granada) Departamento de TECNOLOGÍA Tema : ELECTRÓNICA DIGITAL.- Introducción. 2.- Representación de operadores lógicos. 3.- Álgebra de Boole. 3..- Operadores básicos. 3.2.- Función lógica
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES
 CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
CAPÍTULO 1. PROPAGACIÓN DE LAS ONDAS PLANAS UNIFORMES 1.1 Ecuación de onda. Las ecuaciones de Maxwell se publicaron en 1864, su principal función es predecir la propagación de la energía en formas de Onda.
TEMA V TEORÍA DE CUADRIPOLOS LINEALES. 5.1.-Introducción. 5.2.-Parámetros de Impedancia a circuito abierto.
 TEMA V TEORÍA DE CUADRIPOLOS LINEALES 5.1.-Introducción. 5.2.-Parámetros de Impedancia a circuito abierto. 5.3.-Parámetros de Admitancia a cortocircuito. 5.4.-Parámetros Híbridos (h, g). 5.5.-Parámetros
TEMA V TEORÍA DE CUADRIPOLOS LINEALES 5.1.-Introducción. 5.2.-Parámetros de Impedancia a circuito abierto. 5.3.-Parámetros de Admitancia a cortocircuito. 5.4.-Parámetros Híbridos (h, g). 5.5.-Parámetros
x : N Q 1 x(1) = x 1 2 x(2) = x 2 3 x(3) = x 3
 3 Sucesiones - Fernando Sánchez - - Cálculo I de números racionales 03 10 2015 Los números reales son aproximaciones que se van haciendo con números racionales. Estas aproximaciones se llaman sucesiones
3 Sucesiones - Fernando Sánchez - - Cálculo I de números racionales 03 10 2015 Los números reales son aproximaciones que se van haciendo con números racionales. Estas aproximaciones se llaman sucesiones
Tema 5. Aproximación funcional local: Polinomio de Taylor. 5.1 Polinomio de Taylor
 Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
Capitán de fragata ingeniero AGUSTÍN E. GONZÁLEZ MORALES. ÁLGEBRA PARA INGENIEROS (Solucionario)
 Capitán de fragata ingeniero AGUSTÍN E. GONZÁLEZ MORALES ÁLGEBRA PARA INGENIEROS (Solucionario) 2 Í N D I C E CAPÍTULO : MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES CAPÍTULO 2: ESPACIOS VECTORIALES
Capitán de fragata ingeniero AGUSTÍN E. GONZÁLEZ MORALES ÁLGEBRA PARA INGENIEROS (Solucionario) 2 Í N D I C E CAPÍTULO : MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES CAPÍTULO 2: ESPACIOS VECTORIALES
LÍMITES DE FUNCIONES. CONTINUIDAD
 LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
GUÍA DE EJERCICIOS UNIDAD II
 UNIDAD II: INTEGRAL DEFINIDA UNIVERSIDAD DE CARABOBO FACULTAD DE INGENIERÍA ESTUDIOS BÁSICOS DEPARTAMENTO DE MATEMÁTICA ANÁLISIS MATEMÁTICO II Corregido por: Prof. AOUAD Jamil Prof. LAURENTÍN María Prof.
UNIDAD II: INTEGRAL DEFINIDA UNIVERSIDAD DE CARABOBO FACULTAD DE INGENIERÍA ESTUDIOS BÁSICOS DEPARTAMENTO DE MATEMÁTICA ANÁLISIS MATEMÁTICO II Corregido por: Prof. AOUAD Jamil Prof. LAURENTÍN María Prof.
Los números racionales
 Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Introducción. Ciclo de vida de los Sistemas de Información. Diseño Conceptual
 Introducción Algunas de las personas que trabajan con SGBD relacionales parecen preguntarse porqué deberían preocuparse del diseño de las bases de datos que utilizan. Después de todo, la mayoría de los
Introducción Algunas de las personas que trabajan con SGBD relacionales parecen preguntarse porqué deberían preocuparse del diseño de las bases de datos que utilizan. Después de todo, la mayoría de los
Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos
 Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 1 Conjuntos y Subconjuntos
Apuntes de Matemática Discreta 1. Conjuntos y Subconjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 1 Conjuntos y Subconjuntos
Vectores no colineales.
 Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
Vectores no colineales. Por definición son aquellos vectores que no tienen igual dirección. La resultante de los mismos no surge de la suma algebraica de los módulos de dichos vectores, sino que deben
Errores frecuentes de Matemáticas en sexto de primaria
 CÍRCULO DE LECTURA Errores frecuentes de Matemáticas en sexto de primaria El año 2004 el Ministerio de Educación publicó los resultados de la Evaluación Nacional de Rendimiento Estudiantil. Ahí se indicó
CÍRCULO DE LECTURA Errores frecuentes de Matemáticas en sexto de primaria El año 2004 el Ministerio de Educación publicó los resultados de la Evaluación Nacional de Rendimiento Estudiantil. Ahí se indicó
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 4 La recta en el plano Elaborado por la Profesora Doctora María Teresa
6. VECTORES Y COORDENADAS
 6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
UNIDAD 4 PROCESOS DE MARKOV
 UNIDAD 4 PROCESOS DE MARKOV Anteriormente se han cubierto modelos estáticos, esto es, modelos cuyos parámetros permanecen sin cambio a través del tiempo. Con excepción de programación dinámica donde se
UNIDAD 4 PROCESOS DE MARKOV Anteriormente se han cubierto modelos estáticos, esto es, modelos cuyos parámetros permanecen sin cambio a través del tiempo. Con excepción de programación dinámica donde se
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice
 Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
FORMA CANONICA DE JORDAN Y ECUACIONES DIFERENCIALES LINEALES A COEFICIENTES CONSTANTES
 FORMA CANONICA DE JORDAN Y ECUACIONES DIFERENCIALES LINEALES A COEFICIENTES CONSTANTES Eleonora Catsigeras 6 de mayo de 997 Notas para el curso de Análisis Matemático II Resumen Se enuncia sin demostración
FORMA CANONICA DE JORDAN Y ECUACIONES DIFERENCIALES LINEALES A COEFICIENTES CONSTANTES Eleonora Catsigeras 6 de mayo de 997 Notas para el curso de Análisis Matemático II Resumen Se enuncia sin demostración
Tema 7. Límites y continuidad de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
REPASO NÚMEROS NATURALES Y NÚMEROS ENTEROS
 SUMA REPASO NÚMEROS NATURALES Y NÚMEROS ENTEROS NÚMEROS NATURALES (N) 1. Características: Axiomas de Giuseppe Peano (*): El 1 es un número natural. Si n es un número natural, entonces el sucesor (el siguiente
SUMA REPASO NÚMEROS NATURALES Y NÚMEROS ENTEROS NÚMEROS NATURALES (N) 1. Características: Axiomas de Giuseppe Peano (*): El 1 es un número natural. Si n es un número natural, entonces el sucesor (el siguiente
Lección 24: Lenguaje algebraico y sustituciones
 LECCIÓN Lección : Lenguaje algebraico y sustituciones En lecciones anteriores usted ya trabajó con ecuaciones. Las ecuaciones expresan una igualdad entre ciertas relaciones numéricas en las que se desconoce
LECCIÓN Lección : Lenguaje algebraico y sustituciones En lecciones anteriores usted ya trabajó con ecuaciones. Las ecuaciones expresan una igualdad entre ciertas relaciones numéricas en las que se desconoce
CAPÍTULO 4: ALGORITMOS DE APRENDIZAJE
 Capítulo 4 Algoritmos de Aprendizaje 26 CAPÍTULO 4: ALGORITMOS DE APRENDIZAJE En este capítulo se proporcionan las descripciones matemáticas de los principales algoritmos de aprendizaje para redes neuronales:
Capítulo 4 Algoritmos de Aprendizaje 26 CAPÍTULO 4: ALGORITMOS DE APRENDIZAJE En este capítulo se proporcionan las descripciones matemáticas de los principales algoritmos de aprendizaje para redes neuronales:
1-Comportamiento de una función alrededor de un punto:
 Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Límites y Continuidad de funciones
 CAPITULO Límites y Continuidad de funciones Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr)
CAPITULO Límites y Continuidad de funciones Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr)
Que es el vitíligo? Esenciales: hojas informativas de fácil lectura. Cuál es la causa del vitíligo? Quién tiene vitíligo?
 Esenciaes: hojas informativas de fáci ectura Que es e vitíigo? E vitíigo es una enfermedad de a pie que causa manchas bancas en distintas partes de cuerpo. Esta enfermedad ocurre cuando se destruyen os
Esenciaes: hojas informativas de fáci ectura Que es e vitíigo? E vitíigo es una enfermedad de a pie que causa manchas bancas en distintas partes de cuerpo. Esta enfermedad ocurre cuando se destruyen os
Ejercicios de Programación Lineal
 Ejercicios de Programación Lineal Investigación Operativa Ingeniería Informática, UCM Curso 8/9 Una compañía de transporte dispone de camiones con capacidad de 4 libras y de 5 camiones con capacidad de
Ejercicios de Programación Lineal Investigación Operativa Ingeniería Informática, UCM Curso 8/9 Una compañía de transporte dispone de camiones con capacidad de 4 libras y de 5 camiones con capacidad de
1. INVERSA DE UNA MATRIZ REGULAR
 . INVERSA DE UNA MATRIZ REGULAR Calcular la inversa de una matriz regular es un trabajo bastante tedioso. A través de ejemplos se expondrán diferentes técnicas para calcular la matriz inversa de una matriz
. INVERSA DE UNA MATRIZ REGULAR Calcular la inversa de una matriz regular es un trabajo bastante tedioso. A través de ejemplos se expondrán diferentes técnicas para calcular la matriz inversa de una matriz
PROPIOS. DIAGONALIZACIÓN DE MATRICES CUADRADAS
 Tema 7.- VALORES Y VECTORES PROPIOS. DIAGONALIZACIÓN DE MATRICES CUADRADAS VALORES Y VECTORES PROPIOS MATRICES CUADRADAS DIAGONALIZABLES DIAGONALIZACIÓN N ORTOGONAL DE MATRICES CUADRADAS SIMÉTRICAS 1 Un
Tema 7.- VALORES Y VECTORES PROPIOS. DIAGONALIZACIÓN DE MATRICES CUADRADAS VALORES Y VECTORES PROPIOS MATRICES CUADRADAS DIAGONALIZABLES DIAGONALIZACIÓN N ORTOGONAL DE MATRICES CUADRADAS SIMÉTRICAS 1 Un
Geometría Tridimensional
 Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Capítulo 4 Geometría Tridimensional En dos dimensiones trabajamos en el plano mientras que en tres dimensiones trabajaremos en el espacio, también provisto de un sistema de coordenadas. En el espacio,
Un filtro general de respuesta al impulso finita con n etapas, cada una con un retardo independiente d i y ganancia a i.
 Filtros Digitales Un filtro general de respuesta al impulso finita con n etapas, cada una con un retardo independiente d i y ganancia a i. En electrónica, ciencias computacionales y matemáticas, un filtro
Filtros Digitales Un filtro general de respuesta al impulso finita con n etapas, cada una con un retardo independiente d i y ganancia a i. En electrónica, ciencias computacionales y matemáticas, un filtro
Nivelación de Matemática MTHA UNLP 1. Vectores
 Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
Nivelación de Matemática MTHA UNLP 1 1. Definiciones básicas Vectores 1.1. Magnitudes escalares y vectoriales. Hay magnitudes que quedan determinadas dando un solo número real: su medida. Por ejemplo:
Aplicaciones Lineales
 Aplicaciones Lineales Ejercicio Dada la matriz A = 0 2 0 a) Escribir explícitamente la aplicación lineal f : 2 cuya matriz asociada con respecto a las bases canónicas es A. En primer lugar definimos las
Aplicaciones Lineales Ejercicio Dada la matriz A = 0 2 0 a) Escribir explícitamente la aplicación lineal f : 2 cuya matriz asociada con respecto a las bases canónicas es A. En primer lugar definimos las
Capítulo 3. Estimación de elasticidades
 1 Capítulo 3. Estimación de elasticidades Lo que se busca comprobar en esta investigación a través la estimación econométrica es que, conforme a lo que predice la teoría y lo que ha sido observado en gran
1 Capítulo 3. Estimación de elasticidades Lo que se busca comprobar en esta investigación a través la estimación econométrica es que, conforme a lo que predice la teoría y lo que ha sido observado en gran
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 2º BACHILLERATO (Modalidad: Humanidades y Ciencias Sociales) Desarrollado en Decreto 67/2008, de 19 de junio. B.O.C.M.: 27 de junio de 2008. PROGRAMACIÓN
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 2º BACHILLERATO (Modalidad: Humanidades y Ciencias Sociales) Desarrollado en Decreto 67/2008, de 19 de junio. B.O.C.M.: 27 de junio de 2008. PROGRAMACIÓN
Matrices Invertibles y Elementos de Álgebra Matricial
 Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CCIR/ITESM 12 de enero de 2011 Índice 91 Introducción 1 92 Transpuesta 1 93 Propiedades de la transpuesta 2 94 Matrices
Matrices Invertibles y Elementos de Álgebra Matricial Departamento de Matemáticas, CCIR/ITESM 12 de enero de 2011 Índice 91 Introducción 1 92 Transpuesta 1 93 Propiedades de la transpuesta 2 94 Matrices
Métodos generales de generación de variables aleatorias
 Tema Métodos generales de generación de variables aleatorias.1. Generación de variables discretas A lo largo de esta sección, consideraremos una variable aleatoria X cuya función puntual es probabilidad
Tema Métodos generales de generación de variables aleatorias.1. Generación de variables discretas A lo largo de esta sección, consideraremos una variable aleatoria X cuya función puntual es probabilidad
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II ANDALUCÍA CNVCATRIA JUNI 009 SLUCIÓN DE LA PRUEBA DE ACCES AUTR: José Luis Pérez Sanz pción A Ejercicio En este límite nos encontramos ante la indeterminación. Agrupemos la
Matemáticas II Matemáticas II ANDALUCÍA CNVCATRIA JUNI 009 SLUCIÓN DE LA PRUEBA DE ACCES AUTR: José Luis Pérez Sanz pción A Ejercicio En este límite nos encontramos ante la indeterminación. Agrupemos la
INTRODUCCIÓN A VECTORES Y MAGNITUDES
 C U R S O: FÍSIC Mención MTERIL: FM-01 INTRODUCCIÓN VECTORES Y MGNITUDES La Física tiene por objetivo describir los fenómenos que ocurren en la naturaleza, a través de relaciones entre magnitudes físicas.
C U R S O: FÍSIC Mención MTERIL: FM-01 INTRODUCCIÓN VECTORES Y MGNITUDES La Física tiene por objetivo describir los fenómenos que ocurren en la naturaleza, a través de relaciones entre magnitudes físicas.
PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2.
![PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2. PROBLEMA 1. 1. [1.5 puntos] Obtener la ecuación de la recta tangente en el punto ( 2, 1) a la curva dada implícitamente por y 3 +3y 2 = x 4 3x 2.](/thumbs/27/11795036.jpg) PROBLEMA. ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica en Diseño Industrial Fundamentos Matemáticos de la Ingeniería Soluciones correspondientes a los problemas del Primer Parcial 7/8.
PROBLEMA. ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA Ingeniería Técnica en Diseño Industrial Fundamentos Matemáticos de la Ingeniería Soluciones correspondientes a los problemas del Primer Parcial 7/8.
Problemas a la carta
 Problemas a la carta Enseñanza Alfinio Flores Peñafiel y Nora G. Ramírez Arizona State University Maricopa Community Colleges resumen Se presentan cinco problemas que pueden ser resueltos mediante la utilización
Problemas a la carta Enseñanza Alfinio Flores Peñafiel y Nora G. Ramírez Arizona State University Maricopa Community Colleges resumen Se presentan cinco problemas que pueden ser resueltos mediante la utilización
Instrucción IrA (GoTo). Saltos no naturales en el flujo normal de un programa. Pseudocódigo y diagramas de flujo. (CU00182A)
 aprenderaprogramar.com Instrucción IrA (GoTo). Saltos no naturales en el flujo normal de un programa. Pseudocódigo y diagramas de flujo. (CU00182A) Sección: Cursos Categoría: Curso Bases de la programación
aprenderaprogramar.com Instrucción IrA (GoTo). Saltos no naturales en el flujo normal de un programa. Pseudocódigo y diagramas de flujo. (CU00182A) Sección: Cursos Categoría: Curso Bases de la programación
El rincón de los problemas. Oportunidades para estimular el pensamiento matemático. Triángulos de área máxima o de área mínima Problema
 www.fisem.org/web/union El rincón de los problemas ISSN: 1815-0640 Número 37. Marzo 2014 páginas 139-145 Pontificia Universidad Católica del Perú umalasp@pucp.edu.pe Oportunidades para estimular el pensamiento
www.fisem.org/web/union El rincón de los problemas ISSN: 1815-0640 Número 37. Marzo 2014 páginas 139-145 Pontificia Universidad Católica del Perú umalasp@pucp.edu.pe Oportunidades para estimular el pensamiento
Sistemas de Generación de Energía Eléctrica HIDROLOGÍA BÁSICA. Universidad Tecnológica De Pereira
 2010 Sistemas de Generación de Energía Eléctrica HIDROLOGÍA BÁSICA Universidad Tecnológica De Pereira Conceptos Básicos de Hidrología La hidrología es una ciencia clave en el estudio de los sistemas de
2010 Sistemas de Generación de Energía Eléctrica HIDROLOGÍA BÁSICA Universidad Tecnológica De Pereira Conceptos Básicos de Hidrología La hidrología es una ciencia clave en el estudio de los sistemas de
Objetivos de Análisis de Evaluación Económica
 Evauación Económica Objetivo de Anáisis Criterios Naturaeza Pecuiaridades Comparación de Criterios Enfoque Recomendado Massachusetts Institute of Technoogy Evauación Económica Transparencia 1 de 15 Objetivos
Evauación Económica Objetivo de Anáisis Criterios Naturaeza Pecuiaridades Comparación de Criterios Enfoque Recomendado Massachusetts Institute of Technoogy Evauación Económica Transparencia 1 de 15 Objetivos
Por ello, también será importante la estructura del juego constituyente para efectuar una predicción del resultado.
 8.5 Juegos repetidos con horizonte finito. Los equilibrios en los juegos repetidos con horizonte finito serán sustancialmente diferentes de los obtenidos en los juegos repetidos con horizonte infinito.
8.5 Juegos repetidos con horizonte finito. Los equilibrios en los juegos repetidos con horizonte finito serán sustancialmente diferentes de los obtenidos en los juegos repetidos con horizonte infinito.
UN PROBLEMA CON INTERÉS Y CALCULADORA
 UN PROBLEMA CON INTERÉS Y CALCULADORA José Antonio Mora Sánchez. Alacant Las calculadoras ofrecen la posibilidad de modificar la óptica desde la que se abordan ciertos problemas matemáticos, esto hace
UN PROBLEMA CON INTERÉS Y CALCULADORA José Antonio Mora Sánchez. Alacant Las calculadoras ofrecen la posibilidad de modificar la óptica desde la que se abordan ciertos problemas matemáticos, esto hace
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo
 Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Teóricas de Análisis Matemático (28) - Práctica 4 - Límite de funciones. 1. Límites en el infinito - Asíntotas horizontales
 Práctica 4 - Parte Límite de funciones En lo que sigue, veremos cómo la noción de límite introducida para sucesiones se etiende al caso de funciones reales. Esto nos permitirá estudiar el comportamiento
Práctica 4 - Parte Límite de funciones En lo que sigue, veremos cómo la noción de límite introducida para sucesiones se etiende al caso de funciones reales. Esto nos permitirá estudiar el comportamiento
Recomendaciones para la preparación de las P.A.U. en la materia MATEMÁTICAS para Mayores de 25 años.
 MATEMÁTICAS para Mayores de 25 años Recomendaciones para la preparación de las P.A.U. en la materia MATEMÁTICAS para Mayores de 25 años. Curso 2014-2015 Conviene recordar que los contenidos y criterios
MATEMÁTICAS para Mayores de 25 años Recomendaciones para la preparación de las P.A.U. en la materia MATEMÁTICAS para Mayores de 25 años. Curso 2014-2015 Conviene recordar que los contenidos y criterios
Índice Introducción Números Polinomios Funciones y su Representación. Curso 0: Matemáticas y sus Aplicaciones Tema 1. Números, Polinomios y Funciones
 Curso 0: Matemáticas y sus Aplicaciones Tema 1. Números, Polinomios y Funciones Leandro Marín Dpto. de Matemática Aplicada Universidad de Murcia 2012 1 Números 2 Polinomios 3 Funciones y su Representación
Curso 0: Matemáticas y sus Aplicaciones Tema 1. Números, Polinomios y Funciones Leandro Marín Dpto. de Matemática Aplicada Universidad de Murcia 2012 1 Números 2 Polinomios 3 Funciones y su Representación
Unidad: Representación gráfica del movimiento
 Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
Unidad: Representación gráfica del movimiento Aplicando y repasando el concepto de rapidez Esta primera actividad repasa el concepto de rapidez definido anteriormente. Posición Esta actividad introduce
EL DISEÑO FACTORIAL COMPLETO 2 2
 EL DISEÑO FACTORIAL COMPLETO 2 2 Joan Ferré Grupo de Quimiometría y Cualimetría Departamento de Química Analítica y Química Orgánica Universidad Rovira i Virgili (Tarragona) INTRODUCCIÓN Para optimizar
EL DISEÑO FACTORIAL COMPLETO 2 2 Joan Ferré Grupo de Quimiometría y Cualimetría Departamento de Química Analítica y Química Orgánica Universidad Rovira i Virgili (Tarragona) INTRODUCCIÓN Para optimizar
Capítulo 5: Pruebas y evaluación del sistema. A continuación se muestran una serie de pruebas propuestas para evaluar varias
 Capítulo 5: Pruebas y evaluación del sistema 5.1 Definición de pruebas para la aplicación A continuación se muestran una serie de pruebas propuestas para evaluar varias características importantes del
Capítulo 5: Pruebas y evaluación del sistema 5.1 Definición de pruebas para la aplicación A continuación se muestran una serie de pruebas propuestas para evaluar varias características importantes del
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Introducción Por qué La Geometría? La Geometría tiene como objetivo fundamental
HERRAMIENTAS DE EXCEL PARA EL ANALISIS Y VALORACION DE PROYECTOS DE INVERSION (I)
 Revista de Dirección y Administración de Empresas. Número 10, diciembre 2002 págs. 59-76 Enpresen Zuzendaritza eta Administraziorako Aldizkaria. 10. zenbakia, 2002 abendua 59-76 orr. HERRAMIENTAS DE EXCEL
Revista de Dirección y Administración de Empresas. Número 10, diciembre 2002 págs. 59-76 Enpresen Zuzendaritza eta Administraziorako Aldizkaria. 10. zenbakia, 2002 abendua 59-76 orr. HERRAMIENTAS DE EXCEL
Conclusiones, aportaciones y sugerencias para futuros trabajos
 Capítulo 7 Conclusiones, aportaciones y sugerencias para futuros trabajos En este último capítulo se va a realizar una recapitulación de las conclusiones extraídas en cada uno de los capítulos del presente
Capítulo 7 Conclusiones, aportaciones y sugerencias para futuros trabajos En este último capítulo se va a realizar una recapitulación de las conclusiones extraídas en cada uno de los capítulos del presente
EL MÉTODO DE LA BISECCIÓN
 EL MÉTODO DE LA BISECCIÓN Teorema de Bolzano Sea f : [a, b] IR IR una función continua en [a, b] tal que f(a) f(b) < 0, es decir, que tiene distinto signo en a y en b. Entonces, existe c (a, b) tal que
EL MÉTODO DE LA BISECCIÓN Teorema de Bolzano Sea f : [a, b] IR IR una función continua en [a, b] tal que f(a) f(b) < 0, es decir, que tiene distinto signo en a y en b. Entonces, existe c (a, b) tal que
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 7 Funciones reales de una variable real Elaborado por la Profesora Doctora
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema 7 Funciones reales de una variable real Elaborado por la Profesora Doctora
INFORMACIÓN ACADÉMICA
 ASIGNATURA: MATEMÁTICAS CURSO: 4º ESO INFORMACIÓN ACADÉMICA OBJETIVOS ESPECÍFICOS DEL ÁREA La enseñanza de las Matemáticas en esta etapa tendrá como objetivo el desarrollo de las siguientes capacidades:
ASIGNATURA: MATEMÁTICAS CURSO: 4º ESO INFORMACIÓN ACADÉMICA OBJETIVOS ESPECÍFICOS DEL ÁREA La enseñanza de las Matemáticas en esta etapa tendrá como objetivo el desarrollo de las siguientes capacidades:
ASEGURAMIENTO DE LA CALIDAD EN LABORATORIO
 FUNDACION NEXUS ASEGURAMIENTO DE LA CALIDAD EN LABORATORIO Marzo de 2012 CALIDAD, CONTROL DE LA CALIDAD Y ASEGURAMIENTO DE LA CALIDAD El laboratorio de análisis ofrece a sus clientes un servicio que se
FUNDACION NEXUS ASEGURAMIENTO DE LA CALIDAD EN LABORATORIO Marzo de 2012 CALIDAD, CONTROL DE LA CALIDAD Y ASEGURAMIENTO DE LA CALIDAD El laboratorio de análisis ofrece a sus clientes un servicio que se
PRUEBA ESPECÍFICA PRUEBA 2014
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES DE 5 AÑOS PRUEBA ESPECÍFICA PRUEBA 014 PRUEBA SOLUCIONARIO HAUTAPROBAK 5 URTETIK 014ko MAIATZA DE 5 AÑOS MAYO 014 Aclaraciones previas Tiempo de duración de la
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES DE 5 AÑOS PRUEBA ESPECÍFICA PRUEBA 014 PRUEBA SOLUCIONARIO HAUTAPROBAK 5 URTETIK 014ko MAIATZA DE 5 AÑOS MAYO 014 Aclaraciones previas Tiempo de duración de la
Valoración financiera y contable de carteras con participaciones cruzadas mediante arbitraje: existencia y unicidad de solución general
 Valoración financiera y contable de carteras con participaciones cruzadas mediante arbitrae: existencia y unicidad de solución general Lluís Planas i Casamitana Universitat de Girona lluis.planas@udg.es
Valoración financiera y contable de carteras con participaciones cruzadas mediante arbitrae: existencia y unicidad de solución general Lluís Planas i Casamitana Universitat de Girona lluis.planas@udg.es
Centro de Capacitación en Informática
 Fórmulas y Funciones Las fórmulas constituyen el núcleo de cualquier hoja de cálculo, y por tanto de Excel. Mediante fórmulas, se llevan a cabo todos los cálculos que se necesitan en una hoja de cálculo.
Fórmulas y Funciones Las fórmulas constituyen el núcleo de cualquier hoja de cálculo, y por tanto de Excel. Mediante fórmulas, se llevan a cabo todos los cálculos que se necesitan en una hoja de cálculo.
Subespacios vectoriales en R n
 Subespacios vectoriales en R n Víctor Domínguez Octubre 2011 1. Introducción Con estas notas resumimos los conceptos fundamentales del tema 3 que, en pocas palabras, se puede resumir en técnicas de manejo
Subespacios vectoriales en R n Víctor Domínguez Octubre 2011 1. Introducción Con estas notas resumimos los conceptos fundamentales del tema 3 que, en pocas palabras, se puede resumir en técnicas de manejo
1) Desaparición de gran parte de los carnés profesionales :
 Información relativa a las cualificaciones profesionales en el ámbito de seguridad industrial y minera establecida en la legislación actual (reguladas en general según la normativa anterior mediante carnés
Información relativa a las cualificaciones profesionales en el ámbito de seguridad industrial y minera establecida en la legislación actual (reguladas en general según la normativa anterior mediante carnés
CAPÍTULO 2 IMPORTANCIA DE LA ASIGNATURA OUTSOURCING EN TECNOLOGÍAS DE INFORMACIÓN
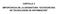 CAPÍTULO 2 IMPORTANCIA DE LA ASIGNATURA OUTSOURCING EN TECNOLOGÍAS DE INFORMACIÓN CAPÍTULO 2 IMPORTANCIA DE LA ASIGNATURA OUTSOURCING EN TECNOLOGÍAS DE INFORMACIÓN 2.1 INTRODUCCIÓN. En este capítulo se
CAPÍTULO 2 IMPORTANCIA DE LA ASIGNATURA OUTSOURCING EN TECNOLOGÍAS DE INFORMACIÓN CAPÍTULO 2 IMPORTANCIA DE LA ASIGNATURA OUTSOURCING EN TECNOLOGÍAS DE INFORMACIÓN 2.1 INTRODUCCIÓN. En este capítulo se
Uso de las tecnologias de la informacion en las PyMES de los municipios de Comalcalco y Cunduacán
 Uso de las tecnologias de la informacion en las PyMES de los municipios de Comalcalco y Cunduacán M.A. María del Carmen Vásquez García M.C. Marbella Araceli Gómez Lemus Pasante Edwin Fabián Hernández Pérez
Uso de las tecnologias de la informacion en las PyMES de los municipios de Comalcalco y Cunduacán M.A. María del Carmen Vásquez García M.C. Marbella Araceli Gómez Lemus Pasante Edwin Fabián Hernández Pérez
MATEMÁTICAS aplicadas a las Ciencias Sociales II
 MATEMÁTICAS aplicadas a las Ciencias Sociales II UNIDAD 1: SISTEMAS DE ECUACIONES. MÉODO DE GAUSS Sistemas de ecuaciones lineales Sistemas equivalentes. Transformaciones que mantienen la equivalencia.
MATEMÁTICAS aplicadas a las Ciencias Sociales II UNIDAD 1: SISTEMAS DE ECUACIONES. MÉODO DE GAUSS Sistemas de ecuaciones lineales Sistemas equivalentes. Transformaciones que mantienen la equivalencia.
CONSIDERACIONES TEÓRICAS GENERALES.
 DUREZA VICKERS OBJETIVO DEL ENSAYO. Determinar experimentalmente la dureza Vickers. Estudiar su campo de aplicación. CONSIDERACIONES TEÓRICAS GENERALES. Definición de dureza: Se entiende por dureza la
DUREZA VICKERS OBJETIVO DEL ENSAYO. Determinar experimentalmente la dureza Vickers. Estudiar su campo de aplicación. CONSIDERACIONES TEÓRICAS GENERALES. Definición de dureza: Se entiende por dureza la
Potencial eléctrico. du = - F dl
 Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
Introducción Como la fuerza gravitatoria, la fuerza eléctrica es conservativa. Existe una función energía potencial asociada con la fuerza eléctrica. Como veremos, la energía potencial asociada a una partícula
SECRETARÍA DE EDUCACIÓN PÚBLICA SUBSECRETARÍA DE EDUCACIÓN SUPERIOR COORDINACIÓN GENERAL DE UNIVERSIDADES TECNOLÓGICAS
 SECRETARÍA DE EDUCACIÓN PÚBLICA SUBSECRETARÍA DE EDUCACIÓN SUPERIOR COORDINACIÓN GENERAL DE UNIVERSIDADES TECNOLÓGICAS CRITERIOS GENERALES PARA LA PLANEACIÓN, EL DESARROLLO Y LA EVALUACIÓN, EN LA IMPLANTACIÓN
SECRETARÍA DE EDUCACIÓN PÚBLICA SUBSECRETARÍA DE EDUCACIÓN SUPERIOR COORDINACIÓN GENERAL DE UNIVERSIDADES TECNOLÓGICAS CRITERIOS GENERALES PARA LA PLANEACIÓN, EL DESARROLLO Y LA EVALUACIÓN, EN LA IMPLANTACIÓN
Líneas Equipotenciales
 Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
Líneas Equipotenciales A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. En esta experiencia se estudia
