APUNTES DE VARIABLE COMPLEJA PARA INGENIEROS DE TELECOMUNICACION Elaborados por José Manuel Rodríguez Versión abreviada de Dmitry Yakubovich (2011)

Transcripción

1 APUNTES DE VARIABLE COMPLEJA PARA INGENIEROS DE TELECOMUNICACION Elbordos por José Mnuel Rodríguez Versión brevid de Dmitry Ykubovich (20). INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS Se define el conjunto de los números complejos como C = {x + iy : x, y R}, donde i =. Si z = x + iy, diremos que x es l prte rel de z y que y es l prte imginri de z, y lo denotremos por Re z = x e Im z = y. Conviene destcr que tnto l prte rel como l prte imginri son números reles, y que los números reles son tmbién números complejos (de hecho, son los números complejos con prte imginri 0). Los números complejos con prte rel 0 se denominn imginrios puros. El único número rel que es tmbién imginrio puro es el 0. Si identificmos el número complejo x + iy con el pr ordendo (x, y), podemos representr el conjunto de los números complejos como el plno R 2. En delnte llmremos eje rel l eje de bsciss (el eje horizontl) y eje imginrio l eje de ordends (el eje verticl). A prtir de est identificción podemos hblr del plno complejo y de sus coordends polres r = z, θ = rg z, el módulo y el rgumento, relcionds con z = x + iy 0 de l siguiente form x = r cos θ, y = r sen θ. Obsérvese que r 2 = x 2 + y 2. Como es bien conocido, el rgumento θ no está definido de mner únic, y que θ + 2π, θ + 4π y en generl θ + 2kπ, con k culquier número entero, representn el mismo ángulo que θ. Por tnto, l hor de hblr de rgumento hy que elegir uno de ellos; ls elecciones más hbitules son θ [0, 2π) ó θ ( π, π]. Si z = x + iy es un número complejo, denotremos hbitulmente su módulo por r = z y su rgumento por θ = rg z. Está clro que no existe un determinción continu de l función rg z en C \ {0}. Sin embrgo, si S es un semirrect culquier en el plno complejo que comienz en el origen de coordends, entonces existe un determinción continu de l función rg z en C \ S. Definición. Se definen l sum y el producto de los números complejos z = x + iy y z 2 = x 2 + iy 2 respectivmente como z + z 2 = x + iy + x 2 + iy 2 = (x + x 2 ) + i(y + y 2 ), z z 2 = (x + iy ) (x 2 + iy 2 ) = x x 2 + ix y 2 + ix 2 y + i 2 y y 2 = (x x 2 y y 2 ) + i(x y 2 + x 2 y ). L interpretción geométric de l sum de números complejos es sencill: si identificmos un número complejo z con el vector de R 2 que tiene como origen el origen de coordends y por extremo el punto z, el número complejo z + z 2 es el extremo del vector sum de z y z 2. L interpretción geométric del producto de números complejos es un poco más complicd: z z 2 es el número complejo cuyo módulo es el producto de los módulos de z y z 2, y cuyo rgumento es l sum de los rgumentos de z y z 2. Definición. Se define el conjugdo z del número complejo z = x + iy como z = x iy. Desde el punto de vist geométrico, z es el punto simétrico de z con respecto l eje rel. Es evidente que z 2 = x 2 + y 2 = (x + iy)(x iy) = z z. Por tnto, el inverso de z 0 con respecto l multiplicción es z = z = z z z = z z 2. Es fácil probr que el conjunto de los números complejos con ls operciones de sum y producto tiene estructur de cuerpo.

2 Pueden deducirse ls siguientes propieddes: z + z 2 z + z 2, z z 2 z z 2, Re z z, Im z z, Re z = z + z 2, Im z = z z 2i z + z 2 = z + z 2, z z 2 = z z 2, (z n ) = z n, z = z, rg z = rg z, z z 2 = z z 2, z z = z 2 z 2, zn = z n,, ( z z 2 ) = z z 2, n z = n z. Ddo que si θ es un rgumento de un número complejo, θ + 2kπ tmbién lo es pr culquier k Z, ls siguientes fórmuls deben ser entendids en culquier de los dos siguientes sentidos: ) rg(z z 2 ) = rg z + rg z 2 signific que pr culquier elección de rg z y rg z 2, se tiene que rg z +rg z 2 es un rgumento de z z 2 ; b) ls fórmuls son igulddes entre conjuntos si se consider rg z como el conjunto de todos los rgumentos de z. ( ) rg(z z 2 ) = rg z + rg z 2, rg = rg z = rg z, ( z z ) rg = rg z rg z 2, rg(z n ) = n rg z, z 2 rg( n z ) = rg z n = { φ + 2kπ n : φ rg z, k Z Tmbién es destcble l fórmul de De Moivre (cos θ + i sen θ) n = cos nθ + i sen nθ. Si definimos e iθ = cos θ + i sen θ, l fórmul nterior result más fmilir : (e iθ ) n = e inθ. Est sugerente notción se justificrá en los dos próximos cpítulos. Ahor podemos clculr ríces de orden n de números complejos de form sencill, teniendo en cuent que θ y θ + 2kπ representn el mismo ángulo pr culquier k Z: }. n z = n r e iθ = n r e i(θ+2kπ) = n r e i(θ+2kπ)/n, k Z. Si dmos los vlores k = 0,,..., n se obtienen ls n ríces n-ésims de z n r e iθ/n, n r e i(θ+2π)/n,..., n r e i(θ+2(n )π)/n, y es fácil probr que pr culquier vlor de k Z se obtiene uno de estos n números complejos. En prticulr, todo número rel tiene n ríces complejs. Por ejemplo, si considermos el cso n = 2 (ls ríces cudrds), se obtienen dos ríces cudrds { r e iθ/2, r e i(θ+2π)/2} = { r e iθ/2, r e iθ/2+iπ} = ± r e iθ/2. 2. FUNCIONES HOLOMORFAS Definiciones previs. Por D(z 0, ε) = {z C : z z 0 < ε} denotremos el disco de centro z 0 y rdio ε. Ls nociones de un subconjunto bierto o cerrdo en C coinciden con ls correspondientes nociones pr subconjuntos de R 2. Ddo Ω C decimos que: () Un conjunto bierto Ω es conexo si pr todo z, z 2 Ω, existe un curv continu : [, b] Ω uniendo z con z 2, es decir, tl que () = z, (b) = z 2. (2) Ω es un región o dominio si es un bierto conexo. (3) Ω es simplemente conexo si es conexo y tod curv cerrd (es decir, tl que () = (b)) contenid en Ω puede deformrse continumente dentro de Ω en un punto. Esto es equivlente que Ω se conexo y que no exist ningun curv cerrd contenid en Ω que rodee lgún punto que no pertenezc Ω (es decir, Ω no tiene gujeros ). 2

3 Dd un función f : Ω C, los conceptos de límite y continuidd coinciden con los estudidos principios del curso pr funciones reles sin más que considerr f : Ω R 2 R 2. Además, se tienen los mismos resultdos pr sums, rests, productos y cocientes de funciones. Ejercicio. Probr que si existe lim z z0 f(z) = w, entonces () lim z z0 f(z) = w, (b) limz z0 Re f(z) = Re w, (c) lim z z0 Im f(z) = Im w, (d) lim z z0 f(z) = w, es decir, que ls funciones z, Re z, Im z y z son continus. Sin embrgo, l función rgumento no es continu en C, unque sí es continu en C menos un semirrect que comience en 0. Ejercicio. Probr que lim z z0 f(z) = w si y sólo si lim z z0 Re f(z) = Re w y lim z z0 Im f(z) = Im w. Dd un función f : Ω C, l hor de definir el concepto de derivd podemos doptr pr tl fin l definición de función diferencible f : R 2 R 2 que y se estudió nteriormente en este curso. Sin embrgo, es más decudo doptr l estrtegi prentemente inocente de definir l derivd de form uni-dimensionl (como en el cso de funciones f : R R) provechndo l estructur de cuerpo de C: Definición. Sen Ω bierto, f : Ω C, z 0 Ω. Decimos que f es derivble (ó derivble en el sentido complejo) en z 0 si existe el límite (donde z, z 0, h C) f f(z) f(z 0 ) f(z 0 + h) f(z 0 ) (z 0 ) = lim = lim. z z 0 z z 0 h 0 h Se tienen ls misms regls pr el cálculo de derivds con ls misms demostrciones. Teorem. Sen f, g funciones derivbles en z 0, y sen α, β C. Entonces: () αf + βg es derivble en z 0, y se tiene (2) fg es derivble en z 0, y (3) Si g(z 0 ) 0, f/g es derivble en z 0, y (αf + βg) (z 0 ) = α f (z 0 ) + β g (z 0 ). (fg) (z 0 ) = f (z 0 ) g(z 0 ) + f(z 0 ) g (z 0 ). ( f g ) (z0 ) = f (z 0 ) g(z 0 ) f(z 0 ) g (z 0 ) g(z 0 ) 2. Teorem 2. Si f es derivble en z 0 y g lo es en f(z 0 ), entonces g f es derivble en z 0, y se verific l regl de l cden: (g f) (z 0 ) = g (f(z 0 )) f (z 0 ). Teorem 3. Si f es derivble en z 0, entonces f es continu en z 0. Teorem 4. Se f = u + iv, donde u = Re f, v = Im f. Entonces son equivlentes ls siguientes firmciones: () f es derivble en z 0. (2) f es diferencible (en sentido rel) en z 0, y demás f y (z 0 ) = if x (z 0 ). (3) u, v son diferencibles en z 0 y se cumplen ls ecuciones de Cuchy-Riemnn en z 0 { ux = v y, u y = v x. Además, si f es derivble en z 0, entonces f (z 0 ) = f x (z 0 ). Demostrción (de lguns prtes). () = (2) f x (z 0 ) = f (z 0 ) z x = f (z 0 ) ; f y (z 0 ) = f (z 0 ) z y = if (z 0 ) = if x (z 0 ). (2) (3) f y = if x u y + iv y = i(u x + iv x ). Ejemplos. Ls funciones rcionles, es decir, los cocientes de polinomios, son derivbles (excepto en los ceros del denomindor). Ejemplo. L derivd de f(z) = z 2 /(z + ) es f (z) = (z 2 + 2z)/(z + ) 2. 3

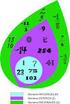
4 Ejemplo. Pr comprobr l derivbilidd de l función exp(z), podemos comprobr directmente ls condiciones de Cuchy-Riemnn: exp(z) = u(z) + iv(z), u(z) = e x cos(y), v(z) = e x sen (y), z = x + iy; u x = e x cos(y) = v y, u y = e x sen (y) = v x. Ejemplo. A cmbio, por ejemplo, poniendo f(z) = z = u + iv, vemos que u(x, y) = Re f(z) = x, v(x, y) = Im f(z) = y, sí que u x =, v y =. Por lo tnto, l función f(z) = z no es derivble en ningún punto del plno complejo. Ejemplo. Ls funciones Re z y z tienen l mism propiedd. Es importnte observr que ls funciones z, Re z son infinitmente derivbles en el sentido rel. Un comentrio sobre el sentido geométrico de l derivd complej. Suponiendo que existe f (z 0 ) 0, escribimos f(z 0, h) = f(z 0 ) + f (z 0 )h + o(h), h 0, f (z 0 )h = e i rg f (z 0) f (z 0 ) h. Ests fórmuls significn que l plicción que llev el incremento h = (z 0 + h) z 0 de l vrible independiente en el incremento f(z 0, h) = f(z 0 +h) f(z 0 ) de l función en l primer proximción consiste en l diltción f (z 0 ) veces con l posterior rotción l ángulo rg f (z 0 ). En prticulr, podemos firmr que l función f conserv los ángulos entre ls curvs que empiezn en z 0, mntiene l orientción del plno y que tods ests curvs se diltn en un número igul de veces en z 0 (es decir, en f (z 0 ) veces). Definición. L función f : G Ω se llm plicción conforme de G Ω si es biyectiv y derivble en el sentido complejo. Se puede demostrr que en este cso, f (z) no se nul en G. Por tnto, un plicción conforme conserv l orientción y conserv los ángulos entre ls curvs. Ver Figs. y 2, donde se ve que se conserv l ortogonlidd de línes Fig. : Un mlldo del disco unidd utilizndo círculos concéntricos círculos concéntricos y rdios 4

5 Según el Teorem de Riemnn (que no se demuestr en este curso), dds dos regiones simplemente conexs culesquier Ω, Ω 2 que no coinciden con C y puntos z Ω, z 2 Ω 2, siempre existe un únic plicción conforme f : Ω Ω 2 tl que f(z ) = z 2 y f (z ) (0, + ) Fig. 2: El correspondiente mlldo de l imgen del disco unidd por un plicción conforme Definición. Decimos que f es holomorf en un bierto Ω si es derivble en todos los puntos de Ω. Tmbién decimos que f es holomorf en z 0 si lo es en lgún disco centrdo en z 0. Ejemplos. Si Ω es un dominio y f : Ω R es derivble en z 0 Ω, se tiene que f (z 0 ) = 0; si demás f es derivble en todos los puntos de Ω, entonces f 0 en Ω. Consecuentemente, ls constntes son ls únics funciones holomorfs en un dominio que sólo tomn vlores reles. Por tnto, funciones como Re z, Im z, z, rg z no son holomorfs en ningún bierto. L función z 2 sólo es derivble en 0, y por tnto, no es holomorf en ningún bierto. Ejemplo. f(z) = e z/(z2 +) es holomorf en C \ { i, i}. Teorem 5. Si f es holomorf en un bierto Ω, entonces f es holomorf en Ω. Demostrción (si f es de clse C 2 en sentido rel). L función f es de clse C en Ω y, por tnto, es diferencible en Ω (en sentido rel). Por otro ldo, como f es derivble en Ω verific ls ecuciones de Cuchy-Riemnn (en Ω) con lo que f tmbién ls verific, puesto que { Ux = ( u f x )x = U + iv = u x + iv x = = ( v y )x = ( ) v x y = V y, U y = ( ) u x = ( ) u y y = ( ) v x x = V x x. Corolrio. Pr tod funcin holomorf f : Ω C, ls derivds f (n) : Ω C (en el sentido complejo) están definids pr todo n N (y tods son holomorfs). Definición. Si Ω es un bierto de R 2, un función u : Ω R de clse C 2 es rmónic en Ω si u = u xx + u yy = 0 en Ω. Teorem 6. Si f es holomorf en el bierto Ω y es de clse C 2 en Ω, entonces Re f e Im f son rmónics en Ω. 5

6 Definiciones y resultdos previos.. Si ω n = n + ib n, ω = + ib, 3. SERIES NUMÉRICAS COMPLEJAS lim ω n = ω ε > 0, N tl que ω n ω < ε, n N n lim n = y lim b n = b. n n 2. {ω n } se dice convergente si tiene límite finito. 3. Decimos que lim n ω n = si lim n ω n =. Ejemplos. e n + i(n + )/n, ( ) n n, i n. 4. L serie n= ω n es, por definición, el límite lim N N n= ω n, y se dice que es convergente si dicho límite es finito. 5. Si n= ω n converge, entonces lim n ω n = 0. Es decir, si lim n ω n es distinto de 0 o no existe, l serie diverge. (El recíproco es flso). 6. L serie n= ω n se dice bsolutmente convergente si n= ω n converge. 7. Si n= ω n converge, entonces n= ω n converge. (El recíproco es flso). 8. Se n 0. () Si existe lim n /n n = r, entonces r > = n= 0 r < = n n= diverge, n converge. n+ (2) Si n > 0 y existe lim n =r, entonces r =lim n /n n y se concluye lo mismo que en (). n + i2 n Ejemplo. 3 n + in. n= 9. Sen f n : Ω C. Decimos que {f n } converge (puntulmente) f en Ω, si lim f n(z) = f(z), z Ω, n es decir, si z Ω, ε > 0, N = N(z, ε) tl que f n (z) f(z) < ε, n N. 0. Dd un sucesión {b n } R, el límite superior de {b n } es el supremo del conjunto formdo por todos los límites de subsucesiones de {b n }. Por tnto, lim sup n b n existe siempre (unque pued ser infinito). Además, se tiene que: () lim n b n = lim sup n b n = lim n b n. (b) lim sup n ( n + b n ) lim sup n n + lim sup n b n. (c) Si n 0 y existe lim n n (0, + ) = lim sup n n b n = (lim n n ) (lim sup n b n ). (d) Si n, b n 0, lim sup n n b n (lim sup n n ) (lim sup n b n ). (e) Si n 0 y α > 0, entonces lim sup n α n = (lim sup n n ) α. (f) Si f es un función continu y creciente, entonces lim sup n f( n ) = f(lim sup n n ). n Ejemplos. lim sup =, lim sup( ) n n =, lim sup no tiene sentido. n n + n n n + i 6

7 4. SERIES DE POTENCIAS Definición. Un serie de potencis centrd en z 0 es un serie de l form () φ(x) := n (z z 0 ) n. Teorem. L serie () () converge bsolutmente en D(z 0, R) = {z : z z 0 < R}, donde R viene ddo por l fórmul de Cuchy -Hdmrd 0 R := lim sup n n. /n (b) diverge pr todo z tl que z z 0 > R. (c) Si el rdio R no es nulo, l sum φ(z) de l serie () es holomorf en D(z 0, R). (d) L serie derivd ( ) ψ(z) := n n (z z 0 ) n converge en el mismo disco D(z 0, R). Si R 0, l derivd complej de φ es igul ψ: n= φ (z) = ψ(z), z D(z 0, R). El número R se llm el rdio de convergenci de l serie y el disco D(z 0, R) se llm el disco de convergenci de l mism. Si R = 0, l serie () sólo converge pr z = z 0. Si R = +, l serie () converge pr todo z en el plno complejo (que se tom por el disco de convergenci de l serie en este cso). Se dice que l serie ( ) se obtiene de l serie () derivndo término término. El siguiente teorem permite clculr con fcilidd el rdio de convergenci en muchos csos: Teorem 2. Si existe lim n n+ / n, entonces el rdio de convergenci R de () verific que R = lim n+. n n Ejemplos. zn /n!, ( )n z 2n /(2n)!, n7 z n. Hbitulmente, cundo los coeficientes de un serie son comprbles con n α (pr lgún α R), el rdio de convergenci suele ser. El Teorem nos permite segurr l convergenci de () en el interior del disco de convergenci. L convergenci en l fronter de dicho disco es mucho más delicd, puesto que, en generl, puede ocurrir culquier cos. Definición. Un función f : Ω C es nlític en z 0 si existe un disco D(z 0, r) Ω tl que f se represent como l sum de un serie de potencis centrd en z 0, que converge en D(z 0, r). Un función es nlític en un dominio Ω si es nlític en todos los puntos de Ω. Por qué l serie rel de l función f(x) = + x 2 = ( ) n x 2n converge sólo si { x < }, siendo f un n= función de clse C (y de hecho nlític) en todo el eje rel? Cuándo un función rel es nlític? Y hemos visto que ls funciones nlítics son holomorfs. El siguiente teorem, conocido como Teorem de Tylor infinito, nos dice que el recíproco tmbién es cierto. Es decir, responde l pregunt qué funciones son nlítics?; demás, tmbién responde l pregunt cuál es el rdio de convergenci de l serie? 7

8 Teorem 3. f es holomorf en el bierto Ω si y sólo si f es nlític en Ω. Además, si Ω y r es l mínim distnci de Ω l punto, se verific que (2) f(z) = f (n) () n! (z ) n, pr todo z D(, r). En el enuncido de este Teorem, se entiende que r = + si Ω coincide con todo el plno complejo C. En este cso, D(, + ) = C, y l serie en (2) converge pr todo z. Este resultdo permite extrer lguns importntes consecuencis: Corolrio 4. Si f es holomorf en l región Ω, y existe un punto Ω tl que entonces f es constnte en Ω. 0 = f () = = f (n) () =, pr todo n, Corolrio 5 (Ceros de funciones holomorfs). Si f es holomorf y no constnte en Ω, y Ω es un cero de f, (es decir, f() = 0), entonces existe un mínimo entero k > 0 tl que donde g es holomorf en Ω, y g() 0. f(z) = (z ) k g(z), Definición. En ls condiciones del corolrio nterior, se dice que f tiene en un cero de orden k. Corolrio 6. Si f es holomorf en l región Ω y existe un sucesión { n } n= contenid en Ω con todos los n distintos, y tl que lim n n = Ω, y f( n ) = 0, n, entonces f(z) = 0 pr todo z Ω. 5. FUNCIONES ELEMENTALES L función exponencil. L definimos medinte l serie de potencis (que tiene rdio de convergenci infinito) () e z := f(z) = z n n!, z C. Con est definición es fácil verificr ls principles propieddes de l función exponencil:. Si x R, f(x) = e x, es decir f(x) coincide con l función exponencil rel. En efecto, usndo el Teorem del vlor medio tenemos que e x N y l propiedd es un consecuenci de que 2. f(z) f(w) = f(z + w), z, w C. En efecto x n n! = f (n+) x n+ (ξ) (N + )! E N(x), 0 < ξ < x, (ó x < ξ < 0), E N (x) e x x N+ - (N + )! 0. N ( z k )( f(z) f(w) = k! k=0 m=0 n z j = j! = j=0 w m ) = m! w n j (n j)! = (z + w) n = f(z + w). n! 8 k=0 m=0 n! z k w m n j=0 k!m! ( n j ) z j w n j

9 3. Si y R, entonces f(iy) = cos y + i sen y = e iy puesto que por lo que, sumndo cos y = ( ) n y2n (2n)! = i sen y = i ( ) n y 2n+ (2n + )! = cos y + i sen y = (iy) 2n (2n)! (iy) n = e iy. n!, (iy) 2n+ (2n + )!, 4. Si z = x + iy C, entonces f(x + iy) = f(x) f(iy) = e x e iy = e x (cos y + i sen y), lo que justific l definición de () como l función exponencil. 5. L función exponencil tiene período 2πi, puesto que e z+2πi = e z e 2πi = e z (cos 2π + i sen 2π) = e z. 6. Según el Teorem de l seccin nterior, l funcin e z es holomorf en todo el plno complejo. 7. Derivndo l serie () término término obtenemos que (e z ) = e z. 8. e z = e Re z, rg e z = Im z. 9. e z = e z. L función logritmo. Decimos que w = log z z = e w. Poniendo w = log z = u + iv, z = re iθ, tenemos que z = re iθ = e w = e u e iv = { r = e u, θ = v. = { u = log r, v = θ. Por tnto, log z = log z + i rg z. Pr que log z se un función univlud (un uténtic función) hy que elegir un intervlo de rgumentos de longitud 2π. L rm principl del logritmo se obtiene l tomr rg z ( π, π]. Por otr prte, ls ecuciones de Cuchy-Riemnn nos dicen que log z es un función holomorf en l región en que es un función continu. Así pues, log z es holomorf en C \ (, 0] si se tomn los rgumentos en el intervlo ( π, π). Es fácil comprobr que (log z) = /z, hllndo l derivd prcil de log z con respecto x, o bien usndo que el logritmo es l función invers de l exponencil. L función potencil. Si C, l funciónes f(z) = z y g(z) = z se definen como z = e z log ( 0), z = e log z. Por tnto, z es holomorf en todo C, mientrs que z es holomorf en C \ (, 0]; si Z, z es holomorf en C \ {0}, y si N, z es holomorf en todo C. Ls funciones trigonométrics. Ls funciones seno y coseno se definen por medio de ls siguientes series de potencis que tienen rdio de convergenci infinito, cos z = ( ) n z2n (2n)!, sen z = ( ) n z2n+ (2n + )!. Con ls misms mnipulciones que en el cso z = y R, se tiene entonces que (2) e iz = cos z + i sen z, z C. Por simple inspección de ls series que definen sen z y cos z, vemos que cos( z) = cos z y que sen ( z) = sen z, por lo que (3) e iz = cos z i sen z. 9

10 Sumndo y restndo (2) y (3) obtenemos que (4) cos z = eiz + e iz 2, sen z = eiz e iz Ls restntes funciones trigonométrics se definen prtir de ells: tn z = sen z cos z, cos z cotn z = sen z, sec z = cos z, cosec z = sen z, y son holomorfs en todo C slvo en los ceros de los denomindores respectivos. Utilizndo ls relciones (4) es sencillo obtener muchs de ls relciones conocids pr el cso rel, por ejemplo, cos 2 z + sen 2 z =, sen 2z = 2 sen z cos z, cos 2z = cos 2 z sen 2 z. 2i. Ls funciones hiperbólics. Como en el cso rel se definen como (5) senh z = ez e z que son holomorfs en todo C, y 2, cosh z = ez + e z 2, tnh z = senh z cosh z, cosh z cotnh z = senh z, sech z = cosh z, cosech z = senh z, que son holomorfs en todo C slvo en los ceros de los denomindores respectivos. Es interesnte conocer ls relciones con ls funciones trigonométrics que se siguen de (4) y (5) y que implicn ls relciones cos z = cosh(iz), sen z = i senh (iz), cosh z = cos(iz), senh z = i sen (iz), cosh 2 z senh 2 z =, senh 2z = 2 senh z cosh z, cosh 2z = cosh 2 z + senh 2 z. 5. SERIES DE LAURENT Y RESIDUOS Teorem (Teorem de Lurent). () Si f es holomorf en Ω = {z : r < z < R} (0 r < R ), entonces existe un sucesión de números complejos {c n } n= tl que f(z) = c n (z ) n, z Ω. n= L serie converge en culquier punto de Ω. (b) Supongmos que f no se extiende como función holomorf de Ω ningún nillo más grnde Ω = {z : r < z < R } Ω, con r < r o R > R. Entonces se tiene que r = lim sup c n /n, n R = lim sup c n /n. n Ejemplo. Desrrollr en serie de Lurent f(z) = /(z 2 4z + 3), en ls regiones { z < }, { < z < 3} y { z > 3}. Definición. Se f : D(f) C. Un punto es un singulridd isld de f, si f está definid y es holomorf en D(, ε) \ {} pr lgún rdio ε > 0, donde el disco perfordo D(, ε) \ {} se contiene en el dominio de definicón D(f) de f. Definición. Se un singulridd isld de f. Por el desrrollo de f en serie de Lurent en torno de z = se entiende el el desrrollo de f en un serie de Lurent en un disco perfordo D(, R) \ {z}, donde el rdio R es positivo (este disco perfordo es un cso prticulr del nillo {z : r < z < R}, cundo el rdio interior r es nulo). 0

11 Definición. Si es un singulridd isld de f, el residuo de f en z = es el coeficiente c de su desrrollo en serie de Lurent en torno de z =. Se escribe Res (f, ) = c. Se es un singulridd isld de f y se () f(z) = n= c n (z ) n, z, 0 < z < ϵ un desrrollo de Lurent de f en torno de z =. Entonces puede ocurrir un de ls tres siguientes posibiliddes: () Que se un singulridd evitble de f, es decir, existe el límite de f cundo z tiende l punto, y si se define f() := lim z f(z), entonces f es holomorf en un entorno de (incluyendo el punto ). Teorem. Sen Ω un bierto y Ω. Se f un función holomorf en Ω \ {}. Entonces son equivlentes ls siguientes firmciones: ) f está cotd en un entorno de ; 2) Existe un límite lim z f(z) C; 3) es un singulridd evitble de f. (2) Que se un polo de f. Por definición, ésto ocurre si lim f(z) =. z Proposición. Sen Ω un bierto, Ω y f un función holomorf en Ω \ {}. Entonces, es un polo de f si y sólo si existe un número entero k (k se denomin el orden del polo de f en ) tl que con g holomorf en Ω, y g() 0. f(z) = g(z) (z ) k, (3) Que se un singulridd esencil de f. Por definición esto ocurre si no ocurre ni () ni (2). El fmoso Teorem grnde de Picrd, dice que es un singulridd esencil de f si y sólo si, pr todo ε > 0, f(d(, ε) \ {}) es todo C slvo, lo sumo, un punto. En prticulr, pr todo w C, existe un sucesión n con f( n ) w. L relción entre l serie de Lurent y el tipo de singulridd isld ) Si es un singulridd evitble de f, entonces f dmite un desrrollo de Tylor en un cierto disco D(, r). f(z) = c n (z ) n 2) Si f tiene en un polo de orden k, entonces f dmite un desrrollo de Lurent del tipo f(z) = c k (z ) k + + c z + c n (z ) n = n= k c n (z ) n, c k 0, en un disco perfordo D(, r) \ {}. 3) Por último, si f tiene en un singulridd esencil, entonces f dmite un desrrollo de Lurent del tipo f(z) = c n (z ) n, con infinitos c n (n N) distintos de cero. n=

12 Ejemplo. El origen es un singulridd esencil de l función f(z) = e /z, pues e /z = m=0 ) m 0 z = m!( n z ( n)!, z 0. n= Ejemplo. El origen es un singulridd esencil de l función f(z) = e /z, pues e /z = m=0 ) m 0 z = m!( n z ( n)!, z 0. n= Un ejemplo de cálculo de residuos. Consideremos l función rcionl Su descomposición en frcciones simples es f(z) = z 2 (z 2 + ). f(z) = z 2 + i/2 z i i/2 z + i. Sus singulriddes evitbles son los puntos = 0, = i y = i. Ls estudimos por seprdo.. L singulridd isld = 0 de f. L función i/2 z i i/2 z+i es holomorf en el disco D(0, ). Según el Teorem de l Sección 4, l serie de Lurent de l función f centrd en = 0 converge en 0 < z < y tiene l form f(z) = z 2 + n z n, donde nz n es l serie de Tylor de l función i/2 z i i/2 z+i centrd en = 0. (Se dice que es l prte z2 principl de l serie de Lurent de f en el punto = 0). Por tnto, = 0 es un polo doble de f, y Res (f, 0) = Ls singulriddes islds = ±i. De l mism mner, vemos que l prte principl de l serie de Lurent de f en el punto = i es i/2 z i, mientrs que l prte principl de l serie de Lurent de f en el punto i es i/2 z+i. Los puntos i, i son polos simples de f, y Res (f, i) = i 2, Res (f, i) = i 2. Fórmuls de cálculo de residuos () Si f tiene en un polo de orden (es decir, un polo simple), entonces (2) Si f tiene en un polo de orden k, entonces Res (f, ) = Res (f, ) = lim z (z )f(z), (k )! lim z d k ( ) dz k (z ) k f(z). (3) Si f tiene en un singulridd esencil, NO existe un fórmul pr el residuo de f en ; l form de hllr el residuo es encontrr el coeficiente c de l potenci (z ) del desrrollo en serie Lurent de f (éste método tmbién es válido si es un polo de f). Si f tiene un singulridd isld en y lim z (z )f(z) = l existe y es distinto de 0 y de, entonces f tiene en un polo de orden y su residuo es l. Definición. f es meromorf en Ω si sólo tiene singulriddes islds en Ω, y ésts son o bien evitbles, o bien son polos. Teorem 2. f es meromorf en el bierto Ω si y sólo si f = g/h con g, h funciones holomorfs en Ω y h no es idénticmente nul. 2

13 6. INTEGRACION COMPLEJA Integrción lo lrgo de curvs. Tods ls curvs : [, b] C que se consideren de hor en delnte serán de clse C trozos. Si f : [, b] C, es un función con vlores complejos, f = u + iv, y sus prtes rel e imginri u, v son integrgles en [, b], l integrl de f en [, b] se define como b f(t) dt = b u(t) dt + i b v(t) dt. Ls propieddes de l integrl de Riemnn de funciones reles de vrible rel implicn inmeditmente que: () (2) b b (αf + βg) = α f b f. b f + β b g, α, β C. Recordemos que si : [, b] C es un curv, (t) = (x(t), y(t)) = x(t) + iy(t), l integrl lo lrgo de de un -form P dx + Q dy (o del cmpo vectoril (P, Q)) se define medinte P dx + Q dy = b ( ) P (x(t), y(t)) x (t) + Q(x(t), y(t)) y (t) dt. Vmos usr est definición en el cso de funciones P, Q complejs. Si f está definid sobre, es decir f : ([, b]) C y, por ejemplo, es continu, entonces tiene sentido definir f(z) dz = f dx + if dy. Por tnto, f(z) dz = b y como x (t) + iy (t) = (t), tenemos que ( ) f((t)) x (t) + if((t)) y (t) dt = f(z) dz = b b f((t)) (t) dt. Ejemplos. z dz, donde (t) = t + 2ti pr t [0, ]; z = dz/z. f((t)) (x (t) + iy (t)) dt, Reprmetrizciones. Si t = t(s) es un reprmetrizción de, es decir, t : [c, d] [, b] es C y creciente, entonces (t) es tmbién un función de clse C trozos que describe l curv ([, b]), y se tiene que b f((t)) (t) dt = d c f((t(s))) (t(s)) t (s) ds = d c f(( t)(s)) ( t) (s) ds, es decir, que l definición de f no depende de l prmetrizción elegid de l curv, siempre que consideremos prmetrizciones con l mism orientción. Cmbio de orientción. El rco opuesto : [, b] C es el rco : [ b, ] C ddo por (t) = ( t) y, por tnto, se tiene que f(z) dz = b f(( t)) ( ( t)) dt = b f((t)) (t) dt = f(z) dz, y, por tnto, un cmbio de orientción en l curv lo lrgo de l cul se integr, produce un cmbio de signo en l integrl. Integrción respecto l longitud de rco. Definimos l integrl de f respecto l longitud de rco en como b f(z) dz = f((t)) (t) dt = f ds, 3

14 donde s denot el prámetro rco. Es sencillo comprobr que este tipo de integrción es no sólo independiente respecto los cmbios de prmetrizción, sino tmbién de orientción: f(z) dz = f(z) dz. Teorem. Sen, i curvs, α, β C, y f, g funciones continus. Si long = dz denot l longitud de, entonces: () (α f + β g) dz = α f dz + β g dz, (2) f dz = f dz + + f dz, si long ( i j ) = 0 pr i j, n n (3) f(z) dz f(z) dz, (4) si f M sobre, entonces f dz M long. Teorem 2. Si f : Ω C es continu en el bierto Ω y f tiene primitiv en Ω, es decir, si existe un función F holomorf en Ω tl que f(z) = F (z) pr todo z Ω, entonces, dd culquier curv : [, b] Ω, se tiene () f(z) dz = F ((b)) F (()), (2) f(z) dz = 0, si es cerrd (es decir, si () = (b)). Demostrción. () es un consecuenci de l regls de Brrow y de l cden: b b b f(z) dz = f((t)) (t) dt = F ((t)) (t) dt = (F ) (t) dt = F ((b)) F (()). L prte (2) es un consecuenci inmedit de (). Ejemplo. Pr tod curv cerrd, e z dz = 0. Ejemplo 2. α dz = 0, pr tod curv cerrd que no pse por el origen. z2 6. EL TEOREMA DE CAUCHY, EL TEOREMA DE LOS RESIDUOS Y SUS APLICACIONES Teorem (Teorem integrl de Cuchy). Si f : Ω C es holomorf en el bierto simplemente conexo Ω, se tiene que f = 0, pr tod curv cerrd Ω. Demostrción (si f es continu). Si es un curv cerrd simple, se S el dominio encerrdo por. Por el Teorem de Green con P (x, y) = f(z), Q(x, y) = i f(z), se tiene que ( Q f(z) dz = f(z) dx + i f(z) dy = x P ) dx dy = (if x f y ) dx dy = 0, y S S donde l últim iguldd es consecuenci de ls ecuciones de Cuchy-Riemnn. Si no es simple, es unión de curvs cerrds simples y l integrl lo lrgo de cd un de ells es cero por lo nterior. Ejemplos. Si es culquier curv cerrd, se tiene e z2 dz = 0. Si es culquier curv cerrd contenid en el semiplno superior, se tiene e z2 + e cos z dz = 0. z + De hecho, no es difícil generlizr el teorem nterior funciones holomorfs con un número finito de singulriddes. 4 S

15 Si es un curv cerrd simple, el conocido teorem de l curv de Jordn, nos segur que divide l plno complejo en dos regiones: Ext (que contiene un entorno del punto del infinito) e Int (que es simplemente conex). Observción: Siempre que no se dig explícitmente lo contrrio, supondremos que ls curvs cerrds simples están orientds positivmente, es decir, en sentido contrrio l movimiento de ls gujs del reloj. Se tiene l siguiente mrvillos fórmul: Teorem 2 (Fórmul integrl de Cuchy). Se Ω un dominio simplemente conexo en el plno complejo. Se f : Ω C un funcin holomorf. Si es un curv cerrd simple contenid en Ω, orientd positivmente, entonces 2πi { f(z) f(), si Int, z dz = 0, si Ext. En prticulr, si es l fronter de un disco, se tiene lo siguiente. Corolrio. Si f es holomorf en el bierto Ω, y D es un disco tl que D Ω, entonces f(z) = f(w) 2πi D w z dw, z D. L Fórmul Integrl de Cuchy nos dice que los vlores en Int de ls funciones holomorfs están prescritos por sus vlores sobre. De hecho, ls demostrciones complets de los Teorems de Secciones 2 y 3 se bsn en l fórmul integrl de Cuchy. Teorem 3 (Teorem de los residuos) Sen Ω un bierto simplemente conexo, f un función holomorf en Ω slvo en un conjunto { j } de singulriddes islds. Se D un dominio tl que D Ω y cuy fronter no contiene ningún j. Entonces f(z) dz = 2πi Res (f, j ) (se elige l orientción positiv de ). Corolrio. Si z,..., z n son números complejos distintos y P (z) es un polinomio de grdo menor que n, se tiene l descomposición en frcciones simples Q(z) = j D P (z) (z z ) (z z n ) = Res (Q, z ) + + Res (Q, z n), con Res (Q, z j ) = lim (z z j )Q(z). (z z ) (z z n ) z z j Teorem 4 (Desiguldd de Cuchy). Si f es holomorf en D(, r) = {z C : z r}, y si M r = mx{ f(z) : z = r}, entonces Demostrción. f (n) () n! 2π D r f (n) () M r n! r n. f(z) n! dz z n+ 2π D r M r r n+ dz = M r n! r n. Consecuencis sencills de est desiguldd son los conocidos resultdos siguientes: Corolrio (Teorem de Liouville). Si f es enter (holomorf en C) y cotd, entonces es constnte. Corolrio 2 (Teorem fundmentl del Algebr). Todo polinomio (con coeficientes complejos) de grdo n tiene n ríces complejs (contdo su multiplicidd ). 5

16 Aplicción: Trnsformd de Lplce. Si f : [0, ) C es continu trozos y verific que lim x f(x) e x = 0 pr lgún R, entonces l función (l trnsformd de Lplce de f) Lf(z) = es holomorf en el semiplno {z C : Re z > }. Ejemplo. Descomponer en frcciones simples z 3 z. Proposición. 2π 0 R(cos θ, sen θ) dθ = Introducimos l notción 2π 0 ( e iθ + e iθ R 2 0 f(x) e zx dx, eiθ e iθ ) ie iθ dθ ( 2i ie iθ = R z + z = 2( ), ( z )) dz z 2i z iz. R v.p. f(x) dx def = lim f(x) dx. R + R Proposición 2. Se f un función que es nlític en un dominio que conteng l clusur del semiplno superior H = {z C : Im z > 0}, slvo en un número finito de singulriddes, que no están sobre el eje rel. () Si lim z z f(z) = 0, tenemos que (2) Si lim z f(z) = 0, y c > 0, entonces v.p. f(x) dx = 2πi Res (f, ) Sing(f) Im >0 v.p. f(x) e icx dx = 2πi Res ( f(z) e icz, ) Sing(f) Im >0 Se firm, en prticulr, que los vlores principles de ests integrles existen. 6