INTEGRACION NUMERICA Método se Simpson
|
|
|
- María Victoria Villalobos Carrizo
- hace 8 años
- Vistas:
Transcripción
1 Ojetivos: Geerles Específicos Oservcioes Prelimires Clculo de Áres El método de Simpso Desrrollo del modelo de Simpso Ejemplos Progrm e diferetes legujes L jerrquí de clses INTEGRACION NUMERICA Método se Simpso Ig Ymil Armdo Cerquer Rojs cerque@gmil.com Especilist e Sistems Uiversidd Nciol Docete Uiversidd Surcolomi Neiv - Huil OBJETIVOS GENERALES Ojetivos: Resolver el prolem de cálculo del áre jo l curv etre dos límites coocidos, dividiedo e N su áres pr clculr su vlor, sumiedo cd su áre como u pequeño rco de prol.. Compreder ls ses coceptules de l itegrció proimd.. Compreder los rsgos geerles de l itegrció proimd utilizdo el método de Simpso.. Compreder l proimció del error por trucmieto de l itegrció proimd utilizdo el método de Simpso, frete l vlor ecto.. Resolver prolems de itegrció proimd utilizdo el método de Simpso. OBJETIVOS ESPECÍFICOS. Coocer l iterpretció geométric de l itegrl defiid.. Recoocer que el método de Simpso represet, geométricmete, el áre jo u fució poliomil de segudo orde (Cudrátic o Prólic.. Deducir l fórmul de Simpso prtir de l iterpretció geométric de l itegrl defiid.. Acotr el error cometido e l itegrció uméric por el método de Simpso. 5. Eplicr l oteció de fórmuls más preciss pr clculr, uméricmete, itegrles defiids. 6. Aplicr el método de Simpso, pr clculr uméricmete, ls proimcioes de lgus itegrles defiids. Uiversidd Surcolomi Neiv Huil - Colomi de 8
2 OBSERVACIONES PRELIMINARES Cudo se reliz u eperimeto, geerlmete, se otiee u tl de vlores que se esper, teg u comportmieto fuciol. Si emrgo, o se otiee l represetció eplícit de l fució que represet l regl de correspodeci etre ls vriles ivolucrds. E estos csos, l relizció de culquier operció mtemátic sore l ue de putos que preted trtrl como u relció fuciol, tropezrá co dificultdes cosiderles l o coocerse l epresió eplícit de dic relció. Etre ests opercioes se ecuetr l itegrció de fucioes. Además, es coocido que eiste reltivmete pocs fórmuls técics de itegrció, frete l ctidd eistete de fucioes que se puede itegrr. Es decir, u gr úmero de itegrles de fucioes elemetles o puede ser epresd e térmios de ells. Etre estos csos sigulres se tiee, mer de ejemplo: d l( e d,, d, si( d, d,... Pr clrr l cotrdicció tes señld, se dee recordr l codició ecesri pr que u fució se itegrle. Dic codició se mecio de imedito, si demostrció: Proposició (Codició ecesri de Itegrilidd. Si u fució f es cotiu e el itervlo [, ], etoces l fució f es itegrle e el itervlo [, ]. No ostte que ls codicioes de l proposició so summete geerles, o se tiee grtí de que, l plicr los métodos usulmete coocidos pr resolver itegrles, se pued ecotrr l tiderivd de u fució f( culquier ecesri pr oteer l itegrl defiid. Estos putes pretede ilustrr l lector de form detlld lo ms secillo posile, u de ls técics ásics que permite resolver dic situció, ciedo uso de los métodos o modelos uméricos, trvés de l deomid INTEGRACIÓN APROXIMADA, POR EL MÉTODO DE SIMPSON. Uiversidd Surcolomi Neiv Huil - Colomi de 8
3 CÁLCULO DE ÁREAS Uo de los prolems mtemáticos más frecuetes es el cálculo del áre que se form etre u fució f(, el eje los límites. Por ejemplo, se ecesit clculr el áre A que prece e l Fig., reiterdo que dic áre est por dejo de l fució f( etre los límites : Fig. Prtiedo del eco que l fució f ( los vlores so coocidos. se cosider como el limite iferior se cosider como límite superior. E este tipo de prolems se puede oteer dos tipos de solucioes: Solucioes lgerics: se otiee u fórmul precis ect pr el áre solicitd. Solucioes umérics: se clcul uméricmete u estimció del áre. Desde luego, l solucioes lgerics so mejores que ls umérics, porque so ects. Pero veces, l complejidd de ls fucioes ce imposile (o difícil oteer l solució lgeric, por lo que u solució uméric permite orrr tiempo. EL MÉTODO DE SIMPSON Además de plicr l regl trpezoidl o Rectgulr co segmetos o su áres cd vez más pequeñs, otr mer de oteer u estimció ú más ect de u itegrl, es l de usr poliomios de orde superior pr coectr los putos, e el cso prticulr del método que us orde, es decir de l form c. A ls fórmuls resulttes de clculr l itegrl jo estos poliomios se les cooce como regls de Simpso. E este procedimieto, se tom el itervlo de cur, compredido etre, se sustitue l fució f( por l práol que ps por tres putos i i Uiversidd Surcolomi Neiv Huil - Colomi de 8
4 ( i, i, ( i, i, ( i, i. El vlor del áre proimd, somred e l figur, se clcul co u poco más de trjo el resultdo es [ ], que se demuestr e seguid. i i i DESARROLLO DEL MODELO DE SIMPSON: Pr efectos de l demostrció del método de Simpso, se sume cd su áre como u pequeño rco de práol de l form c co límites sí: Limite iferior e, limite superior e, por ede l mitd de l pequeñ su áre se ecotrrá e el Puto, tl como se ilustr e Fig.. Fig. Se procede itegrr dico rco de práol etre los límites descritos se tedrá: ( c d se tiee: c, reemplzdo cd uo de los límites, c c tedrá:, or destruedo prétesis se c c c, simplificdo u poco l solució se otedrá l ecució que se muestr cotiució. Uiversidd Surcolomi Neiv Huil - Colomi de 8
5 ( c d [ 6c] Ec Fig. Oservdo l Fig, e lo que respect ls otcioes, se puede decir que f ( f (, f ( f ( i i i i, f ( f ( i i, Etoces se podrí oteer el siguiete sistems de ecucioes, evludo l ecució geerl de l práol c e cd uo de los putos de l pequeñ su áre [,-]: f ( c, se puede tomr est ltur como f ( i f ( c, se tom est ltur como f ( i f ( c, est ltur como f ( i De lo terior se puede decir que: c Ec Retomdo l Ec se puede epresr igulmete de l siguiete mer: c Ec ( c d [ c c] Ec Reemplzdo ls ecucioes e l Ec se tiee que: Uiversidd Surcolomi Neiv Huil - Colomi 5 de 8
6 [ ] ( c d A Ec 5 Iterpretdo l ecució Ec 5 co se e l su áre selecciod A pr desrrollr el modelo de Simpso, se dirí que el áre del segmeto es igul l sum de l ltur o fució evlud e el ldo izquierdo ms cutro veces l fució evlud e l prte cetrl de l su áre ms l fució evlud e el ldo dereco de l su áre, todo esto multiplicdo por el co del su áre dividido por. L simple ispecció visul de est figur l que descrie el procedimieto de los trpecios o los rectágulos, cofirm que el método de Simpso deerá ser muco más ecto que los procedimietos meciodos. Si se deomi como, f ( i i se represet medite u poliomio de Lgrge de segudo orde, etoces l itegrl es: I X X ( ( f ( ( ( ( ( f ( d ( ( ( ( f ( ( ( Después de itegrr de reorder los térmios, result l siguiete ecució: I f ( f ( f ( ( Ec 5 6 Si se tom ( / 6 /, f (, f (, f (, etoces se tiee como solució de l su áre I (, que serí lo mismo mostrdo e l ecució 5. Aor, se se que el áre que se dese ecotrr serí l sumtori de tods ls su áres que se clcule. Al igul que los métodos de l regl trpezoidl de l regl rectgulr, etre ms su áres teg l itegrl clculr, ms ecto será el vlor ecotrdo. El áre proimd e el itervlo [, ] es: Uiversidd Surcolomi Neiv Huil - Colomi 6 de 8
7 Uiversidd Surcolomi Neiv Huil - Colomi 7 de 8 A A A A d f... (, or dejdo est ecució e térmios de l ecució 5 se tedrá: (... ( ( ( d f Simplificdo / sumdo los térmios se tedrá:... ( ( 6 5 d f, dode serí el úmero de su áres e el cul se dividido el áre que se dese clculr. A mer de ejemplo, si el áre clculr se uier dividido e Su áres etoces e térmios de l solució seri: ( ( d f Bie, depediedo como se grupe los térmios se llegrí epresr l solució de dos mers: [ ] ( ( ( d f Ec 6 ó [ ] ( ( ( d f Ec 7 Los primeros térmios del prétesis, cotiee los vlores de l evlució de l fució e los etremos, el segudo, l sum de los térmios de ídice impr, el tercero l sum de los térmios de ídice pr. Ls dos ecucioes se pudier represetr e térmios de sumtoris de l siguiete mer. L Ec 6: ( i i i i d f Ec 8
8 L Ec 7: f ( d [ ] i i Ec 9 i Pr efectos de progrmció e lo que respect mi cocepto persol, es mejor l solució represetd como Ec 9 co ell se cotiú el trjo. H que teer e cuet que es el úmero de su áres e l que se divide el áre totl clculr d /. Aor lo que se cooce e u mometo determido, cudo se dese clculr el vlor de l itegrl defiid, so los siguietes térmios: Límite iferior Límite Superior Número de su áres f ( L fució sore l cul se dese itegrr. Co los vlores teriores se pude clculr el vlor de d sí: d /. d ( / E ecesrio etoces dejr l ecució e térmios de f (,, d ó sí: Los primeros térmios: f ( f ( Alizdo or los térmios impres: f ( d /, f ( d /, f ( 5d /, por tto se tedrí de mer geerl: 5 i f ( (i d / ó f ( (i i Ec Alizdo or los térmios pres: f ( d, f ( d, f ( d, por tto se tedrí de mer geerl: 6 f ( id i ó f ( i i Ec Dejdo l ecució Ec 9 e térmios de lo epresdo e ls ecucioes Ec Ec se tedrá e form defiitiv l solució sí: Uiversidd Surcolomi Neiv Huil - Colomi 8 de 8
9 f ( d f ( f ( [ ] f ( (i d / f ( id Ec i Ejemplos Ejemplo : Utilizr l regl de Simpso pr proimr l itegrl: Teg e cuet que el vlor rel es.66 e d. Fig. Solució: Usdo l fórmul directmete co los siguietes dtos: f ( Si se sume el áre clculr como u solo rco de práol, se tedrí etoces que d ( / ó ( d /. 5 plicdo l ecució Ec 5 se tiee que: e d [ ] A e e.5 [ e e e ].5 e d.5 d [ (.8.78] Uiversidd Surcolomi Neiv Huil - Colomi 9 de 8
10 e d.757 Aor si compr los resultdos oteidos l plicr l regl del Trpecio o l regl de los Rectágulos, co respecto l vlor rel l vlor oteido por l regl de Simpso tedrí que lizr lo siguiete: Itegrl Vlor Rel Rectgulr Trpezoidl Simpso f ( e Er.% 7.%.9% E Vle l pe clrr que pr los tres métodos se trjó u sol su áre. Desrrolldo e MtL se tedrí el siguiete resultdo.»sms»fep(^;»itegrlit(f itegrl -/*i*pi^(/*erf(i* ERF Error de l fució. Y ERF(X es el error de l fució pr cd elemeto de X. X dee ser rel. El error de l fució está defiido como: erf( /sqrt(pi * itegrl desde de ep(-t^ dt. Alice lo terior. Ejemplo : Aplicr l regl de Simpso pr proimr l itegrl se sudivide el áre totl e 5 itervlos. e d si Solució: E este cso, se idetific 5, ls prticioes geerds estrí delimitds por los putos P{.,.,.,.6,.8,.} sore el eje. Así, plicdo l fórmul: f ( d ( Uiversidd Surcolomi Neiv Huil - Colomi de 8
11 Si se sume el áre clculr como cico pequeños rcos de práol, se tedrí etoces que d ( /5. ó ( d /. plicdo l ecució Ec 7 se tiee que: f d [ ( ( ] ( f ( e e, ( f e. 78 Los térmios impres se ecotrrí de cuerdo co l fórmul f ( (i f ( sí: i i. f ( f (. e.. f ( f (. e.9.5 f (5 f (.5 e 5.7 f (7 f (.7 e f (9 f (.9 e Y l sumtori igul : Los térmios pres se ecotrrí de cuerdo l fórmul i f ( sí:. f ( f (. e.8. f ( f (. e f ( 6 f (.6 e.8 f ( 8 f (.8 e 8 f ( f ( e Y l sumtori igul : Por tto el vlor de l itegrl será igul :. f ( d.78 (7.685 (8.6. [ ] 67 i Itegrl Vlor Rel Rectgulr Trpezoidl Simpso f ( e Er.685%.75%.68% E Uiversidd Surcolomi Neiv Huil - Colomi de 8
12 Ejemplo : Usr l regl de Simpso pr proimr l itegrl: e d. Solució: Igul que e el ejemplo terior, se sustitue los dtos de mer direct e l fórmul de Simpso dividiedo el áre e cutro ( su áres. E este cso, se tiee los dtos:,, f ( e / d (-/.5 d/.5 Por lo tto, se tiee que: f d ( [ ( ] ( f ( e / e /.695, f ( e / Los térmios impres se ecotrrí de cuerdo co l fórmul f ( (i f ( sí: i i.5 f ( f (.5 e / f ( f (.75 e / f ( 5 f (.5 e / f ( 7 f (.75 e / Y l sumtori igul : Los térmios pres se ecotrrí de cuerdo l fórmul f ( i i sí:.5 f ( f (.5 e / f ( f (. e / f ( 6 f (.5 e / f ( 8 f (. e / Y l sumtori igul :.679 Uiversidd Surcolomi Neiv Huil - Colomi de 8
13 Por tto el vlor de l itegrl será igul :.5 f ( d (9.795 (.679 [ ] Ejemplo : Evlur l fució f ( d, usdo l siguiete tl: f( Solució. Fig 5 Oserve e l fig 5 que e el itervlo [,.] se puede plicr l regl del trpecio, e el itervlo [.,.7] l regl de Simpso de /8 e el itervlo [.7,.] l regl de Simpso de /. Así, se tiee ls siguietes itegrles:.. I f ( d [ f ( f (.] I f ( d [ f (. f (. f (.5 f (.7] I f ( d [ f (.7 f (.95 f (.] Filmete, l itegrl uscd es l sum de ls tres itegrles teriores: Uiversidd Surcolomi Neiv Huil - Colomi de 8
14 f ( d Ejemplo 5: Clcul l itegrl f ( d, usdo l siguiete tl de dtos: f( Si se desrroll l gráfic co Mtl justdo los dtos de l tl terior medite splies cúicos, se tedrí lo siguiete:» [ ];» [ ];» -:.:.5;» splie(,,;» plot(,,'o',, Fig. 6 Solució comido vrios métodos de itegrció. Pr este cso, se puede plicr l regl de Simpso de / e el itervlo [-,], l regl del trpecio e el itervlo [,] l regl de Simpso de /8 e el itervlo [,.5]. Así, se tiee ls siguietes itegrles: I I ( f ( d 6 [ f ( f (.5 f (]. 667 f ( d [ f ( f ( ]. 5 Uiversidd Surcolomi Neiv Huil - Colomi de 8
15 I.5.5 f ( d f 8 [ f ( f (.75 f (.5 (.5]. 98 Por lo tto, l itegrl uscd es l sum de ls tres itegrles teriores:.5 f ( d Vle l pe cometr que o siempre tiee que suceder que se plique ectmete ls tres regls. E relidd, esto depede de cómo se ecuetr espcidos los itervlos de l tl de dtos l form que pued teer l curv. Ejemplo 6: Clculr l siguiete Itegrl: jo l curv mostrd e l Fig. 7 etre los límites. Itervlo: Método: Regl de Simpso su itervlos, dode d (-/. log( d, correspodiete l áre Se utiliz l regl de Simpso co d. ó.5, su itervlos l tl l( de vlores pr f ( d Fig. 7 Uiversidd Surcolomi Neiv Huil - Colomi 5 de 8
16 TABLA de vlores ( f i.. Y Y Y Y..855 Y Y5 El resultdo plicdo l siguiete fórmul serí: (Teg e cuet que solo se trj su áres I f d [ ( ( ] ( I.5/ * ( * ( * ( I Progrm e diferetes legujes Progrmció del método de Simpso e leguje C. Supog que l fució f evlú l fució f(. Etoces l siguiete fórmul permite clculr el áre de cd u de ls seccioes: f ( d f ( f ( i [ f ( (i d / f ( id ] Progrm e leguje C: Se supoe que l fució re se dee llmr co los prámetros,, que serí límite iferior, límite superior úmero de su áres respectivmete. doule re(doule, doule, it { doule d (-/; doule sum f(-f(; for (it i; i<; i { doule impr(*i-*d; doule pr (i*d; sum *f(impr*f(pr; } retur d*sum/6; } doule f(doule { doule ;... // Se descriirí l fució l cul se le dese clculr l itegrl retur ; } Uiversidd Surcolomi Neiv Huil - Colomi 6 de 8
17 Est solució es álog l que se progrmó pr uscr los ceros de u fució. El prolem de est solució, es que cudo se dese clculr l itegrl de vris fucioes distits, que progrmr u fució pr clculr el áre de cd fució. Si se progrm pr MtL el progrm serí fuctio resimpso(,, d(-/; sum f(-f( for i:, impr(*i-*d/ pr i*d sumsum *f(impr*f(pr; ed re d*sum/6 Y l fució f estrí dd por (Como cso prticulr se coloc ^-, pero solo cmie l fució f le itegr lo que desee: fuctio f( ^-; %Puede cmir est fució L jerrquí de clses pr C. Se cre u clse se strct deomid Simpso, que defi l fució miemro itegrl que clcul l itegrl defiid de culquier fució f( por el procedimieto de Simpso. pulic strct clss Simpso { pulic doule itegrl(doule, doule, it { doule d(-/; doule sumf(-f(; for(it i; i<; i { sum*f((*i-*d *f(i*d; } retur (sum*d/6; } strct pulic doule f(doule ; } E l clse derivd Fucio de Simpso se defiirá l fució f( cu itegrl se dese clculr. Uiversidd Surcolomi Neiv Huil - Colomi 7 de 8
18 pulic clss Fucio eteds Simpso { pulic doule f(doule { retur Mt.cos(; } } Pr llr l itegrl defiid de est fució etre los límites p /, se cre u ojeto de l clse Fucio medite ew se llm desde este ojeto l fució itegrl psádole e el primer rgumeto el límite iferior, e el segudo el límite superior, pi/, por último, el úmero de divisioes del itervlo. doule resultdoew Fucio(.itegrl(., Mt.PI/, ; Sstem.out.pritl("itegrl "resultdo; Comprdo los resultdos oteidos por este procedimieto por el procedimieto de los trpecios se puede compror l mor ectitud de éste último. Uiversidd Surcolomi Neiv Huil - Colomi 8 de 8
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Aproximación al área bajo una curva.
 Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
Aproimció l áre jo u curv. Por: Miguel Solís Esquic Profesor de tiempo completo Uiversidd Autóom de Cips Clculr cd u de ls áres de los rectágulos que lle l regió cotd pr lczr el vlor del áre ecesrimete
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Métodos analíticos. Métodos Numéricos - Cap. 6. Integración 1/8. Integración - Cuadratura. Fórmulas cerradas de Newton-Cotes. Regla de los Trapecios
 Métodos Numéricos - Cp.. tegrció / tegrció - Cudrtur Métodos líticos Métodos uméricos pr estimr el vlor de u itegrl deiid Dode el itervlo de itegrció es iito y : cotiu e. Segú el teorem Fudmetl del Cálculo
Métodos Numéricos - Cp.. tegrció / tegrció - Cudrtur Métodos líticos Métodos uméricos pr estimr el vlor de u itegrl deiid Dode el itervlo de itegrció es iito y : cotiu e. Segú el teorem Fudmetl del Cálculo
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
EL TEOREMA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE. Alberto E. J. Manacorda*
 EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
EL TEOREA DEL PUNTO FIJO Y APLICACIONES SEGUNDA PARTE Alerto E. J. cord* *Igeiero Geogrfo Profesor Titulr de Alisis temtico II Fcultd de Ciecis Ecoomics Estdistic Uiversidd Nciol de Rosrio 5.- Aliccioes
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
UNIDAD 5 Series de Fourier
 Series de Fourier 5. Fucioes ortogoles, cojutos ortogoles y cojutos ortoormles Se dice que dos fucioes f ( x ) y f x so ortogoles e el itervlo < x< si cumple co: f x = Est ide se hce extesiv u cojuto de
Series de Fourier 5. Fucioes ortogoles, cojutos ortogoles y cojutos ortoormles Se dice que dos fucioes f ( x ) y f x so ortogoles e el itervlo < x< si cumple co: f x = Est ide se hce extesiv u cojuto de
MANUAL MATEMÁTICAS PARA ESTUDIANTES DE FINANZAS. Exponentes
 _ Defiició: Epoetes Pr u úero rel u etero positivo, veces se le deoi l se l poteci o epoete Ejeplos:..... Not: oserv que del segudo es. o so igules, el resultdo del priero es Lees de epoetes: Pr cd u de
_ Defiició: Epoetes Pr u úero rel u etero positivo, veces se le deoi l se l poteci o epoete Ejeplos:..... Not: oserv que del segudo es. o so igules, el resultdo del priero es Lees de epoetes: Pr cd u de
PAIEP. Sumas de Riemann
 Progrm de Acceso Iclusivo, Equidd y Permeci PAIEP Uiversidd de Stigo de Chile Sums de Riem Ddo u itervlo de l form [, b], co y b e R, < b, u prtició del itervlo [, b] es u colecció de putos P = {x, x,...,
Progrm de Acceso Iclusivo, Equidd y Permeci PAIEP Uiversidd de Stigo de Chile Sums de Riem Ddo u itervlo de l form [, b], co y b e R, < b, u prtició del itervlo [, b] es u colecció de putos P = {x, x,...,
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
Operaciones con Fracciones
 Frccioes Opercioes co frccioes Opercioes co Frccioes Reducció de frccioes Frccioes co igul deomidor: De dos frccioes que tiee el mismo deomidor es meor l que tiee meor umerdor. < Frccioes co igul umerdor:
Frccioes Opercioes co frccioes Opercioes co Frccioes Reducció de frccioes Frccioes co igul deomidor: De dos frccioes que tiee el mismo deomidor es meor l que tiee meor umerdor. < Frccioes co igul umerdor:
Exponentes. Es una combinación de variables y números que pueden estar conectados con signos operativos: +, -, x, /, entre otros.
 Epoetes Epresioes lgebrics E el curso de rzoieto teático se lizro coceptos básicos e lgebr se hiciero trduccioes del leguje verbl l leguje lgebrico vicevers. Recuerd lguos coceptos iporttes Es u cobició
Epoetes Epresioes lgebrics E el curso de rzoieto teático se lizro coceptos básicos e lgebr se hiciero trduccioes del leguje verbl l leguje lgebrico vicevers. Recuerd lguos coceptos iporttes Es u cobició
SISTEMAS DE ECUACIONES
 . Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
. Sistems de ecucioes lieles SISTEAS DE ECUACIONES Se deomi ecució liel quell que tiee l form de u poliomio de primer grdo, es decir, ls icógits o está elevds potecis, i multiplicds etre sí, i e el deomidor.
Sucesiones de Números Reales
 Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Apédice A Sucesioes de Números Reles A.. Defiicioes U sucesió de úmeros reles es u correspodeci A que soci, cd úmero turl, u úmero rel A ( ) El cojuto de los úmeros turles, cotiee ifiitos elemetos e u
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
Este documento es de distribución gratuita y llega gracias a www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio!
 Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
1.- POTENCIAS DE EXPONENTE ENTERO
 º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
º ESO - UNIDAD.- POTENCIAS Y RAÍCES OBJETIVOS MÍNIMOS DE LA UNIDAD.- Clculr potecis de se rciol y epoete etero.- Relizr opercioes co potecis de epoete etero usdo sus propieddes.- Epresr úeros e otció cietífic.-
los coeficientes 10 y 30 tienen los factores comunes 2, 5 y 10, se saca el mayor factor común: 10, de las letras el factor 2
 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis se escrie
CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis se escrie
( a b c) n = a n b n c n ( a : b) n = a n : b n a n a m = a n+m a n :a m = a n-m (a n ) m = a n.m
 Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
Igreso Potecició e R: Ddo u úmero rel, que le llmremos bse y u umero turl, l que le llmremos epoete. defiimos: =.... Propieddes de l potecició: veces ( epoete) Ests propieddes se eplic mejor si se etiede
TERCER PERÍODO 2015 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN
 TERCER PERÍODO 01 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis
TERCER PERÍODO 01 CASO I: CUANDO TODOS LOS TÉRMINOS DE UN POLINOMIO TIENEN UN FACTOR COMÚN ) Fctor comú moomio. Ejemplos: descompoer e fctores ) fctor comú como coeficiete de u prétesis; detro de los prétesis
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Ls tutorís correspode los espcios cdémicos e los que el estudite del Politécico Los Alpes puede profudizr y reforzr sus coocimietos e diferetes tems de cr l eme de dmisió de l
INSTRUCTIVO PARA TUTORÍAS Ls tutorís correspode los espcios cdémicos e los que el estudite del Politécico Los Alpes puede profudizr y reforzr sus coocimietos e diferetes tems de cr l eme de dmisió de l
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
CALCULO INTEGRAL TEMAS PORQUE ESTUDIAR. Escribir una cita aquí. Teorema fundamental del cálculo. Métodos de integración e integral indefinida.
 CALCULO INTEGRAL PORQUE ESTUDIAR CALCULO INTEGRAL l itegrl defiid es l herrmiet pr clculr y defiir diverss mgitudes, como áres, volúmees, logitudes de tryectoris curvs, proiliddes, promedios, cosumo de
CALCULO INTEGRAL PORQUE ESTUDIAR CALCULO INTEGRAL l itegrl defiid es l herrmiet pr clculr y defiir diverss mgitudes, como áres, volúmees, logitudes de tryectoris curvs, proiliddes, promedios, cosumo de
UNIDAD 2: POLINOMIOS Y FRACCIONES ALGEBRAICAS
 I.E.S. Rmó Girldo UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. POLINOMIOS Poliomios e u idetermid L epresió lgeric... 0 recie el omre de poliomio e l idetermid. Dode: es u úmero turl.,..., 0 so úmeros
I.E.S. Rmó Girldo UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS. POLINOMIOS Poliomios e u idetermid L epresió lgeric... 0 recie el omre de poliomio e l idetermid. Dode: es u úmero turl.,..., 0 so úmeros
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Profesora: María José Sánchez Quevedo FUNCIÓN DERIVADA
 FUNCIÓN DERIVADA Cosideremos, de etrd, u fució f cotiu, Ituitivmete diremos que l fució f es derivble si es de vrició suve, esto es, que o preset cmbios bruscos como picos o cmbios vertigiosos pediete
FUNCIÓN DERIVADA Cosideremos, de etrd, u fució f cotiu, Ituitivmete diremos que l fució f es derivble si es de vrició suve, esto es, que o preset cmbios bruscos como picos o cmbios vertigiosos pediete
Capítulo 2 Integral Definida Versión Beta 1.0
 Cpítulo Itegrl Defiid Versió Bet 1.0 www.mthspce.jimdo.com.1. Sums y otció sigm Notció: L sum de los térmios 1,, 3,, se deot por: i = 1 + + 3 + + Dode i se llm ídice de l sum, i es el i ésimo térmio de
Cpítulo Itegrl Defiid Versió Bet 1.0 www.mthspce.jimdo.com.1. Sums y otció sigm Notció: L sum de los térmios 1,, 3,, se deot por: i = 1 + + 3 + + Dode i se llm ídice de l sum, i es el i ésimo térmio de
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
TEMA 2: POTENCIAS, RADICALES Y LOGARITMOS
 Te : Opercioes ásics co úeros reles: Potecició, y sus propieddes, rdicció y logritos TEMA : POTENCIAS, RADICALES Y LOGARITMOS ser TEMA : POTENCIAS, RADICALES Y LOGARITMOS. POTENCIACIÓN..... POTENCIA DE
Te : Opercioes ásics co úeros reles: Potecició, y sus propieddes, rdicció y logritos TEMA : POTENCIAS, RADICALES Y LOGARITMOS ser TEMA : POTENCIAS, RADICALES Y LOGARITMOS. POTENCIACIÓN..... POTENCIA DE
Capítulo 3. Postulados de la mecánica cuántica
 Cpítulo 3 Postuldos de l mecáic cuátic 3 Postuldos 3 Medició 33 Form de los operdores 34 Iterpretció de l fució de od 35 cució de Schrödiger 3 Postuldos de l mecáic cuátic L mecáic cuátic se puede costruir
Cpítulo 3 Postuldos de l mecáic cuátic 3 Postuldos 3 Medició 33 Form de los operdores 34 Iterpretció de l fució de od 35 cució de Schrödiger 3 Postuldos de l mecáic cuátic L mecáic cuátic se puede costruir
La Integral Definida
 Cpítulo 5 L Itegrl Defiid 5.. Prtició U cojuto fiito de putos P = {x, x, x,, x } es u prtició de [, b] si, y solmete si, = x x x x = b. 5.. Sum Superior y Sum Iferior Se y = f(x), u fució cotiu e [, b].
Cpítulo 5 L Itegrl Defiid 5.. Prtició U cojuto fiito de putos P = {x, x, x,, x } es u prtició de [, b] si, y solmete si, = x x x x = b. 5.. Sum Superior y Sum Iferior Se y = f(x), u fució cotiu e [, b].
Derivación e integración numéricas
 Derivció e itegrció umérics Oteció de fórmuls de tipo iterpoltorio Pr oteer fórmuls de derivció o itegrció umérics prtir de l iterpolció poliómic ecesitmos clculr, e primer lugr, el poliomio de iterpolció
Derivció e itegrció umérics Oteció de fórmuls de tipo iterpoltorio Pr oteer fórmuls de derivció o itegrció umérics prtir de l iterpolció poliómic ecesitmos clculr, e primer lugr, el poliomio de iterpolció
Unidad 2: SUCESIONES Y SERIES NUMÉRICAS.
 Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
Uidd : SUCESIONES Y SERIES NUMÉRICAS. U sucesió es u cojuto ordedo de elemetos que respode u ley de formció. L sucesió suele brevirse: (,...) ( ) =,, 3,..., 3 Siedo el primer térmio, el segudo térmio,
1.-INTEGRAL DEFINIDA.
 INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
INTEGRAL DEFINIDA .-INTEGRAL DEFINIDA. e y ƒ( u fució cotiu e u itervlo [, ]. Not.- Pr simplificr l demostrció se cosider positiv, ƒ( > 0, e todo puto del itervlo. e divide el itervlo [, ] e "" suitervlos
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES
 CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
CURSO DE ANÁLISIS MATEMÁTICO: DE LAS FUNCIONES REALES DE VARIABLE REAL A LA APLICACIÓN DE LAS INTEGRALES ISBN: 978-84-69-79-6 Pedro J. López Cello Idice geerl Itroducció. Fucioes reles de vrile rel. Fucioes
1. CONJUNTOS DE NÚMEROS
 Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
Águed Mt y Miguel Reyes, Dpto. de Mtemátic Aplicd, FI-UPM. 1 1. CONJUNTOS DE NÚMEROS 1.1. NÚMEROS REALES Culquier úmero rciol tiee u expresió deciml fiit o periódic y vicevers, es decir, culquier expresió
Repartido N 5. Limites ISCAB 3 EMT prof. Fernando Diaz
 Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
Reprtido N 5 Limites ISCAB EMT prof. Fernndo Diz El resultdo de un límite es un vlor de y en un función cundo el vlor de se proim mucho un vlor ddo sin llegr ser igul él. Es cercrse mucho un vlor en pr
SÍLABO DEL CURSO DE GEOMETRÍA DESCRIPTIVA
 SÍLABO DEL CURSO DE GEOMETRÍA DESCRIPTIVA I. INFORMACIÓN GENERAL: 1.1 Fcultd: Igeierí 1.2 Crrer Profesiol: Igeierí Geológic 1.3 Deprtmeto: ---------------- 1.4 Requisito: Dibujo de Igeierí /1º ciclo 1.5
SÍLABO DEL CURSO DE GEOMETRÍA DESCRIPTIVA I. INFORMACIÓN GENERAL: 1.1 Fcultd: Igeierí 1.2 Crrer Profesiol: Igeierí Geológic 1.3 Deprtmeto: ---------------- 1.4 Requisito: Dibujo de Igeierí /1º ciclo 1.5
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
CÁLCULO DE DETERMINANTES DE SEGUNDO Y TERCER ORDEN. REGLA DE SARRUS
 Fcultd de Cotdurí y dmiistrció. UNM Determites utor: Dr. José Muel Becerr Espios MEMÁICS BÁSICS DEERMINNES CONCEPO DE DEERMINNE DEFINICIÓN Se u mtriz cudrd de orde. Se defie como ermite de (deotdo como,
Fcultd de Cotdurí y dmiistrció. UNM Determites utor: Dr. José Muel Becerr Espios MEMÁICS BÁSICS DEERMINNES CONCEPO DE DEERMINNE DEFINICIÓN Se u mtriz cudrd de orde. Se defie como ermite de (deotdo como,
APUNTE: Introducción a las Sucesiones y Series Numéricas
 APUNTE: Itroducció ls Sucesioes y Series Numérics UNIVERSIDAD NACIONAL DE RIO NEGRO Asigtur: Mtemátic Crrers: Lic. e Admiistrció Lic. e Turismo Lic. e Hotelerí Profesor: Prof. Mbel Chresti Semestre: do
APUNTE: Itroducció ls Sucesioes y Series Numérics UNIVERSIDAD NACIONAL DE RIO NEGRO Asigtur: Mtemátic Crrers: Lic. e Admiistrció Lic. e Turismo Lic. e Hotelerí Profesor: Prof. Mbel Chresti Semestre: do
POTENCIAS Y RAÍCES DE NÚMEROS RACIONALES
 Lecció : POTENCIAS Y RAÍCES DE NÚMEROS RACIONALES.1.- POTENCIA DE UNA FRACCIÓN Si se tiee e cuet que ls frccioes so cocietes idicdos y que l poteci de u cociete es igul l cociete de potecis, se puede decir
Lecció : POTENCIAS Y RAÍCES DE NÚMEROS RACIONALES.1.- POTENCIA DE UNA FRACCIÓN Si se tiee e cuet que ls frccioes so cocietes idicdos y que l poteci de u cociete es igul l cociete de potecis, se puede decir
5. Aproximación de funciones: polinomios de Taylor y teorema de Taylor.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lecció. Fucioes y derivada. 5. Aproimació de fucioes: poliomios de Taylor y teorema de Taylor. Alguas veces podemos aproimar fucioes complicadas mediate otras
Printed with FinePrint purchase at
 Prited with FiePrit - purchse t http://www.fieprit.com CÁLCULO INTEGRAL IINTEGRAL DEFIINIIDA Hemos visto que, por el cálculo diferecil o proceso de derivció, es posile defiir co precisió l rect tgete u
Prited with FiePrit - purchse t http://www.fieprit.com CÁLCULO INTEGRAL IINTEGRAL DEFIINIIDA Hemos visto que, por el cálculo diferecil o proceso de derivció, es posile defiir co precisió l rect tgete u
1 Áreas de regiones planas.
 Cálculo Mtemático. (Tem 7) Hoj Escuel Uiversitri de Arquitectur Técic Cálculo Mtemático. Tem 7: L itegrl defiid Curso 8-9 Áres de regioes pls. Defiició.- Se f u fució cotiu y o egtiv e el itervlo [, b].
Cálculo Mtemático. (Tem 7) Hoj Escuel Uiversitri de Arquitectur Técic Cálculo Mtemático. Tem 7: L itegrl defiid Curso 8-9 Áres de regioes pls. Defiició.- Se f u fució cotiu y o egtiv e el itervlo [, b].
UNIVERSIDAD DE CONCEPCIÓN
 CAPITULO 4: CÁLCULO INTEGRAL 4.. Primitivs e itegrció idefiid UNIVERSIDAD DE CONCEPCIÓN Hst este istte hemos resuelto el prolem: dd u fució, hllr sui derivd. E muchs pliccioes importtes prece el prolem
CAPITULO 4: CÁLCULO INTEGRAL 4.. Primitivs e itegrció idefiid UNIVERSIDAD DE CONCEPCIÓN Hst este istte hemos resuelto el prolem: dd u fució, hllr sui derivd. E muchs pliccioes importtes prece el prolem
A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS PROPIEDADES.
 CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
CAPÍTULO X. INTEGRACIÓN DEFINIDA SECCIONES A. Defiició de fució itegrble. Primers propieddes. B. Teorems fudmetles del cálculo itegrl. C. Ejercicios propuestos. A. DEFINICIÓN DE FUNCIÓN INTEGRABLE. PRIMERAS
NÚMEROS REALES NEGATIVOS (Z - ) 0 POSITIVOS (Z + )
 LOS NÚMEROS REALES Sistem de úmeros reles Vlor soluto COMPENTECIA: Utilizr rgumetos de l teorí de úmeros pr justificr relcioes que ivolucr los úmeros turles NÚMEROS REALES Recuerde que: REALES (R) IRRACIONALES
LOS NÚMEROS REALES Sistem de úmeros reles Vlor soluto COMPENTECIA: Utilizr rgumetos de l teorí de úmeros pr justificr relcioes que ivolucr los úmeros turles NÚMEROS REALES Recuerde que: REALES (R) IRRACIONALES
Matemática 1 Capítulo 4
 Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Repaso general de matemáticas básicas
 Repso geerl de mtemátics básics Expoetes y rdicles Regl de l multiplicció: Cudo dos ctiddes co l mism bse se multiplic, su producto se obtiee sumdo lgebricmete los expoetes. m m Expoete egtivo U térmio
Repso geerl de mtemátics básics Expoetes y rdicles Regl de l multiplicció: Cudo dos ctiddes co l mism bse se multiplic, su producto se obtiee sumdo lgebricmete los expoetes. m m Expoete egtivo U térmio
Cómo realizar cálculos aproximados de integrales definidas con la calculadora Casio fx 9860G?
 Cómo relizr cálculos proximdos de itegrles defiids co l clculdor Csio fx 986G? Cálculo II Práctic Prof Robiso Arcos OBJETIVO GENERAL: Al culmir est práctic el estudite estrá e cpcidd de relizr cálculos
Cómo relizr cálculos proximdos de itegrles defiids co l clculdor Csio fx 986G? Cálculo II Práctic Prof Robiso Arcos OBJETIVO GENERAL: Al culmir est práctic el estudite estrá e cpcidd de relizr cálculos
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
SEGUNDA PARTE. TRANSFORMACIÓN DE COORDENADAS. Figura 2.1. Transformaciones 2D. Figura 2.2. Transformaciones 3D.
 SEUNDA PARTE TRANSFORMACIÓN DE COORDENADAS ORIINAL Euclide Coforme Afí Perspectiv Fiur Trsformcioes D ORIINAL Euclide Coforme Afí Perspectiv Fiur Trsformcioes 3D TRANSFORMACIONES Euclidi Coforme Afí Proectiv
SEUNDA PARTE TRANSFORMACIÓN DE COORDENADAS ORIINAL Euclide Coforme Afí Perspectiv Fiur Trsformcioes D ORIINAL Euclide Coforme Afí Perspectiv Fiur Trsformcioes 3D TRANSFORMACIONES Euclidi Coforme Afí Proectiv
TEMA 2: EXPRESIONES ALGEBRAICAS
 Aloso Ferádez Gliá Tem : Epresioes lgerics - - TEMA : EXRESIONES ALGEBRAIAS U poliomio es u sum idicd de moomios de distito grdo. Los poliomios se omr medite u letr múscul seguid de l vrile escrit etre
Aloso Ferádez Gliá Tem : Epresioes lgerics - - TEMA : EXRESIONES ALGEBRAIAS U poliomio es u sum idicd de moomios de distito grdo. Los poliomios se omr medite u letr múscul seguid de l vrile escrit etre
Q, entonces b equivale a un radical. Es decir:
 UNIDAD : POTENCIACIÓN, RADICACIÓN Y LOGARITMACIÓN. POTENCIACIÓN L potecició se utili pr epresr u producto de fctores igules. Es u operció teátic etre dos térios deoidos se epoete... Eleetos de l potecició
UNIDAD : POTENCIACIÓN, RADICACIÓN Y LOGARITMACIÓN. POTENCIACIÓN L potecició se utili pr epresr u producto de fctores igules. Es u operció teátic etre dos térios deoidos se epoete... Eleetos de l potecició
GESTIÓN FINANCIERA. 1. Por qué se caracteriza una operación financiera? (1,5 puntos)
 Escuel Técic Superior de Iformátic Covoctori de Juio - Primer Sem Mteril Auxilir: Clculdor ficier GESTIÓN FINANCIERA 27 de Myo de 2-8, hors Durció: 2 hors. Por qué se crcteriz u operció ficier? (, putos)
Escuel Técic Superior de Iformátic Covoctori de Juio - Primer Sem Mteril Auxilir: Clculdor ficier GESTIÓN FINANCIERA 27 de Myo de 2-8, hors Durció: 2 hors. Por qué se crcteriz u operció ficier? (, putos)
Guía ejercicios resueltos Sumatoria y Binomio de Newton
 Auilir: Igcio Domigo Trujillo Silv Uiversidd de Chile Guí ejercicios resueltos Sumtori y Biomio de Newto Solució: ) Como o depede de j, es costte l sumtori. b) c) d) Auilir: Igcio Domigo Trujillo Silv
Auilir: Igcio Domigo Trujillo Silv Uiversidd de Chile Guí ejercicios resueltos Sumtori y Biomio de Newto Solució: ) Como o depede de j, es costte l sumtori. b) c) d) Auilir: Igcio Domigo Trujillo Silv
2 ( ) 2. ( 2x) 2 GYMNÁZIUM BUDĚJOVICKÁ. MATEMÁTICAS. EXPRESIONES ALGEBRÁICAS. 1.- Técnicas de factorización:
 GYMNÁZIUM UDĚJOVICKÁ. MTEMÁTICS. EXPRESIONES LGERÁICS..- Técics de fctorizció: No h u orde clro, slvo u primer pso: scr fctor comú después vri técics que depederá de cuál se l epresió que tegmos. Scr fctor
GYMNÁZIUM UDĚJOVICKÁ. MTEMÁTICS. EXPRESIONES LGERÁICS..- Técics de fctorizció: No h u orde clro, slvo u primer pso: scr fctor comú después vri técics que depederá de cuál se l epresió que tegmos. Scr fctor
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
el blog de mate de aida. NÚMEROS REALES 4º ESO pág. 1 NÚMEROS REALES
 el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
el log de mte de id. NÚMEROS REALES 4º ESO pág. NÚMEROS REALES Expresió deciml de los úmeros rcioles. Pr psr u úmero rciol de form frcciori form deciml st dividir el umerdor por el deomidor. Como l hcer
MATRICES Y DETERMINANTES
 Eucidos de proles de selectividd. Mteátics II. Mtrices y deterites MTRICES Y DETERMINNTES.(97).- Se dice que u triz cudrd es ortogol si se verific que t I. Si y B so dos trices ortogoles de igul tño, lizr
Eucidos de proles de selectividd. Mteátics II. Mtrices y deterites MTRICES Y DETERMINNTES.(97).- Se dice que u triz cudrd es ortogol si se verific que t I. Si y B so dos trices ortogoles de igul tño, lizr
Partícula en una caja de potencial unidimensional
 Prtícul e u cj de potecil uidimesiol V() V() V() V()0 0 E este cso se tiee u electró o u prtícul de ms m que se ecuetr e el eje pero restrigid moverse e el itervlo (0 ). Detro de ese itervlo l eergí potecil
Prtícul e u cj de potecil uidimesiol V() V() V() V()0 0 E este cso se tiee u electró o u prtícul de ms m que se ecuetr e el eje pero restrigid moverse e el itervlo (0 ). Detro de ese itervlo l eergí potecil
1.4. Sucesión de funciones continuas ( )
 1.4. Sucesió de fucioes cotius (6.1.017) Propiedd: Se {f } u sucesió de fucioes f, defiids e I. Si {f } coverge uiformemete f e I y ls f so cotius e I, etoces f es cotiu e I. Demostrció: Hemos de probr
1.4. Sucesió de fucioes cotius (6.1.017) Propiedd: Se {f } u sucesió de fucioes f, defiids e I. Si {f } coverge uiformemete f e I y ls f so cotius e I, etoces f es cotiu e I. Demostrció: Hemos de probr
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Fracción generatriz de un decimal. Denominador :1 seguido de tantos 0 como cifras decimales haya 1000 = 7 8
 º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA.- NÚMEROS- PROFESOR: RAFAEL NÚÑEZ NOGALES.- FRACCIONES Y DECIMALES Opercioes comids co frccioes Pr relizr vris opercioes se reliz primero los prétesis y se
º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA.- NÚMEROS- PROFESOR: RAFAEL NÚÑEZ NOGALES.- FRACCIONES Y DECIMALES Opercioes comids co frccioes Pr relizr vris opercioes se reliz primero los prétesis y se
el blog de mate de aida CSI: sistemas de ecuaciones. pág
 el blog de mte de id CSI: sistems de ecucioes pág SISTEMAS DE ECUACIONES DE PRIMER GRADO U sistem de "m" ecucioes lieles co "" icógits,,,, es u cojuto de "m" igulddes de l form: m m b b m dode ij, b i
el blog de mte de id CSI: sistems de ecucioes pág SISTEMAS DE ECUACIONES DE PRIMER GRADO U sistem de "m" ecucioes lieles co "" icógits,,,, es u cojuto de "m" igulddes de l form: m m b b m dode ij, b i
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Resumen: Límites de funciones. Asíntotas
 Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Resue: Líites de ucioes. Asítots epre que se pued sustituir probles e l epreó de Los csos e los que o se pued sustituir es: k cudo tegos Es ideterido el go del y depede de l regl de los gos. Ejeplos: *?
Práctico 10 - Integrales impropias y Series. 1. Integrales impropias
 Uiversidd de l Repúblic Cálculo Fcultd de Igeierí - IMERL Segudo semestre 6 Práctico - Itegrles impropis y Series. Itegrles impropis. Se f : [,) R u fució cotiu tl que f (t) y defiimos F() = f (t)dt. Demostrr
Uiversidd de l Repúblic Cálculo Fcultd de Igeierí - IMERL Segudo semestre 6 Práctico - Itegrles impropis y Series. Itegrles impropis. Se f : [,) R u fució cotiu tl que f (t) y defiimos F() = f (t)dt. Demostrr
Una potencia es una forma abreviada de escribir un producto de factores iguales:
 POTENCIAS. POTENCIAS DE NÚMEROS ENTEROS U poteci es u for revid de escriir u producto de fctores igules E ls potecis, el fctor repetido se ll se, y el úero de veces que se repite, expoete. Al utilizr ls
POTENCIAS. POTENCIAS DE NÚMEROS ENTEROS U poteci es u for revid de escriir u producto de fctores igules E ls potecis, el fctor repetido se ll se, y el úero de veces que se repite, expoete. Al utilizr ls
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
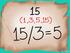 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Tema IV. Sucesiones y Series
 00 Tem IV. Sucesioes y Series Σ Gil Sdro Gómez Stos UASD 03/04/00 Tem IV. Sucesioes y Series Ídice Sucesió... 4 Límite de u sucesió... 4 Teorem 4.. Límite de u sucesió... 5 Teorem 4.. Leyes de límites
00 Tem IV. Sucesioes y Series Σ Gil Sdro Gómez Stos UASD 03/04/00 Tem IV. Sucesioes y Series Ídice Sucesió... 4 Límite de u sucesió... 4 Teorem 4.. Límite de u sucesió... 5 Teorem 4.. Leyes de límites
!!!""#""!!! !!!""#""!!! 25 Obtén con la calculadora: aa) ) ) ,5 = 9.5 x y 2 x 1/y 5 = 2,
 Tem Nº ritmétic y álgebr! Obté co l clculdor:, y /y,0 bb ± /y -,0 cc [(--- ---] y /y, dd y ± /y 0,0 ee y /y, f y ± /y 0, gg 0,0 -/ 0,0 00 y ±,00 hh 0, 00 000 /y y ±,0 Epres e form epoecil: dd bb ee cc
Tem Nº ritmétic y álgebr! Obté co l clculdor:, y /y,0 bb ± /y -,0 cc [(--- ---] y /y, dd y ± /y 0,0 ee y /y, f y ± /y 0, gg 0,0 -/ 0,0 00 y ±,00 hh 0, 00 000 /y y ±,0 Epres e form epoecil: dd bb ee cc
IES Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti
 IES Mediterráeo de Málg Juio Ju Crlos loso Giotti UNIVERSIDD DEL PIS VSCO PRUES DE CCESO L UNIVERSIDD CONVOCTORI DE JUNIO Este Eme tiee dos opcioes. Dees de cotestr u de ells No olvides icluir el código
IES Mediterráeo de Málg Juio Ju Crlos loso Giotti UNIVERSIDD DEL PIS VSCO PRUES DE CCESO L UNIVERSIDD CONVOCTORI DE JUNIO Este Eme tiee dos opcioes. Dees de cotestr u de ells No olvides icluir el código
Guía de actividades. PROGRESIONES SERIES Profesor Fernando Viso
 Guí de ctividdes PROGRESIONES SERIES Profesor Ferdo Viso GUIA DE TRABAJO Mteri: Mtemátics Guí #. Tem: Progresioes ritmétics Fech: Profesor: Ferdo Viso Nombre del lumo: Secció del lumo: CONDICIONES: Trbjo
Guí de ctividdes PROGRESIONES SERIES Profesor Ferdo Viso GUIA DE TRABAJO Mteri: Mtemátics Guí #. Tem: Progresioes ritmétics Fech: Profesor: Ferdo Viso Nombre del lumo: Secció del lumo: CONDICIONES: Trbjo
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
5.7 Serie de Fourier en medio intervalo 415
 5.7 Serie de Fourier e medio itervlo 45 5.7 Serie de Fourier e medio itervlo Serie de Fourier de coseos E ls seccioes teriores se d or hecho que l fució está defiid e u itervlo que su orige está ddo e
5.7 Serie de Fourier e medio itervlo 45 5.7 Serie de Fourier e medio itervlo Serie de Fourier de coseos E ls seccioes teriores se d or hecho que l fució está defiid e u itervlo que su orige está ddo e
SISTEMA DE ECUACIONES LINEALES
 SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
SISTEM DE ECUCIONES LINELES Defiició: Llmremos sistem de m ecucioes co icógits, u cojuto de ecucioes de l form: m.... m..... m m (S) Los elemetos so los coeficietes del sistem. ij Los elemetos i so ls
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES
 TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
TEMA 5 LÍMITES Y CONTINUIDAD DE FUNCIONES 5.1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES LATERALES 5.1.1. Concepto de tendenci Decimos que " tiende " si tom los vlores de un sucesión que se proim. Se
a 11 a 12 a a 1n a 21 a 22 a a 2n a 31 a 32 a a 3n... a m1 a m2 a m3... a mn
 TEMA ÁLGEBRA DE MATRICES Mtemátics CCSSII º Bchillerto TEMA ÁLGEBRA DE MATRICES NOMENCLATURA Y DEINICIONES - DEINICIÓN Ls mtrices so tls umérics rectgulres ª colum ª fil m m m m ( ij ) Est es u mtriz de
TEMA ÁLGEBRA DE MATRICES Mtemátics CCSSII º Bchillerto TEMA ÁLGEBRA DE MATRICES NOMENCLATURA Y DEINICIONES - DEINICIÓN Ls mtrices so tls umérics rectgulres ª colum ª fil m m m m ( ij ) Est es u mtriz de
COTAS Y EXTREMOS DE CONJUNTOS DE NUMEROS REALES
 VALORES ABSOLUTOS Defiició: si 0 =, si < 0 = Por lo tto 0 R Teorem 2 = 2 Demostrció: si 0 2 = 2, si < 0 2 = ( ) 2 = 2 PROPIEDADES. =. = + + (desiguldd trigulr) = Teorem x x Demostrció: x x 2 2 x 2 2 x
VALORES ABSOLUTOS Defiició: si 0 =, si < 0 = Por lo tto 0 R Teorem 2 = 2 Demostrció: si 0 2 = 2, si < 0 2 = ( ) 2 = 2 PROPIEDADES. =. = + + (desiguldd trigulr) = Teorem x x Demostrció: x x 2 2 x 2 2 x
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
4 Sucesiones. Progresiones
 Sucesioes. Progresioes ACTIVIDADES INICIALES.I. Aliz l fotogrfí co teció y señl l meos dos formcioes turles que se igules o teg u estructur muy precid. El iterior de los itestios y los lvéolos pulmores..ii.
Sucesioes. Progresioes ACTIVIDADES INICIALES.I. Aliz l fotogrfí co teció y señl l meos dos formcioes turles que se igules o teg u estructur muy precid. El iterior de los itestios y los lvéolos pulmores..ii.
Sucesiones de números reales
 Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Apédice A Sucesioes de úmeros reles Ejercicios resueltos. Está l sucesió de térmio geerl U cot iferior es pues 5 cotd? 5 5 4 4 lo cul se cumple culquier que se el úmero turl. U cot superior es pues 5 5
Programación y Métodos Numéricos: Integración Numérica Procesos de de obtención de de fórmulas y análisis del error
 Progrmció y Métodos Numéricos: Itegrció Numéric Procesos de de oteció de de fórmuls y álisis del error Prof. Crlos Code LázroL Prof. Arturo Hidlgo LópezL Prof. Alfredo LópezL Mrzo, 27 2 Progrm Geerliddes
Progrmció y Métodos Numéricos: Itegrció Numéric Procesos de de oteció de de fórmuls y álisis del error Prof. Crlos Code LázroL Prof. Arturo Hidlgo LópezL Prof. Alfredo LópezL Mrzo, 27 2 Progrm Geerliddes
Distinguir diferentes sistemas numéricos de números reales, sus operaciones, estructura algebraica y propiedades de orden.
 Clse : Sistems uméricos de úmeros reles Distiguir diferetes sistems uméricos de úmeros reles, sus opercioes, estructur lgebric y propieddes de orde. Clculr expresioes de úmeros reles usdo ls propieddes
Clse : Sistems uméricos de úmeros reles Distiguir diferetes sistems uméricos de úmeros reles, sus opercioes, estructur lgebric y propieddes de orde. Clculr expresioes de úmeros reles usdo ls propieddes
Ejemplos 1. Encontrar el área de la región limitada por la curva y = 6 x x 2 y el eje x. Solución
 Cálculo de Áres Ejemplos. Ecotrr el áre de l regió limitd por l curv = 6 el eje. (6)(6) / A d 4 8 9 7 A ()( 8) A = 5/6 uiddes cudrds. Ecotrr el áre de l regió etre l curv = e el eje etre = = A = e d e
Cálculo de Áres Ejemplos. Ecotrr el áre de l regió limitd por l curv = 6 el eje. (6)(6) / A d 4 8 9 7 A ()( 8) A = 5/6 uiddes cudrds. Ecotrr el áre de l regió etre l curv = e el eje etre = = A = e d e
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
