FENÓMENOS ISOPÍCNICOS Y BAROTRÓPICOS: TENSIÓN INTERFACIAL, SIMULACIÓN MOLECULAR EN MEZCLAS BINARIAS Y EXTENSIÓN A SISTEMAS TERNARIOS

Transcripción

1 Universidad de Concepción Facultad de Ingeniería Departamento de Ingeniería Química FENÓMENOS ISOPÍCNICOS Y BAROTRÓPICOS: TENSIÓN INTERFACIAL, SIMULACIÓN MOLECULAR EN MEZCLAS BINARIAS Y EXTENSIÓN A SISTEMAS TERNARIOS María José Tardón Sepúlveda Tesis presentada a la Escuela de Graduados de la Universidad de Concepción para optar al grado de Doctor en Ciencias de la Ingeniería con mención en Ingeniería Química Concepción, Chile, Noviembre de 2012 Comisión Evaluadora: Dr. Andrés Mejía Matallana Profesor Guía: Dr. Hugo Segura Gómez Dr. Marcelo Zabaloy

2 A mis padres y a mi hijo, símbolos de transición de vida, de apoyo, de fuerza y de alegría. A mis amigos incondicionales. A la vida.

3 Esta Tesis Doctoral ha sido posible gracias al apoyo financiero de la Comisión Nacional de Ciencia y Tecnología- CONICYT-, Chile.

4 Prefacio Esta tesis se presenta como parte del cumplimiento de los requisitos para la obtención del grado académico de Doctor en Ciencias de la Ingeniería con mención en Ingeniería Química en la Universidad de Concepción, Concepción, Chile. El proyecto ha sido financiado por la Comisión Nacional de Ciencia y Tecnología (CONICYT). El trabajo presentado en esta tesis se ha llevado a cabo entre Agosto de 2009 a Diciembre de 2011 en el seno del grupo de investigación de equilibrio de fases e interfases en el Departamento de Ingeniería Química. El trabajo ha sido supervisado en una primera etapa por el Profesor Hugo Segura Gómez y el Profesor Andrés Mejía Matallana, y en una segunda fase por el Profesor asociado Marcelo Zabaloy. La realización de esta tesis, tal como se ha señalado es un producto que se gestó hace dos años y un poco más. Inició como una extensión a partir de la visión de trabajo futuro de la memoria de título de Ingeniero Civil Químico, titulada: Fenómenos barotrópicos e isopícnicos en mezclas binarias. La propuesta que originalmente abordada el proyecto de tesis, conformaba ambiciosamente medición experimental y correlación teórica, predicción de propiedades interfaciales a partir de data experimental y contraste mediante simulación molecular, fue acotada a los tiempos de realización como una investigación teórica. En un principio, mis ideas a realizar una tesis que involucrase extender los principios transicionales determinados en mi trabajo de memoria de título y caracterizar el comportamiento desde un punto de vista interfacial, fueron románticas. Enamorada del fenómeno de la inversión molar, cada día encontraba nuevas características. Cada sistema analizado era distinto al siguiente y al anterior. Invertía tiempo en completar diagramas y analizar exhaustivamente un rango de aplicación conforme a encontrar nuevos mecanismos, semejanzas y diferencias y vinculaciones a diferentes procesos. Recuerdos nostálgicos de muchas y largas pruebas de programaciones, que en un principio y como siempre me sucedió no estuvieron exentos de errores, que me hicieron perder la razón y cuyas mejoras dieron paso a esa sonrisa de satisfacción y origen a las más bellas gráficas. IV

5 Si bien, toda la belleza de aquello, me animaban a seguir estudiando, analizando y describiendo, de pronto me di cuenta que si no acotaba podría terminar siendo románticamente abrumadora nuestra relación. Así que finalmente, la investigación relaciona y extiende el mecanismo críticos de ocurrencia de la fenomenología a mezcla multicomponentes, a partir del análisis descriptivo de 7 mezclas ternarias y la descripción cualitativa de propiedades interfaciales de mezclas binarias tipo II, III, IV y V mediante un modelo sencillo de ecuación de estado y validación de resultados posteriormente, con un modelo más sofisticado acoplando además, la simulación molecular. Agradezco la paciencia de aquellos, que han esperando con ansias conocer el resultado de lo que he investigado durante un poco más de dos años. LEY MÁXIMA DE MANLY La Lógica es un método sistemático para llegar con absoluta certeza a la conclusión equivocada. V

6 Resumen Las mezclas compuestas por CO2+hidrocarburos están asociadas a una cantidad generosa de operaciones de separación típicas de la industria de procesos químicos como la extracción fluido-fluido (en diversos rangos de presión), absorción, adsorción y destilación y donde os fenómenos interfaciales juegan un rol clave en su desempeño eficiente. Generalmente, los procesos de separación se encuentran caracterizados por bajas tensiones interfaciales entre las fases inhomogéneas líquidas-vapor o líquida-líquida, y por lo tanto la tensión interfacial es una propiedad física importante que los controla. La recuperación de gas por condensación cercana al punto crítico o la recuperación de aceites en tratamientos secundarios o terciarios mediante un agente de desplazamiento, tal como ocurre con la introducción de un solvente supercrítico como el dióxido de carbono en los procesos de separación, ha tenido muchas ventajas económicas y ambientales. Sin embargo, el desarrollo de técnicas modernas más eficientes de separación como aquellas, tiene un intrincado nexo con el comportamiento de las fases en mezcla, las que pueden desarrollar una compleja gama de comportamientos que deben tenerse en cuenta tanto en etapas preliminares, como el diseño del proceso y en etapas posteriores, como la determinación de las condiciones óptimas de operación. Una manera de predicción fiable de diferentes propiedades, condiciones y los singulares tipos de equilibrio de fases de mezclas, son las ecuaciones de estado. Modelos capacitado para predecir el equilibrio de fases de los fluidos puros, de las mezclas que estos constituyen y las propiedades termo-físicas que están vinculadas a estados fluidos homogéneos y heterogéneos. Existen numerosos métodos para determinación de propiedades interfaciales de fluidos puros y mezclas, y entre ellos destaca una teoría exitosamente aplicada para calcular la tensión superficial de mezclas binarias y ternarias y en la que se incorpora a través de un modelo de ecuación de estado, como la de van der Waals, el cálculo del equilibrio de fases y el cálculo de las propiedades interfaciales: La teoría del Gradiente. El primer objetivo de la tesis de investigación corresponde a la caracterización del fenómeno de inversión de densidad molar en condiciones de equilibrio de fases de mezclas binarias, a nivel de fase seno e interfases mediante un enfoque descriptivo muy VI

7 completo: la aplicación de la teoría del gradiente y técnicas de simulación molecular (Dinámica molecular).la descripción de los sistemas binarios se lleva a cabo mediante el cálculo de propiedades interfaciales tales como, tensión interfacial, perfiles interfaciales de concentración, espesor de interfase y transición de mojabilidad, en condiciones de temperatura y presión pre-, en y post- inversión de densidad. Como segundo objetivo, se encuentra la predicción y estudio de la fenomenología de inversión de densidad molar de sistemas ternarios, para establecer por criterio de semejanza de las condiciones matemáticas descriptivas del mecanismo de transición crítica de la inversión de densidad en sistemas binarios, una extensión a sistemas multicomponentes. El análisis del efecto de la adición de un tercer componente permite detectar la complejidad del comportamiento de inversión molar de densidad desarrollado en la mezcla ternaria, interpretados por la aparición de estados múltiples de inversión o en la desaparición de la fenomenología. Eventos que determinan la existencia de una condición necesaria detonante la inversión de densidad relacionada directamente con la naturaleza molecular de los constituyentes de una mezcla fluida, tales como la geometría molecular y las interacciones de fuerza de los componentes. El presente informe se estructura en cuatro secciones: I. Introducción: Se describe en forma detallada y vinculada a distintas áreas de la tecnología, el estado del arte del estudio y caracterización de la fenomenología de inversión de fase en mezclas. Fundamentos que constituye la motivación al trabajo de tesis. II. Fundamentos teóricos: Se entregan los conceptos y antecedentes fundamentales de sobre las ecuaciones de estado como herramientas de predicción comportamientos de equilibrios de fases. Se expresan las ecuaciones del equilibrio de fases en términos de fracción molar, temperatura y el volumen- funcionalidades de la energía de Helmholtz- y los fundamentos teóricos de la tensión interfacial y su cálculo mediante la técnica del gradiente III. Resultados: Caracterización de los sistemas con inversión de densidad molar a través del cálculo de las propiedades interfaciales mediante EOS para mezclas fluidas vdw y Lennard-Jones. Descripción y caracterización de las envolventes de densidad de sistemas ternarios, definiendo las condiciones y criterios predeterminan, inhiben y VII

8 detonan el fenómeno de inversión de fases. IV. Conclusiones y trabajo futuro: expresan las conclusiones generales del trabajo realizado y se perfila una perspectiva de desarrollo en trabajos posteriores. VIII

9 Agradecimientos Me gustaría expresar mi gratitud y mi agradecimiento a los supervisores por su inspiración y fructíferos debates de temas relacionados con esta tesis y otros no tan relacionados, pero igualmente retributivo. Destaco sentirme orgullosa el de pertenecer a un grupo de investigación tan humano. Esquema, que ha resultado en una colaboración muy productiva y exitosa. En particular, el Profesor Hugo Segura, de los conocimientos y ánimo que ha compartido y por darme la oportunidad de trabajar con él. También agradecer a Profesor Andrés Mejía por su ayuda y orientación, y obviamente para el cuidado de una gran cantidad de problemas administrativos. Estoy muy agradecida con Marcela Cartes por su valiosa asistencia y ayuda inestimable en el laboratorio. A mis colegas, Héctor Quinteros-Lama y José Matías Garrido, más conocidos como Tito y Chema, que han trabajado y ayudado, consciente e inconsciente, en contribución de esta tesis. A mis amigos de siempre y de la Universidad y a los que he conocido, donde quiera que he estado en los últimos años, a través de las ayudantías, cursos, seminarios y congresos, gracias por su paciencia y entendimiento. A la Escuela de Graduados de la Universidad de Concepción por el financiamiento otorgado durante el periodo y 2011 bajo el contexto de becas de estudio para posgrado. Por último, a mi familia por su apoyo en todas las decisiones que he tomado. LEY DE EVANS Y BJORN No importa lo que salga mal, siempre hay alguien que ya lo sabía..." IX

10 LEY DE FELSON Robar ideas a una persona es plagio. Robárselas a muchas es investigación. X

11 Tabla de Contenidos Lista de Tablas...XV Lista de Figuras... XVII Nomenclatura... XXIII Abreviaciones... XXVII Parte I: Introducción Capítulo 1. Introducción Introducción Antecedentes preliminares: una revisión de la fenomenología de inversión de fases Estado del arte en fenómenos de inversión de fases en mezclas binarias y ternarias Observación y medición experimental Modelación y predicción Modelo matemático descriptivo Presentación de la Investigación Hipótesis Contribución de ésta tesis Objetivos Objetivo General Objetivos Específicos Estructura de esta tesis Referencias Parte II: Fundamentos Teóricos Capítulo 2. Ecuaciones de Estado y termodinámica del equilibrio de fases Introducción Ecuación de estado de van der Waals Reglas cuadráticas de mezclado para vdw Ventajas y desventajas de la EOS de vdw Ecuación de estado para fluido Lennard-Jones Potencial intermolecular de Lennard-Jones Ecuación de estado para fluido Lennard-Jones Ecuación de estado de un fluido Lennard-Jones de Johnson et al Extensión del modelo de ecuación de estado de un fluido Lennard-Jones a mezclas binarias Termodinámica de equilibrio de fases Equilibrio de fases Criterios de estabilidad del equilibrio de fase Criterios del estado crítico Fenómenos críticos en mezclas binarias Fenómenos críticos en mezclas ternarias Fenómenos críticos superiores y Diagrama Global de fases Principios Transicionales XI

12 2.5.2 Algoritmos de cálculo de contornos transicionales del GPD Referencias Capítulo 3. Tensión interfacial, teoría del gradiente y simulación molecular Introducción Terminología y origen de la tensión interfacial Terminología Origen de la Tensión Interfacial Termodinámica Clásica de Interfases Energía libre y estructura de interfases Transiciones de mojabilidad en interfases fluidas Modelo de caracterización del comportamiento interfacial Ecuaciones fundamentales de GT Parámetros de influencia Transformación de coordenadas Procedimiento numérico para el cálculo de propiedades interfaciales por medio de GT Teoría de simulación molecular Potencial de interacción molecular y colectivos estadísticos Simulación molecular: Método Montecarlo (MC) y Dinámica Molecular (MD) Simulación de Dinámica Molecular (MD) Referencias Parte III: Resultados Capítulo 4. Inversión de densidad másica y molar Introducción Fenómenos de inversión: MaDI y MoDI en mezclas binarias asimétricas Descripción del comportamiento de inversión de densidad Límites de conectividad del comportamiento de inversión de densidad másica y molar Geometría de las envolventes de densidad másica y derivación del mecanismo de inversión másica Conclusiones Referencias Capítulo 5. Propiedades interfaciales basadas en la Teoría del Gradiente y la EOS vdw Introducción Detalles de la aplicación y procedimiento de cálculo Actividad interfacial y la transferencia de masa Distribución de densidad a través de la interfase Caracterización y descripción de la estructura interfacial de mezclas fluidas con inversión de densidad molar Sistema tipo II Sistema tipo III Sistema binario tipo IV Sistema binario tipo V XII

13 5.6. Puntos estacionarios y estructura interfacial en la condición de inversión de densidad molar Tensión interfacial y transiciones de mojabilidad en mezclas fluidas con inversión de densidad molar Tensión interfacial e inversión de densidad molar Transición de mojabilidad e Inversión de densidad molar Conclusiones Referencias Capítulo 6. Caracterización interfacial del comportamiento MoDI en fluidos Lennard-Jones Introducción Metodología de caracterización interfacial de sistemas binarios con inversión de densidad molar Detalle de la aplicación de la Teoría del Gradiente y la ecuación de estado JZG: GT-LJ Detalle de la aplicación de Dinámica Molecular (MD) Resultados y Análisis Caracterización interfacial de mezclas fluidas tipo Lennard-Jones basada en la teoría del gradiente: GT-LJ Propiedades interfaciales mediante dinámica molecular Discusión y Conclusiones Referencias Capítulo 7. Inversión de densidad molar en mezclas ternarias Introducción Fenómenos de inversión de densidad en mezclas ternarias Metodología de caracterización de la inversión de densidad en sistemas ternarios Efecto de la adición de un tercer componente en el comportamiento de inversión molar de una mezcla binaria: Efecto cosolvente Caracterización del equilibrio trifásico Resultados y Análisis Efecto cosolvente: Sistema 1 (I-I-III y I-II-III) Efecto cosolvente: Sistema 2 (II-III-III y II-III-VI) Efecto cosolvente: Sistema 3(III-III-IV) Efecto cosolvente Sistema 4:I-I-III y I-II-II Caracterización de la inversión de densidad molar en el equilibrio trifásico Geometría de las envolventes de densidad sistemas ternarios Conclusiones Referencias Parte IV: Conclusiones y trabajo futuro Capítulo 8. Conclusiones y trabajo futuro Conclusiones Trabajo Futuro Apéndices XIII

14 Apéndice A: Termodinámica clásica de interfases Apéndice B: Técnicas de medición de tensión interfacial Apéndice C: Coeficiente de esparcimiento XIV

15 Lista de Tablas Tabla 1.1: Estado del arte en investigación experimental de sistemas binarios con inversión de fases.. 41 Tabla 1.2: Estado del arte en investigación experimental de sistemas ternarios con inversión de fases Tabla 1.3: Estado del arte en investigación predictiva o contraste experimental con ecuaciones de estado de sistemas binarios con inversión de fases Tabla 2.1: Expresiones explícitas de la presión para modelos de ecuación de estado enmarcados en el enfoque de van der Waals [19] Tabla 2.2: Funciones de temperatura de los parámetros ai de la ecuación de estado de Johnson et al.. 85 Tabla 2.3: Funciones de temperatura de los parámetros bi de la ecuación de estado de Johnson et al.. 86 Tabla 2.4: Parámetros lineales de la ecuación de estado de Johnson et al Tabla 2.5: Coeficiente Gi dependientes de la densidad reducida para la expresión de la energía de Helmholtz de la ecuación de estado de Johnson et al Tabla 2.6: Algoritmo de cálculo de líneas críticas de sistemas ternarios Tabla 2.7 Ecuaciones fundamentales de cálculo de líneas y contornos transicionales del diagrama global de fases (GPD) Tabla 2.8 Algoritmos de cálculo de líneas y contornos transicionales del diagrama global de fases (GPD) Tabla 3.1 Tipos de colectivos estadísticos para la simulación molecular [32] Tabla 4.1: Propiedades críticas, parámetros de interacción y globales de una mezcla binaria tipo van der Waals que exhibe fenómeno de inversión de densidad molar y másica Tabla 4.2: Coordenadas del punto crítico MoDI y MaDI mezcla binaria tipo van der Waals de comportamiento global tipo III-m estudiado Tabla 5.1: Propiedades críticas, parámetros de interacción y globales de una mezcla binaria van der Waals tipo I que exhibe fenómeno de inversión de densidad molar Tabla 5.2: Condiciones de temperatura y presión de análisis de la influencia de la inversión de densidad molar en la distribución de densidad de un sistema binario tipo III Tabla 5.3: Propiedades críticas, parámetros de interacción y globales de una mezcla binaria van der Waals tipo III que exhibe fenómeno de inversión de densidad molar Tabla 5.4: Condiciones de temperatura y presión de análisis de la influencia de la inversión de densidad molar en la distribución de densidad de un sistema binario tipo III Tabla 5.5: Propiedades críticas, parámetros de interacción y globales de una mezcla binaria van der Waals tipo IV que exhibe fenómeno de inversión de densidad molar Tabla 5.6: Condiciones de temperatura y presión de análisis de la influencia de la inversión de densidad molar en la distribución de densidad de un sistema binario tipo IV Tabla 5.7: Propiedades críticas, parámetros de interacción y globales de una mezcla binaria van der Waals tipo V que exhibe fenómeno de inversión de densidad molar XV

16 Tabla 5.8: Condiciones de temperatura y presión de análisis de la influencia de la inversión de densidad molar en la distribución de densidad de un sistema binario tipo V Tabla 5.9: Condiciones de temperatura y presión del colapso de los puntos estacionarios de enriquecimiento interfacial en la condición de inversión de densidad molar Tabla 6.1: Parámetros críticos de una mezcla binaria tipo Lennard-Jones que exhibe fenómeno de inversión de densidad molar Tabla 6.2: Algoritmo de cálculo de propiedades interfaciales mediante GT en sistemas binarios Tabla 6.3: Condiciones de temperatura y presión de análisis de los perfiles de distribución de densidad de un sistema binario tipo III con GT-EOS LJ Tabla 6.4: Condiciones de análisis del comportamiento MoDI mediante MD en un sistema binario LJ tipo III Tabla 6.5: Tensión interfacial calculada mediante GT y MD para una mezcla binaria L-J tipo III que exhibe fenómeno de inversión de densidad molar Tabla 7.1: Estado del arte en investigación experimental de sistemas ternarios con inversión de fases Tabla 7.2: Clasificación en sub-sistemas binarios de una mezcla ternaria para el estudio del comportamiento MoDI Tabla 7.3: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria 1-A tipo van der Waals I-I-III que exhibe fenómeno de inversión de densidad molar Tabla 7.4: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria 1-B tipo van der Waals I-II-III que exhibe fenómeno de inversión de densidad molar en el binario tipo III Tabla 7.5: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria 2-A tipo van der Waals II-III-III que exhibe fenómeno de inversión de densidad molar en los binarios tipo III. 261 Tabla 7.6: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria 2-B tipo van der Waals II-III-IV que exhibe fenómeno de inversión de densidad molar en los binarios tipo III y IV Tabla 7.7: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria 2-A tipo van der Waals II-III-III que exhibe fenómeno de inversión de densidad molar en los binarios tipo III. 265 Tabla 7.8: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria tipo van der Waals III-III-IV que exhibe fenómeno de inversión de densidad molar en tres binarios constituyentes Tabla 7.9: Propiedades críticas, parámetros de interacción y globales de una mezcla ternaria tipo van der Waals I-II-II que exhibe fenómeno de inversión de densidad molar en tres binarios constituyentes XVI

17 Lista de Figuras Fig. 1.1: Comportamiento del equilibrio de fases para el sistema PAO+CO2 a 5 C.Inversión de densidad másica a P=40.0bar Fig. 1.2: Estructuras morfológicas de la inversión de fases mediante la interacción entre gotas Fig Diagrama de fase para la segregación o separación espinodal Fig. 1.4: Separación de fases y el fenómeno de la inversión de densidad Fig. 1.5: Esquema de proyecciones de presión y temperatura de los seis tipos de comportamiento de fase fluida en mezclas binarias de acuerdo a la clasificación de van Konynenburg y Scott Fig. 1.6: Transición esquemática de sistemas tipo II a III vía tipo IV. Evolución del equilibrio trifásico a medida que aumenta el número de carbones en la mezcla binaria CO2+n-alcano Fig. 1.7: Proyecciones Presión-Temperatura de sistemas tipo II y III ( a y b) que han sido observados en mezclas binarias de hidrocauros +agua Fig. 2.2 Desarrollo del concepto de estabilidad desde el punto mecánico de la función de Gibbs Fig. 2.3: Esquema de proyecciones de presión y temperatura de los seis tipos de comportamiento de fase fluida en mezclas binarias de acuerdo a la clasificación de van Konynenburg y Scott Fig. 2.4: Esquema de proyecciones de presión y temperatura de los sistemas binarios de comportamiento tipo VI y VII siguiendo la clasificación de van Konynenburg y Scott Fig. 2.5 Diagrama Global de fases de fluidos van der Waals para moléculas de igual diámetro Fig. 3.1: Proyección z para una interface plana en el equilibrio de fases de un fluido puro y una mezcla binaria con adsorción de una de las especies en la zona interfacial. ( ): Perfil de densidad para los componentes 1 y 2, ( ): Densidades de las fases, ( ): Punto estacionario de adsorción Fig. 3.2: Esquema de la proyección de equilibrio de fuerzas atracctivas entre las moléculas en una interface plana en el equilibrio bifásico. Contracción de la interface plana debido al desequilibro de fuerzas atractivas en la interface de contacto bifásico (fase liviana-fase pesada) Fig. 3.3: Enfoque físico-mecánico de la tensión interfacial:trabajo/área- Fuerza/longitud Fig. 3.4: Formas características de los perfiles de concentración para fluidos puros y mezclas de alcanos Fig. 3.5: Formas características de los perfiles de concentración Fig. 3.6: Proyección z para una interface plana en el equilibrio de fases que muestra la ubicación en la interfase las separación y regiones del perfil de densidad que contribuyen al valor final de la densidad en la interfases Fig. 3.7: Régimen de equilibrio trifásico Fig. 3.8: Mojabilidad y comportamiento interfacial en interfases fluidas Fig. 3.9: Sistema trifásico compuesto por las fases homogéneas α, β, γ que están en contacto mutuo a lo largo de una línea de tensión Fig. 3.10: Proyección ρ1-ρ2 de un sitema binario Fig. 3.11: Proyección z para una interface plana en el equilibrio de fases de una mezcla binaria con adsorción de una de las especies en la zona interfacial XVII

18 Fig. 4.1: Proyección P-T de una mezcla tipo van der Waals de comportamiento global tipo III-m y de propiedades críticas indicadas en tabla Fig. 4.2: Detalle de la proyección P-T (Fig.4.1) de la mezcla binaria tipo van der Waals tipo III-m que muestra el comportamiento de inversión de densidad desarrollado entre la la línea LLV y línea crítica Fig. 4.3: Detalle de la proyección P-T (Fig. 4.1) de la mezcla binaria tipo vdw-tipo III-m que muestra el comportamiento de inversión de densidad en la vecidad de la línea de equilibrio trifásico (LLV) Fig. 4.4: Proyecciones para las fases presentes a lo largo del equilibrio trifásico (LLV) para el sistema binario vdw-tipo III-m Fig. 4.5: Envolventes de densidad para de la mezcla binaria tipo vdw-tipo III-m en la vecindad de desarrollo del comportamiento de inversión de densidad molar (a) y másica (b), líneas MoDI y MaDI respectivamente Fig. 4.6: Detalle esqueático de las envolventes de densidad molar para de la mezcla binaria tipo vdwtipo III-m en la vecindad crítica del comportamiento MoDI Fig. 5.1 Diagrama Global de fases de fluidos van der Waals para moléculas de diámetro 1/3 (ξ=0.5) Fig. 5.2: Proyecciones de Concentración-espacio ( -z) Fig. 5.3: Proyecciones de Concentración-espacio (-z) ) en condicionamiento pre-, post- e inversión de densidad molar de una mezcla binaria. Actividad interfacial nula en la condición de inversión de densidad Fig. 5.4: Proyecciones de concentración-espacio ( -z). Deformación de los perfiles monótonos de distribución de densidad dando origen a puntos estacionario de máximo y mínimo Fig. 5.5: Proyección esquemática de concentración-espacio ( -z) vía inversión de densidad molar Fig. 5.6: Proyecciones de Concentración-espacio ( -z) Tipo (1). Condición MoDI caracterizada por la aparición de un punto estacionario de densidad de máximo: adsorción Fig. 5.7: Proyecciones de Concentración-espacio ( -z) Tipo (2). Condición MoDI caracterizada por la aparición de un punto estacionario mínimo de densidad: desorción Fig. 5.8: Proyecciones de Concentración-espacio (i -z)en la condición MoDI caracterizada por la aparición de puntos estacionarios de densidad de ad- y des-sorción Fig. 5.9: Perfil de densidad total a lo largode la interfaz (-z) en codiciones Pre-MoDI, MoDI y Post- MoDI. Aparición de adsorción en la condición MoDI (Tipo 1) Fig. 5.10: Perfil de densidad total a lo ancho de la interfaz (-z) en codiciones Pre-MoDI, MoDI y Post- MoDI. Aparición de desorción en la condición MoDI (Tipo 2) Fig. 5.11: Perfil de densidad total a lo ancho de la interfaz (-z) en codiciones Pre-MoDI, MoDI y Post- MoDI.Aparición de adsorción y desorción en la condición MoDI (tipo 3) Fig. 5.12: Proyección P-T sistema tipo II. EOS vdw Fig. 5.13: Proyección P-T sistema tipo III de las condiciones de de análisis del comportamiento interfacial con GT-EOS vdw Fig. 5.14: Perfiles de densidad parcial -espacio (i -z) a T/Tc1= y T/Tc1= XVIII

19 Fig. 5.15: Perfiles de densidad parcial -espacio (i -z) a T/Tc1= y T/Tc1= Fig. 5.16: Perfiles de densidad total -espacio (= - -z ) a T/Tc1= y T/Tc1= Fig. 5.17: Perfiles de densidad total -espacio (= - -z ) a T/Tc1= Fig. 5.18: Perfiles de densidad total -espacio (= - -z) a T/Tc1= Fig. 5.19: Esquema de topología interfacial ( -z) alrededor de la condición MoDI en un sistema tipo II.Condición MoDI caracterizada por un punto estacionario de densidad de máximo: adsorción Fig. 5.20: Proyección P-T sistema tipo III. EOS vdw Fig. 5.21: Proyección P-T sistema tipo III de las condiciones de de análisis del comportamiento interfacial con GT-EOS vdw Fig. 5.22: Perfiles de densidad parcial -espacio (i -z) a T/Tc1=1.50, 2.00, 2.20 para el sistema tipo III190 Fig. 5.23: Perfiles de densidad parcial -espacio (i -z) a T/Tc1= Fig. 5.24: Perfiles de densidad total en la interfase (- -z ) a T/Tc1=1.50 y T/Tc1= Fig. 5.25: Perfiles de densidad total espacio a T/Tc1=2.20 y T/Tc1= Fig. 5.26: Perfiles de densidad total espacio a T/Tc1=2.20 y T/Tc1= Fig. 5.27: Proyección P-T sistema tipo IV. EOS vdw Fig. 5.28: Proyección P-T sistema tipo IV de las condiciones de de análisis del comportamiento interfacial con GT-EOS vdw Fig. 5.29: Perfiles de densidad parcial -espacio (i -z) a T/Tc1=0.9946, , y Fig. 5.30: Perfiles de densidad total -espacio (= - -z) a T/Tc1=0.9946, , y Fig. 5.31: Proyección P-T sistema tipo V. EOS vdw Fig. 5.32: Proyección P-T sistema tipo V de las condiciones de de análisis del comportamiento interfacial con GT-EOS vdw Fig. 5.33: Perfiles de densidad parcial (i -z) a T/Tc1= y T/Tc1= Fig. 5.34: Perfiles de densidad parcial (i -z) a T/Tc1= Fig. 5.35: Perfiles de densidad total (-z) a T/Tc1= Fig. 5.36: Perfiles de densidad parcial (i -z) y total ( -z) a T/Tc1= Fig. 5.37: Proyección ρ1-ρ2 de las condiciones pre-modi, MoDI y post-modi para el sitema tipo II a T/Tc1= Fig. 5.38: Proyección ρ1-ρ2 de las condiciones pre-modi, MoDI y post-modi para el ssitema tipo III a T/Tc1= Fig. 5.39: Proyección ρ1-ρ2 de las condiciones pre-modi, MoDI y post-modi para el sitema tipo IV yv 208 Fig. 5.40: Perfiles de densidad (1-2) a lo largo de la condición MoDI para los sistemas tipo III,IV y V. Relación de inversión de densidad molar y puntos estacionarios de adsorción Fig. 5.41: Perfiles de densidad (1-2) a lo largo de la condición MoDI para los sistemas tipo III,IV y V. Relación de inversión de densidad molar y puntos estacionarios de adsorción Fig. 5.42: Isotermas de tensión interfacial (σ- P y σ- x1) del sistema tipo III. Relación entre la inversión de densidad molar y punto aneotropo Fig. 5.43: Isotermas de tensión interfacial (σ- P y σ- x1) del sistema tipo III. Relación entre la inversión de densidad molar y punto aneotropo XIX

20 Fig. 5.44: Isotermas de tensión interfacial (σ- P y σ- x1) del sistema tipo IV Fig. 5.45: Isotermas de tensión interfacial (σ- P y σ- x1) del sistema tipo V Fig. 5.46: Relación entre transición de mojabilidad e inversión de densidad molar en la proyección P-T sistema tipo II Fig. 5.47: Relación entre transición de mojabilidad e inversión de densidad molar en la proyección P-T de sistema binario tipo III, IV y V Fig. 6.1: Proyección P-T para un sistema tipo III fluido LJ Fig. 6.2 Esquema de perfiles de concentración a lo ancho de la interfase asociados a la condición MoDI obtenidos a través de GT-EOS vdw Fig. 6.3: Proyección P-T sistema tipo III. Condiciones de Temperatura y presión de análisis Fig. 6.4: Proyecciones de Concentración-espacio (i -z) Fig. 6.5 Esquema de la simulación de la inversión de fases en densidad molar mediante el colectivo Canónico y perfiles de concentración a lo ancho de la interfase asociados a la condición Pre- y Post- MoDI Fig. 6.6: Proyección P-T sistema tipo III delas condiciones de de análisis comparativo GT-EOS LJ y MD Fig. 6.7: Diagramas de equilibrio y proyecciones de densidad en las condiciones del punto P1 Pre- y Post-MoDI Fig. 6.8: Diagramas de equilibrio y proyecciones de densidad en las condiciones del punto P2 Pre- y Post-MoDI Fig. 6.9: Proyecciones de Concentración-espacio (i -z) a P/Pc1= Fig. 6.10: Proyecciones de Concentración-espacio (i -z) a P/Pc1= Fig. 6.11:Dependencia de la tensión interfacial en presión y fración molar (σ- P y σ- x1) del sistema tipo III Fig. 7.1: Proyección P-T de los sistemas binarios tipo van der Waals constituyentes del ternario I-I-III Fig. 7.2: Evolución en fracción molar del tercer componente de las envolventes de densida a P/Pc1= del sistema ternario 1-A Fig. 7.3: Evolución en fracción molar del tercer componente de las envolventes de densidad molar a P/Pc1= del sistema ternario 1-A Fig. 7.4: Diagramas de fase (T-ρ) en condiciones isobáricas para un sistema binario Fig. 7.5: Diagramas de equilibrio T- a P/Pc1=2. División de la envolvente de densidad molar de la mezcla ternaria 1-A Fig. 7.6: Diagramas de equilibrio T- a P/Pc1=1.0 del sistema 1-B Fig. 7.7: Dicotomía del equilibrio bifásico en el diagramas de equilibrio T- a P/Pc1=1.0 del sistema 1-B Fig. 7.8: Evolución de las envolventes de densidad molar en fracción molar del componente (3) del sistema ternario 2-A a P/Pc1= XX

21 Fig. 7.9: Comportamineto crítico de las envolventes de densidad molar en fracción molar del componente (3) del sistema ternario 2-A a P/Pc1= Fig. 7.10: Diagramas de equilibrio T- a P/Pc1=6.00 del sistema 2-B. Efecto de la adición del componente (3) en el sistema binario tipo III da origen a la aparición de múltiples estados de inversión en condición isobárica Fig. 7.11: Diagramas T- del colapso crítico del comportamiento de inversión de densidad del sistema 2-B Fig. 7.12: Proyección T-del equilibrio MoDI del sistema 3 (III-III-IV) a P/Pc1= Fig. 7.13: Comportamiento del equilibrio de fases MoDI del sistema 3 III-III-IV a P/Pc1= Fig. 7.14: Proyección T-ρ del comportamiento del equilibrio de fases del sistema 3 III-III-IV a P/Pc1=4.00 en la medida de la adición del tercer componente Fig. 7.15: Envolventes de densidad a P/Pc1=0.100 del sistema 4-I-II-II. Aparición de inversión de densidad por adición del tercer componente a una mezcla binaria tipo III Fig. 7.16: Diagramas de equilibrio T- a P/Pc1=1.00 del sistema 4-B (I-II-II) Fig. 7.17: Proyección T-ρ del equilibrio trifásico del sistema I-I-III. a P/Pc1= y P/Pc1= Fig. 7.18: Proyección T-ρ del equilibrio trifásico del sistema I-I-III. a P/Pc1= Equilibrio MoDI ρ c =ρ α Fig. 7.19: Equilibrio trifásico (T-ρ) del sistema I-I-III. a P/Pc1=1.1750, , Aparición de dos estados de inversión entre las fases α-β que culminan en estado tangente de densidad Fig. 7.20: Diagrama de equilibrio MoDI (P-T) y (P-ρ) del sistema I-I-III. Seguimiento de los estados de inversión entre las fases α-β y α-γ desarrollado en el equilibrio trifásico Fig. 7.21: Proyección T-ρ del equilibrio trifásico del sistema I-II-III. a P/Pc1= Equilibrio MoDI α- β Fig. 7.22: Equilibrio trifásico del sistema tipo I-II-III (T-ρ). Colapso del equilibrio MoDI en la condición crítica Fig. 7.23: Diagrama de equilibrio MoDI (P-T) y (P-ρ) sistema I-II-III. Seguimiento de los estados de inversión entre las fases α-β desarrollado en el equilibrio trifásico Fig. 7.24: Equilibrio trifásico del sistema tipo II-III-III (T-ρ). Aparición de múltiples puntos de equilibrio MoDI Fig. 7.25: Equilibrio trifásico del sistema tipo II-III-III (T-ρ) Fig. 7.26:. Proyecciones (P-T) y (P-ρ) del seguimiento de los estados de inversión entre las fases α-β y α-γ desarrollado en el equilibrio trifásico del sistema II-III-III Fig. 7.27:Diagrama de equilibrio trifásico (T-ρ) del sistema II-III-IV en condiciones isobáricas. Aparición de múltiples puntos de equilibrio MoDI entre las fases α-β, β-γ y α-γ Fig. 7.28:. Proyecciones (T-ρ) y (P-ρ) del seguimiento de los estados de inversión entre las fases α-β, α-γ y β-γ desarrollado en el equilibrio trifásico del sistema II-III-IV Fig. 7.29:Diagrama (T-ρ) del equilibrio trifásico del sistema tipo III-III-IV. Estados MoDI: α-β, α - γ Fig. 7.30:Diagrama (T-ρ) del equilibrio trifásico del sistema tipo III-III-IV XXI

22 Fig. 7.31: Seguimiento de los estados de inversión entre las fases α-β, α-γ y β-γ desarrollado en el equilibrio trifásico del sistema III-III-IV en proyecciones (P-T) y (P-ρ) Fig. 7.32: Diagrama (T-ρ) del equilibrio trifásico del sistema tipo I-II-III en condiciones isobáricas en el rango 0.01<P/Pc1< Fig. 7.33: Seguimiento de los estados de inversión entre las fases α-β desarrollado en el equilibrio trifásico del sistema I-II-III en las proyecciones P-T y P-ρ Fig. 7.34: Geometría de las envolventes de densidad de sistemas binarios y ternarios Fig. 7.35: Evolución de la envolvente de densidad isobara de sistemas binarios. Extensión conceptual a sistemas multicomponentes Fig. 7.36: Proyección densidad-concentración molar (ρ-x1) en condiciones isobaricas caracteriazada por un línea de conexión de equilibrio isopícnico molar Fig. 7.37: Proyecciones bidimensionales de densidad-concentración molar (ρ-xi) y concentraciónconcentración (x1-x2) a lo largo del equilibrio isopícnico molar del ternario I-I-III Fig. 7.38: Proyecciones de densidad-concentración (-xi), presión-temperatura (P-T) y presióndensidad (P-ρ) para la mezcla ternario I-I-III a lo largo del equilibrio isopícnico molar desarrollado en condiciones isobáricas Fig. 7.39: Proyecciones de densidad-concentración (-xi), presión-temperatura (P-T) y presióndensidad (P-ρ) para la mezcla ternaria I-II-III a lo largo del equilibrio isopícnico molar desarrollado en condiciones isobáricas XXII

23 Nomenclatura Lista de símbolos a : Término de cohesión ( Pa m 6 kmol 2 ) b : Covolumen ( m 3 kmol ) A : Energía de Helmholtz ( J ) * A : Energía de Helmholtz adimensional A : Área superficial (m 2 ) a 0 : Densidad de energía de Helmholtz (J kmol m -3 ) A0, B0, C 0 : Parámetros de la ecuación de estado Benedict- Webb-Rubin a0, b0, c 0 : Parámetros de la ecuación de estado Benedict- Webb-Rubin a i, b i : Parámetros de la ecuación de estado para fluido Lennard-Jones C ij : Parámetro de influencia entre la especie i y j D, d Diámetro ecuatorial y distancia medida desde la parte superior de la elongación de la caída de la gota (m). d s : Diámetro horizontal de gota o burbuja (m) d e : Diámetro desde del ápice de gota o burbuja hasta la medida d s(m) F : Fuerza (N) G : Energía de Gibbs ( J ) G i : Funciones en términos de funciones exponenciales dependientes de la densidad g : Constante gravitacional (m s -2 ) G : Energía de mezclado de Gibbs ( J ) H : Entalpía ( J ) k ij : Parámetro de interacción entre la especie i y j Lx, Ly, Lz : Dimensiones de un paralelepípedo. m : Número de componentes n : Número de moles XXIII

24 N 1,N 2 : Distribución de moléculas 1 y 2. P : Presión ( Pa ) P* : Parámetro de presión adimensional para la ecuación de estado para fluido Lennard-Jones R : Constante universal de los gases( J K -1 Kmol -1 ) r ij : Distancia entre los centro de los átomo i y j ( Å ) r c : Distancia límite entre los centro de los átomo i y j (Å ) r : Distancia intermolecular S : Entropía ( J K 1 ) S β,αγ : Parámetro de esparcimiento de la fase β sobre la interface αγ T : Temperatura (K) T 0 : Temperatura de equilibrio(k) T* Parámetro de temperatura adimensional para la ecuación de estado para fluido Lennard-Jones U : Energía interna (J) U* : Energía interna adimensional V : Volumen ( m 3 ) V 0 : Volumen en condiciones de equilibrio(m 3 ) w : trabajo requerido para crear una unidad de área : Primer determinante en derivadas parciales de la 1 energía de Helmholtz x : Fracción molar x : Longitud (m) x i : Parámetros lineales de la ecuación de estado de Johnson et al. M : Segundo determinante en derivadas parciales de 1 la energía de Helmholtz N : Tercer determinante en derivadas parciales de la 1 energía de Helmholtz z : Dirección normal a una superficie o interfase Superíndices ab, : Fase anexas ad : Fase adicional XXIV

25 E : Exceso c : Fase crítica L : Líquido V : Vapor Subíndices c : Propiedad crítica gen : Generado i : i-ésimo componente j : j-ésimo componente M nt : n-ésima derivada parcial de la propiedad M con respecto a la temperatura M np : n-ésima derivada parcial de la propiedad M con respecto a la presión M nv : n-ésima derivada parcial de la propiedad M con respecto al volumen M nx : n-ésima derivada parcial de la propiedad M con respecto a la fracción molar N : Dirección normal Alfabeto griego T : Dirección tangencial α,β,γ : Fases en equilibrio 0, : Parámetros de la ecuación de estado Benedict-Webb- 0 Rubin γ : Parámetro no lineal de la ecuación de estado de fluido Lennard-Jones, : Diámetro molecular y profundidad de pozo intermolecular : Tensión interfacial : Coordenada paramétrica del Diagrama global de fases relacionada a la diferencia entre los componentes puros : Factor de simetría o razón de tamaño molecular : Coordenada paramétrica del Diagrama global de fases relacionada a la sinergia : Potencial químico XXV

26 Matrices y Vectores χ : Parámetro de simetría Ж : Parámetro que representa la variable estado del sistema: temperatura, presión y fracción molar : Coordenada paramétrica del Diagrama Global de fase relacionada a la razón de tamaño molecular : -ésima fase en equilibrio ρ : Densidad molar ρ* : Densidad adimensional ρ 0 : Densidad molar en condiciones de equilibrio r : Potencial intermolecular para fluido Lennard-Jones. ji : adsorción de Gibbs de la especie j con respecto a la especie i en la interfase (). : Gran potencial termodinámico : Parámetros de la ecuación de estado tipo cúbica ab, HG : Matriz hessiana de la energía de Gibbs T : Gradiente de temperatura P : Gradiente de presión : Gradiente de potencial químico 0 : Vector nulo XXVI

27 Abreviaciones APACT : Associated Perturbed Anisotropic Chain Theory BMoDI : Binary Molar Density Inversion Point BMoDIEP : Binary Molar Density Inversion End Point BWR : Benedict Webb Rubin CEP : Critical End Point CMoDIP : Critical Molar Density inversión Point CPA : Cubic Plus Association CPSP : Critical pressure step point DCEP : Double critical end point ELL : Equilibrio liquido-líquido ELLG : Equilibrio líquido-líquido-gas EOS : Ecuación de estado Equation Of State GPD : Global phase diagram GT : Gradient theory HS : Hard sphere #romano : Sistema tipo # ILs : Ionic Liquids JZG : Johnson-Zollweg-Gubbins LLV : Equilibrio Líquido-líquido-gas L-J/LJ : Lennard-Jones L-V : Equilibrio Líquido-vapor L : Líquido LCEP : Lower critical end point LCST : Lower critical solution phenomena temperature LCMoDIP : Lower critical molar density inversion point MBWR : Modified BWR MD : Molecular dynamics MoDI : Molar Density Inversion Pont MoDIEP : Molar Density Inversion End Point MoDI- LCEP : Equilibrio de fases entre una fase adicional y LCEP en condiciones de inversión molar MoDI- : Equilibrio de fases entre una fase adicional y UCEP en XXVII

28 UCEP condiciones de inversión molar PACT : Perturbed Anisotropic Chain Theory PHCT : Perturbed Hard Chain Theory PC-SAFT : Perturbed Chain- Statistical Associating Fluid Theory PR : Peng-Robinson PAO : Polialfaolefina PAG : Polialquilenglicol PAP : Partial adsorption point PDP : Partial desorption point PIA : Partial interfacial activity POE : Polioéster PVT : Presión-volumen-temperatura SRK : Soave-Redlich-Kwong SAFT : Statistical Associating Fluid Theory SCPEP : Stationary critical pressure end point SW : Square well TAP : Total adsorption point TDP : Total desorption point TIA : Total Interfacial Activity TMoDI : Ternary Molar Density Inversion Point TMoDIEP : Ternary Molar Density Inversion End Point UCEP : upper critical end point UCMoDIP Upper critical molar density inversion point UCST : Upper critical solution temperature vdw : Van der Waals V : Vapor WP : Wetting Point ZT : Zero temperature line XXVIII

29 Parte I: Introducción

30 Capítulo 1. Introducción Contenido 1.1. Introducción Antecedentes preliminares: una revisión de la fenomenología de inversión de fases Estado del arte en fenómenos de inversión de fases en mezclas binarias y ternarias Observación y medición experimental Modelación y predicción Modelo matemático descriptivo Presentación de la Investigación Hipótesis Contribución de ésta tesis Objetivos Objetivo General Objetivos Específicos Estructura de esta tesis Referencias Innegable es el hecho que desde el comienzo de la historia, la investigación científica ha estado estrechamente ligada a los avances en tecnología. La invención y la mejora de técnicas han sido dos tópicos importantemente tratados mediante la investigación científica, en donde, dada la naturaleza compleja de un determinado sistema de estudio -por ejemplo una mezcla multicomponente- es necesaria la aislación y/o separación y simplificación de éste, de forma de determinar las características, funciones y fenomenología en forma esencial y fundamental. De forma tal de extender las funcionalidades y caracterizaciones fenomenológicas encontradas dentro de la mezcla. En este capítulo se describe la importancia, motivación y vinculación existente entre la fenomenología de inversión de fases en densidad y procesos naturales, químicos e industriales, dejando a la vista la relevancia de la caracterización cualitativa y matemática de la fenomenología, desde un punto de vista simplificado, como son los modelos de mezclas binarias y ternarias. 30

31 Capítulo 1: Introducción 1.1. Introducción En ingeniería química, las mezclas son una parte inherente de los procesos de cinética de reacción [1]-[3], extracción líquido-líquido [4]-[6], separación por destilación [7][8] y otros procesos típicos de operaciones de separación, todos ellos involucrando sistemas multicomponentes [9]. Sin ir más allá de nuestra vida cotidiana, los ejemplos más comunes de mezclas multicomponentes son; la gasolina, una mezcla de hidrocarburos alifáticos y aromáticos, materiales plásticos como bolsas y botellas, corresponden a mezclas de polímeros y detergentes y por último, champús, siendo estos una mezcla de surfactantes, polímeros y estabilizadores. Tal como es posible percibir, en muchos de los procesos químicos y aplicaciones como ejemplo anteriormente mencionadas, es muy importante la manera en que dos fases han de ser contactadas y posteriormente separadas, puesto que esta etapa va a determinar finalmente en la calidad del producto obtenido y la eficiencia del proceso. En este punto, es necesario destacar que el contacto, mezcla y la separación de fases-en condiciones de equilibrio-se encuentra directamente relacionada con la propiedad termofísica de la tensión interfacial [10]-[12]. Más aún, procesos químicos que incluyen la formación de películas delgadas y la nucleación de gotas [13][14], microemulsiones [15], sistemas coloidales [16] y flujo de fluidos a través de microporos y membranas [24][25], dependen directamente de grado de humectación y mojabilidad [17]-[23] entre las fases. He ahí la importancia de estudio del comportamiento del equilibrio de fases, cálculo de propiedades termo-físicas de mezclas y caracterización de interfaces a través de la tensión interfacial, perfil interfacial, ángulo de contacto y transición de mojabilidad. La aplicación sistemática de la termodinámica del equilibrio de fases, mediante la comprensión y cálculo de las propiedades termo-físicas de mezclas, permite el estudio del comportamiento del equilibrio de fases de mezclas, ciertamente involucradas en muchas aplicaciones apostadas al desarrollo de nuevas tecnologías y en el sentido de la optimización de recursos [26]. El desarrollo de técnicas modernas más eficientes de separación, basadas en la introducción de solventes supercríticos como por ejemplo dióxido de carbono, fluoro-carbono y xenón, resulta transformarse en un conjunto de mezclas asimétricas que pueden desarrollar una gama compleja de comportamiento de fase [27][28]. El complejo comportamiento de mezclas multicomponentes hace que sean difíciles de comprender y modelar termodinámicamente [28][29], siendo un punto primordial en las etapas previas de diseño de los procesos y en donde las ecuaciones de 31

32 Capítulo 1: Introducción estado desempeñan un papel importante. Las ecuaciones de estado permiten aproximar la naturaleza de un proceso mediante un modelo matemático, capacitado para predecir el equilibrio de fases de los fluidos puros, de las mezclas que estos constituyen y las propiedades termo-físicas, tanto en fase homogénea como heterogénea. Los complejos comportamientos de equilibrio de fases; tales como rangos exclusivos de miscibilidad parcial o total o extendidos de inmiscibilidad, desarrollo de equilibrios líquido-líquido-vapor [30][31] o condensación retrógrada [32][33]o doble retrógrada [34] usualmente encontrada en condiciones críticas en algunos procesos industriales [35], aparecen como respuesta a cambios de las variables que controlan el equilibrio de fases. Cambios de temperatura y/o presión, no solamente provocan un cambio en la concentración de las fases, sino que también cambios en otras propiedades físicas, como la densidad de las fases [27]. Cambio, que eventualmente puede provocar inversión de densidad. La inversión de fases en densidad, ocurre cuando una fase liviana se vuelve de pronto más pesada. En la literatura, dos fenómenos de inversión de densidad han sido identificadas en mezclas : (1) Inversión de densidad másica de fases, denominada barotropía, en cuyo punto de inversión la densidad másica de las fases iguala y por otro lado, (2) la inversión de densidad molar, denominada isopicnia, corresponde al caso en el que la densidad molar de las fases iguala. Las perspectivas de desarrollo tecnológico en base al conocimiento y predicción de la inversión de fases en densidad- másica o molar- son innumerables, debido a la extensa manifestación de la fenomenología como un especial comportamiento del equilibrio de fases, que debe ser considerada como factor determinante para la selección adecuada de parámetros de operación para un óptimo rendimiento en los procesos Antecedentes preliminares: una revisión de la fenomenología de inversión de fases Al comienzo de la investigación y durante el proceso de recopilación de información y revisión bibliográfica sobre la fenomenología de la inversión de fases en densidad, fue perceptible la dificultad de poder encontrar una definición precisa que les diera un significado único y universal al fenómeno, indicándose y asociándose barotropía e isopícnia a un mismo concepto de inversión independiente y alejados de los conceptos diferenciados: másico y molar. Es más, los conceptos de barotropía (del griego: baro-: baro, peso, pesado presión y tropía: tropikos, dar la vuelta) e isopicnia (del griego: iso-: is, 32

33 Capítulo 1: Introducción igual y pícnia: picknos, densidad) fueron introducidas para expresar el hecho que el comportamiento de fases depende de la densidad, centrándose el primer término al proceso de inversión de fases, mientras que el segundo aplicado conceptualmente, al punto de inversión de densidad. De aquella búsqueda y tal como ahora se presenta en este trabajo, una más reciente revisión bibliográfica, permitió observar e interpretar la manera en que han sido estudiados ambas fenomenologías en diferentes perspectivas; como la física, en fenómenos de nucleación asociada a la formación de emulsiones [36]-[38]. En química, en fenómenos de absorción y adhesividad [39], lubricación y circuitos de refrigeración [27][40][41] y recuperación de petróleo y aceites esenciales [42][43] mediante solventes supercríticos [44]-[46]. En biología: centrifugación de proteínas y separación de mezclas fosfolípidicas, perfilamiento de material genético [47]. En geografía, en actividad volcánica [48] y fenómenos atmosféricos modelados y simulados bajo el concepto de flujo [49]. Finalmente, en oceanografía, fenómenos en océanos y lagos, como la formación y propagación de ondas superficiales e internas provocadas por gradientes térmicos y másicos[50]-[51]. Siendo estos algunos casos, en donde se les confiere un sentido distinto pero muy importante a la inversión de fases que luego brevemente se describirá. Casi al mismo tiempo, que ha surgido la necesidad de marcar una conceptualización concreta sobre la inversión de fases en densidad molar y másica, a partir de información bibliográfica, nace como manifiesto de esta misma conceptualización, la siguiente necesidad de describir y caracterizar el comportamiento de inversión de fases. Tempranamente en 1906, el efecto barotrópico fue descubierto por Kamerlingh, Onnes y Keesom, durante la experimentación pionera con el sistema binario hidrógenohelio [52]. El objetivo de la experimentación consistía en determinar las condiciones de temperatura y presión en las que el helio solubilizaba con hidrógeno. Consecuentemente del trabajo experimental, se concluyó que no existía condición de presión que pudiese lograr que los dos componentes formasen solución homogénea y observándose que, frente el aumento de la presión, la fase gaseosa compuesta principalmente por helio se volvía más pesada que la fase líquida rica en hidrógeno, quedando la primera atrapada en el fondo de la celda de trabajo. Este fenómeno mecánico de inversión de densidad fue reconocido como barotropía [52]. El descubrimiento de la inversión de densidad en el sistema hidrógeno-helio, 33

34 Capítulo 1: Introducción marca el inicio de la investigación de la inversión de densidad en mezclas multicomponente. Interesantemente el análisis y descripción de la inversión de densidad del sistema de hidrógeno y helio tiene gran importancia en el modelado realístico de atmósferas planetarias, donde no solamente la ocurrencia del fenómeno barotrópico de la fase gaseosa y la fase líquida [53] es considerado en las simulaciones, sino también las inversiones de densidad entre el líquido y la fase sólida. Fenómeno observado experimentalmente a altas presiones (20-75 kbar) y fracción molar de helio en fase líquida superior a 0.06 [54]. Las emulsiones son mezclas multicomponente, definidas como sistemas formados por dos fases parcial o totalmente inmiscibles, en donde una de ellas forma la llamada fase continua (o dispersante) y la otra la fase discreta (o dispersa) [55]. Las emulsiones submicrónicas, incluyendo miniemulsiones, han atraído una atención considerable en los últimos años [55][56], especialmente aplicadas en cosméticos, agroquímicos, productos farmacéuticos y revestimientos de superficies, obteniéndose mediante el uso de homogeneización a alta presión o una técnica ultrasónica[55]. Una forma alternativa de producir esas emulsiones es mediante la técnica de la inversión de fases [55]-[57]. Esta técnica suele ser más barata y consume menos energía que la emulsificación de alta presión. Hay dos tipos de inversión de fases [55]: (1) Inversión de fases catastrófica (Catastrofic Phase Inversion CPI). En este proceso, el aumento de la coalescencia entre gotas hará que la fase dispersa se convierta en la fase continua, ocurriendo la inversión que por lo general no da origen a buenos productos, donde el tamaño de gota o burbuja del componente activo es de importancia para la aplicación en un sustrato de interés. Por otro lado, el otro procedimiento es llamado (2) inversión de las fases de transición (Transition Phase Inversion TPI) donde la hidrofilicidad del surfactante se altera de tal manera que la inversión de fase ocurre modificando las micelas que contienen la fase discreta en fase continua o viceversa [55][37]. La TPI conlleva a una inversión morfológica de la emulsión en donde la curvatura de la emulsión se invierte. El cambio morfológico de la emulsión, se alcanza, por ejemplo, reduciendo la temperatura, alcanzándose un mínimo de la tensión interfacial coincidente con la temperatura de inversión de fase [37]. Es así, que la técnica de inversión de fases, ha sido extendida y aplicada con la finalidad de construir estructuras poliméricas con porosidad controlada y definida - 34

35 Capítulo 1: Introducción solidification of emulsified polymer solutions via phase inversión (SEPPI) [58]-. El método permite la creación de materiales a partir de una solución de polímeros, emulsionado y luego solidificada por medio del contacto con las gotas en la emulsión en condiciones de inversión de densidad, que actúan como plantilla esférica para crear poros de tamaño definido. El comportamiento de las fases de los sistemas coloidales incorpora muchos fenómenos interesantes, como la formación de superestructuras estables y el equilibrio de fases con participación de varias fases [59]. En estos sistemas, las moléculas que los componen, les permite transitar de fase desordenada -isotrópica- (sin orden ni orientación, compuesta por partículas gruesas) a ordenada orientacionalmente -nemática- (compuesta por partículas finas), por fases intermedias, llamadas mesofases [60]. En el equilibrio de estas dos fases inhomogéneas, nemática e isotrópica, puede darse también una inversión de la densidad, en donde la fase isótropa se vuelve más densa que la nemática. A pesar que la fase nemática tiene una concentración de partículas superior a la fase isotrópica, la densidad másica cae por debajo de la fase isotrópica debido a un alto fraccionamiento en partículas finas de poca masa [59]. En la industria del petróleo, el agua puede estar presente en los yacimientos de petróleo, en aguas de formación o inclusión por rompimiento de fuentes adyacentes. Por lo tanto, el petróleo será trasladado con frecuencia como una mezcla orgánica-acuosa desde los pozos a la superficie en las tuberías [61]. Dependiendo de las condiciones de funcionamiento, esta mezcla puede formar la fase continua, como una dispersión estable de gotas finas[62]. En este tipo de mezclas la inversión de fase se refiere a un fenómeno por el cual-con un pequeño cambio en las condiciones de operación- la fase continua y dispersa espontáneamente puede invertir [62][63]. Esta transición es generalmente asociada con un cambio abrupto en las tasas de transferencia de momento, calor y masa entre las fases continua y dispersa [63][64], y por lo tanto, la consideración del fenómeno de la inversión es un factor importante a la hora del diseño de tuberías, en relación a la corrosión de los conductos de transporte [64] que implica en gran medida la identidad de la fase que moja. Para las aplicaciones prácticas este resultado es muy importante, ya que abre la posibilidad de evitar o posponer la inversión de fase [65][66], la cual provoca una alta caída de presión o baja tasa de flujo, mediante una inyección gradual de la fase dispersa en la fase continua. La inversión de fase y su efecto sobre el gradiente de presión en el flujo de dispersión de dos líquidos inmiscibles se ha estudiado, determinando la fracción de 35

36 Capítulo 1: Introducción volumen de la fase dispersa, llamado volumen crítico, en la que se produce la inversión de fase. Otra mezcla de interesante estudio es dióxido de carbono y agua. En 1986 una letal erupción de un volcán fue causada por una súbita inversión de las aguas cargadas de dióxido de carbono desde el fondo del lago Nyos, en Camerún [48]. La explicación de esta erupción volcánica recae en el hecho que existen condiciones de presión y temperatura en donde el dióxido de carbono queda atrapado y distribuido en forma dispersa en la fase acuosa. Las condiciones de presión y temperatura para lograr esta emulsión equivalen a que la densidad másica del gas sea igual a la del agua líquida -condiciones encapsulación-, logrando un estado estable durante un largo periodo de tiempo (en este caso aproximadamente 500años) en la cámara de magma. Posteriormente, un enfriamiento a lo largo de la profundidad del volcán (3km-1kBar), induce una mecánica de inversión de densidad: (1) una inversión limitada estrictamente entre las aguas profundas cargadas de dióxido de carbono y (2) una segunda inversión de densidad en las aguas superficiales. El dióxido de carbono, es utilizado en cromatografía de fluidos supercríticos (Supercritical Fluid Chromatography: SFC) como una fase de transporte [67] y cuyas propiedades pueden ser ampliamente moduladas, esto dentro de los rangos de temperatura y presión operacionales, dando lugar a valores muy diferentes de factores de retención y de eficiencia de la columna de análisis[67][68]. La retención y eficiencia, son correlacionados directamente con la densidad de la fase de transporte y, en menor medida, con la temperatura y presión de la columna, de manera que las propiedades físicas del dióxido de carbono sean relevantes para la operación adecuada de los sistemas cromatográficos[68] [69]. La centrifugación es la técnica más utilizada para la purificación y separación de partículas por diferencia de tamaño, forma y densidad[70]. La centrifugación isopícnica, separa las partículas, principalmente debido a las diferencias en su densidad de flotación [71][72]. Esta separación se hace en un gradiente de densidad a través del cual las partículas se mueven bajo el efecto del campo centrífugo, que finaliza hasta que la densidad es la misma que la del medio circundante[73]. La técnica es usada en biología, para la obtención de fragmentos de organelos subcelulares [74]. La técnica de centrifugación por gradiente de densidad o centrifugación isopícnica, es rápida, versátil, no destructivo, eficiente, escalable y reproducible. En esta sección se ha expuesto la diversidad de procesos en donde la inversión de 36

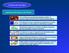
37 Capítulo 1: Introducción fases por densidad juega un rol principal en más de un campo tradicional de investigación y aplicación Estado del arte en fenómenos de inversión de fases en mezclas binarias y ternarias En esta sección se describe el estado del arte de la fenomenología de inversión de fase en mezclas, que constituyen el fundamento de este trabajo de tesis. La presente sección está organizada en tres sub-secciones, donde la primera se describe el estado del arte de la observación y medición experimental de la inversión de fases en densidad molar y másica, la segunda describe el estado del arte de la orientación a un enfoque de modelación y predicción relacionada con ecuaciones de estado y por último, el estado del arte en cuanto a descripción matemática de la fenómeno Observación y medición experimental Hauk y Weidner [75] han observado el comportamiento de fase de mezclas binarias de lubricantes y dióxido de carbono por medio de una celda de alta presión, esto con el objetivo de clasificar y recomendar los aceites que funcionarán correctamente a través del desarrollo de miscibilidad limitada o completa (cerrada o abierta). El comportamiento de las fases de los aceites con dióxido de carbono se pueden dividir en tres tipos diferentes: los sistemas binarios con espacios cerrados de miscibilidad, con espacios abiertos de miscibilidad y sistemas que muestran inversión de densidad. P=1.0bar P=50bar P=40.0bar P=150bar Fig. 1.1: Comportamiento del equilibrio de fases para el sistema PAO+CO2 a 5 C.Inversión de densidad másica a P=40.0bar. El comportamiento de inversión de densidad másica o barotrópico fue observado para la mezcla binaria de CO 2+ poly(r-olefin) (PAO) a 5 C y 40 bar. La Fig. 1.1 muestra una fase mixta en la que el lubricante PAO comienza a nadar en la fase líquida de CO 2. Al aumentar la presión 40 a 50bar y luego a 150 bar, se observa claramente la inversión densidad y el equilibrio queda formado por una fase 37