Opciones bajo la distribución normal
|
|
|
- Gonzalo Godoy Toledo
- hace 8 años
- Vistas:
Transcripción
1 Opciones bajo la distribución normal Jesús Besada Juez Gustavo Plaza González 07 de Julio de 2015 Abstract En este artículo se analizan las opciones de estilo europeo bajo la única suposición de que los precios del subyacente siguen una distribución normal. Muchos traders (entre los que se incluyen los autores) piensan que una distribución normal, en vez de la ampliamente aceptada lognormal, en muchas casos describe adecuadamente el comportamiento del mercado. Independientemente de que se esté de acuerdo con la afirmación anterior, salvo en ciertas condiciones (tiempos muy largos hasta vencimiento y/o volatilidades muy altas), los resultados son muy similares con los obtenidos por las fórmulas de Black Scholes (BS en adelante). Las formulas bajo la distribución normal son sensiblemente más sencillas e interpretables que las obtenidas por BS, por lo que tienen un valor pedagógico muy alto, obteniéndose resultados muy importantes que son igualmente válidos usando la formulación BS. Key words: Opciones, Black Sholes, Distribución normal, Distribución lognormal, volatilidad implicada. 1. Formulación Para el cálculo del precio de una opción, se va a realizar únicamente una suposición, que la distribución de precios del subyacente hasta el vencimiento sigue una distribución normal. No se va a realizar la suposición de que el subyacente siga una distribución lognormal ni que se encuentre gobernado por una constante de dirección (drift rate). Esto supone hacer cero el término r (típicamente el risk free interest rate ) en BS. Independientemente de que sea más o menos cuestionable si el subyacente se encuentra gobernado por un drift rate, no cabe ninguna duda que el enfoque anterior es completamente neutro y no introduce ningún tipo de sesgo en el comportamiento del subyacente. Como se verá más adelante, añadir el término r resulta trivial para aquellos interesados en tenerlo en cuenta. Una de los aspectos más discutibles del modelo BS es el sobreprecio que introduce en los Calls, esto se explica tanto por el uso de la distribución lognormal como por la introducción del término r. La formulación aquí obtenida no introduce este sesgo y es uno de los puntos a favor a considerar. Se usará el argumento de no arbitraje para derivar la fórmula del precio. Esto se traduce al ser una opción de tipo europeo en que la esperanza matemática debe ser cero al vencimiento. El resultado que se obtiene es el siguiente (ver el apéndice para la deducción matemática): C = φ(x) + (S K) Φ(x) (1) Dónde: desviación típica de la distribucción normal asociada φ(x) valor de la distribucción normal estándar
2 S valor del subyacente K Strike Price seleccionado Φ(x) valor de la distribucción normal acumulada estandar x = S K Hay que hacer notar, que es la desviación típica de la distribución normal asociada del subyacente, y no se encuentra anualizada como suelen representar los traders a la volatilidad V. Por lo que: Siendo T el tiempo hasta el vencimiento expresado en años. En el caso de que V esté en porcentaje, además hay que multiplicar por S. De forma similar, se obtiene que el valor de un Put es: = V T (2) P = φ(x) + (K S) Φ( x) (3) Tal y como se indicaba anteriormente, si se desea incluir el término r, se obtiene la siguiente fórmula: C = e r T ( φ(x) + (S K) Φ(x)) 2. Análisis de los resultados Para las conclusiones que siguen, se parte de la fórmula obtenida del valor de un Call en (1). Put-Call parity Se comprueba de forma sencilla que si se resta el valor de un Call y de un Put se obtiene la conocida expresión Put-Call parity : C P = S K (4) Se deriva que la relación de paridad entre un Call y un Put se mantiene bajo la distribución normal. Valor at the money Si se calcula el valor de un Call at the money (K=S), se obtiene: C K=S = π (5) Este resultado puede sorprender a primera vista, ya que concluye que el valor de un Call o de un Put at the money depende únicamente de la desviación típica, o lo que es lo mismo, de la volatilidad según la ecuación (2).
3 A mayor volatilidad, más caro resultará la opción y viceversa: Calcular el valor de un Call at the money con los siguientes datos: Valor del subyacente= días hasta vencimiento. Volatilidad anual=10%. Usando la aproximación en (5): = = 2.87, C = El valor obtenido bajo el modelo completo de BS es de 1.144, lo que da una idea de la alta precisión que se obtiene. Greeks Se obtienen a continuación las conocidas Greeks de una opción: Delta: = C S = Φ(x) Gamma: Γ = S = φ(x) V T Vega: ν = C = φ(x) T V Theta: Θ = C V φ(x) = T 2 T Se extraen conclusiones inmediatas a tenor de las formulas anteriores: Gamma, Vega y Theta dependen directamente de la distribución normal estándar. Por lo tanto serán máximas en K=S. Gamma es mayor cuando hay menor volatilidad y menor tiempo hasta vencimiento. Vega es mayor cuando más tiempo hasta vencimiento queda. Theta depende de la volatilidad y aumenta más rápidamente cuanto menos tiempo queda hasta vencimiento. Ratios Utilizando las greeks anteriores, es posible calcular los ratios entre ellas para analizar las condiciones más favorables para una estrategia en concreto. Por ejemplo, si se usa una estrategia que depende de la dirección (incluso una estrategia direccional y neutra pero que requiere movimiento como un strangle ), Gamma es nuestro amigo y Theta nuestro enemigo, por lo que hay que maximizar el siguiente ratio:
4 Γ Θ = 2 V 2 Se observa que sólo depende de la volatilidad, por lo que cualquier estrategia de este tipo debería montarse cuando la volatilidad sea lo más baja posible. Ni siquiera el paso del tiempo altera el ratio, lo que significa que lo que aumenta Gamma, decrece Theta al mismo ritmo y viceversa. Si lo que se quiere es comprar volatilidad esperando que suba, Vega es nuestro amigo y Theta nuestro enemigo. En este caso hay que maximizar el siguiente ratio: ν Θ = 2 T V Nuevamente, cuanto más baja sea la volatilidad mejor será el ratio. Sin embargo, esta vez, el ratio irá empeorando a medida que queden menos días para el vencimiento. Por lo tanto, se debe montar esta estrategia con volatilidades bajas y un tiempo suficiente hasta vencimiento. Para analizar la exposición a Gamma y Vega: Γ ν = 1 V T Razonamientos similares se pueden hacer para las ventas, buscando el mínimo del ratio en vez del máximo. Delta de una opción Retomando la expresión obtenida para Delta: C = = Φ(x) S (6) Este resultado es muy ilustrativo, ya que bajo el supuesto de distribución normal, el delta de un Call representa también exactamente la probabilidad de que el subyacente sea mayor que K al vencimiento. Tanto es así, que se puede reescribir la ecuación (1) como: C = φ(x) + (S K) Esta nueva expresión ilustra de forma clara que el precio de la opción se encuentra gobernado por dos factores. Factores que gobiernan el precio de una opción El primer término representa el valor de la opción por las posibilidades que tiene de ser valioso a vencimiento, gobernado directamente por la volatilidad y siendo máximo en valores at the money, lo que representa un concepto similar al conocido como Time Value. El segundo término representa un concepto similar al valor intrínseco de la opción, que como se concluye, para opciones muy in the money, es decir valores con deltas próximos a 1 se obtiene: C 1 (S K)
5 Call Value El segundo factor se vuelve negativo para valores out the money a diferencia de la definición clásica de valor intrínseco. Hay que tener en cuenta que este factor penaliza a los valores out the money ya que la probabilidad de que la opción termine sin valor aumenta. La siguiente figura muestra la composición de ambos factores que resultan en el valor del Call a diferentes Strike Prices para S=100: Time Value Intrinsic Value Total Value Strike Prices Puntos de interés Se puede observar de la gráfica anterior, que existen varios puntos interesantes a conocer. El primero de ellos ocurre cuando se cruzan ambas curvas, aproximadamente a un delta de 0.7, el coste de ambos factores es el mismo, es decir, la opción cuesta lo mismo por su Time Value que por su Valor Intrínseco. Para valores mayores de delta, el factor que predomina es el intrínseco y la opción cada vez se asemeja más a su subyacente. El segundo punto interesante ocurre exactamente a un delta de 0.5, es decir, una opción at the money tiene un valor intrínseco de cero, y todo su coste se debe a su probabilidad de ser valioso a vencimiento, es decir, a su volatilidad. El tercer punto de interés es el mínimo para la curva de valor intrínseco. A partir de este punto, el valor intrínseco vuelve a subir, convergiendo asintóticamente a cero. Este punto es el menor coste posible intrínseco y puede considerarse como un punto de equilibrio interesante entre el coste de la opción y las probabilidades de que termine con valor. Calculando el mínimo del factor intrínseco, se obtiene: S eq S (7) eq 0.22 Es decir, este punto de equilibrio se encuentra aproximadamente a 0.75 veces la desviación típica, o lo que es lo mismo, a un delta de 0.22.
6 3. Esperanza matemática Se analiza a continuación la esperanza matemática de la compra de un Call bajo la suposición de que el subyacente sigue una distribución normal. A vencimiento Este caso es el más sencillo, y de forma directa se obtiene que la esperanza matemática a vencimiento de la compra de un Call resulta: EV = r φ(x r ) i φ(x i ) + (S K) (Φ(x r ) Φ(x i )) Dónde se ha utilizado el subíndice i para indicar la volatilidad implicada o esperada y el subíndice r para indicar la volatilidad real que finalmente resultó. Si se calcula la esperanza matemática en vencimiento at the money se obtiene: EV K=S = 1 2 π ( r i ) (8) Este resultado es imprescindible para cualquier trader. La esperanza matemática de las opciones depende de la diferencia entra la volatilidad implicada y la volatilidad real. Si la volatilidad real fue mayor que la esperada, la esperanza matemática es positiva, de lo contrario es negativa. Es imposible a largo plazo obtener beneficios de las opciones si no se tiene una opinión correcta sobre las volatilidades. La ecuación anterior ilustra claramente una regla que los traders de opciones conocen muy bien, comprar volatilidad baja y vender volatilidad alta. Durante la vida de la opción Este caso no resulta trivial ya que la integral de la distribución acumulada no puede ser expresada en funciones elementales. De forma indirecta se puede encontrar la solución a este problema (cuyo desarrollo matemático excede la longitud pretendida del presente artículo): EV K=S = 1 2 π ( r 2 1 ) (9) Dónde se ha utilizado el subíndice 1 para indicar la volatilidad implicada en el momento de la compra, el subíndice 2 para indicar la volatilidad implicada en un momento posterior y el subíndice r para indicar la volatilidad real que finalmente resultó en ese periodo. Este resultado tiene múltiples usos. Se analiza a continuación un caso real, con fecha 10 de Julio del 2015, donde el subyacente (Twitter) tiene un evento importante (su anuncio de resultados trimestrales) el 28 de Julio. Se observa las volatilidades implicadas de las tres opciones más próximas at the money : Fecha Vencimiento Días hasta vencimiento Volatilidad implicada 17-Julio % 21 Agosto % 18 Septiembre %
7 Este comportamiento es el típico en las volatilidades ante un gran evento, donde las opciones que expiran antes del evento no se ven afectadas y las opciones que expiran después del evento aumentan sus volatilidades, siendo mayor el aumento cuanto más próximo al mismo. Por lo tanto, el comportamiento esperado es que a medida que se aproxima la fecha del evento, la volatilidad de Agosto aumentará significativamente y la de Septiembre aumentará moderadamente. Una vez pasado el evento, ambas volatilidades se desplomarán a un valor base en las próximas horas o días. A continuación se muestra una gráfica histórica de Twitter 1 del último año, donde se observa claramente este comportamiento que se repite cada trimestre, donde la serie de color amarillo es la volatilidad implicada y la serie azul es la volatilidad histórica: Usando el resultado de la esperanza matemática es posible responder a preguntas claves para cualquiera que quiera operar este patrón. Cuánto aumentará la volatilidad de Agosto justo antes del evento? Usando la ecuación (9) y suponiendo no arbitraje, se iguala la esperanza matemática a cero y se despeja V2, obteniendo: V 2 = V 1 2 T 1 V r 2 (T 1 T 2 ) T 2 Despejando valores, donde V1=57.7%, Vr=40.1%, T1=42 y T2=18, se obtiene V2=67.97%, lo que representa un aumento de más del 10% en 18 días. Cuánto se desplomará la volatilidad de Agosto justo después del evento? Si por ejemplo no estuviese disponible la opción de Julio, o estamos en un momento posterior al 17 de Julio, no se podría observar de forma directa la volatilidad base. Una opción es utilizar datos históricos para estimar el salto después del evento, pero suele ser mucho mejor enfoque utilizar las volatilidades implicadas que se observan en el mercado. 1 Gráfica por cortesía de CBOE IVolatility Services
8 Volatility (%) Nuevamente, utilizando el resultado en (9), se obtiene: V r = V 1 2 T 1 V 2 2 T 2 T 1 T 2 Este resultado es idéntico al usado por los traders para calcular de forward volatility usando el hecho de que la varianza (ponderada por el tiempo) es aditiva, lo que ratifica la validez del presente enfoque. Despejando valores, donde V1=57.7%, V2=51.5%, T1=42 y T2=70, se obtiene Vr=40.46%. Resumen Se puede concluir que en 18 días la volatilidad implicada de Agosto subirá hasta un valor aproximado del 68%, para luego caer en apenas uno o dos días hasta un 40%. Una estrategia que compre volatilidad ahora y la venda antes del evento se beneficiará de una subida de un 10%, mientras que una estrategia que venda volatilidad antes del evento y la compré después, se beneficiará de un salto del 28%. Estas dos estrategias tienen un perfil de riesgo completamente distinto y debe tenerse en cuenta a la hora de seleccionar la más adecuada. 4. Skew Este modelo normal frente al BS presenta pequeñas diferencias en valores muy out the money o in the money. Es interesante remarcar, que aunque las diferencias sean pequeñas, el modelo BS subvalora las opciones in the money y sobrevalora las opciones out the money con respecto al modelo neutro. Este comportamiento puede explicar una parte del Skew que presentan gran parte de lo assets, como las acciones. Sin embargo, las diferencias no son tan grandes como para explicar completamente el Skew. Lo que es incuestionable, es que el uso del modelo normal, conduciría a un Skew menor. Parte del Skew restante podría explicarse debido a que gran parte de las opciones se usan para hedge, siendo la protección más demandada la compra de Puts. La siguiente figura muestra el resultado de calcular las volatilidades implicadas según el precio de mercado de los call del ES-Sep19 a diferentes Strike Prices para el modelo BS y para el modelo normal, con S=1969, T=73 días y r=0: IV BS IV Normal Strike Prices
9 5. Conclusiones Se ha presentado una forma alternativa de valorar las opciones, suponiendo únicamente una distribución normal de los precios del subyacente. Este enfoque, a pesar de tener sus inconvenientes (como llegar a permitir precios negativos), representa un enfoque más natural y neutro del comportamiento del mercado en muchas situaciones. Las ecuaciones que se obtienen son más sencillas y mucho más interpretables que las derivadas de BS. Todas las interpretaciones y conclusiones que se han presentado son igual de válidas para el modelo BS; por lo que como mínimo tienen un gran valor pedagógico. Así mismo, en muchas condiciones, ambos modelos son similares, pudiendo aplicar cualquier conjunto de ecuaciones con diferencias muy poco significativas. Se ha derivado la fórmula de esperanza matemática bajo este enfoque y se ha utilizado para estimar saltos en las volatilidades ante eventos del subyacente, obteniendo un resultado muy valioso para operar este tipo de patrones. Se ha comprobado que el uso de este modelo normal conllevaría a una pequeña reducción del Skew que presentan la mayoría de Assets, sin embargo, con tiempos largos hasta vencimiento y volatilidades altas es donde se producen las mayores diferencias de los dos enfoques.
10 6. Anexo Para obtener el valor de una opción de estilo europeo bajo el supuesto de que los precios del subyacente siguen una distribución normal, se utiliza el argumento de no arbitraje, es decir, que la esperanza matemática al vencimiento sea cero. El valor de un Call a vencimiento se muestra en la siguiente figura: S K C Que es equivalente a descomponer el valor en una constante y una recta para x>k. La esperanza matemática de una constante bajo cualquier distribución sigue siendo la misma constante, por lo que sólo hay que obtener la esperanza matemática de la recta para x>k para obtener el valor del Call. EV = x=k Aplicando el siguiente cambio de variable: Se obtiene: EV = y = y= K S 1 2π e 1 2 (x S ) 2 (x K)dx x S, dx = dy, x = y + S 1 (φ(y) y + φ(y) (S K)) dy Siendo φ(y) la distribución normal estándar. Integrando se obtiene: EV = φ(y) ] K S + Φ(y) (S K)] K S Siendo Φ(y) la distribución acumulada normal estándar. Finalmente, utilizando las propiedades de la distribución estándar se obtiene: S K K EV = φ ( ) + Φ (S ) (S K)
11 Polígono Industrial Urtinsa, Edificio Antares C/ Las Fábricas 8, Oficina Alcorcón (Madrid). Tlf Fax
Consideraciones al precio de un warrant. El precio del warrant: la prima. Factores que afectan al precio de un warrant
 Consideraciones al precio de un warrant El precio del warrant: la prima La prima es el precio que se paga por comprar un warrant. El inversor adquiere así el derecho a comprar (warrant Call) o vender (warrant
Consideraciones al precio de un warrant El precio del warrant: la prima La prima es el precio que se paga por comprar un warrant. El inversor adquiere así el derecho a comprar (warrant Call) o vender (warrant
Las Griegas de las Opciones
 ANÁLISIS Y OPINIÓN Las Griegas de las Opciones 134 Mtro. Sergio García Quintana, Integrante de la Comisión de Finanzas y Sistema Financiero del Colegio de Contadores Públicos de México, A.C. Son medidas
ANÁLISIS Y OPINIÓN Las Griegas de las Opciones 134 Mtro. Sergio García Quintana, Integrante de la Comisión de Finanzas y Sistema Financiero del Colegio de Contadores Públicos de México, A.C. Son medidas
Aumentando x 10 mis posibilidades de ganar. Las griegas
 Aumentando x 10 mis posibilidades de ganar Las griegas Esto es lo que aprenderás en este video: - Delta, Gamma, Theta, Vega y Rho. - Aplicaciones de Delta. 3 Cuánto más se aproxima uno al sueño, más se
Aumentando x 10 mis posibilidades de ganar Las griegas Esto es lo que aprenderás en este video: - Delta, Gamma, Theta, Vega y Rho. - Aplicaciones de Delta. 3 Cuánto más se aproxima uno al sueño, más se
3. OPCIONES. 3. Opciones. Definición de Opciones:
 3. OPCIONES Definición de Opciones: Es un contrato mediante el cual el comprador de la opción adquiere el derecho más no la obligación de comprar o vender un bien (subyacente) dentro de un plazo determinado
3. OPCIONES Definición de Opciones: Es un contrato mediante el cual el comprador de la opción adquiere el derecho más no la obligación de comprar o vender un bien (subyacente) dentro de un plazo determinado
CAPÍTULO 5 ANÁLISIS DE CONVERGENCIA DEL MÉTODO BINOMIAL AL MODELO DE BLACK & SCHOLES
 CAPÍTULO 5 ANÁLISIS DE CONVERGENCIA DEL MÉTODO BINOMIAL AL MODELO DE BLACK & SCHOLES Para la valuación de opciones hay dos modelos ampliamente reconocidos como son el modelo binomial y el modelo de Black
CAPÍTULO 5 ANÁLISIS DE CONVERGENCIA DEL MÉTODO BINOMIAL AL MODELO DE BLACK & SCHOLES Para la valuación de opciones hay dos modelos ampliamente reconocidos como son el modelo binomial y el modelo de Black
Precio de Opción de Opción de Ejercicio Compra Venta
 Clasificación de los contratos de opción por su precio de ejercicio Los Contratos de Opciones pueden ser clasificados por la diferencia entre su precio de ejercicio y el valor del activo subyacente al
Clasificación de los contratos de opción por su precio de ejercicio Los Contratos de Opciones pueden ser clasificados por la diferencia entre su precio de ejercicio y el valor del activo subyacente al
ANEXO DERIVADOS EL USO DE LAS OPCIONES EN LA INVERSIÓN FINANCIERA
 ANEXO DERIVADOS EL USO DE LAS OPCIONES EN LA INVERSIÓN FINANCIERA ANEXO 2 1- Las opciones como cobertura de riesgo Las Opciones de compra o venta son un instrumento perfecto para realizar coberturas, es
ANEXO DERIVADOS EL USO DE LAS OPCIONES EN LA INVERSIÓN FINANCIERA ANEXO 2 1- Las opciones como cobertura de riesgo Las Opciones de compra o venta son un instrumento perfecto para realizar coberturas, es
3. Qué warrant elegir?
 3 QUE WARRANT ELEGIR? 3.1. Qué subyacente? 3.2. Qué vencimiento? 3.3. Qué strike? 3.4. La relación sensibilidad - delta 3.5. Ejercicios del capítulo 3 3.6. Respuestas a los ejercicios 3. Qué warrant elegir?
3 QUE WARRANT ELEGIR? 3.1. Qué subyacente? 3.2. Qué vencimiento? 3.3. Qué strike? 3.4. La relación sensibilidad - delta 3.5. Ejercicios del capítulo 3 3.6. Respuestas a los ejercicios 3. Qué warrant elegir?
ACCIONES Y OTROS TÍTULOS DE INVERSIÓN
 ACCIONES Y OTROS TÍTULOS DE INVERSIÓN TASAS EFECTIVAS DE RENDIMIENTO ANUAL Y MENSUAL: Es aquélla que se emplea en la compraventa de algunos valores en el Mercado Bursátil o Bolsa de Valores. Estas tasas
ACCIONES Y OTROS TÍTULOS DE INVERSIÓN TASAS EFECTIVAS DE RENDIMIENTO ANUAL Y MENSUAL: Es aquélla que se emplea en la compraventa de algunos valores en el Mercado Bursátil o Bolsa de Valores. Estas tasas
Aumentando x 10 mis posibilidades de ganar. Las opciones financieras
 Aumentando x 10 mis posibilidades de ganar Las opciones financieras Esto es lo que aprenderás en este video: - Características de las opciones. - Descripción de los contratos de opciones. - Tipos de opciones.
Aumentando x 10 mis posibilidades de ganar Las opciones financieras Esto es lo que aprenderás en este video: - Características de las opciones. - Descripción de los contratos de opciones. - Tipos de opciones.
1.4.- D E S I G U A L D A D E S
 1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
Covarianza y coeficiente de correlación
 Covarianza y coeficiente de correlación Cuando analizábamos las variables unidimensionales considerábamos, entre otras medidas importantes, la media y la varianza. Ahora hemos visto que estas medidas también
Covarianza y coeficiente de correlación Cuando analizábamos las variables unidimensionales considerábamos, entre otras medidas importantes, la media y la varianza. Ahora hemos visto que estas medidas también
Foro de Opciones. 1. Introducción. 2. Determinación del precio. 3. Acerca de la volatilidad. 4. Estándares de mercado I.
 Foro de Opciones El objetivo de esta presentación es acercar a los Ingresarios en un nivel básico a los instrumentos de opciones, esta se dividirá en 4 partes de la siguiente manera: 1. Introducción 2.
Foro de Opciones El objetivo de esta presentación es acercar a los Ingresarios en un nivel básico a los instrumentos de opciones, esta se dividirá en 4 partes de la siguiente manera: 1. Introducción 2.
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 3 CAPITALIZACIÓN COMPUESTA
 CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 3 CAPITALIZACIÓN COMPUESTA Javier Bilbao García 1 1.- Capitalización Compuesta Definición: Operación financiera que persigue sustituir un capital por
CESMA BUSINESS SCHOOL MATEMÁTICAS FINANCIERAS. TEMA 3 CAPITALIZACIÓN COMPUESTA Javier Bilbao García 1 1.- Capitalización Compuesta Definición: Operación financiera que persigue sustituir un capital por
Dos meses después, en la fecha de vencimiento del Warrant, suponemos que Telefónica ha subido y se ha revalorizado hasta los 16 euros.
 1. Cómo funcionan los Warrants La inversión en Warrants puede tener como finalidad: La Inversión, o toma de posiciones basada en las expectativas que tenga el inversor acerca del comportamiento futuro
1. Cómo funcionan los Warrants La inversión en Warrants puede tener como finalidad: La Inversión, o toma de posiciones basada en las expectativas que tenga el inversor acerca del comportamiento futuro
Divisibilidad y números primos
 Divisibilidad y números primos Divisibilidad En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos
Divisibilidad y números primos Divisibilidad En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos
Cómo utilizar los warrants?: Principales Estrategias
 Cómo utilizar los warrants?: Principales Estrategias El Warrant frente a la acción: el apalancamiento La principal diferencia entre la inversión en warrants y la inversión directa en acciones radica en
Cómo utilizar los warrants?: Principales Estrategias El Warrant frente a la acción: el apalancamiento La principal diferencia entre la inversión en warrants y la inversión directa en acciones radica en
Registro contable de Supuesto 10 Determinación del derivados OTC valor de una prima de opción (2)
 Ejercicio 10 10 DETERMINACIÓN DE UNA PRIMA EN UNA OPCION (MODELO DE BLACK SCHOLES) Instrucciones Vamos a calcular cual es el importe al que asciende una prima en una opción aplicando el modelo más extendido
Ejercicio 10 10 DETERMINACIÓN DE UNA PRIMA EN UNA OPCION (MODELO DE BLACK SCHOLES) Instrucciones Vamos a calcular cual es el importe al que asciende una prima en una opción aplicando el modelo más extendido
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Tema 3. Medidas de tendencia central. 3.1. Introducción. Contenido
 Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Opciones (Resumen libro Hull)
 Dos tipos básicos de opciones: CALL y PUT Opciones (Resumen libro Hull) CALL = opción de compra. Comprador: pagó (prima) para adquirir el derecho a comprar un activo (activo subyacente) a un precio determinado
Dos tipos básicos de opciones: CALL y PUT Opciones (Resumen libro Hull) CALL = opción de compra. Comprador: pagó (prima) para adquirir el derecho a comprar un activo (activo subyacente) a un precio determinado
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA. La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros.
 QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
MICROECONOMÍA II. PRÁCTICA TEMA II: Equilibrio parcial
 MICROECONOMÍA II PRÁCTICA TEMA II: Equilibrio parcial EJERCICIO 1 A) En equilibrio, la cantidad demandada coincide con la cantidad ofrecida, así como el precio de oferta y demanda. Por lo tanto, para hallar
MICROECONOMÍA II PRÁCTICA TEMA II: Equilibrio parcial EJERCICIO 1 A) En equilibrio, la cantidad demandada coincide con la cantidad ofrecida, así como el precio de oferta y demanda. Por lo tanto, para hallar
PARTE 3 ECUACIONES DE EQUIVALENCIA FINANCIERA T E M A S
 PARTE 3 ECUACIONES DE EQUIVALENCIA FINANCIERA Valor del dinero en el tiempo Conceptos de capitalización y descuento Ecuaciones de equivalencia financiera Ejercicio de reestructuración de deuda T E M A
PARTE 3 ECUACIONES DE EQUIVALENCIA FINANCIERA Valor del dinero en el tiempo Conceptos de capitalización y descuento Ecuaciones de equivalencia financiera Ejercicio de reestructuración de deuda T E M A
Productos de Divisa Tipos de Cambio Exportador
 Productos de Divisa Tipos de Cambio Derivados de Divisa Versión 3.1 Comunicación publicitaria Página 1 Una presencia global: un banco global en los mercados de alto potencial BBVA y Corporate and Investment
Productos de Divisa Tipos de Cambio Derivados de Divisa Versión 3.1 Comunicación publicitaria Página 1 Una presencia global: un banco global en los mercados de alto potencial BBVA y Corporate and Investment
I. RENTABILIDAD FINANCIERA
 I. RENTABILIDAD FINANCIERA En un sentido general, la rentabilidad es la medida del rendimiento que, en un determinado período de tiempo (el ejercicio), producen las magnitudes utilizadas en el mismo, o
I. RENTABILIDAD FINANCIERA En un sentido general, la rentabilidad es la medida del rendimiento que, en un determinado período de tiempo (el ejercicio), producen las magnitudes utilizadas en el mismo, o
CASOS PRACTICOS CON WARRANTS
 4 CASOS PRACTICOS CON WARRANTS 4.1. Aprovechar la subida de una acción 4.2. Aprovechar una bajada de una acción 4.3. Jugar al spread 4.4. Ganar en bolsa con las divisas 4.5. Cubrir una posición a un plazo
4 CASOS PRACTICOS CON WARRANTS 4.1. Aprovechar la subida de una acción 4.2. Aprovechar una bajada de una acción 4.3. Jugar al spread 4.4. Ganar en bolsa con las divisas 4.5. Cubrir una posición a un plazo
Metodología. del ajuste estacional. Tablero de Indicadores Económicos
 Metodología del ajuste estacional Tablero de Indicadores Económicos Metodología del ajuste estacional Componentes de una serie de tiempo Las series de tiempo están constituidas por varios componentes que,
Metodología del ajuste estacional Tablero de Indicadores Económicos Metodología del ajuste estacional Componentes de una serie de tiempo Las series de tiempo están constituidas por varios componentes que,
DOMINIO Y RANGO página 89. Cuando se grafica una función existen las siguientes posibilidades:
 DOMINIO Y RANGO página 89 3. CONCEPTOS Y DEFINICIONES Cuando se grafica una función eisten las siguientes posibilidades: a) Que la gráfica ocupe todo el plano horizontalmente (sobre el eje de las ). b)
DOMINIO Y RANGO página 89 3. CONCEPTOS Y DEFINICIONES Cuando se grafica una función eisten las siguientes posibilidades: a) Que la gráfica ocupe todo el plano horizontalmente (sobre el eje de las ). b)
OPERACIONES EN RÉGIMEN DE COMPUESTA
 OPERACIONES EN RÉGIMEN DE COMPUESTA Las operaciones en régimen de compuesta se caracterizan porque los intereses, a diferencia de lo que ocurre en régimen de simple, a medida que se van generando pasan
OPERACIONES EN RÉGIMEN DE COMPUESTA Las operaciones en régimen de compuesta se caracterizan porque los intereses, a diferencia de lo que ocurre en régimen de simple, a medida que se van generando pasan
Gustavo D Agostino Ezequiel Di Nardo Florencia Enrique Sebastián Marques Federico Reif Javier García Fronti
 VOLATILIDAD IMPLÍCITA EN OPCIONES. EL ROL DE LA FÓRMULA DE BLACK AND SCHOLES Y LA POSIBILIDAD DE CÁLCULO SIN ASUMIR UN MODELO DETERMINADO INTRODUCCIÓN Gustavo D Agostino Ezequiel Di Nardo Florencia Enrique
VOLATILIDAD IMPLÍCITA EN OPCIONES. EL ROL DE LA FÓRMULA DE BLACK AND SCHOLES Y LA POSIBILIDAD DE CÁLCULO SIN ASUMIR UN MODELO DETERMINADO INTRODUCCIÓN Gustavo D Agostino Ezequiel Di Nardo Florencia Enrique
Determinación de primas de acuerdo al Apetito de riesgo de la Compañía por medio de simulaciones
 Determinación de primas de acuerdo al Apetito de riesgo de la Compañía por medio de simulaciones Introducción Las Compañías aseguradoras determinan sus precios basadas en modelos y en información histórica
Determinación de primas de acuerdo al Apetito de riesgo de la Compañía por medio de simulaciones Introducción Las Compañías aseguradoras determinan sus precios basadas en modelos y en información histórica
Técnicas de valor presente para calcular el valor en uso
 Normas Internacionales de Información Financiera NIC - NIIF Guía NIC - NIIF NIC 36 Fundación NIC-NIIF Técnicas de valor presente para calcular el valor en uso Este documento proporciona una guía para utilizar
Normas Internacionales de Información Financiera NIC - NIIF Guía NIC - NIIF NIC 36 Fundación NIC-NIIF Técnicas de valor presente para calcular el valor en uso Este documento proporciona una guía para utilizar
Opciones Financieras : Análisis y Estrategias
 1 Opciones Financieras : Análisis y Estrategias E N LA PRESENTE EXPOSICIÓN TRATAREMOS DE EXPLICAR FACTORES QUE INCIDEN SOBRE EL VALOR DE LAS OPCIONES, DISTINTAS ESTRATEGIAS QUE SE PUEDEN REALIZAR Y LOS
1 Opciones Financieras : Análisis y Estrategias E N LA PRESENTE EXPOSICIÓN TRATAREMOS DE EXPLICAR FACTORES QUE INCIDEN SOBRE EL VALOR DE LAS OPCIONES, DISTINTAS ESTRATEGIAS QUE SE PUEDEN REALIZAR Y LOS
CIIF CENTRO INTERNACIONAL DE INVESTIGACION FINANCIERA
 I E S E Universidad de Navarra CIIF CENTRO INTERNACIONAL DE INVESTIGACION FINANCIERA INFORME SOBRE LA RELACION ENTRE CONSUMO, MOROSIDAD Y CICLOS BURSATILES Miguel A. Ariño* María Coello de Portugal** DOCUMENTO
I E S E Universidad de Navarra CIIF CENTRO INTERNACIONAL DE INVESTIGACION FINANCIERA INFORME SOBRE LA RELACION ENTRE CONSUMO, MOROSIDAD Y CICLOS BURSATILES Miguel A. Ariño* María Coello de Portugal** DOCUMENTO
1.1. Introducción y conceptos básicos
 Tema 1 Variables estadísticas Contenido 1.1. Introducción y conceptos básicos.................. 1 1.2. Tipos de variables estadísticas................... 2 1.3. Distribuciones de frecuencias....................
Tema 1 Variables estadísticas Contenido 1.1. Introducción y conceptos básicos.................. 1 1.2. Tipos de variables estadísticas................... 2 1.3. Distribuciones de frecuencias....................
FUNDACION NIC-NIIF www.nicniif.org
 NORMAS INTERNACIONALES DE INFORMACION FINANCIERA NIC-NIIF Identificación de un contrato de seguro, para que sea de aplicación la NIFF 4 o bien en su defecto otra norma con la NIC 39 si por ejemplo se trata
NORMAS INTERNACIONALES DE INFORMACION FINANCIERA NIC-NIIF Identificación de un contrato de seguro, para que sea de aplicación la NIFF 4 o bien en su defecto otra norma con la NIC 39 si por ejemplo se trata
x 10000 y 8000 x + y 15000 a) La región factible asociada a las restricciones anteriores es la siguiente: Pedro Castro Ortega lasmatematicas.
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Septiembre 2012 - Propuesta A 1. Queremos realizar una inversión en dos tipos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Septiembre 2012 - Propuesta A 1. Queremos realizar una inversión en dos tipos
DIVISAS Evolución y análisis de tipos de cambio(1980-1995)
 DIVISAS Evolución y análisis de tipos de cambio(1980-1995) Pablo Fernández y Miguel Angel Ariño 1. Evolución de los tipos de cambio 2. Rentabilidad de las divisas 3.Volatilidad de las divisas 4. Autocorrelación
DIVISAS Evolución y análisis de tipos de cambio(1980-1995) Pablo Fernández y Miguel Angel Ariño 1. Evolución de los tipos de cambio 2. Rentabilidad de las divisas 3.Volatilidad de las divisas 4. Autocorrelación
ESTRATEGIAS CON OPCIONES
 ESTRATEGIAS CON OPCIONES Por Pablo García Estévez Pablo García Estévez. Doctor en Económicas y Empresariales por la Universidad Complutense de Madrid. Acreditado Doctor por la ACAP. Miembro del IEEE. Es
ESTRATEGIAS CON OPCIONES Por Pablo García Estévez Pablo García Estévez. Doctor en Económicas y Empresariales por la Universidad Complutense de Madrid. Acreditado Doctor por la ACAP. Miembro del IEEE. Es
ANEXO II TEORÍA SOBRE OPCIONES FINANCIERAS
 ANEXO II TEORÍA SOBRE OPCIONES FINANCIERAS OPCIÓN FINANCIERA: Contrato que proporciona a su poseedor (comprador) el derecho (no la obligación) a comprar o vender un determinado activo (activo básico o
ANEXO II TEORÍA SOBRE OPCIONES FINANCIERAS OPCIÓN FINANCIERA: Contrato que proporciona a su poseedor (comprador) el derecho (no la obligación) a comprar o vender un determinado activo (activo básico o
MERCADO DE CAPITALES ERICK J. ESTRADA O. INVESTIGACIÓN EN INTERNET
 MERCADO DE CAPITALES ERICK J. ESTRADA O. INVESTIGACIÓN EN INTERNET Una opción es un contrato entre dos partes (una compradora y otra vendedora), en donde el que compra la opción adquiere el derecho a ejercer
MERCADO DE CAPITALES ERICK J. ESTRADA O. INVESTIGACIÓN EN INTERNET Una opción es un contrato entre dos partes (una compradora y otra vendedora), en donde el que compra la opción adquiere el derecho a ejercer
Inversión. Inversión. Arbitraje. Descuento. Tema 5
 Inversión Tema 5 Inversión Los bienes de inversión obligan a gastar hoy para obtener ganancias en el futuro Vamos a estudiar cómo se valoran los pagos futuros Por ejemplo, la promesa de recibir euro dentro
Inversión Tema 5 Inversión Los bienes de inversión obligan a gastar hoy para obtener ganancias en el futuro Vamos a estudiar cómo se valoran los pagos futuros Por ejemplo, la promesa de recibir euro dentro
Guía warrants BBVA. Le gusta invertir?
 Guía warrants BBVA Le gusta invertir? Índice 1. Qué son los warrants? 5 2. Características de los warrants 7 3. Tipos de warrants 11 4. Particularidades de los warrants 15 5. La prima de un warrant 17
Guía warrants BBVA Le gusta invertir? Índice 1. Qué son los warrants? 5 2. Características de los warrants 7 3. Tipos de warrants 11 4. Particularidades de los warrants 15 5. La prima de un warrant 17
Análisis y cuantificación del Riesgo
 Análisis y cuantificación del Riesgo 1 Qué es el análisis del Riesgo? 2. Métodos M de Análisis de riesgos 3. Método M de Montecarlo 4. Modelo de Análisis de Riesgos 5. Qué pasos de deben seguir para el
Análisis y cuantificación del Riesgo 1 Qué es el análisis del Riesgo? 2. Métodos M de Análisis de riesgos 3. Método M de Montecarlo 4. Modelo de Análisis de Riesgos 5. Qué pasos de deben seguir para el
MANUAL OPCIONES FUTUROS
 MANUAL DE OPCIONES Y FUTUROS Segunda Edición 4 LA VOLATILIDAD 4.1. Qué es la volatilidad? 4.2. Información y volatilidad 4.3. La volatilidad como medida de probabilidad 4.4. Tipos de volatilidad 4.5. Sensibilidades
MANUAL DE OPCIONES Y FUTUROS Segunda Edición 4 LA VOLATILIDAD 4.1. Qué es la volatilidad? 4.2. Información y volatilidad 4.3. La volatilidad como medida de probabilidad 4.4. Tipos de volatilidad 4.5. Sensibilidades
Aumentando x 10 mis posibilidades de ganar. Compra de opciones Call
 Aumentando x 10 mis posibilidades de ganar Compra de opciones Call Esto es lo que aprenderás en este video: - Valor intrínseco de las opciones. - Valor extrínseco de las opciones. - Compra de opciones
Aumentando x 10 mis posibilidades de ganar Compra de opciones Call Esto es lo que aprenderás en este video: - Valor intrínseco de las opciones. - Valor extrínseco de las opciones. - Compra de opciones
E 1 E 2 E 2 E 3 E 4 E 5 2E 4
 Problemas resueltos de Espacios Vectoriales: 1- Para cada uno de los conjuntos de vectores que se dan a continuación estudia si son linealmente independientes, sistema generador o base: a) (2, 1, 1, 1),
Problemas resueltos de Espacios Vectoriales: 1- Para cada uno de los conjuntos de vectores que se dan a continuación estudia si son linealmente independientes, sistema generador o base: a) (2, 1, 1, 1),
Aula Banca Privada. La importancia de la diversificación
 Aula Banca Privada La importancia de la diversificación La importancia de la diversificación La diversificación de carteras es el principio básico de la operativa en mercados financieros, según el cual
Aula Banca Privada La importancia de la diversificación La importancia de la diversificación La diversificación de carteras es el principio básico de la operativa en mercados financieros, según el cual
ANÁLISIS DE VARIANZA EMPLEANDO EXCEL y WINSTATS
 ANÁLISIS DE VARIANZA EMPLEANDO EXCEL y WINSTATS 1) INTRODUCCIÓN El análisis de varianza es una técnica que se puede utilizar para decidir si las medias de dos o más poblaciones son iguales. La prueba se
ANÁLISIS DE VARIANZA EMPLEANDO EXCEL y WINSTATS 1) INTRODUCCIÓN El análisis de varianza es una técnica que se puede utilizar para decidir si las medias de dos o más poblaciones son iguales. La prueba se
DISCOUNT CALL+ DISCOUNT PUT+
 DISCOUNT CALL+ DISCOUNT PUT+ www.productoscotizados.com 900 801 801 El banco para un mundo en evolución Quiere posicionarse de forma apalancada sobre una evolución lateral del Ibex-35? Al apalancamiento
DISCOUNT CALL+ DISCOUNT PUT+ www.productoscotizados.com 900 801 801 El banco para un mundo en evolución Quiere posicionarse de forma apalancada sobre una evolución lateral del Ibex-35? Al apalancamiento
DESCRIPCIÓN DE LA METODOLOGÍA UTILIZADA EN EL PROGRAMA DE CESTAS REDUCIDAS ÓPTIMAS
 DESCRIPCIÓN DE LA METODOLOGÍA UTILIZADA EN EL PROGRAMA DE CESTAS REDUCIDAS ÓPTIMAS Replicar un índice Formar una cartera que replique un índice (o un futuro) como el IBEX 35, no es más que hacerse con
DESCRIPCIÓN DE LA METODOLOGÍA UTILIZADA EN EL PROGRAMA DE CESTAS REDUCIDAS ÓPTIMAS Replicar un índice Formar una cartera que replique un índice (o un futuro) como el IBEX 35, no es más que hacerse con
Medias Móviles: Señales para invertir en la Bolsa
 www.gacetafinanciera.com Medias Móviles: Señales para invertir en la Bolsa Juan P López..www.futuros.com Las medias móviles continúan siendo una herramienta básica en lo que se refiere a determinar tendencias
www.gacetafinanciera.com Medias Móviles: Señales para invertir en la Bolsa Juan P López..www.futuros.com Las medias móviles continúan siendo una herramienta básica en lo que se refiere a determinar tendencias
EJERCICIOS DE MATEMÁTICAS I HOJA 4. Ejercicio 1. Se consideran los vectores
 EJERCICIOS DE MATEMÁTICAS I HOJA 4 Ejercicio 1. Se consideran los vectores u 1 = (1, 1, 0, 1), u 2 = (0, 2, 1, 0), u 3 = ( 1, 1, 1, 1), u 4 = (2, 2, 1, 0) de R 4. Expresa, si es posible, los vectores u
EJERCICIOS DE MATEMÁTICAS I HOJA 4 Ejercicio 1. Se consideran los vectores u 1 = (1, 1, 0, 1), u 2 = (0, 2, 1, 0), u 3 = ( 1, 1, 1, 1), u 4 = (2, 2, 1, 0) de R 4. Expresa, si es posible, los vectores u
Como se mencionó en la parte de la teoría, no existe consenso en cuanto a la
 4. Metodología Definición de empleo informal Como se mencionó en la parte de la teoría, no existe consenso en cuanto a la definición de empleo informal y diferentes estudios han utilizado matices distintas
4. Metodología Definición de empleo informal Como se mencionó en la parte de la teoría, no existe consenso en cuanto a la definición de empleo informal y diferentes estudios han utilizado matices distintas
3.1 Opciones reales Opciones Call Opciones Put Compra de Call
 3.1 Opciones reales La teoría de opciones tiene un origen puramente financiero, se usa ampliamente como estrategia de cobertura de riesgos para inversiones en valores o acciones e inclusive existen opciones
3.1 Opciones reales La teoría de opciones tiene un origen puramente financiero, se usa ampliamente como estrategia de cobertura de riesgos para inversiones en valores o acciones e inclusive existen opciones
FONDO MUTUO SURA SELECCION ACCIONES USA SERIE A Folleto Informativo al cierre de septiembre 2015
 FONDO MUTUO SURA SELECCION ACCIONES USA SERIE A Administradora RUN Patrimonio Serie Monto Mínimo S.A. 8915 CLP $2.016.700.184 $5.000 Rentabilidad en Pesos desde 21/03/2012 a 90% 1 Mes -3,98% Anual de Costos
FONDO MUTUO SURA SELECCION ACCIONES USA SERIE A Administradora RUN Patrimonio Serie Monto Mínimo S.A. 8915 CLP $2.016.700.184 $5.000 Rentabilidad en Pesos desde 21/03/2012 a 90% 1 Mes -3,98% Anual de Costos
Inferencia Estadística
 EYP14 Estadística para Construcción Civil 1 Inferencia Estadística El campo de la inferencia estadística está formado por los métodos utilizados para tomar decisiones o para obtener conclusiones sobre
EYP14 Estadística para Construcción Civil 1 Inferencia Estadística El campo de la inferencia estadística está formado por los métodos utilizados para tomar decisiones o para obtener conclusiones sobre
La derivada de y respecto a x es lo que varía y por cada unidad que varía x. Ese valor se designa por dy dx.
 Conceptos de derivada y de diferencial Roberto C. Redondo Melchor, Norberto Redondo Melchor, Félix Redondo Quintela 1 Universidad de Salamanca 18 de agosto de 2012 v1.3: 17 de septiembre de 2012 Aunque
Conceptos de derivada y de diferencial Roberto C. Redondo Melchor, Norberto Redondo Melchor, Félix Redondo Quintela 1 Universidad de Salamanca 18 de agosto de 2012 v1.3: 17 de septiembre de 2012 Aunque
FONDO MUTUO SURA SELECCION ACCIONES CHILE SERIE A Folleto Informativo al cierre de septiembre 2015
 FONDO MUTUO SURA SELECCION ACCIONES CHILE SERIE A Administradora RUN Patrimonio Serie Monto Mínimo S.A. 8685 CLP $504.867.977 $5.000 Plazo : 10 días Rentabilidad en Pesos desde 01/10/2010 a 3% 1 Mes -3,55%
FONDO MUTUO SURA SELECCION ACCIONES CHILE SERIE A Administradora RUN Patrimonio Serie Monto Mínimo S.A. 8685 CLP $504.867.977 $5.000 Plazo : 10 días Rentabilidad en Pesos desde 01/10/2010 a 3% 1 Mes -3,55%
MEDIDAS DE TENDENCIA CENTRAL
 CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
ORGANIZACIÓN INDUSTRIAL (16691-ECO) PARTE II: MODELOS DE COMPETENCIA IMPERFECTA TEMA 2: EL MONOPOLIO SOLUCIÓN A LOS PROBLEMAS PROPUESTOS
 ORGANIZACIÓN INDUSTRIAL (16691-ECO) PARTE II: MODELOS DE COMPETENCIA IMPERFECTA TEMA 2: EL MONOPOLIO 2.1 ANÁLISIS DE EQUILIBRIO 2.2. DISCRIMINACIÓN DE PRECIOS Y REGULACIÓN SOLUCIÓN A LOS PROBLEMAS PROPUESTOS
ORGANIZACIÓN INDUSTRIAL (16691-ECO) PARTE II: MODELOS DE COMPETENCIA IMPERFECTA TEMA 2: EL MONOPOLIO 2.1 ANÁLISIS DE EQUILIBRIO 2.2. DISCRIMINACIÓN DE PRECIOS Y REGULACIÓN SOLUCIÓN A LOS PROBLEMAS PROPUESTOS
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
RESPUESTAS A LAS PREGUNTAS DEL TEMA 3
 RESPUESTAS A LAS PREGUNTAS DEL TEMA 3 Las respuestas en algún caso (primera pregunta) son más largas de lo requerido para que sirva de explicación 1. Explica brevemente qué significan cada una de las curvas
RESPUESTAS A LAS PREGUNTAS DEL TEMA 3 Las respuestas en algún caso (primera pregunta) son más largas de lo requerido para que sirva de explicación 1. Explica brevemente qué significan cada una de las curvas
Marialejandra Castillo Torres Carlos Enrique Vecino Arenas, Ph. D
 Marialejandra Castillo orres Carlos Enrique Vecino Arenas, Ph. D Las opciones son transadas en los mercados financieros. Una opción call le da a su propietario el derecho más no la obligación de comprar
Marialejandra Castillo orres Carlos Enrique Vecino Arenas, Ph. D Las opciones son transadas en los mercados financieros. Una opción call le da a su propietario el derecho más no la obligación de comprar
SISTEMAS DE ECUACIONES LINEALES
 SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
Diferenciabilidad. Definición 1 (Función diferenciable). Cálculo. Segundo parcial. Curso 2004-2005
 Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 2004-2005 Diferenciabilidad. 1. Definición de función diferenciable Después del estudio de los ites de funciones
Univ. de Alcalá de Henares Ingeniería de Telecomunicación Cálculo. Segundo parcial. Curso 2004-2005 Diferenciabilidad. 1. Definición de función diferenciable Después del estudio de los ites de funciones
CAPÍTULO IV METODOLOGÍA PARA EL CONTROL DE INVENTARIOS. En este capítulo se presenta los pasos que se siguieron para la elaboración de un sistema de
 CAPÍTULO IV METODOLOGÍA PARA EL CONTROL DE INVENTARIOS En este capítulo se presenta los pasos que se siguieron para la elaboración de un sistema de inventarios para lograr un control de los productos.
CAPÍTULO IV METODOLOGÍA PARA EL CONTROL DE INVENTARIOS En este capítulo se presenta los pasos que se siguieron para la elaboración de un sistema de inventarios para lograr un control de los productos.
SÍNTESIS Y PERSPECTIVAS
 SÍNTESIS Y PERSPECTIVAS Los invitamos a observar, a identificar problemas, pero al mismo tiempo a buscar oportunidades de mejoras en sus empresas. REVISIÓN DE CONCEPTOS. Esta es la última clase del curso.
SÍNTESIS Y PERSPECTIVAS Los invitamos a observar, a identificar problemas, pero al mismo tiempo a buscar oportunidades de mejoras en sus empresas. REVISIÓN DE CONCEPTOS. Esta es la última clase del curso.
ANÁLISIS DE BONOS. Fuente: Alexander, Sharpe, Bailey; Fundamentos de Inversiones: Teoría y Práctica; Tercera edición, 2003
 ANÁLISIS DE BONOS Fuente: Alexander, Sharpe, Bailey; Fundamentos de Inversiones: Teoría y Práctica; Tercera edición, 2003 Métodos de Análisis Una forma de analizar un bono es comparar su rendimiento al
ANÁLISIS DE BONOS Fuente: Alexander, Sharpe, Bailey; Fundamentos de Inversiones: Teoría y Práctica; Tercera edición, 2003 Métodos de Análisis Una forma de analizar un bono es comparar su rendimiento al
El palacio de la Alhambra: La primera expansión. El favor de los visires
 El palacio de la Alhambra: La primera expansión El favor de los visires Traducido al español por javche Esta expansión contiene cuatro módulos diferentes, que pueden combinarse individualmente o todos
El palacio de la Alhambra: La primera expansión El favor de los visires Traducido al español por javche Esta expansión contiene cuatro módulos diferentes, que pueden combinarse individualmente o todos
1 de cada 5 ticos usa redes Sociales
 1 de cada 5 ticos usa redes Sociales el NSE o el nivel educativo mayor es el uso de redes sociales. Se entrevistó a 1210 personas costarricenses entre 18 y 69 años de edad, residentes en todo el territorio
1 de cada 5 ticos usa redes Sociales el NSE o el nivel educativo mayor es el uso de redes sociales. Se entrevistó a 1210 personas costarricenses entre 18 y 69 años de edad, residentes en todo el territorio
Módulo 9 Sistema matemático y operaciones binarias
 Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Módulo 9 Sistema matemático y operaciones binarias OBJETIVO: Identificar los conjuntos de números naturales, enteros, racionales e irracionales; resolver una operación binaria, representar un número racional
Pablo Fernández. IESE. Valoración de opciones por simulación 1 VALORACIÓN DE OPCIONES POR SIMULACIÓN Pablo Fernández IESE
 Pablo Fernández. IESE. Valoración de opciones por simulación 1 VALORACIÓN DE OPCIONES POR SIMULACIÓN Pablo Fernández IESE 1. Fórmulas utilizadas en la simulación de la evolución del precio de una acción
Pablo Fernández. IESE. Valoración de opciones por simulación 1 VALORACIÓN DE OPCIONES POR SIMULACIÓN Pablo Fernández IESE 1. Fórmulas utilizadas en la simulación de la evolución del precio de una acción
Antes de invertir... Cómo comprar y vender opciones y futuros?
 123456789 Antes de invertir... Cómo comprar y vender opciones y futuros? Los productos derivados, al igual que otros productos financieros negociables, se pueden comprar y vender en el mercado secundario
123456789 Antes de invertir... Cómo comprar y vender opciones y futuros? Los productos derivados, al igual que otros productos financieros negociables, se pueden comprar y vender en el mercado secundario
Modelo de fuerza deportiva NOTA TÉCNICA
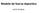 Modelo de fuerza deportiva NOTA TÉCNICA Contenido 1 Motivación 3 2 El modelo de fuerza deportiva 3 2.1 Supuestos del modelo 3 2.2 Críticas al modelo 4 2.3 Formulación 4 2.4 Estimación de los parámetros
Modelo de fuerza deportiva NOTA TÉCNICA Contenido 1 Motivación 3 2 El modelo de fuerza deportiva 3 2.1 Supuestos del modelo 3 2.2 Críticas al modelo 4 2.3 Formulación 4 2.4 Estimación de los parámetros
A estas alturas de nuestros conocimientos vamos a establecer dos reglas muy prácticas de cómo sumar dos números reales:
 ADICIÓN Y RESTA DE NUMEROS REALES ADICIÓN L a adición o suma de números reales se representa mediante el símbolo más (+) y es considerada una operación binaria porque se aplica a una pareja de números,
ADICIÓN Y RESTA DE NUMEROS REALES ADICIÓN L a adición o suma de números reales se representa mediante el símbolo más (+) y es considerada una operación binaria porque se aplica a una pareja de números,
OPERACIONES ESTRUCTURADAS -- NEGOCIACIÓN DE VOLATILIDAD DE TASA DE CAMBIO CON AJUSTE (VCA)
 OPERACIONES ESTRUCTURADAS -- NEGOCIACIÓN DE VOLATILIDAD DE TASA DE CAMBIO CON AJUSTE (VCA) Actualmente, la BM&F autoriza para negociación un conjunto de operaciones estructuradas de volatilidad que incluye
OPERACIONES ESTRUCTURADAS -- NEGOCIACIÓN DE VOLATILIDAD DE TASA DE CAMBIO CON AJUSTE (VCA) Actualmente, la BM&F autoriza para negociación un conjunto de operaciones estructuradas de volatilidad que incluye
Un problema sobre repetidas apuestas al azar
 Un problema sobre repetidas apuestas al azar Eleonora Catsigeras 1 10 de marzo de 2003. Resumen En estas notas se da el enunciado y una demostración de un conocido resultado sobre la probabilidad de éxito
Un problema sobre repetidas apuestas al azar Eleonora Catsigeras 1 10 de marzo de 2003. Resumen En estas notas se da el enunciado y una demostración de un conocido resultado sobre la probabilidad de éxito
TIPO DE CAMBIO, TIPOS DE INTERES Y MOVIMIENTOS DE CAPITAL
 TIPO DE CAMBIO, TIPOS DE INTERES Y MOVIMIENTOS DE CAPITAL En esta breve nota se intentan analizar las relaciones existentes en el sector español entre tipo de cambio, tasa de inflación y tipos de interés,
TIPO DE CAMBIO, TIPOS DE INTERES Y MOVIMIENTOS DE CAPITAL En esta breve nota se intentan analizar las relaciones existentes en el sector español entre tipo de cambio, tasa de inflación y tipos de interés,
1. Lección 5 - Comparación y Sustitución de capitales
 Apuntes: Matemáticas Financieras 1. Lección 5 - Comparación y Sustitución de capitales 1.1. Comparación de Capitales Se dice que dos capitales son equivalentes cuando tienen el mismo valor en la fecha
Apuntes: Matemáticas Financieras 1. Lección 5 - Comparación y Sustitución de capitales 1.1. Comparación de Capitales Se dice que dos capitales son equivalentes cuando tienen el mismo valor en la fecha
TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d.
![TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d. TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d.](/thumbs/31/15114944.jpg) C U R S O: FÍSICA COMÚN MATERIAL: FC-09 TRABAJO Y ENERGÍA La energía desempeña un papel muy importante en el mundo actual, por lo cual se justifica que la conozcamos mejor. Iniciamos nuestro estudio presentando
C U R S O: FÍSICA COMÚN MATERIAL: FC-09 TRABAJO Y ENERGÍA La energía desempeña un papel muy importante en el mundo actual, por lo cual se justifica que la conozcamos mejor. Iniciamos nuestro estudio presentando
Información sobre la naturaleza y riesgos de instrumentos de inversión derivados
 En cumplimiento de sus obligaciones de informarle sobre la naturaleza y riesgos de los productos financieros de inversión, con anterioridad a su contratación, Banco de Caja España de Inversiones, Salamanca
En cumplimiento de sus obligaciones de informarle sobre la naturaleza y riesgos de los productos financieros de inversión, con anterioridad a su contratación, Banco de Caja España de Inversiones, Salamanca
Warrants: una nueva forma de invertir
 Warrants: una nueva forma de invertir José Manuel Alonso Cada vez más personas en todo el mundo invierten sus ahorros en la Bolsa, porque su rentabilidad suele ser mayor que la de otras formas de inversión
Warrants: una nueva forma de invertir José Manuel Alonso Cada vez más personas en todo el mundo invierten sus ahorros en la Bolsa, porque su rentabilidad suele ser mayor que la de otras formas de inversión
POLITICAS DE LA COMPETENCIA Licenciatura en Economía, 4º Curso (Grupos I y II) Profesor: Georges Siotis. Hoja 5: Integración vertical
 POLITICAS DE LA COMPETENCIA Licenciatura en Economía, 4º Curso (Grupos I y II) Profesor: Georges Siotis Hoja 5: Integración vertical Inversiones específicas 1. Imagine una imprenta, que pertenece y es
POLITICAS DE LA COMPETENCIA Licenciatura en Economía, 4º Curso (Grupos I y II) Profesor: Georges Siotis Hoja 5: Integración vertical Inversiones específicas 1. Imagine una imprenta, que pertenece y es
LÍMITES Y CONTINUIDAD DE FUNCIONES
 Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Instrumentos Derivados del Mercado Local: Tipologías y Valorización a Mercado. Santiago, 29 de marzo de 2012 ADV
 Instrumentos Derivados del Mercado Local: Tipologías y Valorización a Mercado Santiago, 29 de marzo de 2012 1 Contenidos Descripción de los Instrumentos Condiciones de Mercado Valorización de Mercado 2
Instrumentos Derivados del Mercado Local: Tipologías y Valorización a Mercado Santiago, 29 de marzo de 2012 1 Contenidos Descripción de los Instrumentos Condiciones de Mercado Valorización de Mercado 2
C A P Í T U L O 1 LA PROBABILIDAD DE HELADA Y EL RIESGO DE DAÑO IMPORTANCIA DE LA PROBABILIDAD Y DEL RIESGO
 C A P Í T U L O 1 LA PROBABILIDAD DE HELADA Y EL RIESGO DE DAÑO IMPORTANCIA DE LA PROBABILIDAD Y DEL RIESGO Los métodos más eficaces de protección contra las heladas son la plantación de cultivos que no
C A P Í T U L O 1 LA PROBABILIDAD DE HELADA Y EL RIESGO DE DAÑO IMPORTANCIA DE LA PROBABILIDAD Y DEL RIESGO Los métodos más eficaces de protección contra las heladas son la plantación de cultivos que no
En un primer momento puede parecer que las opciones son un producto de innovación financiera, pero en realidad tienen una larga tradición.
 Este manual ha sido elaborado por La Caixa como ayuda y soporte a la necesaria formación que se requiere para la inversión en WARRANTS, La Caixa no asume responsabilidad alguna por la exactitud o falta
Este manual ha sido elaborado por La Caixa como ayuda y soporte a la necesaria formación que se requiere para la inversión en WARRANTS, La Caixa no asume responsabilidad alguna por la exactitud o falta
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
Apuntes de Matemática Discreta 9. Funciones
 Apuntes de Matemática Discreta 9. Funciones Francisco José González Gutiérrez Cádiz, Octubre de 004 Universidad de Cádiz Departamento de Matemáticas ii Lección 9 Funciones Contenido 9.1 Definiciones y
Apuntes de Matemática Discreta 9. Funciones Francisco José González Gutiérrez Cádiz, Octubre de 004 Universidad de Cádiz Departamento de Matemáticas ii Lección 9 Funciones Contenido 9.1 Definiciones y
FONDO MUTUO SURA RENTA DEPOSITO CHILE SERIE A Folleto Informativo al cierre de noviembre 2015
 FONDO MUTUO SURA RENTA DEPOSITO CHILE SERIE A Administradora RUN Patrimonio Serie Monto Mínimo S.A. 8678 CLP $18.936.876.967 $5.000 Rentabilidad en Pesos desde 01/12/2010 a 24% Rentabilidades Nominales
FONDO MUTUO SURA RENTA DEPOSITO CHILE SERIE A Administradora RUN Patrimonio Serie Monto Mínimo S.A. 8678 CLP $18.936.876.967 $5.000 Rentabilidad en Pesos desde 01/12/2010 a 24% Rentabilidades Nominales
Cifras significativas e incertidumbre en las mediciones
 Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
Aproximación de patrones estacionales en el mercado cambiario de Costa Rica: octubre 2006 - junio 2014. Allechar Serrano López
 Aproximación de patrones estacionales en el mercado cambiario de Costa Rica: octubre 2006 - junio 2014 Allechar Serrano López Documento de Trabajo DT-09-2014 Departamento de Investigación Económica División
Aproximación de patrones estacionales en el mercado cambiario de Costa Rica: octubre 2006 - junio 2014 Allechar Serrano López Documento de Trabajo DT-09-2014 Departamento de Investigación Económica División
Operativa en Acciones: Introducción a la Bolsa
 Operativa en Acciones: Introducción a la Bolsa Índice 1. Introducción 2. Mercado de acciones 3. Libro de órdenes 4. Ordenes Básicas 5. Liquidez 6. Información Básica Conceptos 7. Operativa Ejemplo 8. Horarios
Operativa en Acciones: Introducción a la Bolsa Índice 1. Introducción 2. Mercado de acciones 3. Libro de órdenes 4. Ordenes Básicas 5. Liquidez 6. Información Básica Conceptos 7. Operativa Ejemplo 8. Horarios
Productos Cotizados de Apalancamiento de BNP Paribas WARRANTS
 Productos Cotizados de Apalancamiento de BNP Paribas WARRANTS En los últimos tiempos los Hedge Funds se han hecho muy famosos por sus capacidades de obtener rentabilidad sea cual sea la tendencia de mercado,
Productos Cotizados de Apalancamiento de BNP Paribas WARRANTS En los últimos tiempos los Hedge Funds se han hecho muy famosos por sus capacidades de obtener rentabilidad sea cual sea la tendencia de mercado,
Unidad 6 Cálculo de máximos y mínimos
 Unidad 6 Cálculo de máimos y mínimos Objetivos Al terminar la unidad, el alumno: Utilizará la derivada para decidir cuándo una función es creciente o decreciente. Usará la derivada para calcular los etremos
Unidad 6 Cálculo de máimos y mínimos Objetivos Al terminar la unidad, el alumno: Utilizará la derivada para decidir cuándo una función es creciente o decreciente. Usará la derivada para calcular los etremos
UNA COMPARACIÓN DE LAS PROYECCIONES DE POBLACIÓN PARA ESPAÑA, LA ZONA DEL EURO Y ESTADOS UNIDOS
 UNA COMPARACIÓN DE LAS PROYECCIONES DE POBLACIÓN PARA, LA ZONA DEL EURO Y Una comparación de las proyecciones de población para España, la zona del euro y Estados Unidos Este artículo ha sido elaborado
UNA COMPARACIÓN DE LAS PROYECCIONES DE POBLACIÓN PARA, LA ZONA DEL EURO Y Una comparación de las proyecciones de población para España, la zona del euro y Estados Unidos Este artículo ha sido elaborado
