PROBLEMAS CAPÍTULO 5 V I = R = X 1 X
|
|
|
- María Nieves Correa Soler
- hace 8 años
- Vistas:
Transcripción
1 PROBLEMAS APÍULO 5.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina.000 VAR. Se pide, calcula: a) El valo de R,, y L. b) La potencia disipada en R si po accidente se desconecta. c) uál es el valo de paa el cual el facto de potencia del conjunto es de 0,9 en etaso?. RESOLUIÓN: a) Paa obtene los valoes de R, ó L de una impedancia, conocido su tiángulo de potencias, es necesaio calcula el valo de la tensión ente los extemos de la misma, o la coiente que cicula po ella, ya que: V P= R R I = R R Q= X L, I L, V = X L, L, Paa el condensado es conocida la tensión ente sus extemos, po tanto: 300= 00 ; X = 33,3 Ω X = x π x f x X ; = 3,9µ F Del esto de los elementos pasivos no es conocido ni la tensión ente sus extemos ni la coiente que cicula po ellos. Paa posegui, se han de agupa los elementos hasta una sección del cicuito en la que se conozca o bien la tensión o bien la coiente. En este caso, se habán de agupa L, R y ya que es conocida la tensión en los extemos de.
2 Haciendo el agupamiento se obtiene el esquema de la figua. El tiángulo de potencias del conjunto se obtiene de la siguiente foma: Q= Q L P = PR = 300 W - Q = =700 VAR S = P +Q =76,6 VA ( onocida la tensión en los extemos del conjunto de cagas se puede calcula la coiente que fluye hacia 76, ellas, así se tiene que: S =V I ; I = = 3,8 A 00 omo esta coiente cicula po la bobina, y es conocido su tiángulo de potencias, se llega a:.000 = X L 3,8 ; X L = 69 Ω X L L= ; x π x f x L L= 0 mh Habá que agupa R y ya que es conocida la coiente que cicula po la bobina. El tiángulo de potencias del conjunto seá: P = PR = 300W ; Q= Q = 300VAR( a ; S = P + Q = 44,3VA po tanto, la tensión ente los extemos de R y vendá dada po: 44,3 =V x 3,8 ; V =,4 V,4 Paa la esistencia R, se tiene que: 300= R ; R= 4,4 Ω y paa el condensado se obtiene: 300=,4 ; X = 4,4 Ω X = x π x f x X ; =77 µ F b) Al supimi vaía la impedancia del conjunto inicial R, L,. Po tanto, vaía la coiente que cicula po la bobina y po consiguiente la tensión ente los extemos de la esistencia. Así la nueva configuación tendá
3 un nuevo tiángulo de potencias. eniendo en cuenta que los valoes de R y L pemanecen invaiables, la impedancia del conjunto seá: Z = 4,4 + j 69= 80,4 59 Ω 00 omo la tensión pemanece igual, la coiente po la impedancia Z vendá dada po: I = =,5 A 80,4 Po tanto, la potencia disipada po la esistencia seá: PR = 4,4 x,5 = 56 W c) En el apatado a), se obtuvo el tiángulo de potencias del conjunto de cagas exceptuado. Repesentando dicho tiángulo y el tiángulo de potencias del condensado tal que el tiángulo de potencias total tenga un facto de potencia de 0,9 en etaso, se tiene el diagama de la figua. En él que se ha epesentado: P = 300 W ; Q=700 VAR( ; S =76,VA ; fp = 0,39( ; θ = 66,8 Paa el nuevo facto de potencia se tiene que: f p= 0,9( ; θ = 5, Q Del tiángulo de potencias, con el facto de potencias coegido: tg 5,8 = ; Q = 554,7 VAR( 300 a
4 Q V = =V x x π x f x ; = 44 µ F X.- Paa alimenta una estación aeopotuaia se utiliza un tansfomado monofásico de 50 kva, 0 V, 50 Hz. En dicha instalación existen las siguientes cagas: 0 motoes de inducción monofásicos de 5 V, 0 V, 50 Hz, fp= 0,84 en etaso cada uno de ellos. 40 tubos fluoescentes, paa alumbado geneal, de 60 W, 0 Hz, fp= 0,5 en etaso, po unidad. Distintas tomas de alimentación con un consumo total de kw, 0 V, 50 Hz y facto de potencia unidad. Al conjunto de cagas anteiomente citadas se le petende añadi un equipo de aie acondicionado, cuya placa de caacteísticas es: 3.70 W, 0 V, 50 Hz, 8,8 A, siendo el equipo inductivo. Se pide, obtene la foma más sencilla de conecta todas las cagas, paa que funcionen coecta y simultáneamente todos los elementos involucados, haciendo los cálculos petinentes paa llega a dicha solución. RESOLUIÓN: Paa que todas las cagas funcionen adecuada y simultáneamente, se han de conecta en paalelo con la fuente, en este caso el tansfomado, ya que todas las cagas han de funciona a 0 V. El tansfomado tiene un capacidad máxima de 50 kva, cuyo valo no ha de sobepasase. El coecto funcionamiento se compobaá analizando el tiángulo de potencias total y viendo si la potencia apaente total del conjunto es mayo, meno o igual a la potencia apaente nominal del tansfomado. Paa los motoes: PM = 0 x 5 x736 = W ; QM = PM +QM = 3.770,4VAR( PM S M = = = ,5 VA fpm 0, Paa los tubos fluoescentes: PF = 40 x 60=.400 W ; S F = = 4.800VA ; Q 0,5 Paa las tomas de alimentación: P =.000W ; Q = 0 VAR ; S =.000VA Paa el equipo de aie acondicionado: PE = 3.70W ; S E = 0 x 8,8 = 4.36 VA ; El tiángulo de potencias total, del conjunto de cagas, viene dado po: P = PM + PF + P + PE = W Q = Q +Q +Q +Q = 9.755,5 VAR( M S F = VA _ 54 kva E F = 4.56,9VAR Q E ( =.88,VAR Po tanto, la potencia apaente total del conjunto de cagas es supeio a la potencia apaente nominal del tansfomado, con lo que éste no puede alimenta todas las cagas. Si se conecta un condensado en paalelo con el conjunto de cagas, al mantenese constante la tensión de alimentación, las cagas funcionaán adecuadamente y el efecto del condensado seá el de educi la (
5 coiente de alimentación y po tanto disminui la potencia apaente del conjunto cagas-condensado. Este efecto se muesta en el diagama de la figua. Del tiángulo de potencias del conjunto caga-condensado tiene que: S = P +( Q - Q ) Q =7.776 VAR ( a desestimándose la solución de la potencia eactiva caga-condensado en adelanto. V omo la tensión se mantiene a 0 V, se obtiene: X = ; X = 6, Ω ; = 5,4 µ F Q 3.- Un cicuito de luces paa la navegación aéea se puede epesenta, en deteminadas condiciones de funcionamiento, po el esquema mostado en la siguiente figua. Medido el facto de potencia de tabajo del geneado de coiente se obtiene un valo de 0'9 en etaso. La impedancia Z A de tipo inductivo, que epesenta las luces con sus tansfomadoes de aislamiento, disipan una potencia apaente de 5'8 kva con un facto de potencia 0'86 en etaso. La impedancia Z de tipo capacitivo, que epesenta efectos esistivo capacitivos, disipa una potencia apaente de,5 kva. Po último, la impedancia Z B de tipo inductivo, que simula pédidas del conjunto del cicuito, consume una potencia apaente de 5 kva. Medida la potencia apaente total del conjunto Z B, se obtiene un valo de 5'6 kva. Se pide: a) alcula las potencias activa y eactiva de Z B y Z, así como las suministadas po el geneado. b) Si la coiente del geneado es de 6,6 A, 50 Hz, calcula la capacidad del condensado que había de se
6 conectado en seie con el geneado de coiente paa que el facto de potencia del conjunto sea la unidad. RESOLUIÓN: a) Se epesenta en la figua, el tiángulo de potencias de la caga Z A, así como las potencias apaentes de Z B, Z y del conjunto de ambos Z B,. El tiángulo de potencias total, debido a Z A, Z B y Z, se puede obtene a pati de la epesentación de la S + 5,8-5,6 figua, calculando peviamente el ángulo δ: cos δ = = 0,9964 x 5,8 x S δ = 30,68-5,84 = 4,84 A pati del teoema del coseno se tiene que: S -,56 S +,8 = 0 S = 5,78 + _ 5,78 -,8 =,4 kva La ota solución, S = 0,0 kva, no es válida ya que implicaía un valo de S B, no coecto en elación a los valoes de S B y S. En la figua se muestan las dos soluciones a S.
7 El tiángulo de potencias total se obtiene conocido el facto de potencia del geneado, po tanto: P = S x fp = 0,6 kw Q = S - Q = 4,97 kvar( El tiángulo de potencias total se puede pone como suma: P = PB, + PA Q = Q +Q B, A como: P A = S A cos θ A= 5 8 x 0 86 = 5 kw ; Q = S A - P A = A 9 kvar( po tanto: PB, = 5 3 kw ; Q = B, kvar( S B, = P B, +Q = 5 B, 7 kva ; fpb, = 0 93( ; α = ac cos 0 93= 6 5, ,5 Po ota pate: cos β = = 0,894 ; β = 6,5 x 5,6 x 5 así pues: α + β = 4 8 po tanto: PB = S B x cos ( α + β )= 3,3 kw Q = S B x sen ( α + β )= 3,7 kvar B ( y además: P = PB, - PB = kw Q = Q - Q = 6 kvar B, B ( a b) Paa que el facto de potencia del conjunto sea la unidad, la potencia eactiva del condensado conectado en seie debeá se igual a la potencia eactiva del conjunto de cagas, así se tiene que: Facto de potencia unidad => Q = 0 Q = - Q = 4 97 kvar( a QOND = X x I => X = 567 Ω = 5 6 µ F OND 4.- Paa el cicuito de la figua, se pide:.- on el inteupto K abieto: a) La lectua del vatímeto cuando sus teminales de tensión A y B se conectan a los teminales y D espectivamente. b) La lectua del vatímeto cuando sus teminales de tensión A y B se conectan a los teminales M y N espectivamente..- on el inteupto K ceado, la lectua del vatímeto es de 85 W, con la conexión descita en a), y de W con la conexión descita en b), calcula el valo de la impedancia Z θ.
8 RESOLUIÓN:.- a) Llamando a la coiente que cicula po la impedancia 4 + j 3 Ω, se tiene que: 0-90 I = = 44-6,87 A 5 36,57 El diagama fasoial con la epesentación de la tensión y de la coiente es el de la figua. po tanto, la lectua del vatímeto vendá dada po: W = 5 x 44 x cos ( 6,87 )= W Este valo de la potencia no tiene ningún significado físico, es deci, no coesponde a la potencia disipada po una impedancia. b) El nuevo diagama fasoial seá el de la figua y la nueva lectua del vatímeto vendá dada po: W = 0 x 44 x cos ( 6,87-90 )=7.744 W
9 En este caso, la lectua coesponde a la potencia disipada po la impedancia 4 + j 3 Ω, cuyo valo coincide con el calculado a tavés de la potencia disipada po su pate esistiva: P = R x I = 4 x 44 =7.744 W.- Llamando I = I - α, a la coiente suministada po el geneado de tensión 0-90º voltios, se puede epesenta el diagama fasoial de la figua. La posición del faso ha de se la indicada, en el cuato cuadante, ya que en caso contaio las lectuas de los vatímetos no seían las indicadas. Así, si el faso coiente estuviese en el pime cuadante la segunda lectua seía negativa, si estuviese en el segundo cuadante las dos lectuas seían negativas y si estuviese en el tece cuadante la pimea lectua seía negativa. De las lectuas de los vatímetos se tiene que: 85= 5 x I x cosα = 0 x I x cos ( 90 -α ) de estas dos ecuaciones se obtiene: α = 88,99 ; I = 38,6 A I = 38,6-88,99 A La impedancia total, agupación de la impedancia 4 + j 3 Ω y Z θ vendá dada po: 0-90 Z = = 5,7 -,0 Ω 38,6-88, ,87 x Z θ como ambas impedancias están en paalelo: 5,7 -,0 = 5 36,87 + Z θ Z θ = 8,05-8,88 = - j 8 Ω
V = R 2 2 EJERCICIOS DE POTENCIAS EN CIRCUITOS MONOFASICOS
 EJERIIOS DE POENIAS EN IRUIOS MONOFASIOS EJERIIO 1.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina 1.000 VAR. Se pide, calcula: a) El valo de
EJERIIOS DE POENIAS EN IRUIOS MONOFASIOS EJERIIO 1.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina 1.000 VAR. Se pide, calcula: a) El valo de
CUESTIONES Y PROBLEMAS DE CAMPO ELÉCTRICO. Ejercicio nº1 Cómo se manifiesta la propiedad de la materia denominada carga eléctrica?
 UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
UESTIONES Y POBLEMAS DE AMPO ELÉTIO Ejecicio nº ómo se manifiesta la popiedad de la mateia denominada caga eléctica? La popiedad de la mateia denominada caga eléctica se manifiesta mediante fuezas de atacción
Tablas y formulas prácticas
 Tablas y fomulas pácticas ECCÓN Automation Technology Poducts Tablas y fómulas pácticas NDCE Tabla de esquemas típicos en sistemas de conmutación (tansfeencias)... Tabla de potencias y coientes nominales...
Tablas y fomulas pácticas ECCÓN Automation Technology Poducts Tablas y fómulas pácticas NDCE Tabla de esquemas típicos en sistemas de conmutación (tansfeencias)... Tabla de potencias y coientes nominales...
INDUCCIÓN ELECTROMAGNÉTCA Y ENERGÍA DEL CAMPO MAGNÉTICO
 NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
NDUCCÓN EECTROMAGNÉTCA Y ENERGÍA 1. ey de inducción de Faaday. ey de enz.. Ejemplos: fem de movimiento y po vaiación tempoal de. 3. Autoinductancia. 4. Enegía magnética. OGRAFÍA:. DE CAMPO MAGNÉTCO -Tiple-Mosca.
Adaptación de impedancias
 .- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
.- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
PROBLEMAS DE ELECTROESTÁTICA
 PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
PBLMAS D LCTSTÁTICA I CAMP LCTIC N L VACI. Cagas puntuales. Cagas lineales. Cagas supeficiales 4. Flujo le de Gauss 5. Distibuciones cúbicas de caga 6. Tabajo enegía electostática 7. Poblemas Pof. J. Matín
CAMPO GRAVITATORIO FCA 10 ANDALUCÍA
 CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
CMPO GRVIORIO FC 0 NDLUCÍ. a) Explique qué se entiende po velocidad de escape y deduzca azonadamente su expesión. b) Razone qué enegía había que comunica a un objeto de masa m, situado a una altua h sobe
IES Fco Ayala de Granada Junio de 2014 (Modelo 1) Soluciones Germán-Jesús Rubio Luna. Opción A. Ejercicio 2 opción A, modelo_1 Junio 2014
 IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
IES Fco Ayala de Ganada Junio de 014 (Modelo 1) Soluciones Gemán-Jesús Rubio Luna Opción A Ejecicio 1 opción A, modelo_1 Junio 014 Sea f : R R definida po f(x) x + ax + bx + c. [1 7 puntos] Halla a, b
Física Universitaria 2 5 de junio 2006 Enrique Sánchez y Aguilera, Rodolfo Estrada Guerrero, Abraham Vilchis CONSTANTE DIELÉCTRICA RELATIVA
 CONSTANTE DIELÉCTRICA RELATIVA OBJETIVO: El alumno podá detemina la constante dieléctica elativa de divesos mateiales dielécticos mediante la medición de la capacitancia de un condensado de placas paalelas.
CONSTANTE DIELÉCTRICA RELATIVA OBJETIVO: El alumno podá detemina la constante dieléctica elativa de divesos mateiales dielécticos mediante la medición de la capacitancia de un condensado de placas paalelas.
2.4 La circunferencia y el círculo
 UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
UNI Geometía. La cicunfeencia y el cículo. La cicunfeencia y el cículo JTIVS alcula el áea del cículo y el peímeto de la cicunfeencia. alcula el áea y el peímeto de sectoes y segmentos ciculaes. alcula
GEOMETRÍA. punto, la recta y el plano.
 MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
MISIÓN 011-II GEMETRÍ STUS GEMETRÍ a geometía es la ama de las Matemáticas que tiene po objeto el estudio de las figuas geométicas. Se denomina figua geomética a cualquie conjunto no vacío de puntos del
Parte 3: Electricidad y Magnetismo
 Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
Pate 3: Electicidad y Magnetismo 1 Pate 3: Electicidad y Magnetismo Los fenómenos ligados a la electicidad y al magnetismo, han sido obsevados y estudiados desde hace muchos siglos. No obstante ello, las
Sistemas y Circuitos
 Sistemas y Circuitos Práctica 4: Circuitos Analógicos Curso Académico 09/10 Objetivos En esta práctica el alumno aprenderá a calcular impedancias equivalentes analizar filtros de primer orden Normas La
Sistemas y Circuitos Práctica 4: Circuitos Analógicos Curso Académico 09/10 Objetivos En esta práctica el alumno aprenderá a calcular impedancias equivalentes analizar filtros de primer orden Normas La
MAGNITUDES VECTORIALES:
 Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Magnitudes ectoiales MAGNITUDES VECTORIALES: Índice 1 Magnitudes escalaes ectoiales Suma de ectoes libes Poducto de un escala po un ecto 3 Sistema de coodenadas ectoiales. Vectoes unitaios 3 Módulo de
Potencial eléctrico. Trabajo y energía potencial en el campo eléctrico. Potencial de una carga puntual: Principio de superposición
 Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
Potencial eléctico Intoducción. Tabajo y enegía potencial en el campo eléctico Potencial eléctico. Gadiente. Potencial de una caga puntual: Pincipio de supeposición Potencial eléctico de distibuciones
www.fisicaeingenieria.es Vectores y campos
 www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
www.fisicaeingenieia.es Vectoes y campos www.fisicaeingenieia.es www.fisicaeingenieia.es ) Dados los vectoes a = 4$ i + 3$ j + k$ y c = $ i + $ j 7k$, enconta las componente de oto vecto unitaio, paa que
Ejercicios resueltos
 Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
Ejecicios esueltos Boletín 2 Campo gavitatoio y movimiento de satélites Ejecicio 1 En el punto A(2,0) se sitúa una masa de 2 kg y en el punto B(5,0) se coloca ota masa de 4 kg. Calcula la fueza esultante
5 Procedimiento general para obtener el esquema equivalente de un transformador
 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado 45 5 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado En este capítulo se encontaá el esquema equivalente de
Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado 45 5 Pocedimiento geneal paa obtene el esquema equivalente de un tansfomado En este capítulo se encontaá el esquema equivalente de
RECTAS Y ÁNGULOS. SEMIRRECTA.- Un punto de una recta la divide en dos semirrectas. La semirrecta tiene principio pero no tiene fin.
 RECTAS Y ÁNGULOS 5º de E. Pimaia RECTAS Y ÁNGULOS -TEMA 5 RECTA.- Es una sucesión infinita de puntos que tienen la misma diección. La ecta no tiene ni pincipio ni fin. Po dos puntos del plano pasa una
RECTAS Y ÁNGULOS 5º de E. Pimaia RECTAS Y ÁNGULOS -TEMA 5 RECTA.- Es una sucesión infinita de puntos que tienen la misma diección. La ecta no tiene ni pincipio ni fin. Po dos puntos del plano pasa una
UNIDAD DE TRABAJO Nº2. INSTALACIONES DE MEGAFONÍA. UNIDAD DE TRABAJO Nº2.1. Descripción de Componentes. Simbología AURICULARES
 UNIDAD DE TRABAJO Nº2. INSTALACIONES DE MEGAFONÍA UNIDAD DE TRABAJO Nº2.1. Descripción de Componentes. Simbología 2. Auriculares. Descripción. AURICULARES Son transductores electroacústicos que, al igual
UNIDAD DE TRABAJO Nº2. INSTALACIONES DE MEGAFONÍA UNIDAD DE TRABAJO Nº2.1. Descripción de Componentes. Simbología 2. Auriculares. Descripción. AURICULARES Son transductores electroacústicos que, al igual
Circuitos. Corriente Alterna Monofásica Mayo La lectura del Voltímetro en el circuito de la figura es de
 icuitos. oiente ltena Monofásica POLM 7.1 La lectua del oltímeto en el cicuito de la figua es de Z -60 0 oltios. alcula el módulo de la tensión ente los extemos y. Z 60 Solución: 0 POLM 7.2 L 1 L 2 n el
icuitos. oiente ltena Monofásica POLM 7.1 La lectua del oltímeto en el cicuito de la figua es de Z -60 0 oltios. alcula el módulo de la tensión ente los extemos y. Z 60 Solución: 0 POLM 7.2 L 1 L 2 n el
Cómo Reducir la Factura de Energía Eléctrica Corrigiendo el Factor de Potencia
 Cómo Reducir la Factura de Energía Eléctrica Corrigiendo el Factor de Potencia Por Ing. José Luís Ola García ( 1 ) RESUMEN El elevado consumo de la Potencia Reactiva (aumento de la necesidad de magnetizar
Cómo Reducir la Factura de Energía Eléctrica Corrigiendo el Factor de Potencia Por Ing. José Luís Ola García ( 1 ) RESUMEN El elevado consumo de la Potencia Reactiva (aumento de la necesidad de magnetizar
TEMA 9 Cicloconvertidores
 TEMA 9 Cicloconvertidores 9.1.- Introducción.... 1 9.2.- Principio de Funcionamiento... 1 9.3.- Montajes utilizados.... 4 9.4.- Estudio de la tensión de salida.... 6 9.5.- Modos de funcionamiento... 7
TEMA 9 Cicloconvertidores 9.1.- Introducción.... 1 9.2.- Principio de Funcionamiento... 1 9.3.- Montajes utilizados.... 4 9.4.- Estudio de la tensión de salida.... 6 9.5.- Modos de funcionamiento... 7
Instrumentación Nuclear Conf. # 2 Tema I. Procesamiento y Conformación de Pulsos.
 Instumentación Nuclea onf. # 2 Tema I. Pocesamiento y onfomación de Pulsos. Sumaio: aacteísticas geneales de los pulsos. oncepto de Ancho de Banda y su elación con el tiempo de subida de un pulso. Objetivo
Instumentación Nuclea onf. # 2 Tema I. Pocesamiento y onfomación de Pulsos. Sumaio: aacteísticas geneales de los pulsos. oncepto de Ancho de Banda y su elación con el tiempo de subida de un pulso. Objetivo
avance de un sacacorchos que gira como lo hacemos para llevar el primer vector sobre el segundo por el
 /5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
/5 Conceptos pevios PRODUCTO VECTORIAL DE DO VECTORE. Es oto vecto cuyo módulo viene dado po: a b a b senα. u diección es pependicula al plano en el ue se encuentan los dos vectoes y su sentido viene dado
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
Máster Universitario en Profesorado
 Máster Universitario en Profesorado Complementos para la formación disciplinar en Tecnología y procesos industriales Aspectos básicos de la Tecnología Eléctrica Contenido (II) SEGUNDA PARTE: corriente
Máster Universitario en Profesorado Complementos para la formación disciplinar en Tecnología y procesos industriales Aspectos básicos de la Tecnología Eléctrica Contenido (II) SEGUNDA PARTE: corriente
P9: ENSAYO DE VACÍO Y CORTOCIRCUITO DEL TRANSFORMADOR MONOFÁSICO FUNDAMENTOS DE TECNOLOGÍA ELÉCTRICA
 ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P9:
Resolución de problemas. Temas: VOR e ILS
 Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
Resolución de problemas. Temas: VOR e ILS Autor: Mario E. Casado García 3er Curso ITT ST Índice 1. Problema tema 5: VOR......3 2. Problema tema 7: ILS.....7 3. Referencias..12 2 1. Problema tema 5: VOR
TRANSFORMADORES EN PARALELO
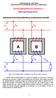 UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
CAMPO GRAVITATORIO FCA 04 ANDALUCÍA
 CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
CAPO GAVIAOIO FCA 04 ANDALUCÍA. a) Al desplazase un cuepo desde una posición A hasta ota B, su enegía potencial disminuye. Puede aseguase que su enegía cinética en B es mayo que en A? azone la espuesta.
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO
 PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
PAUTA ACTIVIDADES: COMENZANDO CON EL LENGUAJE ALGEBRAICO Joaquín ha comenzado a utiliza letas paa epesenta distintas situaciones numéicas. Obseve lo que ealiza con el siguiente enunciado: A Matías le egalaon
1. La tarifación eléctrica
 1. La tarifación eléctrica El sistema de tarifas eléctricas es el medio por el que se establece la forma de cobrar a los consumidores el suministro de energía eléctrica en BT y AT. La tarifa eléctrica
1. La tarifación eléctrica El sistema de tarifas eléctricas es el medio por el que se establece la forma de cobrar a los consumidores el suministro de energía eléctrica en BT y AT. La tarifa eléctrica
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
Es el producto escalar de la fuerza aplicada al cuerpo por el vector r r Por lo tanto es una magnitud escalar.
 TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
TRABAJO Y ENERGÍA TRABAJO Es el poducto escala de la fueza aplicada al cuepo po el vecto desplazamiento. Po lo tanto es una magnitud escala. W = F.D = F.D. cos a Su unidad en el sistema intenacional es
FACTOR DE POTENCIA. Cos φ
 FACTOR DE POTENCIA Cos φ El Factor de Potencia, es el indicador del correcto aprovechamiento de la energía Eléctrica y puede tomar valores, entre 0 y 1, lo que significa que: Factor de Potencia, es un
FACTOR DE POTENCIA Cos φ El Factor de Potencia, es el indicador del correcto aprovechamiento de la energía Eléctrica y puede tomar valores, entre 0 y 1, lo que significa que: Factor de Potencia, es un
CAPITULO 6 POTENCIA COMPLEJA 6.1 INTRODUCCION. Si V VmSen wt v. P Vm Sen wt v Sen wt i. Cos v i Cos wt v i 2 2. P VICos v i.
 CAULO 6 OENCA COMLEJA 6. NRODUCCON La potencia compleja (cuya magnitud se conoce como potencia aparente) de un circuito eléctrico de corriente alterna, es la suma (vectorial) de la potencia que disipa
CAULO 6 OENCA COMLEJA 6. NRODUCCON La potencia compleja (cuya magnitud se conoce como potencia aparente) de un circuito eléctrico de corriente alterna, es la suma (vectorial) de la potencia que disipa
D.1.- Considere el movimiento de una partícula de masa m bajo la acción de una fuerza central del tipo. n ˆ
 Cuso Mecánica (FI-1A), Listado de ejecicios. Edito: P. Aceituno 34 Escuela de Ingenieía. Facultad de Ciencias Físicas y Matemáticas. Univesidad de Chile. D: FUERZAS CENTRALES Y MOVIMIENTOS PLANETARIOS
Cuso Mecánica (FI-1A), Listado de ejecicios. Edito: P. Aceituno 34 Escuela de Ingenieía. Facultad de Ciencias Físicas y Matemáticas. Univesidad de Chile. D: FUERZAS CENTRALES Y MOVIMIENTOS PLANETARIOS
Campo eléctrico. Introducción a la Física Ambiental. Tema 7. Tema 7.- Campo eléctrico.
 Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
Campo eléctico. Intoducción a la Física Ambiental. Tema 7. Tema7. IFA (Pof. RAMOS) 1 Tema 7.- Campo eléctico. El campo eléctico: unidades. Líneas del campo eléctico. Potencial eléctico: unidades. Fueza
MEDICIÓN DE ENERGÍA ELÉCTRICA ACTIVA
 ELT 8.MEDICION DE ENERGIA ELECTRICA ACTIVA.- INTRODUCIÓN MEDICIÓN DE ENERGÍA ELÉCTRICA ACTIVA La medición de energía eléctrica activa se realiza con el medidor de KWH de tipo inducción y con el medidor
ELT 8.MEDICION DE ENERGIA ELECTRICA ACTIVA.- INTRODUCIÓN MEDICIÓN DE ENERGÍA ELÉCTRICA ACTIVA La medición de energía eléctrica activa se realiza con el medidor de KWH de tipo inducción y con el medidor
INTRODUCCION AL ANALISIS VECTORIAL
 JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
JOSÉ MILCIDEZ DÍZ, REL CSTILLO, ERNNDO VEG PONTIICI UNIVERSIDD JVERIN, DEPRTMENTO DE ÍSIC INTRODUCCION L NLISIS VECTORIL Intoducción Pate Pate 3 Pate 4 (Pate ) Donde encuente el símbolo..! conduce a una
Tema 3. Campo eléctrico
 Tema 3 Campo eléctico Pogama 1. Inteacción eléctica. Campo eléctico.. Repesentación mediante líneas de campo. Flujo eléctico: Ley de Gauss. 3. Enegía y potencial elécticos. Supeficies equipotenciales.
Tema 3 Campo eléctico Pogama 1. Inteacción eléctica. Campo eléctico.. Repesentación mediante líneas de campo. Flujo eléctico: Ley de Gauss. 3. Enegía y potencial elécticos. Supeficies equipotenciales.
4.1. Índice del tema...1 4.2. El Condensador...2 4.2.1. Introducción...2 4.2.2. Potencia...3 4.2.3. Energía...3 4.2.4. Condición de continuidad...
 TEMA 4: CAPACITORES E INDUCTORES 4.1. Índice del tema 4.1. Índice del tema...1 4.2. El Condensador...2 4.2.1. Introducción...2 4.2.2. Potencia...3 4.2.3. Energía...3 4.2.4. Condición de continuidad...4
TEMA 4: CAPACITORES E INDUCTORES 4.1. Índice del tema 4.1. Índice del tema...1 4.2. El Condensador...2 4.2.1. Introducción...2 4.2.2. Potencia...3 4.2.3. Energía...3 4.2.4. Condición de continuidad...4
omprender el concepto del Factor de Potencia con respecto al comportamiento de circuitos reactivos capacitivos e inductivos.
 Universidad Don Bosco Facultad de Ingeniería Escuela de Ingeniería Eléctrica Sistemas Eléctricos Lineales I Práctica No.9 Medición de Sistemas de Potencia y Factor de Potencia Objetivos: tilizar instrumentos
Universidad Don Bosco Facultad de Ingeniería Escuela de Ingeniería Eléctrica Sistemas Eléctricos Lineales I Práctica No.9 Medición de Sistemas de Potencia y Factor de Potencia Objetivos: tilizar instrumentos
TEMA 9 POTENCIA EN SISTEMAS TRIFÁSICOS.
 TEMA 9 POTENCIA EN SISTEMAS TRIFÁSICOS. 9.. Potencias en sistemas equilibrados y simétricos en tensiones Un sistema trifásico puede considerarse como circuitos monofásicos, por lo que la potencia total
TEMA 9 POTENCIA EN SISTEMAS TRIFÁSICOS. 9.. Potencias en sistemas equilibrados y simétricos en tensiones Un sistema trifásico puede considerarse como circuitos monofásicos, por lo que la potencia total
DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN DE UN TRANSFORMADOR DE POTENCIA
 PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN DE UN TRANSFORMADOR DE POTENCIA Departamento de Ingeniería Eléctrica E.T.S.I.I. Página 1 de 14 PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN
PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN DE UN TRANSFORMADOR DE POTENCIA Departamento de Ingeniería Eléctrica E.T.S.I.I. Página 1 de 14 PRÁCTICA Nº 8 DETERMINACIÓN DE LAS CAÍDAS DE TENSIÓN
Proyecto: Determinación del Factor de Potencia de un Circuito RLC en Serie
 Universidad Nacional de Tucumán Facultad de iencias Exactas y Tecnología Departamento de Física José Würschmidt Sistema de Enseñanza Aprendizaje por Proyectos Experimentales Simples y por Simulación en
Universidad Nacional de Tucumán Facultad de iencias Exactas y Tecnología Departamento de Física José Würschmidt Sistema de Enseñanza Aprendizaje por Proyectos Experimentales Simples y por Simulación en
MEDICIONES ELECTRICAS I
 Año:... Alumno:... Comisión:... MEDICIONES ELECTRICAS I Trabajo Práctico N 6 Tema: PUENTES DE CORRIENTE CONTINUA Y DE CORRIENTE ALTERNA. Q - METER Introducción Las mediciones de precisión de los valores
Año:... Alumno:... Comisión:... MEDICIONES ELECTRICAS I Trabajo Práctico N 6 Tema: PUENTES DE CORRIENTE CONTINUA Y DE CORRIENTE ALTERNA. Q - METER Introducción Las mediciones de precisión de los valores
Cómo puede la corrección del Factor de Potencia ser parte de tu plan de ahorro? Consulta a nuestros expertos en Uso Eficiente de la Energía
 Cómo puede la corrección del Factor de Potencia ser parte de tu plan de ahorro? Consulta a nuestros expertos en Uso Eficiente de la Energía 1 2 > Introducción Teoría Básica del Factor de Potencia (FP)
Cómo puede la corrección del Factor de Potencia ser parte de tu plan de ahorro? Consulta a nuestros expertos en Uso Eficiente de la Energía 1 2 > Introducción Teoría Básica del Factor de Potencia (FP)
PROGRAMA DE TECNOLOGÍA ELECTRICA - UTP LABORATORIO DE CIRCUITOS - PRÁCTICA 6: EQUILIBRIO DE POTENCIA Y MÁXIMA TRANSFERENCIA DE POTENCIA.
 PROGRAMA DE TECNOLOGÍA ELECTRICA - UTP LABORATORIO DE CIRCUITOS - PRÁCTICA 6: EQUILIBRIO DE POTENCIA Y MÁXIMA TRANSFERENCIA DE POTENCIA. 1. OBJETIVOS. Seleccionar adecuadamente el amperímetro y el voltímetro
PROGRAMA DE TECNOLOGÍA ELECTRICA - UTP LABORATORIO DE CIRCUITOS - PRÁCTICA 6: EQUILIBRIO DE POTENCIA Y MÁXIMA TRANSFERENCIA DE POTENCIA. 1. OBJETIVOS. Seleccionar adecuadamente el amperímetro y el voltímetro
Aptitud Matemática ( ) ( ) EDADES RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN RESOLUCIÓN. 3x x = 75 3x 5x = 75 x = 15 3(x) = 45. 1 + 2α = 9 + α RPTA.: B RPTA.
 EDADES 1 Teófilo tiene el triple de la edad de Pedro Cuando Pedro tenga la edad de Teófilo, este tendrá 75 años Cuál es la edad de Teófilo? A) 30 B) 35 C) 40 D) 45 E) 50 3 Las edades de tres amigos son
EDADES 1 Teófilo tiene el triple de la edad de Pedro Cuando Pedro tenga la edad de Teófilo, este tendrá 75 años Cuál es la edad de Teófilo? A) 30 B) 35 C) 40 D) 45 E) 50 3 Las edades de tres amigos son
UNIVERSIDAD DE COSTA RICA FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA ELÉCTRICA LABORATORIO DE MÁQUINAS ELÉCTRICAS I
 UNIVERSIDAD DE COSTA RICA FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA ELÉCTRICA LABORATORIO DE MÁQUINAS ELÉCTRICAS I Reporte 1 INTEGRANTES FÉLIX SUÁREZ BONILLA A45276 FECHA DE ENTREGA JUEVES, 15 DE FEBRERO
UNIVERSIDAD DE COSTA RICA FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA ELÉCTRICA LABORATORIO DE MÁQUINAS ELÉCTRICAS I Reporte 1 INTEGRANTES FÉLIX SUÁREZ BONILLA A45276 FECHA DE ENTREGA JUEVES, 15 DE FEBRERO
Fenómenos Ondulatorios: Interferencias
 Fenómenos Ondulatoios: Inteeencias Fenómenos de supeposición de ondas. Inteeencias (pags 67-76 Guadiel) Cuando en un punto de un medio coinciden dos o más ondas (petubaciones) se dice que en ese punto
Fenómenos Ondulatoios: Inteeencias Fenómenos de supeposición de ondas. Inteeencias (pags 67-76 Guadiel) Cuando en un punto de un medio coinciden dos o más ondas (petubaciones) se dice que en ese punto
FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO
 FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO Determinar la capacidad de un regulador según la placa de datos:
FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO Determinar la capacidad de un regulador según la placa de datos:
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 ELECTROTECNIA. CÓDIGO 148
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 ELECTROTECNIA. CÓDIGO 148 Elige una de las dos opciones de examen siguientes (opción A u opción B). No pueden contestarse
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA ALUMNOS DE BACHILLERATO LOE Junio 2010 ELECTROTECNIA. CÓDIGO 148 Elige una de las dos opciones de examen siguientes (opción A u opción B). No pueden contestarse
P5: CORRIENTE ALTERNA MONOFÁSICA II FUNDAMENTOS DE TECNOLOGÍA ELÉCTRICA D. FAUSTINO DE LA BODEGA Y BILBAO CURSO 2º GRUPO 01
 ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P5:
ESCUELA UNIVERSITARIA DE INGENIERÍA TÉCNICA INDUSTRIAL (BILBAO) Departamento de Ingeniería Eléctrica INDUSTRI INGENIARITZA TEKNIKORAKO UNIBERTSITATE-ESKOLA (BILBO) Ingeniaritza Elektriko Saila ALUMNO P5:
ESTUDIO DE LOS EJEMPLOS RESUELTOS 7.1, 7.2 Y 7.8 DEL LIBRO DE FUNDAMENTOS FÍSICOS DE LA INFORMÁTICA.
 ESTUIO E LOS EJEMPLOS RESUELTOS.1,.2 Y.8 EL LIRO E FUNMENTOS FÍSIOS E L INFORMÁTI. Resolver un circuito implica conocer las intensidades que circula por cada una de sus ramas lo que permite conocer la
ESTUIO E LOS EJEMPLOS RESUELTOS.1,.2 Y.8 EL LIRO E FUNMENTOS FÍSIOS E L INFORMÁTI. Resolver un circuito implica conocer las intensidades que circula por cada una de sus ramas lo que permite conocer la
OSCILADOR U.H.F CON TRANSISTOR MOSFET
 Dep R.F y Micro Ondas OSCILADOR U.H.F CON TRANSISTOR MOSFET Javier Arribas Lázaro st06596@salleurl.edu 1.Objetivos El objetivo del trabajo es el desarrollo y el montaje de un oscilador basado en un único
Dep R.F y Micro Ondas OSCILADOR U.H.F CON TRANSISTOR MOSFET Javier Arribas Lázaro st06596@salleurl.edu 1.Objetivos El objetivo del trabajo es el desarrollo y el montaje de un oscilador basado en un único
Districte Universitari de Catalunya
 Proves d accés a la universitat Convocatòria 2014 Electrotecnia Serie 3 La prueba consta de dos partes de dos ejercicios cada una. La primera parte es común y la segunda tiene dos opciones (A y B). Resuelva
Proves d accés a la universitat Convocatòria 2014 Electrotecnia Serie 3 La prueba consta de dos partes de dos ejercicios cada una. La primera parte es común y la segunda tiene dos opciones (A y B). Resuelva
Parametrizando la epicicloide
 1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
1 Paametizando la epicicloide De la figua se obseva que cos(θ) = x 0 + ( 0 + ) cos(θ) = x sen(θ) = y 0 + ( 0 + ) sen(θ) = y po tanto las coodenadas del punto A son: A = (( 0 + ) cos(θ), ( 0 + ) sen(θ))
Instrucciones: No se permitirá el uso de calculadoras programables ni gráficas. La puntuación de cada pregunta está indicada en las mismas.
 PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B ELECTROTECNIA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: No se permitirá
PRUEBA ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR OPCIÓN B ELECTROTECNIA DATOS DEL ASPIRANTE Apellidos: CALIFICACIÓN PRUEBA Nombre: D.N.I. o Pasaporte: Fecha de nacimiento: / / Instrucciones: No se permitirá
Inversión en el plano
 Inversión en el plano Radio de la circunferencia x 2 + y 2 + Ax + By + D = 0 Circunferencia de centro (a, b) y radio r: (x a) 2 + (y b) 2 = r 2. Comparando: x 2 + y 2 2ax 2by + a 2 + b 2 r 2 = 0 con x
Inversión en el plano Radio de la circunferencia x 2 + y 2 + Ax + By + D = 0 Circunferencia de centro (a, b) y radio r: (x a) 2 + (y b) 2 = r 2. Comparando: x 2 + y 2 2ax 2by + a 2 + b 2 r 2 = 0 con x
+ + h. 8 v A. = = 2026 m s 1 3 1,3 10 6 m
 m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
m A + ( ) G P m ( ) 0 + G P m R P + h R P h A B R P eniendo en cuenta que h R P /, la anteio expesión queda como: G A P 8 A 3 Sustituyendo datos numéicos, esulta: 6,67 0 N m kg, 0 3 kg A 06 m s 3,3 0 6
Experimento 6 LAS LEYES DE KIRCHHOFF. Objetivos. Teoría. Figura 1 Un circuito con dos lazos y varios elementos
 Experimento 6 LAS LEYES DE KIRCHHOFF Objetivos 1. Describir las características de las ramas, los nodos y los lazos de un circuito, 2. Aplicar las leyes de Kirchhoff para analizar circuitos con dos lazos,
Experimento 6 LAS LEYES DE KIRCHHOFF Objetivos 1. Describir las características de las ramas, los nodos y los lazos de un circuito, 2. Aplicar las leyes de Kirchhoff para analizar circuitos con dos lazos,
GUÍA 9: CÁLCULO DE POTENCIAS Y FACTOR DE POTENCIA
 GUÍA 9: CÁCUO DE POTECIA Y FACTOR DE POTECIA 1. Triángulo de potencias Del triángulo se definen tres tipos de potencias encontradas en cargas inductivas y capacitivas, cuando están siendo alimentadas por
GUÍA 9: CÁCUO DE POTECIA Y FACTOR DE POTECIA 1. Triángulo de potencias Del triángulo se definen tres tipos de potencias encontradas en cargas inductivas y capacitivas, cuando están siendo alimentadas por
CAPITULO 3 REDES HIBRIDAS-COMPLEJAS. 3.1 Descripción de la Red Híbrida Compleja (HCNN)
 CAPITULO 3 REDES HIBRIDAS-COMPLEJAS 3.1 Descripción de la Red Híbrida Compleja (HCNN) La predicción de eventos caóticos que se presentan en un mundo que nos rodea es de gran interés. Especialmente en aquellos
CAPITULO 3 REDES HIBRIDAS-COMPLEJAS 3.1 Descripción de la Red Híbrida Compleja (HCNN) La predicción de eventos caóticos que se presentan en un mundo que nos rodea es de gran interés. Especialmente en aquellos
PROBLEMAS DE ELECTROTECNIA
 PROBLEMAS DE ELECTROTECNIA MATERIAL DIDÁCTICO Ingenierías nº 23 Otros títulos de la colección. 1 Planos acotados: expresión gráfica (2ª ed.) Ricardo Bartolomé Ramírez 2003, 306 pags. ISBN 84-95301-74-1
PROBLEMAS DE ELECTROTECNIA MATERIAL DIDÁCTICO Ingenierías nº 23 Otros títulos de la colección. 1 Planos acotados: expresión gráfica (2ª ed.) Ricardo Bartolomé Ramírez 2003, 306 pags. ISBN 84-95301-74-1
Motores Eléctricos Eficiencia, Factor de Potencia y Carga.
 Motores Eléctricos Eficiencia, Factor de Potencia y Carga. Un programa de ahorro y conservación energética, pasa primero por conocer a profundidad los conceptos de eficiencia y características de operación
Motores Eléctricos Eficiencia, Factor de Potencia y Carga. Un programa de ahorro y conservación energética, pasa primero por conocer a profundidad los conceptos de eficiencia y características de operación
Importancia de la corrección del factor de potencia (PFC)
 www.fuentes-switching.electrosoft.cl Importancia de la corrección del factor de potencia (PFC) M. Patricio Cohen Introducción Al conectar una carga a la red eléctrica, la potencia que podemos consumir
www.fuentes-switching.electrosoft.cl Importancia de la corrección del factor de potencia (PFC) M. Patricio Cohen Introducción Al conectar una carga a la red eléctrica, la potencia que podemos consumir
CAPITULO 5 COMPENSACION DEL FACTOR DE POTENCIA Y CONTROL DE ARMONICAS EN REDES INDUSTRIALES INTRODUCCION
 CAPITULO 5 COMPENSACION DEL FACTOR DE POTENCIA Y CONTROL DE ARMONICAS EN REDES INDUSTRIALES INTRODUCCION Son conocidos los problemas causados por un bajo factor de potencia en sistemas eléctricos, como
CAPITULO 5 COMPENSACION DEL FACTOR DE POTENCIA Y CONTROL DE ARMONICAS EN REDES INDUSTRIALES INTRODUCCION Son conocidos los problemas causados por un bajo factor de potencia en sistemas eléctricos, como
LOS CONDENSADORES TEMA 4. Son elementos capaces de almacenar pequeñas cantidades de Energía Eléctrica. Aplicaciones de los condensadores:
 TEMA 4 LOS ONDENSADORES Son elementos capaces de almacenar pequeñas cantidades de Energía Eléctrica. Aplicaciones de los condensadores: Tiempos de carga y descarga para temporizadores. Filtros en rectificadores.
TEMA 4 LOS ONDENSADORES Son elementos capaces de almacenar pequeñas cantidades de Energía Eléctrica. Aplicaciones de los condensadores: Tiempos de carga y descarga para temporizadores. Filtros en rectificadores.
E 1 - E 2 = I 1. r 1 + (I 1 - I). r 2 E 1 - E 2 = I 1. (r 1 + r 2 ) - I. r 2. E 2 = I. R + (I - I 1 ). r 2 E 2 = I. (R + r 2 ) - I 1.
 Dos pilas de f.e.m. y resistencias internas diferentes se conectan en paralelo para formar un único generador. Determinar la f.e.m. y resistencia interna equivalentes. Denominamos E i a las f.e.m. de las
Dos pilas de f.e.m. y resistencias internas diferentes se conectan en paralelo para formar un único generador. Determinar la f.e.m. y resistencia interna equivalentes. Denominamos E i a las f.e.m. de las
Distribución del consumo de energía por sectores
 Guía Práctica para el uso de la Energía Presentación El uso eficiente de la energía eléctrica en los diversos sectores de consumo, es uno de los objetivos más importantes que todo consumidor de Electricidad
Guía Práctica para el uso de la Energía Presentación El uso eficiente de la energía eléctrica en los diversos sectores de consumo, es uno de los objetivos más importantes que todo consumidor de Electricidad
TEMA: ANÁLISIS DE CIRCUITOS ELÉCTRICOS
 CUSO: º DSOLLO D PODUCTOS LCTÓNICOS. MÓDULO: LCTÓNIC NLÓGIC TM: NÁLISIS D CICUITOS LÉCTICOS NÁLISIS D CICUITOS LÉCTICOS. INTODUCCIÓN.. LYS D KICHOFF.. NÁLISIS D CICUITOS N COINT CONTÍNU. 4. OTOS MÉTODOS
CUSO: º DSOLLO D PODUCTOS LCTÓNICOS. MÓDULO: LCTÓNIC NLÓGIC TM: NÁLISIS D CICUITOS LÉCTICOS NÁLISIS D CICUITOS LÉCTICOS. INTODUCCIÓN.. LYS D KICHOFF.. NÁLISIS D CICUITOS N COINT CONTÍNU. 4. OTOS MÉTODOS
TEMA 8: LÍMITES DE FUNCIONES. CONTINUIDAD
 TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d.
![TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d. TRABAJO Y ENERGÍA. W = F d [Joule] W = F d cos α. Donde F y d son los módulos de la fuerza y el desplazamiento, y α es el ángulo que forman F y d.](/thumbs/31/15114944.jpg) C U R S O: FÍSICA COMÚN MATERIAL: FC-09 TRABAJO Y ENERGÍA La energía desempeña un papel muy importante en el mundo actual, por lo cual se justifica que la conozcamos mejor. Iniciamos nuestro estudio presentando
C U R S O: FÍSICA COMÚN MATERIAL: FC-09 TRABAJO Y ENERGÍA La energía desempeña un papel muy importante en el mundo actual, por lo cual se justifica que la conozcamos mejor. Iniciamos nuestro estudio presentando
Una vez conocido el manejo básico, antes de venir al Laboratorio a manejarlo, puedes practicar con un osciloscopio virtual en el enlace
 PRACTICA 3. EL OSCILOSCOPIO ANALOGICO 1. INTRODUCCION. El Osciloscopio es un voltímetro que nos permite representar en su pantalla valores de tensión durante un intervalo de tiempo. Es decir, nos permite
PRACTICA 3. EL OSCILOSCOPIO ANALOGICO 1. INTRODUCCION. El Osciloscopio es un voltímetro que nos permite representar en su pantalla valores de tensión durante un intervalo de tiempo. Es decir, nos permite
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES
 PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES.- Halla dos númeos que sumados den cuo poducto sea máimo. Sean e los númeos buscados. El poblema a esolve es el siguiente: máimo Llamamos p al poducto de los dos
EJERCICIOS DE AUTOEVALUACIÓN "CIRCUITOS ALIMENTADOS EN CORRIENTE ALTERNA"
 EJERCICIOS DE AUTOEVALUACIÓN "CIRCUITOS ALIMENTADOS EN CORRIENTE ALTERNA" EJERCICIO 1 Simular con PSIM el siguiente circuito y obtener: a) Valores eficaces de la tensión en el generador, en la resistencia
EJERCICIOS DE AUTOEVALUACIÓN "CIRCUITOS ALIMENTADOS EN CORRIENTE ALTERNA" EJERCICIO 1 Simular con PSIM el siguiente circuito y obtener: a) Valores eficaces de la tensión en el generador, en la resistencia
Condensadores Eléctricos
 ondensadores Eléctricos R S T R S T c R S T c ONDENSADORES Generalidades El condensador es un componente eléctrico cuya función es la de almacenar carga eléctrica y su aplicación más importante es la de
ondensadores Eléctricos R S T R S T c R S T c ONDENSADORES Generalidades El condensador es un componente eléctrico cuya función es la de almacenar carga eléctrica y su aplicación más importante es la de
Práctica E4: Medida de potencia en circuitos trifásicos
 Medida de potencia en circuitos triásicos: ráctica E4 ráctica E4: Medida de potencia en circuitos triásicos. Objetivos os objetivos de la práctica son:.- Medida de la potencia activa, reactiva y el actor
Medida de potencia en circuitos triásicos: ráctica E4 ráctica E4: Medida de potencia en circuitos triásicos. Objetivos os objetivos de la práctica son:.- Medida de la potencia activa, reactiva y el actor
Unidad Didáctica. Transformadores Trifásicos
 Unidad Didáctica Transformadores Trifásicos Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION
Unidad Didáctica Transformadores Trifásicos Programa de Formación Abierta y Flexible Obra colectiva de FONDO FORMACION Coordinación Diseño y maquetación Servicio de Producción Didáctica de FONDO FORMACION
PRINCIPADO DE ASTURIAS / SEPTIEMBRE 04. LOGSE / FÍSICA / EXAMEN COMPLETO
 PINCIPADO D ASUIAS / SPIM 04. LOGS / FÍSICA / XAMN COMPLO XAMN COMPLO PUAS D APIUD PAA L ACCSO A LA UNIVSIDAD LOGS Cso 00-004 FÍSICA l almno elegiá CUAO de las seis opciones popestas Opción.- Demosta qe
PINCIPADO D ASUIAS / SPIM 04. LOGS / FÍSICA / XAMN COMPLO XAMN COMPLO PUAS D APIUD PAA L ACCSO A LA UNIVSIDAD LOGS Cso 00-004 FÍSICA l almno elegiá CUAO de las seis opciones popestas Opción.- Demosta qe
Kronotek: Configuración de Red para VoIP
 Konotek: Configuación de Red paa VoIP Contenido 1. Intoducción... 2 2. Impotancia de la Configuación de Red... 2 3. Pasos Pevios: Cálculo del númeo de líneas de voz... 3 Pime paso: obtención del ancho
Konotek: Configuación de Red paa VoIP Contenido 1. Intoducción... 2 2. Impotancia de la Configuación de Red... 2 3. Pasos Pevios: Cálculo del númeo de líneas de voz... 3 Pime paso: obtención del ancho
TEMA 2 POLINOMIOS Y FRACCIONES ALGEBRAICAS
 Matemáticas B 4º E.S.O. Tema : Polinomios y fracciones algebraicas. 1 TEMA POLINOMIOS Y FRACCIONES ALGEBRAICAS.1 COCIENTE DE POLINOMIOS 4º.1.1 COCIENTE DE MONOMIOS 4º El cociente de un monomio entre otro
Matemáticas B 4º E.S.O. Tema : Polinomios y fracciones algebraicas. 1 TEMA POLINOMIOS Y FRACCIONES ALGEBRAICAS.1 COCIENTE DE POLINOMIOS 4º.1.1 COCIENTE DE MONOMIOS 4º El cociente de un monomio entre otro
1.1 La Bobina Ideal. Preguntas conceptuales
 1. RESPUESTA DEL CIRCUITO EN ESTADO TRANSITORIO (DOMINIO DEL TIEMPO) 1.1 La Bobina Ideal Preguntas conceptuales 1. La inductancia de cierta bobina está determinada por la ecuación 1.2. Si se desea construir
1. RESPUESTA DEL CIRCUITO EN ESTADO TRANSITORIO (DOMINIO DEL TIEMPO) 1.1 La Bobina Ideal Preguntas conceptuales 1. La inductancia de cierta bobina está determinada por la ecuación 1.2. Si se desea construir
Instalación eléctrica y domotización de un edificio de viviendas ANEXO A CÁLCULOS
 Pág.1 ANEXO A CÁLCULOS Pág. Pág.3 Sumario A.1.- Cálculos.... 5 A.1.1.- Cálculo de conductores activos.... 5 A.1..- Cálculo de conductores de protección.... 8 A.1.3.- Cálculo de la puesta a tierra.... 9
Pág.1 ANEXO A CÁLCULOS Pág. Pág.3 Sumario A.1.- Cálculos.... 5 A.1.1.- Cálculo de conductores activos.... 5 A.1..- Cálculo de conductores de protección.... 8 A.1.3.- Cálculo de la puesta a tierra.... 9
PARALELO DE TRANSFORMADORES
 GUIA DE TRABAJOS PRACTICOS DE LABORATORIO TPN 2 PARALELO DE TRANSFORMADORES 1. Objetivos Estudio teórico y práctico de las condiciones que se deben cumplir para realizar el conexionado en paralelo de dos
GUIA DE TRABAJOS PRACTICOS DE LABORATORIO TPN 2 PARALELO DE TRANSFORMADORES 1. Objetivos Estudio teórico y práctico de las condiciones que se deben cumplir para realizar el conexionado en paralelo de dos
Un sencillo medidor vectorial de impedancias eléctricas para el laboratorio Fernando Valcarce Codes
 Enseñanza Un sencillo medido vectoial de impedancias elécticas paa el laboatoio Fenando Valcace Codes An aangement fo vectoial electical-impedance measuements is descibed which is pecise and accuate enough
Enseñanza Un sencillo medido vectoial de impedancias elécticas paa el laboatoio Fenando Valcace Codes An aangement fo vectoial electical-impedance measuements is descibed which is pecise and accuate enough
Bloque II: Principios de máquinas
 Bloque II: Principios de máquinas 1. Conceptos Fundamentales A. Trabajo En términos de la física y suponiendo un movimiento rectilíneo de un objeto al que se le aplica una fuerza F, se define como el producto
Bloque II: Principios de máquinas 1. Conceptos Fundamentales A. Trabajo En términos de la física y suponiendo un movimiento rectilíneo de un objeto al que se le aplica una fuerza F, se define como el producto
LÍMITES DE FUNCIONES. CONTINUIDAD
 LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
LÍMITES DE FUNCIONES. CONTINUIDAD Página REFLEXIONA Y RESUELVE Algunos ites elementales Utiliza tu sentido común para dar el valor de los siguientes ites: a,, b,, @ c,, 5 + d,, @ @ + e,, @ f,, 0 @ 0 @
TECNUN MEDIDA DE IMPEDANCIAS
 ESCUELA SUPEROR DE NGENEROS DE SAN SEBASTÁN TECNUN UNERSDAD DE NAARRA Práctica de Laboratorio MEDDA DE MPEDANCAS Circuitos. Medida de mpedancias. OBJETO DE LA PRÁCTCA Con esta práctica se pretende que
ESCUELA SUPEROR DE NGENEROS DE SAN SEBASTÁN TECNUN UNERSDAD DE NAARRA Práctica de Laboratorio MEDDA DE MPEDANCAS Circuitos. Medida de mpedancias. OBJETO DE LA PRÁCTCA Con esta práctica se pretende que
Tema 7. MOTORES ELÉCTRICOS DE CORRIENTE CONTINUA
 Tema 7. MOTORES ELÉCTRICOS DE CORRIENTE CONTINUA 1. MAGNETISMO Y ELECTRICIDAD...2 Fuerza electromotriz inducida (Ley de inducción de Faraday)...2 Fuerza electromagnética (2ª Ley de Laplace)...2 2. LAS
Tema 7. MOTORES ELÉCTRICOS DE CORRIENTE CONTINUA 1. MAGNETISMO Y ELECTRICIDAD...2 Fuerza electromotriz inducida (Ley de inducción de Faraday)...2 Fuerza electromagnética (2ª Ley de Laplace)...2 2. LAS
(a) El triángulo dado se descompone en tres segmentos de recta que parametrizamos de la siguiente forma: (0 t 1); y = 0. { x = 1 t y = t. (0 t 1).
 INTEGRALES DE LÍNEA. 15. alcular las siguientes integrales: (a) (x + y) ds donde es el borde del triángulo con vértices (, ), (1, ), (, 1). (b) x + y ds donde es la circunferencia x + y ax (a > ). (a)
INTEGRALES DE LÍNEA. 15. alcular las siguientes integrales: (a) (x + y) ds donde es el borde del triángulo con vértices (, ), (1, ), (, 1). (b) x + y ds donde es la circunferencia x + y ax (a > ). (a)
1. PLANTEAMIENTO DEL PROBLEMA. 1.1 Descripción del problema
 1. PLANTEAMIENTO DEL PROBLEMA 1.1 Descripción del problema Son muchas las necesidades que presentan los niños y las niñas en el nivel de Educación Parvularia, debido a que es el primer peldaño de la educación
1. PLANTEAMIENTO DEL PROBLEMA 1.1 Descripción del problema Son muchas las necesidades que presentan los niños y las niñas en el nivel de Educación Parvularia, debido a que es el primer peldaño de la educación
PRÁCTICA Nº 6. Hipermetropía, parte 2: neutralización óptica de un ojo hipermétrope
 Departamento de Óptica, Farmacología y Anatomía PRÁCTICAS DE ÓPTICA VISUA I HIPERMETROPÍA, PARTE 2, curso 2011-12 PRÁCTICA Nº 6 Hipermetropía, parte 2: neutralización óptica de un ojo hipermétrope OBJETIVO:
Departamento de Óptica, Farmacología y Anatomía PRÁCTICAS DE ÓPTICA VISUA I HIPERMETROPÍA, PARTE 2, curso 2011-12 PRÁCTICA Nº 6 Hipermetropía, parte 2: neutralización óptica de un ojo hipermétrope OBJETIVO:
Experimento Nº 1: El transformador monofásico y los sistemas trifásicos
 Curso: Laboratorio de Transformadores y Máquinas Eléctricas Experimento Nº 1: El transformador monofásico y los sistemas trifásicos I. Objetivo: Al finalizar este experimento, el estudiante estará en capacidad
Curso: Laboratorio de Transformadores y Máquinas Eléctricas Experimento Nº 1: El transformador monofásico y los sistemas trifásicos I. Objetivo: Al finalizar este experimento, el estudiante estará en capacidad
CORRECCION del FACTOR de POTENCIA
 CORRECCION del FACTOR de POTENCIA Las cargas generan perturbaciones CARGA Armónicas Potencia Reactiva Cargas Asimétricas Flicker RED 2 Diferentes aspectos de la calidad de energía eléctrica Perturbaciones
CORRECCION del FACTOR de POTENCIA Las cargas generan perturbaciones CARGA Armónicas Potencia Reactiva Cargas Asimétricas Flicker RED 2 Diferentes aspectos de la calidad de energía eléctrica Perturbaciones
TEMA I. Teoría de Circuitos
 TEMA I Teoría de Circuitos Electrónica II 2009-2010 1 1 Teoría de Circuitos 1.1 Introducción. 1.2 Elementos básicos 1.3 Leyes de Kirchhoff. 1.4 Métodos de análisis: mallas y nodos. 1.5 Teoremas de circuitos:
TEMA I Teoría de Circuitos Electrónica II 2009-2010 1 1 Teoría de Circuitos 1.1 Introducción. 1.2 Elementos básicos 1.3 Leyes de Kirchhoff. 1.4 Métodos de análisis: mallas y nodos. 1.5 Teoremas de circuitos:
