Análisis de componentes principales. a.k.a.: PCA Principal components analysis
|
|
|
- Magdalena Vidal Soto
- hace 7 años
- Vistas:
Transcripción
1 Análisis de componentes principales a.k.a.: PCA Principal components analysis 1
2 Outline Motivación Derivación Ejemplos 2
3 Motivación general Tenemos un dataset X con n datos y p dimensiones, centrado (medias 0). Queremos encontrar una representación de esos mismos datos en un espacio de menor dimensión Para visualizarlos (entenderlos!) Para modelarlos mejor Cuál es la proyección óptima? 3
4 Motivación Queremos una proyección lineal tal que los datos conserven lo más posible su estructura (relación de distancias). Ejemplo: Datos en 2 dimensiones. Proyectamos sobre una recta Cuál es la recta que introduce menos distorsión? 4
5 Motivación La recta debe pasar cerca de la mayoría de los puntos. La distancia entre los puntos y entre sus proyecciones sobre la recta deben parecerse lo más posible 5
6 Notación a 1 Versor paralelo a la recta a 1 =(a 11,a 12,,a 1p ) Z 1 =a 1 X 1 Z 1 =Z 1 a 1 Pitágoras: x 1 x 1 =Z 1 2+r 1 2 Para que los Z y los X sean similares tenemos que minimizar a los r 6
7 Motivación El primer miembro es constante Para minimizar el último sumando tengo que maximizar el primer sumando. Como los Z tienen media cero, estamos: MAXIMIZANDO LA VARIANZA DE LAS PROYECCIONES 7
8 Definición La primer componente principal es la dirección en la cual los datos tienen máxima varianza Dirección=combinación lineal de las variables originales La segunda componente principal es la dirección ortogonal a la anterior en la cual hay máxima varianza Es la primer componente del subespacio que queda hasta p 8
9 Derivación Buscamos los vectores: tales que la var(z) sea máxima. Como Z tiene media 0: donde S es la matriz de covarianza de los datos. Para que el problema tenga sentido pedimos que a sea de modulo unitario: 9
10 Derivación La restricción se introduce con un multiplicador de Lagrange: Queremos el máximo, derivamos: 10
11 Derivación Las direcciones principales son los autovectores de la matriz de covarianza Como: La varianza de z es el autovalor. La primer DP es la del mayor autovalor. Las otras sucesivamente. 11
12 Complejidad Es del orden de O(np 2 +p 3 ) Para calcular S: np 2 Para autovalores de S: p 3 Lineal en n, pero cúbico en p! 12
13 Uso práctico Cuántas dimensiones necesito conservar? Varianza explicada: / Dejar las direcciones que conservan casi toda la varianza 13
14 Correlación Datos sin normalizar distintas varianzas para cada variable original Cuando las relaciones entre las variables tienen sentido físico-real 14
15 Covarianza Datos normalizados previamente (z-scores) Cuando las variables son inconmensurables (no tienen relación) La mayoría de los casos reales 15
16 Ejemplos Detección de outliers usando PCA 16
17 Ejemplos en R datos<-crea.datos(2000,d=9,n.ce=0,c=1) plot(datos[,1:5],col=datos[,10]) datos.pca<-prcomp(datos[,-10],ret.x=t) x11() plot(datos.pca) x11() plot(datos.pca$x[,1:2],pch=17,col=datos[,10]) #en 100 dimensiones: datos<-crea.datos(2000,d=100,n.ce=0,c=0.3) x11() plot(datos[,1:5],col=datos[,101]) #verificar que son las mismas variables datos.pca<-prcomp(datos[,-101],ret.x=t) x11() plot(datos.pca$x[,1:2],pch=17,col=datos[,101]) 17
18 Interpretación PCA hace una proyección lineal, un giro de los ejes. Cada eje principal es una combinación lineal de las variables originales. Se puede buscar evidencia sobre la importancia de las variables originales evaluando su aporte a las PC. Se suele hacer gráficamente 18
19 Interpretación: gráficas >biplot(prcomp(iris[,-5], scale = TRUE)) 19
20 Interpretación: gráficas >biplot(prcomp(mtcars, scale = TRUE),choices=c(1,2),cex=0.8) 20
21 Resumen PCA: Proyecciones lineales en bajas dimensiones que explican los datos lo mejor posible. Las direcciones principales son los autovectores de la matriz de covarianza. La importancia de cada dirección esta relacionada con su varianza explicada (autovalores). 21
22 Extra: Multi-Dimensional Scaling MDS. Método general. Busca representar los datos en un espacio de menor dimensión respetando las distancias entre los objetos. PCA es un caso muy particular de MDS MDS se basa sólo en distancias entre puntos. No se necesita que los puntos estén en un espacio vectorial. Sólo las distancias. Por ejemplo: grados arbitrarios de similitud entre vinos cantidad de nodos entre dos computadoras 22
23 Ejemplo de MDS Código R: loc <- cmdscale(eurodist) x <- loc[,1] y <- -loc[,2] plot(x, y, type="n", xlab="", ylab="", main="cmdscale(eurodist)") text(x, y, rownames(loc), cex=0.8) 23
Análisis Factorial General.
 Capítulo 1 Análisis Factorial General. 1.1. Análisis Factorial General (AFG). Introducción. Sea una tabla rectangular de valores numéricos, representados por una matriz X n p, con términos x ij. Nos planteamos
Capítulo 1 Análisis Factorial General. 1.1. Análisis Factorial General (AFG). Introducción. Sea una tabla rectangular de valores numéricos, representados por una matriz X n p, con términos x ij. Nos planteamos
Componentes principales y dimensionalidad
 Universisad de San Andrés y CONICET Dos problemas Bienestar 19 dimensiones del bienestar en Argentina Ingreso, educacion, tipo de trabajo, paga en cuotas, etc. Realmente el bienestar tiene 19 dimensiones?
Universisad de San Andrés y CONICET Dos problemas Bienestar 19 dimensiones del bienestar en Argentina Ingreso, educacion, tipo de trabajo, paga en cuotas, etc. Realmente el bienestar tiene 19 dimensiones?
2.5 Ejercicios... 59
 Índice General 1 Espacios vectoriales 1 1.1 Espacios vectoriales y subespacios......................... 1 1.1.1 Preliminares................................. 1 1.1.2 Espacios vectoriales.............................
Índice General 1 Espacios vectoriales 1 1.1 Espacios vectoriales y subespacios......................... 1 1.1.1 Preliminares................................. 1 1.1.2 Espacios vectoriales.............................
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
ANÁLISIS DE COMPONENTES PRINCIPALES
 CAPÍTULO 4 ANÁLISIS DE COMPONENTES PRINCIPALES 4.1 Introducción Al investigar un fenómeno desconocido se pretende abordarlo con muestras de diferentes variables, en las cuales muchas veces existe una fuerte
CAPÍTULO 4 ANÁLISIS DE COMPONENTES PRINCIPALES 4.1 Introducción Al investigar un fenómeno desconocido se pretende abordarlo con muestras de diferentes variables, en las cuales muchas veces existe una fuerte
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2.3
 ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
ÁLGEBRA LINEAL II Algunas soluciones a la práctica 2. Transformaciones ortogonales (Curso 2010 2011) 1. Se considera el espacio vectorial euclídeo IR referido a una base ortonormal. Obtener la expresión
Análisis de componentes principales
 Capítulo 2 Análisis de componentes principales 2.1. Teoría Sea X una muestra de datos (de la variable/población x N ( µ, Σ)) donde el elemento x ij corresponde al individuo i y a la variable continua j
Capítulo 2 Análisis de componentes principales 2.1. Teoría Sea X una muestra de datos (de la variable/población x N ( µ, Σ)) donde el elemento x ij corresponde al individuo i y a la variable continua j
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
Edgar Acuna/ ESMA 6665 Lecc La SVD y Componentes Principales
 Edgar Acuna/ ESMA 6665 Lecc 7 75 6.2 La SVD y Componentes Principales El objetivo de componentes principales es hacer una reducción de la información disponible. Es decir, la información contenida en p
Edgar Acuna/ ESMA 6665 Lecc 7 75 6.2 La SVD y Componentes Principales El objetivo de componentes principales es hacer una reducción de la información disponible. Es decir, la información contenida en p
1. Determina cuáles de los siguientes conjuntos son subespacios vectoriales. Para aquellos que lo sean, halla una base.
 EJERCICIOS PROPUESTOS 1. Espacios vectoriales. Sistemas de ecuaciones. 1. Determina cuáles de los siguientes conjuntos son subespacios vectoriales. Para aquellos que lo sean, halla una base. (a) S = {
EJERCICIOS PROPUESTOS 1. Espacios vectoriales. Sistemas de ecuaciones. 1. Determina cuáles de los siguientes conjuntos son subespacios vectoriales. Para aquellos que lo sean, halla una base. (a) S = {
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1. Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 3, Opción A Reserva, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 3, Opción A Reserva, Ejercicio
Solución de problemas III 1
 Solución de problemas III Álgebra II Curso 25-6. Espacio Afín.. Ejercicios Ejercicio.4.3 Encontrar la expresión analítica de las siguientes aplicaciones afines de R 2 : a Giro de centro (, ángulo π/2 b
Solución de problemas III Álgebra II Curso 25-6. Espacio Afín.. Ejercicios Ejercicio.4.3 Encontrar la expresión analítica de las siguientes aplicaciones afines de R 2 : a Giro de centro (, ángulo π/2 b
Técnicas de inteligencia artificial. Visión Artificial Reconocimiento de objetos
 Técnicas de inteligencia artificial Visión Artificial Reconocimiento de objetos Indice Introducción Reconocimiento mediante características PCA Introducción El reconocimiento de objetos consiste en, dado
Técnicas de inteligencia artificial Visión Artificial Reconocimiento de objetos Indice Introducción Reconocimiento mediante características PCA Introducción El reconocimiento de objetos consiste en, dado
como el número real que resulta del producto matricial y se nota por:
 Espacio euclídeo 2 2. ESPACIO EUCLÍDEO 2.. PRODUCTO ESCALAR En el espacio vectorial se define el producto escalar de dos vectores y como el número real que resulta del producto matricial y se nota por:,
Espacio euclídeo 2 2. ESPACIO EUCLÍDEO 2.. PRODUCTO ESCALAR En el espacio vectorial se define el producto escalar de dos vectores y como el número real que resulta del producto matricial y se nota por:,
Ortogonalización de Gram Schmidt
 Ortogonalización de Gram Schmidt Objetivos. Estudiar el proceso de ortogonalización de Gram Schmidt que permite construir de una lista arbitraria de vectores a,..., a m una lista ortogonal b,..., b m que
Ortogonalización de Gram Schmidt Objetivos. Estudiar el proceso de ortogonalización de Gram Schmidt que permite construir de una lista arbitraria de vectores a,..., a m una lista ortogonal b,..., b m que
Álgebra Lineal y Geometría I. Prueba 3. Grupo A. 12 de marzo de (
 Álgebra Lineal y Geometría I. Prueba 3. Grupo A. 2 de marzo de 208. Apellidos: Nombre: DNI: Ejercicio.-(4 puntos) Se considera la matriz siguiente: A = 2 0 3 0 2. Calcule W = null(a 2I), W 2 = null(a 4I)
Álgebra Lineal y Geometría I. Prueba 3. Grupo A. 2 de marzo de 208. Apellidos: Nombre: DNI: Ejercicio.-(4 puntos) Se considera la matriz siguiente: A = 2 0 3 0 2. Calcule W = null(a 2I), W 2 = null(a 4I)
Se usa para encontrar un numero relativamente pequeño de variables nuevas que contengan la mayor cantidad de info posible del conjunto de datos
 Analisis Estadístico de Datos Climáticos Análisis de componentes principales Analisis de componentes principales Se usa para encontrar un numero relativamente pequeño de variables nuevas que contengan
Analisis Estadístico de Datos Climáticos Análisis de componentes principales Analisis de componentes principales Se usa para encontrar un numero relativamente pequeño de variables nuevas que contengan
Trabajo Práctico N 4: I) VECTORES EN R 2 Y R 3
 Trabajo Práctico N 4: I) VECTORES EN R Y R Ejercicio 1: Las fuerzas que actúan en un cuerpo se localizan en un plano, entonces se pueden representar mediante elementos de R. Determine la fuerza que hay
Trabajo Práctico N 4: I) VECTORES EN R Y R Ejercicio 1: Las fuerzas que actúan en un cuerpo se localizan en un plano, entonces se pueden representar mediante elementos de R. Determine la fuerza que hay
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
(PCA) Análisis de Componentes Principales
 PCA Pricipal Component Analysis Técnica multivariante que trata de reducir el número de variables originales (X1, X2,...,Xn) a un número menor de variables (CP1, CP2,...,CPp), denominadas componentes principales
PCA Pricipal Component Analysis Técnica multivariante que trata de reducir el número de variables originales (X1, X2,...,Xn) a un número menor de variables (CP1, CP2,...,CPp), denominadas componentes principales
7 Aplicaciones ortogonales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 7 Aplicaciones ortogonales 7.1 Aplicación ortogonal Se llama aplicación ortogonal a un endomorfismo f : V V sobre un espacio vectorial
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 7 Aplicaciones ortogonales 7.1 Aplicación ortogonal Se llama aplicación ortogonal a un endomorfismo f : V V sobre un espacio vectorial
ALGEBRA LINEAL. Capítulo III: Vectores en los espacios bidimensional y tridimensional. MsC. Andrés Baquero. jueves, 2 de julio de 15
 ALGEBRA LINEAL Capítulo III: Vectores en los espacios bidimensional y tridimensional MsC. Andrés Baquero jueves, 2 de julio de 15 Introducción a los vectores Vectores Geométricos Vectores Geométricos Vectores
ALGEBRA LINEAL Capítulo III: Vectores en los espacios bidimensional y tridimensional MsC. Andrés Baquero jueves, 2 de julio de 15 Introducción a los vectores Vectores Geométricos Vectores Geométricos Vectores
Esta definición se puede ampliar a cualquier par de bases de los espacio inicial y final MATRIZ DE UNA APLICACIÓN LINEAL EN BASES ARBITRARIAS
 Cambios de base 3 3. CAMBIOS DE BASE Dada una aplicación lineal : y la base,,, se ha definido matriz en bases canónicas de la aplicación lineal a la matriz,, cuyas columnas son las coordenadas de en la
Cambios de base 3 3. CAMBIOS DE BASE Dada una aplicación lineal : y la base,,, se ha definido matriz en bases canónicas de la aplicación lineal a la matriz,, cuyas columnas son las coordenadas de en la
Espacios Vectoriales www.math.com.mx
 Espacios Vectoriales Definiciones básicas de Espacios Vectoriales www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 007-009 Contenido. Espacios Vectoriales.. Idea Básica de Espacio Vectorial.................................
Espacios Vectoriales Definiciones básicas de Espacios Vectoriales www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 007-009 Contenido. Espacios Vectoriales.. Idea Básica de Espacio Vectorial.................................
NOTAS DE ESTUDIO DE ÁLGEBRA LINEAL M.C. MARCOS CAMPOS NAVA TEC DE ATITALAQUIA
 Hasta ahora se han discutido algunas de las propiedades de objetos matemáticos llamados matrices. Un caso de especial interés son las matrices cuadradas, por ejemplo: Se sabe que esta matriz es invertible
Hasta ahora se han discutido algunas de las propiedades de objetos matemáticos llamados matrices. Un caso de especial interés son las matrices cuadradas, por ejemplo: Se sabe que esta matriz es invertible
Problemas métricos. Ángulo entre rectas y planos
 Problemas métricos Ángulo entre rectas y planos Ángulo entre dos rectas El ángulo que forman dos rectas es el ángulo agudo que determinan entre sí sus vectores directores. Dos rectas son perpendiculares
Problemas métricos Ángulo entre rectas y planos Ángulo entre dos rectas El ángulo que forman dos rectas es el ángulo agudo que determinan entre sí sus vectores directores. Dos rectas son perpendiculares
Soluciones a los ejercicios del examen final C =. 1 0
 Universidade de Vigo Departamento de Matemática Aplicada II E T S E de Minas Álgebra Lineal Curso 205/6 de enero de 206 Soluciones a los ejercicios del examen final Se considera el subespacio U {X M 2
Universidade de Vigo Departamento de Matemática Aplicada II E T S E de Minas Álgebra Lineal Curso 205/6 de enero de 206 Soluciones a los ejercicios del examen final Se considera el subespacio U {X M 2
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II REGIÓN DE MURCIA CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Bloque A Para saber si la matriz tiene inversa, el determinante de la
Matemáticas II Matemáticas II REGIÓN DE MURCIA CONVOCATORIA SEPTIEMBRE 9 SOLUCIÓN DE LA PRUEBA DE ACCESO AUTOR: José Luis Pérez Sanz Bloque A Para saber si la matriz tiene inversa, el determinante de la
a) u.(v+w) = u.v + u.w b) c) k (u x v) = ku x v = u x kv, siendo k un escalar d) u.(v x w) = w. (u x v) = v.(w x u)
 Trabajo Práctico N 4: I) VECTORES EN R 2 Y R 3 Ejercicio 1: Las fuerzas que actúan en un cuerpo se localizan en un plano, entonces se pueden representar mediante elementos de R 2. Determine la fuerza que
Trabajo Práctico N 4: I) VECTORES EN R 2 Y R 3 Ejercicio 1: Las fuerzas que actúan en un cuerpo se localizan en un plano, entonces se pueden representar mediante elementos de R 2. Determine la fuerza que
SEGUNDO PARCIAL - EJERCICIOS DE REPASO
 Algebra y Geometría 28 SEGUNDO PARCIAL - EJERCICIOS DE REPASO 3-6-8 ESPACIOS VECTORIALES. Construya en R 2 un subconjunto que sea: a cerrado para la suma y resta de vectores, pero no para la multiplicacion
Algebra y Geometría 28 SEGUNDO PARCIAL - EJERCICIOS DE REPASO 3-6-8 ESPACIOS VECTORIALES. Construya en R 2 un subconjunto que sea: a cerrado para la suma y resta de vectores, pero no para la multiplicacion
Revisión del algoritmo de Corte Normalizado
 Capítulo 2 Revisión del algoritmo de Corte Normalizado El algoritmo Ncut realiza la segmentación planteando un problema de división de grafos, en el cual se pretende maximizar tanto la disimilitud entre
Capítulo 2 Revisión del algoritmo de Corte Normalizado El algoritmo Ncut realiza la segmentación planteando un problema de división de grafos, en el cual se pretende maximizar tanto la disimilitud entre
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 . ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
. ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
Geometría del plano y el espacio
 Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
Geometría del plano y el espacio AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Geometría del plano y el espacio 1 / 21 Objetivos Al final de este tema tendréis que Conocer
Problemas de Geometría Analítica del Espacio
 1) Dados los vectores u(4, 4, 8), v( 2,, 5), w(3, 5, 8) y a(22,, 11). Hallar los valores de x, y, z que verifican la combinación lineal a = x u + y v + z w. 2) Dados los vectores a( 5, 19, n) y b( h, 3,
1) Dados los vectores u(4, 4, 8), v( 2,, 5), w(3, 5, 8) y a(22,, 11). Hallar los valores de x, y, z que verifican la combinación lineal a = x u + y v + z w. 2) Dados los vectores a( 5, 19, n) y b( h, 3,
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
Tema 6: Espacios euclídeos
 Águeda Mata y Miguel Reyes, Dpto de Matemática Aplicada, FI-UPM 1 Tema 6: Espacios euclídeos Ejercicios 1 Demuestra que la aplicación < A, B >= traza(ab t ), A, B M m n (R), es un producto escalar sobre
Águeda Mata y Miguel Reyes, Dpto de Matemática Aplicada, FI-UPM 1 Tema 6: Espacios euclídeos Ejercicios 1 Demuestra que la aplicación < A, B >= traza(ab t ), A, B M m n (R), es un producto escalar sobre
Examen Final Ejercicio 2 (1 hora y 30 min.) 27 de mayo de 2011
 Álgebra Lineal II Eamen Final Ejercicio 2 ( hora 30 min 27 de mao de 20 En el espacio afín euclideo usual consideramos una pirámide triangular ABCD de la cual sabemos: - A (0, 0, 0, B (, 0, 0, C (0,, -
Álgebra Lineal II Eamen Final Ejercicio 2 ( hora 30 min 27 de mao de 20 En el espacio afín euclideo usual consideramos una pirámide triangular ABCD de la cual sabemos: - A (0, 0, 0, B (, 0, 0, C (0,, -
ALGEBRA LINEAL Segundo Semestre. Parte II
 1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
Extremos Restringidos (Multiplicadores de Lagrange)
 Extremos Restringidos (Multiplicadores de Lagrange) Dada la curva en el plano (x h) a + (y k) b = 1. Esta es una elipse con centro en (h,k) y queremos encontrar qué punto de esta elipse se encuentra más
Extremos Restringidos (Multiplicadores de Lagrange) Dada la curva en el plano (x h) a + (y k) b = 1. Esta es una elipse con centro en (h,k) y queremos encontrar qué punto de esta elipse se encuentra más
Física I CIBEX enviar correcciones a:
 Física I CIBEX - 2017 enviar correcciones a: Departamento de Física - UNLP silva@fisica.unlp.edu.ar Práctica 0: Vectores Figura 1: Componentes de un vector en coordenadas cartesianas Dado un sistema cartesiano
Física I CIBEX - 2017 enviar correcciones a: Departamento de Física - UNLP silva@fisica.unlp.edu.ar Práctica 0: Vectores Figura 1: Componentes de un vector en coordenadas cartesianas Dado un sistema cartesiano
COMPONENTES PRINCIPALES
 COMPONENTES PRINCIPALES Jorge Galbiati R. El método de Componentes Principales tiene por objeto reducir la dimensionalidad de un problema de múltiples variables, aplicando una sucesión de transformaciones
COMPONENTES PRINCIPALES Jorge Galbiati R. El método de Componentes Principales tiene por objeto reducir la dimensionalidad de un problema de múltiples variables, aplicando una sucesión de transformaciones
1 Isometrías vectoriales.
 Eugenia Rosado ETSM Curso 9-. Isometrías vectoriales. Sea E un espacio vectorial euclídeo. De nición Una aplicación f : E! E se dice transformación ortogonal o isometría vectorial si conserva el producto
Eugenia Rosado ETSM Curso 9-. Isometrías vectoriales. Sea E un espacio vectorial euclídeo. De nición Una aplicación f : E! E se dice transformación ortogonal o isometría vectorial si conserva el producto
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
VECTORES 1.2 CONCEPTOS Y DEFINICIONES FUNDAMENTALES. En este capítulo estudiaremos los vectores y su álgebra.
 CAPITULO I CALCULO II VECTORES 1.1 INTRODUCCIÓN Los vectores son un auxiliar utilísimo para la geometría del espacio. En esta unidad partiendo de lo que ya se sabe de vectores en el plano, se contemplan
CAPITULO I CALCULO II VECTORES 1.1 INTRODUCCIÓN Los vectores son un auxiliar utilísimo para la geometría del espacio. En esta unidad partiendo de lo que ya se sabe de vectores en el plano, se contemplan
UNIVERSIDAD NACIONAL EXPERIMENTAL DE GUAYANA GERENCIA ACADEMICA COORDINACION DE PREGRADO PROYECTO INGENIERIA 1272-416/ALGEBRA DE ESTRUCTURAS SEMESTRE:
 GERENCIA ACADEMICA COORDINACION DE PREGRADO PROYECTO INGENIERIA PROGRAMA: ALGEBRA LINEAL CÓDIGO ASIGNATURA: 1272-521 PRE-REQUISITO: 1272-416/ALGEBRA DE ESTRUCTURAS SEMESTRE: 90-II UNIDADES DE CRÉDITO:
GERENCIA ACADEMICA COORDINACION DE PREGRADO PROYECTO INGENIERIA PROGRAMA: ALGEBRA LINEAL CÓDIGO ASIGNATURA: 1272-521 PRE-REQUISITO: 1272-416/ALGEBRA DE ESTRUCTURAS SEMESTRE: 90-II UNIDADES DE CRÉDITO:
Tema 3.1. Espacio eucĺıdeo. Diagonalización ortogonal
 Tema 3.1. Espacio eucĺıdeo. Diagonalización ortogonal Definición 1. Sea V un espacio vectorial sobre un cuerpo K. Llamamos forma bilineal a toda aplicación f : V V K ( x, y) f( x, y) que verifica: 1. f(
Tema 3.1. Espacio eucĺıdeo. Diagonalización ortogonal Definición 1. Sea V un espacio vectorial sobre un cuerpo K. Llamamos forma bilineal a toda aplicación f : V V K ( x, y) f( x, y) que verifica: 1. f(
MAT 1102 Geometría Solución Control N 5
 Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática Primer Semestre de 2001 MAT 1102 Geometría Solución Control N 5 Versión A 1. Dadas las rectas l 1 : 2x y = 0,
Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática Primer Semestre de 2001 MAT 1102 Geometría Solución Control N 5 Versión A 1. Dadas las rectas l 1 : 2x y = 0,
EVIDENCIAS DE APRENDIZAJE
 GESTIÓN DEL COCIMIENTO Y DOCENCIA VERÓN 04 PLAN DE S Página 1 de 10 FACULTAD CIENCIAS BÁCAS DIVIÓN: INGENIERÍAS, ARQUITECTURA AGNATURA: ÁLGEBRA LINEAL AREA: MATEMÁTICAS PROFESOR: NELSON O. CÁCERES MUÑOZ
GESTIÓN DEL COCIMIENTO Y DOCENCIA VERÓN 04 PLAN DE S Página 1 de 10 FACULTAD CIENCIAS BÁCAS DIVIÓN: INGENIERÍAS, ARQUITECTURA AGNATURA: ÁLGEBRA LINEAL AREA: MATEMÁTICAS PROFESOR: NELSON O. CÁCERES MUÑOZ
Clase 10: Extremos condicionados y multiplicadores de Lagrange
 Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Riesgo de tipos de interés Componentes principales
 Riesgo de tipos de interés Componentes principales 16 de mayo de 2006 Contenidos Componentes principales Componentes principales Generalidades Componentes principales Controlar el comportamiento de la
Riesgo de tipos de interés Componentes principales 16 de mayo de 2006 Contenidos Componentes principales Componentes principales Generalidades Componentes principales Controlar el comportamiento de la
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
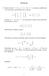 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
ESCUELA DE INGENIERÍAS INDUSTRIALES. UNIVERSIDAD DE VALLADOLID SEMINARIO 1. Vectores VECTORES
 Vectores 1.- Características de los vectores 2.- Clasificación de los vectores 3.- Operaciones con vectores 1.- Características de los vectores La representación gráfica de una magnitud vectorial es un
Vectores 1.- Características de los vectores 2.- Clasificación de los vectores 3.- Operaciones con vectores 1.- Características de los vectores La representación gráfica de una magnitud vectorial es un
Multiplicadores de Lagrange
 Funciones de R n en R 1 Multiplicadores de Lagrange Para entender el método de los multiplicadores de Lagrange ilustraremos las ideas con un ejemplo Ejemplo Sea f : R 2 R dada por fx, y) = x + 1) 2 + y
Funciones de R n en R 1 Multiplicadores de Lagrange Para entender el método de los multiplicadores de Lagrange ilustraremos las ideas con un ejemplo Ejemplo Sea f : R 2 R dada por fx, y) = x + 1) 2 + y
ALGEBRA LINEAL - Práctica N 8 - Segundo cuatrimestre de 2017 Espacios vectoriales con producto interno
 Departamento de Matemática - Facultad de Ciencias Exactas y Naturales - UBA ALGEBRA LINEAL - Práctica N 8 - Segundo cuatrimestre de 07 Espacios vectoriales con producto interno En esta práctica, todos
Departamento de Matemática - Facultad de Ciencias Exactas y Naturales - UBA ALGEBRA LINEAL - Práctica N 8 - Segundo cuatrimestre de 07 Espacios vectoriales con producto interno En esta práctica, todos
Diagonalización de matrices.
 Diagonalización de matrices. 1. Diagonalización de matrices. Definición 1.1 Sea A una matriz cuadrada,, decimos que es un autovalor de A si existe un vector no nulo tal que En esta situación decimos que
Diagonalización de matrices. 1. Diagonalización de matrices. Definición 1.1 Sea A una matriz cuadrada,, decimos que es un autovalor de A si existe un vector no nulo tal que En esta situación decimos que
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2009 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2009 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2009 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
Tema 2 Campo de velocidades del sólido rígido
 Mecánica Clásica Tema Campo de velocidades del sólido rígido EIAE 5 de septiembre de 011 Velocidad de un punto del sólido. Deducción matricial.................................. Tensor velocidad angular......................................................
Mecánica Clásica Tema Campo de velocidades del sólido rígido EIAE 5 de septiembre de 011 Velocidad de un punto del sólido. Deducción matricial.................................. Tensor velocidad angular......................................................
Resumen teórico de los conceptos necesarios para resolver el práctico 1. Vectores VECTORES
 Resumen teórico de los conceptos necesarios para resolver el práctico 1. Vectores En física algunas cantidades se pueden representar mediante un valor y su correspondiente unidad (1 litro, 10 kilogramos).
Resumen teórico de los conceptos necesarios para resolver el práctico 1. Vectores En física algunas cantidades se pueden representar mediante un valor y su correspondiente unidad (1 litro, 10 kilogramos).
TEMA 5. VECTORES. Dados dos puntos del plano y.
 TEMA 5. VECTORES. Dados dos puntos del plano y. Se define el vector de origen A y extremo B como el segmento orientado caracterizado por su módulo (su longitud), dirección (la de la recta que lo contiene)
TEMA 5. VECTORES. Dados dos puntos del plano y. Se define el vector de origen A y extremo B como el segmento orientado caracterizado por su módulo (su longitud), dirección (la de la recta que lo contiene)
Análisis en Componentes Principales
 This is page i Printer: Opaque this Análisis en Componentes Principales Dr. Oldemar Rodríguez Rojas 24 de mayo de 2009 ii This is page iii Printer: Opaque this Contents. Análisis en Componentes Principales
This is page i Printer: Opaque this Análisis en Componentes Principales Dr. Oldemar Rodríguez Rojas 24 de mayo de 2009 ii This is page iii Printer: Opaque this Contents. Análisis en Componentes Principales
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
Análisis Matemático II Curso 2018 Práctica introductoria
 Análisis Matemático II Curso 018 Práctica introductoria Cónicas - Sus ecuaciones y gráficas 1. Encontrar la forma estándar de cada cónica y graficar. a) x + y 6y = 0 b) x + y 1 = 0 c) x(x + 1) y = 4 d)
Análisis Matemático II Curso 018 Práctica introductoria Cónicas - Sus ecuaciones y gráficas 1. Encontrar la forma estándar de cada cónica y graficar. a) x + y 6y = 0 b) x + y 1 = 0 c) x(x + 1) y = 4 d)
Bases ortogonales. Profesores Omar Darío Saldarriaga Ortíz. Hernán Giraldo
 Bases ortogonales Profesores Omar Darío Saldarriaga Ortíz Iván Dario Gómez Hernán Giraldo 9 Definición Sea V un espacio vectorial y {v,..., v n} una base para V. decimos que {v,..., v n} es una base ortogonal
Bases ortogonales Profesores Omar Darío Saldarriaga Ortíz Iván Dario Gómez Hernán Giraldo 9 Definición Sea V un espacio vectorial y {v,..., v n} una base para V. decimos que {v,..., v n} es una base ortogonal
A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES
 RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
Diagonalización de matrices, Semejanza.
 diagonalizacion.nb 1 Diagonalización de matrices, Semejanza. Practica 8, 28 de abril de 2004 En esta práctica aprenderemos/repasaremos los comandos: Eigenvalues[ matriz ] Calcula los autovalores de una
diagonalizacion.nb 1 Diagonalización de matrices, Semejanza. Practica 8, 28 de abril de 2004 En esta práctica aprenderemos/repasaremos los comandos: Eigenvalues[ matriz ] Calcula los autovalores de una
GEOMETRÍA EN EL ESPACIO
 GEOMETRÍA EN EL ESPACIO 1. PUNTOS Y VECTORES OPERACIÓN TEORÍA Y FORMULACIÓN EJEMPLO Coordenadas de un punto Punto medio de un segmento Dividir un segmento en n partes iguales Coordenadas de un vector (
GEOMETRÍA EN EL ESPACIO 1. PUNTOS Y VECTORES OPERACIÓN TEORÍA Y FORMULACIÓN EJEMPLO Coordenadas de un punto Punto medio de un segmento Dividir un segmento en n partes iguales Coordenadas de un vector (
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Álgebra Lineal. Maestría en Ciencias Matemáticas. x y + z = 1 x y z = 3 2x y z = 1. x + y + 2z = 1 4x 2ty + 5z = 2 x y + tz = 1
 Álgebra Lineal Maestría en Ciencias Matemáticas Resuelva el siguiente sistema usando la factorización LU o P T LU (según sea el caso) x y + z = x y z = 3 2x y z = 2 Calcule A usando el algoritmo de Gauss-Jordan:
Álgebra Lineal Maestría en Ciencias Matemáticas Resuelva el siguiente sistema usando la factorización LU o P T LU (según sea el caso) x y + z = x y z = 3 2x y z = 2 Calcule A usando el algoritmo de Gauss-Jordan:
PAIEP. Complemento Ortogonal
 Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Complemento Ortogonal Veamos ahora una aplicación de los vectores ortogonales a la caracterización de subespacios
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Complemento Ortogonal Veamos ahora una aplicación de los vectores ortogonales a la caracterización de subespacios
Tema 3: Transformaciones Geométricas
 J. Ribelles SIE020: Síntesis de Imagen y Animación Institute of New Imaging Technologies, Universitat Jaume I Contenido Introducción 1 Introducción 2 Traslación Escalado Rotación 3 4 5 6 Introducción Por
J. Ribelles SIE020: Síntesis de Imagen y Animación Institute of New Imaging Technologies, Universitat Jaume I Contenido Introducción 1 Introducción 2 Traslación Escalado Rotación 3 4 5 6 Introducción Por
Diseño óptimo de estructuras. p. 1/30. mecánicas bajo incertidumbre en las cargas
 Diseño óptimo de estructuras mecánicas bajo incertidumbre en las cargas Felipe Alvarez y Miguel Carrasco II Encuentro Núcleo Científico Milenio Sistemas Complejos de Ingeniería Universidad de Chile 15-16
Diseño óptimo de estructuras mecánicas bajo incertidumbre en las cargas Felipe Alvarez y Miguel Carrasco II Encuentro Núcleo Científico Milenio Sistemas Complejos de Ingeniería Universidad de Chile 15-16
SOLUCIONES DEL SEGUNDO PARCIAL (17/12/2013)
 ÁLGEBRA LINEAL 1S1M-b SOLUCIONES DEL SEGUNDO PARCIAL 17/12/2013 1. Dada una aplicación lineal f : de manera que : Se pide, obtener su matriz con respecto a las bases canónicas. Calculamos =col 2. Calcular
ÁLGEBRA LINEAL 1S1M-b SOLUCIONES DEL SEGUNDO PARCIAL 17/12/2013 1. Dada una aplicación lineal f : de manera que : Se pide, obtener su matriz con respecto a las bases canónicas. Calculamos =col 2. Calcular
Semana 11 Matrices y vectores - Sistemas de EDOs - Modelica. Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería
 Matemáticas Aplicadas MA101 Semana 11 Matrices y vectores - Sistemas de EDOs - Modelica Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Matrices y vectores Sean dos
Matemáticas Aplicadas MA101 Semana 11 Matrices y vectores - Sistemas de EDOs - Modelica Elizabeth Villota Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Matrices y vectores Sean dos
Interpretación proyectiva de propiedades euclídeas. Elementos
 Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
TEMA 11.- VECTORES EN EL ESPACIO
 TEMA 11.- VECTORES EN EL ESPACIO 1.- INTRODUCCIÓN Un vector fijo AB del espacio (también lo era en el plano) es un segmento orientado que tiene su origen en un punto A y su extremo en otro punto B. Estos
TEMA 11.- VECTORES EN EL ESPACIO 1.- INTRODUCCIÓN Un vector fijo AB del espacio (también lo era en el plano) es un segmento orientado que tiene su origen en un punto A y su extremo en otro punto B. Estos
Álgebra Lineal UCR. Sétimo tema, 2013
 Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
TEMA No 3.- VECTORES EN EL PLANO.
 3.1.- CONCEPTO DE VECTOR. UNIDAD EDUCATIVA ROMULO GALLEGOS TEMA No 3.- VECTORES EN EL PLANO. Mérida, 4 de mayo de 2017 Un vector fijo es un segmento de recta orientado y dirigido que tiene su origen en
3.1.- CONCEPTO DE VECTOR. UNIDAD EDUCATIVA ROMULO GALLEGOS TEMA No 3.- VECTORES EN EL PLANO. Mérida, 4 de mayo de 2017 Un vector fijo es un segmento de recta orientado y dirigido que tiene su origen en
RECONOCIMIENTO DE PAUTAS
 RECONOCIMIENTO DE PAUTAS ANÁLISIS DISCRIMINANTE (Discriminant analysis) Reconocimiento de pautas supervisado si se cuenta con objetos cuya pertenencia a un grupo es conocida métodos: análisis de discriminantes
RECONOCIMIENTO DE PAUTAS ANÁLISIS DISCRIMINANTE (Discriminant analysis) Reconocimiento de pautas supervisado si se cuenta con objetos cuya pertenencia a un grupo es conocida métodos: análisis de discriminantes
Análisis en Componentes Principales
 This is page i Printer: Opaque this Análisis en Componentes Principales Dr. Oldemar Rodríguez Rojas 29 de mayo de 2008 ii This is page iii Printer: Opaque this Contents. Análisis en Componentes Principales
This is page i Printer: Opaque this Análisis en Componentes Principales Dr. Oldemar Rodríguez Rojas 29 de mayo de 2008 ii This is page iii Printer: Opaque this Contents. Análisis en Componentes Principales
Repaso de conceptos de álgebra lineal
 MÉTODOS AVANZADOS EN APRENDIZAJE ARTIFICIAL: TEORÍA Y APLICACIONES A PROBLEMAS DE PREDICCIÓN Manuel Sánchez-Montañés Luis Lago Ana González Escuela Politécnica Superior Universidad Autónoma de Madrid Repaso
MÉTODOS AVANZADOS EN APRENDIZAJE ARTIFICIAL: TEORÍA Y APLICACIONES A PROBLEMAS DE PREDICCIÓN Manuel Sánchez-Montañés Luis Lago Ana González Escuela Politécnica Superior Universidad Autónoma de Madrid Repaso
Análisis multivariante II
 Análisis multivariante II Tema 1: Introducción Pedro Galeano Departamento de Estadística Universidad Carlos III de Madrid pedro.galeano@uc3m.es Curso 2016/2017 Grado en Estadística y Empresa Pedro Galeano
Análisis multivariante II Tema 1: Introducción Pedro Galeano Departamento de Estadística Universidad Carlos III de Madrid pedro.galeano@uc3m.es Curso 2016/2017 Grado en Estadística y Empresa Pedro Galeano
Solución de problemas I 1
 Universidad Autónoma de Madrid Álgebra II. Físicas. Curso 5 6 Solución de problemas I Álgebra II Curso 5-6. Proyecciones en el producto escalar estándar Ejercicio 7.7. (a) Dada la ecuación x + y z, dar
Universidad Autónoma de Madrid Álgebra II. Físicas. Curso 5 6 Solución de problemas I Álgebra II Curso 5-6. Proyecciones en el producto escalar estándar Ejercicio 7.7. (a) Dada la ecuación x + y z, dar
Ejercicio 5: Dados los vectores u = -2i+j+4k y v = -i+j-3k, encuentre a) u.v y v.u b) u v y v u c) Un versor perpendicular a u y v
 Trabajo Práctico N 4: I) VECTORES EN R 2 Y R 3 Ejercicio 1: Las fuerzas que actúan en un cuerpo se localizan en un plano, por lo que pueden ser representadas mediante elementos de R 2. Considere un cuerpo
Trabajo Práctico N 4: I) VECTORES EN R 2 Y R 3 Ejercicio 1: Las fuerzas que actúan en un cuerpo se localizan en un plano, por lo que pueden ser representadas mediante elementos de R 2. Considere un cuerpo
AUTOVALORES Y AUTOVECTORES EL SUBESPACIO CARACTERÍSTICO
 Todos los derechos de propiedad intelectual de esta obra pertenecen en exclusiva a la Universidad Europea de Madrid, S.L.U. Queda terminantemente prohibida la reproducción, puesta a disposición del público
Todos los derechos de propiedad intelectual de esta obra pertenecen en exclusiva a la Universidad Europea de Madrid, S.L.U. Queda terminantemente prohibida la reproducción, puesta a disposición del público
FACULTAD DE INGENIERIA-UBA ALGEBRA II. Primer cuatrimestre de 2016 EXAMEN PARCIAL - 21 de mayo de 2016
 ALGEBRA II. Primer cuatrimestre de 216 EXAMEN PARCIAL - 21 de mayo de 216 TEMA 1 El examen se aprueba resolviendo correctamente 3 ejercicios 1. Halle todos los valores de r R para los cuales {[2 1 r] T,
ALGEBRA II. Primer cuatrimestre de 216 EXAMEN PARCIAL - 21 de mayo de 216 TEMA 1 El examen se aprueba resolviendo correctamente 3 ejercicios 1. Halle todos los valores de r R para los cuales {[2 1 r] T,
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
6.8. Descomposición mediante valores singulares. v 2 =
 68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
El reconocimiento de patrones desde un punto de vista estadístico es la selección o extracción de características.
 ANÁLISIS DE COMPONENTES PRINCIPALES El reconocimiento de patrones desde un punto de vista estadístico es la selección o extracción de características Esta selección se refiere a procesos donde el espacio
ANÁLISIS DE COMPONENTES PRINCIPALES El reconocimiento de patrones desde un punto de vista estadístico es la selección o extracción de características Esta selección se refiere a procesos donde el espacio
EXAMEN A PP 1A SEMANA
 EXAMEN A PP A SEMANA XAVI AZNAR Ejercicio. Defina. Simetría. Proyección. Homotecia vectorial y escriba sus polinomios mínimos. Demostración.. Una simetría σ de base B y dirección D es un endomorfismo tal
EXAMEN A PP A SEMANA XAVI AZNAR Ejercicio. Defina. Simetría. Proyección. Homotecia vectorial y escriba sus polinomios mínimos. Demostración.. Una simetría σ de base B y dirección D es un endomorfismo tal
ESPACIOS EUCLÍDEOS LA TRANSFORMACIÓN ORTOGONAL
 Todos los derechos de propiedad intelectual de esta obra pertenecen en exclusiva a la Universidad Europea de Madrid, S.L.U. Queda terminantemente prohibida la reproducción, puesta a disposición del público
Todos los derechos de propiedad intelectual de esta obra pertenecen en exclusiva a la Universidad Europea de Madrid, S.L.U. Queda terminantemente prohibida la reproducción, puesta a disposición del público
Nombre y Apellido. Bottino,Viviana. Juncos, Sebastián
 INSTITUTO DE CIENCIAS POLARES, AMBIENTE Y RECURSOS NATURALES Año: 2017 PROGRAMA DE LA ASIGNATURA: Matemática Avanzada para Ciencias Naturales (0109) CARÁCTER: CUATRIMESTRAL (2do) TIPO: OBLIGATORIA NIVEL:
INSTITUTO DE CIENCIAS POLARES, AMBIENTE Y RECURSOS NATURALES Año: 2017 PROGRAMA DE LA ASIGNATURA: Matemática Avanzada para Ciencias Naturales (0109) CARÁCTER: CUATRIMESTRAL (2do) TIPO: OBLIGATORIA NIVEL:
Tema 6. Análisis Factorial.
 Tema 6 Análisis Factorial El modelo Sea Y = (Y,, Y p ) t un vector aleatorio con vector de medias µ y matriz de covarianzas Σ Supondremos que existe un número entero m < p, una matriz L de orden p m de
Tema 6 Análisis Factorial El modelo Sea Y = (Y,, Y p ) t un vector aleatorio con vector de medias µ y matriz de covarianzas Σ Supondremos que existe un número entero m < p, una matriz L de orden p m de
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS
 RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
RESUMEN DEL TEMA 7 VALORES Y VECTORES PROPIOS 1. Determinantes El determinante de una matriz cuadrada n n A = a 21 a 22 a 2n a n1 a n2 a nn es un número real, y se representa por: A = a 21 a 22 a 2n a
1. Hallar el rango de cada una de las siguientes matrices
 Tarea 5 Hallar el rango de cada una de las siguientes matrices 5 5 a) = 7 6 5 5 b) = 5 8 Solución: a) rang ( ) = b) rang ( ) = Determinar si cada uno de los siguientes conjuntos de vectores es linealmente
Tarea 5 Hallar el rango de cada una de las siguientes matrices 5 5 a) = 7 6 5 5 b) = 5 8 Solución: a) rang ( ) = b) rang ( ) = Determinar si cada uno de los siguientes conjuntos de vectores es linealmente
