- Palabras claves: espacio tridimensional vector polígono prisma cono cilindro esfera traslación rotación generatriz superficie área volumen

Transcripción

1 Descripción curricular: - Nivel: 4º medio - Sector: Matemática - Unidad temática: Geometría. - Palabras claves: espacio tridimensional vector polígono prisma cono cilindro esfera traslación rotación generatriz superficie área volumen - Contenidos curriculares: - Resolución de problemas sencillos sobre áreas y volúmenes de cuerpos generados por rotación o traslación de figuras planas. Resolución de problemas que plantean diversas relaciones entre cuerpos geométricos; por ejemplo, uno inscrito en otro. - Rectas en el espacio, oblicuas y coplanares. Planos en el espacio, determinación por tres puntos no colineales. Planos paralelos, intersección de dos planos. Ángulos diedros, planos perpendiculares, intersección de tres o más planos. Coordenadas cartesianas en el espacio. - Contenidos relacionados: - 1º medio: Traslaciones, simetrías y rotaciones de figuras planas. Construcción de figuras por traslación, por simetría y por rotación en 60, 90, 10 y 180 grados. Traslación y simetrías de figuras en sistemas de coordenadas. - º medio: Ángulos del centro y ángulos inscritos en una circunferencia. Teorema que relaciona la medida del ángulo del centro con la del correspondiente ángulo inscrito. - 4º medio: Rectas en el espacio, oblicuas y coplanares. Planos en el espacio, determinación por tres puntos no colineales. Planos paralelos, intersección de dos planos. Ángulos diedros, planos perpendiculares, intersección de tres o más planos. Coordenadas cartesianas en el espacio. - Aprendizajes esperados: Conocen y utilizan la operatoria básica con vectores en el plano y en el espacio (adición, sustracción y ponderación por un escalar), y la relacionan con traslaciones y homotecias de figuras geométricas. Conocen y valoran la capacidad del modelo vectorial para representar fenómenos físicos como desplazamientos y fuerzas. Resuelven problemas relativos al cálculo de áreas y volúmenes de cuerpos generados por rotación o traslación de figuras planas. - Aprendizajes esperados de esta actividad: Utilizan la operatoria básica con vectores en el plano y en el espacio (adición, sustracción y ponderación por un escalar), y la relacionan con traslaciones de figuras geométricas.

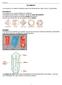
2 Resuelven problemas relativos al cálculo de áreas y volúmenes de cuerpos generados por rotación o traslación de figuras planas. - Recursos digitales asociados de - Ficha: Área y Volumen - Diapositivas digitales (ppt): Superficies de revolución - Juego: Quién sabe más? Área y volumen - Actividades propuestas para este tema: En este documento encontrará dos actividades que pretenden poner en práctica los contenidos abordados en la tercera unidad de NM4: Geometría. En estas actividades sus estudiantes determinarán qué sucede al trasladar o rotar una figura geométrica en el espacio tridimensional. Además, determinarán el área y el volumen de los cuerpos geométricos obtenidos. - Actividad, Qué obtenemos si trasladamos una figura plana? : referida a encontrar el cuerpo geométrico obtenido luego de trasladar una figura plana según un vector tridimensional. Determinar áreas y volúmenes. - Actividad, Si rotamos una figura plana Qué obtenemos? : referida a encontrar el cuerpo geométrico obtenido luego de rotar una figura plana en torno a uno de sus lados. Determinar áreas y volúmenes. A continuación encontrará los contenidos tratados en estas actividades y sugerencias sobre cómo desarrollarlas con sus estudiantes. Actividad: Qué obtenemos si trasladamos una figura plana? Duración: horas pedagógicas. 1. Mapa de contenidos tratados. Espacio Tridimensional Vector Polígono Traslación Cuerpos geométricos Prismas Área Volumen. Desarrollo de la actividad. Esta actividad requiere que sus alumnos, al menos, conozcan la operatoria básica con vectores en el plano y el espacio y que sean capaces de realizar una traslación en el plano cartesiano.

3 Se sugiere realizar la actividad en la sala de clases utilizando la guía del alumno. Paso 1: Para activar los conocimientos de sus alumnos, ya abordados en el desarrollo de la unidad, puede dar inicio a esta actividad realizando preguntas como: Qué nos indica la punta de la flecha de un vector? Qué nos indica su módulo? Con esta pregunta se espera que sus alumnos recuerden cómo se compone un vector y qué nos indican su dirección, sentido y módulo, pues de acuerdo a estas características podremos determinar una traslación. Qué requerimos para trasladarnos en el espacio? Guíe a sus alumnos para que sus respuestas coincidan con las características principales de un vector, de esta forma completará la idea inicial que se pretendía abordar, una traslación queda determinada por una figura y un vector de traslación. Cuál es la diferencia principal entre un cuerpo geométrico y un polígono? Si sus alumnos no pueden responder inmediatamente, realice comparaciones entre objetos presentes en la sala de clases, como por ejemplo, una imagen o fotografía de una persona versus una persona real; una hoja de papel versus un cuaderno. Debe cerciorarse de que sus alumnos comprendan que a un cuerpo geométrico se le pueden asociar las medidas de área y volumen, a diferencia de un polígono, el cuál por ser plano es una superficie sin volumen. Si requiere ahondar en las definiciones de los conceptos que se pretenden activar en el inicio de esta clase, puede hacer uso de la ficha Área y Volumen que se encuentra disponible en el portal Educarchile (recursos asociados). Paso : Si desea armar equipos, se sugiere trabajo en parejas. El material permite trabajo individual. Haga entrega de la guía para el estudiante Qué obtenemos si trasladamos una figura plana? disponible en el portal Educarchile. A través de la observación y/o preguntas dirigidas asegúrese de que sus alumnos están desarrollando debidamente la guía. A continuación, se presenta la guía del alumno con las respuestas (o sugerencias de respuestas) en color azul. FICHAS TEMÁTICAS: Nivel: 4º Medio Subsector: Matemática Unidad temática: Geometría Actividad: Qué obtenemos si trasladamos una figura plana? I. Creando un cuerpo por traslación. Crees que es posible generar volumen mediante una traslación? Sugerencia: Las respuestas de sus alumnos pueden ser variadas, por lo que es recomendable pedirles que las argumenten claramente, pueden dar ejemplos si así lo desean

4 Dibuja en el espacio tridimensional el polígono de vértices A(0, 0, ), B(, 0, 0), C(0, 0, 0) y el vector v(0, 6, 0). Ahora, traslada el polígono ABC según el vector v. Marca el rastro dejado por la traslación. Qué características tiene la figura final al trazar los vectores y la figura trasladada? Sugerencia: La figura final es un cuerpo geométrico. Este cuerpo posee volumen ya que ocupa un lugar en el espacio. Posee tres caras laterales rectangulares y dos caras basales triangulares Sabes qué nombre recibe esta figura? Si no lo sabes a qué objeto que conoces se parece? Este cuerpo geométrico es llamado prisma triangular recto. Sugerencia: Los techos de algunas casas tienen esta forma. Cómo podemos determinar el valor del área de esta figura? Sugerencia: Permita a sus alumnos buscar distintas estrategias para calcular el área del prisma. La manera tradicional se desarrollará a continuación en esta guía.

5 II. Separar para calcular. De cuántas figuras planas está formado el prisma que construiste? de 5 figuras Dibújalas por separado y determina el área de cada una. Prisma: Cara 1. Cara. Rectángulo de Rectángulo de base u y altura 6u. base u y altura 6u. Á1=u x 6u = 1u Á=u x 6u = 1u Cara 3. Cara 4. Cara 5. Rectángulo de base u Triángulo de base u Triángulo de base u y altura 6u y altura u y altura u 1 Á3= u x 6u = 1 u Á4= x u x u = u Á5= 1 x u x u = u Sugerencia: No olvides que: base altura Á = Entonces, el área total del prisma que has construido es: Á total = Á1 + Á + Á3 + Á4 + Á5 Á total = 1u + 1u + 1 u + u + u Á total = 8u + 1 u

6 III. Ahora el volumen. El volumen de un prisma se obtiene multiplicando el área de la base por la altura de dicho prisma. Volumen Prisma: Vp = Área base x altura El volumen del prisma que tú construiste es: Á base = u y h=6u Entonces: Vp = u x 6u Vp = 1u 3 IV. Y esto dónde se aplica? Una empresa desea fabricar carpas con las siguientes dimensiones: 1,0 m de alto; 1,80 m de ancho, pero no se han decidido por la profundidad de éstas. Si la lona con la que cuentan para cubrir toda una carpa (tapas, base y techo) es 16,56 m. Cuál deberá ser la profundidad de cada carpa para aprovechar al máximo la lona? Las caras 1 y poseen iguales medidas y corresponden a las caras basales del prisma. 1,80m 1,0m Á(bases) = =,16 m Para obtener el valor de x haremos uso del teorema de Pitágoras: 1,80m x = (1,0m) + x = 1,5m Las caras 3 y 4 poseen iguales medidas. Á(3 y 4) = (1,5 m ym) = 3y m, donde y metros es la medida de la profundidad de la carpa. El área de la cara 5, base de la carpa, es: Á(5) = 1,80m ym =1,80y m. Como el área total del prisma, área de la lona, es 16,56 m, entonces: 16,56 m =,16 m + 3y m + 1,80y m y = 3 Por lo tanto, para aprovechar al máximo la lona, la profundidad de cada carpa debe ser 3m.

7 Paso 3: Para concluir la actividad, se sugiere entablar una discusión sobre la pregunta de la guía Qué obtenemos si trasladamos una figura plana?. A partir de las respuestas de sus alumnos debe evidenciarse si han comprendido que dado un vector en el espacio y un polígono cualquiera, pueden construir un cuerpo geométrico y determinar el área y volumen de éste. Anote las conclusiones en la pizarra para poder hacer una síntesis al final de la clase. Es en este momento cuándo debe hacer lo posible por detectar las posibles ideas erróneas de sus alumnos y corregirlas. Contraste estas respuestas con las dadas al inicio de la clase. Conduzca la discusión de tal manera que la mayor cantidad de alumnos pueda opinar. Actividad: Si rotamos una figura plana Qué obtenemos? Duración: horas pedagógicas. 1. Mapa de contenidos tratados. Espacio Tridimensional Figuras geométricas. Polígonos Lados Rotación Cuerpos geométricos Cilindros Conos Esferas Área Volumen. Desarrollo de la actividad. Esta actividad requiere que sus alumnos, al menos, tengan noción de los conceptos de triángulos rectángulos, rectángulos y circunferencias, junto con las fórmulas para calcular el área de ellas. Se sugiere desarrollar la actividad en la sala de clases utilizando la guía del alumno. Paso 1: Para activar los conocimientos de sus alumnos, ya abordados en el desarrollo de la unidad, puede dar inicio a esta actividad realizando preguntas como: Cuál es la diferencia principal entre un cuerpo geométrico y un polígono? Si sus alumnos no pueden responder inmediatamente, realice comparaciones entre objetos presentes en la sala de clases, como por ejemplo, una imagen o fotografía de una persona versus una persona real; una hoja de papel versus un cuaderno. Debe cerciorarse de que sus

8 alumnos comprendan que a un cuerpo geométrico se le pueden asociar las medidas de área y volumen, a diferencia de un polígono, el cuál por ser plano es una superficie sin volumen. Pregunte a sus alumnos si es posible obtener una esfera a partir de alguna figura geométrica y la traslación de ésta de acuerdo a algún vector tridimensional. Probablemente lo que imaginen sus alumnos se aproxime a un semicilindro. Sin embargo, la respuesta a su pregunta será negativa. Con esta discusión de inicio a la clase. Si requiere ahondar en las definiciones de los conceptos que se pretenden activar en el inicio de esta clase, puede hacer uso de la ficha Área y Volumen que se encuentra disponible en el portal Educarchile (recursos asociados). Paso : Si desea armar equipos, se sugiere trabajo en parejas. El material permite trabajo individual. Haga entrega de la guía para el estudiante Si rotamos una figura plana Qué obtenemos? disponible en el portal Educarchile. A través de la observación y/o preguntas dirigidas asegúrese que sus alumnos están desarrollando debidamente la guía. A continuación, se presenta la guía del alumno con las respuestas (o sugerencias de respuestas) en color azul. Nivel: 4º Medio Subsector: Matemática Unidad temática: Geometría Actividad: Si rotamos una figura plana Qué obtenemos? I. Creando un cuerpo por rotación. Crees que es posible generar volumen mediante una rotación? Sugerencia: Las respuestas de sus alumnos pueden ser variadas, por lo que es recomendable pedirles que las argumenten claramente, pueden dar ejemplos si así lo desean Imagina qué resulta al girar las siguientes figuras respecto a uno de sus lados y siguiendo la flecha. Haz un bosquejo en el recuadro correspondiente.

9 En cada caso Qué características tiene la figura final luego de la rotación? En todos los casos, la figura inicial, luego de la rotación en torno a uno de sus lados, se ha transformado en un cuerpo geométrico, con volumen. Sabes qué nombre reciben estas figuras? Si no lo sabes a qué objeto que conoces se parecen? El primer cuerpo geométrico es un cono, como el de los helados o los embudos. El segundo cuerpo geométrico es un cilindro, Cómo podemos determinar el valor del área de estas figuras? Sugerencia: Las respuestas de sus alumnos pueden ser variadas, por lo que es recomendable pedirles que las argumenten claramente, pueden dar ejemplos si así lo desean II. Estirar y calcular. a) Iniciemos con el cono. h es la altura del cono (altura del triángulo que lo generó) r es el radio basal del cono (base del triángulo que lo generó). g es la generatriz del cono (hipotenusa del triángulo que lo generó) El perímetro basal del cono es π r ya que la base del cono es una circunferencia de radio r. Al estirar este cuerpo geométrico se obtiene la siguiente figura. g Observa que hemos completado la semicircunferencia de radio g, donde: π r g Ásemicírculo = π π g Psemicircunferencia = = πg

10 Estableciendo una sencilla proporción tenemos que: Área semicírculo Área cono = Perímetro semicircunferencia Perímetro basal cono Reemplazando: π g X Despejando X tenemos que: π g =, donde X es el área del cono que desconocemos. π r X = π Por lo tanto, el área lateral del cono es: Área cono = π g r Si al cono se le agrega la base, basta sumar el área del círculo, de radio r. Entonces, el área total del cono es: g r Á total = π r g + π r b) El área del cilindro. Donde h es la altura del cilindro (lado del rectángulo que genera el cilindro) r es el radio del cilindro (base del rectángulo que genera el cilindro) Al estirar este cuerpo geométrico se obtiene la siguiente figura. Dibújala h r El área lateral del cilindro es: El perímetro de la circunferencia que forma la base del cilindro es: P( ) = π La medida de la base del rectángulo es igual al perímetro de la circunferencia. r El área del rectángulo equivale al área lateral del cilindro, por lo tanto: Álateral _ cilindro = π r h

11 Si el cilindro tiene bases superior e inferior (las tapas) el área total del cilindro es: El área de cada tapa será: A= π r Como ambas tapas son iguales, el área basal es: Ábasal = A = π r El área total del cilindro es: Átotal = Álateral _ cilindro + Átotal = π r h + π r Átotal = π r ( h + r) Ábasal Desafío: Haciendo un análisis similar al anterior, calcula el área de la esfera generada por rotación. III. El volumen de estos cuerpos. a) Volumen de un cono. V cono = 3 1 área de la base x altura Para resolver: Encuentra el volumen del cono generado por la revolución de un triángulo rectángulo isósceles cuyo perímetro es de cm. Supongamos que r es el radio basal del cono Si el triángulo que genera al cono es rectángulo isósceles: r + r = g donde g es la generatriz del cono e hipotenusa del triángulo. g = r cm Como el perímetro es cm: r + r + g = r = + El volumen del cono es: 1 1 V cono = π r r = π b) Volumen de un cilindro. V cilindro = π r x h

12 Resolviendo: El volumen de un cilindro de revolución es 000π cm 3. Hallar el área total de este cilindro, sabiendo que tiene 0 cm. de altura. Según la fórmula del volumen:.000π cm 3 = π r x 0cm r = 10cm Como Átotal = π r ( h + r) Átotal = π 10(0+ 10) cm Átotal = 600π cm c) Volumen de una esfera. V = 4 π 3 r 3 Aplicando la fórmula: La diferencia entre los volúmenes de dos esferas concéntricas es 84π cm 3. Si la menor tiene 1 cm. de radio, hallar el radio de la mayor. V (esfera1) = 4 π 3 r 3 4 ; V (esfera1) = π ; V (esfera1) - V (esfera1) = 84π cm 3 Entonces: 4 π 3 r 3-4 π = 84π cm 3 r = 4cm Paso 3: Para concluir la actividad, se sugiere entablar una discusión sobre la pregunta de la guía Si rotamos una figura plana Qué obtenemos?. A partir de las respuestas de sus alumnos debe evidenciarse si han comprendido que dado un polígono cualquiera, al girarlo en torno a un lado de éste, pueden construir un cuerpo geométrico y determinar su área y volumen. Anote las conclusiones en la pizarra para poder hacer una síntesis al final de la clase. Es en este momento cuándo debe hacer lo posible por detectar las posibles ideas erróneas de sus alumnos y corregirlas. Contraste estas respuestas con las dadas al inicio de la clase. Conduzca la discusión de tal manera que la mayor cantidad de alumnos pueda opinar. Como recurso anexo para esta unidad, puede asistir al laboratorio de computación y pedir a sus alumnos que jueguen el juego Quién sabe más Área y Volumen. Destine al menos 10 minutos para analizar los resultados obtenidos en el juego y resuelvan en conjunto las preguntas que presentaron mayores dificultades.