dx? Justifica la respuesta.
|
|
|
- Joaquín Márquez Vega
- hace 7 años
- Vistas:
Transcripción
1 . PROBLEMAS DE CÁLCULO. (*) El caudal de agua que vacía un depósito de litros es variable y viene dado por la ecuación C(t) 5 't (t en minutos, C en litros/minuto). a) Dibuja la gráfica del caudal en función del tiempo. b) Calcula el área bajo la curva en el intervalo [,5]. Interpretar el resultado. c) Dibuja la función que determina el volumen de agua del depósito en función del tiempo.. Las gráficas i), ii) y iii) corresponden, no necesariamente por ese orden, a las de una función derivable f, su función derivada f ' y una primitiva F de f. Identifica cada gráfica con la función justificando la respuesta. (i) (ii) (iii). De una función integrable f: [,] se sabe que para cada en dicho intervalo se tiene f ( ). De los números,,, '5 y '75, cuáles pueden ser el valor de la integral f ( ) d? Justifica la respuesta..4 La figura siguiente representa la gráfica de una función f: [,7]. Y X Sea F : [,7] la función definida por F( ) f ( t) dt. a) Calcula F(4) y F(7). b) Dibuja la gráfica de F eplicando cómo lo haces..5 La velocidad de un móvil que parte del origen viene dada en m/s por la gráfica. v a) Calcula la función espacio recorrido. 4 5 t b) Dibuja la gráfica de la función espacio recorrido-tiempo. c) Prueba que el área bajo la curva que da la velocidad coincide con el espacio total recorrido. 7
2 .6 Un objeto se mueve a lo largo de una línea recta debido a la acción de una fuerza F que depende continuamente de la posición del objeto en dicha línea recta. Se sabe que el trabajo realizado por la fuerza para mover el objeto desde a hasta b, viene dado por N F( ) d. b a. Si la fuerza es F ( ), calcula el trabajo para ir desde hasta 5. ( ). Determina razonadamente si la fuerza G ( ) realiza más o menos trabajo que ( ) la fuerza F anterior para el mismo desplazamiento..7 (*) De todas las primitivas de la función f: dada por f ( ), determina aquella cuya gráfica pasa por el punto (, )..8 La función f definida por f ( ) ( a ) a si si es derivable en toda la recta real.. Cuánto vale a?. Para dicho valor de a, cuánto vale f '()?.9 De una función f: se sabe que si F: es una primitiva suya, entonces también lo es la función G dada por G() F (). Puedes determinar f ()? y f (5)? y el valor de f ( ) d? Justifica las respuestas y, en los casos de respuestas afirmativa, calcula los valores correspondientes.. Sea f: una función derivable en ; sean a y b dos raíces de la derivada f '() tales que entre ellas no hay ninguna otra raíz de f '(). Razonar debidamente si puede ocurrir cada una de las siguientes posibilidades:. Entre a y b no eiste ninguna raíz de f ().. Entre a y b eiste una sola raíz de f ().. Entre a y b eisten dos o más raíces de f ().. (*) Sea f una función continua tal que para cualquiera que sea > se cumple que f f. Prueba que, entonces, se verifica que f () f () para todo >. 5 8
3 . a) Esboza la gráfica de la función dada por f ( ) 4 b) Es la integral positiva o negativa? Justifica tu respuesta. 4 c) Calcula el valor de la integral del apartado b) descomponiendo el integrando en fracciones simples. d) Un amigo te sugiere que esa integral se hace más fácil con la sustitución secθ. Tú qué piensas?. De una cierta función f conocemos algunos valores, dados en la siguiente tabla: '9 '97 ' ' '9 '99 4 4' 4' f () '5 6'6 6'95 7 7'59 7'5 8 8'8 8'98 9 9'. Usa esta tabla para aproimar el valor de la derivada de f en.. A partir de la información que te da esta tabla, crees que f () es derivable en 4? Justifica tu respuesta. f ( ) f ().4 Supón que f es una función para la que lím. Cuáles de las siguientes afirmaciones tienen que ser verdaderas, cuáles pueden ser verdaderas y cuáles son obligatoriamente falsas? ) f '() ; ) f () ; ) lím f ( ) f () ; 4) f es continua en ; 5) f es continua en..5 Dice la eperiencia que el área encerrada por un segmento parabólico es dos tercios del producto de su altura h por la longitud de su base b. Confirma que esta fórmula es correcta, utilizando el teorema fundamental del cálculo para obtener el área en cuestión..6 Cuatro estudiantes no se ponen de acuerdo sobre el valor de la integral π 8 sen d. Anto- 5π π nio dice que es igual a π, Beatriz dice que vale, Carlos, que vale 8 9 y Diana afirma que es π. Uno de ellos está en lo cierto. Quién es? No intentes calcular esta integral. Elimina, justificadamente, las tres respuestas erróneas..7 Considera la función h() f () g() donde las gráficas de f y g son las que te damos a continuación. 9
4 Gráfica de f Gráfica de g a). Calcula h() y h(). Calcula aproimadamente f '(), f '(), g'() y g'().. Calcula aproimadamente h'(), h'(). b) Con las mismas gráficas que en el apartado anterior, sea h() f [g()].. Calcula h() y h(). Es h'() positivo, negativo o cero? Eplica cómo puedes saberlo.. Es h'() positivo, negativo o cero? Eplica cómo lo averiguas..8 (*) Supón que f y g son funciones derivables para las que se verifican las dos condiciones siguientes: ) f () y g() ; ) f '() g() y g'() f (). a) Sea h() f () g (). Calcula h'() y utiliza el resultado que obtengas para demostrar que f () g () para todo. b) Supón que F y G son otro par de funciones derivables que satisfacen las condiciones ) y ) y sea k() [F() f ()] [G() g()]. Calcula k'() y utiliza el resultado que obtengas para deducir qué relación eiste entre f () y F() y entre g() y G(). c) Muestra un par de funciones f y g que satisfagan las condiciones ) y ). Puede haber otras? Justifica tu respuesta..9 Piensas que alguna las siguientes gráficas es parte de la gráfica de la función f () sen e? Justifica tu respuesta. A B C
5 . a) Si f es derivable y f '() para cualquier número real, cuántas soluciones puede tener la ecuación f ()? Eplica tu respuesta. b) Si f es derivable y la ecuación f '() tiene solamente una solución, cuántas soluciones puede tener la ecuación f ()? Justifica tu respuesta. c) Si f es derivable y la ecuación f '() tiene n soluciones, cuántas soluciones puede tener la ecuación f ()? Justifica tu respuesta.. (*) Demuestra que la ecuación cos sen tiene eactamente dos raíces reales.. Sea f: [a, a] con a > una función continua tal que f. Responde razonadamente a las siguientes preguntas: ) Es necesariamente f () para todo [a, a]? ) Es necesariamente f ( ) d? ) Es necesariamente f ( ) d? a a a a aa. ( d? 4) Cuánto vale ( f ) ) a a ) Estudia, según los valores de b, la derivabilidad de la función f definida por f ( ) b si < si ) Calcula f ( ) d.4 Cuántos puntos del intervalo [, ] satisfacen la igualdad cos? Justifica la respuesta y enuncia algunos de los teoremas importantes que utilices..5 (*) Dada la función f: definida por f ( ) ( ) cos( ) sen( ) si si > a) Determina los puntos en los que f es continua y los puntos en los que f es derivable. b) Cumple f en [, ] las condiciones del teorema de Rolle?
6 .6 Considera la función f: definida por f ( ). a) Determina los puntos donde f es derivable y halla sus máimos y mínimos locales. b) Calcula f ( ) d..7 (*) Considera la función f: definida por f () 5 ( ) 4 ( ). a) Demuestra que la ecuación f '() tiene al menos una solución en el intervalo (, ). b) Demuestra que la ecuación f () tiene eactamente una solución menor que. c) Demuestra que la ecuación f () no tiene ninguna solución mayor que..8 La gráfica de la derivada de una cierta función f es a) Cuántas soluciones puede tener la ecuación f ()? b) Si la ecuación f () tiene eactamente dos soluciones distintas, pueden ser éstas del mismo signo?.9 Determina todas las funciones f de la forma f () a b c d con a y que verifican f '() f '(). Alguna de las funciones determinadas anteriormente verifica f () f ()? Justifica las respuestas.. Encuentra todas las funciones continuas f: [a, b] tales que para toda función continua f '. b a g: [a, b] se cumple que f ( ) g( ) d. a) Sea I [a, b] y f : I una función continua tal que f () I. b a Demostrar que si f ( ) d, entonces f es la función nula. (Si no has hecho el problema anterior, hazlo ahora, después de hacer el apartado a) de éste). b) Eiste alguna función continua g: [, ] y algún número real a tales que g () [, ] y g ( ) d ; g ( ) d a y g( ) d a? Problemas sobre máimos y mínimos. De entre todos los triángulos isósceles de perímetro 6 cm, calcula las dimensiones del de mayor área. (Utiliza funciones trigonométricas).. En un rectángulo de 4 m. de perímetro, se sustituyen los lados por semicircunferencias eteriores. Entre qué valores está comprendida el área de la figura resultante?
7 .4 En un rectángulo de 4 m. de perímetro se sustituyen dos lados opuestos por semicircunferencias eteriores. Estudiar si eiste un rectángulo para el que la figura formada tenga máima área..5 Se tiene un alambre de m. de longitud y se desea dividirlo en dos partes para formar con la primera un cuadrado y con la segunda un círculo. Hallar la longitud de cada parte resultante para que la suma de las áreas de las dos figuras sea: a) Máima; b) Mínima..6 (*) Hallar el punto de la parábola 4y de abscisa no negativa que menos diste de,..7 Dados a, a, a, definimos la función f () ( a ) ( a ) ( a ). Dónde alcanza f el mínimo?.8 Un camión ha de recorrer km. en una carretera llana a velocidad constante de Km/h. Las leyes de circulación prescriben que Se supone que el carburante cuesta ptas. por litro y que el consumo es de litros por hora. Si el conductor cobra P ptas. por hora y obedece todas las leyes de tráfico, determinar la velocidad más económica y el coste del viaje si a) P ; b) P 6..9 Los beneficios de una fábrica de camisas dependen del número de camisas que se fabrican cada día según la función f () donde mide el número de miles de camisas producidas al día y f () la ganancia (o pérdida) en millones de ptas. al mes. Debido al número de máquinas y personal que hay en la fábrica, el gerente de ésta puede decidir fabricar un número de camisas diario comprendido entre y 4. Cuántas camisas debe fabricar para obtener un beneficio máimo?.4 Tenemos una valla de m. de larga y m. de alambre, con los que queremos delimitar un campo rectangular que, conteniendo a la valla como parte de un lado, encierre área máima. Calcular las dimensiones del rectángulo..4 En un jardín eiste un paseo cerrado que consta de media circunferencia de radio m y de su diámetro correspondiente. En el interior de la figura anterior se va a instalar un parterre rectangular, uno de cuyos lados está sobre el diámetro y el opuesto a él tiene sus etremos en la parte curva. El parterre se plantará de camelias, que ocupan '5 m cada una. Cuál es el número máimo de camelias que pueden ubicarse?
8 Nota: Resuélvelo como te sea más familiar, pero inténtalo también introduciendo alguna función trigonométrica..4 El número de bacterias de cierto cultivo en un instante t viene dado por la fórmula N (5 t e t/ ) para t. a) En qué instantes de ese intervalo, t, hay un número máimo y un número mínimo de bacterias? b) En qué instante es más lento el crecimiento o decrecimiento del número de bacterias?.4 Calcula las dimensiones del trapecio de perímetro máimo que se puede inscribir en una semicircunferencia de radio r si una base del trapecio ocupa todo el diámetro de la semicircunferencia. (Utiliza funciones trigonométricas)..44 En un triángulo isósceles ABC, el lado desigual AC mide a y la altura correspondiente a ese lado mide h. Determina los puntos P sobre la altura mencionada para que la suma de las distancias de P hasta los tres vértices sea a) mínima; b) máima..45 Para cada r se define la función f r : [, ) [, ) mediante f r () r. a) Determina la ecuación de la recta tangente a la gráfica de f r en el punto (, ). b) Calcula el área A(r) de la región limitada por la gráfica de f r, su tangente en el punto (, ) y el eje OX. c) Para qué valor de r es el área A(r) máima?.46 Para obtener el máimo beneficio, un cargamento de frutas debe llegar al mercado lo más pronto posible después de la recogida. Si un cultivador envía su producción inmediatamente después de la recogida, obtendrá cajas con un beneficio de euros por caja. Si espera, podrá enviar 5 cajas más por semana pero, como también los competidores producirán más, el beneficio bajará euro por caja y por semana. Cuándo debe enviar la fruta para que el beneficio sea máimo? Calcula éste..47 (*) Las palomas domésticas no suelen volar sobre etensiones grandes de agua a menos que se vean forzadas a ello, posiblemente porque se requiera más energía para mantener la altitud sobre el agua fría. Supongamos que se suelta una paloma desde un barco situado a Km de la costa estando el palomar a km del punto de la costa más cercano al barco. Si la paloma gasta dos veces más energía volando sobre el agua que sobre la tierra firme y sigue un camino que hace mínima la energía gastada, calcula el punto donde debe abandonar el mar. 4
9 .48 (*) Dos pasillos de anchura 8 y 7 se cortan en ángulo recto. Hallar la máima longitud que puede tener una viga que pueda pasar por esa esquina. Límite de una sucesión.49 Considera las sucesiones a n :,,,, L y b n : 5, 5, 5, Los términos de {a n } se aproiman a y los de {b n } se aproiman a 5 4. En qué caso crees que la aproimación es más intensa? Escribe algún párrafo que pudiera responder a esa cuestión y, en cualquier caso, trabaja las cuestiones siguientes.. Vamos a intentar rodear a en un caso, y a 5 4 en el otro, de unas murallas, a ver si conseguimos que traspasen esa muralla la menor cantidad de elementos posibles. Esas murallas van a ser, simplemente, intervalos abiertos centrados en los números en cuestión: y 5 4. a) Cuántos elementos de {a n } hay fuera del intervalo de centro y radio? Cuántos elementos de {b n } hay fuera del intervalo de centro 5 4 y radio? Cuántos se han colado, pues, a través de esas murallas en cada caso? b) Responde a las mismas preguntas que en a) para intervalos de radio en cada caso. c) Responde a las mismas preguntas que en a) para intervalos de radio en cada caso.. Tienes ahora, con la información obtenida en el apartado ), algún argumento que te permita decidir en qué caso es más intensa la aproimación? 4. Continuemos estrechando las murallas. Vamos a pensar ahora en intervalos de radio una cienmilésima. a) Cuántos elementos de {a n } hay fuera del intervalo de centro y radio 5? b) Cuántos elementos de {b n } hay fuera del intervalo de centro y radio 5? c) En qué caso crees ahora que es más intensa la aproimación? Justifica de alguna manera tu respuesta. 5. Observa lo que ocurre en {a n } y por mucho que estrechemos la muralla que rodea a. Se cuelan prácticamente todos. Completa la siguiente frase: 5
10 Dada la sucesión a n :,,,,... considerando, intervalo centrado en, resulta que fuera de ese intervalo hay solamente, una cantidad 4 finita de términos de la sucesión. 6. Esos niveles de aproimación son los que nos interesan en este capítulo. Decimos que es el límite de la sucesión a n :,,,,... Da tú una definición: El número l 4 es el límite de la sucesión {a n } si... En lo que sigue, vamos a intentar sacarle partido a la definición que has dado de límite de una sucesión. 7. Posiblemente recuerdes lo que es una sucesión monótona creciente. También lo que es una sucesión acotada superiormente. (Si estos conceptos te suenan solamente para funciones, recuerda que una sucesión {a n } es eactamente una función f : donde f (n) a n ). Escribe una definición de esos dos conceptos. 8. Piensa si es verosímil construir una sucesión, monótona creciente, acotada superiormente y que no tuviera límite. Crees que no es posible? Enuncia, entonces, un teorema que relacione esas tres ideas Con lo que sabes hasta ahora, puedes dar una demostración rigurosa del teorema que has enunciado. Inténtalo:.... Piensa en la sucesión,,,,... Obviamente es una sucesión acotada. Demuestra que ningún número real es límite de esa sucesión.. Has visto sucesiones acotadas que no tienen límite. Piensa en el teorema recíproco. Crees que hay sucesiones con límite que no estén acotadas?. Enuncia y demuestra algún teorema que relacione las ideas de estar acotada y tener límite.. Dada una sucesión {a n }, un compañero tuyo ha demostrado que tiene por límite y otro que tiene por límite. Crees que alguno tiene que estar equivocado? Da una demostración rigurosa de que alguno está equivocado. 4. Enuncia y demuestra algún teorema que diga algo sobre el número de límites de una sucesión. 6
11 .5 Si has trabajado bien las catorce cuestiones anteriores, ya sabes perfectamente lo que es el límite de una sucesión. Ocurre, sin embargo, que, posiblemente, tengas un recuerdo de algo mucho más engorroso; algo que mezclaba los valores absolutos con las letras griegas, con los eiste y para todo, y para terminar, lo mezclaba todo con las desigualdades. Vamos a ver dos cosas: una, que eso es eactamente lo mismo que has visto en estas cuestiones y, dos, que tus tetos o tus profesores no te han dicho eso con ánimo de liarte sino que es la única vía para demostrar cosas tan elementales como, por ejemplo, que el límite de una sucesión obtenida como suma de dos que tengan límite es, precisamente, la suma de los límites.. Observa que el intervalo abierto (, 7) es { / < < 7}. Completa esta frase: { / < < 7} { / < }.. Completa esta frase: (ar, ar) { / < }.. Recuerda: lím a n l si fuera de cada intervalo abierto centrado en l hay solamente una cantidad finita de términos de la sucesión. Decir que hay fuera una cantidad finita de términos de la sucesión, equivale a decir que, a partir de uno dado, todos están. 4. Supongamos que la sucesión {a n } verifica que fuera del intervalo de centro l y radio están solamente a, a, a 7, a. Completa la siguiente frase: Dado r, resulta que para cualquier n a n (l, l ), o sea, a n <., se verifica que Para cada número positivo r, hay un intervalo centrado en a y radio r. Así pues, en lugar de hablar sobre cada intervalo centrado en a, diremos cosas sobre cada número positivo r. 5. Observa la evolución de la definición de límite que conoces, a esa otra que, posiblemente, recuerdes con terror. ) lím a n a si para cada intervalo centrado en a, tenemos que fuera de ese intervalo hay solamente una cantidad finita de términos de la sucesión. ) lím a n a si para cada intervalo centrado en a, eiste un número natural n, tal que todos los términos de la sucesión, a partir de a n, están dentro de ese intervalo. ) lím a n a si para cada r >, eiste un número natural n, tal que si n n, entonces a n (ar, ar). 7
12 4) lím a n a si para cada r >, eiste un número natural n, tal que si n n, a n a < r. 5) lím a n a si r >, n / n n a n a < r. 6. Supón que tienes dos sucesiones {a n } y {b n } tales que lím {a n } a y lím {b n } b. Crees que eiste lím {a n b n }? Cuánto vale? 7. En el ejercicio anterior has conjeturado un teorema sobre el límite de la suma de dos sucesiones convergentes (Decir sucesión convergente es lo mismo que decir sucesión con límite ). Vamos a intentar probar ese teorema. Empecemos con un caso particular. Sea a n n y b n n n 5 a) Demuestra, aplicando la definición que conoces, que lím a n y lím b n. b) Fija un número positivo: por ejemplo ε. Encuentra un n, tal que si n n, entonces a n < y un n tal que si n n, b n <. (No tienen por qué ser los menores n y n con esa propiedad). No sabemos cuál has elegido mayor, si n o n. Sea n el máimo de los dos. Así que: si n n, entonces se verifica a n < y b n <. c) Suma miembro a miembro esas dos desigualdades y utiliza propiedades del valor absoluto y demuestra que a b ( ) <, si n n. n n 8. Cambian mucho las cosas si escribimos en lugar de, y los números a, b y ε (ε > )? Demuestra que si lím a n a, y lím b n b, entonces lím (a n b n ) a b. 9. Vamos ahora con el producto. Enuncia el teorema que está pensando. Vamos a probarlo. Tú quieres encontrar un n tal que si n n, entonces a n b n ab < ε, donde ε > es un número que te han dado. Observa que a n b n ab a n b n a n b a n b ab. Puedes hacer pequeño a n a y b n b. Escribe a n b n ab en función de epresiones que puedas acotar.. Es posible que en el ejercicio anterior, hayas escrito a n b n ab a n b n a n b a n b ab a n (b n b) b (a n a) a n b n b b a n a. Como {a n } es una sucesión acotada, mira el apartado del ejercicio anterior, podrás hacer a n menor que un cierto número positivo y como {b n } converge a b y {a n } a a, podrás hacer b n b y a n a tan pequeño como quieras a partir de un cier- 8
13 to n. Con esto ya habrías probado que {a n b n } converge a a b, pero antes de probarlo en general, sigue todos estos pasos para, por ejemplo a n n y n n b n. n En concreto: dado, por ejemplo, ε, encuentra a) Un número M > tal que a n M para todo n. b) Un número natural n tal que b n < c) Un número natural n tal que a n < ε para todo n n. M ε b para todo n n. Sea n má {n, n }. Qué ocurre si n n?. Vuelve a hacer el ejercicio pero no para un caso concreto, sino para cualesquiera sucesiones {a n } y {b n } tales que lím a n a y lím b n b.. Modifica los puntos que te hagan falta en tu ejercicio para aquellas sucesiones {b n } en las que lím b n. 9
14 SOLUCIONES A LOS EJERCICIOS CON ASTERISCO (*). a) Por la fórmula que nos indican, y litros 5 por la naturaleza del problema, si t > 5, C(t), es decir, a partir de los 5 minutos no sale nada de 5 minutos agua. b) Como el caudal de vaciamiento (número de litros desalojados por unidad de tiempo) no es constante, para calcular el número de litros desalojados en un cierto intervalo [t, t ], tenemos que calcular C ( t) dt. t t El número de litros desalojados en el intervalo [, 5] sería precisamente el área bajo la curva en [, 5] y, para calcular ese área, no merece la pena hacer la integral, pues tal área, en litros, es el área del triángulo de base 5 y altura 5, o sea, 5 litros. c) El volumen de agua que queda en el depósito en un cierto instante t será el total ( litros) menos lo desalojado hasta ese instante; es decir, volumen que queda en el instante t es V (t) (5 ') d 5t t. t ' ' Dibujemos, pues, V ( t) t 5t en [, 5]. Se trata de una parábola, con las ramas hacia arriba, pues el coeficiente de t es positivo y con vértice en t siendo V (t ). ' V (t) t 5; V (t) t 5, V (5) litros 5 Obsérvese que, a partir de t 5, no se desaloja nada de agua, por lo que el volumen que queda se mantendrá en 5 litros. 5 4
15 .7 Escribamos f () a trozos lo que nos facilitará el cálculo de sus primitivas. f ) ( si si <. Una primitiva de f () es C si F ( ) donde los números C y C no C si < son cualesquiera. En concreto: como F (), deberá ocurrir que Así pues 4 C C. 4 si F ( ) pero como F es derivable (su derivada es C si < f ()), debe ser continua, en particular continua en por lo que con lo que lím F( ) lím F( ), es decir 4 si < F ( ) 4 si 4 C C 4 Nos dicen que f o sea: f para todo mayor que cero. f, es decir,, afirmación válida f f Naturalmente todas las funciones que verifiquen f () f (), es decir, funciones cuya gráfica es simétrica respecto del origen (funciones impares) verifican la condición puesta. Pero nos piden que veamos que son las únicas, es decir que si f, entonces f () f (). Pensemos en la función G () f, que sabemos que es la función idénticamente nula, por lo que G (). Definimos H() f ( t) dt. Así G () H() H() con H (t) f (t) pues f es continua. 4
16 Así pues G () H () H ()() H () H () f () f (), por lo que.8 f () f (). a) h () f () f () g () g () y, por la condición ), h () f () f () f () f (). Así pues, h() es una función constante, y como h() f () g (), que por la condición ) vale, se sigue que h() f () g () para todo. b) k ( ) [ F( ) f ( ) ][ F ( ) f ( ) ] [ G( ) g( ) ][ G ( ) g ( ) ] Nos dicen que F y G satisfacen las condiciones ) y ), es decir: [ F( ) f ( ) ][ G( ) g( ) ] [ G( ) g( ) ][ f ( ) F( )] k ( ) y desarrollando llegamos a que k (). Como, por otra parte, () [ F () f ()] [ G() g() ] k ya que F y G satisfacen la condición ), se sigue que k() es la función idénticamente nula, es decir, F () f () y G () g (), de donde se deduce que F () f () y G () g (). c) Un par de funciones que satisfacen las condiciones ) y ) son f () sen, g () cos y, por lo que acabamos de ver, si hubiera otro par que verificara esas dos condiciones, sería el mismo. Nota. Observa que f () g () f () y g () f () g (), es decir, que f () f () g () g (). Por otra parte, f () y f () g () con lo que la función f () sen es la única función que satisface la ecuación y y con las condiciones y(), y () y, análogamente, la función g () cos es la única función que satisface la ecuación y y con las condiciones y(), y ().. Observa que el problema que se te plantea es probar que la función continua f () cos sen se anula eactamente dos veces. Para probarlo, veamos en primer lugar que se anula al menos dos veces, encontrando intervalos adecuados a los que aplicar el teorema de Bolzano. f (π) < Así pues, f se anulará al menos una vez en (π, ) y al menos una f () vez en (, π) con lo que ya hemos visto que f se anula al menos dos f (π) < veces. 4
17 .5.7 Si se anulara más de dos veces, su derivada se anularía más de una vez (piensa en el teorema de Rolle). Veamos, entonces, su derivada. f () sen sen cos (cos ) Pero f () (cos ) se anula solamente una vez, en, por lo que f no se puede anular más de dos veces y, como vimos que se anulaba al menos dos veces, hemos demostrado que se anula eactamente dos veces. a) De entrada f es derivable, y por tanto continua, en {}. Analicemos ahora la continuidad en lím f ( ) cos sen ( ) sen t y lím f ( ) lím lím t t Como f (), se sigue que f es continua en. Veamos ahora las derivadas laterales en. Si coinciden, f es derivable en f () lím f () h f ( h) f () ( h ) cos( h ) lím h h h lím h h cosh senh lím lím h h h senh f ( h) f () sen lím h h h lím h h h h h cosh senh lím lím. h h h Así pues f es continua en y derivable sólo en {}. b) Como f no es derivable en (,), f no verifica las condiciones del teorema de Rolle en el intervalo [, ]. Parece razonable empezar calculando f () f () 4( ) ( ) ( ) 4 ( ) ( ) ( ) [4 8 ] ( ) ( ) (7 5). a) Observa que la función continua f no verifica eactamente las condiciones del teorema de Bolzano en el intervalo [, ] pues f () f () pero sí podemos encontrar un intervalo contenido en él donde sí las verifique. Para verlo, lo mejor es esbozar la gráfica de f -polinomio de grado 6- que será algo así: 4
18 5 7 Observemos que, por ejemplo, f toma valores de diferente signo en los etremos del intervalo [, ]. Comprobémoslo: f () (8) () () > f () () 4 5 < Así pues, aplicando el teorema de Bolzano a la función continua f en [, ], concluimos que se anula al menos una vez en dicho intervalo, y, por tanto, en [, ]. b) Probemos, en primer lugar, que la ecuación f () tiene al menos una solución menor que. f () 5 y lím f ( ) pues f es un polinomio de grado impar y coeficiente principal positivo. Así pues, por la continuidad de f, la ecuación f () tiene al menos una solución menor que. Si hubiera más de una, f se anularía al menos una vez en < ( por qué?) pero las soluciones de f () son, y 5, ninguna menor que. 7 c) Una forma cómoda -puede resultarte un tanto larga- es comprobar que f no tiene soluciones en 5 5,,, 7 7 y [, ), con lo que habríamos visto que no hay ninguna solución mayor que. Calculemos f en estos puntos y estudiemos luego el crecimiento de f. 5 f () 5, f > y f () En,, f () > y como f () 5, f es siempre positiva en ese intervalo. 7 5 En,, f () <, es decir f es decreciente, pero como f () >, f es positiva en 7 ese intervalo. Finalmente f es siempre positiva en (, ) pues f () 5 y f () > en ese intervalo..6 Llamemos T a (, /) y P (, y) al punto buscado. Hay que hacer mínima d ( T, P) y. La abscisa de P se mueve en [, ), por lo que hay que encontrar el mínimo de f () en [, ), siendo 44
19 45 4 ) ( f Derivando, vemos que 4 4 ) ( f. Al resolver f (), llegamos a con lo que, ya que 4 8 nunca se hace cero. Como para >, f () >, el mínimo de f en [, ) se alcanza en, de donde el punto de la parábola 4y que menos dista del (, /) es el origen..47 Sea E la energía consumida por Km de vuelo en la costa y E la consumida por Km en el mar. El camino que debería recorrer es el indicado en la figura y la energía gastada es ) ( 9 ) ( E E f. Hay que hallar el mínimo de f en [, ] e 9 9 ) ( E E E f f () si y ± De las soluciones de f () la única que está en [, ] es, por lo que el mínimo de f se alcanzará en ó ó. Calculemos la imagen en cada uno de estos puntos y observamos que el mínimo se alcanza en. f () E E 6E P T t M Km Km
20 f () E 9.48 ( ) E E( ) ( )E f Sea la viga AB de la figura la de longitud más pequeña de las que no pueden pasar por la A esquina. Cualquier viga de longitud menor que AB, pasa por la α esquina. Obtengamos AB en función de α. T 8 7 AB AT TB f ( α) senα cosα B Calculemos el mínimo de f en (, π/) f ( 8cosα 7senα 8cos α 7sen α ) sen α cos α sen αcos α α f (α) si 7 sen α 8 cos α α arctg α. Si α > α, entonces f (α) > f creciente. Si α < α, entonces f (α) < f decreciente. Así pues el mínimo de las longitudes de vigas que no pueden pasar por la esquina se alcanza en α α y vale Calculémoslo: 8 7 senα cosα. 4 tgα cosα y 9 cos α 8 7 senα, por lo que AB m, con lo que cual- quier viga que mida menos de m debe pasar por esa esquina. 46
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
Funciones reales. Números complejos
 Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6 1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg) ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
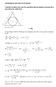 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
 Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD
 DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
3.3 Funciones crecientes y decrecientes y el criterio de la primera derivada
 SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
La circunferencia y el círculo
 La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
sen sen sen a 2 a cos cos 2 a
 BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones.
 Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
6. Optimización de funciones de una variable.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. 6. Optimización de funciones de una variable. En esta sección estudiaremos cómo calcular los extremos absolutos (si estos existen) de una función suficientemente
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. 6. Optimización de funciones de una variable. En esta sección estudiaremos cómo calcular los extremos absolutos (si estos existen) de una función suficientemente
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
APLICACIONES DE LAS DERIVADAS
 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
Trigonometría y problemas métricos
 Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
a) A la mitad del número le sumo 3 y el resultado es 8 ( ) 9 b) En la ecuación 3x = 54 Qué valor puede tomar x? ( ) Rombo
 Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
si este límite es finito, y en este caso decimos que f es integrable (impropia)
 Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
LA INTEGRAL DEFINIDA. APLICACIONES
 LA INTEGRAL DEFINIDA. APLICACIONES Página 6 REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
LA INTEGRAL DEFINIDA. APLICACIONES Página 6 REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
Sucesiones y series de números reales
 Capítulo 2 Sucesiones y series de números reales 2.. Sucesiones de números reales 2... Introducción Definición 2... Llamamos sucesión de números reales a una función f : N R, n f(n) = x n. Habitualmente
Capítulo 2 Sucesiones y series de números reales 2.. Sucesiones de números reales 2... Introducción Definición 2... Llamamos sucesión de números reales a una función f : N R, n f(n) = x n. Habitualmente
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS
 SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
SELECTIVIDAD APLICACIÓN DE LAS DERIVADAS Septiembre 008: Calcula los valores del número real a sabiendo que punto) 0 a e a = 8. ( Septiembre 008: Hallar, de entre los puntos de la parábola de ecuación
TEMA 4: DERIVADAS. En símbolos, la pendiente de la curva en P = lim Q P (pendiente de P Q).
 TEMA 4: DERIVADAS 1. La derivada de una función. Reglas de derivación 1.1. La pendiente de una curva. La pendiente de una curva en un punto P es una medida de la inclinación de la curva en ese punto. Si
TEMA 4: DERIVADAS 1. La derivada de una función. Reglas de derivación 1.1. La pendiente de una curva. La pendiente de una curva en un punto P es una medida de la inclinación de la curva en ese punto. Si
6 EXPRESIONES FRACCIONARIAS Y RADICALES
 EJERCICIOS PROPUESTOS. Halla el valor numérico de la fracción 7 0 para los valores, 0 y. 8 Para : Para 0: 0 0 Para : 7 0 0. Valor indeterminado. 8 0 7 0 0 0 5 0 8 8. 7 0. No eiste valor numérico. 8 0.
EJERCICIOS PROPUESTOS. Halla el valor numérico de la fracción 7 0 para los valores, 0 y. 8 Para : Para 0: 0 0 Para : 7 0 0. Valor indeterminado. 8 0 7 0 0 0 5 0 8 8. 7 0. No eiste valor numérico. 8 0.
Espacio de Funciones Medibles
 Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
PROBLEMAS DE CONTINUIDAD Y DERIVABILIDAD
 PROBLEMAS DE CONTINUIDAD Y DERIVABILIDAD Considera la función f(x)= x 3 + px donde p es un número real. Escribir (en función de p) la ecuación de la recta tangente a la grafica f(x) en el punto de abscisa
PROBLEMAS DE CONTINUIDAD Y DERIVABILIDAD Considera la función f(x)= x 3 + px donde p es un número real. Escribir (en función de p) la ecuación de la recta tangente a la grafica f(x) en el punto de abscisa
8. y = Solución: x 4. 9. y = 3 5x. Solución: y' = 5 3 5x L 3. 10. y = Solución: 4 4 (5x) 3. 11. y = Solución: (x 2 + 1) 2. 12.
 7 Cálculo de derivadas. Reglas de derivación. Tabla de derivadas Aplica la teoría Deriva en función de :. y = 8. y = 5 3 5 4. y = ( ) 5 0( ) 4 9. y = 3 5 5 3 5 L 3 3. y = 7 + 3 4. y = e e 5. y = 7 7 +
7 Cálculo de derivadas. Reglas de derivación. Tabla de derivadas Aplica la teoría Deriva en función de :. y = 8. y = 5 3 5 4. y = ( ) 5 0( ) 4 9. y = 3 5 5 3 5 L 3 3. y = 7 + 3 4. y = e e 5. y = 7 7 +
5 Operaciones. con polinomios. 1. Polinomios. Suma y resta
 5 Operaciones con polinomios 1. Polinomios. Suma y resta Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A() = 6 2 b) V() = 3 P I E N S A Y C A L C U L A 1 Dado el prisma
5 Operaciones con polinomios 1. Polinomios. Suma y resta Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A() = 6 2 b) V() = 3 P I E N S A Y C A L C U L A 1 Dado el prisma
APLICACIONES DE LAS DERIVADAS
 0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
Cálculo Diferencial e Integral - Recta tangente y velocidad. Farith J. Briceño N.
 Cálculo Diferencial e Integral - Recta tangente y velocidad. Farit J. Briceño N. Objetivos a cubrir Código : MAT-CDI.7 Problema: Recta tangente a una curva en un punto 0. Problema: Velocidad promedio y
Cálculo Diferencial e Integral - Recta tangente y velocidad. Farit J. Briceño N. Objetivos a cubrir Código : MAT-CDI.7 Problema: Recta tangente a una curva en un punto 0. Problema: Velocidad promedio y
Seminario de problemas-bachillerato. Curso 2012-13. Hoja 4
 Seminario de problemas-bachillerato. Curso 2012-13. Hoja 4 25. El número 2 x es la mayor potencia entera de 2 entre las que tienen nueve dígitos en base 10, y sus nueve dígitos son distintos. Usando que
Seminario de problemas-bachillerato. Curso 2012-13. Hoja 4 25. El número 2 x es la mayor potencia entera de 2 entre las que tienen nueve dígitos en base 10, y sus nueve dígitos son distintos. Usando que
Unidad 2: Resolución de triángulos
 Ejercicio 1 Unidad : Resolución de triángulos En las siguientes figuras, calcula las medidas de los segmentos desconocidos indicados por letras (ambos triángulos son rectángulos en A): cm 16'5 7'5 cm a
Ejercicio 1 Unidad : Resolución de triángulos En las siguientes figuras, calcula las medidas de los segmentos desconocidos indicados por letras (ambos triángulos son rectángulos en A): cm 16'5 7'5 cm a
En las figuras anteriores vemos algunos casos (no todos) que pueden presentarse al pasar por un punto x 0. (en este caso, para x 0 =2)
 UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 3. Trigonometría
 TRIGONOMETRÍA La trigonometría se inicia estudiando la relación entre los ángulos y los lados de un triángulo, surgiendo las razones trigonométricas de un ángulo y a partir de ellas las funciones trigonométricas.
TRIGONOMETRÍA La trigonometría se inicia estudiando la relación entre los ángulos y los lados de un triángulo, surgiendo las razones trigonométricas de un ángulo y a partir de ellas las funciones trigonométricas.
f (x) (1+[f (x)] 2 ) 3 2 κ(x) =
![f (x) (1+[f (x)] 2 ) 3 2 κ(x) = f (x) (1+[f (x)] 2 ) 3 2 κ(x) =](/thumbs/40/20918876.jpg) MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
RELACION DE PROBLEMAS DE GEOMETRIA. Problemas propuestos para la prueba de acceso del curso 1996/97.
 RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
RELACION DE PROBLEMAS DE GEOMETRIA Problemas propuestos para la prueba de acceso del curso 996/97. º. - Explica cómo se puede hallar el área de un triángulo, a partir de sus coordenadas, en el espacio
Figuras Planas. 100 Ejercicios para practicar con soluciones. 1 Comprueba si los siguientes ángulos son complementarios: a) 72 + 35.
 Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Máximo o mínimo de una función. Solución: El mínimo de una función se da en los puntos que anulan su derivada y tiene derivada segunda positiva.
 Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
Integral definida. 1. Integral definida. Piensa y calcula. Aplica la teoría. 3. Siendo x el valor absoluto o módulo de x, calcula la. 2.
 Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. e) f) es divisible por 6. a) b) c) d) e) f)
 1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
1. Aplique el método de inducción matemática para probar las siguientes proposiciones. a) b) c) d) e) f) es divisible por 6. g) 2. Halle la solución de las siguientes desigualdades de primer orden. g)
TEMAS 10 LAS FUNCIONES ELEMENTALES 1º BACH MATE I
 TEMA 0 FUNCIONES ELEMENTALES MATEMÁTICAS I º Bach. TEMAS 0 LAS FUNCIONES ELEMENTALES º BACH MATE I Son funciones? Ejercicio : Indica cuáles de las siguientes representaciones corresponden a la gráfica
TEMA 0 FUNCIONES ELEMENTALES MATEMÁTICAS I º Bach. TEMAS 0 LAS FUNCIONES ELEMENTALES º BACH MATE I Son funciones? Ejercicio : Indica cuáles de las siguientes representaciones corresponden a la gráfica
Propiedades de las funciones derivables. Representación gráfica de funciones. Determinar los puntos de inflexión. (Junio 1997)
 Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
ejerciciosyexamenes.com
 ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
ejerciciosyeamenes.com Eamen de derivadas 1. Razona la verdad o falsedad de las siguientes afirmaciones: a) f() toma todos los valores entre f(a) y f(b), es continua? b) Si f'() > 0 y g'() > 0 en [a,b]
EXAMEN GEOMETRÍA. 5. Halla el perímetro y el área de un triángulo isósceles cuyos lados miden 5, 5 y 8 cms., respectivamente.
 1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/78/78369935.jpg) cos(3) - e + a 1. [ANDA] [EXT-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte. 2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso
cos(3) - e + a 1. [ANDA] [EXT-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte. 2. [ANDA] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso
MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA. 3. Determinar analíticamente cuando dos rectas son paralelas o perpendiculares.
 ESTUDIO ANALÍTICO DE LA LÍNEA RECTA Y APLICACIONES SEMESTRE II VERSIÓN 03 FECHA: Septiembre 29 de 2011 MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA LOGROS: 1. Hallar la dirección, la
ESTUDIO ANALÍTICO DE LA LÍNEA RECTA Y APLICACIONES SEMESTRE II VERSIÓN 03 FECHA: Septiembre 29 de 2011 MUNICIPIO DE MEDELLÍN ÁREA DE MATEMÁTICAS: GEOMETRÍA ANALÍTICA LOGROS: 1. Hallar la dirección, la
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Aplicaciones de la derivada.
 Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
FUNCIONES TRIGONOMÉTRICAS, EXPONENCIALES Y LOGARÍTMICAS
 UNIDAD 5 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES Y LOGARÍTMICAS Página. La distancia al suelo de una barquilla de la noria varía conforme ésta gira. Representamos gráficamente la función que da la altura
UNIDAD 5 FUNCIONES TRIGONOMÉTRICAS, EPONENCIALES Y LOGARÍTMICAS Página. La distancia al suelo de una barquilla de la noria varía conforme ésta gira. Representamos gráficamente la función que da la altura
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL
 EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
1. CIRCUITO. a) Irene se dio un paseo por este circuito y salió convertida en el 17. Qué itinerario siguió y qué número era al principio?
 1. CIRCUITO Este circuito solo reconoce números naturales (0, 1, 2,,...). Cuando un número entra en este circuito se coloca en la casilla de Entrada y siguiendo las flechas va avanzando hasta llegar a
1. CIRCUITO Este circuito solo reconoce números naturales (0, 1, 2,,...). Cuando un número entra en este circuito se coloca en la casilla de Entrada y siguiendo las flechas va avanzando hasta llegar a
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
www.matesxronda.net José A. Jiménez Nieto
 NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
NÚMEROS REALES 1. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal es exacta
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
Representación gráfica de funciones. De la fórmula a la tabla. Resolución de problemas
 REPRESENTACIÓN DE PUNTOS EN EL PLANO RELACIÓN ENTRE DOS MAGNITUDES Ejes de coordenadas y coordenadas de puntos FUNCIÓN Tipos: - Lineal. - Afín. - Constante. - De proporcionalidad inversa. - Cuadrática.
REPRESENTACIÓN DE PUNTOS EN EL PLANO RELACIÓN ENTRE DOS MAGNITUDES Ejes de coordenadas y coordenadas de puntos FUNCIÓN Tipos: - Lineal. - Afín. - Constante. - De proporcionalidad inversa. - Cuadrática.
a) Calcular las asíntotas, el máximo y el mínimo absolutos de f (x). 4. (SEP 04) Sabiendo que una función f (x) tiene como derivada
 Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Matemáticas II - Curso - EJERCICIOS DE CÁLCULO DIFERENCIAL E INTEGRAL PROPUESTOS EN LAS PRUEBAS DE ACCESO COMUNIDAD DE MADRID (JUN ) Calcular la base y la altura del triángulo isósceles de perímetro 8
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
1. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado:
 CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
1. NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de Matemáticas I)
 . NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de ). Calcula las potencias: a) -, (-), (-) -, - - (/) -, (-/), -(-/) - - (/) - 0 ( ) d) e) 0 0 + + 8 [sol] a) ; 7 ; ( 7; ; 7 d) e) 0 7 7 7. Simplifica
. NÚMEROS REALES. LOGARITMOS Y EXPONENCIALES. (Pendientes de ). Calcula las potencias: a) -, (-), (-) -, - - (/) -, (-/), -(-/) - - (/) - 0 ( ) d) e) 0 0 + + 8 [sol] a) ; 7 ; ( 7; ; 7 d) e) 0 7 7 7. Simplifica
PROBLEMAS METRICOS. r 3
 PROBLEMAS METRICOS 1. Hallar el área del triángulo de vértices A(1,1), B(2,3) y C(5,2). 2. Halla las ecuaciones de las bisectrices determinadas por las rectas y=3x e y=1/3 x. Comprueba que ambas bisectrices
PROBLEMAS METRICOS 1. Hallar el área del triángulo de vértices A(1,1), B(2,3) y C(5,2). 2. Halla las ecuaciones de las bisectrices determinadas por las rectas y=3x e y=1/3 x. Comprueba que ambas bisectrices
x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =
![x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) = x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =](/thumbs/76/74425342.jpg) Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
Ecuaciones de segundo grado
 Ecuaciones de segundo grado Contenidos 1. Expresiones algebraicas Identidad y ecuación Solución de una ecuación. Ecuaciones de primer grado Definición Método de resolución Resolución de problemas 3. Ecuaciones
Ecuaciones de segundo grado Contenidos 1. Expresiones algebraicas Identidad y ecuación Solución de una ecuación. Ecuaciones de primer grado Definición Método de resolución Resolución de problemas 3. Ecuaciones
LA RECTA. Recuerda: Ejercicios de autoaprendizaje 1. Sea la gráfica siguiente:
 LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
ACTIVIDADES INICIALES. 14.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 25, 25 5,...
 Solucionario 4 Integral definida ACTIVIDADES INICIALES 4.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 5, 5 5,... 4.II. Epresa la función f
Solucionario 4 Integral definida ACTIVIDADES INICIALES 4.I. Con ayuda de la calculadora, obtén la suma de los cien primeros términos de esta progresión: 5, 5, 5 5, 5, 5 5,... 4.II. Epresa la función f
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO Página 133 REFLEXIONA Y RESUELVE Relaciones trigonométricas en el triángulo Halla el área de este paralelogramo en función del ángulo a: cm a cm Área = sen a = 40 sen a cm Halla
VECTORES EN EL ESPACIO Página 133 REFLEXIONA Y RESUELVE Relaciones trigonométricas en el triángulo Halla el área de este paralelogramo en función del ángulo a: cm a cm Área = sen a = 40 sen a cm Halla
Perímetro de un polígono regular: Si la longitud de un lado es y hay cantidad de lados en un polígono regular entonces el perímetro es.
 Materia: Matemática de Séptimo Tema: Área de Polígonos Qué pasa si te piden que encuentres la distancia del Pentágono en Arlington, VA? El Pentágono, que también alberga el Departamento de Defensa de EE.UU.,
Materia: Matemática de Séptimo Tema: Área de Polígonos Qué pasa si te piden que encuentres la distancia del Pentágono en Arlington, VA? El Pentágono, que también alberga el Departamento de Defensa de EE.UU.,
EJERCICIOS BLOQUE III: GEOMETRÍA
 EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
EJERCICIOS BLOQUE III: GEOMETRÍA (00-M-A-4) (5 puntos) Determina el centro y el radio de la circunferencia que pasa por el origen de coordenadas, tiene su centro en el semieje positivo de abscisas y es
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN
 FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
EJERCICIOS Nº 10: GEOMETRIA ANALITICA. se extiende hacia cada extremo en una longitud igual a su longitud original. Halle las coordenadas de
 EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
EJERCICIOS Nº 1: GEOMETRIA ANALITICA 1) Determine x si el punto A (x,3) equidista de B ( 3, ) y de C (7,4) Respuesta ) Determine los puntos de trisección del segmento de recta AB donde A( 6, 9), B(6,9)
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
ANÁLISIS DE FUNCIONES
 ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
ANÁLISIS DE FUNCIONES.- Calcula f() de manera que f () = Ln( + ) y que f(0) = 0. (nota: Ln significa logaritmo neperiano). Universidad de Andalucía Se trata de resolver la integral que hemos de hacerlo
TEMA 2: DERIVADA DE UNA FUNCIÓN
 TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
Teorema de máximos y mínimos para funciones continuas:
 Matemática II 7 Modulo 4 Estudio de funciones. Valores etremos de funciones En muchos casos las funciones que se presentan no pueden graficarse hallando unos pocos puntos, a que no es fácil deducir el
Matemática II 7 Modulo 4 Estudio de funciones. Valores etremos de funciones En muchos casos las funciones que se presentan no pueden graficarse hallando unos pocos puntos, a que no es fácil deducir el
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE
 DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
FUNCIONES LINEALES Y AFINES
 www.matesronda.net José A. Jiménez Nieto FUNCIONES LINEALES Y AFINES. LA FUNCIÓN LINEAL = m El tren AVE lleva una velocidad media de 40 km/h. La siguiente tabla nos da el espacio que recorre en función
www.matesronda.net José A. Jiménez Nieto FUNCIONES LINEALES Y AFINES. LA FUNCIÓN LINEAL = m El tren AVE lleva una velocidad media de 40 km/h. La siguiente tabla nos da el espacio que recorre en función
FUNCIONES Y GRÁFICAS
 FUNCIONES Y GRÁFICAS 1. DEPENDENCIA ENTRE MAGNITUDES Relaciones dadas por tablas En una clase de laboratorio un alumno ha medido la temperatura de un líquido según se calentaba. Los resultados del eperimento
FUNCIONES Y GRÁFICAS 1. DEPENDENCIA ENTRE MAGNITUDES Relaciones dadas por tablas En una clase de laboratorio un alumno ha medido la temperatura de un líquido según se calentaba. Los resultados del eperimento
3. Un triángulo rectángulo es semejante a otro cuyos catetos miden 3 cm y 4 cm. Su hipotenusa vale 2,5 cm. Halla las medidas de sus catetos.
 RELACIÓN DE ACTIVIDADES MATEMÁTICAS º ESO TEMA 7: RESOLUCIÓN DE TRIÁNGULOS Y TRIGONOMETRÍA Contesta razonadamente a las siguientes preguntas:. Halla la incógnita en los siguientes triángulos rectángulos:
RELACIÓN DE ACTIVIDADES MATEMÁTICAS º ESO TEMA 7: RESOLUCIÓN DE TRIÁNGULOS Y TRIGONOMETRÍA Contesta razonadamente a las siguientes preguntas:. Halla la incógnita en los siguientes triángulos rectángulos:
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Las Figuras Planas. Vértice. Ángulo. Diagonal. Lado. Los polígonos. El Polígono. CEPA Carmen Conde Abellán Matemáticas II
 Las Figuras Planas Melilla Los polígonos Te has fijado alguna vez en el metro que usan los carpinteros? Está formado por segmentos de madera que se pliegan con facilidad. Este instrumento tiene forma de
Las Figuras Planas Melilla Los polígonos Te has fijado alguna vez en el metro que usan los carpinteros? Está formado por segmentos de madera que se pliegan con facilidad. Este instrumento tiene forma de
