UNIDAD 2 Geometría 2.2 Triángulos 10
|
|
|
- Francisco Quintana Castilla
- hace 7 años
- Vistas:
Transcripción
1 UNI Geometrí. Triánguos 10. Triánguos OJETIVOS ur e áre e perímetro de triánguos. Otener os dos ánguos de triánguos utiizndo s reiones entre otros ánguos en figurs geométris. ur os dos de un triánguo usndo e teorem de Pitágors s propieddes de os triánguos semejntes. efiniión En Geometrí, un triánguo es un poígono formdo por tres rets que se ortn dos dos en tres puntos, que no están inedos. Los puntos de interseión de s rets se es m vérties os segmentos de ret que formn e triánguo se mn dos. d pr de dos en un triánguo formn un ánguo interno, por o tnto un triánguo tiene 3 dos 3 ánguos internos, omo se muestr en figur siguiente sifiión de triánguos Los triánguos se pueden sifir en se medid de sus dos o ien en se medid de sus ánguos. Por sus dos: Por s ongitudes de sus dos, os triánguos se sifin omo: Triánguo equiátero: Es e triánguo que tiene 3 dos igues tres ánguos igues, d ánguo tiene un medid de 60º. Triánguo isósees: Es e que tiene dos dos igues. Los ánguos opuestos esos dos son igues. Triánguo eseno: Es e que tiene sus tres dos on diferente ongitud. En e triánguo eseno os tres ánguos tienen diferente medid. 60º 60º 60º Triánguo equiátero Triánguo isósees Triánguo eseno
2 UNI Geometrí. Triánguos 11 Por sus ánguos: Por medid de sus ánguos, os triánguos se sifin omo: Triánguo utánguo: Es e triánguo en e que todos sus ánguos internos son gudos. Triánguo retánguo: Es e que tiene un ánguo reto, es deir su medid es 90º. Triánguo otusánguo: Es e que tiene un ánguo otuso, es deir un ánguo que mide más de 90º menos de 180º. 90º Triánguo utánguo Triánguo retánguo Triánguo otusánguo Propieddes generes de triánguo L figur muestr un triánguo en donde os ánguos internos son,. Tmién se muestr e ánguo eterno, e u se form proongr uno de os dos de triánguo. utro de s propieddes generes son: 1. L sum de os ánguos internos de un triánguo es igu 180º, es deir que. L medid de un ánguo eterno es igu sum de s medids de os ánguos internos opuestos, es deir 3. En un triánguo retánguo os ánguos gudos son ompementrios, es deir que sus medids sumn 90º. 4. L sum de s medids de dos dos de un triánguo, siempre es mor que medid de otro do, es deir 180º,, tur de un triánguo: Es e segmento que v desde uno de sus vérties ret que ontiene do opuesto que es perpendiur di ret. Puesto que un triánguo tiene 3 vérties, un tur orrespondiente d uno, es deir que un triánguo tiene 3 turs. En os triánguos otusos pr trzr dos de sus turs es neesrio proongr os dos opuestos, omo se muestr en figur siguiente
3 UNI Geometrí. Triánguos Ejempo 1: undo ánguos en triánguos En figur se muestr un áro que se enuentr en prte superior de un oin que form un ánguo de 0º on orizont. Un oservdor situdo en un punto sore oin mide e ánguo formdo entre oin punt de áro en 4º. ue medid de ánguo. 4º Souión 0º Identifindo on etrs músus os puntos importntes de figur se tiene 4º E 0º L medid de ánguo es 90º 0º 70º pues en un triánguo retánguo, os ánguos gudos son ompementrios. omo os ánguos E son supementrios se otiene E 180º 180º 70º 110º Finmente, se puede otener e ánguo que sum de os ánguos internos de un triánguo es 180º, entones 180º 4º E 180º 4º 110º 46º
4 UNI Geometrí. Triánguos 13 Triánguos semejntes os triánguos son semejntes si sus ánguos orrespondientes son igues sus dos orrespondientes son proporiones, en figur se muestrn os triánguos semejntes. En form simói pr indir que dos triánguos son semejntes se esrie E ánguo es orrespondiente on e ánguo por o tnto son igues, es deir. E ánguo es orrespondiente on e ánguo, entones. Finmente e ánguo es orrespondiente on e ánguo, entones. Los dos orrespondientes son os que están opuestos os ánguos orrespondientes, sí tenemos que e do es orrespondiente on e do, e do es orrespondiente on e do e do es orrespondiente on e do. Puesto que os dos orrespondientes son proporiones, undo dos triánguos son semejntes se pueden esteer s reiones siguientes Pr esteer que dos triánguos son semejntes poder sí utiizr s euiones que se derivn de proporionidd de sus dos, se puede utiizr e postudo de os triánguos semejntes P o s t u d o s o r e s e m e j n z d e t r i á n g u o s Si dos ánguos de un triánguo son igues dos ánguos de otro triánguo, os triánguos son semejntes. diionmente en e udro siguiente se presentn gunos teorems sore semejnz, que pueden resutr de mu utiidd en souión de proems. Estos teorems se pueden demostrr utiizndo e postudo de semejnz de triánguos s reiones entre ánguos estudids en seión nterior T e o r e m s s o r e s e m e j n z d e t r i á n g u o s 1. Si dos triánguos son semejntes, rzón de sus perímetros es igu rzón de uquier pr de dos orrespondientes.. Si un ret es pre uno de os dos de un triánguo, ret divide os otros dos dos en segmentos que son proporiones. 3. Si dos triánguos son semejntes, sus turs orrespondientes están en mism rzón que uquier pr de dos orrespondientes. 4. En un triánguo retánguo, tur perpendiur ipotenus form dos triánguos que son semejntes entre sí semejntes triánguo ddo.
5 UNI Geometrí. Triánguos 14 Ejempo : Semejnz de triánguos do e triánguo, donde E, 40, E 8 E 6. Enuentre ongitud de segmento E. 6 Souión 8 E 40 Un ret pre uno de os dos de un triánguo form dos triánguos semejntes, que estos tienen un ánguo omún demás os ánguos orrespondientes entre pres son igues, entones os triánguos E son semejntes. Utiizndo proporionidd entre sus dos se otiene E E Sustituendo informión dd despejndo (6)(40) 8(6 ) (6)(40) 8 6 (6)(40) Respuest: ongitud de segmento E es proimdmente uniddes. Ejempo 3: tur de un poste de uz Pr determinr tur de un poste de uz, un person de 6 pies de tur se oo un distni de 8 pies de se de poste. Se mide que ongitud de somr que person proet sore e sueo tiene 1 pies de rgo. etermine tur de poste. Souión L figur iustr e proem. Puede oservrse que se formn dos triánguos semejntes que tienen un ánguo omún demás mos tienen un ánguo de 90º pues son triánguos retánguos
6 UNI Geometrí. Triánguos 15 Si es tur de poste, se estee proporionidd entre tur de triánguo grnde on tur de triánguo pequeño se de triánguo grnde (8+1), on se de triánguo pequeño, oteniéndose euión despejr se otiene tur de poste Respuest: tur de poste es de 10 pies (0)(6) 1 Teorem de Pitágors Junto on proporionidd de os dos orrespondientes en os triánguos semejntes, e Teorem de Pitágors es un de s epresiones más utiizds en souión de proems geométrios, éste teorem estee que T e o r e m d e P i t á g o r s En todo triánguo retánguo, e udrdo de ipotenus es igu sum de os udrdos de os tetos. Si es ipotenus, son os tetos de triánguo, entones emostrión H mus mners de demostrr e teorem de Pitágors, un de es onsiste en utiizr semejnz de triánguos, que es que se present quí. trzr tur orrespondiente ipotenus, se formn dos nuevos triánguos, que son semejntes entre sí que son semejntes triánguo ddo (vése teorems de semejnz). Se tur de triánguo ddo, os tetos de os triánguos formdos, omo se muestr en figur
7 UNI Geometrí. Triánguos 16 E triánguo es semejnte triánguo. Esteiendo igudd entre os oientes de s ipotenuss on e oiente entre os tetos mores se otiene e donde se otiene que En form simir, e triánguo es semejnte triánguo. Esteiendo igudd entre os oientes de s ipotenuss on e oiente entre os tetos mores se otiene e donde se otiene que Sumndo s epresiones otenids pr se tiene ( ) omo, se puede sustituir, por pr ompetr demostrión de teorem Quedndo sí demostrdo e teorem. ( ) ( ) Ejempo 4: Utiizndo e teorem de Pitágors L figur muestr un triánguo retánguo on ipotenus de ongitud 1 m uno de sus tetos on ongitud 6 m. Enuentre Souión L ongitud de teto puede epresrse omo 4 3. pindo e teorem de Pitágors se tiene Resoviendo euión pr enontrr
8 UNI Geometrí. Triánguos esrtndo souión negtiv pues e vor de dee ser positivo Pr enontrr se pi nuevmente e teorem de Pitágors, or en e triánguo retánguo pequeño 6 Sustituendo 3 despejndo se tiene 36 ( 3) 36 4(3) 48 esrtndo nuevmente souión negtiv se tiene que Respuest: Triánguos espeies os de os triánguos más utiizdos en geometrí son e triánguo retánguo que tiene ánguos gudos on medids de 30º 60º e triánguo retánguo isósees que tiene dos ánguos gudos igues de 45º. Triánguo 30º- 60º- 90º undo se trz un de s turs en un triánguo equiátero, se formn dos triánguos igues que tienen ánguos de 30º, 60º 90º, omo se muestr en figur. 30º 60º / Si ipotenus tiene ongitud, se tiene ongitud / que es mitd de uno de os dos de triánguo equiátero. Pr epresr tur en términos de ongitud de ipotenus se utiiz e teorem de Pitágors. espejndo en términos de se tiene.
9 UNI Geometrí. Triánguos 18 Triánguo 45º- 45º- 90º Este triánguo es e únio que tiene rterísti de ser simutánemente retánguo e isósees. L figur muestr un triánguo 45º - 45º - 90º u ipotenus tiene un ongitud os tetos igues tienen ongitud. 45º 45º Pr epresr ongitud de os tetos en términos de se utiiz e teorem de Pitágors Áre perímetro de triánguo En un triánguo de dos,, tur, donde orresponde do de ongitud, omo se indi en figur. E áre e perímetro se un on s fórmus siguientes re 1 Perímetro Ejempo 5: undo áres de triánguos En figur RS PQ. Enuentre e áre somred. R 5 S 6 P 10 Q
10 UNI Geometrí. Triánguos 19 Souión Si s rets son pres, os triánguos son semejntes que tienen dos de sus ánguos igues pues son ánguos ternos internos entre pres. Si es tur de triánguo de se 10, tur de triánguo de se 5 es 6 Por semejnz de triánguos se tiene (6 ) Entones e triánguo de se 10 tiene tur 4 e triánguo pequeño tiene tur. áre tot es sum de s áres de os dos triánguos 1 1 (10)(4) 1 (5)() Respuest: E áre somred es 5 uniddes udrds. Ejeriios de seión. 1. Enuentre medid de os ánguos º 40º 39º. Enuentre medid de os ánguos Enuentre medid de os ánguos. 84º 5. Si m, enuentre medid de ánguo. 65º 6º 3. Si m, enuentre medid de os ánguos. 4º 35º 1 m 40º 6. Si m, enuentre medid de ánguo. 75º m m
11 UNI Geometrí. Triánguos 0 7. Si es equiátero, enuentre medid de os ánguos. 1. Enuentre. E º 8. Si es equiátero, enuentre medid de os ánguos. 13. Enuentre E Eprese en términos de. 9. Enuentre E segmento es preo segmento E. u Enuentre 4 1 E Enuentre. 11. Enuentre Eprese en términos de r. 3 r 4
12 UNI Geometrí. Triánguos Eprese en términos de. 7. Se insrie un triánguo retánguo isósees dentro de un triánguo retánguo de se 5 m tur 10 m. Enuentre e áre somred Eprese en términos de En figur de proem nterior. Eprese z en términos de. 1. Un person min 7 km i e norte, uego 6 km i e este finmente 4 km i e norte. qué distni está de punto de prtid?. Los dos igues de un triánguo isósees miden 6 m. Si se de triánguo mide 10 m. Enontrr tur trzd se. 3. Enontrr tur de un triánguo equiátero uo do mide 6 m. 4. L ipotenus de un triánguo retánguo isósees mide 8 m. Enontrr medid de os tetos. 5. E do de un triánguo equiátero es igu tur de otro triánguo equiátero. En qué rzón están e perímetro de triánguo mor e perímetro de triánguo menor? 6. Si, eprese ongitud de do en términos de. z 30º 8. Un triánguo isósees tiene dos igues de 8 m se de 6 m. Se trz un pre se un distni de 5 m de e. 5 () ue e áre de os triánguos formdos. () ue rzón de perímetro de triánguo menor on de triánguo mor. () ue rzón en que se enuentr e áre de triánguo mor on de menor. 9. Los dos de un triánguo miden 10, 17 1 m. Enontrr tur trzd do de 1 m. (Sugereni: use dos vries) 30. Enontrr e perímetro de un triánguo equiátero de áre Enuentre ongitud 60º º 3. Enuentre e áre somred 60º 30º 30º 4
13 UNI Geometrí. Triánguos 33. Si medid de ánguo es 30º, ue e áre somred 35. Si e do de triánguo equiátero más grnde mide 4 m todos os triánguos insritos son equiáteros, ue e áre somred do un triánguo equiátero de do 6 m, se trz un segmento preo se un tur de 4 m. Enuentre en que rzón se enuentrn e áre de triánguo pequeño que se formdo on respeto áre de triánguo ddo. 36. L figur muestr dos postes de turs metros seprdos entre sí por un distni de 0 metros. E e que sostiene os postes está ndo sueo en e punto P. Si, enuentre ongitud tot de e P
DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS
 7 REPSO Y POYO OJETIVO DISTINGUIR LS RZONES TRIGONOMÉTRICS Nomre: Curso: Feh: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
7 REPSO Y POYO OJETIVO DISTINGUIR LS RZONES TRIGONOMÉTRICS Nomre: Curso: Feh: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
NOMBRE: CURSO: FECHA: coseno. a (cateto contiguo dividido entre hipotenusa) cos α = c a = 4 5
 00 _ 00-06.qd 9/7/0 9:7 Págin RAZONES OBJETIVO TRIGONOMÉTRICAS Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen = (teto opuesto dividido entre ipotenus)
00 _ 00-06.qd 9/7/0 9:7 Págin RAZONES OBJETIVO TRIGONOMÉTRICAS Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen = (teto opuesto dividido entre ipotenus)
UNIDAD VI LA ELIPSE 6.1. ECUACIÓN EN FORMA COMÚN O CANÓNICA DE LA ELIPSE
 UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
UNIDAD VI LA ELIPSE OBJETIVO PARTIULAR Al onluir l unidd, el lumno onoerá plirá ls propieddes relionds on el lugr geométrio llmdo elipse, determinndo los distintos prámetros, su euión respetiv vievers.
En donde x representa la incógnita, y a, b y c son constantes.
 FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
FUNCIÓN CUADRÁTICA. Cundo los elementos de un onjunto los elementos de un onjunto se soin medinte un regl de orrespondeni definid por un euión de segundo grdo en, l llmmos funión de segundo grdo o udráti.
ECUACIONES DE PRIMER Y SEGUNDO GRADO
 UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
UNIDAD ECUACIONES DE PRIMER Y SEGUNDO GRADO EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd resolverás ejeriios y prolems que involuren l soluión de euiones de primer grdo y de segundo grdo Ojetivo.
DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS
 7 REPASO Y APOYO OBJETIVO DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS Nomre: Curso: Fe: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
7 REPASO Y APOYO OBJETIVO DISTINGUIR LAS RAZONES TRIGONOMÉTRICAS Nomre: Curso: Fe: Ddo un triánguo retánguo, definimos s rzones trigonométris de uno de sus ánguos gudos : seno sen oseno os tngente tg (teto
Tema 5. Semejanza. Tema 5. Semejanza
 Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
1. Definición de Semejanza. Escalas
 Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Tem 5. Semejnz Tem 5. Semejnz 1. Definiión de Semejnz. Esls. Teorem de Tles 3. Semejnz de Triángulos. riterios 4. riterios de Semejnz en triángulos retángulos 5. Teorems en triángulos retángulos 6. Relión
Semejanza. 2. Relación entre perímetros, áreas y volúmenes de figuras semejantes 51
 Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
Semejnz 1. Teorem de Tles 50 2. Relión entre perímetros, áres y volúmenes de figurs semejntes 51 3. Teorem de Pitágors, teorem del teto y teorem de l ltur 52 4. Rzones trigonométris de un ángulo gudo y
7 Semejanza. y trigonometría. 1. Teorema de Thales
 7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
7 Semejnz y trigonometrí 1. Teorem de Tles Si un person que mide 1,70 m proyet un sombr de,40 m y el mismo dí, l mism or y en el mismo lugr l sombr de un árbol mide 15 m, uánto mide de lto el árbol? Se
Los triángulos se clasifican según la magnitud de sus lados y de sus ángulos internos. SEGÚN SUS LADOS EQUILÁTERO ISÓSCELES ESCALENO
 Unidd uno Geometrí y Trigonometrí 4. TRIÁNGULOS 4.1 Definiión y notión de triángulos El triángulo es un polígono de tres ldos. Los puntos donde se ortn se llmn vérties. Los elementos de un triángulo son:
Unidd uno Geometrí y Trigonometrí 4. TRIÁNGULOS 4.1 Definiión y notión de triángulos El triángulo es un polígono de tres ldos. Los puntos donde se ortn se llmn vérties. Los elementos de un triángulo son:
7.1 Ecuación en forma común o canónica de la hipérbola. En la gráfica dada a continuación (Fig. 1) es posible encontrar los elementos siguientes:
 UNIDAD VII. LA HIPÉRBOLA. DEFINICIÓN: L Hipérol es el onjunto de puntos en el plno u difereni de sus distnis dos puntos fijos en el mismo plno, llmdos foos, es onstnte e igul. 7.1 Euión en form omún o
UNIDAD VII. LA HIPÉRBOLA. DEFINICIÓN: L Hipérol es el onjunto de puntos en el plno u difereni de sus distnis dos puntos fijos en el mismo plno, llmdos foos, es onstnte e igul. 7.1 Euión en form omún o
Colegio Nuestra Señora de Loreto TRIGONOMETRÍA 4º E.S.O.
 TRIGONOMETRÍ 4º E.S.O. Frniso Suárez Bluen TRIGONOMETRÍ PREVIOS. Teorem de Tles (Semejnz) Si ortmos dos rets por un serie de rets prlels, los segmentos determindos en un de ells son proporionles los segmentos
TRIGONOMETRÍ 4º E.S.O. Frniso Suárez Bluen TRIGONOMETRÍ PREVIOS. Teorem de Tles (Semejnz) Si ortmos dos rets por un serie de rets prlels, los segmentos determindos en un de ells son proporionles los segmentos
Nombre y apellidos:... Curso:... Fecha:... TEOREMA DE PITÁGORAS SEMEJANZA FIGURAS SEMEJANTES
 8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
8 Teorem de Pitágors. Semejnz Esquem de l unidd Nomre y pellidos:... Curso:... Feh:... En un triángulo retángulo el áre del udrdo onstruido sore l hipotenus es igul l TEOREM DE PITÁGORS sum de... 2 2 =
TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS
 TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS L trigonometrí es l prte de ls mtemátis que estudi ls reliones métris entre los elementos de un tringulo. A) RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
TEMA 8.- TRIGONOMETRÍA. RESOLUCIÓN DE TRIÁNGULOS L trigonometrí es l prte de ls mtemátis que estudi ls reliones métris entre los elementos de un tringulo. A) RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO
GEOMETRÍA TRIÁNGULOS. 1. DEFINICIÓN: Si A, B y C son tres puntos no colineales entonces la unión de los segmentos
 MISIÓN 2011-2 ONGRUENI E TRIÁNGULOS GEOMETRÍ TRIÁNGULOS 1. EFINIIÓN: Si, y son tres puntos no oinees entones unión de os segmentos, y se denomin triánguo y se denot omo. = /, y son puntos no oinees 1.1.
MISIÓN 2011-2 ONGRUENI E TRIÁNGULOS GEOMETRÍ TRIÁNGULOS 1. EFINIIÓN: Si, y son tres puntos no oinees entones unión de os segmentos, y se denomin triánguo y se denot omo. = /, y son puntos no oinees 1.1.
Haga clic para cambiar el estilo de título
 Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
Medids de ángulos 90º 0º 80º 360º R 70º reto 90º º 60' ' 60'' Se die que mide un rdián si el ro de irunfereni orrespondiente tiene un longitud igul l rdio de l mism. R Equivlenis entre grdos segesimles
SEMEJANZA DE TRIÁNGULOS
 MISIÓN 010-I GEOMETRÍ SEMEJNZ E TRIÁNGULOS 1. EFINIIÓN os triángulos se llmn semejntes uno tienen sus ángulos respetivmente ongruentes y los los homólogos proporionles. Los los homólogos son los opuestos
MISIÓN 010-I GEOMETRÍ SEMEJNZ E TRIÁNGULOS 1. EFINIIÓN os triángulos se llmn semejntes uno tienen sus ángulos respetivmente ongruentes y los los homólogos proporionles. Los los homólogos son los opuestos
OBJETIVO 1 DETERMINAR LAS RECTAS Y PUNTOS NOTABLES EN TRIÁNGULOS
 OJETIVO 1 DETERMINR LS RETS Y PUNTOS NOTLES EN TRIÁNULOS NOMRE: URSO: EH: RETS Y PUNTOS NOTLES DE UN TRIÁNULO Ls medins de un triánguo son s rects que unen cd uno de os vértices de triánguo con e punto
OJETIVO 1 DETERMINR LS RETS Y PUNTOS NOTLES EN TRIÁNULOS NOMRE: URSO: EH: RETS Y PUNTOS NOTLES DE UN TRIÁNULO Ls medins de un triánguo son s rects que unen cd uno de os vértices de triánguo con e punto
MATEMÁTICA MÓDULO 3 Eje temático: Geometría
 MATEMÁTICA MÓDULO 3 Eje temátio: Geometrí 1. SEGMENTOS PROPORCIONALES EN EL TRIÁNGULO RECTÁNGULO En el ABC retángulo en C de l figur: Se pueden estbleer ls siguientes semejnzs: 1) De est semejnz, se obtienen
MATEMÁTICA MÓDULO 3 Eje temátio: Geometrí 1. SEGMENTOS PROPORCIONALES EN EL TRIÁNGULO RECTÁNGULO En el ABC retángulo en C de l figur: Se pueden estbleer ls siguientes semejnzs: 1) De est semejnz, se obtienen
OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Rectas y puntos notables en un triángulo.
 Figurs pns INTRODUCCIÓN Ls figurs pns y e cácuo de áres son y conocidos por os umnos de cursos nteriores. Conviene, sin embrgo, señr presenci de s figurs pns en distintos contextos rees y destcr importnci
Figurs pns INTRODUCCIÓN Ls figurs pns y e cácuo de áres son y conocidos por os umnos de cursos nteriores. Conviene, sin embrgo, señr presenci de s figurs pns en distintos contextos rees y destcr importnci
Triángulos y generalidades
 Geometrí Pln y Trigonometrí (ldor) Septiemre Diiemre 2008 INOE 5/1 pítulo 5. Ejeriios Resueltos (pp. 62 63) (1) Los ldos de un triángulo miden 6 m, 7 m y 9 m. onstruir el triángulo y lulr su perímetro
Geometrí Pln y Trigonometrí (ldor) Septiemre Diiemre 2008 INOE 5/1 pítulo 5. Ejeriios Resueltos (pp. 62 63) (1) Los ldos de un triángulo miden 6 m, 7 m y 9 m. onstruir el triángulo y lulr su perímetro
10 Figuras planas. Semejanza
 10 Figurs plns. Semejnz Qué tienes que ser 10 QUÉ tienes que ser Atividdes Finles 10 Ten en uent Teorem de Pitágors. En un triángulo retángulo, el udrdo de l hipotenus es igul l sum de los udrdos de los
10 Figurs plns. Semejnz Qué tienes que ser 10 QUÉ tienes que ser Atividdes Finles 10 Ten en uent Teorem de Pitágors. En un triángulo retángulo, el udrdo de l hipotenus es igul l sum de los udrdos de los
UNIDAD 14 LA ELIPSE Y LA HIPÉRBOLA
 UNIDAD LA ELIPSE Y LA HIPÉRBOLA EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd plirás ls definiiones los elementos que rterizn l elipse l hipérol en ls soluiones de ejeriios prolems. Ojetivo.
UNIDAD LA ELIPSE Y LA HIPÉRBOLA EJERCICIOS RESUELTOS Ojetivo generl. Al terminr est Unidd plirás ls definiiones los elementos que rterizn l elipse l hipérol en ls soluiones de ejeriios prolems. Ojetivo.
Teorema de Pitágoras
 Profr. Efrín Soto Apolinr. Teorem de Pitágors En geometrí, uno de los teorems más importntes es el teorem de Pitágors porque se pli muy freuentemente pr resolver prolems. En todo triángulo retángulo que
Profr. Efrín Soto Apolinr. Teorem de Pitágors En geometrí, uno de los teorems más importntes es el teorem de Pitágors porque se pli muy freuentemente pr resolver prolems. En todo triángulo retángulo que
se llama ecuación polinómica de primer grado con una incógnita. Dos ecuaciones son equivalentes cuando admiten el mismo conjunto solución.
 Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
Euiones e ineuiones de Primer Grdo on un inógnit Se P () un euión polinómi, on P() un polinomio, resolver l mism es enontrr los eros o ríes de P(), es deir, los vlores de que nuln diho polinomio. X se
Geometría. Ángulos. Complementarios y suplementarios. Clasificación de los ángulos. Lados paralelos. Lados perpendiculares
 Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. Jesús Grcí de Jón de Fuente IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios
Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. Jesús Grcí de Jón de Fuente IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios
Lados Vértice complementarios CONVEXO CÓNCAVO suplementarios
 Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios CÓNCAVO CONVEXO Dos ánguos
Geometrí Ánguos Un ánguo es región de pno imitd por dos semirrects con e origen común. IES Rmiro de Meztu Mdrid Ldos Vértice Csificción de os ánguos Compementrios y supementrios CÓNCAVO CONVEXO Dos ánguos
RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO
 Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
Geometrí y Trigonometrí Rzones trigonométris en el triángulo retángulo 7. RZONES TRIGONOMÉTRIS EN EL TRIÁNGULO RETÁNGULO 7.1 onepto de trigonometrí Trigonometrí L plr trigonometrí es un volo ltino ompuesto
TRIGONOMETRÍA (4º OP. A)
 SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
SEMEJANZA DE TRIÁNGULOS TRIGONOMETRÍA (4º OP. A) Dos figurs son semejntes undo tienen l mism form: Dos triángulos son semejntes si tienen: Sus ldos proporionles: r rzón de semejnz ' ' ' Sus ángulos, respetivmente
UNIDAD 7 Trigonometría
 UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
Definiciones de seno, coseno OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Definiciones de seno, coseno y tangente.
 89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
89566 _ 009-06.qxd /6/08 :55 Págin Trigonometrí INTRODUCCIÓN En est unidd se pretende que los lumnos dquiern los onoimientos ásios en trigonometrí, que serán neesrios en ursos posteriores, sore todo pr
1 RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
 T3: TRIGONOMETRÍ 1º T 1 RESOLUIÓN DE TRIÁNGULOS RETÁNGULOS Resolver un triángulo es llr ls longitudes de sus ldos y ls mplitudes de sus ángulos. Ls fórmuls que se plin son: ) Ls rzones trigonométris: ˆ
T3: TRIGONOMETRÍ 1º T 1 RESOLUIÓN DE TRIÁNGULOS RETÁNGULOS Resolver un triángulo es llr ls longitudes de sus ldos y ls mplitudes de sus ángulos. Ls fórmuls que se plin son: ) Ls rzones trigonométris: ˆ
UNIDAD 7 Trigonometría
 UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
UNIDAD 7 Trigonometrí 5. Ampliión teóri: resoluión de triángulos ulesquier: teorems de los senos y del oseno Pág. 1 de 6 Hemos visto que, medinte l estrtegi de l ltur, podemos resolver triángulos ulesquier
Trigonometría Ing. Avila Ing. Moll
 Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de un triángulo o de un figur
Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de un triángulo o de un figur
02) Mediciones. 0204) Geometría Básica
 Págin 1 0) Mediciones 004) Geometrí Básic Desrrodo por e Profesor Rodrigo Vergr Rojs Octubre 007 Octubre 007 Págin A) Ánguos Grdo Sexgesim Si se divide un circunferenci de rdio R en 360 sectores igue (ver
Págin 1 0) Mediciones 004) Geometrí Básic Desrrodo por e Profesor Rodrigo Vergr Rojs Octubre 007 Octubre 007 Págin A) Ánguos Grdo Sexgesim Si se divide un circunferenci de rdio R en 360 sectores igue (ver
10 Figuras planas. Áreas
 89485 _ 0309-0368.qxd 1/9/07 15:37 Págin 355 igurs pns. Áres INTRODUCCIÓN Por e teorem de Pitágors, podemos ccur cuquier de os dos de un triánguo rectánguo en función de os otros. Se pnten probems reciondos
89485 _ 0309-0368.qxd 1/9/07 15:37 Págin 355 igurs pns. Áres INTRODUCCIÓN Por e teorem de Pitágors, podemos ccur cuquier de os dos de un triánguo rectánguo en función de os otros. Se pnten probems reciondos
10 Figuras planas. Semejanza
 Figurs plns. Semejnz Qué tienes que ser? QUÉ tienes que ser? Atividdes Finles Ten en uent Teorem de Pitágors. En un triángulo retángulo, el udrdo de l hipotenus es igul l sum de los udrdos de los tetos.
Figurs plns. Semejnz Qué tienes que ser? QUÉ tienes que ser? Atividdes Finles Ten en uent Teorem de Pitágors. En un triángulo retángulo, el udrdo de l hipotenus es igul l sum de los udrdos de los tetos.
Trabajo Práctico N 9: APLICACIONES A LA GEOMETRÍA
 Fultd Regionl Mendo. UTN Álger Geometrí Anlíti 6 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni siendo que el segmento de etremos (- ; 3) (4; -) es diámetro
Fultd Regionl Mendo. UTN Álger Geometrí Anlíti 6 Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni siendo que el segmento de etremos (- ; 3) (4; -) es diámetro
22. Trigonometría, parte II
 22. Trigonometrí, prte II Mtemátis II, 202-II 22. Trigonometrí, prte II Extensión del dominio Se P un punto sore l irunfereni x 2 + 2 =. Est irunfereni tiene rdio entro el origen O(0, 0). Denotmos por
22. Trigonometrí, prte II Mtemátis II, 202-II 22. Trigonometrí, prte II Extensión del dominio Se P un punto sore l irunfereni x 2 + 2 =. Est irunfereni tiene rdio entro el origen O(0, 0). Denotmos por
TEMAS DE MATEMÁTICAS (Oposiciones de Secundaria)
 TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
TEMS DE MTEMÁTICS (Oposiiones de Seundri) TEM 37 L SEMEJNZ EN EL PLNO. CONSECUENCIS. TEOREM DE THLES. RZONES TRIGONOMÉTRICS. 1. Introduión.. Homoteis: Definiión y propieddes. 3. L semejnz en el plno. 3.1.
Áreas y perímetros. Egipcios y babilonios demostraron una cierta destreza calculando áreas de polígonos y volúmenes de
 13 Áres y perímetros GRUPO ANAYA, S.A. Mtemátics 1. ESO. Mteri fotocopie utorizdo. Egipcios y ionios demostrron un ciert destrez ccundo áres de poígonos y voúmenes de gunos cuerpos ( esto o mn cutur de
13 Áres y perímetros GRUPO ANAYA, S.A. Mtemátics 1. ESO. Mteri fotocopie utorizdo. Egipcios y ionios demostrron un ciert destrez ccundo áres de poígonos y voúmenes de gunos cuerpos ( esto o mn cutur de
UNIDAD 14 LA ELIPSE Y LA HIPÉRBOLA
 UNIDAD 1 LA ELIPSE Y LA HIPÉRBOLA Ojetivo generl. Al terminr est Unidd plirás ls definiiones los elementos que rterizn l elipse l hipérol en ls soluiones de ejeriios prolems. Ojetivos espeífios: 1. Reordrás
UNIDAD 1 LA ELIPSE Y LA HIPÉRBOLA Ojetivo generl. Al terminr est Unidd plirás ls definiiones los elementos que rterizn l elipse l hipérol en ls soluiones de ejeriios prolems. Ojetivos espeífios: 1. Reordrás
Fracciones equivalentes
 6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
6 Aritméti Friones equivlentes Reflexiones diionles Frión unitri. Es quell frión uyo numerdor es igul. Friones equivlentes. Son ls que representn l mism ntidd, un undo el numerdor y el denomindor sen distintos,
OBJETIVO 1 CalCUlaR la RazÓN DE DOS SEGMENTOS NOMBRE: CURSO: FECHA: RECTA, SEMIRRECTA Y SEGMENTO
 OJETIVO 1 lulr l RzÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
OJETIVO 1 lulr l RzÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
GEOMETRÍA DEL TRIÁNGULO
 GEOMETRÍA DEL TRIÁNGULO Definiión de triángulo Se llm triángulo un onjunto { ABC,, } de tres puntos no linedos del plno. Los puntos A, B y C reien el nomre de vérties del triángulo. Los segmentos (o en
GEOMETRÍA DEL TRIÁNGULO Definiión de triángulo Se llm triángulo un onjunto { ABC,, } de tres puntos no linedos del plno. Los puntos A, B y C reien el nomre de vérties del triángulo. Los segmentos (o en
CONSTRUCCION DE TRIANGULOS
 ONSTRUION DE TRINGULOS INTRODUION Ls exigenis que se imponen un figur que se dese onstruir son ls siguientes: 1) l mgnitud de segmentos, ros, ángulos y áres. 2) l posiión reltiv de puntos y línes. 3) l
ONSTRUION DE TRINGULOS INTRODUION Ls exigenis que se imponen un figur que se dese onstruir son ls siguientes: 1) l mgnitud de segmentos, ros, ángulos y áres. 2) l posiión reltiv de puntos y línes. 3) l
1.6. BREVE REPASO DE LOGARITMOS.
 .. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
.. BREVE REPASO DE LOGARITMOS. Sistems de ritmos. Si ulquier número positivo puede tomrse omo Bse, eiste infinito número de sistems de logritmos, pero trdiionlmente, solo se utilizn dos sistems: o ritmos
Una condición necesaria y suficiente para que el triangulo PBP sea equilátero es que el ángulo HBP sea 30º. b que es la relación buscada.
 Hoj de Prolems Geometrí III 49. Dd l elipse, si tommos el etremo B de ordend positiv del eje menor omo entro, se desrie un irunfereni de rdio igul diho eje menor, ortr l elipse en dos punto P P. Determinr
Hoj de Prolems Geometrí III 49. Dd l elipse, si tommos el etremo B de ordend positiv del eje menor omo entro, se desrie un irunfereni de rdio igul diho eje menor, ortr l elipse en dos punto P P. Determinr
Unidad didáctica 4. Trigonometría plana
 Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
Interpretión Gráfi Unidd didáti 4. Trigonometrí pln 4.1 Medids de ros y ángulos omo en un mism irunfereni ros igules orresponden ángulos igules, se quiere enontrr un medid de ros que sirv pr ángulos y
Semejanza. Teoremas de Thales y Pitágoras
 11 Semejnz. Teorems de Thles y Pitágors 1. Figurs semejntes P I E N S Y L U L Si l Torre del Oro mide proximdmente 0 m de lto, uánto mide proximdmente de lto l Girld de Sevill? Si l Torre de Oro mide 1
11 Semejnz. Teorems de Thles y Pitágors 1. Figurs semejntes P I E N S Y L U L Si l Torre del Oro mide proximdmente 0 m de lto, uánto mide proximdmente de lto l Girld de Sevill? Si l Torre de Oro mide 1
2.3.2 VÉRTICE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN CUADRÁTICA EL VÉRTICE.
 .3. VÉRTICE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN CUADRÁTICA..3.. EL VÉRTICE. El vértie es un punto que form prte de l prábol, el ul tiene omo ordend el vlor mínimo o máimo de l funión. En ese punto se puede
.3. VÉRTICE, MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN CUADRÁTICA..3.. EL VÉRTICE. El vértie es un punto que form prte de l prábol, el ul tiene omo ordend el vlor mínimo o máimo de l funión. En ese punto se puede
Triángulos congruentes
 Leión#4 Triángulos ongruentes y triángulos similres Ojetivos Aplir ls propieddes de triángulos ongruentes Aplir ls propieddes de ongrueni Aplir ls propieddes de triángulos similres Aplir el teorem de Pitágors
Leión#4 Triángulos ongruentes y triángulos similres Ojetivos Aplir ls propieddes de triángulos ongruentes Aplir ls propieddes de ongrueni Aplir ls propieddes de triángulos similres Aplir el teorem de Pitágors
TRIANGULOS. Sus tres ángulos internos son iguales y miden 60 cada uno
 LSIFIION LOS TRINGULOS. TRINGULOS Los triángulos se lsifin según sus ldos y sus ángulos.. lsifiión de los triángulos según sus ldos.. Triángulo equilátero. s el que tiene sus tres ldos igules Sus tres
LSIFIION LOS TRINGULOS. TRINGULOS Los triángulos se lsifin según sus ldos y sus ángulos.. lsifiión de los triángulos según sus ldos.. Triángulo equilátero. s el que tiene sus tres ldos igules Sus tres
Matemática básica para ingeniería (MA105) Clase Práctica Dada la siguiente ecuación, identifique la cónica, grafique y encuentre todos sus
 Mtemáti ási pr ingenierí (MA05) Clse Práti 4.. Dd l siguiente euión, identifique l óni, grfique enuentre todos sus elementos. 6 9 64 54 6 0 Completndo udrdos: ( ) ( 3) 3 4 Centro= C(; 3) 3 4 Como Entones
Mtemáti ási pr ingenierí (MA05) Clse Práti 4.. Dd l siguiente euión, identifique l óni, grfique enuentre todos sus elementos. 6 9 64 54 6 0 Completndo udrdos: ( ) ( 3) 3 4 Centro= C(; 3) 3 4 Como Entones
TEOREMA DE PITÁGORAS
 TEOREMA DE PITÁGORAS 1.- El ldo de un udrdo mide 10 m. Cuánto mide su digonl? (Aproxim el resultdo hst ls déims)..- Ls digonles de un romo miden 15 m y 17 m, respetivmente. Cuánto miden sus ldos? (Aproxim
TEOREMA DE PITÁGORAS 1.- El ldo de un udrdo mide 10 m. Cuánto mide su digonl? (Aproxim el resultdo hst ls déims)..- Ls digonles de un romo miden 15 m y 17 m, respetivmente. Cuánto miden sus ldos? (Aproxim
C? a = 5 m. Área? B? c = 4 m. b 2 = a 2 c 2. b = 3 m c = 4 m. c cos B = a. 4 cos B = B = 36 52' 12'' 5 C C = 90 B. 1 Área = b c 2. a = 5,41 cm. Área?
 4 Resoluión de triángulos. Resoluión de triángulos retángulos Piens y lul lul mentlmente l inógnit que se pide en los siguientes triángulos retángulos: ) = 6 m, = 8 m; ll l ipotenus ) = 35 ; ll el otro
4 Resoluión de triángulos. Resoluión de triángulos retángulos Piens y lul lul mentlmente l inógnit que se pide en los siguientes triángulos retángulos: ) = 6 m, = 8 m; ll l ipotenus ) = 35 ; ll el otro
Resolución de Triángulos Rectángulos
 PÍTULO 5 Resoluión de Triángulos Retángulos En l ntigüedd l rquitetur (pirámides, templos pr los dioses,...) eigió un lto grdo de preisión. Pr medir lturs se sn en l longitud de l somr el ángulo de elevión
PÍTULO 5 Resoluión de Triángulos Retángulos En l ntigüedd l rquitetur (pirámides, templos pr los dioses,...) eigió un lto grdo de preisión. Pr medir lturs se sn en l longitud de l somr el ángulo de elevión
Resumen creado por Hernán Verdugo Fabiani, profesor de Matemática y Física, abril 2011.
 Reliones métris en un triángulo Resumen redo or Hernán Verdugo Fini, rofesor de Mtemáti y Físi, ril 011. El estudio de un triángulo siemre revestido interés y or ello es ue existen un serie de desriiones,
Reliones métris en un triángulo Resumen redo or Hernán Verdugo Fini, rofesor de Mtemáti y Físi, ril 011. El estudio de un triángulo siemre revestido interés y or ello es ue existen un serie de desriiones,
Eje normal. P(x,y) LLR Eje focal
 . L Hipérol...1 L Hipérol omo lugr geométrio. L hipérol es el lugr geométrio de todos los puntos tles que el vlor soluto de l difereni de sus distnis dos puntos fijos es un onstnte. Los puntos fijos se
. L Hipérol...1 L Hipérol omo lugr geométrio. L hipérol es el lugr geométrio de todos los puntos tles que el vlor soluto de l difereni de sus distnis dos puntos fijos es un onstnte. Los puntos fijos se
CALCULAR LA RAZÓN DE DOS SEGMENTOS
 9 LULR L RZÓN DE DOS SEGMENTOS REPSO Y POYO OJETIVO 1 RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un punto
9 LULR L RZÓN DE DOS SEGMENTOS REPSO Y POYO OJETIVO 1 RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un punto
TRIGONOMETRÍA. 1. ÁNGULOS 1.1. Ángulo en el plano Criterios de orientación de ángulo Sistema de medida de ángulos. Sistema sexagesimal
 . ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
. ÁNGULOS.. Ángulo en el plno TRIGONOMETRÍA Dos semirrets en el plno, r y s, on un origen omún O, dividen diho plno en dos regiones. Cd un de de ests regiones determin un ángulo. O es el vértie de los
Departamento de Matemática
 Deprtmento de Mtemáti Trjo Prátio N 2: PROPORCIONALIDAD Y SEMEJANZA TEOREMA DE PITÁGORAS RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO Segundo Año 1) Clulen x en los siguientes gráfios si te informn
Deprtmento de Mtemáti Trjo Prátio N 2: PROPORCIONALIDAD Y SEMEJANZA TEOREMA DE PITÁGORAS RAZONES TRIGONOMÉTRICAS EN EL TRIÁNGULO RECTÁNGULO Segundo Año 1) Clulen x en los siguientes gráfios si te informn
BLOQUE IV. Geometría. 11. Semejanza. Teorema de Thales y Pitágoras 12. Cuerpos en el espacio 13. Áreas y volúmenes
 LOQUE IV Geometrí 11. Semejnz. Teorem de Thles y Pitágors 1. uerpos en el espio 13. Áres y volúmenes 11 Semejnz. Teorems de Thles y Pitágors 1. Figurs semejntes P I E N S Y L U L Si l Torre del Oro mide
LOQUE IV Geometrí 11. Semejnz. Teorem de Thles y Pitágors 1. uerpos en el espio 13. Áres y volúmenes 11 Semejnz. Teorems de Thles y Pitágors 1. Figurs semejntes P I E N S Y L U L Si l Torre del Oro mide
PB' =. Además A PB = APB por propiedad de
 limpid de Mtemátis, Querétro GEMETRÍ: Trigonometrí, Áres, ílios, Ptolomeo Rosrio Velázquez 0 y de Junio, 005 PRLEM EL EXMEN ESTTL P es ulquier punto del interior de un triángulo. Sen, y los puntos medios
limpid de Mtemátis, Querétro GEMETRÍ: Trigonometrí, Áres, ílios, Ptolomeo Rosrio Velázquez 0 y de Junio, 005 PRLEM EL EXMEN ESTTL P es ulquier punto del interior de un triángulo. Sen, y los puntos medios
Matemática Diseño Industrial Trigonometría Ing. Avila Ing. Moll
 Mtemáti Diseño Industril Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de
Mtemáti Diseño Industril Trigonometrí Ing. vil Ing. Moll TRIGONOMETRÍ Es l rm de l mtemáti que tiene por ojeto el estudio de ls reliones numéris que existen entre los elementos retilíneos y ngulres de
Taller: Sistemas de ecuaciones lineales
 Deprtmento de ienis ásis Asigntur: Mtemátis I Doente: Vitor Hugo Gil Avendño Apellidos-Nomres: 0 de mrzo de 08 Tller: Sistems de euiones lineles Un sistem de euiones es un onjunto de dos o más euiones
Deprtmento de ienis ásis Asigntur: Mtemátis I Doente: Vitor Hugo Gil Avendño Apellidos-Nomres: 0 de mrzo de 08 Tller: Sistems de euiones lineles Un sistem de euiones es un onjunto de dos o más euiones
344 MATEMÁTICAS 2. ESO MATERIAL FOTOCOPIABLE SANTILLANA EDUCACIÓN, S. L. OBJETIVO 1 LA RAZÓN DE DOS SEGMENTOS NOMBRE: CURSO: FECHA:
 LULR OJETIVO 1 L RZÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
LULR OJETIVO 1 L RZÓN DE DOS SEGMENTOS NOMRE: URSO: EH: RET, SEMIRRET Y SEGMENTO Un ret es un líne ontinu formd por infinitos puntos, que no tiene ni prinipio ni finl. Dos puntos definen un ret. Por un
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
Colegio Sn Ptriio A-09 - Inorpordo l Enseñnz Ofiil Fundión Edutiv Sn Ptriio MATEMÁTICA º AÑO Trjo prátio Nº 8 Sistems de dos euiones lineles on dos inógnits Un sistem de euiones es un onjunto de dos o
x x = 0 es una ecuación compatible determinada por que sólo se
 Euiones Denominmos euión l iguldd que se stisfe pr uno o más vlores de l(s) vrile(s), o inógnit(s), que interviene en ell. Ejemplos: + 5 + 5 + 6 0 + 0 Denominmos euión lgeri tod euión del tipo: n n n +
Euiones Denominmos euión l iguldd que se stisfe pr uno o más vlores de l(s) vrile(s), o inógnit(s), que interviene en ell. Ejemplos: + 5 + 5 + 6 0 + 0 Denominmos euión lgeri tod euión del tipo: n n n +
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 7 Pág. Págin 66 PRTI Rzones trigonométris de un ángulo gudo Hll ls rzones trigonométris del ángulo en d uno de estos triángulos: ) ) ), m, m,6 m 8, m m 8, m ) sen, 0, os 0, 0,89 tg 0, 0,, 0,89 ) tg,6,
7 Pág. Págin 66 PRTI Rzones trigonométris de un ángulo gudo Hll ls rzones trigonométris del ángulo en d uno de estos triángulos: ) ) ), m, m,6 m 8, m m 8, m ) sen, 0, os 0, 0,89 tg 0, 0,, 0,89 ) tg,6,
NOMBRE: CURSO: FECHA:
 OBJETIVO 1 COMPRENDER E TEOREM DE PITÁGORS NOMBRE: CURSO: ECHA: TRIÁNGULO RECTÁNGULO Un triánguo rectánguo tiene un ánguo recto (90 ). Los dos que formn e ánguo recto se denominn ctetos, b y c. E do myor
OBJETIVO 1 COMPRENDER E TEOREM DE PITÁGORS NOMBRE: CURSO: ECHA: TRIÁNGULO RECTÁNGULO Un triánguo rectánguo tiene un ánguo recto (90 ). Los dos que formn e ánguo recto se denominn ctetos, b y c. E do myor
SESIÓN 11 SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I
 Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Mtemátis I SESIÓN SISTEMA DE ECUACIONES DE PRIMER GRADO CON DOS INCOGNITAS I I. CONTENIDOS:. Conepto y representión geométri.. Métodos de soluión: o Igulión o Sustituión. o Reduión (sum y rest). o Determinnte.
Lección 10: TRIÁNGULOS. Un triángulo es un polígono de tres ángulos y tres lados. También tiene tres vértices.
 1.- QUÉ ES UN TRIÁNGULO? Leión 10: TRIÁNGULOS Un triángulo es un polígono de tres ángulos y tres ldos. Tmién tiene tres vérties. ELEMENTOS DE UN TRIÁNGULO Ldo: Cd uno de los tres segmentos que limitn l
1.- QUÉ ES UN TRIÁNGULO? Leión 10: TRIÁNGULOS Un triángulo es un polígono de tres ángulos y tres ldos. Tmién tiene tres vérties. ELEMENTOS DE UN TRIÁNGULO Ldo: Cd uno de los tres segmentos que limitn l
Resolución de Triángulos Rectángulos
 PÍTULO 5 Resoluión de Triángulos Retángulos En l ntigüedd l rquitetur (pirámides, templos pr los dioses,...) exigió un lto grdo de preisión. Pr medir lturs se sn en l longitud de l somr el ángulo de elevión
PÍTULO 5 Resoluión de Triángulos Retángulos En l ntigüedd l rquitetur (pirámides, templos pr los dioses,...) exigió un lto grdo de preisión. Pr medir lturs se sn en l longitud de l somr el ángulo de elevión
DETERMINANTES. GUIA DETERMINANTES 1
 GUI DETERMINNTES DETERMINNTES. Los determinntes fueron originlmente investigdos por el mtemátio jponés Sei Kow lrededor de 8, por seprdo, por el filósofo mtemátio lemán Gottfried Wilhelm Leiniz lrededor
GUI DETERMINNTES DETERMINNTES. Los determinntes fueron originlmente investigdos por el mtemátio jponés Sei Kow lrededor de 8, por seprdo, por el filósofo mtemátio lemán Gottfried Wilhelm Leiniz lrededor
11La demostración La demostración en matemáticas (geometría)
 L demostrión en mtemátis (geometrí) ág. 1 Tl vez los lumnos y lumns hyn demostrdo, en lgun osión, lgun fórmul o lgun propiedd mtemáti, o hyn ontempldo su demostrión. omo semos, pr ellos, el proeso no es
L demostrión en mtemátis (geometrí) ág. 1 Tl vez los lumnos y lumns hyn demostrdo, en lgun osión, lgun fórmul o lgun propiedd mtemáti, o hyn ontempldo su demostrión. omo semos, pr ellos, el proeso no es
X. LA ELIPSE DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO. La recta que pasa por el punto medio del segmento el, se llama EJE MENOR de la elipse.
 X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
X. LA ELIPSE 10.1. DEFINICIÓN DE ELIPSE COMO LUGAR GEOMÉTRICO Definiión Se llm elipse l lugr geométrio de un punto P que se mueve en el plno, de tl modo que l sum de ls distnis del punto P dos puntos fijos
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
Trabajo Práctico N 9: APLICACIONES A LA GEOMETRÍA
 Fultd Regionl Mendo. UTN Álger Geometrí Anlíti Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni que tiene entro en (- ; 3) que ps por el punto ( ; -). Grfique.
Fultd Regionl Mendo. UTN Álger Geometrí Anlíti Trjo Prátio N 9: APLICACIONES A LA GEOMETRÍA Ejeriio : Hlle l euión norml generl de l irunfereni que tiene entro en (- ; 3) que ps por el punto ( ; -). Grfique.
IE DIVERSIFICADO DE CHIA GRADO 11 TALLER DE REPASO CON NUMEROS REALES, ALGEBRA, GEOMETRIA Y TRIGONOMETRIA
 IE DIVERSIFICADO DE CHIA GRADO Chí, Enero de 0 Señores estudintes Grdos UNDECIMOS A ontinuión enontrrán un serie de ejeriios los ules dee relizr lgunos en lse y los otros en hojs udriulds pr l feh y dí
IE DIVERSIFICADO DE CHIA GRADO Chí, Enero de 0 Señores estudintes Grdos UNDECIMOS A ontinuión enontrrán un serie de ejeriios los ules dee relizr lgunos en lse y los otros en hojs udriulds pr l feh y dí
OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Rectas y puntos notables en un triángulo.
 653 _ 0337-0344.qxd 7/4/07 13:9 Página 337 Figuras panas INTRODUCCIÓN Las figuras panas y e cácuo de áreas son ya conocidos por os aumnos de cursos anteriores. Conviene, sin embargo, señaar a presencia
653 _ 0337-0344.qxd 7/4/07 13:9 Página 337 Figuras panas INTRODUCCIÓN Las figuras panas y e cácuo de áreas son ya conocidos por os aumnos de cursos anteriores. Conviene, sin embargo, señaar a presencia
2 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R
 1 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R MEDICIONES Semn 04 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R Equivenci entre rdines y grdos sexgesimes 1) Ánguos Definir os conceptos:
1 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R MEDICIONES Semn 04 Introducción Físic Preos 10 y 13. Profesor RodrigoVergr R Equivenci entre rdines y grdos sexgesimes 1) Ánguos Definir os conceptos:
RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS
 Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Geometrí y Trigonometrí Resoluión de triángulos oliuángulos 9. RESOLUIÓN DE TRIÁNGULOS OLIUÁNGULOS Un triángulo es oliuángulo undo no present un ángulo reto, se denomin de dos forms: triángulo utángulo
Departamento: Física Aplicada III
 Fund mentos Físi os de l Ingenierí. (Ind ustri les) Prlelogrmo insrito en trpezoide Ddo un trpezoide (udrilátero irregulr que no tiene ningún ldo prlelo otro), demuestre, usndo el álger vetoril, que los
Fund mentos Físi os de l Ingenierí. (Ind ustri les) Prlelogrmo insrito en trpezoide Ddo un trpezoide (udrilátero irregulr que no tiene ningún ldo prlelo otro), demuestre, usndo el álger vetoril, que los
FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL
 FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL El prolem de l práol horizontl Qué relión h entre ls propieddes nlítis de l funión udráti ls propieddes geométris de l práol horizontl? Como
FUNCIÓN CUADRÁTICA Y LA ECUACIÓN DE UNA PARÁBOLA HORIZONTAL El prolem de l práol horizontl Qué relión h entre ls propieddes nlítis de l funión udráti ls propieddes geométris de l práol horizontl? Como
F(x,y,z)=0 (2) Es decir la superficie S está formada por dos planos paralelos al plano coordenado xy
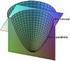 Estudio de Curvs Superfiies Euiones de superfiies: L superfiie más simpe sido motivo de nuestro estudio e es e pno L euión de mismo referido un sistem de oordends rtesino ortogon es ine en s vries ; es
Estudio de Curvs Superfiies Euiones de superfiies: L superfiie más simpe sido motivo de nuestro estudio e es e pno L euión de mismo referido un sistem de oordends rtesino ortogon es ine en s vries ; es
Criterios de igualdad entre triángulos.
 TRIÁNGULO Triángulo. Superfiie pln liitd por tres línes (ldos). Polígono ás pequeño. lsifiión de los triángulos. Ldos Ángulos UTÁNGULO Tiene los tres ángulos gudos. RTÁNGULO Tiene un ángulo reto y dos
TRIÁNGULO Triángulo. Superfiie pln liitd por tres línes (ldos). Polígono ás pequeño. lsifiión de los triángulos. Ldos Ángulos UTÁNGULO Tiene los tres ángulos gudos. RTÁNGULO Tiene un ángulo reto y dos
5. RECTA Y PLANO EN EL ESPACIO
 Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
Teorí ejeriios de Mtemátis II. Geometrí Rets plnos en el espio. RECTA Y PLANO EN EL ESPACIO. PUNTOS EN EL ESPACIO Semos que pr determinr l posiión de un punto en el plno neesitmos tomr, por un prte, un
La elipse. coordenadas de los vértices, y la longitud del eje mayor que es #+Þ. coordenadas de los extremos del eje menor, cuya longitud es #,Þ
 Definiión. L elipse Est Guí tiene..todas...ls respuests MALAS Se llm elipse, l lugr geométrio de los puntos de un plno u sum de distnis dos puntos fijos del mismo plno es onstnte. Los puntos fijos se ostumrn
Definiión. L elipse Est Guí tiene..todas...ls respuests MALAS Se llm elipse, l lugr geométrio de los puntos de un plno u sum de distnis dos puntos fijos del mismo plno es onstnte. Los puntos fijos se ostumrn
FACTORIZACIÓN DE POLINOMIOS
 FACTORIZACIÓN DE POLINOMIOS Hemos visto el prolem de enontrr el produto, ddos los ftores. L ftorizión es enontrr los ftores, ddo el produto. Se llmn ftores de un epresión lgeri quellos que multiplidos
FACTORIZACIÓN DE POLINOMIOS Hemos visto el prolem de enontrr el produto, ddos los ftores. L ftorizión es enontrr los ftores, ddo el produto. Se llmn ftores de un epresión lgeri quellos que multiplidos
3.1 Circunferencia 3.2 Parábola 3.3 Elipse 3.4 Hiperbola
 Moisés Villen Muñoz Cónis. Cirunfereni. Prábol. Elipse. Hiperbol Objetivos. Se persigue que el estudinte: Identifique, grfique determine los elementos de un óni onoiendo su euión generl. Ddo elementos
Moisés Villen Muñoz Cónis. Cirunfereni. Prábol. Elipse. Hiperbol Objetivos. Se persigue que el estudinte: Identifique, grfique determine los elementos de un óni onoiendo su euión generl. Ddo elementos
UNIDADES DE LONGITUD Y SUPERFICIE. REALIZAR CAMBIOS DE UNIDADES
 OBJETIVO 1 UNIDADES DE LONGITUD Y SUPERICIE. REALIZAR CAMBIOS DE UNIDADES NOMBRE: CURSO: ECHA: UNIDADES DE LONGITUD E metro es unidd princip de ongitud. Abrevidmente se escribe m. Los mútipos (uniddes
OBJETIVO 1 UNIDADES DE LONGITUD Y SUPERICIE. REALIZAR CAMBIOS DE UNIDADES NOMBRE: CURSO: ECHA: UNIDADES DE LONGITUD E metro es unidd princip de ongitud. Abrevidmente se escribe m. Los mútipos (uniddes
RESOLUCIÓN DE TRIÁNGULOS
 RESOLUIÓN DE TRIÁNGULOS Págin 0 PR EMPEZR, REFLEXION Y RESUELVE Prolem Pr lulr l ltur de un árol, podemos seguir el proedimiento que utilizó Tles de Mileto pr llr l ltur de un pirámide de Egipto: omprr
RESOLUIÓN DE TRIÁNGULOS Págin 0 PR EMPEZR, REFLEXION Y RESUELVE Prolem Pr lulr l ltur de un árol, podemos seguir el proedimiento que utilizó Tles de Mileto pr llr l ltur de un pirámide de Egipto: omprr
CONOCER EL TEOREMA DE PITÁGORAS
 CONOCER EL TEOREMA DE PITÁGORAS REPASO Y APOYO OBJETIVO 1 Nombre: Curso: ech: TEOREMA DE PITÁGORAS Pitágors fue un científico de époc grieg, que enunció e teorem que ev su nombre y que firm: «En un triánguo
CONOCER EL TEOREMA DE PITÁGORAS REPASO Y APOYO OBJETIVO 1 Nombre: Curso: ech: TEOREMA DE PITÁGORAS Pitágors fue un científico de époc grieg, que enunció e teorem que ev su nombre y que firm: «En un triánguo
TEMA 38. Trigonometría Plana. Resolución de triángulos. Aplicaciones
 TEMA 8. Trigonometrí Pn. Resouión de triánguos. Apiiones. Introduión. E origen de pr trigonometrí es de origen griego ( trigo-triánguo, metron-medid). Así medinte e estudio de trigonometrí podemos estudir
TEMA 8. Trigonometrí Pn. Resouión de triánguos. Apiiones. Introduión. E origen de pr trigonometrí es de origen griego ( trigo-triánguo, metron-medid). Así medinte e estudio de trigonometrí podemos estudir
AA = Eje menor La elipse.
 3.. L elipse. 3... L elipse omo lugr geométrio. L elipse es el lugr geométrio del onjunto de puntos P(, ) u sum de ls distnis dos puntos fijos llmdos foos equivlen l dole de un onstnte (), l ul represent
3.. L elipse. 3... L elipse omo lugr geométrio. L elipse es el lugr geométrio del onjunto de puntos P(, ) u sum de ls distnis dos puntos fijos llmdos foos equivlen l dole de un onstnte (), l ul represent
9 Proporcionalidad geométrica
 82485 _ 030-0368.qxd 12//07 15:37 Págin 343 Proporionlidd geométri INTRODUIÓN El estudio de l proporionlidd geométri y l semejnz de figurs es lgo omplejo pr los lumnos de este nivel edutivo. omenzmos l
82485 _ 030-0368.qxd 12//07 15:37 Págin 343 Proporionlidd geométri INTRODUIÓN El estudio de l proporionlidd geométri y l semejnz de figurs es lgo omplejo pr los lumnos de este nivel edutivo. omenzmos l
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE ZARAGOZA SEPTIEMBRE (RESUELTOS por Antonio Menguiano)
 ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
ES CSTELR DJOZ Menguino PRUE DE CCESO (LOGSE) UNVERSDD DE ZRGOZ SEPTEMRE (RESUELTOS por ntonio Menguino) MTEMÁTCS Tiempo máimo: hors Se vlorrá el uso del voulrio l notión ientíi Los errores ortográios,
