Derivadas de las funciones trigonométricas
|
|
|
- María José Domínguez Ríos
- hace 7 años
- Vistas:
Transcripción
1 Tema 8 Derivadas de las funciones trigonométricas Completamos en este tema la derivación de las principales funciones reales de variable real que venimos manejando, estudiando la derivabilidad de las funciones trigonométricas y sus inversas. Ello nos permitirá, como una nueva aplicación del Teorema del Valor Medio, probar las identidades trigonométricas más usuales y, en general, mejorar sustancialmente el conocimiento de las funciones trigonométricas y sus inversas. Encontraremos también nuevas aplicaciones de las reglas de l Hôpital, así como el ejemplo, varias veces prometido, de una función derivable en un intervalo cuya derivada no es continua. 8.. Derivada del arco coseno Para la derivación de las funciones trigonométricas seguiremos el mismo camino usado en su momento para definirlas, empezando por la función arco coseno. La función arco coseno es derivable en ],[ con arccos x) = x x ],[ ) y no es derivable en ni en. Para la demostración debemos obviamente recordar la función arco coseno y la notación que se usó para definirla. La semicircunferencia unidad era la curva Γ : [,] R dada por Γt) = t,ψt) ) = t, t ) t [,] Usaremos que la función ψ es derivable en ], [ con ψ t) = t t t ],[ 95
2 8. Derivadas de las funciones trigonométricas 96 Sabemos que Γ es rectificable con longitud ΛΓ) = π. Para x [,] denotamos por Γ x a la restricción de Γ al intervalo [x,], que también es rectificable, y recordamos la definición del arco coseno: arccos : [,] [0,π], arccos x = ΛΓ x ) x [,] Dados x,y [,] con x < y, denotamos por γ x,y a la restricción de Γ al intervalo [x,y], que también es una curva rectificable, verificándose que arccos x arccos y = Λγ x,y ) ) Pues bien, suponiendo x 0, el Teorema del Valor Medio nos dará estimaciones por defecto y por exceso de esta longitud, que nos llevarán fácilmente al resultado deseado. Suponemos 0 x < y < y aplicamos el Teorema del Valor Medio a la restricción de ψ al intervalo [x,y], que es derivable en dicho intervalo, obteniendo c ]x,y[ tal que ψy) ψx) = ψ c)y x) = c y x) c Denotando como siempre por d a la distancia euclídea en el plano, deducimos claramente que Λγ x,y ) d Γx),Γy) ) = [y x) + ψy) ψx) ) ] / = [ + ψ c) ] / y x) = c y x) x y x) 3) y tenemos la estimación por defecto que buscábamos. Para obtener la estimación por exceso, fijamos una partición P = {x = t 0 < t <... < t n = y} del intervalo [x,y]. Para k =,,...,n, aplicamos de nuevo el Teorema del Valor Medio a la restricción de ψ al intervalo [t k,t k ], obteniendo c k ]t k,t k [ tal que ψt k ) ψt k ) = ψ c k )t k t k ) = Razonando como ya hicimos antes obtenemos c k c k y x) d Γt k ),Γt k ) ) = t k t k ) ck y t k t k ) Para la longitud de la poligonal asociada a la partición P obtenemos entonces que λγ x,y,p) = n d Γt k ),Γt k ) ) k= y n k= t k t k ) = y x) y Puesto que esta desigualdad es válida para toda partición P del intervalo [x,y] deducimos Λγ x,y ) que es la estimación por exceso buscada. y x) 4) y
3 8. Derivadas de las funciones trigonométricas 97 En resumen, en vista de ), las desigualdades 3) y 4) nos dicen que 0 x < y < = y x ψx) arccos x arccos y y x ψy) Equivalentemente, dividiendo por el número negativo x y, las desigualdades se invierten y obtenemos 0 x < y < = ψy) arccos x arccos y x y ψx) Las cosas son ya bastante inmediatas, pues esta desigualdad encierra toda la información que necesitamos. Sea f : [0, [ R la restricción de la función arco coseno al intervalo [0, [. Para a ]0, [, podemos aplicar 5) con y = a, y usando la continuidad de la función ψ obtenemos claramente f f x) f a) a ) = lím x a x a = ψa) Por otra parte, para a [0,[ podemos tomar en 5) x = a y de nuevo la continuidad de ψ nos da f f y) f a) a+) = lím = y a+ y a ψa) Por tanto, f es derivable en [0,[ con f x) = ψx) = x x [0,[ Sea ahora g la restricción del arco coseno al intervalo ],0]. Sabemos que gx) = arccos x = π arccos x) = π f x) x ],0] luego la regla de la cadena nos dice que g es derivable en ],0] con 5) g x) = f x) = x x ],0] Ha llegado el momento de eliminar las restricciones. Para x ],[ con x 0, el carácter local del concepto de derivada junto con la derivabilidad de f si x > 0) o la de g si x < 0) nos dicen que la función arco coseno es derivable en x y su derivada tiene el valor esperado. Para x = 0 simplemente tenemos arccos 0+) = f 0) = = g 0) = arccos 0 ) luego también tenemos la derivabilidad en 0 con el valor esperado de la derivada. Así pues, hemos probado que la función arco coseno es derivable en ],[ verificándose ). Finalmente, puesto que la función arco coseno es continua en [,], derivable en ],[ y su función derivada diverge negativamente tanto en como en, un corolario de la primera regla de l Hôpital visto en el tema anterior nos dice que la función arco coseno no es derivable en dichos puntos.
4 8. Derivadas de las funciones trigonométricas Derivadas del seno y el coseno Estudiada la derivabilidad de la función arco coseno, para lo que ha sido esencial el Teorema del Valor Medio, la derivación de las funciones trigonométricas y sus inversas se deduce ya casi mecánicamente de las reglas de derivación. Sólo en un punto concreto necesitaremos el mismo corolario de la primera regla de l Hôpital que acabamos de usar. Las funciones seno y coseno son derivables en R con sen x) = cos x, y cos x) = sen x x R 6) Para x ]0,π[ tomamos y = arccos x con lo que tenemos y ],[ con cos y = x. Puesto que el arco coseno es derivable en y con arccos y) 0, y su inversa, que es la restricción de la función coseno al intervalo [0,π], es continua en x, la regla de derivación de la función inversa nos dice que dicha restricción es derivable en x y su derivada se calculará enseguida. El carácter local del concepto de derivada nos dice que la función coseno es derivable en el punto x con cos x) = arccos y) = y = cos x = senx x ]0,π[ Nótese que en los puntos 0 y π la regla de derivación de la función inversa no da información. Usamos ahora que senx = cos x) / para todo x ]0,π[, con lo que la reglas básicas de derivación, y otra vez el carácter local de la derivada, nos dicen que la función seno es derivable en ]0, π[ con sen x) = cos x) / cos x) sen x) = cos x x ]0,π[ Sea k Z y consideremos el intervalo J =]kπ,k +)π[. Para x J tenemos x kπ ]0,π[ y sabemos que cos x = ) k cosx kπ), sen x = ) k senx kπ) Lo ya demostrado, la regla de la cadena y el carácter local de la derivada nos dicen que las funciones seno y coseno son derivables en J con cos x = ) k cos x kπ) = ) k senx kπ) = sen x sen x = ) k sen x kπ) = ) k cosx kπ) = cos x Si x / {mπ : m Z} podemos tomar en el razonamiento anterior k = Ex/π) con lo que x J y por tanto seno y coseno son derivables en el punto x con las derivadas deseadas. Finalmente, si x = mπ con m Z, usamos el intervalo I =]m )π,m + )π[. Sabemos que las funciones seno y coseno son continuas en I, derivables en I \ {x} y sus funciones derivadas tienen límite en el punto x. El corolario ya comentado de la primera regla de l Hôpital nos dice que las funciones seno y coseno son también derivables en x con cos x) = lím y x cos y) = sen x, sen x) = lím y x sen y) = cos x
5 8. Derivadas de las funciones trigonométricas 99 Resaltemos dos límites de funciones que merece la pena recordar. El primero no es más que la derivabilidad en 0 de la función seno, el segundo se deduce de la primera regla de l Hôpital: sen x lím x 0 x =, lím x 0 cos x x = lím x 0 sen x x El uso del Teorema del Valor Medio para derivar el arco coseno, y el de la regla de l Hôpital para el seno y el coseno, explican que hayamos esperado hasta ahora para calcular esas derivadas. Veamos ahora una útil caracterización de las funciones seno y coseno: Sean f, g : R R funciones derivables en R verificando que: f x) = gx) x R, f 0) = 0 g x) = f x) x R, g0) = = Se tiene entonces que f x) = sen x y gx) = cos x para todo x R. Considerando la función h : R R definida por: hx) = f x) sen x ) + gx) cos x ) x R basta evidentemente probar que h es idénticamente nula. Usando la hipótesis, junto con las derivadas del seno y el coseno, se comprueba sin ninguna dificultad que h es derivable en R con h x) = 0 para todo x R. Por tanto h es constante, pero es claro que h0) = 0, luego hx) = 0 para todo x R, como se quería Fórmulas de adición Podemos ya probar muy fácilmente lo siguiente: Para cualesquiera x, y R se tiene: senx + y) = sen x cos y + cos x sen y cosx + y) = cos x cos y sen x sen y Para comprobarlo usamos una idea recién aprendida. Fijado y R, consideramos la función h : R R definida por: hx) = senx + y) sen x cosy cos x sen y ) + cosx + y) cos x cos y + sen x sen y ) Observamos sin dificultad que h es derivable en R con h x) = 0 para todo x R, luego h es constante en R, pero es evidente que h0) = 0, luego h es idénticamente nula, de donde se deducen claramente las dos igualdades buscadas.
6 8. Derivadas de las funciones trigonométricas 00 De las fórmulas de adición se deduce que las funciones seno y coseno pueden obtenerse una de otra mediante una traslación, así como otras identidades trigonométricas útiles. Enunciamos algunas de ellas, cuya comprobación es inmediata: Para cualesquiera x, y R, se tiene: cos x = sen sen x = sen x cos x, x + π ), sen x = cos x π ) sen x + sen y = sen x + y cos x = cos x sen x cos x y 8.4. Una derivada que no es continua, cos x + cos y = cos x + y cos x y Podemos ya presentar un ejemplo de una función derivable en un intervalo, cuya derivada no es continua en dicho intervalo. Construir tal ejemplo sin usar las funciones trigonométricas hubiera sido más laborioso. La función f : R R definida por f x) = x sen/x) x R, f 0) = 0 es derivable en R, pero su derivada no es continua en 0. Tenemos claramente que f es derivable en R con f x) = x sen/x) cos/x) x R f x) pero también es claro que f es derivable en 0, ya que lím = lím x sen/x) = 0. Que { )} x 0 x x 0 f no es continua en 0 se deduce de f = { ) n+}. nπ La función f del ejemplo anterior nos sirve para mostrar, como ya habíamos avisado, que las implicaciones de la primera regla de l Hôpital lo hacemos sólo para una de ellas) no son reversibles. En efecto, tomando gx) = x para todo x R, las funciones f y g cumplen las hipótesis de dicha regla: son incluso funciones derivables en R con g x) ) = 0 para todo x R y f 0) = g0) = 0. Además, hemos visto que lím f x)/gx) = f 0) = 0, pero x 0 también hemos visto que el cociente f /g = f no tiene límite en 0.
7 8. Derivadas de las funciones trigonométricas Otras funciones trigonométricas Obtenidas las derivadas de las funciones seno y coseno, probar que las otras cuatro funciones trigonométricas son derivables en todo su conjunto de definición y calcular sus derivadas es pura rutina. Enunciamos los resultados, que se deducen de las reglas básicas de derivación. Consideremos los conjuntos A = {x R : cos x 0} = R \ {π/) + kπ : k Z} B = {x R : sen x 0} = R \ {kπ : k Z} La función tangente es derivable en A con tg x) = sec x = + tg x x A. La función secante es derivable en A con sec x) = sec x tg x x A. La función cotangente es derivable en B con cotg x) = cosec x x B. La función cosecante es derivable en B con cosec x) = cosecx cotgx x B. Con respecto a las funciones trigonométricas inversas, estudiado ya el arco coseno, veamos la derivabilidad del arco seno, inversa de la restricción del seno al intervalo [ π/, π/]. Puesto que sen x) = cos x 0 para x ] π/,π/[, pero sen π/) = sen π/) = 0, obtenemos lo siguiente. La función arco seno es derivable en ],[ con arcsen x) = x x ],[ y no es derivable en los puntos y. En efecto, para x ],[, tomamos y = arcsen x ] π/,π/[ y obtenemos arcsen x) = sen y) = cos y = x Observamos que la suma de las funciones arco coseno y arco seno es una función continua en [,] y derivable en ],[ con derivada idénticamente nula, luego es constante. De hecho tenemos arccos x + arcsenx = π x [,] Concluimos con el arco tangente, función inversa de la restricción de la tangente al intervalo ] π/,π/[. Tenemos ahora tg x) 0 para todo x ] π/,π/[, de donde deducimos lo siguiente. La función arco tangente es derivable en R con: arctg x) = + x x R En efecto, para x R, tomamos y = arctgx y obtenemos que arctg x) = tg y) = + tg y = + x
8 8. Derivadas de las funciones trigonométricas Ejercicios. Probar que cosπ/4) = senπ/4) = / cosπ/3) = senπ/6) = / cosπ/6) = senπ/3) = 3/. Sean a,b R con a +b = y a. Sea x ] π,π[ tal que cos x = a y sen x = b. Probar que x = arctg b + a 3. Probar que arctgx + arctg x = π x x x R 4. Dado a R, determinar la imagen de la función f : R \ {/a} R definida por arctga + arctgx arctg a + x ax x R \ {/a} 5. Probar que para todo x ]0, π/[ se tiene cos x > x y x π < sen x < x < tg x 6. Calcular las imágenes de las funciones f, g : R R dadas por f x) = arctgx x + x x R, gx) = arctgx x x R, g0) = 7. Probar que sennx) n sen x x R, n N 8. Dado α R, se considera la función f : R + 0 R definida por f x) = x α sen x x R +, f 0) = 0 Estudiar la continuidad y derivabilidad de f, así como la continuidad de su derivada. 9. Estudiar el comportamiento en + de las funciones f,g : R + R dadas por f x) = x sen x log x, gx) = sen x + sen x x R +
9 8. Derivadas de las funciones trigonométricas Estudiar el comportamiento en el origen de la función h : A R en cada uno de los siguientes casos: a) A = R +, hx) = cos x x x A b) A =]0,π/[, hx) = sen x + cos x) /x x A ) /x c) A =]0,π/[, hx) = cos x + x x A d) A =]0,π/[, hx) = + tg x ) /x x A e) A = R +, hx) = x sen x x A f) A =]0,π/[, hx) = x arctgx sen 3 x x A. Estudiar la convergencia de las siguientes sucesiones: { } n e e sen/n) a) n n sen/n) { ) + tg/n) n } b) tg/n) { n 3 sen/n) log } + n) c) n + ) cos ) πn+ 4n+. Dado α R, estudiar la convergencia de las siguientes series: a) b) c) n n n sen ) α n tg n sen ) α n )) log n α log n sen n
Reglas de derivación. 4.1. Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, pasamos a desarrollar las reglas básicas para el cálculo de derivadas o, lo que viene a ser lo mismo, a analizar la estabilidad de las funciones
Tema 4 Reglas de derivación Aclarado el concepto de derivada, pasamos a desarrollar las reglas básicas para el cálculo de derivadas o, lo que viene a ser lo mismo, a analizar la estabilidad de las funciones
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
12.1. Definición de las derivadas sucesivas
 Tema 12 Derivadas sucesivas El proceso de derivación de funciones reales de variable real puede obviamente iterarse, obteniendo la segunda y sucesivas derivadas de una función. Como es lógico, para n N,
Tema 12 Derivadas sucesivas El proceso de derivación de funciones reales de variable real puede obviamente iterarse, obteniendo la segunda y sucesivas derivadas de una función. Como es lógico, para n N,
Funciones trigonométricas
 Tema 0 Funciones trigonométricas Para estudiar esta nueva familia de funciones utilizamos una estrategia similar a la seguida en el tema anterior. Igual que ocurrió con el logaritmo, una integral indefinida
Tema 0 Funciones trigonométricas Para estudiar esta nueva familia de funciones utilizamos una estrategia similar a la seguida en el tema anterior. Igual que ocurrió con el logaritmo, una integral indefinida
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.4: La derivada y sus propiedades básicas. La Regla de la cadena. El concepto de derivada aparece en muchas situaciones en la ciencias: en matemáticas
Grado en Química Bloque Funciones de una variable Sección.4: La derivada y sus propiedades básicas. La Regla de la cadena. El concepto de derivada aparece en muchas situaciones en la ciencias: en matemáticas
Reglas de l Hôpital Teorema del Valor Medio Generalizado. Tema 7
 Tema 7 Reglas de l Hôpital Estudiamos en este tema el método práctico más efectivo para calcular ites de funciones en los que se presenta una indeterminación del tipo [0/0], o [ / ]. Este método se atribuye
Tema 7 Reglas de l Hôpital Estudiamos en este tema el método práctico más efectivo para calcular ites de funciones en los que se presenta una indeterminación del tipo [0/0], o [ / ]. Este método se atribuye
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
Reglas de derivación Sumas, productos y cocientes. Tema 4
 Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Tema 4 Reglas de derivación Aclarado el concepto de derivada, su significado analítico y sus interpretaciones geométrica y física, pasamos a desarrollar las reglas básicas para el cálculo de derivadas
Práctica 2. Diferenciabilidad de campos escalares Ejercicios resueltos
 Práctica. Diferenciabilidad de campos escalares Ejercicios resueltos 1. Estudiar la continuidad, la diferenciabilidad y la continuidad de las derivadas parciales, de los campos escalares f, g, h : R R
Práctica. Diferenciabilidad de campos escalares Ejercicios resueltos 1. Estudiar la continuidad, la diferenciabilidad y la continuidad de las derivadas parciales, de los campos escalares f, g, h : R R
Funciones convexas Definición de función convexa. Tema 10
 Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEMA 4: DERIVADAS. En símbolos, la pendiente de la curva en P = lim Q P (pendiente de P Q).
 TEMA 4: DERIVADAS 1. La derivada de una función. Reglas de derivación 1.1. La pendiente de una curva. La pendiente de una curva en un punto P es una medida de la inclinación de la curva en ese punto. Si
TEMA 4: DERIVADAS 1. La derivada de una función. Reglas de derivación 1.1. La pendiente de una curva. La pendiente de una curva en un punto P es una medida de la inclinación de la curva en ese punto. Si
Espacio de Funciones Medibles
 Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Las Funciones Trigonométricas Inversas
 Capítulo 4 Las Funciones Trigonométricas Inversas 4.1. Relaciones y sus inversas Recordemos que una relación es un subconjunto de un producto cartesiano, es decir R A B o bien R : A B, en tanto que su
Capítulo 4 Las Funciones Trigonométricas Inversas 4.1. Relaciones y sus inversas Recordemos que una relación es un subconjunto de un producto cartesiano, es decir R A B o bien R : A B, en tanto que su
Cálculo de Derivadas
 Cálculo de Derivadas Sean a, b y k constantes (números reales) y consideremos a: u y v como funciones. Derivada de una constante Derivada de x Derivada de la función lineal Derivada de una potencia Derivada
Cálculo de Derivadas Sean a, b y k constantes (números reales) y consideremos a: u y v como funciones. Derivada de una constante Derivada de x Derivada de la función lineal Derivada de una potencia Derivada
Límites en el infinito, funciones divergentes
 Tema 2 Límites en el infinito, funciones divergentes Nuestro próximo objetivo es usar las sucesiones divergentes para ampliar la noción de límite funcional en dos sentidos. Por una parte, analizaremos
Tema 2 Límites en el infinito, funciones divergentes Nuestro próximo objetivo es usar las sucesiones divergentes para ampliar la noción de límite funcional en dos sentidos. Por una parte, analizaremos
A.1 Razones trigonométricas de un triángulo rectángulo: Las razones trigonométricas de un triángulo rectángulo son las siguientes funciones:
 MATEMÁTICAS EJERCICIOS RESUELTOS DE TRIGONOMETRÍA Juan Jesús Pascual TRIGONOMETRÍA A. Introducción teórica A. Razones trigonométricas de un triángulo rectángulo. A.. Valores del seno, coseno tangente para
MATEMÁTICAS EJERCICIOS RESUELTOS DE TRIGONOMETRÍA Juan Jesús Pascual TRIGONOMETRÍA A. Introducción teórica A. Razones trigonométricas de un triángulo rectángulo. A.. Valores del seno, coseno tangente para
Reglas de l Hôpital Teorema del Valor Medio Generalizado. Tema 5
 Tema 5 Reglas de l Hôpital Estudiamos en este tema un método práctico para resolver indeterminaciones del tipo [0/0] o [ / ], que lleva el nombre de un aristócrata y matemático francés, el marqués de l
Tema 5 Reglas de l Hôpital Estudiamos en este tema un método práctico para resolver indeterminaciones del tipo [0/0] o [ / ], que lleva el nombre de un aristócrata y matemático francés, el marqués de l
Funciones convexas Definición de función convexa. Tema 7
 Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
FUNCIONES ELEMENTALES.
 Departamento de Análisis Matemático FUNCIONES ELEMENTALES.. Polinomios p : R R : p(x) = a n x n + +a x+a 0, x R, donde a 0,a,...,a n son constantes reales. Propiedades de los polinomios: a) p es continuo
Departamento de Análisis Matemático FUNCIONES ELEMENTALES.. Polinomios p : R R : p(x) = a n x n + +a x+a 0, x R, donde a 0,a,...,a n son constantes reales. Propiedades de los polinomios: a) p es continuo
Figura 1. Círculo unidad. Definición. 1. Llamamos número π (pi) al valor de la integral
 ANÁLISIS MATEMÁTICO BÁSICO. LAS FUNCIONES TRIGONOMÉTRICAS. La función f(x) = 1 x 2 es continua en el intervalo [ 1, 1]. Su gráfica como vimos es la semicircunferencia de radio uno centro el origen de coordenadas.
ANÁLISIS MATEMÁTICO BÁSICO. LAS FUNCIONES TRIGONOMÉTRICAS. La función f(x) = 1 x 2 es continua en el intervalo [ 1, 1]. Su gráfica como vimos es la semicircunferencia de radio uno centro el origen de coordenadas.
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
Funciones. Definiciones. Dominio, rango e imagen
 Funciones La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números, podemos
Funciones La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números, podemos
Práctica 1. Continuidad Ejercicios resueltos
 Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
Práctica 1. Continuidad Ejercicios resueltos 1. Estudiar la continuidad de los campos escalares definidos por f(x, y) = x y x 2 + y 2 g(x, y) = x2 y x 2 + y 4 h(x, y) = x y2 x 2 + y 4 para todo (x, y)
En este capítulo obtendremos los resultados básicos del cálculo diferencial para funciones reales definidas sobre R o sobre intervalos.
 Capítulo 6 Derivadas 61 Introducción En este capítulo obtendremos los resultados básicos del cálculo diferencial para funciones reales definidas sobre R o sobre intervalos Definición 61 Sea I R, I, f :
Capítulo 6 Derivadas 61 Introducción En este capítulo obtendremos los resultados básicos del cálculo diferencial para funciones reales definidas sobre R o sobre intervalos Definición 61 Sea I R, I, f :
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Herramientas digitales de auto-aprendizaje para Matemáticas
 Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice la cadena Tabla de Dada una función f : D R R,
Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice la cadena Tabla de Dada una función f : D R R,
Curso Propedéutico de Cálculo Sesión 3: Derivadas
 Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Funciones convexas Definición de función convexa. Tema 14
 Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Funciones elementales. A.1 Funciones potenciales. A.2 Función exponencial
 Funciones potenciales A A. Funciones potenciales La función potencial f : R + R definida como f (x) = x b tiene sentido para cualquier exponente b real. En el caso particular de potencias naturales, se
Funciones potenciales A A. Funciones potenciales La función potencial f : R + R definida como f (x) = x b tiene sentido para cualquier exponente b real. En el caso particular de potencias naturales, se
x y = x x y = x
 FUNCIONES ELEMENTALES: Indice: Algebraicas Polinómicas Racionales Irracionales Trascendentes Exponencial Logarítmica Trigonométrica Trigonométricas recíprocas Algebraicas Funciones polinómicas: X f(x)=
FUNCIONES ELEMENTALES: Indice: Algebraicas Polinómicas Racionales Irracionales Trascendentes Exponencial Logarítmica Trigonométrica Trigonométricas recíprocas Algebraicas Funciones polinómicas: X f(x)=
1. Teorema Fundamental del Cálculo
 1. Teorema Fundamental del Cálculo Vamos a considerar dos clases de funciones, definidas como es de otras funciones Funciones es. F (t) = t a f(x)dx donde f : R R, y F (t) = f(x, t)dx A donde f : R n R
1. Teorema Fundamental del Cálculo Vamos a considerar dos clases de funciones, definidas como es de otras funciones Funciones es. F (t) = t a f(x)dx donde f : R R, y F (t) = f(x, t)dx A donde f : R n R
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones.
 Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Teorema del Valor Medio
 Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Sucesiones y funciones divergentes
 Tema 2 Sucesiones y funciones divergentes Nuestro próximo objetivo es ampliar el estudio de los dos tipos de convergencia, o de las dos nociones de límite, que hasta ahora conocemos: el límite de una sucesión
Tema 2 Sucesiones y funciones divergentes Nuestro próximo objetivo es ampliar el estudio de los dos tipos de convergencia, o de las dos nociones de límite, que hasta ahora conocemos: el límite de una sucesión
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD
 DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
2.1 CONTINUIDAD EN UN PUNTO 2.2 CONTINUIDAD DE FUNCIONES CONOCIDAS 2.3 CONTINUIDAD EN OPERACIONES CON
 Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Teoría Tema 3 Teoremas de derivabilidad
 página 1/10 Teoría Tema 3 Teoremas de derivabilidad Índice de contenido Teorema de Rolle...2 Teorema del valor medio de Lagrange (o de los incrementos finitos)...4 Teorema de Cauchy...6 Regla de L'Hôpital...8
página 1/10 Teoría Tema 3 Teoremas de derivabilidad Índice de contenido Teorema de Rolle...2 Teorema del valor medio de Lagrange (o de los incrementos finitos)...4 Teorema de Cauchy...6 Regla de L'Hôpital...8
DERIVADA DE UNA FUNCIÓN
 DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
Por ser un cociente entre dos longitudes, el radián no tiene dimensión. De la definición obtenemos la relación entre radianes y grados:
 E.T.S.I. Industriales y Telecomunicación Curso 011-01 Medida de ángulos Unidad Como unidad del tamaño de un ángulo se utiliza el radián, más natural y con más sentido geométrico que el grado. Recordemos
E.T.S.I. Industriales y Telecomunicación Curso 011-01 Medida de ángulos Unidad Como unidad del tamaño de un ángulo se utiliza el radián, más natural y con más sentido geométrico que el grado. Recordemos
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
Anexo C. Introducción a las series de potencias. Series de potencias
 Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Anexo C Introducción a las series de potencias Este apéndice tiene como objetivo repasar los conceptos relativos a las series de potencias y al desarrollo de una función ne serie de potencias en torno
Ejercicios resueltos de trigonometría
 Ejercicios resueltos de trigonometría 1) Convierte las siguientes medidas de grados en radianes: a) 45º b) 60º c) 180º d) 270º e) 30º f) 225º g) 150º h) 135º i) -90º j) 720º 2) Expresa las siguientes razones
Ejercicios resueltos de trigonometría 1) Convierte las siguientes medidas de grados en radianes: a) 45º b) 60º c) 180º d) 270º e) 30º f) 225º g) 150º h) 135º i) -90º j) 720º 2) Expresa las siguientes razones
si este límite es finito, y en este caso decimos que f es integrable (impropia)
 Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
II Concurso de Resolución de Problemas Curso 2011-2012
 II Concurso de Resolución de Problemas Curso - Solución del Problema de ecuaciones funcionales. Este ejercicio versa sobre ecuaciones funcionales. Es éste un tema poco tratado en la carrera de Matemáticas
II Concurso de Resolución de Problemas Curso - Solución del Problema de ecuaciones funcionales. Este ejercicio versa sobre ecuaciones funcionales. Es éste un tema poco tratado en la carrera de Matemáticas
Funciones elementales
 Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
DERIVADA DE UNA FUNCIÓN
 www.fisicanet.com www.fisicaweb.com DERIVADA DE UNA FUNCIÓN fisicanet@interlap.com.ar Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función.
www.fisicanet.com www.fisicaweb.com DERIVADA DE UNA FUNCIÓN fisicanet@interlap.com.ar Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función.
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Teorema del Valor Medio
 Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 5 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tipos de funciones. Clasificación de funciones. Funciones algebraicas
 Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
CONTINUIDAD Y DERIVABILIDAD. DERIVADAS
 CONTINUIDAD Y DERIVABILIDAD. DERIVADAS. Dada la función f (), (, ), definir f () y f () de forma que f sea continua sen(π ) en todo el intervalo cerrado [, ]. : f () f () π 5 si. Estudiar la continuidad
CONTINUIDAD Y DERIVABILIDAD. DERIVADAS. Dada la función f (), (, ), definir f () y f () de forma que f sea continua sen(π ) en todo el intervalo cerrado [, ]. : f () f () π 5 si. Estudiar la continuidad
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE
 DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIV. DE UNA FUNC. EN UN PUNTO
 DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
Cuadro de derivadas. Cuadro de Derivadas. y = k La derivada de una cte es igual a cero. Es decir: y = 0
 Cuadro de derivadas y = k La derivada de una cte es igual a cero. Es decir: 0 y = x y = + g(x) y = g(x) y = k y = g(x) La derivada de la función identidad es igual a. Es decir: La derivada de una suma
Cuadro de derivadas y = k La derivada de una cte es igual a cero. Es decir: 0 y = x y = + g(x) y = g(x) y = k y = g(x) La derivada de la función identidad es igual a. Es decir: La derivada de una suma
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
RAZONES TRIGONOMÉTRICAS
 RAZONES TRIGONOMÉTRICAS.- PRIMERAS DEFINICIONES Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Ángulo central es el ángulo
RAZONES TRIGONOMÉTRICAS.- PRIMERAS DEFINICIONES Se denomina ángulo en el plano a la porción de plano comprendida entre dos semirrectas con un origen común denominado vértice. Ángulo central es el ángulo
Funciones. A.1 Definiciones. Dominio, rango e imagen A.1.1
 Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
MATEMATICAS GRADO DECIMO
 MATEMATICAS GRADO DECIMO TERCER PERIODO TEMAS Funciones Trigonométricas. Funciones trigonométricas. Son relaciones angulares; guardan relación con el estudio de la geometría de los triángulos y son de
MATEMATICAS GRADO DECIMO TERCER PERIODO TEMAS Funciones Trigonométricas. Funciones trigonométricas. Son relaciones angulares; guardan relación con el estudio de la geometría de los triángulos y son de
Se define la derivada de una función f(x) en un punto "a" como el resultado, del siguiente límite:
 TEMA: DERIVADAS. Derivada de una función en un punto Se define la derivada de una función f() en un punto "a" como el resultado, del siguiente límite: f ( a + ) f ( a) f '( a) lim Si el límite eiste es
TEMA: DERIVADAS. Derivada de una función en un punto Se define la derivada de una función f() en un punto "a" como el resultado, del siguiente límite: f ( a + ) f ( a) f '( a) lim Si el límite eiste es
Aplicaciones de las Derivadas
 Tema 4 Aplicaciones de las Derivadas 4.1 Introducción Repasaremos en este Tema algunas de las aplicaciones fundamentales de las derivadas. Muchas de ellas son ya conocidas por tratarse de conceptos explicados
Tema 4 Aplicaciones de las Derivadas 4.1 Introducción Repasaremos en este Tema algunas de las aplicaciones fundamentales de las derivadas. Muchas de ellas son ya conocidas por tratarse de conceptos explicados
Decimos que f es derivable en dicho punto si existe y es finito: Lím. En tal
 UNIDAD : DERIVADAS Y APLICACIONES.- DERIVADA DE UNA FUNCIÓN EN UN PUNTO. Definición : Sea f una función definida en un a, b Dom f. Se llama tasa de intervalo [ ] variación media de f en dicho intervalo
UNIDAD : DERIVADAS Y APLICACIONES.- DERIVADA DE UNA FUNCIÓN EN UN PUNTO. Definición : Sea f una función definida en un a, b Dom f. Se llama tasa de intervalo [ ] variación media de f en dicho intervalo
Apuntes Trigonometría. 4º ESO.
 Apuntes Trigonometría. 4º ESO. Conceptos previos: Notación: En un triángulo, los vértices se denotan con letras mayúsculas (A, B y C). Los lados se denotan con la letra minúscula del vértice opuesto al
Apuntes Trigonometría. 4º ESO. Conceptos previos: Notación: En un triángulo, los vértices se denotan con letras mayúsculas (A, B y C). Los lados se denotan con la letra minúscula del vértice opuesto al
Un ángulo es una porción de plano limitada por dos semirrectas, los lados, que parten de un mismo punto llamado vértice.
 6. Trigonometría 37 6 Trigonometría Un ángulo es una porción de plano limitada por dos semirrectas, los lados, que parten de un mismo punto llamado vértice. A efectos representativos y de medición, el
6. Trigonometría 37 6 Trigonometría Un ángulo es una porción de plano limitada por dos semirrectas, los lados, que parten de un mismo punto llamado vértice. A efectos representativos y de medición, el
TEMA 2: DERIVADA DE UNA FUNCIÓN
 TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
TEMA : DERIVADA DE UNA FUNCIÓN Tasa de variación Dada una función y = f(x), se define la tasa de variación en el intervalo [a, a +h] como: f(a + h) f(a) f(a+h) f(a) y se define la tasa de variación media
Dependencia e independencia lineal
 CAPíTULO 3 Dependencia e independencia lineal En este capítulo estudiaremos tres conceptos de gran importancia para el desarrollo del álgebra lineal: el concepto de conjunto generador, el concepto de conjunto
CAPíTULO 3 Dependencia e independencia lineal En este capítulo estudiaremos tres conceptos de gran importancia para el desarrollo del álgebra lineal: el concepto de conjunto generador, el concepto de conjunto
94' = 1º 34' 66.14'' = 1' 6.14'' +
 UNIDAD : Trigonometría I. INTRODUCCIÓN. SISTEMAS DE MEDIDAS DE ÁNGULOS Trigonometría proviene del griego: trigonos (triángulo) y metrón (medida). También a veces se usa el término Goniometría, que proviene
UNIDAD : Trigonometría I. INTRODUCCIÓN. SISTEMAS DE MEDIDAS DE ÁNGULOS Trigonometría proviene del griego: trigonos (triángulo) y metrón (medida). También a veces se usa el término Goniometría, que proviene
Por extensión, también se puede hablar de la preimagen de un conjunto. Si B 0 B, la preimagen de B 0 es
 Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
Definiciones A La idea de función aparece por todas partes: cada persona tiene una edad o un número de hijos o una cantidad de dinero en el bolsillo. No necesariamente tenemos que referirnos a números,
2. Ortogonalidad. En todo el capítulo trabajaremos sobre un espacio vectorial euclídeo U.
 2 Ortogonalidad En todo el capítulo trabajaremos sobre un espacio vectorial euclídeo U 1 Vectores ortogonales Definición 11 Dos vectores x, ȳ U se dicen ortogonales si: x ȳ = 0 Veamos algunas propiedades
2 Ortogonalidad En todo el capítulo trabajaremos sobre un espacio vectorial euclídeo U 1 Vectores ortogonales Definición 11 Dos vectores x, ȳ U se dicen ortogonales si: x ȳ = 0 Veamos algunas propiedades
Funciones trigonométricas
 Tema 4 Funciones trigonométricas Va a aparecer aquí una nueva familia de funciones reales de variable real: las funciones trigonométricas. Existen varias formas de introducir estas funciones, ninguna de
Tema 4 Funciones trigonométricas Va a aparecer aquí una nueva familia de funciones reales de variable real: las funciones trigonométricas. Existen varias formas de introducir estas funciones, ninguna de
Tema 2. Grupos. 3. El conjunto de matrices de orden 2 con coeficientes enteros (o reales) con la suma es un grupo conmutativo.
 Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Métodos Numéricos: Resumen y ejemplos Tema 5: Resolución aproximada de ecuaciones
 Métodos Numéricos: Resumen y ejemplos Tema 5: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril 009,
Métodos Numéricos: Resumen y ejemplos Tema 5: Resolución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Abril 009,
= x x x. v p Este cociente indica cómo desciende las ventas al aumentar el precio en una unidad.
 TASA DE VARIACIÓN MEDIA La tasa de variación media de una función nos da una idea de la rapidez con que crece o decrece en un intervalo. Sea y f() una función que relaciona la variable dependiente (y)
TASA DE VARIACIÓN MEDIA La tasa de variación media de una función nos da una idea de la rapidez con que crece o decrece en un intervalo. Sea y f() una función que relaciona la variable dependiente (y)
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Sucesiones y series de números reales
 Capítulo 2 Sucesiones y series de números reales 2.. Sucesiones de números reales 2... Introducción Definición 2... Llamamos sucesión de números reales a una función f : N R, n f(n) = x n. Habitualmente
Capítulo 2 Sucesiones y series de números reales 2.. Sucesiones de números reales 2... Introducción Definición 2... Llamamos sucesión de números reales a una función f : N R, n f(n) = x n. Habitualmente
UNIDAD ÍNDICE DE CONTENIDOS
 UNIDAD 9 Cálculo de derivadas ÍNDICE DE CONTENIDOS 1. Concepto de derivada.................................... 195 1.1. Tasa de Variación Media................................ 195 1.2. Derivada en un punto.
UNIDAD 9 Cálculo de derivadas ÍNDICE DE CONTENIDOS 1. Concepto de derivada.................................... 195 1.1. Tasa de Variación Media................................ 195 1.2. Derivada en un punto.
Funciones Exponenciales y Logarítmicas
 Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Derivadas. Contenido Introducción. ( α) Definición de Derivada. (α) Pendiente de la recta tangente. (α) Funciones diferenciables.
 Derivadas. Contenido 1. Introducción. (α) 2. Definición de Derivada. (α) 3. Pendiente de la recta tangente. (α) 4. Funciones diferenciables. (α) 5. Función derivada. (α) 6. Propiedades de la derivada.
Derivadas. Contenido 1. Introducción. (α) 2. Definición de Derivada. (α) 3. Pendiente de la recta tangente. (α) 4. Funciones diferenciables. (α) 5. Función derivada. (α) 6. Propiedades de la derivada.
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
1º Bachillerato Matemáticas I Tema 3: Trigonometría Ana Pascua García
 . MEDIDAS DE ÁNGULOS. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO Para medir los ángulos solemos utilizar las siguientes unidades: el grado sexagesimal y el radián. Grado sexagesimal: Se denomina grado
. MEDIDAS DE ÁNGULOS. RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO Para medir los ángulos solemos utilizar las siguientes unidades: el grado sexagesimal y el radián. Grado sexagesimal: Se denomina grado
Funciones Hiperbólicas. Who? Verónica Briceño V. When? noviembre 2013
 Funciones Hiperbólicas Funciones Hiperbólicas Who? Verónica Briceño V. When? noviembre 2013 En esta Presentación... En esta Presentación veremos: Definición de Funciones Hiperbólicas En esta Presentación...
Funciones Hiperbólicas Funciones Hiperbólicas Who? Verónica Briceño V. When? noviembre 2013 En esta Presentación... En esta Presentación veremos: Definición de Funciones Hiperbólicas En esta Presentación...
Gráficamente: una función es continua en un punto si en dicho punto su gráfica no se rompe. Función continua en x = 0 Función no continua en x = 0
 Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
Cociente incremental. Mide la variación media de f(x) en (x 0, x 0 + x)
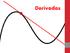 Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Continuidad y derivación de funciones reales de variable real
 Tema 2 Continuidad y derivación de funciones reales de variable real 2.. Funciones. Definiciones básicas. Operaciones con funciones 2... Definiciones Una función real de (una) variable real es una aplicación
Tema 2 Continuidad y derivación de funciones reales de variable real 2.. Funciones. Definiciones básicas. Operaciones con funciones 2... Definiciones Una función real de (una) variable real es una aplicación
PLAN DE ESTUDIOS DE MS
 PLAN DE ESTUDIOS DE MS Temario para desarrollar a lo largo de las clases 11 y 12. CLASE 11: I. ELEMENTOS DE ÁLGEBRA LINEAL. a) Revisión de conceptos Estructura de espacio vectorial. Propiedades de los
PLAN DE ESTUDIOS DE MS Temario para desarrollar a lo largo de las clases 11 y 12. CLASE 11: I. ELEMENTOS DE ÁLGEBRA LINEAL. a) Revisión de conceptos Estructura de espacio vectorial. Propiedades de los
CÁLCULO DIFERENCIAL 9. UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS
 CÁLCULO DIFERENCIAL 9 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS SOLUCIONES DE LA COLECCIÓN DE PROBLEMAS - CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD
CÁLCULO DIFERENCIAL 9 UNIVERSIDAD CARLOS III DE MADRID Departamento de Matemáticas MATEMÁTICAS SOLUCIONES DE LA COLECCIÓN DE PROBLEMAS - CAPÍTULO 3 CURSO PREPARATORIO DE LA PRUEBA DE ACCESO A LA UNIVERSIDAD
Funciones de Una Variable Real I. Derivadas
 Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
Límite Funcional Puntos de acumulación. Tema 1
 Tema 1 Límite Funcional Estudiamos en este tema el concepto de límite para funciones reales de variable real, que guarda una estrecha relación con la continuidad. 1.1. Puntos de acumulación Pretendemos
Tema 1 Límite Funcional Estudiamos en este tema el concepto de límite para funciones reales de variable real, que guarda una estrecha relación con la continuidad. 1.1. Puntos de acumulación Pretendemos
Derivadas Parciales y Derivadas Direccionales
 Tema 3 Derivadas Parciales y Derivadas Direccionales En este tema y en el siguiente presentaremos los conceptos fundamentales del Cálculo Diferencial para funciones de varias variables. Comenzaremos con
Tema 3 Derivadas Parciales y Derivadas Direccionales En este tema y en el siguiente presentaremos los conceptos fundamentales del Cálculo Diferencial para funciones de varias variables. Comenzaremos con
rad, y rad = 360 Ejercicio 1 Realizar las conversiones de grados a radianes y de radianes a grados de los siguientes ángulos:
 Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
Trigonometría 1.- Ángulos En la medida de ángulos, y por tanto en trigonometría, se emplean dos unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 3 Especifico) Solucíon Germán-Jesús Rubio Luna. Opción A
 Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Opción A Ejercicio opción A, modelo 3 Septiembre 03 específico x Sea f la función definida por f(x) = para x > 0, x (donde ln denota el logaritmo neperiano) ln(x) [ 5 puntos] Estudia y determina las asíntotas
Cardinalidad. Teorema 0.3 Todo conjunto infinito contiene un subconjunto infinito numerable.
 Cardinalidad Dados dos conjuntos A y B, decimos que A es equivalente a B, o que A y B tienen la misma potencia, y lo notamos A B, si existe una biyección de A en B Es fácil probar que es una relación de
Cardinalidad Dados dos conjuntos A y B, decimos que A es equivalente a B, o que A y B tienen la misma potencia, y lo notamos A B, si existe una biyección de A en B Es fácil probar que es una relación de
- Ángulos positivos. Los que tienen el sentido de giro en contra de la agujas del reloj.
 Ángulos. TRIGONOMETRÍA - Ángulo en el plano. Dos semirrectas con un origen común dividen al plano, en dos regiones, cada una de las cuales determina un ángulo ( α, β ). Al origen común se le llama vértice.
Ángulos. TRIGONOMETRÍA - Ángulo en el plano. Dos semirrectas con un origen común dividen al plano, en dos regiones, cada una de las cuales determina un ángulo ( α, β ). Al origen común se le llama vértice.
Continuidad Funciones reales de variable real. Tema 12
 Tema 12 Continuidad El Análisis Real es la parte del Análisis Matemático que se ocupa de las funciones de una o varias variables reales. Iniciamos aquí el estudio del caso más sencillo: funciones reales
Tema 12 Continuidad El Análisis Real es la parte del Análisis Matemático que se ocupa de las funciones de una o varias variables reales. Iniciamos aquí el estudio del caso más sencillo: funciones reales
