Lección 8: Protocolo de reparto de secretos
|
|
|
- María Rosario Miguélez San Martín
- hace 8 años
- Vistas:
Transcripción
1 Lección 8: Protocolo de reparto de secretos Dr. Luis Hernández Encinas Consejo Superior de Investigaciones Científicas Científico Titular
2 Esquemas de reparto de secretos (I) Un esquema de reparto de secretos es un protocolo que permite obtener una serie de datos o sombras a partir de un secreto, de forma que sea posible recuperar el secreto original a partir de sólo algunas de esas sombras. Estos esquemas fueron propuestos para salvaguardar las claves criptográficas de su posible deterioro, robo o pérdida. 2
3 Esquemas de reparto de secretos (II) Estos protocolos también se conocen como de compartición de secretos y, en general, como secret sharing. En particular, es posible proteger claves secretas, claves privadas, documentos, etc. Actualmente tienen aplicaciones en: El control de accesos, La apertura de cajas de seguridad, La inicialización de dispositivos militares, etc. 3
4 Esquemas umbrales k de n (I) El ejemplo básico de los esquemas para el reparto de secretos son los esquemas (k, n) umbrales, con k y n enteros y 1 k n. En estos protocolos, el usuario determina n sombras a partir del secreto que desea proteger: S 1,, S n, y las almacena o esconde de manera segura. Utilizando k sombras cualesquiera, o más, se podrá recuperar el secreto S. 4
5 Esquemas umbrales k de n (II) Dicho de otro modo, en un esquema umbral (k, n), no es posible obtener información alguna del secreto si sólo se poseen k 1 sombras o menos. Un esquema se dice ideal si cada una de las sombras tiene el mismo tamaño que el secreto original. 5
6 Realización de un protocolo de reparto de secretos Estos protocolos constan de dos fases: Fase 1: generación de sombras. Fase 2: recuperación del secreto. Una de las formas más sencillas de realizar los protocolos de reparto de secretos es mediante polinomios. 6
7 Fase 1: Generación de las sombras (I) 1. Se deciden los valores del esquema: el valor umbral, k, y el número de sombras, n. 2. Se considera un polinomio de grado k 1: p(x) = a k 1 x k 1 +a k 2 x k 2 + +a 1 x+a 0 = Σ k 1 j=0 a j x j, de modo que el secreto sea el coeficiente a 0 = S. 3. A continuación se eligen aleatoriamente los restantes coeficientes, a i, de p(x). 7
8 Fase 1: Generación de las sombras (II) 4. Una vez conocido el polinomio, se calcula su valor para n valores diferentes de x, por ejemplo, para x = 1,,n, de modo que se tienen n parejas de valores: (x i, y i ) = (i, p(x i )), i = 1,, n. 5. Cada uno de estos pares es una sombra. Ninguno de los valores de las sombras guarda relación con el valor del secreto S. 8
9 Fase 2: Recuperación del secreto (I) 1. Se eligen k sombras cualesquiera de las n de que se disponen, por ejemplo: (x j, y j ), j = 1,,k. 2. Se calculan los siguientes k polinomios auxiliares, cada uno de grado k 1: q j (x)= Π k i=1,i j (x x i )/(x j x i ), j = 1,,k. 9
10 Fase 2: Recuperación del secreto (II) 3. Se determina el polinomio buscado: p(x) = Σ k j=1 y j q j (x). 4. Una vez que se ha calculado el polinomio p(x) = a k 1 x k 1 +a k 2 x k 2 + +a 1 x+a 0, su término independiente es el secreto recuperado: a 0 = S. 10
11 Ejemplo (I): Generación de sombras a) Se elige como umbral k = 3, como número de sombras n = 5 y como secreto S = a 0 = 263. b) Se considera el polinomio de grado k 1 = 2: p(x) = 167 x x c) Se calculan las n = 5 sombras, es decir, los 5 puntos siguientes: (x i, y i ) = (i, p(x i )), i = 1,,5: (1, 657), (2, 1385), (3, 2447), (4, 3843), (5, 5573). 11
12 Ejemplo (II): Recuperación del secreto (I) a) Se seleccionan k = 3 sombras cualesquiera de las n = 5 que se tienen: (2, 1385), (3, 2447), (5, 5573). b) Se calculan los k = 3 polinomios auxiliares: q 2 (x)= (x x 3 )(x x 5 )/((x 2 x 3 )(x 2 x 5 )) = x 2 /3 8x/3+5, q 3 (x)= (x x 2 )(x x 5 )/((x 3 x 2 )(x 3 x 5 )) = x 2 /2+7x/2 5, q 5 (x)= (x x 2 )(x x 3 )/((x 5 x 2 )(x 5 x 3 )) = x 2 /6 5x/
13 Ejemplo (II): Recuperación del secreto (II) c) Se determina el polinomio buscado: p(x) = y 2 q 2 (x) + y 3 q 3 (x) + y 5 q 5 (x) = 1385 q 2 (x) q 3 (x) q 5 (x) = 167x x d) El secreto recuperado es S = a 0 =
14 Ejemplo (III): Seguridad (I) a) Si se seleccionan menos de k = 3 sombras es imposible recuperar el secreto. Si se suponen conocidas sólo 2 sombras: (1, 657) y (4, 3843). b) Entonces, sólo se pueden calcular 2 polinomios auxiliares: q 1 (x)= (x x 4 )/(x 1 x 4 ) = x/3+4/3, q 4 (x)= (x x 1 )/(x 4 x 1 ) = x/3 1/3. 14
15 Ejemplo (III): Seguridad (II) c) A partir de los cuales se puede calcular el siguiente polinomio: q(x) = y 1 q 1 (x) + y 4 q 4 (x) = 657 q 1 (x) q 4 (x) = 1062x 405. d) Pero es imposible obtener el secreto original. De hecho, este polinomio es sólo de grado 1. 15
16 Aplicación gráfica Además de las aplicaciones mencionadas, los protocolos de repartos de secretos se pueden emplear para repartir imágenes secretas. En este caso, se determinan n sombras o imágenes del mismo tamaño que la original, pero a partir de las cuales no se obtiene información de la imagen secreta salvo que se unan k de ellas. 16
17 Ejemplo: Esquema gráfico umbral 5 de 5 Las 5 sombras y la imagen original secreta 17
18 Contacto:
VÍDEO intypedia008es LECCIÓN 8: PROTOCOLO DE REPARTO DE SECRETOS. AUTOR: Dr. Luis Hernández Encinas
 VÍDEO intypedia008es LECCIÓN 8: PROTOCOLO DE REPARTO DE SECRETOS AUTOR: Dr. Luis Hernández Encinas Consejo Superior de Investigaciones Científicas, Madrid, España Hola, bienvenidos a intypedia. Hasta ahora
VÍDEO intypedia008es LECCIÓN 8: PROTOCOLO DE REPARTO DE SECRETOS AUTOR: Dr. Luis Hernández Encinas Consejo Superior de Investigaciones Científicas, Madrid, España Hola, bienvenidos a intypedia. Hasta ahora
INTERPOLACIÓN POLINÓMICA Y LA DIVISIÓN DE SECRETOS
 INTERPOLACIÓN POLINÓMICA Y LA DIVISIÓN DE SECRETOS Ángela Rojas Matas, Universidad de Córdoba Alberto Cano Rojas, Universidad de Córdoba RESUMEN. La división o reparto de secretos es un tema de completa
INTERPOLACIÓN POLINÓMICA Y LA DIVISIÓN DE SECRETOS Ángela Rojas Matas, Universidad de Córdoba Alberto Cano Rojas, Universidad de Córdoba RESUMEN. La división o reparto de secretos es un tema de completa
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo
 Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
1. División de polinomios por monomios
 1. División de polinomios por monomios El cociente de dos monomios (si es posible) es igual a otro monomio que tiene: como coeficiente, el cociente de los coeficientes; como parte literal, las letras que
1. División de polinomios por monomios El cociente de dos monomios (si es posible) es igual a otro monomio que tiene: como coeficiente, el cociente de los coeficientes; como parte literal, las letras que
Los polinomios. Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x
 Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
1. El teorema de la función implícita para dos y tres variables.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lección. Aplicaciones de la derivación parcial.. El teorema de la función implícita para dos tres variables. Una ecuación con dos incógnitas. Sea f :( x, ) U f(
GRADO DE INGENIERÍA AEROESPACIAL. CURSO. Lección. Aplicaciones de la derivación parcial.. El teorema de la función implícita para dos tres variables. Una ecuación con dos incógnitas. Sea f :( x, ) U f(
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
POLINOMIOS. División. Regla de Ruffini.
 POLINOMIOS. División. Regla de Ruffini. Recuerda: Un monomio en x es una expresión algebraica de la forma a x tal que a es un número real y n es un número natural. El real a se llama coeficiente y n se
POLINOMIOS. División. Regla de Ruffini. Recuerda: Un monomio en x es una expresión algebraica de la forma a x tal que a es un número real y n es un número natural. El real a se llama coeficiente y n se
Encriptación en Redes
 Encriptación en Redes Integrantes: Patricio Rodríguez. Javier Vergara. Sergio Vergara. Profesor: Agustín González. Fecha: 28 de Julio de 2014. Resumen Un tema importante actualmente en la redes de computadores,
Encriptación en Redes Integrantes: Patricio Rodríguez. Javier Vergara. Sergio Vergara. Profesor: Agustín González. Fecha: 28 de Julio de 2014. Resumen Un tema importante actualmente en la redes de computadores,
Espacios generados, dependencia lineal y bases
 Espacios generados dependencia lineal y bases Departamento de Matemáticas CCIR/ITESM 14 de enero de 2011 Índice 14.1. Introducción............................................... 1 14.2. Espacio Generado............................................
Espacios generados dependencia lineal y bases Departamento de Matemáticas CCIR/ITESM 14 de enero de 2011 Índice 14.1. Introducción............................................... 1 14.2. Espacio Generado............................................
Tema 3. Espacios vectoriales
 Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Tema 3. Espacios vectoriales Estructura del tema. Definición y propiedades. Ejemplos. Dependencia e independencia lineal. Conceptos de base y dimensión. Coordenadas Subespacios vectoriales. 0.1. Definición
Problemas Resueltos del Tema 1
 Tema 1. Probabilidad. 1 Problemas Resueltos del Tema 1 1- Un estudiante responde al azar a dos preguntas de verdadero o falso. Escriba el espacio muestral de este experimento aleatorio.. El espacio muestral
Tema 1. Probabilidad. 1 Problemas Resueltos del Tema 1 1- Un estudiante responde al azar a dos preguntas de verdadero o falso. Escriba el espacio muestral de este experimento aleatorio.. El espacio muestral
CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA
 CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían de una
CRIPTOGRAFÍA SIMÉTRICA Y ASIMÉTRICA Para generar una transmisión segura de datos, debemos contar con un canal que sea seguro, esto es debemos emplear técnicas de forma que los datos que se envían de una
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS 1. EXPRESIONES ALGEBRAICAS. Estas expresiones del área son expresiones algebraicas, ya que además de números aparecen letras. Son también expresiones algebraicas: bac,
EXPRESIONES ALGEBRAICAS. POLINOMIOS 1. EXPRESIONES ALGEBRAICAS. Estas expresiones del área son expresiones algebraicas, ya que además de números aparecen letras. Son también expresiones algebraicas: bac,
LA DUALIDAD PAR-IMPAR. 1. En una reunión de 25 personas. Puede ser que cada una se salude dándose la mano con todas las demás excepto con una?
 NOTAS Un sencillo principio matemático que da mucho más juego del que parece a primera vista es la simple distinción entre los números pares e impares. Conviene tener presente las siguientes propiedades,
NOTAS Un sencillo principio matemático que da mucho más juego del que parece a primera vista es la simple distinción entre los números pares e impares. Conviene tener presente las siguientes propiedades,
Capítulo 1. MANUAL DE USUARIO
 Capítulo 1. MANUAL DE USUARIO 1.1 SUCESIONES GRÁFICAS Lo primero que se hará es mostrar la pantalla que se encontrará el usuario cuando ejecute la aplicación, indicando las zonas en las que se divide esta:
Capítulo 1. MANUAL DE USUARIO 1.1 SUCESIONES GRÁFICAS Lo primero que se hará es mostrar la pantalla que se encontrará el usuario cuando ejecute la aplicación, indicando las zonas en las que se divide esta:
Apéndice A. Manual del usuario.
 Apéndice A. Manual del usuario. 1. Acceso. Para poder utilizar el sistema, los usuarios deben acceder desde cualquier navegador Web que cuente con el Plug-in de Java 2 a la dirección http://localhost:8080/tesis/index.html.
Apéndice A. Manual del usuario. 1. Acceso. Para poder utilizar el sistema, los usuarios deben acceder desde cualquier navegador Web que cuente con el Plug-in de Java 2 a la dirección http://localhost:8080/tesis/index.html.
EL GRADO Y LOS ELEMENTOS QUE FORMAN UN POLINOMIO
 RECONOCER OBJETIVO EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO NOMBRE: CURSO: ECHA: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los términos del polinomio.
RECONOCER OBJETIVO EL GRADO Y LOS ELEMENTOS QUE ORMAN UN POLINOMIO NOMBRE: CURSO: ECHA: Un polinomio es una expresión algebraica formada por la suma algebraica de monomios, que son los términos del polinomio.
OBJETIVOS CONTENIDOS PROCEDIMIENTOS
 82652 _ 0275-0286.qxd 27/4/07 1:20 Página 275 Polinomios INTRODUCCIÓN Son múltiples los contextos en los que aparecen los polinomios: fórmulas económicas, químicas, físicas, de ahí la importancia de comprender
82652 _ 0275-0286.qxd 27/4/07 1:20 Página 275 Polinomios INTRODUCCIÓN Son múltiples los contextos en los que aparecen los polinomios: fórmulas económicas, químicas, físicas, de ahí la importancia de comprender
no descompone no descompone no descompone
 Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
Problema 1. Sea I n el conjunto de los n primeros números naturales impares. Por ejemplo: I 3 = {1, 3, 5, I 6 = {1, 3, 5, 7, 9, 11, etc. Para qué números n el conjunto I n se puede descomponer en dos partes
CAPÍTULO 6 SIMULACIONES Y RESULTADOS
 CAPÍTULO 6 SIMULACIONES Y RESULTADOS 6.1 Proceso de Simulación Las simulaciones fueros llevadas a cabo empleando como herramienta la Versión 6.5 Release 13 de Matlab. Para lo cual fue empleado un banco
CAPÍTULO 6 SIMULACIONES Y RESULTADOS 6.1 Proceso de Simulación Las simulaciones fueros llevadas a cabo empleando como herramienta la Versión 6.5 Release 13 de Matlab. Para lo cual fue empleado un banco
SEMANAS 07 Y 08 CLASES 05 Y 06 VIERNES 25/05/12 Y 01/06/12
 CÁLCULO IV (7) SEMANAS 7 Y 8 CLASES 5 Y 6 VIERNES 5/5/1 Y 1/6/1 1 Observación Las propiedades de una función real de una variable real se reflejan en su gráfica Pero para w = f(), con w complejos, no es
CÁLCULO IV (7) SEMANAS 7 Y 8 CLASES 5 Y 6 VIERNES 5/5/1 Y 1/6/1 1 Observación Las propiedades de una función real de una variable real se reflejan en su gráfica Pero para w = f(), con w complejos, no es
TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1
 TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1 TEMA 10 - FUNCIONES ELEMENTALES 10.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder
TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1 TEMA 10 - FUNCIONES ELEMENTALES 10.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder
Ecuaciones diferenciales de orden superior
 CAPÍTULO 4 Ecuaciones diferenciales de orden superior 4.4.2 ED lineales homogéneas con coeficientes constantes de orden n 3 En la sección anterior hemos obtenido las soluciones de la ED lineal homogénea
CAPÍTULO 4 Ecuaciones diferenciales de orden superior 4.4.2 ED lineales homogéneas con coeficientes constantes de orden n 3 En la sección anterior hemos obtenido las soluciones de la ED lineal homogénea
Práctica 5. Curso 2014-2015
 Prácticas de Seguridad Informática Práctica 5 Grado Ingeniería Informática Curso 2014-2015 Universidad de Zaragoza Escuela de Ingeniería y Arquitectura Departamento de Informática e Ingeniería de Sistemas
Prácticas de Seguridad Informática Práctica 5 Grado Ingeniería Informática Curso 2014-2015 Universidad de Zaragoza Escuela de Ingeniería y Arquitectura Departamento de Informática e Ingeniería de Sistemas
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice
 Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Tema 1: Fundamentos de lógica, teoría de conjuntos y estructuras algebraicas: Apéndice 1 Polinomios Dedicaremos este apartado al repaso de los polinomios. Se define R[x] ={a 0 + a 1 x + a 2 x 2 +... +
Polinomios y fracciones algebraicas
 829566 _ 0249-008.qxd 27/6/08 09:21 Página 27 Polinomios y fracciones algebraicas INTRODUCCIÓN Son múltiples los contextos en los que aparecen los polinomios: fórmulas económicas, químicas, físicas, de
829566 _ 0249-008.qxd 27/6/08 09:21 Página 27 Polinomios y fracciones algebraicas INTRODUCCIÓN Son múltiples los contextos en los que aparecen los polinomios: fórmulas económicas, químicas, físicas, de
Partición del Disco Duro y Manejo del Setup
 Partición del Disco Duro y Manejo del Setup Disco Duro Un Disco Duro es un dispositivo que permite el almacenamiento recuperación de grandes cantidades de información. Los discos duros forman el principal
Partición del Disco Duro y Manejo del Setup Disco Duro Un Disco Duro es un dispositivo que permite el almacenamiento recuperación de grandes cantidades de información. Los discos duros forman el principal
Selectividad Junio 2008 JUNIO 2008 PRUEBA A
 Selectividad Junio 008 JUNIO 008 PRUEBA A 3 a x + a y =.- Sea el sistema: x + a y = 0 a) En función del número de soluciones, clasifica el sistema para los distintos valores del parámetro a. b) Resuélvelo
Selectividad Junio 008 JUNIO 008 PRUEBA A 3 a x + a y =.- Sea el sistema: x + a y = 0 a) En función del número de soluciones, clasifica el sistema para los distintos valores del parámetro a. b) Resuélvelo
Sistema de proceso por lotes: esquema operativo
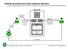 Sistema de proceso por lotes: esquema operativo MAINFRAME CPU Lector de tarjetas MEM SO Impresora Programa de usuario Programadores Sistema de proceso por lotes: características operativas Los programadores
Sistema de proceso por lotes: esquema operativo MAINFRAME CPU Lector de tarjetas MEM SO Impresora Programa de usuario Programadores Sistema de proceso por lotes: características operativas Los programadores
TEMA 2 POLINOMIOS Y FRACCIONES ALGEBRAICAS
 Matemáticas B 4º E.S.O. Tema : Polinomios y fracciones algebraicas. 1 TEMA POLINOMIOS Y FRACCIONES ALGEBRAICAS.1 COCIENTE DE POLINOMIOS 4º.1.1 COCIENTE DE MONOMIOS 4º El cociente de un monomio entre otro
Matemáticas B 4º E.S.O. Tema : Polinomios y fracciones algebraicas. 1 TEMA POLINOMIOS Y FRACCIONES ALGEBRAICAS.1 COCIENTE DE POLINOMIOS 4º.1.1 COCIENTE DE MONOMIOS 4º El cociente de un monomio entre otro
Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1
 Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1 TEMA 4 - FUNCIONES ELEMENTALES 4.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : Una función real de variable real es una aplicación de un subconjunto
Tema 4 Funciones elementales Matemáticas CCSSI 1º Bachillerato 1 TEMA 4 - FUNCIONES ELEMENTALES 4.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : Una función real de variable real es una aplicación de un subconjunto
GENERACIÓN DE TRANSFERENCIAS
 GENERACIÓN DE TRANSFERENCIAS 1 INFORMACIÓN BÁSICA La aplicación de generación de ficheros de transferencias permite generar fácilmente órdenes para que la Caja efectúe transferencias, creando una base
GENERACIÓN DE TRANSFERENCIAS 1 INFORMACIÓN BÁSICA La aplicación de generación de ficheros de transferencias permite generar fácilmente órdenes para que la Caja efectúe transferencias, creando una base
App para realizar consultas al Sistema de Información Estadística de Castilla y León
 App para realizar consultas al Sistema de Información Estadística de Castilla y León Jesús M. Rodríguez Rodríguez rodrodje@jcyl.es Dirección General de Presupuestos y Estadística Consejería de Hacienda
App para realizar consultas al Sistema de Información Estadística de Castilla y León Jesús M. Rodríguez Rodríguez rodrodje@jcyl.es Dirección General de Presupuestos y Estadística Consejería de Hacienda
Seguridad matemática en la Sociedad de la Información
 Pino T. Caballero Gil Profesora Titular de Ciencias de la Computación e Inteligencia Artificial Departamento de Estadística, Investigación Operativa y Computación Universidad de La Laguna Introducción
Pino T. Caballero Gil Profesora Titular de Ciencias de la Computación e Inteligencia Artificial Departamento de Estadística, Investigación Operativa y Computación Universidad de La Laguna Introducción
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP. Universidad de Santiago de Chile. Polinomios
 Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Polinomios Definición: P es un polinomio en el conjunto de los números reales si y sólo si P es una función de
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Polinomios Definición: P es un polinomio en el conjunto de los números reales si y sólo si P es una función de
QUÉ ES BAJO LLAVE? POR QUÉ SER CLIENTE DE BAJO LLAVE?
 QUÉ ES BAJO LLAVE? Bajo Llave es una caja de seguridad electrónica, una aplicación de alta seguridad que usa cifrado de datos y que permite almacenar información personal y profesional, perfectamente clasificada
QUÉ ES BAJO LLAVE? Bajo Llave es una caja de seguridad electrónica, una aplicación de alta seguridad que usa cifrado de datos y que permite almacenar información personal y profesional, perfectamente clasificada
MÓDULO 2. LEYES FINANCIERAS DE CAPITALIZACIÓN Y DESCUENTO SIMPLE
 MÓDULO 2. LEYES FINANCIERAS DE CAPITALIZACIÓN Y DESCUENTO SIMPLE Índice de contenidos: 1. Ley Financiera de capitalización a interés vencido. 1.1. Equivalencia de capitales. 1.2. Tipos de interés equivalentes.
MÓDULO 2. LEYES FINANCIERAS DE CAPITALIZACIÓN Y DESCUENTO SIMPLE Índice de contenidos: 1. Ley Financiera de capitalización a interés vencido. 1.1. Equivalencia de capitales. 1.2. Tipos de interés equivalentes.
TALLER DE MATEMÁTICAS NOTAS. Toda expresión algebraica del tipo. a n x n + a n 1 x n 1 +... + a 1 x + a 0. es un polinomio de grado n, si a n 0.
 NOTAS Toda expresión algebraica del tipo es un polinomio de grado n, si a n 0. a n x n + a n 1 x n 1 +... + a 1 x + a 0 RELACIONES DE DIVISIBILIDAD 1) x n a n = (x a)(x n 1 + ax n 2 + a 2 x n 3 +... +
NOTAS Toda expresión algebraica del tipo es un polinomio de grado n, si a n 0. a n x n + a n 1 x n 1 +... + a 1 x + a 0 RELACIONES DE DIVISIBILIDAD 1) x n a n = (x a)(x n 1 + ax n 2 + a 2 x n 3 +... +
Idea general: Comienzo de la partida:
 Idea general: El Estratega es un juego de estrategia y conquista. Se desarrolla en un planisferio que consta de 42 territorios. Las dimensiones y divisiones políticas fueron modificadas para facilitar
Idea general: El Estratega es un juego de estrategia y conquista. Se desarrolla en un planisferio que consta de 42 territorios. Las dimensiones y divisiones políticas fueron modificadas para facilitar
VII. Estructuras Algebraicas
 VII. Estructuras Algebraicas Objetivo Se analizarán las operaciones binarias y sus propiedades dentro de una estructura algebraica. Definición de operación binaria Operaciones como la suma, resta, multiplicación
VII. Estructuras Algebraicas Objetivo Se analizarán las operaciones binarias y sus propiedades dentro de una estructura algebraica. Definición de operación binaria Operaciones como la suma, resta, multiplicación
Cómo registrarse y crear su cuenta de usuario? < IMAGEN 2.1.1: HAZ CLIC SOBRE EL BOTÓN RESALTADO
 Cómo registrarse y crear su cuenta de usuario? Si es la primera vez que visita la página, y nunca ha creado un usuario para poder acceder a todos los servicios que el sistema ofrece, deberá registrarse
Cómo registrarse y crear su cuenta de usuario? Si es la primera vez que visita la página, y nunca ha creado un usuario para poder acceder a todos los servicios que el sistema ofrece, deberá registrarse
INTRODUCCIÓN A LA PROBABILIDAD.
 INTRODUCCIÓN A LA ROBABILIDAD. Departamento de Matemáticas Se denomina experimento aleatorio a aquel en que jamás se puede predecir el resultado. El conjunto formado por todos los resultados posibles de
INTRODUCCIÓN A LA ROBABILIDAD. Departamento de Matemáticas Se denomina experimento aleatorio a aquel en que jamás se puede predecir el resultado. El conjunto formado por todos los resultados posibles de
Preguntas que se hacen con frecuencia sobre los estudios clínicos
 Preguntas que se hacen con frecuencia sobre los estudios clínicos Son seguros? Todos los ensayos clínicos deben ser aprobados por el gobierno federal y deben cumplir con una reglamentación estricta que
Preguntas que se hacen con frecuencia sobre los estudios clínicos Son seguros? Todos los ensayos clínicos deben ser aprobados por el gobierno federal y deben cumplir con una reglamentación estricta que
SISTEMA DE RASTREO Y MARCADO ANTIRROBO
 Enlaces - Centro de Educación y Tecnología SISTEMA DE RASTREO Y MARCADO ANTIRROBO DESCRIPCIÓN Y MANUAL DE USO SOFTWARE RASTREO PC IMPORTANTE En caso de robo de un computador, y para su posterior recuperación,
Enlaces - Centro de Educación y Tecnología SISTEMA DE RASTREO Y MARCADO ANTIRROBO DESCRIPCIÓN Y MANUAL DE USO SOFTWARE RASTREO PC IMPORTANTE En caso de robo de un computador, y para su posterior recuperación,
Tema 2 Límites de Funciones
 Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
Tema 2 Límites de Funciones 2.1.- Definición de Límite Idea de límite de una función en un punto: Sea la función. Si x tiende a 2, a qué valor se aproxima? Construyendo - + una tabla de valores próximos
SISTEMAS Y MANUALES DE LA CALIDAD
 SISTEMAS Y MANUALES DE LA CALIDAD NORMATIVAS SOBRE SISTEMAS DE CALIDAD Introducción La experiencia de algunos sectores industriales que por las características particulares de sus productos tenían necesidad
SISTEMAS Y MANUALES DE LA CALIDAD NORMATIVAS SOBRE SISTEMAS DE CALIDAD Introducción La experiencia de algunos sectores industriales que por las características particulares de sus productos tenían necesidad
ANALISIS COMBINATORIO
 Universidad de San Carlos de Guatemala Centro Universitario de Occidente División Ciencias de la Salud Carrera de Médico y Cirujano, Primer Año, 2015 Teléfonos: 78730000, EXT. 2227-2221-2345-2244 CUNOC-USAC
Universidad de San Carlos de Guatemala Centro Universitario de Occidente División Ciencias de la Salud Carrera de Médico y Cirujano, Primer Año, 2015 Teléfonos: 78730000, EXT. 2227-2221-2345-2244 CUNOC-USAC
CAPÍTULO 3 RED NEURONAL PARA EL RECONOCIMIENTO DE ROSTROS
 CAPÍTULO 3 RED NEURONAL PARA EL RECONOCIMIENTO DE ROSTROS Descripción de la base de datos Como datos de entrenamiento, en este proyecto, se utilizó la base de datos ORL [1], la cual contiene un conjunto
CAPÍTULO 3 RED NEURONAL PARA EL RECONOCIMIENTO DE ROSTROS Descripción de la base de datos Como datos de entrenamiento, en este proyecto, se utilizó la base de datos ORL [1], la cual contiene un conjunto
La suma se realiza miembro a miembro. La suma de polinomios goza de las mismas propiedades que la suma de números. Ejemplo:
 Tema 4. Polinomios 1. Definición Un polinomio es una expresión hecha con constantes, variables y exponentes, que están combinados. Los exponentes sólo pueden ser 0, 1, 2, 3,... etc. No puede tener un número
Tema 4. Polinomios 1. Definición Un polinomio es una expresión hecha con constantes, variables y exponentes, que están combinados. Los exponentes sólo pueden ser 0, 1, 2, 3,... etc. No puede tener un número
Sea un espacio vectorial sobre y sea un producto interno en ; entonces, : , y los vectores
 FASÍCULO: ESPACIOS CON PRODUCTO INTERNO Teorema. Sea un espacio vectorial sobre y sea un producto interno en ; entonces, : i) ii) iii) iv) Ejemplo: Sean el espacio vectorial con el producto interno definido
FASÍCULO: ESPACIOS CON PRODUCTO INTERNO Teorema. Sea un espacio vectorial sobre y sea un producto interno en ; entonces, : i) ii) iii) iv) Ejemplo: Sean el espacio vectorial con el producto interno definido
FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO
 FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO Determinar la capacidad de un regulador según la placa de datos:
FACULTAD DE MEDICINA VETERINARIA Y ZOOTECNIA SECRETARÍA GENERAL SECRETARÍA DE TECNOLOGÍA EN APOYO A LA DOCENCIA DEPARTAMENTO DE CÓMPUTO Determinar la capacidad de un regulador según la placa de datos:
CERRADURAS RFID PARA TAQUILLAS PASSTECH
 CERRADURAS RFID PARA TAQUILLAS PASSTECH DESCRIPCIÓN DEL PROCESO DE APLICACIÓN EN UN CENTRO DEPORTIVO SECUENCIA NÚMERO 1: CREACIÓN DE TARJETA/PULSERA Las cerraduras RFID para taquillas se controlan a partir
CERRADURAS RFID PARA TAQUILLAS PASSTECH DESCRIPCIÓN DEL PROCESO DE APLICACIÓN EN UN CENTRO DEPORTIVO SECUENCIA NÚMERO 1: CREACIÓN DE TARJETA/PULSERA Las cerraduras RFID para taquillas se controlan a partir
SISTEMAS DE COORDENADAS SISTEMA COORDENADO UNIDIMENSIONAL
 SISTEMAS DE COORDENADAS En la vida diaria, nos encontramos con el problema de ordenar algunos objetos; de tal manera que es necesario agruparlos, identificarlos, seleccionarlos, estereotiparlos, etc.,
SISTEMAS DE COORDENADAS En la vida diaria, nos encontramos con el problema de ordenar algunos objetos; de tal manera que es necesario agruparlos, identificarlos, seleccionarlos, estereotiparlos, etc.,
Unidad IV: Teoría de la Partida Doble
 Unidad IV: Teoría de la Partida Doble 4.1 La cuenta La Cuenta de Pérdidas y Ganancias de una empresa se divide en varios tipos de resultados: Resultado de explotación, calculado como diferencia entre ingresos
Unidad IV: Teoría de la Partida Doble 4.1 La cuenta La Cuenta de Pérdidas y Ganancias de una empresa se divide en varios tipos de resultados: Resultado de explotación, calculado como diferencia entre ingresos
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
Factorización de polinomios
 Factorización de polinomios Polinomios Un polinomio p en la variable x es una expresión de la forma: px a 0 a 1 x a x a n1 x n1 a n x n donde a 0, a 1, a,, a n1, a n son unos números, llamados coeficientes
Factorización de polinomios Polinomios Un polinomio p en la variable x es una expresión de la forma: px a 0 a 1 x a x a n1 x n1 a n x n donde a 0, a 1, a,, a n1, a n son unos números, llamados coeficientes
5.4. Manual de usuario
 5.4. Manual de usuario En esta sección se procederá a explicar cada una de las posibles acciones que puede realizar un usuario, de forma que pueda utilizar todas las funcionalidades del simulador, sin
5.4. Manual de usuario En esta sección se procederá a explicar cada una de las posibles acciones que puede realizar un usuario, de forma que pueda utilizar todas las funcionalidades del simulador, sin
Funciones lineales. Objetivos. Antes de empezar. 1.Función de proporcionalidad directa pág. 170 Definición Representación gráfica
 10 Funciones lineales Objetivos En esta quincena aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
10 Funciones lineales Objetivos En esta quincena aprenderás a: Identificar problemas en los que intervienen magnitudes directamente proporcionales. Calcular la función que relaciona a esas magnitudes a
Sistemas de seguridad en redes inalámbricas: WEP, WAP y WAP2
 Sistemas de seguridad en redes inalámbricas: WEP, WAP y WAP2 Calle San Rafael, 14 28108 Alcobendas (Madrid) 902 90 10 20 www.acens.com Introducción Actualmente una de las formas más utilizadas para conectarse
Sistemas de seguridad en redes inalámbricas: WEP, WAP y WAP2 Calle San Rafael, 14 28108 Alcobendas (Madrid) 902 90 10 20 www.acens.com Introducción Actualmente una de las formas más utilizadas para conectarse
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA. La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros.
 QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
ATAQUE Y CONTRAMEDIAS
 Unidad 3 4-5 3. AUTENTICACIÓN 4. CONTROL DE ACCESO 5. ATAQUE Y CONTRAMEDIAS jun-10 M.C. Gustavo A. Gutiérrez Carreón DEFINICIÓN AUTENTICACIÓN Autenticación o autentificación es el acto de establecimiento
Unidad 3 4-5 3. AUTENTICACIÓN 4. CONTROL DE ACCESO 5. ATAQUE Y CONTRAMEDIAS jun-10 M.C. Gustavo A. Gutiérrez Carreón DEFINICIÓN AUTENTICACIÓN Autenticación o autentificación es el acto de establecimiento
Funciones uno-uno, sobre y biunívocas
 Funciones uno-uno, sobre y biunívocas La inversa (biunívocas) de una función es una regla que actúa en la salida de la función y produce la entrada correspondiente. Así, la inversa deshace o invierte lo
Funciones uno-uno, sobre y biunívocas La inversa (biunívocas) de una función es una regla que actúa en la salida de la función y produce la entrada correspondiente. Así, la inversa deshace o invierte lo
5 Ecuaciones lineales y conceptos elementales de funciones
 Programa Inmersión, Verano 206 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 300 y MATE 3023 Clase #6: martes, 7 de junio de 206. 5 Ecuaciones lineales y conceptos elementales
Programa Inmersión, Verano 206 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 300 y MATE 3023 Clase #6: martes, 7 de junio de 206. 5 Ecuaciones lineales y conceptos elementales
ISEC Labs #11. Despliegue y restauración segura de volúmenes cifrados con TrueCrypt. Javier Moreno jmoreno<arroba>isecauditors.com
 ISEC Labs #11 Despliegue y restauración segura de Javier Moreno jmorenoisecauditors.com 1. RESUMEN 2 2. INTRODUCCIÓN 2 3. RESTAURACIÓN DE VOLÚMENES CIFRADOS 3 4. CONCLUSIÓN 14 5. REFERENCIAS 14
ISEC Labs #11 Despliegue y restauración segura de Javier Moreno jmorenoisecauditors.com 1. RESUMEN 2 2. INTRODUCCIÓN 2 3. RESTAURACIÓN DE VOLÚMENES CIFRADOS 3 4. CONCLUSIÓN 14 5. REFERENCIAS 14
Resumen de Requisitos Técnicos para incorporación de Organismos a la Plataforma Integrada de Servicios Electrónicos del Estado
 Resumen de Requisitos Técnicos para incorporación de Organismos a la Plataforma Integrada de Servicios Electrónicos del Estado Ministerio Secretaría General de la Presidencia Unidad de Modernización y
Resumen de Requisitos Técnicos para incorporación de Organismos a la Plataforma Integrada de Servicios Electrónicos del Estado Ministerio Secretaría General de la Presidencia Unidad de Modernización y
SISTEMA DE RASTREO Y MARCADO ANTIRROBO
 SISTEMA DE RASTREO Y MARCADO ANTIRROBO DESCRIPCIÓN Y MANUAL DE USO Enlaces - Centro de Educación y Tecnología IMPORTANTE En caso de robo de un computador, y para su posterior recuperación, es imprescindible
SISTEMA DE RASTREO Y MARCADO ANTIRROBO DESCRIPCIÓN Y MANUAL DE USO Enlaces - Centro de Educación y Tecnología IMPORTANTE En caso de robo de un computador, y para su posterior recuperación, es imprescindible
ANÁLISIS DE UN JUEGO DE CARTAS: LAS SIETE Y MEDIA
 ANÁLISIS DE UN JUEGO DE CARTAS: LAS SIETE Y MEDIA MaMaEuSch (Management Mathematics for European School) http://www.mathematik.uni-kl.de/~mamaeusch/ Modelos matemáticos orientados a la educación Clases
ANÁLISIS DE UN JUEGO DE CARTAS: LAS SIETE Y MEDIA MaMaEuSch (Management Mathematics for European School) http://www.mathematik.uni-kl.de/~mamaeusch/ Modelos matemáticos orientados a la educación Clases
Nombre/Código: Febrero 21 2015. Examen I. 5 /10pts. Total: /50pts
 1 Álgebra abstracta II Guillermo Mantilla-Soler Nombre/Código: Febrero 21 2015 Examen I Problemas Puntuación 1 /10pts 2 /10pts 3 /10pts 4 /10pts 5 /10pts Total: /50pts 2 Preguntas Problema 1[10 pts]: Sea
1 Álgebra abstracta II Guillermo Mantilla-Soler Nombre/Código: Febrero 21 2015 Examen I Problemas Puntuación 1 /10pts 2 /10pts 3 /10pts 4 /10pts 5 /10pts Total: /50pts 2 Preguntas Problema 1[10 pts]: Sea
MERCANCIAS EN CONSIGNACIÓN UTILIZANDO EL SISTEMA ANALÍTICO.
 MERCANCIAS EN CONSIGNACIÓN UTILIZANDO EL SISTEMA ANALÍTICO. Cuando el sistema que se lleva para el registro y control de las mercancías es el Analítico o Pormenorizado y se presenta la necesidad de manejar
MERCANCIAS EN CONSIGNACIÓN UTILIZANDO EL SISTEMA ANALÍTICO. Cuando el sistema que se lleva para el registro y control de las mercancías es el Analítico o Pormenorizado y se presenta la necesidad de manejar
Empresas. Manual de Usuario. Versión 1.0. Fundación Venezuela sin Límites. Empresas-ManualUsuario-1.0. Página 1 de 20
 Versión 1.0 A.C Fundación Venezuela Sin Límites -ManualUsuario-1.0 Fundación Venezuela sin Límites Manual de Usuario Página 1 de 20 Aprobación Nombre Apellido Cargo Fecha Firma Histórico de Cambios Fecha
Versión 1.0 A.C Fundación Venezuela Sin Límites -ManualUsuario-1.0 Fundación Venezuela sin Límites Manual de Usuario Página 1 de 20 Aprobación Nombre Apellido Cargo Fecha Firma Histórico de Cambios Fecha
LÍMITES Y CONTINUIDAD DE FUNCIONES
 Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Ejemplo: Apuesta? 100 PERA PERA MANZANA La casa gana!!! Apuesta? 300 FRUTILLA FRUTILLA FRUTILLA GANASTE 600!!! Apuesta? 0 Gracias por jugar!!!
 Problema: El Tragamonedas. Pepito fue a un casino de juegos y ganó un montón de dinero apostando al tragamonedas. Quedó tan fascinado con el juego que decidió, una vez en casa, hacer un programa que le
Problema: El Tragamonedas. Pepito fue a un casino de juegos y ganó un montón de dinero apostando al tragamonedas. Quedó tan fascinado con el juego que decidió, una vez en casa, hacer un programa que le
Soluciones de los ejercicios de Selectividad sobre Probabilidad de Matemáticas Aplicadas a las Ciencias Sociales II
 Soluciones de los ejercicios de Selectividad sobre Probabilidad de Antonio Francisco Roldán López de Hierro * Convocatoria de 2008 Las siguientes páginas contienen las soluciones de los ejercicios propuestos
Soluciones de los ejercicios de Selectividad sobre Probabilidad de Antonio Francisco Roldán López de Hierro * Convocatoria de 2008 Las siguientes páginas contienen las soluciones de los ejercicios propuestos
EXPRESIONES ALGEBRAICAS Y POLINOMIOS
 EXPRESIONES ALGEBRAICAS Y POLINOMIOS 1. Dado el polinomio A(x)=x +3. Halla: a) (B(x)) y b)(b(x)) 3. a) Define valor numérico de un polinomio P(x) en x=a. b) Halla el valor numérico del polinomio P(x) =
EXPRESIONES ALGEBRAICAS Y POLINOMIOS 1. Dado el polinomio A(x)=x +3. Halla: a) (B(x)) y b)(b(x)) 3. a) Define valor numérico de un polinomio P(x) en x=a. b) Halla el valor numérico del polinomio P(x) =
FORMA CANONICA DE JORDAN Y ECUACIONES DIFERENCIALES LINEALES A COEFICIENTES CONSTANTES
 FORMA CANONICA DE JORDAN Y ECUACIONES DIFERENCIALES LINEALES A COEFICIENTES CONSTANTES Eleonora Catsigeras 6 de mayo de 997 Notas para el curso de Análisis Matemático II Resumen Se enuncia sin demostración
FORMA CANONICA DE JORDAN Y ECUACIONES DIFERENCIALES LINEALES A COEFICIENTES CONSTANTES Eleonora Catsigeras 6 de mayo de 997 Notas para el curso de Análisis Matemático II Resumen Se enuncia sin demostración
Quién quiere ganar Taller?
 Segundo Semestre, 2011 IC-1801 Taller de Programación Grupo 3 Especificación I Proyecto Programado Formato de desarrollo del primer Examen Parcial Teórico Profesora: Ing.Ericka Solano Fernández Quién quiere
Segundo Semestre, 2011 IC-1801 Taller de Programación Grupo 3 Especificación I Proyecto Programado Formato de desarrollo del primer Examen Parcial Teórico Profesora: Ing.Ericka Solano Fernández Quién quiere
Métodos Numéricos Grado en Ingeniería Informática Univ. Tema de Las 7 Interpolación Palmas de G.C. de funciones 1 / 42II
 Métodos Numéricos Grado en Ingeniería Informática Tema 7 Interpolación de funciones II Luis Alvarez León Univ. de Las Palmas de G.C. Métodos Numéricos Grado en Ingeniería Informática Univ. Tema de Las
Métodos Numéricos Grado en Ingeniería Informática Tema 7 Interpolación de funciones II Luis Alvarez León Univ. de Las Palmas de G.C. Métodos Numéricos Grado en Ingeniería Informática Univ. Tema de Las
Definición 2.1.1. Se llama suceso aleatorio a cualquier subconjunto del espacio muestral.
 Capítulo 2 Probabilidades 2. Definición y propiedades Al realizar un experimento aleatorio nuestro interés es obtener información sobre las leyes que rigen el fenómeno sometido a estudio. El punto de partida
Capítulo 2 Probabilidades 2. Definición y propiedades Al realizar un experimento aleatorio nuestro interés es obtener información sobre las leyes que rigen el fenómeno sometido a estudio. El punto de partida
Tipos de instalaciones
 Tipos de instalaciones Existen este infinidad de configuraciones, pero como técnicos debemos referirnos a las normalizadas por la NTE, la cual diferencia cinco tipos basados en número de circuitos y programas,
Tipos de instalaciones Existen este infinidad de configuraciones, pero como técnicos debemos referirnos a las normalizadas por la NTE, la cual diferencia cinco tipos basados en número de circuitos y programas,
VÍDEO intypedia003es LECCIÓN 3: SISTEMAS DE CIFRA CON CLAVE PÚBLICA. AUTOR: Gonzalo Álvarez Marañón
 VÍDEO intypedia003es LECCIÓN 3: SISTEMAS DE CIFRA CON CLAVE PÚBLICA AUTOR: Gonzalo Álvarez Marañón Consejo Superior de Investigaciones Científicas, Madrid, España Hola, bienvenidos a intypedia. Conocidos
VÍDEO intypedia003es LECCIÓN 3: SISTEMAS DE CIFRA CON CLAVE PÚBLICA AUTOR: Gonzalo Álvarez Marañón Consejo Superior de Investigaciones Científicas, Madrid, España Hola, bienvenidos a intypedia. Conocidos
RELACIONES DE RECURRENCIA
 Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
Capítulo 5. Análisis del software del simulador del sistema de seguridad
 1 Capítulo 5. Análisis del software del simulador del sistema de seguridad Para realizar análisis del simulador de sistema de seguridad se recurrió a diagramas de flujo de datos (DFD s), ya que se consideró
1 Capítulo 5. Análisis del software del simulador del sistema de seguridad Para realizar análisis del simulador de sistema de seguridad se recurrió a diagramas de flujo de datos (DFD s), ya que se consideró
EVALUACIÓN 11 B) 150 1 C) 2 D) 15 E) 30
 EVALUACIÓN 1. Si la probabilidad que llueva en San Pedro en verano es 1/30 y la probabilidad que caigan 100 cc es 1/40, cuál es la probabilidad que no llueva en San Pedro y que no caigan 100 cc? A) 1/1200
EVALUACIÓN 1. Si la probabilidad que llueva en San Pedro en verano es 1/30 y la probabilidad que caigan 100 cc es 1/40, cuál es la probabilidad que no llueva en San Pedro y que no caigan 100 cc? A) 1/1200
Funciones, x, y, gráficos
 Funciones, x, y, gráficos Vamos a ver los siguientes temas: funciones, definición, dominio, codominio, imágenes, gráficos, y algo más. Recordemos el concepto de función: Una función es una relación entre
Funciones, x, y, gráficos Vamos a ver los siguientes temas: funciones, definición, dominio, codominio, imágenes, gráficos, y algo más. Recordemos el concepto de función: Una función es una relación entre
Teorema de Green. 6.1. Curvas de Jordan
 Lección 6 Teorema de Green En la lección anterior, previa caracterización de los campos conservativos, hemos visto que un campo irrotacional puede no ser conservativo. Tenemos por tanto una condición fácil
Lección 6 Teorema de Green En la lección anterior, previa caracterización de los campos conservativos, hemos visto que un campo irrotacional puede no ser conservativo. Tenemos por tanto una condición fácil
MÁSTER UNIVERSITARIO EN INGENIERIA INDUSTRIAL
 Impartido por la Escuela Técnica Superior de Ingenieros Industriales de la UNED PREGUNTAS DE INFORMACIÓN GENERAL Curso 2014 2015 1. Qué titulación se obtiene cuando se superan todos los créditos del Máster
Impartido por la Escuela Técnica Superior de Ingenieros Industriales de la UNED PREGUNTAS DE INFORMACIÓN GENERAL Curso 2014 2015 1. Qué titulación se obtiene cuando se superan todos los créditos del Máster
Ejercicios de divisibilidad con soluciones. 1 De entre los siguientes números: 405, 316, 814, 1085 y 340: a) Hay alguno que sea divisible por 3?
 Ejercicios de divisibilidad con soluciones 1 De entre los siguientes números: 405, 316, 814, 1085 y 340: a) Hay alguno que sea divisible por 3? b) Cuáles son divisibles por 4? c) Cuáles tienen por divisor
Ejercicios de divisibilidad con soluciones 1 De entre los siguientes números: 405, 316, 814, 1085 y 340: a) Hay alguno que sea divisible por 3? b) Cuáles son divisibles por 4? c) Cuáles tienen por divisor
FÓRMULAS DEL PRODUCTO Y DEL COCIENTE
 CAPÍTULO 5 FÓRMULAS DEL PRODUCTO Y DEL COCIENTE 5.1 FÓRMULA DE LA RAÍZ CUADRADA Antes de practicar las fórmulas (7) y (8) del procto y del cociente, conviene decir una fórmula para la raíz cuadrada, en
CAPÍTULO 5 FÓRMULAS DEL PRODUCTO Y DEL COCIENTE 5.1 FÓRMULA DE LA RAÍZ CUADRADA Antes de practicar las fórmulas (7) y (8) del procto y del cociente, conviene decir una fórmula para la raíz cuadrada, en
CAPÍTULO III. FUNCIONES
 CAPÍTULO III LÍMITES DE FUNCIONES SECCIONES A Definición de límite y propiedades básicas B Infinitésimos Infinitésimos equivalentes C Límites infinitos Asíntotas D Ejercicios propuestos 85 A DEFINICIÓN
CAPÍTULO III LÍMITES DE FUNCIONES SECCIONES A Definición de límite y propiedades básicas B Infinitésimos Infinitésimos equivalentes C Límites infinitos Asíntotas D Ejercicios propuestos 85 A DEFINICIÓN
REGLA DE RUFFINI. FACTORIZACIÓN DE POLINOMIOS
 REGLA DE RUFFINI. FACTORIZACIÓN DE POLINOMIOS Si en una división de polinomios el divisor es de la forma (x - a) se puede aplicar la regla de Ruffini para obtener el cociente y el resto de la división.
REGLA DE RUFFINI. FACTORIZACIÓN DE POLINOMIOS Si en una división de polinomios el divisor es de la forma (x - a) se puede aplicar la regla de Ruffini para obtener el cociente y el resto de la división.
DEL LENGUAJE DE LOS NÚMEROS AL LEGUAJE ALGEBRAICO.
 DEL LENGUAJE DE LOS NÚMEROS AL LEGUAJE ALGEBRAICO. En ocasiones, en matemáticas, necesitamos operar con números desconocidos. Para ello, se toman letras para representar esas cantidades desconocidas o
DEL LENGUAJE DE LOS NÚMEROS AL LEGUAJE ALGEBRAICO. En ocasiones, en matemáticas, necesitamos operar con números desconocidos. Para ello, se toman letras para representar esas cantidades desconocidas o
Cifras significativas e incertidumbre en las mediciones
 Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
Unidades de medición Cifras significativas e incertidumbre en las mediciones Todas las mediciones constan de una unidad que nos indica lo que fue medido y un número que indica cuántas de esas unidades
MEDIDAS DE TENDENCIA CENTRAL
 CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
CAPÍTULO 14 MEDIDAS DE TENDENCIA CENTRAL A veces, de los datos recolectados ya organizados en alguna de las formas vistas en capítulos anteriores, se desea encontrar una especie de punto central en función
Polinomios. Jesús García de Jalón de la Fuente. IES Ramiro de Maeztu Madrid
 Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Definición Un polinomio es una operación indicada de sumas y productos entre números y una variable x (indeterminada): P (x) = a n x n + a
Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Definición Un polinomio es una operación indicada de sumas y productos entre números y una variable x (indeterminada): P (x) = a n x n + a
SESIÓN 4: WORD 2013 MODIFICAR EL DISEÑO GENERAL CON LOS TEMAS [SESIÓN 4] WORD 2013 APLICAR TEMAS
![SESIÓN 4: WORD 2013 MODIFICAR EL DISEÑO GENERAL CON LOS TEMAS [SESIÓN 4] WORD 2013 APLICAR TEMAS SESIÓN 4: WORD 2013 MODIFICAR EL DISEÑO GENERAL CON LOS TEMAS [SESIÓN 4] WORD 2013 APLICAR TEMAS](/thumbs/25/4585815.jpg) SESIÓN 4: WORD 2013 MODIFICAR EL DISEÑO GENERAL CON LOS TEMAS APLICAR TEMAS Al igual que los temas en Windows 8, esta herramienta permite guardar una serie de formatos que luego puedes aplicar a tu documento,
SESIÓN 4: WORD 2013 MODIFICAR EL DISEÑO GENERAL CON LOS TEMAS APLICAR TEMAS Al igual que los temas en Windows 8, esta herramienta permite guardar una serie de formatos que luego puedes aplicar a tu documento,
Qué son los monomios?
 Qué son los monomios? Recordemos qué es una expresión algebraica. Definición Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones. Si se observan las siguientes
Qué son los monomios? Recordemos qué es una expresión algebraica. Definición Una expresión algebraica es aquella en la que se utilizan letras, números y signos de operaciones. Si se observan las siguientes
2. Gestionar dispositivos de almacenamiento, describir los procedimientos efectuados y aplicar técnicas para asegurar la integridad de la información.
 0226. SEGURIDAD INFORMÁTICA Atendiendo a lo establecido en la Orden de 7 de julio de 2009 (BOJA núm. 165 de 25 de agosto), que desarrolla el currículo correspondiente al título de Técnico en Sistema Microinformáticos
0226. SEGURIDAD INFORMÁTICA Atendiendo a lo establecido en la Orden de 7 de julio de 2009 (BOJA núm. 165 de 25 de agosto), que desarrolla el currículo correspondiente al título de Técnico en Sistema Microinformáticos
POLINOMIOS Y FRACCIONES ALGEBRAICAS
 POLINOMIOS Y FRACCIONES ALGEBRAICAS Página 66 PARA EMPEZAR, REFLEXIONA Y RESUELVE Múltiplos y divisores. Haz la división: 4 + 5 0 + 5 A la vista del resultado, di dos divisores del polinomio 4 + 5 0. (
POLINOMIOS Y FRACCIONES ALGEBRAICAS Página 66 PARA EMPEZAR, REFLEXIONA Y RESUELVE Múltiplos y divisores. Haz la división: 4 + 5 0 + 5 A la vista del resultado, di dos divisores del polinomio 4 + 5 0. (
Funciones polinomiales de grados cero, uno y dos
 Funciones polinomiales de grados cero, uno y dos A una función p se le llama polinomio si: p x = a n x n + a n 1 x n 1 + + a 2 x 2 + a 1x + a 0 Donde un entero no negativo y los números a 0, a 1, a 2,
Funciones polinomiales de grados cero, uno y dos A una función p se le llama polinomio si: p x = a n x n + a n 1 x n 1 + + a 2 x 2 + a 1x + a 0 Donde un entero no negativo y los números a 0, a 1, a 2,
