Introducció a la Trigonometria 4t ESO
|
|
|
- Francisco Javier Botella González
- hace 7 años
- Vistas:
Transcripción
1 Introducció a la Trigonometria 4t ESO
2 Índex: 1. Unitats de mesura d'angles: graus i radians Raons trigonomètriques bàsiques: sinus, cosinus i tangent. Definicions Relacions entre les raons trigonomètriques bàsiques. Relacions fonamentals Resolució de triangles rectangles Ampliació del concepte d'angle Raons trigonomètriques d'angles de qualsevol amplitud. Circumferència goniomètrica. Signes de les raons Relació entre las raons trigonomètriques d'angles de quadrants diferents Taula de valors Exercicis de reforç Exercicis d'ampliació pàg.
3 1. Unitats de mesura d'angles: graus i radians. Mesura en Graus (DEG): El grau és l'angle pla que, amb el vèrtex al centre d'un cercle, intercepta sobre la circumferència d'aquest cercle un arc de longitud πr/360. El seu símbol és: N. Per tant, un angle complet (una volta, gir o revolució sencera) mesura 360. Altres angles molt importants són: angle recte 90 i angle pla 180. Un grau és igual a 60 minuts (1 =60 ) i un minut és igual a 60 segons (1 =60 ). Mesura en radians (rad): El radian és l'angle pla que, amb el vèrtex al centre d'un cercle, intercepta sobre la circumferència d'aquest cercle un arc de longitud igual al radi. el simbolitzem per rad. Equivalència entre graus i radians: La longitud d'una circumferència és πr, per tant, un angle complet mesura πr/r=π rad, és a dir 360 =π rad, o equivalentment 180 =π rad. Per tant, un radian equival, en graus, a 180/π, la qual cosa té un valor aproximat de: 1 rad = De la mateixa forma, tenim que un grau equival a π/180 rad, és a dir, lo que dóna un valor aproximat: 1 =0, rad 3
4 Per tant, el factor conversió per passar de graus a radians és: π ; i per passar de 180 radians a graus és: 180 π. NOTA: si en fixem en una calculadora científica, observarem que per fer càlculs amb angles podem utilitzar diversos sistemes de mesura. Els principals són els graus i els radians, que apareixen a la pantalla amb les abreviatures DEG o D i RAD o R, les quals s'activen normalment amb la tecla MODE. 4
5 . Raons trigonomètriques bàsiques: sin, cos i tan (tg). Definicions. Sobre un triangle rectangle, les raons trigonomètrics no són més que les raons de proporció que hi ha entre els seus catets i la hipotenusa. S'anomena sinus d'un angle a la raó entre el catet oposat i la hipotenusa. Es designa per: sin x catet oposat sin x= hipotenusa Per exemple, quan diem que sin 30 = 1 (ja veurem perquè més endavant) significa que en un triangle rectangle amb un angle de 30, la hipotenusa és el doble del catet oposat, o lo que és el mateix que el catet oposat és la meitat de la hipotenusa. S'anomena cosinus d'un angle a la raó entre el catet contigu i la hipotenusa. Es designa per: cos x catet contigu cos x= hipotenusa 5
6 S'anomena tangent d'un angle a la raó entre el catet oposat i el catet contigu. Es catet oposat designa per: tg x o tan x tan x= catet contigu Per exemple, en un triangle rectangle quan diem que tan 45 =1 no significa res més els dos catets estan en proporció 1, és a dir, els dos catets són iguals. Finalment, només comentar que existeixen les raons inverses del sinus, del cosinus i de la tangent, que s'anomenen, respectivament, cosecant ( cosec x ), secant ( sec x ) i cotangent ( cotg x ). 6
7 3. Relacions entre les raons trigonomètriques bàsiques. Relacions fonamentals. A partir de les definicions de les tres raons trigonomètriques tenim que: sin A= y h cos A= x h tan A= y x És a dir, la primera relació fonamental és: y h tan A= = sin A A tan A=sin x cos A cos A h tan A= sin A cos A y h x A En el triangle rectangle, d'acord amb el teorema de Pitàgores, tenim que: x y =h També ho podem escriure com: x h y =1 h Finalment, aplicant les definicions trigonomètriques anteriors obtenim la relació fonamental (o relació pitagòrica): cos A sin A=1 A partir d'aquí podem fer, si cos A 0, cosa obtenim: tan A 1=sec A sin A A cos A cos cos A = 1 cos A, amb la qual De forma semblant, podem obtenir: cotg A 1=cosec A Utilitzant aquestes relacions, i les obtingudes a partir de les definicions, podem calcular les raons trigonomètriques d'un angle si en coneixem una raó trigonomètrica qualsevol i també obtenir una infinitat d'altres relacions trigonomètriques. 7
8 Observem el quadre resum: En qualsevol triangle rectangle es verifica que la hipotenusa és més gran que qualsevol dels catets. Per tant, com que el sinus i els cosinus d'un angle són la raó entre u catet i la hipotenusa, es compleix que: 1 sinα 1 1 cosα 1 En canvi, com que la tangent és el quocient entre els dos catets (entre el sinus i el cosinus), pot prendre qualsevol valor real: tg α R 8
9 4. Resolució de triangles rectangles. Resoldre un triangle vol dir trobar els seus elements: els tres costats i els tres angles. Un triangle queda determinat quan es coneixen tres dels seus elements, dels quals un, com a mínim, ha de ser un costat, perquè si els tres elements coneguts fossin angles, resoldríem un qualsevol dels possibles triangles semblants. Quan es tracta de triangles rectangles, sempre es coneix un dels elements que és l'angle recte. Així, ens podem trobar quatre casos de resolució de triangles rectangles: a) Es coneixen la hipotenusa i un catet. b) Es coneixen els dos catets. c) Es coneixen la hipotenusa i un angle. d) Es coneixen un catet i un angle. La nomenclatura utilitzada amb els triangles, normalment és la següent (essent A l'angle recte en el cas dels triangles rectangles): B c a A b C Cas a) Dades a i b; incògnites c, B i C. Càlcul de B: Càlcul de C: C=90 -B. sin B= b a i amb la calculadora científica B=sin 1 b a. Càlcul de c: cos B= c a c=a cos B o també c= a b Cas b) Dades b i c; incògnites a, B i C. Càlcul de B: tg B= b c Càlcul de C: C=90 -B. Càlcul de a: a= b c o també i amb la calculadora B=tg 1 b c. sin B= b a a= b sin B 9
10 Cas c) Dades a i B; incògnites b, c i C. Càlcul de b: sin B= b b=a sin B a Càlcul de c: cos B= c a Càlcul de C: C=90 -B. c=a cos B Cas d) Dades b i B; incògnites a, c i C. Càlcul de a: sin B= b a Càlcul de c: tg B= b c Càlcul de C: C=90 -B. Observem el quadre resum: a= b sin B c= b tg B 10
11 5. Ampliació del concepte d'angle. La interpretació geomètrica de l'angle com una regió plana només permet expressar angles més petits o iguals a 360. Suposem que un mòbil es desplaça en una circumferència de radi r partint de A i girant en sentit contrari a les agulles d'un rellotge. Per exemple, podem imaginar el moviment d'una de les cistelles d'una sínia de fira. Aleshores. * si el mòbil s'atura a P, l'arc recorregut és AP i l'angle corresponent és α. * si el mòbil no s'atura a P, continua girant, passa per A i s'atura la segona vegada que passa per P, el camí recorregut és una volta sencera més l'arc AP i l'angle final seria altre cop α, però havent descrit abans una angle complet. * si el mòbil fa k voltes abans d'aturar-se a P, l'angle descrit seria k angles complets més l'angle α. En aquests dos últims casos no té sentit parlar de sector circular. Però si que podem comparar el camí descrit amb l'arc que determina un radian: el quocient entre l'arc descrit pel mòbil i l'arc d'un radian ens dóna la mesura en radians de l'arc descrit pel mòbil. Així, per exemple, dues voltes equivalen a 4π rad o, fent la conversió, 70. Prenent el semieix positiu com a origen dels angles, quan el gir és en el sentit contrari a les agulles del rellotge se'n diu sentit positiu; i sentit negatiu quan el gir és en el sentit de les agulles del rellotge. Per acabar, a tall d'exemple, com es calcula l'angle més petit que 360 corresponent a 710? Si fem la divisió entera, obtenim: 710 = Això significa que l'angle 710 correspon a donar 0 voltes més un angle de 10, i tot això en sentit positiu. Si fos en sentit negatiu escriuríem: -710 =0 (-360 )+(-10 ) la qual cosa significaria que hem donat 0 voltes en el sentit de les agulles del rellotge i, a més, un angle de 10 en el mateix sentit. 11
12 Observeu el diagrama resum: Els eixos de coordenades divideixen la circumferència en quatre parts, que com sabem s'anomenen quadrants, que com podem comprovar al gràfic, els angles divisoris corresponents són: 0 =0 rad 90 = π/ rad 180 = π rad 70 = 3π/ rad 1
13 6. Raons trigonomètriques d'angles de qualsevol amplitud. Circumferència goniomètrica. Signes de les raons trigonomètriques. Es tracta de generalitzar la definició de raó trigonomètrica a angles no aguts. Per això observem la figura següent i recordem que les raons trigonomètriques no varien sobre triangles semblants, per la qual cosa podem considerar la circumferència de radi 1, la qual rep el nom de goniomètrica: Tenint en compte les definicions de les raons sobre un triangle rectangle, a partir de la figura deduïm que les coordenades del punt P són: (x,y)=(cos α,sin α) i si la circumferència tingués radi r, aleshores, les coordenades serien: sin α= ordenada radi = y r cosα= abscissa radi = x r tg α= ordenada abscissa = y x Això ens permet fer una extensió de les definicions de les raons trigonomètriques d'un angle agut a un angle qualsevol, donat que les raons trigonomètriques no depenen del valor del radi de la circumferència escollida. 13
14 Per tant, per a un angle qualsevol α, la definició de les raons trigonomètriques és la següent: El signe de les raons trigonomètriques es calcula fàcilment si sabem el quadrant en què es troba l'angle, ja que aleshores sabem el signe de l'ordenada i el de l'abscissa (el radi de la circumferència és sempre un valor positiu). Podem comprovar-ho al gràfic següent: El signe de la resta de raons trigonomètriques s'obté a partir del signe del sinus i del cosinus. 14
15 7. Relació entre las raons trigonomètriques d'angles de quadrants diferents. En aquest apartat anem a veure les relacions existents entre les raons trigonomètriques de dos angles que presenten alguna propietat entre ells. Aquest estudi permet reduir qualsevol angle a un altre que es trobi al primer quadrant. En primer lloc cal recordar algunes definicions: Angles complementaris són els angles que sumen 90 o π/ rad. Angles suplementaris són els angles que sumen 180 o π rad. Angles oposats són els angles que sumen 0 o 0 rad o múltiples enters de l'angle complet. Raons trigonomètriques d'angles complementaris ( α i 90 α): Els triangles OEC i OAB de la figura són iguals perquè tenen la hipotenusa i els seus angles iguals. D C 1 B 90-α O α E A D'això se'n dedueix: sin 90 α = CE OC =OA OB =cosα cos 90 α =OE OC =AB OB =sinα Finalment: tg 90 α = CE OE =AB OA = 1 tg α =cotg α 15
16 També es pot deduir a partir d'un triangle rectangle; observa la figura: Raons trigonomètriques d'angles suplementaris ( α i 180 α): Sobre la circumferència unitat, està clar que, per simetria, els dos triangles rectangles de la figura són iguals; aleshores: sin 180 α =y=sin α cos 180 α = x= cos α tg 180 α = y x = y x = tg α 16
17 Raons trigonomètriques d'angles que difereixen 180 (α i α): Observem la figura Els dos triangles rectangles són iguals perquè tenen iguals la hipotenusa (radi) i els seus angles. A partir d'això deduïm: sin 180 α = y= sinα cos 180 α = x= cos α tg 180 α = y x = y x =tg α Raons trigonomètriques d'angles oposats ( α i α o 360 α): Donat que els triangles rectangles OBC i OAC tenen la mateixa hipotenusa i els mateixos angles, són iguals. Per tant: O α -α 1 A B A sin α = CA OC = AB OB = sinα cos α = OA OC =OA OB =cosα C tg α = CA OA = AB OA = tg α 17
18 8. Taula de valors. Si dividim un angle recte en dos o tres parts obtenim els angles de 45, 30 i 60 ; aquests angles també apareixen a l'escaire i al cartabó. La calculadora ens dóna les raons trigonomètriques de qualsevol angle, però en la majoria de casos són aproximacions. Anem a trobar els valors exactes de les raons trigonomètriques dels angles anteriors per tal de construir una taula de valors. Raons trigonomètriques de l'angle 45 : La meitat d'un quadrat ens dóna un triangle rectangle isòsceles com el de la figura, i, per tant, amb angles de 45. Aleshores. c =a a =a c=a Per tant, cos 45 =sin45 = a c = a a = i tg 45 =a a =1 Raons trigonomètriques dels angles 30 i 60 : La meitat d'un triangle equilàter ens determina un triangle rectangle com el de la figura i, per tant, tenim que c=a. Aleshores: b =c a =c c 4 =3 4 c b= 3 c Per tant, sin30 = a c = a a = 1 cos30 = b c = 3 c c = 3 tg 30 = 1 = I, donat que 30 i 60 són angles complementaris: cos60 = 1 sin 60 = 3 tg 60 = 3 18
19 Raons trigonomètriques dels angles 90, 180 i 70 : A partir de les definicions de les raons per angles no aguts, si observem la figura tenim que: sin 90 = 1 cos 90 =0 tg 90 =1/0 tg 90 =± sin 180 = 0 cos 180 =-1 tg 180 =0 sin 70 =-1 cos 70 =0 tg 70 =± D'aquesta manera, obtenim la següent taula: graus radians 0 π/6 π/4 π/3 π/ π 3π/ sin cos tg ± 0 ± Com exercici, es pot ampliar aquesta taula amb els angles de 30, 45 i 60 traslladats als diferents quadrants. 19
20 9. Exercicis de reforç: 1. Calcula la mesura, en graus i radians, de cada un dels següents angles: a) L angle d un triangle equilàter. b) Els angles d un rombe, un dels quals mesura 30.. Utilitza la calculadora per a trobar x en cada un dels següents casos, determinant els angles aguts amb una precisió de segons i arrodonint les raons angulars a las mil lèsimes: x=tan ' ; cos x=0, 7 ; x=sin 75 ; x=cos π 1 ; sin x=0,8 ; tan x=7,35 3. La hipotenusa d un triangle rectangle mesura 13 cm, i un dels seus catets, 1 cm. Troba les raons trigonomètriques de l angle oposat al catet menor i l àrea del triangle. Fes un dibuix per explicar els càlculs realitzats. 4. Les rectes tangents a una circumferència des d un punt exterior, que dista del centre 50 m, formen un angle de 48. Donat que les rectes tangents són perpendiculars als radis en el punt de tangència, troba l àrea del cercle. Fes un dibuix aproximat que t ajudi en els càlculs. 5. Calcula el valor de les raons desconegudes (sin, cos i tan) de l angle agut α en els següents casos: a) sinα=0,8 b) cosα= 1 3 c) tanα= Si x és un angle agut, simplifica tot el que sigui possible les següents expressions: A= 1 cos x 1 sin x 1 cos x 1 sin x B= cos3 x x sin x sin3 cos x 7. Les mesures, en metres, de les diagonals d un rombe són proporcionals als números 6 y 8. Amb aquestes dades, troba els dos angles del rombe. Fes un dibuix que t ajudi a resoldre el problema. 8. S observa el punt més alt, D, d un arbre des d un punt, B, del terra, sota un angle de 30. El punt B dista 18 m del peu, A, de l arbre. Quina és la seva altura? A quina distància d del punt B en la línia AB hauríem de situar-nos per observar el punt D des de un punto C amb un angle de 0? 0
21 9. En la figura, l angle A és de 90, i els segments AD y DC tenen la mateixa mesura. Són iguals els angles α i β? Raona la teva resposta. 10. En el paral lelogram ABCD, calcula la mesura de la diagonal BD i l àrea del paral lelogram. 11. Expressa els següents angles com a suma d un nombre enter de voltes i un angle menor que 360 o π rad: π rad 17 π 3 rad 1. Indica en quin quadrant estan situats cada un dels següents angles: π 5 rad 80 π 7 rad 13. En una circumferència de 0 m de radi, un arc mesura 65 m. Calcula en graus i radians l angle central que li correspon. 14. Donats els angles α = 78, β = -60 i γ = 105, indica en quin quadrant estan situats els següents angles: A=5α 3β 4γ B= 3α β 4 α γ Sense utilitzar la calculadora, calcula el valor exacte de las expressions: A=3 sin70 4 tan135 cos300 B= sin 315 tan900 3 cos540 C= sin tan40 1 cos315 1
22 16. Sabent que α és un angle agut, tal que cosα=0,6, calcula les següents raons trigonomètriques: sin 180 α sin 900 α tan 90 α cos 180 α 17. Amb l ajut de la calculadora i utilitzant el mode angular en graus, troba, amb tres xifres decimals significatives, els valors de les següents raons trigonomètriques: cos385 tan 18 π 7 sin.050 cos 13 π Calcula el valor del sinus i el cosinus d un angle del quart quadrant, la tangent del qual val 3 4. Expressa les solucions en forma fraccionària. 19. Troba, sense fer ús de la calculadora, quins angles de la circumferència goniomètrica compleixen les següents condicions: a) El sinus val 1 b) El cosinus val 3 c) La tangent val Troba els angles x tals que 0 x 360, els quals verifiquen les igualtats següents: a) sin x 60 = 1 b) tan 5x 40 = 1
23 10. Exercicis d ampliació: 1. Sobre una circumferència de radi R, se consideren: a) Per un arc de longitud L=3 R, quant val, en graus, l angle central que determina? b) Para un sector circular de superfície S=R, quant val, en graus, l angle central que avarca?. Calcula l altura de la muntanya de la figura, sabent que dos observadors situats en dos punts A y B, distants 500 metres entre si, observen el cim D sota angles de 30 y 4, respectivament. 3. a) Comprova si és certa la igualtat: sina cos a a cos a sin a =tan 1 tan a b) Simplifica tot el que puguis l expressió: cos 3 a sin a cos a sin a cosa sin 3 a 4. Les bases d un trapezi isòsceles mesuren 4 y 16 cm, i l angle que formen els costats no paral lels és de 30. Troba el perímetre i l àrea del trapezi, fes un dibuix que ajudi a aclarir la solució del problema. 5. En una circumferència de 3 metres de radio es dibuixa una corda AB, tal que l arc definit mesura 5 metres. Determina la longitud d aquesta corda i la distància al centre de la circumferència. 6. En un polígon regular, calcula en graus i radians, en funció del nombre de costats: a) La mesura de l angle central i de l angle interior. b) La suma dels angles interiors del polígon. Aplica els resultats anteriors al cas del dodecàgon. 7. Proba que si A, B i C són las mesures dels angles d un triangle qualsevol, es verifiquen les següents igualtats: sin A=sin B C sin A B C = sin A 3
24 8. Una torre de telefonia està subjecta en el seu extrem superior C por dos cables tensos AC i CB collats a terra formant angles de 40 i 55, respectivament, tal i com mostra la figura (les dades en metres). Troba l altura h de la torre i els metres de cable que s han necessitat per a subjectar-la. 9. Amb les dades que proporciona la figura, sabent que els segments BD y DC tenen la mateixa longitud, troba l àrea del triangle BCD i l angle α amb una precisió de segons. 10. Utilitzant procediments trigonomètrics, demostra el teorema de l altura que diu: «En tot triangle rectangle, el quadrat de l altura és el producte de les projeccions dels catets sobre la hipotenusa», o lo que és el mateix, que h =m n, essent h, m i n les dades assenyalades en la figura. 11. A las tres en punt, las agulles d un rellotge formen un angle recte. A quina hora tornaran a formar, per primera vegada, un angle recte? 4
25 1. Considera un triangle ABC, rectangle en A. Quina relació existeix entre las raons trigonomètriques dels seus angles aguts? És certa la igualtat tan B tan C=1?: 13. Sigui α un angle qualsevol, per el que estan definides les tres raons trigonomètriques sinus, cosinus i tangent. Proba que es verifica la igualtat: tan α tan α sin α=sin α 14. Simplifica tot el que puguis les següents expressions: A=cos 5π x sin π x cos 3π x sin 7π x B= cos x 1 sin x 1 sin x, per a x π cos x 15. Troba totes les solucions de les següents equacions trigonomètriques: cos 4x=sin x 135 cos x sin x 1=0 16. D un angle α, situat en el tercer quadrant, se sap que el seu cosinus és el triple que el seu sinus. Calcula amb exactitud, i sense necessitat de calcular el valor de l angle α, les següents raons: sin 180 α cos π α tan 90 α cos π α 5
TEMA 1: Trigonometria
 TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
Exercicis de trigonometria
 Mesura d'angles 1. En una circumferència de 5 cm de radi, un arc fa 1, m. Troba el seu angle central corresponent en radians i en graus sexagesimals.. Expressa en radians de manera exacta els angles següents,
Mesura d'angles 1. En una circumferència de 5 cm de radi, un arc fa 1, m. Troba el seu angle central corresponent en radians i en graus sexagesimals.. Expressa en radians de manera exacta els angles següents,
Trigonometria Resolució de triangles.
 Trigonometria Resolució de triangles. Raons trigonomètriques d un angle agut. Considerarem el triangle rectangle ABC on A = 90º Recordem que en qualsevol triangle rectangle Es complia el teorema de Pitàgores:
Trigonometria Resolució de triangles. Raons trigonomètriques d un angle agut. Considerarem el triangle rectangle ABC on A = 90º Recordem que en qualsevol triangle rectangle Es complia el teorema de Pitàgores:
UNITAT 3: TRIGONOMETRIA
 UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ 1.2. CLASSIFICACIÓ
 GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
EXERCICIS PROPOSATS. 3 cm
 EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
quaderns de matemàtiques
 1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte xevi.vb@gmail.com CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte xevi.vb@gmail.com CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
8 Geometria analítica
 Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
Geometria analítica INTRODUCCIÓ Els vectors s utilitzen en diverses branques de la física que fan servir magnituds vectorials, per això és important que els alumnes en coneguin els elements i les operacions.
FITXA 1: Polígons. Conceptes
 FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
TRIGONOMETRIA. FUNCIONS TRIGONOMÈTRIQUES. MATEMÀTIQUES-1
 TRIGONOMETRIA. FUNCIONS TRIGONOMÈTRIQUES. 1. Angles i mesura d angles.. Raons trigonomètriques d un angle agut. 3. Resolució de triangles rectangles. 4. Raons trigonomètriques d un angle qualsevol. 5.
TRIGONOMETRIA. FUNCIONS TRIGONOMÈTRIQUES. 1. Angles i mesura d angles.. Raons trigonomètriques d un angle agut. 3. Resolució de triangles rectangles. 4. Raons trigonomètriques d un angle qualsevol. 5.
POLÍGONS, CIRCUMFERÈNCIA I CERCLE
 POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
DIVISIBILITAT. Amb els nombres 5, 7 i 35 podem escriure diverses expressions matemàtiques: 5x7= 35 35 5 35
 ESO Divisibilitat 1 ESO Divisibilitat 2 A. El significat de les paraules. DIVISIBILITAT Amb els nombres 5, 7 i 35 podem escriure diverses expressions matemàtiques: 5x7= 35 35 = 7 5 35 = 5 7 35 7 0 5 35
ESO Divisibilitat 1 ESO Divisibilitat 2 A. El significat de les paraules. DIVISIBILITAT Amb els nombres 5, 7 i 35 podem escriure diverses expressions matemàtiques: 5x7= 35 35 = 7 5 35 = 5 7 35 7 0 5 35
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
La porció limitada per una línia poligonal tancada és un
 PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
Tema 2: Trigonometria
 Tema 2: Trigonometria Alguns d aquests exercicis han estat extrets de la web i de materials elaborats a l IES Antoni Maura (Palma) Vídeos interessants (Com Eratòstenes va mesurar la Terra): https://www.youtube.com/watch?v=siajflyd508
Tema 2: Trigonometria Alguns d aquests exercicis han estat extrets de la web i de materials elaborats a l IES Antoni Maura (Palma) Vídeos interessants (Com Eratòstenes va mesurar la Terra): https://www.youtube.com/watch?v=siajflyd508
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
TRIANGLES. TEOREMA DE PITÀGORES.
 TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
Els catets d un triangle rectangle mesuren 5 i 13 centímetres. Calcula n el valor de la hipotenusa.
 1 LONGITUDS I ÀREES EXERCICIS PER A ENTRENAR-SE Teorema de Pitàgores 1.8 Els catets d un triangle rectangle mesuren i 1 centímetres. Calcula n el valor de la hipotenusa. Si fem servir el teorema de Pitàgores:
1 LONGITUDS I ÀREES EXERCICIS PER A ENTRENAR-SE Teorema de Pitàgores 1.8 Els catets d un triangle rectangle mesuren i 1 centímetres. Calcula n el valor de la hipotenusa. Si fem servir el teorema de Pitàgores:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Matemàtiques 1r d'eso Professora: Lucía Clar Tur DOSSIER DE REPÀS
 DOSSIER DE REPÀS 1. Ordena els nombres de més petit a més gran: 01 0 01 101 0 001 0 001 0 1. Converteix els nombres fraccionaris en nombres decimals i representa ls en la recta: /4 1/ 8/ 11/10. Efectua
DOSSIER DE REPÀS 1. Ordena els nombres de més petit a més gran: 01 0 01 101 0 001 0 001 0 1. Converteix els nombres fraccionaris en nombres decimals i representa ls en la recta: /4 1/ 8/ 11/10. Efectua
UN POLÍGON és una superficie plana
 UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
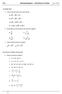 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Sector circular i Segment circular.
 Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
DOSSIER ESTIU 2018 MATEMÀTIQUES
 DOSSIER ESTIU 2018 MATEMÀTIQUES ELS ALUMNES AMB L ASSIGNATURA SUSPESA HAN D ENTREGAR EL DOSSIER CORRECTAMENT PER PODER REALITZAR L EXAMEN DE SETEMBRE. Has de presentar el dossier en fulls apart. S han
DOSSIER ESTIU 2018 MATEMÀTIQUES ELS ALUMNES AMB L ASSIGNATURA SUSPESA HAN D ENTREGAR EL DOSSIER CORRECTAMENT PER PODER REALITZAR L EXAMEN DE SETEMBRE. Has de presentar el dossier en fulls apart. S han
FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES
 FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES Pàgina 8. Encara que el mètode per a resoldre les preguntes següents se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radiants corresponen als
FUNCIONS I FÓRMULES TRIGONOMÈTRIQUES Pàgina 8. Encara que el mètode per a resoldre les preguntes següents se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radiants corresponen als
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
Proporcionalitat i percentatges
 Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
FITXA 1: Angles consecutius i adjacents
 FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
1.- Elements d una recta Vector director d una recta Vector normal d una recta Pendent d una recta
 .- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
.- Elements d una recta..- Vector director d una recta..- Vector normal d una recta.3.- Pendent d una recta.- Equacions d una recta..- Equació ectorial, paramètrica i contínua..- Equació explícita.3.-
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Àmbit de les Matemàtiques, de la Ciència i de la Tecnologia M14 Operacions numèriques UNITAT 1 OPERACIONS AMB ENTERS
 UNITAT 1 OPERACIONS AMB ENTERS 1 Què treballaràs? En acabar la unitat has de ser capaç de... Sumar, restar, multiplicar i dividir nombres enters. Entendre i saber utilitzar les propietats de la suma i
UNITAT 1 OPERACIONS AMB ENTERS 1 Què treballaràs? En acabar la unitat has de ser capaç de... Sumar, restar, multiplicar i dividir nombres enters. Entendre i saber utilitzar les propietats de la suma i
Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 3 ÀREES I VOLUMS. Unitat 3 ÀREES I VOLUMS
 70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
4. EQUACIONS DE PRIMER GRAU AMB UNA INCÒGNITA
 Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
Definició d'equació. Equacions de primer grau amb una incògnita 1. EQUACIONS: DEFINICIONS Equació: igualtat entre dues expressions algebraiques. L'expressió de l'esquerra de la igualtat rep el nom de PRIMER
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
Càlcul d'àrees i volums.
 Càlcul d'àrees i volums. Exemple 1. Donada la figura següent: Calcula'n: superfície volum Resolució: Fixem-nos que la superfície està formada per tres objectes.: 1. la base del cilindre 2. la paret del
Càlcul d'àrees i volums. Exemple 1. Donada la figura següent: Calcula'n: superfície volum Resolució: Fixem-nos que la superfície està formada per tres objectes.: 1. la base del cilindre 2. la paret del
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
UNITAT 8. FIGURES PLANES
 1. Fes servir aquests punts per traçar dues línies poligonals més de cada tipus, apart de les dels exemples: Línia poligonal oberta Línia poligonal oberta creuada Línia poligonal tancada Línia poligonal
1. Fes servir aquests punts per traçar dues línies poligonals més de cada tipus, apart de les dels exemples: Línia poligonal oberta Línia poligonal oberta creuada Línia poligonal tancada Línia poligonal
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
Es important dir que, dos vectors, des del punt de vista matemàtic, són iguals quan els seus mòduls, sentits i direccions són equivalents.
 1 CÀLCUL VECTORIAL Abans de començar a parlar de vectors i ficar-nos plenament en el seu estudi, hem de saber distingir els dos tipus de magnituds que defineixen la física: 1. Magnituds escalars: magnituds
1 CÀLCUL VECTORIAL Abans de començar a parlar de vectors i ficar-nos plenament en el seu estudi, hem de saber distingir els dos tipus de magnituds que defineixen la física: 1. Magnituds escalars: magnituds
GEOMETRIA ANALÍTICA DEL PLA. MATEMÀTIQUES-1
 GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
GEOMETRIA ANALÍTICA DEL PLA. 1. Vectors en el pla.. Equacions de la recta. 3. Posició relativa de dues rectes. 4. Paral lelisme de rectes. 5. Producte escalar de dos vectors. 6. Perpendicularitat de rectes.
ACTIVITATS FINALS. Segments proporcionals. Teorema de Tales. a) AB = 2 cm i CD = 5 cm. b) AB = 7,5 cm i CD = 15 cm. c) AB = 1 m i CD = 30 dm.
 TIVITTS INLS Segments proporcionals 33 34 a) cm i b) 7, i c) m i 30 dm d) 7 mm i 0,4 dm 35 4 5 36 3 7 37 a) cm E GH 0 cm b) E 9 cm GH Teorema de Tales 43 a) b) 3 cm, cm,, 3, 44 a) e) 4,,8 cm cm b) f )
TIVITTS INLS Segments proporcionals 33 34 a) cm i b) 7, i c) m i 30 dm d) 7 mm i 0,4 dm 35 4 5 36 3 7 37 a) cm E GH 0 cm b) E 9 cm GH Teorema de Tales 43 a) b) 3 cm, cm,, 3, 44 a) e) 4,,8 cm cm b) f )
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
TEMES TREBALLATS A 3r d'eso
 TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 85 Activitat 1 Calcula l àrea de la figura prenent com a unitat d àrea la quadrícula que hi ha indicada: Activitat Ens referirem a la unitat d àrea amb el símbol
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 85 Activitat 1 Calcula l àrea de la figura prenent com a unitat d àrea la quadrícula que hi ha indicada: Activitat Ens referirem a la unitat d àrea amb el símbol
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
2.Igualtat. 3.Gir. 4.Simetria. 6.Semblança. 7.Escales
 DIBUIX TÈCNIC 3. TRANSFORMACIONS GEOMÈTRIQUES. ESCALES 1.Transformacions isomètriques 2.Igualtat 3.Gir 4.Simetria 5.Transformacions isomòrfiques 6.Semblança 7.Escales COL LEGI ST. JOSEP SANT SADURNÍ D
DIBUIX TÈCNIC 3. TRANSFORMACIONS GEOMÈTRIQUES. ESCALES 1.Transformacions isomètriques 2.Igualtat 3.Gir 4.Simetria 5.Transformacions isomòrfiques 6.Semblança 7.Escales COL LEGI ST. JOSEP SANT SADURNÍ D
UNITAT DIDÀCTICA 5 F UNCIONS I FÓRMULES TRIGONOMÈTRIQUES
 Pàgina UNITAT DIDÀCTICA. Encara que el mètode per resoldre les preguntes que hi ha a continuació se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radians corresponen als 0 d una circumferència?
Pàgina UNITAT DIDÀCTICA. Encara que el mètode per resoldre les preguntes que hi ha a continuació se sistematitza a la pàgina següent, pots resoldre-les ara: a) Quants radians corresponen als 0 d una circumferència?
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
30. Calculeu l altura d una piràmide de base quadrada de 5 m de costat i 10 m d aresta lateral.
 29. Es vol construir un celler per emmagatzemar bótes de vi de la forma com s indica en el dibui. Si d = 60 cm és el diàmetre de les bótes. Quina ha de ser l altura del celler? 30. Calculeu l altura d
29. Es vol construir un celler per emmagatzemar bótes de vi de la forma com s indica en el dibui. Si d = 60 cm és el diàmetre de les bótes. Quina ha de ser l altura del celler? 30. Calculeu l altura d
Unitat 1. Nombres reals.
 Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
Tema 1: Equacions i problemes de primer grau.
 Tema 1: Equacions i problemes de primer grau. 1.1. Igualtats, identitats i equacions. Dues expressions separades pel signe = és una igualtat. Les igualtats poden ser numèriques (només contenen números)
Tema 1: Equacions i problemes de primer grau. 1.1. Igualtats, identitats i equacions. Dues expressions separades pel signe = és una igualtat. Les igualtats poden ser numèriques (només contenen números)
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
ACTIVITATS COMPLEMENTÀRIES DE TRIGONOMETRIA
 Unitat 1: Angles i triangles. Activitat 1.1 Classifiqueu els angles que observeu en la figura adjunta i mesureu la seva amplitud amb l ajut d un transportador d angles. Activitat 1.2 a) Desprès d una operació
Unitat 1: Angles i triangles. Activitat 1.1 Classifiqueu els angles que observeu en la figura adjunta i mesureu la seva amplitud amb l ajut d un transportador d angles. Activitat 1.2 a) Desprès d una operació
1. Indica si les següents expressions són equacions o identitats: a. b. c. d.
 Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
7. Calcula P (x ) Q (x ): P (x ) = 5x 4 + x 3 2x 2 5 Q (x ) = 7x 4 5x 2 + 3x + 2 P (x ) Q (x ) = 2x 4 + x 3 + 3x 2 3x 7
 50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
Vector unitari Els vectors unitaris tenen de mòdul la unitat. Calculem el vector unitari del vector següent manera: ( ) ( )
 GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
GEOMETRIA EN L ESPAI VECTORS EN L ESPAI OPERACIONS AMB VECTORS Un vector és un segment orientat en l espai que té un mòdul, una direcció i un sentit coneguts: té un extrem i un origen (Exemple: vector
GEOMETRIA Optativa 1r d ESO
 GEOMETRIA Optativa 1r d ESO Dossier d estiu per a recuperar la matèria al setembre. S haurà d entregar el dia de l examen. L examen valdrà un 50% i aquest dossier l altre 50%. S han d escriure tots els
GEOMETRIA Optativa 1r d ESO Dossier d estiu per a recuperar la matèria al setembre. S haurà d entregar el dia de l examen. L examen valdrà un 50% i aquest dossier l altre 50%. S han d escriure tots els
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
TEMA 4: Equacions de primer grau
 TEMA 4: Equacions de primer grau Full de preparació Aquest full s ha de lliurar el dia de la prova Nom:... Curs:... 1. Expressa algèbricament les operacions següents: a) Nombre de rodes necessàries per
TEMA 4: Equacions de primer grau Full de preparació Aquest full s ha de lliurar el dia de la prova Nom:... Curs:... 1. Expressa algèbricament les operacions següents: a) Nombre de rodes necessàries per
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
MATEMÀTIQUES. DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E. Nom i Cognoms (alumne):... Nom professor:...
 zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
Teorema de Tales. Triangles semblants. Teorema de Pitàgores 116 MATEMÀTIQUES A. 1. Angles iguals (amb dos n hi ha prou) Â = Â y Bˆ
 7 Semblança i trigonometria Objectius En aquesta quinzena aprendràs a: Reconèixer triangles semblants. Calcular distàncies inaccessibles aplicant la semblança de triangles. Nocions bàsiques de trigonometria.
7 Semblança i trigonometria Objectius En aquesta quinzena aprendràs a: Reconèixer triangles semblants. Calcular distàncies inaccessibles aplicant la semblança de triangles. Nocions bàsiques de trigonometria.
Problemes de Geometria per a l ESO Calculeu l àrea d un cercle tal que té un hexàgon inscrit de costats consecutius 1, 1, 1, 2, 2, 2.
 Problemes de Geometria per a l SO 7 6- alculeu l àrea d un cercle tal que té un hexàgon inscrit de costats consecutius,,,,, Siga l hexàgon inscrit en la circumferència de centre O i radi r Siga α O, β
Problemes de Geometria per a l SO 7 6- alculeu l àrea d un cercle tal que té un hexàgon inscrit de costats consecutius,,,,, Siga l hexàgon inscrit en la circumferència de centre O i radi r Siga α O, β
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
FITXA 1: Angles rectes, aguts i obtusos
 FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
Geometria. Àrees i volums de cossos geomètrics
 Geometria. Àrees i volums de cossos geomètrics Àrea de figures planes... Àrea dels paral lelograms... Àrea del quadrat... Àrea del rectangle... 3 Àrea del rombe... 4 Àrea del paral lelogram... 4 Àrea dels
Geometria. Àrees i volums de cossos geomètrics Àrea de figures planes... Àrea dels paral lelograms... Àrea del quadrat... Àrea del rectangle... 3 Àrea del rombe... 4 Àrea del paral lelogram... 4 Àrea dels
d) L'angle que forma el costat de 3 cm amb el de 4 cm és rectangle.
 ACTIVITATS PER PRACTICAR r LLIURAMENT Es tracta de què resoleu les qüestions següents llegint atentament els enunciats i, després, comproveu si les vostres respostes coincideixen amb les solucions donades.
ACTIVITATS PER PRACTICAR r LLIURAMENT Es tracta de què resoleu les qüestions següents llegint atentament els enunciats i, després, comproveu si les vostres respostes coincideixen amb les solucions donades.
DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO
 Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
Semblança. Teorema de Pitàgores.
 7 Semblança. Teorema de Pitàgores. Objectius En aquesta quinzena aprendràs a: Aplicar correctament el Teorema de Tales. Reconèixer y dibuixar figures semblants. Aplicar els criteris de semblança de triangles
7 Semblança. Teorema de Pitàgores. Objectius En aquesta quinzena aprendràs a: Aplicar correctament el Teorema de Tales. Reconèixer y dibuixar figures semblants. Aplicar els criteris de semblança de triangles
Geometria / GE 2. Perpendicularitat S. Xambó
 Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Geometria / GE 2. Perpendicularitat S. Xambó Vectors perpendiculars Ortogonal d un subespai Varietats lineals ortogonals Projecció ortogonal Càlcul efectiu de la projecció ortogonal Aplicació: ortonormalització
Foto: El teorema de Tales a la ciutat de París, Autora: Tamara Victoria Fernández
 Foto: El teorema de Tales a la ciutat de París, Autora: Tamara Victoria Fernández Matemàtiques 1r ESO T. tales 1 Matemàtiques 1r ESO T. tales 2 Teorema de Tales A.1 Utilitzant tota la plana apaïsada d
Foto: El teorema de Tales a la ciutat de París, Autora: Tamara Victoria Fernández Matemàtiques 1r ESO T. tales 1 Matemàtiques 1r ESO T. tales 2 Teorema de Tales A.1 Utilitzant tota la plana apaïsada d
Proporcionalitat geomètrica
 Proporcionalitat geomètrica Guió de treball de l alumne/a...del grup... Raó entre dos segments 1. Amb el GeoGebra obriu l arxiu MArao.html, us trobareu dos segments a i b, els quals podeu seleccionar les
Proporcionalitat geomètrica Guió de treball de l alumne/a...del grup... Raó entre dos segments 1. Amb el GeoGebra obriu l arxiu MArao.html, us trobareu dos segments a i b, els quals podeu seleccionar les
Aproximar un nombre decimal consisteix a reduir-lo a un altre nombre decimal exacte el valor del qual sigui molt pròxim al seu.
 Aproximar un nombre decimal consisteix a reduir-lo a un altre nombre decimal exacte el valor del qual sigui molt pròxim al seu. El nombre π és un nombre que té infinites xifres decimals. Sabem que aquest
Aproximar un nombre decimal consisteix a reduir-lo a un altre nombre decimal exacte el valor del qual sigui molt pròxim al seu. El nombre π és un nombre que té infinites xifres decimals. Sabem que aquest
MÍNIM COMÚ MULTIPLE m.c.m
 MÍNIM COMÚ MULTIPLE m.c.m Al calcular el mínim comú múltiple de dos o més nombres el que estem fent és quedar-nos amb el valor més petit de tots els múltiples que són comuns a aquests nombres. És a dir,
MÍNIM COMÚ MULTIPLE m.c.m Al calcular el mínim comú múltiple de dos o més nombres el que estem fent és quedar-nos amb el valor més petit de tots els múltiples que són comuns a aquests nombres. És a dir,
FITXA 1: Angles rectes, aguts i obtusos
 FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC
 PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC 1º A Donada la perspectiva de la figura dibuixa, a mà alçada, les tres vistes de la mateixa Dada la perspectiva
PROVES D ACCÉS A CICLES FORMATIUS DE GRAU SUPERIOR Convocatòria maig de 2005 DIBUIX TÈCNIC 1º A Donada la perspectiva de la figura dibuixa, a mà alçada, les tres vistes de la mateixa Dada la perspectiva
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
1 Problemes de física per a batxillerat... // M. L. Escoda, J. Planella, J. J. Suñol // ISBN: 84-8458-220-5
 1 Problemes de física per a batxillerat... // M. L. Escoda, J. Planella, J. J. Suñol // ISBN: 84-8458-0-5 MESURA FÍSICA: MAGNITUDS i UNITATS Índex P.1. P.. P.3. P.4. P.5. Magnituds físiques. Unitats Anàlisi
1 Problemes de física per a batxillerat... // M. L. Escoda, J. Planella, J. J. Suñol // ISBN: 84-8458-0-5 MESURA FÍSICA: MAGNITUDS i UNITATS Índex P.1. P.. P.3. P.4. P.5. Magnituds físiques. Unitats Anàlisi
