UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
|
|
|
- Nieves Sánchez Paz
- hace 7 años
- Vistas:
Transcripción
1 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como queramos sin más que tomar valores de x suficientemente grandes. En tal caso, se escribe lim x + f(x) = L Ejemplo: lim x + 3X+1 2x = 3 2 lim x f(x) = L Se dice que el límite de f(x) cuando x tiende a - es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como queramos sin más que tomar valores de x suficientemente pequeños. En tal caso, se escribe lim x f(x) = L Ejemplo: lim x 3X+1 2x = 3 2
2 lim x + f(x) = + Se dice que el límite de f(x) cuando x tiende a + es +, si podemos hacer que f (x) sea tan grande como queramos sin más que tomar valores de x suficientemente grandes. En tal caso, se escribe lim x + f(x) = + Ejemplo: lim x + 3X + 1 = + lim x f(x) = + Se dice que el límite de f(x) cuando x tiende a - es +, si podemos hacer que f (x) sea tan grande como queramos sin más que tomar valores de x suficientemente pequeños. En tal caso, se escribe lim x f(x) = + Ejemplo: lim x X + 1 = +
3 lim x + f(x) = Se dice que el límite de f(x) cuando x tiende a + es -, si podemos hacer que f (x) sea tan pequeño como queramos sin más que tomar valores de x suficientemente grandes. En tal caso, se escribe lim x + f(x) = Ejemplo: lim x + X + 1 = lim x f(x) = Se dice que el límite de f(x) cuando x tiende a - es -, si podemos hacer que f (x) sea tan pequeño como queramos sin más que tomar valores de x suficientemente pequeños. En tal caso, se escribe lim x f(x) = Ejemplo: lim x X 3 =
4 2.-Operaciones con límites en el infinito Para facilitar su aprendizaje, en este apartado vamos a trabajar solo con el valor del límite entre paréntesis en lugar de toda la expresión, es decir: Para hablar del lim x ± f(x) = a, usaremos solo (a) Para hablar del lim x ± f(x) = +, usaremos únicamente (+ ) Para hablar del lim x ± f(x) =, usaremos solo (- ) De este modo se cumple: Suma y Resta Producto Cociente (a) + (b) = (a + b) (a) (b) = (a b) (a) (b) = a b con b 0 (a) (b) = (a - b) (a) + (+ ) = (+ ) (a) (+ ) = (+ ) con a 0 (a) (+ ) = (- ) con a<0 Regla de los signos (a) (- ) = (- ) con a 0 (a) (- ) = (+ ) con a<0 (a) (0) = (± ) (a) (± ) = (0) (a) - (+ ) = (- ) Regla de los signos (0) (± ) = IND [0 ] (a) + (- ) = (- ) (+ ) (+ ) = (+ ) (+ ) (- ) = (- ) (- ) (+ ) = (- ) (- ) (- ) = (+ ) (a) - (- ) = (+ ) (+ ) + (+ ) = (+ ) (- ) + (- ) = (- ) (+ ) - (+ ) = IND (+ ) + (- ) =IND Regla de los signos (± ) (a) (0) (± ) = (0) = (+ ) o ( ) con a 0 Regla de los signos (± ) (0) = (± ) (0) (0) = IND (± ) (± ) = IND [ ]
5 Potencias (a) (b) (a) (+ ) (a) ( ) (+ ) (b) (+ ) (± ) (a) (b) = (a b ) con a 0 (0) (b) = (0) con b>0 (0) (b) = (+ ) (a) (+ ) = (+ ) con a>1 (a) (+ ) = (0) con 0<a<1 (a) (+ ) = IND (a) ( ) = (0) con a>1 (a) ( ) = (+ ) con 0<a<1 (a) ( ) = IND (+ ) (b) = (+ ) con b>0 (+ ) (b) = (0) con b<0 (+ ) (b) = IND (+ ) (+ ) = (+ ) (+ ) ( ) = (0) con b<0 con a=1 con a=1 con b=0 [1 ] [1 ] [ 0 ] (0) (b) = IND con b=0 [0 0 ] Se proponen el ejercicio 12.
6 3.- Límite de una función en un punto. Límites laterales lim x a f(x) = L Sea f (x) una función definida en un entorno de x = a. Se dice que el límite de f (x) cuando x tiende hacia a es L, si podemos hacer que f (x) se aproxime a L tanto como queramos sin más que tomar valores de x suficientemente próximos al valor x = a. Lo escribiremos lim x a f(x) = L. Ejemplo: lim x 2 x + 3 = 5 Hemos de tener en cuenta que la definición de límite no depende del valor de la función en x = a, es decir, no tiene porqué cumplirse que f (x) = L, de hecho, ni siquiera tiene que estar definida la función en x = a. La idea de límite analiza lo que ocurre con las imágenes cuando nos acercamos, sin llegar a alcanzar (en principio) el valor x = a. lim x a f(x) = ± Sea f (x) una función definida en un entorno de x = a. Se dice que el límite de f (x) cuando x tiende hacia a es más infinito, si podemos hacer que f (x) tome valores positivos tan grandes como queramos sin más que tomar valores de x suficientemente próximos al valor x = a. Lo escribiremos lim x a f(x) = +. De forma análoga, se define el límite cuando x tiende hacia a es menos infinito.
7 Ejemplo: lim x x = ± Límites Laterales: En determinadas funciones, como por ejemplo las definidas a trozos, los valores que toma alrededor de un punto, dependen si nos acercamos por la izquierda o por la derecha del punto y el comportamiento puede ser muy distinto en ambas direcciones. Por ello, además de las definiciones de límite, conviene llevar a cabo definiciones que tengan en cuenta dicha circunstancia. Nos referimos a las definiciones de límites laterales. Sea f (x) una función definida en un entorno a la izquierda de x = a. Se dice que el límite de f (x) cuando x tiende hacia a por la izquierda es L, si podemos hacer que f (x) se aproxime a L tanto como queramos sin más que tomar valores de x suficientemente próximos al valor a, a través de valores menores que a. Lo escribiremos, lim x a f(x) = L. Ejemplo: De forma análoga se define lim x a + f(x) = L y lim x a ± f(x) = ±
8 Teorema: Sea f(x) una función definida en un entorno de x = a. Entonces, f(x) tiene como límite L cuando x tiende hacia a si, y solo sí, existen los dos límites laterales y ambos valen L. Se proponen los ejercicios 8, 9, 10 y Estudio de las indeterminaciones: Existen en total 7 indeterminaciones que son: a) Resolución de la indeterminación : Este tipo de indeterminaciones aparece normalmente en expresiones del tipo: siendo f(x) y g(x) expresiones polinómicas (a n X n + a n-1 X n-1 + a 2 X 2 + a 1 X + a 0 ) o expresiones con radicales ( ax + b ), una de ellas o ambas. - En el caso de que f(x) y g(x) sean funciones polinómicas, basta simplificar los factores del tipo (x a) mediante factorización, con la regla de Ruffini:
9 Ejemplo: Numerador 2X 2 8 = 2 (X + 2) (X - 2) Denominador X 2 + X 2 = (X - 1) (x + 2) - Si hay radicales, hay que transformarlos en expresiones sin radicales antes de llevar a cabo lo anterior. Esto se consigue multiplicando numerador y denominador por la expresión conjugada conveniente. Ejemplo:
10 b) Resolución de la indeterminación : Este tipo de indeterminaciones aparece normalmente en expresiones del tipo: siendo f(x) y g(x) expresiones polinómicas (a n X n + a n-1 X n-1 + a 2 X 2 + a 1 X + a 0 ) o expresiones con radicales ( b m X m + + b 1 X + b 0 ), una de ellas o ambas. En cualquier caso, se resuelve dividiendo numerador y denominador entre X elevado al mayor exponente de las dos expresiones. Ejemplos: c) Resolución de la indeterminación : Este tipo de indeterminaciones aparece normalmente en expresiones del tipo: siendo alguna de las dos funciones expresiones polinómicas o radicales. Para resolverlas, se transforma en una indeterminación del tipo o.
11 Ejemplos: Se proponen los ejercicios 13 y 14 d) Resolución de la indeterminación 1 : Este tipo de indeterminaciones aparece normalmente en expresiones del tipo: siendo y. Se resuelve usando la función exponencial de la siguiente manera: o
12 Ejemplo: Ejercicio extra: Calcula los siguientes límites: a) d) b) e) c)
13 5.- Asíntotas (verticales, horizontales y oblicuas): El estudio de las asíntotas de una función, que abordaremos a continuación, está íntimamente relacionado tanto con el concepto de límite como con la representación gráfica de funciones. Hay 3 tipos de asíntotas: Verticales, Horizontales y Oblicuas. Veamos cómo se buscan: a) Asíntota Vertical: La función f (x) tiene una asíntota vertical en x = a cuando alguno de sus límites laterales en x = a es infinito, es decir, cuando: Para estudiar la posición de la función respecto a la asíntota vertical se estudian los límites laterales en x = a. Ejemplo: Veamos como la función f(x) = X2 3X+3 X 2 4 tiene dos asíntotas verticales en los puntos donde se anula el denominador: X 2 4 = 0 X 1 = 2 y X 2 = 2 Para el estudio de la posición de la función respecto a la asíntota vertical, se calculan los límites laterales en cada punto: Para la asíntota vertical en X = 2: Para la asíntota vertical en X = -2:
14 b) Asíntota Horizontal: La función f(x) tiene una asíntota horizontal en y = b cuando alguno de sus límites infinitos es b, es decir, cuando: Para estudiar la posición de la función respecto a la asíntota horizontal se estudian los límites infinitos de f (x) b. Ejemplo: Veamos como la función f(x) = X2 3X+3 X 2 4 tiene una asíntota horizontal en y = 1: Para el estudio de la posición de la función respecto a la asíntota horizontal, se calculan los límites infinitos de f (x) 1: f (x) 1 = X2 3X+3 X = 3X+7 X 2 4
15 c) Asíntota Oblicua: La función f(x) tiene una asíntota oblicua en y = m x + n, cuando alguno de los límites infinitos de f(x) - m x + n es cero, es decir, cuando: o si Para hallar la recta m x + n, a la que la función f (x) es oblicua se hace calculando: y Para estudiar la posición de la función respecto a la asíntota oblicua se estudian los límites infinitos de f (x) mx + n y tenemos en cuenta que: - Si se aproxima a 0 positivamente, la función se queda por encima de la recta. - Si se aproxima a 0 negativamente, la función se queda por debajo de la recta. Ejemplos: a) Veamos si la función f(x) = X2 3X+3 X Primero buscamos el valor de m: tiene asíntotas oblicuas: Cuando m resulta 0 o ±, podemos concluir que f(x) no tiene asíntotas oblicuas. b) Estudiemos las asíntotas oblicuas en f(x) = X3 1 X 2 2X : - Primero buscamos el valor de m: - En segundo lugar calculamos el valor de n: Luego f(x) tiene una asíntota oblicua en la recta Y = X Finalmente, se estudia la posición de la función respecto a la asíntota oblicua, con los límites infinitos de f (x) (x + 2):
16 Nota 1: No puede haber simultáneamente asíntotas horizontales y oblicuas en ni en. Lo que sí puede darse es que haya una horizontal en un lado y una oblicua en otro, es decir, puede haber simultáneamente horizontal y oblicua pero no en el mismo lado. Nota 2: Conviene tener en cuenta las siguientes observaciones sobre las asíntotas en el caso de funciones racionales: f(x) = a nx n + +a 1 X+a 0 b m X m + +b 1 X+b 0 f(x) presenta asíntotas verticales en las raíces del denominador (salvo cuando dicha raíz lo es también del numerador). f(x) presenta asíntotas horizontales cuando el grado del numerador es menor o igual que el del denominador. f(x) presentan asíntotas oblicuas cuando el grado del numerador es una unidad más que el del denominador. Se proponen los ejercicios 19, 20, 21, 22 y 23.
17 6.- Continuidad de una función: - Continuidad de f(x) en un punto x = a: Se dice que f(x) es continua en el punto x = a, si, es decir: 1. Existe los límites laterales de f(x) en x=a y ambos coinciden. 2. Existe la imagen de f(x) para x=a. 3. Los límites laterales de f(x) en x=a y la imagen de f(x) en a, coinciden. - Discontinuidad de f(x) en un punto x = a: Se dice que f(x) es discontinua en el punto x = a, si f(x) no es continua en ese punto. Los tipos de discontinuidad son: a) Discontinuidad Esencial (o de salto): Se produce cuando los dos límites laterales existen pero no coinciden. Hay dos tipos de discontinuidades de salto: -De salto finito: cuando los dos límites laterales resultan números reales distintos. En este caso, al valor absoluto de la diferencia de dichos límites lo llamaremos valor del salto. -De salto infinito: cuando al menos uno de los dos límites laterales es infinito.
18 b) Discontinuidad Evitable: Se produce cuando los dos límites laterales existen y coinciden, pero ese valor es distinto al de f(a). c) Discontinuidad de 2ª especie: Se llama de este modo a la discontinuidad que se produce cuando no existe alguno de los límites laterales en el punto estudiado. - Continuidad de f (x) en el intervalo [a, b]: Se dice que f(x) es continua en el intervalo cerrado [a, b], si lo es en todos los puntos del intervalo y además, Nota: Las funciones polinómicas, valor absoluto, racionales, raíces, exponenciales, logarítmica, trigonométricas y las inversas de las trigonométricas son continuas en sus respectivos dominios. Además, la composición de funciones continuas es continua en su dominio correspondiente. Se proponen los ejercicios 24, 25, 26, 27, 28, 29, 30, 31 y 33.
19 7.- Teoremas relativos a funciones continuas en [ a, b]: a) Teorema del valor intermedio de Bolzano: Si f (x) es continua en el intervalo cerrado [a, b] y f(a) f(b) < 0, es decir el signo de f (a) signo de f (b), entonces se cumple que existe, al menos, un número c perteneciente al intervalo abierto ]a, b[ de tal modo que f (c) = 0. Nota: Una de las aplicaciones del Teorema de Bolzano es demostrar que algunas ecuaciones tienen por lo menos 1 solución real y para calcular su valor aproximado. b) Consecuencias del Teorema de Bolzano (Teorema de los valores intermedios): 1.- Sea f (x) continua en el intervalo cerrado [a, b] y f (a) f (b). Se cumple que para todo número real K ϵ ]f(a), f(b)[, existe un valor c perteneciente al intervalo abierto ]a, b[ de tal modo que f (c) = K. (Se demuestra aplicando el Teorema de Bolzano a la función g (x) = f (x) K) 2.- Sea f (x) y g (x) dos funciones continuas en el intervalo cerrado [a, b] y se verifican que f (a) > g (a) y f (b) < g (b), (de igual modo si f (a) < g (a) y f (b) > g (b)), Entonces existe al menos un c ϵ ]a, b[ tal que f (c) = g (c). (Se demuestra aplicando el Teorema de Bolzano a la función h (x) = f (x) g (x))
20 c) Teorema de existencia de extremos absolutos de Weierstrass: Si f (x) es continua en el intervalo cerrado [a, b], entonces existen dos números reales C1 y C2 ϵ [a, b] tales que f (C1) es un máximo absoluto y f (C2) es un mínimo absoluto de f (x). Se proponen los ejercicios 1, 2, 3, 4, 5, 6, 7 y 8 de la relación de ejercicios 2.
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones.
 Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Resumen Tema 3: Derivadas. Concepto. Propiedades. Cálculo de derivadas. Aplicaciones. 0.. Concepto de derivada. Definición. Sea f : S R R, a (b, c) S. Decimos que f es derivable en a si existe: f(x) f(a)
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Límites y continuidad
 Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
TEMA 1.- LÍMITES DE FUNCIONES Y CONTINUIDAD.
 TEMA 1.- LÍMITES DE FUNCIONES Y CONTINUIDAD. 1.LÍMITE DE UNA FUNCIÓN EN UN PUNTO El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes por f de puntos x, cuando los originales
TEMA 1.- LÍMITES DE FUNCIONES Y CONTINUIDAD. 1.LÍMITE DE UNA FUNCIÓN EN UN PUNTO El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes por f de puntos x, cuando los originales
En las figuras anteriores vemos algunos casos (no todos) que pueden presentarse al pasar por un punto x 0. (en este caso, para x 0 =2)
 UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
Límite de una función
 Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es decir el valor al que tienden
Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es decir el valor al que tienden
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
2 o BACHILLERATO ciencias
 . ANÁLISIS 2 o BACHILLERATO ciencias Francisco Navarro Martínez . Tema 1 o - Funciones Continuas 1. Continuidad de una Función 2. Definición de una Función Continua en un punto 3. Tipos de Discontinuidades
. ANÁLISIS 2 o BACHILLERATO ciencias Francisco Navarro Martínez . Tema 1 o - Funciones Continuas 1. Continuidad de una Función 2. Definición de una Función Continua en un punto 3. Tipos de Discontinuidades
LÍMITE DE UNA FUNCIÓN EN UN PUNTO
 pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO c significa que toma valores cada vez más próimos a c. Se lee tiende a c. Por ejemplo: ; `9; `; `; `; `; `9; `; `999; Es una secuencia de números cada vez más próimos
pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO c significa que toma valores cada vez más próimos a c. Se lee tiende a c. Por ejemplo: ; `9; `; `; `; `; `9; `; `999; Es una secuencia de números cada vez más próimos
Tema 6: Límites y continuidad
 Tema 6: Límites y continuidad March 25, 217 Contents 1 *Conceptos relativos a funciones 2 1.1 Dominio de funciones usuales........................................ 2 1.2 Funciones periódicas.............................................
Tema 6: Límites y continuidad March 25, 217 Contents 1 *Conceptos relativos a funciones 2 1.1 Dominio de funciones usuales........................................ 2 1.2 Funciones periódicas.............................................
Procedimiento para determinar las asíntotas verticales de una función
 DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
Veamos ahora el comportamiento de la función parte entera (f(x) = E(x)). Si x se aproxima a 2, a qué valor tiende f(x)?
 LÍMITES Y CONTINUIDAD DE FUNCIONES. C O N C E P T O D E L Í M I T E D E U N A F U N C I Ó N E N U N P U N T O Consideremos la función f(x)x², cuya gráfica es una parábola. Si x se aproxima a, a qué valor
LÍMITES Y CONTINUIDAD DE FUNCIONES. C O N C E P T O D E L Í M I T E D E U N A F U N C I Ó N E N U N P U N T O Consideremos la función f(x)x², cuya gráfica es una parábola. Si x se aproxima a, a qué valor
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Gráficamente: una función es continua en un punto si en dicho punto su gráfica no se rompe. Función continua en x = 0 Función no continua en x = 0
 Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
LÍMITES, CONTINUIDAD, ASÍNTOTAS LÍMITE DE UNA FUNCIÓN. Límite de una función en un punto
 LÍMITES, CONTINUIDAD, ASÍNTOTAS LÍMITE DE UNA FUNCIÓN Límite de una función en un punto xc Se lee: El límite cuando x tiende a c de f(x) es l Notas: - Que x se aproxima a c significa que toma valores muy
LÍMITES, CONTINUIDAD, ASÍNTOTAS LÍMITE DE UNA FUNCIÓN Límite de una función en un punto xc Se lee: El límite cuando x tiende a c de f(x) es l Notas: - Que x se aproxima a c significa que toma valores muy
Tema 7. Límites y continuidad. 7.1 Definición de límite de una función
 Tema 7 Límites y continuidad 7.1 Definición de límite de una función Sea f : I R, I R yseaa I un punto de acumulación de I, decimos que f() tiene límite l R en el punto a f() =l si ε > 0, η > 0: a < η
Tema 7 Límites y continuidad 7.1 Definición de límite de una función Sea f : I R, I R yseaa I un punto de acumulación de I, decimos que f() tiene límite l R en el punto a f() =l si ε > 0, η > 0: a < η
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 4 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 4 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Límites y continuidad
 Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 2º BACHILLERATO
 LÍMITES: OPERACIONES CON INFINITOS LÍMITES: RESOLUCIÓN DE INDETERMINACIONES DEL TIPO 1 Estas indeterminaciones están relacionadas con el número e se calculan de la siguiente forma: 1 DOMINIO E IMAGEN DE
LÍMITES: OPERACIONES CON INFINITOS LÍMITES: RESOLUCIÓN DE INDETERMINACIONES DEL TIPO 1 Estas indeterminaciones están relacionadas con el número e se calculan de la siguiente forma: 1 DOMINIO E IMAGEN DE
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
el blog de mate de aida CSI: Límites y continuidad. . Se lee x tiende a x por la derecha. , se expresa así: , se expresa así: por la derecha)
 pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO gnifica que toma valores cada vez más próimos a. Se lee tiende a. Ejemplo: ;,9;,;,;,8;,;,9;,;,999; Es una secuencia de números cada vez más próimos a. Escribimos.
pág. LÍMITE DE UNA FUNCIÓN EN UN PUNTO gnifica que toma valores cada vez más próimos a. Se lee tiende a. Ejemplo: ;,9;,;,;,8;,;,9;,;,999; Es una secuencia de números cada vez más próimos a. Escribimos.
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN
 FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
2.1. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable x)
 Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
TEMA 2: CONTINUIDAD DE FUNCIONES
 TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
Límites. Continuidad.
 Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Límite finito cuando x tiende a infinito (1) Límite finito cuando x tiende a infinito (2) Se dice que el límite de la función f(x) cuando
Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Límite finito cuando x tiende a infinito (1) Límite finito cuando x tiende a infinito (2) Se dice que el límite de la función f(x) cuando
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
2.1 CONTINUIDAD EN UN PUNTO 2.2 CONTINUIDAD DE FUNCIONES CONOCIDAS 2.3 CONTINUIDAD EN OPERACIONES CON
 Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Tema 5: Continuidad de funciones
 Tema 5: Continuidad de funciones 1. Continuidad de una función en un punto La idea intuitiva de función continua en un punto es bien sencilla, es aquella que no da saltos ni presenta interrupciones, que
Tema 5: Continuidad de funciones 1. Continuidad de una función en un punto La idea intuitiva de función continua en un punto es bien sencilla, es aquella que no da saltos ni presenta interrupciones, que
RESUMEN DE CONTINUIDAD DE FUNCIONES
 RESUMEN DE CONTINUIDAD DE FUNCIONES La idea intuitiva de función continua es la de aquella cuya gráfica se puede dibujar sin levantar el lápiz del papel. Analíticamente, una función f(x) se dice que es
RESUMEN DE CONTINUIDAD DE FUNCIONES La idea intuitiva de función continua es la de aquella cuya gráfica se puede dibujar sin levantar el lápiz del papel. Analíticamente, una función f(x) se dice que es
CONTINUIDAD Y DERIVADA ESTUDIO DE LA CONTINUIDAD DE UNA FUNCIÓN
 Índice Presentación... 3 Continuidad en un punto... 4 Estudio de la continuidad en un punto a partir de un ejemplo... 5 Discontinuidades... 7 Continuidad de las funciones definidas a trozos... 9 Propiedades
Índice Presentación... 3 Continuidad en un punto... 4 Estudio de la continuidad en un punto a partir de un ejemplo... 5 Discontinuidades... 7 Continuidad de las funciones definidas a trozos... 9 Propiedades
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
SOLUCIONES DE LAS ACTIVIDADES Págs. 239 a 257
 TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
TEMA. LÍMITES Y CONTINUIDAD SOLUCIONES DE LAS ACTIVIDADES Págs. 9 a 7 Página 9 Página. a) f() 0. a) f() 0, 0,0 0,00 0,000 f(),,9,99,999,9,99,999,9999 f() 00 0.000 0 6 0 8 b) f() 0 0, 0,0 0,00 0,000 f(),,0,00,000
RESUMEN TEÓRICO DE CLASES
 Página 1 RESUMEN TEÓRICO DE CLASES Página 2 Tema 1. Inecuaciones Las inecuaciones son desigualdades algebraicas en la que sus dos miembros se relacionan por uno de estos signos: >; ;
Página 1 RESUMEN TEÓRICO DE CLASES Página 2 Tema 1. Inecuaciones Las inecuaciones son desigualdades algebraicas en la que sus dos miembros se relacionan por uno de estos signos: >; ;
TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD.
 TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD. 1. Concepto de función.. Dominio e imagen de una función. 3. Tipos de funciones. 4. Operaciones con funciones. 5. Concepto de límite. 6. Cálculo de límites. 7.
TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD. 1. Concepto de función.. Dominio e imagen de una función. 3. Tipos de funciones. 4. Operaciones con funciones. 5. Concepto de límite. 6. Cálculo de límites. 7.
De los tres conceptos que se estudian es este tema, funciones, límites y continuidad, el primero y el último son muy sencillos de comprender.
 INTRODUCCIÓN. FUNCIONES. LÍMITES. Este tema lo iniciamos recordando el concepto de función y dando algunas nociones básicas sobre funciones, para dar paso al estudio del límite de una función, cálculo
INTRODUCCIÓN. FUNCIONES. LÍMITES. Este tema lo iniciamos recordando el concepto de función y dando algunas nociones básicas sobre funciones, para dar paso al estudio del límite de una función, cálculo
LÍMITES Y CONTINUIDAD
 LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
Unidad 10 Continuidad de las funciones
 Unidad 10 Continuidad de las funciones 4 SOLUCIONES 1. La continuidad queda: a) La continuidad en x = 0. No es continua en ese punto al no coincidir los límites laterales. b) La continuidad en x = 3. 2.
Unidad 10 Continuidad de las funciones 4 SOLUCIONES 1. La continuidad queda: a) La continuidad en x = 0. No es continua en ese punto al no coincidir los límites laterales. b) La continuidad en x = 3. 2.
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
DEPARTAMENTO DE MATEMÁTICAS B A C H I L L E R A T O
 DEPARTAMENTO DE MATEMÁTICAS B A C H I L L E R A T O FUNDACIÓN VEDRUNA S E V I L L A COLEGIO SANTA JOAQUINA DE VEDRUNA MATEMÁTICAS I LÍMITES Y CONTINUIDAD DE FUNCIONES Límite finito de una función en un
DEPARTAMENTO DE MATEMÁTICAS B A C H I L L E R A T O FUNDACIÓN VEDRUNA S E V I L L A COLEGIO SANTA JOAQUINA DE VEDRUNA MATEMÁTICAS I LÍMITES Y CONTINUIDAD DE FUNCIONES Límite finito de una función en un
Es evidente la continuidad en En el punto, se tiene:
 Tema 3 Continuidad Ejercicios Resueltos Ejercicio 1 Estudia la continuidad de la función La función puede expresarse como Para representarla basta considerar dos arcos de parábola: Es evidente la continuidad
Tema 3 Continuidad Ejercicios Resueltos Ejercicio 1 Estudia la continuidad de la función La función puede expresarse como Para representarla basta considerar dos arcos de parábola: Es evidente la continuidad
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Solución. - Verticales: En los puntos excluidos del dominio donde el límite quede de la forma k. 3( ) = Asíntota vertical. = + x 2.
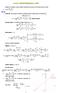 Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
TEMA 10.-LÍMITES DE FUNCIONES Y CONTINUIDAD
 TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
Denominadores: un denominador nunca se puede hacer cero. Ejemplo: 𝑓 𝑥 =
 1. Continuidad de funciones. Una función es continua en 𝑥 = 𝑎, si se cumple: Existe 𝑓(𝑎). lim!! 𝑓 𝑥 = lim!!! 𝑓(𝑥) = lim!!! 𝑓 𝑥 𝒇 𝒂 = 𝐥𝐢𝐦𝒙 𝒂 𝒇 𝒙 Las funciones definidas por expresiones analíticas elementales
1. Continuidad de funciones. Una función es continua en 𝑥 = 𝑎, si se cumple: Existe 𝑓(𝑎). lim!! 𝑓 𝑥 = lim!!! 𝑓(𝑥) = lim!!! 𝑓 𝑥 𝒇 𝒂 = 𝐥𝐢𝐦𝒙 𝒂 𝒇 𝒙 Las funciones definidas por expresiones analíticas elementales
INTRODUCCIÓN. FUNCIONES. LÍMITES.
 INTRODUCCIÓN. FUNCIONES. LÍMITES. Este capítulo puede considerarse como una prolongación y extensión del anterior, límite de sucesiones, al campo de las funciones. Se inicia recordando el concepto de función
INTRODUCCIÓN. FUNCIONES. LÍMITES. Este capítulo puede considerarse como una prolongación y extensión del anterior, límite de sucesiones, al campo de las funciones. Se inicia recordando el concepto de función
2. LÍMITES Y CONTINUIDAD DE LAS FUNCIONES REALES DE VARIABLE REAL.
 2. LÍMITES Y CONTINUIDAD DE LAS FUNCIONES REALES DE VARIABLE REAL. ESQUEMA LÍMITES Y CONTINUIDAD DE LAS FUNCIONES REALES DE VARIABLE REAL Límites. Límite de una función. Tipos de límites. Álgebra de límites.
2. LÍMITES Y CONTINUIDAD DE LAS FUNCIONES REALES DE VARIABLE REAL. ESQUEMA LÍMITES Y CONTINUIDAD DE LAS FUNCIONES REALES DE VARIABLE REAL Límites. Límite de una función. Tipos de límites. Álgebra de límites.
RESUMEN DE FUNCIONES REALES DE VARIABLE REAL. Se dice que una función tiene límite en un punto si los límites laterales toman el mismo valor.
 RESUMEN DE FUNCIONES REALES DE VARIABLE REAL LIMITES Se dice que una función tiene límite en un punto si los límites laterales toman el mismo valor. lim f ( x) = L lim f ( x) = lim f ( x) = L x a x a x
RESUMEN DE FUNCIONES REALES DE VARIABLE REAL LIMITES Se dice que una función tiene límite en un punto si los límites laterales toman el mismo valor. lim f ( x) = L lim f ( x) = lim f ( x) = L x a x a x
1. Conocimientos previos. 2. Sucesión Progresiones aritméticas. 1 CONOCIMIENTOS PREVIOS. 1
 CONOCIMIENTOS PREVIOS. Límites.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Repasar las operaciones básicas con expresiones algebraicas. Repasar
CONOCIMIENTOS PREVIOS. Límites.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Repasar las operaciones básicas con expresiones algebraicas. Repasar
Asíntotas en una función.
 Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Límites de Funciones
 . Introducción y notación Límites de Funciones Hasta ahora, se han visto muchos conceptos sobre las funciones desde un enfoque muy intuitivo. Cosas como la continuidad, el crecimiento o los máximos y los
. Introducción y notación Límites de Funciones Hasta ahora, se han visto muchos conceptos sobre las funciones desde un enfoque muy intuitivo. Cosas como la continuidad, el crecimiento o los máximos y los
TEMA 4: DERIVADAS. En símbolos, la pendiente de la curva en P = lim Q P (pendiente de P Q).
 TEMA 4: DERIVADAS 1. La derivada de una función. Reglas de derivación 1.1. La pendiente de una curva. La pendiente de una curva en un punto P es una medida de la inclinación de la curva en ese punto. Si
TEMA 4: DERIVADAS 1. La derivada de una función. Reglas de derivación 1.1. La pendiente de una curva. La pendiente de una curva en un punto P es una medida de la inclinación de la curva en ese punto. Si
MATE 3031. Dr. Pedro Vásquez UPRM. P. Vásquez (UPRM) Conferencia 1 / 77
 MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
Tema 9. Limite de funciones. Continuidad
 Tema 9. Limite de funciones. Continuidad 1. Límite de una función. Funciones convergentes La idea intuitiva de límite de una función en un punto es fácil de comprender: es el valor hacia el que se aproxima
Tema 9. Limite de funciones. Continuidad 1. Límite de una función. Funciones convergentes La idea intuitiva de límite de una función en un punto es fácil de comprender: es el valor hacia el que se aproxima
LÍMITES Y CONTINUIDAD. 1º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN LÍMITE DE UNA FUNCIÓN EN UN PUNTO CONCEPTO DE LÍMITE DE UNA FUNCIÓN
 LÍMITES Y CONTINUIDAD º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN Sea f() =. Vamos a darle valores a cercanos a y vamos a ver cómo se comporta f()..9.99.999.9999.99999 f() 4.8 4.98 4.998 4.9998
LÍMITES Y CONTINUIDAD º Bto. Sociales. CONCEPTO DE LÍMITE DE UNA FUNCIÓN Sea f() =. Vamos a darle valores a cercanos a y vamos a ver cómo se comporta f()..9.99.999.9999.99999 f() 4.8 4.98 4.998 4.9998
Continuidad, límites y asíntotas. Funciones
 9 Continuidad, ites y asíntotas Funciones Introducción El estudio de la continuidad de una función se inicia desde el análisis de la gráfica de la función. Este análisis, intuitivo y fácil, pero insuficiente
9 Continuidad, ites y asíntotas Funciones Introducción El estudio de la continuidad de una función se inicia desde el análisis de la gráfica de la función. Este análisis, intuitivo y fácil, pero insuficiente
Límite y Continuidad de funciones de una variable
 Introducción Límite y de funciones de una variable Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Límite y de funciones
Introducción Límite y de funciones de una variable Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Límite y de funciones
TEMA 1: FUNCIONES. LÍMITES Y CONTINUIDAD
 Alonso Fernández Galián TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Aunque el concepto de función está implícito en los trabajos de Newton, Leibniz, Euler, no fue hasta el glo XIX en que se definió de manera
Alonso Fernández Galián TEMA : FUNCIONES. LÍMITES Y CONTINUIDAD Aunque el concepto de función está implícito en los trabajos de Newton, Leibniz, Euler, no fue hasta el glo XIX en que se definió de manera
APUNTES. Obtención del dominio de las funciones:
 Materia: Tema: Curso: APUNTES Obtención del dominio de las funciones: - Si f(x) es una constante, la función no presentará problema alguno, el dominio será todos los puntos pertenecientes al conjunto de
Materia: Tema: Curso: APUNTES Obtención del dominio de las funciones: - Si f(x) es una constante, la función no presentará problema alguno, el dominio será todos los puntos pertenecientes al conjunto de
Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados:
 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica
Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica
Tipos de funciones. Clasificación de funciones. Funciones algebraicas
 Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Teoría Tema 9 Representación gráfica de funciones
 página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
CONTINUIDAD DE FUNCIONES
 CONTINUIDAD CONTINUIDAD DE FUNCIONES CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO Una función f es continua en a si y sólo si se cumplen las tres condiciones siguientes: 1) Existe f(a), es decir, a Dom f. 2)
CONTINUIDAD CONTINUIDAD DE FUNCIONES CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO Una función f es continua en a si y sólo si se cumplen las tres condiciones siguientes: 1) Existe f(a), es decir, a Dom f. 2)
Límites y continuidad de funciones reales de variable real
 Límites y continuidad de funciones reales de variable real Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 10 2.1. Funciones
Límites y continuidad de funciones reales de variable real Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 10 2.1. Funciones
Límite de una función Funciones continuas
 Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
tiene por límite L cuando la variable independiente x tiende a x , y se nota por L, cuando al acercarnos todo lo que queramos a x lím( x
 UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN Diremos que una función y f () tiene por ite L cuando la variable independiente tiende a, y se nota por f ( ) L, cuando al acercarnos
UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN Diremos que una función y f () tiene por ite L cuando la variable independiente tiende a, y se nota por f ( ) L, cuando al acercarnos
RELACIÓN ENTRE LA GRÁFICA DE UNA FUNCIÓN f y LA DE SU INVERSA f -1
 RELACIÓN ENTRE LA GRÁFICA DE UNA FUNCIÓN f y LA DE SU INVERSA f -1 Sabemos que la función inversa 1 Si f a b, entonces f b a 1 f (o recíproca) de f cumple la siguiente condición: Por lo tanto: 1 f f 1
RELACIÓN ENTRE LA GRÁFICA DE UNA FUNCIÓN f y LA DE SU INVERSA f -1 Sabemos que la función inversa 1 Si f a b, entonces f b a 1 f (o recíproca) de f cumple la siguiente condición: Por lo tanto: 1 f f 1
Continuidad de funciones
 Apuntes Tema 3 Continuidad de funciones 3.1 Continuidad de funciones Def.: Dada una función f(x), diremos que es continua en x = a, si cumple la siguiente condición: En caso de que no cumpla esta condición,
Apuntes Tema 3 Continuidad de funciones 3.1 Continuidad de funciones Def.: Dada una función f(x), diremos que es continua en x = a, si cumple la siguiente condición: En caso de que no cumpla esta condición,
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS
 1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
PROBLEMAS DE CONTINUIDAD Y DERIVABILIDAD
 PROBLEMAS DE CONTINUIDAD Y DERIVABILIDAD Considera la función f(x)= x 3 + px donde p es un número real. Escribir (en función de p) la ecuación de la recta tangente a la grafica f(x) en el punto de abscisa
PROBLEMAS DE CONTINUIDAD Y DERIVABILIDAD Considera la función f(x)= x 3 + px donde p es un número real. Escribir (en función de p) la ecuación de la recta tangente a la grafica f(x) en el punto de abscisa
Herramientas digitales de auto-aprendizaje para Matemáticas
 Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice la cadena Tabla de Dada una función f : D R R,
Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice la cadena Tabla de Dada una función f : D R R,
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Estudios J.Concha ( fundado en 00) ESO, BACHILLERATO y UNIVERSIDAD Departamento Bachillerato MATEMATICAS º BACHILLERATO Profesores Javier Concha y Ramiro Froilán Tema 8 Límites de funciones, continuidad
Estudios J.Concha ( fundado en 00) ESO, BACHILLERATO y UNIVERSIDAD Departamento Bachillerato MATEMATICAS º BACHILLERATO Profesores Javier Concha y Ramiro Froilán Tema 8 Límites de funciones, continuidad
TEMA 5 LÍMITE DE FUNCIONES. CONTINUIDAD
 TEMA 5 LÍMITE DE FUNCIONES. CONTINUIDAD 5.1. VISIÓN INTUITIVA DE LA CONTINUIDAD. TIPOS DE DISCONTINUIDADES. La idea de función continua es la que puede ser construida con un solo trazo. DISCONTINUIDADES
TEMA 5 LÍMITE DE FUNCIONES. CONTINUIDAD 5.1. VISIÓN INTUITIVA DE LA CONTINUIDAD. TIPOS DE DISCONTINUIDADES. La idea de función continua es la que puede ser construida con un solo trazo. DISCONTINUIDADES
Problemas de 4 o ESO. Isaac Musat Hervás
 Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
Aplicaciones de las Derivadas
 Tema 4 Aplicaciones de las Derivadas 4.1 Introducción Repasaremos en este Tema algunas de las aplicaciones fundamentales de las derivadas. Muchas de ellas son ya conocidas por tratarse de conceptos explicados
Tema 4 Aplicaciones de las Derivadas 4.1 Introducción Repasaremos en este Tema algunas de las aplicaciones fundamentales de las derivadas. Muchas de ellas son ya conocidas por tratarse de conceptos explicados
UNIDAD I LÍMITES Y CONTINUIDAD
 República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD I LÍMITES Y CONTINUIDAD Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, Enero de 2016 UNIDAD
República Bolivariana de Venezuela Universidad Alonso de Ojeda Administración Mención Gerencia y Mercadeo UNIDAD I LÍMITES Y CONTINUIDAD Elaborado por: Ing. Ronny Altuve Ciudad Ojeda, Enero de 2016 UNIDAD
N = {1, 2, 3, 4, 5,...}
 Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Números y Funciones.. Números Los principales tipos de números son:. Los números naturales son aquellos que sirven para contar. N = {,,, 4, 5,...}. Los números enteros incluyen a los naturales y a sus
Límite de una función
 Idea intuitiva de límite Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
Idea intuitiva de límite Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
1.- CONCEPTO DE LÍMITE. LÍMITE DE UNA FUNCIÓN EN UN PUNTO.
 º Bachillerato Matemáticas I Tema 8:Límites y continuidad.- CONCEPTO DE LÍMITE. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. En ocasiones interesa saber hacia qué valor se aproima una función cuando la variable
º Bachillerato Matemáticas I Tema 8:Límites y continuidad.- CONCEPTO DE LÍMITE. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. En ocasiones interesa saber hacia qué valor se aproima una función cuando la variable
CÁLCULO DIFERENCIAL. b) Al darle a x valores suficientemente grandes, los valores de f(x) crecen cada vez más
 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
Tema II: Análisis Límites
 Tema II: Análisis Límites En matemáticas, se usa el concepto del límite para describir la tendencia de una sucesión o una función. La idea es que en una sucesión o una función, decimos que existe el límite
Tema II: Análisis Límites En matemáticas, se usa el concepto del límite para describir la tendencia de una sucesión o una función. La idea es que en una sucesión o una función, decimos que existe el límite
TIPOS DE FUNCIONES. Ing. Caribay Godoy Rangel
 TIPOS DE FUNCIONES Repasar los conceptos de dominio, rango, gráfica, elementos esenciales y transformaciones de las funciones: lineal, cuadrática, racional, trigonométrica, exponencial y logarítmica. FUNCIONES
TIPOS DE FUNCIONES Repasar los conceptos de dominio, rango, gráfica, elementos esenciales y transformaciones de las funciones: lineal, cuadrática, racional, trigonométrica, exponencial y logarítmica. FUNCIONES
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.2. LÍMITES Y CONTINUIDAD
 TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
Repartido 4. Profesor Fernando Díaz Matemática A 3ro E.M.T. Iscab 2016
 Repartido 4 Profesor Fernando Díaz Matemática A 3ro E.M.T. Iscab 2016 6. Estudiar los límites laterales de las siguientes funciones en los puntos que anulan al denominador: A) B) 7. Estudiar la existencia
Repartido 4 Profesor Fernando Díaz Matemática A 3ro E.M.T. Iscab 2016 6. Estudiar los límites laterales de las siguientes funciones en los puntos que anulan al denominador: A) B) 7. Estudiar la existencia
Considermos la función
 Considermos la función f x = x2 9 x 3 Qué sucede si reemplazamos a x por 3? f x = x2 9 x 3 = 32 9 3 3 = 0 0 Tenemos lo que se denomina UNA INDETERMINACIÓN En matemática hay 7 indeterminaciones básicas
Considermos la función f x = x2 9 x 3 Qué sucede si reemplazamos a x por 3? f x = x2 9 x 3 = 32 9 3 3 = 0 0 Tenemos lo que se denomina UNA INDETERMINACIÓN En matemática hay 7 indeterminaciones básicas
Teoría Tema 8 Ejemplos y más ejemplos de límites
 página 1/10 Teoría Tema 8 Ejemplos y más ejemplos de límites Índice de contenido Practicar y practicar...2 página 2/10 Practicar y practicar Como existen infinitas funciones distintas... existen infinitos
página 1/10 Teoría Tema 8 Ejemplos y más ejemplos de límites Índice de contenido Practicar y practicar...2 página 2/10 Practicar y practicar Como existen infinitas funciones distintas... existen infinitos
Apuntes de Continuidad de funciones
 Apuntes de Continuidad de funciones En el tema anterior estudiamos el concepto de función real de variable real y el concepto de límite. Ahora vamos a estudiar la aplicación de los límites en el estudio
Apuntes de Continuidad de funciones En el tema anterior estudiamos el concepto de función real de variable real y el concepto de límite. Ahora vamos a estudiar la aplicación de los límites en el estudio
AUTOEVALUACIÓN DE CÁLCULO I - SOLUCIONES. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable
 AUTOEVALUACIÓN DE CÁLCULO I - SOLUCIONES Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Soluciones del Examen de Autoevaluación
AUTOEVALUACIÓN DE CÁLCULO I - SOLUCIONES Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Soluciones del Examen de Autoevaluación
EJERCICIOS DE REPASO SOBRE LÍMITES Y CONTINUIDAD I
 EJERCICIOS DE REPASO SOBRE LÍMITES Y CONTINUIDAD I Ejercicio 1: En este ejercicio vamos a recordar como se resuelven las indeterminaciones más importantes. En cada indeterminación se describen los primeros
EJERCICIOS DE REPASO SOBRE LÍMITES Y CONTINUIDAD I Ejercicio 1: En este ejercicio vamos a recordar como se resuelven las indeterminaciones más importantes. En cada indeterminación se describen los primeros
Se desea estudiar el comportamiento de una función a medida independiente x se aproxima a un valor específico.
 Tema: Límites de las funciones Objetivos: Comprender el concepto de límite de una función y las propiedades de los límites. Calcular el límite de una función algebraica utilizando las propiedades de los
Tema: Límites de las funciones Objetivos: Comprender el concepto de límite de una función y las propiedades de los límites. Calcular el límite de una función algebraica utilizando las propiedades de los
Matemáticas aplicadas a las Ciencias Sociales II. ANAYA
 Unidad 5 / Límites de funciones Continuidad! PARA RESOLVER a)) Calcula el límite de la función f() cuando,,,, - : f() (-)/( -5) b)) Representa gráficamente los resultados obtenidos. a))! 5! 5 indeterminado,
Unidad 5 / Límites de funciones Continuidad! PARA RESOLVER a)) Calcula el límite de la función f() cuando,,,, - : f() (-)/( -5) b)) Representa gráficamente los resultados obtenidos. a))! 5! 5 indeterminado,
