APLICACIONES DE LAS DERIVADAS
|
|
|
- Patricia Paz Maidana
- hace 7 años
- Vistas:
Transcripción
1 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece f' < 0 Relación de la curvatura con el signo de la segunda derivada Describe el tramo CD y los tramos DE, EF y FG siguientes: A B C D E F G f convea f cóncava f' decreciente f' creciente f'' < 0 f'' > 0 CD 8 f convea 8 f' decreciente 8 f" < 0 DE 8 f cóncava 8 f' creciente 8 f" > 0 EF 8 f convea 8 f' decreciente 8 f" < 0 FG 8 f cóncava 8 f' creciente 8 f" > 0
2 Dibuja la gráfica de una función, f, que cumpla las siguientes condiciones: La función está definida en [0, 7]. Solo toma valores positivos. Pasa por los puntos 0, ),, ) y 7, ). En el intervalo, ), la función es convea. En el intervalo, 4), f''> 0. En el intervalo 4, 6), f' es decreciente. En el intervalo 6, 7), f es cóncava Página 68. Halla las rectas tangentes a la curva: y = en los puntos de abscisas 0,,. Calculamos la derivada de la función: y' = ) ) ) = ) Ordenadas de los puntos: y0) = 0; y) = 4; y) = 50 Recta tangente en 0, 0): y'0) = 8 y = 8 Recta tangente en, 4): y') = 9 y = 4 9 ) = 9 + Recta tangente en, 50): y') = y = 50 + ) = )
3 UNIDAD 7. Halla las ecuaciones de las rectas tangentes a la curva: y = 4 + que sean paralelas a la bisectriz de los cuadrantes segundo y cuarto. y = 4 + Calculamos la derivada: y' = 4 Si son paralelas a la bisectriz del. y 4. cuadrante, la pendiente es. Por tanto: 4 = 8 = 8 = 8 = ± y ) = 6 y ) = 0 Recta tangente en, 6): y = 6 + ) = + 5 Recta tangente en, 0): y = 0 ) = + Página 69. Dada la función y = 9 + 5, averigua: a) Dónde crece. b) Dónde decrece. y' = 6 9 = ) = ) + ) a) < 8 y' > 0 8 f es creciente ) > 8 y' > 0 8 f es creciente en, +@) b) < < 8 y' < 0 8 f es decreciente en, ) Página 7. Comprueba que la función y = / ) tiene solo dos puntos singulares, en = 0 y en = 6. Averigua de qué tipo es cada uno de esos dos puntos singulares; para ello, debes estudiar el signo de la derivada. y' = ) ) = ) ) ) = ) 4 ) 4 = 6 ) = 6) ) )
4 y' = 0 8 6) = 0 = 0 = 6 f' 0,0) > 0 f'0,0) > 0 En = 0 hay un punto de infleión. f'5,99) < 0 f'6,0) > 0 En = 6 hay un mínimo relativo.. a) Halla todos los puntos singulares abscisa y ordenada) de la función y = Mediante una representación adecuada, averigua de qué tipo es cada uno de ellos. b) Ídem para y = a) y' = + = + ) y' = 0 = 0 8 Punto 0, 0) = 8 Punto, ) Dos puntos singulares. Los dos puntos están en el intervalo [ ;,5], donde la función es derivable. Además, f ) = 7 y f,5) =,7. En 0, 0) hay un punto de infleión. En, ) hay un máimo relativo. b) y' = = 4 +) +) +) y' = 0 = 8 Punto, 0) = 8 Punto, ) = 8 Punto, 0) Los tres puntos están en el mismo intervalo [ 4, 0], donde la función es derivable. Además, f 4) = f 0) = 9. Hay un mínimo relativo en, 0), un máimo relativo en, ) y un mínimo relativo en, 0). Tres puntos singulares
5 UNIDAD 7 Página 7. Estudia la curvatura de esta función: y = f') = 4 ; f'') = 6 48 = 0 8 Punto 0, 5) f'') = 0 8 4) = = 8 Punto, 7 ) 4 f''') = 7 48; f'''0)? 0; f''' )? 0) 4 Los puntos 0, 5) y, ) son puntos de infleión. 7 4 La función es cóncava 0) «, +@), pues f'') > 0. La función es convea en el intervalo ) 0, 4. Estudia la curvatura de la función siguiente: y = f') = + 9; f'') = 6, pues f'') < 0. f'') = = 0 8 = 8 Punto, ) f''') = 6; f''')? 0) El punto, ) es un punto de infleión. La función es convea ), pues f'') < 0. La función es cóncava en, +@), pues f'') > 0. Página 75. Halla el número positivo cuya suma con veinticinco veces su inverso sea mínima. Llamamos al número que buscamos. Ha de ser > 0. Tenemos que minimizar la función: 5 f ) = + f') = 5 = 5 = 0 Como lím f ) = +@, lím f ) = +@ y la función es continua en 0, +@), @ hay un mínimo en = 5). Por tanto, el número buscado es = 5. El mínimo es 0. = 5 8 f 5) = 0 = 5 no vale, pues >0) 5
6 . De todos los triángulos rectángulos cuyos catetos suman 0 cm, halla las dimensiones de aquel cuya área es máima. + y = 0 8 y = 0 y 0 ) 0 Área = = =, 0 < < 0 Tenemos que maimizar la función: 0 f ) = y, 0 < < 0 0 f') = = 5 = 0 8 = 5 8 y = 0 5 = 5 5 f 0) = 0; f 0) = 0; f 5) = ; y f es continua. Luego en = 5 está el máimo). Los catetos miden 5 cm cada uno. El área máima es de,5 cm.. Entre todos los rectángulos de perímetro m, cuál es el que tiene la diagonal menor? d = 6 ) +, 0 < < 6 d 6 Tenemos que minimizar la función: f ) = 6 ) +, 0 < < 6 f') = 6 ) + = + 4 = 6 ) + 6 ) + f') = = 0 8 = ) + f 0)= 6; f 6) = 6; f ) = 8 = 4,4; y f ) es continua. Luego en = hay un mínimo). El rectángulo con la diagonal menor es el cuadrado de lado m. 4. Determina las dimensiones que debe tener un recipiente cilíndrico de volumen igual a 6,8 litros para que pueda construirse con la menor cantidad posible de hojalata. Suponemos el recipiente con dos tapas: h r V = 6,8 l = 6,8 dm πr r h Área total = π rh + π r = = π rh + r) 6
7 UNIDAD 7 Como V = π r h =,4 r h = 6,8 8 h = 6,8 =,4 r Así: Áreal total = πr + r) = π + r ) r Tenemos que hallar el mínimo de la función: f r) = π + r ), r >0 f'r) = π + r ) = π ) = r = 0 8 r = = Como lím f r) = +@, lím f r) = +@, y f es continua en 0, +@); en r = r r r r r 8 +@ + r hay un mínimo). r = 8 h = = r = El cilindro tendrá dm de radio y dm de altura. r r 7
8 Página 80 EJERCICIOS Y PROBLEMAS PROPUESTOS PARA PRACTICAR Recta tangente Halla la ecuación de la recta tangente a las siguientes curvas en los puntos cuya abscisa se indica: a) y = en = b) y = 0, 0,0 ) en = 0 +5 c) y = + en = d) y = en = 5 e) y = e en = 0 f) y = sen cos en = g) y = ln + ) en = 0 h)y = ln en = e a) Ordenada en el punto: = 8 y = Pendiente de la recta: y' = 8 y') = Recta tangente: y = ) = + b) Ordenada en el punto: = 0 8 y = = 4 Pendiente de la recta: y' = 0, 0,0 )0, 0,0) 8 y'0) = 0, = 0,4 Recta tangente: y = 4 + 0,4 0) = 0,4 c) Ordenada en el punto: = 8 y = Pendiente de la recta: y' = 8 y' ) = + 7 Recta tangente: y = + + ) = d) Ordenada en el punto: = 8 y = 4 6 π 0 0 Pendiente de la recta: y' = 8 y') = = 5) Recta tangente: y = 4 ) =
9 UNIDAD 7 e) Ordenada en el punto: = 0 8 y = Pendiente de la recta: y' = e 8 y'0) = Recta tangente: y = = + π f) Ordenada en el punto: = 8 y = 0 Pendiente de la recta: y' = cos sen π 8 y' = ) π π Recta tangente: y = = + g) Ordenada en el punto: = 0 8 y = 0 Pendiente de la recta: y' = 8 y'0) = + Recta tangente: y = h) Ordenada en el punto: = e 8 y = e Pendiente de la recta: y' = ln + 8 y'e) = Recta tangente: y = e + e) = e ) s Escribe la ecuación de la tangente a la curva y = + 4 +, que es paralela a la recta 4 y + 5 = 0. Calculamos la pendiente de la recta 4 y + 5 = 0: 5 4 y + 5 = 0 8 y = + 8 Pendiente. y' = + 4 = 8 = 8 y = 4 + = La recta tangente tiene pendiente y pasa por, ): y = + + ) = 8 y = s Halla las tangentes a la curva y = paralelas a la recta que pasa por 0, 0) y por, ). 0 La pendiente de la recta que pasa por 0, 0) y, ) es m = =. 0 Buscamos los puntos en los que la derivada de la función sea igual a : ) y' = = ) ) y' = 8 = 8 = 8 ) = 8 ) ) 8 = 0 = 0, y = 0 =, y = 9
10 Los puntos son 0, 0) y, 4). Las rectas tangentes son: y 0 = 0) 8 y = y 4 = ) 8 y = +8 s4 Escribe las ecuaciones de las tangentes a la función y = 4 en los puntos de corte con el eje de abscisas. Los puntos de corte son 0, 0) y 4, 0). y'0) = 4 pendiente en 0, 0) y' = 4 y'4) = 4 pendiente en 4, 0) Rectas tangentes: En 0, 0) 8 y = 4 En 4, 0) 8 y = 4 4) = Halla los puntos de tangente horizontal en las siguientes funciones y escribe la ecuación de la tangente en esos puntos: a) y = + b) y = c) y = d) y = + a) y' = 4 + = 0 = 8 y = 0, recta tangente en, 0). 4 4 = 8 y =, recta tangente en,. 7 7 b) y' = 4 + = 4 + ) = 0 = 0 8 y = 0, recta tangente en 0, 0). = 8 y =, recta tangente en,. 4 4 ) = 8 y =, recta tangente en,. 4 4 ) 6 + ) 6 c) y' = = = 0 + ) = 8 y =, recta tangente en, ). = 8 y =, recta tangente en, ). 5) 5 + 4) d) y' = = = 0 = 8 y =, recta tangente en, ). = 8 y = 9, recta tangente en, 9) ) 0
11 UNIDAD 7 6 Escribe la ecuación de la tangente a la curva f) = e en el punto donde corta el eje de ordenadas. Punto de corte con el eje de ordenadas: = 0 8 y = e 0 = e 8 0, e ) Pendiente de la recta tangente: f') = e 8 f'0) = e Ecuación de la recta tangente en 0, e ): y = e e = e ) 7 Determina el punto de la curva f) = en el que la tangente es paralela a la bisectriz del primer y tercer cuadrante. Escribe la ecuación de dicha tangente. La pendiente de la bisectriz del primer cuadrante es. Buscamos los puntos en los que f') = : f') = = 8 = f) = = Ecuación de la tangente: y = + ) = Máimos y mínimos 8 Halla los máimos, los mínimos y los puntos de infleión de las siguientes funciones: a) y = ) b) y = c) y = 4 d) y = 4 + e) y = + f) y = e ) a) y = f') = f') = = 0 8 No tiene solución. No tiene ni máimos ni mínimos. f'') = 6 6 = 0 8 = f'' < 0 f'' > 0 Hay un punto de infleión en, 9).
12 b) y = 4 8 f') = 4 = f') = 0 8 ) = 0 = 0 8 y = 0 = 8 y = 4/ f' < 0 f' < 0 f' > Hay un mínimo en, ). f'') = 4 = 0 8 4) = 0 = 0 8 y = 0 = 4/ 8 y = 64/8 f'' > 0 f'' < 0 f'' > Hay un punto de infleión en 0, 0) y otro en, ). 4 c) f') = 4 6 f') = ) = 0 = 0 8 y = 0 = / 8 y = 7/6 f' < 0 f' < 0 f' > Hay un mínimo en, ). 0 f'') = = ) = 0 = 0 8 y = 0 = 8 y = f'' > 0 f'' < 0 f'' > 0 0 Hay un punto de infleión en 0, 0) y otro en, ). d) f') = f') = ) = 0 8 = 0 8 y = 0 f' < 0 f' > 0 0
13 UNIDAD 7 Hay un mínimo en 0, 0). f'') = + 4? 0 para todo. No hay puntos de infleión. e) f') = + ) f') = 0 8 = 0 8 = 0 8 y = f' > 0 f' < 0 0 Hay un máimo en 0, ). f'') = + ) + + ) = + ) + 8 = + ) 4 + ) 6 + ) f'') = 0 8 = ± = ± = ± 8 y = f'' > 0 f'' < 0 f'' > 0 4 Hay un punto de infleión en, ) y otro en, ). 4 4 f) f') = e ) + e = e + ) = e f') = 0 8 e = 0 8 = 0 pues e? 0 para todo ) 8 y = f'' < 0 f'' > 0 0 Hay un mínimo en 0, ). f'') = e + e = e + ) f'') = 0 8 = 8 y = e f'' < 0 f'' > 0 Hay un punto de infleión en ), e.
14 9 Estudia los intervalos de crecimiento y de decrecimiento de las siguientes funciones, y di si tienen máimos o mínimos: a) y = b) y = 4 + c) y = d) y = + a) y =. Dominio = Á {, } 4 f') = = 0 8 = 0 4) Signo de la derivada: f' > 0 f' > 0 f' < 0 f' < 0 0 La función: crece ) «, 0). decrece en 0, ) «, +@). tiene un máimo en 0,. 4 b) y =. Dominio = Á { } + + ) ) f') = = = +) + ) +) f') > 0 para todo?. Por tanto, la función es creciente ) «, +@). No tiene máimos ni mínimos. c) y =. Dominio = Á + + ) + f') = = = + ) + ) f') > 0 8 = 0 8 = 0 Signo de la derivada: f' < 0 f' > 0 ) +) La función: decrece 0). crece en 0, +@). tiene un mínimo en 0, 0). 4
15 UNIDAD 7 d) y =. Dominio = Á {0} ) + f') = = = + f')? 0 para todo? 0. f') > 0 para todo? 0. La función es creciente 0) «0, +@). No tiene máimos ni mínimos. 0 Halla los intervalos de crecimiento y de decrecimiento, y los máimos y los mínimos de las siguientes funciones: 8 a) y = b) y = + c) y = ) d) y = ) ) e) y = f) y = ) 4) 8 8 a) y = =. Dominio = Á {0, } ) 8 ) ) 8 ) ) f') = = = ) ) = ) f') = ± ± = 0 8 = = = 6 6 = 6 ± 8 6 = 4, f4) = / = 4/, f4/) = 9/ Signo de la derivada: f' > 0 f' > 0 f' < 0 f' < La función: es creciente 0) «0, 4 es decreciente en, «, 4). ) ) 4 9 tiene un máimo en,. tiene un mínimo en 4,. ) 4 ) «4, +@). f' > 0 5
16 b) y = +. Dominio = Á {, } ) + ) f') = = = ) ) f') = = 0 8 = 0, f 0) = Signo de la derivada: f' > 0 f' > 0 f' < 0 f' < ) La función: es creciente ) «, 0). es decreciente en 0, ) «, +@). tiene un máimo en 0, ). c) y =. Dominio = Á {, } ) f') = = = = ) ) ) = 0, f0) = 0 f') = 0 8 ) = 0 =, f ) = )/ =, f ) = )/ ) ) Signo de la derivada: f' > 0 f' < 0 f' < 0 f' < 0 f' < 0 f' > 0 0 La función: es creciente ) «, +@). es decreciente en, ) «, ) «, ). tiene un máimo en,. tiene un mínimo en,. tiene un punto de infleión en 0, 0). ) ) d) y =. Dominio = Á {} 4 ) ) ) ) f') = = = ) ) = = 4 + ) ) ) 6
17 UNIDAD 7 f') = = ± 6 4 ± 4 8 = = = Signo de la derivada: 4 ± =, f) = 9 =, f) = f' < 0 f' > 0 f' > 0 f' < 0 La función: es creciente en, ) «, ). es decreciente ) «, +@). tiene un mínimo en, ). tiene un máimo en, 9). e) y = 9. Dominio = Á f') = 6 9 = ) ± 4 + ± 6 ± 4 f') = 0 8 = = = Signo de la derivada: =, f) = 7 =, f ) = 5 f' > 0 f' < 0 f' > 0 La función: es creciente ) «, +@). es decreciente en, ). tiene un máimo en, 5). tiene un mínimo en, 7). 8 8 f) y = =. Dominio = Á {0, } ) 8 6) 8 6) f') = = = 4 ) 4 ) 8 6) ) f') = ) = 0 Signo de la derivada: = 0 no vale) =, f) = f' < 0 f' > 0 f' < 0 0 f' < 0 La función: es creciente en 0, ). es decreciente 0) «, ) «, +@). tiene un máimo en, ). 7
18 Estudia la concavidad, la conveidad y los puntos de infleión de las siguientes funciones: a) y = + 4 b) y = 4 6 c) y = ) 4 d) y = e e) y = f) y = ln + ) + a) y = + 4. Dominio = Á f') = ; f'') = 6 f'') = = 0 8 = 0, f0) = 4 Signo de f''): f'' < 0 f'' > 0 0 La función: es convea 0). es cóncava en 0, +@). tiene un punto de infleión en 0, 4). b) y = 4 6. Dominio = Á f') = 4 ; f'') = =, f ) = 5 f'') = 0 8 ) = 0 =, f) = 5 Signo de f''): f'' > 0 f'' < 0 f'' > 0 La función: es cóncava ) «, +@). es convea en, ). tiene un punto de infleión en, 5) y otro en, 5). c) y = ) 4. Dominio = Á f') = 4 ) ; f'') = ) f'') = 0 8 =, f) = 0 f'') > 0 para? Por tanto, la función es cóncava. No tiene puntos de infleión. d) y = e. Dominio = Á f') = e + e = + )e ; f'') = e + + )e = + )e f'') = 0 8 = e? 0 para todo ), f ) = e 8
19 UNIDAD 7 Signo de f''): f'' < 0 f'' > 0 La función: es convea ). es cóncava en, +@). tiene un punto de infleión en,. e) y =. Dominio = Á { } + + ) ) + f') = = = + ) + ) + ) 6 f'') = + ) f'')? 0 para todo. Signo de f''): f'' < 0 f'' > 0 e ) La función: es convea ). es cóncava en, +@). no tiene puntos de infleión. f) y = ln + ). Dominio =, +@) f') = + f'') = + ) f'') < 0 para é, +@) Por tanto, la función es convea en, +@). Estudia si las siguientes funciones tienen máimos, mínimos o puntos de infleión en el punto de abscisa = : a) y = + ) b) y = + ) 4 c) y = ) 6 a) f') = ) f'') = 6 ) f' > 0 f' > 0 f'' < 0 f'' > 0 Hay un punto de infleión en =. 9
20 b) f') = 4 ) f'') = ) f' < 0 f' > 0 f'' > 0 f'' > 0 Hay un mínimo en =. c) f') = 6 ) 5 f'') = 0 ) 4 f' > 0 f' < 0 f'' < 0 f'' < 0 Hay un máimo en =. Página 8 Problemas de optimización Una discoteca abre a las 0 de la noche y cierra cuando se han marchado todos sus clientes. La epresión que representa el número de clientes en función del número de horas que lleva abierta, t, es Nt) = 80t 0t. a) A qué hora el número de clientes es máimo? Cuántos clientes hay en ese momento? b) A qué hora cerrará la discoteca? a) Buscamos los puntos en los que la derivada es igual a 0: N't) = 80 0t t = 0 8 t = 4 N''t) = 0 < 0; en t = 4, la función tiene un máimo. El número de clientes es máimo a las de la mañana 4 horas después de abrir). Este número de clientes es: N4) = = 60 personas b) Nt) = t 0t t = 0 = 0 8 0t 8 t) = 0 t = 8 Cierra 8 horas después de abrir, a las 6 de la mañana. 4 Una franquicia de tiendas de moda ha estimado que sus beneficios semanales en miles de euros) dependen del número de tiendas que tiene en funcionamiento n) de acuerdo con la epresión: Bn) = 8n + 60n 96n Determina razonadamente: a) El número de tiendas que debe tener para maimizar sus beneficios semanales. b) El valor de dichos beneficios máimos. 0
21 UNIDAD 7 a) Buscamos los puntos en los que la derivada es igual a 0: B'n) = 4n + 0n n + 0n 96 = n 5 ± 5 6 n = + 5n 4 = 0 8 n = n = 4 Para saber cuál es el máimo utilizamos la segunda derivada: B'') = 7 > 0; en n = hay un mínimo. B''n) = 48n + 0 B''4) = 7 < 0; en n = 4 hay un máimo. Debe tener 4 tiendas para que los beneficios semanales sean máimos. b) B4) = = 64 Los beneficios semanales serán de euros. 5 El coste total de producción de unidades de un producto es: C) = C) Se define la función coste medio por unidad como C m ) = Cuántas unidades hay que producir para que el coste por unidad sea mínimo? C) Buscamos el máimo de la función C m ) =, igualando a 0 su derivada: / C m ) = = C' m ) = 8 = 0 8 = 576 Comprobamos que hay un mínimo en = 4: 84 C'' m ) = 8 C'' m 4) > 0 El coste medio por unidad es mínimo si se producen 4 unidades. = 4 = 4 no vale) 6 Una empresa quiere producir Ct) = t unidades de un producto para vender a un precio pt) = 00 t euros por unidad, siendo t el número de días transcurridos desde el inicio de la producción. a) Calcula el beneficio si t = 0. b) Escribe, dependiendo de t, la función de beneficio 0 Ì t Ì 60). c) Deteremina cuándo el beneficio es máimo. a) Si t = 0 C0) = = 00 unidades p0) = 00 0 = 80 por unidad Beneficio: C0) p0) = =
22 b) Bt) = Ct) pt) = t) 00 t) = 0t + 600t si 0 Ì t Ì 60 c) Para hallar el máimo, hacemos B't) = 0: B't) = 40t = 0 8 t = 40 Al cabo de 40 días se obtiene el máimo beneficio, que es: B40) = = Se quiere fabricar una caja de volumen máimo que sea el doble de larga que de ancha y que, además, la suma del ancho más el largo más el alto sea igual a un metro. Calcula las medidas que debe tener la caja y cuál será su volumen. a a b Volumen de la caja: V = a a b = a b a + a + b = 8 b = a V = a a) = a 6a Para hallar el máimo volumen, derivamos e igualamos a cero: V' = 4a 8a = 0 8 a4 8a) = 0 a = 0 no vale) a = 9 Comprobamos si el volumen es máimo para a = : 9 ) V'' = 4 6a 8 V'' = 4 6 = 4 < 0, máimo Si a = m, el largo será = m, y el alto, = m El volumen máimo es: 4 8 V = = m PARA RESOLVER 8 Prueba que la recta y = es tangente a y = Halla el punto de tangencia y estudia si esa recta corta a la curva en otro punto distinto al de tangencia. y' = +8 Veamos para qué valor de tiene pendiente : + 8 = + 9 = 0 = 8 y = = 8 y =
23 UNIDAD 7 El punto, ) verifica la ecuación y =. Veamos los puntos de corte: = = 0 = 0 8 y = ) = 0 = 8 y = El otro punto de corte es 0, 0). s9 Halla la ecuación de la recta tangente a la curva y =4 0 en su punto de infleión. Hallamos el punto de infleión: y' = 4 8 y'' = y''' = 4 y'' = = 0 8 =, y = 4 0 = 8 Comprobamos que, 8) es un punto de infleión: y''') = 4? 0 Pendiente de la recta tangente: m = y') = 4 = Ecuación de la recta tangente: y = 8 ) 8 y = 6 s0 Determina la parábola y = a + b + c que es tangente a la recta y = en el punto A, ) y que pasa por el punto B5, ). y = a + b + c La pendiente de la recta y = es. Debe ser y') =. y' = a + b 8 y') = 8 4a + b = Pasa por A, ) 8 y) = 4a + b + c = Pasa por B5, ) 8 y5) = 5a + 5b + c = Solución del sistema: a =, b = 6, c = 7 8 y = La curva y = + a + b + c corta al eje de abscisas en = y tiene un punto de infleión en, ). Calcula a, b y c. y = + a + b + c f') = + a + b f'') = 6 +a f ) = a b + c = 0 a b + c = a = 6 f ) = a + b + c = 4a + b + c = 7 b = f'') = a = 0 a = 6 c = 0
24 De la función f ) = a + b sabemos que pasa por, ) y que en ese punto tiene tangente paralela a la recta + y = 0. a) Halla a y b. b) Determina sus etremos relativos y sus intervalos de crecimiento y de decrecimiento. a) f ) = a + b; f') = a + b. La pendiente de la recta es. f ) = 8 a + b = a = f ) = + f') = 8 a + b = b = b) f') = 6 +4 f') = 0 8 ) = 0 Signo de la derivada: f' < 0 f' > 0 f' < 0 La función: es decreciente «, +@ ). ) es creciente en, ). ) ) tiene un mínimo en,. tiene un máimo en,. =, f ) = =, f ) = s De la función f ) = + a + b se sabe que: Tiene un mínimo en =. Su gráfica pasa por el punto, ). Teniendo en cuenta estos datos, cuánto vale la función en =? f') = + a Además: Tiene un mínimo en = 8 f') = a = 0 8 a = 4 Su gráfica pasa por, ) 8 f) = 8 + 4) + b = 8 8 b 4 = 8 b = 6 Por tanto: f) = + a + b = + 4) + 6 = 4
25 UNIDAD 7 s4 Calcula p y q de modo que la curva y = + p + q contenga al punto, ) y presente un mínimo en =. y = + p + q 8 f') = + p f ) = 4 p + q = f' ) = ) + p = 0 8 p = 6 ) q = 8 q = 9 ) Sustituimos en f ). Por tanto: p = 6 y q = 9 5 Estudia los intervalos de crecimiento y de concavidad de las siguientes funciones: a) f ) = b) f ) = a) f ) = 8 f') = + f') = 0 8 = 0 8 = ± Signo de la derivada: ) + ) f' < 0 f' > 0 f' < 0 Crece en, ) y decrece ) «, +@). f'') = 6 ) + ) f'') = 0 8 = 0, =, = f'' < 0 f'' > 0 f'' < 0 f'' > 0 0 Es cóncava en, 0) «, +@) y convea ) «0, ). b) f ) = f') = f') = 0 8 = 0, = Signo de la derivada: f' < 0 f' < 0 f' > 0 0 Crece en 0, +@) y decrece 0). 5
26 f'') = f'') = 0 8 =, = Signo de la segunda derivada: f'' > 0 f'' < 0 f'' > 0 Es cóncava ) «, +@) y convea en, ). 6 Comprueba y justifica que la función f ) =e es siempre decreciente y cóncava. f) = e f') = e < 0 para cualquier valor de Por tanto, f) es siempre decreciente. f'') = 9e > 0 para todo Así, f) es cóncava en todo su dominio. Página 8 7 Observando la gráfica de la función f', derivada de f, di: a) Cuáles son los intervalos de crecimiento y de decrecimiento de f. b) Tiene f máimos o mínimos? f' a) f es creciente f' > 0) en el ) y decreciente f' < 0) en, +@). b) f tiene un máimo en =. f') = 0 y la función pasa de creciente a decreciente). 8 Esta es la gráfica de la función derivada de f ). Eplica si f ) tiene máimos, mínimos o puntos de infleión en =, = y = 5. = : en este punto, la función tiene un mínimo, porque pasa de ser decreciente f' < 0) a creciente f' > 0), y f') = 0. = : en este punto, f tiene un punto de infleión, ya que f'') = 0. = 5: en este punto, f tiene un máimo, pues pasa de ser creciente a decreciente y f'5) = 0. f' 6
27 UNIDAD 7 + si Ì 9 Dada la función f ) = : + si > a) Halla su función derivada. b) Tiene f algún punto en el que f') = 0? c) Estudia el crecimiento y decrecimiento de f. d) Escribe la ecuación de la recta tangente a f en = 0. + si Ì f ) = + si > + si < a) f') = si > No es derivable en = porque f' ) =? f' + ) =. b) f') = 0 solo puede darse para + = 0 8 = c) Signo de la derivada: f' < 0 f' > 0 f' > 0 Crece en, +@) y decrece ). d) La pendiente de la recta en = 0 es: m = f'0) = Por tanto: y = f0) + m 0) y = + 0) y = 0 Esta es la gráfica de una función y = f ). a) Indica el signo que tendrá f' en los ),, ) y, +@). b) En qué puntos la gráfica de f' cortará al eje OX? a) f' > 0 f' < 0 f' > 0 b) En = y en =. 7
28 Escribe la ecuación de la recta tangente a la curva y = en su punto de infleión. y = y' = y'' = 48 El punto de infleión será: f'') = = 0 8 = 4 8 4, 7) En ese punto, la pendiente de la recta tangente es: m = f'4) = 4 Así, la ecuación de la recta pedida es: y = f4) + m 4) y = 7 4 4) y = 4 + Dada la curva y = 4 4 : a) Cuál es la función que nos da la pendiente de la recta tangente en un punto cualquiera? b) Halla el punto en el que la pendiente de la recta tangente es máima. a) La función pedida es la de su función derivada: f') = 4 b) Para ello hay que hallar el máimo de la función f': f'') = 4 f'') = = ) = 0 8 = 0 y = Hallamos la tercera derivada: f''') = 4 4 f'''0) = 4 < 0 8 0, 0) es un máimo. f''') = 4 > 0 8, 6) es un mínimo. El punto pedido es el 0, 0). Una feria ganadera permanece abierta al público desde las 0 hasta las 0 horas. Se sabe que el número de visitantes diarios viene dado por: Nt) = 0A t) + B, 0 Ì t Ì 0 Sabiendo que a las 7 horas se alcanza el número máimo de 500 visitantes, determina el valor de A y de B. La función pasa por el punto 7, 500). Su derivada es igual a 0 en t = 7, punto en el que alcanza el máimo: 8
29 UNIDAD 7 N7) = 0A 7) + B = 500 N't) = 40A t) 8 N'7) = 40A 7) = 0 8 A = 7 N7) = 07 7) + B = B = 500 Comprobamos que hay un máimo en t = 7: N''t) = 40 < 0, es un máimo. 4 El número de vehículos que ha pasado cierto día por el peaje de una autopista viene dado por la función: t ) + si 0 Ì t Ì 9 Nt) = t 5 0 ) si 9 Ì t Ì 4 donde N indica el número de vehículos y t el tiempo transcurrido en horas desde las 0:00 h. a) Entre qué horas aumentó el número de vehículos que pasaba por el peaje? b) A qué hora pasó el mayor número de vehículos? Cuántos fueron? a) Para saber cuándo la función es creciente, estudiaremos el signo de su derivada. Las funciones con las que Nt) está definida son continuas y derivables si 0 Ì t < 9 y si 9 < t Ì 4. Estudiamos la derivabilidad en t = 9: t N't) = t 5 ) si 0 Ì t <9 ) si 9 < t Ì 4 N't) = 0 4 N'9 ) = 4 N'9 + ) = N es derivable en t = 9. t ) = 0 8 t = t 5 ) = 0 8 t = 5 Signo de N't): N' t ) < 0 N' t ) > 0 N' t ) < El número de vehículos aumentó entre las h y las 5 h. 9
30 b) El máimo absoluto de una función continua definida en un intervalo cerrado se encuentra entre los máimos relativos de la función o en los etremos del intervalo: N0) = ; N5) = 0; N4) = El mayor número de vehículos pasó a las 5 h, y fueron 0 vehículos. 5 Se desea construir el marco para una ventana rectangular de 6 m de superficie. El metro lineal de tramo horizontal cuesta,50 y el de tramo vertical,. a) Calcula las dimensiones de la ventana para que el coste del marco sea mínimo. b) Cuál será ese coste mínimo? 6 a) Área = y = 6 8 y = 6 m y Perímetro = + y Coste =,5 + y = 5 + 6y 6 C = C' = 5 = 0 8 =,68 m 8 y = 5,4 m C'' = ; C'' ) > 0 8 = es mínimo) Las dimensiones son = m e y = 5 m b) C = = 5 6,8 5 6 Se quiere construir un recipiente cónico cuya generatriz mida 0 cm y que tenga capacidad máima. Cuál debe ser el radio de la base? h + R = 00 8 R = 00 h Volumen = πr h = π 00 h )h = π 00h h ) Tenemos que maimizar la función volumen: 0 cm h f h) = π 00h h ) f'h) = π 00 h ) R f'h) = h = 0 8 h = ± 00 consideramos la raíz positiva, pues h Ó 0). 0
31 UNIDAD 7 f'h) > 0 a la izquierda de h = y f'h) < 0 a la derecha de h = Luego en h = hay un 00 máimo). Por tanto, el radio de la base será: R = 00 h = 00 = 8 R = 00 7 Un artículo ha estado 8 años en el mercado. Su precio Pt), en miles de euros, estaba relacionado con el tiempo, t, en años, que este llevaba en el mercado por la función: 4t + 4 si 0 Ì t Ì Pt) = 5/)t + 5 si < t Ì 8 a) Estudia el crecimiento y decrecimiento de Pt). b) Cuál fue el precio máimo que alcanzó el artículo? c) Cuál fue la tasa de variación media del precio durante los últimos 6 años? 4t + 4 si 0 Ì t Ì Pt) = 5/)t + 5 si < t Ì 8 8t 0 < t < a) P't) = No eiste P'), pues P' )? P' + )). 5/ < t < 8 Pt) es creciente en 0 < t < pues P't) > 0. Pt) es decreciente en < t < 8 pues P't) < 0. b) El máimo se alcanza en t =, P) = 0. P8) P) c) T.V.M. [, 8] = = = = =, Página 8 CUESTIONES TEÓRICAS s8 La función f tiene derivadas primera y segunda y es f'a) = 0 y f''a) = 0. Puede presentar f un máimo relativo en el punto a? En caso afirmativo, pon un ejemplo. Sí puede presentar un máimo. Por ejemplo: f ) = 4 en = 0 es tal que:
32 f' > 0 f' < 0 0 f') = 4 f'') = Por tanto: f'0) = 0 y f''0) = 0 En 0, 0) hay un máimo relativo. 9 Considera la función valor absoluto de ): a) Presenta un mínimo relativo en algún punto? b) En qué puntos es derivable? Razona tus respuestas. a) f) presenta un mínimo relativo en = 0, pues f0) = 0 < f) si? 0. y = De hecho, es el mínimo absoluto de f). si Ì 0 si < 0 b) f) = = ; f') = si > 0 si > 0 f) no es derivable en = 0, pues f'0 ) =? f'0 + ) =. Por tanto, f es derivable para? Si f'a) = 0, qué proposición es cierta?: a) f tiene un máimo o un mínimo en el punto de abscisa = a. b) f tiene un punto de infleión en = a. c) f tiene en el punto = a tangente paralela al eje OX. Si f'a) = 0, solo podemos asegurar que f tiene en = a tangente horizontal paralela al eje OX). Podría tener un máimo, un mínimo o un punto de infleión en = a. Por tanto, solo es cierta la proposición c). 4 Comprueba si eiste algún valor de a para el cual la función: f) = a ln + tenga un punto de infleión en =. Para que eista punto de infleión en =, debe ser f'') = 0: f) = a ln + 8 f') = a + a = + a f'') = f'') = a + 6 = 0 8 a = 6
33 UNIDAD 7 Comprobamos con f''' si eiste punto de infleión: 6 6 f'') = f''') = f''')? 0 Para a = 6, la función tiene un punto de infleión en =. PARA PROFUNDIZAR 4 Estudia la eistencia de máimos y de mínimos relativos y absolutos de la función y = 4. Tiene puntos de infleión? 4 si < f) = + 4 si Ì Ì 4 si > si < f') = si < < si > En = no es derivable, pues f' ) = 4? f' + ) = 4. En = no es derivable, pues f' ) = 4? f' + ) = 4. La derivada se anula en = 0. Signo de la derivada: f' < 0 f' > 0 f' < 0 0 f' > 0 La función tiene un máimo relativo en 0, 4). No tiene máimo absoluto lím f) = lím f) = +@). Tiene un mínimo relativo en, 0) y otro en, 0). En estos puntos, el mínimo también es absoluto, puesto que f) Ó 0 para todo. Puntos de infleión: si < f'') = si < < si > Signo de f'': f'' > 0 f'' < 0 f'' > 0 8 +@ Tiene dos puntos de infleión:, 0) y, 0). Coinciden con los dos mínimos absolutos.
34 4 Estudia el crecimiento, los máimos y los mínimos de la función: y = + Definimos la función por intervalos. Para ello, calculamos los puntos donde f) = 0: ± = 0 8 = = ± 4 = = + si < f ) = + si Ì Ì + si > Hallamos la derivada de f: + si < f') = si < < + si > En = no es derivable, pues f' ) = 4? f' + ) = 4. En = no es derivable, pues f' ) = 4? f' + ) = 4. Veamos dónde se anula la derivada: + = 0 8 = Pero f') = + para < y >. = 0 8 = y f') = para < < Por tanto, f') se anula en = 8 f ) = 4. Signo de la derivada: f' < 0 f' > 0 f' < 0 f' > 0 La función: es creciente en, ) «, +@). es decreciente ) «, ). tiene un máimo en, 4). tiene un mínimo en, 0) y otro en, 0). Son los puntos donde f no es derivable. 4
35 UNIDAD 7 44 Se quiere construir una pista de entrenamiento que consta de un rectángulo y de dos semicírculos adosados a dos lados opuestos del rectángulo. Si se desea que el perímetro de la pista sea de 00 m, halla las dimensiones que hacen máima el área de la región rectangular. y Perímetro de la pista = + π y = Despejamos: y = π Área del rectángulo = y = = π π Derivamos: A' = = 0 8 = 50 m 8 y = m π π π 4 A'' = ; A''50) < 0 8 = 50 es máimo). π 45 Dos postes de m y 8 m de altura distan entre sí 0 m. Se desea tender un cable que una un punto del suelo entre los dos postes con los etremos de estos. Dónde hay que situar el punto del suelo para que la longitud total del cable sea mínima? La longitud total del cable es: m 8 m L) = ) + 8 ; es decir: 0 L) = m L') = + 60 = + 0 = = ) ) ) L') = ) + 44 = = 0) ) = 0) + 44) = ) + 44) 5
36 = = = 0 48 ± ± 5 84 = = = 48 ± 7 = = 60 no vale) En = hay un mínimo, pues L') < 0 a la izquierda de ese valor y L') > 0 a su derecha). Por tanto, el punto del suelo debe situarse a m del poste de m y a 8 m del poste de 8 m). 46 Determina el radio de la base y la altura de un cilindro de 54 cm de área total para que su volumen sea máimo. h r Área total = πrh + πr πrh + πr 54 πr = 54 8 h = πr Volumen = πr h V = πr 54 πr = r7 πr ) = 7r πr πr Buscamos el máimo de V: V' = 7 πr 8 7 πr = 0 8 r 7 9 = = 8 π π 8 r = la solución negativa no vale). π Comprobamos si el volumen es máimo: V'' = 6πr 8 V'' < 0, es un máimo. π ) 7 π 9/π) 8 π 6 π Si r = 8 h = = = π π / π ) π π Por tanto, para que el volumen sea máimo debe ser: 6 π r =,7 cm y h =,4 cm π π 6
37 UNIDAD 7 Página 8 AUTOEVALUACIÓN. Dada la parábola y = + 4 : a) Halla la pendiente de la recta r que une los puntos de la parábola de abscisas = 0 y =. b) Escribe la ecuación de la recta tangente a la parábola que es paralela a la recta r del apartado a). a) El punto de la parábola de abscisa = 0 es el 0, ) y el de = es el, 0). Por tanto, la pendiente de la recta que los une es: 0 m = = = 0 La ecuación de la recta es y =. b) Cualquier recta paralela a r tiene la pendiente igual a. Buscamos los puntos en los que la derivada de la curva es igual a : y' = = 8 =, y = El punto de tangencia es,. 4 Ecuación de la recta tangente: y = + 8 y = 4 4 ) ) ) + 4 = 4. Estudia el crecimiento y decrecimiento de la función y =. Tiene máimos o mínimos? + Estudiamos el signo de la función derivada: + ) ) 4 y' = = +) +) El numerador y el denominador son positivos para cualquier valor de. La función es creciente en todo su dominio, Á {}, porque su derivada es positiva. No tiene máimos ni mínimos, porque es siempre creciente. 7
38 . Halla los máimos, los mínimos y los puntos de infleión de la función: 5 y = Máimos y mínimos: buscamos los puntos en los que la derivada es igual a 0. y' = = y' = ) = 0 5 = = 0 = = Los posibles máimos y mínimos están en = 0, = y =. Comprobamos en la segunda derivada: y'' = y''0) = 0 y'') < 0 8 máimo, 0 y'') > 0 8 mínimo, ) Buscamos los puntos de infleión: ) y'' = = ) = 0 = = = 0 + =,4 = 0,6 Comprobamos en y''' = 4 + 6: Puntos de infleión: ) 0,,,4;,4), 0,6; 0,04) 0 y'''0)? 0 y''',4)? 0 y'''0,6)? 0 8
39 UNIDAD 7 4. La función f ) = + a + b + c verifica que f ) =, f') = 0 y que f no tiene etremo relativo en =. Calcula a, b y c. Si es f') = 0 y no hay etremo relativo, tiene que haber un punto de infleión en =. f) = + a + b + c 8 f') = + a + b 8 f'') = 6 + a f) = 8 + a + b + c = f') = a + b = 0 f'') = a = 0 Resolviendo este sistema, obtenemos: a =, b =, c = 0 Por tanto, la función buscada es: f) = + 5. El número de personas ingresadas en un hospital por una infección después de t semanas viene dado por la función: 50t Nt) = siendo t Ó 0 t t +8 Calcula el máimo de personas ingresadas y la semana en que ocurre. A partir de qué semana, después de alcanzar el máimo, el número de ingresados es menor que 5? Para calcular el máimo, derivamos e igualamos a cero: 50t t + 8) 50t4t ) 50 t +8) N't) = = = 0 8 t t +8) t t +8) 8 t + 8 = 0 8 t = 4 t = no vale, pues t Ó 0) 50 t = 8 N) = = El número máimo de personas ingresadas es 70, y ocurre en la. a semana. 50t Hemos de ver cuándo < 5. t t +8 50t < 50t 75t t 45t + 00 > 0 8 t 7t + 8 > 0 Resolvemos la inecuación: ft) = t 7t + 8 = 0 t = 8 t = 0,5 f t) > 0 f t) < 0 f t) > 0 0,5 8 ft) > 0 para t é 0; 0,5) «8, +@). Después de alcanzar el máimo en t =, a partir de t = 8, el número de personas ingresadas es menor que 5. 9
40 6. Sea B) = a + b la función de beneficios, en miles de euros, de una empresa. El beneficio máimo es de 50 miles de euros para = 00 unidades producidas. Calcula a y b. B) = a + b Sabemos que B00) = 50 y B'00) = 0 B00) = 00a +0b = 50 b b B') = a + 8 B'00) = a + = 0 0 Resolvemos el siguiente sistema: 00a + 0b = 50 b b a + = 0 8 a = 0 0 ) b b b = b = 5 8 b + b = 0 8 b = 0; a = 0 Por tanto, B) = Con una cartulina rectangular de m Ò m, se quiere construir una caja sin tapa. Para ello, se recorta un cuadrado de cada uno de los vértices. Calcula el lado del cuadrado recortado para que el volumen de la caja sea máimo. m m El volumen de la caja es: V) = ) ), é 0, ) V) = V') = V') = ± 8 = 0 8 = V'') = 0 + 4; V''0,9) < 0 ò = 0,9,7 no vale) 0,9 Si = 0,9 m, el volumen es máimo. 40
APLICACIONES DE LAS DERIVADAS
 0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
0 APLICACIONES DE LAS DERIVADAS Página 8 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES
 ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
ESTUDIO Y REPRESENTACIÓN GRÁFICA DE FUNCIONES 1. Sea f : (0, + ) definida como f () = Ln a) Probar que la función derivada f es decreciente en todo su dominio. b) Determinar los intervalos de crecimiento
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL
 EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6
![1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6 1. Calcula la tasa de variación media de la función y = x 2 +x-3 en los intervalos: a) [- 1,0], b) [0,2], c) [2,3]. Sol: a) 0; b) 3; c) 6](/thumbs/40/21103079.jpg) ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
ejerciciosyeamenes.com PROBLEMAS DE DERIVADAS 1. Calcula la tasa de variación media de la función +- en los intervalos: a) [- 1,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación media
Demuestra que el punto de tangencia, T, es el lugar de la recta r desde el que se ve el segmento AB con ángulo máximo.
 Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 7 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura.
Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 7 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura.
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
APLICACIONES DE LAS DERIVADAS
 UNIDAD APLICACIONES DE LAS DERIVADAS Página 98 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f
UNIDAD APLICACIONES DE LAS DERIVADAS Página 98 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días
![5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días 5. [2013] [EXT-A] En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días](/thumbs/40/21102307.jpg) . [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
. [204] [ET-A] Una empresa ha realizado un estudio sobre los beneficios, en miles de euros, que ha obtenido en los últimos 0 años. La función a la que se ajustan dichos beneficios viene dada por B(t) =
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
Las superficies serán: Tapa y superficie lateral S 1 = ( x 2 +4xy ) cm 2 Superficie de la base: S 2 = x 2 cm 2
 MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
MATEMÁTICAS II, º BACHILLERATO F.- Se desea construir una caja cerrada de base cuadrada con una capacidad de 8 cm. Para la tapa y la superficie lateral se usa un material que cuesta /cm y para la base
APLICACIONES DE LAS DERIVADAS
 10 APLICACIONES DE LAS DERIVADAS REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: Relación de la curvatura con el signo de la segunda derivada
10 APLICACIONES DE LAS DERIVADAS REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: Relación de la curvatura con el signo de la segunda derivada
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
JUNIO 2010. Opción A. 1 1.- Dada la parábola y = 3 área máxima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola.
 Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
Junio 00 (Prueba Específica) JUNIO 00 Opción A.- Dada la parábola y 3 área máima que tiene un lado en la recta y los otros dos vértices en la gráfica de la parábola., y la recta y 9, hallar las dimensiones
REPRESENTACIÓN GRÁFICA DE FUNCIONES
 REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
REPRESENTACIÓN GRÁFICA DE FUNCIONES a. Dominio de definición: D = Dom f() = { R eiste f()} b. Puntos de corte con los ejes: Con el eje OX (abscisas): f() = 0 : (,0). Ninguno, uno o más puntos. Con el eje
APLICACIONES DE LA DERIVADA CCSS
 APLICACIONES DE LA DERIVADA CCSS Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en
APLICACIONES DE LA DERIVADA CCSS Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 55 REFLEXIONA Y RESUELVE Tangentes a una curva y f ( 5 5 Halla, mirando la gráfica y las rectas trazadas, f'(, f'( y f'(. f'( 0; f'( ; f'( Di otros tres puntos
Hacia la universidad Análisis matemático
 Hacia la universidad Análisis matemático OPCIÓN A. a) Deriva las funciones f( ) = 8, g ( ) =, h ( ) = e. f( ) si 0 b) Indica si la función m ( ) = es continua en =. g ( ) si < c) Escribe la ecuación de
Hacia la universidad Análisis matemático OPCIÓN A. a) Deriva las funciones f( ) = 8, g ( ) =, h ( ) = e. f( ) si 0 b) Indica si la función m ( ) = es continua en =. g ( ) si < c) Escribe la ecuación de
1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones:
 APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
APLICACIONES DE DERIVADAS 1. Halla los máximos, mínimos y puntos de inflexión de las siguientes funciones: a. 6 9 b. c. 2 d. 2 e. f. 1 2. Estudia los intervalos de crecimiento y decrecimiento de las siguientes
8. y = Solución: x 4. 9. y = 3 5x. Solución: y' = 5 3 5x L 3. 10. y = Solución: 4 4 (5x) 3. 11. y = Solución: (x 2 + 1) 2. 12.
 7 Cálculo de derivadas. Reglas de derivación. Tabla de derivadas Aplica la teoría Deriva en función de :. y = 8. y = 5 3 5 4. y = ( ) 5 0( ) 4 9. y = 3 5 5 3 5 L 3 3. y = 7 + 3 4. y = e e 5. y = 7 7 +
7 Cálculo de derivadas. Reglas de derivación. Tabla de derivadas Aplica la teoría Deriva en función de :. y = 8. y = 5 3 5 4. y = ( ) 5 0( ) 4 9. y = 3 5 5 3 5 L 3 3. y = 7 + 3 4. y = e e 5. y = 7 7 +
CONCEPTO DE DERIVADA
 TASA DE VARIACIÓN MEDIA CONCEPTO DE DERIVADA ACTIVIDADES ) Halla la tasa de variación media de la función f siguientes intervalos: en cada uno de los a), b), c) 0, d), 3 ) Halla la T.V.M. de esta función
TASA DE VARIACIÓN MEDIA CONCEPTO DE DERIVADA ACTIVIDADES ) Halla la tasa de variación media de la función f siguientes intervalos: en cada uno de los a), b), c) 0, d), 3 ) Halla la T.V.M. de esta función
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción B Junio, Ejercicio, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 004 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción B Junio, Ejercicio, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 1, Ejercicio, Opción A Reserva,
APLICACIONES DE LA DERIVADA
 7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
Máximo o mínimo de una función. Solución: El mínimo de una función se da en los puntos que anulan su derivada y tiene derivada segunda positiva.
 Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
FUNCIONES CONTINUAS EN UN INTERVALO. El Tª de Bolzano es útil para determinar en algunas ocasiones si una ecuación tiene soluciones reales:
 FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
FUNCIONES CONTINUAS EN UN INTERVALO Teoremas de continuidad y derivabilidad Teorema de Bolzano Sea una función que verifica las siguientes hipótesis:. Es continua en el intervalo cerrado [, ]. Las imágenes
Tema 2. Derivadas. Aplicaciones de las derivadas Aplicación 2ºA Bach
 1.- Dada la función y = x 3 3x 2 9x + 5 : a) Dónde crece? b) Dónde decrece? Tema 2. Derivadas. Aplicaciones de las derivadas x 3 2.- Comprueba que la función f (x) = tiene solo dos puntos singulares, en
1.- Dada la función y = x 3 3x 2 9x + 5 : a) Dónde crece? b) Dónde decrece? Tema 2. Derivadas. Aplicaciones de las derivadas x 3 2.- Comprueba que la función f (x) = tiene solo dos puntos singulares, en
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
Grado en Química Bloque Funciones de una variable Sección.5: Aplicaciones de la derivada. Máximos y mínimos (absolutos) de una función. Sea f una función definida en un conjunto I que contiene un punto
a) f(x) (x 1) 2 b) f(x) x c) h(x) 1 2 a) f (3) 8 0 f es creciente en x 3.
 6 Aplicando la definición de derivada, calcula la derivada de las siguientes funciones en los puntos que se indican: a) f() en Aplicando la definición de derivada, calcula f () en las funciones que se
6 Aplicando la definición de derivada, calcula la derivada de las siguientes funciones en los puntos que se indican: a) f() en Aplicando la definición de derivada, calcula f () en las funciones que se
PAU: Aplicaciones de la derivada MATEMÁTICAS II 1. 2cos. x 0 x 0
 PAU: Aplicaciones de la derivada MATEMÁTICAS II JULIO 0 ESPECÍFICA. Calcule a para que las siguientes funciones: sen a cos f( ) g() tengan el mismo límite en el punto 0. Calculamos cada límite: sen a 0
PAU: Aplicaciones de la derivada MATEMÁTICAS II JULIO 0 ESPECÍFICA. Calcule a para que las siguientes funciones: sen a cos f( ) g() tengan el mismo límite en el punto 0. Calculamos cada límite: sen a 0
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
9.- DERIVADAS 2.- DERIVADA DE UNA FUNCIÓN. 2 utilizando la definición y halla su valor en xo = REGLAS DE DERIVACIÓN
 9- DERIVADAS - DERIVADA EN UN PUNTO Calcula la derivada de y = + en o = utilizando la definición Solución: y'() = 8 Calcula la derivada de - en o = utilizando la definición Solución: y '() = -6 Calcula
9- DERIVADAS - DERIVADA EN UN PUNTO Calcula la derivada de y = + en o = utilizando la definición Solución: y'() = 8 Calcula la derivada de - en o = utilizando la definición Solución: y '() = -6 Calcula
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2017 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 017 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 017 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
Integral definida. 1. Integral definida. Piensa y calcula. Aplica la teoría. 3. Siendo x el valor absoluto o módulo de x, calcula la. 2.
 Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
Tema: Aplicaciones de derivadas. Sean x e y las dimensiones del rectángulo. Área del rectángulo: A = x y. 36 x. Luego, el área es A(x) =
 JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
APLICACIONES DE LAS DERIVADAS 2º Bachillerato
 APLICACIONES DE LAS DERIVADAS º Bachillerato RECTA TANGENTE A UNA CURVA EN UN PUNTO. Si f es derivable en el punto, la ecuación de la recta tangente a f en el punto es: y = f + f ' Si f es derivable en
APLICACIONES DE LAS DERIVADAS º Bachillerato RECTA TANGENTE A UNA CURVA EN UN PUNTO. Si f es derivable en el punto, la ecuación de la recta tangente a f en el punto es: y = f + f ' Si f es derivable en
Autoevaluación. Bloque IV. Análisis. BACHILLERATO Matemáticas I. Página Observa la gráfica de la función y = f (x) y a partir de ella responde:
 Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 4 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
C u r s o : Matemática Material N 6 GUÍA TEÓRICO PRÁCTICA Nº UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación de la forma, o que
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. Estudia la continuidad derivabilidad de las funciones f() g() si f() si < Estudiamos la continuidad en. f() ( ) - - f() ( ) + + La función f() es continua
RESOLUCIÓN DE ACTIVIDADES Actividades iniciales. Estudia la continuidad derivabilidad de las funciones f() g() si f() si < Estudiamos la continuidad en. f() ( ) - - f() ( ) + + La función f() es continua
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 29-OCTUBRE-1996. (1) 2x 3 > 4.
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 9-OCTUBRE-199 1) 3 > 4. +1 ) Sea la función 3 si 1 a + b si 1 . Encontrar los valores de a, b, c para que la función
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN DE RECUPERACIÓN E1300, 9-OCTUBRE-199 1) 3 > 4. +1 ) Sea la función 3 si 1 a + b si 1 . Encontrar los valores de a, b, c para que la función
FUNCIONES RACIONALES. HIPÉRBOLAS
 www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
FUNCIONES CUADRÁTICAS. PARÁBOLAS
 FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
FUNCIONES CUADRÁTICAS. PARÁBOLAS 1. FUNCIONES CUADRÁTICAS Representemos, en función de la longitud de la base (x), el área (y) de todos los rectángulos de perímetro 1 metros. De ellos, cuáles son las medidas
Derivada de una función
 0 Derivada de una función Derivada de una función L I T E R A T U R A M A T E M Á T I C A S La ciudad Rosa y Roja Aquella princesa de largos y dorados cabellos estaba alarmada al observar que cada día
0 Derivada de una función Derivada de una función L I T E R A T U R A M A T E M Á T I C A S La ciudad Rosa y Roja Aquella princesa de largos y dorados cabellos estaba alarmada al observar que cada día
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
Matemáticas aplicadas a las CC.SS. II
 Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
Tema Nº 8 Aplicaciones de las Derivadas ( 17! Determina las dimensiones de una ventana rectangular que permita pasar la máima cantidad de luz, sabiendo que su marco debe medir 4 m. ---oooo--- La ventana
LA INTEGRAL DEFINIDA. APLICACIONES
 LA INTEGRAL DEFINIDA. APLICACIONES Página 6 REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
LA INTEGRAL DEFINIDA. APLICACIONES Página 6 REFLEXIONA Y RESUELVE Dos trenes Un Talgo y un tren de mercancías salen de la misma estación, por la misma vía y en idéntica dirección, uno tras otro, casi simultáneamente.
LA RECTA. Recuerda: Ejercicios de autoaprendizaje 1. Sea la gráfica siguiente:
 LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
LA RECTA Recuerda: Una recta es una función de la forma y = mx + n, siendo m y n números reales m es la pendiente de la recta y n es la ordenada en el origen La ordenada en el origen nos indica el punto
x = 1 Asíntota vertical
 EJERCICIO Sea la función f ( ). a) Indique el dominio de definición de f, sus puntos de corte con los ejes, sus máimos mínimos, eisten, sus intervalos de crecimiento decrecimiento. b) Obtenga las ecuaciones
EJERCICIO Sea la función f ( ). a) Indique el dominio de definición de f, sus puntos de corte con los ejes, sus máimos mínimos, eisten, sus intervalos de crecimiento decrecimiento. b) Obtenga las ecuaciones
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2014 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 04 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 04 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Examen de Análisis Matemático. a) (1 punto) Calcula las derivadas de las siguientes funciones: (1 + 3x) 1 2
 Curso º Bachillerato 16/05/017 Ejercicio 1 a) (1 punto) Calcula las derivadas de las siguientes funciones: f() = 1+3 ; g() = ln(1 5) + e7 b) (1 punto) Estudia la derivabilidad de la función dada por: a)
Curso º Bachillerato 16/05/017 Ejercicio 1 a) (1 punto) Calcula las derivadas de las siguientes funciones: f() = 1+3 ; g() = ln(1 5) + e7 b) (1 punto) Estudia la derivabilidad de la función dada por: a)
EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Colegio Portocarrero. Curso Departamento de matemáticas. Derivadas; aplicaciones de las derivadas
 Derivadas; aplicaciones de las derivadas Problema 1: La función f(t), 0 t 10, en la que el tiempo t está expresado en años, representa los beneficios de una empresa (en cientos de miles de euros) entre
Derivadas; aplicaciones de las derivadas Problema 1: La función f(t), 0 t 10, en la que el tiempo t está expresado en años, representa los beneficios de una empresa (en cientos de miles de euros) entre
ANÁLISIS. d) No, se podrían haber considerado infinitas funciones diferenciadas en una constante.
 Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
Página 194 EJERCICIOS Y PROBLEMAS PROPUESTOS. Tasa de variación media PARA PRACTICAR UNIDAD
 UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2009 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
, siendo ln(1+x) el logaritmo neperiano de 1+x. x
 Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
Idea de Derivada. Tasa de variación media e instantánea
 TEMA 6. Derivadas Nombre CURSO: BACH CCSS Idea de Derivada. Tasa de variación media e instantánea.- La variación de la altura de un niño con el paso de los años, se recoge en la guiente tabla: Edad (años)
TEMA 6. Derivadas Nombre CURSO: BACH CCSS Idea de Derivada. Tasa de variación media e instantánea.- La variación de la altura de un niño con el paso de los años, se recoge en la guiente tabla: Edad (años)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2008 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 008 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
Demuestra que el punto de tangencia, T, es el lugar de la recta r desde el que se ve el segmento AB con ángulo máximo.
 Resuelve Página 69 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura. A qué distancia se debe acercar para que el ángulo,
Resuelve Página 69 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura. A qué distancia se debe acercar para que el ángulo,
IES Fco Ayala de Granada Septiembre de 2013 (Modelo 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
IES Fco Ayala de Granada Septiembre de 01 (Modelo ) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Septiembre 01 ['5 puntos] Un alambre de 10 metros de longitud se divide en dos trozos.
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA 6.- FUNCIONES. LÍMITES Y CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II FICHA TEMA.- FUNCIONES. LÍMITES CONTINUIDAD PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------.-
Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA
 Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
Fuente: PreUniversitario Pedro de Valdivia Guía Práctica N 11 ECUACIÓN DE SEGUNDO GRADO Y FUNCIÓN CUADRÁTICA Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma a + b + c = 0,
DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES
 UNIDAD 6 DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES Página 5 Problema y f () 5 5 9 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(). f'() 0; f'(9) ; f'() Di otros tres puntos en
UNIDAD 6 DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES Página 5 Problema y f () 5 5 9 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(). f'() 0; f'(9) ; f'() Di otros tres puntos en
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
VECTORES EN EL ESPACIO
 VECTORES EN EL ESPACIO Página 133 REFLEXIONA Y RESUELVE Relaciones trigonométricas en el triángulo Halla el área de este paralelogramo en función del ángulo a: cm a cm Área = sen a = 40 sen a cm Halla
VECTORES EN EL ESPACIO Página 133 REFLEXIONA Y RESUELVE Relaciones trigonométricas en el triángulo Halla el área de este paralelogramo en función del ángulo a: cm a cm Área = sen a = 40 sen a cm Halla
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN
 2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
2º BACHILLERATO. EJERCICIOS DE REPASO 1ª EVALUACIÓN 1.) Resuelve las siguientes derivadas: a) b) c) d) e) f) g) h) i) j) k) l) m) n) o) p) q) r) f(x) = arcsen 2.) Resuelve la siguiente derivada, simplificando
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 009 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA 1. MONOTONÍA (CRECIMIENTO O DECRECIMIENTO) Si una función es derivable en un punto = a, podemos determinar su crecimiento o decrecimiento en ese punto a partir del signo de
APLICACIONES DE LA DERIVADA 1. MONOTONÍA (CRECIMIENTO O DECRECIMIENTO) Si una función es derivable en un punto = a, podemos determinar su crecimiento o decrecimiento en ese punto a partir del signo de
2. Calcula las velocidades medias anteriores tomando valores sobre la ecuación del movimiento de dicha partícula: s = 2
 Unidad. Derivadas Resuelve Página 0 Movimiento de una partícula Un investigador, para estudiar el movimiento de una partícula, la a iluminado con destellos de flas cada décima de segundo (0, s) durante
Unidad. Derivadas Resuelve Página 0 Movimiento de una partícula Un investigador, para estudiar el movimiento de una partícula, la a iluminado con destellos de flas cada décima de segundo (0, s) durante
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
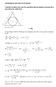 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS GEOMETRÍA
 PROBLEMAS RESUELTOS GEOMETRÍA ) Uno de los vértices de un paralelogramo ABCD es el punto A(, ) y dos de los lados están sobre las rectas r : 3x -y- =, s : 6x -7y- =. Calcula los demás vértices. Como el
PROBLEMAS RESUELTOS GEOMETRÍA ) Uno de los vértices de un paralelogramo ABCD es el punto A(, ) y dos de los lados están sobre las rectas r : 3x -y- =, s : 6x -7y- =. Calcula los demás vértices. Como el
9. Rectas e hipérbolas
 08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO
 EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
EJERCICIOS DE LOS EXÁMENES DE ANÁLISIS MATEMÁTICAS II CURSO 7-8 Ejercicio º.- Se considera la función f : R R dada por: f ( ) ( ) e a) (,5 puntos) Calcula las asíntotas de f. b) (,5 puntos) Calcula la
ANÁLISIS (Selectividad)
 ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
ANÁLISIS (Selectividad) 1 Sea f : R R la función definida por f() ln ( +1). (a) Determina los intervalos de crecimiento y decrecimiento y los etremos relativos de la función f (puntos donde se alcanzan
ECUACIÓN DE LA RECTA. Dibujando los ejes de coordenadas y representando el punto vemos que está situado sobre el eje de abscisas.
 ECUACIÓN DE LA RECTA. El punto (, 0) está situado: a) Sobre el eje de ordenadas. b) En el tercer cuadrante. c) Sobre el eje de abscisas. (Convocatoria junio 00. Examen tipo D) Dibujando los ejes de coordenadas
ECUACIÓN DE LA RECTA. El punto (, 0) está situado: a) Sobre el eje de ordenadas. b) En el tercer cuadrante. c) Sobre el eje de abscisas. (Convocatoria junio 00. Examen tipo D) Dibujando los ejes de coordenadas
EJERCICIOS RESUELTOS. x )
 BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
DERIVADAS EN LA EBAU DE MURCIA. 2x 2 2x 1. 2x + 2x + 1 (2x + 1) 2x + 1. g'(x) = 2xe + x 2xe g'(x) = 2xe (1 + x )
 DERIVADAS EN LA EBAU DE MURCIA a + b 1. (Septiembre 017) Dada la función f() =, donde a y b son números reales, halla el + 1 valor de a y b para que se cumpla que f(0) = 1 y f (0) = 1. b = 1 y a = 1..
DERIVADAS EN LA EBAU DE MURCIA a + b 1. (Septiembre 017) Dada la función f() =, donde a y b son números reales, halla el + 1 valor de a y b para que se cumpla que f(0) = 1 y f (0) = 1. b = 1 y a = 1..
