y con la semiamplitud δ =1. 2.
|
|
|
- María del Carmen Vega Núñez
- hace 7 años
- Vistas:
Transcripción
1 LÍMITE DE UNA FUNCIÓN UNIDAD II II. ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos puede escribirse como: { a δ < < a δ} un valor absoluto: a < δ. Gráicamente se representa así:, o bien como Semiamplitud del intervalo δ Semiamplitud del intervalo δ a - δ a a δ δ Amplitud del intervalo Ejemplo. Obtener el entorno del punto a y con la semiamplitud δ.. Solución. Entorno de a (.,. ) (.,. ) {. < <.} <. esto signiica que el entorno de a son todos los valores de desde. hasta. etremos. Veriicando algunos valores dentro del entorno: si. :... <. si. :.. <.. δ., pero sin incluir a los δ.. δ.
2 Ejemplo. Obtener el entorno del punto a y con la semiamplitud δ.. Solución. Entorno de a (.,.) (.,.) {. < <.} <. esto signiica que el entorno de a son todos los valores de desde. hasta., pero sin incluir a los etremos: si. :... <. si : <. -. δ. - δ. δ. -. Se deine como entorno reducido de un punto a en al entono que ecluye al propio punto a. Es decir, a δ, a δ donde a. es el intervalo abierto ( ) El entorno reducido de a también puede escribirse como: { a δ < < a δ, a} δ como: < a <. Gráicamente esto es:, o bien Semiamplitud del intervalo δ Semiamplitud del intervalo δ a - δ a a δ δ Amplitud del intervalo Ejemplo. Obtener el entorno reducido del punto a y con la semiamplitud. Solución. Entorno reducido de (.,.) (.,.) {. < <., } < <. a si δ
3 esto signiica que el entorno reducido de a son todos los valores de desde. hasta., quitando el y sin incluir a los etremos: si. :.. <. si. :... <.. δ. δ.. δ. Ejemplo. Obtener el entorno reducido del punto a. y con la semiamplitud δ.. Solución. Entorno reducido de a (..,..) (.,.) {. < <.,.} <. <. esto signiica que el entorno reducido de a son todos los valores de desde. hasta., quitando el. y sin incluir a los etremos: si. :... <. si. :....<. -. δ. δ δ. II. DEFINICIÓN DE LÍMITE Si se desea investigar el comportamiento de la unción deinida por ( ) para valores cercanos a tanto menores como mayores a este valor. En la tabla siguiente se muestran los valores de ( ) para valores aproimados pero no iguales a : ( ) ( ) A partir de la tabla, se demuestra que cuando está cada vez más cerca de por cualquiera de los dos se aproima a. Este hecho se epresa al decir que el límite de la unción ( ) lados, ( ) cuando tiende a es igual a. La notación para esta epresión es ( ).
4 Como se puede apreciar del ejemplo anterior, el interés se centra en conocer el valor de la unción ( ) cuando se aproima a un valor a, pero sin ubicarse en dicho valor. Esto es, si se acerca más y más se acerca más y más a un valor L. Esto signiica que a a (pero no es igual a a ), la unción ( ) ( ) tiende a L si tiende a a. La rase " tiende a a " signiica que independientemente de lo próimo que esté del valor a, eiste siempre otro valor de (distinto de a ) en el dominio de que está aún más próimo a a. Deinición de límite: Una unción tiende hacia el límite L en a si para todo ε > eiste algún δ > tal que ( ) L < ε siempre que < a < δ. Se puede deducir de la deinición, que para que eista el límite L de una unción ( ) se orme un entorno de L en ( ) siempre y cuando se pueda generar un entorno reducido de a en. Dado que el entorno de L es: { L ε < y < L ε} { a δ < < a δ a} es necesario que y, el entorno reducido de a es:,, donde δ y ε pueden se tan pequeñas como se desee, por lo que se a. Esto puede a, L. pueden generar una ininidad de entornos cada vez más pequeños, siempre que interpretarse como la ormación de rectángulos cada vez más pequeños que incluyan al punto ( ) Gráicamente esto es: y y () Lε Lε Lε Lε L L-ε L-ε L-ε L-ε a-δ a-δ a-δ a-δ a aδ aδ aδ aδ Nótese como cada entorno L ε i < y < L ε i se orma respondiendo a los entornos a δ i < < a δ i, y a medida que δ tiende a cero (sin llegar a serlo), también ε tiende a cero.
5 En caso de eistir, el límite se representa en orma simbólica como: a ( ) L y se lee: el límite de ( ) cuando tienda hacia a es L. Una unción no puede tender a dos límites distintos a la vez. Esto es, si el límite de una unción eiste, es único: El límite eiste si el límite por la izquierda, y el límite por la derecha, son iguales. a a a ( ) ( ) ( ) Estos dos últimos límites se conocen como límites laterales, lo que signiica que se pueden aproimar los valores de ( ) cumple lo siguiente: a L tanto como se quiera, ya sea por la derecha o por la izquierda. De lo anterior, se a ( ) L ( ) L y ( ) L a Para ines prácticos, para determinar si una unción ( ) tiene límite cuando a basta con aplicar la deinición y establecer una epresión que relacione a δ y ε. En caso de no encontrar una relación, la unción no tendrá límite en ese punto. Ejemplos. A través de la deinición, calcular ormalmente los siguientes límites: ) ( ) Solución: ( ) ( ) aplicando la deinición: ( ) L < ε a < δ < ε < δ < ε < δ ( ) < ε < δ ε < < δ ε δ a
6 el límite eiste y es. ) ( ) Solución: ( ) ( ) aplicando la deinición: ( ) L < ε a < δ ( ) < ε < δ < ε < δ ( )( ) < ε < δ ε < < δ ε δ el límite eiste y es. ) ( ) Solución: ( ) aplicando la deinición: ( ) L < ε a < δ < ε < δ < ε < δ ( )( ) < ε < δ ε < < δ ε δ el límite eiste y es. ) Solución: aplicando la deinición: L < ε a < ( ) δ
7 < ε < < ε < δ ( ) ( ) δ < ε < δ aplicando el valor absoluto a los términos del producto: ( ) < ε < δ ε < < δ ε δ el límite eiste y es. ) Solución: ( ) aplicando la deinición: ( ) L < ε a < δ < ε < δ multiplicando por el conjugado del binomio: ( ) < ε < δ ( ) < ε < δ < ε < δ ( ) ε < < δ ( ) ε δ el límite eiste y es. ) Solución:
8 si se desea aplicar la deinición: L < ε a < ( No eiste) ( ) δ no se puede ya que L no es un valor deinido, por lo tanto, el límite no eiste. II. PROPIEDADES DE LOS LÍMITES Sean ( ), g( ) a. [ c] c a dos límites que eisten y c una constante. Entonces: a El límite de una constante es la misma constante.. [ ] a a El límite de la unción identidad es igual al valor de a.. [ c ( ) ] c ( ) a a El límite de una constante multiplicada por una unción es la constante multiplicada por el límite de la unción.. [ ( ) ± g( ) ] ( ) ± g( ) a a a El límite de una suma algebraica es la suma algebraica de los límites.. [ ( ) g( ) ] ( ) g( ) a a a El límite de un producto es el producto de los límites.. a g ( ) ( ) a g a ( ) ( ) g a ( ) El límite de un cociente es el cociente de los límites. n. [ ( ) ] ( ) a n [ ] n N a El límite de la potencia de una unción es el límite de la unción elevada a la potencia.. n ( ) n ( ) n N (si n es par se asume que ( ) > a a El límite de una raíz es la raíz del límite. Ejemplos. Aplicando las propiedades, calcular los siguientes límites: ) ) a )
9 ) ( ) ( ) ) ( ) ( ) ( ) ( ) ) ( ) ( ) ( ) ( ) ( ) ( ) ) ( ) ) ( ) ( ) ) ( ) ( ) ( ) ) ( ) ) este límite presenta una indeterminación, sin embargo, si se actoriza el denominador: ( )( ) ) para einar la indeterminación se actoriza el numerador: ( )( ) ( ) ) ( ) este límite presenta una indeterminación, sin embargo, si se actoriza tanto el numerador como el denominador: ( ) ( )( ) ) ( ) para einar la indeterminación se actoriza tanto el numerador como el denominador: ( )( ) ( )( ) ) ( )( ) ( ) ( )( ) ( ) ( ) ( )( ) a in de einar la indeterminación se actoriza el numerador y el denominador: ( )( ) ( )( )( ) ( )( ) ( ) ) ( )
10 para einar la indeterminación se actoriza tanto el numerador como el denominador: ) ( ) ( )( ) este límite presenta una indeterminación, sin embargo, si se actoriza tanto el numerador como el denominador: ) ( )( ) ( )( ) ( ) ( ) para einar la indeterminación se actoriza tanto el numerador como el denominador: ) ( )( ) ( )( ) ( ) este límite presenta una indeterminación, sin embargo, si se actoriza el numerador: ( )( ) ) ( )( ) ( ) ( no eiste) ) multiplicando por el binomio conjugado del numerador para deshacer la indeterminación: ( )( ) actorizando el denominador: ( ) ) ( ) para einar la indeterminación se actoriza el denominador: ( ) como no se puede simpliicar, el límite no eiste. ) a in de einar la indeterminación se actoriza el numerador y el denominador: ( )( )( ) ( )( ) ( )( )
11 ( )( ) ) ( )( ) para einar la indeterminación, se eleva al cuadrado: ( ) ( ) ( ) actorizando el numerador: ( )( ) ( ) ( ) ) este límite presenta una indeterminación, sin embargo, elevando al cuadrado: ( ) ( ) ( ) actorizando el denominador: ( )( ) ( no eiste) ) para einar la indeterminación se multiplica por el binomio conjugado del numerador: ( )( ) ( )( ) II. LÍMITES INFINITOS Los tipos de límites en los que una unción ( ) se hace ininita (ya sea positiva o negativa) cuando tiende a a por la izquierda o por la derecha se conocen como límites ininitos. Qué ocurre cuando se aproima o tiende a cero en la unción ( )? Tabulando la unción se aprecia que cuando tiende a cero por la derecha, los valores de la unción que son positivos, son cada vez más grandes. Es decir, los valores de la unción aumentan. Mientras que, cuando tiende a cero por la izquierda, los valores de la unción son negativos, son cada vez más pequeños. Es decir, los valores de la unción disminuyen.
12 ( ) ( ) Gráicamente en ambos casos, ( ) crece o decrece sin tope, sin ronteras. Esto es, y () () - - El símbolo de ininito ( ) no signiica que el límite eista, ya que no representa un número real. Simboliza el comportamiento no acotado (sin ronteras) de ( ) cuando tiende a a. De manera que, al decir que "el límite de ( ) cuando tiende a a es ininito" se interpreta que el límite no eiste. En general, considérese la unción: las raíces del polinomio q ( ) p ( ) q, provocan que la unción no esté deinida, es decir, sus límites son el ininito. Geométricamente, cada raíz representa a una asíntota vertical. ( ) ( )
13 Ejemplos., los límites laterales no son iguales:, el valor que anula al denominador es, así que el límite en el ininito se presenta en la asíntota ) En la unción ( ) ) En la unción ( ),, los valores que anulan al denominador son y asíntotas y., los límites laterales no son iguales: ) En la unción ( ),, los valores que anulan al denominador son, y se presentan en las asíntotas, y., los límites laterales no son iguales:,., así que los límites en el ininito se presentan en las respectivamente, así que los límites en el ininito II. LÍMITES DE FUNCIONES TRIGONOMÉTRICAS Los límites trigonométricos elementales son aquellos que se obtienen directamente, ya que basta sólo con evaluarlos y recordar los valores notables de dichas unciones. Ejemplos. Evaluar los siguientes límites trigonométricos elementales: ) sen sen. π ) cos cos( ) ( ) π ) tan tan ( π ) π π ) cot cot ( ) π
14 ( ) ( ) ( ) ) csc csc( π) ) sec sec π ) cos cos cos ( ) ( ) ( ) Eisten otros límites cuya evaluación no es tan simple. En este sentido, el límite de la unción sen cuando tiende a cero es muy importante ya que la resolución de muchos límites trigonométricos se basan en su aplicación. Por ello, se evalúa en primera instancia: sen sen ( ) aparentemente, el límite no eiste. Sin embargo, si se tabula la unción ( en radianes), se tiene: sen ±. ±.. ±.. ±.. ±.. ±.. ±.. ±.. Como puede apreciarse el límite tiende a la unidad. Por lo tanto: sen Ejemplos. Considerando el resultado anterior y aplicando identidades trigonométricas, obtener los siguientes límites: ) ( ) ( ) ( ) sen sen sen multiplicando y dividiendo por : sen ( )( ) sen ( ) sen ( ) ( ) ( ) sen ) epresando la potencia como producto: La demostración ormal de este límite puede consultarse en la página del libro Cálculo Dierencial e Integral, de J. Stewart incluido en la bibliograía.
15 sen sen sen sen ( ) ) sen sen ( ( ) ) sen ( ) sen sen u En general, u senu ( ) ( ( ) ) ( ) ( ) sen sen sen sen ) sen sen sen multiplicando y dividiendo por sen sen sen sen sen sen cos cos ( ) ) cos aplicando la identidad trigonométrica tan : sen sen tan cos sen sen ( ( ) ) ( ) ) sen ( ) sen ( ( ) ) ( sen )( ) ( )( ) y : ( ) ( ) ( ) ( ) tan ( ) tan tan ( ) ( )( ) ( ) epresando las potencias como productos y multiplicando y dividiendo por y ( )( ) sen ( ) sen sen ( ) sen ( )( ) sen sen sen ( ) sen sen ( )( ) sen multiplicando y dividiendo por : sen sen sen cos cos ) ( )( )( ) ( )( )( )( ) ( )( ) sensen ( ) ( ) aplicando la identidad trigonométrica sen cos : cos sen sen sen ( ) tan tan ( ) ) ( ) sen aplicando la identidad trigonométrica tan : cos ( )( ) ( )( ) :
16 sen tan cos ) csc sen cos cos cos ( ) ( ) aplicando la identidad trigonométrica csc y multiplicando y dividiendo por : sen csc ( ) sen sen tan tan ( π ) ) π π π π sen aplicando las identidades trigonométricas tan tan ( π ) y tan : cos tan tan ( π ) sen( π ) π π π π π π cos π π cos π cos π π cos ( ) ( ) ( ) ( ) ( ) ( ) II. LÍMITES QUE TIENDEN A INFINITO Dada una unción deinida en un intervalo ( a,). Entonces el ( ) L signiica que los valores de ( ) se pueden aproimar a L tanto como se quiera, si se elige una suicientemente grande. Esta epresión se lee como el límite de ( ) cuando tiende a ininito es L. Similarmente, la epresión ( ) L signiica que los valores de ( ) se pueden aproimar a L tanto como se quiera, si se elige una negativa suicientemente grande y se lee como el límite de ( ) cuando tiende a ininito es L. Para saber si eiste el límite de una unción cuando tiende a ininito es necesario analizar su comportamiento particular. Por su importancia, los límites de este tipo que revisten más interés de estudio son los de las unciones algebraicas y de las racionales. En el primer caso, todos los límites de unciones algebraicas que tienden a ininito (o a menos ininito) no eisten. Ejemplos. Calcular los siguientes límites: ) ( ) ( ) ( ) ) ( ) ( ) ( ) ) ( ) ( ) ( ) ( )
17 En el segundo caso, para calcular límites de unciones racionales, normalmente el procedimiento consiste en dividir cada término de la unción por el término en que posee el mayor eponente, se reduce aplicando leyes de eponentes y se toma el límite, considerando que:. Ejemplos. Calcular los siguientes límites: ) ( ) ( ) ( ) Esta es una orma indeterminada, sin embargo, si se divide todo entre se tiene: ) ( ) ( ) ( ) ( ) Es una indeterminación, pero si se divide todo entre se tiene: ) ( ) ( ) ( ) ( ) ( ) Esta es una orma indeterminada, sin embargo, si se divide todo entre se tiene: ( ) no eiste En general, para calcular límites que tienden a ininito (o a menos ininito), de las unciones racionales de la orma: ( ) b b b b a a a a p m m m m m m n n n n n n eisten tres casos posibles: ) Si el grado del numerador es menor que el grado del denominador y el límite de la unción es cero. ( ) p, si m n <
18 ) Si los grados de los polinomios en el numerador y el denominador son iguales, el límite es el cociente del coeiciente del eponente mayor del numerador entre el coeiciente del eponente mayor del denominador. a p b n ( ), n si n m ) Si el grado del numerador es mayor que el del denominador, el límite no eiste. Ejemplos. Calcular los siguientes límites: ) Como n < m, p( ) ) Como ( ) ( no eiste) p, si n > m m p no eiste n >, ( ) ( ) ) Como m ) Como m p no eiste n, p( ) n >, ( ) ( ) ) Como m ) Como n < m, p( ) n, p( ) II. LÍMITES DE FUNCIONES EXPONENCIALES Y LOGARÍTMICAS Una unción eponencial es una unción de la orma: ( ) a donde a es un número real positivo y a. El comportamiento general de esta unción se puede apreciar en las siguientes gráicas:
19 () a y y a > < a < Sus características son: Dominio ( -, ) Rango (, ) La asíntota horizontal es el eje Siempre corta al eje y en el punto P (,) Siempre es creciente si a > y siempre es decreciente si < a < La unción crece más rápido si la base es más grande y decrece más rápido si la base es más pequeña. De acuerdo a lo anterior, se puede inerir que:. a, a >. a, a > a a., < a <., < a <. a Ejemplo. Evaluar numéricamente el límite: ( ) Solución. Tabulando: ( )
20 Como se puede advertir, el límite tiende a un número cercano a.. Dicho límite es el número irracional conocido como e y tiene el valor aproimado de e.. Se llama unción logarítmica a la unción real de variable real : y loga El comportamiento general de esta unción se puede apreciar en las siguientes gráicas: ( ) y () log a y a > < a < La unción logarítmica es una aplicación biyectiva deinida de R en R y sus características son: Dominio (, ) Rango ( -, ) La asíntota vertical es el eje y Siempre corta al eje en el punto P (, ) Siempre es creciente si a > y siempre es decreciente si < a < La unción crece más rápido si la base es más pequeña (cuando a > ) y decrece más rápido si la base es más grande (cuando < a < ) La unción logarítmica de base a es la recíproca de la unción eponencial de base a Por lo anterior, se puede inerir que:. log, a > a. log, a > a. log, < a < a. log, < a < a Ejemplo. Evaluar numéricamente el límite: log Solución. Tabulando:
21 log.....,.,.,. es más grande que su logaritmo, así que a medida que crece, la racción va disminuyendo. Por lo log tanto: II. CONTINUIDAD Una unción es continua en a cuando no hay interrupción en la gráica de en a. Su gráica no aparece con huecos o saltos en. Esto es, una unción es continua si su gráica se puede trazar sin levantar el lápiz del papel. Formalmente, una unción es continua en un punto a si está deinida en ese punto, y además: a ( ) ( a) En caso de no cumplir con la condición se dice que la unción es discontinua. Una unción es continua en un intervalo cuando es continua en todos los puntos de ese intervalo. a ( ) ( a) y y Función continua Función discontinua
22 Ejemplos. ) La unción ( ) ( ) ( ) ( ) es continua en el punto porque ) La unción ( ) sen ( ) ( π ) sen ( π ) ( ) π ) La unción ( ) no eiste. ) La unción ( ) límite eista:. es continua en el punto π es discontinua porque en el punto es discontinua porque en el punto ( )( ) ( ).. porque no está deinida y porque el límite no está deinida, aunque el Nótese como en este último ejemplo la unción original puede reescribirse como: ( ), la cual es continua. En estos casos la discontinuidad recibe el nombre de evitable. Las gráicas de ambas unciones es la misma a ecepción de que en la primera tiene una especie de oriicio en el punto y en y la segunda no. Evitar la discontinuidad consiste en rellenar dicho oriicio tal y como se ve en la siguiente igura: y y Función discontinua en Función continua en Las discontinuidades se clasiican en: evitables y no evitables. Una discontinuidad en se puede redeinir en ese punto. Los siguientes tipos de unciones son continuas en sus dominios: a es evitable si
23 Polinomiales Racionales De raíz Trigonométricas Trigonométricas inversas Eponenciales Logarítmicas Sean y g dos unciones continuas en también son continuas en a : a, entonces las siguientes operaciones de unciones g g g si g ( a) g c, siendo c una constante g g o ( ) ( ( )), si es continua en ( a) g. Ejemplo. Determinar si las siguientes unciones son continuas en el punto dado: ) ( ) en el punto Solución: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) como ( ) ( ) unción polinomial)., la unción sí es continua en (lo cual era de esperarse ya que es una ) ( ) en el punto Solución: como la unción no está deinida en ese punto la unción no es ( ) ( ) continua (no tiene caso calcular el límite porque no hay orma de einar la ineistencia). en el punto ) ( ) Solución: El valor anula al denominador, sin embargo, la unción puede rescribirse como: ( )( ) ( ) ( ) ( )( ) ( ) por lo tanto, la unción es discontinua en el punto pero es evitable.
24 en el punto Solución: ( ) ( ) como la unción no está deinida en ese punto la unción no es continua (no ( ) tiene caso calcular el límite porque no hay orma de einar la discontinuidad). ) ( ) log en el punto ) ( ) Solución: ( ) log ( ) log ( ) log log ( ) log ( ) como ( ) ( ) (lo cual era de esperarse ya que es una unción logarítmica). ) ( ) en el punto Solución: El valor anula al denominador, sin embargo, la unción puede rescribirse como: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) por lo tanto, la unción es discontinua en el punto pero es evitable. Ejemplos. Analizar la continuidad de las siguientes unciones: ) ( ) Solución. Hay continuidad en todo el intervalo ( ) denominador). Además, no es evitable. ) ( ) Solución. ( ) ( ) Hay continuidad en todo el intervalo ( ) anula el denominador). Además, no son evitables., ecepto en el punto, la unción sí es continua en (ya que ahí se anula el, ecepto en los puntos y (ya que ahí se
25 ) ( ) Solución. ( ) ( )( ) ( )( ) Hay continuidad en todo el intervalo ( ) anula el denominador). Sin embargo, en, ecepto en los puntos y es evitable. (ya que ahí se ) ( ) Solución. > ( ) ( ) ( ) ( ) ( ) ( ) ( ) como ( ) ( ) entonces el ( ) Por lo tanto, hay continuidad en el intervalo [,).
MATEMÁTICAS BÁSICAS LÍMITES Y CONTINUIDAD ENTORNOS. a, donde δ es la. = x
 MATEMÁTICAS BÁSICAS LÍMITES Y CONTINUIDAD ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos
MATEMÁTICAS BÁSICAS LÍMITES Y CONTINUIDAD ENTORNOS Se denomina entorno de un punto a en, al intervalo abierto ( δ a δ ) semiamplitud del intervalo. a, donde δ es la El entorno de a, en notación de conjuntos
4.2. Continuidad de una función en un punto. (A) Una función f es continua en un punto x=a, cuando se cumplen las siguientes condiciones:
 4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
4. CONTINUIDAD DE UNA FUNCIÓN. 4.. Noción intuitiva de continuidad de una unción en un punto. La mayor parte de las unciones que manejamos a nivel elemental, presentan en sus gráicas una propiedad característica
Límites y continuidad
 Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
Límites y continuidad.. Límites El ite por la izquierda de una función f en un punto 0, denotado como 0 f() es el valor al que se aproima f() cuando se acerca hacia 0 por la izquierda. De igual forma,
Asíntotas en una función.
 Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
Asíntotas en una unción. Las asíntotas son rectas a las cuales la unción se va aproimando indeinidamente, cuando por lo menos una de las variables ( o y) tienden al ininito. Deinición: Si un punto, y )
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN
 FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
FUNCIONES.FUNCIONES ELEMENTALES. LÍMITES DE UNA FUNCIÓN 1 FUNCIONES FUNCIÓN REAL DE VARIABLE REAL Una función real de variable real es una relación que asocia a cada número real, (variable independiente),
Límites y continuidad
 Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
Estudio de la continuidad de la función en el punto = : Comprobemos, como primera medida, que la función está definida en =. Para =, tenemos que determinar f() = + = 6 + = 8, luego eiste. Calculamos, entonces
TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS
 Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
Tema 8 Límites de funciones, continuidad y asíntotas Matemáticas II º Bach 1 TEMA 8 LÍMITES DE FUNCIONES, CONTINUIDAD Y ASÍNTOTAS 8.1 LÍMITE DE UNA FUNCIÓN 8.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de funciones. Extremos
 (Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de unciones. Etremos INTRODUCCIÓN En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen
(Apuntes en revisión para orientar el aprendizaje) Capítulo IV Variación de unciones. Etremos INTRODUCCIÓN En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen
TEMA 2: CONTINUIDAD DE FUNCIONES
 TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
TEMA : CONTINUIDAD DE FUNCIONES 1. Continuidad de una función en un punto Entre las primeras propiedades de las funciones aparece el concepto de continuidad. Durante mucho tiempo fue asumida como una idea
Capítulo II Límites y Continuidad
 (Apuntes en revisión para orientar el aprendizaje) INTRODUCCIÓN Capítulo II Límites y Continuidad El concepto de límite, después del de función, es el fundamento matemático más importante que ha cimentado
(Apuntes en revisión para orientar el aprendizaje) INTRODUCCIÓN Capítulo II Límites y Continuidad El concepto de límite, después del de función, es el fundamento matemático más importante que ha cimentado
Teoría Tema 9 Representación gráfica de funciones
 página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
página 1/24 Teoría Tema 9 Representación gráfica de funciones Índice de contenido Gráficas de funciones...2 Gráfica de una parábola...3 Gráfica de un polinomio de grado 3...6 Gráfica de un cociente de
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
{( ) ( ) ( ) ( )} 4. FUNCIONES. B y f es una función de A en B definida por y = x 2 1, = x + 3, encuentra 5 pares que pertenezcan a la
 4 FUNCIONES 4 Conceptos básicos Sean A y B dos conjuntos dados, una unción de A en B es una regla de correspondencia que asigna a cada elemento de A uno y solamente uno de B En una unción: A es el dominio
4 FUNCIONES 4 Conceptos básicos Sean A y B dos conjuntos dados, una unción de A en B es una regla de correspondencia que asigna a cada elemento de A uno y solamente uno de B En una unción: A es el dominio
Curso Propedéutico de Cálculo Sesión 2: Límites y Continuidad
 y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
y Laterales Curso Propedéutico de Cálculo Sesión 2: y Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico y Esquema Laterales 1 Laterales 2 y Esquema Laterales
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas Función Derivada Función compuesta Derivada y f x y f x y f g x
 Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
Tabla de derivadas Función Derivada Función compuesta Derivada k ' 0 ' ' n ' ' ' e ' n n n n ' n ' e a ' ln ln log a a a ' ' e a ln ln a Reglas de derivación log a ' ' ' ' ' ' ' ' ' ln ' ' ' ' e a a '
Autor: Antonio Rivero Cuesta, Tutor C.A. Palma de Mallorca
 Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
Ejercicio: 4. 4. El intervalo abierto (,) es el conjunto de los números reales que verifican: a). b) < . - Intervalo abierto (a,b) al conjunto de los números reales, a < < b. 4. El intervalo
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
2.1. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable x)
 Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
= y. Así pues, el domino lo forman los números x para los cuales existe el valor de f (x)
 UAH Actualización de Conocimientos de Matemáticas para Tema 6 Funciones Concepto de función Dados dos conjuntos A y B, una función de A en B es una relación (una ley) que asigna a cada elemento de A uno
UAH Actualización de Conocimientos de Matemáticas para Tema 6 Funciones Concepto de función Dados dos conjuntos A y B, una función de A en B es una relación (una ley) que asigna a cada elemento de A uno
TEMA 2. FUNCIONES REALES DE VARIABLE REAL 2.2. LÍMITES Y CONTINUIDAD
 TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
TEMA. FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD . FUNCIONES REALES DE VARIABLE REAL.. LÍMITES Y CONTINUIDAD... LÍMITE DE UNA FUNCIÓN EN UN PUNTO... LÍMITES INFINITOS... LÍMITES EN EL INFINITO..4.
Solución. - Verticales: En los puntos excluidos del dominio donde el límite quede de la forma k. 3( ) = Asíntota vertical. = + x 2.
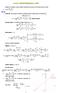 Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
Estudiar sus asíntotas y ramas ininitas valorando la posición de la unción respecto de ellas.. ( ) - Verticales: En los puntos ecluidos del dominio donde el límite quede de la orma D[ ( ) ] R { } 6 : Se
Procedimiento para determinar las asíntotas verticales de una función
 DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
DETERMINACIÓN DE ASÍNTOTAS EN UNA FUNCIÓN Las asíntotas son rectas a las cuales la función se va aproimando indefinidamente, cuando por lo menos una de las variables ( o y) tienden al infinito. Una definición
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS
 REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
REPRESENTACIÓN DE FUNCIONES 11.1 ELEMENTOS FUNDAMENTALES PARA LA CONSTRUCCIÓN DE CURVAS DOMINIO - Polinomio : D = R - Cocientes : D = R {puntos que anulan el denominador} - Raíces de índice par : D = {Lo
Ejemplo. Función parte entera de " x " que se denota como. Se denomina así la función en la que a cada
 (Apuntes en revisión para orientar el aprendizaje) FUNCIONES DEFINIDAS EN VARIOS INTERVALOS En problemas de ingeniería es común trabajar con enómenos que se modelan con unciones que consideran más de una
(Apuntes en revisión para orientar el aprendizaje) FUNCIONES DEFINIDAS EN VARIOS INTERVALOS En problemas de ingeniería es común trabajar con enómenos que se modelan con unciones que consideran más de una
1.5 Límites infinitos
 SECCIÓN.5 Límites infinitos 8.5 Límites infinitos Determinar ites infinitos por la izquierda por la derecha. Encontrar dibujar las asíntotas verticales de la gráfica de una función., cuando Límites infinitos
SECCIÓN.5 Límites infinitos 8.5 Límites infinitos Determinar ites infinitos por la izquierda por la derecha. Encontrar dibujar las asíntotas verticales de la gráfica de una función., cuando Límites infinitos
Profesor: Rafa González Jiménez. Instituto Santa Eulalia ÍNDICE
 TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
TEMA 5: DERIVADAS. APLICACIONES. ÍNDICE 5..- Derivada de una función en un punto. 5...- Tasa de variación media. Interpretación geométrica. 5..2.- Tasa de variación instantánea. Derivada de una función
FUNCIONES. Función. π k π +, k } (los puntos que quitamos anulan el coseno). 2. tg x: {x / x =
 Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
Función FUNCIONES Es una relación entre dos magnitudes variables, de tal manera que a cada valor de la primera, llamada independiente, le corresponde un único valor de la segunda, llamada dependiente.
TEMA 1: Funciones elementales
 MATEMATICAS TEMA 1 CURSO 014/15 TEMA 1: Funciones elementales 8.1 CONCEPTO DE FUNCIÓN: Una función es una ley que asigna a cada elemento de un conjunto un único elemento de otro. Con esto una función hace
MATEMATICAS TEMA 1 CURSO 014/15 TEMA 1: Funciones elementales 8.1 CONCEPTO DE FUNCIÓN: Una función es una ley que asigna a cada elemento de un conjunto un único elemento de otro. Con esto una función hace
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Continuidad, límites y asíntotas. Funciones
 9 Continuidad, ites y asíntotas Funciones Introducción El estudio de la continuidad de una función se inicia desde el análisis de la gráfica de la función. Este análisis, intuitivo y fácil, pero insuficiente
9 Continuidad, ites y asíntotas Funciones Introducción El estudio de la continuidad de una función se inicia desde el análisis de la gráfica de la función. Este análisis, intuitivo y fácil, pero insuficiente
MATE 3031. Dr. Pedro Vásquez UPRM. P. Vásquez (UPRM) Conferencia 1 / 77
 MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
MATE 3031 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 77 P. Vásquez (UPRM) Conferencia 2 / 77 Qué es una función? MATE 3171 En esta parte se recordará la idea de función y su definición formal.
En las figuras anteriores vemos algunos casos (no todos) que pueden presentarse al pasar por un punto x 0. (en este caso, para x 0 =2)
 UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
FUNCIONES RACIONALES. HIPÉRBOLAS
 www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
www.matesronda.net José A. Jiménez Nieto FUNCIONES RACIONALES. HIPÉRBOLAS 1. FUNCIÓN DE PROPORCIONALIDAD INVERSA El área de un rectángulo es 18 cm 2. La siguiente tabla nos muestra algunas medidas que
REGLAS PRÁCTICAS PARA EL CÁLCULO DE LÍMITES DE FUNCIONES
 REGLAS PRÁCTICAS PARA EL CÁLCULO DE LÍMITES DE FUNCIONES Cuadro resumen de las INDETERMINACIONES. Tipo I. k f () a Método: calcular los límites laterales. Ejemplo: 6 0 0 Tipo II. f () a Caso. f() es un
REGLAS PRÁCTICAS PARA EL CÁLCULO DE LÍMITES DE FUNCIONES Cuadro resumen de las INDETERMINACIONES. Tipo I. k f () a Método: calcular los límites laterales. Ejemplo: 6 0 0 Tipo II. f () a Caso. f() es un
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
Matemáticas Febrero 2013 Modelo A
 Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
Matemáticas Febrero 0 Modelo A. Calcular el rango de 0 0 0. 0 a) b) c). Cuál es el cociente de dividir P(x) = x x + 9 entre Q(x) = x +? a) x x + x 6. b) x + x + x + 6. c) x x + 5x 0.. Diga cuál de las
APLICACIONES DE LA DERIVADA I. Ejercicios a resolver en la práctica. = x + 2. Determina y clasifica los puntos o valores
 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 010 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-1111) Fecha de publicación: 0-0-010 Contenido Tercer Parcial APLICACIONES DE LA DERIVADA I Contenidos
TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS
 TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 9.1. LÍMITE DE UNA FUNCIÓN
TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 1 TEMA 9 LÍMITES DE FUNCIONES, CONTINUIDAD Y RAMAS INFINITAS TEMA 9- LÍMITES Y CONTINUIDAD MATEMÁTICAS I 1º BACHILLERATO 9.1. LÍMITE DE UNA FUNCIÓN
Matemática II Clase Nº 14-15
 LA DERIVADA La derivación es una de las operaciones que el Análisis Matemático efectúa con las funciones, permite resolver numerosos problemas de Geometría, Economía, Física otras disciplinas. En matemáticas,
LA DERIVADA La derivación es una de las operaciones que el Análisis Matemático efectúa con las funciones, permite resolver numerosos problemas de Geometría, Economía, Física otras disciplinas. En matemáticas,
TIPOS DE FUNCIONES. Ing. Caribay Godoy Rangel
 TIPOS DE FUNCIONES Repasar los conceptos de dominio, rango, gráfica, elementos esenciales y transformaciones de las funciones: lineal, cuadrática, racional, trigonométrica, exponencial y logarítmica. FUNCIONES
TIPOS DE FUNCIONES Repasar los conceptos de dominio, rango, gráfica, elementos esenciales y transformaciones de las funciones: lineal, cuadrática, racional, trigonométrica, exponencial y logarítmica. FUNCIONES
Página 322. 3. Representa: a) y = b) y = c) y = cos 2x + cos x. a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales:
 Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Página. Representa: e e a) y = b) y = c) y = cos + cos e a) y = Dominio: D = Á {0} No es simétrica. Asíntotas verticales: f () = +@ 8 0 f () = +@ 8 0 + Asíntota vertical: = 0 f () = 0. Además, f () > 0
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Gráficamente: una función es continua en un punto si en dicho punto su gráfica no se rompe. Función continua en x = 0 Función no continua en x = 0
 Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
Funciones continuas Funciones continuas Continuidad de una función Si x 0 es un número, la función f(x) es continua en este punto si el límite de la función en ese punto coincide con el valor de la función
1 Técnicas elementales para el cálculo de límites
 Técnicas elementales para el cálculo de límites. Límites de una función en un punto Todas las funciones elementales son continuas en todos los puntos en los que están definidas. Por lo tanto; para calcular
Técnicas elementales para el cálculo de límites. Límites de una función en un punto Todas las funciones elementales son continuas en todos los puntos en los que están definidas. Por lo tanto; para calcular
Tabla de Derivadas. Función Derivada Función Derivada. f (x) n+1. f (x) y = f (x) y = ln x. y = cotg f (x) y = ( 1 cotg 2 f (x)) f (x) = f (x)
 Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Matemáticas aplicadas a las CCSS - Derivadas Tabla de Derivadas Función Derivada Función Derivada y k y 0 y y y y y f ) y f ) f ) y n y n n y f ) n y n f ) n f ) y y n y y f ) y n n+ y f ) n y f ) f )
Tema 10: Funciones racionales y potenciales. Asíntotas.
 1 Tema 10: Funciones racionales y potenciales. Asíntotas. 1. Funciones racionales. Una función racional es de la forma =p()/q(), donde p() y q() son polinomios, con q()0. El dominio de una función racional
1 Tema 10: Funciones racionales y potenciales. Asíntotas. 1. Funciones racionales. Una función racional es de la forma =p()/q(), donde p() y q() son polinomios, con q()0. El dominio de una función racional
LIMITE. Si f(x)= x 2 -x 6 = (x 3) (x + 2) = x + 3 x + 2 x + 2
 LIMITE Qué se entiende por límite? De ordinario hablamos del precio límite de la velocidad límite del límite de nuestra propia resistencia los límites de la tecnología moderna o de estirar un muelle hasta
LIMITE Qué se entiende por límite? De ordinario hablamos del precio límite de la velocidad límite del límite de nuestra propia resistencia los límites de la tecnología moderna o de estirar un muelle hasta
3.3 Funciones crecientes y decrecientes y el criterio de la primera derivada
 SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
1. LÍMITE DE UNA FUNCIÓN REAL
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resolución Nº 88 de noviembre.8/ Secretaria De Educación Distrital REGISTRO DANE Nº-99 Teléfono 6 Barrio Bastidas Santa Marta DEPARTAMENTO DE MATEMATICAS
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Resolución Nº 88 de noviembre.8/ Secretaria De Educación Distrital REGISTRO DANE Nº-99 Teléfono 6 Barrio Bastidas Santa Marta DEPARTAMENTO DE MATEMATICAS
2.1 CONTINUIDAD EN UN PUNTO 2.2 CONTINUIDAD DE FUNCIONES CONOCIDAS 2.3 CONTINUIDAD EN OPERACIONES CON
 Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Cap. Continuidad de funciones.1 CONTINUIDAD EN UN PUNTO. CONTINUIDAD DE FUNCIONES CONOCIDAS.3 CONTINUIDAD EN OPERACIONES CON FUNCIONES.4 CONTINUIDAD EN UN INTERVALO.5 TEOREMA DEL VALOR INTERMEDIO OBJETIVOS:
Límite, continuidad, asíntotas. Rápidamente aparecen las indeterminaciones y aplicamos las principales herramientas para su
 UNIDAD 4 Límite, continuidad, asíntotas a presente Unidad es la base del denominado L Cálculo Infinitesimal, que es a su vez el sustento del Análisis Matemático Los temas de la Unidad ya fueron tratados
UNIDAD 4 Límite, continuidad, asíntotas a presente Unidad es la base del denominado L Cálculo Infinitesimal, que es a su vez el sustento del Análisis Matemático Los temas de la Unidad ya fueron tratados
RESUMEN TEÓRICO DE CLASES
 Página 1 RESUMEN TEÓRICO DE CLASES Página 2 Tema 1. Inecuaciones Las inecuaciones son desigualdades algebraicas en la que sus dos miembros se relacionan por uno de estos signos: >; ;
Página 1 RESUMEN TEÓRICO DE CLASES Página 2 Tema 1. Inecuaciones Las inecuaciones son desigualdades algebraicas en la que sus dos miembros se relacionan por uno de estos signos: >; ;
Funciones y notación de funciones DEFINICIÓN DE FUNCIÓN REAL DE UNA VARIABLE REAL
 SECCIÓN P. Funciones sus gráicas 9 P. Funciones sus gráicas Usar la notación de unción para representar evaluar unciones. Encontrar el dominio recorrido o rango de una unción. Trazar la gráica de una unción.
SECCIÓN P. Funciones sus gráicas 9 P. Funciones sus gráicas Usar la notación de unción para representar evaluar unciones. Encontrar el dominio recorrido o rango de una unción. Trazar la gráica de una unción.
Teorema de máximos y mínimos para funciones continuas:
 Matemática II 7 Modulo 4 Estudio de funciones. Valores etremos de funciones En muchos casos las funciones que se presentan no pueden graficarse hallando unos pocos puntos, a que no es fácil deducir el
Matemática II 7 Modulo 4 Estudio de funciones. Valores etremos de funciones En muchos casos las funciones que se presentan no pueden graficarse hallando unos pocos puntos, a que no es fácil deducir el
TEMA 10.-LÍMITES DE FUNCIONES Y CONTINUIDAD
 TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
TEMA.-Límites de funciones y continuidad.- Matemáticas I. SUCESIONES DE NÚMEROS REALES TEMA.-LÍMITES DE FUNCIONES Y CONTINUIDAD Una sucesión de números reales es un conjunto de números (a, a, a 3,...,
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE
 DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVACIÓN DE FUNCIONES DE UNA VARIABLE Derivada de una función en un punto. Función derivada. Sea f () una función de una variable definida en un intervalo abierto (a, b) y sea (a, b). Se dice que f es
DERIVADAS DE LAS FUNCIONES ELEMENTALES
 Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1
 TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1 TEMA 11 LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN 11.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función en un
TEMA 11 LÍMITES, CONTINUIDAD Y ASÍNTOTAS MATEMÁTICAS I 1º Bach 1 TEMA 11 LÍMITES, CONTINUIDAD, ASÍNTOTAS 11.1 LÍMITE DE UNA FUNCIÓN 11.1.1 LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función en un
x + x 2 +1 = 1 1 = 0 = lím
 UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
UNIDAD Asíntota horizontal: 8 +@ + + = y = es asíntota horizontal hacia +@ (y > ). + + + + = = = 0 8 @ 8 +@ y = 0 es asíntota horizontal hacia @ (y < 0). CUESTIONES TEÓRICAS 30 Qué podemos decir del grado
LÍMITES Y CONTINUIDAD
 LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
LÍMITES Y CONTINUIDAD Tema 4: LÍMITES Y CONTINUIDAD. Índice:. Límite de una función en un punto. Límites laterales.. Límites en el infinito.. Cálculo de límites... Propiedades de los límites... Límites
V. 2 DISCUSIÓN DE UNA CURVA
 DISCUSIÓN DE ECUACIONES ALGEBRAICAS UNIDAD V Eisten dos problemas fundamentales en la Geometría Analítica:. Dada una ecuación hallar el lugar geométrico que representa.. Dado un lugar geométrico definido
DISCUSIÓN DE ECUACIONES ALGEBRAICAS UNIDAD V Eisten dos problemas fundamentales en la Geometría Analítica:. Dada una ecuación hallar el lugar geométrico que representa.. Dado un lugar geométrico definido
Función es una relación entre dos variables a las que, en general, se les llama x e y. Viene representado por: y f (x)
 TEMA 9: :.- CONCEPTO DE FUNCIÓN: Función es una relación entre dos variables a las que, en general, se les llama e y. Viene representado por: y (, donde es la variable independiente e y es la variable
TEMA 9: :.- CONCEPTO DE FUNCIÓN: Función es una relación entre dos variables a las que, en general, se les llama e y. Viene representado por: y (, donde es la variable independiente e y es la variable
Límite de una función Funciones continuas
 Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
Límite de una función Funciones continuas Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid 2014-2015 1 LÍMITE CUANDO LA VARIABLE TIENDE A INFINITO. 3 1. Límite cuando la variable tiende
Enteras Polinómicas Racionales Algebraicas Fraccionarias Racionales Irracionales Funciones Trigonométricas Trascendentes Exponenciales Logarítmicas
 E.T.S.I. Industriales y Telecomunicación Curso 010-011 Tema : Funciones reales de una variable real Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase y ponga
E.T.S.I. Industriales y Telecomunicación Curso 010-011 Tema : Funciones reales de una variable real Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase y ponga
Funciones algebraicas
 Funciones algebraicas Las funciones polinomiales tienen una gran aplicación en la elaboración de modelos que describen fenómenos reales. Algunos de ellos son: la concentración de una sustancia en un compuesto,
Funciones algebraicas Las funciones polinomiales tienen una gran aplicación en la elaboración de modelos que describen fenómenos reales. Algunos de ellos son: la concentración de una sustancia en un compuesto,
5.3 Dominios de funciones: Polinómicas: Dom f(x): R La X puede tomar cualquier valor entre (, + )
 Tema 5: Funciones. Dominio, Límites, Asíntotas y Continuidad de Funciones 5.1 Concepto de Dominio de una función Función: es una regla que asigna a cada número real X un único número real Y. X Dom R Dom
Tema 5: Funciones. Dominio, Límites, Asíntotas y Continuidad de Funciones 5.1 Concepto de Dominio de una función Función: es una regla que asigna a cada número real X un único número real Y. X Dom R Dom
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (00874) UNIDAD N 2 (LIMITES) Profesora: Yuar Matute Diciembre 20 0 Definición Intuitiva de Límites
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (00874) UNIDAD N 2 (LIMITES) Profesora: Yuar Matute Diciembre 20 0 Definición Intuitiva de Límites
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
REPRESENTACIÓN DE FUNCIONES Ejercicio nº.- Estudia y representa la siguiente unción: ( ) + 6 Ejercicio nº.- Dibuja la gráica de la unción: ( + ) ( ) Ejercicio nº.- Dada la unción: y sen sen, [0, ] a) Halla
TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD.
 TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD. 1. Concepto de función.. Dominio e imagen de una función. 3. Tipos de funciones. 4. Operaciones con funciones. 5. Concepto de límite. 6. Cálculo de límites. 7.
TEMA 8. FUNCIONES, LÍMITES Y CONTINIDAD. 1. Concepto de función.. Dominio e imagen de una función. 3. Tipos de funciones. 4. Operaciones con funciones. 5. Concepto de límite. 6. Cálculo de límites. 7.
UNIDAD III Límites. Límites infinitos. En el límite de una función, cuando x a y resulta que f x crece sin límite, entonces se tendrá: lim
 UNIDAD III Límites Límites ininitos En el límite de una unción, cuando a resulta que crece sin límite, entonces se tendrá: lim a Mientras que cuando a resulta que decrece sin límite, entonces se tendrá:
UNIDAD III Límites Límites ininitos En el límite de una unción, cuando a resulta que crece sin límite, entonces se tendrá: lim a Mientras que cuando a resulta que decrece sin límite, entonces se tendrá:
"""##$##""" !!!""#""!!!
 Unidad nº 9 CARACTERÍSTICAS DE LAS GRÁFICAS! 11 AUTTOEEVALLUACI IÓN 1 Eplica qué significan los símbolos 0 y -. 0 ( tiende a 0) significa que tomamos valores ( 0) cuya distancia a 0, dada por, se hace
Unidad nº 9 CARACTERÍSTICAS DE LAS GRÁFICAS! 11 AUTTOEEVALLUACI IÓN 1 Eplica qué significan los símbolos 0 y -. 0 ( tiende a 0) significa que tomamos valores ( 0) cuya distancia a 0, dada por, se hace
Problemas de 4 o ESO. Isaac Musat Hervás
 Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Problemas de 4 o ESO Isaac Musat Hervás 5 de febrero de 01 Índice general 1. Problemas de Álgebra 7 1.1. Números Reales.......................... 7 1.1.1. Los números....................... 7 1.1.. Intervalos.........................
Funciones: Límites y continuidad.
 Límites finitos de sucesiones. Funciones: límites y continuidad Matemáticas I Funciones: Límites y continuidad. + Decimos que una sucesión numérica ( ) n= tiene por límite r R y se escribe =r o de forma
Límites finitos de sucesiones. Funciones: límites y continuidad Matemáticas I Funciones: Límites y continuidad. + Decimos que una sucesión numérica ( ) n= tiene por límite r R y se escribe =r o de forma
Aplicaciones de la derivada.
 Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
Aplicaciones de la derivada. (Máimos y mínimos) MAXIMOS Y MINIMOS RELATIVOS Entre los valores q puede tener una unción ( ), puede haber uno que sea el más grande y otro que sea el más pequeño. A estos
APUNTE: CONCEPTO DE DERIVADA
 APUNTE: CONCEPTO DE DERIVADA UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática Carreras: Lic en Economia Proesor: Pro Mabel Chrestia Semestre: ero Año: o Introducción al concepto de derivada de
APUNTE: CONCEPTO DE DERIVADA UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática Carreras: Lic en Economia Proesor: Pro Mabel Chrestia Semestre: ero Año: o Introducción al concepto de derivada de
Capítulo 1 LÍMITES Y CONTINUIDAD Versión Beta 1.1
 Capítulo 1 LÍMITES Y CONTINUIDAD Versión Beta 1.1 www.mathspace.jimdo.com Tabla de contenido Capítulo 1...1 LÍMITES Y CONTINUIDAD...1 1.1. LÍMITES...2 1.1.1 Definición formal...2 1.1.2. Cálculo de límites...2
Capítulo 1 LÍMITES Y CONTINUIDAD Versión Beta 1.1 www.mathspace.jimdo.com Tabla de contenido Capítulo 1...1 LÍMITES Y CONTINUIDAD...1 1.1. LÍMITES...2 1.1.1 Definición formal...2 1.1.2. Cálculo de límites...2
EJERCICIOS DE LÍMITES DE FUNCIONES
 EJERCICIOS DE LÍMITES DE FUNCIONES Ejercicio nº.- A partir de la gráica de (), calcula: c) d) e) 5 Ejercicio nº.- La guiente gráica corresponde a la unción (). Sobre ella, calcula los límites: c) d) e)
EJERCICIOS DE LÍMITES DE FUNCIONES Ejercicio nº.- A partir de la gráica de (), calcula: c) d) e) 5 Ejercicio nº.- La guiente gráica corresponde a la unción (). Sobre ella, calcula los límites: c) d) e)
Cálculo Diferencial e Integral orientado para Ciencias Empresariales
 013 Cálculo Diferencial e Integral orientado para Ciencias Empresariales EQUIPO DE MATEMÁTICOS UCV -FILIAL CHICLAYO 17/04/013 ÍNDICE PRESENTACIÓN... 5 PRIMERA UNIDAD... 6 SESIÓN 1... 7 TEMA No. 1. LÍMITE
013 Cálculo Diferencial e Integral orientado para Ciencias Empresariales EQUIPO DE MATEMÁTICOS UCV -FILIAL CHICLAYO 17/04/013 ÍNDICE PRESENTACIÓN... 5 PRIMERA UNIDAD... 6 SESIÓN 1... 7 TEMA No. 1. LÍMITE
Tipos de funciones. Clasificación de funciones. Funciones algebraicas
 Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Tipos de funciones Clasificación de funciones Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación,
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Funciones Exponenciales y Logarítmicas
 Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
DERIVADAS. TÉCNICAS DE DERIVACIÓN Página 5 REFLEXIONA Y RESUELVE Tangentes a una curva y f () 5 5 9 4 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(4). f'() 0; f'(9) ; f'(4) 4 Di otros
Tema 3. LÍMITES Y CONTINUIDAD DE FUNCIONES
 1 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g( ) ENT[ ] h ( ) i ( ) 4 en el punto = Para ello, damos a valores
1 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g( ) ENT[ ] h ( ) i ( ) 4 en el punto = Para ello, damos a valores
3. VARIABLES ALEATORIAS
 . VARIABLES ALEATORIAS L as variables aleatorias se clasiican en discretas y continuas, dependiendo del número de valores que pueden asumir. Una variable aleatoria es discreta si sólo puede tomar una cantidad
. VARIABLES ALEATORIAS L as variables aleatorias se clasiican en discretas y continuas, dependiendo del número de valores que pueden asumir. Una variable aleatoria es discreta si sólo puede tomar una cantidad
EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES
 EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES. Estudiar el crecimiento, el decrecimiento y los etremos relativos de las siguientes funciones: a) f( ) 7 + + b) ln f( ) c) 5 si < f(
EJERCICIOS RESUELTOS DE REPRESENTACIÓN GRÁFICA DE FUNCIONES REALES. Estudiar el crecimiento, el decrecimiento y los etremos relativos de las siguientes funciones: a) f( ) 7 + + b) ln f( ) c) 5 si < f(
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Pendiente exacta de una curva en alguno de sus puntos
 Pendiente eacta de una curva en alguno de sus puntos Para calcular la pendiente de una curva representada mediante la unción y ( en un punto es necesario que el punto considerado pertenezca a esa unción.
Pendiente eacta de una curva en alguno de sus puntos Para calcular la pendiente de una curva representada mediante la unción y ( en un punto es necesario que el punto considerado pertenezca a esa unción.
Un i d a d 2. Co n t i n U i da d. Objetivos. Al inalizar la unidad, el alumno:
 Un i d a d Co n t i n U i da d Objetivos Al inalizar la unidad, el alumno: Identificará cuándo una función es continua en un punto y en un intervalo. Aplicará las operaciones de las funciones continuas
Un i d a d Co n t i n U i da d Objetivos Al inalizar la unidad, el alumno: Identificará cuándo una función es continua en un punto y en un intervalo. Aplicará las operaciones de las funciones continuas
Cálculo Diferencial e Integral - Recta tangente y velocidad. Farith J. Briceño N.
 Cálculo Diferencial e Integral - Recta tangente y velocidad. Farit J. Briceño N. Objetivos a cubrir Código : MAT-CDI.7 Problema: Recta tangente a una curva en un punto 0. Problema: Velocidad promedio y
Cálculo Diferencial e Integral - Recta tangente y velocidad. Farit J. Briceño N. Objetivos a cubrir Código : MAT-CDI.7 Problema: Recta tangente a una curva en un punto 0. Problema: Velocidad promedio y
GUIA DE MATEMATICAS I, CAPITULO III
 UNIVERSIDAD NACIONAL EXPERIMENTAL DE GUAYANA VICE-RECTORADO ACADEMICO DEPARTAMENTO DE CIENCIA Y TECNOLOGIA AREA DE MATEMATICAS GUIA DE MATEMATICAS I, CAPITULO III Prof. Orlando Baisdem Pérez Puerto Ordaz,
UNIVERSIDAD NACIONAL EXPERIMENTAL DE GUAYANA VICE-RECTORADO ACADEMICO DEPARTAMENTO DE CIENCIA Y TECNOLOGIA AREA DE MATEMATICAS GUIA DE MATEMATICAS I, CAPITULO III Prof. Orlando Baisdem Pérez Puerto Ordaz,
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
1 Elabora una tabla de valores de la función f(x) = x 2-4x + 3 en puntos x próximos a x = 2. Sugiere la tabla
 Unidad nº 9 CARACTERÍSTICAS DE LAS GRÁFICAS! 1 PROBLEMAS PROPUESTOS 1 Elabora una tabla de valores de la función f() - + en puntos próimos a. Sugiere la tabla que f() es continua en? 1 9 1 99 1 999 1 01
Unidad nº 9 CARACTERÍSTICAS DE LAS GRÁFICAS! 1 PROBLEMAS PROPUESTOS 1 Elabora una tabla de valores de la función f() - + en puntos próimos a. Sugiere la tabla que f() es continua en? 1 9 1 99 1 999 1 01
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
Límite de una función
 Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es decir el valor al que tienden
Límite de una función El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es decir el valor al que tienden
Tema 3. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) 4 en el punto Para ello, damos a valores próimos
Tema LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) 4 en el punto Para ello, damos a valores próimos
El problema de la recta tangente. 96 CAPÍTULO 2 Derivación
 96 CAPÍTULO Derivación. La derivada el problema de la recta tangente Hallar la pendiente de la recta tangente a una curva en un punto. Usar la definición de ite para calcular la derivada de una función.
96 CAPÍTULO Derivación. La derivada el problema de la recta tangente Hallar la pendiente de la recta tangente a una curva en un punto. Usar la definición de ite para calcular la derivada de una función.
Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados:
 Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica
Tema. Límites y continuidad. HOJA ASÍNTOTAS º Bachillerato de CCSS Determina las asíntotas de las siguientes funciones e interpreta gráficamente los resultados: ) f ( ) 4 f ( ) es una función polinómica
FECHA OBJETIVO CONTENIDO 12 DE MARZO. Introducir el tema de funciones
 Página 1 de 11 INA Turismo Bachillerato por madurez Cronograma 2011 de Matemáticas Profesora: Lordys Serrano Ramírez FECHA OBJETIVO CONTENIDO 12 DE MARZO Introducir el tema de funciones inicio de clases
Página 1 de 11 INA Turismo Bachillerato por madurez Cronograma 2011 de Matemáticas Profesora: Lordys Serrano Ramírez FECHA OBJETIVO CONTENIDO 12 DE MARZO Introducir el tema de funciones inicio de clases
