0. INTRODUCCIÓN. OBJETO
|
|
|
- María del Pilar Rivas Villalba
- hace 8 años
- Vistas:
Transcripción
1 EJEMPLO DE CÁLCULO DE MUROS DE LADRILLO SEGÚN EL CÓDIGO TÉCNICO DE LA EDIFICACIÓN ========================================= ÍNDICE DE CONTENIDO Páginas 0. INTRODUCCIÓN. OBJETO CÁLCULO A ACCIÓN VERTICAL... 6 PROCESO GENERAL DE CÁLCULO... 6 EVALUACIÓN DE ACCIONES CÁLCULO DE EXCENTRICIDADES EN PRIMER ORDEN COMPROBACIÓN DE SECCIONES ANÁLISIS EN PRIMER ORDEN. CÁLCULO DE SOLICITACIONES DISCUSIÓN DE LOS RESULTADOS ANÁLISIS EN SEGUNDO ORDEN. PROCEDIMIENTO CÁLCULO DEL FACTOR REDUCTOR DE LA CAPACIDAD RESISTENTE COMPROBACIÓN DEFINITIVA DE SECCIONES ROZAS Y REBAJES ESTRATEGIAS DE PROYECTO Y DIMENSIONADO CÁLCULO A ACCIÓN DE VIENTO ESTABILIDAD GENERAL ANTE ACCIONES HORIZONTALES COMPROBACIÓN DE LOS MUROS DE CARGA EXTERIORES COMPROBACIÓN DE LOS MUROS DE ARRIOSTRAMIENTO COMPROBACIÓN DE LOS MUROS DE CERRAMIENTO NO CARGADOS JUNTAS VERTICALES DE MOVIMIENTO EN MUROS SUSTENTADOS CONCLUSIONES
2 0. INTRODUCCIÓN. OBJETO El presente documento tiene por objeto el desarrollo pormenorizado de los procesos a seguir para verificar el cumplimiento de las condiciones resistentes y de estabilidad de un edificio convencional proyectado con muros de ladrillo, utilizando tanto el formato catalán, como el formato castellano. El procedimiento utilizado se basa en el contenido del Código Técnico de la Edificación; respetando, en particular, las prescripciones, modelos y parámetros establecidos en los siguientes Documentos Básicos: DB SE ( Seguridad Estructural ) DB SE-AE ( Seguridad Estructural: Acciones en la Edificación ) DB SE-F ( Seguridad Estructural: Fábrica ) Para este objetivo, se ha elegido como ejemplo objeto de estudio un edificio sencillo en cuanto a la geometría se refiere; que tiene, no obstante, un número considerable de situaciones diferentes que afectan al dimensionado de los muros, lo que permite exponer los procedimientos y estrategias a seguir en cada caso. En este documento se presentan los procedimientos básicos para el dimensionado de los elementos a un nivel global de estructura, y las rutinas necesarias para verificar los requisitos de resistencia y estabilidad exigidos por la normativa para cada tipo de muro, utilizando como único recurso el cálculo manual. La descripción del edificio a estudiar y los datos de partida de Proyecto aparecen detallados en la hoja gráfica adjunta. 2
3 3
4 Destacamos a continuación los rasgos esenciales, que tienen trascendencia en los procedimientos de dimensionado. El edificio planteado tiene tres tipos de muros, esencialmente distintos en cuanto a su tratamiento se refiere, que se corresponden con los tipos planteados en el DB SE-F: Muros de carga (sometidos predominantemente a carga vertical) Muros de arriostramiento (sometidos a cortante) Muros de fachada (sometidos a acciones laterales locales) En el ejemplo se desarrolla el análisis y comprobación de todos los muros de carga, sin omitir ninguno, por tener cada uno de ellos condiciones de proyecto muy diferentes. Ello permite extraer conclusiones relativas a la influencia que cada una de las variables tiene en el comportamiento. Además, el muro exterior afectado por la zona de la escalera presenta, a su vez, dos tramos claramente diferenciados entre sí; por lo que se ha realizado un análisis específico para cada uno de ellos, denominados en la documentación gráfica como zona de escalera y zona de planta. Los resultados obtenidos son muy similares en un análisis en primer orden; sin embargo las diferencias son definitivas cuando intervienen las condiciones de esbeltez y arriostramiento, por lo que se han incluido la totalidad de los resultados, aun a costa de parecer repetitivo. Los muros transversos se han diferenciado, para su tratamiento, en dos tipos distintos, denominados muros de fachadas y muros de arriostramiento, aunque debe entenderse que, tanto unos como otros, contribuyen a la estabilidad global de la estructura. La razón de diferenciar los dos tipos consiste en destacar el estado de cargas y solicitaciones que condiciona el dimensionado de cada uno de ellos que, como se verá, son esencialmente distintos. Se ha desarrollado el ejemplo para dos hipótesis de carga fundamentales, denominadas en la documentación gráfica como acción vertical y acción de viento. Cabe desatacar que el análisis realizado no considera la hipótesis de cargas accidentales. En particular, no se ha incluido la hipótesis de carga que incorpora el efecto de la acción del sismo, porque entendemos que el procedimiento de evaluación de ese efecto requiere un estudio específico en otro documento. 4
5 Se han tomado como datos de partida los valores de los parámetros que, habitualmente, son objeto de decisión por parte del proyectista y, en cualquier caso, deben ser especificados en la fase de proyecto. No obstante, los resultados obtenidos en las distintas etapas del cálculo, pueden indicar la necesidad de modificar algunos de ellos; lo cual obliga a reconsiderar el cálculo realizado previamente. En este documento se ha reproducido el proceso completo, intencionadamente, con objeto de poder orientar acerca de la influencia que tiene cada uno de los parámetros en el comportamiento global de la estructura. Cabe destacar que, en todo momento, el análisis de los muros de carga, está íntimamente ligado al análisis de los forjados. Los modelos que se adopten para el análisis y correspondiente dimensionado de estos últimos, condicionan sustancialmente el estado de solicitaciones e, incluso, el de cargas de los primeros, por tratarse de una estructura redundante, con diferentes posibilidades de readaptación de esfuerzos. Por ello, la validez definitiva del dimensionado de los muros debe quedar condicionada a determinadas prescripciones relacionadas, fundamentalmente, con la rigidez y capacidad resistente de los forjados. 5
6 1. CÁLCULO A ACCIÓN VERTICAL PROCESO GENERAL DE CÁLCULO El artículo 3.1, párrafo 4) del Documento Básico Seguridad Estructural (en adelante DB SE), establece tres situaciones de dimensionado sobre las que deben aplicarse las condiciones de verificación correspondientes. Las dos primeras se refieren a situaciones persistentes y transitorias, respectivamente. La tercera se refiere a situaciones accidentales. En este capítulo se desarrolla el procedimiento de comprobación para la primera de las situaciones indicadas. La combinación de carga utilizada es la correspondiente a las acciones permanentes y una acción gravitatoria variable. La acción permanente considerada es el peso propio, tanto de los elementos estructurales (forjados y muros), como de los elementos constructivos que gravitan sobre ellos o cargas muertas (solados, tabiquerías y revestimientos). Es importante destacar que el peso de la tabiquería aparece explícitamente incluido dentro del grupo de acciones permanentes, en el Documento Básico Seguridad estructural: Acciones en la edificación (en adelante DB SE-AE), lo que supone un cambio en el tratamiento de este tipo de acción, respecto de la normativa anterior. En este ejemplo se ha adoptado como peso de tabiquería el valor indicado en el artículo 2.1, párrafo 4) del mencionado documento básico. La acción variable introducida es la sobrecarga de uso, tomada de la tabla 3.1 del DB SE-AE, para edificios de vivienda. Todas las acciones consideradas en este primer capítulo son de naturaleza gravitatoria, por lo que nos referimos a esta combinación con el nombre de acción vertical. El objetivo de este capítulo es sentar las bases fundamentales del dimensionado de los muros de carga, debido a que, para este tipo de muros, la acción vertical constituye la combinación fundamental que condiciona la validez de su capacidad portante. 6
7 El proceso general de verificación de los muros de carga se desarrolla en el artículo 5.2 Muros sometidos predominantemente a carga vertical del Documento Básico Seguridad Estructural: Fábrica (en adelante DB SE-F). El procedimiento consiste, esencialmente, en comparar la capacidad resistente de las secciones más significativas del muro, con el estado de solicitaciones ante la combinación de cargas indicada. La condición de verificación de la capacidad portante de un muro de carga es: N Sd N Rd (DB SE-F artículo párrafo 1) donde: N Sd N Rd es el valor de cálculo de la solicitación es el valor de cálculo de la capacidad resistente deducido de las propiedades del material El tipo de solicitación en las secciones de los muros de carga, ante acción vertical, es de compresión compuesta. Los esfuerzos proceden de la transmisión de la carga de los forjados y del propio peso del muro, considerando los nudos muro-forjado con un cierto grado de rigidez, deducido según se indica para cada caso en apartados sucesivos. La capacidad resistente de las secciones se obtiene con una hipótesis de comportamiento no lineal; suponiendo ausencia total de tracciones, y bloque comprimido con tensión constante igual al valor de cálculo de la resistencia del material. La comprobación debe hacerse en segundo orden, es decir, introduciendo la amplificación de excentricidad que supone el pandeo y las imperfecciones de ejecución, deducida, a su vez, de la esbeltez y condiciones de arriostramiento de cada muro. 7
8 El proceso general, esquemáticamente, comprende las siguientes fases: Evaluación de acciones: debe calcularse la carga procedente de los forjados que gravitan sobre cada muro, así como la carga debida a su propio peso. Obtención del esfuerzo normal: en las tres secciones significativas: sección de cabeza, sección de base y sección central. Obtención del momento flector: (expresado en términos de excentricidad del esfuerzo normal) en las secciones indicadas. El momento flector en la cabeza y en la base de cada muro se obtiene realizando el análisis de nudo correspondiente, admitiendo plastificación total o parcial, según los casos; en la sección central, se deduce del diagrama de momentos flectores a lo largo de la longitud del muro. Comprobación en primer orden: de las secciones de extremo, a compresión compuesta, con las solicitaciones obtenidas anteriormente. Esta primera comprobación es necesaria para reconsiderar el predimensionado de los elementos o el resto de las condiciones de proyecto, si fuere necesario; lo cual implicaría un nuevo análisis con las modificaciones introducidas. Comprobación en segundo orden: de las secciones indicadas, con los esfuerzos amplificados por efecto del pandeo y las imperfecciones de ejecución. El DB SE-F plantea el tratamiento del cálculo en segundo orden en términos de incremento de la excentricidad debida a las cargas. El efecto de pandeo propiamente dicho sólo afecta a la sección central. En las secciones de extremo basta con introducir el incremento de excentricidad por ejecución. 8
9 9
10 EVALUACIÓN DE ACCIONES Las acciones gravitatorias sobre los muros de carga proceden de su propio peso y de los forjados que apoyan en ellos. La acción debida al propio peso de cada muro es función del peso específico de la fábrica y de su espesor. El valor de cálculo de la carga, por unidad de superficie, se obtiene mediante la siguiente expresión: donde: p d γ G p d = γ G ρ t es el valor de cálculo de la carga debida a peso propio (por unidad de superficie) es el coeficiente parcial de seguridad para acciones permanentes ρ es el peso específico de la fábrica (valor adoptado para ladrillo tosco 15 kn/m 3 ) t es el espesor del muro El valor de cálculo de la carga debida al peso propio del muro, en una sección determinada, para un metro de longitud es: P d,i = p d h i donde: P d,i p d h i es el valor de cálculo de la carga en la sección i, por unidad de longitud es el valor de cálculo de la carga superficial debida a peso propio es la altura de la sección considerada, medida desde la cabeza del muro La carga debida a los forjados puede evaluarse, sólo a efectos de conocer el orden de magnitud, suponiendo que cada forjado transmite la mitad de la carga total a cada uno de los dos muros donde apoya. Con esta simplificación, puede obtenerse el valor aproximado de la reacción de los muros sobre el forjado, con las expresiones siguientes: R d = ½ q d L (muro extremo) donde: R d q d L R d = ½ q d (L izq + L der ) (muro interior) es el valor de cálculo de la reacción sobre el forjado, por metro de longitud es el valor de cálculo de la carga superficial del forjado es la luz de cálculo de los tramos correspondientes Sin embargo, este supuesto considera sólo la reacción isostática de los muros sobre los forjados. Debido a que lo habitual es que los forjados sean de hormigón (unidireccional, bidireccional o losa maciza), es preciso considerar la componente 10
11 hiperestática de la reacción, debida a la continuidad en los apoyos y a la rigidez de los nudos. Para una evaluación exacta es preciso tener la estructura totalmente dimensionada y analizada, lo cual no es posible en esta primera fase. En primera aproximación, se puede deducir fácilmente la reacción hiperestática, suponiendo que los forjados se comportan como vigas continuas de sección constante, apoyadas en el eje de los muros. Según el modelo de análisis utilizado para el dimensionado de los forjados (elástico o plástico), se puede obtener el valor del momento de continuidad en los apoyos y la reacción sobre cada muro. En rigor, el valor de la reacción sobre cada muro es la suma de los cortantes del forjado a ambos lados del apoyo. Si los tramos de forjado tienen luz constante, se puede tabular el valor de la reacción sobre los muros, en función del número de tramos: R d = α q d L donde: R d q d L α es el valor de cálculo de la reacción en cada apoyo es el valor de cálculo de la carga superficial del forjado es la luz de los forjados a ejes de muros coeficiente tabulado 11
12 Valor del coeficiente α. Análisis elástico: forjado de un tramo: APOYO 1 APOYO 2 α 0,5 0,5 forjado de dos tramos: APOYO 1 APOYO 2 APOYO 3 α 0,375 1,25 0,375 forjado de tres tramos: APOYO 1 APOYO 2 APOYO 3 APOYO 4 α 0,40 1,10 1,10 0,40 forjado de n tramos: APOYO 1 APOYO 2 APOYO 3... APOYO n APOYO n+1 α 0,40 1,10 1,00 1,00 1,10 0,40 Valor del coeficiente α. Análisis plástico (es lo habitual): forjado de un tramo: APOYO 1 APOYO 2 α 0,5 0,5 forjado de dos tramos: APOYO 1 APOYO 2 APOYO 3 α 0,415 1,170 0,415 forjado de tres tramos: APOYO 1 APOYO 2 APOYO 3 APOYO 4 α 0,415 1,085 1,085 0,415 forjado de n tramos: APOYO 1 APOYO 2 APOYO 3... APOYO n APOYO n+1 α 0,415 1,085 1,00 1,00 1,085 0,415 12
13 Como puede observarse en la tabulación anterior, el efecto hiperestático debido a la continuidad de los forjados sólo tiene ligera influencia en los apoyos extremos, con un valor parecido en análisis elástico o plástico. Por otra parte, en los muros extremos, la magnitud de la carga no es el parámetro fundamental que condiciona su dimensionado, sino la excentricidad en el apoyo. La magnitud de la carga sólo es un parámetro decisivo en los muros interiores, de los cuales, el más cargado (a igualdad de luces) es el inmediato al muro extremo. Por ello, una simplificación aceptable en esta primera fase, a favor de la seguridad, consiste en incrementar el valor isostático de la carga en un 10%, en el primer muro interior, para tener en cuenta el efecto hiperestático; sin necesidad de hacer ninguna corrección en el resto. En el ejemplo analizado, debido a que las luces son diferentes, no es aplicable la tabulación anterior, por lo que ha sido necesario calcular las reacciones hiperestáticas a partir del momento de continuidad. Para evaluar este último, se ha supuesto análisis plástico de los forjados. 13
14 14
15 15
16 16
17 17
18 18
19 CÁLCULO DE EXCENTRICIDADES EN PRIMER ORDEN El procedimiento general para el cálculo de la excentricidad de la carga se establece en el artículo Análisis de solicitaciones del DB SE-F, donde dice textualmente en el primer párrafo que la determinación de esfuerzos se realizará de acuerdo con los métodos generales de análisis estructural, utilizando modelos planos o espaciales. Sin embargo, no indica bajo qué régimen de comportamiento de los materiales (elástico o plástico) deben aplicarse los mencionados métodos. En el segundo párrafo del mencionado artículo sugiere que, ante carga vertical, la interacción entre forjados y muros se puede idealizar según un modelo de comportamiento de pórtico plano, de ancho unidad. En el resto de los párrafos del mismo artículo se indican las pautas para la determinación de los esfuerzos mediante un análisis simplificado de nudos rígidos; en los cuales se permite determinado grado de plastificación, según los casos; pudiéndose llegar, incluso, a considerar plastificación total, lo que implica el cálculo por capacidad. Se indica explícitamente en el párrafo 3) que el análisis nudo a nudo debe hacerse en hipótesis elástica con secciones de la fábrica no fisuradas. Aunque no lo indica explícitamente en la fórmula que aparece como momento de nudo, también supone comportamiento elástico del forjado, aunque esto implica una contradicción con el procedimiento de dimensionado de este último que, de acuerdo con la normativa que lo ampara, suele hacerse admitiendo comportamiento plástico. El análisis de nudo requiere calcular los parámetros de rigidez (módulo de elasticidad, momento de inercia y longitud) de cada barra (muros y forjados de ancho unidad). El momento en el nudo, procedente del empotramiento de los forjados, se equilibra generando momentos en cada barra de valores proporcionales a sus respectivas rigideces. Según el artículo párrafo 3) del DB SE-F, la suma de los momentos en los tramos superior e inferior de un nudo de piso intermedio, puede calcularse según la siguiente expresión: M = (M emp, i M emp, j ) K / K T (1) 19
20 siendo: M emp, i M emp, j K K T los momentos de empotramiento perfecto del forjado a uno y otro lado (para carga uniforme de valor q ; M emp = q L 2 /12, siendo L la luz del forjado) la suma de rigideces de los tramos de muro en cuestión, igual a 4 E I / h donde: E es el módulo de elasticidad del muro ( = 1000 f k) siendo f k el valor característico de la resistencia a compresión de la fábrica I es el momento de inercia del muro ( = t 3 /12, siendo t el espesor del muro) h es la altura libre del paño la suma de rigideces de las piezas que concurren en el nudo analizado (para el forjado se tomará n E I / L) donde: n = 3 si el nudo opuesto es de fachada, 4 si es interior, 0 si es un vuelo E I es la rigidez del forjado (puede tomarse la rigidez de la sección sin fisurar) L es la luz libre del forjado El producto del módulo de elasticidad por el momento de inercia del forjado es un dato facilitado por el fabricante, por unidad de ancho. En la Ficha de Autorización de Uso debe constar el valor E.I especificado como rigidez o módulo de flecha. En la mencionada Ficha aparecen dos valores, de los cuales puede tomarse el que corresponde a sección íntegra (sin fisurar), en concordancia con el método. El reparto del momento así obtenido en cada muro puede ser cualquiera, siempre y cuando se mantenga el equilibrio. En el ejemplo se ha repartido proporcionalmente a la capacidad resistente de cada muro. Los parámetros de rigidez de los muros es necesario calcularlos, en función de sus características geométricas (espesor y altura libre), y mecánicas (resistencia característica de la fábrica). El módulo de elasticidad de la fábrica, se obtiene en función de la resistencia característica (DB SE-F artículo 4.6.5): E fábrica = 1000 f k donde: E fábrica f k es el módulo de elasticidad secante instantáneo de la fábrica es el valor característico de la resistencia a compresión de la fábrica En las hojas gráficas se detalla el cálculo de cada uno de los parámetros de rigidez de las barras que constituyen los nudos. Se ha calculado también el factor de rigidez relativo de cada barra, con objeto de poder sistematizar el análisis de los nudos sin necesidad de repetir las operaciones complejas. 20
21 21
22 Si bien el punto de partida del método expuesto en el DB SE-F artículo párrafo 3), es un análisis de nudos suponiendo comportamiento elástico, tanto de los forjados como de la fábrica, se reconoce explícitamente en el párrafo siguiente que la unión entre el muro y el forjado no es perfectamente rígida, por lo que se admite un determinado porcentaje de plastificación, que puede llegar a ser total bajo determinadas condiciones. En general, se admite plastificación parcial si la tensión vertical media de cálculo en el espesor del muro es menor que 0,25 N/mm 2. La plastificación parcial supone reducir el momento obtenido según la expresión (1), por un coeficiente C, (incrementando, en consecuencia, los momentos de vano de los forjados), de valor: C = (1 k/4) > 0,50 donde: k es la relación de suma de la rigidez a flexión de los forjados a la de los muros Si la tensión es menor que 0,25 N/mm 2, o si la excentricidad calculada según el método anterior es superior al 40% del espesor del muro, se admite plastificación total, o cálculo por capacidad, lo que supone asignar como momento flector en el extremo del muro el valor que corresponde a su capacidad resistente. 22
23 Además, en el mismo artículo del DB SE-F se indica el procedimiento específico para calcular el momento en cabeza de los muros de última planta, asignando directamente un valor establecido para la excentricidad de la carga, sin recurrir al análisis de nudo. También se establece el procedimiento específico para calcular el momento en el arranque del muro sobre la cimentación, indicando que es el correspondiente a la condición de empotramiento perfecto. Para la aplicación de estos criterios, es importante distinguir tres casos diferentes de nudos, con diferentes procedimientos de cálculo del momento flector (DB SE-F artículo 5.2.1): A) NUDOS DE ÚLTIMA PLANTA (párrafo 6) B) NUDOS DE PLANTAS INTERMEDIAS (párrafo 3 y siguientes) C) NUDOS DE ARRANQUE INFERIOR SOBRE CIMENTACIÓN O SOLERA (párrafo 7) El resumen del procedimiento a seguir en cada caso se indica en la hoja gráfica que se adjunta. 23
24 24
25 COMPROBACIÓN DE SECCIONES El análisis expuesto en el apartado anterior permite obtener el valor de los momentos flectores en los extremos de cado muro que, lógicamente, deben equilibrarse en los nudos con los momentos de los forjados implicados. Este análisis permite realizar una primera comprobación del cumplimiento de las secciones de cabeza y base, con objeto de reconsiderar el dimensionado o las condiciones iniciales de proyecto, si fuere necesario. La comprobación de secciones consiste en comparar los valores de la solicitación obtenida con la capacidad resistente de la sección de muro. La comprobación puede hacerse comparando solicitaciones o comparando tensiones. Con objeto de ilustrar los dos procedimientos que conducen, obviamente, a las mismas conclusiones, la comprobación en esta primera fase del proceso, antes de introducir los efectos de segundo orden, se ha realizado en términos de tensión; y la comprobación definitiva, en términos de esfuerzos. En cualquier caso, la comprobación de la validez del muro exige determinar la capacidad resistente, utilizando los parámetros geométricos (en primer orden sólo interviene el espesor t), y los parámetros mecánicos (en comprobación frente a estado límite último sólo interviene la resistencia); todos ellos definidos en proyecto. Hasta ahora sólo se ha utilizado el valor característico de la resistencia a compresión de la fábrica, f k, a efectos de evaluar el módulo resistente para determinar la rigidez relativa en los nudos. La fase de comprobación de secciones exige utilizar el valor de cálculo de la resistencia a compresión, f d ; en el que interviene el coeficiente de seguridad parcial del material, γ M. En general, el valor de cálculo de la resistencia a compresión se obtiene según la expresión siguiente: f d = f k / γ M 25
26 donde: f d es el valor de cálculo de la resistencia a compresión, a utilizar en fase de comprobación f k es el valor característico de la resistencia a compresión (según DB SE-F tabla 4.4) γ M es el coeficiente parcial de seguridad del material (según DB SE-F tabla 4.8) En la determinación del coeficiente parcial de seguridad de la fábrica γ M, intervienen las categorías de control, tanto de la fabricación de las piezas, como de la ejecución de la fábrica. El DB SE-F establece dos categorías del control de la fabricación de las piezas (I y II); y tres categorías de control de la ejecución de la fábrica (A, B y C). En función de las categorías establecidas, el coeficiente parcial de seguridad de la fábrica se obtiene mediante la siguiente tabla: γ M Categoría de la ejecución Situaciones persistentes y transitorias A B C Fábrica Categoría del control de fabricación de piezas I 1,7 2,2 2,7 II 2,0 2,5 3,0 El proceso general de comprobación de secciones, en términos de tensión, consiste en conseguir el equilibrio del nudo, con bloque de tensión rectangular en las secciones extremas de los muros implicados, sin superar el valor de cálculo de la resistencia de la fábrica. 26
27 El proceso operativo comprende los siguientes pasos: A) Nudos superiores de última planta 1. No es necesario realizar análisis de nudo. Se obtiene directamente la excentricidad de la carga según las expresiones siguientes (DB SE-F articulo párrafo 6): muros extremos e = 0,25 t + 0,25 a muros interiores e = 0,25 t (N i N j ) / (N i + N j ) donde: t es el grueso del muro a es el retranqueo de la tabica del forjado respecto del borde exterior N i; N j es la carga que acomete por cada lado 2. Se obtiene la profundidad del bloque de tensión. c = t 2 e 3. Se continúa por el punto 9 del apartado siguiente. B) Nudos de plantas intermedias 1. Se determina el valor de cálculo de la tensión media en la sección. donde: σ d,med N d t σ d,med = N d / t es el valor de cálculo de la tensión media de la sección es el valor de cálculo del esfuerzo normal por unidad de longitud es el espesor del muro 2. Se compara el valor de σ d,med con 0,25 N/mm 2, para determinar si existe posibilidad de plastificación total o parcial. En general, las secciones extremas con σ d,med < 0,25 N/mm 2 no precisan comprobación. 27
28 3. Se obtiene el momento flector a repartir entre los muros, por análisis simplificado de nudo (DB SE-F artículo párrafo 3). M Sd,sup + M Sd,inf = [(K muro sup + K muro inf ) / K total ].(q d,izq L izq 2 /12 q d,der L der 2 /12) donde: M Sd,sup, M Sd,inf K muro sup, K muro inf K total q d izq, q d der L izq, L der son los momentos flectores a obtener en los muros (valores de cálculo) son las rigideces de los muros es la suma de rigideces de muros y forjados son las cargas uniformes en cada tramo del forjado (valores de cálculo) son las luces libres del forjado a cada lado 4. Se obtiene la capacidad resistente de cada muro. muro extremo superior M Rd = N d (t 2 a N d / f d ) / 2 muro extremo inferior y muros interiores M Rd = N d (t N d / f d ) / 2 donde: M Rd es el valor de cálculo de la capacidad resistente de cada muro N d es el valor de cálculo del esfuerzo normal por unidad de longitud a es el retranqueo de la tabica del forjado respecto del borde exterior t es el espesor del muro es el valor de cálculo de la resistencia a compresión de la fábrica f d 5. La suma de momentos obtenida según el punto 6 se reparte proporcionalmente a capacidad resistente de cada muro. M Sd sup = [M Rd sup / (M Rd sup + M Rd inf )].(M Sd sup + M Sd inf ) M Sd inf = [M Rd inf / (M Rd sup + M Rd inf )].(M Sd sup + M Sd inf ) donde: M Rd sup, M Rd inf M Sd sup, M Sd inf son las capacidades resistentes de cada muro (valores de cálculo) son los momentos flectores de cada muro (valores de cálculo) 28
29 6. Si σ d,med > 0,25 N/mm 2 se pasa al proceso propiamente dicho de comprobación. Para ello, se calcula la excentricidad de la carga. donde: M Sd N d e = M Sd / N d es el momento flector en la sección de muro considerado (valor de cálculo) es el valor del esfuerzo normal por unidad de longitud (valor de cálculo) 7. Se compara el valor de la excentricidad con 0,4 t. Si e > 0,4 t se admite el cálculo por capacidad y la sección no precisa comprobación. Si e < 0,4 t se continua el proceso. 8. Se obtiene la profundidad del bloque de tensión. en la cima c = t 2 e en la base c = t 2 e 2 a donde: c es la profundidad del bloque comprimido t es el espesor del muro e es la excentricidad calculada según el punto 6 a es el retranqueo de la tabica del forjado respecto del borde exterior 9. Se obtiene el valor de cálculo de la tensión normal del bloque comprimido. donde: σ d c N d σ d = N d / c es la tensión normal del bloque comprimido (valor de cálculo) es la profundidad del bloque comprimido es el valor de cálculo del esfuerzo normal por unidad de longitud 10. Se compara σ d con la resistencia de cálculo de la fábrica, f d. 11. La validez de la sección implica σ d f d. 12. En las secciones en las que σ d,med es menor que 0,25 N/mm 2, aunque no precisen comprobación, es necesario calcular el momento flector, para seguir el proceso de comprobación en segundo orden de la sección central. Estas secciones admiten plastificación parcial. Se calcula el factor reductor. donde: C k C = (1 k/4) > 0,50 es el coeficiente reductor del momento flector por plastificación parcial es el cociente entre la suma de rigideces de forjados y la suma de rigideces de muros 13. A todos los efectos se toma como momento flector el producto del momento obtenido según el punto 5, por el coeficiente reductor obtenido según el punto
30 14. En las secciones que admiten cálculo por capacidad (cuando σ d,med < 0,25 N/mm 2 o cuando e > 0,4 t), aunque no precisen comprobación, también hay que calcular el momento flector, para seguir el proceso de comprobación en segundo orden de la sección central. En estas secciones, el momento flector coincide con la capacidad resistente, obtenida según el punto 4. C) Nudos de arranque en la cimentación 1. Se obtiene el momento flector suponiendo empotramiento perfecto. donde: M Sd,arranque M Sd,cima M Sd,arranque = - M Sd,cima / 2 es el momento flector en la sección de arranque (valor de cálculo) es el momento flector en la sección superior del muro (valor de cálculo) 2. Se continua el proceso de comprobación a partir del punto 6 del apartado anterior. Debe observarse que en las secciones a las que les corresponde un análisis simplificado de nudo, se obtiene primero el momento, después la excentricidad de las cargas y, posteriormente, la dimensión del bloque comprimido y el valor de la tensión, para proceder a su comprobación. Por el contrario, en las secciones en las que se puede aplicar el cálculo por capacidad, el valor de la tensión es conocido (igual a f d, por lo que no requieren comprobación). A partir de este valor, se obtiene primero la dimensión del bloque comprimido, después la excentricidad máxima de las cargas y, por último, se deduce el máximo valor del momento flector (capacidad resistente de la sección). 30
PUBLICACIONES GRATUITAS PARA EL CÁLCULO DE MUROS DE CARGA DE LADRILLO O TERMOARCILLA
 PUBLICACIONES GRATUITAS PARA EL CÁLCULO DE MUROS DE CARGA DE LADRILLO O TERMOARCILLA Para facilitar al prescriptor el cálculo de estructuras con muros de carga de ladrillo o bloque cerámico, Hispalyt y
PUBLICACIONES GRATUITAS PARA EL CÁLCULO DE MUROS DE CARGA DE LADRILLO O TERMOARCILLA Para facilitar al prescriptor el cálculo de estructuras con muros de carga de ladrillo o bloque cerámico, Hispalyt y
CONFERENCIA CIMENTACIONES EN ANTONIO BLANCO BLASCO
 CONFERENCIA CIMENTACIONES EN EDIFICACIONES ANTONIO BLANCO BLASCO LAS CIMENTACIONES SON ELEMENTOS ESTRUCTURALES QUE TIENEN COMO FUNCIÓN TRANSMITIR LAS CARGAS Y MOMENTOS DE UNA EDIFICACIÓN HACIA EL SUELO,
CONFERENCIA CIMENTACIONES EN EDIFICACIONES ANTONIO BLANCO BLASCO LAS CIMENTACIONES SON ELEMENTOS ESTRUCTURALES QUE TIENEN COMO FUNCIÓN TRANSMITIR LAS CARGAS Y MOMENTOS DE UNA EDIFICACIÓN HACIA EL SUELO,
ARRIOSTRAMIENTOS - 1 -
 1. DE EDIFICIOS INDUSTRIALES Los arriostramientos se consideran habitualmente elementos secundarios en las estructuras, sin embargo conviene no prescindir de ellos para que el comportamiento del conjunto
1. DE EDIFICIOS INDUSTRIALES Los arriostramientos se consideran habitualmente elementos secundarios en las estructuras, sin embargo conviene no prescindir de ellos para que el comportamiento del conjunto
Diseño y cálculo de bases de soporte solicitadas a flexocompresión, compresión o tracción según la combinación considerada
 Diseño y cálculo de bases de soporte solicitadas a flexocompresión, compresión o tracción según la combinación considerada Apellidos, nombre Departamento Centro Arianna Guardiola Víllora (aguardio@mes.upv.es)
Diseño y cálculo de bases de soporte solicitadas a flexocompresión, compresión o tracción según la combinación considerada Apellidos, nombre Departamento Centro Arianna Guardiola Víllora (aguardio@mes.upv.es)
Comprobación de una viga biapoyada de hormigón armado con sección rectangular
 Comprobación de una viga biapoyada de hormigón armado con sección rectangular J. Alcalá * V. Yepes Enero 2014 Índice 1. Introducción 2 2. Descripción del problema 2 2.1. Definición geométrica........................
Comprobación de una viga biapoyada de hormigón armado con sección rectangular J. Alcalá * V. Yepes Enero 2014 Índice 1. Introducción 2 2. Descripción del problema 2 2.1. Definición geométrica........................
Supongamos que se tiene que montar un pilar de referencia"a" localizado en un plano de replanteo.
 EJEMPLOS DE SELECCIÓN DE GRÚAS TELESCÓPICAS Ejemplo 1: selección de la grúa para el montaje de pilares. Supongamos que se tiene que montar un pilar de referencia"a" localizado en un plano de replanteo.
EJEMPLOS DE SELECCIÓN DE GRÚAS TELESCÓPICAS Ejemplo 1: selección de la grúa para el montaje de pilares. Supongamos que se tiene que montar un pilar de referencia"a" localizado en un plano de replanteo.
Objetivos docentes del Tema 8:
 Tema 8:Sistemas estructurales 1. Las acciones mecánicas. Estabilidad y Resistencia. 2. Transmisión de cargas gravitatorias y horizontales. 3. Deformación de la estructura y movimientos del edificio. 4.
Tema 8:Sistemas estructurales 1. Las acciones mecánicas. Estabilidad y Resistencia. 2. Transmisión de cargas gravitatorias y horizontales. 3. Deformación de la estructura y movimientos del edificio. 4.
Ejemplo nueve. Introducción a las Estructuras - Jorge Bernal. Se pide: Secuencia del estudio: Diseño general. Libro: Capítulo doce - Ejemplo 9
 Archivo: ie cap 12 ejem 09 Ejemplo nueve. Se pide: Dimensionar la estructura soporte del tinglado de la figura. Se analizan las solicitaciones actuantes en las correas, cabriadas, vigas y columnas, para
Archivo: ie cap 12 ejem 09 Ejemplo nueve. Se pide: Dimensionar la estructura soporte del tinglado de la figura. Se analizan las solicitaciones actuantes en las correas, cabriadas, vigas y columnas, para
INTERACCIÓN DE UNA CIMENTACIÓN PROFUNDA CON LA ESTRUCTURA
 INTERACCIÓN DE UNA CIMENTACIÓN PROFUNDA CON LA ESTRUCTURA Fernando MUZÁS LABAD, Doctor Ingeniero de Caminos Canales y Puertos Profesor Titular de Mecánica del Suelo ETSAM RESUMEN En el presente artículo
INTERACCIÓN DE UNA CIMENTACIÓN PROFUNDA CON LA ESTRUCTURA Fernando MUZÁS LABAD, Doctor Ingeniero de Caminos Canales y Puertos Profesor Titular de Mecánica del Suelo ETSAM RESUMEN En el presente artículo
CÁLCULOS RELATIVOS A LOS ESTADOS LÍMITE DE SERVICIO
 CAPÍTULO XI CÁLCULOS RELATIVOS A LOS ESTADOS LÍMITE DE SERVICIO Artículo 49º Estado Límite de Fisuración 49.1 Consideraciones generales Para las comprobaciones relativas al Estado Límite de Fisuración,
CAPÍTULO XI CÁLCULOS RELATIVOS A LOS ESTADOS LÍMITE DE SERVICIO Artículo 49º Estado Límite de Fisuración 49.1 Consideraciones generales Para las comprobaciones relativas al Estado Límite de Fisuración,
de la empresa Al finalizar la unidad, el alumno:
 de la empresa Al finalizar la unidad, el alumno: Identificará el concepto de rentabilidad. Identificará cómo afecta a una empresa la rentabilidad. Evaluará la rentabilidad de una empresa, mediante la aplicación
de la empresa Al finalizar la unidad, el alumno: Identificará el concepto de rentabilidad. Identificará cómo afecta a una empresa la rentabilidad. Evaluará la rentabilidad de una empresa, mediante la aplicación
PATOLOGÍAS DE ORIGEN TÉRMICO EN ESTRUCTURAS
 PATOLOGÍAS DE ORIGEN TÉRMICO EN ESTRUCTURAS Ing. Eduardo Pedoja Profesor de Hormigón Armado y Proyecto Facultad de Ingeniería, Universidad de Montevideo Una de las causas más frecuentes de la aparición
PATOLOGÍAS DE ORIGEN TÉRMICO EN ESTRUCTURAS Ing. Eduardo Pedoja Profesor de Hormigón Armado y Proyecto Facultad de Ingeniería, Universidad de Montevideo Una de las causas más frecuentes de la aparición
CAPÍTULO 2 COLUMNAS CORTAS BAJO CARGA AXIAL SIMPLE
 CAPÍTULO 2 COLUMNAS CORTAS BAJO CARGA AXIAL SIMPLE 2.1 Comportamiento, modos de falla y resistencia de elementos sujetos a compresión axial En este capítulo se presentan los procedimientos necesarios para
CAPÍTULO 2 COLUMNAS CORTAS BAJO CARGA AXIAL SIMPLE 2.1 Comportamiento, modos de falla y resistencia de elementos sujetos a compresión axial En este capítulo se presentan los procedimientos necesarios para
Gestión de la Prevención de Riesgos Laborales. 1
 UNIDAD Gestión de la Prevención de Riesgos Laborales. 1 FICHA 1. LA GESTIÓN DE LA PREVENCIÓN DE RIESGOS LABORALES. FICHA 2. EL SISTEMA DE GESTIÓN DE LA PREVENCIÓN DE RIESGOS LABORALES. FICHA 3. MODALIDAD
UNIDAD Gestión de la Prevención de Riesgos Laborales. 1 FICHA 1. LA GESTIÓN DE LA PREVENCIÓN DE RIESGOS LABORALES. FICHA 2. EL SISTEMA DE GESTIÓN DE LA PREVENCIÓN DE RIESGOS LABORALES. FICHA 3. MODALIDAD
Tema 3. Medidas de tendencia central. 3.1. Introducción. Contenido
 Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
Tema 3 Medidas de tendencia central Contenido 31 Introducción 1 32 Media aritmética 2 33 Media ponderada 3 34 Media geométrica 4 35 Mediana 5 351 Cálculo de la mediana para datos agrupados 5 36 Moda 6
CONCEPTOS DE LA FUERZA
 CONCEPTOS DE LA FUERZA PAPEL DE LA FUERZA EN EL RENDIMIENTO DEPORTIVO La mejora de la fuerza es un factor importante en todas las actividades deportivas, y en algunos casos determinantes (en el arbitraje
CONCEPTOS DE LA FUERZA PAPEL DE LA FUERZA EN EL RENDIMIENTO DEPORTIVO La mejora de la fuerza es un factor importante en todas las actividades deportivas, y en algunos casos determinantes (en el arbitraje
Decisión: Indican puntos en que se toman decisiones: sí o no, o se verifica una actividad del flujo grama.
 Diagrama de Flujo La presentación gráfica de un sistema es una forma ampliamente utilizada como herramienta de análisis, ya que permite identificar aspectos relevantes de una manera rápida y simple. El
Diagrama de Flujo La presentación gráfica de un sistema es una forma ampliamente utilizada como herramienta de análisis, ya que permite identificar aspectos relevantes de una manera rápida y simple. El
**********************************************************************
 1..- a) Dimensionar la sección de la viga sabiendo que está compuesta por dos tablones dispuestos como se indica en la figura (se trata de hallar a). Tensión admisible de la madera: σ adm, tracción = 50
1..- a) Dimensionar la sección de la viga sabiendo que está compuesta por dos tablones dispuestos como se indica en la figura (se trata de hallar a). Tensión admisible de la madera: σ adm, tracción = 50
Objetivos docentes del Tema 10: Tema 10:Muros
 Tema 10:Muros 1. La construcción masiva. 2. Comportamiento mecánico del muro. 3. Estabilidad lateral. 4. Tipos de muros. 5. Fábricas y Aparejos. 6. Muros homogéneos. 7. Paneles prefabricados. 8. Discontinuidades
Tema 10:Muros 1. La construcción masiva. 2. Comportamiento mecánico del muro. 3. Estabilidad lateral. 4. Tipos de muros. 5. Fábricas y Aparejos. 6. Muros homogéneos. 7. Paneles prefabricados. 8. Discontinuidades
Tema 12: El contacto con el terreno.
 Tema 12: El contacto con el terreno. Parte I: Cimentación:Transferencia de cargas de la estructura al terreno Parte II: Contención de tierras y mejora de suelos: Cerramientos en contacto con el terreno,
Tema 12: El contacto con el terreno. Parte I: Cimentación:Transferencia de cargas de la estructura al terreno Parte II: Contención de tierras y mejora de suelos: Cerramientos en contacto con el terreno,
ESCALERAS DE HORMIGÓN ARMADO
 ESCALERAS DE HORMIGÓN ARMADO Fuente: www.vitadelia.com Una escalera es uno de los recursos arquitectónicos que, con más frecuencia, se utiliza para comunicar espacios situados en diferentes planos. Breve
ESCALERAS DE HORMIGÓN ARMADO Fuente: www.vitadelia.com Una escalera es uno de los recursos arquitectónicos que, con más frecuencia, se utiliza para comunicar espacios situados en diferentes planos. Breve
Tema 11:Vigas, pilares y pórticos
 Tema 11:Vigas, pilares y pórticos 1. Vigas. El trabajo a flexión: canto y rigidez. 2. Pilares. El trabajo a compresión y el Pandeo. 3. Uniones de elementos estructurales lineales: nudos. 4. El pórtico
Tema 11:Vigas, pilares y pórticos 1. Vigas. El trabajo a flexión: canto y rigidez. 2. Pilares. El trabajo a compresión y el Pandeo. 3. Uniones de elementos estructurales lineales: nudos. 4. El pórtico
CONFERENCIA SOBRE MUROS DE CONTENCIÓN. ANTONIO BLANCO BLASCO
 CONFERENCIA SOBRE MUROS DE CONTENCIÓN. ANTONIO BLANCO BLASCO LOS MUROS DE CONTENCIÓN SON ELEMENTOS QUE SE USAN PARA CONTENER TIERRA, AGUA, GRANOS Y DIFERENTES MINERALES, CUANDO HAY DESNIVELES QUE CUBRIR.
CONFERENCIA SOBRE MUROS DE CONTENCIÓN. ANTONIO BLANCO BLASCO LOS MUROS DE CONTENCIÓN SON ELEMENTOS QUE SE USAN PARA CONTENER TIERRA, AGUA, GRANOS Y DIFERENTES MINERALES, CUANDO HAY DESNIVELES QUE CUBRIR.
19 Losas en dos direcciones - Método de Diseño Directo
 19 Losas en dos direcciones - Método de Diseño Directo CONSIDERACIONES GENERALES El Método de Diseño Directo es un procedimiento aproximado para analizar sistemas de losas en dos direcciones solicitados
19 Losas en dos direcciones - Método de Diseño Directo CONSIDERACIONES GENERALES El Método de Diseño Directo es un procedimiento aproximado para analizar sistemas de losas en dos direcciones solicitados
Los números racionales
 Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Los números racionales Los números racionales Los números fraccionarios o fracciones permiten representar aquellas situaciones en las que se obtiene o se debe una parte de un objeto. Todas las fracciones
Capítulo 5: METODOLOGÍA APLICABLE A LAS NORMAS NE AI
 Capítulo 5: METODOLOGÍA APLICABLE A LAS NORMAS NE AI La segunda fase del NIPE corresponde con la adecuación de las intervenciones de enfermería del sistema de clasificación N.I.C. (Nursing Intervention
Capítulo 5: METODOLOGÍA APLICABLE A LAS NORMAS NE AI La segunda fase del NIPE corresponde con la adecuación de las intervenciones de enfermería del sistema de clasificación N.I.C. (Nursing Intervention
Según el pliego de condiciones económicas administrativas, página 16 de 67 apartado 10: PRESENTACIÓN DE PROPOSICIONES:
 En respuesta a la solicitud de aclaraciones recibida, trasladado su escrito a la Sociedad Municipal de Aparcamientos, (Smassa), se da respuesta a las cuestiones planteadas: Como cuestión previa, decir
En respuesta a la solicitud de aclaraciones recibida, trasladado su escrito a la Sociedad Municipal de Aparcamientos, (Smassa), se da respuesta a las cuestiones planteadas: Como cuestión previa, decir
1.1. Introducción y conceptos básicos
 Tema 1 Variables estadísticas Contenido 1.1. Introducción y conceptos básicos.................. 1 1.2. Tipos de variables estadísticas................... 2 1.3. Distribuciones de frecuencias....................
Tema 1 Variables estadísticas Contenido 1.1. Introducción y conceptos básicos.................. 1 1.2. Tipos de variables estadísticas................... 2 1.3. Distribuciones de frecuencias....................
Ficha de Patología de la Edificación
 Introducción DAÑOS EN ELEMENTOS NO ESTRUCTURALES (PARTE I) Las patologías en elementos estructurales suelen llevar consigo daños en los elementos no estructurales que conforman el conjunto constructivo.
Introducción DAÑOS EN ELEMENTOS NO ESTRUCTURALES (PARTE I) Las patologías en elementos estructurales suelen llevar consigo daños en los elementos no estructurales que conforman el conjunto constructivo.
RESOLUCION DE ESTRUCTURAS POR EL METODO DE LAS DEFORMACIONES
 Facultad de Ingeniería Universidad Nacional de La Plata ESTRUCTURS III RESOLUCION DE ESTRUCTURS POR EL METODO DE LS DEFORMCIONES utor: Ing. Juan P. Durruty RESOLUCION DE ESTRUCTURS POR EL METODO DE LS
Facultad de Ingeniería Universidad Nacional de La Plata ESTRUCTURS III RESOLUCION DE ESTRUCTURS POR EL METODO DE LS DEFORMCIONES utor: Ing. Juan P. Durruty RESOLUCION DE ESTRUCTURS POR EL METODO DE LS
6. RECOMENDACIONES PARA PROYECTO
 6. RECOMENDACIONES PARA PROYECTO En principio, por motivos de confort y mantenimiento de la vía, deben disponerse el mínimo número de aparatos de dilatación de vía. Con esta premisa se ha realizado, en
6. RECOMENDACIONES PARA PROYECTO En principio, por motivos de confort y mantenimiento de la vía, deben disponerse el mínimo número de aparatos de dilatación de vía. Con esta premisa se ha realizado, en
POLIGONO FUNICULAR. Figura 1 - Cable - Estructura trabajando a tracción
 TIDE - ESTRUCTURAS IV 1 POLIGONO FUNICULAR Consideramos en primer término un cable estirado entre dos puntos fijos, con una sola carga aplicada en su punto medio. Bajo la acción de la carga, el cable adopta
TIDE - ESTRUCTURAS IV 1 POLIGONO FUNICULAR Consideramos en primer término un cable estirado entre dos puntos fijos, con una sola carga aplicada en su punto medio. Bajo la acción de la carga, el cable adopta
Bolsa POLÍTICA DE EJECUCIÓN DE ÓRDENES BANESTO BOLSA
 BANESTO BOLSA INDICE 1. ALCANCE... 3 2. AMBITO DE APLICACIÓN... 4 3. CONSIDERACIÓN DE FACTORES... 6 a. Precio... 6 b. Costes... 6 c. Rapidez... 6 d. Probabilidad de la ejecución y la liquidación... 6 e.
BANESTO BOLSA INDICE 1. ALCANCE... 3 2. AMBITO DE APLICACIÓN... 4 3. CONSIDERACIÓN DE FACTORES... 6 a. Precio... 6 b. Costes... 6 c. Rapidez... 6 d. Probabilidad de la ejecución y la liquidación... 6 e.
La importancia de dimensionar correctamente los sistemas de frenado en aerogeneradores residenciales.
 La importancia de dimensionar correctamente los sistemas de frenado en aerogeneradores residenciales. La instalación de aerogeneradores en entornos urbanos requiere la implementación de importantes medidas
La importancia de dimensionar correctamente los sistemas de frenado en aerogeneradores residenciales. La instalación de aerogeneradores en entornos urbanos requiere la implementación de importantes medidas
Cálculo y elección óptima de un depósito de agua 199
 Cálculo y elección óptima de un depósito de agua 199 CAPÍTULO 6 CONCLUSIONES 6.1.- INTRODUCCIÓN En este capítulo se exponen las conclusiones que se derivan de los distintos estudios desarrollados a lo
Cálculo y elección óptima de un depósito de agua 199 CAPÍTULO 6 CONCLUSIONES 6.1.- INTRODUCCIÓN En este capítulo se exponen las conclusiones que se derivan de los distintos estudios desarrollados a lo
Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real VIGAS EN CELOSÍA.
 VIGAS EN CELOSÍA. 1. Introducción. Cuando necesitamos salvar luces importantes (a partir de 10-15 m por ejemplo), o necesitamos tener vigas de cantos importantes, puede resultar más económico utilizar
VIGAS EN CELOSÍA. 1. Introducción. Cuando necesitamos salvar luces importantes (a partir de 10-15 m por ejemplo), o necesitamos tener vigas de cantos importantes, puede resultar más económico utilizar
EXPANSIÓN POR HUMEDAD DE LAS PIEZAS CERÁMICAS
 EXPANSIÓN POR HUMEDAD DE LAS PIEZAS CERÁMICAS 1.- DEFINICIÓN. La expansión por humedad (EPH) es la característica que presentan los materiales de arcilla cocida consistente en aumentar sus dimensiones
EXPANSIÓN POR HUMEDAD DE LAS PIEZAS CERÁMICAS 1.- DEFINICIÓN. La expansión por humedad (EPH) es la característica que presentan los materiales de arcilla cocida consistente en aumentar sus dimensiones
Técnicas de valor presente para calcular el valor en uso
 Normas Internacionales de Información Financiera NIC - NIIF Guía NIC - NIIF NIC 36 Fundación NIC-NIIF Técnicas de valor presente para calcular el valor en uso Este documento proporciona una guía para utilizar
Normas Internacionales de Información Financiera NIC - NIIF Guía NIC - NIIF NIC 36 Fundación NIC-NIIF Técnicas de valor presente para calcular el valor en uso Este documento proporciona una guía para utilizar
CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de
 CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de cualquier modelo en el software Algor. La preparación de un modelo,
CAPÍTULO VI PREPARACIÓN DEL MODELO EN ALGOR. En este capítulo, se hablará acerca de los pasos a seguir para poder realizar el análisis de cualquier modelo en el software Algor. La preparación de un modelo,
E-CONTABILIDAD FINANCIERA: NIVEL II
 E-CONTABILIDAD FINANCIERA: NIVEL II MÓDULO 8: INTRODUCCION AL ANALISIS DE BALANCES OBJETIVOS DEL MÓDULO: Iniciar el estudio de análisis contable. Comprender el significado y necesidad del fondo de maniobra.
E-CONTABILIDAD FINANCIERA: NIVEL II MÓDULO 8: INTRODUCCION AL ANALISIS DE BALANCES OBJETIVOS DEL MÓDULO: Iniciar el estudio de análisis contable. Comprender el significado y necesidad del fondo de maniobra.
Informe Nº: 071013 MEMORIA DE CÁLCULO HABITATGE UNIFAMILIAR AÏLLAT CÁNOVES, BARCELONA
 Página 1 de 21 Informe Nº: 071013 MEMORIA DE CÁLCULO HABITATGE UNIFAMILIAR AÏLLAT CÁNOVES, BARCELONA Descripción Lista de distribución Cálculo de estructura de vivienda unifamiliar en Cánoves, Barcelona.
Página 1 de 21 Informe Nº: 071013 MEMORIA DE CÁLCULO HABITATGE UNIFAMILIAR AÏLLAT CÁNOVES, BARCELONA Descripción Lista de distribución Cálculo de estructura de vivienda unifamiliar en Cánoves, Barcelona.
 Equipos a Presión. Condiciones de Seguridad Industrial y Laboral. Marco Normativo. Calderas. Lugo, 25 de octubre de 2011 1 CAMPAÑA EUROPEA SOBRE MANTENIMIENTO SEGURO Principales Objetivos: Sensibilizar
Equipos a Presión. Condiciones de Seguridad Industrial y Laboral. Marco Normativo. Calderas. Lugo, 25 de octubre de 2011 1 CAMPAÑA EUROPEA SOBRE MANTENIMIENTO SEGURO Principales Objetivos: Sensibilizar
De la lectura de este párrafo podemos llegar a las mismas conclusiones detalladas anteriormente.
 INFORME TÉCNICO SOBRE LA NATURALEZA CONTABLE DE LA AMORTIZACIÓN Y SU IMPLICACIÓN EN EL PROCESO DE CÁLCULO DE LOS COSTES DE LOS PRODUCTOS TERMINADOS Y EN LA CUENTA DE PÉRDIDAS Y GANANCIAS. 1.- OBJETIVO
INFORME TÉCNICO SOBRE LA NATURALEZA CONTABLE DE LA AMORTIZACIÓN Y SU IMPLICACIÓN EN EL PROCESO DE CÁLCULO DE LOS COSTES DE LOS PRODUCTOS TERMINADOS Y EN LA CUENTA DE PÉRDIDAS Y GANANCIAS. 1.- OBJETIVO
TIPO DE CAMBIO, TIPOS DE INTERES Y MOVIMIENTOS DE CAPITAL
 TIPO DE CAMBIO, TIPOS DE INTERES Y MOVIMIENTOS DE CAPITAL En esta breve nota se intentan analizar las relaciones existentes en el sector español entre tipo de cambio, tasa de inflación y tipos de interés,
TIPO DE CAMBIO, TIPOS DE INTERES Y MOVIMIENTOS DE CAPITAL En esta breve nota se intentan analizar las relaciones existentes en el sector español entre tipo de cambio, tasa de inflación y tipos de interés,
Covarianza y coeficiente de correlación
 Covarianza y coeficiente de correlación Cuando analizábamos las variables unidimensionales considerábamos, entre otras medidas importantes, la media y la varianza. Ahora hemos visto que estas medidas también
Covarianza y coeficiente de correlación Cuando analizábamos las variables unidimensionales considerábamos, entre otras medidas importantes, la media y la varianza. Ahora hemos visto que estas medidas también
TIPOS DE RESTRICCIONES
 RESTRICCIONES: Las restricciones son reglas que determinan la posición relativa de las distintas geometrías existentes en el archivo de trabajo. Para poder aplicarlas con rigor es preciso entender el grado
RESTRICCIONES: Las restricciones son reglas que determinan la posición relativa de las distintas geometrías existentes en el archivo de trabajo. Para poder aplicarlas con rigor es preciso entender el grado
COMPARACIÓN DE ÁREAS DE FIGURAS POR ESTUDIANTES DE PRIMERO DE MAGISTERIO
 COMPARACIÓN DE ÁREAS DE FIGURAS POR ESTUDIANTES DE PRIMERO DE MAGISTERIO Sonia Aguilera Piqueras y Pablo Flores Martínez Departamento de Didáctica de la Matemática Universidad de Granada 1. Introducción
COMPARACIÓN DE ÁREAS DE FIGURAS POR ESTUDIANTES DE PRIMERO DE MAGISTERIO Sonia Aguilera Piqueras y Pablo Flores Martínez Departamento de Didáctica de la Matemática Universidad de Granada 1. Introducción
CAPÍTULO 7. CONCLUSIONES FINALES
 CAPÍTULO 7. CONCLUSIONES FINALES Conclusiones finales El grado de protección, UPF, que un tejido proporciona contra el paso de radiación ultravioleta viene influenciado por todos los parámetros de los
CAPÍTULO 7. CONCLUSIONES FINALES Conclusiones finales El grado de protección, UPF, que un tejido proporciona contra el paso de radiación ultravioleta viene influenciado por todos los parámetros de los
Integración de la prevención de riesgos laborales
 Carlos Muñoz Ruiz Técnico de Prevención. INSL Junio 2012 39 Integración de la prevención de riesgos laborales Base legal y conceptos básicos Ley 31/1995, de Prevención de Riesgos Laborales: Artículo 14.
Carlos Muñoz Ruiz Técnico de Prevención. INSL Junio 2012 39 Integración de la prevención de riesgos laborales Base legal y conceptos básicos Ley 31/1995, de Prevención de Riesgos Laborales: Artículo 14.
PUENTE SAN SEBASTIAN
 PUENTE SAN SEBASTIAN Leonardo FERNÁNDEZ TROYANO Dr. Ingeniero de Caminos Carlos Fernández Casado, S.L cfcsl@cfcsl.com Lucía FERNÁNDEZ MUÑOZ Ingeniero de Caminos Carlos Fernández Casado, S.L. luciafm@cfcsl.com
PUENTE SAN SEBASTIAN Leonardo FERNÁNDEZ TROYANO Dr. Ingeniero de Caminos Carlos Fernández Casado, S.L cfcsl@cfcsl.com Lucía FERNÁNDEZ MUÑOZ Ingeniero de Caminos Carlos Fernández Casado, S.L. luciafm@cfcsl.com
SISTEMA MONOFÁSICO Y TRIFÁSICO DE C.A Unidad 1 Magnetismo, electromagnetismo e Inducción electromagnética.
 SISTEMA MONOFÁSICO Y TRIFÁSICO DE C.A Unidad 1 Magnetismo, electromagnetismo e Inducción electromagnética. A diferencia de los sistemas monofásicos de C.A., estudiados hasta ahora, que utilizan dos conductores
SISTEMA MONOFÁSICO Y TRIFÁSICO DE C.A Unidad 1 Magnetismo, electromagnetismo e Inducción electromagnética. A diferencia de los sistemas monofásicos de C.A., estudiados hasta ahora, que utilizan dos conductores
6. VECTORES Y COORDENADAS
 6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
6. VECTORES Y COORDENADAS Página 1 Traslaciones. Vectores Sistema de referencia. Coordenadas. Punto medio de un segmento Ecuaciones de rectas. Paralelismo. Distancias Página 2 1. TRASLACIONES. VECTORES
Enfoque del Marco Lógico (EML)
 Enfoque del Marco Lógico (EML) Qué es el EML? Es una herramienta analítica que se utiliza para la mejorar la planificación y la gestión de proyectos tanto de cooperación al desarrollo como de proyectos
Enfoque del Marco Lógico (EML) Qué es el EML? Es una herramienta analítica que se utiliza para la mejorar la planificación y la gestión de proyectos tanto de cooperación al desarrollo como de proyectos
ANCLAJES Y EMPALMES POR ADHERENCIA
 9.A.- ANCLAJES ANCLAJES Y EMPALMES POR ADHERENCIA 9.A.1.- Anclaje de barras y alambres rectos traccionados 9.A.1.1.- Expresión general El CIRSOC 201-2005, artículo 12.2.3, indica la siguiente expresión
9.A.- ANCLAJES ANCLAJES Y EMPALMES POR ADHERENCIA 9.A.1.- Anclaje de barras y alambres rectos traccionados 9.A.1.1.- Expresión general El CIRSOC 201-2005, artículo 12.2.3, indica la siguiente expresión
Resistencia de Materiales
 Tema 5 - Deflexión en Vigas Resistencia de Materiales Tema 5 Deflexión en vigas Sección 1 - Ecuación diferencial de la elástica Ecuación diferencial de la elástica Para comenzar este tema se debe recordar
Tema 5 - Deflexión en Vigas Resistencia de Materiales Tema 5 Deflexión en vigas Sección 1 - Ecuación diferencial de la elástica Ecuación diferencial de la elástica Para comenzar este tema se debe recordar
Control Estadístico de Procesos
 Control Estadístico de Procesos Gráficos de Control Los gráficos de control o cartas de control son una importante herramienta utilizada en control de calidad de procesos. Básicamente, una Carta de Control
Control Estadístico de Procesos Gráficos de Control Los gráficos de control o cartas de control son una importante herramienta utilizada en control de calidad de procesos. Básicamente, una Carta de Control
Análisis de propuestas de evaluación en las aulas de América Latina
 Este trabajo de evaluación tiene como objetivo la caracterización de figuras del espacio. Para ello el alumno debe establecer la correspondencia entre la representación de la figura y algunas de sus propiedades.
Este trabajo de evaluación tiene como objetivo la caracterización de figuras del espacio. Para ello el alumno debe establecer la correspondencia entre la representación de la figura y algunas de sus propiedades.
Control Estadístico del Proceso. Ing. Claudia Salguero Ing. Alvaro Díaz
 Control Estadístico del Proceso Ing. Claudia Salguero Ing. Alvaro Díaz Control Estadístico del Proceso Es un conjunto de herramientas estadísticas que permiten recopilar, estudiar y analizar la información
Control Estadístico del Proceso Ing. Claudia Salguero Ing. Alvaro Díaz Control Estadístico del Proceso Es un conjunto de herramientas estadísticas que permiten recopilar, estudiar y analizar la información
IAP 1005 - CONSIDERACIONES PARTICULARES SOBRE LA AUDITORÍA DE LAS EMPRESAS DE REDUCIDA DIMENSIÓN
 IAP 1005 - CONSIDERACIONES PARTICULARES SOBRE LA AUDITORÍA DE LAS EMPRESAS DE REDUCIDA DIMENSIÓN Introducción 1. Las Normas Internacionales de Auditoría (NIA) se aplican a la auditoría de la información
IAP 1005 - CONSIDERACIONES PARTICULARES SOBRE LA AUDITORÍA DE LAS EMPRESAS DE REDUCIDA DIMENSIÓN Introducción 1. Las Normas Internacionales de Auditoría (NIA) se aplican a la auditoría de la información
Física de los Procesos Biológicos Curso 2005/6
 Bibliografía: ísica, Kane, Tema 8 ísica de los Procesos Biológicos Curso 2005/6 Grupo 3 TEMA 2 BIOMECÁNICA 2.1 SÓIDO DEORMABE Parte 1 Introducción Vamos a estudiar como los materiales se deforman debido
Bibliografía: ísica, Kane, Tema 8 ísica de los Procesos Biológicos Curso 2005/6 Grupo 3 TEMA 2 BIOMECÁNICA 2.1 SÓIDO DEORMABE Parte 1 Introducción Vamos a estudiar como los materiales se deforman debido
8.1. Introducción... 1. 8.2. Dependencia/independencia estadística... 2. 8.3. Representación gráfica: diagrama de dispersión... 3. 8.4. Regresión...
 Tema 8 Análisis de dos variables: dependencia estadística y regresión Contenido 8.1. Introducción............................. 1 8.2. Dependencia/independencia estadística.............. 2 8.3. Representación
Tema 8 Análisis de dos variables: dependencia estadística y regresión Contenido 8.1. Introducción............................. 1 8.2. Dependencia/independencia estadística.............. 2 8.3. Representación
ANEXO III OBLIGACIONES DEL INDUSTRIAL
 ANEXO III OBLIGACIONES DEL INDUSTRIAL NOTIFICACIÓN ANEXO III OBLIGACIONES DEL INDUSTRIAL Todos los industriales cuyos establecimientos estén afectados por el RD 1254/1999 están obligados a enviar una notificación
ANEXO III OBLIGACIONES DEL INDUSTRIAL NOTIFICACIÓN ANEXO III OBLIGACIONES DEL INDUSTRIAL Todos los industriales cuyos establecimientos estén afectados por el RD 1254/1999 están obligados a enviar una notificación
LISTA DE MATERIALES, BOM (BILL OF MATERIALS)
 LISTA DE MATERIALES, BOM (BILL OF MATERIALS) El desglose de cualquier conjunto complejo que se produzca es un instrumento básico de los departamentos de ingeniería de diseño para la realización de su cometido.
LISTA DE MATERIALES, BOM (BILL OF MATERIALS) El desglose de cualquier conjunto complejo que se produzca es un instrumento básico de los departamentos de ingeniería de diseño para la realización de su cometido.
Fallo estructural del concreto en diagramas de dominio
 Fallo estructural del concreto en diagramas de dominio (Parte II) Eduardo de J. Vidaud Quintana Ingeniero Civil/Maestría en Ingeniería. Su correo electrónico es: evidaud@mail.imcyc.com Ingrid N. Vidaud
Fallo estructural del concreto en diagramas de dominio (Parte II) Eduardo de J. Vidaud Quintana Ingeniero Civil/Maestría en Ingeniería. Su correo electrónico es: evidaud@mail.imcyc.com Ingrid N. Vidaud
ANEXO I Capítulo 6 GENERACIÓN EÓLICA TÉCNICAMENTE ADMISIBLE EN EL SISTEMA ELÉCTRICO PENINSULAR ESPAÑOL. ANEXO I (Capítulo 6)
 ANEXO I Capítulo 6 GENERACIÓN EÓLICA TÉCNICAMENTE ADMISIBLE EN EL SISTEMA ELÉCTRICO PENINSULAR ESPAÑOL RETELGAS 13/09/2002 GENERACIÓN EÓLICA TÉCNICAMENTE ADMISIBLE EN EL SISTEMA ELÉCTRICO PENINSULAR ESPAÑOL
ANEXO I Capítulo 6 GENERACIÓN EÓLICA TÉCNICAMENTE ADMISIBLE EN EL SISTEMA ELÉCTRICO PENINSULAR ESPAÑOL RETELGAS 13/09/2002 GENERACIÓN EÓLICA TÉCNICAMENTE ADMISIBLE EN EL SISTEMA ELÉCTRICO PENINSULAR ESPAÑOL
MINISTERIO DE ECONOM~A Y HACIENDA
 SECRETARIA, DE ESTADO DE ECONOMIA Y En relación con su consulta sobre adaptación de las normas de funcionamiento de los fondos de pensiones a las modificaciones del Reglamento de Planes y Fondos de Pensiones
SECRETARIA, DE ESTADO DE ECONOMIA Y En relación con su consulta sobre adaptación de las normas de funcionamiento de los fondos de pensiones a las modificaciones del Reglamento de Planes y Fondos de Pensiones
CAPITULO II CARACTERISTICAS DE LOS INSTRUMENTOS DE MEDICION
 CAPITULO II CARACTERISTICAS DE LOS INSTRUMENTOS DE MEDICION Como hemos dicho anteriormente, los instrumentos de medición hacen posible la observación de los fenómenos eléctricos y su cuantificación. Ahora
CAPITULO II CARACTERISTICAS DE LOS INSTRUMENTOS DE MEDICION Como hemos dicho anteriormente, los instrumentos de medición hacen posible la observación de los fenómenos eléctricos y su cuantificación. Ahora
TEMA 2. FILOSOFÍA DE LOS GRÁFICOS DE CONTROL. Principios básicos de los gráficos de control. Análisis de patrones.
 TEMA 2. FILOSOFÍA DE LOS GRÁFICOS DE CONTROL. Principios básicos de los gráficos de control. Análisis de patrones. La herramienta que nos indica si el proceso está o no controlado o Estado de Control son
TEMA 2. FILOSOFÍA DE LOS GRÁFICOS DE CONTROL. Principios básicos de los gráficos de control. Análisis de patrones. La herramienta que nos indica si el proceso está o no controlado o Estado de Control son
Planes de montaje de andamios: análisis del RD 2177/2004
 Planes de montaje de andamios: análisis del RD 2177/2004 Apellidos, nombre Oliver Faubel, Inmaculada (inolfau@csa.upv.es) Departamento Centro Construcciones Arquitectónicas ETSIE. Universitat Politècnica
Planes de montaje de andamios: análisis del RD 2177/2004 Apellidos, nombre Oliver Faubel, Inmaculada (inolfau@csa.upv.es) Departamento Centro Construcciones Arquitectónicas ETSIE. Universitat Politècnica
ANÁLISIS DE DATOS NO NUMERICOS
 ANÁLISIS DE DATOS NO NUMERICOS ESCALAS DE MEDIDA CATEGORICAS Jorge Galbiati Riesco Los datos categóricos son datos que provienen de resultados de experimentos en que sus resultados se miden en escalas
ANÁLISIS DE DATOS NO NUMERICOS ESCALAS DE MEDIDA CATEGORICAS Jorge Galbiati Riesco Los datos categóricos son datos que provienen de resultados de experimentos en que sus resultados se miden en escalas
ANÁLISIS DE LOS RESULTADOS DE LAS EVALUACIONES REALIZADAS POR ACSUCYL EVALUACIÓN PREVIA DEL PROFESORADO CONTRATADO
 ANÁLISIS DE LOS RESULTADOS DE LAS EVALUACIONES REALIZADAS POR ACSUCYL EVALUACIÓN PREVIA DEL PROFESORADO CONTRATADO Desde el año 23 ACSUCYL realiza evaluaciones previas a los procesos de selección de profesorado
ANÁLISIS DE LOS RESULTADOS DE LAS EVALUACIONES REALIZADAS POR ACSUCYL EVALUACIÓN PREVIA DEL PROFESORADO CONTRATADO Desde el año 23 ACSUCYL realiza evaluaciones previas a los procesos de selección de profesorado
APROXIMACION AL METODO DE EVALUACION DEL RIESGO DE INCENDIO ESTRUCTURAL Y GLOBAL DE LOS BUQUES
 UNIVERSITAT POLITÈCNICA DE CATALUNYA APROXIMACION AL METODO DE EVALUACION DEL RIESGO DE INCENDIO ESTRUCTURAL Y GLOBAL DE LOS BUQUES Autor: Ricard Mari Sagarra Director: José Mª Fornons Barcelona, febrero
UNIVERSITAT POLITÈCNICA DE CATALUNYA APROXIMACION AL METODO DE EVALUACION DEL RIESGO DE INCENDIO ESTRUCTURAL Y GLOBAL DE LOS BUQUES Autor: Ricard Mari Sagarra Director: José Mª Fornons Barcelona, febrero
Administración de Empresas. 11 Métodos dinámicos de evaluación de inversiones 11.1
 Administración de Empresas. 11 Métodos dinámicos de evaluación de inversiones 11.1 TEMA 11: MÉTODOS DINÁMICOS DE SELECCIÓN DE INVERSIONES ESQUEMA DEL TEMA: 11.1. Valor actualizado neto. 11.2. Tasa interna
Administración de Empresas. 11 Métodos dinámicos de evaluación de inversiones 11.1 TEMA 11: MÉTODOS DINÁMICOS DE SELECCIÓN DE INVERSIONES ESQUEMA DEL TEMA: 11.1. Valor actualizado neto. 11.2. Tasa interna
35 Facultad de Ciencias Universidad de Los Andes Mérida-Venezuela. Potencial Eléctrico
 q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
q 1 q 2 Prof. Félix Aguirre 35 Energía Electrostática Potencial Eléctrico La interacción electrostática es representada muy bien a través de la ley de Coulomb, esto es: mediante fuerzas. Existen, sin embargo,
Conclusiones, aportaciones y sugerencias para futuros trabajos
 Capítulo 7 Conclusiones, aportaciones y sugerencias para futuros trabajos En este último capítulo se va a realizar una recapitulación de las conclusiones extraídas en cada uno de los capítulos del presente
Capítulo 7 Conclusiones, aportaciones y sugerencias para futuros trabajos En este último capítulo se va a realizar una recapitulación de las conclusiones extraídas en cada uno de los capítulos del presente
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA. La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros.
 QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
QUÉ ES LA RENTABILIDAD Y CÓMO MEDIRLA La rentabilidad mide la eficiencia con la cual una empresa utiliza sus recursos financieros. Qué significa esto? Decir que una empresa es eficiente es decir que no
TRANSFORMADORES EN PARALELO
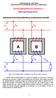 UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
UNIVERIDD DE CNTRI TRNFORMDORE EN PRLELO Miguel ngel Rodríguez Pozueta Condiciones para que varios transformadores se puedan conectar en paralelo Fig. 0: Dos transformadores monofásicos ( y ) conectados
TÉCNICAS DE MEJORA DE TERRENOS
 TÉCNICAS DE MEJORA DE TERRENOS Julio García-Mina Ingeniero de Caminos Director General KELLERTERRA, S.L. TÉCNICAS DE MEJORA DE TERRENOS 1. Introducción La mejora del terreno como solución a la cimentación
TÉCNICAS DE MEJORA DE TERRENOS Julio García-Mina Ingeniero de Caminos Director General KELLERTERRA, S.L. TÉCNICAS DE MEJORA DE TERRENOS 1. Introducción La mejora del terreno como solución a la cimentación
EXIGENCIA DE LA CLASIFICACIÓN POR LAS ADMINISTRACIONES PÚBLICAS
 EXIGENCIA DE LA CLASIFICACIÓN POR LAS ADMINISTRACIONES PÚBLICAS EXIGENCIA DE LA CLASIFICACIÓN POR LAS ADMINISTRACIONES PÚBLICAS El artículo 54.1 de la Ley de Contratos del Sector Público (L.C.S.P.) exige,
EXIGENCIA DE LA CLASIFICACIÓN POR LAS ADMINISTRACIONES PÚBLICAS EXIGENCIA DE LA CLASIFICACIÓN POR LAS ADMINISTRACIONES PÚBLICAS El artículo 54.1 de la Ley de Contratos del Sector Público (L.C.S.P.) exige,
4 Análisis de los principales factores AsociAdos A los resultados en ciencias
 cuada en relación con las posibles futuras profesiones de los estudiantes vinculadas a las ciencias. En segundo lugar, los alumnos opinan que las dificultades en el aprendizaje del nuevo conocimiento científico
cuada en relación con las posibles futuras profesiones de los estudiantes vinculadas a las ciencias. En segundo lugar, los alumnos opinan que las dificultades en el aprendizaje del nuevo conocimiento científico
Estudio de aislamientos acústicos del sistema Silensis en condiciones in situ en las instalaciones de ACUSTTEL.
 Estudio de aislamientos acústicos del sistema Silensis en condiciones in situ en las instalaciones de ACUSTTEL. María José Carpena Ruíz, Iñaki Miralles Martínez. Acusttel 73 INSTRUCCIÓN La publicación
Estudio de aislamientos acústicos del sistema Silensis en condiciones in situ en las instalaciones de ACUSTTEL. María José Carpena Ruíz, Iñaki Miralles Martínez. Acusttel 73 INSTRUCCIÓN La publicación
T R A C C I Ó N periodo de proporcionalidad o elástico. limite elástico o aparente o superior de fluencia.
 T R A C C I Ó N Un cuerpo se encuentra sometido a tracción simple cuando sobre sus secciones transversales se le aplican cargas normales uniformemente repartidas y de modo de tender a producir su alargamiento.
T R A C C I Ó N Un cuerpo se encuentra sometido a tracción simple cuando sobre sus secciones transversales se le aplican cargas normales uniformemente repartidas y de modo de tender a producir su alargamiento.
[ GUIA DE EVALUACION PREVIA DE DAÑOS SISMICOS ] PATRICIO LORCA P. Arquitecto P.U.C Magíster en Arquitectura P.U.C. I.C.A: 7685 pjlorca@puc.
![[ GUIA DE EVALUACION PREVIA DE DAÑOS SISMICOS ] PATRICIO LORCA P. Arquitecto P.U.C Magíster en Arquitectura P.U.C. I.C.A: 7685 pjlorca@puc. [ GUIA DE EVALUACION PREVIA DE DAÑOS SISMICOS ] PATRICIO LORCA P. Arquitecto P.U.C Magíster en Arquitectura P.U.C. I.C.A: 7685 pjlorca@puc.](/thumbs/27/11217710.jpg) 2010 PATRICIO LORCA P. Arquitecto P.U.C Magíster en Arquitectura P.U.C. I.C.A: 7685 pjlorca@puc.cl [ GUIA DE EVALUACION PREVIA DE DAÑOS SISMICOS ] Documento que guiará al interesado para realizar una autoevaluación
2010 PATRICIO LORCA P. Arquitecto P.U.C Magíster en Arquitectura P.U.C. I.C.A: 7685 pjlorca@puc.cl [ GUIA DE EVALUACION PREVIA DE DAÑOS SISMICOS ] Documento que guiará al interesado para realizar una autoevaluación
Geometría analítica. Impreso por Juan Carlos Vila Vilariño Centro I.E.S. PASTORIZA
 Conoce los vectores, sus componentes y las operaciones que se pueden realizar con ellos. Aprende cómo se representan las rectas y sus posiciones relativas. Impreso por Juan Carlos Vila Vilariño Centro
Conoce los vectores, sus componentes y las operaciones que se pueden realizar con ellos. Aprende cómo se representan las rectas y sus posiciones relativas. Impreso por Juan Carlos Vila Vilariño Centro
Coordinación de actividades empresariales
 Coordinación de actividades empresariales Plan General de Actividades Preventivas de la Seguridad Social 2013 Sumario 1. Introducción 3 Qué es? Objetivo Tipos de empresarios 2. Supuestos de concurrencia
Coordinación de actividades empresariales Plan General de Actividades Preventivas de la Seguridad Social 2013 Sumario 1. Introducción 3 Qué es? Objetivo Tipos de empresarios 2. Supuestos de concurrencia
Auditoría de los Sistemas de Gestión de Prevención de Riesgos Laborales
 Auditoría de los Sistemas de Gestión de Prevención de Olga Gómez García Técnico Superior de Prevención de 20/12/2012 Dirección de Prevención de IBERMUTUAMUR Fecha: 20/12/2012 Versión: 1 AUTOR: Olga Gómez
Auditoría de los Sistemas de Gestión de Prevención de Olga Gómez García Técnico Superior de Prevención de 20/12/2012 Dirección de Prevención de IBERMUTUAMUR Fecha: 20/12/2012 Versión: 1 AUTOR: Olga Gómez
Los polinomios. Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x
 Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Los polinomios Los polinomios Un polinomio es una expresión algebraica con una única letra, llamada variable. Ejemplo: 9x 6 3x 4 + x 6 polinomio de variable x Elementos de un polinomio Los términos: cada
Operación de Microsoft Excel
 Representación gráfica de datos Generalidades Excel puede crear gráficos a partir de datos previamente seleccionados en una hoja de cálculo. El usuario puede incrustar un gráfico en una hoja de cálculo,
Representación gráfica de datos Generalidades Excel puede crear gráficos a partir de datos previamente seleccionados en una hoja de cálculo. El usuario puede incrustar un gráfico en una hoja de cálculo,
VECTORES. Módulo, dirección y sentido de un vector fijo En un vector fijo se llama módulo del mismo a la longitud del segmento que lo define.
 VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
VECTORES El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman
SEGURIDAD ESTRUCTURAL en obras de FÁBRICA DE BLOQUES DE HORMIGÓN a través de 13 cuestiones.
 V MAÑANA DE LA EDIFICACIÓN 2008. COATTM SEGURIDAD ESTRUCTURAL en obras de FÁBRICA DE BLOQUES DE HORMIGÓN a través de 13 cuestiones. Ramón Gesto de Dios, arquitecto. Técnico Control Proyectos CPV Profesor
V MAÑANA DE LA EDIFICACIÓN 2008. COATTM SEGURIDAD ESTRUCTURAL en obras de FÁBRICA DE BLOQUES DE HORMIGÓN a través de 13 cuestiones. Ramón Gesto de Dios, arquitecto. Técnico Control Proyectos CPV Profesor
NIFBdM B-12 COMPENSACIÓN DE ACTIVOS FINANCIEROS Y PASIVOS FINANCIEROS
 NIFBdM B-12 COMPENSACIÓN DE ACTIVOS FINANCIEROS Y PASIVOS FINANCIEROS OBJETIVO Establecer los criterios de presentación y revelación relativos a la compensación de activos financieros y pasivos financieros
NIFBdM B-12 COMPENSACIÓN DE ACTIVOS FINANCIEROS Y PASIVOS FINANCIEROS OBJETIVO Establecer los criterios de presentación y revelación relativos a la compensación de activos financieros y pasivos financieros
contabilidad www.directivosconstruccion.com
 040_contabilidad_196.qxp 27/12/2006 18:48 PÆgina 40 contabilidad Aún habrá que esperar unos meses hasta que se apruebe el nuevo Plan General de Contabilidad que se adapte a las normas internacionales de
040_contabilidad_196.qxp 27/12/2006 18:48 PÆgina 40 contabilidad Aún habrá que esperar unos meses hasta que se apruebe el nuevo Plan General de Contabilidad que se adapte a las normas internacionales de
Capítulo 4. FLEXIÓN PURA Y FLEXIÓN SIMPLE
 Roberto Imaz Gutiérrez. Este capítulo se publica bajo Licencia Creative Commons BY NC SA 3.0 Capítulo 4. FLEXIÓN PURA Y FLEXIÓN SIMPLE 4.1 GENERALIDADES Se dice que una pieza está sometida a flexión pura
Roberto Imaz Gutiérrez. Este capítulo se publica bajo Licencia Creative Commons BY NC SA 3.0 Capítulo 4. FLEXIÓN PURA Y FLEXIÓN SIMPLE 4.1 GENERALIDADES Se dice que una pieza está sometida a flexión pura
elojfdþk=^oj^al=v=mobqbkp^al= fåöéåáéê ~=q ÅåáÅ~=ÇÉ=lÄê~ë=m ÄäáÅ~ë= = = = mol_ibj^p= ab=bu^jbk= = = `ìêëç=ommtlmu= = = = = = = = = mêçñk=iìáë=_~
 elojfdþk=^oj^al=v=mobqbkp^al= fåöéåáéê ~=q ÅåáÅ~=ÇÉ=lÄê~ë=m ÄäáÅ~ë= = = = mol_ibj^p= ab=bu^jbk= = = `ìêëç=ommtlmu= = = = = = = = = mêçñk=iìáë=_~ μå=_ä òèìéò= oéëéçåë~ääé=çé=ä~=~ëáöå~íìê~= = mêçñk=p~äî~ççê=bëíéîé=séêç
elojfdþk=^oj^al=v=mobqbkp^al= fåöéåáéê ~=q ÅåáÅ~=ÇÉ=lÄê~ë=m ÄäáÅ~ë= = = = mol_ibj^p= ab=bu^jbk= = = `ìêëç=ommtlmu= = = = = = = = = mêçñk=iìáë=_~ μå=_ä òèìéò= oéëéçåë~ääé=çé=ä~=~ëáöå~íìê~= = mêçñk=p~äî~ççê=bëíéîé=séêç
Operación Microsoft Access 97
 Trabajar con Controles Características de los controles Un control es un objeto gráfico, como por ejemplo un cuadro de texto, un botón de comando o un rectángulo que se coloca en un formulario o informe
Trabajar con Controles Características de los controles Un control es un objeto gráfico, como por ejemplo un cuadro de texto, un botón de comando o un rectángulo que se coloca en un formulario o informe
Tema 2. Análisis gráfico Ejercicios resueltos 1
 Tema 2. Análisis gráfico Ejercicios resueltos 1 Ejercicio resuelto 2.1 En una tienda han anotado los precios de los artículos que han vendido en una hora. Los datos son: 9,95, 19,95, 19,95, 14,95, 29,95,
Tema 2. Análisis gráfico Ejercicios resueltos 1 Ejercicio resuelto 2.1 En una tienda han anotado los precios de los artículos que han vendido en una hora. Los datos son: 9,95, 19,95, 19,95, 14,95, 29,95,
Unidad Formativa UF0525: Gestión Administrativa para el Asesoramiento de Productos de Activo
 Unidad Formativa UF0525: Gestión Administrativa para el Asesoramiento de Productos de Activo TEMA 1. Procedimientos de cálculo financiero básico aplicable a los productos financieros de activo TEMA 2.
Unidad Formativa UF0525: Gestión Administrativa para el Asesoramiento de Productos de Activo TEMA 1. Procedimientos de cálculo financiero básico aplicable a los productos financieros de activo TEMA 2.
La ventana de Microsoft Excel
 Actividad N 1 Conceptos básicos de Planilla de Cálculo La ventana del Microsoft Excel y sus partes. Movimiento del cursor. Tipos de datos. Metodología de trabajo con planillas. La ventana de Microsoft
Actividad N 1 Conceptos básicos de Planilla de Cálculo La ventana del Microsoft Excel y sus partes. Movimiento del cursor. Tipos de datos. Metodología de trabajo con planillas. La ventana de Microsoft
NMÁS1 SYZ VALORES AGENCIA DE VALORES, S.A NMÁS1 SYZ GESTION, SGIIC, S.A. POLÍTICA DE EJECUCIÓN Y GESTIÓN DE ÓRDENES
 NMÁS1 SYZ VALORES AGENCIA DE VALORES, S.A NMÁS1 SYZ GESTION, SGIIC, S.A. POLÍTICA DE EJECUCIÓN Y GESTIÓN DE ÓRDENES Nmás1 Syz Valores Agencia de Valores, S.A., inscrita en el Registro Mercantil de Madrid
NMÁS1 SYZ VALORES AGENCIA DE VALORES, S.A NMÁS1 SYZ GESTION, SGIIC, S.A. POLÍTICA DE EJECUCIÓN Y GESTIÓN DE ÓRDENES Nmás1 Syz Valores Agencia de Valores, S.A., inscrita en el Registro Mercantil de Madrid
