Autómatas finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS. Ejemplo 2. Ejemplo 1
|
|
|
- Juan Manuel Ponce Blázquez
- hace 7 años
- Vistas:
Transcripción
1 Autómts Lengujes regulres Autómts no determinists Cerrdur Autómts finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: Un utómt finito (DFA) está formdo por Un lfeto de entrd Σ Un conjunto finito de estdos Q Un estdo inicil s Q y un conjunto de estdos finles F Q Un función de trnsición δ : Q Σ Q Posgrdo en Cienci e Ingenierí de l Computción Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 2 / 64 Autómts Lengujes regulres Autómts no determinists Cerrdur Ejemplo Autómts Lengujes regulres Autómts no determinists Cerrdur Ejemplo 2 El utómt formdo por Σ = {,, c, d}, Q = {S,, 2, 3, F} y δ descrit por l siguiente tl: Q c d S F F Y que cept el lenguje formdo por cdens que empiezn con, terminn con y enmedio tienen un número indetermindo de c y d. El utómt formdo por Σ = {, }, Q = {S,, 2, F} y δ descrit por l siguiente tl: Q S 2 2 F 2 F F F F Y que cept un lenguje cuy descripción es demsido lrg como pr ser comprensile. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 3 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 4 / 64
2 Autómts Lengujes regulres Autómts no determinists Cerrdur Representción gráfic Autómts Lengujes regulres Autómts no determinists Cerrdur Lengujes regulres c,d S 2 3 F Podemos mplir l función δ un función δ : Q Σ Q de l siguiente form. Sen q Q, Σ y α Σ : δ (q, ɛ) = q δ (q, α) = δ (δ(q, ), α) O lterntivmente S F, δ (q, ɛ) = q δ (q, α) = δ(δ (q, α), ) 2 Not: el lumno puede demostrr que ms definiciones son equivlentes. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 5 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 6 / 64 Autómts Lengujes regulres Autómts no determinists Cerrdur Autómts Lengujes regulres Autómts no determinists Cerrdur Un ejemplo ritmético El siguiente utómt cept el lenguje Ahor podemos definir el lenguje ceptdo por el utómt A = (Q, Σ, S, F, δ): L(A) = {α δ (S, α) F}. 0 {α {0, } α es un múltiplo de 3 en inrio} Un lenguje L Σ es regulr sii exite un utómt finito A tl que L = L(A). 0 núm. representdo por el prefijo leído estdo del utómt 0 mód 3 0 mód 3 2 mód 3 2 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 7 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 8 / 64
3 Autómts Lengujes regulres Autómts no determinists Cerrdur Autómts Lengujes regulres Autómts no determinists Cerrdur Se #α el número denotdo por l cden inri α. Entonces δ (0, α) = #α mód 3 Demostrción. Primero #(αd) = 2(#α) + d d {0, } δ(q, d) = (2q + d) mód 3 Ahor, por inducción en α. Cso ásico δ (0, ɛ) = 0 definición de δ = #ɛ pues #ɛ = 0 = #ɛ mód 3 Hipótesis inductiv: δ (0, α) = #α mód 3. Por demostrr δ (0, αd) = δ(δ (0, α), d) = δ(#α mód 3, d) = (2(#α mód 3) + d) mód 3 = (2(#α) + d) mód 3 = #αd mód 3 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 9 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 0 / 64 Autómts Lengujes regulres Autómts no determinists Cerrdur Autómts no determinists Autómts Lengujes regulres Autómts no determinists Cerrdur Ejemplo Un utómt finito no determinist (NFA) puede elegir uno de vrios estdos posiles cundo lee un crácter. Además, tiene un conjunto de estdos iniciles S., L función de trnsición de un NFA es : Q Σ P(Q). L función nterior se extiende un función : P(Q) Σ P(Q) de est form: S, (A, ɛ) = A (A, α) = q (A,α) (q, ) 2, El lenguje ceptdo es {α (S, α) F } Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 2 / 64
4 Autómts Lengujes regulres Autómts no determinists Cerrdur Equivlenci con los DFA Se N = (Q, Σ,, S, F) un NFA y se D = (Q D, Σ, δ D, s D, F D ) el siguiente utómt DFA Q D = P(Q) δ D (A, ) = (A, ) s D = S F D = {A Q A F } Amos utómts ceptn el mismo lenguje. Autómts Lengujes regulres Autómts no determinists Cerrdur Demostrción. Los tres lems siguientes (A, αβ) = ( (A, α), β) ( A i, α) i = (A i, α) i δd (A, α) = (A, α) se demuestrn por inducción sore β, α y α, en ese orden. Entonces, L(N) = L(D): α L(D) sii δ (s D, α) F D sii (S N, α) F N sii α L(N) Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 3 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 4 / 64 Autómts Lengujes regulres Autómts no determinists Cerrdur Trnsiciones ɛ Autómts Lengujes regulres Autómts no determinists Cerrdur Ejemplo Un utómt finito no determinist con trnsiciones-ɛ es un quintet N = (Q, Σ,, S, F), igul un NFA slvo que ɛ : Q (Σ {ɛ}) P(Q). S ɛ Ahor es posile trnsitr de un estdo otro sin consumir símolos. se define sí, 3 (A, ɛ) = A q A (q, ɛ) (A, α) = q (A,α) (q, ) r (q,ɛ) q (A,α) (r, ) S 2, 2, Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 5 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 6 / 64
5 Autómts Lengujes regulres Autómts no determinists Cerrdur NFA-ɛ es equivlente NFA Autómts Lengujes regulres Autómts no determinists Cerrdur Vrios estdos finles e iniciles Se N = (Q, Σ,, S, F) un NFA-ɛ, y se q Q. Definimos l cerrdur-ɛ de q Se N = (Q, Σ,, S, F ), con 0 ɛ(q) = {q} n+ ɛ (q) = (r, ɛ) r n ɛ (q) ɛ(q) = n ɛ(q) n N (q, ) = (q, ) r ɛ (q) (r, ) F = {q ɛ(q) F } L introducción de trnsiciones-ɛ permite trnsformr utómts con vrios estdos iniciles o finles en utómts con un solo estdo inicil o finl. Est técnic será útil más delnte. Clrmente, L(N) = L(N ) Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 7 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 8 / 64 Autómts Lengujes regulres Autómts no determinists Cerrdur Propieddes de cerrdur Los conjuntos regulres son cerrdos jo ls operciones de: Unión Intersección Complemento Conctención Estrell de Kleene Not: en ls demostrciones siguientes se supondrá que los utómts son completos, i.e., que l función δ no es prcil. Autómts Lengujes regulres Autómts no determinists Cerrdur Demostrción de cerrdur jo Sen D = (Q, Σ, δ, s, F ) y D 2 = (Q 2, Σ, δ 2, s 2, F 2 ) dos DFA. Construiremos un D DFA tl que Definimos D = (Q, Σ, δ, s, F) donde L(D) = L(D ) L(D 2 ). Q = Q Q 2 s = (s, s 2 ) F = (Q F 2 ) (F Q 2 ) δ((q, q 2 ), ) = (δ (q, ), δ(q 2, )) Se puede demostrr por inducción en α que α L(D) sii α L(D ) o ien α L(D 2 ). Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 9 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 20 / 64
6 Autómts Lengujes regulres Autómts no determinists Cerrdur Cerrdur jo y complemento Autómts Lengujes regulres Autómts no determinists Cerrdur Cerrdur jo conctención y estrell de Kleene Intersección Se construye un utómt como en el cso de, slvo que F = F F 2. Complemento Se A = (Q, Σ, δ, s, F) un DFA. Se Ā = (Q, Σ, δ, s, Q F). Clrmente L(Ā) = Σ L(A). Sen A = (Q A, Σ, δ A, s A, F A ) y B = (Q B, Σ, δ B, s B, F B ) dos DFA. El utómt C = (Q C, Σ, C, S C, F C ) se construye de l siguiente form: Q C = Q A Q B S C = {s A } F C = F B (q, ) = {δ A (q, )} si q Q A (q, ) = {δ B (q, )} si q Q B (q, ɛ) = {s B } si q F A C es un NFA-ɛ tl que L(C) = L(A)L(B). Pr construir A tl que L(A ) = L(A), se ñden trnsiciones-ɛ de los estdos en F A s A. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 2 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 22 / 64 Expresiones regulres Ptrones Grmátics Equivlencis Definiciones lterntivs de lengujes regulres Expresiones regulres Ptrones Grmátics Equivlencis Expresiones regulres Existen otrs forms de definir los lengujes regulres: Expresiones regulres Ptrones Grmátics lineles Ls expresiones regulres son un form muy compct de definir lengujes. El lenguje generdo por l expresión α es L(α). He quí un definición inductiv: Si Σ entonces es un expresión regulr y L() = {}. y ɛ son expresiones regulres con L( ) = y L(ɛ) = {ɛ} Ls expresiones regulres α y β genern ls expresiones y lengujes: α + β L(α + β) = L(α) L(β) α β L(α β) = L(α)L(β) α L(α ) = L(α) Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 23 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 24 / 64
7 Expresiones regulres Ptrones Grmátics Equivlencis Ejemplos Expresiones regulres Ptrones Grmátics Equivlencis Ptrones Los números nturles en notción deciml: 0 + (( ) ( ) ) Ls fórmuls tómics del cálculo proposicionl: (p + q + r) + ((p + q + r) N) donde N se refiere l expresión del ejemplo nterior. Ls cdens del lfeto {,, c} con l menos un prición de cd un de ls tres letrs: (AAAcA)+(AAcAA)+(AAAcA)+(AcAAA)+(AcAAA)+(AAcAA) donde A es l expresión ( + + c). Los ptrones son otr form muy común. Tmién se definen inductivmente:, y ɛ son igules que en ls expresiones regulres #, con L(#) = con L(@) = Σ Los ptrones α y β genern los ptrones y lengujes: α + β L(α + β) = L(α) L(β) α β L(α β) = L(α) L(β) αβ L(αβ) = L(α)L(β) α L( α) = Σ L(α) α L(α ) = L(α) α + L(α + ) = L(α) + Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 25 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 26 / 64 Expresiones regulres Ptrones Grmátics Equivlencis Ejemplos Expresiones regulres Ptrones Grmátics Equivlencis Grmátics lineles Ls cdens que contienen priciones de, y c, en ese orden, pero no necesrimente Ls cdens del lfeto {,, c} slvo ls que son repeticiones consecutivs de l cden c: ((c) + ). Culquier símolo del lfeto seguido de culquier cden menos ls repeticiones consecutivs de o cd: # (() + + (cd) + ). Recordtorio. Un grmátic es G = Σ, Γ, S,. Sen A, B Γ y α Σ. Si tods ls regls de G tienen un de ls siguientes dos forms A αb o ien A α se trt de un grmátic linel por l derech. Si tods ls regls de G son de lgun de ls dos forms A Bα o ien A α es un grmátic linel por l izquierd. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 27 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 28 / 64
8 Expresiones regulres Ptrones Grmátics Equivlencis Ejemplos Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre ptrones y expresiones regulres I L grmátic G N = {0,... 9}, {S, N}, S, con regls de producción S 0 N 2N 9N N 0N N... 9N ɛ, gener los números nturles en notción deciml. L grmátic G P = {p, q, r, 0,... 9}, {S, S, N}, S, con ls siguientes regls dicionles ls del ejemplo nterior: S p q r ps qs rs Pr todo ptrón α, existe un expresión regulr β tl que L(α) = L(β). Demostrción. Por inducción en α. Primero los csos ásicos:, ɛ,, # Los tres primeros tienen expresiones regulres equivlentes ovis. En cunto # si Σ = {c,..., c m }, entonces L(#) = L(c + + c m ) y L(@) = L((c + + c m ) ) Hipótesis inductiv. Supongmos que ddos los ptrones α y β, existen expresiones regulres γ y η tles que gener ls fórmuls tómics del cálculo de proposiciones. L(α) = L(γ) L(β) = L(η) Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 29 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 30 / 64 Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre ptrones y expresiones regulres II Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre expresiones regulres y utómts Procedemos pror los csos inductivos con los operdores +, conctención,, + y. Los tres primeros son ovios, pues tmién se encuentrn presentes en ls expresiones regulres. En cunto +, st oservr que α + es equivlente αα. L prue del ptrón α se dej pendiente. Finlmente, el ptrón α β es equivlente l ptrón ( α+ β), el cul qued cuierto por los csos nteriores. Not. L firmción invers es trivilmente ciert. Pr tod expresión regulr α, existe un utómt finito A tl que L(α) = L(A). L demostrción se hrá por inducción en α. Csos ásicos. Pr ls expresiones, ɛ y, se tienen los siguientes utómts: S F S S Csos inductivos. Y se estudió cómo construir utómts que cepten l unión, l conctención y l estrell de Kleene de lengujes regulres. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 3 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 32 / 64
9 Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre utómts y expresiones regulres I Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre utómts y expresiones regulres II Se N = (Q, Σ,, S, F) NFA y sen X Q y p, q Q. Definiremos un expresión regulr α X pq tl que L(α X pq) = {β q ({p}, β) y el cmino ps sólo por estdos en X}. Por inducción en X. Sen,... k todos los símolos de Σ tles que q (p, i ). Si p q { αpq + + = k k k = 0 Si p = q α pq = { + + k + ɛ k ɛ k = 0 Si X, se r X α X pq = α X {r} pq + α X {r} pr (α X {r} rr ) α X {r} rq. Finlmente, si s,..., s n S y f,..., f m F, entonces L(N) = L( n i= m α Q s i f j ) j= Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 33 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 34 / 64 Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre grmátics lineles y utómts I Se G = Σ, Γ, S, un grmátic linel por l derech. Se N NFA-ɛ el siguiente utómt: Entonces Q = {α V Γ, β Σ Γ V βα} {[S]} ([V], ɛ) = {[α] V α} si V Γ ([α], ) = {α} si Σ α Σ Σ Γ {[S]} = estdos iniciles {[ɛ]} = estdos finles. [α] ([S], γ) sii S ηv ηθα. Demostrción. Inducción en. A prtir de este resultdo, es clro que Expresiones regulres Ptrones Grmátics Equivlencis Equivlenci entre grmátics lineles y utómts II A l invers, se A = (Q, Σ, δ, s, F) DFA. Se G = Σ, Q, s, un grmátic con producciones de l form Entonces q r sii δ(q, ) = r q sii δ(q, ) F δ (q, α) = r sii q G αr L(N) = L(G). Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 35 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 36 / 64
10 Teorem del omeo Aplicciones Un lenguje no regulr I Teorem del omeo Aplicciones Un lenguje no regulr II El lenguje { n n } no es regulr. Supongmos que lo es y que A es un utómt determinist con k estdos y L(A) = { n n }. Se l cden m m, con m > k. Durnte su lectur, el utómt dee her psdo l menos dos veces por un mismo estdo (hy menos estdos que copis de ). Se q este estdo repetido. Entonces: δ (s, i ) = q i < m δ (q, j ) = q j 0 δ (q, r m ) = f F i + j + r = m. Como A es determinist, tenemos que pr tod p N δ (q, jp ) = q y en consecuenci δ (s, i jp r m ) = f F Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 37 / 64 Pero i + jp + r m, slvo en el cso en que p =. Por tnto, unque i j p r m L(A), i j p r m { n n }, lo cul es un contrdicción. En conclusión, este lenguje no es regulr. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 38 / 64 Teorem del omeo Aplicciones Teorem del omeo Teorem del omeo Aplicciones Aplicciones del lem del omeo I El resultdo nterior se puede generlizr con el siguiente Teorem. Se L un lenguje regulr. Entonces, k N tl que α, β, γ Σ, si entonces η, θ, φ Σ tles que αβγ L y k β, β = ηθφ y θ ɛ y αηθ i φγ L i N. L demostrción generliz el rgumento del ejemplo nterior, en el que α = ɛ, β = m, η = i, θ = j, φ = r y γ = m. Ejemplo. El lenguje { 2n } no es regulr. Supongmos que lo es y A DFA reconoce este lenguje. Se k el número de estdos de A y se m tl que 2 m > k. El teorem del omeo nos dice que η, θ, φ tles que 2m = αηθ i φγ L(A) i N. Como θ ɛ, l firmción nterior quiere decir que α + η + i θ + φ + γ siempre es un potenci de 2, lo cul es ovimente flso. Por tnto, A no puede existir y { 2n } no es regulr. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 39 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 40 / 64
11 Teorem del omeo Aplicciones Aplicciones del lem del omeo II Minimlizción de estdos Teorem de Myhill-Nerode Minimlizción de estdos Ejemplo 2. Sen α Σ y Σ. Definimos #(α) = el número de priciones de en α. En ocsiones, un utómt A puede reemplzrse con un utómt A que reconoce el mismo lenguje pero que tiene un conjunto de estdos menor: Entonces {α {, } #(α) = #(α)} no es regulr. L demostrción en este cso es indirect: El lenguje { } es regulr. 2 { } {α {, } #(α) = #(α)} = { n n }. 3 Los lengujes regulres son cerrdos jo. 4 Por tnto, {α {, } #(α) = #(α)} no puede ser regulr. S 2, F,,,, S F De hecho, pr cd lenguje regulr existe un único DFA (slvo isomorfismo) con un número mínimo de estdos que lo reconoce., Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 4 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 42 / 64 Minimlizción de estdos Teorem de Myhill-Nerode Autómt cociente Minimlizción de estdos Teorem de Myhill-Nerode Algoritmo de minimlizción I Se A DFA, A = (Q, Σ, δ, s, F). Definimos un relción de equivlenci entre estdos de Q. Sen q, r Q. Entonces: q r sii α. δ (q, α) F sii δ (r, α) F. Ddo que es un relción de equivlenci, designremos con [q] l clse de equivlenci l que pertenece el estdo q. El utómt cociente de A, que denotremos con A/ = (Q, Σ, δ, s, F ), se define sí: Q = {[q] q Q} δ ([q], ) = [δ(q, )] s = [s] F = {[f] f F}. El siguiente lgoritmo permite construir el utómt cociente prtir del utómt A = (Q, Σ, δ, s, F), con Q = {q,..., q k }: Se construye un tl Estdo q... q k q m.... q k Donde m = s si el estdo en el i-ésimo renglón es finl y el estdo en l j-ésim column no es finl o vicevers. En cso contrrio, m = n. 2 Se repite el siguiente procedimiento hst que y no hy cmios: Si (q i, q j ) = n y (δ(q i, ), δ(q j, )) = s, pr lgún Σ, entonces (q i, q j ) := s. 3 Al terminr el pso nterior, q i q j sii (q i, q j ) = n. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 43 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 44 / 64
12 Minimlizción de estdos Teorem de Myhill-Nerode Algoritmo de minimlizción II Minimlizción de estdos Teorem de Myhill-Nerode Relciones de Myhill-Nerode I El lgoritmo tom cundo mucho ( ) n = 2 psos, donde n es el número de estdos. n! 2!(n 2)! Se L un lenguje regulr y se A DFA tl que L(A) = L, con A = (Q, Σ, δ, s, F) y sin estdos inccesiles. Definiremos un relción de equivlenci en Σ : α A β sii δ (s, α) = δ (s, β). L relción A tiene ls siguientes propieddes: Es un congruenci por l derech: 2 Es un finción de L: α A β implic que α A β. α A β implic que α L sii β L. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 45 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 46 / 64 Minimlizción de estdos Teorem de Myhill-Nerode Relciones de Myhill-Nerode II Minimlizción de estdos Teorem de Myhill-Nerode Teorem de Myhill-Nerode 3 Tiene índice finito, es decir, induce un número finito de clses de equivlenci. Un relción que cumple con 3 es un relción de Myhill-Nerode. Se hor R Σ un lenguje ritrrio. L relción de equivlenci R Σ Σ se define de est form: α R β sii γ Σ. αγ R sii βγ R. Se L Σ. Entonces, ls siguientes firmciones son equivlentes: L es regulr. Existe un relción de Myhill-Nerode en L. L relción L tiene índice finito. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 47 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 48 / 64
13 Minimlizción de estdos Teorem de Myhill-Nerode Ejemplo Autómts no determinists y disyunción Considérese el siguiente NFA: El conjunto L = { 2n } no es regulr. Se demostrrá utilizndo el teorem nterior. Considérense ls clses de equivlenci: α L β sii k. α k L sii β k L. S,, Pero α k, β k L sii α + k = β + k = 2 n, pr lgun n N. En pocs plrs, por cd vlor de k hy un clse de equivlenci distint, i.e., L no tiene índice finito. 2, En el estdo inicil, l cden será ceptd si l cden llev un estdo de ceptción prtir del estdo o el estdo 2. Es decir, si l disyunción (, ) F (2, ) F es verdder. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 49 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 50 / 64 Autómts finitos lternntes (AFA) Definiciones preliminres Un utómt lternnte generliz l ide nterior otrs funciones oolens. Por ejemplo, l ceptción de l cden podrí ocurrir si l expresión (, ) F (2, ) F es verdder. En cd estdo de un utómt lternnte, l lectur de un símolo llev l plicción de un función oolen los posiles resultdos de procesr el resto de l cden de entrd. Se Q un conjunto finito de estdos. Un evlución es un función e : Q {V, F}. Se B Q = {e : Q {V, F}}. El conjunto de funciones oolens con rgumentos en Q es { : B Q {V, F}}. Ejemplo. Se Q = {s,, 2}. Un función oolen es = s ( 2). Se e l evlución siguiente e(s) = V e() = F e(2) = V. Entonces, (e) = V. Si = s entonces (e) = F. Not: L función oolen no necesit utilizr todos sus rgumentos, como en el ejemplo de. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 5 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 52 / 64
14 Definición forml Un utómt lternnte es un curteto A = (Q, Σ, δ, s, F), donde δ : Q Σ { : B Q {V, F}}. L función δ se extiende l función δ : Σ { : B Q {V, F}} de l siguiente form: δ (q, ɛ) = q δ (q, α) = δ(q, ) (δ (q, α),..., δ (q n, α)) Se f : Q {V, F} l evlución siguiente: Entonces f(q) = V sii q F. L(A) = {α δ (s, α)(f) = V} Ejemplo Se A = ({s,, 2}, {, }, δ, s, {2}), donde δ está definid sí: Entonces Estdo s δ (s, )(f) = δ (, ) δ (2, ) = δ (2, ) δ (2, ) = δ (2, ɛ) δ (2, ɛ) = 2 2 y finlmente l cden es rechzd, pues 2 2(f) = F Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 53 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 54 / 64 Sistems de ecuciones Ejemplo Un form concis de definir AFA es por medio de sistems de ecuciones. Se Γ el lfeto de entrd. Entonces, ls ecuciones tienen el formto: X = (X,..., X n ) + c... X n = Γ n (X,..., X n ) + c n Γ donde ls i son funciones oolens de n rgumentos y ls c i pueden ser ɛ (en cso de que se un estdo finl) o 0. Los operdores ritméticos y oolenos se interpretn como en ls expresiones regulres o de mner trdicionl. El AFA del ejemplo nterior quedrí descrito por ls siguientes ecuciones: X 0 = (X X 2 ) + (X X 2 ) + 0 X = ( X 2 ) + X + 0 X 2 = X 2 + ( X X 2 ) + ɛ Un resultdo interesnte es que todo sistem de ecuciones corresponde un AFA y vicevers. L regulridd de los AFA se deduce de que los sistems de ecuciones pueden trnsformrse en expresiones regulres. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 55 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 56 / 64
15 Un plicción: reconocimiento de cdens I Supongmos que se tiene un conjunto de cdens X Σ y un cden α Σ y el ojetivo es verificr si lgun cden de X prece en α, es decir si β, γ, η Σ. α = βγη γ X. El lgoritmo ingenuo sigue el método de l ventn corrediz pr cd cden en X: se recorre α crácter por crácter y se verific si un cden de X corresponde l segmento de α que inici con es cden. No es difícil ver que este lgoritmo es muy ineficiente. Hy lgoritmos más eficientes que éste, pero requieren cierts operciones iniciles tmién muy costoss. Si se relizrán úsqueds frecuentes de priciones de cdens de X en cdens ritrris, el costo de ests operciones se puede justificr. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 57 / 64 Diccionrios Se Σ un lfeto. Un diccionrio es un suconjunto finito de Σ que no contiene ɛ. Buscr priciones de cdens de un diccionrio X en cdens ritrris de Σ equivle reconocer el lenguje Σ X. Se α Σ un cden no vcí. Denotremos con Pre(α) los prefijos de α. Si X es un conjunto de cdens, Pre(X) es el conjunto de prefijos de ls cdens de X. Ejemplo. Si α =, Pre(α) = {ɛ,,,, }. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 58 / 64 Autómt trie de un diccionrio Ejemplo de utómt trie El utómt trie de un diccionrio X es el utómt T(X) formdo por. Un conjunto de estdos que comprende un estdo por cd prefijo de ls cdens de X (si más de un cden tienen el mismo prefijo, T(X) sólo incluirá un estdo pr tods) El estdo inicil corresponde ɛ. Los estdos finles son ls cdens de X. L función δ se define sí. Sen p y q los estdos correspondientes ls prefijos α y β, respectivmente, y se Σ. Entonces δ(p, ) = q sii β = α. Considérese el siguiente conjunto de plrs: {,,, }. ɛ Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 59 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 60 / 64
16 Autómt de un diccionrio I Autómt de un diccionrio II Se X un diccionrio. Con se en T(X) se puede construir el utómt del diccionrio X que ceptrá el lenguje Σ X. Se h : Σ X Pre(X) l función siguiente h(α, X) = el sufijo de α de myor longitud tl que pertenece Pre(X). El utómt del diccionrio de X, denotdo por D(X), constrá de los elementos Los mismos estdos de T(X). El mismo estdo inicil. El conjunto de estdos finles es el conjunto de estdos que corresponden ls cdens en Pre(X) Σ X. L función δ definid por δ(p, ) = q sii β = h(α, X), donde p y q los estdos correspondientes ls prefijos α y β, respectivmente, y Σ. D(X) es un utómt completo que cept el lenguje Σ X. Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 6 / 64 Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 62 / 64 Ejemplo de utómt de diccionrio El utómt de diccionrio del ejemplo nterior: ɛ Frncisco Hernández Quiroz Autómts y Lengujes Formles Leng. regulres y utómts finitos 63 / 64
Autómatas finitos TEORÍA DE LA COMPUTACIÓN LENGUAJES REGULARES Y AUTÓMATAS FINITOS. Ejemplo 2. Ejemplo 1
 Autómts finitos TEORÍA DE LA COMPUTACIÓN LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Autómts finitos TEORÍA DE LA COMPUTACIÓN LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Autómatas finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS. Ejemplo 2. Ejemplo 1
 Autómts finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
Autómts finitos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES Y AUTÓMATAS FINITOS Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis, UNAM E-mil: fhq@ciencis.unm.mx Págin We: www.mtemtics.unm.mx/fhq
1 Se construye una tabla. 2 Se repite el siguiente procedimiento hasta que ya no haya cambios: (q i, q j ) := s.
 Minimlizción de estdos Minimlizción de estdos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES II LENGUAJES INDEPENDIENTES DEL CONTEXTO Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis,
Minimlizción de estdos Minimlizción de estdos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES II LENGUAJES INDEPENDIENTES DEL CONTEXTO Frncisco Hernández Quiroz Deprtmento de Mtemátics Fcultd de Ciencis,
1 Se construye una tabla. 2 Se repite lo siguiente hasta que ya no haya cambios: (q i, q j ) := s.
 Minimlizción Reconocimiento de cdens Minimlizción de estdos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES II LENGUAJES INDEPENDIENTES DEL CONTEXTO Frncisco Hernández Quiroz Deprtmento de Mtemátics
Minimlizción Reconocimiento de cdens Minimlizción de estdos AUTÓMATAS Y LENGUAJES FORMALES LENGUAJES REGULARES II LENGUAJES INDEPENDIENTES DEL CONTEXTO Frncisco Hernández Quiroz Deprtmento de Mtemátics
Problemas de Lenguajes y Autómatas
 Trjo VIII Semestre A2005 Prolems Prolems de Lengujes y Autómts 1. Pr los lengujes ddos sore Σ = {, } construir un expresión regulr de él y un Autómt Finito que lo cepte: ) L = {w w tiene un numero pr de
Trjo VIII Semestre A2005 Prolems Prolems de Lengujes y Autómts 1. Pr los lengujes ddos sore Σ = {, } construir un expresión regulr de él y un Autómt Finito que lo cepte: ) L = {w w tiene un numero pr de
Lenguajes y Autómatas finitos
 Trjo VII Semestre A2005 Teorí Lengujes y Autómts finitos 1. Lengujes. Conceptos fundmentles Se Σ un colección finit de símolos. Este conjunto de símolos se denomin lfeto y los elementos letrs. Un plr sore
Trjo VII Semestre A2005 Teorí Lengujes y Autómts finitos 1. Lengujes. Conceptos fundmentles Se Σ un colección finit de símolos. Este conjunto de símolos se denomin lfeto y los elementos letrs. Un plr sore
EJERCICIOS del TEMA 2: Lenguajes Regulares
 EJERCICIOS de MAC 1 ALF (Tem 2) Curso 2010/2011 EJERCICIOS del TEMA 2: Lengujes Regulres Sore AFDs (utómts finitos determinists): 1. Rzon l vercidd o flsedd de l siguientes firmción, poyándote en l teorí
EJERCICIOS de MAC 1 ALF (Tem 2) Curso 2010/2011 EJERCICIOS del TEMA 2: Lengujes Regulres Sore AFDs (utómts finitos determinists): 1. Rzon l vercidd o flsedd de l siguientes firmción, poyándote en l teorí
Fundamentos de Algoritmos y Computabilidad
 Fundmentos de Algoritmos y Computilidd * Autómts finitos * Autómts finitos determinists * Autómts finitos no determinists * Equivlenci entre AFD y AFN Lengujes regulres Tipo Lengujes Tipo de máquin 0 Recursivmente
Fundmentos de Algoritmos y Computilidd * Autómts finitos * Autómts finitos determinists * Autómts finitos no determinists * Equivlenci entre AFD y AFN Lengujes regulres Tipo Lengujes Tipo de máquin 0 Recursivmente
Capítulo 8: Propiedades de Lenguajes Regulares
 Cpítulo 8: Propieddes de Lengujes Regulres 8.1. Identificción de lengujes no regulres 8.1.1. Lem de Boeo 8.1.2. Aplicciones del lem de omeo 8.2. Propieddes de Cierre 8.2.1. Unión, Conctención, Clusur 8.2.2.
Cpítulo 8: Propieddes de Lengujes Regulres 8.1. Identificción de lengujes no regulres 8.1.1. Lem de Boeo 8.1.2. Aplicciones del lem de omeo 8.2. Propieddes de Cierre 8.2.1. Unión, Conctención, Clusur 8.2.2.
AUTÓMATAS FINITOS y LENGUAJES REGULARES
 Dpto. de nformátic (ATC, CCA y LS. Universidd de Vlldolid. TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES ngenierí Técnic en nformátic de Sistems. Curso 2011-12. AUTÓMATAS FNTOS y LENGUAJES REGULARES 1. Sen
Dpto. de nformátic (ATC, CCA y LS. Universidd de Vlldolid. TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES ngenierí Técnic en nformátic de Sistems. Curso 2011-12. AUTÓMATAS FNTOS y LENGUAJES REGULARES 1. Sen
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
1. Indicar el lenguaje aceptado por los siguientes autómatas :
 Universidd Rey Jun Crlos Curso 27 28 Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Hoj de Prolems 4 Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio,
Universidd Rey Jun Crlos Curso 27 28 Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Hoj de Prolems 4 Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio,
Tema 4: Operaciones sobre lenguajes regulares
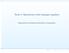 Tem 4: Operciones sore lengujes regulres Deprtmento de Sistems Informáticos y Computción DSIC - UPV http://www.dsic.upv.es p.1/19 Tem 4: Propieddes de los lengujes regulres Lem de omeo pr lengujes regulres.
Tem 4: Operciones sore lengujes regulres Deprtmento de Sistems Informáticos y Computción DSIC - UPV http://www.dsic.upv.es p.1/19 Tem 4: Propieddes de los lengujes regulres Lem de omeo pr lengujes regulres.
Lenguajes Regulares. Departamento de Informática e Ingeniería de Sistemas C.P.S. Universidad de Zaragoza. Última revisión: Feb.
 Lengujes Regulres Deprtmento de Informátic e Ingenierí de Sistems C.P.S. Universidd de Zrgoz Últim revisión: Fe. 2003 LengujesRegulres..ppt 27/03/2006 1 Índice Prolem de especificción de lengujes Lengujes
Lengujes Regulres Deprtmento de Informátic e Ingenierí de Sistems C.P.S. Universidd de Zrgoz Últim revisión: Fe. 2003 LengujesRegulres..ppt 27/03/2006 1 Índice Prolem de especificción de lengujes Lengujes
AUTÓMATAS DE PILA. Dpto. de Informática (ATC, CCIA y LSI). Univiersidad de Valladolid.
 Dpto. de Informátic (ATC, CCIA y SI). Univiersidd de Vlldolid. TEORÍA DE AUTÓMATAS Y ENGUAJES FORMAES II Ingenierí Técnic en Informátic de Sistems. Curso 20-2 AUTÓMATAS DE PIA. Dd l siguiente grmátic independiente
Dpto. de Informátic (ATC, CCIA y SI). Univiersidd de Vlldolid. TEORÍA DE AUTÓMATAS Y ENGUAJES FORMAES II Ingenierí Técnic en Informátic de Sistems. Curso 20-2 AUTÓMATAS DE PIA. Dd l siguiente grmátic independiente
June 24, 2011 DSIC - UPV. Autómatas Finitos. U.D. Computación. Autómata Finito Determinista. Autómata Finito no Determinista
 s s no s s s DSIC - UPV June 24, 2011 (DSIC - UPV) s s June 24, 2011 1 / 41 (AFD) s s no s (AFD) Un (AFD) es un 5-tupl de l siguiente form: A = (Q,Σ,δ, q 0, F), siendo: Q un conjunto finito de estdos Σ
s s no s s s DSIC - UPV June 24, 2011 (DSIC - UPV) s s June 24, 2011 1 / 41 (AFD) s s no s (AFD) Un (AFD) es un 5-tupl de l siguiente form: A = (Q,Σ,δ, q 0, F), siendo: Q un conjunto finito de estdos Σ
AUTOMATAS FINITOS Traductores
 Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
Universidd de Morón Lengujes Formles y Autómts AUTOMATAS FINITOS Trductores AUTOMATAS FINITOS Un utómt finito es un modelo mtemático que posee entrds y slids. Un utomát finito recie los elementos tester
TEORÍA DE AUTÓMATAS I Informática de Sistemas. Soluciones a las cuestiones de examen del curso 2011/12
 TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2011/12 Ferero 12, 1ª semn 1. Considere el lenguje { 2n n c / 0}. Indique cuál de ls siguientes firmciones es fls:
TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2011/12 Ferero 12, 1ª semn 1. Considere el lenguje { 2n n c / 0}. Indique cuál de ls siguientes firmciones es fls:
q 2 q 3 b q 3 q 4 a, b
 M = (Σ E, Q, q, f, F ) donde Reconocedor finito determinist Slide Σ E : lfeto de entrd Q : conjunto de estdos, f inito q Q : estdo inicil f : Q Σ E Q función prcil de trnsición F Q : estdos finles o de
M = (Σ E, Q, q, f, F ) donde Reconocedor finito determinist Slide Σ E : lfeto de entrd Q : conjunto de estdos, f inito q Q : estdo inicil f : Q Σ E Q función prcil de trnsición F Q : estdos finles o de
1. Indicar el lenguaje aceptado por los siguientes autómatas :
 Universidd Rey Jun Crlos Grdo en Ingenierí de Computdores Máquins Secuenciles, Autómts y Lengujes Hoj de Prolems: Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio, ( ) vnzdo.. Indicr
Universidd Rey Jun Crlos Grdo en Ingenierí de Computdores Máquins Secuenciles, Autómts y Lengujes Hoj de Prolems: Autómts Finitos Determinists Nivel del ejercicio : ( ) ásico, ( ) medio, ( ) vnzdo.. Indicr
AUTOMATAS FINITOS CIENCIAS DE LA COMPUTACION I 2009
 AUTOMATAS FINITOS Un utómt finito es un modelo mtemático de un máquin que cept cdens de un lenguje definido sore un lfeto A. Consiste en un conjunto finito de estdos y un conjunto de trnsiciones entre
AUTOMATAS FINITOS Un utómt finito es un modelo mtemático de un máquin que cept cdens de un lenguje definido sore un lfeto A. Consiste en un conjunto finito de estdos y un conjunto de trnsiciones entre
Ciencias de la Computación I
 Ciencis de l Computción I Propieddes de Clusur de Lengujes Regulres y Lengujes Libres del Contexto Propieddes de Clusur de Lengujes Regulres Los lengujes regulres (LR son cerrdos bjo ls siguientes operciones:
Ciencis de l Computción I Propieddes de Clusur de Lengujes Regulres y Lengujes Libres del Contexto Propieddes de Clusur de Lengujes Regulres Los lengujes regulres (LR son cerrdos bjo ls siguientes operciones:
4.2 Gramáticas libres de contexto. 4.1 Introducción
 1 Curso Básico de Computción 4 Grmátics libres de contexto 4.1 Introducción Un grmátic libre de contexto es un conjunto finito de vribles, cd un de ls cules represent un lenguje. Los lengujes representdos
1 Curso Básico de Computción 4 Grmátics libres de contexto 4.1 Introducción Un grmátic libre de contexto es un conjunto finito de vribles, cd un de ls cules represent un lenguje. Los lengujes representdos
TEORÍA DE AUTÓMATAS I Informática de Sistemas. Soluciones a las cuestiones de examen del curso 2010/11
 TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2/ Ferero, ª semn. Indique cuál de ls siguientes firmciones referentes los operdores sore símolos *, y es FALSA:
TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 2/ Ferero, ª semn. Indique cuál de ls siguientes firmciones referentes los operdores sore símolos *, y es FALSA:
Temas. Objetivo. Definición de autómata finito. Autómata finito determinístico y no determinístico. Autómata finito de estados mínimos 14:17
 0 Tems Definición de utómt finito Autómt finito determinístico y no determinístico Autómt finito de estdos mínimos Ojetivo Que el estudinte logre: 1) Identificr conceptos constructivos de l Teorí de l
0 Tems Definición de utómt finito Autómt finito determinístico y no determinístico Autómt finito de estdos mínimos Ojetivo Que el estudinte logre: 1) Identificr conceptos constructivos de l Teorí de l
Determinización: Construcción de Safra
 Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
Determinizción: Construcción de Sfr Ddo: Autómt de Büchi A = (Q,Σ,Q 0,δ,F) Supong que Q = {q 1,...,q n }. Vmos construir un utómt de Rin determinist B tl que L ω (A) = L ω (B), donde B está compuesto por:
Introducción a la Lógica y la Computación
 Introducción l Lógic y l Computción Prte III: Lengujes y Autómts Autores: Alejndro Tiroschi y Pedro Sánchez Terrf Contenidos 1 Introducción 1 2 Lengujes y Autómts 3 2.1 Cdens, lfetos y lengujes.............................
Introducción l Lógic y l Computción Prte III: Lengujes y Autómts Autores: Alejndro Tiroschi y Pedro Sánchez Terrf Contenidos 1 Introducción 1 2 Lengujes y Autómts 3 2.1 Cdens, lfetos y lengujes.............................
TEORÍA DE AUTÓMATAS I Informática de Sistemas
 TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 25/6 Ferero 26, ª semn. Se un utómt finito M={S, Σ, δ, ι, F,}. Sen p,q S;, Σ. Indique cuál de ls siguientes firmciones
TEORÍA DE AUTÓMATAS I Informátic de Sistems Soluciones ls cuestiones de exmen del curso 25/6 Ferero 26, ª semn. Se un utómt finito M={S, Σ, δ, ι, F,}. Sen p,q S;, Σ. Indique cuál de ls siguientes firmciones
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I
 INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 18 de enero de 2008 APELLIDOS Y NOMBRE: DURACIÓN: 3 hors. SOLUCIÓN del EXAMEN L primer pregunt es un test, que const de 8 supregunts corts y puntú
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 18 de enero de 2008 APELLIDOS Y NOMBRE: DURACIÓN: 3 hors. SOLUCIÓN del EXAMEN L primer pregunt es un test, que const de 8 supregunts corts y puntú
3 de marzo de 2011 DSIC - UPV. Tema 5: Expresiones Regulares. U.D. Computación. Definiciones. Propiedades. Construcciones. AFs a partir de ERs
 UD AFs Lem de UD DSIC - UPV 3 de mrzo de 2011 UD (DSIC - UPV) 3 de mrzo de 2011 1 / 40 Índice UD AFs Lem de sore expresiones regulres utómts finitos utómts finitos UD (DSIC - UPV) 3 de mrzo de 2011 2 /
UD AFs Lem de UD DSIC - UPV 3 de mrzo de 2011 UD (DSIC - UPV) 3 de mrzo de 2011 1 / 40 Índice UD AFs Lem de sore expresiones regulres utómts finitos utómts finitos UD (DSIC - UPV) 3 de mrzo de 2011 2 /
Ejercicios resueltos de Lenguajes, Gramáticas y Autómatas ( )
 Ejercicios resueltos de Lengujes, Grmátics y utómts (-2-4). Encuentr el FD mínimo que reconoce el lenguje representdo por l ER ( + + ) ( + ) Pr otener el FD mínimo correspondiente (+ +ɛ) (+) tenemos que
Ejercicios resueltos de Lengujes, Grmátics y utómts (-2-4). Encuentr el FD mínimo que reconoce el lenguje representdo por l ER ( + + ) ( + ) Pr otener el FD mínimo correspondiente (+ +ɛ) (+) tenemos que
Caracterización de lenguajes regulares con expresiones regulares
 Crcterizción de lengujes regulres con expresiones regulres Elvir Myordomo Universidd de Zrgoz 15 de octubre de 2012 Contenido de este tem Recordtorio de expresiones regulres (e.r.) Cómo convertir un e.r.
Crcterizción de lengujes regulres con expresiones regulres Elvir Myordomo Universidd de Zrgoz 15 de octubre de 2012 Contenido de este tem Recordtorio de expresiones regulres (e.r.) Cómo convertir un e.r.
5. Lenguajes Regulares
 5. Lengujes Regulres Arceli Snchis de Miguel Agpito Ledezm Espino José A. Iglesis Mr
5. Lengujes Regulres Arceli Snchis de Miguel Agpito Ledezm Espino José A. Iglesis Mr
Informática Teórica. Tema 4: Autómatas Finitos
 Informátic Teóric Tem 4: Autómts Finitos 1 Autómts Finitos. Biliogrfí M. Alfonsec, J. Sncho y M. Mrtínez. Teorí de Lengujes, Grmátics y Autómts, R.A.E.C., Mdrid, (1998). P. Issi, P. Mrtínez y D. Borrjo.
Informátic Teóric Tem 4: Autómts Finitos 1 Autómts Finitos. Biliogrfí M. Alfonsec, J. Sncho y M. Mrtínez. Teorí de Lengujes, Grmátics y Autómts, R.A.E.C., Mdrid, (1998). P. Issi, P. Mrtínez y D. Borrjo.
Minimización de AFDs, método y problemas
 Minimizción de Fs, método y prolems Elvir Myordomo, Universidd de Zrgoz 8 de octure de. Resultdos sore utómts determinists mínimos El F mínimo existe y es único, es decir Teorem. do unf M = (Q,Σ,δ,q,F),
Minimizción de Fs, método y prolems Elvir Myordomo, Universidd de Zrgoz 8 de octure de. Resultdos sore utómts determinists mínimos El F mínimo existe y es único, es decir Teorem. do unf M = (Q,Σ,δ,q,F),
Relación de ejercicios hechos en clase en los últimos días previos al examen de febrero
 Relción de ejercicios hechos en clse en los últimos dís previos l exmen de ferero De cuerdo con l definición de APND, propón 5 ejemplos de utómt con pil que cepten: - el lenguje Σ * ({f}, Σ, Σ, { ((f,,ε),
Relción de ejercicios hechos en clse en los últimos dís previos l exmen de ferero De cuerdo con l definición de APND, propón 5 ejemplos de utómt con pil que cepten: - el lenguje Σ * ({f}, Σ, Σ, { ((f,,ε),
Relaciones de equivalencia
 Relciones de equivlenci. Un relción de equivlenci en un conjunto X se puede interpretr como el suconjunto de X X ddo por (, ) X X }. Enúnciesen ls propieddes de l relción de equivlenci en términos de dicho
Relciones de equivlenci. Un relción de equivlenci en un conjunto X se puede interpretr como el suconjunto de X X ddo por (, ) X X }. Enúnciesen ls propieddes de l relción de equivlenci en términos de dicho
2. Cálculo de primitivas
 5. Cálculo de primitivs Definición. Se dice que un función F () es un primitiv de otr función f() sobre un intervlo (, b) si pr todo de (, b) se tiene que F () f(). Por ejemplo, l función F () es un primitiv
5. Cálculo de primitivs Definición. Se dice que un función F () es un primitiv de otr función f() sobre un intervlo (, b) si pr todo de (, b) se tiene que F () f(). Por ejemplo, l función F () es un primitiv
Máximo común divisor. 2. Descomposición en primos Ejemplo. Encontrar mcd 504,300 Se descomponen ambos números en primos 504 2 252 2 126 2 63 3 21 3
 Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Autómatas sobre palabras infinitas
 Autómts sobre plbrs infinits Mrcelo Arens M. Arens Autómts sobre plbrs infinits 1 / 46 Teorí de utómts sobre plbrs infinits Los utómts sobre plbrs infinits son un herrmient fundmentl pr l verificción forml.
Autómts sobre plbrs infinits Mrcelo Arens M. Arens Autómts sobre plbrs infinits 1 / 46 Teorí de utómts sobre plbrs infinits Los utómts sobre plbrs infinits son un herrmient fundmentl pr l verificción forml.
INGENIERÍA TÉCNICA EN INFORMÁTICA DE SISTEMAS
 UNIVERSIDAD DE CÓRDOBA ESCUELA POLITÉCNICA SUPERIOR DEPARTAMENTO DE INFORMÁTICA Y ANÁLISIS NUMÉRICO INGENIERÍA TÉCNICA EN INFORMÁTICA DE SISTEMAS SEGUNDO CURSO, SEGUNDO CUATRIMESTRE TEORÍA DE AUTÓMATAS
UNIVERSIDAD DE CÓRDOBA ESCUELA POLITÉCNICA SUPERIOR DEPARTAMENTO DE INFORMÁTICA Y ANÁLISIS NUMÉRICO INGENIERÍA TÉCNICA EN INFORMÁTICA DE SISTEMAS SEGUNDO CURSO, SEGUNDO CUATRIMESTRE TEORÍA DE AUTÓMATAS
3.- Matrices y determinantes.
 3.- Mtrices y determinntes. 3.. Definición de mtriz, notción y orden. Se define un mtriz de orden m x n, un reunión de m x n elementos colocdos en m fils y n columns. Cd elemento que form l mtriz se denot
3.- Mtrices y determinntes. 3.. Definición de mtriz, notción y orden. Se define un mtriz de orden m x n, un reunión de m x n elementos colocdos en m fils y n columns. Cd elemento que form l mtriz se denot
Universidad de Valladolid
 Universidd de Vlldolid Deprtmento de Informátic Teorí de utómts y lengujes formles. 2 o I.T.Informátic. Gestión. Exmen de segund convoctori, 5 de septiemre de 2007 Apellidos, Nomre... Grupo:... Firm: 1
Universidd de Vlldolid Deprtmento de Informátic Teorí de utómts y lengujes formles. 2 o I.T.Informátic. Gestión. Exmen de segund convoctori, 5 de septiemre de 2007 Apellidos, Nomre... Grupo:... Firm: 1
Estructuras Algebraicas. UCR ECCI CI-1204 Matemática Discretas Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 UCR ECCI CI-204 Mtemátic Discrets Prof. M.Sc. Krysci Dvin Rmírez Benvides Se E un conjunto no vcío, un función f f : E E E se llm ley de composición intern (operción) sobre E. Además, l imgen f(,b) se
UCR ECCI CI-204 Mtemátic Discrets Prof. M.Sc. Krysci Dvin Rmírez Benvides Se E un conjunto no vcío, un función f f : E E E se llm ley de composición intern (operción) sobre E. Además, l imgen f(,b) se
INTEGRALES IMPROPIAS
 NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES IMPROPIAS Ing. Jun Scerdoti Deprtmento de Mtemátic Fcultd de Ingenierí Universidd de Buenos Aires V INDICE INTEGRALES IMPROPIAS.- PUNTOS SINGULARES
NOTAS PARA LOS ALUMNOS DE ANALISIS MATEMATICO III INTEGRALES IMPROPIAS Ing. Jun Scerdoti Deprtmento de Mtemátic Fcultd de Ingenierí Universidd de Buenos Aires V INDICE INTEGRALES IMPROPIAS.- PUNTOS SINGULARES
Bases Formales de la Computación
 Gerrdo M. Srri M. Bses Formles de l Computción Gerrdo M. Srri M. Pontifici Universidd Jverin 4 de octure de 2008 Gerrdo M. Srri M. RELACIONES DE SIMULACIÓN El Prolem con l Teorí de Autómts Clásic Gerrdo
Gerrdo M. Srri M. Bses Formles de l Computción Gerrdo M. Srri M. Pontifici Universidd Jverin 4 de octure de 2008 Gerrdo M. Srri M. RELACIONES DE SIMULACIÓN El Prolem con l Teorí de Autómts Clásic Gerrdo
Exámenes de Teoría de Autómatas y Lenguajes Formales. David Castro Esteban
 Exámenes de Teorí de Autómts y Lengujes Formles Dvid Cstro Esten Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Ferero 24 Prolem (2 ptos.) Otener expresiones regulres pr
Exámenes de Teorí de Autómts y Lengujes Formles Dvid Cstro Esten Teorí de Autómts y Lengujes Formles Ingenierí Técnic en Informátic de Sistems Ferero 24 Prolem (2 ptos.) Otener expresiones regulres pr
Resolver inecuaciones como las siguientes. Expresar la solución en forma gráfica y algebraica. Comparar las soluciones de los ejercicios e), f) y g).
 64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
Introducción a la integración numérica
 Tem 7 Introducción l integrción numéric Versión: 13 de ril de 009 7.1 Motivción L integrl definid de un función continu f : [, ] R R en el intervlo [, ], If) = fx) dx 7.1) es el áre de l región del plno
Tem 7 Introducción l integrción numéric Versión: 13 de ril de 009 7.1 Motivción L integrl definid de un función continu f : [, ] R R en el intervlo [, ], If) = fx) dx 7.1) es el áre de l región del plno
DIAPOSITIVAS AUTÓMATAS CON TRANSICIONES ÉPSILON (EJERCICIOS) UNIDAD DE APRENDIZAJE: AUTÓMATAS Y LENGUAJES FORMALES
 DIAPOSITIVAS AUTÓMATAS CON TRANSICIONES ÉPSILON (EJERCICIOS) UNIDAD DE APRENDIZAJE: AUTÓMATAS Y LENGUAJES FORMALES PROGRAMA EDUCATIVO: INGENIERÍA EN COMPUTACIÓN ESPACIO ACADÉMICO: FACULTAD DE INGENIERÍA
DIAPOSITIVAS AUTÓMATAS CON TRANSICIONES ÉPSILON (EJERCICIOS) UNIDAD DE APRENDIZAJE: AUTÓMATAS Y LENGUAJES FORMALES PROGRAMA EDUCATIVO: INGENIERÍA EN COMPUTACIÓN ESPACIO ACADÉMICO: FACULTAD DE INGENIERÍA
Teoría de Lenguajes. Transductores y Máquinas Secuenciales Generalizadas
 Teorí de Lengujes Trnsductores y Máquins Secuenciles Generlizds José M. Sempere Deprtmento de Sistems Informáticos y Computción Universidd Politécnic de Vlenci Trnsductores 1. Preliminres lgericos 2. Relciones
Teorí de Lengujes Trnsductores y Máquins Secuenciles Generlizds José M. Sempere Deprtmento de Sistems Informáticos y Computción Universidd Politécnic de Vlenci Trnsductores 1. Preliminres lgericos 2. Relciones
Funciones de una variable real II Integrales impropias
 Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Aprendizaje de lenguajes incontextuales (II) Autómatas de árboles y gramáticas incontextuales
 prendizje de lengujes incontextules (II) utómts de ároles y grmátics incontextules José M. Sempere Deprtmento de Sistems Informáticos y omputción Universidd Politécnic de Vlenci onceptos ásicos de los
prendizje de lengujes incontextules (II) utómts de ároles y grmátics incontextules José M. Sempere Deprtmento de Sistems Informáticos y omputción Universidd Politécnic de Vlenci onceptos ásicos de los
Estructuras algebraicas. Departamento de Álgebra. Apuntes de teoría
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teorí Autor: Jun González-Meneses. Revisión: Jvier Herrer y José Mrí Uch Tem 3: Anillos. Recordemos que un nillo es un tern (A,
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teorí Autor: Jun González-Meneses. Revisión: Jvier Herrer y José Mrí Uch Tem 3: Anillos. Recordemos que un nillo es un tern (A,
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I
 INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 22 de Junio de 2009 SOLUCIONES 1. (0,5 puntos) Sobre el lfbeto {,b}, d expresiones regulres que denoten los siguientes lengujes: ) El lenguje formdo
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 22 de Junio de 2009 SOLUCIONES 1. (0,5 puntos) Sobre el lfbeto {,b}, d expresiones regulres que denoten los siguientes lengujes: ) El lenguje formdo
Autómatas Finitos. Programación II Margarita Álvarez 0,1 0,1. q 3
 Autómts Finitos 0,1 0,1 q 0 0 q 1 0 q 2 1 q 3 1 Progrmción II Mrgrit Álvrez Autómts Dispositivo mecánico cpz símolos. de procesr cdens de Ddo un lenguje L definido sore un lfeto A y un cden x ritrri, determin
Autómts Finitos 0,1 0,1 q 0 0 q 1 0 q 2 1 q 3 1 Progrmción II Mrgrit Álvrez Autómts Dispositivo mecánico cpz símolos. de procesr cdens de Ddo un lenguje L definido sore un lfeto A y un cden x ritrri, determin
Tema 14. Gramáticas libres del contexto (GLC o CFG) Dr. Luis A. Pineda ISBN: Definición recursiva de lenguajes
 Hy lengujes que no son regulres Tem 4 Grmátics libres del contexto (GLC o CFG) Dr. Luis A. ined ISBN: 97-32-2972-7 l = {w w = w R } {, } l no es regulr: l lem del bombeo: Se n l constnte socid Se w = n
Hy lengujes que no son regulres Tem 4 Grmátics libres del contexto (GLC o CFG) Dr. Luis A. ined ISBN: 97-32-2972-7 l = {w w = w R } {, } l no es regulr: l lem del bombeo: Se n l constnte socid Se w = n
Semánticas de procesos y aplicaciones
 Semántics de procesos y plicciones Clse 06: Puntos Fijos Qué vimos hst hor? cciones: multicciones: α 3 operdores sobre multicciones: α \ β, α β y α operdor de elección: + operdor de secuenci:. operdor
Semántics de procesos y plicciones Clse 06: Puntos Fijos Qué vimos hst hor? cciones: multicciones: α 3 operdores sobre multicciones: α \ β, α β y α operdor de elección: + operdor de secuenci:. operdor
Clase Auxiliar 5. Aútomatas Finitos Determinísticos (Diagramas de Estado)
 CC2A Computción II Auxilir 5 Iván Bustmnte Clse Auxilir 5 Aútomts Finitos Determinísticos (Digrms de Estdo) Un utómt finito determinístico es un modelo de un sistem que tiene un cntidd finit de estdos
CC2A Computción II Auxilir 5 Iván Bustmnte Clse Auxilir 5 Aútomts Finitos Determinísticos (Digrms de Estdo) Un utómt finito determinístico es un modelo de un sistem que tiene un cntidd finit de estdos
Examen Parcial de Autómatas y Lenguajes Formales 12 de diciembre de 2003
 Exmen Prcil de Autómts y Lengujes Formles 2 de diciemre de 23 Resolver los siguientes prolems. Tiempo 2 hors.. Dr un grmátic y demostrr que es correct pr L = { m n 2m < n < 3m}. 2. Dr un utómt de pil determinist
Exmen Prcil de Autómts y Lengujes Formles 2 de diciemre de 23 Resolver los siguientes prolems. Tiempo 2 hors.. Dr un grmátic y demostrr que es correct pr L = { m n 2m < n < 3m}. 2. Dr un utómt de pil determinist
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Formalización de los Números Reales. M. en I. Gerardo Avilés Rosas
 Formlizción de los Números Reles M. en I. Gerrdo Avilés Ross Agosto de 016 Tem Formlizción de los Números Reles Objetivo: El lumno plicrá ls propieddes de los números reles y sus subconjuntos, pr demostrr
Formlizción de los Números Reles M. en I. Gerrdo Avilés Ross Agosto de 016 Tem Formlizción de los Números Reles Objetivo: El lumno plicrá ls propieddes de los números reles y sus subconjuntos, pr demostrr
3. Expresa los siguientes radicales mediante potencias de exponente fraccionario y simplifica: 625 d) 0, 25 e) c) ( ) 4 8
 POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
POTENCIAS. Hll sin clculdor +.. Simplific utilizndo ls propieddes de ls potencis: b c ) 0 b c. Epres los siguientes rdicles medinte potencis de eponente frccionrio y simplific: ). Resuelve sin utilizr
2 Números racionales positivos
 Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
Progrm Inmersión, Verno 0 Nots escrits por Dr. M Nots del cursos. Bsds en los pronturios de MATE 00 y MATE 0 Clse #: miércoles, de junio de 0. Números rcionles positivos. Consceptos básicos del conjunto
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Integral Definida. Tema 6. 6.1 Introducción. 6.2 Definición de Integral Definida
 Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Además de las operaciones tradicionales, es posible expresar otras operaciones binarias. Tabla 1.1. Operación AND.
 Grupos y Cmpos Definición de operción inri Operciones como l sum, rest, multiplicción o división de números son considerds operciones inris, y que socin un pr de números con un resultdo. En generl, un
Grupos y Cmpos Definición de operción inri Operciones como l sum, rest, multiplicción o división de números son considerds operciones inris, y que socin un pr de números con un resultdo. En generl, un
NÚMEROS COMPLEJOS. Números reales Intervalos El conjunto R 2 Discos Números complejos Teorema fundamental del Álgebra
 NÚMEROS COMPLEJOS Números reles Intervlos El conjunto R 2 Discos Números complejos Teorem fundmentl del Álgebr NÚMEROS REALES Números nturles, enteros rcionles e irrcionles En mtemátics son importntes
NÚMEROS COMPLEJOS Números reles Intervlos El conjunto R 2 Discos Números complejos Teorem fundmentl del Álgebr NÚMEROS REALES Números nturles, enteros rcionles e irrcionles En mtemátics son importntes
Construcción de Vardi & Wolper: Paso final
 Construcción de Vrdi & Wolper: Pso finl Pr simplificr el proceso de construcción, usmos un generlizción de los utómts de Büchi: Definición A = (Q,Σ,Q 0,δ, G) es un utómt de Büchi generlizdo sore Σ si:
Construcción de Vrdi & Wolper: Pso finl Pr simplificr el proceso de construcción, usmos un generlizción de los utómts de Büchi: Definición A = (Q,Σ,Q 0,δ, G) es un utómt de Büchi generlizdo sore Σ si:
Integrales Impropias. Capítulo Introducción Integrales de Funciones No Acotadas
 Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
TEMA 1. VECTORES Y MATRICES 1.3. TRAZA Y DETERMINANTE DE UNA MATRIZ
 TEM. VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ . VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ... Concepto de Trz.... Propieddes de l trz.... Determinnte de un mtriz.... Cálculo de determinntes
TEM. VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ . VECTORES Y MTRICES.. TRZ Y DETERMINNTE DE UN MTRIZ... Concepto de Trz.... Propieddes de l trz.... Determinnte de un mtriz.... Cálculo de determinntes
Tema 8.4: Teorema de Runge. Aproximación de funciones holomorfas por funciones racionales
 Tem 8.4: Teorem de Runge. Aproximción de funciones holomorfs por funciones rcionles Fcultd de Ciencis Experimentles, Curso 2008-09 Enrique de Amo, Universidd de Almerí Sbemos que ls funciones holomorfs
Tem 8.4: Teorem de Runge. Aproximción de funciones holomorfs por funciones rcionles Fcultd de Ciencis Experimentles, Curso 2008-09 Enrique de Amo, Universidd de Almerí Sbemos que ls funciones holomorfs
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
MATRICES Y DETERMINANTES
 MATRICES Y DETERMINANTES ) Resolver el siguiente sistem de ecuciones lineles t t z emplendo el método de Guss utilizndo trnsformciones elementles de fils En qué csos es comptible? b) Relcionr ls mtrices
MATRICES Y DETERMINANTES ) Resolver el siguiente sistem de ecuciones lineles t t z emplendo el método de Guss utilizndo trnsformciones elementles de fils En qué csos es comptible? b) Relcionr ls mtrices
Capitulo II. Números Reales
 Cpitulo II. Números Reles Ojetivo. El lumno plicrá ls propieddes de los números reles y sus suconjuntos, pr demostrr lguns proposiciones por medio del método de inducción mtemátic y pr resolver inecuciones.
Cpitulo II. Números Reles Ojetivo. El lumno plicrá ls propieddes de los números reles y sus suconjuntos, pr demostrr lguns proposiciones por medio del método de inducción mtemátic y pr resolver inecuciones.
MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES.
 MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES 1 Mtrices 11 Definición Se K un cuerpo y n, m N Un mtriz n m sobre K es un plicción: A : {1,,n} {1,,m} K Si (i, j) {1,,n} {1,,m} denotremos ij
MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES 1 Mtrices 11 Definición Se K un cuerpo y n, m N Un mtriz n m sobre K es un plicción: A : {1,,n} {1,,m} K Si (i, j) {1,,n} {1,,m} denotremos ij
Tema 22. El lema de bombeo para LR
 Tem 22 Lem de omeo pr LLC Dr. Luis A. Pined IBN: 970-32-2972-7 Cómo podemos decir si un lenguje es lire del contexto? Definir un GLC o diseñr un AP pr el lenguje Pero que tl si el lenguje se descrie por
Tem 22 Lem de omeo pr LLC Dr. Luis A. Pined IBN: 970-32-2972-7 Cómo podemos decir si un lenguje es lire del contexto? Definir un GLC o diseñr un AP pr el lenguje Pero que tl si el lenguje se descrie por
Integral impropia Al definir la integral definida b
 Mte Univ II, 14 FCE-BUAP CÁLCULO INTEGRAL ALEJANDRO RAMÍREZ PÁRAMO 1. Sucesiones y series Integrl impropi Al definir l integrl definid b f(x)dx, pretendimos que l función f estb definid; demás de cotd,
Mte Univ II, 14 FCE-BUAP CÁLCULO INTEGRAL ALEJANDRO RAMÍREZ PÁRAMO 1. Sucesiones y series Integrl impropi Al definir l integrl definid b f(x)dx, pretendimos que l función f estb definid; demás de cotd,
GRAMATICAS REGULARES - EXPRESIONES REGULARES
 CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
CIENCIAS DE LA COMPUTACION I 29 GRAMATICAS REGULARES - EXPRESIONES REGULARES Grmátis Ls grmátis formles definen un lenguje desriiendo ómo se pueden generr ls dens del lenguje. Un grmáti forml es un udrupl
Laboratorio N 7, Asíntotas de funciones.
 Universidd Diego Portles Fcultd de Ingenierí. Instituto de Ciencis Básics Asigntur: Cálculo I Lortorio N 7, Asíntots de funciones. Introducción. Ls síntots de un función son rects que seprn ls regiones
Universidd Diego Portles Fcultd de Ingenierí. Instituto de Ciencis Básics Asigntur: Cálculo I Lortorio N 7, Asíntots de funciones. Introducción. Ls síntots de un función son rects que seprn ls regiones
Tema 3: Sistemas de ecuaciones lineales
 Tem 3: Sistems de ecuciones lineles 1. Introducción Los sistems de ecuciones resuelven problems relciondos con situciones de l vid cotidin, que tiene que ver con ls Ciencis Sociles. Nos centrremos, por
Tem 3: Sistems de ecuciones lineles 1. Introducción Los sistems de ecuciones resuelven problems relciondos con situciones de l vid cotidin, que tiene que ver con ls Ciencis Sociles. Nos centrremos, por
Introducción a la lógica epistémica
 Introducción l lógic epistémic Fernndo Soler Toscno Universidd de Sevill ¾Qué es l lógic epistémic? Sistem forml pr rzonr sore el conocimiento y l creenci Podemos modelr el conocimiento de uno o vrios
Introducción l lógic epistémic Fernndo Soler Toscno Universidd de Sevill ¾Qué es l lógic epistémic? Sistem forml pr rzonr sore el conocimiento y l creenci Podemos modelr el conocimiento de uno o vrios
EXPONENTES. se abrevia n k, es decir que. Por ejemplo, para no escribir , se abrevia 3 6, que visto a la inversa 4 5 significa
 págin 1 págin 16 EXPONENTES L ide de los exponentes nce con l necesidd de revir cierts multiplicciones. Como es sido, cundo se multiplic un cntidd n por sí mism k veces, o se n nn... n k veces se revi
págin 1 págin 16 EXPONENTES L ide de los exponentes nce con l necesidd de revir cierts multiplicciones. Como es sido, cundo se multiplic un cntidd n por sí mism k veces, o se n nn... n k veces se revi
UNIDAD N 3: EXPRESIONES ALGEBRAICAS POLINOMIOS
 Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Mtemátic Unidd - UNIDAD N : EXPRESIONES ALGEBRAICAS POLINOMIOS ÍNDICE GENERAL DE LA UNIDAD Epresiones Algebrics Enters...... Polinomios..... Actividdes... 4 Vlor Numérico del polinomio........ 4 Concepto
Z := Z {0} a partir de este nuevo conjunto construimos el producto cartesiano
 Cpítulo 4 Números Rcionles. Luego de construir los Números Nturles, se presentron ciertos problems como Cuál es el resultdo de 3 menos 5?, pr poder encontrr un solución se creó prtir de N el conjunto de
Cpítulo 4 Números Rcionles. Luego de construir los Números Nturles, se presentron ciertos problems como Cuál es el resultdo de 3 menos 5?, pr poder encontrr un solución se creó prtir de N el conjunto de
LOS CONJUNTOS NUMÉRICOS
 Pontifici Universidd Ctólic de Chile Fcultd de Educción Nivelción de Estudios pr Adultos CREA Educción Mtemátic Nivel 2 Profesor Jun Núñez Fernández LOS CONJUNTOS NUMÉRICOS Como se mencionó en l clse nterior,
Pontifici Universidd Ctólic de Chile Fcultd de Educción Nivelción de Estudios pr Adultos CREA Educción Mtemátic Nivel 2 Profesor Jun Núñez Fernández LOS CONJUNTOS NUMÉRICOS Como se mencionó en l clse nterior,
En este tema supondremos al lector familiarizado con las técnicas más elementales de formas bilineales y cuadráticas sobre un espacio vectorial.
 Cpítulo 4 El espcio euclídeo 4.1 Introducción En este tem supondremos l lector fmilirizdo con ls técnics más elementles de forms bilineles y cudrátics sobre un espcio vectoril. Definición 4.1.1. Un espcio
Cpítulo 4 El espcio euclídeo 4.1 Introducción En este tem supondremos l lector fmilirizdo con ls técnics más elementles de forms bilineles y cudrátics sobre un espcio vectoril. Definición 4.1.1. Un espcio
Héctor Palma Valenzuela. Dpto. de Matemática UdeC Definición e interpretación geométrica
 Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. L Integrl.-. Definición e interpretción geométric Dd un función continu f :[, b] R ynonegtiv (f (), [, b]), vmos considerr l región del plno bjo l gráfic de
Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. L Integrl.-. Definición e interpretción geométric Dd un función continu f :[, b] R ynonegtiv (f (), [, b]), vmos considerr l región del plno bjo l gráfic de
I Resolución de sistemas de ecuaciones lineales
 ESCUELA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA FUNDAMENTOS MATEMÁTICOS I Resolución de sistems de ecuciones lineles Objetivo: El lumno deberá tener
ESCUELA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA FUNDAMENTOS MATEMÁTICOS I Resolución de sistems de ecuciones lineles Objetivo: El lumno deberá tener
Operación Matemática Conceptos y definiciones básicas Operaciones binarias
 ... onceptos y definiciones ásics... onjunto Llmremos conjunto, o clse culquier colección de ojetos llmdos elementos. Si es un elemento que pertenece l conjunto, se denot por. Si x no pertenece l conjunto,
... onceptos y definiciones ásics... onjunto Llmremos conjunto, o clse culquier colección de ojetos llmdos elementos. Si es un elemento que pertenece l conjunto, se denot por. Si x no pertenece l conjunto,
Fórmulas de cuadratura.
 PROYECTO DE ANALISIS MATEMATICO I : Integrción numéric. Ojetivos: Aprender los métodos más sencillos de integrción númeric y plicrlos en diversos prolems. Fórmuls de cudrtur. Se (x un unción continu deinid
PROYECTO DE ANALISIS MATEMATICO I : Integrción numéric. Ojetivos: Aprender los métodos más sencillos de integrción númeric y plicrlos en diversos prolems. Fórmuls de cudrtur. Se (x un unción continu deinid
Los números reales. 1.4 Orden de los números reales CAPÍTULO
 1 CAPÍTULO 1 Los números reles 1 1.4 Orden de los números reles Un número que pertenezc los reles. 2 R / es positivo si está l derech del cero; esto se denot sí: > 0 o bien 0 < : 0 Un número que pertenezc
1 CAPÍTULO 1 Los números reles 1 1.4 Orden de los números reles Un número que pertenezc los reles. 2 R / es positivo si está l derech del cero; esto se denot sí: > 0 o bien 0 < : 0 Un número que pertenezc
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
