Operaciones con matrices
|
|
|
- María Victoria Estefania Juárez Lozano
- hace 7 años
- Vistas:
Transcripción
1 Operaciones con matrices Problemas teóricos En todos los problemas de esta lista se supone que F es un campo (cuerpo). Si no conoce bien el concepto de campo, entonces puede pensar que F = R. Operaciones lineales en F n 1. Definición de las operaciones lineales en F n. Escriba la definición de a + b y λa, donde a, b F n y λ F. 2. Definición de la tupla nula 0 n F n. Escriba la definición de 0 n. 3. Definición de la tupla a. Escriba la definición de a, donde a F n. Basta con resolver 3 de los siguientes 8 problemas, por ejemplo 4, 8 y Sean a, b, c F n. Demuestre que (a + b) + c = a + (b + c). 5. Sea a F n. Demuestre que 6. Sea a F n. Demuestre que 7. Sean a, b F n. Demuestre que a + 0 n = a. a + ( a) = 0 n. a + b = b + a. 8. Sean a, b F n y sea λ F. Demuestre que λ(a + b) = λa + λb. 9. Sea a F n y sean λ, µ F. Demuestre que (λ + µ)a = λa + µa. 10. Sea a F n y sean λ, µ F. Demuestre que λ(µa) = (λµ)a. 11. Sea a F n. Demuestre que 1a = a. Operaciones con matrices, problemas teóricos, página 1 de 18
2 Delta de Kronecker y vectores básicos en F n 12. Definición de la delta de Kronecker. Escriba la definición de δ i,j, donde i, j Z. 13. Propiedad principal de la delta de Kronecker. Simplifique la suma: n δ k,j a k. k=1 Considere dos casos: 1) j {1,..., n} y 2) j / {1,..., n}. Notación: vectores básicos en F n. Sea n un número fijo y sea p {1,..., n}. Denotemos por e p al vector del espacio F n cuya p-ésima componente es 1 y todas las demás son 0. Los vectores e 1,..., e n se llaman también los vectores de la base canónica de F n. Luego vamos a comprender el sentido de estas palabras. 14. Fórmula para las componentes de los vectores e 1,..., e p. Sea p, j {1,..., n}. Escriba una fórmula para la j-ésima componente de e p en términos de la delta de Kronecker: (e p ) j =? 15. Combinación lineal de vectores básicos en F n. Denotamos por e 1,..., e n a los vectores básicos en F n. Sean λ 1,..., λ n F. Calcule la suma: n λ p e p. p=1 16. Producto de una matriz por un vector básico. Sea n un número fijo y sea p {1,..., n}. Denotemos por e p al vector del espacio F n cuya p-ésima componente es 1 y todas las demás son 0. Considere el producto de una matriz arbitraria A M m,n (F) por el vector e p. Enuncie y demuestre la fórmula. Operaciones con matrices, problemas teóricos, página 2 de 18
3 Operaciones lineales con matrices 17. Definición de las operaciones lineales en M m,n (F). Escriba la definición de A + B y λa, donde A, B M m,n (F) y λ F. 18. Definición de la matriz nula 0 m,n. Escriba la definición de 0 m,n. 19. Definición de la matriz A. Escriba la definición de A, donde A M m,n (F). Basta con resolver 3 de los siguientes 8 problemas. Se recomienda demostrar propiedades distintas de las demostradas para F n. 20. Sean A, B, C M m,n (F). Demuestre que (A + B) + C = A + (B + C). 21. Sea A M m,n (F). Demuestre que A + 0 m,n = A. 22. Sea A M m,n (F). Demuestre que A + ( A) = 0 m,n. 23. Sean A, B M m,n (F). Demuestre que A + B = B + A. 24. Sean A, B M m,n (F) y sea λ F. Demuestre que λ(a + B) = λa + λb. 25. Sea A M m,n (F) y sean λ, µ F. Demuestre que (λ + µ)a = λa + µa. 26. Sea A M m,n (F) y sean λ, µ F. Demuestre que λ(µa) = (λµ)a. 27. Sea A M m,n (F). Demuestre que 1A = A. Operaciones con matrices, problemas teóricos, página 3 de 18
4 Multiplicación de matrices: definición y propiedades 28. Definición del producto de matrices. Escriba la definición de AB, donde A M m,n (F) y B M n,p (F). 29. Teorema: la multiplicación de matrices es distributiva por la izquierda respecto la adición. Sean A M m,n (F) y B, C M n,p (F). Demuestre que A(B + C) = AB + AC. 30. Teorema: la multiplicación de matrices es distributiva por la derecha respecto la adición. Sean A, B M m,n (F) y C M n,p (F). Demuestre que (A + B)C = AC + BC. 31. Teorema: la multiplicación de matrices es asociativa. Sean A M m,n (F), B M n,p (F) y C M p,q (F). Demuestre que (AB)C = A(BC). 32. Propiedad homogénea izquierda. Sean A M m,n (F), B M n,p (F) y λ F. Demuestre que (λa)b = λ(ab). 33. Propiedad homogénea derecha. Sean A M m,n (F), B M n,p (F) y λ F. Demuestre que A(λB) = λ(ab). Operaciones con matrices, problemas teóricos, página 4 de 18
5 Multiplicación de matrices por vectores 34. Definición del producto de una matriz por un vector. Escriba la definición de Ax, donde A M m,n (F) y x F n. 35. Sea A M m,n (F) y sea x F n. Escriba el producto Ax como una combinación lineal de las columnas de la matriz A. 36. Sea A M m,n (F) y sean x, y F n. Demuestre que A(x + y) = Ax + Ay. 37. Sea A M m,n (F), sea x F n y sea λ F. Demuestre que A(λx) = λax. Operaciones con matrices, problemas teóricos, página 5 de 18
6 Renglones y columnas del producto de matrices Notación para renglones y columnas de matrices. Sea A M m,n (F). Para todo i {1,..., m} denotamos por A i, al i-ésimo renglón de A: A i, := [ A i,j ] n j=1. Para todo j {1,..., n} denotamos por A,j a la j-ésima columna de A: A,j := [ A i,j ] m i= Sea A M m,n (F) y sea B M n,p (F). Demuestre la siguiente fórmula para el i-ésimo renglón del producto AB: (AB) i, = A i, B. 39. Sea A M m,n (F) y sea B M n,p (F). Demuestre la siguiente fórmula para la j-ésima columna del producto AB: (AB),j = AB,j. Matriz identidad 40. Definición de la matriz identidad. Escriba la definición de I n usando la delta de Kronecker. 41. Teorema: la propiedad principal de la matriz identidad. Usando la delta de Kronecker demuestre que para toda A M m,n (F) I m A = A, AI n = A. Operaciones con matrices, problemas teóricos, página 6 de 18
7 Matrices básicas Notación (matrices básicas). Sea n {1, 2,...} un número fijo. Para todos p, q {1,..., n} definamos la matriz E p,q mediante la siguiente regla: E p,q = [ δ i,p δ j,q ] n i,j= Para n = 3 escriba las matrices E 1,3, E 2,2 y E 3, Ejemplos de productos por matrices básicas. Sea A M 3,2 (F) una matriz con entradas generales: [ ] A1,1 A A = 1,2 A 1,3. A 2,1 A 2,2 A 2,3 Calcule los productos AE 2,1, AE 2,2, E 2,2 A y E 1,3 A. 44. Tabla de multiplicación de las matrices básicas de tamaño 2 2. Calcule todos los productos E p,q E r,s, donde p, q, r, s {1, 2}, y llene la siguiente tabla de multiplicación. En la entrada ubicada en la intersección del renglón E p,q y columna E r,s se escribe el producto E p,q E r,s : E 1,1 E 1,2 E 2,1 E 2,2 E 1,1 E 1,2 E 2,1 E 2,2 45. Matrices escalares conmutan con todas las matrices. Sea λ F y sea X = λi n. Se dice que X es una matriz escalar. Demuestre que X conmuta con cualquier matriz Y perteneciente a M n (F): Y M n (F) XY = Y X. Operaciones con matrices, problemas teóricos, página 7 de 18
8 Propiedades raras de la multiplicación de matrices 46. Construya un ejemplo de matrices A, B M 2 (R) tales que AB BA. 47. Construya un ejemplo de matrices A, B M 2 (R) tales que A 0 2,2, B 0 2,2, AB = 0 2, Construya un ejemplo de una matriz A M 2 (R) tal que A 0 2,2, A 2 = 0 2, Construya un ejemplo de una matriz A M 3 (R) tal que A 0 3,3, A 2 0 3,3, A 3 = 0 3, Construya un ejemplo de matrices A, B, C M 2 (R) tales que A B, C 0 2,2, AC = BC. Operaciones con matrices, problemas teóricos, página 8 de 18
9 Matriz transpuesta 51. Definición de la matriz transpuesta de una matriz. Escriba la definición de A, donde A M m,n (F). 52. La matriz transpuesta de la matriz transpuesta. Sea A M m,n (F). Demuestre que ( A ) = A. 53. La matriz transpuesta de la suma de dos matrices. Sean A, B M m,n (F). Demuestre que (A + B) = A + B. 54. La matriz transpuesta del producto por escalar. Sea A M m,n (F) y sea λ F. Demuestre que (λa) = λa. 55. Teorema: la matriz transpuesta del producto de matrices. Sea A M m,n (F) y sea B M n,p (F). Demuestre que (AB) = B A. 56. La matriz transpuesta de la matriz identidad. Demuestre que (I n ) = I n. Operaciones con matrices, problemas teóricos, página 9 de 18
10 Matrices simétricas y antisimétricas En estos problemas ponemos F = R. 57. Criterio de la matriz simétrica. Sea A M n (R). Demuestre que las siguientes propiedades son equivalentes: (a) A = A. (b) Para todos i, j {1,..., n} se cumple la igualdad A j,i = A i,j. Cualquiera de las dos condiciones (a) y (b) se puede elegir como la definición de matriz simétrica. 58. Criterio de la matriz antisimétrica. Sea A M n (R). Demuestre que las siguientes propiedades son equivalentes: (a) A = A. (b) Para todos i, j {1,..., n} se cumple la igualdad A j,i = A i,j. Cualquiera de las dos condiciones (a) y (b) se puede elegir como la definición de matriz antisimétrica. Campos de característica 2. Se dice que F es un campo de característica 2 si en este campo = 0. Por ejemplo el campo F 2 = {0, 1} es un campo de característica 2, y los campos Q, R, C no son de característica 2. En los campos de característica 2 es imposible la división entre 2 porque en estos campos 2 coincide con Ejemplo de una matriz no nula simétrica y antisimétrica, sobre F 2. Las definiciones de matrices simétricas y antisimétricas se puede escribir para cualquier campo, pero sobre campos de característica 2 una matriz puede ser simétrica, antisimétrica y no nula al mismo tiempo. Construya un ejemplo de matriz A M n (F 2 ) que sea simétrica, antisimétrica y no nula. 60. Entradas diagonales de una matriz antisimétrica son nulas. Sea A M n (R) tal que A = A. Demuestre que A i,i = 0 para todo i {1,..., n}. Operaciones con matrices, problemas teóricos, página 10 de 18
11 61. Si una matriz compleja es simétrica y antisimétrica, entonces es nula. Sea A M n (R) una matriz simétrica y al mismo tiempo antisimétrica. Demuestre que A = 0 n,n. 62. Número máximo de entradas diferentes de una matriz simétrica. Cuántas entradas diferentes puede tener una matriz real simétrica de orden n?. 63. Número máximo de entradas diferentes no nulas de una matriz antisimétrica. Cuántas entradas diferentes y no nulas puede tener una matriz real antisimétrica de orden n?. 64. Descomposición de una matriz cuadrada en una suma de una matriz simétrica y una matriz antisimétrica. Demuestre que para toda matriz A M n (R) existe un único par de matrices B, C M n (R) tales que B es simétrica, C es antisimétrica y A = B + C. 65. Suma y producto por escalar de matrices simétricas. Demuestre que la suma y el producto por escalar de matrices simétricas son matrices simétricas. Sugerencia: use las propiedades de la matriz transpuesta. 66. Suma y producto por escalar de matrices antisimétricas. Demuestre que la suma y el producto por escalar de matrices antisimétricas son matrices antisimétricas. En los siguientes dos problemas se propone hacer una pequeña investigación y determinar si se cumple una propiedad o no. Se recomienda empezar con ejemplos en M 2 (R). 67. Producto de matrices simétricas. Determine si el producto AB siempre es una matriz simétrica para cualesquiera matrices simétricas A, B M n (R) o no. 68. Producto de matrices antisimétricas. Determine si el producto AB siempre es una matriz antisimétrica para cualesquiera matrices antisimétricas A, B M n (R) o no. Operaciones con matrices, problemas teóricos, página 11 de 18
12 La traza de una matriz cuadrada 69. Definición de la traza de una matriz cuadrada. Escriba la definición de tr(a), donde A M n (F). 70. La traza de una matriz diagonal. Calcule tr(a), donde A es la matriz diagonal cuadrada n n con entradas diagonales d 1,..., d n : A = diag(d 1,..., d n ). 71. La traza de la matriz identidad. Calcule tr(i n ). 72. La traza de la suma de dos matrices. Sean A, B M n (F). Demuestre que tr(a + B) = tr(a) + tr(b). 73. La traza del producto de una matriz por un escalar. Sea A M n (F) y sea λ F. Demuestre que tr(λa) = λ tr(a). 74. La traza de la matriz transpuesta. Sea A M n (F). Demuestre que tr(a ) = tr(a). 75. Teorema: la traza del producto no depende del orden de los factores. Sea A M m,n (F) y sea B M n,m (F). Demuestre que tr(ab) = tr(ba). 76. El conmutador de dos matrices no puede ser igual a la matriz identidad. Sean A, B M n (F). La matriz AB BA se llama conmutador de A y B. Muestre que AB BA I n. Operaciones con matrices, problemas teóricos, página 12 de 18
13 Invertibilidad de una matriz (definición y propiedades simples) 77. Definición de matriz inversa izquierda. Sea A M m,n (F). Cuándo se dice que B es una matriz inversa por izquierda a la matriz A?. 78. Definición de matriz inversa derecha. Sea A M m,n (F). Cuándo se dice que B es una matriz inversa por derecha a la matriz A?. 79. Definición de matriz inversa. Sea A M n (F). Cuándo se dice que B es una matriz inversa a la matriz A?. 80. Unicidad de la matriz inversa (en el caso de existencia). Sea A M n (F) y sean B, C M n (F) matrices cada una de las cuales es inversa a la matriz A. Demuestre que B = C. 81. Igualdades de las inversas izquierdas y derechas (en el caso de existencia). Sea A M n (F). Supongamos que B M n (F) es una matriz inversa por izquierda a la matriz A y C M n (F) es una matriz inversa por derecha a la matriz A. Demuestre que B = C. 82. Definición de matriz invertible. Sea A M n (F). Cuándo se dice que A es invertible?. 83. Sea β F. Usando solamente la definición de la matriz inversa demuestre que la matriz [ ] 1 λ A = 0 1 es invertible y calcule su inversa. 84. Ejemplo de una matriz no invertible. Basándose solamente en la definición demuestre que la siguiente matriz no es invertible: [ ] 1 3 A =. 2 6 Operaciones con matrices, problemas teóricos, página 13 de 18
14 85. Invertibilidad de una matriz triangular de orden 2. Usando solamente la definición de la matriz inversa demuestre que la matriz [ ] α β A = 0 γ es invertible si y sólo si α 0 y γ 0. Calcule la matriz inversa (en el caso de su existencia). 86. Toda matriz que tiene un renglón nulo no es invertible. Sea A M n (F) tal que A p, = 0 donde p {1,..., n}. Basándose en la definición de la matriz inversa demuestre que A no es invertible. 87. Toda matriz que tiene una columna nula no es invertible. Sea A M n (F) tal que A,p = 0 donde p {1,..., n}. Basándose en la definición de la matriz inversa demuestre que A no es invertible. 88. Sea A M n (F) una matriz tal que A 4 = I n. Demuestre que A es invertible y exprese A 1 a través de A. 89. Sea A M n (R) una matriz tal que A 7 = 4I n. Demuestre que A es invertible y exprese A 1 a través de A. 90. Sea A M n (F) una matriz tal que la matriz A 5 es invertible, esto es, existe una matriz B M n (F) tal que A 5 B = BA 5 = I n. Demuestre que la matriz A es invertible y exprese A 1 a través de A y B. 91. Invertibilidad de matrices diagonales. Demuestre que una matriz diagonal α A = diag(α 1, α 2, α 3 ) = 0 α α 3 es invertible si, y sólo si, todas sus entradas diagonales son distintas de cero: α 1 0, α 2 0, α 3 0. Operaciones con matrices, problemas teóricos, página 14 de 18
15 92. Inversa de la transpuesta. Sea A M n (F) una matriz invertible. Demuestre que A también es invertible y exprese ( A ) 1 a través de A 1. Indicación: hay que encontrar una matriz B tal que B A = I n y A B = I n. Escriba una fórmula para B y pruebe que se cumplen las últimas dos igualdades. 93. Inversa de una matriz simétrica. Sea A M n (F) una matriz simétrica e invertible. Demuestre que la matriz A 1 también es simétrica. 94. Invertibilidad del producto implica la invertibilidad de los factores. Sean A, B M n (F) tales que la matriz AB es invertible. Demuestre que las matrices A y B también son invertibles. Indicación: muestre que A es invertible por la derecha usando las matrices (AB) 1 y B; de manera similar muestre que A es invertible por la izquierda, B es invertible por la derecha y por la izquierda. Operaciones con matrices, problemas teóricos, página 15 de 18
16 Matrices diagonales Vamos a usar el término matriz diagonal solamente para matrices cuadradas. 95. Definición (matriz diagonal). Escriba la definición de matriz diagonal. Notación: la matriz diagonal con entradas diagonales α 1,..., α n. Sean α 1,..., α n F. Denotemos por diag(α 1,..., α n ) a la matriz diagonal de orden n con entradas diagonales α 1,..., α n. Formalmente, diag(α 1,..., α n ) := [ α i δ i,j ] n i,j= La matriz identidad es diagonal. Demuestre que la matriz I n es diagonal. 97. Toda matriz diagonal es simétrica. Sea A M n (F). Demuestre que A es simétrica. 98. Operaciones lineales con matrices diagonales. Sean A, B M n (F) matrices diagonales: Calcule A + B y λa, donde λ F. A = diag(α 1,..., α n ), B = diag(β 1,..., β n ). 99. Producto de matrices diagonales. Sean A y B matrices diagonales como en el problema anterior. Calcule su producto AB. Operaciones con matrices, problemas teóricos, página 16 de 18
17 Matrices triangulares Notación: matrices triangulares superiores, matrices triangulares inferiores. Denotemos por ut n (F) al conjunto de las matrices triangulares superiores y por lt n (F) al conjunto de las matrices triangulares inferiores: { } ut n (F) = A M n (F): i, j {1,..., n} i > j A i,j = 0 ; lt n (F) = { } A M n (F): i, j {1,..., n} i < j A i,j = Encuentre la intersección ut n (F) lt n (F). (Enuncie la respuesta y demuéstrela.) 101. Sea A M n (F). Demuestre que las siguientes condiciones son equivalentes: A ut n (F) A lt n (F) Demuestre que toda matriz A M n (F) se puede escribir como una suma U + L con U ut n (F) y L lt n (F). La descomposición L + U del problema anterior no es única. Muéstrelo con un ejemplo: 103. Construya algunas matrices U 1, U 2 ut 2 (R) y L 1, L 2 lt 2 (R) tales que U 1 U 2, L 1 L 2, U 1 + L 1 = U 2 + L 2. Operaciones con matrices triangulares superiores: 104. Suma de matrices triangulares superiores. Sean A, B ut n (F). Demuestre que A + B ut n (F) Producto de una matriz triangular superior por un escalar. Sea A ut n (F) y sea λ F. Demuestre que λa ut n (F). Enuncie y demuestre las propiedades similares de las operaciones con matrices triangulares inferiores Teorema del producto de dos matrices triangulares superiores. Sean A, B ut n (F). Demuestre que AB ut n (F). Demuestre que las entradas diagonales del producto AB son productos de las entradas correspondientes de A y B: i {1,..., n} (AB) i,i = A i,i B i,i Teorema del producto de dos matrices triangulares inferiores. Sean A, B lt n (F). Demuestre que AB lt n (F). Demuestre que las entradas diagonales del producto AB son productos de las entradas correspondientes de A y B: i {1,..., n} (AB) i,i = A i,i B i,i. Operaciones con matrices, problemas teóricos, página 17 de 18
18 Potencias naturales de una matriz cuadrada 108. Definición inductiva de las potencias naturales de una matriz cuadrada. Sea A M n (F). Escriba la definición inductiva de A p, donde p {0, 1, 2,...} Calcule A n (escriba la fórmula y demuéstrela por inducción): [ ] 1 λ A = Calcule A n (escriba la fórmula y demuéstrela por inducción): [ ] 1 0 A =. λ Calcule A n (escriba la fórmula y demuéstrela por inducción): [ ] λ 1 A =. 0 λ 112. Calcule A n (escriba la fórmula y demuéstrela por inducción): [ ] λ 0 A =. 1 λ 113. Calcule A n. La parte no trivial consiste en obtener la fórmula correcta para la (1, 3)- ésima entrada de A n. λ 1 0 A = 0 λ λ 114. Calcule AB. Usando la fórmula obtenida calcule A n. [ ] [ cos(α) sen(α) cos(β) sen(β) A =, B = sen(α) cos(α) sen(β) cos(β) ] Calcule A n, donde A = [ ]. Operaciones con matrices, problemas teóricos, página 18 de 18
Operaciones con matrices
 Operaciones con matrices Problemas para examen Operaciones lineales con vectores 1. Programación: la suma de dos vectores. Escriba una función que calcule x + y, donde x, y R n. Calcule el número de flops.
Operaciones con matrices Problemas para examen Operaciones lineales con vectores 1. Programación: la suma de dos vectores. Escriba una función que calcule x + y, donde x, y R n. Calcule el número de flops.
Teoría de Matrices. Julio Yarasca. 30 de junio de 2015. Julio Yarasca
 30 de junio de 2015 Matriz de m por n Definimeros a una matriz A de orden m por n como un arreglo de números de m filas y n columnas. a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A = a 31 a 32 a 33 a 3n....
30 de junio de 2015 Matriz de m por n Definimeros a una matriz A de orden m por n como un arreglo de números de m filas y n columnas. a 11 a 12 a 13 a 1n a 21 a 22 a 23 a 2n A = a 31 a 32 a 33 a 3n....
Métodos directos para resolver sistemas de ecuaciones lineales
 Métodos directos para resolver sistemas de ecuaciones lineales Problemas para examen Si en algún problema se pide calcular el número de flops (operaciones aritméticas con punto flotante), entonces en el
Métodos directos para resolver sistemas de ecuaciones lineales Problemas para examen Si en algún problema se pide calcular el número de flops (operaciones aritméticas con punto flotante), entonces en el
Matrices y sistemas de ecuaciones lineales
 Matrices y sistemas de ecuaciones lineales Problemas para examen Antes de resolver un problema en el caso general, se recomienda considerar casos particulares (por ejemplo, n = 4 y n = 50). En el caso
Matrices y sistemas de ecuaciones lineales Problemas para examen Antes de resolver un problema en el caso general, se recomienda considerar casos particulares (por ejemplo, n = 4 y n = 50). En el caso
Matrices triangulares y matrices ortogonales
 Matrices triangulares y matrices ortogonales Problemas para examen Matrices diagonales 1. Sea a R n. Se denota por diag(a) la matriz diagonal con entradas a 1,..., a n : diag(a) = [ a j δ j,k ] n j,k=1.
Matrices triangulares y matrices ortogonales Problemas para examen Matrices diagonales 1. Sea a R n. Se denota por diag(a) la matriz diagonal con entradas a 1,..., a n : diag(a) = [ a j δ j,k ] n j,k=1.
Vectores y matrices. Problemas para examen
 Vectores y matrices Problemas para examen Operaciones lineales con vectores 1. Programación: la suma de dos vectores. Escriba una función que calcule x + y, donde x, y R n. Calcule el número de flops.
Vectores y matrices Problemas para examen Operaciones lineales con vectores 1. Programación: la suma de dos vectores. Escriba una función que calcule x + y, donde x, y R n. Calcule el número de flops.
Ejemplo 1. Ejemplo introductorio
 . -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
. -Jordan. Ejemplo 1. Ejemplo introductorio. -Jordan Dos especies de insectos se crían juntas en un recipiente de laboratorio. Todos los días se les proporcionan dos tipos de alimento A y B. 1 individuo
Conjunto R n y operaciones lineales en R n
 Conjunto R n y operaciones lineales en R n Objetivos. Definir el conjunto R n y operaciones lineales en R n, estudiar propiedades de las últimas. Requisitos. Conjunto de los números reales R, propiedades
Conjunto R n y operaciones lineales en R n Objetivos. Definir el conjunto R n y operaciones lineales en R n, estudiar propiedades de las últimas. Requisitos. Conjunto de los números reales R, propiedades
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Operaciones con matrices
 Operaciones con matrices Tareas adicionales Los problemas auxiliares de estas tareas adicionales no son muy difíciles y corresponden al nivel obligatorio de conocimientos. Los problemas principales de
Operaciones con matrices Tareas adicionales Los problemas auxiliares de estas tareas adicionales no son muy difíciles y corresponden al nivel obligatorio de conocimientos. Los problemas principales de
Matrices, determinantes, sistemas de ecuaciones lineales.
 UNIVERSIDAD DE MURCIA Departamento de Matemáticas Óptica y Optometría Resúmenes Curso 2007-2008 Matrices, determinantes, sistemas de ecuaciones lineales. Una matriz A de orden m n es una colección de m
UNIVERSIDAD DE MURCIA Departamento de Matemáticas Óptica y Optometría Resúmenes Curso 2007-2008 Matrices, determinantes, sistemas de ecuaciones lineales. Una matriz A de orden m n es una colección de m
Tema 1: Matrices y Determinantes
 Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Tema 1: Matrices y Determinantes September 14, 2009 1 Matrices Definición 11 Una matriz es un arreglo rectangular de números reales a 11 a 12 a 1m a 21 a 22 a 2m A = a n1 a n2 a nm Se dice que una matriz
Capitulo 6. Matrices y determinantes
 Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
Capitulo 6. Matrices y determinantes Objetivo. El alumno aplicará los conceptos fundamentales de las matrices, determinantes y sus propiedades a problemas que requieran de ellos para su resolución. Contenido.
Matrices y Determinantes.
 Matrices y Determinantes. Definición [Matriz] Sea E un conjunto cualquiera, m, n N. Matrices. Generalidades Matriz de orden m n sobre E: a 11 a 12... a 1n a 21 a 22... a 2n...... a m1 a m2... a mn a ij
Matrices y Determinantes. Definición [Matriz] Sea E un conjunto cualquiera, m, n N. Matrices. Generalidades Matriz de orden m n sobre E: a 11 a 12... a 1n a 21 a 22... a 2n...... a m1 a m2... a mn a ij
Números complejos (lista de problemas para examen)
 Números complejos (lista de problemas para examen) En esta lista de problemas trabajamos con la construcción de números complejos (como pares ordenados de los reales) y con su representación en la forma
Números complejos (lista de problemas para examen) En esta lista de problemas trabajamos con la construcción de números complejos (como pares ordenados de los reales) y con su representación en la forma
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; (A ) = A. 2. La inversa de A 1 es A; (A 1 ) 1 = A. 3. (AB) = B A.
 ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
ÁLGEBRA MATRICIAL. 1. La traspuesta de A es A; A = A. 2. La inversa de A 1 es A; A 1 1 = A. 3. AB = B A. 4. Las matrices A A y AA son simétricas. 5. AB 1 = B 1 A 1, si A y B son no singulares. 6. Los escalares
Matriz sobre K = R o C de dimensión m n
 2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
2 Matrices y Determinantes 21 Matrices Matriz sobre K = R o C de dimensión m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Tipos de matrices: Cuadrada: n n = (a ij) i=1,,m j=1,,n Nula: (0) i,j 1 0
Álgebra Lineal, Ejercicios
 Álgebra Lineal, Ejercicios MATRICES 1 Se llama traza de una matriz cuadrada a la suma de los elementos de su diagonal principal Sea G el conjunto de todas las matrices cuadradas de orden n con traza nula
Álgebra Lineal, Ejercicios MATRICES 1 Se llama traza de una matriz cuadrada a la suma de los elementos de su diagonal principal Sea G el conjunto de todas las matrices cuadradas de orden n con traza nula
Bases y dimensión. Problemas teóricos. En todos los problemas se supone que V es un espacio vectorial sobre un campo F. p=1
 Bases y dimensión Problemas teóricos Bases de un espacio vectorial En todos los problemas se supone que V es un espacio vectorial sobre un campo F. Definición de base. Sean b 1,..., b n V. Se dice que
Bases y dimensión Problemas teóricos Bases de un espacio vectorial En todos los problemas se supone que V es un espacio vectorial sobre un campo F. Definición de base. Sean b 1,..., b n V. Se dice que
Definición de la matriz inversa
 Definición de la matriz inversa Ejercicios Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, matriz identidad, habilidades básicas de resolver sistemas de ecuaciones
Definición de la matriz inversa Ejercicios Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, matriz identidad, habilidades básicas de resolver sistemas de ecuaciones
Matrices. p ij = a ik b kj = a i1 b 1j + a i2 b 2j + + a in b nj.
 Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Matrices Introducción Una matriz de m filas y n columnas con elementos en el cuerpo K es un rectángulo de elementos de K (es decir, números) del tipo a a 2 a n a 2 a 22 a 2n A = (a ij ) = a m a m2 a mn
Matrices triangulares y descomposición LU
 Matrices triangulares y descomposición LU Problemas para examen Si en algún problema se pide calcular el número de flops (operaciones aritméticas con punto flotante), entonces en el examen será suficiente
Matrices triangulares y descomposición LU Problemas para examen Si en algún problema se pide calcular el número de flops (operaciones aritméticas con punto flotante), entonces en el examen será suficiente
Vectores y Matrices. Tema 3: Repaso de Álgebra Lineal Parte I. Contenidos
 Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
Tema 3: Repaso de Álgebra Lineal Parte I Virginia Mazzone Contenidos Vectores y Matrices Bases y Ortonormailizaciòn Norma de Vectores Ecuaciones Lineales Algenraicas Ejercicios Vectores y Matrices Los
MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES
 5 de Abril de 2 MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES (Clase ) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela Puntos a tratar. Definición
5 de Abril de 2 MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES LINEALES (Clase ) Departamento de Matemática Aplicada Facultad de Ingeniería Universidad Central de Venezuela Puntos a tratar. Definición
Una matriz es una tabla ordenada (por filas y columnas) de escalares a i j de la forma: ... ... a... ...
 MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
MATRICES Las matrices se utilizan en el cálculo numérico, en la resolución de sistemas de ecuaciones lineales, de las ecuaciones diferenciales y de las derivadas parciales. Tienen también muchas aplicaciones
MENORES, COFACTORES Y DETERMINANTES
 MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
MENORES, COFACTORES Y DETERMINANTES 1. Introducción. 2. Determinante de una matriz de 3 x 3. 3. Menores y cofactores. 4. Determinante de una matriz de n x n. 5. Matriz triangular. 6. Determinante de una
Producto de matrices triangulares superiores
 Producto de matrices triangulares superiores Ejercicios Objetivos Demostrar que el producto de dos matrices triangulares superiores es una matriz triangular superior Deducir una fórmula para las entradas
Producto de matrices triangulares superiores Ejercicios Objetivos Demostrar que el producto de dos matrices triangulares superiores es una matriz triangular superior Deducir una fórmula para las entradas
Ecuaciones matriciales AX = B y XA = B. Cálculo de la matriz inversa
 Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Ecuaciones matriciales AX = B y XA = B Cálculo de la matriz inversa Objetivos Aprender a resolver ecuaciones matriciales de la forma AX = B y XA = B Aprender a calcular la matriz inversa con la eliminación
Matemática 2 MAT022. Clase 1 (Complementos) Departamento de Matemática Universidad Técnica Federico Santa María. Matrices
 Matemática 2 MAT022 Clase 1 (Complementos) Departamento de Matemática Universidad Técnica Federico Santa María Tabla de Contenidos 1 Matrices Propiedades Tabla de Contenidos Matrices 1 Matrices Propiedades
Matemática 2 MAT022 Clase 1 (Complementos) Departamento de Matemática Universidad Técnica Federico Santa María Tabla de Contenidos 1 Matrices Propiedades Tabla de Contenidos Matrices 1 Matrices Propiedades
Contenido. 2 Operatoria con matrices. 3 Determinantes. 4 Matrices elementales. 1 Definición y tipos de matrices
 elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
elementales Diciembre 2010 Contenido Definición y tipos de matrices elementales 1 Definición y tipos de matrices 2 3 4 elementales 5 elementales Definición 1.1 (Matriz) Una matriz de m filas y n columnas
A = , B = 2 2. a 11 a 1n a 21 a 2n A = a m1 a mn
 Máster en Materiales y Sistemas Sensores para Tecnologías Medioambientales Erasmus Mundus NOTAS DE CÁLCULO NUMÉRICO Damián Ginestar Peiró ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEL DISEÑO UNIVERSIDAD POLITÉCNICA
Máster en Materiales y Sistemas Sensores para Tecnologías Medioambientales Erasmus Mundus NOTAS DE CÁLCULO NUMÉRICO Damián Ginestar Peiró ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEL DISEÑO UNIVERSIDAD POLITÉCNICA
Matrices, Determinantes y Sistemas de ecuaciones lineales
 Tema 1 Matrices, Determinantes y Sistemas de ecuaciones lineales 1.1. Matrices Definición: Una MATRIZ es un conjunto de números reales dispuestos en forma de rectángulo, que usualmente se delimitan por
Tema 1 Matrices, Determinantes y Sistemas de ecuaciones lineales 1.1. Matrices Definición: Una MATRIZ es un conjunto de números reales dispuestos en forma de rectángulo, que usualmente se delimitan por
ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250)
 Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
Matrices. José Vicente Romero Bauset. ETSIT-curso 2009/2010. José Vicente Romero Bauset Tema 1.- Matrices. 1
 Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
Matrices José Vicente Romero Bauset ETSIT-curso 2009/2010 José Vicente Romero Bauset Tema 1- Matrices 1 Introducción Por qué estudiar las matrices? Son muchas las situaciones de la vida real en las que
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES.
 BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
BLOQUE DE ÁLGEBRA: TEMA 1: MATRICES. Matrices: Se llama matriz de dimensión m n a un conjunto de números reales dispuestos en m filas y n columnas de la siguiente forma: 11 a 12 a 13... a 1n A= a a 21
Valores y vectores propios
 Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Valores y vectores propios Tareas adicionales Algunos de estos problemas compuso Gustavo Antonio Sandoval Angeles (como parte de su servicio social). Estos problemas son más difíciles o más laboriosos
Determinantes. Problemas teóricos. i=1. 2. De la fórmula general (1) deduzca la fórmula para el determinante de orden 3.
 Determinantes Problemas teóricos Adradezco por varios problemas e ideas a los profesores de la ESFM Myriam Rosalía Maldonado Ramírez y Eliseo Sarmiento Rosales y al estudiante de servicio social Sadi Manuel
Determinantes Problemas teóricos Adradezco por varios problemas e ideas a los profesores de la ESFM Myriam Rosalía Maldonado Ramírez y Eliseo Sarmiento Rosales y al estudiante de servicio social Sadi Manuel
Objetivos: Al inalizar la unidad, el alumno:
 Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Unidad 1 Matrices y determinantes Objetivos: Al inalizar la unidad, el alumno: Identiicará qué es una matriz y cuáles son sus elementos. Distinguirá los principales tipos de matrices. Realizará operaciones
Matrices y determinantes (Curso )
 ÁLGEBRA Práctica 3 Matrices y determinantes (Curso 2008 2009) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz triangular
ÁLGEBRA Práctica 3 Matrices y determinantes (Curso 2008 2009) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz triangular
Definición de la matriz inversa
 Definición de la matriz inversa Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, habilidades básicas de resolver sistemas de ecuaciones Ejemplo El número real
Definición de la matriz inversa Objetivos Aprender la definición de la matriz inversa Requisitos Multiplicación de matrices, habilidades básicas de resolver sistemas de ecuaciones Ejemplo El número real
Tema 1. Álgebra lineal. Matrices
 1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
Mat r i z in v e r s a
 Unidad 2 Método de GaUss Mat r i z in v e r s a M U lt i pli cat i va Objetivos: Al inalizar la unidad, el alumno: Representará un sistema de m ecuaciones lineales con n incógnitas mediante una matriz
Unidad 2 Método de GaUss Mat r i z in v e r s a M U lt i pli cat i va Objetivos: Al inalizar la unidad, el alumno: Representará un sistema de m ecuaciones lineales con n incógnitas mediante una matriz
Matrices: repaso. Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas. Una matriz A M m n es de la forma A =
 Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Matrices: repaso Denotaremos con M m n el conjunto de matrices de tamaño m n, o sea, de m filas y n columnas Una matriz A M m n es de la forma a 11 a 1n A = a m1 a mn Denotaremos A ij = a ij el coeficiente
Una matriz es una arreglo rectangular ordenado de elementos, comúnmente llamados escalares, dispuestos en m renglones y n columnas.
 MATRICES Las matrices tienen una importancia fundamental en el análisis económico sobre todo en el estudio de sistemas de ecuaciones lineales, como en el modelo insumo-producto. Cuando trabajamos con modelos
MATRICES Las matrices tienen una importancia fundamental en el análisis económico sobre todo en el estudio de sistemas de ecuaciones lineales, como en el modelo insumo-producto. Cuando trabajamos con modelos
Matrices. Definiciones básicas de matrices. José de Jesús Angel Angel.
 Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 1 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 1 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Matrices y Determinantes.
 Tema II Capítulo 1 Matrices Álgebra Lineal I Departamento de Métodos Matemáticos y de Representación UDC Tema II Matrices y Determinantes 1 Matrices 1 Definiciones básicas Definición 11 Una matriz A de
Tema II Capítulo 1 Matrices Álgebra Lineal I Departamento de Métodos Matemáticos y de Representación UDC Tema II Matrices y Determinantes 1 Matrices 1 Definiciones básicas Definición 11 Una matriz A de
Cambio de base. Objetivos. Estudiar la relación entre las coordenadas de un vector en dos bases.
 Cambio de base Objetivos Estudiar la relación entre las coordenadas de un vector en dos bases Requisitos Definición de una base, multiplicación de una matriz por un vector, delta de Kronecker Definición
Cambio de base Objetivos Estudiar la relación entre las coordenadas de un vector en dos bases Requisitos Definición de una base, multiplicación de una matriz por un vector, delta de Kronecker Definición
El cuerpo de los números reales
 Capítulo 1 El cuerpo de los números reales 1.1. Introducción Existen diversos enfoques para introducir los números reales: uno de ellos parte de los números naturales 1, 2, 3,... utilizándolos para construir
Capítulo 1 El cuerpo de los números reales 1.1. Introducción Existen diversos enfoques para introducir los números reales: uno de ellos parte de los números naturales 1, 2, 3,... utilizándolos para construir
23/10/14. Algebra Matricial $ $ ' ' ' $ & & & # # I 3 I 2 = 1 0 $ DEFINICION DE MATRIZ 2.1 CONCEPTOS DE MATRICES CONCEPTOS DE MATRICES. $ n. ! a.
 /0/ Algebra Matricial. OPERACIONES DE DEFINICION DE MATRIZ Si A es una matriz de m x n (esto es una matriz con m filas y n columnas) la entrada escalar en la i-ésima fila y la j-ésima columna de A se denota
/0/ Algebra Matricial. OPERACIONES DE DEFINICION DE MATRIZ Si A es una matriz de m x n (esto es una matriz con m filas y n columnas) la entrada escalar en la i-ésima fila y la j-ésima columna de A se denota
Espacios vectoriales con producto interno
 Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Espacios vectoriales con producto interno Problemas teóricos En todos los problemas relacionados con el caso complejo se supone que el producto interno es lineal con respecto al segundo argumento. Definición
Matriz asociada a una transformación lineal respecto a un par de bases
 Matriz asociada a una transformación lineal respecto a un par de bases Objetivos Definir la matriz asociada a una transformación lineal respecto a un par de bases y estudiar la representación matricial
Matriz asociada a una transformación lineal respecto a un par de bases Objetivos Definir la matriz asociada a una transformación lineal respecto a un par de bases y estudiar la representación matricial
TEMA 2: MATRICES. 2.2.1 Operaciones elementales y matrices elementales. 2.2.2 Proceso de escalonamiento de una matriz no nula.
 TEMA 2: MATRICES 21 Generalidades sobre matrices 211 Definición de matriz Tipos de matrices 212 Operaciones algebraicas con matrices 213 Matriz traspuesta y traspuesta-conjugada 214 Submatrices 22 Proceso
TEMA 2: MATRICES 21 Generalidades sobre matrices 211 Definición de matriz Tipos de matrices 212 Operaciones algebraicas con matrices 213 Matriz traspuesta y traspuesta-conjugada 214 Submatrices 22 Proceso
Una matriz es un arreglo rectangular de elementos. Por ejemplo:
 1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
1 MATRICES CONCEPTOS BÁSICOS Definición: Matriz Una matriz es un arreglo rectangular de elementos. Por ejemplo: es una matriz de 3 x 2 (que se lee 3 por 2 ) pues es un arreglo rectangular de números con
2 - Matrices y Determinantes
 Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Nivelación de Matemática MTHA UNLP 1 2 - Matrices y Determinantes 1 Matrices 11 Definición Una matriz A es cualquier ordenamiento rectangular de números o funciones a 11 a 12 a 1n a 21 a 22 a 2n A a m1
Tema 5: Sistemas de Ecuaciones Lineales
 Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Matrices simétricas y antisimétricas
 Matrices simétricas y antisimétricas Ejercicios Objetivos Definir matrices simétricas y antisimétricas estudiar sus propiedades básicas Requisitos Matriz transpuesta propiedades de la matriz transpuesta
Matrices simétricas y antisimétricas Ejercicios Objetivos Definir matrices simétricas y antisimétricas estudiar sus propiedades básicas Requisitos Matriz transpuesta propiedades de la matriz transpuesta
Definición (matriz): Definición (dimensión de una matriz): Si una matriz tiene m renglones y n columnas se dice que es de dimensión m n.
 Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
Índice general 1. Álgebra de Matrices 1 1.1. Conceptos Fundamentales............................ 1 1.1.1. Vectores y Matrices........................... 1 1.1.2. Transpuesta................................
TEMA 3: Matrices y sistemas de ecuaciones lineales. Álgebra y estructuras finitas/discretas (Grupos A)
 TEMA 3: Matrices y sistemas de ecuaciones lineales Álgebra y estructuras finitas/discretas Grupos A Curso 2007-2008 1 2 1 Anillos y cuerpos Definición 1 Un anillo viene dado por un conjunto R y por dos
TEMA 3: Matrices y sistemas de ecuaciones lineales Álgebra y estructuras finitas/discretas Grupos A Curso 2007-2008 1 2 1 Anillos y cuerpos Definición 1 Un anillo viene dado por un conjunto R y por dos
Valores y Vectores Propios
 Valores y Vectores Propios Departamento de Matemáticas, CSI/ITESM de abril de 9 Índice 9.. Definiciones............................................... 9.. Determinación de los valores propios.................................
Valores y Vectores Propios Departamento de Matemáticas, CSI/ITESM de abril de 9 Índice 9.. Definiciones............................................... 9.. Determinación de los valores propios.................................
Matrices escalonadas y escalonadas reducidas
 Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
SISTEMAS DE ECUACIONES LINEALES Y MATRICES
 y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015 1 Visita http://sergiosolanosabie.wikispaces.com y SISTEMAS DE ECUACIONES ES Y MATRICES Sergio Stive Solano 1 Febrero de 2015
Definición Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas.
 Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Tema 1 Matrices 1.1. Conceptos básicos y ejemplos Definición 1.1.1. Dados dos números naturales m y n, una matriz de orden o dimensión m n es una tabla numérica rectangular con m filas y n columnas. NOTA:
Lección 5.1: Matrices y determinantes. Primeros conceptos. Objetivos de esta lección
 Matemáticas Tema 5: Conceptos básicos sobre matrices y vectores Objetivos Lección 5.: y determinantes Philippe Bechouche Departamento de Matemática Aplicada Universidad de Granada 3 4 phbe@ugr.es 5 Qué
Matemáticas Tema 5: Conceptos básicos sobre matrices y vectores Objetivos Lección 5.: y determinantes Philippe Bechouche Departamento de Matemática Aplicada Universidad de Granada 3 4 phbe@ugr.es 5 Qué
ELEMENTOS DE ALGEBRA LINEAL
 ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
ELEMENTOS DE ALGEBRA LINEAL Matriz Una matriz de orden o dimensión n x p es una ordenación rectangular de elementos dispuestos en n filas y p columnas de la siguiente forma: a11 a1 a1p a1 a a p A an1 an
Ing. Ramón Morales Higuera
 MATRICES. Una matriz es un conjunto ordenado de números. Un determinante es un número. CONCEPTO DE MATRIZ. Se llama matriz a un conjunto ordenado de números, dispuestos en filas y Las líneas horizontales
MATRICES. Una matriz es un conjunto ordenado de números. Un determinante es un número. CONCEPTO DE MATRIZ. Se llama matriz a un conjunto ordenado de números, dispuestos en filas y Las líneas horizontales
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Matrices y Sistemas Lineales Natalia Boal María Luisa Sein-Echaluce Universidad de Zaragoza Matrices sobre IR ó C. Definición Dado un conjunto K (IR ó C) y dos conjuntos finitos de índices I = {,, m} J
Operaciones lineales en R 3 y sus propiedades
 Operaciones lineales en R 3 y sus propiedades Ejercicios Objetivos. Aprender a demostrar propiedades de las operaciones lineales en R 3. Requisitos. Conjunto de los números reales R, propiedades de las
Operaciones lineales en R 3 y sus propiedades Ejercicios Objetivos. Aprender a demostrar propiedades de las operaciones lineales en R 3. Requisitos. Conjunto de los números reales R, propiedades de las
APÉNDICE A. Algebra matricial
 APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
APÉNDICE A Algebra matricial El estudio de la econometría requiere cierta familiaridad con el álgebra matricial. La teoría de matrices simplifica la descripción, desarrollo y aplicación de los métodos
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Problemas teóricos Sistemas de ecuaciones lineales con parámetros En los siguientes problemas hay que resolver el sistema de ecuaciones lineales para todo valor del parámetro
Sistemas de ecuaciones lineales Problemas teóricos Sistemas de ecuaciones lineales con parámetros En los siguientes problemas hay que resolver el sistema de ecuaciones lineales para todo valor del parámetro
TEMA 11. Autovalores y autovectores. Diagonalización y formas canónicas.
 TEMA 11 F MATEMÁTICOS TEMA 11 Autovalores y autovectores Diagonalización y formas canónicas 1 Introducción Definición 1 (Matrices semejantes) Sean A y B dos matrices cuadradas de orden n Decimos que A
TEMA 11 F MATEMÁTICOS TEMA 11 Autovalores y autovectores Diagonalización y formas canónicas 1 Introducción Definición 1 (Matrices semejantes) Sean A y B dos matrices cuadradas de orden n Decimos que A
Subespacios de espacios vectoriales
 Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
Subespacios de espacios vectoriales Objetivos. Estudiar la definición, el criterio y algunos ejemplos de subespacios vectoriales. Muchos espacios vectoriales importantes (por ejemplo, espacio de soluciones
ÁLGEBRA LINEAL I Práctica 3
 ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2011 2012) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2011 2012) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
Matrices ortogonales y descomposición QR
 Matrices ortogonales y descomposición QR Problemas para examen Agradezco a Aldo Iván Leal García por varias correcciones importantes. Invertibilidad por la izquierda y por la derecha (repaso) 1. Conceptos
Matrices ortogonales y descomposición QR Problemas para examen Agradezco a Aldo Iván Leal García por varias correcciones importantes. Invertibilidad por la izquierda y por la derecha (repaso) 1. Conceptos
Proyecciones. Producto escalar de vectores. Aplicaciones
 Proyecciones La proyección de un punto A sobre una recta r es el punto B donde la recta perpendicular a r que pasa por A corta a la recta r. Con un dibujo se entiende muy bien. La proyección de un segmento
Proyecciones La proyección de un punto A sobre una recta r es el punto B donde la recta perpendicular a r que pasa por A corta a la recta r. Con un dibujo se entiende muy bien. La proyección de un segmento
Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas.
 1.- CONCEPTO DE MATRIZ. TIPOS DE MATRICES Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas. 1 3 4 Por ejemplo, A = es una matriz de 2 filas y 3 columnas 0 5
1.- CONCEPTO DE MATRIZ. TIPOS DE MATRICES Definición de matriz Una matriz A es un conjunto de números dispuestos en filas y en columnas. 1 3 4 Por ejemplo, A = es una matriz de 2 filas y 3 columnas 0 5
Definición: Dos matrices A y B son iguales si tienen el mismo orden y coinciden los elementos que ocupan el mismo lugar.
 UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
UNIDAD 03: MATRICES Y DETERMINANTES. 3.1 Conceptos de Matrices. 3.1.1 Definición de matriz. Definición: Se lama matriz de orden m x n a un arreglo rectangular de números dispuestos en m renglones y n columnas.
Matrices. Definiciones básicas de matrices. José de Jesús Angel Angel
 Matrices Definiciones básicas de matrices www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2009 Contenido 1. Matrices 3 1.1. Matrices cuadradas.................................
Matrices Definiciones básicas de matrices www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2009 Contenido 1. Matrices 3 1.1. Matrices cuadradas.................................
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES
 Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
Isabel Eguia Ribero Aitziber Unzueta Inchaurbe Elisabete Alberdi Celaya
 FUNDAMENTOS DEL ÁLGEBRA LINEAL. EJERCICIOS Y CUESTIONES. SOLUCIONES CON MATHEMATICA Isabel Eguia Ribero Aitziber Unzueta Inchaurbe Elisabete Alberdi Celaya ISBN: 978-84-606-6054-5 Depósito legal: BI-355-2015
FUNDAMENTOS DEL ÁLGEBRA LINEAL. EJERCICIOS Y CUESTIONES. SOLUCIONES CON MATHEMATICA Isabel Eguia Ribero Aitziber Unzueta Inchaurbe Elisabete Alberdi Celaya ISBN: 978-84-606-6054-5 Depósito legal: BI-355-2015
V 2 : vectores libres en el plano
 V 2 : vectores libres en el plano Egor Maximenko ESFM del IPN 8 de agosto de 2009 Egor Maximenko (ESFM del IPN) V 2 : Vectores libres en el plano 8 de agosto de 2009 1 / 13 Contenido 1 Conjunto V 2 2 Operaciones
V 2 : vectores libres en el plano Egor Maximenko ESFM del IPN 8 de agosto de 2009 Egor Maximenko (ESFM del IPN) V 2 : Vectores libres en el plano 8 de agosto de 2009 1 / 13 Contenido 1 Conjunto V 2 2 Operaciones
Elementos de una matriz.
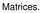 Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Matrices. Elementos de una matriz. Renglón. Columnas. A=[a ij ] A-Nombre de la matriz. a-número. i-renglón. j-columna. i j-orden de la matriz. Ejercicio. Indica el orden de la matriz. Indica el valor de
Sistemas de Ecuaciones y Matrices
 Sistemas de Ecuaciones y Matrices 0.1 Sistemas de ecuaciones Consideremos las gráficas de dos funciones f y g como en la figura siguiente: P Q y = fx y = gx En la práctica, en ocasiones hay que encontrar
Sistemas de Ecuaciones y Matrices 0.1 Sistemas de ecuaciones Consideremos las gráficas de dos funciones f y g como en la figura siguiente: P Q y = fx y = gx En la práctica, en ocasiones hay que encontrar
Sistema de ecuaciones algebraicas
 Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
Sistema de ecuaciones algebraicas Curso: Métodos Numéricos en Ingeniería Profesor: Dr. José A. Otero Hernández Correo: j.a.otero@itesm.mx web: http://metodosnumericoscem.weebly.com Universidad: ITESM CEM
MATEMÁTICA LIC. Y PROF. EN CS. BIOLÓGICAS
 Definición: se llama matriz de m filas y n columnas sobre un cuerpo K (R ó C), a una ordenación rectangular de la forma Notación: a11 a...... a1n a21 a...... a2n A = M M M donde cada elemento a ij Є K
Definición: se llama matriz de m filas y n columnas sobre un cuerpo K (R ó C), a una ordenación rectangular de la forma Notación: a11 a...... a1n a21 a...... a2n A = M M M donde cada elemento a ij Є K
Matrices. Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas.
 Matrices Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Matrices Concepto de matriz Se denomina matriz a todo conjunto de números o expresiones ordenados en filas y columnas. Cada uno de los números de que consta la matriz se denomina elemento. Un elemento
Métodos Estadísticos Multivariados
 Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 34 Álgebra matricial y vectores aleatorios Una matriz es un arreglo
Inversas Generalizadas
 Inversas Generalizadas Departamento de Matemáticas, CSI/IESM 5 de abril de 2 Índice.. Inversas generalizadas..........................................2. Uso de la inversa generalizada.....................................
Inversas Generalizadas Departamento de Matemáticas, CSI/IESM 5 de abril de 2 Índice.. Inversas generalizadas..........................................2. Uso de la inversa generalizada.....................................
ÁLGEBRA LINEAL I Práctica 3
 ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2013 2014) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
ÁLGEBRA LINEAL I Práctica 3 Matrices y determinantes (Curso 2013 2014) 1. En el conjunto de las matrices n n de elementos reales, demostrar que el producto de matrices triangulares inferiores es otra matriz
Algoritmo de factorización LU
 Algoritmo de factorización LU Objetivos. Estudiar el algoritmo de la factorización LU de una matriz cuadrada invertible. Requisitos. Matrices elementales y su relación con operaciones elementales, matriz
Algoritmo de factorización LU Objetivos. Estudiar el algoritmo de la factorización LU de una matriz cuadrada invertible. Requisitos. Matrices elementales y su relación con operaciones elementales, matriz
Números complejos (lista de problemas para examen)
 Números complejos (lista de problemas para examen) En esta lista de problemas trabajamos con la construcción de números complejos (como pares ordenados de los reales) y con su representación en la forma
Números complejos (lista de problemas para examen) En esta lista de problemas trabajamos con la construcción de números complejos (como pares ordenados de los reales) y con su representación en la forma
Conjuntos y matrices. Sistemas de ecuaciones lineales
 1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
Matrices. Álgebra de matrices.
 Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
Matrices. Álgebra de matrices. 1. Definiciones generales Definición 1.1 Si m y n son dos números naturales, se llama matriz de números reales de orden m n a una aplicación A : {1, 2, 3,..., m} {1, 2, 3,...,
ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012. Guía de Estudio y Ejercitación propuesta
 ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012 1 Guía de Estudio y Ejercitación propuesta Esta selección de Temas y Ejercicios están extraídos del texto FUNDAMENTOS DE ALGEBRA LINEAL de R. Larson y D. Falvo.
ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012 1 Guía de Estudio y Ejercitación propuesta Esta selección de Temas y Ejercicios están extraídos del texto FUNDAMENTOS DE ALGEBRA LINEAL de R. Larson y D. Falvo.
Valores y vectores propios
 Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Valores y vectores propios Problemas teóricos El los siguientes problemas se denota por L(V ) conjunto de los operadores lineales en un espacio vectorial V (en otras palabras, de las transformaciones lineales
Seno y coseno de una matriz
 Miscelánea Matemática 5 (200 29 40 SMM Seno y coseno de una matriz Rafael Prieto Curiel Instituto Tecnológico Autónomo de México ITAM rafaelprietocuriel@yahoocom Introducción En muchas áreas de las matemáticas
Miscelánea Matemática 5 (200 29 40 SMM Seno y coseno de una matriz Rafael Prieto Curiel Instituto Tecnológico Autónomo de México ITAM rafaelprietocuriel@yahoocom Introducción En muchas áreas de las matemáticas
Combinación lineal, Independencia Lineal, y Vectores que generan (Sección 6.3 pág. 291)
 Combinación lineal, Independencia Lineal, y Vectores que generan (Sección 6.3 pág. 291) I. Combinación Lineal Definición: Sean v 1, v 2, v 3,, v n vectores en el espacio vectorial V. Entonces cualquier
Combinación lineal, Independencia Lineal, y Vectores que generan (Sección 6.3 pág. 291) I. Combinación Lineal Definición: Sean v 1, v 2, v 3,, v n vectores en el espacio vectorial V. Entonces cualquier
Tema 2. Grupos. 3. El conjunto de matrices de orden 2 con coeficientes enteros (o reales) con la suma es un grupo conmutativo.
 Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
MANUAL DE MATRICES Y DETERMINANTES
 Universidad Politécnica Salesiana Carrera de Ingeniería Mecánica MANUAL DE MATRICES Y DETERMINANTES Msc. Wilson Benavides Wilson Benavides MANUAL DE MATRICES Y DETERMINANTES 2012 Carrera de Ingeniería
Universidad Politécnica Salesiana Carrera de Ingeniería Mecánica MANUAL DE MATRICES Y DETERMINANTES Msc. Wilson Benavides Wilson Benavides MANUAL DE MATRICES Y DETERMINANTES 2012 Carrera de Ingeniería
