RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN Actualizado en el curso 2008/2009
|
|
|
- Sebastián Soriano Hidalgo
- hace 7 años
- Vistas:
Transcripción
1 Actualizado en el curso 008/ Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máima. Calcular dicha suma. Condición: + e, de donde tenemos que e- Función: S(,) ln() + ln() S() ln() + ln(e-) 1 1 e S'( ) S'( ) 0 e 1 1 e 8 S''( ) S''( ) < 0 e ( e ) luego, tenemos que es máimo. e e La suma pedida será: suma ln + ln e ln. Solución: e/ la suma S -ln. Calcula dos números que cumplan que al sumarlos resulte 10 la resta de uno de ellos menos el inverso del otro sea mínima. Condición: + 10, de donde 10- Condición: + 10, de donde 10- La función: 1 f (, ) 1 f ( ) 10 f ( ) f ( ) (10 ) f ( ) 0 9, 11 f ( ) (10 ) f ( 9) < 0 Es un máimo f ( 11) > 0 Es un mínimo Solución: 11, /0.-
2 Actualizado en el curso 008/009. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren reciben como premio tantos euros como decímetros cuadrados tenga de superficie el cuadrilátero construido. Calcula razonadamente la cuantía del máimo premio que se pueda obtener en este concurso. Condición: A(, ) (Función Objetivo) Condición: + 1- Función Objetivo: A(, ) A() (1-) - A ()1- A () / m. A () - A (1/) - < 0 (es un máimo) Solución: 5 dm. e 5 dm., siendo Área 5 dm. Cuantía máima a percibir por el premio 5.. Un jardinero dispone de 160 metros de alambre que va a utilizar para cercar una zona rectangular dividirla en tres partes. Las alambradas de las divisiones deben quedar paralelas a uno de los lados del rectángulo. Qué dimensiones debe tener la zona cercada para que su área sea la maor posible? A(, ) (Función objetivo) Condición: Condición: Función: A(, ) -. /0.-
3 Actualizado en el curso 008/ A() 0- A () 0- A () 0 0 m. A () -1 < 0 (el punto es un máimo) Para 0 m. resulta m. Solución: 0 m, 0 m. 5. Se dispone de 00 metros de alambrada para vallar un solar rectangular. Qué dimensiones deberá tener el solar para que con esa alambrada se limite la maor área posible? Razonar el proceso. Función: A(, ) Condición: + 00 Condición: Función: A(, ) A() (00-) 00- A () 00- A () m A () - < es un máimo, siendo Solución: 100 m. e 100 m., es un cuadrado 6. Un terreno de forma rectangular tiene 00 m va a ser vallado. El precio del metro lineal de valla es de euros. Cuáles serán las dimensiones del solar que hacen que el costo de la valla sea mínimo? 00 m Perímetro del vertedero: P + Coste cerca: P ()+() 8+8 (función objetivo) Condición: /0.-
4 Condición: Coste cerca: C(, ) 8+8 Actualizado en el curso 008/009 C() C () 8- C () 0 00 ± 0; Solución válida 0 m. C () 00 C (0) 0.8 > 0 Es un mínimo Para 0 m., siendo 00 00/0 0 m. Solución: Las dimensiones del solar son cuadradas con 0 m. e 0m. 7. Supongamos que el solar del problema anterior tiene 00 m un lado a lo largo del río requiere una valla más costosa de 5 euros el metro lineal. Qué dimensiones darán el costo más bajo? Río Condición: Función objetivo: C(, ) () C() C () Función: C(, ) () Condición: 00 C ()0 5 ± 15 (Solución válida: 15 m.) C () C (15) > Luego, en 15 ha un mínimo, siendo 0/. Solución: Las dimensiones del solar serán en este caso 15 m. e 0/ m. -. /0.-
5 Actualizado en el curso 008/ Las páginas de un libro deben medir cada una 600 cm de área. Sus márgenes laterales el inferior miden cm. el superior mide cm. Calcular las dimensiones de la página que permitan obtener la maor área impresa posible. Alto de la página impresa: -5 Ancho de la página impresa: - Área impresa (-) (-5) (función objetivo) Área páginas 600 (condición) Condición: / Función: A(, ) (-) ( ) A() A () -5+ A ()0 ± 80 ± 0 (La solución negativa no es válida).800 A ( 0 ) ( ) < 0, es un máimo, siendo Solución: 0 cm. e 5 0 cm. 9. Una hoja de papel debe contener 18 cm de teto impreso. Los márgenes superior e inferior han de tener cm. cada uno, los laterales 1 cm. Halla las dimensiones de la hoja para que el gasto de papel sea mínimo. 1 Función: A(, ) Condición: (-) (-) /0.-
6 Actualizado en el curso 008/009 Condición: (-) (-) Función: A(, ) A() A() 16 0 A () A () (solución negativa no es válida). A () ( ) Solución: 10 cm. e 5 cm. ( 16)( ) ( )( 16 0) ( ) A (10) > 0, es un mínimo. 10. Un pastor dispone de 1000 m de tela metálica para construir una cerca rectangular aprovechando una pared a eistente. Halla las dimensiones de la cerca para que el área encerrada sea máima. Función: f(, ) Condición: f(, ) f() (1.000-) f()1.000 f () f () 0 50 f () - f (50) < 0. Por lo tanto, 50 es un máimo. Solución: 50 metros e 500 metros 11. Un segmento de longitud de 5 cm. apoa sus etremos en los semiejes positivos OX OY, de tal manera que forma con éstos un triángulo. Halla las dimensiones del triángulo de área máima así construido. 5 Función: f(, ) Condición /0.-
7 Actualizado en el curso 008/009 Condición: + 5 Función: f(, ) f ( ) f ( ) 5 5 f ( ) 0 ± (La solución negativa no es válida). (75 f ( ) ( ( 5 )) 5 f < 0 Es un máimo 5 5 Solución: cm, cm ) 1. Se considera una ventana rectangular en la que el lado superior se ha sustituido por un triángulo equilátero. Sabiendo que el perímetro de la ventana es 6,6 m, hallar sus dimensiones para que la superficie sea máima. Función: A total A triángulo + A rectángulo Condición: Condición: A total f(, ) + + f() + ( ) f() f ( ) f ( ) 1 f (1.5) < 0. Luego, 1.5 es máimo. -. 7/0.-
8 Actualizado en el curso 008/009 Solución: 1.5 metros; 0.99 metros 1. Dividir un segmento de 6 cm. de longitud en dos partes, con la propiedad de que la suma de las áreas del cuadrado del triángulo equilátero construidos sobre ellos sea máima. A total A triángulo + A cuadrado Condición: + 6 Condición: Función: A total Sustituimos obtenemos: f() + (6 ) f (, ) + f() f ( ) 86 1 f ( ) 0 18 f ( ) `86 f ( 18) > 0 Luego, en 18 es un mínimo. Por lo tanto el problema no tiene solución a que en el enunciado pedían que fuera máimo. 1. Se considera una ventana como la que se indica en la figura (la parte inferior es rectangular la superior una semicircunferencia). El perímetro de la ventana mide 6 m. Halla las dimensiones e del rectángulo para que la superficie de la ventana sea máima (Epresa el resultado en función de π). -. 8/0.-
9 Actualizado en el curso 008/009 / / π Condición: + + 6, luego 1 π π Funcion : f(, ) + 1 π π f( ) + 8 π f( ) 8 1 f ( ) f ( ) 0 + π π f ''( ) 1 ( π ) 1 π 1 f ( ) 1 < 0 es un máimo + π + π Solución: metros ; + π π metros 15. (El Primer Problema de la Ventana) Una ventana tiene la forma de un rectángulo coronado con un semicírculo. Encuentre las dimensiones de la ventana que deja pasar más luz, si su perímetro mide 5 metros. / r L circunferencia L πr L semicircunferencia L Perímetro rectángulo + Perímetro total ++πr 5 (condición) π r Función: Área: A(, ) + π r -. 9/0.-
10 Actualizado en el curso 008/009 π 10 ( + π ) Condición: π r π / Función: A(, ) + + A() ( π ) π A () 10 π A () m + π A () π < 0 1. es un máimo 10 ( + π ) 10 / + π 0.7 m Solución: Dimensiones de la ventana: Ancho: 1. m.; Alto: + r m. 16. Entre todos los rectángulos de perímetro 1 m. cuál es el que tiene la diagonal menor? Razonar el proceso seguido. Condición: Función: f(, ) + ( ) f( ) + 6 f ( ) f ( ) Para f () 0 tenemos que f ( ) 6 ( ) 1+ 6 sustituimos, f () > 0, por lo tanto es mínimo. Solución: metros e metros -. 10/0.-
11 Actualizado en el curso 008/ Calcula el área máima que puede tiene un triángulo rectángulo tal que la suma de la longitudes de sus dos catetos vale cm. Condición: + ; - Función: Área f(,) / f(, ) f( ) f( ) f ( ) ( ) f ( ) 0 f ( ) 1 f () < 0 de donde tenemos que es máimo. Solución: cm e cm 18. Halla las dimensiones del rectángulo de área máima inscrito en una circunferencia de 10 cm. de radio. Razonar el proceso seguido. Condición: + (0) cm Función Área f(, ) f( ) 00 f ( ) f ( ) 0 ± 10 La solución negativa no es válida /0.-
12 Actualizado en el curso 008/ f ( ) ( ) ( ) 00 f (10 ) < 0 es un mínimo Solución: 10 cm e 10 cm 19. Calcule las dimensiones de tres campos cuadrados de modo que: el perímetro de uno de ellos sea triple del perímetro de otro, se necesiten eactamente 18 metros de valla para vallar los tres la suma de las áreas de los tres campos sea la mínima posible. z Llamamos,, z, a los lados de las tres parcelas. Condiciones: i) z ii) ++z 18 de donde z, entonces 1 Función: S(,,z) + + z S() + (1-) +9 S() S () 5-96 para S () 0 tenemos que 8 S () 5 S (8) > 0, por tanto, es mínimo. Solución: 8 m 10 m z 1 m. -. 1/0.-
13 Actualizado en el curso 008/ Una arquitecta quiere construir un jardín rectangular en un terreno circular de 100 metros de radio. Halla las dimensiones de dicho jardín para que el área sea máima. Condición: + 00, luego tenemos que Función: Área del jardín rectangular 00 A(, ) A( ) 0000 A ( ) A ( ) A ( ) A`() ± 0000 ±100 ±1 1 m A ( ) A (100 ) < 0 Es un máimo 0000 Desechamos la solución ser negativas. por ser negativa a que las dimensiones del jardín no pueden 0000 Solución: Para 11 m e 11 m ( 100 ) m -. 1/0.-
14 Actualizado en el curso 008/ (El Problema del Cable más Corto) Dos postes con longitudes de 6 8 metros respectivamente se colocan verticalmente sobre el piso con sus bases separadas una distancia de 10 metros. Calcule aproimadamente la longitud mínima de un cable que pueda ir desde la punta de uno de los postes hasta un punto en el suelo entre los postes luego hasta la punta del otro poste. Función: L cable Condición: (10-) m. L cable L() (10 ) (10 ) L () (10 ) L () (10 ) (10 ) solucion no validad > 0 L () ( 6 + ) 6 + ( 10 ) L (0/7) > 0 0/7 es un mínimo L(0/7) Solución: Longitud mínima L(0/7) m. -. 1/0.-
15 Actualizado en el curso 008/ Una empresa ha decidido mejorar su seguridad instalando 9 alarmas. Un especialista en el tema señala que dada la estructura de la empresa sólo puede optar por dos tipos de alarmas, de tipo A o de tipo B; además, afirma que la seguridad de la empresa se puede epresar como la décima parte del producto entre el número de alarmas de tipo A instaladas el cuadrado del número de alarmas instaladas de tipo B. Cuántas alarmas de cada tipo se deben instalar en la empresa para maimizar su seguridad? Alarmas tipo A Alarmas tipo B Condición: + 9, luego 9- Función: La Seguridad se epresa como: f(, ) 10 ( 9 ) 10 f (, ) f( ) f( ) f ( ) f ( ) 0 10 los valores de la que anulan la primera derivada son f ( ) f (9) > f () < 0 10 luego, 9 es mínimo es máimo. Solución: Será necesario instalar de tipo A alarmas de tipo B 6 alarmas. 1. Entre todos los triángulos isósceles (dos lados iguales) de perímetro 0 cm., cuál es el de área máima? -. 15/0.-
16 RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN Actualizado en el curso 008/009 0 Condición: + 0 h Función: A (, ) A ( ) A ( ) A ( ) A (10) < 0 Es un máimo Solución: 10 cm, 10 cm -. 16/0.-
17 Actualizado en el curso 008/009. Para la fabricación de un determinado producto, se necesita invertir dinero en contratar empleados comprar máquinas. El dueño de la fábrica ha estimado que si compra máquinas contrata empleados, el número de unidades de producto que podía fabricar vendría dado por la función: f (, ) 90 Cada máquina le supone una inversión de 500 cada contrato de un nuevo empleado otro de 1500 Si el empresario sólo dispone de un presupuesto de 500 para este fin, determine el número de obreros que debe contratar el número de máquinas que debe comprar para maimizar la producción. máquinas. empleados. 5 5 Condición: f, 90 Función: ( ) Solución: máquinas, 10 empleados 5 5 f( ) 90 f ( ) f ( ) f ( ) 0 1 ; 9 f ( ) f () < 0 Es Máimo. f (9) > 0 Es Mínimo.. Una esmeralda pesa 16 grs. sabemos que su valor es proporcional al cuadrado de su peso. Si partimos en dos trozos la esmeralda, halla el peso que debe tener cada uno de ellos para que su valor sea mínimo. Condición: peso de un trozo. peso del otro trozo. La función que queremos optimizar es la que nos da el valor de la esmeralda después de dividirla, que dependerá del peso de cada trozo. Función: f (, ) k + k -. 17/0.-
18 Solución: 8 gramos e 8 gramos. Actualizado en el curso 008/009 k( ) ( + ( 16 ) ) ( + 56) f (, ) + f ( ) k f ( ) k f ( ) k( ) ( ) 0 8 f ( ) k f, consideramos k > 0 f (8) > 0 Es mínimo.. Determina el punto de la gráfica de la función f ( ) en el que la pendiente de la recta tangente es máima. Cuál es la ecuación de la recta tangente en ese punto? Condición: f ( ) Pendiente: p ( ) f ( ) p ( ) 6 + 1, p ( ) 0 p ( ) 6, p () < 0 Es Máimo Solución: Punto buscado: P(, f ()) P(, 7) Ecuación Recta Tangente: 7 p() ( ) 7 5 ( ) 5. Una ingeniera sabe que la cantidad, en millones de euros, que gasta la empresa constructora de una autovía en función del tiempo (t en meses), viene dada por la siguiente función: 0,t si 0 t < f ( ), + 0,0 /( t ) si t < 8,6 + 0,1( t 8) si 8 t 1 Deduce, razonadamente, el valor de t en el que el gasto fue máimo /0.-
19 Actualizado en el curso 008/ Un aparejador sabe que el rendimiento de los operarios de una constructora a medida que avanza la jornada laboral. La función que epresa dicho rendimiento es R(t)0-10,5 t + t, siendo t el número de horas transcurridos desde el inicio de la jornada laboral. Determina cuando se produce el máimo rendimiento el mínimo. R + ( t) t t R ( t) 1t + t R (t) 0 t 0 t 7 R (0) -1 < 0 t 0 es el valor máimo R ( t) 1+ 6t R (7) 1 > 0 t 7 es el valor mínimo Conclusión: Al inicio de la jornada el rendimiento es máimo al final de la misma el rendimiento será mínimo. a) 7. Una bióloga marina sabe que los ingresos por venta de ejemplares de lubina en una planta de cultivo de peces es I(q) 000q 0,0q los costes de alimentación vienen dados por la función C(q) q +0,001q, donde q nº unidades de lubina. Halla: a) La función beneficio. b) Cuántas unidades ha que producir vender para que el beneficio sea máimo?. B( q) 000q 0 0q B( q) 0 01q q 0 001q q b) B ( q) 0 08q B (q) 0 q B ( q) 0 08 B (170 7) < 0 Conclusión: Es el valor que maimiza el beneficio. 8. Un médico ha leído que el número de personas afectadas por la enfermedad de las vacas locas viene dado por la función v() , donde representa el número de años transcurridos desde que se descubrió la enfermedad. Calcula: a) El número de años para que dicha enfermedad desaparezca. b) La tasa de propagación de la enfermedad al cabo de 5 años. c) El momento en que la enfermedad deja de crecer /0.-
20 Actualizado en el curso 008/009 a) La enfermedad nunca desaparece, es crónica TVM f (5) f (0) b) [ 0,5] 5 c) v ( ) + 0 v () 0-0 La enfermedad nunca deja de crecer..- Una bióloga está haciendo un cultivo de Escheritzia coli. Se sabe que el número de bacterias varía con el tiempo en días de acuerdo con la siguiente función N(t) 50 ( t - 15t + 6 t +), se pide: a) Cuántas bacterias había al principio? b) Cuál es el número máimo de bacterias? Cuándo?.- PAU-Junio 007- Hallar una función polinómica de tercer grado tal que tenga un etremo relativo en (1, 1) un punto de infleión en (0, ). Es (1,1) el único etremo de la función?. Determinar los máimos mínimos relativos de f. a) f ( ) a + b + c + d f ( ) a + b + c f ( ) 6a + b La función pasa por los puntos (1,1) (0,), por lo tanto sustituendo tenemos: (1,1) : (0,) : f (1) 0 f (0) 0 a + b + c + d 1 d a 1, a + b + c 0 b 0 b b) f ( ) f () 0 ± 1 0, c -, d f() + f ( ) 6 f ( 1) 9 < 0 f (1) > 0 es un máimo es un mínimo Máimo(-1,5) mínimo(1,1) -. 0/0.-
21 Actualizado en el curso 008/009.- Una tienda vende aceite a,10 el litro. Los costes de producción son de 0, céntimos el litro los de transporte son la centésima parte del cubo del número de litros vendidos. Halla cuántos litros deben venderse para obtener una ganancia máima. 5. Se estima que la ganancia de una empresa en decenas de miles de euros para los próimos 10 años sigue la función: t si 0 t < t + 1 f ( ) t + si t 10 t + 1 Averigua cuando será la ganancia máima. 6.- El precio de venta de un artículo viene dado por al epresión p 1-0,01, donde es el número de artículos fabricados p es el precio en cientos de euros. a) Si se fabrican se venden 500 artículos, cuáles serán los ingresos obtenidos? b) Cuál es la función que representa los ingresos en función de los artículos vendidos? c) Cuántos artículos se deben fabricar par que los ingresos sean máimos? 7.- La función f ( ) + a + b + c verifica que f(1)1, f (1)0 que f no tiene máimo(f``<0) ni mínimo (f``>0) en 1. Calcula a, b, c. Considérese el recinto limitado por la curva la recta : (-, ) (, ) 0 De entre los rectángulos situados como el de la figura anterior, determinar el que tiene área máima -. 1/0.-
22 Actualizado en el curso 008/009 Ejercicios de ampliación 5. La base menor de un trapecio isósceles mide 6 metros la longitud de los lados no paralelos es de metros. Calcula cuánto debe medir la base maor para que el área del trapecio sea máima. h 6 Condición (por Pitágoras): h + h Función: A trapecio ( ) ( 6 ) BASE + base h + h Atrapecio ( + ) h f(, h) ( ) f( ) + f ( ) f ( ) ( ) 1 < 0 Se descarta > f ( ) f ( ) < 0 es máimo Solución: + 1 metros e + 1 metros (el valor 1se descarta) 6. En un jardín con forma semicírculo de radio 10 m se va a instalar un parterre rectangular, uno de cuos lados está sobre el diámetro el opuesto a él tiene sus etremos en la parte curva. Calcula las dimensiones del parterre para que su área sea máima. -. /0.-
23 Actualizado en el curso 008/009 Condición: P(,) pertenece a la Circunferencia Función:f(,) ( ) f, ( ) f f ( ) f ( ) 0 ± 5 (La solución negativa no es válida) 100 f (5 ) < 0 (máimo) Solución: Dimensión del parterre será de base 10 m ; altura 5 m. Siendo el área máima de 100 m. 7. Se divide un alambre de 100 m de longitud en dos segmentos de longitudes Con el de longitud se forma un triángulo equilátero con el otro segmento se forma un cuadrado. Sea f() la suma de las áreas del triángulo del cuadrado. Indicar razonadamente para qué valor de se obtiene que la suma de las áreas del triángulo del cuadrado es mínima. h / (100-)/ Condición: Altura del triángulo h 6 6 Área del triángulo 6 a triangulo 6 -. /0.-
24 Actualizado en el curso 008/009 Área del cuadrado a cuadrado 100 Función: atriángulo + a f() cuadrado 100 f ( ) f ( ) f ( ) f ( ) f (56.5) > es un mínimo 7 Solución: Para 56.5 m. resulta la suma de las áreas mínima. 8. Sea T un triángulo de perímetro 60 cm. Uno de los lados del triángulo T mide cm. los dos lados tienen la misma longitud. a) Deducir razonadamente las epresiones de las funciones A f tales que: A() Área del triángulo T F() {A()} Indicar además entre que valores puede variar. b) Obtener, razonadamente, el valor de para el que f () alcanza el valor máimo. Condición: La altura del triángulo será: h a) -. /0.-
25 Solución: RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN Actualizado en el curso 008/ A (, ) A triangulo A ( ) 60 F(, ) ( A(, ) ) F( ) b) ( 60 ) F( ) 900 F ( ) ( ) F '( ) Por las condiciones del problema descartamos 0, siendo: F ( ) 90 F (0) < 0. Por lo tanto es máimo. Solución: 0 cm e 0 cm 9. Comprueba que el rectángulo de maor área que puede inscribirse en una circunferencia de ecuación + r es un cuadrado de lado r. r b/ h/ Condición: r r h r b b h + b + h Función Área b h -. 5/0.-
26 Actualizado en el curso 008/009 f(, b h) bh f( b) b r b b f ( b) r b f ( b) 0 b r r b ( ) ( ) b b r b + b f ''( b) < 0 r b r b ( ) h r b r r r Solución : El area es maima para: b r; h r -. 6/0.-
27 Actualizado en el curso 008/ En una carretera a través del desierto un automóvil debe de ir desde la ciudad A hasta el oasis P situado a 500 Km de distancia de A. Puede aprovechar para ello una carretera recta que une las ciudades A B que le permite ir a una velocidad de 100 Km/h, mientras que por el desierto la velocidad es de 60 Km/h. Sabiendo que la distancia más corta de P a la carretera que une las ciudades A B es de 00 Km, determina la ruta que deberá usar para ir de A a P en el menor tiempo posible. A M 1 Derivando, t () Si hacemos t () 0 obtenemos La ruta a seguir es AMP Aplicando el teorema de Pitágoras en el triángulo ABP se obtiene: AB En el triángulo MBP se obtiene MP + 00 Y el tiempo que tarda el automóvil en recorrer la distancia AM + MP es: t( ) 1 ± La solución negativa no tiene sentido: AM El automóvil deja la carretera a 175 km de la ciudad A. P B 00 Podemos comprobar que es un mínimo utilizando la segunda derivada: t () 60( + 00 ) 60 ( ) t () + 00 ( ) Para 5 t () > 0, por lo tanto, es un mínimo. Solución: La ruta a seguir es AMP, de A a M ha 175 Km. de M a P ha Km., con lo que recorrerá en total 550 Km. a una velocidad de 100 Km/h /0.-
28 Actualizado en el curso 008/ Determine los puntos de la curva que están a distancia mínima del punto P (, 0). Q 1 Condición: de donde Un punto de la curva tiene la forma P(, ± ) 0 1 P(,0) Función: dpq (, ) ( ) + ( ± ) Q ( ) ( ) dpq (, ) + ± d + ( ) 16 d ( ) d ( ) d ( ) d () > 0 ( + 16) El punto es mínimo. Solución: Q1(, ) Q(, ). Un rectángulo tiene por vértices los puntos de coordenadas ( 0,0), (a,0), ( 0, b ) ( a, b), de modo que el punto ( a, b) tiene coordenadas positivas está situado en la curva 1 de ecuación: +. De todos estos rectángulos hallar razonadamente el de área mínima. 1 Condición: Si (a, b) pertenece a la curva, verifica: b + a 1 1 Función: El área del rectángulo es Aa ( ) a + a + a a -. 8/0.-
29 Actualizado en el curso 008/ A ( a) + A ( a) 0 a± a El valor a -1/ no es valido por que se indica que las coordenadas son positivas. 1 A ( a) A ( ) > 0 (es mínimo) a Solución: Los vértices serán (0,0), (1/,0), (1/,8) (0,8). (Problema del tiempo mínimo).- Un nadador, A, se encuentra a km. De la plaa enfrente de una caseta. Desea ir a B, en la misma plaa, a 6 Km. De la caseta. Sabiendo que nada a km/h que anda por la arena a 5 km/h, averigua a qué lugar debe dirigirse a nado para llegar a B en el menor tiempo posible. P 6 - B h 9 + a Km/h Recorre 6 a 5 Km/h Km A h t ( ) Tiempo empleado: t( ) Haciendo t ( ) ; (No valida) t ( 5) > 0 Es mínimo. Solución: Debe dirigirse a un punto que esté a.5 Km de la caseta. Tiempo que tarda en llegar: t t horas /0.-
30 Actualizado en el curso 008/009. Si un cultivador valenciano planta 00 naranjos por hectárea, el rendimiento promedio es de 00 naranjas por árbol. Por cada árbol adicional que siembre por hectárea, el cultivador obtendrá 15 naranjas menos por árbol. Cuántos árboles por hectárea darán la mejor cosecha? Nº naranjos / hectárea 00 Rendimiento / árbol 00 naranjas nº árboles a plantar R () Rendimiento() ( ) ( ) R( ) R( ) R ( ) R ( ) Solución absurda. Conclusión: Sin plantar árboles la producción que se obtiene es mejor que si aumentamos el número de frutales de esta variedad. 5. El propietario de un edificio tiene alquilados los 0 pisos del mismo a un precio de 600 cada uno. Por cada 60 que el propietario aumenta el precio observa que pierde un inquilino. a qué precio le convienen alquilar los pisos para obtener la maor ganancia posible?(auda: llamar nº de 60 que aumenta o lo que es lo mismo el nº inquilinos perdidos.) 0 pisos 600 euros / cada uno Si aumenta euros por cada piso cobra 600 +, pero alquila 0 60 pisos. La función es el beneficio obtenido: B ( ) (600 + ) 0 con 0 < < B ( ) B ( ) 0 B ( ) B ( ) B (900) < 0 Es Máimo. 0 Solución: Aumentará /0.-
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN
 1. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren
1. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN Actualizado en el curso 2008/2009
 1. Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máxima. Calcular dicha suma. 2. Calcula dos números que cumplan que al sumarlos
1. Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máxima. Calcular dicha suma. 2. Calcula dos números que cumplan que al sumarlos
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN
 1. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren
1. En un concurso se da a cada participante un alambre de dos metros de longitud para que doblándolo convenientemente hagan con el mismo un cuadrilátero con los cuatro ángulos rectos. Aquellos que lo logren
Apuntes Matemáticas 2º de bachillerato. Tema 6. Optimización
 Apuntes Tema 6 Optimización 6.1 Problemas de optimización El cálculo de máximos y mínimos no solo se usa en Matemáticas, sino en muchas otras disciplinas. Precisamente este tipo de problemas fue el que
Apuntes Tema 6 Optimización 6.1 Problemas de optimización El cálculo de máximos y mínimos no solo se usa en Matemáticas, sino en muchas otras disciplinas. Precisamente este tipo de problemas fue el que
Problemas de optimización
 Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN Y APLICACIÓN DE DERIVADAS
 1. Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máxima. Calcular dicha suma. Solución: Los sumandos han de ser e y e. La suma
1. Descomponer el número e en dos sumandos positivos de forma que la suma de los logaritmos neperianos de los sumandos sea máxima. Calcular dicha suma. Solución: Los sumandos han de ser e y e. La suma
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
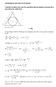 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
SOLUCIONES MINIMOS 2º ESO TEMA 7 TEOREMA DE PITÁGORAS.SEMEJANZA
 SOLUCIONES MINIMOS º ESO TEMA 7 TEOREMA DE PITÁGORAS.SEMEJANZA Ejercicio nº 1.- Los lados de un triángulo miden, respectivamente, 9 cm, 1 cm y 15 cm. Averigua si el triángulo es rectángulo. Según el teorema
SOLUCIONES MINIMOS º ESO TEMA 7 TEOREMA DE PITÁGORAS.SEMEJANZA Ejercicio nº 1.- Los lados de un triángulo miden, respectivamente, 9 cm, 1 cm y 15 cm. Averigua si el triángulo es rectángulo. Según el teorema
Efa Moratalaz PCPI - Matemáticas GEOMETRÍA PLANA
 GEOMETRÍA PLANA Geometría Plana Ficha 1 (Ejercicios Cuadrado) Área de un cuadrado: Perímetro de un cuadrado: 1) Halla el perímetro y el área de un cuadrado de 3 m de lado. 2) Halla el perímetro y el área
GEOMETRÍA PLANA Geometría Plana Ficha 1 (Ejercicios Cuadrado) Área de un cuadrado: Perímetro de un cuadrado: 1) Halla el perímetro y el área de un cuadrado de 3 m de lado. 2) Halla el perímetro y el área
Tema 10 Aplicaciones de la derivada Matemáticas II 2º Bachillerato 1. ( x) 2x x. Hay dos puntos: (1, 2) y (1, 2)
 Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
Tema 0 Aplicaciones de la derivada Matemáticas II º Bachillerato TEMA 0 APLICACIONES DE LA DERIVADA RECTA TANGENTE Escribe e 0 EJERCICIO : la ecuación de la recta tangente a la curva f en 0. Ordenada del
a) A la mitad del número le sumo 3 y el resultado es 8 ( ) 9 b) En la ecuación 3x = 54 Qué valor puede tomar x? ( ) Rombo
 Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Guía Matemáticas 3 ELIGE LA RESPUESTA CORRECTA.. Anota en el paréntesis de la derecha la letra que corresponda. a) A la mitad del número le sumo 3 y el resultado es 8 9 b) En la ecuación 3 = 54 Qué valor
Problemas de optimización
 Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
Problemas de optimización 1º) La producción de cierta hortaliza en un invernadero (Q() en Kg) depende de la temperatura (ºC) según la epresión Q() = ( + 1) 2 (2 ). a) Calcula razonadamente cuál es la temperatura
Figuras Planas. 100 Ejercicios para practicar con soluciones. 1 Comprueba si los siguientes ángulos son complementarios: a) 72 + 35.
 Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
Figuras Planas. 100 Ejercicios para practicar con soluciones 1 Comprueba si los siguientes ángulos son complementarios: a) 7º y 35 b) 6º y 64º a) 7 + 35 = 107 90 No son complementarios. b) 6 + 64 = 90
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES. 2.- La suma de dos números es 15 y su producto es 26. Cuáles son dichos números?
 RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES 1.- El perímetro de un rectángulo es 4 cm y su área es 0 cm. Cuáles son sus dimensiones? Sea = altura ; y = base Como perímetro es 4: + y = 1 y = 1 Como el área
www.academiacae.com!!info@academiacae.com!!91.501.36.88!!28007!madrid!
 CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
CONTINUIDAD Y DERIVABILIDAD. TEOREMAS Y APLICACIONES DE LAS DERIVADAS 1.- junio 1994 Se sabe que y = f (x) e y = g (x) son dos curvas crecientes en x = a. Analícese si la curva y = f(x) g(x) ha de ser,
Máximo o mínimo de una función. Solución: El mínimo de una función se da en los puntos que anulan su derivada y tiene derivada segunda positiva.
 Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
Análisis: Máimos, mínimos, optimización 1 Máimo o mínimo de una función Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 = 5 dm b) 8 = 8 cm P =
APLICACIONES DE LAS DERIVADAS
 7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
7 APLICACIONES DE LAS DERIVADAS Página 67 REFLEXIONA Y RESUELVE Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0
1 Indica cuál es el valor de los ángulo Â, Bˆ. en las siguientes figuras: a) b) 2 Calcula los ángulos dados por letras:
 1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
1 Indica cuál es el valor de los ángulo Â, Bˆ y Ĉ en las siguientes figuras: a) b) Calcula los ángulos dados por letras: 3 Calcula el valor del ángulo A. 4 Dados los ángulos los mismos. a 45 0 30.y b 6
TEMA 5 FUNCIONES ELEMENTALES II
 Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
Tema Funciones elementales Ejercicios resueltos Matemáticas B º ESO TEMA FUNCIONES ELEMENTALES II Rectas EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas
x = 0, la recta tangente a la gráfica de f (x)
 CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
CÁLCULO DIFERENCIAL JUNIO 004 1. Sea la función e y = estúdiese su monotonía, etremos relativos y asíntotas. (Solución: Es derivable en todos los puntos ecepto en =0. Creciente si < 0. No tiene asíntotas
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA
 CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
CÁLCULO DIFERENCIAL (SEMESTRE 01-2010) EJERCICIOS COMPLEMENTARIOS SECCIÓN 1.1 DEL TEXTO GUÍA 1. Expresar el área de un triángulo equilátero como función de la altura h del triángulo. 2. Se va a construir
1 Calcula en la siguiente figura el elemento que falta: 2 Calcula en la siguiente figura el elemento que falta:
 1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
1 Calcula en la siguiente figura el elemento que falta: Calcula en la siguiente figura el elemento que falta: Calcula el valor de la diagonal de un ortoedro de aristas cm, 4 cm y 5 cm. 4 Comprueba la fórmula
FIGURAS PLANAS: RECTÁNGULOS. R1.
 NÚMEROS. N1. Encuentra dos números positivos cuya suma sea 120, tales que el producto de uno de ellos por el cuadrado del otro sea máximo. N2. Expresa el número 90 como suma de tres enteros positivos de
NÚMEROS. N1. Encuentra dos números positivos cuya suma sea 120, tales que el producto de uno de ellos por el cuadrado del otro sea máximo. N2. Expresa el número 90 como suma de tres enteros positivos de
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES
 Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
Etremos y optimización de funciones EXTREMOS Y OPTIMIZACIÓN DE FUNCIONES CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN. EXTREMOS RELATIVOS En 1º de Bachillerato, basándonos en la interpretación geométrica
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
APLICACIONES DE LA DERIVADA Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en un punto
EXAMEN GEOMETRÍA. 5. Halla el perímetro y el área de un triángulo isósceles cuyos lados miden 5, 5 y 8 cms., respectivamente.
 1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
1. Supongamos una circunferencia de radio 90/ð cms. y un ángulo cuyo vértice coincida con el centro de la circunferencia. Halla: a) La longitud de arco de circunferencia que abarca un ángulo de 501. b)
EJERCICIOS RESUELTOS. x )
 BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
BXX5744_08 /6/09 09:59 Página 77 EJERCICIOS RESUELTOS Estudia el crecimiento, decrecimiento y los etremos relativos de la función f() = El dominio de f() es R, por lo tanto eiste en ]0, π[. Calculamos
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES
 CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
CÁLCULO DE PRIMITIVAS Y ÁREAS POR INTEGRALES RELACIÓN DE PROBLEMAS DE SELECTIVIDAD º DE BACHILLERATO CIENCIAS DEPARTAMENTO DE MATEMÁTICAS COLEGIO MARAVILLAS TERESA GONZÁLEZ GÓMEZ .-Hallar una primitiva
EJERCICIOS PAU MATEMÁTICAS II ANDALUCÍA Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.
 FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
FUNCIONES I: LÍMITES, CONTINUIDAD Y DERIVAVILIDAD 1- Sea : definida por a) Halla a, b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1/2 y que la recta tangente en el punto de
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
, siendo ln(1+x) el logaritmo neperiano de 1+x. x
 Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
La circunferencia y el círculo
 La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO Halla la superficie y el perímetro del recinto marrón: Calcula el perímetro y el área de esta figura: Calcula el perímetro y el área de esta figura:
Hoja de problemas nº 7. Introducción a la Geometría
 Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
Hoja de problemas nº 7 Introducción a la Geometría 1. Un rectángulo tiene de área 135 u 2 a. Si sus lados miden números enteros, averigua cuáles pueden ser sus dimensiones. b. Cortamos los vértices como
I.E.S VICENTE ALEIXANDRE BARBATE
 1. Calcula el área y el perímetro de estas figuras:. Un sector circular mide 80 y tiene 10 de radio. Cuál es su área y su perímetro? 3. El área de la zona sombreada es de 35. Cuál es la superficie del
1. Calcula el área y el perímetro de estas figuras:. Un sector circular mide 80 y tiene 10 de radio. Cuál es su área y su perímetro? 3. El área de la zona sombreada es de 35. Cuál es la superficie del
Matemática I - Problemas de Máximos y Mínimos
 Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
Conceptos previos de la materia a considerar: Concepto de Función. Dominio, codominio, imagen. Formas de expresar una función: mediante tablas, mediante gráficas y analíticamente. Funciones crecientes
TEMA 10. CÁLCULO DIFERENCIAL
 TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
TEMA 0. CÁLCULO DIFERENCIAL Problemas que dieron lugar al cálculo diferencial. (Estos dos problemas los resolveremos más adelante) a) Consideremos la ecuación de movimiento de un móvil en caída libre en
6 EXPRESIONES FRACCIONARIAS Y RADICALES
 EJERCICIOS PROPUESTOS. Halla el valor numérico de la fracción 7 0 para los valores, 0 y. 8 Para : Para 0: 0 0 Para : 7 0 0. Valor indeterminado. 8 0 7 0 0 0 5 0 8 8. 7 0. No eiste valor numérico. 8 0.
EJERCICIOS PROPUESTOS. Halla el valor numérico de la fracción 7 0 para los valores, 0 y. 8 Para : Para 0: 0 0 Para : 7 0 0. Valor indeterminado. 8 0 7 0 0 0 5 0 8 8. 7 0. No eiste valor numérico. 8 0.
13 LONGITUDES Y ÁREAS
 EJERCICIOS PROPUESTOS 1.1 Calcula el perímetro de las siguientes figuras., cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Halla el perímetro de estas figuras. a) Un cuadrado de 6 centímetros de lado. b) Un triángulo
EJERCICIOS PROPUESTOS 1.1 Calcula el perímetro de las siguientes figuras., cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Halla el perímetro de estas figuras. a) Un cuadrado de 6 centímetros de lado. b) Un triángulo
PROBLEMAS DE RECTA TANGENTE. 6 en el punto de abscisa 2. Halla la ecuación de la recta tangente a. ( en el punto de abscisa. x 3x
 PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
PROBLEMAS DE RECTA TANGENTE º Bachillerato CCSS Halla la ecuación de la recta tangente a ( ) 6 en el punto de abscisa Halla la ecuación de la recta tangente a Halla la ecuación de la recta tangente a (
PENDIENTES 2º ESO. Tercer examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del tercer examen de recuperación de MATEMÁTICAS DE 2º ESO Curso 2013-2014
 014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
014 015 Preparación del tercer examen de recuperación de MATEMÁTICAS DE º ESO PENDIENTES º ESO Tercer examen DEPARTAMENTO DE MATEMÁTICAS 1.- En un triángulo rectángulo, los catetos miden 5 y 1cm, respectivamente.
APLICACIONES DE LA DERIVADA CCSS
 APLICACIONES DE LA DERIVADA CCSS Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en
APLICACIONES DE LA DERIVADA CCSS Crecimiento y decrecimiento. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto: Una función f() es creciente en
TRANSFORMACIONES DEL PLANO
 PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
PROBLEMAS DE GEOMETRÍA. TRANSFORMACIONES DEL PLANO 1. Un producto de dos simetrías axiales de ejes perpendiculares A qué transformación corresponde? En qué se transforma un segmento vertical? ( ) 2. Cuál
x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =
![x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) = x 1. [ANDA] [SEP-B] Considera la función f:[0,4] definida por: f(x) =](/thumbs/76/74425342.jpg) Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
Selectividad CCNN 00. [ANDA] [SEP-B] Considera la función f:[0,] definida por: f() = +a+b si 0 c si
c) Demuestra que la función f(x) anterior y g(x) = 2x 1 se cortan al menos en un punto. (1 punto) 2
 Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
Junio 010 1A. a) Enuncia el teorema de Bolzano. (0,5 puntos) 1 b) Se puede aplicar dicho teorema a la función f ( x) 1 x en algún intervalo? (1 punto) c) Demuestra que la función f(x) anterior y g(x) =
5 Operaciones. con polinomios. 1. Polinomios. Suma y resta
 5 Operaciones con polinomios 1. Polinomios. Suma y resta Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A() = 6 2 b) V() = 3 P I E N S A Y C A L C U L A 1 Dado el prisma
5 Operaciones con polinomios 1. Polinomios. Suma y resta Dado el cubo de la figura, calcula en función de : a) El área. b) El volumen. a) A() = 6 2 b) V() = 3 P I E N S A Y C A L C U L A 1 Dado el prisma
EJERCICIOS RESUELTOS MÍNIMOS 3º ESO TEMA 8 PROBLEMAS MÉTRICOS DEL PLANO
 EJERCICIOS RESUELTOS MÍNIMOS 3º ESO TEMA 8 PROBLEMAS MÉTRICOS DEL PLANO Ejercicio nº 1.- Calcula la medida de los ángulos desconocidos: a) b) a) A ˆ = 180 35 = 145 Por ser opuestos por el vértice: Bˆ =
EJERCICIOS RESUELTOS MÍNIMOS 3º ESO TEMA 8 PROBLEMAS MÉTRICOS DEL PLANO Ejercicio nº 1.- Calcula la medida de los ángulos desconocidos: a) b) a) A ˆ = 180 35 = 145 Por ser opuestos por el vértice: Bˆ =
MATEMÁTICAS 1º BAC Aplicaciones de las derivadas
 . Queremos construir una caja abierta, de base cuadrada y volumen 56 litros. Halla las dimenones para que la superficie, y por tanto el coste, sea mínimo.. Entre todos los rectángulos de área 6 halla el
. Queremos construir una caja abierta, de base cuadrada y volumen 56 litros. Halla las dimenones para que la superficie, y por tanto el coste, sea mínimo.. Entre todos los rectángulos de área 6 halla el
9. Rectas e hipérbolas
 08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
Profesor: Fernando Ureña Portero
 Optimización de funciones P a s o s p a r a l a r e s o l u c i ó n d e p ro b l e m a : 1. S e p l a n t e a l a f u n c i ón que hay que maximizar o minimizar. 2. S e p l a n t e a u n a e c u a c i
Optimización de funciones P a s o s p a r a l a r e s o l u c i ó n d e p ro b l e m a : 1. S e p l a n t e a l a f u n c i ón que hay que maximizar o minimizar. 2. S e p l a n t e a u n a e c u a c i
ÁNGULOS EN POLÍGONOS. Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c. Ejercicio nº 2.-
 ÁNGULOS EN POLÍGONOS Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c Ejercicio nº.- Halla el valor del ángulo en cada uno de estos casos: a b c Ejercicio nº 3.- Halla el
ÁNGULOS EN POLÍGONOS Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c Ejercicio nº.- Halla el valor del ángulo en cada uno de estos casos: a b c Ejercicio nº 3.- Halla el
TEMA 10 FUNCIÓN DERIVADA. REPRESETACIÓN y aplicaciones.
 A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones polinómicas, a) f( = 5 b) g( = 4 c) h( = 7 d) i( = 4 5 e) i( = 3 + 1 f) j( = 5 4 + 3 g) k( = 3 + 4 + h) l( = 5 3 43 5 i) m( = 4 + 3 3 + 4. Calcula
ÁREAS O SUPERFICIES DE FIGURAS PLANAS
 ÁREAS O SUPERFICIES DE FIGURAS PLANAS CUADRADO --- RECTÁNGULO 1. - Calcula el área de los cuadrados cuyos lados miden: a) 8 cm. b) 3,5 dm c) 10 m. d) 0,5 dm a) b) c) d) 2. - Halla el área o superficie
ÁREAS O SUPERFICIES DE FIGURAS PLANAS CUADRADO --- RECTÁNGULO 1. - Calcula el área de los cuadrados cuyos lados miden: a) 8 cm. b) 3,5 dm c) 10 m. d) 0,5 dm a) b) c) d) 2. - Halla el área o superficie
1.4. Proporcionalidad de perímetros, áreas y volúmenes en objetos semejantes Si dos figuras son semejantes, entonces se verifica que: V = 3
 TEMA 8: SEMEJANZA Y TRIGONOMETRÍA. Teorema de Thales.. Teorema de Thales Si se trazan un conjunto de rectas paralelas entre sí: L, L, L, que cortan a dos rectas r y s, los segmentos que determinan sobre
TEMA 8: SEMEJANZA Y TRIGONOMETRÍA. Teorema de Thales.. Teorema de Thales Si se trazan un conjunto de rectas paralelas entre sí: L, L, L, que cortan a dos rectas r y s, los segmentos que determinan sobre
, hallar su dominio, los puntos de corte con los ejes y la pendiente de la recta x 2-4 tangente a la gráfica de la función en x = 1.
 . [04] [ET-A] El beneficio semanal (en miles de euros) que obtiene una fábrica por la producción de aceite viene dado por la función B(x) = -x +6x-8, donde x representa los hectolitros de aceite producidos
. [04] [ET-A] El beneficio semanal (en miles de euros) que obtiene una fábrica por la producción de aceite viene dado por la función B(x) = -x +6x-8, donde x representa los hectolitros de aceite producidos
a) El beneficio es el resultado de restar los ingresos y gastos. Esto es,
 Análisis: Máimos, mínimos, optimización 1. Una multinacional ha estimado que anualmente sus ingresos en euros vienen dados por la función I( ) 8 6000, mientras que sus gastos (también en euros) pueden
Análisis: Máimos, mínimos, optimización 1. Una multinacional ha estimado que anualmente sus ingresos en euros vienen dados por la función I( ) 8 6000, mientras que sus gastos (también en euros) pueden
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón:
 PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón: 2 ) Calcula el perímetro y el área de esta figura: 3 ) Calcula el perímetro y el área de
PERÍMETROS Y ÁREAS DE FIGURAS PLANAS UNIDADE 13 1º ESO 1 ) Halla la superficie y el perímetro del recinto marrón: 2 ) Calcula el perímetro y el área de esta figura: 3 ) Calcula el perímetro y el área de
P. A. U. LAS PALMAS 2005
 P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
P. A. U. LAS PALMAS 2005 OPCIÓN A: J U N I O 2005 1. Hallar el área encerrada por la gráfica de la función f(x) = x 3 4x 2 + 5x 2 y la rectas y = 0, x = 1 y x = 3. x 3 4x 2 + 5x 2 es una función polinómica
EJERCICIOS DE LA UNIDAD DE TRIÁNGULOS
 EJERCICIOS DE LA UNIDAD DE TRIÁNGULOS TEOREMA DE TALES 1. Usa el Teorema de Tales para calcular x a) b) c) d) 2. Aplicando el teorema de Tales, divide un segmento de 9 centímetros de longitud en 5 partes
EJERCICIOS DE LA UNIDAD DE TRIÁNGULOS TEOREMA DE TALES 1. Usa el Teorema de Tales para calcular x a) b) c) d) 2. Aplicando el teorema de Tales, divide un segmento de 9 centímetros de longitud en 5 partes
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto).
 1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
1.- Punto: Intersección de dos rectas. No tiene dimensiones (ni largo, ni ancho, ni alto). 6.- Espacio: Conjunto de puntos con tres dimensiones: largo, ancho y alto. Es infinito, sin límites. 2.- Recta:
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL
 EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
EJERCICIOS RESUELTOS DE DERIVADAS DE FUNCIONES REALES DE UNA VARIABLE REAL Ejercicio nº 1.- Calcula (), utilizando la definición de derivada, siendo: f () + 5 f ( + ) f () ( + ) + 5( + ) 18 (4 + 4 + )
Tema: Aplicaciones de derivadas. Sean x e y las dimensiones del rectángulo. Área del rectángulo: A = x y. 36 x. Luego, el área es A(x) =
 JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
JUNIO 0 GENERAL. Halle el rectángulo de mayor área inscrito en una circunferencia de radio. Sean e y las dimensiones del rectángulo. Área del rectángulo: A y El triángulo ABC es rectángulo, sus lados miden,
A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar.
 C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
C URSO: º BACHILLERATO DERIVABILIDAD. A) CÁLCULO DE DERIVADAS. 1. Deriva las siguientes funciones pensando antes que tipo de fórmula hay que utilizar. 9 7 a) f ( 4 1 b) f ( 8 4 c) 4 f ( 1 d) ( ) 7 4 f
UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO
 UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO 1. POLÍGONOS: DEFINÍCIÓN, ELEMENTOS Y CLASIFICACIÓN. 2. POLÍGONOS REGULARES E IRREGULARES. 3. TRIÁNGULOS Y CUADRILÁTEROS: CLASIFICACIÓN. 4.
UNIDAD 10. FIGURAS PLANAS: POLÍGONOS CIRCUNFERENCIA Y CÍRCULO 1. POLÍGONOS: DEFINÍCIÓN, ELEMENTOS Y CLASIFICACIÓN. 2. POLÍGONOS REGULARES E IRREGULARES. 3. TRIÁNGULOS Y CUADRILÁTEROS: CLASIFICACIÓN. 4.
Propiedades de las funciones derivables. Representación gráfica de funciones. Determinar los puntos de inflexión. (Junio 1997)
 Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
PRUEBA GEOMETRÍA CDI 2015
 Portal Fuenterrebollo PRUEBA GEOMETRÍA CDI 015 1. Una cruz compuesta por cinco cuadrados iguales está inscrita en un cuadrado. Si el área de la cruz es de 5 cm. Cuál es, en cm, el área del cuadrado? 5
Portal Fuenterrebollo PRUEBA GEOMETRÍA CDI 015 1. Una cruz compuesta por cinco cuadrados iguales está inscrita en un cuadrado. Si el área de la cruz es de 5 cm. Cuál es, en cm, el área del cuadrado? 5
(1-mx)(2x+3) x 2 +4 = 6. x > -1
 . [04] [EXT-A] Sea la función f(x) = e x +ax+b a) Calcular a y b para que f(x) tenga un extremo en el punto (,). b) Calcular los extremos de la función f(x) cuando a = 0 y b = 0.. [04] [EXT-B] En la figura
. [04] [EXT-A] Sea la función f(x) = e x +ax+b a) Calcular a y b para que f(x) tenga un extremo en el punto (,). b) Calcular los extremos de la función f(x) cuando a = 0 y b = 0.. [04] [EXT-B] En la figura
x 2-4 intervalos de crecimiento y decrecimiento, sus máximos y mínimos, sus intervalos de concavidad y convexidad y sus puntos de inflexión.
 . [ANDA] [JUN-A] De la función f: definida por f() = a 3 +b +c+d se sabe que tiene un máimo en = -, que su gráfica corta al eje O en el punto de abscisa = y tiene un punto de infleión en el punto de abscisa
. [ANDA] [JUN-A] De la función f: definida por f() = a 3 +b +c+d se sabe que tiene un máimo en = -, que su gráfica corta al eje O en el punto de abscisa = y tiene un punto de infleión en el punto de abscisa
MÚLTIPLOS Y DIVISORES
 Alumno:......... MÚLTIPLOS Y DIVISORES 1 Cuándo se dice que un número es divisor de otro? Cómo se calculan los divisores de un número dado? Cuántos divisores tiene un número? Cuándo se dice que un número
Alumno:......... MÚLTIPLOS Y DIVISORES 1 Cuándo se dice que un número es divisor de otro? Cómo se calculan los divisores de un número dado? Cuántos divisores tiene un número? Cuándo se dice que un número
Ejercicios de números reales
 Ejercicios de números reales Ejercicio nº.- Clasifica los siguientes números como naturales, enteros, racionales o reales:,7 7 7 Ejercicio nº.- Considera los siguientes números: 9,000000..., 8,... Clasifícalos
Ejercicios de números reales Ejercicio nº.- Clasifica los siguientes números como naturales, enteros, racionales o reales:,7 7 7 Ejercicio nº.- Considera los siguientes números: 9,000000..., 8,... Clasifícalos
Portal Fuenterrebollo Olimpiada Matemáticas Nivel III (3º 4º ESO) OLIMPIADA MATEMÁTICAS NIVEL III (3º - 4º ESO)
 Portal Fuenterrebollo Olimpiada Matemáticas Nivel III (º º ESO) OLIMPIADA MATEMÁTICAS NIVEL III (º - º ESO) 6. Encima de un triángulo equilátero de lado cm, colocamos un círculo de cm de radio, haciendo
Portal Fuenterrebollo Olimpiada Matemáticas Nivel III (º º ESO) OLIMPIADA MATEMÁTICAS NIVEL III (º - º ESO) 6. Encima de un triángulo equilátero de lado cm, colocamos un círculo de cm de radio, haciendo
PRÁCTICA 1: 2) Calcular el valor de x con tres cifras significativas. 2) Determina el valor de x e y en el siguiente dibujo. b) x. 6 x 60.
 PRÁCTICA 1: 1) 2) Calcular el valor de con tres cifras significativas a) b) c) 7 40 20 6 60 d) e) f) 40 6 60 7 20 2) Determina el valor de e y en el siguiente dibujo y 40 6 20 3) Determina el valor de
PRÁCTICA 1: 1) 2) Calcular el valor de con tres cifras significativas a) b) c) 7 40 20 6 60 d) e) f) 40 6 60 7 20 2) Determina el valor de e y en el siguiente dibujo y 40 6 20 3) Determina el valor de
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
sen sen sen a 2 a cos cos 2 a
 BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
BLOQUE I: TRIGONOMETRÍA Y TRIÁNGULOS.- Sabiendo que tg g y cot, calcular tg y cos( ).- Demostrar razonadamente las fórmulas del seno, coseno y tangente del ángulo mitad.- Demostrar las siguientes igualdades:
TEMA 8: TEOREMA DE PITÁGORAS. SEMEJANZA. ÁREAS DE FIGURAS PLANAS. 1. Calcula el área de las figuras siguientes: TEOREMA DE PITÁGORAS
 TEMA 8: TEOREMA DE PITÁGORAS. SEMEJANZA. ÁREAS DE FIGURAS PLANAS 1. Calcula el área de las figuras siguientes: TEOREMA DE PITÁGORAS En un triángulo rectángulo, los lados menores son los que forman el ángulo
TEMA 8: TEOREMA DE PITÁGORAS. SEMEJANZA. ÁREAS DE FIGURAS PLANAS 1. Calcula el área de las figuras siguientes: TEOREMA DE PITÁGORAS En un triángulo rectángulo, los lados menores son los que forman el ángulo
TEOREMA DE PITÁGORAS. SEMEJANZA. (http://profeblog.es/blog/luismiglesias)
 Cuestiones 1. Qué polígonos son semejantes cuando tienen los lados proporcionales? a) Todos. c) Ninguno. b) Los cuadriláteros. d) Los triángulos. 2. La razón entre los perímetros de dos figuras semejantes
Cuestiones 1. Qué polígonos son semejantes cuando tienen los lados proporcionales? a) Todos. c) Ninguno. b) Los cuadriláteros. d) Los triángulos. 2. La razón entre los perímetros de dos figuras semejantes
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
Estudio de funciones mediante límites y derivadas Observación: La mayoría de estos ejercicios se han propuesto en las pruebas de Selectividad, en los distintos distritos universitarios españoles El precio
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES.
 APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
Integral definida. 1. Integral definida. Piensa y calcula. Aplica la teoría. 3. Siendo x el valor absoluto o módulo de x, calcula la. 2.
 Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
Integral definida. Integral definida Piensa y calcula Halla, contando, el área de la ª figura del margen, la que tiene un signo + dentro. Cada cuadradito es una unidad cuadrada. Tiene eactamente 7, u y
16. Dados los puntos A(-1,3), B(2,0) y C(-2,1). Halla las coordenadas de otro punto D para que los vectores y sean equivalentes.
 TEMA 5. VECTORES 5.1. Vectores en el plano. - Definición. - Componentes de un vector. - Módulo. - Vectores equivalentes. 5.2. Operaciones con vectores. - Suma y resta. - Multiplicación por un número real.
TEMA 5. VECTORES 5.1. Vectores en el plano. - Definición. - Componentes de un vector. - Módulo. - Vectores equivalentes. 5.2. Operaciones con vectores. - Suma y resta. - Multiplicación por un número real.
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE
 TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
TEORMAS DE WEIERSTRASS, BOLZANO, ROLLE Y LAGRANGE PROBLEMAS RESUELTOS + Dada F() =, escriba la ecuación de la secante a F que une los puntos (, F( )) y 4 (, F()). Eiste un punto c en el intervalo [, ]
EJERCICIOS. ÁREAS Y VOLÚMENES.
 EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
EJERCICIOS. ÁREAS Y VOLÚMENES. Teorema de Tales 1. Sean los triángulos ABC, AB'C'.Calcula el valor desconocido x. 2. Dos triángulos semejantes tienen una superficie de 20cm 2 y 30cm 2 respectivamente.
TEMA 8 GEOMETRÍA ANALÍTICA
 Tema 8 Geometría Analítica Matemáticas 4º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Halla el punto medio del segmento de extremos P, y Q4,. Las coordenadas del punto medio,
Tema 8 Geometría Analítica Matemáticas 4º ESO TEMA 8 GEOMETRÍA ANALÍTICA RELACIÓN ENTRE PUNTOS DEL PLANO EJERCICIO : Halla el punto medio del segmento de extremos P, y Q4,. Las coordenadas del punto medio,
A = 180-90 - 62 = 28. 8 GEOMETRíA DEL PLA 8 = 720-145 - 125-105 - 130-160 = 55. b) 720 = 90: ~ B- 110 + 8+ 150 + 90 = 440 + 28 ==> B = 140 C
 8 GEOMETRíA DEL PLA EJERCCOS PROPUESTOS Calcula la medida del ángulo que falta en cada figura. a) b) a) En un triángulo, la suma de las medidas de sus ángulos es 180, A = 180-90 - 6 = 8 El ángulo mide
8 GEOMETRíA DEL PLA EJERCCOS PROPUESTOS Calcula la medida del ángulo que falta en cada figura. a) b) a) En un triángulo, la suma de las medidas de sus ángulos es 180, A = 180-90 - 6 = 8 El ángulo mide
TRIANGULOS. La trigonometría se desarrollo con el fin de relacionar los lados y los ángulos de los triángulos.
 TRIANGULOS La trigonometría se desarrollo con el fin de relacionar los lados y los ángulos de los triángulos. CLASIFICACION DE LOS TRIANGULOS Los triángulos se pueden clasificar por la relación entre las
TRIANGULOS La trigonometría se desarrollo con el fin de relacionar los lados y los ángulos de los triángulos. CLASIFICACION DE LOS TRIANGULOS Los triángulos se pueden clasificar por la relación entre las
Colegio C. C. Mª Auxiliadora II Marbella Urb. La Cantera, s/n. 952822586 http:/www.mariaauxiliadora2.com SISTEMAS DE ECUACIONES
 Colegio C. C. Mª Auiliadora II Marbella Urb. La Cantera, s/n. 988 http:/www.mariaauiliadora.com º ESO SISTEMAS DE ECUACIONES º. Une con flechas cada pareja de números con el sistema del que es solución:
Colegio C. C. Mª Auiliadora II Marbella Urb. La Cantera, s/n. 988 http:/www.mariaauiliadora.com º ESO SISTEMAS DE ECUACIONES º. Une con flechas cada pareja de números con el sistema del que es solución:
EXAMEN DE MATEMATICAS II 2ª ENSAYO (1) Apellidos: Nombre:
 EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
EXAMEN DE MATEMATICAS II ª ENSAYO () Apellidos: Nombre: Curso: º Grupo: A Día: CURSO 05 Instrucciones: a) Duración: HORA y 0 MINUTOS. b) Debes elegir entre realizar únicamente los cuatro ejercicios de
Ejercicios de geometría
 Ejercicios de geometría Ejercicio nº 1.- Los lados de un triángulo miden 16 cm, 11 cm y 8 cm. Comprueba si es un triángulo rectángulo. Ejercicio nº 2.- Calcula el área y el perímetro de estas figuras:
Ejercicios de geometría Ejercicio nº 1.- Los lados de un triángulo miden 16 cm, 11 cm y 8 cm. Comprueba si es un triángulo rectángulo. Ejercicio nº 2.- Calcula el área y el perímetro de estas figuras:
Trigonometría y problemas métricos
 Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
Trigonometría y problemas métricos 1) En un triángulo rectángulo, los catetos miden 6 y 8 centímetros. Calcula la medida de la altura sobre la hipotenusa y la distancia desde su pie hasta los extremos.
ANÁLISIS. d) No, se podrían haber considerado infinitas funciones diferenciadas en una constante.
 Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
Pruebas de Acceso a la Universidad de Zaragoza. ANÁLISIS Junio 99. Sea f: una función cuya primera derivada es f () =. Se pide: a) Determinar los intervalos de crecimiento y decrecimiento, de concavidad
POLIGONOS. Nº DE LADOS NOMBRE 3 Triángulos 4 Cuadriláteros 5 Pentágonos 6 Hexágonos 7 Heptágonos 8 Octógonos 9 Eneágonos 10 Decágonos
 1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
1 POLIGONO POLIGONOS Polígono es la superficie plana limitada por una línea poligonal cerrada. Lados Vértices Polígono regular es el que tiene todos sus lados y ángulos iguales, mientras que polígono irregular
ELEMENTOS QUE FORMAN UN POLÍGONO
 ELEMENTOS QUE FORMAN UN POLÍGONO Los lados son los segmentos que forman el polígono. Los ángulos son las zonas que forman los lados al cortarse. Las diagonales son los segmentos que unen dos vértices no
ELEMENTOS QUE FORMAN UN POLÍGONO Los lados son los segmentos que forman el polígono. Los ángulos son las zonas que forman los lados al cortarse. Las diagonales son los segmentos que unen dos vértices no
