( ) 2. Pendiente de una Recta Tangente. Sea f una función que es continua en x. 1. Para definir la pendiente de la recta tangente ( )
|
|
|
- Luis Miguel Juárez Jiménez
- hace 8 años
- Vistas:
Transcripción
1 Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales. 7. Derivaa e la función inversa. 8. Derivaa implícita. 9. Curva lisa. 0. Curva cerraa.. Curva simple.. Derivaas paramétricas.. Derivaas e oren superior. 4. Bibliografía.. Introucción. Una e las ieas básicas en Cálculo Matemático es el concepto e Derivaa. Para introucir icho concepto se recurre generalmente a os problemas: uno Físico, para calcular la velocia instantánea e un móvil, y otro Geométrico, para eterminar la peniente e la recta tangente a una curva en un punto cualquiera e ella. Los os problemas conucen al mismo cálculo: el límite e un cociente e incrementos cuano el enominaor tiene a cero. Puesto que, muchos problemas importantes epenen e la eterminación e la recta tangente a la gráfica e una función en un punto específico, a continuación se introuce el concepto analítico e la peniente e recta tangente a una función en un punto y luego el concepto e erivaa.. Peniente e una Recta Tangente. Sea f una función que es continua en. Para efinir la peniente e la recta tangente a la gráfica e f en el punto ( ) a. Sea ; P ; f, consieremos un intervalo abierto I que contiene Q f otro punto sobre la gráfica e f tal que esté contenio en I. La recta que pase por los puntos P y Q se enomina recta secante. y Figura T P(; f ()) y f () - Q(; f ()) y f () - f ()
2 Lic. Eleazar J. García Observe que es el cambio el valor e a, llamao incremento e, y y es el cambio el valor e y f e f ( ) a f ( ), llamao incremento e y. La peniente e la recta que pasa por los puntos P y Q e la curva e la figura., está eterminaa por: f f ( ) mpq Como +, la peniente puee escribirse así: ( + ) f f mpq Consieremos ahora el punto P como un punto fijo, y que el punto Q se mueve a lo largo e la curva hacia P. Esto es igual a ecir que tiene a cero. Si esto sucee la recta secante gira sobre el punto P hasta convertirse en una recta tangente a la curva en el punto P, por lo tanto, la peniente e la recta tangente en icho punto puee ser calculaa meiante la siguiente ecuación: m lím 0 ( + ) f f La notación m( ) nos inica que la peniente que calculemos con la ecuación (A) es la e la recta tangente a la gráfica e la función y f en el punto, f ( ). Ejercicios resueltos. ( A) ( ).) Calcule la peniente e la recta tangente a la parábola f + 4 en el punto Solución: Es eviente que, por lo tanto, aplicano la ecuación (A) tenemos: ( ) ( ) f + f m( ) lím lím lím lím lím lím( 8+ ) Luego, la peniente eigia es: m 8..) Determine la peniente e la recta tangente a la curva f sen en el punto ( π ),. Solución: Apliquemos la ecuación (A), con π m ( π) sen lím 0 ( π + ) sen( π) : ;.
3 Derivaa e Funciones ( π) ( ) + ( ) ( π) ( π) sen cos sen cos sen lím 0 ( ) + ( ) ( π) ( π) sen cos sen cos lím 0 ( ) ( ) ( π) ( π) sen cos sen cos lím + lím 0 0 cos sen sen( π) lím + cos( π) lím 0 0 Ahora, cuano ( ) 0, cos y sen, entonces, ( ) 0 cos sen lím lím lím 0 y lím lím lím, por consiguiente: m ( π) π cos sen sen π lím cos lím sen 0 cos π + π + π 0 0 cos 0. Por lo tanto, la peniente buscaa es: m 0.. Derivaa e una Función. La erivaa e una función f, es una función enotaa por f, tal que para cualquier el ominio e f está aa por: f ( + ) f f lím ( B) 0 si este límite eiste. Si es un número el ominio e f, entonces: f ( + ) f ( ) f ( ) lím 0 si este límite eiste. ( C) El proceso e calcular la erivaa e una función se enomina erivación o iferenciación, es ecir, la erivación o iferenciación es el proceso meiante el cual se
4 4 Lic. Eleazar J. García obtiene f a partir e f. Si una función tiene erivaa en too su ominio, se ice que es una función iferenciable. Ejercicios resueltos..) Determine la erivaa e f, aplicano la ecuación (B). Solución: ( + ) f f f lím lím lím 0 0 ( ) ( ) ( + ( ) + ( ) + ( )) ( ) ( ) 0 lím 0 lím ( ) + ( ) + ( ) lím Por lo tanto, f.) Determine la erivaa e la función g. Solución: Apliquemos la ecuación (B), + + g g g lím lím 0 0
5 Derivaa e Funciones lím lím 0 0 ( + ( ) + ( ) ) lím lím( + ( ) + ( ) ) En conclusión, g.) Determine la erivaa e la función h tg. Aplicano la ecuación (B), tenemos, ( + ) tg( + ) h h - tg h lím lím 0 0 Por consiguiente : tg + tg tg tg tg tg + tg tg + tg tg lím lím tg tg tg lím ( + tg ) lím ( + tg ) sec 0 0 sec h Otras notaciones para la erivaa e una función f son: f y D f. Ejercicios propuestos A. Determine la erivaa e caa una e las siguientes funciones : ) 8 ) 7 5 ) + 4 4) f f f f ) f 6) f 7) f + 8) f ) f 0) f cos ) f 5 + ) f cos + sen
6 6 Lic. Eleazar J. García Teorema. Si una función f es iferenciable en un punto, entonces, f es continua en. Una función f puee no ser iferenciable en c por alguna e las siguientes razones:. La función es iscontinua en c. (Ver figura ). La función es continua en c, pero la gráfica e f tiene una recta tangente vertical en el punto one c. (Ver figura ). La función f es continua en c, pero la gráfica e f no tiene recta tangente en el punto one c. (Ver figura 4). La continuia no implica iferenciabilia. y Figura y Figura (c; f (c)) (c; f (c)) y Figura 4 Y Figura 5 (c; f (c)) T T T T4 (a; f (a)) (b; f (b)) X
7 Derivaa e Funciones 7 La figura 5 muestra la gráfica e una función que no es iferenciable en los puntos one a y b. La gráfica está compuesta por tres curvas. En el punto ( a; f ( a )) se han trazao las siguientes rectas: T tangente a la curva e la izquiera y T tangente a la curva central, las cuales evientemente tienen penientes iferentes. Igualmente se han trazao en el punto ( b; f ( b )) las rectas tangentes T y T 4 que igualmente tienen iferentes penientes. Esta eperiencia nos conuce a pensar en erivaas laterales, lo que estuiaremos a continuación. 4. Derivaas Laterales. i) Si f es una función efinia en, entonces, la erivaa por la erecha e f en, enotaa por f ( ), + lím está efinia por: f + f f f f f lím si el límite eiste., ii) Si f es una función efinia en, entonces, la erivaa por la izquiera e f en enotaa por si el límite eiste. f, está efinia por: f + f f f f lím f lím 0 Ejercicios resueltos..) Determine si la función f es iferenciable en. + si 4 f 4 6 si 4 < Puesto que f está efinia por trozos, se calculan las erivaas laterales en 4. f f f ( 4) lím lím lím lím f f f + ( 4) lím lím lím lím lím + 4
8 8 Lic. Eleazar J. García Como f f 4 4, entonces, f no es iferenciable en 4. +.) Decia si la función g 4 es iferenciable en. Puesto que: 4 si 4, entonces, 4 si < ( 4 + ) ( 4 ) ( + ) g g g lím lím 0 0 ( ) 4 4+ lím lím lím ( + ) g g g + lím lím ( + 4) ( 4) lím lím lím Ahora, sieno g g, entonces, g no es iferenciable en. +.) Determine si la función h cos ( π) h lím 0 cos ( π ) + cos es iferenciable en π. π cos π cos sen π sen cos π lím 0 ( ( ) ) π ( ) cos π cos sen sen lím 0 cos sen cos π lím sen π lím 0 0 ( ) 0, cos y sen ( ), entonces, Ahora, cuano
9 Derivaa e Funciones 9 ( ) 0 cos sen lím lím lím 0 y lím lím lím, luego, cos sen h ( π) cos π lím sen π lím 0 0 cos π 0 sen π sen π ( π) h + lím + 0 cos ( π ) + cos cos π cos sen π sen cos π lím+ 0 ( ( ) ) π ( ) cos π cos sen sen lím+ 0 cos sen cos π lím sen π lím Cuano π 0, cos y sen, entonces, + ( ) 0 cos sen lím lím lím 0 y lím lím lím, luego, cos sen h + ( π) cos π lím sen π lím cos π 0 sen π sen π Puesto que, h ( π) h ( π) entonces, h es iferenciable en π. +,
10 0 Lic. Eleazar J. García Ejercicios propuestos B. Determine si la función aa es iferenciable en. < si < 4 si ) f ) f 7 si si si < si 0 ) f 4) f 0 ( ) si si 0< 5) f + + 6) f + 7) f 0 El proceso el cálculo e la erivaa e una función aplicano la fórmula (B) es muy largo y laborioso, por lo tanto, a continuación se proporcionan algunos teoremas que permiten eterminar las erivaas con mayor facilia; con la finalia e familiarizarnos con las notaciones, la erivaa se epresará con alguna e las tres epresiones equivalentes f, D f, ó f. Teorema. Derivaa e una función constante. f c one c es una constante, entonces: Si, Ejemplo. Si f ( ) 6, entonces, f 0. 0 f Teorema. Derivaa e una función potencial. n Si f, one n es un número racional, entonces: Ejemplo. Si f 6 5, entonces, f n n D n 6. Teorema 4. Derivaa el proucto e una función por una constante. Si g es una función efinia por g c f, one f es una función y c una constante, entonces: Ejemplo. f Si g c f , entonces, D( ) D( )
11 Derivaa e Funciones A partir el resultao obtenio en el ejemplo anterior, poemos enunciar el siguiente teorema. Teorema 5. Derivaa el proucto e una función potencial por una constante. n Si f c, one n es un número entero positivo y c una constante, entonces: n n n ( ) D c c D c n Teorema 6. Derivaa e una aición e funciones. Si f, f, f, f4,, fn son funciones y si f es una función efinia por: y si f f f f f f f f f Ejemplo. n,,,,, n eisten, entonces: f f f f f f 4 Determine f si 4 n f ( 4 ) ( ) + ( 5) 4 D( ) D( ) D D f D D D D D Teorema 7. Derivaa e un proucto e funciones. y Si f y g son funciones y h una función efinia por h f g, y si f g eisten, entonces: Ejemplo. h f g f g g f + +, etermine h. Sea h ( )( ) Apliquemos el teorema 7: h + D + D ( ) ( ) ( ) ( ) ( ) ( )( ) Teorema 8. Derivaa e un cociente e funciones. f Si f y g son funciones y h una función efinia por h g, one 0 si f y g eisten, entonces: g y
12 Lic. Eleazar J. García f g D f f D g D g g Ejemplo. Calcule D. + Debemos aplicar el teorema 8: ( + ) + D D D Ejercicios propuestos C. Calcule la erivaa e las funciones aas : + ) f + ) f ( )( 5 + 6) ) f 4) f ) D ( 5)( 4 ) 6) D ( 4 5)( ) ) D + + 8) ) ( 7 ) 0) ( ) ) Para eterminar la erivaa e una función compuesta, se aplica uno e los teoremas más importantes el Cálculo llamao Regla e la Caena. 5. Teorema 9. Derivaa e una función compuesta (Regla e la Caena). Si g es una función iferenciable en y la función h es iferenciable en g( ), entonces, la función compuesta f ( h g) es iferenciable en, y su erivaa es: Ejemplo. ( ) f h g h g g Sean f y g Determinar ( ). f g La función f g está efinia por ( f g) f g + 49.
13 Derivaa e Funciones g ( ) Para aplicar la regla e la caena necesitamos calcular f g f, entonces, f y. Como, y así: f g g Aemás, + como g + 4 9, luego, g 6 4. Por lo tanto, ( ) f g f g g Calcular la erivaa e numerosas funciones aplicano la fórmula (B) es muy laborioso y complicao, por tal razón, a continuación se suministra la siguiente tabla: 6. Tabla e erivaas usuales. n... f k... f 0 f... f f f n n n n... g... f g f g f n g g f g f ln... f g ln... g ±... ±... + g g h g h... f h h... g g ln g g... f ln k g k logb( e) log... f g f f g h f g h f g h f g h g h f f e f e f e f g e f k f k k f k f f b log... f b g f g e logb g h h h f g... f h g ln g + h g g f g... f g g ln g + g g g g g
14 4 Lic. Eleazar J. García... ( ln + ) sen ( )... cos( ) cos ( )... sen( ) tg ( )... f sec ( g ) g cotg ( )... csc ( ) sec ( )... sec( ) tg( ) csc ( )... f csc( g ) cotg ( g ). g g arcsen ( )... ( g ) g arccos ( )... ( g ) g arctg ( )... f + ( g ) g arccotg ( )... + ( g ) g arcsec ( )... g ( g ) g arccsc ( )... f g ( g ) senh ( )... cosh( ) cosh ( )... senh( ) tgh ( )... sech ( ) cotgh ( )... csch ( ) sech ( )... sech( ) tgh( ) csch ( )... csch( ) cotgh( ) g arg senh ( )... + ( g ) g arg cosh ( )... ( g ) f f f g f g g f g f g g f g f g f g g f g f g g g f g f g f f g f f g f g f f g f f g f g f g g f g f g g f g f g g f g f g g f g f g g g f g f g g g f g f f g f
15 Derivaa e Funciones 5 g f arg tgh... f g f arg cotgh ( g )... f + f arg sech g... f g arg csch... f f g g g g ( g ) g g + g Ejercicios resueltos 4. 4.) Calcule la erivaa e la función f ln +. Debemos aplicar el teorema 8 y la regla e la caena, así: ( ln ) ( ) ( ln )( ) ( ) ln + + f + + ( ln )( ln ) ( + ) ( ln ) ( ) ( ln )( + ) ln + + ( + ) + ( + ) ( + ) ( + ) ( + ) ( ) ln ln 6 ln ln ln ln 6 ln ln ln + + Por ene, f ln ln + ( + )
16 6 Lic. Eleazar J. García 8 + cos 4, etermine g. 4.) Daa la función + g 5 ( 5 ) Apliquemos la regla e la caena en caa sumano. En efecto, g 8 + cos ( 4 ) 8 + cos ( 4 ) ( 5) ( 8 ) ln 8 cos ( 4 ) cos( 4 ) ( ln 8)( 4 )( 8 ) cos ( 4 ) sen ( 4 ) ( 4 ) ( ln 8)( 4 )( 8 ) 60 cos ( 4 ) sen( 4 ) + Por consiguiente, + ln cos ( 4 5 ) sen( 4 5 ) g + 4.) Derive la función h + 7+ ln. + 4 Apliquemos la fórmula para erivar el logaritmo neperiano e una función y resolvamos las erivaas inicaas. Efectivamente, h ln ( + 7+ ) ( + 4) ( + 7+ )( + 4) ( + 4) ( + 7)( + 4) ( 7+ )( )
17 Derivaa e Funciones 7 Por lo tanto, h f e tg. 4.4) Determine la erivaa e la función Apliquemos el teorema 7 y resolvamos las erivaas señalaas, así, f e tg e tg + e tg e tg + e tg tg tg + tg sec e e En conclusión, + f e tg e tg sec 4.5) Calcule la erivaa e la función f + arctg. Aplicano la fórmula que aparece en tabla e erivaas usuales, tenemos que, + + f arctg ( )
18 8 Lic. Eleazar J. García + + ( + )( + ) Por lo tanto, f + 4.6) Daa la función g ( + )( + + ) ln, 4 4 ( ) ( ) ( ) 4 ( + + ) ( ) calcular g. En efecto, ( + )( + + ) 4 g ln ln 4 ( + ) + ln( + + ) ln( ) ln + + ln + + ln Consecuentemente, + 4 g Derivaa e la función inversa. y f Si la función es iferenciable con respecto e, entonces, f ( y) iferenciable con respecto e y, y se verifica la siguiente relación: es f f ( y) ( D)
19 Derivaa e Funciones 9 Ejercicios resueltos 5. 5.) Determine la erivaa e la función f arccos, aplicano la relación (D). Si y arccos, entonces, cos y, por ene, aplicano la relación (D), tenemos que, f sen y ( cos y) cos y Por lo tanto, f 5.) Sea g tg, calcule g usano la relación (D). Puesto que, y tg, entonces, arctg y, luego, si usamos la relación (D), obtenemos, g + y + tg sec Por consiguiente, g sec ( arctg y) + y 5.) Empleano la relación (D), etermine la erivaa e h Como, y h ( ) y ln, entonces, e en consecuencia, y ( e ), y ln e e Por ene, h ln.
20 0 Lic. Eleazar J. García 5.4) Valiénonos e la relación (D), calcule la erivaa e f +. Sieno y, + entonces, ( y ), así que, f y ( y ) En consecuencia, f 5.5) Daa la función sen g 0, calcule g utilizano la relación (D). sen Ya que, g( ) 0, entonces, ( y) arcsen log, luego, ( log y) y ( log y) g ( ) log e ( log ) log e arcsen log y y y ( log y) sen sen 0 log0 sen sen 0 sen cos 0 log e log e log e sen ln0 cos 0 ; recuere que : logbe ln b. Por lo tanto, g ln0 cos 0 sen 8. Derivaa implícita. Eisten funciones que no pueen epresarse eplícitamente. Por ejemplo, no se puee resolver la ecuación 4+ y + 5y + 4 para y en términos e. Pueen eistir una o más funciones y f tales que f f ; cuano esto es así, se ice que la función f está efinia implícitamente. Ahora, la erivaa e y con respecto a puee eterminarse meiante la iferenciación implícita.
21 Derivaa e Funciones Ejercicios resueltos 6. 6.) Determinemos, aa la ecuación 4+ y + 5y + 4. Para calcular la erivaa peia, iferenciemos ambos miembros e la ecuación con respecto e y espejemos D( y), así: ( 4 + ) ( ) D D y y y ( ) ( 4 ) + ( ) + ( 5 ) + D D D D y D y D y 6.) Sea ( y) y D y yd y D y y y D y D y 0y cos + y y sen, hallar. Diferenciemos ambos miembros con respecto e y espejemos : ( cos( + y) ) ( y sen ) sen + + sen + sen ( y) ( y) y sen( + y) + sen + y cos sen( + y) sen( + y) sen + y cos sen + sen( + y) sen( + y) y cos
22 Lic. Eleazar J. García 6.) Sieno, y ( y) ( + ) cos + sen( + ) sen y y sen y cos +, hallar. Diferenciano ambos miembros con respecto e y espejano, cos( + y) obtenemos, sen + + ( y) ( y) sen( + y) + sen( + y) sen( + y) ( + y) sen + sen + y 6.4) Determine, e la ecuación ( y ) sen. Debemos iferenciar ambos miembros con respecto e y luego espejemos. sen( y) cos( y) ( y) cos( y) y+
23 Derivaa e Funciones y cos( y) + cos( y) Ejercicios propuestos D ( y) y cos cos y Determine la erivaa e y con respecto a : ) + y 5 ) + y 8y ) + y y 4) y sen y 5) y + y y y + y y + y y y 5 6) sen cos 9 7) sen cos 8) cotg 0 9) Supongamos que una partícula se mueve en un plano, e manera tal que sus coorenaas ( ; y ), e su posición en cualquier tiempo t, están aas por las ecuaciones: f t y y g( t). Para caa número t el ominio común e f y g, la partícula se encuentra en el punto f t ; g t, y el conjunto e toos estos puntos escribe una curva plana C recorria por ( ) la partícula. Las ecuaciones f ( t) y y g( t), se llaman ecuaciones paramétricas e C y la variable t se llama parámetro. Si eliminamos el parámetro e las ecuaciones paramétricas, se obtiene una ecuación en e y, la cual es enominaa ecuación cartesiana e C. A partir e una ecuación cartesiana poemos obtener una ecuación paramétrica, y viceversa. Ejemplos. ) Para eterminar unas ecuaciones paramétricas e y, se procee e la manera siguiente: puesto que, la variable y está epresaa en función e, hacemos t e y t, por lo tanto, las ecuaciones paramétricas e y son: t y y t ) Obtenga la ecuación cartesiana e la curva efinia por las ecuaciones paramétricas 5cos t y y 5sen t Para eliminar el parámetro t, se elevan al cuarao los os miembros e caa ecuación paramétrica y se suman, así: + y 5cos t+ 5sen t ( 5cost) y 5( cos t sen t) + + y ( 5sen t) + y 5 A continuación se arán tres efiniciones e términos relacionaos con las curvas planas, las cuales serán aplicaas posteriormente.
24 4 Lic. Eleazar J. García 9. Curca lisa. Una curva plana C efinia por las ecuaciones paramétricas f t y g t a t b y se ice que es lisa o suave en el intervalo cerrao [ ; ] y aemás, f ( t) y g ( t) no son cero simultáneamente en caa t ( a b) Ejemplo. Sea C la curva efinia por las ecuaciones paramétricas f t t g t t t π Como a b si f y g son continuas en [ a b ] ;. 5cos y 5sen 0 f ( t) 5sen t y g ( t) 5cost son continuas para too t [ 0; π], son cero simultáneamente en cualquier t, entonces la curva C es lisa. ;, y aemás, no Si un intervalo I puee partirse en un número finito e subintervalos en los que la curva C es suave, entonces se ice que C es lisa a trozos en I. 0. Curva cerraa. Una curva plana C efinia por las ecuaciones paramétricas f t y g t a t b y se ice que es cerraa si el punto inicial ; B f ( b) ; g( b ). Fig..5 A f a g a coincie con el punto final A B La figura.5 muestra una curva cerraa y lisa one los puntos A y B coincien.. Curva simple. Una curva plana C efinia por las ecuaciones paramétricas f t y g t a t b y se ice que es simple entre los puntos A( f ( a) ; g( a )) y B( f ( b) ; g( b )) si f ( t) ; g( t ) es iferente el punto ( ; ) ( a; b ). Una curva simple no se cruza a sí misma. f t g t para too t y t iferentes el intervalo abierto
25 Derivaa e Funciones 5 En la figura.5 se muestra una curva cerraa simple lisa.. Derivaas paramétricas. Supongamos que una curva lisa C está efinia paramétricamente por f ( t) y y g( t), y que éste par e ecuaciones efine al menos una función iferenciable h para la cual y h. La erivaa e caa función h, enotaa por, está relacionaa con y t meiante la siguiente ecuación:. t t t Si t 0, poemos iviir miembro a miembro entre para obtener: t t. t y Para hallar la erivaa, a la iguala anterior la erivamos con respecto a : y y t t t t t t t t t t t t t t t t t t t t y t t t t t Para hallar la erivaa manera similar para eterminar y erivamos 4 5 y y,, etc. 4 5 y con respecto a, y se procee e Puesto que, las erivaas paramétricas que hemos consierano son funciones epenientes el parámetro t, las siguientes fórmulas son alternativas para hallar las erivaas paramétricas: Primera erivaa paramétrica: t t
26 6 Lic. Eleazar J. García Seguna erivaa paramétrica: Tercera erivaa paramétrica: y t t t t y y Cuarta erivaa paramétrica: t t 4 y y 4 n-ésima erivaa paramétrica: n n y y n n t. t Ejercicio resuelto 7. Daas las ecuaciones paramétricas t y 5 y t + t, etermine y. y Como 4 4 t, 4, 5t t t t + y y 0 t, t entonces 4 t 5t + y 4t t y 54 ( 4 )( 0 ) ( 5 )( 4) y t t t t t t t + 80t 0t 4 5t. ( 4t) 64t 6t t Usano la fórmula alternativa tenemos que: 4 ( 0t )( 4t) ( 5t + )( 4) 4 4 y 5t + 5t. t t 4t 4t ( 4t) 4t 6t t
27 Derivaa e Funciones 7 Ejercicios propuestos E y Determine las erivaas y. ) cos, sen ) sen, cos ) cos, sen a t y b t a t t y a t a t y b t at at 4), y 5) ln ( cotg t), y tgt+ cotg t 6) 4sen t, y 4 cost + t + t 5 7) cos t, y sen t 8) t + t, y 5t t 9) cos t, y sen t. Derivaa e oren superior. Si la función f es iferenciable en too su ominio, entonces su erivaa f se le llama primera erivaa e f o primera función erivaa. Si la función f es también iferenciable, entonces la erivaa f se enomina seguna erivaa e f o seguna ( n) función erivaa Si continuamos erivano n veces, entonces la erivaa f es llamaa n- ésima erivaa e f. La función f puee representarse como A continuación conoceremos las istintas notaciones para las erivaas e oren superior: Primera erivaa: y, f,, f, D f y,,,, Seguna erivaa: y f f D f y,,,, Tercera erivaa: y f f D f 4 4 y,,,, 4 4 (4) (4) 4 Cuarta erivaa: y f f D f n n y,,,,. n n ( n) ( n) n n-ésima erivaa: y f f D f Para familiarizarnos con la erivación e oren superior, veamos con etenimiento el esarrollo e los siguientes ejemplos. Ejercicios resueltos 8. f, f (4), f (5) ) Las erivaas y f ( ) e f 0. f 5 + son:
28 8 Lic. Eleazar J. García f f f f (4) 5 4 f f ( ) (5) (4) 4 f f (4) 6 8.) Las erivaas f, f, f y f ( ) e sen f son: 6 5 f f sen 6sen cos f f 6sen cos 0sen cos 6 sen f f 0 sen cos 6sen 0sen cos 66sen (4) 5 4 f f 0sen cos 66sen 60sen cos 450sen. 4. Bibliografía [] Rabuffetti Hebe T. Introucción al Análisis Matemático, écima eición. [] Apostol Tom M. Calculus, seguna eición. Trabajo enviao por: Eleazar José García eleagarcia95@hotmail.com Profesión: Licenciao en Matemática País: Venezuela
DEFINICION DE DERIVADA Sea una función definida en un intervalo abierto que contiene a a Diremos que f es Derivable en a si: si este límite existe
 DERIVADA DEFINICION DE DERIVADA Sea una función efinia en un intervalo abierto que contiene a a Diremos que f es Derivable en a si: si este límite eiste Dicho límite, cuano eiste, se llama DERIVADA e f
DERIVADA DEFINICION DE DERIVADA Sea una función efinia en un intervalo abierto que contiene a a Diremos que f es Derivable en a si: si este límite eiste Dicho límite, cuano eiste, se llama DERIVADA e f
(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)
![(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x) (f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)](/thumbs/24/2434623.jpg) Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
LA DERIVADA POR FÓRMULAS
 CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
Información importante
 Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
Universia Técnica Feerico Santa María Departamento e Matemática Coorinación e Matemática I (MAT021) 1 er Semestre e 2010 Semana 9: Lunes 17 viernes 21 e Mayo Información importante El control Q2A es el
DERIVADA. Interpretación Geométrica Encontrar la pendiente de la recta tangente a una curva en un punto dado de ella.
 DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
DERIVADA Interpretación Geométrica Objetivo: Encontrar la peniente e la recta tangente a una curva en un punto ao e ella. Para precisar correctamente la iea e tangente a una curva en un punto, se utilizará
Cálculo I. Índice Reglas Fundamentales para el Cálculo de Derivadas. Julio C. Carrillo E. * 1. Introducción 1. 2.
 3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
3.2. Reglas Funamentales para el Cálculo e Derivaas Julio C. Carrillo E. * Ínice 1. Introucción 1 2. Reglas básicas 3 3. El Álgebra e funciones erivables 4 4. Regla e la caena 8 * Profesor Escuela e Matemáticas,
Teoría de Conjuntos y Funciones
 Elaborado por: Lic. Eleazar J. García República Bolivariana de Venezuela. Tinaco.- Estado Cojedes Teoría de Conjuntos Funciones Este capítulo comienza con el estudio de las nociones de la teoría de conjuntos
Elaborado por: Lic. Eleazar J. García República Bolivariana de Venezuela. Tinaco.- Estado Cojedes Teoría de Conjuntos Funciones Este capítulo comienza con el estudio de las nociones de la teoría de conjuntos
Tema 8: Derivación. José M. Salazar. Noviembre de 2016
 Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Tema 8: Derivación. José M. Salazar Noviembre e 2016 Tema 8: Derivación. Lección 9. Derivación: teoría funamental. Lección 10. Aplicaciones e la erivación. Ínice 1 Derivaas. Principales nociones y resultaos.
Funciones hiperbólicas inversas (19.09.2012)
 Funciones hiperbólicas inversas 9.09.0 a Argumento seno hiperbólico. y = arg shx = x = senh y = ey e y = x = e y e y. Multiplicando por e y, xe y = e y = e y xe y = 0, de donde e y = x ± x +. Para el signo
Funciones hiperbólicas inversas 9.09.0 a Argumento seno hiperbólico. y = arg shx = x = senh y = ey e y = x = e y e y. Multiplicando por e y, xe y = e y = e y xe y = 0, de donde e y = x ± x +. Para el signo
Logaritmo Natural. Z x. 1 t dt = ln(x) = I 1 1. ln(x) < 0 para x 2 (0; 1) y ln(x) > 0 para x 2 (1; 1)
 Logaritmo Natural Si n 6= ya sabemos que R x t n t = n+ xn+ + C, con C una constante. De nición. La regla e corresponencia ln(x) = Z x t t = Z x I e ne una función con ominio D ln = (0; ): A esta función
Logaritmo Natural Si n 6= ya sabemos que R x t n t = n+ xn+ + C, con C una constante. De nición. La regla e corresponencia ln(x) = Z x t t = Z x I e ne una función con ominio D ln = (0; ): A esta función
4. CÁLCULO INTEGRAL...71
 Inice. FUNCIONES..... NATURALEZA Y DEFINICIÓN DE FUNCIÓN MATEMÀTICA..... PRINCIPALES TIPOS DE FUNCIONES...9.. APLICACIONES DE LAS FUNCIONES.... LÍMITES..... LÌMITE DE UNA FUNCIÒN..... PROPIEDADES DE LOS
Inice. FUNCIONES..... NATURALEZA Y DEFINICIÓN DE FUNCIÓN MATEMÀTICA..... PRINCIPALES TIPOS DE FUNCIONES...9.. APLICACIONES DE LAS FUNCIONES.... LÍMITES..... LÌMITE DE UNA FUNCIÒN..... PROPIEDADES DE LOS
48 Apuntes de Matemáticas II para preparar el examen de la PAU
 48 Apuntes de Matemáticas II para preparar el eamen de la PAU Unidad. Funciones. Derivabilidad TEMA FUNCIONES.DERIVABILIDAD.. Tasa de variación media. Derivada en un punto. Interpretación.. Tasa de variación
48 Apuntes de Matemáticas II para preparar el eamen de la PAU Unidad. Funciones. Derivabilidad TEMA FUNCIONES.DERIVABILIDAD.. Tasa de variación media. Derivada en un punto. Interpretación.. Tasa de variación
3. Operaciones con funciones.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lección. Funciones derivada. 3. Operaciones con funciones. En esta sección veremos cómo podemos combinar funciones para construir otras nuevas. Especialmente
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 00. Lección. Funciones derivada. 3. Operaciones con funciones. En esta sección veremos cómo podemos combinar funciones para construir otras nuevas. Especialmente
Derivación de funciones de una variable real
 Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Capítulo 4 Derivación e funciones e una variable real 4.1. Derivaa e una función 4.1.1. Introucción Definición 4.1.1. Sea f : (a, b) R R y x 0 (a, b). Se ice que la función f es erivable en el punto x
Se llama dominio de una función f(x) a todos los valores de x para los que f(x) existe. El dominio se denota como Dom(f)
 MATEMÁTICAS EJERCICIOS RESUELTOS DE FUNCIONES FUNCIONES A. Introducción teórica A.1. Definición de función A.. Dominio y recorrido de una función, f() A.. Crecimiento y decrecimiento de una función en
MATEMÁTICAS EJERCICIOS RESUELTOS DE FUNCIONES FUNCIONES A. Introducción teórica A.1. Definición de función A.. Dominio y recorrido de una función, f() A.. Crecimiento y decrecimiento de una función en
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 FUNCIONES CONOCIDAS. FUNCIONES LINEALES. Se llaman funciones lineales a aquellas que se representan mediante rectas. Su epresión en forma eplícita es y f ( ) a b. En sentido más estricto, se llaman funciones
FUNCIONES CONOCIDAS. FUNCIONES LINEALES. Se llaman funciones lineales a aquellas que se representan mediante rectas. Su epresión en forma eplícita es y f ( ) a b. En sentido más estricto, se llaman funciones
UNIVERSIDAD DE CASTILLA-LA MANCHA Departamento de Matemáticas.
 UNIVERSIDAD DE CASTILLA-LA MANCHA Departamento de Matemáticas. PROBLEMAS DE CÁLCULO INFORMÁTICA DE SISTEMAS . Cálculo diferencial. Probar que a si y sólo si a a, siendo a >. Utilizar estas desigualdades
UNIVERSIDAD DE CASTILLA-LA MANCHA Departamento de Matemáticas. PROBLEMAS DE CÁLCULO INFORMÁTICA DE SISTEMAS . Cálculo diferencial. Probar que a si y sólo si a a, siendo a >. Utilizar estas desigualdades
Tema 07. LÍMITES Y CONTINUIDAD DE FUNCIONES
 Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
Tema 07 LÍMITES Y CONTINUIDAD DE FUNCIONES Límite de una función en un punto Vamos a estudiar el comportamiento de las funciones f ( ) g ( ) ENT[ ] h ( ) i ( ) en el punto Para ello, damos a valores próimos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2010 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 010 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio 1, Opción A Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción
Juan Antonio González Mota Profesor de Matemáticas del Colegio Juan XIII Zaidín de Granada
 FUNCIONES CONTINUAS. La mayor parte de las funciones que manejamos, a nivel elemental, presentan en sus gráficas una propiedad característica que es la continuidad. La continuidad de una función definida
FUNCIONES CONTINUAS. La mayor parte de las funciones que manejamos, a nivel elemental, presentan en sus gráficas una propiedad característica que es la continuidad. La continuidad de una función definida
Electromagnetismo Pedagogía en Física R. Lagos. PROBLEMAS RESUELTOS
 PROBLEMAS RESUELTOS. Un capacitor e lleno e aire está compuesto e os placas paralela, caa una con un área e 7 6 [ 2 ], separaas por una istancia e,8 [mm]. Si se aplica una iferencia e potencial e 20 [V]
PROBLEMAS RESUELTOS. Un capacitor e lleno e aire está compuesto e os placas paralela, caa una con un área e 7 6 [ 2 ], separaas por una istancia e,8 [mm]. Si se aplica una iferencia e potencial e 20 [V]
DERIVADAS DE LAS FUNCIONES ELEMENTALES
 Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
DERIVADA DE UNA FUNCIÓN DEFINIDA EN FORMA PARAMÉTRICA
 (Apuntes en revisión para orientar el aprendizaje) DERIVADA DE UNA FUNCIÓN DEFINIDA EN FORMA PARAMÉTRICA f( t) f: ; t a, b y g() t De la regla de la cadena dy dy dt d dt d En donde dt se puede calcular
(Apuntes en revisión para orientar el aprendizaje) DERIVADA DE UNA FUNCIÓN DEFINIDA EN FORMA PARAMÉTRICA f( t) f: ; t a, b y g() t De la regla de la cadena dy dy dt d dt d En donde dt se puede calcular
Reglas de derivación
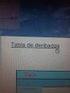 CAPÍTULO 6 Reglas e erivación 6. Regla e la caena En las reglas básicas e erivación se aplican fórmulas apropiaas para calcular las erivaas e las funciones f C g (suma), f g (iferencia), fg (proucto) y
CAPÍTULO 6 Reglas e erivación 6. Regla e la caena En las reglas básicas e erivación se aplican fórmulas apropiaas para calcular las erivaas e las funciones f C g (suma), f g (iferencia), fg (proucto) y
1.4.- D E S I G U A L D A D E S
 1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
1.4.- D E S I G U A L D A D E S OBJETIVO: Que el alumno conozca y maneje las reglas empleadas en la resolución de desigualdades y las use para determinar el conjunto solución de una desigualdad dada y
Apuntes Matemáticas 2º de bachillerato. Tema 2. Límites de funciones
 Apuntes Tema 2 Límites de funciones 2.1 Límites de funciones Def.: Dada una función f(), diremos que su límite cuando tiende hacia a es el número L, y lo escribiremos, lim f() L si eisten los límites laterales
Apuntes Tema 2 Límites de funciones 2.1 Límites de funciones Def.: Dada una función f(), diremos que su límite cuando tiende hacia a es el número L, y lo escribiremos, lim f() L si eisten los límites laterales
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
INECUACIONES NOTA IMPORTANTE: El signo de desigualdad de una inecuación puede ser,, < o >. Para las cuestiones teóricas que se desarrollan en esta unidad únicamente se utilizará la desigualdad >, siendo
RELACIONES DE RECURRENCIA
 Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
SECCIÓN.5 Derivación implícita.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. EXPLORACIÓN Representación gráfica e una
Continuidad y ramas infinitas. El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A = 2. lm í
 Unidad. Límites de funciones. Continuidad y ramas infinitas Resuelve Página 7 A través de una lupa AUMENTO DISTANCIA (dm) El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A
Unidad. Límites de funciones. Continuidad y ramas infinitas Resuelve Página 7 A través de una lupa AUMENTO DISTANCIA (dm) El aumento A producido por cierta lupa viene dado por la siguiente ecuación: A
TEMA 8: LÍMITES DE FUNCIONES. CONTINUIDAD
 TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
TEMA 8: DE FUNCIONES. CONTINUIDAD 1. EN EL INFINITO En ocasiones interesa estudiar el comportamiento de una función (la tendencia) cuando los valores de se hacen enormemente grandes ( ) o enormemente pequeños
Derivación. (x c) que pasa por el punto fijo (c, f(c)) y el punto móvil (c + h, f(c + h)) cuando h tiende a 0.
 Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Derivación Definición y propieaes básicas Definición. Una función f efinia en un entorno e un punto c R es erivable en c si y sólo si el ite f c = f fc + h fc f fc c := = h h c c eiste y toma un valor
Una función f es derivable en un punto a de su dominio si existe el límite. f(x) f(a) Si f y g son derivables en a, entonces fg es derivable en a y
 4. Derivabilidad 1 Una función f es derivable en un punto a de su dominio si existe el límite f (a) = lím x a f(x) f(a) x a f(a + h) f(a) = lím, h 0 h y es un número real. El número f (a) se denomina derivada
4. Derivabilidad 1 Una función f es derivable en un punto a de su dominio si existe el límite f (a) = lím x a f(x) f(a) x a f(a + h) f(a) = lím, h 0 h y es un número real. El número f (a) se denomina derivada
Las Funciones Analíticas. f (z 0 + h) f (z 0 ) lim. h=z z 0. = lim
 Las Funciones Analíticas 1 Las Funciones Analíticas Definición 12.1 (Derivada de una función compleja). Sea D C un conjunto abierto. Sea z 0 un punto fijo en D y sea f una función compleja, f : D C C.
Las Funciones Analíticas 1 Las Funciones Analíticas Definición 12.1 (Derivada de una función compleja). Sea D C un conjunto abierto. Sea z 0 un punto fijo en D y sea f una función compleja, f : D C C.
Límites. 1. Calcula los límites de las siguientes funciones en los puntos que se indican: 2 2 2 a) lim b) lim c) lim d) lim
 Límites CIT_H. Calcula los límites de las siguientes funciones en los puntos que se indican: ( ) + + + a) lim b) lim c) lim d) lim + + + + + e) lim f) lim g) lim h) lim + 0 + + 9 + j) lim k) lim l) lim
Límites CIT_H. Calcula los límites de las siguientes funciones en los puntos que se indican: ( ) + + + a) lim b) lim c) lim d) lim + + + + + e) lim f) lim g) lim h) lim + 0 + + 9 + j) lim k) lim l) lim
Tema 6: Derivadas, Técnicas de Derivación
 Matemáticas º Bacillerato CCNN Tema 6: Derivaas, Técnicas e Derivación.- Introucción.- Tasa e Variación Meia.- Derivaa e una unción en un punto..- Derivaas Laterales...- Interpretación geométrica e la
Matemáticas º Bacillerato CCNN Tema 6: Derivaas, Técnicas e Derivación.- Introucción.- Tasa e Variación Meia.- Derivaa e una unción en un punto..- Derivaas Laterales...- Interpretación geométrica e la
1. Hallar la derivada por definición de f ( x) x x 1. Solución: para resolver la derivada aplicaremos la definición de la derivada: f '( x)
 . Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
. Hallar la erivaa por efinición e f ( ) Solución: para resolver la erivaa aplicaremos la efinición e la erivaa: f '( ) lim 0 f ( ) f ( ) f ( ) f '( ) lim 0 ara allar la erivaa meiante efinición ebemos
Integrales y ejemplos de aplicación
 Integrales y ejemplos de aplicación I. PROPÓSITO DE ESTOS APUNTES Estas notas tienen como finalidad darle al lector una breve introducción a la noción de integral. De ninguna manera se pretende seguir
Integrales y ejemplos de aplicación I. PROPÓSITO DE ESTOS APUNTES Estas notas tienen como finalidad darle al lector una breve introducción a la noción de integral. De ninguna manera se pretende seguir
Tema 7. Límites y continuidad de funciones
 Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
Matemáticas II (Bachillerato de Ciencias) Análisis: Límites y continuidad de funciones 55 Límite de una función en un punto Tema 7 Límites y continuidad de funciones Idea inicial Si una función f está
TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1
 TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1 TEMA 10 - FUNCIONES ELEMENTALES 10.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder
TEMA 10 FUNCIONES ELEMENTALES MATEMÁTICAS I 1º Bach. 1 TEMA 10 - FUNCIONES ELEMENTALES 10.1 CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder
Tema 5 Elasticidades. Economía Aplicada
 Tema 5 lasticiaes conomía Aplicaa Curso 2008-2009 Ínice 1. Introucción 2. lasticia e la emana 2.1. lasticia-precio 2.2. lasticia-renta 2.3. lasticia cruzaa 3. lasticia-precio e la oferta 4. lasticia-precio
Tema 5 lasticiaes conomía Aplicaa Curso 2008-2009 Ínice 1. Introucción 2. lasticia e la emana 2.1. lasticia-precio 2.2. lasticia-renta 2.3. lasticia cruzaa 3. lasticia-precio e la oferta 4. lasticia-precio
1. Función exponencial y funciones definidas mediante la exponencial
 TEMA 3 FUNCIONES COMPLEJAS ELEMENTALES 1. Función exponencial funciones efinias meiante la exponencial 1.1 La función exponencial 1. Funciones trigonométricas 1.3 Funciones hiperbólicas. Función logaritmo
TEMA 3 FUNCIONES COMPLEJAS ELEMENTALES 1. Función exponencial funciones efinias meiante la exponencial 1.1 La función exponencial 1. Funciones trigonométricas 1.3 Funciones hiperbólicas. Función logaritmo
UNIDAD 4: PLANO CARTESIANO, RELACIONES Y FUNCIONES. OBJETIVO DE APRENDIZAJE: Representar gráficamente relaciones y funciones en el plano cartesiano.
 UNIDAD 4: PLANO CARTESIANO, RELACIONES Y FUNCIONES OBJETIVO DE APRENDIZAJE: Representar gráficamente relaciones y funciones en el plano cartesiano. EL PLANO CARTESIANO. El plano cartesiano está formado
UNIDAD 4: PLANO CARTESIANO, RELACIONES Y FUNCIONES OBJETIVO DE APRENDIZAJE: Representar gráficamente relaciones y funciones en el plano cartesiano. EL PLANO CARTESIANO. El plano cartesiano está formado
UNIDAD IV.- CÁLCULO INTEGRAL
 UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
UNIDAD IV.- CÁLCULO INTEGRAL En la práctica e cualquier campo científico es frecuente que se presenten prolemas relacionaos con el cálculo e áreas, algunas veces e figuras regulares y muchas otras, con
LA DERIVADA UNIDAD III III.1 INCREMENTOS. y, esto es:
 Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
Página el Colegio e Matemáticas e la ENP-UNAM La erivaa Autor: Dr. José Manuel Becerra Espinosa LA DERIVADA UNIDAD III III. INCREMENTOS Se eine como incremento e la variable al aumento o isminución que
UNIVERSIDAD DIEGO PORTALES GUÍA N 11 CÁLCULO I. Profesor: Carlos Ruz Leiva DERIVADAS. Derivadas de orden superior. Ejemplos
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS Profesor: Carlos Ruz Leiva GUÍA N CÁLCULO I DERIVADAS Derivaas e oren superior Ejemplos Hallar las siguientes
Una desigualdad se obtiene al escribir dos expresiones numéricas o algebraicas relacionadas con alguno de los símbolos
 MATEMÁTICAS BÁSICAS DESIGUALDADES DESIGUALDADES DE PRIMER GRADO EN UNA VARIABLE La epresión a b significa que "a" no es igual a "b ". Según los valores particulares de a de b, puede tenerse a > b, que
MATEMÁTICAS BÁSICAS DESIGUALDADES DESIGUALDADES DE PRIMER GRADO EN UNA VARIABLE La epresión a b significa que "a" no es igual a "b ". Según los valores particulares de a de b, puede tenerse a > b, que
Departamento de Matemáticas
 MA5 Clase 9: Campos Direccionales, Curvas Integrales. Eistencia y Unicidad Elaborado por los profesores Edgar Cabello y Marcos González La ecuación y = f(, y) determina el coeficiente angular de la tangente
MA5 Clase 9: Campos Direccionales, Curvas Integrales. Eistencia y Unicidad Elaborado por los profesores Edgar Cabello y Marcos González La ecuación y = f(, y) determina el coeficiente angular de la tangente
2. Vector tangente y gráficas en coordenadas polares.
 GRADO DE INGENIERÍA AEROESPACIAL CURSO 0 Vector tangente y gráficas en coordenadas polares De la misma forma que la ecuación cartesiana y = yx ( ) define una curva en el plano, aquella formada por los
GRADO DE INGENIERÍA AEROESPACIAL CURSO 0 Vector tangente y gráficas en coordenadas polares De la misma forma que la ecuación cartesiana y = yx ( ) define una curva en el plano, aquella formada por los
EJERCICIOS DE FUNCIONES REALES
 EJERCICIOS DE FUNCIONES REALES.- La ley que relaciona el valor del área de un cuadrado con la longitud de su lado es una función. Sabemos que la epresión que nos relacionas ambas variables es. Observa
EJERCICIOS DE FUNCIONES REALES.- La ley que relaciona el valor del área de un cuadrado con la longitud de su lado es una función. Sabemos que la epresión que nos relacionas ambas variables es. Observa
3.1. DERIVADAS DE SEGUNDO ORDEN
 .. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
.. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
Análisis Matemático I (Lic. en Cs. Biológicas) Práctica 4: Derivadas. Primer cuatrimestre de 2009
 Análisis Matemático I (Lic. en Cs. Biológicas) Primer cuatrimestre de 2009 Práctica 4: Derivadas Notaciones: Dada una función f : R R, un punto a R y un número R que llamaremos incremento en, se define
Análisis Matemático I (Lic. en Cs. Biológicas) Primer cuatrimestre de 2009 Práctica 4: Derivadas Notaciones: Dada una función f : R R, un punto a R y un número R que llamaremos incremento en, se define
Polinomios de Taylor.
 Tema 7 Polinomios de Taylor. 7.1 Polinomios de Taylor. Definición 7.1 Recibe el nombre de polinomio de Taylor de grado n para la función f en el punto a, denotado por P n,a, el polinomio: P n,a (x) = f(a)
Tema 7 Polinomios de Taylor. 7.1 Polinomios de Taylor. Definición 7.1 Recibe el nombre de polinomio de Taylor de grado n para la función f en el punto a, denotado por P n,a, el polinomio: P n,a (x) = f(a)
I. RELACIONES Y FUNCIONES 1.1. PRODUCTO CARTESIANO { }
 I. RELACIONES Y FUNCIONES PAREJAS ORDENADAS Una pareja ordenada se compone de dos elementos x y y, escribiéndose ( x, y ) donde x es el primer elemento y y el segundo elemento. Teniéndose que dos parejas
I. RELACIONES Y FUNCIONES PAREJAS ORDENADAS Una pareja ordenada se compone de dos elementos x y y, escribiéndose ( x, y ) donde x es el primer elemento y y el segundo elemento. Teniéndose que dos parejas
Profr. Efraín Soto Apolinar. Función Inversa
 Función Inversa Una función es una relación entre dos variables, de manera que para cada valor de la variable independiente eiste a lo más un único valor asignado a la variable independiente por la función.
Función Inversa Una función es una relación entre dos variables, de manera que para cada valor de la variable independiente eiste a lo más un único valor asignado a la variable independiente por la función.
MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas
 Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema Representación gráfica de funciones reales de una variable real Elaborado
Universidad de Cádiz Departamento de Matemáticas MATEMÁTICAS para estudiantes de primer curso de facultades y escuelas técnicas Tema Representación gráfica de funciones reales de una variable real Elaborado
TEMA 4: Transformaciones 3D
 TEMA 4: Transformaciones D Ínice. Sistemas e Coorenaas. Transformaciones Básicas. Traslación. Escalao. Rotación lana 4. Afilamiento 5. Deformaciones. Composición e Transformaciones 4. Rotación General
TEMA 4: Transformaciones D Ínice. Sistemas e Coorenaas. Transformaciones Básicas. Traslación. Escalao. Rotación lana 4. Afilamiento 5. Deformaciones. Composición e Transformaciones 4. Rotación General
CAPÍTULO III. FUNCIONES
 CAPÍTULO III LÍMITES DE FUNCIONES SECCIONES A Definición de límite y propiedades básicas B Infinitésimos Infinitésimos equivalentes C Límites infinitos Asíntotas D Ejercicios propuestos 85 A DEFINICIÓN
CAPÍTULO III LÍMITES DE FUNCIONES SECCIONES A Definición de límite y propiedades básicas B Infinitésimos Infinitésimos equivalentes C Límites infinitos Asíntotas D Ejercicios propuestos 85 A DEFINICIÓN
Cálculo Diferencial en una variable
 Tema 3 Cálculo Diferencial en una variable 3.1 Introucción Analizaremos en este Tema los conceptos funamentales acerca e las erivaas e las funciones reales e variable real. En el tema siguiente estuiaremos
Tema 3 Cálculo Diferencial en una variable 3.1 Introucción Analizaremos en este Tema los conceptos funamentales acerca e las erivaas e las funciones reales e variable real. En el tema siguiente estuiaremos
1-Comportamiento de una función alrededor de un punto:
 Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Matemática II 7 Modulo Límites continuidad En esta sección desarrollaremos el concepto de límite, una de las nociones fundamentales del cálculo. A partir de este concepto se desarrollan también los conceptos
Esta es la forma vectorial de la recta. Si desarrollamos las dos posibles ecuaciones, tendremos las ecuaciones paramétricas de la recta:
 Todo el mundo sabe que dos puntos definen una recta, pero los matemáticos son un poco diferentes y, aún aceptando la máxima universal, ellos prefieren decir que un punto y un vector nos definen una recta.
Todo el mundo sabe que dos puntos definen una recta, pero los matemáticos son un poco diferentes y, aún aceptando la máxima universal, ellos prefieren decir que un punto y un vector nos definen una recta.
Hasta ahora hemos estudiado potencias pertenecientes a distintos campos numéricos. n N, ( a 0 ) m a. m Z, n N
 EXPONENCIALES Y LOGARITMOS FUNCIÓN EXPONENCIAL Hasta ahora hemos estudiado potencias pertenecientes a distintos campos numéricos. Potencias de eponente natural: a n = a. a. a... a n N n veces Potencias
EXPONENCIALES Y LOGARITMOS FUNCIÓN EXPONENCIAL Hasta ahora hemos estudiado potencias pertenecientes a distintos campos numéricos. Potencias de eponente natural: a n = a. a. a... a n N n veces Potencias
DOMINIO Y RANGO página 89. Cuando se grafica una función existen las siguientes posibilidades:
 DOMINIO Y RANGO página 89 3. CONCEPTOS Y DEFINICIONES Cuando se grafica una función eisten las siguientes posibilidades: a) Que la gráfica ocupe todo el plano horizontalmente (sobre el eje de las ). b)
DOMINIO Y RANGO página 89 3. CONCEPTOS Y DEFINICIONES Cuando se grafica una función eisten las siguientes posibilidades: a) Que la gráfica ocupe todo el plano horizontalmente (sobre el eje de las ). b)
FUNCIONES CUADRÁTICAS Y RACIONALES
 www.matesronda.net José A. Jiménez Nieto FUNCIONES CUADRÁTICAS Y RACIONALES 1. FUNCIONES CUADRÁTICAS. Representemos, en función de la longitud de la base (), el área (y) de todos los rectángulos de perímetro
www.matesronda.net José A. Jiménez Nieto FUNCIONES CUADRÁTICAS Y RACIONALES 1. FUNCIONES CUADRÁTICAS. Representemos, en función de la longitud de la base (), el área (y) de todos los rectángulos de perímetro
Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada
![Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada Semana 14-Derivadas I[1/29] Derivada. 7 de junio de Derivada](/thumbs/71/65048770.jpg) Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
Semana 14-s I[1/9] 7 e junio e 007 s Introucción Semana 14-s I[/9] Introucción P f Q Consieremos el gráfico e una función f con ominio R. Sea P = (x 0, y 0 ) un punto el gráfico e f y sea Q = (x 1, y 1
Manual de la Práctica 2: Análisis de sistemas discretos
 Control por computaor Manual e la Práctica : Análisis e sistemas iscretos Jorge Pomares Baeza Fracisco Anrés Canelas Herías Grupo e Innovación Eucativa en Automática 009 GITE IEA - - Introucción En la
Control por computaor Manual e la Práctica : Análisis e sistemas iscretos Jorge Pomares Baeza Fracisco Anrés Canelas Herías Grupo e Innovación Eucativa en Automática 009 GITE IEA - - Introucción En la
BASES Y DIMENSIÓN. Propiedades de las bases. Ejemplos de bases.
 BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
BASES Y DIMENSIÓN Definición: Base. Se llama base de un espacio (o subespacio) vectorial a un sistema generador de dicho espacio o subespacio, que sea a la vez linealmente independiente. β Propiedades
Tema 9. Funciones de varias variables.
 Tema 9. Funciones de varias variables. 9.1 Introducción 9.2 Límite continuidad. 9.3 Derivadas parciales. Derivadas de orden superior. Teorema Schwart. 9.4 Diferencial. 9.5 Regla de la cadena. Derivación
Tema 9. Funciones de varias variables. 9.1 Introducción 9.2 Límite continuidad. 9.3 Derivadas parciales. Derivadas de orden superior. Teorema Schwart. 9.4 Diferencial. 9.5 Regla de la cadena. Derivación
1. Dominio, simetría, puntos de corte y periodicidad
 Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
Estudio y representación de funciones 1. Dominio, simetría, puntos de corte y periodicidad 1.1. Dominio Al conjunto de valores de x para los cuales está definida la función se le denomina dominio. Se suele
DERIVADAS. * Definición de derivada. Se llama derivada de la función f en el punto x=a al siguiente límite, si es que existe: lim
 DERIVADAS. CONTENIDOS. Recta tangente a una curva en un punto. Idea intuitiva del concepto de derivada de una función en un punto. Función derivada. sucesivas. Reglas de derivación Aplicación de la derivada
DERIVADAS. CONTENIDOS. Recta tangente a una curva en un punto. Idea intuitiva del concepto de derivada de una función en un punto. Función derivada. sucesivas. Reglas de derivación Aplicación de la derivada
Vectores. Las cantidades físicas que estudiaremos en los cursos de física son escalares o vectoriales.
 Cantidades vectoriales escalares Vectores Las cantidades físicas que estudiaremos en los cursos de física son escalares o vectoriales. Una cantidad escalar es la que está especificada completamente por
Cantidades vectoriales escalares Vectores Las cantidades físicas que estudiaremos en los cursos de física son escalares o vectoriales. Una cantidad escalar es la que está especificada completamente por
LÍMITES Y CONTINUIDAD DE FUNCIONES
 Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Capítulo 9 LÍMITES Y CONTINUIDAD DE FUNCIONES 9.. Introducción El concepto de ite en Matemáticas tiene el sentido de lugar hacia el que se dirige una función en un determinado punto o en el infinito. Veamos
Ejercicios de Análisis propuestos en Selectividad
 Ejercicios de Análisis propuestos en Selectividad.- Dada la parábola y 4, se considera el triángulo rectángulo T( r ) formado por los ejes coordenados y la tangente a la parábola en el punto de abscisa
Ejercicios de Análisis propuestos en Selectividad.- Dada la parábola y 4, se considera el triángulo rectángulo T( r ) formado por los ejes coordenados y la tangente a la parábola en el punto de abscisa
Ejercicios de derivadas e integrales
 Ejercicios e erivaas e integrales Este material puee escargarse ese http://wwwuves/~montes/biologia/matceropf Departament Estaística i Investigació Operativa Universitat e València Derivaas Reglas e erivación
Ejercicios e erivaas e integrales Este material puee escargarse ese http://wwwuves/~montes/biologia/matceropf Departament Estaística i Investigació Operativa Universitat e València Derivaas Reglas e erivación
MATEMÁTICAS. TEMA 5 Límites y Continuidad
 MATEMÁTICAS TEMA 5 Límites y Continuidad MATEMÁTICAS º BACHILLERATO CCSS. TEMA 5: LÍMITES Y CONTINUIDAD ÍNDICE. Introducción. Concepto de función. 3. Dominio e imagen de una función. 4. Gráfica de algunas
MATEMÁTICAS TEMA 5 Límites y Continuidad MATEMÁTICAS º BACHILLERATO CCSS. TEMA 5: LÍMITES Y CONTINUIDAD ÍNDICE. Introducción. Concepto de función. 3. Dominio e imagen de una función. 4. Gráfica de algunas
MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS x = x - x y2 = f(x2) y = y - y y = f(x )
 Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
Faculta e Contauría Aministración. UNAM Derivaa Autor: Dr. José Manuel Becerra Espinosa MATEMÁTICAS BÁSICAS DERIVADA INCREMENTOS Se eine como incremento e la variable al aumento o isminución que eperimenta,
Integral definida. 4. La integral definida de una suma de funciones es igual a la suma de integrales (Propiedad de linealidad)
 Integral definida Dada una función f(x) de variable real y un intervalo [a,b] R, la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y rectas x = a y x = b. bb
Integral definida Dada una función f(x) de variable real y un intervalo [a,b] R, la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y rectas x = a y x = b. bb
Capítulo 2: Concepto y Cálculo de Límites
 Capítulo : Concepto y Cálculo de Límites Geovany Sanabria Contenido Concepto de Límite Una definición intuitiva de Límite Ejercicios 6 Problemas con la utilización de sucesiones para calcular límites 7
Capítulo : Concepto y Cálculo de Límites Geovany Sanabria Contenido Concepto de Límite Una definición intuitiva de Límite Ejercicios 6 Problemas con la utilización de sucesiones para calcular límites 7
Información importante
 Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Vectores: Producto escalar y vectorial
 Nivelación de Matemática MTHA UNLP 1 Vectores: Producto escalar y vectorial Versores fundamentales Dado un sistema de coordenadas ortogonales, se considera sobre cada uno de los ejes y coincidiendo con
Nivelación de Matemática MTHA UNLP 1 Vectores: Producto escalar y vectorial Versores fundamentales Dado un sistema de coordenadas ortogonales, se considera sobre cada uno de los ejes y coincidiendo con
Seminario Universitario Material para estudiantes. Física. Unidad 2. Vectores en el plano. Lic. Fabiana Prodanoff
 Seminario Universitario Material para estudiantes Física Unidad 2. Vectores en el plano Lic. Fabiana Prodanoff CONTENIDOS Vectores en el plano. Operaciones con vectores. Suma y producto por un número escalar.
Seminario Universitario Material para estudiantes Física Unidad 2. Vectores en el plano Lic. Fabiana Prodanoff CONTENIDOS Vectores en el plano. Operaciones con vectores. Suma y producto por un número escalar.
DERIVACIÓN. mtan. y x x. lim lim y ' f '( x) CAPÍTULO IV
 75 CAPÍTULO IV DERIVACIÓN. LA DERIVADA COMO PENDIENTE DE UNA CURVA La peniente e una curva en un punto ao, es iual a la peniente e la recta tanente a la curva en icho punto. Δ Q, Δ Q Q P, La peniente e
75 CAPÍTULO IV DERIVACIÓN. LA DERIVADA COMO PENDIENTE DE UNA CURVA La peniente e una curva en un punto ao, es iual a la peniente e la recta tanente a la curva en icho punto. Δ Q, Δ Q Q P, La peniente e
Estudio de ceros de ecuaciones funcionales
 Capítulo 1 Estudio de ceros de ecuaciones funcionales Problema 1.1 Calcular el número de ceros de la ecuación arctang(x) = 4 x, dando un intervalo 5 donde se localicen. Solución: Denimos f(x) = arctan(x)
Capítulo 1 Estudio de ceros de ecuaciones funcionales Problema 1.1 Calcular el número de ceros de la ecuación arctang(x) = 4 x, dando un intervalo 5 donde se localicen. Solución: Denimos f(x) = arctan(x)
2.1.5 Teoremas sobre derivadas
 si x < 0. f(x) = x si x 0 x o = 0 Teoremas sobre derivadas 9 2. f(x) = x 3, x o = 3 a. Determine si f es continua en x o. b. Halle f +(x o ) y f (x o ). c. Determine si f es derivable en x o. d. Haga la
si x < 0. f(x) = x si x 0 x o = 0 Teoremas sobre derivadas 9 2. f(x) = x 3, x o = 3 a. Determine si f es continua en x o. b. Halle f +(x o ) y f (x o ). c. Determine si f es derivable en x o. d. Haga la
Apuntes de Matemática Discreta 9. Funciones
 Apuntes de Matemática Discreta 9. Funciones Francisco José González Gutiérrez Cádiz, Octubre de 004 Universidad de Cádiz Departamento de Matemáticas ii Lección 9 Funciones Contenido 9.1 Definiciones y
Apuntes de Matemática Discreta 9. Funciones Francisco José González Gutiérrez Cádiz, Octubre de 004 Universidad de Cádiz Departamento de Matemáticas ii Lección 9 Funciones Contenido 9.1 Definiciones y
Análisis Dinámico: Integración
 Análisis Dinámico: Integración Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Análisis Dinámico: Integración 1 / 57 Integración indefinida
Análisis Dinámico: Integración Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Análisis Dinámico: Integración 1 / 57 Integración indefinida
FÓRMULAS DE DERIVACIÓN
 SESIÓN Nº 1 Derivaas e Funciones Trigonométricas, Eponenciales y Logarítmicas Ahora correspone revisar las fórmulas principales e erivación y algunos ejemplos e aplicación. FÓRMULAS DE DERIVACIÓN 1) (
SESIÓN Nº 1 Derivaas e Funciones Trigonométricas, Eponenciales y Logarítmicas Ahora correspone revisar las fórmulas principales e erivación y algunos ejemplos e aplicación. FÓRMULAS DE DERIVACIÓN 1) (
MÉTODOS DE ELIMINACIÓN Son tres los métodos de eliminación más utilizados: Método de igualación, de sustitución y de suma o resta.
 ECUACIONES SIMULTÁNEAS DE PRIMER GRADO CON DOS INCÓGNITAS. Dos o más ecuaciones con dos incógnitas son simultáneas cuando satisfacen iguales valores de las incógnitas. Para resolver ecuaciones de esta
ECUACIONES SIMULTÁNEAS DE PRIMER GRADO CON DOS INCÓGNITAS. Dos o más ecuaciones con dos incógnitas son simultáneas cuando satisfacen iguales valores de las incógnitas. Para resolver ecuaciones de esta
M a t e m á t i c a s I I 1
 Matemáticas II Matemáticas II ANDALUCÍA CNVCATRIA JUNI 009 SLUCIÓN DE LA PRUEBA DE ACCES AUTR: José Luis Pérez Sanz pción A Ejercicio En este límite nos encontramos ante la indeterminación. Agrupemos la
Matemáticas II Matemáticas II ANDALUCÍA CNVCATRIA JUNI 009 SLUCIÓN DE LA PRUEBA DE ACCES AUTR: José Luis Pérez Sanz pción A Ejercicio En este límite nos encontramos ante la indeterminación. Agrupemos la
1. Ecuaciones no lineales
 1. Ecuaciones no lineales 1.1 Ejercicios resueltos Ejercicio 1.1 Dada la ecuación xe x 1 = 0, se pide: a) Estudiar gráficamente sus raíces reales y acotarlas. b) Aplicar el método de la bisección y acotar
1. Ecuaciones no lineales 1.1 Ejercicios resueltos Ejercicio 1.1 Dada la ecuación xe x 1 = 0, se pide: a) Estudiar gráficamente sus raíces reales y acotarlas. b) Aplicar el método de la bisección y acotar
(A) Primer parcial. si 1 x 1; x 3 si x>1. (B) Segundo parcial
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E700 1) x 5 > 1. A) Primer parcial ) Sean las funciones ft) t +,gy) y 4&hw) w. Encontrar f/h, g f, f g y sus dominios. ) Graficar la función x + six
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E700 1) x 5 > 1. A) Primer parcial ) Sean las funciones ft) t +,gy) y 4&hw) w. Encontrar f/h, g f, f g y sus dominios. ) Graficar la función x + six
Ecuaciones de primer grado con dos incógnitas
 Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
Ecuaciones de primer grado con dos incógnitas Si decimos: "las edades de mis padres suman 120 años", podemos expresar esta frase algebraicamente de la siguiente forma: Entonces, Denominamos x a la edad
LA DERIVADA. Introducción:
 LA DERIVADA Introucción: Fue Isaac Newton que estuiano las lees el movimiento e los planetas que Kepler había escubierto meio siglo antes, llegó a la iea e incremento e una función como se nos ofrece en
LA DERIVADA Introucción: Fue Isaac Newton que estuiano las lees el movimiento e los planetas que Kepler había escubierto meio siglo antes, llegó a la iea e incremento e una función como se nos ofrece en
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
Límite de una función
 Límite de una función Idea intuitiva de límite El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
Límite de una función Idea intuitiva de límite El límite de la función f(x) en el punto x 0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x 0. Es
10 Cálculo. de derivadas. 1. La derivada. Piensa y calcula. Aplica la teoría
 0 Cálculo de derivadas. La derivada Piensa y calcula Calcula mentalmente sobre la primera gráfica del margen: a) la pendiente de la recta secante, r, que pasa por A y B b) la pendiente de la recta tangente,
0 Cálculo de derivadas. La derivada Piensa y calcula Calcula mentalmente sobre la primera gráfica del margen: a) la pendiente de la recta secante, r, que pasa por A y B b) la pendiente de la recta tangente,
DOMINIO Y RANGO DE UNA FUNCIÓN I N D I C E. martilloatomico@gmail.com. Página. Titulo:
 Titulo: DOMINIO Y RANGO I N D I C E Página DE UNA FUNCIÓN Año escolar: 4to. Año de Bachillerato Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela
Titulo: DOMINIO Y RANGO I N D I C E Página DE UNA FUNCIÓN Año escolar: 4to. Año de Bachillerato Autor: José Luis Albornoz Salazar Ocupación: Ing Civil. Docente Universitario País de residencia: Venezuela
Ejemplo: Resolvemos Sin solución. O siempre es positiva o siempre es negativa. Damos un valor cualquiera Siempre + D(f) =
 T1 Dominios, Límites, Asíntotas, Derivadas y Representación Gráfica. 1.1 Dominios de funciones: Polinómicas: D( = La X puede tomar cualquier valor entre Ejemplos: D( = Función racional: es el cociente
T1 Dominios, Límites, Asíntotas, Derivadas y Representación Gráfica. 1.1 Dominios de funciones: Polinómicas: D( = La X puede tomar cualquier valor entre Ejemplos: D( = Función racional: es el cociente
Ecuaciones Diferenciales Tema 2. Trasformada de Laplace
 Ecuaciones Diferenciales Tema 2. Trasformada de Laplace Ester Simó Mezquita Matemática Aplicada IV 1 1. Transformada de Laplace de una función admisible 2. Propiedades básicas de la transformada de Laplace
Ecuaciones Diferenciales Tema 2. Trasformada de Laplace Ester Simó Mezquita Matemática Aplicada IV 1 1. Transformada de Laplace de una función admisible 2. Propiedades básicas de la transformada de Laplace
