MATEMÁTICAS II. x x x d) ( ) b) Como el grado del numerador y del denominador son iguales, hay que empezar por hacer la división.
|
|
|
- Rubén Gutiérrez Maldonado
- hace 7 años
- Vistas:
Transcripción
1 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio Calcula la siguienes inegrales a) d b) d c) 6 d d) 3 d e) d 9 e a) Haciendo el cambio de variable d d. d d d ln C ln ( ) C d ln ( ) C b) Como el grado del numerador y del denominador son iguales, hay que empezar por hacer la división. Comprueba que 6 6 Haciendo lo cálculos habiuales obenemos la descomposición en fracciones simples: Con los resulados aneriores podemos afirmar que: ( 3) 8ln( ) C 3 ln c) La inegral se resuelve por descomposición en fracciones simples, previa división del numerador por el denominador. Para comprobar us resulados puedes uilizar la orden Epandir de la pesaña Simplificar en DERIVE, según se indica a coninuación. d d d d ( ) ln C d) 3 d I d d I I I d d ln 9 C 9 9 d 3 arcan ( 3) 3 C La primera es una logarímica: La segunda un arco angene: ( ) - -
2 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas arcan ( 3) I I 3I 3 ln 9 d C 9 e) d se resuelve con un cambio de variable e e ln d d, que llevado a nuesra inegral: d, que es de ipo racional. ( ) A B ( A B) B A ( A B) B ( ) ( ) B d d I ln ln Deshaciendo el cambio: I ln e ln e ln d e e Ejercicio d. b) Uilizar el cambio de variable e e para calcular Indicación: Para deshacer el cambio uilícese ln a) Calcula: 3 ln d Madrid: sepiembre 8 a) Se resuelve por pares: d u ln du dv v d 3 3 b) e e d e e d 3 ln I ln d d ( e e ) d I d e e e e e e e e e e e e e e e e ln C 6 ( e e ) Llevando ese resulado a la inegral pedida: ( e e ) d ( e e ) d I d d c e e ( e e ) Como en la indicación nos dicen cómo se deshace el cambio, el problema esá erminado: d ln C - -
3 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas O ambién: d ln ( ) C porque ( ) podemos considerar ln ce. incluido en C. ln ln ln y NOTA: Nos han dado la epresión que deshace el cambio de variable, pero si no hubiera sido así, la habríamos obenido de la siguiene forma: e z e e z z z z z z Se raa de resolver una ecuación de segundo grado en z, de coeficienes: a, b, c z e z e ln Ejercicio 3 a) Hallar los máimos y mínimos y los punos de infleión de f b) Deerminar la función F ( ) al que su derivada sea 3 3 f f críicos. Signo de f Crecimieno, decrecimieno de f ( ) ( ) ( ) 3 3 F f y además Madrid: sepiembre 7. D f R y en y la función iene sus punos La función f ( ) alcanza un máimo relaivo en (, f ) (,7 ) y un mínimo relaivo en, f ( ), ( ) ( ) 3 f f ; 3 f ± El Como en esos punos se anula la segunda derivada es nula, y la primero no se anulaba, los res son punos de infleión: ( f ) ( f ) f 3, 3 3,3 3 ;,,3 y 3, 3 3,3 3 3 b) d d 3 d ( ) ln F C 3. ( ) ln F C F 3-3 -
4 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio a) Deerminar las funciones reales de variable real que saisfacen la condición de que la, y de su gráfica viene dada por la pendiene de la reca angene en un puno genérico epresión e. b) Hallar máimo y mínimo locales y los inervalos de crecimieno y decrecimieno de,. aquella de las funciones del aparado anerior que pasa por el puno Madrid: junio 998 Que la pendiene de la angene en cualquier puno venga dada por e, equivale a decir que f e, por lo que la funciones pedidas son las primiivas de ésa. f e f e d, que se hace por pares y se obiene: f e e C. es En el segundo aparado se pide el esudio de, enre las aneriores, la función que pasa por (,), es decir, aquella para la cual f () C C, luego: f e e. El esudio que se pide se hace a parir de - Signo de f f ) ( e. Como e, : > sig ( f ) sig( ) Monoonía de f La función iene un mínimo relaivo en (, f ()) (,). Ejercicio De la función derivable () A y que su derivada es: si f ( ) si > a) Hallar la epresión de f (). b) Obener la ecuación de la reca angene a f () en f se sabe que pasa por el puno (, ) si ( ) f f a si si >. ln b si > Las consanes a y b se deerminan imponiendo dos condiciones: Madrid: Prueba ipo 999- Su gráfica pasa por el puno A(, ) f ( ) 3 a f () es derivable f () coninua lím f lím f 3 a b - -
5 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Resolviendo el sisema: 3 a b 3 f ln si si > Como f () ln > f (), la ecuación de la angene en es: : y ln ( ) Ejercicio 6 Si la derivada de f ( ) es f ( ) 3 ( ), si pide: a) Los inervalos de crecimieno y decrecimieno de f. b) Los valores de en los que f iene eremos relaivos o punos de infleión. f c) La función f sabiendo que Madrid: Junio de 9 a) Para el esudio del crecimieno y decrecimieno esudiamos el signo de f ( ) 3 ( ) f b) Por los resulados del aparado anerior, podemos concluir que en la función alcanza un máimo relaivo y en un mínimo relaivo. Para las infleiones necesiamos la segunda derivada. 3 3 ( ) ( ) 3( ) ( ) ( ) ( ) ( 3( ) ( ) ) f ( ) ( ) f f Podríamos hacer el esudio del signo de f para averiguar si en o la gráfica de f iene alguna infleión, pero no es necesario, pues ya sabemos que en hay un eremo relaivo, por lo que sólo hay un puno de infleión, en. La función f, primiiva de f, se obiene si desarrollamos ésa: 3 3 ( ) ( ) f f ( ) C. 3 f 6 8 C 3 f
6 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas Ejercicio 7 Dada la función f ( ) ln, se pide: a) Deerminar el dominio de f y sus asínoas. y f en. b) Calcular la reca angene a la curva c) Calcular f d. Madrid junio de > >, a) f (, ) { } D f (, ) { } Hay dos posible asínoas vericales: y. Comprobamos si definiivamene lo son. ( ) ( ) ln ln lím f lím lím lím ( ) ln Como lím lím f La reca es una asínoa verical ln ( ) ln ( ) lím f lím lím lím ± No es necesario hacer los límies laerales para saber que la reca ± 3 ln 3 3 es una asínoa verical Viso el dominio de f, el esudio de las asínoas horizonales, y oblicuas si procede, se reduce a cuando. ( ) ln lím f lím lím ln ( ) ( L'H) lím lím b) lím f ln ( ) ln ( ) f f (, ( ) ) (, ) f ( ) 3 A f m y es una asínoa horizonal ( ) ( ) 3 : y ( ) ( ) ln - 6 -
7 Albero Enero Conde Maie González Juarrero Inegral indefinida. Cálculo de primiivas c) ( ) d d ln C u ln d ln ( ) d ln ( ) C u u f d ln ln C NOTA: Si no e das cuena de que la segunda es inmediaa, puedes hacer un cambio de variable ln ( ) e ln ( ) e d e d. d d d C. e Deshaciendo el cambio: ( ) ln ln d C - 7 -
El sistema es incompatible. b) El sistema es compatible determinado. Lo resolvemos por la regla de Cramer.
 Prueba de Acceso a la Universidad. JUNIO 0. Maemáicas II. El alumno debe responder a una de las dos opciones propuesas, A o B. En cada preguna se señala la punuación máima. OPCIÓN A a y z A. Sean a un
Prueba de Acceso a la Universidad. JUNIO 0. Maemáicas II. El alumno debe responder a una de las dos opciones propuesas, A o B. En cada preguna se señala la punuación máima. OPCIÓN A a y z A. Sean a un
DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =
![DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función = DERIVACIÓN BAJO EL SIGNO INTEGRAL. 1. Hallar el punto del intervalo [0,2] en el que la función =](/thumbs/52/30419199.jpg) DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
DERIVACIÓN BAJO EL SIGNO INTEGRAL. Hallar el puno del inervalo [,] en el que la función F () d alcanza su valor mínimo. El mínimo de una función se alcanza en los punos donde su primera derivada es nula
INTEGRACIÓN POR CAMBIO DE VARIABLE
 INTEGRCIÓN POR CMBIO DE VRIBLE Dada la inegral f( ) d, si consideramos como una función de ora variable, = g(), enonces d = g'() d, y susiuyendo en la inegral inicial se obiene f( g( )) g'( ) d. En el
INTEGRCIÓN POR CMBIO DE VRIBLE Dada la inegral f( ) d, si consideramos como una función de ora variable, = g(), enonces d = g'() d, y susiuyendo en la inegral inicial se obiene f( g( )) g'( ) d. En el
EXAMEN DE MATEMÁTICAS I 8 de febrero de 2006
 EXAMEN DE MATEMÁTICAS I 8 de febrero de 006 MATEMÁTICAS I Eamen del º PARCIAL 8 de febrero de 006 Sólo una respuesa a cada cuesión es correca. Respuesa correca: 0. punos. Respuesa incorreca: -0. punos
EXAMEN DE MATEMÁTICAS I 8 de febrero de 006 MATEMÁTICAS I Eamen del º PARCIAL 8 de febrero de 006 Sólo una respuesa a cada cuesión es correca. Respuesa correca: 0. punos. Respuesa incorreca: -0. punos
C cos x sen x 0 x sen x x cos x x sen x cos x x C 1 x 0. Calculamos la matriz adjunta de C: sen x 0 cox 0 cos x sen x. sen x x 1 x 1 sen x
 Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
Prueba de Acceso a la Universidad. SEPTIEMBRE. Maemáicas II. Insrucciones: Se proponen dos opciones A y B. Debe elegirse una y conesar a sus cuesiones. La punuación de cada cuesión aparece en la misma.
EXAMEN DE MATEMÁTICAS I (Primer Parcial) 11 de febrero de 2009
 EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
EXAMEN DE MATEMÁTICAS I (Primer Parcial) de febrero de 9 Sólo una respuesa a cada cuesión es correca. Respuesa correca:. punos. Respuesa incorreca: -. punos Respuesa en blanco: punos.- Sea ABC un riángulo
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 I.E.S. CASTELAR BADAJOZ A. Menguiano PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE - 8 (RESUELTOS por Anonio Menguiano) MATEMÁTICAS II Tiempo máimo: horas minuos Se valorará la corrección
I.E.S. CASTELAR BADAJOZ A. Menguiano PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES SEPTIEMBRE - 8 (RESUELTOS por Anonio Menguiano) MATEMÁTICAS II Tiempo máimo: horas minuos Se valorará la corrección
SEGUNDO EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
MATEMÁTICAS II (G I T I SEGUNDO EXAMEN 13 1 EJERCICIOS RESUELTOS EJERCICIO 1 Considera el cuerpo de revolución que se genera al girar alrededor del eje OX la gráfica de la función x α f(x = x (, + (x +
45 EJERCICIOS de INTEGRAL DEFINIDA 2º BACH. ( )
 5 EJERCICIOS de INTEGRAL DEFINIDA º BACH. Inegral definida:. Enunciar la regla de Barrow. Calcular:. Calcular:. (S) Calcular: d (Soluc: ) a + b a ( ) a + b d Soluc : b d (Soluc: 5/). Calcular: 5. Calcular:
5 EJERCICIOS de INTEGRAL DEFINIDA º BACH. Inegral definida:. Enunciar la regla de Barrow. Calcular:. Calcular:. (S) Calcular: d (Soluc: ) a + b a ( ) a + b d Soluc : b d (Soluc: 5/). Calcular: 5. Calcular:
NOTA: En todos los ejercicios se deberá justificar la respuesta explicando el procedimiento seguido en la resolución del ejercicio.
 NOTA: En odos los ejercicios se deberá jusificar la respuesa eplicando el procedimieno seguido en la resolución del ejercicio. CURSO 10-11 JUNIO CURSO 10 11 1 Aplicando ransformadas de Laplace, hallar
NOTA: En odos los ejercicios se deberá jusificar la respuesa eplicando el procedimieno seguido en la resolución del ejercicio. CURSO 10-11 JUNIO CURSO 10 11 1 Aplicando ransformadas de Laplace, hallar
EJERCICIOS RESUELTOS DE INTEGRALES INDEFINIDAS. 3t t dt 3 dt 3t C 3 x2 1 C. 2 2x 2 1 dx 1 arctg 2x C. 5x dx arctg 5x3 C. Ln t C Ln Ln x C.
 EJERCICIOS RESUELTOS DE INTEGRALES INDEFINIDAS. Para resolverla planeamos la susiución, de la que se sigue que d. Por ano,. 5 5.986 d d d C C. 5 5.986 Ln 5.986 C.. arcg C.. 5 5. 5 6 5 5 6 5 5 arcg5 C.
EJERCICIOS RESUELTOS DE INTEGRALES INDEFINIDAS. Para resolverla planeamos la susiución, de la que se sigue que d. Por ano,. 5 5.986 d d d C C. 5 5.986 Ln 5.986 C.. arcg C.. 5 5. 5 6 5 5 6 5 5 arcg5 C.
a) en [0, 2] ; b) en [-1, 1]
![a) en [0, 2] ; b) en [-1, 1] a) en [0, 2] ; b) en [-1, 1]](/thumbs/80/82443407.jpg) UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO FACULTAD DE CIENCIAS NATURALES CATEDRA: Maemáica I CURSO: 04 TRABAJO PRACTICO Nº -Tercera Pare Pare III. Aplicaciones de la derivada TEOREMA DE ROLLE
UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO FACULTAD DE CIENCIAS NATURALES CATEDRA: Maemáica I CURSO: 04 TRABAJO PRACTICO Nº -Tercera Pare Pare III. Aplicaciones de la derivada TEOREMA DE ROLLE
CÁLCULO DE INTEGRALES. Solución: Todas ellas se resuelven por partes y la fórmula del método es
 CÁLCULO DE NTEGRALES.-Calcula las siguienes inegrales: a) d ; b) sen d ; c) Ld ; e Todas ellas se resuelven por pares y la fórmula del méodo es u. dv u. v v. du a) e d. u du d dv e. d v e d e e e d e e
CÁLCULO DE NTEGRALES.-Calcula las siguienes inegrales: a) d ; b) sen d ; c) Ld ; e Todas ellas se resuelven por pares y la fórmula del méodo es u. dv u. v v. du a) e d. u du d dv e. d v e d e e e d e e
ECUACIONES DIFERENCIALES
 Tema 1 ECUACIONES DIFERENCIALES EJERCICIO 1 Comprobar que la función y() = c 2 ++3 es una solución del problema de valor inicial 2 y 2y + 2y = 6, y(0) = 3, y (0) = 1, (1.1) en <
Tema 1 ECUACIONES DIFERENCIALES EJERCICIO 1 Comprobar que la función y() = c 2 ++3 es una solución del problema de valor inicial 2 y 2y + 2y = 6, y(0) = 3, y (0) = 1, (1.1) en <
Opción A Ejercicio 1.-
 Soluciones modelo (Sepiembre de 009) Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f( ) -+. Deermina la asínoa de la gráfica Evidenemene, la función no iene asínoas vericales,
Soluciones modelo (Sepiembre de 009) Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f( ) -+. Deermina la asínoa de la gráfica Evidenemene, la función no iene asínoas vericales,
Cálculo Diferencial e Integral - Funciones trascendentales. Prof. Farith J. Briceño N.
 Cálculo Diferencial e Inegral - Funciones rascenenales. Prof. Farih J. Briceño N. Objeivos a cubrir Función logarimo y eponencial. Propieaes. Derivaa e inegración. Cóigo : MAT-CDI.5 Ejercicios resuelos
Cálculo Diferencial e Inegral - Funciones rascenenales. Prof. Farih J. Briceño N. Objeivos a cubrir Función logarimo y eponencial. Propieaes. Derivaa e inegración. Cóigo : MAT-CDI.5 Ejercicios resuelos
REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA
 Represenación de curvas planas dadas en forma paramérica REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA PLANTEAMIENTO DEL PROBLEMA Sean x e y dos funciones reales de variable real, de dominios
Represenación de curvas planas dadas en forma paramérica REPRESENTACIÓN DE CURVAS PLANAS DADAS EN FORMA PARAMÉTRICA PLANTEAMIENTO DEL PROBLEMA Sean x e y dos funciones reales de variable real, de dominios
. Podemos afirmar: Dom f. c) f es creciente en un entorno de x 0. = y(t) 9.- Sean las ecuaciones paramétricas de una curva plana.
 1.- Sea una función coninua y = f() al que el dominio de f() =[a,b], enonces: a) El máimo absoluo de f() se alcanza en uno de los valores ales que f ()=0. b) No iene porque ener máimo absoluo. c) El máimo
1.- Sea una función coninua y = f() al que el dominio de f() =[a,b], enonces: a) El máimo absoluo de f() se alcanza en uno de los valores ales que f ()=0. b) No iene porque ener máimo absoluo. c) El máimo
MODELO JUNIO 2005 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
 Modelo de eamen Junio MODELO JUNIO MTEMÁTICS PLICDS LS CIENCIS SOCILES II OPCIÓN. (Punuación máima: punos) Se dice que una mari cuadrada es orogonal si T I: Noa: La noación T significa mari ranspuesa de.
Modelo de eamen Junio MODELO JUNIO MTEMÁTICS PLICDS LS CIENCIS SOCILES II OPCIÓN. (Punuación máima: punos) Se dice que una mari cuadrada es orogonal si T I: Noa: La noación T significa mari ranspuesa de.
1. Derivadas de funciones de una variable. Recta tangente.
 1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
1. Derivadas de funciones de una variable. Reca angene. Derivadas Vamos a ver en ese capíulo la generalización del concepo de derivada de funciones reales de una variable a funciones vecoriales con varias
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO 2011 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
 IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
IES CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE BLERES JUNIO (GENERL) (RESUELTOS por nonio Menguiano) MTEMÁTICS II Tiempo máimo: horas y minuos Conese de manera clara y razonada una de las dos opciones
Autoevaluación Cálculo Integral. sen(x) dx (i) cos(x)
 Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
Auoevaluación Cálculo Inegral Ejercicio 6. Calcular las siguienes inegrales indefinidas: ln d d ln( + d (a (b (c g cos + e d e + (d (e e + e d (f d cos( sen (g sen ( d (h ( + sen( d (i cos( cos ( + d (j
Examen de Matemáticas II 2º de Bachillerato
 º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
º Bachillerao - Maemáicas II 1. Calcular el siguiene límie: Eamen e Maemáicas II º e Bachillerao 1 cos lim 0 e 1. Encuenra el puno e la reca y, que cumpla que la suma e los cuaraos e sus coorenaas sea
Unidad 6 Derivadas PÁGINA 135 SOLUCIONES. 1. La solución en cada caso es: = lím. lím. = h. 2. Queda: La recta debe tener una forma: y = x + b 5
 Unidad 6 Derivadas PÁGINA 15 SOLUCIONES 1. La solución en cada caso es: f ( ) f () ( ) 5 17 1 a) lím lím lím lím (1 ) 1 0 0 0 0 b) g ( ) g ( ) ( ) 1 1 lím lím lím 0 ( 1 1) 1. Queda: 1 La reca debe ener
Unidad 6 Derivadas PÁGINA 15 SOLUCIONES 1. La solución en cada caso es: f ( ) f () ( ) 5 17 1 a) lím lím lím lím (1 ) 1 0 0 0 0 b) g ( ) g ( ) ( ) 1 1 lím lím lím 0 ( 1 1) 1. Queda: 1 La reca debe ener
prepara TU SElECTIVIDAD
 prepara TU SElECTIVIDAD Se considera la función f ( ) = ( + a) e a siendo a un parámero real. a) Razone a qué es igual el dominio de f ( ). b) Deermine el valor de a para que la gráfica de f() pase por
prepara TU SElECTIVIDAD Se considera la función f ( ) = ( + a) e a siendo a un parámero real. a) Razone a qué es igual el dominio de f ( ). b) Deermine el valor de a para que la gráfica de f() pase por
Unidad 9 Funciones exponenciales, logarítmicas y trigonométricas
 Unidad 9 Funciones eponenciales, logarímicas y rigonoméricas PÁGINA 177 SOLUCIONES 1. En cada uno de los res casos: a) Domf = Imf = Esricamene creciene en odo su dominio. No acoada. Simérica respeco al
Unidad 9 Funciones eponenciales, logarímicas y rigonoméricas PÁGINA 177 SOLUCIONES 1. En cada uno de los res casos: a) Domf = Imf = Esricamene creciene en odo su dominio. No acoada. Simérica respeco al
GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA
 GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA Una curva C se dice definida paraméricamene por medio de un parámero, si las coordenadas afines de sus punos M se expresan en función de ese parámero, cuando varía
GRÁFICA DE CURVAS EN FORMA PARAMÉTRICA Una curva C se dice definida paraméricamene por medio de un parámero, si las coordenadas afines de sus punos M se expresan en función de ese parámero, cuando varía
130 Matemáticas I. Parte IV. I.T.I. en Electricidad. Prof: Jos Antonio Abia Vian
 30 Maemáicas I Pare IV Cálculo inegral en IR 3 Maemáicas I : Cálculo inegral en IR Tema Cálculo de primiivas. Primiiva de una función Definición 55.- Diremos ue la función F coninua en [a, b], es una primiiva
30 Maemáicas I Pare IV Cálculo inegral en IR 3 Maemáicas I : Cálculo inegral en IR Tema Cálculo de primiivas. Primiiva de una función Definición 55.- Diremos ue la función F coninua en [a, b], es una primiiva
( ) ( 15 50) 0
 PRUE DE CCESO L UNIVERSIDD JUNIO 7 OPCION ) Deermina dos números reales posiivos sabiendo que su suma es y que el produco de sus cuadrados es máximo. Sean x e y los números reales que suman y P x y odos
PRUE DE CCESO L UNIVERSIDD JUNIO 7 OPCION ) Deermina dos números reales posiivos sabiendo que su suma es y que el produco de sus cuadrados es máximo. Sean x e y los números reales que suman y P x y odos
(a-3)x+(a-2)y+2z=-1 (2a-6)x+(3a-6)y+5z=-1 (3-a)x+(a-2)z=a 2-4a+5. a-3. a 2-4a a 2-4a+3
 EXTRAORDINARIO DE 8. PROBLEMA A. Esudia el siguiene sisema de ecuaciones lineales dependiene del parámero real a y resuélvelo en los casos en que es compaible: Aplicamos el méodo de Gauss: a-3 (a-3) 3-a
EXTRAORDINARIO DE 8. PROBLEMA A. Esudia el siguiene sisema de ecuaciones lineales dependiene del parámero real a y resuélvelo en los casos en que es compaible: Aplicamos el méodo de Gauss: a-3 (a-3) 3-a
IES CASTELAR BADAJOZ Examen Junio de 2011(General) Solución Antonio Mengiano Corbacho
 IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
IES CASTELAR BADAJOZ Eamen Junio de (General) Anonio Mengiano Corbacho PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE BALEARES JUNIO (GENERAL) MATEMÁTICAS II Tiempo máimo: horas y minuos Conese de manera clara
Examen Final de Ecuaciones Diferenciales Septiembre 2007
 Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
Eamen Final de Ecuaciones Diferenciales Sepiembre 007 Problema La siguiene ecuación diferencial de primer orden se puede resolver por diferenes méodos según cómo se planee. d d = + () Conesar las siguienes
x t, x t, x dx dt sustituyendo e integrando, obtenemos: 3
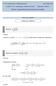 E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
E.T.S.I. Indusriales y Telecomunicación Curso - Grados E.T.S.I. Indusriales y Telecomunicación Tema 5: Inegración de funciones de una variable. Ejercicios resuelos Inegración indefinida Resolver. d 6 Hacemos
Opción A Ejercicio 1.-
 Colegio Lux Mundi (Cajar-Granada) Examen Sepiembre de 009 Javier Cosillo Iciarra Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f ( x ) x -x+x. Deermina la asínoa de la
Colegio Lux Mundi (Cajar-Granada) Examen Sepiembre de 009 Javier Cosillo Iciarra Opción A Ejercicio.- ['5 punos] Se considera la función f: [, + ) R definida por f ( x ) x -x+x. Deermina la asínoa de la
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-V--00-208 CURSO: Maemáica Inermedia CÓDIGO DEL CURSO: 07 SEMESTRE: Primer Semesre JORNADA: Vesperina
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-07-2-V--00-208 CURSO: Maemáica Inermedia CÓDIGO DEL CURSO: 07 SEMESTRE: Primer Semesre JORNADA: Vesperina
1 a 1 a 1. 0 a 1 a a 0. 0 a 1 a 1 a a 1 a 1 a 1 a 1 a a 1 a 1 a 1 a 1. a 1 a 1 a 1 a 1 0 a 1, a 1
 Pruebas de Apiud para el Acceso a la Universidad. JUNIO 1998. Maemáicas II. OPCIÓN A 1. Discuir el sisema a z solución del mismo cuando a = [1 puno] (a 1) y a z 1 (a 1) y (a 1) z según sea el valor del
Pruebas de Apiud para el Acceso a la Universidad. JUNIO 1998. Maemáicas II. OPCIÓN A 1. Discuir el sisema a z solución del mismo cuando a = [1 puno] (a 1) y a z 1 (a 1) y (a 1) z según sea el valor del
Ecuaciones de primer orden
 Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
Capíulo 1 Ecuaciones de primer orden Problema 1.1 Hallar la solución general de la ecuación + 1 + 2 = 0. Hallar la solución que verifica (0) = 0 y la que verifica (1) = 0. k=-5 k=5 k=-1 Figura 1.1: Soluciones
TRABAJO PRÁCTICO N 3: Derivadas - Diferencial
 TRABAJO PRÁCTICO N : Derivadas - Diferencial ) Definición de derivada en un puno: La derivada de la función f es aquella función, denoada por f ', al que su valor en un número del dominio de f esá dado
TRABAJO PRÁCTICO N : Derivadas - Diferencial ) Definición de derivada en un puno: La derivada de la función f es aquella función, denoada por f ', al que su valor en un número del dominio de f esá dado
CAPÍTULO 5. INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS 5.1. Introducción 5.2. Cambios de variable 5.3. Transformación en sumas 5.4. Problemas resueltos
 CAPÍTULO 5. INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS 5.. Inroducción 5.. Cambios de variable 5.3. Transformación en sumas 5.4. Problemas resuelos 5.5. Inegración por recurrencia Capíulo 5 Inegración de
CAPÍTULO 5. INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS 5.. Inroducción 5.. Cambios de variable 5.3. Transformación en sumas 5.4. Problemas resuelos 5.5. Inegración por recurrencia Capíulo 5 Inegración de
PROBLEMA 3. a) Determina el valor de a para que la siguiente función sea continua en x = 1:
 EXAMEN COMPLETO Baremo: Se elegirá el o el EJERCICIO B, del que SOLO se harán TRES de los cuaro problemas. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada esudiane podrá disponer de una calculadora cienífica
EXAMEN COMPLETO Baremo: Se elegirá el o el EJERCICIO B, del que SOLO se harán TRES de los cuaro problemas. LOS TRES PROBLEMAS PUNTÚAN POR IGUAL. Cada esudiane podrá disponer de una calculadora cienífica
IES Fco Ayala de Granada Suplente Junio de 2017 (Modelo 4) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Suplene Junio de 07 (Modelo 4) Germán-Jesús Rubio Luna Opción A Ejercicio opción A, Suplene Junio 07 (modelo 4) x+ si x < 0 Se sabe que la función f : R R dada por f(x) = x + acos(x)
IES Fco Ayala de Granada Suplene Junio de 07 (Modelo 4) Germán-Jesús Rubio Luna Opción A Ejercicio opción A, Suplene Junio 07 (modelo 4) x+ si x < 0 Se sabe que la función f : R R dada por f(x) = x + acos(x)
LA INTEGRAL INDEFINIDA
 Inegrales LA INTEGRAL INDEFINIDA Inegral indefinida: Primiiva (aniderivada) Primiivas (Aniderivadas) Dada la función F( es fácil hallar su derivada F (. El proceso inverso: enconrar F ( a parir de F (
Inegrales LA INTEGRAL INDEFINIDA Inegral indefinida: Primiiva (aniderivada) Primiivas (Aniderivadas) Dada la función F( es fácil hallar su derivada F (. El proceso inverso: enconrar F ( a parir de F (
Propuesta A. 1. Dadas las matrices: C = B = A =
 Pruebas de Acceso a Enseñanzas Univerarias Oiciales de Grado 6 Maeria: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá conesar a una de las dos opciones propuesas A ób. Se podrá uilizar
Pruebas de Acceso a Enseñanzas Univerarias Oiciales de Grado 6 Maeria: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II El alumno deberá conesar a una de las dos opciones propuesas A ób. Se podrá uilizar
PRIMER EXAMEN EJERCICIOS RESUELTOS
 MATEMÁTICAS II (G. I. T. I.) PRIMER EXAMEN 03 04 EJERCICIOS RESUELTOS EJERCICIO. Dada la curva cuya ecuación en coordenadas polares es r θ para 0 θ, se pide: () Deermina la ecuación de la reca angene a
MATEMÁTICAS II (G. I. T. I.) PRIMER EXAMEN 03 04 EJERCICIOS RESUELTOS EJERCICIO. Dada la curva cuya ecuación en coordenadas polares es r θ para 0 θ, se pide: () Deermina la ecuación de la reca angene a
Unidad 5 Geometría afín en el espacio
 Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
Unidad 5 Geomería afín en el espacio 5 SOLUCIONES. a) Los componenes de los vecores pedidos son: b) Eisen infinias parejas de punos C D que cumplan la condición pedida. Por ejemplo, C(,,) D (,,). c) Sea
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Junio, Ejercicio, Opción A Reserva, Ejercicio, Opción A Reserva, Ejercicio,
ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1
 ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1 A) Hallar la pendiene de la reca secane a la parábola y + 8,cuyas abscisas de los punos de inersección son 1 y 4 f ( ) f ( a) B) Dada la siguiene epresión
ANÁLISIS MATEMÁTICO I TEMA IV : DERIVADA Hoja 1 A) Hallar la pendiene de la reca secane a la parábola y + 8,cuyas abscisas de los punos de inersección son 1 y 4 f ( ) f ( a) B) Dada la siguiene epresión
Como podrás observar, los valores de la última columna no son iguales a qué se debe esto, si para una función lineal sí resultaron iguales?
 Razón de cambio de una función cuadráica Ejemplo.5 Un puno se desplaza en el plano describiendo el lugar geomérico correspondiene a la función f ( x x 6x 3. Obén la razón promedio de cambio. Considera
Razón de cambio de una función cuadráica Ejemplo.5 Un puno se desplaza en el plano describiendo el lugar geomérico correspondiene a la función f ( x x 6x 3. Obén la razón promedio de cambio. Considera
RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN. Razón de cambio instantánea y la derivada de una función
 RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN Razón de cambio insanánea y la derivada de una función anerior Reomemos nuevamene el problema del proyecil esudiado en la secuencia
RELACIÓN ENTRE LA RAZÓN DE CAMBIO INSTANTÁNEA Y LA DERIVADA DE UNA FUNCIÓN Razón de cambio insanánea y la derivada de una función anerior Reomemos nuevamene el problema del proyecil esudiado en la secuencia
Propuesta A. y B = 1 0
 Pruebas de cceso a Enseñanzas Univerarias Oiciales de Grado Maeria: MEMÁIS PLIDS LS IENIS SOILES II El alumno deberá conesar a una de las dos opciones propuesas o. Se podrá uilizar cualquier ipo de calculadora..
Pruebas de cceso a Enseñanzas Univerarias Oiciales de Grado Maeria: MEMÁIS PLIDS LS IENIS SOILES II El alumno deberá conesar a una de las dos opciones propuesas o. Se podrá uilizar cualquier ipo de calculadora..
U.P.R. Departamento de Ciencias Matemáticas RUM MATE 3031 Examen Final 3 de diciembre de 2007
 U.P.R. Dearameno de Ciencias Maemáicas RUM MATE 33 Eamen Final 3 de diciembre de 7 Nombre: Profesor: Sección: Insrucciones: Lea cada reguna minuciosamene y muesre odo su rabajo. Esá rohibido coiar, consular
U.P.R. Dearameno de Ciencias Maemáicas RUM MATE 33 Eamen Final 3 de diciembre de 7 Nombre: Profesor: Sección: Insrucciones: Lea cada reguna minuciosamene y muesre odo su rabajo. Esá rohibido coiar, consular
a) Dar la definición de dominio y rango de una función. b) Explicar cada una de las siguientes funciones y dar tres ejemplos de cada una.
 UNIVERSIDAD DE LONDRES PREPARATORIA GUIA DE MATEMÁTICAS VI Áreas I-II Plan : 9 Clave maeria : 00 Clave UNAM : Unidad I. Funciones Objeivos Que el alumno idenifique disinos ipos de funciones, esablezca
UNIVERSIDAD DE LONDRES PREPARATORIA GUIA DE MATEMÁTICAS VI Áreas I-II Plan : 9 Clave maeria : 00 Clave UNAM : Unidad I. Funciones Objeivos Que el alumno idenifique disinos ipos de funciones, esablezca
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES 2.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS
 CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS Hasa ahora conocemos la represenación de una grafica mediane una ecuación con dos variables. En ese
CURVAS PLANAS, ECUACIONES PARAMETRICAS Y COORDENADAS POLARES.1 CURVAS PLANAS Y ECUACIONES PARAMETRICAS Hasa ahora conocemos la represenación de una grafica mediane una ecuación con dos variables. En ese
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica TERCER EXAMEN PARCIAL CÁLCULO. Miércoles 3 de setiembre de 2014
 Universidad de Cosa Rica Insiuo Tecnológico de Cosa Rica TERCER EXAMEN PARCIAL CÁLCULO Miércoles 3 de seiembre de 4 INSTRUCCIONES Lea cuidadosamene, cada insrucción y preguna, anes de conesar. Uilice únicamene
Universidad de Cosa Rica Insiuo Tecnológico de Cosa Rica TERCER EXAMEN PARCIAL CÁLCULO Miércoles 3 de seiembre de 4 INSTRUCCIONES Lea cuidadosamene, cada insrucción y preguna, anes de conesar. Uilice únicamene
Matemáticas II TEMA 10 La integral indefinida
 nálisis. Inegral Indefinida Maemáicas II TEM 0 La inegral indefinida. oncepo de inegral indefinida La derivada de una función permie conocer la asa de variación (el cambio insanáneo) de un deerminado fenómeno
nálisis. Inegral Indefinida Maemáicas II TEM 0 La inegral indefinida. oncepo de inegral indefinida La derivada de una función permie conocer la asa de variación (el cambio insanáneo) de un deerminado fenómeno
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
 INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
Geometría del espacio
 Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
Geomería del espacio º) Dados los vecores u = (,, ) v = (,, ), calcula: a) sus módulos. b) su produco escalar. c) el coseno del ángulo que forman. d) el valor de w para que el vecor w (w,, ) sea perpendicular
TEMA 2: CINETICA DE LA TRASLACIÓN
 TEMA 2: CINETICA DE LA TRASLACIÓN 1.1. Inroducción. Para ener caracerizado un movimieno mecánico cualquiera, hay que esablecer primero respeco a que cuerpo (s) se va a considerar dicho movimieno. Ese cuerpo
TEMA 2: CINETICA DE LA TRASLACIÓN 1.1. Inroducción. Para ener caracerizado un movimieno mecánico cualquiera, hay que esablecer primero respeco a que cuerpo (s) se va a considerar dicho movimieno. Ese cuerpo
Técnicas cualitativas para las Ecuaciones diferenciales de primer orden: Campos de pendientes y ĺıneas de fase. Campos de pendientes
 Lección 5 Técnicas cualiaivas para las Ecuaciones diferenciales de primer orden: Campos de pendienes y ĺıneas de fase Campos de pendienes () solución de = f (, ) pendiene de la reca angene a la gráfica
Lección 5 Técnicas cualiaivas para las Ecuaciones diferenciales de primer orden: Campos de pendienes y ĺıneas de fase Campos de pendienes () solución de = f (, ) pendiene de la reca angene a la gráfica
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA
 DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL Septiembre de 00 APELLIDOS: NOMBRE: DNI CUESTIONARIO DE RESPUESTA MÚLTIPLE (50%) (Cada respuesta incorrecta
DEPARTAMENTO DE FUNDAMENTOS DE ECONOMÍA E HISTORIA ECONÓMICA Análisis Matemático I EXAMEN FINAL Septiembre de 00 APELLIDOS: NOMBRE: DNI CUESTIONARIO DE RESPUESTA MÚLTIPLE (50%) (Cada respuesta incorrecta
Modelo 2 OPCIÓN A. A y B AB se puede realizar porqueel n decolumnas de Aesigual al n de filas de B AB. t t t
 Insrucciones: a) Duración: 1 hora y 3 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida. c) En cada ejercicio, pare o aparado se indica la punuación máxima
Insrucciones: a) Duración: 1 hora y 3 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida. c) En cada ejercicio, pare o aparado se indica la punuación máxima
Soluciones a los ejercicios propuestos Unidad 3. Ecuaciones, inecuaciones y sistemas Matemáticas aplicadas a las Ciencias Sociales
 Soluciones a los ejercicios propuesos Unidad cuaciones inecuaciones sisemas Maemáicas aplicadas a las Ciencias Sociales CUACIONS D SGUNDO GRADO Resuelve e inerprea gráficamene las soluciones de las ecuaciones:
Soluciones a los ejercicios propuesos Unidad cuaciones inecuaciones sisemas Maemáicas aplicadas a las Ciencias Sociales CUACIONS D SGUNDO GRADO Resuelve e inerprea gráficamene las soluciones de las ecuaciones:
Representación gráfica de curvas en forma paramétrica x a(t sent) 1.- Representar la curva dada por
 Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
Represenación gráfica de curvas en forma paramérica x a( sen) 1.- Represenar la curva dada por, siendo a > 0. y a(1 cos).- Emparejar cada curva con su gráfica ì ì x = a) ï x = í b) ï ì í ï c) ï x = - sen
1 DEFINICION. INTEGRALES INMEDIATAS
 DEFNCON. NTEGRALES NMEDATAS CAMBO DE VARABLE NTEGRACON POR PARTES SUSTTUCONES TRGONOMETRCAS 5 NTEGRACÓN POR RECURRENCA 6 NTEGRACÓN DE FUNCONES RACONALES. METODO DE HERMTE 7 NTEGRACÓN DE FUNCONES RRACONALES
DEFNCON. NTEGRALES NMEDATAS CAMBO DE VARABLE NTEGRACON POR PARTES SUSTTUCONES TRGONOMETRCAS 5 NTEGRACÓN POR RECURRENCA 6 NTEGRACÓN DE FUNCONES RACONALES. METODO DE HERMTE 7 NTEGRACÓN DE FUNCONES RRACONALES
LA INTEGRAL INDEFINIDA
 Inegrales LA INTEGRAL INDEFINIDA Inegral indeinida: Primiiva (aniderivada) Primiivas (Aniderivadas) Dada la unción F (, es ácil hallar su derivada F (. El proceso inverso, enconrar F ( a parir de F ( se
Inegrales LA INTEGRAL INDEFINIDA Inegral indeinida: Primiiva (aniderivada) Primiivas (Aniderivadas) Dada la unción F (, es ácil hallar su derivada F (. El proceso inverso, enconrar F ( a parir de F ( se
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 5 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 OPCIÓN A 0 1 0 0 1 1 Sean las marices C = 1 0 1 y D = 1 0 1. 0 1 0 1 1 0 a) (1.5 punos) Resuelva la ecuación maricial 2 X C D = ( I 3 + D) C. b) (1 puno) Si las marices C y D son las marices de adyacencia
OPCIÓN A 0 1 0 0 1 1 Sean las marices C = 1 0 1 y D = 1 0 1. 0 1 0 1 1 0 a) (1.5 punos) Resuelva la ecuación maricial 2 X C D = ( I 3 + D) C. b) (1 puno) Si las marices C y D son las marices de adyacencia
Relación de ejercicios. Ecuaciones diferenciales
 Relación de ejercicios. Ecuaciones diferenciales Abraham Rueda Zoca Ejercicio 1. [ punos] Resolver la ecuación diferencial: x = 2 + x + x 2 2. Solución. Veamos que se raa de una ecuación homogénea. Si
Relación de ejercicios. Ecuaciones diferenciales Abraham Rueda Zoca Ejercicio 1. [ punos] Resolver la ecuación diferencial: x = 2 + x + x 2 2. Solución. Veamos que se raa de una ecuación homogénea. Si
ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2015
 GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
GEOMETRÍA (Selecividad 15) 1 ALGUNOS PROBLEMAS DE GEOMETRÍA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 15 1 Andalucía, junio 15 Sean los punos A(, 1, 1), B(, 1, ), C( 1,, ) y D(, 1, m) a) [,75 punos]
BLOQUE 2 CÁLCULO INTEGRAL
 BLOQUE CÁLCULO INTEGRAL INTEGRALES INDEFINIDAS. Primeras deiniciones.propiedades De: Se dice que F es FUNCIÓN PRIMITIVA de si F = EJEMPLO: Es evidene que es una primiiva de ya que ( ) = Pero ambién + es
BLOQUE CÁLCULO INTEGRAL INTEGRALES INDEFINIDAS. Primeras deiniciones.propiedades De: Se dice que F es FUNCIÓN PRIMITIVA de si F = EJEMPLO: Es evidene que es una primiiva de ya que ( ) = Pero ambién + es
ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN 2013
 GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
GEOMETRÍA (Selecividad ) ALGUNOS PROBLEMAS DE SELECTIVIDAD PROPUESTOS EN Aragón junio a) Pueden eisir vecores u v ales que u v u v = 8? Jusifica la respuesa b) Deermina odos los posibles vecores u = (a
Ondas y Rotaciones. Principios fundamentales II
 Ondas y Roaciones rincipios fundamenales II Jaime Feliciano Hernández Universidad Auónoma Meropoliana - Izapalapa México, D. F. 5 de agoso de 0 INTRODUCCIÓN. Generalmene el esudio del movimieno se realiza
Ondas y Roaciones rincipios fundamenales II Jaime Feliciano Hernández Universidad Auónoma Meropoliana - Izapalapa México, D. F. 5 de agoso de 0 INTRODUCCIÓN. Generalmene el esudio del movimieno se realiza
5. Planos y rectas en el espacio
 5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
5. Planos recas en el espacio ACTIVIDADES INICIALES 5.I Calcula el valor de los siguienes deerminanes a) 5 b) 5 4 c) d) 5.II Esudia la compaibilidad de los siguienes sisemas resuélvelos en los casos en
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA MATEMÁTICAS II TEMA 3: ESPACIO AFÍN Y EUCLÍDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 6 MATEMÁTICAS II TEMA : ESPACIO AFÍN Y EUCLÍDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio 4, Opción
PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE Apellidos Nombre. DNI / NIE Centro de examen
 CALIFICACIÓN: Consejería de Educación, Ciencia y Culura PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE 011 Resolución de 9 de marzo de 011 (DOCM de 5 de abril)
CALIFICACIÓN: Consejería de Educación, Ciencia y Culura PRUEBAS DE ACCESO A CICLOS FORMATIVOS DE GRADO SUPERIOR DE FORMACIÓN PROFESIONAL SEPTIEMBRE 011 Resolución de 9 de marzo de 011 (DOCM de 5 de abril)
MATEMÁTICAS II Examen del 28/05/2012 Solución Importante
 MATEMÁTICAS II Examen del 8/05/0 Solución Imporane Las calificaciones se harán públicas en el aula virual el 08/06/0. La revisión será el /06/0 y el /06/0 de -3 horas en la sala D-4-. MATEMÁTICAS II 8/05/0
MATEMÁTICAS II Examen del 8/05/0 Solución Imporane Las calificaciones se harán públicas en el aula virual el 08/06/0. La revisión será el /06/0 y el /06/0 de -3 horas en la sala D-4-. MATEMÁTICAS II 8/05/0
Departamento de Matemáticas Página 1 PROBLEMAS DE SELECTIVIDAD. INTEGRAL INDEFINIDA. (Sugerencia: cambio de variable
 Departamento de Matemáticas Página PROBLEMAS DE SELECTIVIDAD. INTEGRAL INDEFINIDA. d 4.0.- Calcula ( ) (Sugerencia: cambio de variable t ) 4-0.- Sea f : R R la función definida por Sea f ( ) e cos ( )
Departamento de Matemáticas Página PROBLEMAS DE SELECTIVIDAD. INTEGRAL INDEFINIDA. d 4.0.- Calcula ( ) (Sugerencia: cambio de variable t ) 4-0.- Sea f : R R la función definida por Sea f ( ) e cos ( )
OPCIÓN A MATEMÁTICAS 2º BACHILLERATO B
 MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
MTEMÁTICS º BCHILLERTO B -5-11 OPCIÓN 1.- 1 Dadas las funciones f( x) = x x+, gx ( ) = x+ 1 a) Esboza sus gráficas y calcula su puno de core b) Señala el recino limiado por las gráficas de ambas funciones
x 1; Soluciones dobles
 EJERCICIOS TIPO EXAMEN ECUACIONES INECUACIONES Y SISTEMAS.- Resuelve las ecuaciones siguienes, facorizando previamene en los casos que eso sea posible: a) Solución: Por raarse de una ecuación de grado
EJERCICIOS TIPO EXAMEN ECUACIONES INECUACIONES Y SISTEMAS.- Resuelve las ecuaciones siguienes, facorizando previamene en los casos que eso sea posible: a) Solución: Por raarse de una ecuación de grado
5. Métodos de integración y aplicaciones de la integral denida 5.5 Fracciones parciales. Métodos de Integración. Método de Euler
 Méodos de Inegración Méodo de Euler Para resolver inegrales de la forma ax + bx + c El maemáico suízo Leonard Euler, ideó unas susiuciones que permien ransformar esas inegrales a inegrales de funciones
Méodos de Inegración Méodo de Euler Para resolver inegrales de la forma ax + bx + c El maemáico suízo Leonard Euler, ideó unas susiuciones que permien ransformar esas inegrales a inegrales de funciones
MATEMÁTICAS II. ANDALUCÍA Pruebas de acceso a la Universidad SOLUCIONES 1. (2001-1A-3) Tienen inversa las matrices A y D.
 MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
MTEMÁTICS II NDLUCÍ Pruebas de acceso a la Universidad ÁLGEBR SOLUCIONES. (--) Tienen inversa las marices y D. = y D =. (-B-) a) Rango de. Si a y Si a = o Sisema = B a, ( ) R = a =, ( ) R = Si a y a, S.C.D.
ANDALUCÍA JUNIO 2004
 ANDALUCÍA JUNIO 004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Insrucciones: a) Duración: 1 hora y 0 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida.
ANDALUCÍA JUNIO 004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II Insrucciones: a) Duración: 1 hora y 0 minuos. b) Elija una de las dos opciones propuesas y conese los ejercicios de la opción elegida.
Matemáticas 1 1 EJERCICIOS RESUELTOS: Funciones de varias variables. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C.
 Maemáicas 1 1 EJERCICIOS RESUELTOS: Funciones de varias variables Elena Álvarez Sáiz Dpo. Maemáica Aplicada C. Compuación Universidad de Canabria Ingeniería de Telecomunicación Ejercicios: Func. varias
Maemáicas 1 1 EJERCICIOS RESUELTOS: Funciones de varias variables Elena Álvarez Sáiz Dpo. Maemáica Aplicada C. Compuación Universidad de Canabria Ingeniería de Telecomunicación Ejercicios: Func. varias
EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A
 Ejercicio 1. (2,5 puntos) EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A Dada la función f (x)= 3 x 2 +3 x a) (1,25 puntos) Indicar el dominio de definición de la función f y hallar
Ejercicio 1. (2,5 puntos) EXAMEN I RESUELTO PRIMERA EVALUACIÓN MATEMÁTICAS II 08/11/2017 OPCIÓN A Dada la función f (x)= 3 x 2 +3 x a) (1,25 puntos) Indicar el dominio de definición de la función f y hallar
Actividades de recuperación
 Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
Acividades de recuperación.- Dados los vecores a y b de la figura. Calcula: a) a + b ; b) a b + c ; c) a ; d) a b..- Dados los punos A(3, -), B(4, 3) y C(5, -3), se pide: a) Hallar las coordenadas de los
= A, entonces A = 0. Y si A es una matriz. y comprobar el resultado. ,, ;,, es el mismo que el generado
 EJERCICIOS. APLICACIONES DE LOS DETERMINANTES. 1. Calcular el siguiene deerminane de orden n: 1 n n n n n n n n n n n n n. Demosrar que si A es una mariz al que n n, se verifica lo anerior? A = A, enonces
EJERCICIOS. APLICACIONES DE LOS DETERMINANTES. 1. Calcular el siguiene deerminane de orden n: 1 n n n n n n n n n n n n n. Demosrar que si A es una mariz al que n n, se verifica lo anerior? A = A, enonces
Por lo tanto el polinomio de Newton basado en diferencias divididas será:
 Universidad Nacional de Ingeniería 7--6 Faculad de Ingeniería Mecánica P.A. 5- Área de Ciencias Básicas y Humanidades SE PERMITE UNA HOJA DE FORMULARIO. Problema ARIO - EXAMEN FINAL DE CALCULO NUMERICO
Universidad Nacional de Ingeniería 7--6 Faculad de Ingeniería Mecánica P.A. 5- Área de Ciencias Básicas y Humanidades SE PERMITE UNA HOJA DE FORMULARIO. Problema ARIO - EXAMEN FINAL DE CALCULO NUMERICO
y = x ln x ; con los datos obtenidos representa su gráfica. f x es continua y derivable en 0, por ser producto de funciones continuas y derivables.
 Matemáticas II Curso 0/4 Opción A (ª evaluación) Ejercicio. (Puntuación máima: puntos) Estudia las características de la función = ln = ( 0, + ) ( + ) f Dom f y = ln ; con los datos obtenidos representa
Matemáticas II Curso 0/4 Opción A (ª evaluación) Ejercicio. (Puntuación máima: puntos) Estudia las características de la función = ln = ( 0, + ) ( + ) f Dom f y = ln ; con los datos obtenidos representa
ÁLGEBRA (Selectividad 2014) 1 ALGUNOS PROBLEMAS DE ÁLGEBRA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2014
 ÁLGEBR (Selecividad 04) LGUNOS PROBLEMS DE ÁLGEBR PROPUESTOS EN LS PRUEBS DE SELECTIVIDD DE 04 Casilla y León, junio 4 a a+ a+ Sea la mariz = a a+ 3 a+ 4 a a+ 5 a+ 6 a) Discuir su rango en función de los
ÁLGEBR (Selecividad 04) LGUNOS PROBLEMS DE ÁLGEBR PROPUESTOS EN LS PRUEBS DE SELECTIVIDD DE 04 Casilla y León, junio 4 a a+ a+ Sea la mariz = a a+ 3 a+ 4 a a+ 5 a+ 6 a) Discuir su rango en función de los
03) Rapidez de Cambio. 0302) Rapidez de Cambio
 Página 3) Rapidez de Cambio 3) Rapidez de Cambio Desarrollado por el Profesor Rodrigo Vergara Rojas Ocubre 7 Ocubre 7 Página A) Rapidez media de cambio Considere una canidad física (), como la mosrada
Página 3) Rapidez de Cambio 3) Rapidez de Cambio Desarrollado por el Profesor Rodrigo Vergara Rojas Ocubre 7 Ocubre 7 Página A) Rapidez media de cambio Considere una canidad física (), como la mosrada
, se denomina primitiva de esta función a otra F(x)
 1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE)
 UNIVERSIDDES PÚLICS DE L COUNIDD DE DRID PRUET DE CCESO ESTUDIOS UNIVERSITRIOS (LOGSE) Curso 8-9 (Sepiebre) TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN El aluno conesará a los cuaro ejercicios de
UNIVERSIDDES PÚLICS DE L COUNIDD DE DRID PRUET DE CCESO ESTUDIOS UNIVERSITRIOS (LOGSE) Curso 8-9 (Sepiebre) TERI: TEÁTICS II INSTRUCCIONES GENERLES Y VLORCIÓN El aluno conesará a los cuaro ejercicios de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE)
 UNIVERSIDADES PÚBLICAS DE LA COUNIDAD DE ADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 8-9 (Sepiebre) ATERIA: ATEÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El aluno conesará a los
UNIVERSIDADES PÚBLICAS DE LA COUNIDAD DE ADRID PRUETBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Curso 8-9 (Sepiebre) ATERIA: ATEÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El aluno conesará a los
Técnicas analíticas para las Ecuaciones diferenciales de primer orden: Ecuaciones Exactas y Cambios de Variables
 Lección 3 Técnicas analíicas para las Ecuaciones diferenciales de primer orden: Ecuaciones Exacas y Cambios de Variables 3.1. Ecuaciones Exacas Las ecuaciones exacas esán relacionadas con las llamadas
Lección 3 Técnicas analíicas para las Ecuaciones diferenciales de primer orden: Ecuaciones Exacas y Cambios de Variables 3.1. Ecuaciones Exacas Las ecuaciones exacas esán relacionadas con las llamadas
Montesion. Examen final 2ª evaluación Tel.:
 Montesion. Eamen final ª evaluación Tel.: 665.516.510 1º Los gastos de mantenimiento de la maquinaria de una determinada empresa, G () (en miles de euros), vienen dados en función del tiempo, en meses,
Montesion. Eamen final ª evaluación Tel.: 665.516.510 1º Los gastos de mantenimiento de la maquinaria de una determinada empresa, G () (en miles de euros), vienen dados en función del tiempo, en meses,
