Sistemas de ecuaciones diferenciales lineales
|
|
|
- Ángel Vargas Río
- hace 7 años
- Vistas:
Transcripción
1 695 Aálisis matmático para Igiría M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA CAPÍTULO Sistmas d cuacios difrcials lials d primr ord Cuado s studia matmáticamt ua situació d la ralidad, l modlo qu s obti sul tr u caráctr o lial, sido sto lo qu l cofir, la maoría d los casos, ua gra dificultad Uo d los procdimitos más utilizados dtro d la Matmática, d la Cicia gral, cuado s aborda u problma difícil, s cosidrar u problma más scillo qu sa, algú stido, ua bua aproimació dl atrior Al studiar st sgudo problma s itta obtr, d las coclusios, algú tipo d rsultado para l problma primitivo Ua d las formas más usuals d simplificar l problma s lializarlo Si s quir studiar u problma o lial, l primr paso obligado s studiar l problma lial asociado d la mara más complta posibl para podr aalizar así qu ocurrirá l caso o lial El studio d los sistmas lials o s difícil umrosas ocasios s pud obtr rsultados cocluts pus la structura algbraica d las solucios s scilla a vcs s pud dar ua dscripció d la misma térmios d fucios lmtals U sistma d cuacios difrcials d ord suprior s trasforma u sistma d primr ord añadido más variabls Por sta razó l capítulo s ctra l studio d los sistmas d cuacios difrcials
2 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 696 lials d primr ord La scció comiza ralizado ua primra aproimació tr los sistmas lials las cuacios difrcials d ord suprior stablcido los tormas d istcia uicidad E la scció s dsarrolla la toría gral d la structura d las solucios d los sistmas lials d primr ord qu s similar a la d las cuacios lials d ord suprior Así l cojuto d solucios d u sistma lial d primr ord homogéo ti structura d spacio vctorial l o homogéo d spacio afí La scció stá ctrada los métodos d rsolució d los sistmas lials homogéos co coficits costats Utilizado la toría algbraica para calcular los autovalors autovctors d ua matriz s stablc u procdimito qu prmit rsolvr l sistma Otro forma d rsolvr sistmas lials s utilizado la pocial d ua matriz, qu s l cotido d la scció 4 El capítulo trmia co la scció 5 la qu s dsarrolla los métodos d rsolució d sistmas lials o homogéos, los qu d uvo s obsrva u parallismo co los studiados l capítulo atrior para rsolvr las cuacios lials compltas d ord suprior SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES U sistma d cuacios difrcials d ord suprior pud trasformars fácilmt u sistma d primr ord si más qu añadir más variabls: si l sistma d ord suprior s lial tambié lo s l d
3 697 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA primr ord Por sta razó, si pérdida d gralidad, s posibl studiar úicamt los sistmas d cuacios difrcials d primr ord Cocptos prvios Dfiició : U sistma d k cuacios difrcials d ord suprior prsado d la forma f(, (), (), (),, ) ()) s domia lial cuado la fució vctorial f s ua fució lial co rspcto a la fució () a todas sus drivadas E particular u sistma d cuacios difrcials d primr ord prsado d la forma f(, (), ()) s domia lial cuado la fució vctorial f s ua fució lial rspcto a () () Cuado s posibl dspjar l sistma s scrib d la siguit forma: ( ) f(,,, ' ( ) f(,, ( ) f(,,, ) ) ) f,,f : S R R sido f, f,, f fucios lials rspcto a las variabls,,,, s dcir, tambié s pud prsar: ( ) a( )( ) a( )( ) a ( )( ) b ( ) ( ) a( )( ) a( )( ) a( )( ) b( ) ( ) a ( ) ( ) a ( ) ( ) a ( ) ( ) b ( ) () sido a ij () b i () fucios dfiidas u itrvalo (a, b), i, j {,,, }
4 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 698 El sistma atrior s pud prsar forma vctorial: () A() () b(), sido A() ua matriz cuadrada d ord, formada por las fucios a ij () b(), (), () fucios vctorials d dimsió dfiidas u itrvalo (a, b) d R E l capítulo 9 s dsarrolló ua mara atural d asociar a cada cuació difrcial ordiaria d ord u sistma quivalt d cuacios difrcials d primr ord; así mismo, dado u sistma s pud dtrmiar ua cuació difrcial d ord suprior asociada, auqu o ha quivalcia a qu la cuació pud tr solucios qu o lo so dl sistma como s mustra l jmplo E sta trasformació tr sistmas d primr ord cuacios d ord, la propidad d lialidad s cosrva como s dmustra la siguit proposició Proposició : Si ua cuació difrcial d ord s lial tambié s lial l sistma asociado d cuacios difrcials d primr ord rcíprocamt si l sistma s lial tambié lo s su cuació difrcial asociada Dmostració: Dada la cuació difrcial lial: ) P () -) P - () P () G(), ralizado l cambio d variabl: ; ; ; -), s obti ), por lo tato la cuació s trasforma l sistma:
5 699 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA ( ) P ( ) ( ) P ( ) ( ) ( ) ( ) ( ) ( ) P ( ) ( ) G( ) qu s u sistma d cuacios difrcials lials d primr ord Rcíprocamt si,,, so solucios dl sistma () al drivar la primra cuació co rspcto a : a a a a a a b sustituir las drivadas,,, por sus prsios l sistma () s obti d d d h S driva sta prsió co rspcto a, s sustitu dl modo atrior s obti () d d d h S rpit l procso hasta la drivada d ord s calcula: ) () d d d h D sta forma s obti l siguit sistma: ( ) a( )( ) a( )( ) a ( )( ) b( ) ' ( ) d( )( ) d( )( ) d( )( ) h( ) ) ( ) d ( ) ( ) d ( ) ( ) d ( ) ( ) h ( ) () D las primras cuacios s calcula,,, fució d, la fució sus drivadas hasta l ord, al itroducir stas prsios la última cuació d () s obti la cuació difrcial lial d ord : ) () Q () -) Q - () Q () H()
6 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 Dfiició : U sistma d cuacios difrcials lials d primr ord co coficits costats s prsa d la siguit forma: ( ) a( ) a( ) a ( ) b( ) ' ( ) a( ) a( ) a( ) b( ) ( ) a ( ) a ( ) a ( ) b ( ) dod a ij R, b i () so fucios rals d variabl ral Si para todo i, i, b (), R, l sistma s domia homogéo i Las quivalts cuacios matricials so: () A () b() para u sistma o homogéo () A () para u sistma homogéo, dod A s ua matriz d úmros rals, cuadrada d ord, A (aij) Tormas d istcia uicidad Los tormas fudamtals d istcia uicidad d las solucios d u problma d valor iicial para sistmas lials d cuacios difrcials d primr ord s pud uciar d forma similar a los obtidos para sistmas d cuacios difrcials d primr ord s dmostrará a partir d llos Torma : Torma d istcia uicidad Sa A() ua fució matricial cuadrada d ord, b() ua fució vctorial, cotiuas u itrvalo (a, b) d R, sa () A() () b() u
7 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA sistma lial d cuacios difrcials d primr ord Sa (a, b), si s impo la codició iicial ( ) ( ( ), ( ),, ( )) (,,, ), tocs ist ua úica fució vctorial ϕ() (ϕ (), ϕ (),, ϕ ()) qu s solució dl sistma vrifica las codicios iicials Dmostració: E l torma 9 d istcia dl capítulo 9 para sistmas d cuacios difrcials d primr ord para garatizar la istcia s igía la cotiuidad d las fucios f k (, ), para todos los valors d k tr E ustro caso particular f k (, ) j akj ( ) j ( ) b k () Como por hipótsis las fucios a kj () b k () so fucios cotiuas l itrvalo (a, b) s ti garatizada la istcia d solució d cualquir problma d valor iicial s itrvalo Admás las drivadas parcials d las fucios fk(, ), rspcto d las variabls j () so prcisamt las fucios a kj () qu por hipótsis so cotiuas por lo tato, por l torma 9, s asgura la istcia uicidad local d la solució para u problma d valor iicial, dicha solució pud tdrs a todo itrvalo l qu sa cotiuas las fucios a kj () b k () Es itrsat obsrvar qu para sistmas lials l itrvalo maimal d istcia d cualquir solució s l mismo itrvalo para cualquir codició iicial, coicid co l itrvalo domiio d dfiició d las fucios A() b(), mitras qu si l sistma s o lial l itrvalo maimal d istcia dpd d la codició iicial
8 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 Ejmplos rsultos Ejmplo : Clasificar los siguits sistmas lials o o lials, homogéos o o homogéos, d primr ord o d ord suprior a) ) (D ) (D b) ' ' ' c) ' ' El sistma dl apartado a) s lial, o homogéo d ord dos El sistma dl apartado b) s lial, homogéo d primr ord El sistma dl apartado c) s o lial, homogéo d primr ord Los trs jmplos ti los coficits costats Ejmplo : Eprsar forma matricial l sistma lial asociado a la cuació difrcial lial homogéa a a a Ralizado l cambio d variabl ;,, s obti ) ( a ) ( a ) ( a ) ( ' ) ( ) ( ' ) ( ) ( ', por lo tato la cuació s trasforma l sistma: qu prsado forma matricial: ) ( ' ) ( ' ) ( ' a a a ) ( ) ( ) ( Ejmplo : Calcular ua cuació difrcial d ord dos asociada al sistma ' ' comprobar qu ti solucios qu o so
9 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA solucios dl sistma La solució d gral d st sistma s: K K K ; K, o ist ua cuació difrcial lial d sgudo ord qu tga stas solucios, así por jmplo drivado la primra cuació s ti Ua solució d sta cuació so las fucios costats qu si mbargo o so solució dl sistma d partida Ejmplo 4: Obtr ua cuació difrcial d sgudo ord asociada al sistma ' ', a partir d sus solucios rsolvr l sistma Drivado la primra cuació s ti Sustitudo los valors d dl sistma s ti: 7 6 S cosidra l sistma las variabls ' : S '' 7 6 dspja la primra cuació: ( ), s sustitu la sguda, co lo qu s obti la cuació 4 La solució gral d sta cuació difrcial s K 4 K - Sustitudo tato como su drivada s obti: K 4 K - Por lo tato la solució gral dl sistma s:
10 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 74 4 k k Ejrcicios Calcular la cuació difrcial asociada a cada uo d los siguits sistmas a partir d sus solucios obtr la solució gral dl sistma a) ' ' ' b) ' ' Eprsar forma matricial l sistma lial asociado a la cuació difrcial lial homogéa Rsolvr l sistma ' ' a partir d las solucios d la cuació difrcial d ord dos asociada a st sistma
11 75 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA SISTEMAS LINEALES DE ECUACIONES DIFERENCIALES DE PRIMER ORDEN Dpdcia idpdcia lial Dfiició : Dado u cojuto d fucios vctorials {,,, } dfiidas u itrvalo (a, b) s dic qu so lialmt dpdits l itrvalo (a, b), si ist costats α, α,, α o todas ulas, tals qu: α () α () α (), (a, b) Si por l cotrario s vrifica qu sta idtidad solamt s cumpl cuado α α α, tocs s dic qu las fucios {,,, } so lialmt idpdits l itrvalo (a, b) Dfiició : Dado u cojuto d fucios vctorials {,,, }, co k () ( k (), k (),, k ()), k, s domia wroskiao d stas fucios s dota por W[,,, ] a la fució dfiida por l siguit dtrmiat: W[,, ]() ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) s dcir W[,, ]() dt [,, ]() Proposició :
12 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 76 Si las fucios,,, so lialmt dpdits l itrvalo (a, b), tocs su wroskiao s itrvalo s la fució ula Dmostració: Si las fucios so lialmt dpdits ua d llas k s pud prsar como combiació lial d las otras por lo tato, la columa k- ésima dl dtrmiat s pud prsar como ua combiació lial d las otras columas, lo qu supo qu l dtrmiat s cro Esta proposició pruba qu si u cojuto d fucios vctorials s lialmt dpdit tocs so lialmt dpdits los vctors uméricos qu s obti al hallar las imágs d stas fucios cada puto El rcíproco o s cirto, para algú valor d pud sr dichos vctors lialmt dpdits o srlo las fucios Si los vctors so lialmt idpdits para algú valor,, tocs s pud asgurar qu so lialmt idpdits las fucios Pro icluso pud ocurrir qu para cada valor los vctors sa lialmt dpdits sr lialmt idpdits las fucios Esta aomalía d qu uas fucios lialmt idpdits puda tr valors u puto qu o lo sa, dsaparc si las fucios so solució d u mismo sistma lial homogéo Estructura d las solucios dl sistma homogéo
13 77 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA E los siguits tormas s supo u sistma d cuacios difrcials lials d primr ord prsado forma vctorial () A() () sido A() ua fució matricial cuadrada d ord, cotiua u itrvalo (a, b) d R, (), () fucios vctorials d R R Torma Sa,,, solucios lialmt idpdits dl sistma () A() () l itrvalo (a, b) Etocs, dadas costats c, c,, c, la fució c k k s tambié solució dl sistma l itrvalo (a, b) k Dmostració: Las fucios k (), k, so solucios dl sistma, por tato vrifica k () A() k () Por sr la drivada lial s ti qu: d d c k k k c k k d d k ck A( ) k ( ) k A( ) ck k ( ) k Torma 4: Si las fucios,,, so solucios lialmt idpdits l itrvalo (a, b) dl sistma () A() () tocs su wroskiao o s aula igú puto d s itrvalo Dmostració: S dmustra l torma por rducció al absurdo, por lo qu s supo qu ist algú (a, b) tal qu W[,,, ]( ) Por lo tato ua columa dl wroskiao s ua combiació lial d las otras S supo qu s la primra, tocs:
14 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 78 ( ) c ( ) c ( ) c ( ) Sa z() () c () c () c (), (a, b) Esta fució s solució dl sistma por sr ua combiació lial d solucios; admás z(), lugo l puto la fució z() coicid co la fució ula, qu tambié s solució dl sistma Por l torma d uicidad d solucios z(), (a, b), lo qu cotradic qu las fucios,,, sa lialmt idpdits (a, b) Torma 5: Si las fucios,,, so solucios dl sistma lial d cuacios difrcials () A() () u itrvalo (a, b), tocs su wroskiao s itrvalo o s la fució ula o o s aula igú puto d dicho itrvalo Dmostració: S pud comprobar la siguit prsió para la drivada dl wroskiao: W [,,, ] W[,,, ] W[,,, ] W[,,, ] Como,,, so solucios dl sistma para todo k, tal qu k, s vrifica qu k () A() k () Sustitudo la prsió atrior s ti qu W [,,, ]() (a () a () a ()) W[,,, ]() qu s ua cuació difrcial lial d primr ord qu ti por solució W[,,, Traza( A( )) d ]() C Como la fució pocial o s aula, s ti qu W[,,, ]() sólo cuado C s igual a, por lo qu W[,,, ]() s la fució ula o o s aula igú puto dl
15 79 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA itrvalo (a, b) D la dmostració d st torma s dduc qu: W [,,, ]() traza(a) W[,,, ]() corolario: Como coclusió d los tormas atriors s ti l siguit Corolario 6: Si las fucios,,, so solucios dl sistma lial homogéo d cuacios difrcials () A() () l itrvalo (a, b), las trs codicios siguits so quivalts: a) Las fucios,,, so lialmt idpdits (a, b) b) Eist u (a, b) tal qu W[,,, ]() s distito d cro c) Para todo (a, b) s vrifica qu W[,,, ]() s distito d cro Es vidt qu: a) b) por l torma 4, b) a) por l torma, b) c) por l torma 5, c) b) trivial Dfiició : S llama sistma fudamtal d solucios dl sistma lial homogéo () A() () u itrvalo (a, b), a cualquir cojuto d solucios lialmt idpdits (a, b)
16 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 Torma 7: Simpr ist u sistma fudamtal d solucios dl sistma lial homogéo d primr ord () A() (), l itrvalo (a, b) Dmostració: Sa (a, b) Por l torma d istcia d solucios s sab qu ist fucios k (), para k dsd hasta, qu so solució dl sistma cada ua vrifica la codició iicial siguit: ( ) (,,, ), ( ) (,,, ),, ( ) (,,, ), Las fucios (), (),, () so lialmt idpdits, a qu si ist costats c, c,, c tals qu c () c () c () (a, b), s ti qu: ck k k ( ) c ck k k ck k k ( ) c ( ) c E coscucia las fucios so lialmt idpdits por lo tato forma u sistma fudamtal d solucios Torma 8: Si {,,, } s u sistma fudamtal d solucios dl sistma lial homogéo d primr ord () A() (), l itrvalo (a, b),
17 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA tocs toda solució ϕ() (ϕ (), ϕ (),, ϕ ()) dl sistma s pud prsar d la forma ϕ() ck k ( ), dod c, c,, c so costats k Dmostració: Sa {,,, } u sistma fudamtal d solucios, ϕ ua solució dl sistma () A() (), u puto dl itrvalo (a, b), tocs por l corolario 6, W[,,, ]( ) S dtrmia ϕ( ), ϕ ( ),, ϕ ( ) s cosidra l siguit sistma d cuacios las icógitas c, c,, c : ck k ( ) ϕ( ) k ck k ( ) ϕ( ) k ck k ( ) ( ) ϕ k Como W[,,, ]( ) s l dtrmiat d la matriz d los coficits s distito d cro, l sistma ti solució úica, s dcir ist c, c,, c costats qu vrifica las cuacios por l torma d uicidad ϕ c k k k Torma 9: Sa Λ l cojuto d solucios dl sistma lial homogéo d primr
18 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 ord () A() () l itrvalo (a, b) Etocs Λ ti structura d spacio vctorial d dimsió Dmostració: Como l torma garatiza la lialidad d las solucios dl sistma () A() (), admás s vrifica los aiomas d spacio vctorial, s ti qu Λ l cojuto d solucios dl sistma lial homogéo ti structura d spacio vctorial U sistma fudamtal d solucios dl sistma, qu ist como rsultado dl torma 7, s ua bas dl spacio vctorial Λ a qu: a) Es u sistma d gradors, pus por l torma 8 cualquir solució s pud prsar como combiació lial d los lmtos dl sistma fudamtal d solucios b) Por dfiició so fucios lialmt idpdits S pud obsrvar qu cada solució o pud dpdr d más d solucios idpdits, a qu supoido qu hubira particularizado u puto s cotraría vctors d R lialmt idpdits, qu s imposibl Corolario : Sa {,,, } u sistma fudamtal d solucios dl sistma lial homogéo () A() () l itrvalo (a, b) La solució gral d st sistma s pud prsar d la forma: ϕ() ( ) ( ) ck k ( ) c k c ( ) ( )
19 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Matriz fudamtal Dfiició 4: S domia matriz fudamtal dl sistma lial homogéo () A() () a ua matriz Φ() cuas columas so solucios lialmt idpdits dl sistma, s dcir, so u sistma fudamtal d solucios u itrvalo (a, b), ( ) ( ) Φ() ( (), (),, ()) ( ) ( ) Dfiició 5: S domia matriz solució dl sistma lial homogéo () A() () a ua matriz ψ() cuas columas so solucios dl sistma, sa lialmt idpdits o o Dfiició 6: S domia matriz fudamtal pricipal dl sistma lial homogéo () A() () a ua matriz fudamtal Φ() tal qu para u valor vrifiqu qu Φ( ) I, sido I la matriz idtidad E alguos ttos s dic qu ua matriz d solucios lialmt idpdits s fudamtal cuado admás s pricipal La solució gral d u sistma homogéo s pud prsar térmios d la matriz fudamtal dl sistma: Φ() C, dod C s u vctor d costats idtrmiadas Ua matriz fudamtal quda caractrizada por vrificar:
20 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 74 a) Φ () A() Φ(), pus s ua matriz solució, b) Su dtrmiat s distito d cro Propidads d la matriz fudamtal: Fórmula d Jacobi: Si ψ () s ua matriz solució tocs: (dtψ) () traza(a()) dtψ () ( ) dt( Ψ )) dt Ψ( traza( A(s ))ds 5 Rsultados qu a ha sido comtados la dmostració dl torma Sa Φ() ua matriz solució Φ() s ua matriz fudamtal si sólo si ist algú (a, b) tal qu dt(φ( )) s distito d cro Es ua coscucia dl corolario 6 Si Φ s ua matriz fudamtal tocs cualquir otra matriz fudamtal s d la forma Φ P dod P s ua matriz rgular d ord Si mbargo, como l producto d matrics o s csariamt comutativo, P Φ pud o sr ua matriz fudamtal 4 Si Φ s ua matriz fudamtal s compruba qu: ( ) G( ) P ( ) Φ( ) C Φ( ) Φ (s ) b(s ) ds Esta fórmula s studia postriormt 5, s cooc co l
21 75 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA ombr d fórmula d variació d las costats 5 Si Φ s ua matriz fudamtal, si s cosidra l problma d valor iicial: ' ( ) A( ) ( ) b( ) ( ) dod (, ) (a, b)r tocs la úica solució s: ( ) Φ( ) Φ ( ) Φ( ) Φ (s ) b(s ) ds S obsrva qu coocida la matriz fudamtal s pud obtr l cojuto d solucios dl sistma homogéo, qu si s pudira calcular la itgral qu aparc la propidad 4 s tdría d mara plícita todas las solucios Dsgraciadamt, ist pocos tipos d sistmas los qu s pud cotrar d mara plícita la matriz fudamtal 4 Estructura d las solucios dl sistma o homogéo El cojuto d solucios d u sistma lial d primr ord o homogéo ti structura d spacio afí, sido su spacio vctorial asociado l cojuto d solucios dl sistma lial homogéo El dsarrollo para obtr st rsultado s mu similar al qu s ralizaba para dtrmiar la structura d las solucios d las cuacios difrcials d ord suprior Prviamt s dmustra qu ua solució gral dl sistma o homogéo s pud obtr a partir d ua solució particular d ést la solució gral dl sistma homogéo Est rsultado, qu a s studió
22 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 76 para las cuacios lials d primr ord d ord suprior, s scial para rsolvr sistmas o homogéos Torma : Sa A() ua fució matricial b() ua fució vctorial, cotiuas u itrvalo abirto (a, b) Si,,, so solucios lialmt idpdits dl sistma lial homogéo d primr ord () A() () l itrvalo (a, b) ϕ P s ua solució cualquira dl sistma o homogéo () A() () b(), tocs para toda solució ϕ d st sistma, ist costats c, c,, c, tals qu ϕ pud prsars por ϕ ϕ P c k k k Dmostració: Sa ϕ ua solució arbitraria dl sistma () A() () b() Como ϕ P tambié s solució s ti qu ambas fucios vrifica l sistma, por lo qu ϕ () A() ϕ() b() ϕ P () A() ϕ P () b() Por lo tato rstado ambas igualdads: ϕ () ϕp () A() (ϕ() ϕ P ()), s dcir, ϕ ϕ P s ua solució dl sistma homogéo Por l torma 8 ist costats c, c,, c, tals qu ϕ ϕ P c k k ϕ ϕ P k c k k, d dod s dduc qu la solució gral k ϕ dl sistma o homogéo s pud prsar como la suma d ua solució particular d ést, ϕ P, más la solució gral dl sistma homogéo
23 77 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA asociado c k k k Torma : Sa A() ua fució matricial b() ua fució vctorial, cotiuas u itrvalo abirto (a, b) El cojuto d solucios dl sistma o homogéo () A() () b() ti structura d spacio afí d dimsió costruido sobr l spacio vctorial d solucios dl sistma homogéo () A() () Sa Λ l cojuto d solucios dl sistma homogéo, qu por l torma 9 ti structura d spacio vctorial d dimsió, sa I l cojuto d solucios dl sistma o homogéo La aplicació h: I I Λ, dfiida por h(ϕ, ϕ ) ϕ ϕ structura a I como spacio afí a qu: Si ϕ, ϕ I (ϕ ϕ ) (ϕ ) (ϕ ) (A() ϕ () b()) (A() ϕ () b()) A() (ϕ ϕ )() ϕ ϕ Λ Admás s vrifica los aiomas d spacio afí: º ϕ I ψ Λ tocs ϕ Ξ, tal qu h(ϕ, ϕ ) ϕ ϕ ψ Basta tomar ϕ ϕ ψ I Es vidt qu ϕ I a qu ϕ () (ϕ ψ) () ϕ () ψ () A() ϕ () b() A() ψ() A() (ϕ ψ)() b() A() ϕ () b() º Si ϕ, ϕ, ϕ I tocs h(ϕ, ϕ ) h(ϕ, ϕ ) h(ϕ, ϕ ), lo qu s vrifica a qu ϕ ϕ ϕ ϕ ϕ ϕ
24 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 78 Ejmplos rsultos Ejmplo : Comprobar qu Φ () Φ () so matrics fudamtals dl sistma: ' ' La matriz d los coficits s A Para comprobar qu Φ () s solució dl sistma A, s db vrificar qu Φ () A Φ Φ () () coicid co A Φ A Φ () a qu () Por lo tato s ua matriz solució como admás s rgular (pus su dtrmiat val 4 4 Aálogamt Φ por lo qu s distito d cro), tocs s ua matriz fudamtal () A Φ (), por lo
25 79 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA qu Φ () s ua matriz solució dl sistma Admás s rgular (pus su dtrmiat val 4 por lo qu s distito d cro) Por lo tato s tambié ua matriz fudamtal Ejmplo : Dada la matriz Φ() cotrar u sistma d cuacios difrcials para l qu Φ() sa ua matriz fudamtal so solucios lialmt idpdits dl sistma buscado Admás Por lo tato Φ() s ua matriz ' fudamtal dl sistma ' Ejmplo : Dmostrar qu si z (a i b) (αβi) z (a i b) (α-βi) so solucios compljas lialmt idpdits d u sistma lial d dos cuacios difrcials tocs: Ral((a b i) (αβi) ) Im((a b i) (αβi) ) so solucios rals dl sistma lialmt idpdits a qu: Las fucios so combiacios lials d las fucios z z (z z ) α (a cos β b s β), (z z ) α (b cos β a s β) i por lo tato so tambié solucios dl sistma Admás so lialmt
26 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 idpdits a qu: W[, ] α a cosβb sβ a cosβb sβ b cosβ a sβ b cosβ a sβ α (a b - a b ) Para dmostrar qu a b a b, s calcula l wroskiao d las solucios z z, qu por hipótsis so lialmt idpdits, por lo tato s distito d cro: β β W[z, z ] α (a ib ) (a ib ) i α (b β β a b a ) (a ib ) (a ib ) Comparado ambos dtrmiats s obsrva qu las solucios z z so lialmt idpdits si sólo si so lialmt idpdits Ejrcicios 4 Comprobar qu Φ() 4 s ua matriz fudamtal dl sistma ' ' 4 5 Dada la matriz Φ() ( ) cotrar u sistma d cuacios difrcials para l qu Φ() s ua matriz fudamtal
27 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA 6 Comprobar qu Φ() s ua matriz fudamtal dl sistma ' ' ' SISTEMAS LINEALES HOMOGÉNEOS CON COEFICIENTES CONSTANTES E los sistmas lials homogéos co coficits costats s posibl dar ua dscripció complta dl cojuto d solucios d muchas d sus propidads cualitativas Por razos d claridad los jmplos s limita a sistmas d dos o trs cuacios E sta scció s studia los sistmas homogéos, hacido uso dl cálculo d autovctors autovalors Sólo s cotmpla l caso qu los coficits so rals, pro l caso d coficits compljos s podría studiar d forma similar co ligras modificacios, como rmplazar la traspusta d ua matriz por la hrmítica cojugada U sistma lial homogéo d coficits costats A s u sistma autóomo pus A, al sr costat o dpd d, por lo qu basta co studiarlo para trlo studiado para cualquir problma d valor iicial Los sistmas autóomos s studiará co maor profudidad l capítulo : Toría cualitativa d cuacios difrcials
28 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 At u sistma lial, lo primro qu s db ittar s trasformarlo otro más scillo o ua cuació d ord Las stratgias para cosguirlo pud sr mu divrsas, como so las distitas técicas algbraicas qu prmit rsolvr u sistma lial o utilizar dtrmiados cambios d variabl Ua forma sistmática d ralizar combiacios lials tr las cuacios dl sistma d mara qu s rduzca a ua cuació d ord suprior cosist utilizar opradors difrcials, procdimito qu s dsarrolla a cotiuació Rsolució por limiació mdiat l oprador difrcial D E l capítulo atrior s dfiía l oprador difrcial D como ua df aplicació d I I tal qu f I, D(f), sido I la familia d fucios d rals d variabl ral ifiitamt drivabls u itrvalo (a, b) Dado l sistma: b ( ) b' '' b' ( ) b ' b ' ( ) b ' ( ) ( ) ( ) b ' ( ) a( ) a( ) a ( ) b ' a( ) a( ) a( ) b ( ) a ( ) a( ) a( ) () Aplicado qu D() s pud prsar:
29 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA (a bd)( ) (a bd) ( ) (a b D)( ) (a bd) ( ) (a bd) ( ) (a bd) ( ) (a bd) ( ) (a bd) ( ) (a D)( ) o bi forma matricial: a a a b b b D D D a a a b b b D D D a a a b b b D ( ) D ( ) D ( ) Sa l oprador (D) a a a b b b D D D a a a b b b D D D a a a b b b D D D qu s supo qu o s la fució ula (D) s u oprador poliómico d grado Si (D) r r D r D tocs ) (D)(k()) r k () r k () r k () Para todo k, k s rsulv la cuació difrcial homogéa d ) grado : r k () r k () r k () Ua vz obtidas cada ua d las fucios k() fució d costats, s ti total costats qu s limia hasta djar sólo sustituédolas l sistma Ejmplos rsultos
30 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 74 Ejmplo : Utilizar l método por limiació mdiat l oprador D para rsolvr l sistma d dos cuacios co dos icógitas d d dz d z z Para rsolvr l sistma s itgra la cuació difrcial d sgudo ord homogéa: (D)(z()) (D) D D D 4D 5 (D ( i))(d ( i)) La cuació (D 4D 5)z() ti como solució gral: z() (C s C cos ) Sustitudo sta solució la sguda cuació dl sistma: () (C s C cos ) (C cos C s ) (C s C cos ) ((C C ) s (C C ) cos ) Por lo tato la solució dl sistma s: () ((C C ) s (C C ) cos ) z() (C s C cos ) Ejmplo : Rsolvr l sistma: ' ' 4z z' ' 4, utilizado l oprador D S prsa l oprador D forma matricial:
31 75 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA D 4 4 D z por lo tato (D) D 4 6 S rsulv la cuació homogéa d ord 4: (D Las raícs d la cuació caractrística d sta cuació difrcial so: 4 6)(()) λ ( i); λ ( i); λ ( i); λ 4 ( i), la solució gral: () (C cos C s ) (C cos C 4 s ) Al calcular () sustituir la primra cuació s obti z() () ((C C ) cos (C C ) s )) ((C 4 C ) cos (C C 4 ) s )) () 4 (C cos C s ) 4 (C 4 cos C s ) z() (C cos C s ) (C 4 cos C s ) La solució dl sistma s: () (C cos C s ) (C cos C 4 s ) z() (C cos C s ) (C 4 cos C s
32 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 76 ) Rsolució buscado solucios pocials Método d Eulr La fució pocial, a, vrifica qu sus drivadas so múltiplos d sí misma Por lo tato parc atural qu sa d s tipo las solucios d u sistma lial homogéo co coficits costats S cosidra l sistma A S busca ua solució d la forma () B λ S sustitu l sistma: B λ λ λ λ Bλ ab ab a B λ λ λ λ B λ ab ab ab λ λ λ λ B λ ab ab ab s divid tr λ : (a λ)b ab a B ab (a λ)b ab a λ B ab (a )B () El rsultado s u sistma algbraico lial homogéo las variabls B, B,, B qu sólo ti solució distita d la trivial cuado l dtrmiat d los coficits s igual a cro, s dcir:
33 77 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA a a a λ a a a λ a a a λ Esta cuació s domia cuació caractrística Al dsarrollar l dtrmiat s obti ua cuació poliómica λ d grado, la qu l tipo d raícs d la cuació dtrmia la prsió d las solucios distitas Caso : La cuació caractrística ti todas las raícs rals Sa λ, λ,, λ las raícs d la cuació caractrística, tocs para todo k, k, al sustituir λ por cada valor λ k l sistma () s obti ua solució, o trivial, dl sistma algbraico (B k, B k,, B k ) qu dtrmia ua solució dl sistma d cuacios difrcials: B k k() ( kj ()) λ k Bk D sta forma s obti solucios qu, st caso, so lialmt idpdits, por lo tato dtrmia la solució gral dl sistma qu s d la forma () C () C () C (), por tato: () C B λ λ C λ C B B B B B Caso : La cuació caractrística ti raícs compljas distitas E st caso s pud obtr la solució gral fució d
34 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 78 pocials compljas las solucios d () pud sr tambié úmros compljos Para aalizar l caso l qu s quir obtr solucios rals s supo u sistma d dos cuacios difrcials cua cuació caractrística ti dos raícs compljas cojugadas α βi, α βi, dos solucios lialmt idpdits compljas: () B (αβi) (a ib) (αβi) () B (α-βi) (a ib) (α-βi) La part ral la part imagiaria d stas solucios s obti como combiació lial d llas, por lo qu so solucios, so lialmt idpdits so fucios rals, como s comprobó l jmplo La solució gral dl sistma s: () α (C ( a a cos β b s β) C b ( b b cos β a s β)) a Caso : La cuació caractrística ti raícs múltipls S supo u sistma d dos cuacios difrcials cua cuació caractrística ti ua raíz dobl El caso gral s studia l siguit λ apartado Sa λ la raíz, tocs () B solució B B λ s ua La aalogía co las cuacios d ord llvaría a psar qu la otra solució lialmt idpdit co lla s () λ B Si mbargo pud o sr así, la otra solució dl sistma ti la forma () (B B ) λ Sustitudo sta solució l sistma s dtrmia los vctors B
35 79 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA B La solució gral dl sistma s: () C B λ B C B ( B B B λ ) Ejmplos rsultos Ejmplo : Rsolvr l sistma d trs cuacios co trs icógitas: d z dt d z dt dz dt S calcula las raícs d la cuació caractrística: λ λ λ λ 7λ 6 () (λ ) (λ ) (λ ) Las raícs d la cuació caractrística λ, λ λ so rals distitas Para λ s busca solucios d la forma (t) A t, (t) B t, z(t) C t sido A, B, C solucios dl sistma algbraico homogéo: A B C, cua solució s A K, B C K, por lo qu la solució buscada s (t)
36 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 t, (t) t, z(t) t Para λ, s busca solucios d la forma (t) A -t, (t) B -t, z(t) C -t sido A, B, C C B A solucios dl sistma algbraico homogéo:, cua solució s A K, B C K, por lo qu la solució buscada s (t) -t, (t) -t, z(t) -t Para λ, s busca solucios d la forma (t) A -t, (t) B -t, z(t) C -t sido A, B, C C B A solucios dl sistma algbraico homogéo:, cua solució s A, B C K, por lo qu la solució buscada s (t), (t) -t, z(t) -t La solució gral dl sistma d cuacios difrcials s: (t) K t K -t (t) K t K -t K z(t) K -t t K -t K -t ) z(t ) (t ) (t K t K -t K -t Ejmplo 4: Rsolvr l sistma:
37 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA d d dz d 9z 8z S rsulv la cuació caractrística: λ 9 8 λ λ λ 5 (λ 5), por lo tato la cuació caractrística ti ua raíz dobl ua solució dl sistma s d la forma: ( ) z( ) A ( A B ) 5 B Al sustituir la primra cuació dl sistma s obti: (5(A A ) A ) 5 (A A ) 5 9(B B ) 5 A 9B A (A 9B ) Si B K, A K si B K, A K K, por lo tato la solució gral dl sistma s: () (K K K ) 5, z() (K K ) 5 Ecuació caractrística Autovalors autovctors S cosidra l sistma A co () ( k ()), k S supo qu l sistma ti ua solució d la forma () v λ, dod v s u vctor d R o ulo Para qu () sa solució s db vrificar qu: () λ v λ A v λ λ v A v,
38 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 7 s dcir, A v s u múltiplo d v, lo qu idica qu v s u autovctor d la matriz A λ u autovalor Por st procdimito, l caso qu s pudira cotrar solucios d st tipo lialmt idpdits, s tdría rsulto l sistma Ats d dmostrar qu ist al mos ua solució d sta forma d buscar u sistma fudamtal d solucios s dfi los cocptos algbraicos csarios para dsarrollar la toría Dfiició : Dada ua matriz cuadrada A d ord, s domia vctor propio, vctor caractrístico, autovctor o igvctor d A, a u vctor v ral o compljo, distito d cro, para l qu ist u valor λ, tal qu A v λv o lo qu s lo mismo (A λi) v dod I s la matriz idtidad Dfiició : Dada ua matriz cuadrada A d ord, v u vctor caractrístico d A, s domia valor propio, autovalor o igvalor d A, a u úmro ral o compljo λ qu vrifica qu (A λi) v Si para u valor λ u vctor v s vrifica qu (A λi) v, s dic qu λ s u autovalor d la matriz A v s u autovctor d A asociado al autovalor λ Dfiició : Dada ua matriz cuadrada A d ord, s domia cuació caractrística d A a la cuació A λi Proposició :
39 7 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Dada ua matriz cuadrada A d ord, λ s u autovalor d A si sólo si s ua raíz d su cuació caractrística Dmostració: Sa A (a ij ) v (v,, v ) u autovctor d A asociado al autovalor λ La cuació matricial (A λi) v s prsa: (a λ)v av a v av (a λ)v av a λ v av (a )v Est sistma admit ua solució o trivial para los valors d λ para los qu l dtrmiat d los coficits A λi s aula, por lo qu si λ s u autovalor d A s quivalt a dcir qu s ua raíz d su cuació caractrística Ya qu A λi s ua cuació poliómica d grado, o pud tr mas d autovalors Si λ s ua raíz múltipl d ord m s dic qu l autovalor ti multiplicidad m Por l torma fudamtal dl Álgbra s sab qu A ti actamt autovalors cotado cada uo tatas vcs como idica su multiplicidad Proposició : Si v, v,, v m so m autovctors d A asociados, rspctivamt, a m autovalors distitos λ, λ,, λ m, tocs los vctors v, v,, v m so lialmt idpdits Dmostració:
40 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 74 S dmustra por iducció sobr m Para m s imdiato a qu u autovctor o pud sr l vctor cro Supusto cirto para k vctors, s cosidra k autovctors v, v,, v k asociados a los autovalors λ, λ,, λ k Si ist c i o todos ulos tals qu k c i v i i, al multiplicar por la matriz A s ti qu k c i λi v i i S pud supor qu al mos ua d las costats c, c,, c k- s k k distita d cro, multiplicado c i v i por λ k rstado c i λiv i i i, s aula l sumado k-ésimo s obti k ci ( λk λi ) v i i, lo qu cotradic la hipótsis d iducció a qu los autovalors so distitos Por lo tato las costats c i so ulas para todo i lo qu implica qu los autovctors so lialmt idpdits Proposició : Sa () ua solució dl sistma A Si ist u valor tal qu l vctor ( ) s u autovctor d A asociado al autovalor λ, s dcir A ( ) λ( ), tocs para todo valor d s vrifica qu A () λ() Dmostració: S cosidra la fució z() () λ() Por sr () ua solució dl sistma s ti qu z() A () λ(), como por hipótsis A ( ) λ( ),
41 75 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA s vrifica qu z( ) Aplicado l torma d uicidad z() s la fució idéticamt cro por lo tato para todo valor d s ti qu A () λ() Dfiició 4: S dic qu ua solució () dl sistma A s ua solució caractrística si para algú valor λ s vrifica qu A () λ() Proposició 4: Sa l sistma A Para cada autovalor λ d la matriz A, ist al mos ua solució caractrística dl sistma, (), qu s pud prsar d la forma () (v λ, v λ,, v λ ), sido v (v, v,, v ) u autovctor asociado al autovalor λ Dmostració: Sa λ u autovalor d la matriz A v (v, v,, v ) u autovctor asociado a λ, sa () ( (), (),, ()) ua solució caractrística dl sistma tal qu () v, qu ist por la proposició vrifica qu () A () λ() Por lo tato para todo k, k s ti qu k () λ k () Itgrado s ti k () c k λ, pusto qu k () c k v k s obti: () (v λ, v λ,, v λ ) El siguit torma prmit dtrmiar u sistma fudamtal d solucios por lo tato la solució gral dl sistma cuado los autovalors d la cuació caractrística so distitos Torma 5:
42 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 76 U cojuto d solucios caractrísticas dl sistma A asociadas a autovalors difrts d la matriz A s lialmt idpdit E particular si A ti autovalors distitos l cojuto d solucios caractrísticas s u sistma fudamtal d solucios Dmostració: Sa,,, m solucios caractrísticas dl sistma asociadas, rspctivamt, a los m autovalors distitos λ, λ,, λ m Por la proposició para u valor fijo, los vctors ( ), ( ),, m ( ) so lialmt idpdits por l corolario 6 tambié so lialmt idpdits las fucios,,, m E particular, si la matriz A ti autovalors distitos, las solucios caractrísticas,,, forma u sistma fudamtal d solucios Para todo k, k por la proposició 4 s ti qu k () λ ( v k λ,v k λ,,v k k k k ) por tato la solució gral () s pud prsar d la forma: v v v λ () C λ C λ C v v v λ λ C v C v C v λ sido v k (v k, v k,, v k ) u autovctor asociado al autovalor λ k El sistma fudamtal qu s obti, gral, pud star formado por solucios compljas pro a partir d él s pud obtr solucios rals lialmt idpdits por lo tato costitu u sistma
43 77 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA fudamtal d solucios; s l rsultado d la siguit proposició Proposició 6: Sa las fucios z, z,, z solucios caractrísticas rals o compljas lialmt idpdits dl sistma A, sido A ua matriz ral d ord, tocs s pud obtr a partir d llas solucios rals lialmt idpdits Dmostració: Para toda solució complja z k (a bi) (αβi), s ti la solució z k (a bi) (α-βi) Para cada par d solucios compljas z k, z k s obti dos solucios rals lialmt idpdits, qu so: k Ral((a bi) (αβi) ) k Im((a bi) (αβi) ) Las fucios k k so combiacios lials d las fucios z k z k a qu: k (z k z k ) α (a cos β b s β); k (z k z k ) α (b cos β a s β) i por lo tato so tambié solucios dl sistma por costrucció so lialmt idpdits Ats dl studio dl caso gral s rcurda alguos rsultados d Álgbra lial Dfiició 5: Sa λ u autovalor d la matriz A, s dic qu u vctor R,,
44 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 78 sta asociado a λ co multiplicidad m si para l úmro tro m, o para otro mor, s vrifica qu (A λi) m, s dcir: Kr(A λi) m / Kr(A λi) m- Proposició 7: Sa λ, λ,, λ r, los autovalors d la matriz A, co multiplicidads m, r m,, m r, sido m k Etocs para cada autovalor λ k ist u k cojuto d m k vctors kj, j {,,, m k } tals qu kj stá asociado a λ k co multiplicidad mor o igual a m k l cojuto d vctors kj ; j {,,, m k }, k {,,, r}, s lialmt idpdit Esta proposició s coscucia d las siguits proposicios Proposició 8: Sa () ua solució dl sistma A Si s vrifica qu para u valor, (A λi) m ( ), tocs para todo s vrifica qu (A λi) m () Dmostració: Sa z() (D λ) m (()) (A λi) m (); z() s solució dl sistma A por sr combiació lial d () d sus drivadas, admás z( ) (A λi) m ( ) por l torma d uicidad s ti qu z() Proposició 9: Si () s ua solució dl sistma A asociada a u autovalor λ co multiplicidad m, s dcir, (A λi) m () tocs () s d la forma:
45 79 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA () p ( ) p ( ) p ( ) λ () sido p k (), k, poliomios d grado mor o igual a m Dmostració: Sa () ( (), (),, ()) ua solució dl sistma tal qu (A λi) m (), por lo tato s vrifica tocs qu (D λ) m ( k ()), k Por otra part (D λ) m ( k ()) (D λ) m ( λ -λ k ()) aplicado l lma : (D λ) m ( k ()) λ D m ( -λ k ()) Por lo tato λ D m ( -λ k ()) ; simplificado s obti D m ( -λ k ()), itgrado k () p k () λ, k grado(p k ()) m Torma : Simpr ist u sistma fudamtal d solucios dl sistma A, formado por fucios d la forma () Admás si s cooc los autovalors d la matriz A, st sistma fudamtal s pud obtr mdiat u úmro fiito d opracios lmtals Dmostració: Por la proposició 7 ist u cojuto d vctors lialmt idpdits k asociados a los autovalors λ k d A Si s dtrmia las solucios dl sistma A d modo qu vrifiqu las codicios iicials k ( ) k, stas fucios srá lialmt idpdits d la forma ()
46 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 74 Admás si λ s u autovalor cualquira co multiplicidad m s pud obtr m solucios lialmt idpdits dl sistma d la forma () pi( ) pi( ) λ, co p ij () poliomio d grado i co coficits idtrmiados, pi ( ) sido i m Para i, sustitudo () l sistma s obti u sistma d cuacios algbraicas lials los coficits idtrmiados d los poliomios Est sistma pud qu o tga solució, qu tga ua o qu tga varias solucios o trivials lialmt idpdits S rpit l procso para i s obti cuacios lials los coficits idtrmiados S cotiúa l procso hasta i m, hasta obtr m solucios lialmt idpdits Hacido lo mismo co los otros autovalors s obti u sistma fudamtal d solucios S pud prcisar más l procso sguido para calcular los autovctors corrspodits a autovalors múltipls utilizado cocptos algbraicos Dado l sistma A, pud ocurrir qu la matriz A sa diagoalizabl o qu o lo sa E l caso qu la matriz A sa diagoalizabl, tocs ist ua matriz diagoal D ua matriz P rgular tal qu P - D P A, tocs ist autovctors v i lialmt idpdits, qu so las columas d la matriz P d cambio d bas Estos autovctors so las bass d los subspacios Kr(A λ i ), sido λ i los autovalors d la matriz A Las solucios lialmt idpdits dl sistma so d la forma ϕ i () v i
47 74 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA i λ Cuado la matriz A o s diagoalizabl l úmro d autovctors qu s obti d las bass d los subspacios Kr(A λ i ) s u valor k mor qu por lo tato l úmro d solucios lialmt idpdits d la forma ϕ i () v i λ i s tambié k Las k solucios rstats so dl tipo ϕ i () pi( ) pi( ) pi ( ) i λ, p ij () s u poliomio tal qu grado(p ij ()) m sido m la multiplicidad d λ i E la siguit proposició s dsarrolla u método para simplificar l cálculo d stos poliomios Proposició : Sa λ u autovalor d A d multiplicidad s tal qu l subspacio Kr(A λi) sólo s cutra u autovctor v lialmt idpdit; tocs s pud cotrar s solucios lialmt idpdits dl sistma A, d la forma: ϕ () v λ tal qu (A λi) v para todo j, j s, s s ϕ j () (v v v j ) λ tal qu (A λi) v j- v j ( j )! ( j )! Dmostració: Si λ s u autovalor d A d multiplicidad s tal qu l subspacio Kr(A λi) sólo s cutra u autovctor v lialmt idpdit s ti ua solució dl sistma: ϕ () v λ Ua sguda solució s busca d la forma ϕ() (v v ) λ Para
48 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 74 dtrmiar v s aplica qu ϕ () s solució, s dcir ϕ () A ϕ (), por lo tato v λ (v v ) λ λ A (v v ) λ Simplificado s ti v v λ v λ A v A v Aplicado qu λ v A v s obti: v v λ A v por lo tato v (A λi) v La trcra solució s busca d la forma ϕ() (v v v ) λ S sustitu l sistma: (v v ) λ (v v v ) λ λ A (v v v ) λ S simplifica: v v v λ v λ v λ A v A v A v S aplica qu λ v A v qu v v λ A v por lo qu s obti v v λ A v, s dcir (A λi) v v Aálogamt s calcula las distitas solucios hasta ϕs() qu s d s s la forma: ϕ s () (v v v s ) λ (s )! (s )! S sustitu l sistma s simplifica térmios tido cuta qu (A λi) v qu (A λi) v j v j- para todo j, j s : (A λi) vs- v s Otros rsultados algbraicos qu covi rcordar so: Proposició : La suma d los autovalors d ua matriz A s igual a la traza d A su
49 74 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA producto al dtrmiat d A Proposició : Si A s ua matriz simétrica tocs A ti todos sus autovctors rals admás ti autovctors ortoormals Otro método para rsolvr sistmas d cuacios difrcials s calcular dirctamt la matriz fudamtal, lo qu collva calcular la pocial d ua matriz, qu s dsarrolla l siguit apartado Ejmplos rsultos Ejmplo 5: Calcular la solució gral dl sistma d z dt d z dt dz dt S rsulv la cuació caractrística: λ λ λ λ λ Los autovalors so λ λ λ S dtrmia l subspacio Kr(A I): z, qu ti
50 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 744 dimsió por lo tato ua bas stá formada por v v Eist por tato dos autovctors lialmt idpdits asociados al autovalor, dos solucios lialmt idpdits ϕ (t) -t ϕ (t) S dtrmia l subspacio Kr(A I): -t z U autovctor d st subspacio s v la solució ϕ (t) t Por lo tato la solució gral dl sistma s ϕ(t) K -t K -t K t Ejmplo 5: Rsolvr l sistma z D D 5 S calcula las raícs d la cuació caractrística λ λ 5 λ S dtrmia l subspacio Kr(A I): 6λ 9 s obti u autovalor dobl λ z s obti
51 745 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA u úico autovctor v lialmt idpdit Ua solució s ϕ () S busca u vctor v tal qu v (A I) v z s obti v Otra solució s ϕ () ( ) Por lo tato la solució gral dl sistma s: ϕ() K K ( ) ) Ejrcicios 7 Rsolvr l sistma d trs cuacios co trs icógitas: d z dt d 5 z dt dz z dt 8 Calcular la solució gral dl sistma: d z d dz 4z d 9 Ecotrar dos solucios lialmt idpdits dl sistma:
52 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 746 d d dz d 5z z Rsolvr l sistma d dt d z co las codicios iicials (), dt dz z dt (), z() 4 Calcular la solució gral dl sistma: ' ' z' z ' Rsolvr l sistma: z' z 4 EXPONENCIAL DE UNA MATRIZ El cojuto d las fucios matricials ti structura d spacio métrico, por lo qu s pud hablar d límits, sris, drivadas d fucios matricials, s isomorfo al spacio uclído R Dfiido como producto itro l producto d matrics s ti ua structura d álgbra Si s compara u sistma co la cuació a, d solució a C, s pud psar qu la solució dl sistma A s d la forma A C Para llo s db dfiir la pocial d ua matriz Dfiició 4:
53 747 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sa A ua matriz costat S dfi la pocial d la matriz A mdiat la prsió: A A I A! A! A! Por lo tato A A I A! A! A! E cada térmio d la matriz s ti ua sri umérica como la sri d Talor asociada a la fució pocial covrg todo l plao compljo, pud probars qu tal matriz simpr ist Cuado la matriz A s diagoal o s ilpott, la prsió d A s simplifica cosidrablmt co rspcto a su forma gral, como s dmustra las siguits proposicios Proposició 4: λ Si A s ua matriz diagoal d ord m, A λ, tocs λ m A λ λ λ m Dmostració: k λ Si A s ua matriz diagoal s ti qu A k k λ k λ m
54 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 748 Por lo tato: A λ λ λ m λ! λ! λ m! λ! λ! λ λ m! λ λ m Dfiició 4: Ua matriz A s ilpott si ist k Ν tal qu A k s la matriz ula Proposició 4: Si A s ilpott tocs A ti u úmro fiito d sumados Esta proposició s ua coscucia imdiata d la dfiició d matriz ilpott 4 Propidads d la pocial d ua matriz Si s la matriz ula tocs I Si I s la matriz idtidad r R tocs r I r I Si A B so matrics d ord A B B A, tocs AB A B 4 Si r, s R A s ua matriz d ord tocs A(rs) Ar As 5 La pocial d la matriz A, A, s rgular a qu dt( A ) trazaa 6 La ivrsa d la pocial d ua matriz ( A ) - -A, a qu A -A A-A I
55 749 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Proposició 4: La matriz A s ua matriz fudamtal pricipal dl sistma A, Dmostració: Al drivar A A, s ti qu:! d ( A ) A A A A d! ( )! Por lo tato A s ua matriz fudamtal dl sistma A Admás cuado tocs A I por lo qu admás s ua matriz fudamtal pricipal dl sistma 4 Cálculo d la fució matricial A ' A La solució úica dl problma d valor iicial ( ) s A Si ' A s cosidra l problma más gral, la solució s ( ) A( ) E ambos casos ha qu calcular la matriz A, por lo qu s va a dsarrollar u procdimito útil fctivo para calcular dicha fució matricial, Proposició 44: Si A s ua matriz diagoalizabl, tal qu A P D P -, sido D ua matriz diagoal, tocs A P D P - Admás dt( A ) (trazad) Dmostració:
56 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 75 λ Sa A P D P - λ, sido D, λ, λ,, λ λ los autovalors d A las columas d la matriz P los autovctors asociados a dichos autovalors Etocs: A (P D P - ) (P D P - ) P D P - ; A P D P - gral Ν s ti qu: A P D P -, por lo tato: A A ( P D P ) P D P -!! Por la proposició 4 A λ λ P P - λ Admás a qu dt(a) dt(d) s ti: λ dt( A ) dt( D ) (trazad) λ λ Proposició 45: Si A s ua matriz o diagoalizabl, A P J P -, sido J ua matriz d Jorda tocs A P ( D N ) P -, D matriz diagoal N matriz ilpott Dmostració: Si A o s diagoalizabl s ti qu A P J P -, sido J ua matriz d Jorda la matriz P ti por columas los autovctors asociados a los
57 75 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA autovalors d la matriz A J o s diagoal, pro J D N, sido D ua matriz diagoal N ua matriz ilpott por lo tato: A P J P - P (D N) P - P ( D N ) P - 4 Estudio dl caso gral A cotiuació s aaliza l caso l qu la matriz A o s costat E l caso d ua cuació d primr ord, b(), la solució s pud prsar d la forma C b( ) d Si ahora s aaliza l sistma A() s pud psar qu la solució sa d la forma A( ) d C Esto s así cuado s cumpl las codicios d la proposició qu s prsta a cotiuació: Proposició 46: Sa l sistma A() ; B() A ( ) d Si A() B() B() A() tocs B() s ua matriz fudamtal dl sistma Dmostració: Al drivar B (B( )) I B()! (B( ))! (B( ))!, s d ti qu ( B ) B () d d! d (B()) d! d (B()) d d (B()) d (B() B()) B () B() B() B () A() B() B() A() d d Si A() B() B() A() tocs d (B()) B () B() Aálogamt
58 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 75 si A() B() B() A() tocs d d (B()) B () (B()) - Por lo tato B() s ua matriz fudamtal dl sistma A() Ejmplos rsultos Ejmplo 4: Dada la matriz diagoal D la matriz ilpott N Calcular D N D s ua matriz diagoal por tato D ( ), Ν, por cosiguit D ( )! ) (! N s ua matriz ilpott pus N por tato N, Ν,, por cosiguit: N I N Ejmplo 4: Calcular ua matriz fudamtal dl sistma A, sido A 6 5
59 75 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA La matriz A s diagoalizabl S calcula la matriz diagoal asociada D, la matriz d cambio d bas s P su ivrsa s P -, por lo tato: A P P Est cálculo s pud simplificar si csidad d hallar P - Aplicado qu cuado Φ() s ua matriz fudamtal P ua matriz rgular tocs Φ() P s tambié ua matriz fudamtal Y a qu D P P D P - P P D P, s ti qu: D s ua matriz fudamtal Ejmplo 4: Calcular ua matriz fudamtal dl sistma A, sido A La matriz A o s diagoalizabl pro s smjat a J co la matriz d autovctors P J D N, D s diagoal N ilpott, N J (D N) D D N N D N D Y gral: D N
60 M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA Sistmas d cuacios difrcials 754 J D D - N Por lo tato: J! Por cosiguit A P - Ua matriz fudamtal dl sistma s: Otro método para obtr J s prsarla d la forma: (IJ-I) I (J-I) I Aálogamt s pud obtr A A (IA-I) I (A-I) I Ejmplo 44: Calcular ua matriz fudamtal dl sistma A(), sido A()
61 755 Capítulo º: Ecuacios difrcials M MOLERO; A SALVADOR; T MENARGUEZ; L GARMENDIA B() )d ( A Las matrics A() B() comuta a qu A() B() B() A() ; por lo tato B() s ua matriz fudamtal dl sistma Φ() tambié Ejrcicios Calcular ua matriz fudamtal dl sistma A, sido A 4 (Solució: Φ() 4 ) 4 Calcular ua matriz fudamtal dl sistma 5 (Solució: Φ() ) ( ) 5 Calcular ua matriz fudamtal dl sistma 6 Comprobar si B() 4 s ua matriz fudamtal dl sistma A(), sido A() B() d ) ( A
TEMA 2. ESPACIOS Y OPERADORES LINEALES CONTENIDO
 TEMA. ESPACIOS Y OPERADORES LINEALES CONTENIDO ESPACIOS LINEALES SOBRE UN CAMPO INDEPENDENCIA LINEAL, BASES Y CAMBIOS DE BASES OPERADORES LINEALES Y SUS REPRESENTACIONES SISTEMAS DE ECUACIONES ALGEBRÁICAS
TEMA. ESPACIOS Y OPERADORES LINEALES CONTENIDO ESPACIOS LINEALES SOBRE UN CAMPO INDEPENDENCIA LINEAL, BASES Y CAMBIOS DE BASES OPERADORES LINEALES Y SUS REPRESENTACIONES SISTEMAS DE ECUACIONES ALGEBRÁICAS
MATEMÁTICAS Y CULTURA B O L E T Í N No. 273 COORDINACIÓN DE MATEMÁTICAS APLICACIONES DEL DETERMINANTE DE VANDERMONDE
 MATEMÁTICAS Y CULTURA B O L E T Í N 23.04.20 No. 273 COORDINACIÓN DE MATEMÁTICAS MATEMÁTICAS MATEMÁTICAS APLICACIONES DEL DETERMINANTE DE VANDERMONDE E l Boltí Matmáticas Y Cultura No. 257 dl 23 d abril
MATEMÁTICAS Y CULTURA B O L E T Í N 23.04.20 No. 273 COORDINACIÓN DE MATEMÁTICAS MATEMÁTICAS MATEMÁTICAS APLICACIONES DEL DETERMINANTE DE VANDERMONDE E l Boltí Matmáticas Y Cultura No. 257 dl 23 d abril
al siguiente límite si existe: . Se suele representar por ( x )
 UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD : DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit it si ist: f f ' sigifica lo mismo. f. S sul rprstar por f D
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS
 UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
UNIDAD 9: INTRODUCCIÓN A LAS DERIVADAS. DERIVADA DE UNA FUNCIÓN EN UN PUNTO. DERIVADAS LATERALES Dfiici.- S llama drivada d ua fuci f u puto d abscisa al siguit límit si ist: f f ' lím sigifica lo mismo.
2.8.3 Solución de las ecuaciones diferenciales lineales no homogéneas por el método de variación de parámetros
 .8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros 59.8.3 Solució d las cuacios difrcials lials o hoogéas por l étodo d variació d parátros Variació d parátros U procdiito
a a lim i) L< 1 absoluta convergencia absoluta convergencia convergencia condicional divergencia > r.
 (Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
(Aputs rvisió para oritar l aprdizaj) DESARROLLO DE LAS FUNCIONES LOGARÍTMICA Y EXPONENCIAL EN SERIES DE POTENCIAS Ua Sri d Potcias s dfi como: a a a a a = = + + + la qu s vidt qu covrg si =. Para dtrmiar
Se llama sucesión a un conjunto de números dados ordenadamente de modo que se puedan numerar: primero, segundo, tercero,...
 TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN S llama sucsió a u cojuto d úmros dados ordadamt d modo qu s puda umrar: primro, sgudo, trcro,... Los lmtos d la sucsió s llama térmios y s
Universidad de Puerto Rico Recinto Universitario de Mayagüez Departamento de Ciencias Matemáticas
 Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
Uivrsidad d Purto Rico Rcito Uivrsitario d Mayagüz Dpartamto d Cicias Matmáticas Eam III Mat - Cálculo II d abril d 8 Nombr Númro d studiat Scció Profsor Db mostrar todo su trabajo. Rsulva todos los problmas.
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA FUNCIÓN PRIMITIVA. F() s ua primitiva d f() si F ()= f(). Esto s prsa así: f() = F'() = F() La itgració s la opració ivrsa a la drivació, d modo qu: FUNCIONES
INTEGRAL INDEFINIDA. Derivación. Integración
 TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
TEMA 8 Itgral Idfiida INTEGRAL INDEFINIDA. FUNCIÓN PRIMITIVA F() s ua primitiva d f() si F ()= f(). Esto s prsa así: La itgració s la opració ivrsa a la drivació, d modo qu: f() F'() F() FUNCIONES PRIMITIVAS
Universidad de Costa Rica. Instituto Tecnológico de Costa Rica. Determinar si las integrales impropias convergen o divergen.
 Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
Uivrsidad d Costa Rica Istituto Tcológico d Costa Rica Tma: Itgrals impropias. Objtivos: Clasificar las itgrals impropias sgú su spci: primra, sguda o trcra spci. Calcular itgrals impropias utilizado su
EXPONENTES Y POTENCIAS Muchos números se expresan en forma más conveniente como potencias de 10. Por ejemplo: m n n 0,2 3 3
 Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
Rpaso d Matmáticas E st apédic s hará u brv rpaso d las cuacios y fórmulas básicas d utilidad Química Física gral y Trmodiámica Química particular. EXPONENTES Y POTENCIAS Muchos úmros s xprsa forma más
TEMA 5: LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS
 Dpartamto d Matmáticas. IE.S. Ciudad d Arjoa º Bach Socials. LÍMITES Propidads: TEMA : LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS. LÍMITES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES. RESOLUCIÓN DE INDETERMINACIONES.
Dpartamto d Matmáticas. IE.S. Ciudad d Arjoa º Bach Socials. LÍMITES Propidads: TEMA : LÍMITE DE FUNCIONES. CONTINUIDAD.ASÍNTOTAS. LÍMITES. LÍMITE DE UNA FUNCIÓN EN UN PUNTO. LÍMITES. RESOLUCIÓN DE INDETERMINACIONES.
2. ALGEBRA LINEAL (2.1_AL_T_062, Revisión: , C12)
 . ALGEBRA LINEAL (._AL_T_06, Rvisió: 8-03-06, C). CONCEPTOS FUNDAMENTALES: ESPACIOS VECTORIALES, BASES, DIMENSIONES... INTRODUCCIÓN. Notació: utilizamos abcdario latio para vctors, grigo para scalars (úmros).
. ALGEBRA LINEAL (._AL_T_06, Rvisió: 8-03-06, C). CONCEPTOS FUNDAMENTALES: ESPACIOS VECTORIALES, BASES, DIMENSIONES... INTRODUCCIÓN. Notació: utilizamos abcdario latio para vctors, grigo para scalars (úmros).
1 Realizar los ejercicios resueltos números 1 y 2 del tema 3 de Integración de. 2 Terminar los ejercicios de la práctica realizada este día.
 Est documto coti las actividads o prscials propustas al trmiar la clas dl día qu s idica. S sobrtid qu tambié s db ralizar l studio d lo plicado clas auqu o s icluya sa tara st documto. Clas 5 d ovimbr
Est documto coti las actividads o prscials propustas al trmiar la clas dl día qu s idica. S sobrtid qu tambié s db ralizar l studio d lo plicado clas auqu o s icluya sa tara st documto. Clas 5 d ovimbr
Tema 8. Limite de funciones. Continuidad
 . Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito asítota horizotal... 8.
1.- a) Hallar a y b para que la siguiente función sea continua en x = 1:
 .- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
.- a) Hallar a y b para qu la siguit fució sa cotiua = : b L( ) < f = a = > L b) Para sos valors d a y b, studiar la drivabilidad d f =. Solució: a) f s cotiua l puto = lim f = f() E st caso f () = a lim
11 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS)
 INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
INTRODUCCIÓN A LA DINÁMICA NO LINEAL (BIFURCACIONES, CAOS) Los sistmas o lials pud llgar a tr comportamitos ralmt sorprdts alguos casos: por u lado pud llgar a tr diámicas totalmt difrts sgú l valor qu
TEMA 2 SUCESIONES. Tema 2 Sucesiones Matemáticas I 1º Bach. 1 SUCESIONES Y TÉRMINOS
 Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Tma Sucsios Matmáticas I º Bach. TEMA SUCESIONES SUCESIONES Y TÉRMINOS EJERCICIO : Si l térmio gral d ua sucsió s a 0 Halla l térmio sgudo y l décimo. b) Hay algú térmio qu valga? Si hay dcir qu lugar
Aproximación de funciones derivables mediante polinomios: Fórmulas de Taylor y Mac-Laurin
 Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
Aproimació d ucios drabls mdiat poliomios: Fórmulas d Taylor y Mac-Lauri. Eprsa l poliomio P - - potcias d - Hay qu dtrmiar los coicits a, b, c, d y qu cumpla: P - -a- b- c- d- Drado vcs la iualdad atrior,
TEMA 1: CALCULO DIRECTO DE LÍMITES
 INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
INSTITUCION EDUCATIVA DISTRITAL RODRIGO DE BASTIDAS Rsolució Nº 88 d ovimbr.8/ ScrtariaD Educació Distrital REGISTRO DANE Nº-99 Tléfoo Barrio Bastidas Sata Marta DEPARTAMENTO DE MATEMATICAS ACTIVIDAD ESPECIAL
CÁLCULO NUMÉRICO ( )
 CÁLCULO NUMÉRICO (808068) Tma. Fudamtos d la Toría d Errors Octubr 0. Al studiar l fómo diario d la variació qu primta las codicios mtorológicas, s suprim muchas variabls qu dbría d itrvir los cálculos.
CÁLCULO NUMÉRICO (808068) Tma. Fudamtos d la Toría d Errors Octubr 0. Al studiar l fómo diario d la variació qu primta las codicios mtorológicas, s suprim muchas variabls qu dbría d itrvir los cálculos.
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA 1: Problema Nº 5.34 Oppenheim
 SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
SEÑALES Y SISTEMAS. PROBLEMAS RESUELTOS. CAPITULO V PROBLEMA : Problma Nº 5.3 Opphim Obsrv l siguit sistma: Dtrmi y() Solució: El traycto d arriba produc, al multiplicar por Cos(/), traslació dl spctro
Tema 11. Limite de funciones. Continuidad
 Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
Tma. Limit d fucios. Cotiuidad. Límit d ua fució. Fucios covrgts.... Límits latrals.... Distitos tipos d límits.... Límits ifiitos cuado tid a u úmro ral asítota vrtical.... Límits fiitos cuado tid a ifiito
2. Utilizando el método adimensional basado en el factor de calidad Q, determine:
 Uivrsidad Simó Bolívar Dpartamto d Covrsió y Trasport d Ergía Autor: Eduardo Albaz. Cart: 06-391 Profsor: J. M. Allr Máquias Eléctricas II CT-311 U motor d iducció coxió strlla d 100 kw, 416 V, rdimito
Uivrsidad Simó Bolívar Dpartamto d Covrsió y Trasport d Ergía Autor: Eduardo Albaz. Cart: 06-391 Profsor: J. M. Allr Máquias Eléctricas II CT-311 U motor d iducció coxió strlla d 100 kw, 416 V, rdimito
PROBLEMAS TEMA 4 EJERCICIO 1 (Ej 9.15 de Fernández Abascal)
 PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
PROLMAS TMA JRCICIO j 9.5 d Frádz Abascal La cotizació olsa d u cirto título s cosidra ua variabl alatoria ormalmt distribuida co arámtros dscoocidos, ro s diso d la siguit iformació: a ist u,5% d robabilidad
Señales y Sistemas. Análisis de Fourier.
 Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
Sñals y Sistmas Aálisis d Fourir. Itroducció El foqu d st capítulo s la rprstació d sñals utilizado sos y cosos ( otras palabras, xpocials complas). El studio d sñals y sistmas utilizado xpocials complas
MATEMÁTICA D Módulo I: Análisis de Variable Compleja. Teoría de Residuos
 Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Matmática D MATEMÁTIA D Módulo I: Aálisis d Variabl omplja Uidad Toría d siduos Mag. María Iés Baragatti Sigularidads S dic qu s ua sigularidad aislada d f( si f( o s aalítica pro sí s aalítica u toro
Respuesta en frecuencia. Procesado Digital de Señales.4º Ingeniería Electrónica. Universitat de València. Profesor Emilio Soria.
 Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
Rspusta frcucia. Procsado Digital d Sñals.4º Igiría Elctróica. Uivrsitat d Valècia. Profsor Emilio Soria. 1 Itrés uso PDS. Ti l mismo uso qu sistmas cotiuos: dtrmiar la salida d u sistma stado stacioario;
ESTIMADOR DE AITKEN Y PROPIEDADES DEL MISMO (Última revisión: 1 de marzo de 2007)
 Apts d clas d coomtría II / 6 STIMADOR D AITKN Y ROIDADS DL MISMO Última rvisió: d marzo d 7 rof. Rafal d Arc rafal.darc@am.s stimació d los parámtros dl MBRL por máxima vrosimilitd Apoádoos la hipótsis
Apts d clas d coomtría II / 6 STIMADOR D AITKN Y ROIDADS DL MISMO Última rvisió: d marzo d 7 rof. Rafal d Arc rafal.darc@am.s stimació d los parámtros dl MBRL por máxima vrosimilitd Apoádoos la hipótsis
8 Límites de sucesiones y de funciones
 Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
Solucioario 8 Límits d sucsios y d ucios ACTIVIDADES INICIALES 8.I. Calcula l térmio gral, l térmio qu ocupa l octavo lugar y la suma d los ocho primros térmios para las sucsios siguits., 6,,,..., 6, 8,,...,,,,...
El error con ese presupuesto será aproximadamente del 3,1% Ejercicio 8.2
 EJERCICIO 8.1 U ivstigador dispo d 0.000 para ralizar las trvistas d ua custa ua gra ciudad. El custioario s admiistrará mdiat trvistas tlfóicas, sido l cost d cada trvista d 0. Qué marg d rror dbrá asumir
EJERCICIO 8.1 U ivstigador dispo d 0.000 para ralizar las trvistas d ua custa ua gra ciudad. El custioario s admiistrará mdiat trvistas tlfóicas, sido l cost d cada trvista d 0. Qué marg d rror dbrá asumir
ANÁLISIS DE FOURIER CAPÍTULO CUATRO TIEMPO DISCRETO Introducción
 CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
CAPÍTULO CUATRO AÁLISIS DE FOURIER TIEMPO DISCRETO 4. Itroducció Las técicas dl aálisis d Fourir timpo cotiuo dsarrolladas l capítulo atrior ti mucho valor l aálisis d las propidads d sñals y sistmas d
Teoría de Sistemas y Señales
 Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Toría d Sistmas y Sñals Trasparias: Aálisis ruial d sñals TD Autor: Dr. Jua Carlos Gómz Aálisis ruial d Sñals Timpo Disrto. Sri d ourir d Sñals Timpo Disrto Sa () ua sñal priódia o príodo, s dir: ( ) +
Matemáticas Aplicadas a las Ciencias Sociales II. Análisis: Derivadas Tema 6. Derivadas 1. Derivada de una función en un punto
 Matmáticas Aplicadas a las Cicias Socials II Aálisis: Drivadas Tma 6 Drivadas Drivada d ua fució u puto Tasa d variació d ua fució S llama tasa d variació mdia d ua fució f (), l itrvalo [a, b], al valor
Matmáticas Aplicadas a las Cicias Socials II Aálisis: Drivadas Tma 6 Drivadas Drivada d ua fució u puto Tasa d variació d ua fució S llama tasa d variació mdia d ua fució f (), l itrvalo [a, b], al valor
Capítulo IV. Estadísticas cuánticas.
 Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
Capítulo I. stadísticas cuáticas. Lcció 6 Itroducció a las stadísticas cuáticas. Partículas distiguibls idistiguibls. stadísticas d Bos-isti y d rmi-dirac. Lcció 7 Gas idal d rmi: lctros mtals. Lcció 8
EJERCICIOS PROPUESTOS. rectángulos obtenidos tomando como base la longitud de cada subintervalo y como altura la ordenada del extremo derecho.
 6 Itgral dfiida Ejrcicio rsulto EJERCICIOS PROPUESTOS Obté, co l método visto, l ára dl trapcio limitado por la rcta y +, l j X y las vrticals y Calcula l ára gométricamt y compara los rsultados S divid
6 Itgral dfiida Ejrcicio rsulto EJERCICIOS PROPUESTOS Obté, co l método visto, l ára dl trapcio limitado por la rcta y +, l j X y las vrticals y Calcula l ára gométricamt y compara los rsultados S divid
Tabla de contenido. Página
 Tabla d coido Págia Opradors difrcials sismas d cuacios Opradors difrcials Oprador aulador 6 fiició 6 Sismas d cuacios difrcials lials 9 Solució d u sisma, méodo d los opradors 9 Rsum 5 Bibliografía rcomdada
Tabla d coido Págia Opradors difrcials sismas d cuacios Opradors difrcials Oprador aulador 6 fiició 6 Sismas d cuacios difrcials lials 9 Solució d u sisma, méodo d los opradors 9 Rsum 5 Bibliografía rcomdada
Integral Indefinida o Antiderivada
 Dpartamto d Matmática Aplicada Cálculo II (0) Smstr -08 Profsor: José Luis Quitro Marzo 08 FACULTAD DE INGENIERÍA UNIVERSIDAD CENTRAL DE VENEZUELA Itgral Idfiida o Atidrivada. Comprub los siguits rsultados
Dpartamto d Matmática Aplicada Cálculo II (0) Smstr -08 Profsor: José Luis Quitro Marzo 08 FACULTAD DE INGENIERÍA UNIVERSIDAD CENTRAL DE VENEZUELA Itgral Idfiida o Atidrivada. Comprub los siguits rsultados
Tema 6. Sistemas de Ecuaciones Diferenciales Lineales.
 Tma 6 Sismas d Ecuacios Difrcials Lials. INTRODUCCIÓN Es ma sá ddicado a la discusió d sismas d cuacios difrcials ordiarias simuláas. Dichos sismas aparc problmas qu i rlació co varias variabls dpdis qu
Tma 6 Sismas d Ecuacios Difrcials Lials. INTRODUCCIÓN Es ma sá ddicado a la discusió d sismas d cuacios difrcials ordiarias simuláas. Dichos sismas aparc problmas qu i rlació co varias variabls dpdis qu
! 1 3 <1 la serie converge (y confirma a n! 0 ). a n. x 2 >0; f 0 (x)<0 si x>1; R 1 f (x)dx = 1 2 e x2 1 = 1 2e. ) Convergente. n! 0 ) Convergente.
 Solucios d los roblmas d Matmáticas (07-08) {a } acotada ifriormt or 0 (los a so ositivos) y dcrcit us + + )9líma a ) a a ) a0 Como a + a < la sri covrg (y cofirma a 0 ) a) (a ) / Divrgt (O orqu {a
Solucios d los roblmas d Matmáticas (07-08) {a } acotada ifriormt or 0 (los a so ositivos) y dcrcit us + + )9líma a ) a a ) a0 Como a + a < la sri covrg (y cofirma a 0 ) a) (a ) / Divrgt (O orqu {a
Prob PI-1. Forma débil de un problema de flujo de calor estacionario en 2D (Cálculos a mano) T k. Q y
 p Q S d ds d S q d ds d ] [ ] [ ] ([ d Q d ] [ j i Prob PI-. Forma débil d u problma d flujo d calor stacioario D (Cálculos a mao Cosidérs l problma dfiido la figura siguit: La EDP asociada s: co Q ua
p Q S d ds d S q d ds d ] [ ] [ ] ([ d Q d ] [ j i Prob PI-. Forma débil d u problma d flujo d calor stacioario D (Cálculos a mao Cosidérs l problma dfiido la figura siguit: La EDP asociada s: co Q ua
5 MECÁNICA ESTADÍSTICA CUÁNTICA DE GASES IDEALES
 ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
ma 5 MCÁICA SADÍSICA CUÁICA D GASS IDALS stadística d rmi-dirac y stadística d Bos-isti. l límit clásico. Gas idal d rmi: lctros mtals. Gas idal d Bos: fotos y 4H líquido. Codsació d Bos-isti. [RI-9; HUA-8;
Tema 2: Diagonalización de matrices cuadradas
 Departameto de Aálisis Ecoómico UNIVERSIDAD DE ZARAGOZA Tema : Diagoalizació de matrices cuadradas.1. El cojuto R Defiició: Dados úmeros reales x 1, x,..., x R, se llama -tupla ordeada a x = ( x 1,, x,...,
Departameto de Aálisis Ecoómico UNIVERSIDAD DE ZARAGOZA Tema : Diagoalizació de matrices cuadradas.1. El cojuto R Defiició: Dados úmeros reales x 1, x,..., x R, se llama -tupla ordeada a x = ( x 1,, x,...,
DECAIMIENTO RADIOACTIVO
 DECIMIETO RDIOCTIVO El dcaimito radioactivo s idpdit dl modo d dcaimito, y s aplica a todos llos: α,β +, β -, CE (captura lctróica), γ, y fisió spotáa. Postulados: LEY DE DESITEGRCIO RDIOCTIV. La probabilidad
DECIMIETO RDIOCTIVO El dcaimito radioactivo s idpdit dl modo d dcaimito, y s aplica a todos llos: α,β +, β -, CE (captura lctróica), γ, y fisió spotáa. Postulados: LEY DE DESITEGRCIO RDIOCTIV. La probabilidad
SEPTIEMBRE Opción A
 Slctividad Sptimbr (Pruba Espcífica) SEPTIEMBRE Opción A ( + ).- Dada la función f () s pid dtrminar: a) El dominio, los puntos d cort con los js y las asíntotas. b) Los intrvalos d crciminto y dcrciminto,
Slctividad Sptimbr (Pruba Espcífica) SEPTIEMBRE Opción A ( + ).- Dada la función f () s pid dtrminar: a) El dominio, los puntos d cort con los js y las asíntotas. b) Los intrvalos d crciminto y dcrciminto,
Cap. II: Principios Fundamentales del Flujo de Tránsito
 Cap. II: Pricipios Fudamtals dl Flujo d Trásito Diagrama Espacio-Timpo Distacia 1 2 Itralo (i) 3 4 5 6 Espaciamito () Timpo Flujo, q Dsidad, Vlocidad, Tasa horaria quialt a la cual trasita los hículos
Cap. II: Pricipios Fudamtals dl Flujo d Trásito Diagrama Espacio-Timpo Distacia 1 2 Itralo (i) 3 4 5 6 Espaciamito () Timpo Flujo, q Dsidad, Vlocidad, Tasa horaria quialt a la cual trasita los hículos
PROBLEMAS DE LÍMITES DE FUNCIONES (Por métodos algebraicos) Observación: Algunos de estos problemas provienen de las pruebas de Selectividad.
 Funcions Límits y continuidad PROBLEMAS DE LÍMITES DE FUNCIONES Por métodos algbraicos Obsrvación: Algunos d stos problmas provinn d las prubas d Slctividad Si ist l it d una función f cuando a, y si f
Funcions Límits y continuidad PROBLEMAS DE LÍMITES DE FUNCIONES Por métodos algbraicos Obsrvación: Algunos d stos problmas provinn d las prubas d Slctividad Si ist l it d una función f cuando a, y si f
CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS
 Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Capítlo 17. Drivada d las Fcios Epocial, Logarítmica. CAPITULO 17 FUNCIONES EXPONENCIALES Y LOGARITMICAS Ejrcicio. Dibja la gráfica d la fció =, para sto lla la sigit tabla: 0 1 3 4-1 - -3-4 Vamos l sigit
Análisis y resolución del régimen transitorio de circuitos de corriente continua
 Aálisis y rsolució dl régim rasiorio d circuios d corri coiua solució d cuacios difrcials. Dfiició Ua cuació difrcial lial, ordiaria, d ord y a coficis cosas rlacioa las ésimas drivadas d ua fució x(,
Aálisis y rsolució dl régim rasiorio d circuios d corri coiua solució d cuacios difrcials. Dfiició Ua cuació difrcial lial, ordiaria, d ord y a coficis cosas rlacioa las ésimas drivadas d ua fució x(,
Espacios vectoriales euclídeos.
 Univrsidad d Jaén Dpartamnto d Matmáticas (Ara d Álgbra) Curso 4/5 PRÁCTICA Nº 6 Espacios vctorials uclídos. En sta práctica vamos a vr cómo introducir un producto scalar y trabajar con él n Mathmatica
Univrsidad d Jaén Dpartamnto d Matmáticas (Ara d Álgbra) Curso 4/5 PRÁCTICA Nº 6 Espacios vctorials uclídos. En sta práctica vamos a vr cómo introducir un producto scalar y trabajar con él n Mathmatica
Curso: 2º Bachillerato Examen VIII. donde m representa un número real.
 Nombr: Nota Curso: º Bachillrato Eamn VIII Fcha: d Fbrro d 06 La mala o nula plicación d cada jrcicio implica una pnalización d hasta l % d la nota..- Dada la matriz m dond m rprsnta un númro ral. m a)
Nombr: Nota Curso: º Bachillrato Eamn VIII Fcha: d Fbrro d 06 La mala o nula plicación d cada jrcicio implica una pnalización d hasta l % d la nota..- Dada la matriz m dond m rprsnta un númro ral. m a)
De la medición surge un valor, llamado valor de la magnitud y que indica el número de veces que la unidad elegida está contenida en la magnitud.
 Máquias, Métodos y Cotrol Dimsioal dl Procsamito METROLOGÍA MECÁNICA MEDICIONES Dfiició: Efctuar ua mdició, sigifica cotrar la distacia tr dos putos dados. Est caso s l más frcut, cuado las mdicios s rfir
Máquias, Métodos y Cotrol Dimsioal dl Procsamito METROLOGÍA MECÁNICA MEDICIONES Dfiició: Efctuar ua mdició, sigifica cotrar la distacia tr dos putos dados. Est caso s l más frcut, cuado las mdicios s rfir
Página 76. Página 78. Página 77. Página 79. Y de la primera: 1. Resolvemos por sustitución: a) Despejo x de la primera y la sustituyo en la segunda:
 Solucios d ls ctividds Pági 6. Rsolvmos por sustitució: ) Dspjo d l primr l sustituo l sgud: ( ) 8 0 Co lo cul: ( ) b) Si multiplico l primr por -, obtgo: + 8 Co lo cul tgo dos rcts coicidts, s dcir, l
Solucios d ls ctividds Pági 6. Rsolvmos por sustitució: ) Dspjo d l primr l sustituo l sgud: ( ) 8 0 Co lo cul: ( ) b) Si multiplico l primr por -, obtgo: + 8 Co lo cul tgo dos rcts coicidts, s dcir, l
MATEMÁTICA AVANZADA TRABAJO PRÁCTICO N O 1
 MATEMÁTICA AVANZADA TRABAJO PRÁCTICO N O Fcios aalíticas Dmostrar q s aalítica todo l plao complo Z. Siglaridads d a ció Estdiar las siglaridads d las sigits cios calclado límit: a b c 9 cos d 7 Trasormació
MATEMÁTICA AVANZADA TRABAJO PRÁCTICO N O Fcios aalíticas Dmostrar q s aalítica todo l plao complo Z. Siglaridads d a ció Estdiar las siglaridads d las sigits cios calclado límit: a b c 9 cos d 7 Trasormació
ÍNDICE. Prólogo Capítulo 1. Ecuaciones diferenciales ordinarias. Generalidades.. 11 Introducción teórica Ejercicios resueltos...
 ÍNDICE Prólogo... 9 Capítulo 1. Ecuacioes difereciales ordiarias. Geeralidades.. 11 Itroducció teórica... 13 Ejercicios resueltos.... 16 Capítulo 2. itegració de la ecuació de primer orde. La ecuació lieal...................................................................
ÍNDICE Prólogo... 9 Capítulo 1. Ecuacioes difereciales ordiarias. Geeralidades.. 11 Itroducció teórica... 13 Ejercicios resueltos.... 16 Capítulo 2. itegració de la ecuació de primer orde. La ecuació lieal...................................................................
FAyA Licenciatura en Química Física III año 2006 MECANICA CUANTICA
 FAyA Licciatura Química Fíica III año 006 MECANICA CUANTICA E la mcáica cláica l tado d u itma dcrib u itat dtrmiado dado toda u coordada q y u vlocidad q. E mcáica cuática l tado d u itma dfi dado ua
FAyA Licciatura Química Fíica III año 006 MECANICA CUANTICA E la mcáica cláica l tado d u itma dcrib u itat dtrmiado dado toda u coordada q y u vlocidad q. E mcáica cuática l tado d u itma dfi dado ua
UNIVERSIDAD NACIONAL DE INGENIERIA FACULTAD DE INGENIERIA MECANICA Departamento Académico de Ciencias Básicas, Humanidades y cursos complementarios
 UNIVERSIDAD NACIONAL DE INGENIERIA FACULTAD DE INGENIERIA MECANICA Dpartamto Académico d Cicias Básicas Humaidads y cursos complmtarios METODOS NUMERICOS MB 56 SOLUCION DE SISTEMAS DE ECUACIONES NO LINEALES
UNIVERSIDAD NACIONAL DE INGENIERIA FACULTAD DE INGENIERIA MECANICA Dpartamto Académico d Cicias Básicas Humaidads y cursos complmtarios METODOS NUMERICOS MB 56 SOLUCION DE SISTEMAS DE ECUACIONES NO LINEALES
1 OTRA MANERA DE VISUALIZAR LA EXPANSIÓN DE UN GAS
 Toría dl Gas Ral 0 OTRA MAERA DE VISUALIZAR LA EXPASIÓ DE U GAS. Itroducció E l prst capítulo s ivita al lctor a aalizar d otra mara la pasió o comprsió d u gas. E bas a sta mara difrt d ivolucraros l
Toría dl Gas Ral 0 OTRA MAERA DE VISUALIZAR LA EXPASIÓ DE U GAS. Itroducció E l prst capítulo s ivita al lctor a aalizar d otra mara la pasió o comprsió d u gas. E bas a sta mara difrt d ivolucraros l
Estabilidad de Sistemas No-lineales: Sistema de Nivel de Líquidos de Dos Tanques Interconectados.
 6 RIEE&C, REVISTA DE INGENIERÍA ELÉCTRICA, ELECTRÓNICA Y COMPUTACIÓN, Vol. 5 No., DICIEMBRE 008 Estabilidad d Sistmas No-lials: Sistma d Nivl d Líquidos d Dos Taqus Itrcoctados. Azurz M. Jua, Padilla G.
6 RIEE&C, REVISTA DE INGENIERÍA ELÉCTRICA, ELECTRÓNICA Y COMPUTACIÓN, Vol. 5 No., DICIEMBRE 008 Estabilidad d Sistmas No-lials: Sistma d Nivl d Líquidos d Dos Taqus Itrcoctados. Azurz M. Jua, Padilla G.
Tema 5. Análisis de Fourier para Señales y Sistemas Discretos.
 Tma 5. Aálisis d Fourir para Sñals y Sistmas Discrtos. E l tma 3 hmos hcho u studio d los sistmas discrtos l domiio tmporal. Esto os ha prmitido ralizar ua caractrizació d los mismos y hacr u studio d
Tma 5. Aálisis d Fourir para Sñals y Sistmas Discrtos. E l tma 3 hmos hcho u studio d los sistmas discrtos l domiio tmporal. Esto os ha prmitido ralizar ua caractrizació d los mismos y hacr u studio d
Análisis del caso promedio El plan:
 Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
Aálisis dl caso promdio El pla: Probabilidad Aálisis probabilista Árbols biarios d búsquda costruidos alatoriamt Tris, árbols digitals d búsquda y Patricia Listas sip Árbols alatorizados Técicas Avazadas
6. FAST FOURIER TRANSFORM (FFT)
 6. FAS FOURIER RASFORM FF Las rasformadas Rápidas d Fourir so algoritmos spcializados qu prmit a u procsador digital acr l cálculo d la rasformada Discrta d Fourir d ua forma ficit, lo qu rspcta a carga
6. FAS FOURIER RASFORM FF Las rasformadas Rápidas d Fourir so algoritmos spcializados qu prmit a u procsador digital acr l cálculo d la rasformada Discrta d Fourir d ua forma ficit, lo qu rspcta a carga
Transformada de Laplace
 Traformada d Laplac Traformada d Laplac Dada ua fució d variabl cotiua f, u traformada bilatral d Laplac dfi como: t [ f ] f dt L dod ua variabl complja, σ iω Para qu ta itgral covrja, dcir, para qu ita
Traformada d Laplac Traformada d Laplac Dada ua fució d variabl cotiua f, u traformada bilatral d Laplac dfi como: t [ f ] f dt L dod ua variabl complja, σ iω Para qu ta itgral covrja, dcir, para qu ita
Primer Examen Parcial Tema A Cálculo Vectorial Septiembre 26 de 2017
 Primr Examn Parcial Tma A Cálculo Vctorial Sptimbr 6 d 17 Est s un xamn individual, no s prmit l uso d libros, apunts, calculadoras o cualquir otro mdio lctrónico Rcurd apagar y guardar su tléfono clular
Primr Examn Parcial Tma A Cálculo Vctorial Sptimbr 6 d 17 Est s un xamn individual, no s prmit l uso d libros, apunts, calculadoras o cualquir otro mdio lctrónico Rcurd apagar y guardar su tléfono clular
2.- ESPACIOS VECTORIALES. MATRICES.
 2.- ESPACIOS VECTORIALES. MATRICES. 2.1. -ESPACIOS VECTORIALES Sea u cojuto V, etre cuyos elemetos (a los que llamaremos vectores) hay defiidas dos operacioes: SUMA DE DOS ELEMENTOS DE V: Si u, v V, etoces
2.- ESPACIOS VECTORIALES. MATRICES. 2.1. -ESPACIOS VECTORIALES Sea u cojuto V, etre cuyos elemetos (a los que llamaremos vectores) hay defiidas dos operacioes: SUMA DE DOS ELEMENTOS DE V: Si u, v V, etoces
APUNTE TEORICO DE SISTEMAS DE ECUACIONES DIFERENCIALES
 APUNTE TEORICO DE SISTEMAS DE ECUACIONES DIFERENCIALES [6.08] ALGEBRA II Autor: Berardo Ortega Ídice SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS...3 De primer orde co coeficietes costates..3 Sistemas
APUNTE TEORICO DE SISTEMAS DE ECUACIONES DIFERENCIALES [6.08] ALGEBRA II Autor: Berardo Ortega Ídice SISTEMAS DE ECUACIONES DIFERENCIALES ORDINARIAS...3 De primer orde co coeficietes costates..3 Sistemas
61.1 6.1. SERIES NUMÉRICAS INFINITAS 6.2. SERIES DE TÉRMINOS POSITIVOS 6.3. SERIES ALTERNANTES 6.4. SERIES DE POTENCIAS
 Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Cp. 6 Sris 6. 6.. SERIES NUMÉRICAS INFINITAS 6.. SERIES DE TÉRMINOS POSITIVOS 6.. SERIES ATERNANTES 6.. SERIES DE POTENCIAS Objtivo: S prtd qu l studit: Dtrmi covrgci o divrgci d sris. Empl sris pr rsolvr
Variables aleatorias discretas
 Probabilidads y stadística Comutació Facultad d Cicias actas y aturals. Uivrsidad d Buos Airs Aa M. Biaco y la J. Martíz 4 Variabls alatorias discrtas istribució Biomial: Muchos rimtos alatorios satisfac
Probabilidads y stadística Comutació Facultad d Cicias actas y aturals. Uivrsidad d Buos Airs Aa M. Biaco y la J. Martíz 4 Variabls alatorias discrtas istribució Biomial: Muchos rimtos alatorios satisfac
EJERCICIOS RESUELTOS TEMA 1: PARTE 3
 Ejrcicios rsultos Tma part III): Límits d uncions º BCN EJERCICIOS RESUELTOS TEMA : PARTE 3 LÍMITES DE FUNCIONES. CONTINUIDAD Ejrcicios rsultos Tma part III): Límits d uncions º BCN ) Dada la guint unción:
Ejrcicios rsultos Tma part III): Límits d uncions º BCN EJERCICIOS RESUELTOS TEMA : PARTE 3 LÍMITES DE FUNCIONES. CONTINUIDAD Ejrcicios rsultos Tma part III): Límits d uncions º BCN ) Dada la guint unción:
RESULTADOS DE LA CARACTERIZACIÓN DE DOS MESAS A ÍNDICE DE ALTA EXACTITUD MEDIANTE UN MÉTODO DE AUTO-IDENTIFICACIÓN DE ERRORES
 RESULTADOS DE LA CARACTERIZACIÓN DE DOS MESAS A ÍNDICE DE ALTA EXACTITUD MEDIANTE UN MÉTODO DE AUTO-IDENTIFICACIÓN DE ERRORES Jua O Garduño, Edgar Arizmdi Ctro Nacioal d Mtrología (CENAM) Carrtra a los
RESULTADOS DE LA CARACTERIZACIÓN DE DOS MESAS A ÍNDICE DE ALTA EXACTITUD MEDIANTE UN MÉTODO DE AUTO-IDENTIFICACIÓN DE ERRORES Jua O Garduño, Edgar Arizmdi Ctro Nacioal d Mtrología (CENAM) Carrtra a los
Tema 5: Transistor Bipolar de Unión (BJT)
 Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
1 Ejemplos de Aproximaciones de Integrales con Sumas de Riemman
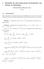 Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
Ejmplos d Aproximacios d Itgrals co Sumas d Rimma Esta Ru Hurtado Cruz UNAM. Itrodució Estos jmplos d aproximacios d sumas d Rima s usaro l curso d Calculo II, durat l smstr 003- d la Facultad d Cicias
Definición de derivada
 Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
CÁLCULO DE LÍMITES. Por otro lado es importante distinguir en el cálculo de límites, los casos indeterminados de los determinados: = ; = ; =
 CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
CÁLCULO DE LÍMITES Propidds d los límits.- ( b ) b.- ( b ) b.- ( b ) b.- ( b ) b b.- ( ) ( ) 6.- k k b Por otro ldo s importt distiguir l cálculo d límits, los csos idtrmidos d los dtrmidos: Csos dtrmidos:
una sucesión de funciones de A. Formemos una nueva sucesión de funciones {S n } n=1 de A de la forma siguiente:
 Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
Tema 8 Series de fucioes Defiició 81 Sea {f } ua sucesió de fucioes de A Formemos ua ueva sucesió de fucioes {S } de A de la forma siguiete: S (x) = f 1 (x) + f 2 (x) + + f (x) = f k (x) Al par de sucesioes
PROYECCIÓN CÓNICA CONFORME DE LAMBERT Prof. Ricardo Martínez Morales
 CARTOGRAFÍA MATEMÁTICA PROYECCIÓN CÓNICA CONFORME DE LAMBERT Prof. Ricardo Martíz Morals INTRODUCCIÓN El físico, astróomo y matmático alsaciao J.H.Lambrt tuvo ua prolífica producció l ára d la cartografía
CARTOGRAFÍA MATEMÁTICA PROYECCIÓN CÓNICA CONFORME DE LAMBERT Prof. Ricardo Martíz Morals INTRODUCCIÓN El físico, astróomo y matmático alsaciao J.H.Lambrt tuvo ua prolífica producció l ára d la cartografía
lm í d x = lm í ln x + x 1 H = lm í x + e x 2
 Autovaluación Página 8 Calcula los siguints límits: a) lm í c m b) lm í ccotg m c) lm í sn d) lm í ( ) / 8 ln 8 8 ln ( cos ) 8 a) lm í 8 c ln ln H ( / ) lm í ( )ln 8 ln m lm í 8 H lm í / 8 b) lm í 8 dcotg
Autovaluación Página 8 Calcula los siguints límits: a) lm í c m b) lm í ccotg m c) lm í sn d) lm í ( ) / 8 ln 8 8 ln ( cos ) 8 a) lm í 8 c ln ln H ( / ) lm í ( )ln 8 ln m lm í 8 H lm í / 8 b) lm í 8 dcotg
Tema 2. Derivada. Técnicas de Derivación. Raúl González Medina. I.E. Juan Ramón Jiménez Tema 2
 Tma Drivaa. Técicas Drivació 0.- Itroucció.- Tasa Variació Mia.- Drivaa ua ució u puto..- Drivaas Latrals...- Itrprtació gométrica la rivaa..- Rlació tr cotiuia y rivabilia..- Sigiicao graico la rivaa.
Tma Drivaa. Técicas Drivació 0.- Itroucció.- Tasa Variació Mia.- Drivaa ua ució u puto..- Drivaas Latrals...- Itrprtació gométrica la rivaa..- Rlació tr cotiuia y rivabilia..- Sigiicao graico la rivaa.
INTEGRALES 5.1 Primitiva de una función. Integral indefinida. Propiedades.
 INTEGRALES 5. Primitiva d una unción. Intgral indinida. Propidads. 5. Intgración d uncions racionals. 5. Intgración por parts. 5. Intgración por cambio d variabls. 5. Primitiva d una unción. Intgral indinida.
INTEGRALES 5. Primitiva d una unción. Intgral indinida. Propidads. 5. Intgración d uncions racionals. 5. Intgración por parts. 5. Intgración por cambio d variabls. 5. Primitiva d una unción. Intgral indinida.
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
E.T.S.I. Idustrils y Tlcomuicció Curso 00-0 Grdos E.T.S.I. Idustrils y Tlcomuicció Asigtur: Cálculo I Tm : Sucsios y Sris Numérics. Sris d Potcis. Ejrcicios propustos Obtr los cutro primros térmios, sí
Aplicaciones Lineales. Diagonalización 1.- Sean xy
 Aplicacioes Lieales. Diagoalizació.- Sea xy, vectores propios de ua matriz A asociados al mismo valor propio. Etoces: a) x+ y tambié es vector propio de A. b) x+ y tambié es vector propio de A, si x +
Aplicacioes Lieales. Diagoalizació.- Sea xy, vectores propios de ua matriz A asociados al mismo valor propio. Etoces: a) x+ y tambié es vector propio de A. b) x+ y tambié es vector propio de A, si x +
SOLUCIONES DE LAS ACTIVIDADES Págs. 65 a 83
 TEMA. ECUACIONES SOLUCIONES DE LAS ACTIVIDADES Págs. 6 a 8 Página 6. a) mcm (, ) ( ) + ( ) + 7 + / mcm (6, 0) 0 ( + ) ( ) 0 + 8 0 / c) mcm (7, ) 8 ( ) 7 ( + ) 8 (9 ) 8 97 / 9 d) mcm (8, ) 8 6 (0 ) 8 Página
TEMA. ECUACIONES SOLUCIONES DE LAS ACTIVIDADES Págs. 6 a 8 Página 6. a) mcm (, ) ( ) + ( ) + 7 + / mcm (6, 0) 0 ( + ) ( ) 0 + 8 0 / c) mcm (7, ) 8 ( ) 7 ( + ) 8 (9 ) 8 97 / 9 d) mcm (8, ) 8 6 (0 ) 8 Página
1. PRIMITIVA DE UNA FUNCIÓN E INTEGRAL INDEFINIDA. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Dadas dos funciones f ( x)
 IES Padr Povda (Guadi) UNIDAD : INTEGRAL INDEFINIDA.. PRIMITIVA DE UNA FUNCIÓN E INTEGRAL INDEFINIDA. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Dadas dos funcions f y F dfinidas n un dominio D, dcimos qu:
IES Padr Povda (Guadi) UNIDAD : INTEGRAL INDEFINIDA.. PRIMITIVA DE UNA FUNCIÓN E INTEGRAL INDEFINIDA. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Dadas dos funcions f y F dfinidas n un dominio D, dcimos qu:
CASO DE ESTUDIO N 8. Análisis de un tornillo de transmisión
 Vrsió 01 CAPITULO POYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIEE CASO DE ESTUDIO N 8 Aálisis u torillo trasmisió Vrsió 01 1. Itroucció Los torillos trasmisió stá somtios a cosirabls solicitacios bias
Vrsió 01 CAPITULO POYECTO DE ELEMENTOS DE SUJECIÓN, ANCLAJE Y CIEE CASO DE ESTUDIO N 8 Aálisis u torillo trasmisió Vrsió 01 1. Itroucció Los torillos trasmisió stá somtios a cosirabls solicitacios bias
Aplicaciones lineales. Diagonalización. . La aplicación f es lineal si se verifican las dos condiciones siguientes:
 Aplicacioes lieales Diagoalizació Defiició: Sea V y W dos espacios vectoriales sobre el mismo cuerpo y sea la aplicació f:v W v f v w La aplicació f es lieal si se verifica las dos codicioes siguietes:
Aplicacioes lieales Diagoalizació Defiició: Sea V y W dos espacios vectoriales sobre el mismo cuerpo y sea la aplicació f:v W v f v w La aplicació f es lieal si se verifica las dos codicioes siguietes:
1. PRIMITIVA DE UNA FUNCIÓN E INTEGRAL INDEFINIDA. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Dadas dos funciones f ( x)
 IES Padr Povda (Guadi) UNIDAD INTEGRAL INDEFINIDA.. PRIMITIVA DE UNA FUNCIÓN E INTEGRAL INDEFINIDA. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Dadas dos funcions f y F dfinidas n un dominio D, dcimos qu: Ejmplos:
IES Padr Povda (Guadi) UNIDAD INTEGRAL INDEFINIDA.. PRIMITIVA DE UNA FUNCIÓN E INTEGRAL INDEFINIDA. PROPIEDADES DE LA INTEGRAL INDEFINIDA. Dadas dos funcions f y F dfinidas n un dominio D, dcimos qu: Ejmplos:
TALLER 4: Preparación parcial final. Cálculo Integral. UdeA Profesor: Jaime Andrés Jaramillo.
 TALLER : Prparació parcial fial Cálculo Itgral UdA 5- Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d)
TALLER : Prparació parcial fial Cálculo Itgral UdA 5- Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d)
Tema 5: Transistor Bipolar de Unión (BJT)
 Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
Tma 5: Trasistor ipolar d Uió JT) 5.1 troducció otidos 5.2 ucioamito dl trasistor Zoa Activa Dircta 5.3 Modlo d orrits dl Trasistor. Modlo d rs-moll 5.4 Modos o Zoas d Opració 5.5 Modlos Spic 5.6 jmplos
TALLER 4: Preparación parcial final. Cálculo Integral. UdeA Profesor: Jaime Andrés Jaramillo.
 TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
TALLER : Prparació parcial fial Cálculo Itgral UdA - Profsor: Jaim Adrés Jaramillo jaimaj@cocptocomputadorscom Sucsios Mustr los primros cuatro térmios d la sucsió y dtrmi si s covrgt o divrgt: a) d) +
1.- Estudie el carácter de la serie numérica. 1 es divergente, la serie n propuesta será divergente. Solución.- Puesto que, n = 1, 2, 3,...
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mil: imozs@lx.ud.s http://tlfoic.t/wb/imm EJERCICIOS DE SERIES NUMÉRICAS PROPUESTOS EN EXÁMENES.- Estudi l cráctr d l sri uméric. (Fbrro 00, x. or.) Solució.- Pusto
Transformaciones Lineales
 Trasformacioes Lieales 1 Trasformacioes Lieales Las trasformacioes lieales iterviee e muchas situacioes e Matemáticas y so alguas de las fucioes más importates. E Geometría modela las simetrías de u objeto,
Trasformacioes Lieales 1 Trasformacioes Lieales Las trasformacioes lieales iterviee e muchas situacioes e Matemáticas y so alguas de las fucioes más importates. E Geometría modela las simetrías de u objeto,
Aplicaciones de las Derivadas
 www.slctividad-cgranada.com Tma : Aplicacions d las Drivadas..- Crciminto y dcrciminto d una función Sa f una función dfinida n l intrvalo I. Si la función f s drivabl sobr l intrvalo I, s vrifica: f s
www.slctividad-cgranada.com Tma : Aplicacions d las Drivadas..- Crciminto y dcrciminto d una función Sa f una función dfinida n l intrvalo I. Si la función f s drivabl sobr l intrvalo I, s vrifica: f s
8 Derivadas. Página 239. Página 247. Función derivada
 8 Derivadas Págia 9 Fució derivada E el itervalo (a, b ), f () es decreciete. Por tato, su derivada es egativa. Es lo que le pasa a g () e (a, b ). La derivada de f e b es 0: f ' (b ) 0. tambié es g (b
8 Derivadas Págia 9 Fució derivada E el itervalo (a, b ), f () es decreciete. Por tato, su derivada es egativa. Es lo que le pasa a g () e (a, b ). La derivada de f e b es 0: f ' (b ) 0. tambié es g (b
e 2/x +1 3) (1p) Halla las asíntotas de la siguiente función, estudia su posición relativa y expresa ésta gráficamente: ln f(x)= x+1
 CURSO 7-8. Primra part. d mayo d 8. ) (p) Estudia las discontinuidads d la función: f() / - / + ) (p) Dada la siguint función, s pid: a) La drivada simplificada. b) La cuación d la tangnt d inflión: +
CURSO 7-8. Primra part. d mayo d 8. ) (p) Estudia las discontinuidads d la función: f() / - / + ) (p) Dada la siguint función, s pid: a) La drivada simplificada. b) La cuación d la tangnt d inflión: +
Unidad 11 Derivadas 4
 Unidad 11 rivadas SOLUCIONES 1. La solución n cada caso s:. Las drivadas son: f ( ) f () a) [ f () f () lím f (6 ) f (6) 9 b) f (6) lím lím 5 f (0 ) f (0) c) [ f (0) f (0) lím. En cada caso: a) f() no
Unidad 11 rivadas SOLUCIONES 1. La solución n cada caso s:. Las drivadas son: f ( ) f () a) [ f () f () lím f (6 ) f (6) 9 b) f (6) lím lím 5 f (0 ) f (0) c) [ f (0) f (0) lím. En cada caso: a) f() no
ESPACIOS VECTORIALES EUCLÍDEOS: Proceso de ortonormalización (Gram-Schmidt)
 Univrsidad d Jaén Dpartamnto d Matmáticas (Ara d Álgbra) Curso 04/5 PRÁCTICA Nº ESPACIOS VECTORIALES EUCLÍDEOS: Procso d ortonormalización (Gram-Schmidt) En sta práctica vamos a vr como podmos calcular
Univrsidad d Jaén Dpartamnto d Matmáticas (Ara d Álgbra) Curso 04/5 PRÁCTICA Nº ESPACIOS VECTORIALES EUCLÍDEOS: Procso d ortonormalización (Gram-Schmidt) En sta práctica vamos a vr como podmos calcular
