ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ
|
|
|
- Salvador Paz Giménez
- hace 7 años
- Vistas:
Transcripción
1 ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ
2 Probabilidad - Período de retorno y riesgo La probabilidad de ocurrencia de un fenómeno en hidrología puede citarse de varias Formas: El evento hidrológico posee una probabilidad de ocurrencia del % El evento hidrológico se presenta una vez cada 10 años. Existe una relación entre probabilidad de ocurrencia de un evento hidrológico y tiempo de recurrencia el fenómeno. Por ejemplo: Si un suceso hidrológico se presenta (en promedio) una vez cada 10 años, su probabilidad de ocurrencia será 0.1 (10%). Si la probabilidad de ocurrencia de un determinado fenómeno hidrológico es de 0.04 (4%), significa que dicho fenómeno se presentará ( en promedio) 4 veces en 100 años, es decir, una vez cada 5 años.
3 Período de retorno (r) Se define el período de retorno, r, de un evento de cierta magnitud como el tiempo promedio que transcurre entre la ocurrencia de ese evento y la próxima ocurrencia de ese evento con la misma magnitud. Se define también como el tiempo que transcurre para que un evento sea excedido o igualado, al menos una vez en promedio. Si P es la probabilidad de excedencia, entonces: P = 1 r
4 Riesgo Supóngase que se calcula un cierto caudal para el periodo de retorno de 50 años, entonces la probabilidad de que se produzca dicho caudal este año será de 0.0 (1/50). Si este año no se produce dicho caudal, La probabilidad de que se produzca el año siguiente sigue siendo 0.0. en cualquier año la probabilidad es 0.0. Surge una pregunta: Cual es la probabilidad de que se presente dicho caudal durante los próximos n años?: Probabilidad de que un suceso de periodo de retorno se presente este año.. 1/ Probabilidad de que un suceso de periodo de retorno NO se presente este año 1-1/ Probabilidad de que un suceso de periodo de retorno NO se presente en dos años.(1-1/) (1-1/) Probabilidad de que un suceso de periodo de retorno NO se presente en n años..(1-1/)^n Probabilidad de que un suceso de periodo de retorno SI se presente en n años.. 1- (1-1/)^n Entonces la probabilidad de que sí se presente alguna vez un suceso hidrológico con periodo de retorno de durante los próximos n años se denomina Riesgo. n 1 r R = 1-1
5 Ejemplo1: Se va a construir un canal cuya vida útil es de 75 años. Si el caudal supera el valor correspondiente al período de retorno de 100 años se desbordará. Cual es la probabilidad de que se produzca algún desbordamiento en los próximos 75 años. 1 R =1-1 r n % Ejemplo: Se esta diseñando una obra cuya vida útil se estima en 50 años y se admite que el riesgo de daño sea del 10%. Cual debe ser el periodo de retorno del caudal de diseño? (area)
6 Factor de frecuencia Recordando el proceso de estandarización típico de la distribución normal, la variable aleatoria estandarizada se definía como: Por tanto se puede inferir que: Y para una muestra poblacional: z i x i x zis x Es decir, el valor esperado de una variable aleatoria para para un determinado periodo de retorno (xt) depende de su media y será proporcional a su desviación estándar, en general: x Donde la constante de proporcionalidad kt se conoce como factor de frecuencia y depende, de la probabilidad de ocurrencia (el periodo de retorno) y su fdp. x x i i zi x k s x
7 Intervalos de confianza Cuando se desea hallar cualquier estadístico, por ejemplo la media, generalmente se dispone de una muestra de tamaño limitado. Se quiere saber qué tan cercano puede estar ese estimado al verdadero valor desconocido de la población. En otras palabras, se quisiera conocer con una cierta certeza (probabilidad) la franja de valores entre los cuales se encontraría el verdadero valor de la población. Franja grande: mucha incertidumbre.
8 : Nivel de confianza o nivel de probabilidad. S : Error estándar. X i Z1 / S E El error estándar, S, es una medida de la desviación estándar de la magnitud de un evento calculado a partir de una muestra respecto a la verdadera magnitud del evento. S E = σˆ x N 1+ K 1
9 Ejemplo: Caudales de río Escondido Cual es el caudal correspondiente a un R =100 años, si tienen una distribución normal. N=5 años. =83.5 m 3 /s σ=4.8 m 3 /s En este caso se puede escribir: P= 1/r = 0.01 Fu(K) = 1 - P = 0.99 K= z = F u -1 (0.99) abla K=.36
10 Q K Q Intervalos de confianza para =5%: s m S z X abla z z E / / K 1+ N σˆ = S x E 1
11 DISRIBUCIONES DE PROBABILIDAD EN EL ANÁLISIS DE FRECUENCIAS
12 Distribuciones simétricas y asimétricas Muchas variables naturales se ajustan a la distribución simétrica propuesta por Gaus. Sin embargo existen casos en los que no existe la misma proporción de los pequeños que de los grandes. Dando como resultado una fdp asimétrica. En hidrología los caudales y las precipitaciones medias anuales suelen ajustarse a la distribución simétrica de Gaus. Pero los caudales y las precipitaciones máximas o mínimas (extremos) no. Estos últimos suelen ajustarse a campanas asimétricas
13 Distribuciones de probabilidad para análisis de frecuencias. Los matemáticos han encontrado para nosotros las ecuaciones de muchas de las campanas asimétricas. Distribuciones Asimétricas continuas: Distribución General de Valor Extremos (Gumbel) Distribución Gamma (Pearson) Distribución Log Normal Distribución Log Gumbel Distribución Log Pearson. Para cada distribución existen ecuaciones que permiten determinar el factor de frecuencia para un determinado r y su respectiva banda de error.
14 Distribución General de Valor Extremo Los valores extremos son valores máximos y mínimos seleccionados de un conjuntos de datos. Las distribuciones de valores extremos seleccionados de conjuntos de muestras de cualquier distribución de probabilidad convergen en una de las tres formas de distribución de valor extremo, llamadas: ipo I: Gumbel ipo II: Frechet ipo III: Weibull Función de Distribución de probabilidad para la GEV x F(x) = exp -1-1/
15 Donde:, y son parámetros que deben ser determinados. Los tres casos limitantes son: 1. = 0 Distribución de Valor Extremo ipo I (Gumbel) f(x) 1 = exp - x - - exp - x - Rango: - x Estimación de parámetros: x ˆ = 6 ˆ
16 . < 0 Distribución de Valor Extremo ipo II (Frechet) f(x) x = exp -1-1/ Rango: ( / ) x 3. > 0 Distribución de Valor Extremo ipo III (Weibull) f(x) x = exp -1-1/ Rango: x ( / )
17 La fda y el factor de frecuencias es: Distribución Gumbel F(x) exp-exp x x K = ln ln r - ln r -1 Intervalos de confianza: Que tan cercano puede estar el estimado al valor verdadero desconocido de la población. : Nivel de confianza o nivel de probabilidad S : Error estándar ^ S = N X u 1- S = K+1.1K 1/
18 Como ajustar la fda de la distribución Gumbel a una muestra de datos (Fácil) Método 1: (rápido, buenos resultados) F(x) exp -exp ax b x Siendo: a 1.85 S x b X 0. 45S x Método : (EL mejor, mas preciso) a F(x) S y x c exp a x b -exp b X c y a
19 Ejemplo 1: Gumbel De una serie de 55 caudales extremos se sabe que su media es 1.97 m3/s y la desviación estándar es de 13. m3/s. a) calcular la probabilidad de que se supere un caudal de 60 m3/s. b) Cuál caudal se superará el 1% de los años?. Por el método 1)
20 Ejemplo 3 : Distribución Gumbel Los caudales máximos del rio Nare tienen una distribución Gumbel, determinar el caudal con r de 100 años si se sabe que el valor medio es de los máximos es de y su desviación de.45 y sus intervalos de confianza 6 K lnln R ln( R 1) K r=100 = 3.13
21 Ejemplo: Distribución Gumbel Qr 95S S = N = K+1.1K 1/ Intervalos de confianza: δ = 3.91 S = 14.6 Q R 1.6* m 3 /s
22 Distribución Gamma ( Parámetros) Una de las mas usadas en Hidrología. Crecientes máximas anuales Caudales mínimos Volúmenes de flujo anuales y estacionales Valores de precipitaciones extremas Volúmenes de lluvia de corta duración f(x) = 1 x ( ) -1 e x - iene ó 3 parámetros (Pearson ipo III).
23 Parámetros y Factor de frecuencia (Parámetro de escala) > 0 (Parámetro de forma) () es la función Gamma completa ( ) = 0 z -1 e -z dz Estimación de parámetros: Método de los momentos = =
24 Distribución Gamma 3 Parámetros(Pearson ipo III) Función de distribución de probabilidad Función de densidad acumulada Parámetros y, parámetros de escala y forma respectivamente. x o parámetro de localización. α x - x - exp α x - x Γ(β) α 1 = f(x) o o β-1 dz e z = ) ( -z -1 0 X x x dx x x e x X P ) ( 1 ) (
25 Parámetros e Intervalos de confianza (Función Gamma) Estimación de Parámetros: Método de los momentos ˆ = ˆ ˆ = ˆ ˆ Xˆ0 = ˆ ˆ ˆ Que tan cercano puede estar el estimado al verdadero valor desconocido de la población: Conocer con cierta certeza. Franja grande: mucha incertidumbre. : Nivel de confianza o nivel de probabilidad S : Error estándar X S = u 1 N S
26 abla Factor de frecuencia Pearson tipo III
27 Valores de para la Distribución Gamma ó Pearson tipo III
28 Ejemplo: Distribución Gamma Hallar el Q R=100. Si la distribución de los caudales de la estación de Nare es Gamma. μ = m 3 /s y σ =.45 m 3 /s, γ = μ Y = 4.5 y σ Y = 0.337, Y = De tabla: K =.3 Q R=100 = *.45 = Intervalos de confianza: X u 1 S
29 De tabla δ=4.7, N= 36 datos. S N De tabla 95 =1.6 S = ,4 1.6* m 3 /s
30 Distribución Log Normal En general, cuando la variable aleatoria X es el producto de un gran número de otras variables aleatorias, la distribución de los logaritmos de X puede aproximarse a la Normal, ya que los logaritmos de X son la suma de los logaritmos de los factores contribuyentes. Si se tiene una variable aleatoria X y ln X = Y, se ajusta a una distribución Normal, se dice que la variable aleatoria X es log normalmente distribuida. Función de Distribución de Probabilidad Asumiendo Y = log a (X) 1 1 y -μ f(x) = exp - σyx π σy y
31 Parámetros y Factor de frecuencia Media (Parámetro de escala) Desviación estandar (Parámetro de forma) Estimación de parámetros: Método de los momentos 1 N N N ˆ Y log a(xi) 1 ˆ Y log a(x i) ˆ Y i1 N i1 1 ln = + K X y y K es la misma de la distribución normal Si se quiere trabajar con la variable no transformada en el campo logarítmico se tiene que: expk K = ln 1+ Cv ln 1+ - Cv Cv 1/ -1
32 1 1 F u 1 K = F -1 u r Es el inverso de la función de distribución Normal estandarizada acumulada y Cv es el coeficiente de variación Intervalos de confianza : Nivel de confianza o significancia S : Error estándar ln u1- S X S = Y N = 1+ K 1/
33 Ejemplo: Distribución Log Normal La media y desviación estándar de los Q max anuales de la estación del río Nare son: μ=94.35 m 3 /s y σ=.45 m 3 /s μ Y =4.5 y σ Y =0.337 Hallar el Q R=100 si los Q max tienen una distribución Log Normal. K=.36 Q Y r=100 = *0.37 Q r=100 =159 m 3 /s Intervalos de Confianza: Ln(Q R=100 ) μ 95 S
34 Es un intervalo de dos colas, con una probabilidad en cada una de 5% 1/ = Y S K = 1 + N δ=1.9 S = * Q Y m 3 /s
35 Distribución Log Pearson ipo III Función de distribución de probabilidad f x (x) = x 1 ln(x) - ( ) y o -1 e ln(x)- - y o Parámetros y, parámetros de escala y forma y y o parámetro de localización Estimación de Parámetros Método de los momentos ˆ ˆy ˆ = ˆ y ˆ y yˆ 0 ˆ y ˆ ˆ
36 Factor de Frecuencia: Y = ln X = ˆ y +K ˆ y Intervalos de Confianza: Que tan cercano puede estar el estimado al verdadero valor desconocido de la población: Conocer con cierta certeza. Franja grande: mucha incertidumbre. : Nivel de confianza o nivel de probabilidad S : Error estándar X u 1- S S = ˆ y N lnx S 1 /
METODOS ESTADÍSTICOS
 METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
ANÁLISIS DE FRECUENCIAS
 ANÁLISIS DE FRECUENCIAS EXPRESIONES PARA EL CÁLCULO DE LOS EVENTOS PARA EL PERÍODO DE RETORNO T Y DE LOS RESPECTIVOS ERRORES ESTÁNDAR DE ESTIMACIÓN REQUERIDOS PARA LA DETERMINACIÓN DE LOS INTERVALOS DE
ANÁLISIS DE FRECUENCIAS EXPRESIONES PARA EL CÁLCULO DE LOS EVENTOS PARA EL PERÍODO DE RETORNO T Y DE LOS RESPECTIVOS ERRORES ESTÁNDAR DE ESTIMACIÓN REQUERIDOS PARA LA DETERMINACIÓN DE LOS INTERVALOS DE
ANALISIS DE FRECUENCIA EN HIDROLOGIA
 ANALISIS DE FRECUENCIA EN HIDROLOGIA Luis F. Carvajal Julián D. Rojo Universidad Nacional de Colombia Facultad de Minas Escuela de Geociencias y Medio Ambiente Introducción 1. Los eventos hidrológicos
ANALISIS DE FRECUENCIA EN HIDROLOGIA Luis F. Carvajal Julián D. Rojo Universidad Nacional de Colombia Facultad de Minas Escuela de Geociencias y Medio Ambiente Introducción 1. Los eventos hidrológicos
CLASE X ANÁLISIS PROBABILISTICO DE LAS VARIABLES PRECIPITACIÓN TOTAL ANUAL Y CAUDAL MEDIO ANUAL
 Universidad Nacional Agraria La Molina IA-406 Hidrología Aplicada CLASE X ANÁLISIS PROBABILISTICO DE LAS VARIABLES PRECIPITACIÓN TOTAL ANUAL Y CAUDAL MEDIO ANUAL 1. Longitud necesaria de registro Diversos
Universidad Nacional Agraria La Molina IA-406 Hidrología Aplicada CLASE X ANÁLISIS PROBABILISTICO DE LAS VARIABLES PRECIPITACIÓN TOTAL ANUAL Y CAUDAL MEDIO ANUAL 1. Longitud necesaria de registro Diversos
Distribución Exponencial
 Distribución Exponencial Hay dos casos especiales importantes de la distribución gamma, que resultan de restricciones particulares sobre los parámetros α y β. El primero es cuando se tiene α = 1, entonces
Distribución Exponencial Hay dos casos especiales importantes de la distribución gamma, que resultan de restricciones particulares sobre los parámetros α y β. El primero es cuando se tiene α = 1, entonces
Algunas Distribuciones Continuas de Probabilidad. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
3. ANÁLISIS DE DATOS DE PRECIPITACIÓN.
 3. ANÁLISIS DE DATOS DE PRECIPITACIÓN. Teniendo en cuenta que la mayoría de procesos estadísticos se comportan de forma totalmente aleatoria, es decir, un evento dado no está influenciado por los demás,
3. ANÁLISIS DE DATOS DE PRECIPITACIÓN. Teniendo en cuenta que la mayoría de procesos estadísticos se comportan de forma totalmente aleatoria, es decir, un evento dado no está influenciado por los demás,
GENERACION DE NUMEROS ALEATORIOS Y VARIABLES ALEATORIAS
 GENERACION DE NUMEROS ALEATORIOS Y VARIABLES ALEATORIAS La simulación de eventos se basa en la ocurrencia aleatoria de los mismos, por ello los números aleatorios y las variables aleatorias son de especial
GENERACION DE NUMEROS ALEATORIOS Y VARIABLES ALEATORIAS La simulación de eventos se basa en la ocurrencia aleatoria de los mismos, por ello los números aleatorios y las variables aleatorias son de especial
ANEXO ANÁLISIS DE FRECUENCIA EMPLEANDO EL MODELO HYFRAN
 000114 ANEXO 4.2.5-3 ANÁLISIS DE FRECUENCIA EMPLEANDO EL MODELO HYFRAN Recrecimiento del Embalse de relaves Quebrada Honda 000115 ESTACIÓN QUEBRADA HONDA (ALTA) El análisis de frecuencia parte de la adopción
000114 ANEXO 4.2.5-3 ANÁLISIS DE FRECUENCIA EMPLEANDO EL MODELO HYFRAN Recrecimiento del Embalse de relaves Quebrada Honda 000115 ESTACIÓN QUEBRADA HONDA (ALTA) El análisis de frecuencia parte de la adopción
DRENAJE AGRICOLA. Determinación de Lluvias Máximas. Análisis de Frecuencia
 DRENAJE AGRICOLA Prof. Ricardo Trezza Determinación de Lluvias Máximas Las obras relacionadas con el manejo y control del agua, así como toda actividad agrícola, son afectadas y determinadas por eventos
DRENAJE AGRICOLA Prof. Ricardo Trezza Determinación de Lluvias Máximas Las obras relacionadas con el manejo y control del agua, así como toda actividad agrícola, son afectadas y determinadas por eventos
( ) DISTRIBUCIÓN UNIFORME (o rectangular) 1 b a. para x > b DISTRIBUCIÓN DE CAUCHY. x ) DISTRIBUCIÓN EXPONENCIAL. α α 2 DISTRIBUCIÓN DE LAPLACE
 Estudiamos algunos ejemplos de distribuciones de variables aleatorias continuas. De ellas merecen especial mención las derivadas de la distribución normal (χ, t de Student y F de Snedecor), por su importancia
Estudiamos algunos ejemplos de distribuciones de variables aleatorias continuas. De ellas merecen especial mención las derivadas de la distribución normal (χ, t de Student y F de Snedecor), por su importancia
El diseño de las redes de Saneamiento: Caudales en las Redes de Saneamiento
 SECCIÓN 3: MÉTODOS ESTADÍSTICOS El diseño de las redes de saneamiento, están siempre relacionadas con eventos lluviosos. Evento que debe pronosticarse con objeto de determinar adecuadamente las secciones
SECCIÓN 3: MÉTODOS ESTADÍSTICOS El diseño de las redes de saneamiento, están siempre relacionadas con eventos lluviosos. Evento que debe pronosticarse con objeto de determinar adecuadamente las secciones
GENERACION DE NUMEROS ALEATORIOS Y VARIABLES ALEATORIAS
 GENERACION DE NUMEROS ALEATORIOS Y VARIABLES ALEATORIAS La simulación de eventos se basa en la ocurrencia aleatoria de los mismos, por ello los números aleatorios y las variables aleatorias son de especial
GENERACION DE NUMEROS ALEATORIOS Y VARIABLES ALEATORIAS La simulación de eventos se basa en la ocurrencia aleatoria de los mismos, por ello los números aleatorios y las variables aleatorias son de especial
ANALISIS DE FRECUENCIA
 ANALISIS DE FRECUENCIA HIDROLOGÍA Determinística: enfoque en el cual los parámetros se calculan en base a relaciones físicas para procesos dinámicos del ciclo hidrológico. Estocástico: Enfoque en el cual
ANALISIS DE FRECUENCIA HIDROLOGÍA Determinística: enfoque en el cual los parámetros se calculan en base a relaciones físicas para procesos dinámicos del ciclo hidrológico. Estocástico: Enfoque en el cual
Transformaciones y esperanza
 Capítulo 3 Transformaciones y esperanza 3.1. Introducción Por lo general estamos en condiciones de modelar un fenómeno en términos de una variable aleatoria X cuya función de distribución acumulada es
Capítulo 3 Transformaciones y esperanza 3.1. Introducción Por lo general estamos en condiciones de modelar un fenómeno en términos de una variable aleatoria X cuya función de distribución acumulada es
= f ( intensidad de lluvia, área de aportación)
 Redes de saneamiento (III): Estadística hidrológica 1 Cuánta agua entra a través de este imbornal en la alcantarilla? = f ( intensidad de lluvia, área de aportación) 2 Mapas de isoyetas Mapa de isoyetas
Redes de saneamiento (III): Estadística hidrológica 1 Cuánta agua entra a través de este imbornal en la alcantarilla? = f ( intensidad de lluvia, área de aportación) 2 Mapas de isoyetas Mapa de isoyetas
GEOESTADÍSTICA APLICADA
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO GEOESTADÍSTICA APLICADA Tema: Análisis Exploratorio de Datos Instructores: Dr. Martín A. Díaz Viera (mdiazv@imp.mx) Dr. Ricardo Casar González (rcasar@imp.mx) 2009
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO GEOESTADÍSTICA APLICADA Tema: Análisis Exploratorio de Datos Instructores: Dr. Martín A. Díaz Viera (mdiazv@imp.mx) Dr. Ricardo Casar González (rcasar@imp.mx) 2009
ANÁLISIS DE FRECUENCIA (CURVAS INTENSIDAD DURACIÓN - FRECUENCIA) Y RIESGO HIDROLÓGICO
 Facultad de Ingeniería Escuela de Civil Hidrología ANÁLISIS DE FRECUENCIA (CURVAS INTENSIDAD DURACIÓN - FRECUENCIA) Y RIESGO HIDROLÓGICO Prof. Ada Moreno ANÁLISIS DE FRECUENCIA Es un procedimiento para
Facultad de Ingeniería Escuela de Civil Hidrología ANÁLISIS DE FRECUENCIA (CURVAS INTENSIDAD DURACIÓN - FRECUENCIA) Y RIESGO HIDROLÓGICO Prof. Ada Moreno ANÁLISIS DE FRECUENCIA Es un procedimiento para
INDICE 1. PROCESAMIENTO ESTADISTICO DE LOS DATOS 1 2. INTERPOLACION 3 3. COMPARACION DE RESULTADOS DE 1 Y MODELO DE BELL Y YANCE TUEROS 6
 RESUMEN En el presente informe se desarrollara la solución del examen parcial, la cual cuenta con el análisis de datos estadísticos de las precipitaciones registradas en la estación de Jaén y una posterior
RESUMEN En el presente informe se desarrollara la solución del examen parcial, la cual cuenta con el análisis de datos estadísticos de las precipitaciones registradas en la estación de Jaén y una posterior
Part I. Momentos de una variable aleatoria. Esperanza y varianza. Modelos de Probabilidad. Mario Francisco. Esperanza de una variable aleatoria
 una una típica Part I Momentos. Esperanza y varianza Esperanza una una típica Definición Sea X una discreta que toma los valores x i con probabilidades p i. Supuesto que i x i p i
una una típica Part I Momentos. Esperanza y varianza Esperanza una una típica Definición Sea X una discreta que toma los valores x i con probabilidades p i. Supuesto que i x i p i
PPTCEG061EM33-A17V1. Distribución normal 1
 PPTCEG061EM33-A17V1 Distribución normal 1 Propiedades distribución normal Distribución normal tipificada Es una distribución estadística continua cuya función de densidad es simétrica, y cuya forma se
PPTCEG061EM33-A17V1 Distribución normal 1 Propiedades distribución normal Distribución normal tipificada Es una distribución estadística continua cuya función de densidad es simétrica, y cuya forma se
ANÁLISIS DEL RÉGIMEN DE CAUDALES
 ANÁLISIS DEL RÉGIMEN DE CAUDALES JOSÉ CARLOS ROBREDO SÁNCHEZ PROFESOR TITULAR DE UNIVERSIDAD UNIDAD DOCENTE DE HIDRÁULICA E HIDROLOGÍA DEPARTAMENTO DE INGENIERÍA FORESTAL E.T.S. DE INGENIEROS DE MONTES
ANÁLISIS DEL RÉGIMEN DE CAUDALES JOSÉ CARLOS ROBREDO SÁNCHEZ PROFESOR TITULAR DE UNIVERSIDAD UNIDAD DOCENTE DE HIDRÁULICA E HIDROLOGÍA DEPARTAMENTO DE INGENIERÍA FORESTAL E.T.S. DE INGENIEROS DE MONTES
Part I. Variables aleatorias unidimensionales. Estadística I. Mario Francisco. Definición de variable aleatoria. Variables aleatorias discretas
 Part I unidimensionales de s de s Definición Dado un experimento aleatorio, con espacio muestral asociado Ω, una es cualquier función, X, X : Ω R que asocia a cada suceso elemental un número real, verificando
Part I unidimensionales de s de s Definición Dado un experimento aleatorio, con espacio muestral asociado Ω, una es cualquier función, X, X : Ω R que asocia a cada suceso elemental un número real, verificando
PROBABILIDADES Trabajo Práctico 5. 0 si x<0. x3 si 0 x<2 1 si x 2
 PROBABILIDADES Trabajo Práctico 5 1. Sea X una variable aleatoria con función de distribución acumulada a) Calcular, usando F X, P (X 1) P (0.5 X 1) P (X >1.5) b) Hallar la mediana de esta distribución.
PROBABILIDADES Trabajo Práctico 5 1. Sea X una variable aleatoria con función de distribución acumulada a) Calcular, usando F X, P (X 1) P (0.5 X 1) P (X >1.5) b) Hallar la mediana de esta distribución.
Teorema Central del Límite
 Teorema Central del Límite TCL: indica que, en condiciones muy generales, la distribución de la suma de v.a. tiende a una distribución normal cuando la cantidad de variables es muy grande. 156 Sea X 1,
Teorema Central del Límite TCL: indica que, en condiciones muy generales, la distribución de la suma de v.a. tiende a una distribución normal cuando la cantidad de variables es muy grande. 156 Sea X 1,
PP: gran cantidad de faltantes. Mejor solución no siempre es la misma: 1) Trabajar con datos incompletos (ojo con no sesgar la serie!!
 PP: gran cantidad de faltantes Mejor solución no siempre es la misma: 1) Trabajar con datos incompletos (ojo con no sesgar la serie!!) 2) Completar con algún método Definición: Homegeneidad 2 estaciones
PP: gran cantidad de faltantes Mejor solución no siempre es la misma: 1) Trabajar con datos incompletos (ojo con no sesgar la serie!!) 2) Completar con algún método Definición: Homegeneidad 2 estaciones
INGENIERO EN COMPUTACIÓN DISTRIBUCIONES DE PROBABILIDAD CONTINUA ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN DISTRIBUCIONES DE PROBABILIDAD CONTINUA ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACIÓN DISTRIBUCIONES DE PROBABILIDAD CONTINUA ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: AGOSTO DE 2017
Desempeño del modelo DIT ante distintas distribuciones teoricas de probabilidad: caso idt de la ciudad de La Rioja
 Desempeño del modelo DIT ante distintas distribuciones teoricas de probabilidad: caso idt de la ciudad de La Rioja Laboratorio de Hidráulica, Departamento de Ingeniería Civil, Facultad Regional Córdoba,
Desempeño del modelo DIT ante distintas distribuciones teoricas de probabilidad: caso idt de la ciudad de La Rioja Laboratorio de Hidráulica, Departamento de Ingeniería Civil, Facultad Regional Córdoba,
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 2013 Selectividad-Opción A Tiempo: 90 minutos Problema 1 2 puntos Se consideran las matrices A = 3 8. 3 5 0 2 3 0 y B = a Calcúlese la matriz
Examen de Matemáticas Aplicadas a las CC. Sociales II Septiembre 2013 Selectividad-Opción A Tiempo: 90 minutos Problema 1 2 puntos Se consideran las matrices A = 3 8. 3 5 0 2 3 0 y B = a Calcúlese la matriz
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos 0 2 Problema 1 (2 puntos) Se consideran las matrices A y B 3 0 3 8. 3 5 a) Calcúlese la
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2013) Selectividad-Opción A Tiempo: 90 minutos 0 2 Problema 1 (2 puntos) Se consideran las matrices A y B 3 0 3 8. 3 5 a) Calcúlese la
SECCIÓN 3: APLICACIÓN
 SECCIÓN 3: APLICACIÓN Tiempo de concentración. Período de retorno. Introducción. Cálculo de intensidades medias máximas de lluvia, I t. Superficie considerada. Cálculo del caudal de aguas blancas teórico..
SECCIÓN 3: APLICACIÓN Tiempo de concentración. Período de retorno. Introducción. Cálculo de intensidades medias máximas de lluvia, I t. Superficie considerada. Cálculo del caudal de aguas blancas teórico..
Tema 6. Variables aleatorias continuas
 Tema 6. Variables aleatorias continuas Resumen del tema 6.1. Definición de variable aleatoria continua Identificación de una variable aleatoria continua X: es preciso conocer su función de densidad, f(x),
Tema 6. Variables aleatorias continuas Resumen del tema 6.1. Definición de variable aleatoria continua Identificación de una variable aleatoria continua X: es preciso conocer su función de densidad, f(x),
Lecciones aprendidas de estudios hidrológicos en las cuencas de los ríos Coyolate y Villalobos.
 Lecciones aprendidas de estudios hidrológicos en las cuencas de los ríos Coyolate y Villalobos. Algunos conceptos básicos Evento extremo Probabilidad de no excedencia q P(X xo) P(T 40 C) Probabilidad de
Lecciones aprendidas de estudios hidrológicos en las cuencas de los ríos Coyolate y Villalobos. Algunos conceptos básicos Evento extremo Probabilidad de no excedencia q P(X xo) P(T 40 C) Probabilidad de
INTRODUCCIÓN AL ANÁLISIS DE DATOS ORIENTACIONES (TEMA Nº 7)
 TEMA Nº 7 DISTRIBUCIONES CONTINUAS DE PROBABILIDAD OBJETIVOS DE APRENDIZAJE: Conocer las características de la distribución normal como distribución de probabilidad de una variable y la aproximación de
TEMA Nº 7 DISTRIBUCIONES CONTINUAS DE PROBABILIDAD OBJETIVOS DE APRENDIZAJE: Conocer las características de la distribución normal como distribución de probabilidad de una variable y la aproximación de
Formulario. Estadística Administrativa. Módulo 1. Introducción al análisis estadístico
 Formulario. Estadística Administrativa Módulo 1. Introducción al análisis estadístico Histogramas El número de intervalos de clase, k, se elige de tal forma que el valor 2 k sea menor (pero el valor más
Formulario. Estadística Administrativa Módulo 1. Introducción al análisis estadístico Histogramas El número de intervalos de clase, k, se elige de tal forma que el valor 2 k sea menor (pero el valor más
ESTADISTICA INFERENCIAL DR. JORGE ACUÑA A.
 ESTADISTICA INFERENCIAL DR. JORGE ACUÑA A. 1 PROBABILIDAD Probabilidad de un evento es la posibilidad relativa de que este ocurra al realizar el experimento Es la frecuencia de que algo ocurra dividido
ESTADISTICA INFERENCIAL DR. JORGE ACUÑA A. 1 PROBABILIDAD Probabilidad de un evento es la posibilidad relativa de que este ocurra al realizar el experimento Es la frecuencia de que algo ocurra dividido
Inferencia Bayesiana en la distribución Gumbel: aplicación en el modelamiento de intensidades de lluvia
 Inferencia Bayesiana en la distribución Gumbel: aplicación en el modelamiento de intensidades de lluvia Ignacio Vidal G.. ividal@utalca.cl Universidad de Talca, Chile. Seminario FONDEF-D08I1054, Santiago
Inferencia Bayesiana en la distribución Gumbel: aplicación en el modelamiento de intensidades de lluvia Ignacio Vidal G.. ividal@utalca.cl Universidad de Talca, Chile. Seminario FONDEF-D08I1054, Santiago
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 3 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. Sea X 1,..., X n una muestra aleatoria
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 3 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. Sea X 1,..., X n una muestra aleatoria
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2010) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 200) Selectividad-Opción A Tiempo: 90 minutos Problema (3 puntos) Se considera el siguiente sistema lineal de ecuaciones dependiente de
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 200) Selectividad-Opción A Tiempo: 90 minutos Problema (3 puntos) Se considera el siguiente sistema lineal de ecuaciones dependiente de
CAPÍTULO 5 DISTRIBUCIONES TEÓRICAS
 CAPÍTULO 5 DISTRIBUCIONES TEÓRICAS Hugo Grisales Romero Profesor titular CONCEPTOS BÁSICOS Experimento: Variable aleatoria: Clasificación: Proceso por medio del cual una medición se obtiene. Aquella que
CAPÍTULO 5 DISTRIBUCIONES TEÓRICAS Hugo Grisales Romero Profesor titular CONCEPTOS BÁSICOS Experimento: Variable aleatoria: Clasificación: Proceso por medio del cual una medición se obtiene. Aquella que
Ejercicios de Variables Aleatorias
 Ejercicios de Variables Aleatorias Elisa M. Molanes-López, Depto. Estadística, UC3M Transformaciones de variables aleatorias Ejercicio. Sea X una v.a. continua con función de densidad dada por: /, si
Ejercicios de Variables Aleatorias Elisa M. Molanes-López, Depto. Estadística, UC3M Transformaciones de variables aleatorias Ejercicio. Sea X una v.a. continua con función de densidad dada por: /, si
[1,75 PUNTOS] Considerando la matriz A del apartado anterior con a = 1, resuelve la ecuación C. 6 si x 1
![[1,75 PUNTOS] Considerando la matriz A del apartado anterior con a = 1, resuelve la ecuación C. 6 si x 1 [1,75 PUNTOS] Considerando la matriz A del apartado anterior con a = 1, resuelve la ecuación C. 6 si x 1](/thumbs/84/90666921.jpg) MATEMÁTICAS CCSS º DE BACHILLERATO 014 OPCIÓN DE EXAMEN Nº 1 Ejercicio 1 [,5 PUNTOS] A. [1,75 PUNTOS] Determina para qué valores de a la matriz 1 A 5 a 1 1 a no tiene inversa. [1,75 PUNTOS] Considerando
MATEMÁTICAS CCSS º DE BACHILLERATO 014 OPCIÓN DE EXAMEN Nº 1 Ejercicio 1 [,5 PUNTOS] A. [1,75 PUNTOS] Determina para qué valores de a la matriz 1 A 5 a 1 1 a no tiene inversa. [1,75 PUNTOS] Considerando
Variables aleatorias: El caso continuo. Random variables: The continuous case. Rincón de la Bioestadística
 Variables aleatorias: El caso continuo Gabriel Cavada Ch. 1 1 División de Bioestadística, Escuela de Salud Pública, Universidad de Chile. Random variables: The continuous case E l tratamiento de una variable
Variables aleatorias: El caso continuo Gabriel Cavada Ch. 1 1 División de Bioestadística, Escuela de Salud Pública, Universidad de Chile. Random variables: The continuous case E l tratamiento de una variable
CI 41C HIDROLOGÍA HIDROLOGÍA PROBABILÍSTICA
 CI 41C HIDROLOGÍA HIDROLOGÍA PROBABILÍSTICA alcantarilla Puente? Badén http://www.disasternews.net/multimedia/files/drought5_9412.jpg Fenómenos en Ingeniería (según certeza de ocurrencia) determinísticos
CI 41C HIDROLOGÍA HIDROLOGÍA PROBABILÍSTICA alcantarilla Puente? Badén http://www.disasternews.net/multimedia/files/drought5_9412.jpg Fenómenos en Ingeniería (según certeza de ocurrencia) determinísticos
HIDROLOGÍA. CALSE 10: Precipitación Parte III. Julián David Rojo Hdz. I.C. Msc. Recursos Hidráulicos
 HIDROLOGÍA CALSE 10: Precipitación Parte III Julián David Rojo Hdz. I.C. Msc. Recursos Hidráulicos ANÁLISIS DE LLUVIAS INTENSAS CURVAS INTENSIDAD - FRECUENCIA - DURACION i m ktr ( c d ) n Para cada Tr
HIDROLOGÍA CALSE 10: Precipitación Parte III Julián David Rojo Hdz. I.C. Msc. Recursos Hidráulicos ANÁLISIS DE LLUVIAS INTENSAS CURVAS INTENSIDAD - FRECUENCIA - DURACION i m ktr ( c d ) n Para cada Tr
11.5. Septiembre Opción A
 .5. Septiembre 200 - Opción A Problema.5. (3 puntos) Se considera el siguiente sistema lineal de ecuaciones dependiente de un parámetro real a: 2 x + 3 2 4 a ( y z a) Discútase el sistema para los diferentes
.5. Septiembre 200 - Opción A Problema.5. (3 puntos) Se considera el siguiente sistema lineal de ecuaciones dependiente de un parámetro real a: 2 x + 3 2 4 a ( y z a) Discútase el sistema para los diferentes
Estimación de Parámetros.
 Estimación de Parámetros. Un estimador es un valor que puede calcularse a partir de los datos muestrales y que proporciona información sobre el valor del parámetro. Por ejemplo la media muestral es un
Estimación de Parámetros. Un estimador es un valor que puede calcularse a partir de los datos muestrales y que proporciona información sobre el valor del parámetro. Por ejemplo la media muestral es un
Algunas distribuciones teóricas continuas
 Algunas distribuciones teóricas continuas Dr. Pastore, Juan Ignacio Profesor Adjunto. Algunas Distribuciones Estadísticas Teóricas Distribución Continuas: a) Distribución Uniforme b) Distribución de Exponencial
Algunas distribuciones teóricas continuas Dr. Pastore, Juan Ignacio Profesor Adjunto. Algunas Distribuciones Estadísticas Teóricas Distribución Continuas: a) Distribución Uniforme b) Distribución de Exponencial
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos 5 7 C = 1 5
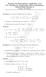 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Considérense las matrices ( ) ( ) ( ) 1 2 3 2 5 7 A =,
software para cálculos hidrológicos,
 Villón Bejar, Máximo. HidroEsta, software para cálculos hidrológicos. Tecnología en Marcha. Vol. 18 N. 2 Especial. HidroEsta, software para cálculos hidrológicos Máximo Villón Bejar 1 Palabras clave Precipitación,
Villón Bejar, Máximo. HidroEsta, software para cálculos hidrológicos. Tecnología en Marcha. Vol. 18 N. 2 Especial. HidroEsta, software para cálculos hidrológicos Máximo Villón Bejar 1 Palabras clave Precipitación,
Estimación. Diseño Estadístico y Herramientas para la Calidad. Estimación. Estimación. Inferencia Estadística
 Diseño Estadístico y Herramientas para la Calidad Estimación Epositor: Dr. Juan José Flores Romero juanf@umich.m http://lsc.fie.umich.m/~juan M. en Calidad Total y Competitividad Estimación Inferencia
Diseño Estadístico y Herramientas para la Calidad Estimación Epositor: Dr. Juan José Flores Romero juanf@umich.m http://lsc.fie.umich.m/~juan M. en Calidad Total y Competitividad Estimación Inferencia
UNIDAD 4: DISTRIBUCIÓN DE PROBABILIDAD
 UNIDAD 4: DISTRIBUCIÓN DE PROBABILIDAD La Distribución de Probabilidad (DP) es la relación que se da entre los diferentes eventos de un espacio muestral y sus respectivas probabilidades de ocurrencia.
UNIDAD 4: DISTRIBUCIÓN DE PROBABILIDAD La Distribución de Probabilidad (DP) es la relación que se da entre los diferentes eventos de un espacio muestral y sus respectivas probabilidades de ocurrencia.
Estadística Clase 2. Maestría en Finanzas Universidad del CEMA. Profesor: Alberto Landro Asistente: Julián R. Siri
 Estadística 010 Clase Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri Clase 1. La distribución de Bernoulli. La distribución binomial 3. La distribución de
Estadística 010 Clase Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri Clase 1. La distribución de Bernoulli. La distribución binomial 3. La distribución de
Estadística Clase 2. Maestría en Finanzas Universidad del CEMA. Profesor: Alberto Landro Asistente: Julián R. Siri
 Estadística 011 Clase Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri Clase 1. La distribución de Bernoulli. La distribución binomial 3. La distribución de
Estadística 011 Clase Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri Clase 1. La distribución de Bernoulli. La distribución binomial 3. La distribución de
Tema 6: Modelos de probabilidad.
 Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Cálculo de Probabilidades II Preguntas Tema 2
 Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Cálculo de Probabilidades II Preguntas Tema 2 1. Demuestre que la suma de n v.a. Bernuolli(p) independientes tiene una distribución Binomial con parametros (n, p). 2. Se dice que una v.a tiene una distribución
Tema 4: Probabilidad y Teoría de Muestras
 Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
CAPÍTULO 1. GENERALIDADES
 CAPÍTULO 1 GENERALIDADES 1.1. ESTADÍSTICA HIDROLÓGICA: DISTRIBUCIONES DE PROBABILIDAD Los procesos hidrológicos, como todo proceso natural, son de carácter aleatorio, es decir, que se rigen por las leyes
CAPÍTULO 1 GENERALIDADES 1.1. ESTADÍSTICA HIDROLÓGICA: DISTRIBUCIONES DE PROBABILIDAD Los procesos hidrológicos, como todo proceso natural, son de carácter aleatorio, es decir, que se rigen por las leyes
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDADES PAUTA DE CORRECCIÓN PRUEBA N 3 Profesor: Hugo S. Salinas. Segundo Semestre 200. Se investiga el diámetro
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDADES PAUTA DE CORRECCIÓN PRUEBA N 3 Profesor: Hugo S. Salinas. Segundo Semestre 200. Se investiga el diámetro
ANÁLISIS DE CAUDALES (II) Profesor Luis Fernando Carvajal
 ANÁLISIS DE CAUDALES (II) Profesor Luis Fernando Carvajal Relaciones nivel-caudal 1. El objetivo de aforar una corriente, durante varias épocas del año en una sección determinada, es determinar lo que
ANÁLISIS DE CAUDALES (II) Profesor Luis Fernando Carvajal Relaciones nivel-caudal 1. El objetivo de aforar una corriente, durante varias épocas del año en una sección determinada, es determinar lo que
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 P (X > 0) P ( 0,5 < X < 0,5) P ( X > 0,25) 1 si 2 x P (X 1) P (0,5 X 1) P (0,5 < X 1 X < 1)
 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad { 0,75 (1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular:
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 3 1. Sea X una v.a. con función de densidad { 0,75 (1 x f X (x) = 2 ) 1 x 1 0 en otro caso. a) Verificar que f X es realmente una función de densidad. b) Calcular:
Cálculos Estadísticos en Hidrología
 Cálculos Estadísticos en Hidrología Para extraer conclusiones estadísticas a partir de series de datos de precipitaciones o aforos, es necesario disponer de series históricas de más de 2 ó valores, cuanto
Cálculos Estadísticos en Hidrología Para extraer conclusiones estadísticas a partir de series de datos de precipitaciones o aforos, es necesario disponer de series históricas de más de 2 ó valores, cuanto
Unidad IV: Distribuciones muestrales
 Unidad IV: Distribuciones muestrales 4.1 Función de probabilidad En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia
Unidad IV: Distribuciones muestrales 4.1 Función de probabilidad En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia
Variables aleatorias continuas
 Variables aleatorias continuas VARIABLE ALEATORIA UNIFORME Definición Se dice que una variable X tiene una distribución uniforme en el intervalo [a;b] si la fdp de X es: 1 si a x b f(x)= b-a 0 en otro
Variables aleatorias continuas VARIABLE ALEATORIA UNIFORME Definición Se dice que una variable X tiene una distribución uniforme en el intervalo [a;b] si la fdp de X es: 1 si a x b f(x)= b-a 0 en otro
1. Conceptos de Regresión y Correlación. 2. Variables aleatorias bidimensionales. 3. Ajuste de una recta a una nube de puntos
 TEMA 10 (curso anterior): REGRESIÓN Y CORRELACIÓN 1 Conceptos de Regresión y Correlación 2 Variables aleatorias bidimensionales 3 Ajuste de una recta a una nube de puntos 4 El modelo de la correlación
TEMA 10 (curso anterior): REGRESIÓN Y CORRELACIÓN 1 Conceptos de Regresión y Correlación 2 Variables aleatorias bidimensionales 3 Ajuste de una recta a una nube de puntos 4 El modelo de la correlación
Técnicas Cuantitativas para el Management y los Negocios I
 Técnicas Cuantitativas para el Management y los Negocios I Licenciado en Administración Módulo II: ESTADÍSTICA INFERENCIAL Contenidos Módulo II Unidad 4. Probabilidad Conceptos básicos de probabilidad:
Técnicas Cuantitativas para el Management y los Negocios I Licenciado en Administración Módulo II: ESTADÍSTICA INFERENCIAL Contenidos Módulo II Unidad 4. Probabilidad Conceptos básicos de probabilidad:
TEMA 7 CÁLCULO DE PERIODO DE RETORNO
 Lourdes Bello Mendoza Sara Jane Velázquez Juárez TEMA 7 CÁLCULO DE PERIODO DE RETORNO Introducción La precipitación es la cantidad de agua que llega al suelo ya sea de manera líquida o sólida en forma
Lourdes Bello Mendoza Sara Jane Velázquez Juárez TEMA 7 CÁLCULO DE PERIODO DE RETORNO Introducción La precipitación es la cantidad de agua que llega al suelo ya sea de manera líquida o sólida en forma
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015-coincidente) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 ( puntos) Se considera el sistema de ecuaciones dependiente del parámetro
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 015-coincidente) Selectividad-Opción A Tiempo: 90 minutos Problema 1 ( puntos) Se considera el sistema de ecuaciones dependiente del parámetro
PyE_ EF2_TIPO1_
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD Y ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS COORDINACIÓN DE CIENCIAS APLICADAS DEPARTAMENTO DE PROBABILIDAD Y ESTADÍSTICA SEGUNDO EXAMEN FINAL RESOLUCIÓN
USO DE LAS HERRAMIENTAS ESTADÍSTICAS DE EXCEL EN EL ANÁLISIS DE FRECUENCIAS DE CAUDALES MÁXIMOS
 REVISA ELECRÓICA AFEI DIGIAL Año,., Ene-Jun. 05 USO DE LAS HERRAMIEAS ESADÍSICAS DE EXCEL E EL AÁLISIS DE FRECUECIAS DE CAUDALES MÁXIMOS J. A. Raynal Villaseñor RESUME Se propone el uso de herramientas
REVISA ELECRÓICA AFEI DIGIAL Año,., Ene-Jun. 05 USO DE LAS HERRAMIEAS ESADÍSICAS DE EXCEL E EL AÁLISIS DE FRECUECIAS DE CAUDALES MÁXIMOS J. A. Raynal Villaseñor RESUME Se propone el uso de herramientas
Tema 4: Variables aleatorias. Tema 4: Variables Aleatorias. Tema 4: Variables aleatorias. Objetivos del tema:
 Tema 4: Variables aleatorias Tema 4: Variables Aleatorias Distribución de Bernouilli Distribución Binomial Distribución de Poisson Distribución Exponencial Objetivos del tema: Al final del tema el alumno
Tema 4: Variables aleatorias Tema 4: Variables Aleatorias Distribución de Bernouilli Distribución Binomial Distribución de Poisson Distribución Exponencial Objetivos del tema: Al final del tema el alumno
Distribuciones unidimensionales continuas
 Estadística II Universidad de Salamanca Curso 2011/2012 Outline 1 Distribución uniforme continua 2 Estándar 3 Distribución χ 2 de Pearson 4 Distribución uniforme continua Definición Es una variable continua
Estadística II Universidad de Salamanca Curso 2011/2012 Outline 1 Distribución uniforme continua 2 Estándar 3 Distribución χ 2 de Pearson 4 Distribución uniforme continua Definición Es una variable continua
TH. DE CHEBYSHEV DISTRIB. NORMAL.
 f ( x) 1 2 2 ( x) e 2 2 TH. DE CHEBYSHEV DISTRIB. NORMAL El Desvío Estándar y el Teorema de Chebyshev Es conocida en el área de la probabilidad y estadística, la desigualdad de Chebyshev, matemático Ruso
f ( x) 1 2 2 ( x) e 2 2 TH. DE CHEBYSHEV DISTRIB. NORMAL El Desvío Estándar y el Teorema de Chebyshev Es conocida en el área de la probabilidad y estadística, la desigualdad de Chebyshev, matemático Ruso
UNIVERSIDAD TECNICA PARTICULAR DE LOJA ESTADISTICA Y PROBABILIDAD ENSAYO N 4
 UNIVERSIDAD TECNICA PARTICULAR DE LOJA ESTADISTICA Y PROBABILIDAD ENSAYO N 4 DOCENTE: Ing. Patricio Puchaicela ALUMNA: Andrea C. Puchaicela G. CURSO: 4to. Ciclo de Electrónica y Telecomunicaciones AÑO
UNIVERSIDAD TECNICA PARTICULAR DE LOJA ESTADISTICA Y PROBABILIDAD ENSAYO N 4 DOCENTE: Ing. Patricio Puchaicela ALUMNA: Andrea C. Puchaicela G. CURSO: 4to. Ciclo de Electrónica y Telecomunicaciones AÑO
ANÁLISIS DE REGRESIÓN
 ANÁLISIS DE REGRESIÓN INTRODUCCIÓN Francis Galtón DEFINICIÓN Análisis de Regresión Es una técnica estadística que se usa para investigar y modelar la relación entre variables. Respuesta Independiente Y
ANÁLISIS DE REGRESIÓN INTRODUCCIÓN Francis Galtón DEFINICIÓN Análisis de Regresión Es una técnica estadística que se usa para investigar y modelar la relación entre variables. Respuesta Independiente Y
Agenda 1 Variable aleatoria Continua Valor esperado de una variable aleatoria continua. Varianza. 2
 Curso de nivelación Estadística y Matemática Cuarta clase: Distribuciones de probablidad continuas Programa Técnico en Riesgo, 2016 Agenda 1 Variable aleatoria Continua Valor esperado de una variable aleatoria
Curso de nivelación Estadística y Matemática Cuarta clase: Distribuciones de probablidad continuas Programa Técnico en Riesgo, 2016 Agenda 1 Variable aleatoria Continua Valor esperado de una variable aleatoria
Tema 2 Variables Aleatorias
 Tema 2 Variables Aleatorias Introducción El análisis estructural consiste en determinar la forma en que se comporta una estructura hecha de un material específico ante un sistema de cargas dado, el estudio
Tema 2 Variables Aleatorias Introducción El análisis estructural consiste en determinar la forma en que se comporta una estructura hecha de un material específico ante un sistema de cargas dado, el estudio
INTRODUCCIÓN AL ANÁLISIS DE DATOS ORIENTACIONES (TEMA Nº 8) TEMA Nº 8 ESTIMACIÓN
 OBJETIVOS DE APRENDIZAJE: TEMA Nº 8 ESTIMACIÓN Conocer las relaciones entre muestra, análisis estadístico descriptivo y análisis estadístico inferencial. Conocer los conceptos de muestra aleatoria y muestra
OBJETIVOS DE APRENDIZAJE: TEMA Nº 8 ESTIMACIÓN Conocer las relaciones entre muestra, análisis estadístico descriptivo y análisis estadístico inferencial. Conocer los conceptos de muestra aleatoria y muestra
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos k 1 0 Problema 1 (2 puntos) Se considera la matriz A = 7 k k 1 1 k a) Estudíese para qué
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2016) Selectividad-Opción A Tiempo: 90 minutos k 1 0 Problema 1 (2 puntos) Se considera la matriz A = 7 k k 1 1 k a) Estudíese para qué
Qué es? Primer paso Representación en un sistema de coordenadas. numéricos Cada punto muestra el valor de cada pareja de datos (X e Y)
 Gráfico de dispersión Qué es? Primer paso Representación en un sistema de coordenadas cartesianas de los datos numéricos Cada punto muestra el valor de cada pareja de datos (X e Y) Gráfico de dispersión
Gráfico de dispersión Qué es? Primer paso Representación en un sistema de coordenadas cartesianas de los datos numéricos Cada punto muestra el valor de cada pareja de datos (X e Y) Gráfico de dispersión
Estadística Clase 4. Maestría en Finanzas Universidad del CEMA. Profesor: Alberto Landro Asistente: Julián R. Siri
 Estadística 011 Clase 4 Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri Clase 4 1. Pasos en un proceso estadístico. Inferencia Estadística 3. Estimación Puntual
Estadística 011 Clase 4 Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri Clase 4 1. Pasos en un proceso estadístico. Inferencia Estadística 3. Estimación Puntual
Departamento de Matemática Aplicada a las T.I.C. SOLUCIONES
 Departamento de Matemática Aplicada a las T.I.C. ASIGNATURA: ESTADÍSTICA Y PROCESOS ESTOCÁSTICOS EAMEN FINAL Otoño 25-6 FECHA: 5 de Enero de 26 Fecha publicación notas: 22 de Enero de 26 Fecha revisión
Departamento de Matemática Aplicada a las T.I.C. ASIGNATURA: ESTADÍSTICA Y PROCESOS ESTOCÁSTICOS EAMEN FINAL Otoño 25-6 FECHA: 5 de Enero de 26 Fecha publicación notas: 22 de Enero de 26 Fecha revisión
MATEMÁTICAS II PROBABILIDAD DISTRIBUCIÓN BINOMIAL DISTRIBUCIÓN NORMAL
 MATEMÁTICAS II PROBABILIDAD DISTRIBUCIÓN BINOMIAL DISTRIBUCIÓN NORMAL 1) PROBABILIDAD Experimentos aleatorios. Concepto de espacio muestral y de suceso elemental. Operaciones con sucesos. Leyes de De Morgan.
MATEMÁTICAS II PROBABILIDAD DISTRIBUCIÓN BINOMIAL DISTRIBUCIÓN NORMAL 1) PROBABILIDAD Experimentos aleatorios. Concepto de espacio muestral y de suceso elemental. Operaciones con sucesos. Leyes de De Morgan.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema de ecuaciones dependiente del parámetro real a:
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema de ecuaciones dependiente del parámetro real a:
1. ANTECEDENTES TEÓRICOS
 1. Antecedentes Teóricos 1. ANTECEDENTES TEÓRICOS La planeación y el diseño de obras hidráulicas están relacionados con eventos hidrológicos futuros, cuyo tiempo de ocurrencia o magnitud no pueden predecirse,
1. Antecedentes Teóricos 1. ANTECEDENTES TEÓRICOS La planeación y el diseño de obras hidráulicas están relacionados con eventos hidrológicos futuros, cuyo tiempo de ocurrencia o magnitud no pueden predecirse,
ESTADÍSTICA Y PROBABILIDAD
 (distribución normal) 1 1.- Calcular las probabilidades de los siguientes intervalos, empleando para ello las tablas de la distribución de probabilidad normal estándar N(0, 1): (1) P(z 2 14) (2) P(z 0
(distribución normal) 1 1.- Calcular las probabilidades de los siguientes intervalos, empleando para ello las tablas de la distribución de probabilidad normal estándar N(0, 1): (1) P(z 2 14) (2) P(z 0
Variables aleatorias continuas y Teorema Central del Limite
 Variables aleatorias continuas y Teorema Central del Limite FaMAF 17 de marzo, 2015 Variables aleatorias continuas Definición Una variable aleatoria X se dice (absolutamente continua) si existe f : R R
Variables aleatorias continuas y Teorema Central del Limite FaMAF 17 de marzo, 2015 Variables aleatorias continuas Definición Una variable aleatoria X se dice (absolutamente continua) si existe f : R R
Modelos de probabilidad. Modelos de probabilidad. Modelos de probabilidad. Proceso de Bernoulli. Objetivos del tema:
 Modelos de probabilidad Modelos de probabilidad Distribución de Bernoulli Distribución Binomial Distribución de Poisson Distribución Exponencial Objetivos del tema: Al final del tema el alumno será capaz
Modelos de probabilidad Modelos de probabilidad Distribución de Bernoulli Distribución Binomial Distribución de Poisson Distribución Exponencial Objetivos del tema: Al final del tema el alumno será capaz
Juan Carlos Colonia INFERENCIA ESTADÍSTICA
 Juan Carlos Colonia INFERENCIA ESTADÍSTICA PARÁMETROS Y ESTADÍSTICAS Es fundamental entender la diferencia entre parámetros y estadísticos. Los parámetros se refieren a la distribución de la población
Juan Carlos Colonia INFERENCIA ESTADÍSTICA PARÁMETROS Y ESTADÍSTICAS Es fundamental entender la diferencia entre parámetros y estadísticos. Los parámetros se refieren a la distribución de la población
TEMA: Avenidas. TEMA: Avenidas
 ÍNDICE TEMA: Avenidas Introducción Métodos Métodos empíricos Métodos hidrológicos Métodos estadísticos Correlación con otras cuencas Propagación de avenidas Introducción TEMA: Avenidas Caudal circulante
ÍNDICE TEMA: Avenidas Introducción Métodos Métodos empíricos Métodos hidrológicos Métodos estadísticos Correlación con otras cuencas Propagación de avenidas Introducción TEMA: Avenidas Caudal circulante
BLOQUE III: INFERENCIA ESTADISTICA. X, variable aleatoria de interés sobre una determinada población
 BLOQUE III: INFERENCIA ESTADISTICA TEMA 8. MUESTREO Y DISTRIBUCIONES DE MUESTREO 1. Introducción a la Inferencia Estadística X, variable aleatoria de interés sobre una determinada población Observar el
BLOQUE III: INFERENCIA ESTADISTICA TEMA 8. MUESTREO Y DISTRIBUCIONES DE MUESTREO 1. Introducción a la Inferencia Estadística X, variable aleatoria de interés sobre una determinada población Observar el
SOLUCIÓN EXAMEN IV Nombres: Apellidos: C.I.: Firma: Fecha: 19/11/2004
 Nombres: Apellidos: C.I.: Firma: Fecha: 19/11/004 MÉTODOS ESTADÍSTICOS I EXAMEN IV PARTE I: Encierre con un círculo la respuesta correcta (0,5 puntos c/u): 1. (V F) Los contrastes de hipótesis de dos muestras
Nombres: Apellidos: C.I.: Firma: Fecha: 19/11/004 MÉTODOS ESTADÍSTICOS I EXAMEN IV PARTE I: Encierre con un círculo la respuesta correcta (0,5 puntos c/u): 1. (V F) Los contrastes de hipótesis de dos muestras
Estadística Clase 3. Maestría en Finanzas Universidad del CEMA. Profesor: Alberto Landro Asistente: Julián R. Siri
 Estadística 010 Clase 3 Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri 1. Pasos en un proceso estadístico 1. Plantear una hipótesis sobre una población.. Diseñar
Estadística 010 Clase 3 Maestría en Finanzas Universidad del CEMA Profesor: Alberto Landro Asistente: Julián R. Siri 1. Pasos en un proceso estadístico 1. Plantear una hipótesis sobre una población.. Diseñar
Distribuciones de probabilidad II
 II Facultad de Estudios Superiores Acatlán Licenciatura en Economía 20 de abril 2017 José A. Huitrón Mendoza Distribuciones de probabilidad de Poisson Enmarca el estudio de una variable aleatoria discreta
II Facultad de Estudios Superiores Acatlán Licenciatura en Economía 20 de abril 2017 José A. Huitrón Mendoza Distribuciones de probabilidad de Poisson Enmarca el estudio de una variable aleatoria discreta
