Genera 10 parejas de números. Escríbelos, colocando entre ellos el signo adecuado de desigualdad. Intervalo [ 4,5] (0,3) [ 6,8) ( 7, 1] Desigualdad
|
|
|
- Elvira Valdéz Villalba
- hace 7 años
- Vistas:
Transcripción
1 Hoja de trabajo personal Nº 1. EVALUACIÓN INICIAL Uso de los signos de desigualdad. Genera 10 parejas de números. Escríbelos, colocando entre ellos el signo adecuado de desigualdad. Intervalos sobre la recta real. 1. Escribe como desigualdad los intervalos siguientes: Intervalo [ 4,5] (0,3) [ 6,8) ( 7, 1] Desigualdad 2. Representa sobre la recta real: 2 x 3 Representación [ 5,0] Representación 5 < x < 2 (1,6) 1 x < 2 [ 6, 2) 7 < x 0 ( 3,3] 3. Escribe los intervalos definidos por las siguientes desigualdades: Desigualdad 8 x 1 5 < x < 9 4 x < 0 7 < x 7 Intervalo Representación de rectas en los ejes de coordenadas. Representa las rectas, con la ayuda de una tabla de valores: Recta Tabla Representación: y = x + 1 y = 2x 2 y = 3x 2 y = 2x y = 3x + 2
2 Hoja de trabajo personal Nº 2. RELACIONES DE ORDEN. Relaciones de orden, sumas y restas. 1.- Anota dos números A y B en este orden. Escribe entre ellos la desigualdad que corresponde. 2.- Suma a cada uno de ellos la cantidad que desees (la misma para ambos). Anota los resultados en el mismo orden (el resultado obtenido de A a la izquierda), y escribe entre ellos la desigualdad correspondiente. 3.- Resta cada uno de ellos la cantidad que desees (la misma para ambos). Anota los resultados también por orden, y escribe entre ellos la desigualdad correspondiente. Repite el proceso con nuevos números tres veces: A desigualdad B Qué ocurre al sumar? Qué ocurre al restar? Escribe la regla general: En una desigualdad, sumar o restar una misma cantidad a cada lado... Relaciones de orden y producto por una cantidad positiva. 1.- Anota dos números A y B en este orden. Escribe entre ellos la desigualdad que corresponde. 2.- Multiplica cada uno de ellos por la misma cantidad positiva. Anota los resultados en el mismo orden (el resultado obtenido de A a la izquierda), y escribe entre ellos la desigualdad correspondiente. Repite el proceso con nuevos números tres veces: A desigualdad B Qué ocurre al multiplicar por la misma cantidad positiva? Escribe la regla general: En una desigualdad, multiplicar por una misma cantidad positiva a cada lado... Relaciones de orden y producto por una cantidad negativa. 1.- Anota dos números A y B en este orden. Escribe entre ellos la desigualdad que corresponde. 2.- Multiplica cada uno de ellos por la misma cantidad negativa. Anota los resultados en el mismo orden (el resultado obtenido de A a la izquierda), y escribe entre ellos la desigualdad correspondiente. Repite el proceso con nuevos números tres veces: A desigualdad B Qué ocurre al multiplicar por la misma cantidad negativa? Escribe la regla general: En una desigualdad, multiplicar por una misma cantidad negativa a cada lado...
3 Hoja de trabajo personal Nº 3. INECUACIONES DE PRIMER GRADO. Resuelve el ejemplo 1. 5x + 7 2x +13 Resuelve el ejemplo 2. x 3 x < Resuelve el ejemplo 3. 2x + 4 x 3x + < Resuelve las inecuaciones siguientes: a) 2x + 3(x+1) 23 b) 4 x 1 x + 1 < 3 2 c) 2x + 1 x x 2 d) 3 x 4 2x 1 x e) 4 x 3 x x x
4 Hoja de trabajo personal Nº 4. RESOL. INECUACIONES PRIMER GRADO. Resuelve gráficamente las inecuaciones siguientes. Recta Tabla y operaciones Representación: Solución 2x + 3 < 0 x x x + 4 > 3 5x 0 2x > 0 Resuelve analíticamente las siguientes inecuaciones. Inecuación Resolución y solución Inecuación Resolución y solución 2x + 5 < 0 2x + 7 > 3 3x x 0 2x x > 0 Resuelve por el método que prefieras. x + 2 < 1+ 5 x 2 5x 2 x 8 x + 14 > x + 4 x 4 3x x 1 x 2 2 4
5 Hoja de trabajo personal Nº 5. INECUACIONES DE SEGUNDO GRADO. Desarrolla en la hoja de trabajo los ejemplos siguientes. Ejemplo Operaciones y factorización Ejemplo Operaciones y factorización x 2 + 7x x 2 3x + 2 2x 2 10x x 2 3x 10 Halla el vértice de las siguientes parábolas. Parábola Vértice Parábola Vértice Parábola Vértice y = x 2 4 y = x 2 5x +4 y = x 2 +2x +3 Representa gráficamente las parábolas que siguen. y = x 2 1 y = x 2 2,5x +1,5 y = x 2 +5x 4
6 Hoja de trabajo personal Nº 6. RESOL. INEC. DE SEGUNDO GRADO. Resuelve gráficamente. x 2 4 < 0 x 2 5x x 2 +2x +3 0 Resuelve analíticamente. x 2 4 < 0 x 2 5x x 2 +2x +3 0
7 Hoja de trabajo personal Nº 7. INECUACIONES CON COCIENTES. Resuelve las siguientes inecuaciones con cocientes. x + 5 < 0 x 2 3 x 0 x + 4 x 0 x + 6 x 3 0 x + 1
8 Hoja de trabajo personal Nº 8. ACTIVIDADES FINALES I. Resuelve las inecuaciones de primer grado que siguen. 2x 1 x 3 x x 5 4 x x 2 a) + 1 b) > x x + 1 x x x + 1 x + 1 d) + + > 3 e) c) 2(5x + 3) 5 x 1 4 2
9 Hoja de trabajo personal Nº 9. ACTIVIDADES FINALES II. Resuelve las inecuaciones de segundo grado que siguen. a) x 2 x 6 0 b) x 2 25 > 0 c) x > 0 d) x 2 +5x 6 0 e) x 2 6x 7 > 0
10 Hoja de trabajo personal Nº 10. ACTIVIDADES FINALES III. Resuelve las siguientes inecuaciones con cocientes. x + 3 a) < 0 x + 2 x b) > 0 x 5 x + 6 c) 0 x 1 2 x d) 0 x 5 x e) > 0 x + 5
TEMA 4 NÚMEROS ENTEROS
 TEMA 4 NÚMEROS ENTEROS 1 2 3 Recta numérica. -9-8 -7-6 -5-4 -3-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 Enteros negativos A la izquierda del 0 están los números enteros negativos Enteros positivos A la derecha
TEMA 4 NÚMEROS ENTEROS 1 2 3 Recta numérica. -9-8 -7-6 -5-4 -3-2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 Enteros negativos A la izquierda del 0 están los números enteros negativos Enteros positivos A la derecha
Desigualdades o inecuaciones lineales en una variable. Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo
 Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,, para representar
Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,, para representar
INTERVALOS Y SEMIRRECTAS.
 el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
Desigualdades o Inecuaciones Desigualdades lineales en una variable
 Desigualdades o Inecuaciones Desigualdades lineales en una variable Una desigualdad, es una oración que incluye un signo de desigualdad. Los signos de desigualdad son: ,,. (Estos se leen: menor que,
Desigualdades o Inecuaciones Desigualdades lineales en una variable Una desigualdad, es una oración que incluye un signo de desigualdad. Los signos de desigualdad son: ,,. (Estos se leen: menor que,
EXAMEN DE MATEMÁTICAS APLICADAS I
 EXAMEN DE MATEMÁTICAS APLICADAS I 1 Calcula y simplifica: a (0,4 puntos 1 6 : (0, puntos ( 4x 1 4x( x x (0,7 puntos Factoriza el polinomio P( x (0,9 puntos Simplifica las siguientes fracciones algebraicas:
EXAMEN DE MATEMÁTICAS APLICADAS I 1 Calcula y simplifica: a (0,4 puntos 1 6 : (0, puntos ( 4x 1 4x( x x (0,7 puntos Factoriza el polinomio P( x (0,9 puntos Simplifica las siguientes fracciones algebraicas:
EXAMEN DE INECUACIONES Y SUS SISTEMAS
 EXAMEN DE INECUACIONES Y SUS SISTEMAS Se recomienda: a) Antes de hacer algo, leer todo el examen. b) Resolver antes las preguntas que se te den mejor. c) Responde a cada parte del examen en una hoja distinta.
EXAMEN DE INECUACIONES Y SUS SISTEMAS Se recomienda: a) Antes de hacer algo, leer todo el examen. b) Resolver antes las preguntas que se te den mejor. c) Responde a cada parte del examen en una hoja distinta.
1º Bachillerato Capítulo 2: Inecuaciones
 Matemáticas Aplicadas a las Ciencias Sociales I 1º Bachillerato Capítulo 2: Inecuaciones 43 Índice 2. INECUACIONES DE PRIMER Y SEGUNDO GRADO 2.3. RESOLUCIÓN DE INECUACIONES DE PRIMER GRADO Y SU INTERPRETACIÓN
Matemáticas Aplicadas a las Ciencias Sociales I 1º Bachillerato Capítulo 2: Inecuaciones 43 Índice 2. INECUACIONES DE PRIMER Y SEGUNDO GRADO 2.3. RESOLUCIÓN DE INECUACIONES DE PRIMER GRADO Y SU INTERPRETACIÓN
Desigualdades lineales en una variable. Prof. Anneliesse Sánchez Adaptada por Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo
 Desigualdades lineales en una variable Prof. Anneliesse Sánchez Adaptada por Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades o Inecuaciones Una desigualdad, es una oración
Desigualdades lineales en una variable Prof. Anneliesse Sánchez Adaptada por Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades o Inecuaciones Una desigualdad, es una oración
Clase 6 Tema: Solución de un sistema de ecuaciones por sustitución
 Matemáticas 9 Bimestre: II Número de clase: 6 Clase 6 Tema: Solución de un sistema de ecuaciones por sustitución Actividad 0 Observe la manera en la que se solucionó el sistema de ecuaciones. 4 + = 8 +
Matemáticas 9 Bimestre: II Número de clase: 6 Clase 6 Tema: Solución de un sistema de ecuaciones por sustitución Actividad 0 Observe la manera en la que se solucionó el sistema de ecuaciones. 4 + = 8 +
FUNCIÓN. La Respuesta correcta es D
 FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
Desigualdades lineales en una variable. Prof. Anneliesse Sánchez Adaptada por Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo
 Desigualdades lineales en una variable Prof. Anneliesse Sánchez Adaptada por Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades o Inecuaciones Una inecuación o desigualdad,
Desigualdades lineales en una variable Prof. Anneliesse Sánchez Adaptada por Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades o Inecuaciones Una inecuación o desigualdad,
Unidad #1: DESIGUALDAD o inecuaciones COLEGIO BENIGNO TOMÁS ARGOTE UNIDAD # 1
 ÁREA: Algebra COLEGIO BENIGNO TOMÁS ARGOTE UNIDAD # 1 ASIGNATURA: Matemática. NIVEL: Duodécimo grado ( CIENCIAS ) PROFESOR: José Alexander Echeverría Ruiz TRIMESTRE: I TÍTULO DE LA UNIDAD DIDÁCTICA: 1.
ÁREA: Algebra COLEGIO BENIGNO TOMÁS ARGOTE UNIDAD # 1 ASIGNATURA: Matemática. NIVEL: Duodécimo grado ( CIENCIAS ) PROFESOR: José Alexander Echeverría Ruiz TRIMESTRE: I TÍTULO DE LA UNIDAD DIDÁCTICA: 1.
Desigualdades o inecuaciones lineales en una variable
 Desigualdades o inecuaciones lineales en una variable Sec 3.5 3.6 Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,,
Desigualdades o inecuaciones lineales en una variable Sec 3.5 3.6 Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,,
Revisora: María Molero
 57 Capítulo 5: INECUACIONES. Matemáticas 4ºB ESO 1. INTERVALOS 1.1. Tipos de intervalos Intervalo abierto: I = (a, b) = {x a < x < b}. Intervalo cerrado: I = [a, b] = {x a x b}. Intervalo semiabierto por
57 Capítulo 5: INECUACIONES. Matemáticas 4ºB ESO 1. INTERVALOS 1.1. Tipos de intervalos Intervalo abierto: I = (a, b) = {x a < x < b}. Intervalo cerrado: I = [a, b] = {x a x b}. Intervalo semiabierto por
4º ESO ACADÉMICAS INECUACIONES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa INECUACIONES
 INECUACIONES.- DESIGUALDADES E INECUACIONES Mientras que en una ecuación se trata de buscar el valor que hace que sean iguales dos epresiones algebraicas, en las inecuaciones intentamos localizar los valores
INECUACIONES.- DESIGUALDADES E INECUACIONES Mientras que en una ecuación se trata de buscar el valor que hace que sean iguales dos epresiones algebraicas, en las inecuaciones intentamos localizar los valores
Tema 1: NUMEROS ENTEROS
 COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS 1º ESO. NÚMEROS ENTEROS Tema 1: NUMEROS ENTEROS Los números enteros (representados por la letra Z), son un conjunto de número
COLEGIO EL LIMONAR. MÁLAGA DEPARTAMENTO DE MÁTEMÁTICAS RELACIONES DE EJERCICIOS 1º ESO. NÚMEROS ENTEROS Tema 1: NUMEROS ENTEROS Los números enteros (representados por la letra Z), son un conjunto de número
EJERCICIOS RESUELTOS DE SISTEMAS DE INECUACIONES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones y de inecuaciones EJERCICIOS RESUELTOS DE SISTEMAS DE INECUACIONES 1. Resolver el sistema de inecuaciones + 5 4 0 3 4 + 8 < 3( 1) Se
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones y de inecuaciones EJERCICIOS RESUELTOS DE SISTEMAS DE INECUACIONES 1. Resolver el sistema de inecuaciones + 5 4 0 3 4 + 8 < 3( 1) Se
Chapter Audio Summary for McDougal Littell Pre-Algebra
 Chapter Audio Summary for McDougal Littell Pre-Algebra Chapter 5 Rational Numbers and Equations En el capítulo 5 aprendiste a escribir, comparar y ordenar números racionales. Después aprendiste a sumar
Chapter Audio Summary for McDougal Littell Pre-Algebra Chapter 5 Rational Numbers and Equations En el capítulo 5 aprendiste a escribir, comparar y ordenar números racionales. Después aprendiste a sumar
1 LAS PROPIEDADES DE LOS NÚMEROS REALES SOBRE OPERACIONES BÁSICAS
 LAS PROPIEDADES DE LOS NÚMEROS REALES SOBRE OPERACIONES BÁSICAS Afectan directamente a los procesos de simplificación de operaciones con números, con expresiones algebraicas y a los procesos de solución
LAS PROPIEDADES DE LOS NÚMEROS REALES SOBRE OPERACIONES BÁSICAS Afectan directamente a los procesos de simplificación de operaciones con números, con expresiones algebraicas y a los procesos de solución
Divisibilidad I. Nombre Curso Fecha
 Matemáticas 2.º ESO Unidad 1 Ficha 1 Divisibilidad I Un número b es divisor de otro número a si al dividir a entre b la división es exacta. Se dice también que a es múltiplo de b. 1. Completa con la palabra
Matemáticas 2.º ESO Unidad 1 Ficha 1 Divisibilidad I Un número b es divisor de otro número a si al dividir a entre b la división es exacta. Se dice también que a es múltiplo de b. 1. Completa con la palabra
Solucionario Unidad 6: Inecuaciones
 Solucionario Unidad 6: Inecuaciones Ejercicio 1 Resuelve las siguientes inecuaciones: a 0 La ecuación correspondiente no tiene solución, por tanto, las soluciones de la inecuación son todos los números
Solucionario Unidad 6: Inecuaciones Ejercicio 1 Resuelve las siguientes inecuaciones: a 0 La ecuación correspondiente no tiene solución, por tanto, las soluciones de la inecuación son todos los números
EXAMEN DE INECUACIONES Y SUS SISTEMAS
 EXAMEN DE INECUACIONES Y SUS SISTEMAS Se recomienda: a) Antes de hacer algo, leer todo el examen. b) Resolver antes las preguntas que se te den mejor. c) Responde a cada parte del examen en una hoja distinta.
EXAMEN DE INECUACIONES Y SUS SISTEMAS Se recomienda: a) Antes de hacer algo, leer todo el examen. b) Resolver antes las preguntas que se te den mejor. c) Responde a cada parte del examen en una hoja distinta.
1. x = 2. Solución : x = 2 o x = x = 2. Solución x = 2 o x= x = 0. Solución: x = 0
 Problemas que involucran igualdades con valor absoluto. x =. Solución : x = o x = -. x =. Solución x = o x= -.. x = 0. Solución: x = 0. x =. No hay solución posible. No existen valores absolutos negativos.
Problemas que involucran igualdades con valor absoluto. x =. Solución : x = o x = -. x =. Solución x = o x= -.. x = 0. Solución: x = 0. x =. No hay solución posible. No existen valores absolutos negativos.
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 1º Año Ciclo Básico de Secundaria Teoría Nº 2 Segundo Trimestre
 CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
CONJUNTO DE LOS NÚMEROS ENTEROS Los números enteros están formados por: los números naturales (o enteros positivos y el cero) y los números negativos. El cero no tiene signo, no es ni positivo ni negativo.
Inecuaciones con valor absoluto
 Inecuaciones con valor absoluto El valor absoluto de un número real a se denota por a y está definido por: Propiedades a a si a si a 0 a < 0 i a y b son números reales y n es un número entero, entonces:
Inecuaciones con valor absoluto El valor absoluto de un número real a se denota por a y está definido por: Propiedades a a si a si a 0 a < 0 i a y b son números reales y n es un número entero, entonces:
UNIDAD DIDÁCTICA #1 CONTENIDO
 UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
UNIDAD DIDÁCTICA #1 CONTENIDO OPERACIONES CON DECIMALES MULTIPLICACION DE DECIMALES DIVISIÓN DE DECIMALES OPERACIONES COMBINADAS CON DECIMALES POTENCIACIÓN DE DECIMALES HOJA DE EVALUACIÓN BIBLIOGRAFÍA
1. (2 puntos) Escribe la expresión analítica de cada una de las siguientes funciones: a)
 Departamento de Matemáticas III Control º Nivel: 4º ESO B Fecha: 0 de abril de 00. ( puntos) Escribe la epresión analítica de cada una de las siguientes funciones: a) b) c). ( puntos) Representa la siguiente
Departamento de Matemáticas III Control º Nivel: 4º ESO B Fecha: 0 de abril de 00. ( puntos) Escribe la epresión analítica de cada una de las siguientes funciones: a) b) c). ( puntos) Representa la siguiente
Inecuaciones lineales y cuadráticas
 Inecuaciones lineales y cuadráticas 0.1. Inecuaciones lineales Una inecuación lineal tiene la forma ax + b < 0 ó ax + b > 0 ó ax + b 0 ó ax + b 0. El objetivo consiste en hallar el conjunto solución de
Inecuaciones lineales y cuadráticas 0.1. Inecuaciones lineales Una inecuación lineal tiene la forma ax + b < 0 ó ax + b > 0 ó ax + b 0 ó ax + b 0. El objetivo consiste en hallar el conjunto solución de
FUNDAMENTOS NUMÉRICOS SEMANA 4
 FUNDAMENTOS NUMÉRICOS SEMANA 4 ÍNDICE INECUACIONES Y DESIGUALDADES... 3 APRENDIZAJES ESPERADOS... 3 INTRODUCCIÓN... 3 INECUACIONES... 4 REGLAS DE LAS DESIGUALDADES... 4 INECUACIONES LINEALES... 5 INECUACIONES
FUNDAMENTOS NUMÉRICOS SEMANA 4 ÍNDICE INECUACIONES Y DESIGUALDADES... 3 APRENDIZAJES ESPERADOS... 3 INTRODUCCIÓN... 3 INECUACIONES... 4 REGLAS DE LAS DESIGUALDADES... 4 INECUACIONES LINEALES... 5 INECUACIONES
MATEMÁTICAS 1º BACHILLERATO Curso EJERCICIOS RESUELTOS DE INECUACIONES
 MATEMÁTICAS 1º BACHILLERATO Curso 9-1 EJERCICIOS RESUELTOS DE INECUACIONES EJERCICIOS RESUELTOS DE INECUACIONES A. Inecuaciones lineales con una incógnita x x1 x3 > 1 3 4 x x1 x3 4( x ) 3( x1) 6( x3) 1
MATEMÁTICAS 1º BACHILLERATO Curso 9-1 EJERCICIOS RESUELTOS DE INECUACIONES EJERCICIOS RESUELTOS DE INECUACIONES A. Inecuaciones lineales con una incógnita x x1 x3 > 1 3 4 x x1 x3 4( x ) 3( x1) 6( x3) 1
INTERVALOS, DESIGUALDADES Y VALOR ABSOLUTO
 INTERVALOS INTERVALOS, DESIGUALDADES Y VALOR ABSOLUTO Los Intervalos son una herramienta matemática que se utiliza para delimitar un conjunto determinado de números reales. Por ejemplo el intervalo [-5,3]
INTERVALOS INTERVALOS, DESIGUALDADES Y VALOR ABSOLUTO Los Intervalos son una herramienta matemática que se utiliza para delimitar un conjunto determinado de números reales. Por ejemplo el intervalo [-5,3]
Colegio Portocarrero. Curso Departamento de matemáticas. Ejercicios tipo 1-2 de selectividad. ( años )
 Colegio Portocarrero. Curso 04-05. Ejercicios tipo - de selectividad ( años 005-007) Cuaderno de verano º Bachillerato mates aplicadas. Alumno: Cuaderno de verano º Bachillerato, matemáticas aplicadas.
Colegio Portocarrero. Curso 04-05. Ejercicios tipo - de selectividad ( años 005-007) Cuaderno de verano º Bachillerato mates aplicadas. Alumno: Cuaderno de verano º Bachillerato, matemáticas aplicadas.
REPASO DE ÁLGEBRA PRIMERA PARTE: RADICALES, LOGARITMOS Y POLINOMIOS
 Ejercicio nº.- Simplifica: REPASO DE ÁLGEBRA PRIMERA PARTE: RADICALES, LOGARITMOS Y POLINOMIOS a) b) a a Ejercicio nº.- Epresa en forma de intervalo las soluciones de la desigualdad: El intervalo [, 6].
Ejercicio nº.- Simplifica: REPASO DE ÁLGEBRA PRIMERA PARTE: RADICALES, LOGARITMOS Y POLINOMIOS a) b) a a Ejercicio nº.- Epresa en forma de intervalo las soluciones de la desigualdad: El intervalo [, 6].
8.1. Traslación de puntos. Investigación: Figuras en movimiento CONDENSADA
 LECCIÓN CONDENSADA 8.1 Traslación de puntos En esta lección trasladarás figuras en el plano de coordenadas definirás una traslación al describir cómo afecta un punto general (, ) Una regla matemática que
LECCIÓN CONDENSADA 8.1 Traslación de puntos En esta lección trasladarás figuras en el plano de coordenadas definirás una traslación al describir cómo afecta un punto general (, ) Una regla matemática que
3.2 Calcula el número de soluciones de las siguientes ecuaciones SIN resolverlas: d) 2x 2 + 8x + 8 = 0 e) x 2 + 2x + 4 = 0 f) x 2 x + 1 = 0
 3. ECUACIONES, INECUACIONES Y SISTEMAS: Ecuaciones polinómicas, logarítmicas, exponenciales e irracionales. Sistemas de ecuaciones lineales y no lineales. Inecuaciones 3.1 Resuelve las siguientes ecuaciones:
3. ECUACIONES, INECUACIONES Y SISTEMAS: Ecuaciones polinómicas, logarítmicas, exponenciales e irracionales. Sistemas de ecuaciones lineales y no lineales. Inecuaciones 3.1 Resuelve las siguientes ecuaciones:
Colegio Portocarrero. Curso Departamento de matemáticas. Números Reales.
 Números Reales. Lo primero que hemos hecho en este primer curso de bachillerato, es repasar lo visto en cursos anteriores, para resolver cualquier duda que pudiésemos tener, y asentar bien la base, para
Números Reales. Lo primero que hemos hecho en este primer curso de bachillerato, es repasar lo visto en cursos anteriores, para resolver cualquier duda que pudiésemos tener, y asentar bien la base, para
1. dejar a una lado de la igualdad la expresión que contenga una raíz.
 1. Resuelve las siguientes ecuaciones reales: Solución x 1 + x = 0 ; 3 x = 3 ; ln(x 1) + 4 = ln 3 Ecuaciones con raíces: No todas las ecuaciones de este tipo son sencillas de resolver, pero podemos intentar
1. Resuelve las siguientes ecuaciones reales: Solución x 1 + x = 0 ; 3 x = 3 ; ln(x 1) + 4 = ln 3 Ecuaciones con raíces: No todas las ecuaciones de este tipo son sencillas de resolver, pero podemos intentar
Colegio Beato Carlos Manuel Rodríguez Departamento de Matemáticas. Mapa curricular Pre-Cálculo 12 mo grado
 Colegio Beato Carlos Manuel Rodríguez Departamento de Matemáticas Mapa curricular Pre-Cálculo 12 mo grado Colegio Beato Carlos Manuel Rodríguez Mapa curricular Pre-Cálculo 12 mo grado periodo contenido
Colegio Beato Carlos Manuel Rodríguez Departamento de Matemáticas Mapa curricular Pre-Cálculo 12 mo grado Colegio Beato Carlos Manuel Rodríguez Mapa curricular Pre-Cálculo 12 mo grado periodo contenido
Ordenada en el origen: Es el valor de la función cuando la variable x es 0 También llamado corte con el eje de ordenadas o corte Oy.
 Función polinómica: La función polinómica está compuesta por una serie de operaciones; sumas, restas, productos potencias. Todas ellas están perfectamente definidas en el conjunto de los números reales.
Función polinómica: La función polinómica está compuesta por una serie de operaciones; sumas, restas, productos potencias. Todas ellas están perfectamente definidas en el conjunto de los números reales.
COLEGIO NUESTRA SEÑORA DEL CARMEN HATILLO, PUERTO RICO
 MATERIA: Matemática 6to grado MES/AÑO: agosto septiembre 2015 LIBRO: Matemáticas para Crecer (Santillana) DIAS agosto 10-14 17-21 -escribirá en palabras los números. -escribirá números cardinales en notación
MATERIA: Matemática 6to grado MES/AÑO: agosto septiembre 2015 LIBRO: Matemáticas para Crecer (Santillana) DIAS agosto 10-14 17-21 -escribirá en palabras los números. -escribirá números cardinales en notación
Como introducción a este tema se te propone que resuelvas el siguiente problema utilizando el tradicional sistema de tanteo.
 Como introducción a este tema se te propone que resuelvas el siguiente problema utilizando el tradicional sistema de tanteo. Busca todos los números reales que al sumarlos, por separado, a tu edad den
Como introducción a este tema se te propone que resuelvas el siguiente problema utilizando el tradicional sistema de tanteo. Busca todos los números reales que al sumarlos, por separado, a tu edad den
GUÍAS DE ESTUDIO. Programa de alfabetización, educación básica y media para jóvenes y adultos
 GUÍAS DE ESTUDIO Código PGA-02-R02 1 INSTITUCIÓN EDUCATIVA CASD Programa de alfabetización, educación básica y media para jóvenes y adultos UNIDAD DE TRABAJO Nº 1 PERIODO 1 1. ÁREA INTEGRADA: MATEMÁTICAS
GUÍAS DE ESTUDIO Código PGA-02-R02 1 INSTITUCIÓN EDUCATIVA CASD Programa de alfabetización, educación básica y media para jóvenes y adultos UNIDAD DE TRABAJO Nº 1 PERIODO 1 1. ÁREA INTEGRADA: MATEMÁTICAS
REPRESENTACIÓN DE CURVAS - CCSS
 REPRESENTACIÓN DE CURVAS - CCSS Esquema Para representar gráficamente una función se debe estudiar: 1. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
REPRESENTACIÓN DE CURVAS - CCSS Esquema Para representar gráficamente una función se debe estudiar: 1. Dominio. Puntos de corte con los ejes coordenados. Paridad y periodicidad 4. Asíntotas 5. Monotonía
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es 1 Índice 1. Definiciones 3 2. Herramientas 5 2.1. Factorización de polinomios: Regla
de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es 1 Índice 1. Definiciones 3 2. Herramientas 5 2.1. Factorización de polinomios: Regla
INDICE Capitulo 1. Ecuaciones Fundamentos Teóricos Capitulo 2. Polinomios
 INDICE Prólogo X Introducción XI Capitulo 1. Ecuaciones 1 Revisión de Álgebra Elemental 1 1. Conceptos Básicos 1 1.a. Expresión algebraica 1, 1.b. Valor numérico de un polinomio 2 2. Operaciones con Polinomios
INDICE Prólogo X Introducción XI Capitulo 1. Ecuaciones 1 Revisión de Álgebra Elemental 1 1. Conceptos Básicos 1 1.a. Expresión algebraica 1, 1.b. Valor numérico de un polinomio 2 2. Operaciones con Polinomios
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros. Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros. Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Alumno/a:... Lo primero que debes tener en cuenta cuando trabajes con radicales es que no son más que potencias con exponente fraccionario.
 Hoja Cálculos con radicales Calificación Alumno/a:... Curso: º E.S.O. A Definición de radical Lo primero que debes tener en cuenta cuando trabajes con radicales es que no son más que potencias con exponente
Hoja Cálculos con radicales Calificación Alumno/a:... Curso: º E.S.O. A Definición de radical Lo primero que debes tener en cuenta cuando trabajes con radicales es que no son más que potencias con exponente
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones
 Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
Ecuaciones e inecuaciones. Sistemas de ecuaciones e inecuaciones Álvarez S., Caballero M.V. y Sánchez M. a M. salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Herramientas 6 1.1. Factorización
REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_ DE 6
 REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_2016 1 DE 6 Nombre: Fecha: REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_2016 2 DE 6 REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_2016 3 DE 6 VOCABULARIO
REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_2016 1 DE 6 Nombre: Fecha: REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_2016 2 DE 6 REPASO_RECUPERACION_III_PERIODO_MATEMATICAS_9_2016 3 DE 6 VOCABULARIO
Operaciones de números racionales
 Operaciones de números racionales Yuitza T. Humarán Martínez Adapatado por Caroline Rodriguez Departamento de Matemáticas Universidad de Puerto Rico en Arecibo El conjunto de los números racionales consiste
Operaciones de números racionales Yuitza T. Humarán Martínez Adapatado por Caroline Rodriguez Departamento de Matemáticas Universidad de Puerto Rico en Arecibo El conjunto de los números racionales consiste
Guía de Matemática NM 3: Inecuaciones
 Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Guía de Matemática NM : Inecuaciones Nombre(s): Curso: Fecha. Contenido:
Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Guía de Matemática NM : Inecuaciones Nombre(s): Curso: Fecha. Contenido:
Inecuaciones: Actividades de recuperación.
 Inecuaciones: Actividades de recuperación. 1.- Escribe la inecuación que corresponde a los siguientes enunciados: a) El perímetro de un triángulo equilátero es menor que 4. (x = lado del triángulo) b)
Inecuaciones: Actividades de recuperación. 1.- Escribe la inecuación que corresponde a los siguientes enunciados: a) El perímetro de un triángulo equilátero es menor que 4. (x = lado del triángulo) b)
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS
 TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
TEMA 2: NÚMEROS ENTEROS 1º ESO. MATEMÁTICAS Por qué aparecen los números enteros? Por qué aparecen los números enteros? La cueva de Voronia, es la cueva conocida más profunda de la Tierra, localizada
UAH. FACULTAD DE CIENCIAS ECONÓMICAS ACTUALIZACIÓN DE CONOCIMIENTOS MATEMÁTICOS EXAMEN FINAL JULIO a) Halla los siguientes límites: 2 + 3x
 UAH FACULTAD DE CIENCIAS ECONÓMICAS ACTUALIZACIÓN DE CONOCIMIENTOS MATEMÁTICOS EXAMEN FINAL JULIO 0 Observación: Cada respuesta correcta vale punto a) Una serie de números se define como sigue: a ; a +
UAH FACULTAD DE CIENCIAS ECONÓMICAS ACTUALIZACIÓN DE CONOCIMIENTOS MATEMÁTICOS EXAMEN FINAL JULIO 0 Observación: Cada respuesta correcta vale punto a) Una serie de números se define como sigue: a ; a +
TEMA 7. FUNCIONES ELEMENTALES
 TEMA 7. FUNCIONES ELEMENTALES 8.1. Funciones cuya gráfica es una recta. - Función constante. - Función de proporcionalidad. - Función lineal. - Pendiente. 8.2. Función cuadrática. - Representación gráfica
TEMA 7. FUNCIONES ELEMENTALES 8.1. Funciones cuya gráfica es una recta. - Función constante. - Función de proporcionalidad. - Función lineal. - Pendiente. 8.2. Función cuadrática. - Representación gráfica
FUNCIONES RECUERDE QUE EL USO DE GRAFICADORES ES UNA HERRAMIENTA ÚTIL PARA CORROBORAR SUS RESULTADOS
 FUNCIONES mathspace.jimdo@gmail.com www.mathspace.jimdo.com RECUERDE QUE EL USO DE GRAFICADORES ES UNA HERRAMIENTA ÚTIL PARA CORROBORAR SUS RESULTADOS 1. Eprese la regla dada en forma de función y determine
FUNCIONES mathspace.jimdo@gmail.com www.mathspace.jimdo.com RECUERDE QUE EL USO DE GRAFICADORES ES UNA HERRAMIENTA ÚTIL PARA CORROBORAR SUS RESULTADOS 1. Eprese la regla dada en forma de función y determine
Repaso para el dominio de la materia
 LECCIÓN 0.5 Repaso para el dominio de la materia Usar con las páginas 685 a 690 OBJETIVO Resolver ecuaciones cuadráticas completando el cuadrado. Vocabulario En una epresión de la forma 2 b, puedes sumar
LECCIÓN 0.5 Repaso para el dominio de la materia Usar con las páginas 685 a 690 OBJETIVO Resolver ecuaciones cuadráticas completando el cuadrado. Vocabulario En una epresión de la forma 2 b, puedes sumar
5.1 Números Reales Mate 3041 Milena Salcedo V. Copyright Cengage Learning. All rights reserved.
 5.1 Números Reales Mate 3041 Milena Salcedo V R Copyright Cengage Learning. All rights reserved. Números Reales Números Naturales: N = 1,2,3, Números Enteros no negativos (Cardinales): 0,1,2,3, Números
5.1 Números Reales Mate 3041 Milena Salcedo V R Copyright Cengage Learning. All rights reserved. Números Reales Números Naturales: N = 1,2,3, Números Enteros no negativos (Cardinales): 0,1,2,3, Números
Dos inecuaciones se dice que son equivalentes cuando ambas tienen las mismas soluciones.
 10. INECUACIONES Definición de inecuación Una inecuación es una desigualdad entre dos expresiones algebraicas. 2x + 3 < 5 ; x 2 5x > 6 ; x x 1 0 Inecuaciones equivalentes Dos inecuaciones se dice que son
10. INECUACIONES Definición de inecuación Una inecuación es una desigualdad entre dos expresiones algebraicas. 2x + 3 < 5 ; x 2 5x > 6 ; x x 1 0 Inecuaciones equivalentes Dos inecuaciones se dice que son
PAUTA ACTIVIDADES: PROPIEDADES DE LAS POTENCIAS DE BASE ENTERA Y EXPONENTE NATURAL
 PAUTA ACTIVIDADES: PROPIEDADES DE LAS POTENCIAS DE BASE ENTERA Y EXPONENTE NATURAL I. Antes de partir, resuelve los siguientes ejercicios utilizando propiedades de las potencias de base y exponente natural:
PAUTA ACTIVIDADES: PROPIEDADES DE LAS POTENCIAS DE BASE ENTERA Y EXPONENTE NATURAL I. Antes de partir, resuelve los siguientes ejercicios utilizando propiedades de las potencias de base y exponente natural:
Desigualdades o inecuaciones lineales en una variable. Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo
 Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Usamos los símbolos de una desigualdad son: ,, para representar
Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Usamos los símbolos de una desigualdad son: ,, para representar
UNIDAD 2. INECUACIONES Y SISTEMAS DE INECUACIONES
 UNIDAD. INECUACIONES Y SISTEMAS DE INECUACIONES Actividad a) Soluciones: = y =. b) Soluciones: = y =. Actividad Soluciones: = y =. Actividad a) Por ejemplo ; ;. b) 8 > ; > ; >. c) < ; < 8; < 7. Actividad
UNIDAD. INECUACIONES Y SISTEMAS DE INECUACIONES Actividad a) Soluciones: = y =. b) Soluciones: = y =. Actividad Soluciones: = y =. Actividad a) Por ejemplo ; ;. b) 8 > ; > ; >. c) < ; < 8; < 7. Actividad
MATEMÁTICAS Versión impresa INECUACIONES
 MATEMÁTICAS Versión impresa INECUACIONES 1. INTRODUCCIÓN Imaginen que queremos abrir una nueva librería en el centro de la ciudad. Y que tenemos un presupuesto de 800 $ como máximo para comprar los libros.
MATEMÁTICAS Versión impresa INECUACIONES 1. INTRODUCCIÓN Imaginen que queremos abrir una nueva librería en el centro de la ciudad. Y que tenemos un presupuesto de 800 $ como máximo para comprar los libros.
Tema 1. Racionales 2 2'4 0'1 2'1 1'15 3'1 1' Representa en la recta racional las siguientes fracciones:
 Tema 1. Racionales 1.- Representa en la recta racional las siguientes fracciones: -1 y 4 b) - y 1. Calcula el valor de las siguientes expresiones: 7 5 4 1 4 b ) : c ) d) 8 4 1 5 5 : : 10 7 9 7 5 6 1 6
Tema 1. Racionales 1.- Representa en la recta racional las siguientes fracciones: -1 y 4 b) - y 1. Calcula el valor de las siguientes expresiones: 7 5 4 1 4 b ) : c ) d) 8 4 1 5 5 : : 10 7 9 7 5 6 1 6
EXAMEN DE FUNCIONES ELEMENTALES
 EXAMEN DE FUNCIONES ELEMENTALES Se recomienda: a) Antes de hacer algo, lee todo el eamen. b) Resuelve antes las preguntas que se te den mejor. c) Responde a cada parte del eamen en una hoja distinta. d)
EXAMEN DE FUNCIONES ELEMENTALES Se recomienda: a) Antes de hacer algo, lee todo el eamen. b) Resuelve antes las preguntas que se te den mejor. c) Responde a cada parte del eamen en una hoja distinta. d)
Problemas Tema 1 Solución a problemas de Repaso 4ºESO - Hoja 22 - Todos resueltos
 página 1/10 Problemas Tema 1 Solución a problemas de Repaso 4ºESO - Hoja 22 - Todos resueltos Hoja 22. Problema 1 1. Representa gráficamente y= 2 x 3 + x 1. Rompemos el primer valor absoluto. 2 x 3=0 x=
página 1/10 Problemas Tema 1 Solución a problemas de Repaso 4ºESO - Hoja 22 - Todos resueltos Hoja 22. Problema 1 1. Representa gráficamente y= 2 x 3 + x 1. Rompemos el primer valor absoluto. 2 x 3=0 x=
TEMA 3: NÚMEROS REALES
 . Intervalos y semirrectas TEMA : NÚMEROS REALES Ejemplo Dados los siguientes intervalos y semirrectas, exprésalos en forma de conjunto y represéntalos sobre la recta real:. El intervalo abierto de extremos
. Intervalos y semirrectas TEMA : NÚMEROS REALES Ejemplo Dados los siguientes intervalos y semirrectas, exprésalos en forma de conjunto y represéntalos sobre la recta real:. El intervalo abierto de extremos
EJERCICIOS DE REPASO DE MATEMÁTICAS DE 4º ESO. 1. Realiza las siguientes operaciones simplificando el resultado:
 EJERCICIOS DE REPASO DE MATEMÁTICAS DE 4º ESO. Realiza las siguientes operaciones simplificando el resultado: 56 4 8 4 6 5. Racionaliza las siguientes fracciones: 7 7 4 5. Realiza las siguientes operaciones
EJERCICIOS DE REPASO DE MATEMÁTICAS DE 4º ESO. Realiza las siguientes operaciones simplificando el resultado: 56 4 8 4 6 5. Racionaliza las siguientes fracciones: 7 7 4 5. Realiza las siguientes operaciones
Tema 9 Funciones elementales
 Tema 9 Funciones elementales 9.1Gráfica de una función. Signo simetría. PÁGINA 175 EJERCICIOS 1. Encuentra los puntos de corte con los ejes de las siguientes funciones estudia su signo. 3 c) f 1 c.1) Cortes
Tema 9 Funciones elementales 9.1Gráfica de una función. Signo simetría. PÁGINA 175 EJERCICIOS 1. Encuentra los puntos de corte con los ejes de las siguientes funciones estudia su signo. 3 c) f 1 c.1) Cortes
Módulo de Revisión para la Evaluación de Febrero
 Módulo de Revisión para la Evaluación de Febrero Matemática to año B Profesora Fátima R. Urquieta Año 07: Nombre del Alumno: CONTENIDOS: Geometría y Álgebra Semejanza de figuras planas. Teorema de Thales.
Módulo de Revisión para la Evaluación de Febrero Matemática to año B Profesora Fátima R. Urquieta Año 07: Nombre del Alumno: CONTENIDOS: Geometría y Álgebra Semejanza de figuras planas. Teorema de Thales.
FUNCIONES REALES DE VARIABLE REAL
 MatemáticasNM Curso 0- FUNCIONES REALES DE VARIABLE REAL. Determina gráficamente el dominio y recorrido de cada una de las siguientes funciones: a) f() = b) f() = c) f() = d) f() = + d) f() = + e) f()
MatemáticasNM Curso 0- FUNCIONES REALES DE VARIABLE REAL. Determina gráficamente el dominio y recorrido de cada una de las siguientes funciones: a) f() = b) f() = c) f() = d) f() = + d) f() = + e) f()
LOS NÚMEROS ENTEROS. Para restar un número entero, se quita el paréntesis y se pone al número el signo contrario al que tenía.
 Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Melilla Los números Enteros y operaciones elementales LOS NÚMEROS ENTEROS 1º LOS NÚMEROS ENTEROS. El conjunto de los números enteros Z está formado por los números naturales (enteros positivos) el cero
Vectores equipolentes. Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.
 TEMA 9: GEOMETRIA ANALÍTICA VECTORES EN EL PLANO Un vector fijo AB es un segmento orientado que va del punto A (origen) al punto B (extremo). Si las coordenadas de A son (x1, y1) y las de B, (X, y), las
TEMA 9: GEOMETRIA ANALÍTICA VECTORES EN EL PLANO Un vector fijo AB es un segmento orientado que va del punto A (origen) al punto B (extremo). Si las coordenadas de A son (x1, y1) y las de B, (X, y), las
Inecuaciones lineales
 Inecuaciones lineales 1. Desigualdades 1.1. Definición: Una desigualdad es una comparación entre "a" y "b" tal que: a > b a < b Se lee "a" mayor que "b", cuando la diferencia a - b es positiva Se lee "a"
Inecuaciones lineales 1. Desigualdades 1.1. Definición: Una desigualdad es una comparación entre "a" y "b" tal que: a > b a < b Se lee "a" mayor que "b", cuando la diferencia a - b es positiva Se lee "a"
Guía 1: Operaciones numéricas en los Números enteros (Z)
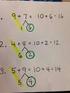 Guía 1: Operaciones numéricas en los Números enteros (Z) NÚMEROS ENTEROS (Z): Existen números con signo, que son los números enteros (Z+ son los positivos y Z- son los negativos). Según se sabe, nos los
Guía 1: Operaciones numéricas en los Números enteros (Z) NÚMEROS ENTEROS (Z): Existen números con signo, que son los números enteros (Z+ son los positivos y Z- son los negativos). Según se sabe, nos los
NUMEROS ENTEROS ( Z)
 NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
NUMEROS ENTEROS ( Z) En N la resta sólo está definida si el minuendo es mayor o igual al sustraendo. Para que dicha operación no sea tan restringida se creó el conjunto de enteros negativos ( notado por
Repaso para el dominio de la materia
 LECCIÓN Repaso para el dominio de la materia Usar con las páginas 398 a 03 OBJETIVO Resolver ecuaciones de valor absoluto. Vocabulario Una ecuación de valor absoluto, como x 5 3 es una ecuación que contiene
LECCIÓN Repaso para el dominio de la materia Usar con las páginas 398 a 03 OBJETIVO Resolver ecuaciones de valor absoluto. Vocabulario Una ecuación de valor absoluto, como x 5 3 es una ecuación que contiene
Matemáticas, 3º de ESO Trabajo de repaso para las recuperaciones
 Matemáticas, 3º de ESO Trabajo de repaso para las recuperaciones Tema 1. Racionales 1.- Representa en la recta racional las siguientes fracciones: -1 y 4 b) -3 y 1 3 3. Calcula el valor de las siguientes
Matemáticas, 3º de ESO Trabajo de repaso para las recuperaciones Tema 1. Racionales 1.- Representa en la recta racional las siguientes fracciones: -1 y 4 b) -3 y 1 3 3. Calcula el valor de las siguientes
ECUACIONES E INECUACIONES CON VALOR ABSOLUTO QUE SE PUEDEN EXPRESAR EN UNA DE LAS SIGUIENTES FORMAS TÍPICAS :
 CALCULO PCI INECUACIONES E INECUACIONES CON VALOR ABSOLUTO Si a es un número real el Valor Absoluto de a es: a = a a si = a si a < 0 a 0 Sean a y b son números reales Entonces: a = 0 si y solo si a = 0
CALCULO PCI INECUACIONES E INECUACIONES CON VALOR ABSOLUTO Si a es un número real el Valor Absoluto de a es: a = a a si = a si a < 0 a 0 Sean a y b son números reales Entonces: a = 0 si y solo si a = 0
Las desigualdades absolutas son aquellas que se cumplen sea cual sea el valor real que se sustituye. Por ejemplo:
 MATEMÁTICAS BÁSICAS INECUACIONES INTERVALOS DE NÚMEROS REALES Una desigualdad es la epresión de dos cantidades tales que una es mayor que otra. Las desigualdades en general se clasifican en absolutas y
MATEMÁTICAS BÁSICAS INECUACIONES INTERVALOS DE NÚMEROS REALES Una desigualdad es la epresión de dos cantidades tales que una es mayor que otra. Las desigualdades en general se clasifican en absolutas y
FUNCIONES REALES DE UNA VARIABLE CONCEPTOS FUNDAMENTALES
 FUNCIONES REALES DE UNA VARIABLE Índice Presentación... 3 Conjunto de los números reales... 4 Los intervalos... 6 Las potencias... 7 Los polinomios... 8 La factorización de polinomios (I)... 9 La factorización
FUNCIONES REALES DE UNA VARIABLE Índice Presentación... 3 Conjunto de los números reales... 4 Los intervalos... 6 Las potencias... 7 Los polinomios... 8 La factorización de polinomios (I)... 9 La factorización
EXAMEN DE JUNIO DE MAS I
 EXAMEN DE JUNIO DE MAS I Se recomienda: a) Antes de hacer algo, lee todo el eamen. b) Resuelve antes las preguntas que se te den mejor. c) Responde a cada parte del eamen en una hoja distinta. d) Es una
EXAMEN DE JUNIO DE MAS I Se recomienda: a) Antes de hacer algo, lee todo el eamen. b) Resuelve antes las preguntas que se te den mejor. c) Responde a cada parte del eamen en una hoja distinta. d) Es una
UNIDAD DE APRENDIZAJE II
 UNIDAD DE APRENDIZAJE II Saberes procedimentales 1. Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. 2. Relaciona una ecuación algebraica con a
UNIDAD DE APRENDIZAJE II Saberes procedimentales 1. Emplea de manera sistemática conceptos algebraicos, geométricos, trigonométricos y de geometría analítica. 2. Relaciona una ecuación algebraica con a
EJERCICIOS ECUACIONES E INECUACIONES
 EJERCICIOS ECUACIONES E INECUACIONES Ejercicio nº.- Halla las soluciones de las siguientes ecuaciones: a) b) a) b) Cambio: z z z z z Dos soluciones:, z z (no vale) Ejercicio nº.- Resuelve: a) b) a) Comprobación:
EJERCICIOS ECUACIONES E INECUACIONES Ejercicio nº.- Halla las soluciones de las siguientes ecuaciones: a) b) a) b) Cambio: z z z z z Dos soluciones:, z z (no vale) Ejercicio nº.- Resuelve: a) b) a) Comprobación:
GUIA DE ESTUDIO FUNCIONES CUADRÁTICAS. Se llama FUNCION POLINOMICA DE SEGUNDO GRADO o FUNCION CUADRÁTICA a la función:
 GUIA DE ESTUDIO FUNCIONES CUADRÁTICAS Se llama FUNCION POLINOMICA DE SEGUNDO GRADO o FUNCION CUADRÁTICA a la función: f: R R f(x) = ax + bx + c a 0 y a, b, c R El término ax se denomina término cuadrático,
GUIA DE ESTUDIO FUNCIONES CUADRÁTICAS Se llama FUNCION POLINOMICA DE SEGUNDO GRADO o FUNCION CUADRÁTICA a la función: f: R R f(x) = ax + bx + c a 0 y a, b, c R El término ax se denomina término cuadrático,
"""##$##""" !!!""#""!!! """##$##""" (c) Verdadero siempre que los términos en grado p = q se anulen.
 Unidad nº 0 FFUNCI IONEES POLLI INÓMICAS YY RACIONALLEES! 7 AUTOEVALUACIÓN Halla la suma y el producto de los polinomios P() y Q() - - 5 -. P() + Q() 5 - +.. P() Q() ( ) ( 5 ) - 6 5 5 + + 0 + - 6 5 + 5
Unidad nº 0 FFUNCI IONEES POLLI INÓMICAS YY RACIONALLEES! 7 AUTOEVALUACIÓN Halla la suma y el producto de los polinomios P() y Q() - - 5 -. P() + Q() 5 - +.. P() Q() ( ) ( 5 ) - 6 5 5 + + 0 + - 6 5 + 5
Listo para seguir? Intervención de destrezas
 Listo para seguir? Intervención de destrezas 1-1 Variables y expresiones Busca estas palabras de vocabulario en la Lección 1-1 y el Glosario multilingüe. Vocabulario variable constante expresión numérica
Listo para seguir? Intervención de destrezas 1-1 Variables y expresiones Busca estas palabras de vocabulario en la Lección 1-1 y el Glosario multilingüe. Vocabulario variable constante expresión numérica
Tema 2.- Va de funciones. Ejercicios Definición de funciones y funciones sencillas. Forma de dar una función.
 Tema 2.- Va de funciones. Ejercicios 2.1.- Definición de funciones y funciones sencillas. Forma de dar una función. 1. En un triángulo isosceles de perímetro 20, expresa la base como función del otro lado.
Tema 2.- Va de funciones. Ejercicios 2.1.- Definición de funciones y funciones sencillas. Forma de dar una función. 1. En un triángulo isosceles de perímetro 20, expresa la base como función del otro lado.
Cuando se enumeran todos los elementos que componen el conjunto. A = { 1, 2, 3, 4, 5 }
 LOS NÚMEROS REALES TEMA 1 IDEAS SOBRE CONJUNTOS Partiremos de la idea natural de conjunto y del conocimiento de si un elemento pertenece (* ) o no pertenece (* ) a un conjunto. Los conjuntos se pueden
LOS NÚMEROS REALES TEMA 1 IDEAS SOBRE CONJUNTOS Partiremos de la idea natural de conjunto y del conocimiento de si un elemento pertenece (* ) o no pertenece (* ) a un conjunto. Los conjuntos se pueden
ARITMÉTICA Y ÁLGEBRA
 ARITMÉTICA Y ÁLGEBRA Serie 1 Ejercicio nº 1.- a) Aproxima hasta las décimas cada uno de los siguientes números: A = 1,84 B = 39,174 b) Halla el error absoluto y el error relativo que se cometen al tomar
ARITMÉTICA Y ÁLGEBRA Serie 1 Ejercicio nº 1.- a) Aproxima hasta las décimas cada uno de los siguientes números: A = 1,84 B = 39,174 b) Halla el error absoluto y el error relativo que se cometen al tomar
INECUACIONES Y SISTEMAS
 www.matesronda.net José A. Jiménez Nieto INECUACIONES Y SISTEMAS. DESIGUALDADES E INECUACIONES En todos los ámbitos encontramos epresiones numéricas o algebraicas que hacen referencia a la desigualdad
www.matesronda.net José A. Jiménez Nieto INECUACIONES Y SISTEMAS. DESIGUALDADES E INECUACIONES En todos los ámbitos encontramos epresiones numéricas o algebraicas que hacen referencia a la desigualdad
Números enteros. Los números enteros son los formados por los números naturales (1), sus opuestos (2) y el número 0
 Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Los números enteros son los formados por los números naturales, sus opuestos (2) y el número 0 Números enteros Los números naturales son aquellos que nos permiten contar las cosas. Ej. 2 sillas, 4 patas,
Instituto Superior del Profesorado Dr. Joaquín V. González Profesorado de Informática Ingreso Matemática GUÍA DE ACTIVIDADES
 1) Resolver las siguientes ecuaciones: Instituto Superior del Profesorado Dr. Joaquín V. González GUÍA DE ACTIVIDADES d) e) f) g) h) i) j) k) l) ll) m) n) 2) Dadas las siguientes ecuaciones, verificar
1) Resolver las siguientes ecuaciones: Instituto Superior del Profesorado Dr. Joaquín V. González GUÍA DE ACTIVIDADES d) e) f) g) h) i) j) k) l) ll) m) n) 2) Dadas las siguientes ecuaciones, verificar
La lección de hoy es sobre cómo encontrar el Punto Medio de un Segmento. Es cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1.
 CGT.5.G.1-Jennifer Goff-Midpoint of a Segment. La lección de hoy es sobre cómo encontrar el Punto Medio de un Segmento. Es cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1. Qué es el
CGT.5.G.1-Jennifer Goff-Midpoint of a Segment. La lección de hoy es sobre cómo encontrar el Punto Medio de un Segmento. Es cuál es la expectativa para el aprendizaje del estudiante CGT.5.G.1. Qué es el
INSTEC PENSAMIENTO NUMERICO VARIACIONAL GUIA 1 - GRADO 11
 1.. LOS NUMEROS REALES CONDUCTA DE ENTRADA La figura muestra una recta real -1 0 1 Teniendo en cuenta la Figura responde en minutos a. Cuantos números Reales hay entre -1 y 1. b. Cuantos números naturales
1.. LOS NUMEROS REALES CONDUCTA DE ENTRADA La figura muestra una recta real -1 0 1 Teniendo en cuenta la Figura responde en minutos a. Cuantos números Reales hay entre -1 y 1. b. Cuantos números naturales
Lic. Manuel de Jesús Campos Boc
 UNIVERSIDAD MARIANO GÁLVEZ DE GUATEMALA FACULTAD DE CIENCIAS DE LA ADMINISTRACIÓN DIRECCIÓN GENERAL DE CENTRO UNIVERSITARIOS CENTRO UNIVERSITARIO DE VILLA NUEVA CURSO MATEMÁTICAS APLICADA I 05 Lic. Manuel
UNIVERSIDAD MARIANO GÁLVEZ DE GUATEMALA FACULTAD DE CIENCIAS DE LA ADMINISTRACIÓN DIRECCIÓN GENERAL DE CENTRO UNIVERSITARIOS CENTRO UNIVERSITARIO DE VILLA NUEVA CURSO MATEMÁTICAS APLICADA I 05 Lic. Manuel
CURSO: Matemáticas. Undécimo NOMBRE DEL ESTUDIANTE: REPASO
 COLEGIO JUAN LUIS LONDOÑO TALLER PREPARATORIO TRIMESTRE 1 L-GE-13 Vigente desde: 04-06-2013 ÁREA: Matemáticas NOMBRE DEL PROFESOR: David Melo Leguizamón ASIGNATURA: CURSO: Matemáticas Undécimo NOMBRE DEL
COLEGIO JUAN LUIS LONDOÑO TALLER PREPARATORIO TRIMESTRE 1 L-GE-13 Vigente desde: 04-06-2013 ÁREA: Matemáticas NOMBRE DEL PROFESOR: David Melo Leguizamón ASIGNATURA: CURSO: Matemáticas Undécimo NOMBRE DEL
Fundamentos matemáticos. Tema 1 Números reales. Polinomios
 Grado en Ingeniería agrícola y del medio rural Tema 1 Números reales. Polinomios José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative
Grado en Ingeniería agrícola y del medio rural Tema 1 Números reales. Polinomios José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative
Unidad didáctica 1. Operaciones básicas con números enteros
 Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
Unidad didáctica 1 Operaciones básicas con números enteros 1.- Representación y ordenación de números enteros Para representar números enteros en una recta hay que seguir estos pasos: a) Se dibuja una
