Teoremas de Convergencia
|
|
|
- María del Pilar Lozano Montero
- hace 7 años
- Vistas:
Transcripción
1 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y lim, es decir para que (24.1) lim f k = lim f k. En este capítulo consideraremos otras condiciones bajo las que sea cierta la fórmula A lo largo de él hemos de tener presente que siempre que unas determinadas hipótesis conduzcan a la validez de la igualdad anterior, esas hipótesis restringidas a un conjunto medible B garantizan también, si no se dice nada en contra, la validez de la misma sobre B, es decir (24.2) lim f k = lim f k, B De igual modo, estas hipótesis sólo deberán ser verificadas normalmente en casi todo punto. Convergencia monótona El teorema de la convergencia monótona para funciones no negativas proporciona, invirtiendo las hipótesis, un teorema de convergencia para funciones no positivas. Por lo que, hasta aquí, tendríamos un teorema de convergencia para sucesiones no decrecientes de funciones no negativas (0 f k ), y otro para sucesiones no crecientes de funciones no positivas (0 f k ). En general las hipótesis de estos dos teoremas no podrán ser intercambiadas. Así, para una sucesión no creciente de funciones no negativas (0 f k ) no es seguro que la fórmula 24.1 sea válida: 239 B
2 240 Teoremas de Convergencia 24.1 Ejemplo 24.1 Sea {f k } la sucesión de funciones f k (x) = 1/k. Esta sucesión es claramente no decreciente, todas las funciones son no positivas y converge puntualmente a 0. Es inmediato comprobar que f k = +, k, y por tanto + = lim f k lim f k = 0 = 0. No obstante, manteniendo la monotonía de la sucesión pero sin hacer referencia alguna al signo de las funciones, aún es posible obtener un buen teorema de convergencia: Teorema 24.2 (De la convergencia monótona generalizado) Sea {f k } una sucesión monótona (da igual que sea creciente o decreciente) de funciones medibles. Si alguna de las funciones de esta sucesión es integrable, entonces las dos expresiones, lim f k y lim f k, existen y lim f k = lim f k. Demostración. Supongamos, para concretar, que la sucesión es no decreciente y que la función f k es integrable. Consideremos entonces la sucesión no decreciente de funciones medibles y no negativas, definida c.s., {f s f k } s k. Si llamamos f = lim f s, es claro que 0 f s f k f f k (c.s.) luego, por el teorema de la convergencia monótona para funciones no negativas, lim (f s f k ) = (f f k ) s y, por tanto, si fuese cierto que (24.3) (f s f k ) = f s f k ; (f f k ) = f f k,
3 24.3 Teoremas de Convergencia 241 se tendría lim f s f k = f f k lim f s = f. Veamos pues que 24.3 se verifica: Escribamos f s = (f s f k ) + f k. Entonces, puesto que f k es integrable y (f s f k ) 0, se satisfacen las condiciones de la proposición para deducir que f s = (f s f k ) + f k (f s f k ) = f s De igual modo se demuestra que (f f k ) = f f k. El resultado siguiente nos servirá de lema para la demostración de otro teorema de convergencia muy utilizado, el teorema de la convergencia dominada de Lebesgue. Teorema 24.3 (Lema de Fatou) (a) Si {f k } es una sucesión de funciones medibles no negativas, entonces limf k lim f k. (b) Si {f k } una sucesión de funciones medibles no positivas negativas, entonces limf k lim f k. f k. Demostración. (a) Sea g k = j k f j. Obviamente, {g k } es una sucesión no decreciente de funciones medibles y no negativas y lim g k = limf k, luego limf k = lim g k = lim g k lim f k, donde la desigualdad, lim g k lim f k, se obtiene así: De la definición de g k se deduce que g k f j, para cada j k, por tanto g k f j, j k g k inf f j lim g k lim f k. j k (b) Resulta de (a) aplicado a la sucesión { f k }.
4 242 Teoremas de Convergencia 24.4 Convergencia dominada Teorema 24.4 Sea {f k } una sucesión de funciones medibles que converge puntualmente a la función f y supongamos que existe una función integrable F tal que f k F, entonces (a) f es integrable. (b) f = lim f k. Demostración. De la condición f k F y la convergencia puntual de la sucesión f k hacia la función f, se deduce trivialmente que f F, lo que implica (por F integrable) que cada función f k y f son funciones integrables. Veamos que f = lim f k. Tenemos por hipótesis que F f k F, para todo k. Aplicando entonces el lema de Fatou (a) a la sucesión de funciones no negativas {f k + F }, resulta (f + F ) = lim(f k + F ) lim (f k + F ), de donde se deduce, haciendo uso de la linealidad del operador integral, que f lim f k. Análogamente, aplicando de nuevo el teorema de Fatou, ahora a la sucesión de funciones no positivas {f k F }, obtendríamos f lim f k. y uniendo ambas desigualdades, teniendo en cuenta que el límite inferior de una sucesión de numeros reales es menor o igual que el límite superior, se tiene ya f lim f k lim f k lo que implica que todas las desigualdades anteriores son, en realidad, igualdades y por tanto, que existe lim f k (por coincidir el límite superior y el inferior) y es igual a f. El corolario siguiente proporciona una versión fuerte del teorema de la convergencia dominada. f,
5 24.6 Teoremas de Convergencia 243 Corolario 24.5 Sean {f k } y f como en el teorema anterior. Entonces lim f k f = 0. Demostración. Vamos a aplicar lo obtenido antes a la sucesión { f k f }. Por hipótesis la sucesión de funciones { f k f } converge a 0 en cada uno de los puntos x en que estén definidas las funciones f k f, luego en c.t.p., pues f k y f son funciones integrables. f k f 2 F, siendo la función 2 F integrable, luego lim f k f = 0. En el teorema anterior hemos hecho referencia a una versión fuerte del mismo, pareciendo indicar con ello que lim f k f = 0 lim f k = f? Esto es verdad, pero siempre que existan las integrales f k, concretamente: Proposición 24.6 Sean {f k } y f funciones medibles y supongamos que para cada k, f k, entonces lim f k f = 0 f, y lim f k = f. Demostración. Para ε > 0 sea ν N tal que f k f < ε si k ν. Supongamos en primer lugar que todas las funciones f k, k ν son integrables. Entonces, se tiene que (f k f) = f k f, por lo que podemos escribir f k f = (f k f) f k f < ε, luego, lim fk = f. Supongamos que existe p ν tal que f p = y escribamos f = (f f p ) + f p. De las hipótesis y del teorema de aditividad de la integral (Proposición 23.13) se deduce que f existe y (24.4) f = (f f p ) + f p =.
6 244 Teoremas de Convergencia 24.6 Por otra parte, escribiendo f k = (f k f) + f vemos que f k =, para todo k ν. Luego, también en este caso, lim fk = f. Ejemplos triviales que muestran que la condición lim fk f = 0 no implica la existencia de las integrales f k, pueden construirse sin más que tomar f k = f para todo k, y f una función medible, cuya integral no existe (por ejemplo f(x) = 1, si x 0; f(x) = 1, si x > 0). Por otra parte, el nuevo ejemplo prueba que la condición lim fk = f no implica que lim fk f = 0. Ejemplo. Sea f k = 1/k X [ k,0] + 1/k X [0,k] ; f = 0. Como f k = 0, se tiene que lim f k = f = 0. En cambio, lim f k f = 2 0. Vamos a ver a continuación dos casos particulares del teorema de la convergencia dominada: Corolario 24.7 Sea B un conjunto medible y de medida finita, y sea {f k } una sucesión de funciones medibles sobre B, que converge puntualmente sobre B a una función f. Supongamos que se satisface una de las dos condiciones siguientes: (i) Existe una constante M tal que f k (x) M, para cada x B. (ii) La sucesión {f k } converge uniformemente en B a la función f. Entonces, lim f k f = 0. B Demostración. La condición i) significa que f k X B MX B.
7 24.9 Teoremas de Convergencia 245 Puesto que la función F = MX B es integrable ( MX B = M m(b) < ) y {f k X B } f, aplicando el teorema de la convergencia dominada, se tiene que 0 = lim f k X B fx B = lim f k f. B De la condición ii) se deduce que, dado ε > 0, f k f X B εx B para k suficientemente grande. Por lo que, aplicando de nuevo el teorema de la convergencia dominada, resulta lo que queremos. Consecuencias 24.8 Si {f k } es una sucesión de funciones medibles, no negativas, entonces fk = f k. Para probarlo sólo hay que aplicar el teorema de la convergencia monótona y la aditividad del operador integral a la sucesión de funciones no negativas g k = k f i. i= Si {B k } es una sucesión de conjuntos medibles disjuntos dos a dos, f una función medible sobre B k, y suponemos que existe su integral sobre B k, entonces f = f. B k B k Si f 0, entonces, del resultado anterior y la igualdad fx Bk = fx Bk, se deduce que fx Bk = fx Bk = B k f.
8 246 Teoremas de Convergencia 24.9 En el caso general, supongamos por ejemplo que B k f + <, entonces f = f + f = f + f, B k B k B k B k B k que nos dice que B k f es la diferencia de dos series de términos positivos, siendo la primera de ellas convergente. Se tiene entonces que f = f + f = ( f + f ) = f. B k B k B k B k B k B k Para escribir las igualdades anteriores hemos utilizado el siguiente resultado, cuya demostración constituye un sencillo ejercicio: Si a k, bk son dos series de términos positivos, y suponemos que una de ellas es convergente, entonces ak b k = (a k b k ) Sea B 1 B 2... una sucesión no decreciente de conjuntos medibles, y supongamos que f es una función medible cuya integral sobre B k existe, entonces f = lim B k f. B k Si f 0, la demostración resulta de aplicar el teorema de la convergencia monótona a la sucesión no decreciente {fx Bk }. En el caso general se procede como antes Sea B 1 B 2... una sucesión no creciente de conjuntos medibles, y supongamos que f es una función integrable sobre algún B k, entonces f = lim f. B k B k En caso de ser f 0, la demostración resultará de aplicar el teorema 24.2 a la sucesión {fx Bk }, de ahí la necesidad de la hipótesis f integrable sobre algún B k. El caso general, como en los resultados precedentes.
9 24.13 Teoremas de Convergencia Sea {B k } una sucesión de conjuntos medibles, tal que lim m(b k) = 0. Entonces, si f es una función integrable, se tiene que lim f = 0. B k Demostración. El resultado es evidentemente cierto si f es una función acotada, pues entonces f c f f cm(b k ) 0. B k B k En general, denotemos por C α = {x: f(x) α}. Entonces f = B k f + B k C α B k C c α f f + αm(b k ). C α Por tanto en particular, lim f B k f, α > 0, C α lim f B k f, p = 1, 2,... C p Pero la sucesión de integrales, C p f, tiende a 0 en virtud de 24.11, ya que obviamente C 1 C Se deduce pues que lim B k f = 0. Corolario (Continuidad absoluta) Si f es una función integrable, entonces para cada ε > 0 existe un δ > 0 tal que m(b) < δ B f < ε. Demostración. De lo contrario, existiría un ε > 0 y una sucesión de conjuntos {B k } tales que m(b k ) < 1/k, mientras que B k f > ε, lo cual contradice
10 248 Teoremas de Convergencia 24A Ejercicios 24A Sea f una función integrable y B p = {x: f(x) p}. (a) Probar que lim p p m(b p ) = 0. (b) Probar que p m(b p+1 \ B p )) < +. p=0 (c) Probar que la condición sobre f en el apartado (a) no implica f integrable. La condición en el apartado (b) implica que f es integrable si {x : f(x) 0} es de medida finita. 24B Encontrar sucesiones monótonas {f k } que no satisfagan las hipótesis de ninguno de los teoremas de convergencia monótona y tales que f k =, k. lim f k lim f k lim f k = lim f k 24C (a) Probar que si {f k } es una sucesión de funciones integrables que converge uniformemente a una función f sobre un conjunto B de medida finita, entonces f es integrable sobre B y f = lim f k. B B (b) Demostrar que la condición del apartado anterior, B de medida finita, no se puede quitar. (c) Construir una sucesión de funciones {f k } que converja uniformemente en un conjunto de medida finita B y tal que para todo k f k =. B 24D Probar que si B k y B son conjuntos medibles tales que m(b k B) 0, entonces lim f = B k B para toda f integrable. 24E Demostrar que si f es una función integrable entonces lim m 0 e m sen2 x f(x) = 0.
11 24K Teoremas de Convergencia F Consideremos la sucesión de funciones f p (x, y) = px2 px y cos 1 px y. (a) Probar que se trata de una sucesión de funciones medibles que converge c.s. hacia qué función? (b) Se puede aplicar el teorema de la convergencia dominada en B = {(x, y): 0 < y < x < 1}. 24G Probar que si f es una función medible sobre el intervalo [a, b] y para cada x [a, b] se tiene que x c.s. f = 0, entonces f = 0. a indicación. Observar que f = 0 para cada semintervalo contenido en [a, b] y I utilizar la continuidad absoluta de la integral. 24H Sea f L 1 (R) derivable en 0 y tal que f(0) = 0. Probar que la función g(x) = f(x)/x es integrable en R. 24I Sea f k una sucesión monótona de funciones reales e integrables que converge puntualmente a una función f. Es cierto entonces que lim f fk = 0? 24J Sea f k una sucesión de funciones medibles que converge puntualmente a una función f. Probar que si existe M > 0 tal que f k M entonces f M. 24K Sea f k una sucesión de funciones medibles no negativas que converge puntualmente a una función integrable f y sea para cada k, B k = {x : f(x) f k (x)}. (a) Probar que (b) Probar que lim (f f k ) = 0. B k f f k = (f f k ) + 2 (f f k ). B k (c) Deducir de los apartados anteriores que si, además de las hipótesis iniciales sobre {f k } y f, se tiene que lim f k = f, entonces lim f f k = 0. Puede suprimirse la hipótesis f k 0 para cada k? y la hipótesis f integrable?
12
El Teorema de la Convergencia Dominada
 Capítulo 22 l Teorema de la Convergencia Dominada Los dos teoremas de convergencia básicos en la integración Lebesgue son el teorema de la convergencia monótona (Lema 19.10), que vimos el capítulo y el
Capítulo 22 l Teorema de la Convergencia Dominada Los dos teoremas de convergencia básicos en la integración Lebesgue son el teorema de la convergencia monótona (Lema 19.10), que vimos el capítulo y el
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
El Teorema de Fubini-Tonelli
 Capítulo 23 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 23 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
El Teorema de Fubini-Tonelli
 Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Capítulo 26 El Teorema de Fubini-Tonelli Veremos en este capítulo que el cálculo de una integral múltiple se reduce al de integrales simples. Concretamente se va a probar que si f(x, y) es una función
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
 Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Apuntes sobre la integral de Lebesgue
 Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
Apuntes sobre la integral de Lebesgue Miguel Lacruz Martín Universidad de Sevilla 1. Medida de Lebesgue 1.1. Introducción La longitud l(i) de un intervalo I R se define habitualmente como la distancia
1. MEDIDA E INTEGRACIÓN.
 1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
La Medida de Lebesgue. Problema de la Medida
 Capítulo 19 La Medida de Lebesgue. Problema de la Medida Hemos demostrado en el capítulo anterior que la medida exterior de Lebesgue es una medida sobre la familia M de los conjuntos medibles. Por definición,
Capítulo 19 La Medida de Lebesgue. Problema de la Medida Hemos demostrado en el capítulo anterior que la medida exterior de Lebesgue es una medida sobre la familia M de los conjuntos medibles. Por definición,
1. Convergencia en medida
 FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
FACULTAD CS. FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA3801 Teoría de la Medida. Semestre 2009-02 Profesor: Jaime San Martín Auxiliares: Andrés Fielbaum y Cristóbal Guzmán Clase auxiliar 7 21 de Septiembre
1. Funciones Medibles
 1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
1. Medibles Medibles simples... Hasta ahora hemos estudiado la medida de Lebesgue definida sobre los conjuntos de R n y sus propiedades. Vamos a aplicar ahora esta teoría al estudio de las funciones escalares
Cambio de Variables en la Integral Múltiple
 Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 27 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Cambio de Variables en la Integral Múltiple
 Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Capítulo 24 Cambio de Variables en la Integral Múltiple n la demostración del teorema del cambio de variable utilizaremos con frecuencia que el carácter medible de los conjuntos es una propiedad que se
Conjuntos Medibles. Preliminares
 Capítulo 18 Conjuntos Medibles Preliminares En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos de R
Capítulo 18 Conjuntos Medibles Preliminares En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos de R
Funciones continuas e inyectivas
 Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
2 Obtener el término general de las siguientes sucesiones definidas por recurrencia: y0 = a > 0
 CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
Conjuntos Medibles. La identidad de Caratheodory
 Capítulo 18 Conjuntos Medibles La identidad de Caratheodory En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos
Capítulo 18 Conjuntos Medibles La identidad de Caratheodory En el capítulo anterior vimos que la medida exterior de Lebesgue no resulta σ-aditiva en todo R n. Ahora vamos a construir una familia M de subconjuntos
Parte 4: Teoremas de convergencia.
 Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
Parte 4: Teoremas de convergencia. Como siempre, si no se dice lo contrario, se supone que (, M, µ) es un espacio de medida y trabajamos con funciones de dominio y recorrido contenido en C o R o R. Empezamos
3. INTEGRACION. La (µ)-integral de una función simple no negativa es, por definición:
 3. INTEGRACION La (µ)-integral de una función simple no negativa es, por definición: En este caso se sigue la convención de que si µ(y E i ) = pero como a i = 0 entonces a i µ(y E i ) = 0. Evidentemente,
3. INTEGRACION La (µ)-integral de una función simple no negativa es, por definición: En este caso se sigue la convención de que si µ(y E i ) = pero como a i = 0 entonces a i µ(y E i ) = 0. Evidentemente,
1. Medida Exterior. Medida de Lebesgue en R n
 1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
CÁLCULO NUMÉRICO I (Tema 2 - Relación 1)
 CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
La propiedad de compacidad
 En un artículo anterior hemos obtenido dos importantes resultados relacionados con la continuidad de una función en un intervalo: el teorema de los ceros de Bolzano y el teorema del valor intermedio. De
En un artículo anterior hemos obtenido dos importantes resultados relacionados con la continuidad de una función en un intervalo: el teorema de los ceros de Bolzano y el teorema del valor intermedio. De
Parte III. Medida e Integración en R n
 Parte III Medida e Integración en R n Capítulo 17 La Medida Exterior de Lebesgue en R n El cálculo de longitudes, áreas y volúmenes es uno de los asuntos matemáticos con más larga tradición histórica,
Parte III Medida e Integración en R n Capítulo 17 La Medida Exterior de Lebesgue en R n El cálculo de longitudes, áreas y volúmenes es uno de los asuntos matemáticos con más larga tradición histórica,
Medida y Probabilidad
 Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
Medida y Probabilidad Jorge Salazar 1 Enero 2015 1 Con el apoyo del Programa PROMETEO/SENESCYT del Gobierno del Ecuador. ii Contents 7 Integral de Lebesgue 1 7.1 Integración de funciones simples.................
CÁLCULO II. Grado M+I. Sucesiones y series de funciones. Sucesiones y series de funciones 1 / 27. Grado M+I () CÁLCULO II
 CÁLCULO II Grado M+I Sucesiones y series de funciones Sucesiones y series de funciones 1 / Sucesiones funciones. Convergencia puntual Sucesión de funciones Definición Una sucesión de funciones será cualquier
CÁLCULO II Grado M+I Sucesiones y series de funciones Sucesiones y series de funciones 1 / Sucesiones funciones. Convergencia puntual Sucesión de funciones Definición Una sucesión de funciones será cualquier
1. Continuidad. Universidad de Chile Subsucesiones. Ingeniería Matemática
 1. Continuidad 1.1. Subsucesiones Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Importante: Visita regularmente http://www.dim.uchile.cl/~calculo.
1. Continuidad 1.1. Subsucesiones Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Importante: Visita regularmente http://www.dim.uchile.cl/~calculo.
Modos de convergencia
 Modos de convergencia Favio Pirán, Christian Caticha Resumen En este documento intentaremos generar intuiciones acerca de distintos tipos de convergencia de sucesiones de funciones reales medibles, mediante
Modos de convergencia Favio Pirán, Christian Caticha Resumen En este documento intentaremos generar intuiciones acerca de distintos tipos de convergencia de sucesiones de funciones reales medibles, mediante
Aplicaciones de las derivadas. El teorema del valor medio
 Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Derivada de la función compuesta. Regla de la cadena
 Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Derivada de la función compuesta. Regla de la cadena Cuando en las matemáticas de bachillerato se introduce el concepto de derivada, su significado y su interpretación geométrica, se pasa al cálculo de
Observación: Aceptaremos que la función f no este definida para un número finito de términos como por ejemplo f(n) = n 5.
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07- Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07- Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
El Teorema de Stone-Weierstrass
 Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Capítulo 3 El Teorema de Stone-Weierstrass Vamos a ver en esta lección el teorema clásico de Weierstrass y la importante generalización del mismo dada por Stone. El teorema de Weierstrass El teorema de
Sucesiones y Series Sucesiones
 Capítulo 6 Sucesiones y Series 6.. Sucesiones En particular estudiaremos las sucesiones de números reales, es decir, las que verifican la siguiente definición. Definición 6... Llamaremos sucesión a la
Capítulo 6 Sucesiones y Series 6.. Sucesiones En particular estudiaremos las sucesiones de números reales, es decir, las que verifican la siguiente definición. Definición 6... Llamaremos sucesión a la
Funciones de Clase C 1
 Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Capítulo 7 Funciones de Clase C 1 Vamos a considerar ahora la extensión a varias variables del concepto de función de clase C 1. Cada vez que establezcamos una propiedad de las funciones diferenciables,
Medidas. Problemas para examen. Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez.
 Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Derivadas Parciales de Orden Superior
 Capítulo 9 Derivadas Parciales de Orden Superior La extensión a funciones de varias variables del concepto de derivada de orden superior, aunque teóricamente no ofrece ninguna dificultad, presenta ciertas
Capítulo 9 Derivadas Parciales de Orden Superior La extensión a funciones de varias variables del concepto de derivada de orden superior, aunque teóricamente no ofrece ninguna dificultad, presenta ciertas
Espacio de Funciones Medibles
 Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Espacios compactos. 7.1 Espacios compactos
 58 Capítulo 7 Espacios compactos 7.1 Espacios compactos Definición 7.1.1 (Recubrimiento). Sea X un conjunto y sea S X. Un recubrimiento de S es una familia A = {A i } i I de subconjuntos de X tales que
58 Capítulo 7 Espacios compactos 7.1 Espacios compactos Definición 7.1.1 (Recubrimiento). Sea X un conjunto y sea S X. Un recubrimiento de S es una familia A = {A i } i I de subconjuntos de X tales que
Series de Fourier absolutamente convergentes
 Series de Fourier absolutamente convergentes Objetivos. Estudiar las propiedades principales de series de Fourier absolutamente convergentes. Ya hemos mostrado que los caracteres del grupo Z se pueden
Series de Fourier absolutamente convergentes Objetivos. Estudiar las propiedades principales de series de Fourier absolutamente convergentes. Ya hemos mostrado que los caracteres del grupo Z se pueden
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Espacios conexos. 6.1 Conexos
 Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Teoremas de Tonelli y Fubini
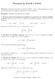 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Elementos Básicos de Análisis Funcional en. Dr. Oldemar Rodríguez Rojas
 Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Elementos Básicos de Análisis Funcional en Análisis Numérico Dr. Oldemar Rodríguez Rojas Agosto 2008 Contents 1 Elementos Básicos de Análisis Funcional 2 1.1 Espacios normados...........................
Integrales impropias múltiples
 Integrales impropias múltiples ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Caracterización de la integrabilidad impropia 2 3.
Integrales impropias múltiples ISABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Caracterización de la integrabilidad impropia 2 3.
1. Unicidad de Medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2. Lección n 3: Construcción de medidas, Medida de Lebesgue EPN, verano 2009 1. Unicidad de Medidas = Es imposible
Principio de acotación uniforme
 Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Funciones continuas. Definición y propiedades
 Funciones continuas. Definición y propiedades Para la lectura de este artículo es recomendable haber leído con anterioridad otros tres artículos relacionados con las sucesiones de números reales y las
Funciones continuas. Definición y propiedades Para la lectura de este artículo es recomendable haber leído con anterioridad otros tres artículos relacionados con las sucesiones de números reales y las
El teorema del valor intermedio
 Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Parte II. Cálculo Diferencial para Funciones de Varias Variables Reales
 Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
Parte II Cálculo Diferencial para Funciones de Varias Variables Reales Capítulo 5 Derivadas Direccionales y Derivadas Parciales Iniciamos, con este capítulo, el cálculo diferencial para funciones de varias
Departamento de Matemáticas
 MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
MA5 Clase : Series de números reales Definición de Serie Elaborado por los profesores Edgar Cabello y Marcos González Definicion Dada una sucesión de escalares (a n ), definimos su sucesión de sumas parciales
Ejercicios de aplicaciones de las derivadas y del teorema del valor medio
 Se proponen a continuación varios ejercicios relacionados con las derivadas y sus aplicaciones (por ejemplo, cálculo de etremos, monotonía, cálculo de la imagen de una función, soluciones de ciertas ecuaciones...).
Se proponen a continuación varios ejercicios relacionados con las derivadas y sus aplicaciones (por ejemplo, cálculo de etremos, monotonía, cálculo de la imagen de una función, soluciones de ciertas ecuaciones...).
Teoremas de Taylor. Capítulo 7
 Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Ejercicios de teoría de la medida
 Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Ejercicios de teoría de la medida Pedro Alegría Capítulo. Dada una aplicación F : Ω Ω, demostrar que: a) Si A es una σ-álgebra de Ω, A = {B Ω : F B) A} lo es de Ω. b) Si A es una σ-álgebra de Ω, A = F
Taller de Cálculo Avanzado - Segundo Cuatrimestre de Práctica 3
 Taller de Cálculo Avanzado - Segundo Cuatrimestre de 2008 Práctica 3 Topología. Decir qué propiedades (abierto, cerrado, acotado) tienen los siguientes conjuntos. (a) Q. (b) N. (c) {x R : x > 0}. (d) (0,
Taller de Cálculo Avanzado - Segundo Cuatrimestre de 2008 Práctica 3 Topología. Decir qué propiedades (abierto, cerrado, acotado) tienen los siguientes conjuntos. (a) Q. (b) N. (c) {x R : x > 0}. (d) (0,
diám A = x,y A d(x,y) si A es acotado si A no es acotado. {d(x,y) : x,y A}
 Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 6 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple
 Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Órdenes de la convergencia de sucesiones. Condiciones de la convergencia lineal y cuadrática del método de iteración simple Estos apuntes están redactados por Maria de los Angeles Isidro Pérez y Egor Maximenko.
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
sup si A no es acotado.
 Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Capítulo 6 Espacios completos 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y
Análisis Matemático I
 Análisis Matemático I Funciones Implícitas Francisco Montalvo Curso 2011/12 Índice 1. Teorema de existencia de Funciones Implícitas 1 1.1. Punto fijo.............................. 1 1.2. Planteamiento............................
Análisis Matemático I Funciones Implícitas Francisco Montalvo Curso 2011/12 Índice 1. Teorema de existencia de Funciones Implícitas 1 1.1. Punto fijo.............................. 1 1.2. Planteamiento............................
Funciones integrables en R n
 Capítulo 1 Funciones integrables en R n Sean un subconjunto acotado de R n, y f : R una función acotada. Sea R = [a 1, b 1 ]... [a n, b n ] un rectángulo que contenga a. Siempre puede suponerse que f está
Capítulo 1 Funciones integrables en R n Sean un subconjunto acotado de R n, y f : R una función acotada. Sea R = [a 1, b 1 ]... [a n, b n ] un rectángulo que contenga a. Siempre puede suponerse que f está
Definición 11.1 Sea f : A E F una aplicación r-veces diferenciable en un punto a A. o
 Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Teoría de la Probabilidad Tema 2: Teorema de Extensión
 Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Teoría de la Probabilidad Tema 2: Teorema de Extensión Alberto Rodríguez Casal 25 de septiembre de 2015 Definición Una clase (no vacía) A de subconjuntos de Ω se dice que es un álgebra si A es cerrada
Tema 1 EL TEOREMA DE PEANO. 1 Compacidad en C(I; R N ): el Teorema de Ascoli-
 Tema 1 EL TEOREMA DE PEANO En este tema vamos a probar que bajo la hipótesis de ser f continua en un entorno del punto (, y 0 ), se puede garantizar la existencia, aunque no necesariamente la unicidad,
Tema 1 EL TEOREMA DE PEANO En este tema vamos a probar que bajo la hipótesis de ser f continua en un entorno del punto (, y 0 ), se puede garantizar la existencia, aunque no necesariamente la unicidad,
Nombre y Apellidos: x e 1 x 1 x f(x) = ln(x) x
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Nombre y Apellidos: Cálculo I Convocatoria de Diciembre de Diciembre de 008 DNI: (6.5 p.) ) Se considera la función f : R R definida
Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas.
 Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas. Beatriz Porras 1 Límites Las definiciones de ĺımite de funciones de varias variables son similares a las de los ĺımites de funciones
Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas. Beatriz Porras 1 Límites Las definiciones de ĺımite de funciones de varias variables son similares a las de los ĺımites de funciones
Cálculo infinitesimal Grado en Matemáticas Curso 20014/15 Clave de soluciones n o 6. Derivadas de orden superior
 Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Cálculo infinitesimal Grado en Matemáticas Curso 2004/5 Clave de soluciones n o 6 Derivadas de orden superior 70. Hallar los polinomios de Taylor del grado indicado y en el punto indicado para las siguientes
Funciones convexas Definición de función convexa. Tema 7
 Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Espacios compactos. Se pretenden alcanzar las siguientes competencias específicas:
 4 Espacios compactos En este capítulo introducimos los conceptos de espacio y subespacio compacto. Se estudian propiedades de los conjuntos compactos, así como relación entre la compacidad y las funciones
4 Espacios compactos En este capítulo introducimos los conceptos de espacio y subespacio compacto. Se estudian propiedades de los conjuntos compactos, así como relación entre la compacidad y las funciones
Examen de Cálculo infinitesimal PROBLEMAS. 1 + a + a a n a n+1
 Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
Examen de Cálculo infinitesimal. 4-2-203. PROBLEMAS. Calcular el límite de la sucesión definida por donde a >. + a + a 2 + + a n a n+ Solución. Sea x n = + a + a 2 + + a n, y n = a n+. Es claro que y n
1. Cuáles de los siguientes algoritmos son finitos?
 . Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
. Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Funciones convexas Definición de función convexa. Tema 14
 Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
1. Cuáles de los siguientes algoritmos son finitos?
 . Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
. Cuáles de los siguientes algoritmos son finitos? a Cálculo del producto de dos números enteros. b Cálculo de la división de dos números enteros. c Cálculo de la raíz cuadrada de un número natural. d
Conceptos clave para el examen de Análisis Matemático
 Conceptos clave para el examen de Análisis Matemático 1. Axioma de Dedekind. Existencia de supremos e ínfimos. Sucesiones monótonas y acotadas. Axioma de Dedekind: Dados dos subconjuntos no vacíos A y
Conceptos clave para el examen de Análisis Matemático 1. Axioma de Dedekind. Existencia de supremos e ínfimos. Sucesiones monótonas y acotadas. Axioma de Dedekind: Dados dos subconjuntos no vacíos A y
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. Conjuntos invariantes
 ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. CONJUNTOS INVARIANTES Y CONJUNTOS LÍMITE. ESTABILIDAD POR EL MÉTODO DE LIAPUNOV. Conjuntos invariantes 1. Definición. Se dice que un conjunto D Ω es positivamente
ECUACIONES DIFERENCIALES ORDINARIAS. HOJA 8. CONJUNTOS INVARIANTES Y CONJUNTOS LÍMITE. ESTABILIDAD POR EL MÉTODO DE LIAPUNOV. Conjuntos invariantes 1. Definición. Se dice que un conjunto D Ω es positivamente
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
El teorema de Lebesgue
 Capítulo 3 El teorema de Lebesgue En este capítulo estudiaremos un teorema que nos dice exactamente qué funciones son integrables y cuán grande puede ser la frontera de un conjunto para que éste tenga
Capítulo 3 El teorema de Lebesgue En este capítulo estudiaremos un teorema que nos dice exactamente qué funciones son integrables y cuán grande puede ser la frontera de un conjunto para que éste tenga
BORRADOR. Sucesiones y series numéricas Sucesiones. es un conjunto ordenado de números
 Capítulo 4 Sucesiones y series numéricas 4.1. Sucesiones Una sucesión {s n } es un conjunto ordenado de números {s 1,s 2,s 3,...,s n,...}. Técnicamente, una sucesión puede considerarse como una aplicación
Capítulo 4 Sucesiones y series numéricas 4.1. Sucesiones Una sucesión {s n } es un conjunto ordenado de números {s 1,s 2,s 3,...,s n,...}. Técnicamente, una sucesión puede considerarse como una aplicación
1.3. El teorema de los valores intermedios
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07-2 Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 07-2 Importante: Visita regularmente http://www.dim.uchile.cl/calculo. Ahí encontrarás
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Espacios métricos completos
 5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
5 Espacios métricos completos Comenzamos introduciendo las sucesiones de Cauchy, que relacionamos con las sucesiones convergentes. En el caso de que coincidan, se trata de un espacio métrico completo.
Extremos de funciones de varias variables
 Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Mariano Suárez-Alvarez. 7 de mayo, Límites superiores y límites inferiores
 ĺımsup y ĺıminf Mariano Suárez-Alvarez 7 de mayo, 2013 1.1. Definiciones 1. Límites superiores y límites inferiores 1.1. Sea (a n ) n 1 una sucesión de números reales que es acotada superiormente. Si para
ĺımsup y ĺıminf Mariano Suárez-Alvarez 7 de mayo, 2013 1.1. Definiciones 1. Límites superiores y límites inferiores 1.1. Sea (a n ) n 1 una sucesión de números reales que es acotada superiormente. Si para
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
1. Propiedades básicas de las medidas
 AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
AMARUN www.amarun.net Comisión de Pedagogía - Diego Chamorro Teoría de la medida (Nivel 2). Lección n 2: σ-álgebras y medidas EPN, verano 2009 1. Propiedades básicas de las medidas Marco de trabajo: la
Sucesiones y series de funciones
 Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
Sucesiones y series de funciones Renato Álvarez Nodarse Departamento de Análisis Matemático Facultad de Matemáticas. Universidad de Sevilla http://euler.us.es/ renato/ 8 de octubre de 2012 Sucesiones y
La Diferencial de Fréchet
 Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
U de Talca. Funciones y series de potencias Introducción. Temas Métodos para determinar series de potencias de nuevas funciones.
 Sesión 28 Funciones y series de potencias Temas Métodos para determinar series de potencias de nuevas funciones. 28. Introducción Colin Maclaurin Escocés. (698-6. Capacidades Conocer y aplicar el método
Sesión 28 Funciones y series de potencias Temas Métodos para determinar series de potencias de nuevas funciones. 28. Introducción Colin Maclaurin Escocés. (698-6. Capacidades Conocer y aplicar el método
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites. Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites
 Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites 1. Definición de límite DEF. Sea f : A R R y a A Se dice que l R es el límite de f cuando x tiende a a, si para todo entorno de l, existe un entorno
Tema X: LÍMITES Y CONTINUIDAD DE FUNCIONES X.2. Límites 1. Definición de límite DEF. Sea f : A R R y a A Se dice que l R es el límite de f cuando x tiende a a, si para todo entorno de l, existe un entorno
A continuación daremos algunos teoremas de unicidad para un problema de valores iniciales de la siguiente forma x = f (t, x) (3.1)
 3 Teoremas de Unicidad A continuación daremos algunos teoremas de unicidad para un problema de valores iniciales de la siguiente forma x = f (t, x) (3.1) x(t ) = x. 3.1 Teorema de Unicidad de Peano Teorem
3 Teoremas de Unicidad A continuación daremos algunos teoremas de unicidad para un problema de valores iniciales de la siguiente forma x = f (t, x) (3.1) x(t ) = x. 3.1 Teorema de Unicidad de Peano Teorem
Cálculo diferencial e integral I. Eleonora Catsigeras
 Cálculo diferencial e integral I Eleonora Catsigeras Universidad de la República Montevideo, Uruguay 01 de setiembre de 2011. CLASE 14 complementaria. Sobre sucesiones y conjuntos en la recta real. Sucesiones
Cálculo diferencial e integral I Eleonora Catsigeras Universidad de la República Montevideo, Uruguay 01 de setiembre de 2011. CLASE 14 complementaria. Sobre sucesiones y conjuntos en la recta real. Sucesiones
El Espacio Normado R n
 Capítulo 1 El Espacio Normado R n 1. Conceptos básicos En este curso supondremos conocida la estructura de R y su topología, así como las propiedades de las funciones continuas o derivables de una variable.
Capítulo 1 El Espacio Normado R n 1. Conceptos básicos En este curso supondremos conocida la estructura de R y su topología, así como las propiedades de las funciones continuas o derivables de una variable.
Pauta 1 : Sucesiones y Continuidad
 MA1002-2 Cálculo Diferencial e Integral Profesor: Mauricio Telias Auxiliar: Arturo Merino P1. [Función por partes] Pauta 1 : Sucesiones y Continuidad 8 de agosto del 2017 Sea a R \ {0, 1} y b R. Consideremos
MA1002-2 Cálculo Diferencial e Integral Profesor: Mauricio Telias Auxiliar: Arturo Merino P1. [Función por partes] Pauta 1 : Sucesiones y Continuidad 8 de agosto del 2017 Sea a R \ {0, 1} y b R. Consideremos
Sucesiones Introducción
 Temas Límites de sucesiones. convergentes. Sucesiones divergentes. Sucesiones Capacidades Conocer y manejar conceptos de sucesiones convergentes y divergentes. Conocer las principales propiedades de las
Temas Límites de sucesiones. convergentes. Sucesiones divergentes. Sucesiones Capacidades Conocer y manejar conceptos de sucesiones convergentes y divergentes. Conocer las principales propiedades de las
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Teorema del valor medio
 Práctica 6 - Parte 1 Teorema del valor medio El teorema del valor medio para derivadas (o teorema de Lagrange) es un resultado central en la teoría de funciones reales. Este teorema relaciona valores de
Práctica 6 - Parte 1 Teorema del valor medio El teorema del valor medio para derivadas (o teorema de Lagrange) es un resultado central en la teoría de funciones reales. Este teorema relaciona valores de
