Sucesiones de Funciones
|
|
|
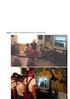
- Luz Parra Crespo
- hace 7 años
- Vistas:
Transcripción
1 Cpítulo 9 Sucesiones de Funciones 9.1. Sucesiones de Funciones. En los cpítulos 3 y 4 vimos que un sucesión de números reles es, simplemente, un colección numerble y ordend de números reles. De mner similr, un sucesión de funciones es un colección numerble y ordend de funciones. En generl supondremos que el conjunto de índices es N, unque ocsionlmente usremos los enteros no-negtivos o Z. Usremos l notción (f n ) n 1 o f n : n N} pr indicr un sucesión de funciones. Ejemplos Ls funciones f n : [, 1] R, n 1 definids por f n (x) = x n formn un sucesión cuyo conjunto de índices es N. 2. Ls funciones f : R R, n Z definids por f n (x) = nx, tmbién formn un sucesión pero con índices en Z. Definición 9.1 Se S R un conjunto y (f n ) n 1 un sucesión de funciones f n : S R y se tmbién f un función de S en R. Decimos que l sucesión (f n ) n 1 converge puntulmente f en S si, pr todo s S, l sucesión (f n (s)) n 1 converge f(s): f(s) = lim n f n(s) y entonces escribimos f n f (puntulmente). Desrrollndo esto en detlle, pr cd s S y cd ɛ > existe N N tl que f n (s) f(s) < ɛ, siempre que n N. Es fundmentl observr que l selección de N se hce luego de conocer s y ɛ, de modo que N puede depender de mbos.
2 156 CAPÍTULO 9. SUCESIONES DE FUNCIONES Ejemplos S = [, 1], f n : S R definid por 1 ns si s 1/n, f n (s) = si 1/n < s 1, y se f : S R definid por f(s) = si < s 1 1 si s =. Es trivil ver que f n () converge f() = 1, mientrs que si < s 1 y ɛ > tenemos f n (s) f(s) = f n (s) = < ɛ si n > 1/s, por lo tnto f n f puntulmente en S. f(x) 1.. f 1 f 2 f x Figur 9.1: L sucesión f n. 2. S = [, 1] y pr n N, f n : S R está definid por f n (s) = s n. Se f : S R definid por si s < 1, f(s) = 1 si s = 1... f(x). 1. Figur 9.2: L sucesión f n. Es fácil ver que f n (1) f(1) = 1, mientrs que si s < 1, f n (s) f(s) = s n < ɛ si n > log ɛ/ log s. En este cso l dependenci de N en ɛ y s es clr.. 1 x..
3 9.1. SUCESIONES DE FUNCIONES S = R y pr n N se f n : S R definid por f n (s) = s/n. Definimos f : S R por f(s) = pr s R. De nuevo es clro que f n f puntulmente en R: si s R y ɛ >, f n (s) f(s) = s n < ɛ s si n > ɛ. f(x).. ε ε f 1 f 2. f 3 f 4 f 5... x Figur 9.3: L sucesión f n. Por lo tnto el menor vlor de N pr el cul l firmción: f n (s) f(s) < ɛ cundo n > N es ciert es l prte enter de s /ɛ, y está clro que ddo ɛ > no podemos escoger un único N que hg ciert l firmción nterior pr todo s. 4. Si en el ejemplo nterior tommos S = [, 1] tenemos, por supuesto, que f n f en S, pero en este cso si ɛ > y N = [1/ɛ] entonces f n (s) f(s) < ɛ pr n > N y todo s S. L diferenci es que hor, ddo ɛ podemos hllr un N que sirve pr todo s S. f(x) f 1 ε. f 2. f x.. Figur 9.4: L sucesión f n.
4 158 CAPÍTULO 9. SUCESIONES DE FUNCIONES 5. S = [, 1], f n (s) = ns(1 s) n pr n N, entonces f n (s) pr todo s [, 1]. Observmos que f n tiene un máximo locl en s = 1/(n + 1) de modo que, medid que n crece, este máximo se desplz hci l izquierd. Además ( 1 ) ( n ) n+1 f n = e 1 n + 1 n + 1 El problem principl que nos plntemos hor es determinr si cierts propieddes de ls funciones de l sucesión, tmbién son comprtids por l función límite; en prticulr, si ls funciones f n son continus, diferencibles o integrbles, es lo mismo cierto pr f? qué relción hy entre f n y f, o entre ls integrles de ls funciones f n y l de f? Por ejemplo, si f n f puntulmente, decir que f es continu en x quiere decir que lim f(t) = f(x) t x o se lim lim f n(t) = lim f n(x) t x n n de modo que si ls funciones f n son continus en x esto es lim lim f n(t) = lim lim f n(t) t x n n t x y l pregunt que nos estmos hciendo es si d lo mismo tomr los límites en culquier orden. En generl esto no es posible sin fectr el resultdo: en los ejemplos y 2 vemos funciones discontinus que son límite de sucesiones de funciones continus. Ejemplos Pr m y n N definimos f m (x) = lim (cos m!πx)2n n Cundo m!x es entero, f m (x) = 1. Pr culquier otro vlor de x, f m (x) =. Se f(x) = lim m f m(x). Pr x irrcionl, f m (x) = y por lo tnto f(x) =. Pr x rcionl, x = p/q digmos, vemos que m!x es entero si m q y entonces f(x) = 1. Por lo tnto lim lim (cos m n m!πx)2n = si x es irrcionl, 1 si x es rcionl.
5 9.1. SUCESIONES DE FUNCIONES Se f n (x) = 1 n sennx x R, n N f(x) = lim n f n(x) = entonces f (x) = y f n(x) = n cos nx, de modo que f n no converge f, por ejemplo, f n() = n (n ) mientrs que f () =. 3. Se f n (x) = n 2 x(1 x 2 ) n pr x [, 1], n N. Podemos escribir 1 x 2 = 1 x2 1+y donde y = 1 x y por lo tnto 2 Por el teorem binomil (1 x 2 ) n = (1 + y) n = n k= pr culquier j n. Si j > 2 1 (1 + y) n. ( ) n y k > k ( ) n y j j n 2 (1 x 2 ) n n 2 = (1 + y) n < n2 ) = n 2 y j ( n j n! j!(n j)! yj y como j está fijo, j > 2, esto tiende cundo n. Por lo tnto, lim n f n (x) =. Por otro ldo es fácil ver que 1 de modo que x(1 x 2 ) n dx = 1 1 2(n + 1) (1 x2 ) n+1 1 = 1 2n + 2 f n (x)dx = n2 2n + 2. Si en lugr de f n (x) = n 2 x(1 x 2 ) n tenemos nx(1 x 2 ) n entonces lim n 1 n f n (x)dx = lim n 2n + 2 = 1 2.
6 16 CAPÍTULO 9. SUCESIONES DE FUNCIONES Ejercicios Hlle el límite puntul (si existe) de l sucesión (f n ) de funciones de S en R en cd uno de los siguientes csos: i) S = R, f n (x) = nx 1 + n 2 x 2 ii) S = R, f n (x) = n si n x n, si x > n 1 si n x n, iii) S = [, 1], f n (x) = nx(1 x 2 ) n iv) S = R, f n (x) = si x > n v) S = [, 1], f n(x) = xn nx si x 1/n vi) S = [, 1], f n(x) = n(1 x) n si 1/n < x 1 n 1 vii) S = [, 1], f n (x) = ix) S = [, 1], f n(x) = xn 1 + x n viii) S = [, ), f n (x) = xn n + x n x n x) S = R, f n(x) = x2 + nx x si x n 1 si x > n 2. Se f : I R un función continu slvo en un único punto c del intervlo I. Obteng un sucesión de funciones continus f n : I R que converj puntulmente f. Generlice pr un función f con un número finito de discontinuiddes Convergenci Uniforme. Definición 9.2 Se S R un conjunto, (f n ) n 1 un sucesión de funciones de S en R y f : S R. Decimos que l sucesión (f n ) n 1 converge uniformemente f en S si pr cd ɛ > existe N N tl que f n (s), f(s) < ɛ si n > N y s S. (9.1) Decimos que f es el límite uniforme de (f n ) y que f n f uniformemente en S. Es importnte observr que en este cso el vlor de N prtir del cul vle l relción (9.1) es el mismo pr todo s S. Ejemplo Se S = s: s > } y pr n N definimos f n (s) = s ; f(s) =. 1 + ns
7 9.2. CONVERGENCIA UNIFORME. 161 Si s S tenemos f n (s) f(s) = s 1 + ns < s ns = 1 n < ɛ pr n > 1/ɛ. Por lo tnto (f n ) converge uniformemente f en S. Si Y R podemos ilustrr l noción de convergenci uniforme con un digrm. Si f n : [, b] R converge uniformemente f, ddo ɛ > existe N tl que f(x) ɛ < f n (x) < f(x) + ɛ siempre que x [, b] y n > N. Esto quiere decir que si n > N l gráfic de l función f n debe estr dentro de l bnd del digrm. f(x).. f(x) f(x) ε f(x) + ε Figur 9.5: Convergenci Uniforme. x... Es evidente prtir de ls definiciones que si (f n ) n 1 converge uniformemente f entonces tmbién converge puntulmente. Teorem 9.1 (Condición uniforme de Cuchy) L sucesión de funciones (f n ) definids en S con vlores en R converge uniformemente en S si y sólo si pr cd ɛ > existe un entero N tl que si m N, n N, y s S entonces f n (s) f m (s) < ɛ. (9.2) Demostrción. Supongmos que f n f uniformemente en S, entonces existe N N tl que si n N y s S de modo que f n (s) f(s) ɛ 2 f n (s) f m (s) f n (s) f(s) + f(s) f m (s) ɛ siempre que n N, m N y s S. Supongmos hor que l condición de Cuchy es válid. Por l completitud de los números reles, pr cd s S l sucesión (f n (s)) converge un límite en R que llmremos f(s). Por lo tnto l sucesión (f n ) converge f en S. Flt ver que l convergenci es uniforme.
8 162 CAPÍTULO 9. SUCESIONES DE FUNCIONES Se ɛ > ddo y tomemos N de modo que (9.2) se cierto. Fijndo n y hciendo m obtenemos f n (s) f(s) < ɛ pr todo n N y todo s S. Teorem 9.2 Supongmos que f n f puntulmente en S y se M n = sup s S f n (s) f(s). Entonces f n f uniformemente en S si y sólo si M n cundo n. Demostrción. Inmedito prtir de l definición. Ejercicios En cd uno de los csos del ejercicio 2.1 determine si l convergenci es uniforme o no. 2. Estudie l convergenci uniforme de l sucesión f n (x) = x n i) en X = [, η] pr < η < 1; ii) en X = [, 1]; iii) en [, 1). 3. Verifique que l convergenci uniforme sobre un intervlo I de un sucesión de funciones es equivlente l condición siguiente: Existe un sucesión ( n) de números reles que tienden tl que pr n suficientemente grnde y pr todo x I se tiene que f n(x) n. 4. Supong que f n f uniformemente en S y g n g uniformemente en S. Demuestre que f n + g n f + g uniformemente en S. 5. Supong que f : R R es uniformemente continu y pr n N definimos f n(x) = f(x + 1/n) sobre R. Demuestre que (f n) converge uniformemente. 6. Se K un conjunto compcto y (f n) un sucesión de funciones reles continus definids sobre K que convergen puntulmente en K l función continu f. Si f n+1(x) f n(x) pr todo x K y todo n N entonces f n converge uniformemente f. 7. Definimos ls siguientes sucesiones de funciones f n (x) = x(1 + 1 ), si x R, n 1, n g n (x) = 1, n b + 1 n, si x = o x es irrcionl, si x es rcionl, x =, b >,, b primos reltivos. b Demuestre que (f n) y (g n) convergen uniformemente en todo intervlo finito pero su producto h n (x) = f n (x) g n (x) no converge uniformemente en ningún intervlo finito. 8. Supong que f n f uniformemente en S y g n g uniformemente en S. Se h n (x) = f n (x) g n (x), h(x) = f(x) g(x). El ejercicio nterior muestr que, en generl, no es cierto que h n h uniformemente en S. Demuestre que bjo l hipótesis dicionl de que ls funciones f n y g n son cotds, el resultdo sí es válido.
9 9.3. CONVERGENCIA UNIFORME Y CONTINUIDAD Convergenci Uniforme y Continuidd. Teorem 9.3 Si (f n ) es un sucesión de funciones continus de S R en R que convergen uniformemente f : S R entonces f es continu. Demostrción. Tenemos que mostrr que si x S y ɛ > entonces pr lgún δ > f(x) f(t) < ɛ si x t < δ. Supongmos que x S y ɛ >, como f n f uniformemente en S, existe N N tl que f n (t) f(t) < ɛ si n > N y t S. 3 Escogemos n > N, como f n es continu existe δ > tl que f n (x) f n (t) < ɛ 3 si x t < δ. Por lo tnto, si d x t < δ f(x) f(t) f(x) f n (x) + f n (x) f n (t) + f n (t) f(t) y cd uno de los términos de l derech es menor que ɛ/3, el primero y el último por (9.3), y que n > N, y el segundo por (9.3), y que x t < δ. Por lo tnto f(x) f(t) < ɛ si x t < δ. y esto concluye l demostrción. Observción 9.1 En el ejemplo l convergenci no es uniforme pero l función límite es continu. Esto muestr que l condición del teorem es suficiente pero no necesri. Pr S R llmremos C(S) l fmili de ls funciones reles continus y cotds definids en S. Si S es compcto entonces bst con pedir que ls funciones sen continus. Pr cd función f C(S) definimos l norm supremo de f por f = sup f(x). x S Como hemos supuesto que f es cotd, f <. Además, f = si y sólo si f(x) = pr todo x S. Finlmente, si g C(S) y definimos h(x) = f(x) + g(x) entonces h C(S) y tenemos h(x) = f(x) + g(x) f(x) + g(x) f + g pr culquier x S. Por lo tnto f + g f + g. Ests tres propieddes muestrn que l función : C(S) R + es un norm.
10 164 CAPÍTULO 9. SUCESIONES DE FUNCIONES Pr f, g C(S) definimos l distnci entre ells por ρ(f, g) = f g = sup f(x) g(x). x S Lo nterior muestr que ρ es un métric sobre el espcio C(S) y el Teorem 9.2 nos dice que l sucesión (f n ) en C(S) converge f C(S) si y sólo si f n f uniformemente en S. Teorem 9.4 (C(S), ρ) es un espcio métrico completo. Demostrción. Usr los Teorems 9.1 y 9.3. Ejercicios Dé contrejemplos que muestren que si l convergenci no es uniforme, el límite no tiene por que ser continuo. 2. Supong que (f n ) es un sucesión de funciones continus de [, 1] en R que converge uniformemente un función f : [, 1] R. Pr n N definimos g n (x) = f n (x + 1/n). Demuestre que l sucesión (g n ) converge puntulmente f. 3. Si (f n ) es un sucesión de funciones continus de R en R que converge uniformemente l función f : R R, entonces pr todo x R y culquier sucesión (x n ) que converj x, se tiene que (f n (x n )) converge f(x). 4. Si ls funciones f n : E R son uniformemente continus en E y f n f uniformemente en E entonces f es uniformemente continu en E Convergenci Uniforme y Diferencición Se I R un intervlo y f n : I R, n N un sucesión de funciones que convergen puntulmente f : I R. Si pr lgún I y pr todo n N, f n es diferencible en, es nturl preguntrse si f es diferencible en y si (f n()) converge f (). Plnteds de est mner, mbs pregunts tienen respuests negtiv. Es posible que f no se diferencible en y si lo es, puede suceder que (f n()) no converj f () o simplemente que no converj en bsoluto. Ejemplos Se I = R, f n (x) = x 1+nx pr x R y n N, y f(x) = pr x R. 2 Entonces si x, f n (x) 1 n x cundo n y como f n () =, vemos que f n f puntulmente en R. Evidentemente f () = y f n(x) = 1 nx2 (1+nx 2 ), f n() = 1 de modo que f n() no converge f () ún 2 cundo (f n()) converge.
11 9.4. CONVERGENCIA UNIFORME Y DIFERENCIACIÓN Se I = R, f n (x) = nx 1+n 2 x 2 pr x R, n N y f(x) = pr todo x R. Es fácil ver de nuevo que f n f puntulmente en R y que demás f n() = n. En este cso f es diferencible en pero f n() no converge. 3. Se I = (, ), f n (x) = 1 x 1+x n pr x I, n N y f : I R definid por f(x) = 1 x si < x 1, si x > 1 No es difícil ver que f n f puntulmente en I y que f no es diferencible en 1. Como f n(1) = 1/2, (f n(1)) converge pero f no es diferencible en Se I = (, ), f n (x) = xn 1+x n pr x I, n N y si < x < 1, f(x) = 1/2 si x = 1 1 si x > 1. De nuevo es posible mostrr que f n f puntulmente en I y que f n(1) = n/4 de modo que f no es diferencible en 1 y (f n(1)) no converge. Teorem 9.5 Se (f n ) un sucesión de funciones reles que son diferencibles en el intervlo (, b). Supongmos que l menos pr un punto x (, b) l sucesión (f n (x )) converge. Supongmos demás que existe un función g tl que f n g uniformemente en (, b). Entonces i) Existe un función f tl que f n f uniformemente en (, b). ii) Pr todo x (, b) l derivd f (x) existe y es igul g(x). Demostrción. Fijmos z (, b) y definimos un nuev sucesión de funciones g n g n (x) = fn(x) f n(z) x z, si x z, f n(z), si x = z. (9.3) Est sucesión depende de l selección de z. L sucesión g n (z) = f n(z) converge por hipótesis. Vemos que (g n ) converge uniformemente en (, b). Si x z tenemos h(x) h(z) g n (x) g m (x) = x z donde h(x) = f n (x) f m (x). Por hipótesis h (x) existe pr todo x (, b) y vle f n(x) f m(x). Usndo el Teorem del Vlor Medio obtenemos g n (x) g m (x) = f n(ξ) f m(ξ),
12 166 CAPÍTULO 9. SUCESIONES DE FUNCIONES donde ξ está entre x y z. Como, por hipótesis, (f n) converge uniformemente en (, b), podemos usr est relción y el criterio de Cuchy pr deducir que (g n ) converge uniformemente en (, b). Vemos hor que (f n ) converge uniformemente en (, b) Tomemos z = x y recordemos que por hipótesis (f n (x )) converge. A prtir de 9.3 obtenemos f n (x) = f n (x ) + (x x )g n (x) que es válid pr todo x (, b). Por lo tnto f n (x) f m (x) = f n (x ) f m (x ) + (x x )(g n (x) g m (x)). Usndo de nuevo el criterio de Cuchy, est ecución demuestr l convergenci uniforme de (f n ) en (, b). Esto demuestr (i). Pr demostrr (ii) se G(x) = lim n g n (x) donde g n se define por (9.3) pr un punto rbitrrio z (, b) Como por hipótesis l derivd f n existe, se tiene que lim x z g n (x) = g n (z), es decir, ls funciones g n son continus en z. Como g n G uniformemente en (, b), l función límite G tmbién es continu en z. Esto quiere decir que Pero pr x z tenemos G(z) = lim x z G(x), (9.4) G(x) = lim g f n (x) f n (z) n(x) = lim = n n x z f(x) f(z). x z Por lo tnto (9.4) dice que l derivd f (z) existe y es igul G(z). Pero G(z) = lim n g n(z) = lim n f n(z) = g(z), y en consecuenci f (z) = g(z). Como z (, b) es rbitrrio esto concluye l demostrción. Observción 9.2 Ls condiciones del teorem son suficientes pero no necesris. Por ejemplo, en el intervlo [, 1], f n (x) = x n /n converge f(x) = pr todo x [, 1] y f n f puntulmente pero no uniformemente Ejercicios Pr n N definimos f n : R R por f n (x) = x/(1 + nx 2 ). Muestre que (f n ) converge uniformemente un función f y que l ecución f (x) = lim f n(x) es válid. 2. Estudie l convergenci de l serie Σe n cos n 2 x y demuestre que su sum es un función infinitmente diferencible en R.
13 9.5. INTEGRACIÓN DE SUCESIONES DE FUNCIONES Demuestre l convergenci uniforme en R de l serie 1 cos n 2 x n 2. Converge uniformemente l serie de derivds? 4. Considere l sucesión ( 1 f n(x) = n + x2) 1/2 2 Demuestre que f n converge uniformemente en [ 1, 1] un función f(x). Determine si f es diferencible. Pr cuáles vlores de x es cierto que lím n f n(x) = f (x)? 5. Se f n(x) = x/(1 + nx 2 ) pr x R, n 1. Hlle f(x) = lím n f n(x) y g(x) = lím n f n(x) ) Demuestre que f (x) existe pr todo x pero que f () g(). Pr qué vlores de x se tiene que f (x) = g(x)? b) En cuáles subintervlos de R se tiene que f n f uniformemente? c) En cuáles subintervlos de R se tiene que f n g uniformemente? 6. Se f n (x) = e n2 x 2 /n pr x R, n 1. Demuestre que f n uniformemente en R, que f n putulmente en R pero que l convergenci de (f n) no es uniforme en ningún intervlo que conteng l origen Integrción de sucesiones de funciones. Después de l discusión de ls secciones nteriores es nturl plnterse si dd un sucesión f n R[, b] con límite puntul f es cierto que f R[, b] y si lim n f n dx = fdx. Ejemplos Se q n, n 1} un enumerción de los rcionles en [, 1]. Pr n N definimos f n : [, 1] R por 1 si x q 1,..., q n } f n (x) = si no Pr cd n tenemos que 1 f ndx =, pero l sucesión f n converge puntulmente l función f : [, 1] R definid por 1 si x es rcionl f(x) = si x es irrcionl y f / R[, b].
14 168 CAPÍTULO 9. SUCESIONES DE FUNCIONES 2. Definimos f n : [, 1] R por f n (x) = n si x (, 1/n) si no entonces f n R[, 1] y 1 f ndx = 1. Por otro ldo f n f en [, 1] donde f(x) = pr x [, 1]. En este cso f R[, 1] pero 1 lim n f n dx = 1 1 fdx. Teorem 9.6 Se f n un sucesión en R[, b] que converge uniformemente en [, b] f : [, b] R. Entonces f R[, b] y lim n f n dx = fdx. Demostrción. Se ɛ >, pr lgún N N f n (x) f(x) < ɛ 4(b ) si n N, x [, b], (9.5) de donde obtenemos f(x) < f N (x) + ɛ 4(b ) pr todo x [, b], de modo que f es cotd. Pr n N definimos g n = f f n. A prtir de (9.5) obtenemos que si E [, b] no es vcío, ɛ 4(b ) m(g ɛ n, E) M(g n, E) 4(b ) si n N, donde m(g n, E) = infg n (x): x E} y M(g n, E) = supg n (x): x E}. Por lo tnto pr culquier P P[, b] S(P, g n ) I(P, g n ) ɛ 2 si n N y demás S(P, f n + g n ) S(P, f n ) + S(P, g n ) I(P, f n + g n ) I(P, f n ) + I(P, g n ). Escogemos n N y lo fijmos. Como f n R[, b] existe P P[, b] tl que S(P, f n ) I(P, f n ) < ɛ 2
15 9.5. INTEGRACIÓN DE SUCESIONES DE FUNCIONES. 169 de donde obtenemos S(P, f) I(P, f) = S(P, f n + g n ) I(P, f n + g n ) S(P, f n ) I(P, f n ) + S(P, g n ) I(P, g n ) < ɛ de modo que f R[, b]. Además, por (9.5) y monotoní, si n N y entonces si n N. Por lo tnto f f n dx (f f n )dx y esto concluye l demostrción. f n dx ɛ 4(b ) dx = ɛ 4 f f n dx < ɛ fdx Corolrio 9.1 Si (f n ) es un sucesión de funciones en C[, b] que converge uniformemente en [, b] f : [, b] R, entonces f R[, b] y lim n f n dx = lim f n dx = n fdx. Ejercicios Se (f n ) un sucesión de funciones reles y continus que converge uniformemente en [, b] f. Definimos F n y F en [, b] por F n (x) = x f ndt, F (x) = fdt pr x [, b]. Demuestre que Fn converge uniformemente F en [, b]. x 2. Considere ls siguientes sucesiones de funciones en [, 1] () f n (x) = n 2 x si x 1 n ; (b) f n (x) = n 2 (x 2 n ) si 1 n x 2 n : (c) f n(x) = si 2 n x 1. En cd cso dibuje l gráfic de f n, hlle el límite de l sucesión (f n ) y clcule 1 fn(x)dx. Qué concluye? 3. Si g es un función rel y continu definid sobre [, b] y (f n ) es un sucesión de funciones reles y continus que converge uniformemente en [, b] f, entonces lim n f n(x)g(x)dx = f(x)g(x)dx. 4. Supong que g y f n, n N, están definids sobre (, ), son integrbles sobre [t, T ] pr culesquier < t < T <, f n g, f n f uniformemente en culquier subconjunto compcto de (, ) y g(x)dx <. Pruebe que lim n f n (x)dx = f(x)dx.
16 17 CAPÍTULO 9. SUCESIONES DE FUNCIONES 5. Pr ls siguientes sucesiones de funciones f n : [, 1] R clcule lím n f n(x) y determine si l convergenci es uniforme. Determine tmbién si es posible intercmbir límites e integrles. ) f n (x) = nx (1 + n 2 x 2 ), b) f n 2 x n(x) = 2 (1 + n 2 x 2 ) 2 6. Se (f n ) un sucesión de funciones reles continus definids en [, 1] y supong que f n f uniformemente en [, 1]. Es cierto que 1 1/n lím n f n (x) dx = 1 f(x) dx? 9.6. Convergenci Acotd Definición 9.3 Se (f n ) un sucesión de funciones definids en un conjunto E. Decimos que (f n ) es cotd (puntulmente) en E si pr cd x E l sucesión de números reles (f n (x)) es cotd, es decir, existe un función φ : E R tl que f n (x) φ(x), x E, n 1. Decimos que (f n ) es uniformemente cotd en E si existe un número M tl que f n (x) M, x E, n 1. Definición 9.4 Un sucesión de funciones (f n ) converge cotdmente en T si (f n ) converge puntulmente y es uniformente cotd. Teorem 9.7 (Arzelá) Se (f n ) un sucesión que converge cotdmente f en [, b] y supongmos que cd f n es integrble según Riemnn en [, b] y tmbién f R[, b]. Entonces lim n f n (x) dx = lim f n(x) dx = n f(x) dx. Demostrción. Se g n (x) = f n (x) f(x), demostrremos que lim n g n (x) dx =. Pr esto vmos definir un nuev sucesión de funciones (h n ) de l siguiente mner: Observmos que h n (x) = supg n (x), g n+1 (x),... } si x [, b], n 1. g n (x) h n (x), h n+1 (x) h n (x), lim n h n(x) =.
17 9.6. CONVERGENCIA ACOTADA 171 Por lo tnto g n (x) dx = g n (x) dx h n (x) dx I n. Est últim integrl inferior existe porque ls h n son funciones cotds en [, b]. Sin embrgo, h n puede no ser integrble según Riemnn. Por otro ldo g n sí es integrble según Riemnn. Pr demostrr el teorem bst con ver que I n cundo n. Observmos que est sucesión converge un límite no negtivo y que I n+1 I n. Se I = lim n I n. Vemos que l desiguldd I > nos llev un contrdicción. Supongmos que I >. Como I n I > I/2 pr todo n, existe un prtición P n de [, b] tl que l sum inferior de Riemnn I(P n, h n ) stisfce I(P n, h n ) > I/2. (9.6) Se ε = I/2(M + b ) donde M es un cot uniforme pr (h n ) en [, b]. Entonces l sum inferior I(P n, h n ) se puede dividir en dos prtes de l siguiente mner: I(P n, h n ) = m i (h n ) x i + m i (h n ) x i i A(n) i/ A(n) donde A(n) = i : m i (h n ) > ε}. L ecución (9.6) implic I 2 < i A(n) M x i + ε i / A(n) x i M i A(n) x i + ε(b ), de donde obtenemos que i A(n) x i > ε. Como el refinmiento de un prtición ument ls sums inferiores, no hy pérdid de generlidd en suponer que ls prticiones son monótons: P n P n+1. Se S n l unión de los subintervlos [x i 1, x i ] de P n pr los cules i A(n). Entonces S n es cerrdo y x i > ε. i A(n) Esto implic que hy l menos un x que pertenece infinitos conjuntos S n y pr este x tenemos que h n (x) > ε, lo que contrdice l hipótesis de que h n (x) cundo n pr todo x. Est contrdicción implic que I =. Ejercicios Supong que l sucesión f n : E R converge uniformemente l función f. Demuestre que f es cotd si y solmente si existe N N tl que f n es cotd pr todo n N. En cso firmtivo demuestre que f = lim n f n. 2. Si l sucesión f n : E R es cotd y f n f uniformemente en E entonces f es cotd y (f n) es un sucesión uniformemente cotd.
18 172 CAPÍTULO 9. SUCESIONES DE FUNCIONES 9.7. Equicontinuidd Nuestro objetivo hor es determinr bjo qué condiciones podemos grntizr que un colección E de funciones continus definids sobre un dominio común, tiene un subsucesión uniformemente convergente. Sbemos que pr un conjunto de números reles E l condición necesri y suficiente pr que tod sucesión x n E teng un subsucesión convergente es que el conjunto E se cotdo. En el cso de funciones est condición no es suficiente. Incluso si (f n ) es un sucesión uniformemente cotd de funciones continus definids sobre un conjunto compcto K, no necesrimente existe un subsucesión que converj puntulmente en K. Ejemplo 9.7 Se f n (x) = sen nx, pr x 2π, n 1. Supongmos que existe un sucesión (n k ) tl que (sen n k x) converge pr todo x [, 2π]. En ese cso se debe tener lim (sen n kx sen n k+1 x) =, pr x 2π. k Por lo tnto tmbién se tiene lim (sen n kx sen n k+1 x) 2 =, pr x 2π. k Por el teorem 9.7 esto implic que 2π lim k Sin embrgo, no es difícil demostrr que 2π lim k (sen n k x sen n k+1 x) 2 =. (sen n k x sen n k+1 x) 2 = 2π. y esto es un contrdicción que viene de suponer que existe un subsucesión convergente. L segund pregunt es si tod tod sucesión convergente contiene un subsucesión uniformemente convergente. El siguiente ejemplo muestr que esto no es cierto en generl, ún si l sucesión es uniformemente cotd en un conjunto compcto. Ejemplo 9.8 Se n 2 x pr x 1/n 2, f n (x) = n2 x n n 1 pr 1/n 2 x 1/n, pr 1/n x 1.
19 9.7. EQUICONTINUIDAD 173 Pr est sucesión de funciones se tiene que f n (x) 1, de modo que (f n ) es uniformemente cotd en [, 1] y se tiene que lim n f n (x) = pr todo x [, 1]. Sin embrgo, f n ( 1 n 2 ) = 1, n 1, de modo que ningun subsucesión puede converger uniformemente en [, 1]. El concepto que necesitmos pr responder ests pregunts es el de equicontinuidd. Definición 9.5 Se F un conjunto de funciones reles definids sobre un dominio común E. Decimos que F es equicontinu si ddo culquier ε > existe δ > tl que si x, y E pr tod f F x y < δ f(x) f(y) < ε, Como vemos, est condición es más fuerte que continuidd uniforme, porque se pide que ddo ε > exist un δ que sirv pr tods ls funciones de l fmili F. Por lo tnto, tod función en un fmili equicontinu, es uniformemente continu. Ejemplos L sucesión de funciones continus f n (x) = nx definids en todo R no es equicontinu en ningún punto x R. En efecto, ddo ε = 1/2 pr culquier δ > podemos hllr n N tl que (1/n) < δ y en este cso el punto y = x + (1/n) cumple y x < δ pero f n (y) f n (x) = 1 > ε. 2. Se F un conjunto de funciones derivbles en un intervlo I tles que f (x) c pr ciert constnte c > pr tod f F y todo x I. Entonces F es equicontinu. En efecto, se x I, ddo ε > tomemos δ = ε/c. Si y I con x y < δ entonces por el Teorem del Vlor Medio tenemos que f(y) f(x) c y x < ε pr tod f F. Teorem 9.8 Si un sucesión equicontinu de funciones f n : E R converge puntulmente en un subconjunto denso D E, entonces converge uniformemente en cd subconjunto compcto K E. Demostrción. Ddo ε > demostrremos que existe N N tl que m, n N f m (x) f n (x) < ε x K,
20 174 CAPÍTULO 9. SUCESIONES DE FUNCIONES y por el criterio de Cuchy pr convergenci uniforme esto es suficiente pr demostrr el teorem. Como l sucesión (f n ) converge puntulmente en D, pr todo d D existe N d N tl que m, n N d f m (d) f n (d) < ε 3. (9.7) Por otro ldo l equicontinuidd de l sucesión de funciones implic que pr todo y K existe un intervlo bierto J y de centro y tl que x, z E J y f n (x) f n (z) < ε, n N. (9.8) 3 Como K es c ompcto y y J y es un cubrimiento bierto de K, podemos extrer un subcubrimiento finito: K J 1 J r. Como D es denso en E, en cd bierto J i podemos escoger d i J i D. Se N = máxn d1, N d2,..., N dr }, entonces si m, n N y x K existe i tl que x J i y en consecuenci f m (x) f n (x) f m (x) f m (d i ) + f m (d i ) f n (d i ) + f n (d i ) f n (x) Usndo (9.7) y (9.8) obtenemos que m, n N, x K f m (x) f n (x) < ε. Teorem 9.9 Se E R un conjunto numerble. Tod sucesión cotd de funciones f n : E R tiene un subsucesión que converge puntulmente. Demostrción. Se E = x 1, x 2... }. L sucesión de números reles (f n (x 1 )) n 1 es cotd y por lo tnto posee un subsucesión convergente. Por lo tnto hy un sucesión (n (1) k ) de números nturles tl que existe 1 = lim f k n (1) k (x 1 ). Ahor considermos l sucesión (f (1) n (x 2 )) k 1, que tmbién es un sucesión k cotd de números reles y por lo tnto tiene un subsucesión convergente. Es decir, existe (n (2) k ) subsucesión de (n(1) k ) tl que existe 2 = lim f k n (2) k (x 2 ). Procediendo inductivmente de est mner pr cd nturl i obtenemos un sucesión (n (i) k ), que es subsucesión de (n(i 1) k ), tl que existe i = lim f k n (i) k (x i ).
21 9.7. EQUICONTINUIDAD 175 Definimos hor un nuev sucesión infinit (m i ) i 1 tomndo como i-ésimo elemento el número n (i) i, es decir, el i-ésimo elemento de l i-ésim sucesión. L sucesión de funciones (f mi ) i 1 converge en todos los puntos de E porque pr culquier punto x r E, l sucesión (f mi (x r )) i 1 es, prtir del r-ésimo elemento, un subsucesión de (f (r) n (x r )) i 1, que converge r. i Teorem 9.1 (Arzelá-Ascoli) Se E R un conjunto compcto. Tod sucesión equicontinu y cotd de funciones f n : E R tiene un subsucesión uniformemente convergente. Demostrción. Como E es compcto tiene un subconjunto numerble y denso D E. Por el teorem 9.9, (f n ) tiene un subsucesión que converge puntulmente en D. Est mism subsucesión converge uniformemente en E por el teorem 9.8. Teorem 9.11 Se F un fmili de funciones continus definids en un conjunto compcto K R. Ls siguientes proposiciones son equivlentes (1) F es equicontinu y uniformemente cotd. (2) F es equicontinu y cotd. (3) Tod sucesión de funciones f n F tiene un subsucesión uniformemente convergente. Demostrción. Es evidente que (1) (2) y por el teorem nterior tenemos que (2) (3). Flt demostrr que (3) (1). Supongmos que esto es flso, entonces: (3) es cierto pero existe un punto x K en el cul F no es equicontinu, es decir, existe ε > pr el cul podemos obtener un sucesión de puntos x n K con x n x < 1/n y funciones f n F tles que f n (x n ) f n (x ) ε, n 1. Psndo un subsucesión si es necesrio, por l hipótesis (3), tenemos que f n f uniformemente en K. Entonces l sucesión (f n ) es equicontinu: Existe δ > tl que x K, x x < δ f n (x) f n (x ) ε pr todo n N. En prticulr, si tommos n > 1/δ obtenemos que x n x < δ, de donde f n (x n ) f n (x ) < ε, lo que es un contrdicción. Por lo tnto (3) implic que F es equicontinu. Finlmente vemos que F es uniformemente cotd. Si no fuese sí, pr cd n podrímos hllr un función f n F tl que sup x K f n (x) > n. En consecuenci ningun subsucesión serí uniformemente cotd, y esto contrdice l hipótesis en virtud del ejercicio
22 176 CAPÍTULO 9. SUCESIONES DE FUNCIONES Ejercicios 9.7 Pr lgunos de los siguientes ejercicios necesitmos l siguiente definición. Un fmili F de funciones reles definids en un conjunto E de un espcio métrico X es equicontinu en un punto x E si ddo ε > existe δ > tl que f(x) f(y) < ε siempre que d(x, y) < δ, y E y f F. Si est condición se cumple en todos los puntos del conjunto E decimos que F es equicontinu puntulmente en E. 1. Si los conjuntos de funciones reles F 1,..., F n definids sobre un dominio común E son equicontinuos en el punto x, entonces l unión F 1 F n es equicontinu en x. 2. Demuestre que l sucesión de funciones del ejemplo 9.8 es equicontinu en todo punto mientrs que l del ejemplo 9.7 no lo es en ningún punto. 3. L sucesión de funciones f n (x) = nx 2 posee derivds cotds en pero no es equicontinu en ese punto. 4. Si un sucesión de funciones continus F n : E R converge uniformemente f : E R, entonces el conjunto F = f, f 1,..., f n,... } es equicontinuo. 5. Un conjunto de polinomios de grdo menor o igul que k uniformemente cotdos en un intervlo compcto es equicontinuo en ese intervlo. 6. Decimos que un sucesión de funciones f n : E R converge debilmente un función f : E R si f n (x) f(x) en todo punto x E en el cul f se continu. Se D R denso. Demuestre que si un sucesión de funciones monótons f n : R R converge puntulmente en D un función f : R R entonces (f n) converge debilmente f en R. 7. Tod sucesión cotd de funciones monótons f n : R R tiene un subsucesión que converge debilmente un función monóton f : R R, l cul se puede tomr continu por l derech. (Sugerenci: use el teorem 9.9). 8. Se (f n ) un sucesión equicontinu y cotd definid en un compcto E R. Si tod subsucesión uniformemente convergente en E tiene el mismo límite f : E R entonces f n f uniformemente en E. 9. Dd un sucesión de funciones dos veces diferencibles f n : E R donde E es un intervlo, supong que f n f puntulmente en E, que (f n(x )) es cotd pr lgún x E y que (f n ) es uniformemente cotd en E. Demuestre que f C El Teorem de Aproximción de Weierstrss Definimos l sucesión ϕ n (x) = µ n (1 x 2 ) n si 1 x 1 en otro cso, donde µ n = (2n + 1) n
23 9.8. EL TEOREMA DE APROXIMACIÓN DE WEIERSTRASS177 se escoge de modo que ϕ n (x) dx = 1. (9.9) A medid que n crece ests funciones se concentrn más y más lrededor del origen. Lem 9.1 Pr todo ε > y todo δ > existe un entero N tl que pr n N, δ 1 1 ε < δ δ ϕ n (x) dx + ϕ n (x) dx 1, (9.1) 1 δ ϕ n (x) dx < ε. (9.11) Demostrción. Comenzmos con l demostrción de (9.11). Y que l función ϕ n es simétric, bst considerr el cso x. Como 1 x 2 1 x pr x 1, tenemos 1 (1 x 2 ) n dx 1 (1 x) n dx = 1 n + 1 y en consecuenci µ n (n + 1)/2. Por lo tnto tenemos, pr δ x 1 ϕ n (x) ϕ n (δ) n + 1 (1 δ 2 ) n. 2 Pero (n + 1)(1 δ 2 ) n y en consecuenci, pr n suficientemente grnde ϕ n (x) ε/2 pr δ x 1. Ahor (9.11) se obtiene prtir de ls propieddes de l integrl. Ls desigulddes en (9.1) se obtienen restndo (9.11) de (9.9). Un sucesión que stisfce (9.9), (9.1) y (9.11) se conoce como un sucesión de Dirc. Teorem 9.12 (de Aproximción de Weierstrss) Se f : [, b] R un función continu. Pr todo ε > existe un polinomio p(x) tl que p(x) f(x) < ε pr todo x [, b] (9.12) Demostrción. Podemos suponer que < < b < 1 pues en cso contrrio podemos usr un trnsformción de l form x α + βx pr constntes decuds α y β. Luego extendemos f(x) un función continu en [, 1], por ejemplo poniendo f(x) = f() pr x < y f(x) = f(b) pr b < x 1. Ahor, pr ξ [, b] definimos p n (ξ) = 1 1 f(x)ϕ n (x ξ) dx = µ n f(x)(1 (x ξ) 2 ) n dx. (9.13)
24 178 CAPÍTULO 9. SUCESIONES DE FUNCIONES Pr clculr el error cometido l proximr f(ξ) por p n (ξ) usmos l desiguldd tringulr f(ξ) p n (ξ) + 1 ξ+δ + f(ξ) f(x)ϕ n (x ξ) dx ξ δ ξ+δ f(x)ϕ n (x ξ) dx ξ δ ξ+δ ξ δ ξ+δ ξ δ f(x)ϕ n (x ξ) dx f(ξ)ϕ n (x ξ) dx ϕ n (x ξ) dx f(ξ). (9.14) Ahor fijmos ε >. Como f es continu en [, 1], es uniformemente continu y por lo tnto existe δ > independiente de ξ tl que x ξ < 2δ f(x) f(ξ) < ε. (9.15) Podemos escoger δ de modo que δ y δ 1 b. Por lo tnto siempre tenemos que [ξ δ, ξ + δ] [, 1]. Además l función f(x) es cotd: existe M tl que f(x) M pr todo x [, 1]. Los tres términos l derech de l ecución (9.14) se pueden cotr de l siguiente mner: Pr el primero usmos l cotción de f y l ecución (9.11): ξ δ 1 f(x)ϕ n (x ξ) dx + δ 1 ξ+δ f(y + ξ) ϕ n (y) dy + f(x)ϕ n (x ξ) dx 1 δ f(y + ξ) ϕ n (y) dy Mε. (9.16) De mner similr se cot el tercer término. Finlmente el segundo término está cotdo por ξ+δ ξ δ En consecuenci tenemos f(x) f(ξ) ϕ n (x ξ) dx ε. f(ξ) p n (ξ) (2M + 1)ε pr n suficientemente grnde. Esto demuestr el teorem. Corolrio 9.2 Pr todo intervlo [, ] existe un sucesión (p n ) de polinomios reles que converge x uniformemente en [, ] pr los cules se tiene que p n () =. Demostrción. Por el teorem nterior existe un sucesión de polinomios (p n) que converge x uniformemente en [, ]. En prticulr p n() cundo n. Los polinomios p n (x) = p n(x) p n() tienen ls propieddes deseds.
25 9.8. EL TEOREMA DE APROXIMACIÓN DE WEIERSTRASS179 Definición 9.6 Un fmili de funciones reles A definids en un conjunto E es un álgebr si pr f, g A, λ R se tiene que 1. f + g A. 2. fg A. 3. λf A. Si demás se tiene que f A siempre que f se el límite uniforme de l sucesión (f n ) con f n A decimos que A es uniformemente cerrd. Se B el conjunto de ls funciones que son límite de sucesiones uniformemente convergentes de elementos de A. Decimos que B es l clusur uniforme de A. Por ejemplo, el conjunto de los polinomios es un álgebr y el teorem de proximción de Weierstrss dice que l clse de ls funciones continus en [, b] es l clusur uniforme del conjunto de los polinomios en [, b]. Teorem 9.13 Se B l clusur uniforme de un álgebr A de funciones cotds. Entonces B es un álgebr uniformemente cerrd. Demostrción. Si f, g B existen sucesiones (f n ), (g n ) que convergen uniformemente f y g respectivmente y f n A, g n A. Como ls funciones son cotds es fácil mostrr que f n + g n f + g, f n g n fg, λf n λf, donde λ R y l convergenci es uniforme en todos los csos. En consecuenci f + g B, fg B y λf B, de modo que B es un álgebr. Por lo tnto, B es uniformemente cerrd. Definición 9.7 Se A un fmili de funciones definids sobre un conjunto E. Decimos que A sepr puntos en E si pr todo pr de puntos distintos x, y en E existe un función f A tl que f(x) f(y). Si pr cd punto x E existe un función g A tl que g(x), decimos que A nunc se nul en E. El álgebr de los polinomios de un vrible tiene ests propieddes en R. Un ejemplo de un álgebr que no sepr puntos en el conjuntos de los polinomios de grdo pr en [ 1, 1], y que f( x) = f(x) pr tod función pr f. Teorem 9.14 Se A un álgebr de funciones en un conjunto E tl que A sepr puntos en E y A no se nul en ningún punto de E. Se x, y puntos distintos de E y λ, µ constntes. Entonces A contiene un función f tl que f(x) = λ, f(y) = µ.
26 18 CAPÍTULO 9. SUCESIONES DE FUNCIONES Demostrción. Por hipótesis podemos encontrr funciones g, h y k tles que Ponemos g(x) g(y), h(x), k(y). u = gk g(x)k, v = gh g(y)h. Entonces u, v A, u(x) = v(y) =, u(y) y v(x). Por lo tnto f = λv v(x) + µu u(y) tiene ls propieddes que buscmos. Teorem 9.15 (Stone-Weierstrss) Se A un álgebr de funciones reles continus sobre un conjunto compcto K. Si A sepr puntos en K y si A no se nul en ningún punto de K, entonces l clusur uniforme B de A consiste de tods ls funciones reles y continus sobre K. Demostrción. Dividimos l prueb en cutro psos. Pso 1. Si f B entonces f B. Demostrción. Se = sup x K f(x) y se ε > ddo. Por el corolrio 9.2 existen números reles c 1,..., c n tles que n c i y i y < ε, pr y. (9.17) i=1 Como B es un álgebr, l función g(x) = n c i f i (x) i=1 pertenece B. Por l definición de y (9.17) tenemos g(x) f(x) < ε pr x K. Como B es uniformemente cerrd esto muestr que f B. Pso 2. Si f, g B entonces máx(f, g) B y min(f, g) B. Demostrción. El pso 2 sigue del pso 1 y ls identiddes máx(f, g) = f + g f g +, 2 2 min(f, g) = f + g f g. 2 2 Iterndo el resultdo puede extenderse culquier conjunto finito de funciones: Si f 1,... f n B entonces máx(f 1,..., f n ) B y min(f 1,..., f n ) B.
27 9.8. EL TEOREMA DE APROXIMACIÓN DE WEIERSTRASS181 Pso 3. Dd un función rel f, continu sobre K, un punto x K, y ε >, existe un función g x B tl que g x (x) = f(x) y g x (t) > f(t) ε pr todo t K. (9.18) Demostrción. Como A B y A stisfce ls hipótesis del teorem 9.14, tmbién ls stisfce B. Por lo tnto pr todo y K podemos hllr un función h y B tl que h y (x) = f(x), h y (y) = f(y). (9.19) Por l continuidd de h y existe un conjunto bierto J y que contiene y tl que h y (t) > f(t) ε pr t J y. (9.2) Como K es compcto, existe un conjunto finito de puntos y 1,..., y n tl que Ponemos K J y1 J yn. (9.21) g x = máx(h y1,..., h yn ). Por el segundo pso, g B y ls relciones (9.19) (9.21) muestrn que g x tiene ls demás propieddes. Pso 4. Dd un función rel f continu en K, y ε >, existe un función h B tl que h(x) f(x) < ε pr todo x K (9.22) Como B es uniformemente cerrd, esto es equivlente l conclusión del teorem. Demostrción. Consideremos ls funciones g x pr x K que construimos en el pso nterior. Por l continuidd de g x existen conjuntos biertos V x que contienen x tles que g x (t) < f(t) + ε pr todo t V x. (9.23) Como K es compcto, existe un conjunto finito de puntos x 1,..., x m tles que K V x1 V xm. (9.24) Ponemos h = min(g x1,..., g xm ). Por el pso 2, h B y por (9.18) mientrs que (9.23) y (9.24) implicn h(t) > f(t) ε pr t K, (9.25) h(t) < f(t) + ε pr t K. (9.26) Finlmente (9.22) sigue de (9.25) y (9.26).
28 182 CAPÍTULO 9. SUCESIONES DE FUNCIONES Ejemplo 9.1 El siguiente ejemplo muestr que l hipótesis de compcidd en K es importnte. Consideremos un conjunto K que no se compcto, por ejemplo K = R y se x n un sucesión que no tiene ningun subsucesión convergente, por ejemplo x n = n. Considermos A = f C(R) : lim n f(x n ) existe }. Si b son números reles escogemo N N tl que n siempre que n > N y definmos el conjunto E = b} x n : n > N} y l función f(x) = dist(x, E) dist(x, ) + dist(x, E) entonces f() = 1, f(b) =, f C(R y lim n f(x n ) =. Por lo tnto f A y A sepr puntos. Por otro ldo, como A contiene l función 1, A no se nul en ningún punto de R. Vemos que l clusur uniforme de A no es C(R). Se S = x 2k, k N}, T = x 2k 1, k N} y g(x) = dist(x, T ) dist(x, T ) + dist(x, S). Entonces g (R) y g(x) = 1 si x S mientrs que g(x) = si x T, de modo que l sucesión g(x n ) no converge cundo n y por lo tnto no puede proximrse de mner uniforme por un función en A. De hecho, g f 1/2 pr tod f A. Ejercicios Demuestre que ϕ n (x) = ( n ) 1/2 e nx2, n 1, π es un sucesión de Dirc, es decir, stisfce ls condiciones (9.9), (9.1) y (9.11). Est fue l sucesión que Weierstrss usó en su demostrción. 2. Se ϕ n(x) = n si x 1/2n, en otro cso. Demuestre que pr tod función continu f(x) se tiene pr todo ξ (, b). lim n 3. Se p = y defin pr n ϕ n(x ξ)f(x)dx = f(ξ) p n+1(x) = p n(x) (x2 p n(x)). Demuestre que p n (x) x uniformemente en [ 1, 1]. (Ayud: Use l identidd x p n+1 (x) = ( x p n (x) )( 1 1 ) 2 ( x + p n(x))
29 9.8. EL TEOREMA DE APROXIMACIÓN DE WEIERSTRASS183 pr demostrr que p n(x) p n+1(x) x si x 1, y que si x 1). ( x p n (x) x 1 x 2 ) n < 2 n Use el Teorem de Aproximción de Weierstrss e inducción pr demostrr que si f tiene k derivds continus en un intervlo [, b] entonces existe un sucesión de polinomios (p n) que stisfcen p n f uniformemente en [, b] p n f uniformemente en [, b]. p (k) n f (k) uniformemente en [, b] 5. Se A un conjunto y 1 A l función indicdor de A: 1 si x A 1 A (x) = si x / A Decimos que l función g es simple si se puede escribir como g(x) = n c j 1 Aj, j=1 con A j = [ j, b j]. Demuestre que un función continu en el intervlo [, b] es el límite uniforme de funciones simples. 6. Si f es un función continu en [, b] y si f(x)p(x) dx = pr todo polinomio p, demuestre que f debe ser idénticmente igul cero.
7.1. Definición de la Integral de Riemann
 Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
Cpítulo 7 Integrl de Riemnn 71 Definición de l Integrl de Riemnn En este cpítulo supondremos, menos que se indique lo contrrio, que < b y f : [, b] R es un función cotd Definición 71 Un prtición del intervlo
Funciones continuas. Mariano Suárez-Alvarez. 4 de junio, Índice
 Funciones continus Mrino Suárez-Alvrez 4 de junio, 2013 Índice 1. Funciones continus................... 1 2. Alguns propieddes básics............ 3 3. Los teorems de Weierstrss y Bolzno... 6 4. Funciones
Funciones continus Mrino Suárez-Alvrez 4 de junio, 2013 Índice 1. Funciones continus................... 1 2. Alguns propieddes básics............ 3 3. Los teorems de Weierstrss y Bolzno... 6 4. Funciones
Integrales Impropias. Capítulo Introducción Integrales de Funciones No Acotadas
 Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
Cpítulo 8 Integrles Impropis 8.. Introducción L integrl de Riemnn tl como l hemos estudido, está definid únicmente pr funciones cotds y definids sobre intervlos cerrdos y cotdos. En este cpítulo estudiremos
El Teorema de Arzela-Ascoli Rodrigo Vargas
 El Teorem de Arzel-Ascoli Rodrigo Vrgs Definición 1. Sen M, N espcios métricos y E un conjunto de plicciones f : M N. El conjunto E se dice equicontinuo en el punto M cundo, pr todo ε > eiste δ > tl que
El Teorem de Arzel-Ascoli Rodrigo Vrgs Definición 1. Sen M, N espcios métricos y E un conjunto de plicciones f : M N. El conjunto E se dice equicontinuo en el punto M cundo, pr todo ε > eiste δ > tl que
Tema 9. La Integral de Riemann Construcción de la integral de Riemann.
 Tem 9 L Integrl de Riemnn. 9.1. Construcción de l integrl de Riemnn. Definición 9.1.1. Se I = [, b] R un intervlo cerrdo y cotdo (compcto). Se llm prtición de I todo conjunto de puntos P = {x 0, x 1,,
Tem 9 L Integrl de Riemnn. 9.1. Construcción de l integrl de Riemnn. Definición 9.1.1. Se I = [, b] R un intervlo cerrdo y cotdo (compcto). Se llm prtición de I todo conjunto de puntos P = {x 0, x 1,,
1.4. Sucesión de funciones continuas ( )
 1.4. Sucesión de funciones continus (18.04.2017) Se {f n } un sucesión de funciones f n, definids en I. Si {f n } converge uniformemente f en I y ls f n son continus en I, entonces f es continu en I. D:
1.4. Sucesión de funciones continus (18.04.2017) Se {f n } un sucesión de funciones f n, definids en I. Si {f n } converge uniformemente f en I y ls f n son continus en I, entonces f es continu en I. D:
Primitivas e Integrales
 Cpítulo 25 Primitivs e Integrles En este cpítulo vmos trbjr con funciones de un vrible. En él estbleceremos un cso prticulr del Teorem Fundmentl del Cálculo Integrl (ver [3] pr el cso generl), con el que
Cpítulo 25 Primitivs e Integrles En este cpítulo vmos trbjr con funciones de un vrible. En él estbleceremos un cso prticulr del Teorem Fundmentl del Cálculo Integrl (ver [3] pr el cso generl), con el que
4. Definición: Convergencia uniforme de una sucesión de funciones
 1. Teorem de l funcion invers Se A un ierto de R N, f : A R m un funcion de clse n (n 1), se A tl que det(jf()) 0. Entonces existe un entorno U de tl que U A tl que: (1). det(jf (x)) 0 pr todo x U (2).
1. Teorem de l funcion invers Se A un ierto de R N, f : A R m un funcion de clse n (n 1), se A tl que det(jf()) 0. Entonces existe un entorno U de tl que U A tl que: (1). det(jf (x)) 0 pr todo x U (2).
La Integral de Riemann
 Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función potencil Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función
Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función potencil Sums de Riemnn Funciones integrbles Riemnn Cálculo de l integrl Teorems de integrbilidd L función
Sucesiones y Series Numéricas
 FCEIA - Universidd Ncionl de Rosrio Métodos Numéricos - LCC 27 Profesor: Alejndro G. Mrchetti Sucesiones y Series Numérics Sucesiones Numérics Definición. Un sucesión es un función de N en R. f : N R Un
FCEIA - Universidd Ncionl de Rosrio Métodos Numéricos - LCC 27 Profesor: Alejndro G. Mrchetti Sucesiones y Series Numérics Sucesiones Numérics Definición. Un sucesión es un función de N en R. f : N R Un
Anexo 3: Demostraciones
 170 Mtemátics I : Cálculo integrl en IR Anexo 3: Demostrciones Integrl de Riemnn Demostrción de: Propieddes 264 de l págin 142 Propieddes 264.- Se f: [, b] IR un función cotd. ) Pr tod P P[, b], se verific
170 Mtemátics I : Cálculo integrl en IR Anexo 3: Demostrciones Integrl de Riemnn Demostrción de: Propieddes 264 de l págin 142 Propieddes 264.- Se f: [, b] IR un función cotd. ) Pr tod P P[, b], se verific
Pequeña síntesis de conceptos sobre sucesiones y series para la cátedra de Matemática II.
 Pequeñ síntesis de conceptos sobre sucesiones y series pr l cátedr de Mtemátic II. Altmirnd Enzo - enzo.lt@gmil.com - V1.0 15 de diciembre de 2010 Este texto fue hecho en L A TEX con los puntes tomdos
Pequeñ síntesis de conceptos sobre sucesiones y series pr l cátedr de Mtemátic II. Altmirnd Enzo - enzo.lt@gmil.com - V1.0 15 de diciembre de 2010 Este texto fue hecho en L A TEX con los puntes tomdos
Funciones de una variable real II Integrales impropias
 Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 202-203 (22/04/203??/05/203)
Notas de Integral de Riemann-Stieltjes
 Nots de Integrl de Riemnn-Stieltjes 1. Definición y propieddes Dds funciones g, F : [, b] R que cumpln ciertos requisitos, definiremos l expresión g(x)df(x) de tl mner que cundo consideremos el cso prticulr
Nots de Integrl de Riemnn-Stieltjes 1. Definición y propieddes Dds funciones g, F : [, b] R que cumpln ciertos requisitos, definiremos l expresión g(x)df(x) de tl mner que cundo consideremos el cso prticulr
La integral de Riemann
 L integrl de Riemnn Mrí Muñoz Guillermo mri.mg@upct.es U.P.C.T. Mtemátics I (1 o Ingenierí Electrónic Industril y Automátic) M. Muñoz (U.P.C.T.) L integrl de Riemnn Mtemátics I 1 / 33 Sums superior e inferior
L integrl de Riemnn Mrí Muñoz Guillermo mri.mg@upct.es U.P.C.T. Mtemátics I (1 o Ingenierí Electrónic Industril y Automátic) M. Muñoz (U.P.C.T.) L integrl de Riemnn Mtemátics I 1 / 33 Sums superior e inferior
La Integral Definida
 Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
Nivelción de Mtemátic MTHA UNLP ID Introducción Prtición L Integrl Definid Un prtición del intervlo [, b] es un sucesión de números = x x x x n = b, entre y b, tl que x i x i+ (i =,,, n ) Ejemplo: se llm
Tema 8.4: Teorema de Runge. Aproximación de funciones holomorfas por funciones racionales
 Tem 8.4: Teorem de Runge. Aproximción de funciones holomorfs por funciones rcionles Fcultd de Ciencis Experimentles, Curso 2008-09 Enrique de Amo, Universidd de Almerí Sbemos que ls funciones holomorfs
Tem 8.4: Teorem de Runge. Aproximción de funciones holomorfs por funciones rcionles Fcultd de Ciencis Experimentles, Curso 2008-09 Enrique de Amo, Universidd de Almerí Sbemos que ls funciones holomorfs
7.1. Definición de integral impropia y primeras propiedades
 Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Cpítulo 7 Integrles impropis 7.. Definición de integrl impropi y primers propieddes El concepto de integrl se etiende de mner csi espontáne situciones más generles que ls que hemos emindo hst hor. Consideremos,
Teorema del punto fijo Rodrigo Vargas
 Teorem del punto fijo Rodrigo Vrgs Definición 1. Un punto fijo de un plicción f : M M es un punto x M tl que f(x) = x. Definición 2. Sen M, N espcios métricos. Un plicción f : M N es un contrcción cundo
Teorem del punto fijo Rodrigo Vrgs Definición 1. Un punto fijo de un plicción f : M M es un punto x M tl que f(x) = x. Definición 2. Sen M, N espcios métricos. Un plicción f : M N es un contrcción cundo
Teoremas de convergencia
 Cpítulo 3 Teorems de convergenci L necesidd de considerr límites de sucesiones o series de funciones es básic en el estudio del nálisis. Por tnto, es nturl preguntrse bjo qué condiciones se tiene que un
Cpítulo 3 Teorems de convergenci L necesidd de considerr límites de sucesiones o series de funciones es básic en el estudio del nálisis. Por tnto, es nturl preguntrse bjo qué condiciones se tiene que un
5.2 Integral Definida
 80 CÁLCULO / CIENCIAS AMBIENTALES / TEMA 5 5.2 Integrl Definid Definición de Integrl Definid El concepto de integrl definid se construye prtir de l ide de psr l límite un sum cundo el número de sumndos
80 CÁLCULO / CIENCIAS AMBIENTALES / TEMA 5 5.2 Integrl Definid Definición de Integrl Definid El concepto de integrl definid se construye prtir de l ide de psr l límite un sum cundo el número de sumndos
7 Integral triple de Riemann
 Miguel eyes, pto. de Mtemátic Aplicd, FI-UPM 1 7 Integrl triple de iemnn 7.1 efinición Llmremos rectángulo cerrdo de 3 (prlelepípedo) l producto de tres intervlos cerrdos y cotdos de, es decir = [, b]
Miguel eyes, pto. de Mtemátic Aplicd, FI-UPM 1 7 Integrl triple de iemnn 7.1 efinición Llmremos rectángulo cerrdo de 3 (prlelepípedo) l producto de tres intervlos cerrdos y cotdos de, es decir = [, b]
Teorema fundamental del Cálculo.
 Sesión Teorem fundmentl del Cálculo (TFC) Tems Teorem fundmentl del Cálculo. Cpciddes Conocer y comprender el TFC. Aplicr el TFC en el cálculo de derivds e integrles definids.. Introducción I. Brrow Inglés.
Sesión Teorem fundmentl del Cálculo (TFC) Tems Teorem fundmentl del Cálculo. Cpciddes Conocer y comprender el TFC. Aplicr el TFC en el cálculo de derivds e integrles definids.. Introducción I. Brrow Inglés.
El problema del área. Tema 5: Integración. Integral de Riemann. Particiones de un intervalo. Sumas superior e inferior
 Construcción Funciones integrbles TFCI Construcción Funciones integrbles TFCI Prticiones de un intervlo El problem del áre Tem 5: Integrción. Integrl de Riemnn El objetivo finl del tem es hllr el áre de
Construcción Funciones integrbles TFCI Construcción Funciones integrbles TFCI Prticiones de un intervlo El problem del áre Tem 5: Integrción. Integrl de Riemnn El objetivo finl del tem es hllr el áre de
Héctor Palma Valenzuela. Dpto. de Matemática UdeC Definición e interpretación geométrica
 Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. L Integrl.-. Definición e interpretción geométric Dd un función continu f :[, b] R ynonegtiv (f (), [, b]), vmos considerr l región del plno bjo l gráfic de
Héctor Plm Vlenzuel. Dpto. de Mtemátic UdeC. L Integrl.-. Definición e interpretción geométric Dd un función continu f :[, b] R ynonegtiv (f (), [, b]), vmos considerr l región del plno bjo l gráfic de
Lecturas de Análisis Matemático II. Oswaldo Sevilla
 Lecturs de Análisis Mtemático II Oswldo Sevill Febrero-Myo 203 ditdo por Muricio Zely Aguilr en www.write L A TX.com Medid de Lebesgue Un medid es un función m : M M P() A M : ma 0. s deseble que M = P()
Lecturs de Análisis Mtemático II Oswldo Sevill Febrero-Myo 203 ditdo por Muricio Zely Aguilr en www.write L A TX.com Medid de Lebesgue Un medid es un función m : M M P() A M : ma 0. s deseble que M = P()
El Teorema Fundamental del Cálculo
 del Cálculo Deprtmento de Análise Mtemátic Fcultde de Mtemátics Universidde de Sntigo de Compostel Sntigo, 2011 L Regl de Brrow: un resultdo sorprendente Recordemos que f es integrble en I = [, b] y su
del Cálculo Deprtmento de Análise Mtemátic Fcultde de Mtemátics Universidde de Sntigo de Compostel Sntigo, 2011 L Regl de Brrow: un resultdo sorprendente Recordemos que f es integrble en I = [, b] y su
Apunte sobre. Cálculo II Licenciatura en Matemática Aplicada Facultad de Ingeniería Química Universidad Nacional del litoral. 1. Integración numérica
 Apunte sobre Integrción Numéric y Polinomios de Tylor Cálculo II Licencitur en Mtemátic Aplicd Fcultd de Ingenierí Químic Universidd Ncionl del litorl 1. Integrción numéric En este tem veremos sólo dos
Apunte sobre Integrción Numéric y Polinomios de Tylor Cálculo II Licencitur en Mtemátic Aplicd Fcultd de Ingenierí Químic Universidd Ncionl del litorl 1. Integrción numéric En este tem veremos sólo dos
SEMANA 8: INTEGRAL DE RIEMANN
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Ingenierí Mtemátic Universidd de Chile SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 08-2 Ingenierí Mtemátic Universidd de Chile SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl
4.6. Teorema Fundamental del Cálculo
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 07-2 SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl del Cálculo Proposición 4.5. Se un
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Dierencil e Integrl 07-2 SEMANA 8: INTEGRAL DE RIEMANN 4.6. Teorem Fundmentl del Cálculo Proposición 4.5. Se un
2. PROBLEMAS DE VALOR INICIAL EN R n. EXISTENCIA, UNICIDAD, DEPENDENCIA CONTINUA O DIFERENCIABLE DE LA CONDICIÓN INICIAL. Teoremas de punto fijo
 2. PROBLEMAS DE VALOR INICIAL EN R n. EXISTENCIA, UNICIDAD, DEPENDENCIA CONTINUA O DIFERENCIABLE DE LA CONDICIÓN INICIAL. Teorems de punto fijo Definición 1. Se X un espcio vectoril rel. Se dice que un
2. PROBLEMAS DE VALOR INICIAL EN R n. EXISTENCIA, UNICIDAD, DEPENDENCIA CONTINUA O DIFERENCIABLE DE LA CONDICIÓN INICIAL. Teorems de punto fijo Definición 1. Se X un espcio vectoril rel. Se dice que un
Funciones de variable compleja
 Funciones de vrible complej Integrles impropis. Mrí Eugeni Torres Universidd Ncionl de Entre Ríos Fcultd de Ingenierí Funciones de Vrible Complej (Bioingenierí, Pln 28) Myo 29 Integrles impropis Alcnce
Funciones de vrible complej Integrles impropis. Mrí Eugeni Torres Universidd Ncionl de Entre Ríos Fcultd de Ingenierí Funciones de Vrible Complej (Bioingenierí, Pln 28) Myo 29 Integrles impropis Alcnce
Tema 9: Cálculo de primitivas. Integrales definidas e impropias.
 Integrl definid y sus plicciones. Integrles impropis. Tem 9: Cálculo de primitivs. Integrles definids e impropis. José M. Slzr Noviembre de 206 Integrl definid y sus plicciones. Integrles impropis. Tem
Integrl definid y sus plicciones. Integrles impropis. Tem 9: Cálculo de primitivs. Integrles definids e impropis. José M. Slzr Noviembre de 206 Integrl definid y sus plicciones. Integrles impropis. Tem
Clase No. 19: Integrales impropias MAT 251. Joaquín Peña (CIMAT) Métodos Numéricos (MAT 251) / 17
 Clse No. 19: Integrles impropis MAT 251 Joquín Peñ (CIMAT) Métodos Numéricos (MAT 251) 23.1.213 1 / 17 Integrndos con singulriddes (I) Cundo el integrndo o lgun de sus derivds de bjo orden tienen un singulridd
Clse No. 19: Integrles impropis MAT 251 Joquín Peñ (CIMAT) Métodos Numéricos (MAT 251) 23.1.213 1 / 17 Integrndos con singulriddes (I) Cundo el integrndo o lgun de sus derivds de bjo orden tienen un singulridd
Integral Definida. Tema 6. 6.1 Introducción. 6.2 Definición de Integral Definida
 Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Tem 6 Integrl Definid 6.1 Introducción En este tem estudiremos l Integrl Definid o Integrl de Riemnn, un concepto mtemático que esencilmente puede describirse como el límite de un sum cundo el número de
Examen con soluciones
 Cálculo Numérico I. Grdo en Mtemátics. Exmen con soluciones. Decidir rzondmente si ls siguientes firmciones son verdders o flss, buscndo un contrejemplo en el cso de ser flss (.5 puntos): () Si f(x) cmbi
Cálculo Numérico I. Grdo en Mtemátics. Exmen con soluciones. Decidir rzondmente si ls siguientes firmciones son verdders o flss, buscndo un contrejemplo en el cso de ser flss (.5 puntos): () Si f(x) cmbi
f : [a, b] R, acotada
![f : [a, b] R, acotada f : [a, b] R, acotada](/thumbs/85/92696353.jpg) 6. Integrción 6.1 Integrl definid Problem del áre. Ejemplos: 1 3 f(x 0, x [, b] f : [, b] R, cotd Figur 1 P n = { = x 0 < x 1
6. Integrción 6.1 Integrl definid Problem del áre. Ejemplos: 1 3 f(x 0, x [, b] f : [, b] R, cotd Figur 1 P n = { = x 0 < x 1
Integral impropia Al definir la integral definida b
 Mte Univ II, 14 FCE-BUAP CÁLCULO INTEGRAL ALEJANDRO RAMÍREZ PÁRAMO 1. Sucesiones y series Integrl impropi Al definir l integrl definid b f(x)dx, pretendimos que l función f estb definid; demás de cotd,
Mte Univ II, 14 FCE-BUAP CÁLCULO INTEGRAL ALEJANDRO RAMÍREZ PÁRAMO 1. Sucesiones y series Integrl impropi Al definir l integrl definid b f(x)dx, pretendimos que l función f estb definid; demás de cotd,
La integral de Riemann
 L integrl de Riemnn 1 Vmos dr un definición precis de l integrl de un función definid en un intervlo. Este tiene que ser un intervlo cerrdo y cotdo, es decir [,] con < R, y l definición que dremos de integrl
L integrl de Riemnn 1 Vmos dr un definición precis de l integrl de un función definid en un intervlo. Este tiene que ser un intervlo cerrdo y cotdo, es decir [,] con < R, y l definición que dremos de integrl
Integración numérica: Regla del trapecio Método de Romberg
 Clse No. 18: Integrción numéric: Regl del trpecio Método de Romberg MAT 251 Dr. Alonso Rmírez Mnznres CIMAT A.C. e-mil: lrm@ cimt.mx web: http://www.cimt.mx/ lrm/met_num/ Dr. Joquín Peñ Acevedo CIMAT A.C.
Clse No. 18: Integrción numéric: Regl del trpecio Método de Romberg MAT 251 Dr. Alonso Rmírez Mnznres CIMAT A.C. e-mil: lrm@ cimt.mx web: http://www.cimt.mx/ lrm/met_num/ Dr. Joquín Peñ Acevedo CIMAT A.C.
Grado en Química Bloque 1 Funciones de una variable
 Grdo en Químic Bloque Funciones de un vrible Sección.6: Integrción y plicciones. L integrl sirve pr clculr áres de figurs plns limitds por curvs. Pr definir l integrl de un función f : [, b] R se utilizn
Grdo en Químic Bloque Funciones de un vrible Sección.6: Integrción y plicciones. L integrl sirve pr clculr áres de figurs plns limitds por curvs. Pr definir l integrl de un función f : [, b] R se utilizn
Cálculo integral de funciones de una variable
 Lino Alvrez - Aure Mrtínez CÁLCULO II Cálculo integrl de funciones de un vrible 1 L integrl de Riemnn Se f : [, b] R R un función cotd en [, b]. Definición 1.- Un prtición P = {t 0, t 1,..., t n } del
Lino Alvrez - Aure Mrtínez CÁLCULO II Cálculo integrl de funciones de un vrible 1 L integrl de Riemnn Se f : [, b] R R un función cotd en [, b]. Definición 1.- Un prtición P = {t 0, t 1,..., t n } del
La integral indefinida Métodos de integración Integración de funciones de una variable real Integración impropia Aplicaciones de la integral
 Febrero, 2005 Índice generl Se f : I IR. Definición Diremos que F es primitiv de f en I si F (x) = f (x), x I. Teorem Si F y G son dos primitivs de un mism función f en un intervlo I, entonces, / k IR
Febrero, 2005 Índice generl Se f : I IR. Definición Diremos que F es primitiv de f en I si F (x) = f (x), x I. Teorem Si F y G son dos primitivs de un mism función f en un intervlo I, entonces, / k IR
Funciones de una variable real II Integrales impropias
 Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 203-204 Contents
Universidd de Murci Deprtmento Mtemátics Funciones de un vrible rel II Integrles impropis B. Cscles, J. M. Mir y L. Oncin Deprtmento de Mtemátics Universidd de Murci Grdo en Mtemátics 203-204 Contents
Matemáticas Empresariales I. Integral Definida
 Mtemátics Empresriles I Lección 8 Integrl Definid Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 31 Construcción de l integrl definid Se f un función definid
Mtemátics Empresriles I Lección 8 Integrl Definid Mnuel León Nvrro Colegio Universitrio Crdenl Cisneros M. León Mtemátics Empresriles I 1 / 31 Construcción de l integrl definid Se f un función definid
C alculo Octubre 2010
 Cálculo Octubre 2010 c Dpto. de Mtemátics UDC c Dpto. de Mtemátics UDC L integrl indefinid Sen I R un intervlo bierto y f : I IR Definición Diremos que F es primitiv de f en I si F (x) = f (x), x I Teorem
Cálculo Octubre 2010 c Dpto. de Mtemátics UDC c Dpto. de Mtemátics UDC L integrl indefinid Sen I R un intervlo bierto y f : I IR Definición Diremos que F es primitiv de f en I si F (x) = f (x), x I Teorem
Integrales de funciones de una variable.
 Tem Integrles de funciones de un vrible... L integrl definid como áre. L integrl definid de un función cotd y positiv corresponde l áre encerrd entre l curv y fx) y el eje OX desde y f x f x un punto hst
Tem Integrles de funciones de un vrible... L integrl definid como áre. L integrl definid de un función cotd y positiv corresponde l áre encerrd entre l curv y fx) y el eje OX desde y f x f x un punto hst
SEGUNDA PARTE. ANALÍTICAS Y TEORÍA DE CAUCHY.
 42 Funciones de vrible complej. Eleonor Ctsigers. 25 Abril 2006. FUNCIONES SEGUNDA PARTE. ANALÍTICAS Y TEORÍA DE CAUCHY. Resumen Se prueb que tod función holomorf es nlític, y recíprocmente. Se desrroll
42 Funciones de vrible complej. Eleonor Ctsigers. 25 Abril 2006. FUNCIONES SEGUNDA PARTE. ANALÍTICAS Y TEORÍA DE CAUCHY. Resumen Se prueb que tod función holomorf es nlític, y recíprocmente. Se desrroll
Integrales de funciones de una variable.
 Tem Integrles de funciones de un vrible... L integrl definid como áre. L integrl definid de un función cotd y positiv corresponde l áre encerrd entre l curv y f (x) y el eje OX desde un punto y fx fx hst
Tem Integrles de funciones de un vrible... L integrl definid como áre. L integrl definid de un función cotd y positiv corresponde l áre encerrd entre l curv y f (x) y el eje OX desde un punto y fx fx hst
P 1 P 2 = Figura 1. Distancia entre dos puntos.
 ANÁLISIS MATEMÁTICO BÁSICO. LONGITUD DE UNA CURVA PARAMÉTRICA. Ddos dos puntos P 1 = (x 1, x 2,..., x n ), P 2 = (y 1, y 2,..., y n ) R n (pensemos en puntos del espcio, de R 3 ) sbemos clculr l distnci
ANÁLISIS MATEMÁTICO BÁSICO. LONGITUD DE UNA CURVA PARAMÉTRICA. Ddos dos puntos P 1 = (x 1, x 2,..., x n ), P 2 = (y 1, y 2,..., y n ) R n (pensemos en puntos del espcio, de R 3 ) sbemos clculr l distnci
Integración de funciones de una variable real
 Cpítulo 5 Integrción de funciones de un vrible rel 5.1. Introducción Los inicios del Cálculo Integrl se remontn Arquímedes, mtemático, físico e ingeniero griego del S.III A.C., quién clculó el áre de numeross
Cpítulo 5 Integrción de funciones de un vrible rel 5.1. Introducción Los inicios del Cálculo Integrl se remontn Arquímedes, mtemático, físico e ingeniero griego del S.III A.C., quién clculó el áre de numeross
Integrales impropias
 Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrles impropis En todo el estudio hecho hst hor se hn utilizdo dos propieddes fundmentles: l función tení que ser cotd y el intervlo de integrción tení que ser cerrdo y cotdo. En est últim sección
Integrales de ĺınea complejas
 Tem Integrles de ĺıne complejs. Integrles de líne.. Funciones complejs de vrible rel Un función complej de vrible rel llev socid un función vectoril de vrible rel, por lo que ls definiciones y resultdos
Tem Integrles de ĺıne complejs. Integrles de líne.. Funciones complejs de vrible rel Un función complej de vrible rel llev socid un función vectoril de vrible rel, por lo que ls definiciones y resultdos
LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.
![LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b. LA INTEGRAL DEFINIDA Si f(x) es una función continua y no negativa definida en el intervalo x [a, b], entonces la integral definida b.](/thumbs/52/29237757.jpg) Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
Tem 4 Integrción 4.. Primitivs LA INTEGRAL DEFINIDA Si f(x) es un función continu y no negtiv definid en el intervlo x [, b], entonces l integrl definid f(x) represent el áre bjo l gráfic de l función
Herramientas digitales de auto-aprendizaje para Matemáticas
 Mtemático Tem: L integrl Integrl Herrmients digitles de uto-prendizje pr Mtemátics, Grupo de Innovción Didáctic Deprtmento de Mtemátics Universidd de Extremdur Mtemático Tem: L integrl Integrl Mtemático
Mtemático Tem: L integrl Integrl Herrmients digitles de uto-prendizje pr Mtemátics, Grupo de Innovción Didáctic Deprtmento de Mtemátics Universidd de Extremdur Mtemático Tem: L integrl Integrl Mtemático
6.1 Sumas de Riemann e integral definida
 Tem 6 Integrción Definid 6.1 Sums de Riemnn e integrl definid Supongmos que estmos interesdos en clculr el áre que se encuentr bjo un curv y = f(x) en un intervlo [, b] (pr simplificr, consideremos el
Tem 6 Integrción Definid 6.1 Sums de Riemnn e integrl definid Supongmos que estmos interesdos en clculr el áre que se encuentr bjo un curv y = f(x) en un intervlo [, b] (pr simplificr, consideremos el
Integración numérica: Regla del trapecio Método de Romberg
 Clse No. 18: MAT 251 Integrción numéric: Regl del trpecio Método de Romberg Joquín Peñ (CIMAT) Métodos Numéricos (MAT 251) 19.10.2011 1 / 14 Integrción numéric Dd un función f : [, b] R continu, queremos
Clse No. 18: MAT 251 Integrción numéric: Regl del trpecio Método de Romberg Joquín Peñ (CIMAT) Métodos Numéricos (MAT 251) 19.10.2011 1 / 14 Integrción numéric Dd un función f : [, b] R continu, queremos
n f j (x). j=0 f n Los teoremas que hemos obtenido anteriormente para sucesiones de funciones pueden aplicarse a las series de funciones.
 Cpítulo 10 Series de Funciones 10.1. Series de Funciones Definición 10.1 Se X R y (f n ) n N un sucesión de funciones reles sobre X. Pr n N definimos S n : X R por S n (x) = f j (x). Llmmos (S n ) n N
Cpítulo 10 Series de Funciones 10.1. Series de Funciones Definición 10.1 Se X R y (f n ) n N un sucesión de funciones reles sobre X. Pr n N definimos S n : X R por S n (x) = f j (x). Llmmos (S n ) n N
ANALISIS MATEMATICO II INTEGRAL DEFINIDA
 ANALISIS MATEMATICO II INTEGRAL DEFINIDA Mrí Susn Montelr Fcultd de Ciencis Excts, Ingenierí y Agrimensur - UNR El problem del áre Dd f : [, b] R, tl que f(x) 0 pr todo x [, b] b x Se f un función no negtiv
ANALISIS MATEMATICO II INTEGRAL DEFINIDA Mrí Susn Montelr Fcultd de Ciencis Excts, Ingenierí y Agrimensur - UNR El problem del áre Dd f : [, b] R, tl que f(x) 0 pr todo x [, b] b x Se f un función no negtiv
TEMA 5: INTEGRACIÓN. f(x) dx.
 TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
TEMA 5: INTEGRACIÓN. L integrl indefinid En muchos spectos, l operción llmd integrción que vmos estudir quí es l operción invers l derivción. Definición.. L función F es un ntiderivd (o primitiv) de l
Métodos Numéricos: Resumen y ejemplos Tema 3: Integración numérica
 Métodos Numéricos: Resumen y ejemplos em 3: Integrción numéric Frncisco Plcios Escuel Politécnic uperior de Ingenierí de Mnres Universidd Politécnic de Ctluñ Mrzo 8, versión.4 Contenido. Fórmuls de cudrtur.
Métodos Numéricos: Resumen y ejemplos em 3: Integrción numéric Frncisco Plcios Escuel Politécnic uperior de Ingenierí de Mnres Universidd Politécnic de Ctluñ Mrzo 8, versión.4 Contenido. Fórmuls de cudrtur.
Cálculo integral y series de funciones
 UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE MATEMÁTICA LABORATORIO DE FORMAS EN GRUPOS Cálculo integrl y series de funciones Rmón Bruzul Mrisel Domínguez Crcs, Venezuel Febrero 2005
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE MATEMÁTICA LABORATORIO DE FORMAS EN GRUPOS Cálculo integrl y series de funciones Rmón Bruzul Mrisel Domínguez Crcs, Venezuel Febrero 2005
Examen de Admisión a la Maestría 8 de Enero de 2016
 Exmen de Admisión l Mtrí 8 de Enero de 1 Nombre: Instruccion: En cd rectivo seleccione l rput correct encerrndo en un círculo l letr corrpondiente. Puede hcer cálculos en ls hojs que se le proporcionron.
Exmen de Admisión l Mtrí 8 de Enero de 1 Nombre: Instruccion: En cd rectivo seleccione l rput correct encerrndo en un círculo l letr corrpondiente. Puede hcer cálculos en ls hojs que se le proporcionron.
Capítulo 2. Espacios normados Introducción
 Cpítulo 2 Espcios normdos 2.1. Introducción Hbímos visto en el cpítulo nterior que en los espcios de prehilbertinos se podí definir un norm trvés del producto esclr por l fórmul x = (x y) 1/2, y que ést
Cpítulo 2 Espcios normdos 2.1. Introducción Hbímos visto en el cpítulo nterior que en los espcios de prehilbertinos se podí definir un norm trvés del producto esclr por l fórmul x = (x y) 1/2, y que ést
1 Aproximación de funciones por polinomios.
 GEODESIA Y FUNCIONES OTOGONALES Enrique Clero Curso GPS en Geodesi y Crtogrfí Crtgen de Indis Aproximción de funciones por polinomios. Consideremos el conjunto de funciones S = ; x; x ; x 3 ; x ; :::::
GEODESIA Y FUNCIONES OTOGONALES Enrique Clero Curso GPS en Geodesi y Crtogrfí Crtgen de Indis Aproximción de funciones por polinomios. Consideremos el conjunto de funciones S = ; x; x ; x 3 ; x ; :::::
CÁLCULO ELEMENTAL APUNTES. Valor absoluto. Definición 1. El valor absoluto del número real a, que se designa por a, se define por. a si a < 0.
 CÁLCULO ELEMENTAL APUNTES Vlor bsoluto Definición 1. El vlor bsoluto del número rel, que se design por, se define por { si 0, = si < 0. Definición 2. L distnci entre los números x 1 y x 2 de l rect rel
CÁLCULO ELEMENTAL APUNTES Vlor bsoluto Definición 1. El vlor bsoluto del número rel, que se design por, se define por { si 0, = si < 0. Definición 2. L distnci entre los números x 1 y x 2 de l rect rel
4. EL TEOREMA DE RADON-NIKODYM.
 4. EL TEOREMA DE RADON-NIKODYM. 1. MEDIDAS CON SIGNO. TEOREMA DE DESCOMPOSICIÓN DE HAHN. Ddo un espcio de medid (X, Σ, µ), nuestro objetivo es crcterizr ls medids con densidd. Pr ello necesitmos el concepto
4. EL TEOREMA DE RADON-NIKODYM. 1. MEDIDAS CON SIGNO. TEOREMA DE DESCOMPOSICIÓN DE HAHN. Ddo un espcio de medid (X, Σ, µ), nuestro objetivo es crcterizr ls medids con densidd. Pr ello necesitmos el concepto
1 TECNICAS DE INTEGRACION
 UNIVERSIDAD DE CONCEPCION DEPARTAMENTO DE MATEMATICA Prof Jorge Ruiz Cstillo TECNICAS DE INTEGRACION Integrción por prtes Teorem- Sen f g dos funciones derivbles sobre [, b] de mner que f g sen continus
UNIVERSIDAD DE CONCEPCION DEPARTAMENTO DE MATEMATICA Prof Jorge Ruiz Cstillo TECNICAS DE INTEGRACION Integrción por prtes Teorem- Sen f g dos funciones derivbles sobre [, b] de mner que f g sen continus
Parte 7. Derivación e integración numérica
 Prte 7. Derivción e integrción numéric Gustvo Montero Escuel Técnic Superior de Ingenieros Industriles Universidd de Ls Plms de Grn Cnri Curso 006-007 Los problems de derivción e integrción numéric El
Prte 7. Derivción e integrción numéric Gustvo Montero Escuel Técnic Superior de Ingenieros Industriles Universidd de Ls Plms de Grn Cnri Curso 006-007 Los problems de derivción e integrción numéric El
Introducir los elementos básicos del cálculo diferencial e integral de funciones numéricas de una variable real.
 2003 en delnte MA 12-A CALCULO (Curso Anul - 20 U.D.) DISTRIBUCION HORARIA: 4.5 hrs. clses/semn 1.5 hrs. de ejercicios semnles 4.0 hrs. de trbjo personl REQUISITOS: no tiene OBJETIVOS: Introducir los elementos
2003 en delnte MA 12-A CALCULO (Curso Anul - 20 U.D.) DISTRIBUCION HORARIA: 4.5 hrs. clses/semn 1.5 hrs. de ejercicios semnles 4.0 hrs. de trbjo personl REQUISITOS: no tiene OBJETIVOS: Introducir los elementos
Integración. 1. El cálculo de áreas, longitudes de arco y volúmenes.
 Integrción El cálculo integrl es de grn importnci en muchs áres de estudio, como l economí, l biologí, l químic, l físic y l mtemátic en generl. Ls plicciones más conocids del cálculo integrl son en: 1.
Integrción El cálculo integrl es de grn importnci en muchs áres de estudio, como l economí, l biologí, l químic, l físic y l mtemátic en generl. Ls plicciones más conocids del cálculo integrl son en: 1.
Unidad Temática Integral definida
 Integrl definid Unidd Temátic 5 5.2 Integrl definid Análisis Mtemático (Ingenierí Informátic) Deprtmento de Mtemátic Aplicd Fcultd de Informátic Universidd Politécnic de Vlenci S. Cmp, J.A. Conejero y
Integrl definid Unidd Temátic 5 5.2 Integrl definid Análisis Mtemático (Ingenierí Informátic) Deprtmento de Mtemátic Aplicd Fcultd de Informátic Universidd Politécnic de Vlenci S. Cmp, J.A. Conejero y
Dpto. Matemática Aplicada Universidad de Málaga
 ndlucitech Integrción Integrción Dpto. Mtemátic Aplicd Universidd de Málg ndlucitech Integrción Resumen 1 Integrción 2 Áres Volúmenes Longitudes y superficies ndlucitech Integrción Motivción Cálculo de
ndlucitech Integrción Integrción Dpto. Mtemátic Aplicd Universidd de Málg ndlucitech Integrción Resumen 1 Integrción 2 Áres Volúmenes Longitudes y superficies ndlucitech Integrción Motivción Cálculo de
Integrales. Jesús García de Jalón de la Fuente. IES Ramiro de Maeztu Madrid
 Jesús Grcí de Jlón de l Fuente IES Rmiro de Meztu Mdrid Diferencil de un función Diferencil de un función Definición L diferencil de un función f es igul su derivd por un incremento rbitrrio de l vrible.
Jesús Grcí de Jlón de l Fuente IES Rmiro de Meztu Mdrid Diferencil de un función Diferencil de un función Definición L diferencil de un función f es igul su derivd por un incremento rbitrrio de l vrible.
Apuntes de cálculo infinitesimal Una introducción al análisis matemático
 Apuntes de cálculo infinitesiml Un introducción l nálisis mtemático Miguel Lcruz Mrtín Año cdémico 17/18 The clculus ws the first chievement of modern mthemtics, nd it is difficult to overestimte its importnce.
Apuntes de cálculo infinitesiml Un introducción l nálisis mtemático Miguel Lcruz Mrtín Año cdémico 17/18 The clculus ws the first chievement of modern mthemtics, nd it is difficult to overestimte its importnce.
5. Integral y Aplicaciones
 Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
Métodos Mtemáticos (Curso 203 204) Grdo en Óptic y Optometrí 29 5. Integrl y Aplicciones Primitiv de un función Un función F es un primitiv de f, en un intervlo I, si F (x) = f(x) pr todo x en I. Observción
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
2. Estimar el área debajo de la gráfica de f(x) = cosx desde x = 0 hasta x = π/2, usando cuatro rectángulos
 1. Estimr el áre debjo de l gráfic de f(x) = cosx desde x = hst x = π/2, usndo cutro rectángulos de proximción y como puntos muestr, los extremos derechos de los intervlos. Dibuje l curv y los rectángulos
1. Estimr el áre debjo de l gráfic de f(x) = cosx desde x = hst x = π/2, usndo cutro rectángulos de proximción y como puntos muestr, los extremos derechos de los intervlos. Dibuje l curv y los rectángulos
PROBABILIDAD II Cuarto Artículo: Integral de Riemann-Stieltjes
 PROBABILIDAD II Curto Artículo: Integrl de Riemnn-Stieltjes Resumen En est escrito estudiremos un modo especil de integrción, introducido por primer vez por el mtemático lemán Thoms Jonnes Stieltjes en
PROBABILIDAD II Curto Artículo: Integrl de Riemnn-Stieltjes Resumen En est escrito estudiremos un modo especil de integrción, introducido por primer vez por el mtemático lemán Thoms Jonnes Stieltjes en
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 6 Curso preprtorio de l prueb de cceso l universidd pr myores de 5 ños curso 1/11 Nuri Torrdo Robles Deprtmento de Estdístic Universidd Crlos III de Mdrid
DEFINICIÓN DE LA INTEGRAL DE RIEMANN. Sea una función f : [a, b] R, positiva (f 0) y cuya gráfica presenta una situación del tipo:
![DEFINICIÓN DE LA INTEGRAL DE RIEMANN. Sea una función f : [a, b] R, positiva (f 0) y cuya gráfica presenta una situación del tipo: DEFINICIÓN DE LA INTEGRAL DE RIEMANN. Sea una función f : [a, b] R, positiva (f 0) y cuya gráfica presenta una situación del tipo:](/thumbs/88/115327044.jpg) ANÁLISIS MATEMÁTICO BÁSICO. DEFINICIÓN DE LA INTEGRAL DE RIEMANN. Se un función f : [, b] R, positiv (f 0) y cuy gráfic present un situción del tipo: Figur 1. Aproximción por rectángulos. Antes de proximr
ANÁLISIS MATEMÁTICO BÁSICO. DEFINICIÓN DE LA INTEGRAL DE RIEMANN. Se un función f : [, b] R, positiv (f 0) y cuy gráfic present un situción del tipo: Figur 1. Aproximción por rectángulos. Antes de proximr
Práctico 8 - Integrabilidad y Teorema Fundamental. 1. Integrales geometricas
 Universidd de l Repúblic Cálculo Fcultd de Ingenierí - IMERL Segundo semestre 6 Práctico 8 - Integrbilidd y Teorem Fundmentl. Integrles geometrics En est sección se trbjr con l ide intuitiv de integrles,
Universidd de l Repúblic Cálculo Fcultd de Ingenierí - IMERL Segundo semestre 6 Práctico 8 - Integrbilidd y Teorem Fundmentl. Integrles geometrics En est sección se trbjr con l ide intuitiv de integrles,
Integración de funciones reales de una variable real. 24 de octubre de 2014
 Cálculo Integrción de funciones reles de un vrible rel 24 de octubre de 2014 c Dpto. de Mtemátics UDC Integrción de funciones reles de un vrible rel L integrl indefinid. Cálculo de primitivs L integrl
Cálculo Integrción de funciones reles de un vrible rel 24 de octubre de 2014 c Dpto. de Mtemátics UDC Integrción de funciones reles de un vrible rel L integrl indefinid. Cálculo de primitivs L integrl
Las integrales que vamos a tratar de resolver numéricamente son de la forma I = f(x)dx
 Cpítulo 3 Integrción Numéric 3.1. Introducción Ls integrles que vmos trtr de resolver numéricmente son de l form f(x)dx donde [, b] es un intervlo finito. Sbemos que l integrl definid (de Riemnn) de un
Cpítulo 3 Integrción Numéric 3.1. Introducción Ls integrles que vmos trtr de resolver numéricmente son de l form f(x)dx donde [, b] es un intervlo finito. Sbemos que l integrl definid (de Riemnn) de un
TEMA 4. Cálculo integral
 TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
TEMA 4. Cálculo integrl En este tem considerremos el cálculo integrl, que es un complemento nturl del cálculo diferencil y tiene múltiples plicciones en otrs ciencis. 4.. Introducción l cálculo integrl
Curvas en el plano y en el espacio
 Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Cpítulo 1 Curvs en el plno y en el espcio 1.1. Curvs prmetrizds Definición 1.1.1 (Curv prmetrizd). Un curv prmetrizd diferencible α : I R n, es un plicción de clse C, donde I R es un intervlo bierto, que
Tema 4. Integración de Funciones de Variable Compleja
 Tem 4. Integrción de Funciones de Vrible omplej Prof. Willim L ruz Bstids 7 de octubre de 22 Tem 4 Integrción de Funciones de Vrible omplej 4. Integrl definid Se F (t) un función de vrible rel con vlores
Tem 4. Integrción de Funciones de Vrible omplej Prof. Willim L ruz Bstids 7 de octubre de 22 Tem 4 Integrción de Funciones de Vrible omplej 4. Integrl definid Se F (t) un función de vrible rel con vlores
Grado en Biología Tema 3 Integración. La regla del trapecio.
 Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Grdo en Biologí Tem Integrción Sección.: Aproximción numéric de integrles definids. Hy funciones de ls que no se puede hllr un primitiv en términos de funciones elementles. Esto sucede, por ejemplo, con
Clase 5: La Convolución.
 Clse 5: L Convolución. Peter Hummelgens 10 de diciembre de 2006 1. Soporte de un distribución. Se T D (R) y se O R un bierto. Denotremos por D(O) el subespcio linel de ls ϕ D(R) tl que sop(ϕ) O (sí D(O)
Clse 5: L Convolución. Peter Hummelgens 10 de diciembre de 2006 1. Soporte de un distribución. Se T D (R) y se O R un bierto. Denotremos por D(O) el subespcio linel de ls ϕ D(R) tl que sop(ϕ) O (sí D(O)
Solución Examen. (1 + a)x + y + z + u = α x + (1 + a)y + z + u = β x + y + (1 + a)z + u = γ x + y + z + (1 + a)u = δ.
 Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Algebr Linel MA 0, 0/08/3, Profs. J. González, R. Gouet. Solución Exmen. Considere el siguiente sistem de ecuciones lineles,
Ingenierí Mtemátic FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Algebr Linel MA 0, 0/08/3, Profs. J. González, R. Gouet. Solución Exmen. Considere el siguiente sistem de ecuciones lineles,
CURSO DE MATEMÁTICA 1. Facultad de Ciencias
 CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
CURSO DE MATEMÁTICA 1. Fcultd de Ciencis Reprtido Teórico 1 Mrzo de 2008 1. Conceptos Básicos de Funciones Definiciones 1. Si A y B son conjuntos no vcíos, un función de A en B es un correspondenci tl
Curvas en el espacio.
 Curvs en el espcio. Tod curv en el espcio R n se puede considerr como l imgen de un función vectoril r : [, b] R n, r(t) = (x 1 (t),..., x n (t)), que recibe el nombre de prmetrizción de l curv. Los puntos
Curvs en el espcio. Tod curv en el espcio R n se puede considerr como l imgen de un función vectoril r : [, b] R n, r(t) = (x 1 (t),..., x n (t)), que recibe el nombre de prmetrizción de l curv. Los puntos
Primitiva de una función.
 Primitiv de un función. 1 / 29 Definición. Un función derivble F es primitiv de l función f en el intervlo I si F (x) = f(x), pr todo x I. Ejemplos 2 / 29 Ejemplo. Se f : R R tl que f(x) = 4x 3. i) F(x)
Primitiv de un función. 1 / 29 Definición. Un función derivble F es primitiv de l función f en el intervlo I si F (x) = f(x), pr todo x I. Ejemplos 2 / 29 Ejemplo. Se f : R R tl que f(x) = 4x 3. i) F(x)
Series de funciones e integral de Lebesgue Curso 14/15 Grupo A
 Curso 14/15 Grupo A Frncisco José Freniche Ibáñez Modificdo el 16 de octubre de 2014 Primer prte 1. Sucesiones y series de funciones Se estudin propieddes de funciones f definids como límites o sums de
Curso 14/15 Grupo A Frncisco José Freniche Ibáñez Modificdo el 16 de octubre de 2014 Primer prte 1. Sucesiones y series de funciones Se estudin propieddes de funciones f definids como límites o sums de
Integrando Derivadas. f = F (b) F (a) F (x ) = F (x i) F (x i 1 ) i. S(f, P ) F (b) F (a) S(f, P ) f = F (b) F (a) f = f(b) f(a)
 Unidd 2 Teorem Fundmentl del Cálculo 2. L integrl como función del límite superior Integrndo Derivds Denición. Un función F es un ntiderivd de un función f sobre un conjunto A si tnto F, f estn denidos
Unidd 2 Teorem Fundmentl del Cálculo 2. L integrl como función del límite superior Integrndo Derivds Denición. Un función F es un ntiderivd de un función f sobre un conjunto A si tnto F, f estn denidos
TRABAJOS DE MATEMATICA
 UNIVERSIDAD NACIONAL DE CÓRDOBA FACULTAD DE MATEMÁTICA, ASTRONOMÍA Y FÍSICA SERIE C TRABAJOS DE MATEMATICA Nº 36/07 Un segundo curso de Cálculo Crin Boyllin, Elid Ferreyr, Mrt Urciuolo, Cynthi Will Editores:
UNIVERSIDAD NACIONAL DE CÓRDOBA FACULTAD DE MATEMÁTICA, ASTRONOMÍA Y FÍSICA SERIE C TRABAJOS DE MATEMATICA Nº 36/07 Un segundo curso de Cálculo Crin Boyllin, Elid Ferreyr, Mrt Urciuolo, Cynthi Will Editores:
Aproximación e interpolación mediante polinomios
 LA GACETA DE LA RSME, Vol. 5.3 (2002), Págs. 621 627 621 Aproximción e interpolción medinte polinomios por Miguel Mrno y Mrt Mrcolini En este trbjo se muestr un relción entre los conceptos de interpolción
LA GACETA DE LA RSME, Vol. 5.3 (2002), Págs. 621 627 621 Aproximción e interpolción medinte polinomios por Miguel Mrno y Mrt Mrcolini En este trbjo se muestr un relción entre los conceptos de interpolción
