MECÁNICA DE FLUIDOS I GUÍA DE EJERCICIOS TEMA 4 SOLUCIÓN
|
|
|
- María del Rosario Villanueva Araya
- hace 7 años
- Vistas:
Transcripción
1 Ejercicio 1 Un campo de velocidades viene dado por MECÁNICA DE FUIDOS I GUÍA DE EJERCICIOS TEMA 4 SOUCIÓN V = 4txi 2t 2 yj + 4xzk Es el flujo estacionario o no estacionario? Es bidimensional o tridimensional? Calcule, en el punto (x,y,z)=(-1,1,0), (a) el vector aceleración y (b) un vector unitario normal a la aceleración. - El flujo es no estacionario porque la variable tiempo (t) aparece explícitamente en las componentes del velocidad (es decir, la velocidad depende del tiempo). - El flujo es tridimensional porque el vector velocidad tiene componentes no nulas en todas las direcciones del espacio. (a) El vector aceleración tiene la siguiente forma (recordar el concepto de derivada material): Resolviendo para cada componente: dt = V V V V V + V V = t t du dt = t = 4x + 4tx 4t 2t xz 0 = 4x + 16t 2 x dv dt = v v v v t = 4ty + 4tx 0 2t2 y 2t 2 + 4xz 0 = 4ty + 4t 4 y dw dt = w w w w t = 0 + 4tx 4z 2t2 y 0 + 4xz 4x = 16txz + 14x 2 z Agrupando términos por componente tenemos: dt = 4x + 16t2 x i + 4ty + 4t 4 y j + 16txz + 14x 2 z k Finalmente, evaluando para (x,y,z)=(-1,1,0): dt = t2 i 4t 1 t 3 j + 0k (b) En el punto donde se calculó la aceleración (-1,1,0) existen muchos vectores unitarios normales a dicha aceleración. El más obvio es k.
2 Ejercicio 2 Un flujo incompresible idealizado tiene la siguiente distribución tridimensional de velocidades: V = 4xy 2 i + f y j zy 2 k Determine la forma que debe tener la función f(y) para que se cumpla la ecuación de continuidad. En un flujo incompresible, la ecuación de continuidad viene dada por: y + w z = 0 Sustituyendo las componentes de la velocidad, queda x 4xy2 + y f y + z zy2 = 4y 2 + df(y) dy y2 = 0 Entonces: Separando variables e integrando: df(y) dy = 3y2 f y = ( 3y 2 )dy f y = y 3 + constante
3 Ejercicio 3 Si z es vertical, positiva hacia arriba, qué condiciones deben cumplir las constantes a y b para que el campo de velocidades u = ay, v = bx, w = 0 sea una solución exacta de las ecuaciones del movimiento (continuidad y Navier-Stokes) de un fluido incompresible? Primero se examina la ecuación de continuidad: y + w z = x ay + y bx + z 0 = = 0 (Se cumple para cualquier a y b). A continuación se examinan las ecuaciones de cantidad de movimiento, si se puede encontrar una distribución de presiones única, la solución es exacta. Como z es vertical y positiva hacia arriba entonces g x = g y = 0. Para la componente x tenemos: ρg x x u x 2 + u + u ρ(0) x x 2 ay + ay + z 2 ay t ay + ay x ay + bx y ay + 0 z (ay) De manera similar, para la componente y: ay 0 + bx a + 0 x x = ρabx ρg y y v x 2 + v + v v v v v ρ(0) y x 2 bx + bx + z 2 bx t bx + ay x bx + bx y bx + 0 z (bx) aby + bx y y = ρaby
4 Y para la componente z: ρg z z w x 2 + w + w w w w w ρ( g) z x z 2 0 t 0 + ay x 0 + bx y z (0) ρg z z = ρg (En la dirección z el gradiente de presiones es hidrostático). Para conseguir la distribución de presiones integramos parcialmente cada uno de los gradientes (para cada dirección, manteniendo las variables de las otras direcciones como constantes), comparando en cada paso con los restantes. Comenzamos con P/ x: P = x dx = ( ρabx)dx = 1 2 ρabx2 + f 1 (y, z) a constante de integración que aparece es una función de las variables no integradas (y y z). Derivando parcialmente este resultado con respecto a y y comparando con el P/ y obtenido anteriormente, tenemos: f 1 y = ρaby Entonces, f 1 = ( ρaby)dy = 1 2 ρaby2 + f 2 (z) Agrupando términos, la distribución de presiones se convierte en: P = 1 2 ρabx2 1 2 ρaby2 + f 2 (z) Derivando esta expresión respecto a z y comparando con el gradiente correspondiente, tenemos: Donde, f 2 z = ρg f 2 = ( ρg)dz = ρgz + C Finalmente, la distribución de presiones buscada es: P = 1 2 ρabx2 1 2 ρaby2 ρgz + C (El campo de velocidades dado es una solución exacta y es independiente de los valores de a y b).
5 Ejercicio 4 Un campo fluido incompresible bidimensional está definido por las componentes de velocidad u = 2V x y ; v = 2V y Donde V y son constantes. En caso de existir, determine la función de corriente y el potencial de velocidades. En primer lugar debemos verificar si se cumple la ecuación de continuidad y la condición de irrotacionalidad: y = 2V 2V = 0 (Se cumple, por lo tanto existe). V = v x y k = 0 + 2V 0 (No se cumple, por lo tanto no existe). Para determinar la función de corriente, utilizamos la definición de u y v e integramos: u = Ψ y = 2V x y Ψ = 2V x y dy = 2V xy y2 2 + f(x) Derivando esta expresión respecto a x y comparando con la definición de v: Entonces, Ψ x = 2Vy + df 2Vy = v = dx df dx = 0 Integrando / x respecto a x tenemos, finalmente: Ψ = V 2xy y2 + C
Problema 1. Calcula las derivadas parciales de las siguientes funciones: (d) f(x, y) = arctan x + y. (e) f(x, y) = cos(3x) sin(3y),
 Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Mecánica de Fluidos. Análisis Diferencial
 Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
Métodos de solución de ED de primer orden
 CAPÍTULO 2 Métodos de solución de ED de primer orden 2.6 Ecuaciones diferenciales exactas Antes de abordar este tema, sugerimos al lector revise la última sección de este capítulo, la cual trata sobre
CAPÍTULO 2 Métodos de solución de ED de primer orden 2.6 Ecuaciones diferenciales exactas Antes de abordar este tema, sugerimos al lector revise la última sección de este capítulo, la cual trata sobre
Integrales de Línea. Sabemos que una curva cerrada C paramétrica para a t b (en donde t es el parámetro), se representa por:
 r (t) =x (t) î + y (t) ĵ + z (t) ˆk dr (t) =dx (t) î + dy (t) ĵ + dz (t) ˆk Las integrales que incluyen vectores de desplazamiento diferencial d r se llaman integrales de línea. onsideremos las siguientes
r (t) =x (t) î + y (t) ĵ + z (t) ˆk dr (t) =dx (t) î + dy (t) ĵ + dz (t) ˆk Las integrales que incluyen vectores de desplazamiento diferencial d r se llaman integrales de línea. onsideremos las siguientes
4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II
 4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II 4.1. Ecuaciones lineales La e.d.o. de primer orden lineal es Si g(x) = 0: ecuación lineal homogénea. a 1 (x) +
4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II 4.1. Ecuaciones lineales La e.d.o. de primer orden lineal es Si g(x) = 0: ecuación lineal homogénea. a 1 (x) +
TEMA II.7. Lagrange y Euler. Dr. Juan Pablo Torres-Papaqui. Departamento de Astronomía Universidad de Guanajuato DA-UG (México)
 TEMA II.7 Lagrange y Euler Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus Guanajuato,
TEMA II.7 Lagrange y Euler Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus Guanajuato,
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE V
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-112-4-V-1--217 CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 112 TIPO DE EXAMEN: Examen Final Parcial FECHA DE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-112-4-V-1--217 CURSO: SEMESTRE: Primero CÓDIGO DEL CURSO: 112 TIPO DE EXAMEN: Examen Final Parcial FECHA DE
2.4 Ecuaciones diferenciales de Bernoulli
 .4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
.4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Ejercicio 3.1. Sea el campo de velocidades de un escurrimiento definido por : v = x 2 yē x + x 2 tē y (3.1)
 Ejercicio 3.1. Sea el campo de velocidades de un escurrimiento definido por : Se pide: v = x yē x + x tē y (3.1) a. A qué tipo de formalismo corresponde este análisis del escurrimiento, lagrangeano o eulereano?
Ejercicio 3.1. Sea el campo de velocidades de un escurrimiento definido por : Se pide: v = x yē x + x tē y (3.1) a. A qué tipo de formalismo corresponde este análisis del escurrimiento, lagrangeano o eulereano?
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 . DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
. DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
2 Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
ANÁLISIS II Computación. Práctica 4. x 3. x 2 + y 2 si (x, y) (0, 0)
 facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
i j k xy yz xz = = Div Rot F = x y z
 Div Rot F, si F = ( xy, yz, xz) 1. Hallar: primero, debemos hallar rotor de la función vectorial. i j k Rot ( F ) = ( xy, yz, xz) =,, ( xy, yz, xz) = x y z xy yz xz ( xz) ( yz) ( xy) ( xz) ( yz) ( xy)
Div Rot F, si F = ( xy, yz, xz) 1. Hallar: primero, debemos hallar rotor de la función vectorial. i j k Rot ( F ) = ( xy, yz, xz) =,, ( xy, yz, xz) = x y z xy yz xz ( xz) ( yz) ( xy) ( xz) ( yz) ( xy)
Nombre: Cédula: Sección: SEGUNDO PARCIAL TEORÍA 1. Mencione los supuestos necesarios para que sea válida la ecuación de Bernoulli.
 U.L.A. FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA MECÁNICA MECÁNICA DE FLUIDOS Mérida, 05/02/2009 Nombre: Cédula: Sección: SEGUNDO PARCIAL TEORÍA 1. Mencione los supuestos necesarios para que sea válida
U.L.A. FACULTAD DE INGENIERÍA ESCUELA DE INGENIERÍA MECÁNICA MECÁNICA DE FLUIDOS Mérida, 05/02/2009 Nombre: Cédula: Sección: SEGUNDO PARCIAL TEORÍA 1. Mencione los supuestos necesarios para que sea válida
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
70 Ecuaciones diferenciales. ln e/ D e.0 1/ D e ) C D e: D e: y. y ln. 11..x 2 8xy 4y 2 / dy D.x 2 C 2xy 4y 2 / dx.
 70 Ecuaciones diferenciales Considerando la condición inicial.1/ D e: ( ) 1 C D e ln D e.ln 1 e ln e/ D e.0 1/ D e ) C D e: Por lo tanto, la solución del PVI es ln ( ) x D e: Ejercicios 2.5.1 Ecuaciones
70 Ecuaciones diferenciales Considerando la condición inicial.1/ D e: ( ) 1 C D e ln D e.ln 1 e ln e/ D e.0 1/ D e ) C D e: Por lo tanto, la solución del PVI es ln ( ) x D e: Ejercicios 2.5.1 Ecuaciones
3. Expresar las siguientes figuras en (i) coordenadas cilíndricas (ii) coordenadas esféricas (a) x 2 + y 2 + z 2 = 25 (b) z 2 = 2(x 2 + y 2 ) B + 3
 ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO ACADÉMICO DE INGENIERÍA ELÉCTRICA ACADEMIA DE MATEMÁTICAS GUÍA DE LA MATERIA DE CÁLCULO VECTORIAL TURNO VESPERTINO Junio 2011 I. SISTEMAS
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO ACADÉMICO DE INGENIERÍA ELÉCTRICA ACADEMIA DE MATEMÁTICAS GUÍA DE LA MATERIA DE CÁLCULO VECTORIAL TURNO VESPERTINO Junio 2011 I. SISTEMAS
Guía de Estudio para la Sección de Matemáticas del Examen de Admisión
 1 Guía de Estudio para la Sección de Matemáticas del Examen de Admisión 215-1 El material relativo al temario puede ser consultado en la amplia bibliografía que allí se menciona o en alguno de los muchísimos
1 Guía de Estudio para la Sección de Matemáticas del Examen de Admisión 215-1 El material relativo al temario puede ser consultado en la amplia bibliografía que allí se menciona o en alguno de los muchísimos
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Teorema de Stokes Introducción
 EIÓN 1 1.1 Introducción En la presente sesión se revisa el último teorema clave del cálculo vectorial, el teorema de tokes. Este teorema establece una relación entre una integral de línea sobre una curva
EIÓN 1 1.1 Introducción En la presente sesión se revisa el último teorema clave del cálculo vectorial, el teorema de tokes. Este teorema establece una relación entre una integral de línea sobre una curva
Temas 1 y 2: Cálculo Diferencial y Optimización ENUNCIADO Y RESPUESTA AL EJERCICIO: ENUNCIADO
 CÁLCULO II. Ejercicio de Examen Final Temas 1 y : Cálculo Diferencial y Optimización FECHA: 1/07/1 TIEMPO RECOMENDADO: 40 m Puntuación/TOTAL:,5/10 ENUNCIADO Y RESPUESTA AL EJERCICIO: ENUNCIADO w w 1. Dada
CÁLCULO II. Ejercicio de Examen Final Temas 1 y : Cálculo Diferencial y Optimización FECHA: 1/07/1 TIEMPO RECOMENDADO: 40 m Puntuación/TOTAL:,5/10 ENUNCIADO Y RESPUESTA AL EJERCICIO: ENUNCIADO w w 1. Dada
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
CAMPOS VECTORIALES. Presenta: M.E.M. Enrique Arenas Sánchez. 21 de septiembre de 2016
 Presenta: M.E.M. Enrique Arenas Sánchez 21 de septiembre de 2016 Definición de Campo Escalar. Se llama campo escalar a una función que asocia a cada punto del dominio de una función un valor escalar. Ejemplo:
Presenta: M.E.M. Enrique Arenas Sánchez 21 de septiembre de 2016 Definición de Campo Escalar. Se llama campo escalar a una función que asocia a cada punto del dominio de una función un valor escalar. Ejemplo:
PEP Acumulativa. segundo después? (Suponga que la pelota cae una distancia s = 16t 2 [m] en t segundos).
![PEP Acumulativa. segundo después? (Suponga que la pelota cae una distancia s = 16t 2 [m] en t segundos). PEP Acumulativa. segundo después? (Suponga que la pelota cae una distancia s = 16t 2 [m] en t segundos).](/thumbs/63/49822063.jpg) Universidad de Santiago de Chile, Facultad de Ciencia, Departamento de Matemática y C.C. Asignatura Cálculo I, Módulo Básico Ingeniería, Primer Semestre 01 PEP Acumulativa Problema 1. (0 pts.) { (1.1)
Universidad de Santiago de Chile, Facultad de Ciencia, Departamento de Matemática y C.C. Asignatura Cálculo I, Módulo Básico Ingeniería, Primer Semestre 01 PEP Acumulativa Problema 1. (0 pts.) { (1.1)
Problemas de Análisis Vectorial y Estadístico
 Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS
 195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
P xx ( r) P xy ( r) P xz ( r) P xy ( r) P yy ( r) P yz ( r) P xz ( r) P yz ( r) P zz ( r) d S = ds ˆn( r) (2)
 EL TENSOR DE PRESIONES La discusión siguiente se centra en el tensor de presiones; sin embargo, los conceptos matemáticos pueden ser extendidos a otras clases de tensores. El tensor de presiones es un
EL TENSOR DE PRESIONES La discusión siguiente se centra en el tensor de presiones; sin embargo, los conceptos matemáticos pueden ser extendidos a otras clases de tensores. El tensor de presiones es un
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
ANALISIS II Computación. Práctica 4. x 3. x 2 + y 2. x 2 + y 2 si (x, y) (0, 0) 0 si (x, y) = (0, 0)
 facultad de ciencias exactas y naturales uba curso de verano 2006 ANALISIS II Computación Práctica 4 Derivadas parciales 1. Calcular (a) f xy y (2, 1) para f(x, y) = + x y (b) f z (1, 1, 1) para f(x, y,
facultad de ciencias exactas y naturales uba curso de verano 2006 ANALISIS II Computación Práctica 4 Derivadas parciales 1. Calcular (a) f xy y (2, 1) para f(x, y) = + x y (b) f z (1, 1, 1) para f(x, y,
TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL
 Capítulo 4 TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL 4.1 Introducción En el tema anterior hemos estudiado los principios fundamentales de la dinámica. La segunda ley de Newton, que relaciona
Capítulo 4 TEOREMAS GENERALES DE LA DINÁMICA DEL PUNTO MATERIAL 4.1 Introducción En el tema anterior hemos estudiado los principios fundamentales de la dinámica. La segunda ley de Newton, que relaciona
Primer Examen Parcial Tema A Cálculo Vectorial Marzo 5 de 2016
 rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
Universidad Nacional de Córdoba. Facultad de Ciencias Exactas Físicas y Naturales. Cátedra de Mecánica de los Fluidos. Carrea de Ingeniería Civil
 Universidad Nacional de Córdoba Facultad de Ciencias Exactas Físicas y Naturales Cátedra de Mecánica de los Fluidos Carrea de Ingeniería Civil FLUJO COMPRESIBLE DR. ING. CARLOS MARCELO GARCÍA 2011 A modo
Universidad Nacional de Córdoba Facultad de Ciencias Exactas Físicas y Naturales Cátedra de Mecánica de los Fluidos Carrea de Ingeniería Civil FLUJO COMPRESIBLE DR. ING. CARLOS MARCELO GARCÍA 2011 A modo
Problema de Valor Inicial (PVI):
 Problema de Valor Inicial (PVI): Con frecuencia nos interesan problemas en los que se busca la solución y () de una ecuación diferencial de modo que y () satifaga condiciones adicionales impuestas a la
Problema de Valor Inicial (PVI): Con frecuencia nos interesan problemas en los que se busca la solución y () de una ecuación diferencial de modo que y () satifaga condiciones adicionales impuestas a la
Física General III. Ayudantía 8. Mecánica de fluidos: Paradoja de la hidrostática y viscosidad. El alumno una vez finalizado la guía debe ser capaz:
 Física General III Ayudantía 8 Mecánica de fluidos: Paradoja de la hidrostática y viscosidad. El alumno una vez finalizado la guía debe ser capaz: Entender y aplicar los conceptos de viscosidad de un fluido.
Física General III Ayudantía 8 Mecánica de fluidos: Paradoja de la hidrostática y viscosidad. El alumno una vez finalizado la guía debe ser capaz: Entender y aplicar los conceptos de viscosidad de un fluido.
APUNTES DE MATEMÁTICAS UNIVERSIDAD DE SEVILLA GRADOS EN ECONOMÍA Y ADMINISTRACIÓN DE EMPRESAS PRIMER CURSO
 APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
CINEMATICA DE FLUIDOS ING. GIOVENE PEREZ CAMPOMANES
 CINEMATICA DE FLUIDOS ING. GIOVENE PEREZ CAMPOMANES 3.1 OBJETIVOS Representar mediante ecuaciones matemáticas y gráficas el movimiento de los fluidos. Aplicar las ecuaciones fundamentales de líneas de
CINEMATICA DE FLUIDOS ING. GIOVENE PEREZ CAMPOMANES 3.1 OBJETIVOS Representar mediante ecuaciones matemáticas y gráficas el movimiento de los fluidos. Aplicar las ecuaciones fundamentales de líneas de
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-114-1-M-2-00-2017 CURSO: Matemática Intermedia 3 SEMESTRE: Segundo CÓDIGO DEL CURSO: 114 TIPO DE EXAMEN: Primer
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-114-1-M-2-00-2017 CURSO: Matemática Intermedia 3 SEMESTRE: Segundo CÓDIGO DEL CURSO: 114 TIPO DE EXAMEN: Primer
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
FLUJO POTENCIAL. Mecánica de Fluidos Avanzada UNIVERSIDAD NACIONAL DE INGENIERÍA FACULTAD DE INGENIERÍA CIVIL DEPARTAMENTO DE HIDRÁULICA E HIDROLOGÍA
 FLUJO POTENCIAL Mecánica de Fluidos Avanzada UNIVERSIDAD NACIONAL DE INGENIERÍA FACULTAD DE INGENIERÍA CIVIL DEPARTAMENTO DE HIDRÁULICA E HIDROLOGÍA CIRCULACIÓN La circulación del vector velocidad se define
FLUJO POTENCIAL Mecánica de Fluidos Avanzada UNIVERSIDAD NACIONAL DE INGENIERÍA FACULTAD DE INGENIERÍA CIVIL DEPARTAMENTO DE HIDRÁULICA E HIDROLOGÍA CIRCULACIÓN La circulación del vector velocidad se define
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Práctica 9 Campos conservativos - Teorema de Green
 ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
Clase 10: Extremos condicionados y multiplicadores de Lagrange
 Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Clase 4. Campos Vectorialesy OperadoresDiferenciales
 lase 4. ampos Vectorialesy Operadoresiferenciales Un campo vectorial en R n es una función F : R n R n. i F es un campo vectorial, una línea de flujo (línea de corriente o curva integral) para F es una
lase 4. ampos Vectorialesy Operadoresiferenciales Un campo vectorial en R n es una función F : R n R n. i F es un campo vectorial, una línea de flujo (línea de corriente o curva integral) para F es una
Andrés Aceña Relatividad: por qué la mecánica newtoniana no funciona?
 Relatividad General I El programa Teorías actuales. Problemas abiertos en Relatividad General Clásica. Fundamentos de la teoría. Espacios topológicos. Variedades. La métrica. Geodésicas. El tensor de curvatura.
Relatividad General I El programa Teorías actuales. Problemas abiertos en Relatividad General Clásica. Fundamentos de la teoría. Espacios topológicos. Variedades. La métrica. Geodésicas. El tensor de curvatura.
2. Actividad inicial: Crecimiento del dinero.
 Índice 1. Introducción 6 2. Actividad inicial: Crecimiento del dinero. 6 3. EDO de variables separables 7 3.1. Técnica de resolución de una ODE de variables separables........... 8 3.2. Ejemplos desarrollados...............................
Índice 1. Introducción 6 2. Actividad inicial: Crecimiento del dinero. 6 3. EDO de variables separables 7 3.1. Técnica de resolución de una ODE de variables separables........... 8 3.2. Ejemplos desarrollados...............................
EXAMEN TIPO TEST NÚMERO 1. MODELO 1 RESOLUCIÓN. El ángulo tiene que ser adimensional de modo que: Respuesta correcta: c)
 EXAMEN TIPO TEST NÚMERO 1. MODELO 1 RESOLUCIÓN 1.-Si en la expresión xcos(cρt) "x" es espacio, "t" es tiempo y ρ densidad, la constante C tiene dimensiones de: a) ML -3 T b) L c) M -1 L 3 T -1 d) L -1
EXAMEN TIPO TEST NÚMERO 1. MODELO 1 RESOLUCIÓN 1.-Si en la expresión xcos(cρt) "x" es espacio, "t" es tiempo y ρ densidad, la constante C tiene dimensiones de: a) ML -3 T b) L c) M -1 L 3 T -1 d) L -1
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
CLAVE DE EXAMEN Matemática Básica 2 código de curso: 103
 universidad de san carlos Facultad de Ingeniería Escuela de Ciencias Departamento de Matemática clave-103-4-v-2-00-2013 CLAVE DE EXAMEN Matemática Básica 2 código de curso: 103 Datos de la clave Elaborada
universidad de san carlos Facultad de Ingeniería Escuela de Ciencias Departamento de Matemática clave-103-4-v-2-00-2013 CLAVE DE EXAMEN Matemática Básica 2 código de curso: 103 Datos de la clave Elaborada
Definir la Integral del campo vectorial F sobre una superficie S como una suma de Riemann.
 .7. Integral de superfície de campos vectoriales. Otra de las aplicaciones importantes de la integral de superficies, es cuando se integra un campo vectorial sobre ella. El significado que adquiere este
.7. Integral de superfície de campos vectoriales. Otra de las aplicaciones importantes de la integral de superficies, es cuando se integra un campo vectorial sobre ella. El significado que adquiere este
Soluciones Matemáticas II Examen Final 2º Parcial 3-Julio-07. 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =.
 Soluciones Matemáticas II Examen Final º Parcial 3-Julio-07 3x 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =. x + y a) Hallar la curva de nivel (isoterma) que pasa por el punto
Soluciones Matemáticas II Examen Final º Parcial 3-Julio-07 3x 1) La temperatura en un punto (x, y) de una lámina metálica es T(x, y) =. x + y a) Hallar la curva de nivel (isoterma) que pasa por el punto
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3! + x5
 Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
Cálculo I (Grado en Ingeniería Informática Problemas resueltos, -, -4 y 4-5 (tercera parte Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić, Luis Guijarro (coordinadores,
ECUACIONES GENERALES DE LA HIDRAULICA EN MEDIOS POROSOS
 ECUACIONES GENERALES DE LA HIDRAULICA EN MEDIOS POROSOS CONSERVACION DE MASA PARA FLUJO EN UN MEDIO SATURADO Consideremos un volumen de control rectangular. Este volumen de control tiene dimensiones Δx,
ECUACIONES GENERALES DE LA HIDRAULICA EN MEDIOS POROSOS CONSERVACION DE MASA PARA FLUJO EN UN MEDIO SATURADO Consideremos un volumen de control rectangular. Este volumen de control tiene dimensiones Δx,
TEMA II.9. Ecuación de Bernoulli. Dr. Juan Pablo Torres-Papaqui
 TEMA II.9 Ecuación de Bernoulli Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus
TEMA II.9 Ecuación de Bernoulli Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus
Soluciones a los ejercicios del examen final
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
REGIMENES DE CORRIENTES O FLUJOS
 LINEAS DE CORRIENTE Ø Las líneas de corriente son líneas imaginarias dibujadas a través de un fluido en movimiento y que indican la dirección de éste en los diversos puntos del flujo de fluidos. Ø Una
LINEAS DE CORRIENTE Ø Las líneas de corriente son líneas imaginarias dibujadas a través de un fluido en movimiento y que indican la dirección de éste en los diversos puntos del flujo de fluidos. Ø Una
5.1 Primera ley de la termodinámica
 55 Capítulo 5 Energía En este capítulo se verán los aspectos energéticos asociados al flujo de un fluido cualquiera. Para ésto se introduce, en una primera etapa, la primera ley de la termodinámica que
55 Capítulo 5 Energía En este capítulo se verán los aspectos energéticos asociados al flujo de un fluido cualquiera. Para ésto se introduce, en una primera etapa, la primera ley de la termodinámica que
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Funciones reales de varias variables.
 Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Extremos Restringidos (Multiplicadores de Lagrange)
 Extremos Restringidos (Multiplicadores de Lagrange) Dada la curva en el plano (x h) a + (y k) b = 1. Esta es una elipse con centro en (h,k) y queremos encontrar qué punto de esta elipse se encuentra más
Extremos Restringidos (Multiplicadores de Lagrange) Dada la curva en el plano (x h) a + (y k) b = 1. Esta es una elipse con centro en (h,k) y queremos encontrar qué punto de esta elipse se encuentra más
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Soluciones a los ejercicios propuestos: Matemáticas III. Curso Tema 4. (a) Determinar si f es localmente invertible en (0, 0, 0).
 Soluciones a los ejercicios propuestos: Matemáticas III Curso 08 09 36 Tema 4 1 Sea f : IR 3 IR 3 definida por fx, y, z = e x+y, cosz, e z a Determinar si f es localmente invertible en 0, 0, 0 J fx, y,
Soluciones a los ejercicios propuestos: Matemáticas III Curso 08 09 36 Tema 4 1 Sea f : IR 3 IR 3 definida por fx, y, z = e x+y, cosz, e z a Determinar si f es localmente invertible en 0, 0, 0 J fx, y,
Tema 6 Funciones reales de varias variables
 Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
EXAMEN DE FISICA I (I.I. e I.Q.)
 EXAMEN DE FISICA I (I.I. e I.Q.) 11-2-26 CUESTIONES 1) Una partícula describe el movimiento parabólico de la figura. Obtener las expresiones para la máxima altura y el alcance a lo largo del eje X. Demostrar
EXAMEN DE FISICA I (I.I. e I.Q.) 11-2-26 CUESTIONES 1) Una partícula describe el movimiento parabólico de la figura. Obtener las expresiones para la máxima altura y el alcance a lo largo del eje X. Demostrar
DINAMICA DE FLUIDOS ING. GIOVENE PEREZ CAMPOMANES
 DINAMICA DE FLUIDOS ING. GIOVENE PEREZ CAMPOMANES 4.1 OBJETIVOS Aplicar los principios de la física sobre la: conservación de masa, cantidad de movimiento y de la energía. Representar los conceptos del
DINAMICA DE FLUIDOS ING. GIOVENE PEREZ CAMPOMANES 4.1 OBJETIVOS Aplicar los principios de la física sobre la: conservación de masa, cantidad de movimiento y de la energía. Representar los conceptos del
Ayudantía Regla de la Cadena. Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática
 / 010 Ayudantía 4 1. Regla de la Cadena Proposición 1 Regla de la Cadena - 1. Sea f : U R n R diferenciable y γ : I R R n una curva diferenciable contenida en U. Entonces, la función gt = f γt es derivable
/ 010 Ayudantía 4 1. Regla de la Cadena Proposición 1 Regla de la Cadena - 1. Sea f : U R n R diferenciable y γ : I R R n una curva diferenciable contenida en U. Entonces, la función gt = f γt es derivable
4.3 Teorema del transporte de Reynolds. Enfoque diferencial
 Cinemática de fluidos 4.3 Teorema del transporte de Reynolds. Enfoque diferencial Apliquemos el teorema del transporte de Reynolds para estudiar la variación de la densidad ρ en un volumen de control infinitesimal,
Cinemática de fluidos 4.3 Teorema del transporte de Reynolds. Enfoque diferencial Apliquemos el teorema del transporte de Reynolds para estudiar la variación de la densidad ρ en un volumen de control infinitesimal,
Transferencia de Momentum
 Transferencia de Momentum 1740-014-03-18 1ª. Es bueno distinguir lo esencial de lo superfluo ups! Qué se celebraba el 18 de Maro? Contenido Ejercicios Flujo en tabla inclinada.; Flujo en tubo cilíndrico
Transferencia de Momentum 1740-014-03-18 1ª. Es bueno distinguir lo esencial de lo superfluo ups! Qué se celebraba el 18 de Maro? Contenido Ejercicios Flujo en tabla inclinada.; Flujo en tubo cilíndrico
EXAMEN TEMA 2:Funciones de varias variables
 GRUPO 4Mb (16-17) CÁLCULO ETSI Informática (UPM) 8 de Junio - 217 Tiempo: 2 horas Nombre y Apellidos: Nº de Matrícula: Pr 1 Pr 2 Pr3 Pr4 Nota EXAMEN TEMA 2:Funciones de varias variables 2x 3 y 3 +yx 2
GRUPO 4Mb (16-17) CÁLCULO ETSI Informática (UPM) 8 de Junio - 217 Tiempo: 2 horas Nombre y Apellidos: Nº de Matrícula: Pr 1 Pr 2 Pr3 Pr4 Nota EXAMEN TEMA 2:Funciones de varias variables 2x 3 y 3 +yx 2
Lección 11: Derivadas parciales y direccionales. Gradiente. Introducción al Cálculo Infinitesimal I.T.I. Gestión
 Lección 11: Derivadas parciales y direccionales. Gradiente Introducción al Cálculo Infinitesimal I.T.I. Gestión Recordar: - Cálculo de ĺımites - Reglas de derivación Derivadas parciales f : R 2 R función
Lección 11: Derivadas parciales y direccionales. Gradiente Introducción al Cálculo Infinitesimal I.T.I. Gestión Recordar: - Cálculo de ĺımites - Reglas de derivación Derivadas parciales f : R 2 R función
2xy 3x 2 y 2 y(0) = 1
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA DEPARTAMENTO DE MATEMÁTICA APLICADA II Ingeniería Técnica Industrial. Especialidad en Mecánica Soluciones al Primer Parcial de Ampliación de Matemáticas. Curso
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA DEPARTAMENTO DE MATEMÁTICA APLICADA II Ingeniería Técnica Industrial. Especialidad en Mecánica Soluciones al Primer Parcial de Ampliación de Matemáticas. Curso
IES Fco Ayala de Granada Modelo 5 del Solución Germán-Jesús Rubio Luna. Opción A. Ejercicio 1 de la opción A del modelo 5 de 1999.
 IES Fco Ayala de Granada Modelo 5 del 999. Germán-Jesús Rubio Luna Opción A Ejercicio de la opción A del modelo 5 de 999. [ 5 puntos] Haciendo el cambio de variable t = e x, calcula Calculamos primero
IES Fco Ayala de Granada Modelo 5 del 999. Germán-Jesús Rubio Luna Opción A Ejercicio de la opción A del modelo 5 de 999. [ 5 puntos] Haciendo el cambio de variable t = e x, calcula Calculamos primero
Contenido. 2. Ecuaciones diferenciales de primer orden. 1 / Omar De la Peña-Seaman IFUAP Ecuaciones Diferenciales Facultad de Ingeniería 1/29 29
 Contenido 2. Ecuaciones diferenciales de primer orden 1 / Omar De la Peña-Seaman IFUAP Ecuaciones Diferenciales Facultad de Ingeniería 1/29 29 Contenido: Tema 02 2. Ecuaciones diferenciales de primer orden
Contenido 2. Ecuaciones diferenciales de primer orden 1 / Omar De la Peña-Seaman IFUAP Ecuaciones Diferenciales Facultad de Ingeniería 1/29 29 Contenido: Tema 02 2. Ecuaciones diferenciales de primer orden
Tema 7: Fundamentos del movimiento de fluidos
 Tema 7: Fundamentos del movimiento de fluidos INTRODUCCIÓN La Cinemática de fluidos es la parte de la Mecánica de Fluidos que estudia las propiedades geométricas del movimiento de los fluidos. El estudio
Tema 7: Fundamentos del movimiento de fluidos INTRODUCCIÓN La Cinemática de fluidos es la parte de la Mecánica de Fluidos que estudia las propiedades geométricas del movimiento de los fluidos. El estudio
Tema 11: Diferenciabilidad en varias variables.
 Tema 11: Diferenciabilidad en varias variables. José M. Salazar Noviembre de 2016 Tema 11: Diferenciabilidad en varias variables. Lección 14. Diferenciabilidad en varias variables. Lección 15. Aplicaciones
Tema 11: Diferenciabilidad en varias variables. José M. Salazar Noviembre de 2016 Tema 11: Diferenciabilidad en varias variables. Lección 14. Diferenciabilidad en varias variables. Lección 15. Aplicaciones
1. ECUACIONES DIFERENCIALES ORDINARIAS
 1 1. ECUACIONES DIFERENCIALES ORDINARIAS 1.1. PRIMERAS DEFINICIONES. PROBLEMA DEL VALOR INICIAL Definición 1.1. Una ecuación diferencial es una ecuación en la que intervienen una variable dependiente y
1 1. ECUACIONES DIFERENCIALES ORDINARIAS 1.1. PRIMERAS DEFINICIONES. PROBLEMA DEL VALOR INICIAL Definición 1.1. Una ecuación diferencial es una ecuación en la que intervienen una variable dependiente y
ρ t + ρu x = 0, ρu t + P = ρrt 0 Eliminando la presión, nos quedan dos ecuaciones acopladas para la densidad y la velocidad: ρ x = 0, (1) = 0.
 Solución Tarea 2 Problema 1 (a) Poniendo las derivadas con respecto a y y z iguales a cero en las ecuaciones de Euler, obtenemos las ecuaciones de continuidad y momento 1D: ρ t + ρu x =, ρu t + x (ρu2
Solución Tarea 2 Problema 1 (a) Poniendo las derivadas con respecto a y y z iguales a cero en las ecuaciones de Euler, obtenemos las ecuaciones de continuidad y momento 1D: ρ t + ρu x =, ρu t + x (ρu2
MATEMÁTICAS VI. CÁLCULO INTEGRAL UNIDAD II MÉTODOS DE INTEGRACIÓN
 MÉTODOS DE INTEGRACIÓN UNIDAD II MÉTODOS DE INTEGRACIÓN No todas las funciones en un integrando se pueden resolver mediante reglas inmediatas de integración, y requieren ser tratadas con técnicas especiales.
MÉTODOS DE INTEGRACIÓN UNIDAD II MÉTODOS DE INTEGRACIÓN No todas las funciones en un integrando se pueden resolver mediante reglas inmediatas de integración, y requieren ser tratadas con técnicas especiales.
Soluciones de los ejercicios del examen final de la primera convocatoria
 Matemáticas III GI, curso 2015 2016 oluciones de los ejercicios del examen final de la primera convocatoria EJERIIO 1. De un campo escalar fx, y, z se sabe que es de clase R 3 y que su gradiente en el
Matemáticas III GI, curso 2015 2016 oluciones de los ejercicios del examen final de la primera convocatoria EJERIIO 1. De un campo escalar fx, y, z se sabe que es de clase R 3 y que su gradiente en el
Prueba de Funciones de varias variables. 5 de noviembre de 2012 GRUPO A
 5 de noviembre de 1 GRUPO A xy5 si y x x y 1.- Consideremos f(xy)=. Se pide: 1 si y=x a) Existe el límite: lím f(xy)? xy 1 b) Es continua la función en (1)? c) Es diferenciable la función en (1)? ( puntos).-
5 de noviembre de 1 GRUPO A xy5 si y x x y 1.- Consideremos f(xy)=. Se pide: 1 si y=x a) Existe el límite: lím f(xy)? xy 1 b) Es continua la función en (1)? c) Es diferenciable la función en (1)? ( puntos).-
Ley de Newton. Masa Acceleración = Fuerza. ρ dv!" = F!"
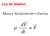 Ley de Newton Masa Acceleración = Fuerza ρ dv!" dt = F!" Fuerzas F = m a F! m = a = F / m F Presión + F Coriolis + F gravedad + F marea + F fricción! Fx m = F Presión fv + F gravedad + F marea + F fricción!
Ley de Newton Masa Acceleración = Fuerza ρ dv!" dt = F!" Fuerzas F = m a F! m = a = F / m F Presión + F Coriolis + F gravedad + F marea + F fricción! Fx m = F Presión fv + F gravedad + F marea + F fricción!
Integrales de lı nea y de superficie
 EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
1.6 Ejercicios resueltos
 Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Breviario de cálculo vectorial
 Apéndice A Breviario de cálculo vectorial versión 16 de octubre de 2006 Este apéndice no pretende ser mas que un resumen de definiciones y fórmulas útiles acerca de la función delta de Dirac, cálculo vectorial
Apéndice A Breviario de cálculo vectorial versión 16 de octubre de 2006 Este apéndice no pretende ser mas que un resumen de definiciones y fórmulas útiles acerca de la función delta de Dirac, cálculo vectorial
TEMA II.10. Gasto o Caudal. Dr. Juan Pablo Torres-Papaqui. Departamento de Astronomía Universidad de Guanajuato DA-UG (México)
 TEMA II.10 Gasto o Caudal Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus Guanajuato,
TEMA II.10 Gasto o Caudal Dr. Juan Pablo Torres-Papaqui Departamento de Astronomía Universidad de Guanajuato DA-UG (México) papaqui@astro.ugto.mx División de Ciencias Naturales y Exactas, Campus Guanajuato,
Pauta Examen Final - Ecuaciones Diferenciales
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERIA Y CIENCIAS INSTITUTO DE CIENCIAS BÁSICAS ECUACIONES DIFERENCIALES Pauta Examen Final - Ecuaciones Diferenciales P1.- Indicar el tipo de EDO de las siguientes
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERIA Y CIENCIAS INSTITUTO DE CIENCIAS BÁSICAS ECUACIONES DIFERENCIALES Pauta Examen Final - Ecuaciones Diferenciales P1.- Indicar el tipo de EDO de las siguientes
Pauta Prueba Solemne 2. y(x) = C 1 x 2 2C 2 x 2. Notemos que el determinante del Wronskiano de u y v esta dado por.
 Pauta Prueba Solemne 1. Determine si las siguientes afirmaciones son verdaderas o falsas. Justifique su respuesta. a) (0.5pt) Suponga que las funciones u(x) = x y v(x) = x son soluciones de una ecuación
Pauta Prueba Solemne 1. Determine si las siguientes afirmaciones son verdaderas o falsas. Justifique su respuesta. a) (0.5pt) Suponga que las funciones u(x) = x y v(x) = x son soluciones de una ecuación
DINÁMICA DE FLUIDOS 1. Propiedades de los Fluidos. 2. Cinemática de fluidos.
 DINÁMICA DE FLUIDOS 1. Propiedades de los Fluidos. Concepto de fluido. Fluido ideal. Fluidos reales. Viscosidad Tensión superficial. Capilaridad Estática. Presión en un punto. Ecuación general de la estática.
DINÁMICA DE FLUIDOS 1. Propiedades de los Fluidos. Concepto de fluido. Fluido ideal. Fluidos reales. Viscosidad Tensión superficial. Capilaridad Estática. Presión en un punto. Ecuación general de la estática.
1 Unidad I: Ecuaciones Diferenciales de Primer Orden
 ITESM, Campus Monterrey Departamento de Matemáticas MA-841: Ecuaciones Diferenciales Lectura #6 Profesor: Victor Segura 1 Unidad I: Ecuaciones Diferenciales de Primer Orden 1.3.4 Factores Integrantes Dentro
ITESM, Campus Monterrey Departamento de Matemáticas MA-841: Ecuaciones Diferenciales Lectura #6 Profesor: Victor Segura 1 Unidad I: Ecuaciones Diferenciales de Primer Orden 1.3.4 Factores Integrantes Dentro
CAMPOS VECTORIALES CONSERVATIVOS
 1 CAMPOS VECTORIALES CONSERVATIVOS DEFINICION DE CAMPO VECTORIAL. Sean M y N funciones de las variables x e y definidas en una región R del plano. La función definida por F(x, y) = Mi + Nj se llama campo
1 CAMPOS VECTORIALES CONSERVATIVOS DEFINICION DE CAMPO VECTORIAL. Sean M y N funciones de las variables x e y definidas en una región R del plano. La función definida por F(x, y) = Mi + Nj se llama campo
Física de Fluidos Aplicada Tema 1: INTRODUCCIÓN A LA FÍSICA DE FLUIDOS 3 er curso de Licenciado en Ciencias Ambientales
 Física de Fluidos Aplicada Tema 1: INTRODUCCIÓN A LA FÍSICA DE FLUIDOS 3 er curso de Licenciado en Ciencias Ambientales Dr. Eduardo García Ortega Departamento de Química y Física Aplicadas. Área de Física
Física de Fluidos Aplicada Tema 1: INTRODUCCIÓN A LA FÍSICA DE FLUIDOS 3 er curso de Licenciado en Ciencias Ambientales Dr. Eduardo García Ortega Departamento de Química y Física Aplicadas. Área de Física
MÉTODOS MATEMÁTICOS II
 MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
MÉTODOS MATEMÁTICOS II (Licenciatura de Física. Curso 2007-2008) Boletín de problemas a evaluar correspondientes a los Temas I y II Fecha de entrega: Viernes, 23 de Noviembre de 2007 1. Calcula los siguientes
