Integral de superficie.
|
|
|
- María Luz Ortiz Santos
- hace 7 años
- Vistas:
Transcripción
1 Tema 4 Integral de superficie. 4.1 uperficies. Definición 4.1 ean IR 2 un conjunto conexo y κ: IR 3 una función continua. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una parametrización de o que es una representación paramétrica de la superficie. Los conjuntos de IR 3 que forman superficies no sólo se obtienen de esta forma sino que el conjunto puede venir definido de otras maneras. unque, para el estudio de la integral de superficie, las superficies van a manejarse siempre mediante su representación paramétrica hay otras formas de representar superficies en el espacio y que es conveniente conocer Expresión analítica de una superficie. Representación impĺıcita. 4.2 Dada una función real F que toma valores en IR 3, el conjunto de puntos { } = x, y, z IR 3 : F x, y, z = constituye una superficie en IR 3, y de la expresión F x, y, z = se dice que es una representación implícita de la superficie. Representación expĺıcita. 4.3 Dada una función real f que toma valores en IR 2, el conjunto de puntos { } = x, y, z IR 3 : z = fx, y conforma una superficie en IR 3 y de la expresión z = fx, y se dice que es una representación explícita de la superficie. nálogamente, para x = fy, z ó y = fx, z. Ejemplo 4.4 El plano x + 2y + 3z = 4 es una superficie en IR 3. i consideramos la función F x, y, z = x + 2y + 3z 4, la expresión x + 2y + 3z 4 = es una representación implícita del plano. Despejando, por ejemplo x en la expresión anterior, x = 4 2y 3z = fy, z es una representación explícita del plano. Haciendo u = y y v = z, la función κ: IR 2 IR 3 con κu, v = 4 2u 3v, u, v es una parametrización del plano. Integrales de Línea y uperficie. 47
2 4.1 uperficies uperficies cuadráticas. Una de las familias más importantes de superficies de IR 3 son las llamadas cuádricas o superficies cuadráticas, que se obtienen de igualar a cero una función polinómica de tres variables y grado 2, es decir, una expresión de la forma a 11 + a 22 y 2 + a 33 z 2 + a 12 xy + a 13 xz + a 23 yz + a 1 x + a 2 y + a 3 z + a =. Mediante giros y translaciones se pueden escribir en la forma a + a 1 x c 1 n 1 + a 2 y c 2 n 2 + a 3 z c 3 n 3 = donde los n i son 1 ó 2 y algunos de los a i pueden ser cero en los casos siguientes pueden observarse algunos de estos tipos Elipsoide. El elipsoide de semiejes a, b, c > viene dado por la ecuación b 2 + z2 c 2 1 =. Una representación parámetrica se obtiene con una pequeña modificación de las coordenadas esféricas recordemos que en el caso particular a = b = c el elipsoide es una esfera mediante κ: [, 2π] [, π] IR 3 con κθ, ϕ = a cos θ sen ϕ, b sen θ sen ϕ, c cos ϕ. La superficie completa del elipsoide no puede expresarse explícitamente, aunque sí por trozos. Por ejemplo, para z y z se tienen las mitades superior e inferior del elipsoide representadas por z = c 1 x2 b 2 z = c 1 x2 b 2 Fig Elipsoide. Curvas de intersección con los planos coordenados Hiperboloide de una hoja. El hiperboloide elíptico de una hoja viene dado por la ecuación a, b, c > b 2 z2 c 2 1 =. Integrales de Línea y uperficie. 48
3 4.1 uperficies. Una representación paramétrica se obtiene, de manera sencilla, haciendo v = z c a polares en la ecuación x2 + y2 = z Por tanto, κ: [, 2π] IR IR 3 con a 2 b 2 c 2 κθ, v = a v cos θ, b v sen θ, cv. y el cambio Puede evitarse la raiz haciendo uso de las funciones hiperbólicas mediante v = sh t y se obtiene κ: [, 2π] IR IR 3 con κθ, t = a ch t cos θ, b ch t sen θ, c sh t. La superficie completa del hiperboloide no puede expresarse explícitamente, aunque sí por trozos. Por ejemplo, para z y z se tienen las partes superior e inferior del hiperboloide representadas por x z = c 2 b 2 1 z = c b 2 1 Fig Hiperboloide de una hoja. Curvas de intersección con los planos coordenados Hiperboloide de dos hojas. El hiperboloide elíptico de dos hojas está formado por la unión de dos superficies conexas. Cada una de las hojas viene dada por la ecuación a, b, c > b 2 z2 c = con z > y con z <. Una representación paramétrica, para cada una de las hojas, se obtiene como en el caso anterior mediante κ: [, 2π] [1, + IR 3 con κθ, v = y κ: [, 2π], 1] IR 3 con κθ, v = a v 2 1 cos θ, b v 2 1 sen θ, cv, a v 2 1 cos θ, b v 2 1 sen θ, cv. La superficie de cada hoja del hiperboloide puede expresarse explícitamente, para z c y z c, por z = c b z = c b Integrales de Línea y uperficie. 49
4 4.1 uperficies. Fig Hiperboloide de dos hojas Cono elíptico. El cono elíptico viene dado por la ecuación a, b, c > b 2 z2 c 2 =. Una representación paramétrica se obtiene, de manera sencilla, haciendo v = z c a polares en la ecuación x2 + y2 = z2. Por tanto, κ: [, 2π] IR IR 3 con a 2 b 2 c 2 y el cambio κθ, v = a v cos θ, b v sen θ, cv. La superficie completa del cono no puede expresarse explícitamente, aunque sí por trozos. Por ejemplo, para z y z se tienen las partes superior e inferior del cono representadas por z = c b 2 z = c b 2 Fig Cono elíptico Paraboloide elíptico. El paraboloide elíptico viene dado por la ecuación a, b, c > b 2 z c =. Integrales de Línea y uperficie. 5
5 4.1 uperficies. La representación explícita se obtiene fácilmente por x 2 z = c b 2. Una representación paramétrica se obtiene de lo anterior por κ: IR 2 IR 3 con κu, v = au, bv, cu 2 + v 2. Fig Paraboloide elíptico Paraboloide hiperbólico. El paraboloide hiperbólico viene dado por la ecuación a, b, c > a 2 y2 b 2 z c =. La representación explícita se obtiene fácilmente por x 2 z = c a 2 y2 b 2. Una representación paramétrica se obtiene de lo anterior por κ: IR 2 IR 3 con κu, v = au, bv, cu 2 v 2. Fig Paraboloide hiperbólico. Integrales de Línea y uperficie. 51
6 4.1 uperficies Cilindros. Los cilindros de obtienen cuando en la expresión de F x, y, z = alguna de las variables no aparece, y heredan el apelativo de la curva que en IR 2 representa la expresión. sí, si F x, y, z = fx, y = y la curva fx, y = es una elípse, hipérbola o parábola, el cilindro es elíptico, hiperbólico o parabólico. La representación paramétrica se obtiene a partir de una parametrización de la curva, es decir, si αt = α 1 t, α 2 t es una parametrización de la curva, entonces la aplicación κt, z = α 1 t, α 2 t, z es una parametrización del cilindro. Para el cilindro elíptico x2 + y2 1 =, una parametrización es κ: [, 2π] IR IR 3 a 2 b 2 con κt, z = a cos t, b sen t, z. Para el cilindro parabólico x2 a 2 y b =, una parametrización se tiene de κ: IR2 IR 3 con κt, z = at, bt 2, z. El cilindro hiperbólico x2 y2 1 = tiene dos hojas, una por cada rama de la hipérbola, a 2 b 2 y pueden parametrizarse por κ: IR 2 IR 3 de expresiones κt, z = a ch t, b sh t, z y κt, z = a ch t, b sh t, z, para cada una de las hojas. Fig Cilindro elíptico. Fig Cilindro hiperbólico uperficies de revolución. Las superficies de revolución son superficies que se obtienen girando una curva plana respecto a una recta. sí, una esfera es una superficie de revolución que se obtiene al girar una semicircunferencia alrededor del diámetro que une los extremos, o un cilindro circular se obtiene de girar una recta respecto a otra paralela ver figura 4.9. ea C una curva plana, supongamos que contenida en el plano XZ, y sea la superficie de revolución obtenida al girar esta curva respecto al eje OZ. Entonces, si αt = α 1 t, α 2 t = xt, zt es una parametrización de C, los puntos de son los de las circunferencias que se obtienen al girar cada punto de C alrededor del eje. Es decir, cada punto xt, zt determina, al girar, una circunferencia plana en, que está situada a altura zt y tiene por radio la distancia del punto al eje OZ, que es xt. En consecuencia, κt, θ = xt cos θ, xt sen θ, zt donde κ: [a, b] [, 2π] IR 3 es una parametrización de. = α 1 t cos θ, α 1 t sen θ, α 2 t Integrales de Línea y uperficie. 52
7 4.1 uperficies. Fig Nota: Las parametrizaciones de la esfera y el cilindro y por tanto, los cambios a coordenadas esféricas y cilíndricas se obtienen de esta forma. Hágase como ejercicio. Ejemplo 4.5 Hallar una parametrización del toro obtenido al girar la circunferencia y b 2 + z 2 = a 2 con b > a, contenida en el plano Y Z, alrededor del eje OZ. olución: Una parametrización de la circunferencia es αϕ = b + a cos ϕ, a sen ϕ con ϕ [, 2π], luego κ: [, 2π] [, 2π] IR 3 donde κϕ, θ = b + a cos ϕ cos θ, b + a cos ϕ sen θ, a sen ϕ, es la parametrización buscada. Fig Parametrización del toro uperficies regulares. Definición 4.6 ean IR 3 un conjunto conexo y κ: IR 3 una función de clase 1. La imagen = κ se llama superficie descrita por κ. También se dice que κ es una parametrización de. El punto κu, v de se dice regular si el rango de la matriz κ u, v es 2. En caso contrario se dice que es singular. Una superficie se dice regular si todos sus puntos lo son. Integrales de Línea y uperficie. 53
8 4.1 uperficies. Definición 4.7 ean IR 2 conexo y κ: IR 3 de clase 1. Para cada u, v, consideremos los vectores D 1 κu, v = D 1 κ 1 u, v, D 1 κ 2 u, v, D 1 κ 3 u, v D 2 κu, v = D 2 κ 1 u, v, D 2 κ 2 u, v, D 2 κ 3 u, v. l vector pvfu, v = D 1 κu, v D 2 κu, v, se le llama vector producto vectorial fundamental de la superficie descrita por κ, y tiene por componentes i j k D D 1 κ D 2 κ = D 1 κ 1 D 1 κ 2 D 1 κ 3 = 1 κ 2 D 1 κ 3 D D 2 κ 1 D 2 κ 2 D 2 κ 3 2 κ 2 D 2 κ 3, D 1 κ 1 D 1 κ 3 D 2 κ 1 D 2 κ 3, D 1 κ 1 D 1 κ 2. D 2 κ 1 D 2 κ 2 i pvfu, v, al vector nu, v = pvfu, v pvfu, v = D 1 κu, v D 2 κu, v D 1 κu, v D 2 κu, v se le denomina vector normal a la superficie en el punto κu, v. Proposición 4.8 ean IR 2 conexo, κ: IR 3 de clase 1 y = κ. El punto κu, v es regular si, y sólo si, pvfu, v. Demostración: Como entonces D pvf = 1 κ 2 D 1 κ 3 D 2 κ 2 D 2 κ 3, pvfu, v rg D 1 κ 3 D 1 κ 1 D 2 κ 3 D 2 κ 1, D 1 κ 1 D 1 κ 2, D 2 κ 1 D 2 κ 2 D1 κ 1 u, v D 1 κ 2 u, v D 1 κ 3 u, v D 2 κ 1 u, v D 2 κ 2 u, v D 2 κ 3 u, v Representación paramétrica obtenida de una explícita. ean f: IR 2 IR y la superficie representada por z = fx, y, entonces la función κ: IR 3 dada por κu, v = u, v, fu, v es una representación paramétrica de. i f es de clase 1, κ es de clase 1 y como pvfu, v = D 1 κu, v D 2 κu, v = 1,, D 1 fu, v = D 1 fu, v, D 2 fu, v, 1,, es una superficie regular. = 2., 1, D 2 fu, v Representación explícita local obtenida de una paramétrica. ea IR 2 conexo y κ: IR 3 de clase 1. Entonces, se puede construir una representación explícita de la superficie dada por κ en un entorno de cada punto regular. En efecto. ea x = κu, v un punto regular, entonces alguna de las coordenadas del vector pvfu, v es distinta de cero. upongamos que es la tercera componente, es decir, que D 1 κ 1 u, v D 1 κ 2 u, v D 2 κ 1 u, v D 2 κ 2 u, v Integrales de Línea y uperficie. 54
9 4.1 uperficies. y, consideremos los valores de x, y, z IR tales que x κ 1 u, v = ; y κ 2 u, v = ; z κ 3 u, v =. ea U IR 4 un abierto tal que x, y, u, v U y construyamos h: U IR 2 dada por hx, y, u, v = x κ 1 u, v, y κ 2 u, v = x x, y y. hx, y, u, v = x x, y y =,. Como x = κ 1 u, v e y = κ 2 u, v, h x, y, u, v = D y 1 κ 1 u, v D 1 κ 2 u, v D 2 κ 1 u, v D 2 κ 2 u, v. 1 D1 κ 1 u, v D 1 κ 2 u, v 1 D 2 κ 1 u, v D 2 κ 2 u, v Entonces, por el teorema de la función implícita, existen un abierto W IR 2 que contiene a x, y, un abierto V IR 2 que contiene a u, v y una función g: W V tal que gx, y = u, v, para todo x, y W. Entonces, la función f: W IR definida por fx, y = κ 3 g 1 x, y, g 2 x, y nos da la representación pedida, pues de z κ 3 u, v = se tiene que Plano tangente y recta normal. fx, y = κ 3 g 1 x, y, g 2 x, y = κ 3 u, v = z. Proposición 4.9 ean IR 2 conexo, C una curva regular contenida en y = κ una superficie regular. Entonces C = κc es una curva regular contenida en y, en cada punto de C, el vector producto vectorial fundamental a la superficie es perpendicular al vector tangente a la curva. Demostración: ea α: [a, b] una parametrización regular de C. Entonces, β: [a, b] definida por βt = καt es una parametrización de C de clase 1 y, para cada t a, b, β t = κ αtα t = D 1 κ 1 αt D 2 κ 1 αt D 1 κ 2 αt D 2 κ 2 αt D 1 κ 3 αt D 2 κ 3 αt = α 1tD 1 καt + α 2tD 2 καt α 1 t α 2 t pues, como κ es regular los vectores D 1 καt y D 2 καt son linealmente independientes rg κ αt = 2 y, como α es regular α t = α 1 t, α 2 t,. En consecuencia, β es una parametrización regular de C. demás, como el vector D 1 καt D 2 καt es ortogonal a D 1 καt y a D 2 καt, es también ortogonal a β t, que es el vector tangente a la curva C en el punto. Definición 4.1 ea IR 2 conexo y = κ una superficie regular. El plano que pasa por el punto κu, v y es paralelo a los vectores D 1 κu, v y D 2 κu, v, se llama plano tangente a la superficie en dicho punto y tiene por ecuación vectorial y = κu, v + λd 1 κu, v + µd 2 κu, v. La recta que pasa por el punto κu, v y es paralela al vector pvfu, v, se llama recta normal a la superficie en dicho punto y tiene por ecuación vectorial y = κu, v + λ D 1 κu, v D 2 κu, v. Integrales de Línea y uperficie. 55
10 4.1 uperficies. Ejemplo 4.11 Hallar la ecuación del plano tangente y la recta normal a la superficie del hiperboloide parabólico κu, v = u, v, u 2 v 2 en el punto κ1, 1. olución: Como D 1 κu, v = 1,, 2u y D 2 κu, v =, 1, 2v, se tiene que pvf1, 1 = D 1 κ1, 1 D 2 κ1, 1 = 1,, 2, 1, 2 = 2, 2, 1 luego el plano tangente en κ1, 1 = 1, 1, es y la recta normal y = 1, 1, + λ1,, 2 + µ, 1, 2 = 1 + λ, 1 + µ, 2λ 2µ y = 1, 1, + λ 2, 2, 1 = 1 2λ, 1 + 2λ, λ Área de una superficie. Definición 4.12 ean IR 2 un conjunto conexo y acotado y κ: IR 3 de clase 1, inyectiva en int. El área de la superficie = κ se define como el valor = pvfu, v du dv. Observación 4.13 i una superficie viene dada en explícitas, z = fx, y, con f: IR, tomando κx, y = x, y, fx, y en, = pvfx, y dx dy = 1,, D 1 fx, y, 1, D 2 fx, y dx dy = D 1 fx, y, D 2 fx, y, 1 dx dy = 1 + D 1 fx, y 2 + D 2 fx, y 2 dx dy Usando la notación clásica D 1 fx, y = f x x, y y D 2fx, y = f y x, y, tenemos que = 1 + D 1 f 2 + D 2 f 2 dx dy = 1 + f 2 x + f 2 y dx dy. Ejemplo 4.14 ea = [, 2π] [, π]. Calcular el área de la esfera descrita por la función κ: IR 3 con κθ, ϕ = a cos θ sen ϕ, a sen θ sen ϕ, a cos ϕ. olución: κ es de clase 1 y luego D 1 κθ, ϕ = a sen θ sen ϕ, a cos θ sen ϕ, D 2 κθ, ϕ = a cos θ cos ϕ, a sen θ cos ϕ, a sen ϕ pvfθ, ϕ = a sen θ sen ϕ, a cos θ sen ϕ, a cos θ cos ϕ, a sen θ cos ϕ, a sen ϕ = a 2 cos θ sen 2 ϕ, a 2 sen θ sen 2 ϕ, a 2 sen ϕ cos ϕ = a 4 cos 2 θ sen 4 ϕ + a 4 sen 2 θ sen 4 ϕ + a 4 sen 2 ϕ cos 2 ϕ = a 4 sen 2 ϕ[cos 2 θ + sen 2 θ] sen 2 ϕ + cos 2 ϕ = a 2 sen ϕ sen 2 ϕ + cos 2 ϕ = a 2 sen ϕ = a 2 sen ϕ. Integrales de Línea y uperficie. 56
11 4.2 Integral de superficie de funciones reales. Entonces = = π pvfθ, ϕ dθ dϕ = a 2 sen ϕ dθ dϕ = 2π a 2 sen ϕ dϕ dθ = a 2 cos ϕ ] π 2π π 2π = 4πa 2. a 2 sen ϕ dϕ dθ 4.2 Integral de superficie de funciones reales. Definición 4.15 ea IR 2 un conjunto conexo y acotado, κ: IR 3 una función de clase 1, = κ y f: IR acotada tal que la función compuesta f κ es integrable en. La integral de superficie de f sobre se define por f = f dκ = fκu, v pvfu, v du dv. Ejemplo 4.16 Calcular la integral de superficie z 2, siendo la superficie de la esfera unidad en el primer octante. olución: El conjunto, puede parametrizarse por κθ, ϕ = cos θ sen ϕ, sen θ sen ϕ, cos ϕ, donde κ: [, π 2 ] [, π 2 ] IR3. Entonces, como pvfθ, ϕ = sen ϕ ver ejemplo 4.14, se tiene π 2 f = fκθ, ϕ pvfθ, ϕ dθ dϕ = π 2 cos 2 ϕ sen ϕ dθ dϕ = π plicaciones a la mecánica. ean IR 2 un conjunto conexo y acotado y κ: IR 3 una función de clase 1. Consideremos una lámina delgada que tenga la forma de la superficie = κ y que su densidad en cada punto viene dada por una función acotada f: IR tal que la función compuesta f κ es integrable en. Entonces, la masa M de la lámina viene dada por M = f El centro de masas de la lámina, de coordenadas ξ, η, γ se obtiene de ξ = 1 M xf η = 1 M yf γ = 1 M y, el momento de inercia I L de la lámina respecto de la recta L es I L = δ 2 f donde, para cada x, y, z, δx, y, z representa la distancia del punto x, y, z a la recta L. Ejemplo 4.17 Una hoja de papel homogénea rectangular de base 2πa y altura h se enrolla formando una superficie cilíndrica de radio a. Calcular el momento de inercia de respecto de la recta que contenga un diámetro de la base circular. zf Integrales de Línea y uperficie. 57
12 4.3 Flujo de un campo vectorial. olución: ituamos el cilindro formado por la lámina sobre el plano XY siendo eje OZ su eje longitudinal, es decir, formando la superficie = {x, y, z : + y 2 = a 2 ; z h}. Por ser homogénea, la función densidad f: IR viene dada por fx, y, z = k, para algún valor constante k; y si tomamos como recta L uno de los otros ejes, por ejemplo, el eje OX, se tiene que δx, y, z = y 2 + z 2. Una parametrización para viene dada por κ: = [, 2π] [, h] IR 3, de expresión κθ, z = a cos θ, a sen θ, z y con pvfθ, z = a cos θ, a sen θ, = a. Luego I L = δ 2 x, y, zk = ky 2 + z 2 = ka 2 sen 2 θ + z 2 a dθ dz = ka2π ha2 2 + h Flujo de un campo vectorial. Definición 4.18 ea IR 2 un conjunto conexo y acotado, κ: IR 3 una función de clase 1 y = κ. ea f: IR 3 la función que representa el vector densidad de flujo de la corriente de un fluido, entonces la masa de fluido que atraviesa la superficie en la unidad de tiempo el flujo a través de la superficie, en la dirección del vector normal, viene dado por f n = f n dκ. Observación 4.19 Usando la definición de integral de superficie y que n = f n dκ = fκu, v pvf pvf, se tiene que pvfu, v pvfu, v du dv = fκu, v pvfu, v du dv. pvfu, v Ejemplo 4.2 La corriente de un fluido tiene como vector densidad de flujo en cada punto a la función fx, y, z = yz, xz, xy. ea la superficie del plano x + y + z = 1 situada en el primer octante y n el vector normal a. Calcular la masa de fluido que atraviesa la superficie en la unidad de tiempo en la dirección de n. olución: La superficie es un trozo del plano z = 1 x y, luego puede parametrizarse con κ: IR 3, donde κx, y = x, y, 1 x y y = {x, y : x 1, y 1 x}. Como pvfx, y = 1,, 1, 1, 1 = 1, 1, 1 y fκx, y = y1 x y, x1 x y, xy, el flujo a través de la superficie en la dirección del vector normal es n Fig f n = 1 1 x y1 x y + x1 x y + xy dy dx = 1 8. Integrales de Línea y uperficie. 58
13 4.3 Flujo de un campo vectorial Teorema de tokes. Definición 4.21 ean IR 3 un conjunto abierto y f: IR 3 una función con derivadas parciales en. e llama rotacional de f a la función rot f: IR 3 definida como rot f = D 2 f 3 D 3 f 2, D 3 f 1 D 1 f 3, D 1 f 2 D 2 f 1. Proposición 4.22 ean IR 3 un conjunto abierto y convexo y f: IR 3 una función de clase 1 en. Entonces f es un gradiente en si, y sólo si, rot f = en. Demostración: Como el conjunto es convexo, f es un gradiente en i, j, D i f j = D j f i en rot f = en. Teorema de tokes o del rotacional 4.23 ea C una curva simple cerrada y regular a trozos de IR 2 parametrizada por α: [a, b] IR 2, que la recorre en sentido positivo. ean el conjunto encerrado por C y = κ una superficie regular descrita por κ, función de clase 2. i f: IR 3 es de clase 1, entonces f = rot f n, κc donde la curva κc está recorrida en el sentido inducido por α. Ejemplo 4.24 Calcular la integral de línea de fx, y, z = xz, y, y a lo largo de la frontera del triángulo de vértices a = 2,,, b =, 6, y c =,, 2 recorrida en este sentido. olución: El triángulo T es el trozo del plano 3x + y + 3z = 6 en el primer octante, que se parametriza por κ: IR 3, donde κx, y = x, y, 2 x y 3 y = {x, y : x [, 2], y 6 3x}. demás, si recorremos en sentido positivo, vamos de, a 2, y, en T = κ z y T T y x x Fig vamos de κ, =,, 2 a κ2, = 2,,, luego el sentido del recorrido inducido en T es el buscado. En consecuencia, por el teorema de tokes, 2 6 3x f = rot f n =, x 2xy, 1, 1 3, 1 dx dy = + x 2xy 3 dy dx = 4 T T 3. Integrales de Línea y uperficie. 59
14 4.3 Flujo de un campo vectorial Rotacional y divergencia de un campo vectorial. Definición 4.25 ean IR n abierto y f: IR n una función cuyas componentes tienen derivadas parciales en. e llama divergencia de f a la función div f: IR definida por div f = D 1 f 1 + D 2 f D n f n. Proposición 4.26 ean IR 3 abierto y g: IR 3 una función de clase 2. Entonces divrot g = en. Demostración: Como en el abierto la función g es de clase 2, se tiene que D ij g k = D ji g k, i, j, k. Luego divrot g = div D 2 g 3 D 3 g 2, D 3 g 1 D 1 g 3, D 1 g 2 D 2 g 1 = D 1 D 2 g 3 D 3 g 2 + D 2 D 3 g 1 D 1 g 3 + D 3 D 1 g 2 D 2 g 1 = D 21 g 3 D 31 g 2 + D 32 g 1 D 12 g 3 + D 13 g 2 D 23 g 1 = D 21 g 3 D 12 g 3 + D 13 g 2 D 31 g 2 + D 32 g 1 D 23 g 1 = Corolario 4.27 Con las hipótesis del teorema anterior, una condición necesaria para que una función f sea el rotacional de otra función g en un abierto es que div f = en. Proposición 4.28 ean IR 3 un rectángulo abierto y f: IR 3 de clase 1 tal que div f = en. Entonces, existe una función g: IR 3 tal que rot g = f en. Demostración: ea x, y, z un punto fijo. La función g: IR 3 de componentes g 1 = ; g 2 = x z f 3 t, y, z dt f 1 x, y, t dt; x z x g 3 = f 2 t, y, z dt; x verifica que rot g = f en. En efecto, x x z D 2 g 3 D 3 g 2 = D 2 f 2 t, y, z dt D 3 f 3 t, y, z dt f 1 x, y, t dt x x z x x z = D 2 f 2 t, y, z dt D 3 f 3 t, y, z dt + D 3 f 1 x, y, t dt x x z Por las integrales dependientes de un parámetro las dos primeras y, por ser una función integral la tercera, se tiene que = = x x x x D 2 f 2 t, y, z dt D 3 f 3 t, y, z dt + f 1 x, y, z x x D 2 f 2 t, y, z D 3 f 3 t, y, z dt + f 1 x, y, z Como = div f = D 1 f 1 + D 2 f 2 + D 3 f 3, se tiene que D 1 f 1 = D 2 f 2 D 3 f 3. Luego x = D 1 f 1 t, y, z dt + f 1 x, y, z x = f 1 x, y, z f 1 x, y, z + f 1 x, y, z = f 1 x, y, z. Integrales de Línea y uperficie. 6
15 4.3 Flujo de un campo vectorial. x D 3 g 1 D 1 g 3 = + D 1 f 2 t, y, z dt = f 2 x, y, z. x x z D 1 g 2 D 2 g 1 = D 1 f 3 t, y, z dt f 1 x, y, t dt x z x z = D 1 f 3 t, y, z dt D 1 f 1 x, y, t dt = f 3 x, y, z = f 3 x, y, z. x z Ejemplo 4.29 Demostrar que el campo fx, y, z = y z, z x, x y es un rotacional en IR 3 y determinar g tal que rot g = f. olución: En IR 3, div f = D 1 f 1 + D 2 f 2 + D 3 f 3 = + + =, luego existe g: IR 3 IR 3 tal que rot g = f. ea el punto fijo de IR 3, por la proposición anterior, g 1 x, y, z = ; g 2 x, y, z = x g 3 x, y, z = x z f 3 t, y, z dt f 2 t, y, z dt = f 1, y, t dt = x x z t dt = zx + x2 2. z t y dt y t dt = x2 z2 yx yz ; luego gx, y, z =, x2 +z 2 2 yx + z, x2 2 xz Teorema de la divergencia. Teorema de la divergencia o de Gauss 4.3 ean una superficie que encierra un volumen V, = κ donde κ es de clase 1 e inyectiva salvo quizá en un conjunto de medida nula, f: V IR 3 de clase 1 y n el vector normal unitario exterior a la superficie. Entonces, f n = V div f. Ejemplo 4.31 La corriente de un fluido tiene como vector densidad de flujo en cada punto fx, y, z = x, y 2, 2yz. Calcular la masa de fluido que atraviesa la superficie exterior del hemisferio = {x, y, z : + y 2 + z 2 1, z } en la unidad de tiempo y en la dirección del vector normal exterior. olución: Por el teorema de la divergencia, si denotamos por = V la superficie exterior del sólido, se tiene que f n = div f. Como div fx, y, z = 1 + 2y 2y = 1, entonces f n = V V div f = V 1 = VV = π 2. Integrales de Línea y uperficie. 61
16 4.4 Ejercicios. 4.4 Ejercicios. 4.1 Para cada una de las cuádricas de la subseccion 4.1.2, encontrar el vector producto vectorial fundamental asociado a las parametrizaciones allí construidas, indicando la dirección de dicho vector. 4.2 Hallar el vector unitario normal a la superficie de revolución dada por la función κu, v = fu cos v, fu sen v, gu, donde f y g son funciones reales de clase Calcular el área del toro engendrado al girar entorno al eje OZ la circunferencia de radio a situada en el plano XZ con centro en el eje OX a una distancia b b > a del origen 4.4 Calcular el área de la porción de la semiesfera + y 2 + z 2 = a 2, z, interior al cilindro + y 2 = ax. 4.5 Calcular el área de la porción del plano x + y + z = a, interior al cilindro + y 2 = a El plano y + z = a divide a la superficie esférica + y 2 + = a 2 en dos partes. Designando por el casquete de menor área, calcular la integral de superficie de la función fx, y, z = yz sobre. 4.7 Calcular la integral de línea de fx, y, z = xz, y, y a lo largo de la curva intersección del cilindro + y 2 = a 2 y el plano x a + z b = 1, con a, b >. Indíquese el sentido del recorrido. 4.8 Consideremos el cubo de lado 2 situado en el primer octante y con un vértice en el origen. Cortando dicho cubo con un plano que pasa por el centro del cubo y es perpendicular a la diagonal del cubo con extremo en el origen, queda definido un exagono regular H. Calcular el valor de la integral de línea de fx, y, z = y 2 z 2, z 2, y 2 a lo largo de H, indicando el sentido del recorrido. Hacerlo de dos formas distintas. 4.9 ean un rectángulo abierto de IR 3 y f y g dos gradientes de clase 1 en. Probar que f g es un rotacional en. 4.1 Calcular la integral de superficie f n siendo fx, y, z =, y 2, z 2, la superficie exterior total del cono sólido C = {x, y, z : x2 a 2 normal exterior. + y2 a 2 z2 b 2, z b} y n el vector 4.11 ea V el conjunto V = {x, y, z : z y 2 ; +y 2 2y; z } y sea f: V IR 3 definida por fx, y, z = 6y, 6x, 2x. Hallar integrando en la superficie frontera de V el flujo saliente y comprobarlo mediante el teorema de la divergencia Demostrar el principio de rquímedes: el empuje de un fluido sobre un sólido V es igual al peso del fluido desalojado por V. Integrales de Línea y uperficie. 62
Integral de superficie
 2 Métodos Matemáticos I : Integral de superficie Tema 4 Integral de superficie 4.1 uperficies Definición 114.- ean IR 2 un conjunto coneo y κ: IR 3 una función continua. La imagen = κ se llama superficie
2 Métodos Matemáticos I : Integral de superficie Tema 4 Integral de superficie 4.1 uperficies Definición 114.- ean IR 2 un conjunto coneo y κ: IR 3 una función continua. La imagen = κ se llama superficie
GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE. 2) Para cada una de las superficies dadas determine un vector normal y la ecuación del
 GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE PLANO TANGENTE Y VECTOR NORMAL. AREA DE UNA SUPERFICIE 1) En cada uno de los siguientes ejercicios se presenta una S dada en forma paramétrica,
GUIA DE ESTUDIO PARA EL TEMA 2: INTEGRALES DE SUPERFICIE PLANO TANGENTE Y VECTOR NORMAL. AREA DE UNA SUPERFICIE 1) En cada uno de los siguientes ejercicios se presenta una S dada en forma paramétrica,
Integrales de lı nea y de superficie
 EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
EJERIIO DE A LULO II PARA GRADO DE INGENIERI A Elaborados por Domingo Pestana y Jose Manuel Rodrı guez, con Arturo de Pablo y Elena Romera 4 4.1 Integrales de lı nea y de superficie Integrales sobre curvas
Coordinación de Matemática IV Guía-Apunte de Preparación del CAR. 2 do Semestre Contenidos del Certamen
 Universidad Técnica Federico anta aría Coordinación de atemática IV Guía-Apunte de Preparación del CAR 2 do emestre 2011 Información Contenidos del Certamen Teorema de Green, Teorema de Green para Regiones
Universidad Técnica Federico anta aría Coordinación de atemática IV Guía-Apunte de Preparación del CAR 2 do emestre 2011 Información Contenidos del Certamen Teorema de Green, Teorema de Green para Regiones
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
Problemas de Análisis Vectorial y Estadístico
 Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
ANALISIS MATEMATICO II (Ciencias- 2011) Trabajo Práctico 8
 ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
Integración sobre superficies
 Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Parametrizaciones 1 2. Área de una superficie
Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Parametrizaciones 1 2. Área de una superficie
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
ANALISIS II 12/2/08 COLOQUIO TEMA 1
 ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Práctica 9 Campos conservativos - Teorema de Green
 ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
Matemáticas III Tema 6 Integrales de superficie
 Matemáticas III Tema 6 Integrales de superficie Rodríguez ánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba,. 214. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative Commons Attribution- NonComercial-hareAlike
Matemáticas III Tema 6 Integrales de superficie Rodríguez ánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba,. 214. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative Commons Attribution- NonComercial-hareAlike
Lista de Ejercicios Complementarios
 Lista de Ejercicios omplementarios Matemáticas VI (MA-3) Verano. ean α >, β > y a, b R constantes. ea la superficie que es la porción del cono de ecuación z = α x + y que resulta de su intersección con
Lista de Ejercicios omplementarios Matemáticas VI (MA-3) Verano. ean α >, β > y a, b R constantes. ea la superficie que es la porción del cono de ecuación z = α x + y que resulta de su intersección con
sea a lo largo de la curva solución de la ecuación diferencial xy, = 5x
 1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
1. Hallar κ de manera que el flujo saliente del campo f ( x, = (x + y + z, 6y a través de la frontera del cuerpo x + y + z 16 x + y κ, 0 < k < 4 f : R R un campo vectorial definido por:. Sea γ ( t ) =
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
AMPLIACIÓN DE CÁLCULO
 AMPLIACIÓN DE CÁLCULO Problemas propuestos Departamento de Matemáticas del Área Industrial Programa de Ampliación de Cálculo. Curso 2014/15 1. Cálculo de integrales múltiples Integrales dobles en rectángulos;
AMPLIACIÓN DE CÁLCULO Problemas propuestos Departamento de Matemáticas del Área Industrial Programa de Ampliación de Cálculo. Curso 2014/15 1. Cálculo de integrales múltiples Integrales dobles en rectángulos;
AMPLIACIÓN DE CÁLCULO
 AMPLIACIÓN DE CÁLCULO Problemas propuestos Departamento de Matemáticas del Área Industrial Índice general Programa III Tema 1. Enunciados 1 Tema 2. Enunciados 6 Tema 3. Enunciados 12 Tema 4. Enunciados
AMPLIACIÓN DE CÁLCULO Problemas propuestos Departamento de Matemáticas del Área Industrial Índice general Programa III Tema 1. Enunciados 1 Tema 2. Enunciados 6 Tema 3. Enunciados 12 Tema 4. Enunciados
El Teorema de Green. Una curva dada por r(t) = x(t) i + y(t) j, a t b, se dice simple si no se corta consigo misma, es decir, r(c) Curva no simple
 El Teorema de Green Una curva dada por r(t) x(t) i + y(t) j, a t b, se dice simple si no se corta consigo misma, es decir, r(c) r(d) si c d. urva simple urva no simple urva orientada positivamente La curva
El Teorema de Green Una curva dada por r(t) x(t) i + y(t) j, a t b, se dice simple si no se corta consigo misma, es decir, r(c) r(d) si c d. urva simple urva no simple urva orientada positivamente La curva
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Universidad Técnica Federico Santamaría
 Integral de uperficie - Mate 4 UPEFICIE PAAMÉTICA e forma similar a como se describe una curva mediante una función vectorial r(t), en función de un parámetro t,se puede describir una superficie mediante
Integral de uperficie - Mate 4 UPEFICIE PAAMÉTICA e forma similar a como se describe una curva mediante una función vectorial r(t), en función de un parámetro t,se puede describir una superficie mediante
CALCULO VECTORIAL GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES
 GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
Soluciones de los ejercicios del segundo examen parcial
 Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
Matemáticas III GIC, curso 5 6 Soluciones de los ejercicios del segundo examen parcial EJERCICIO. Considera la integral doble π π ibuja la región del plano XY en la que se está integrando. Usa el teorema
1. INTEGRALES MÚLTIPLES
 1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Primer curso de Ingeniero de Telecomunicación Segundo Examen Parcial. 14 de Junio de 2000
 ÁLULO Primer curso de ngeniero de elecomunicación egundo Examen Parcial. de Junio de Ejercicio. Hallar los extremos absolutos de la función f (x, y, z) =x + y + z, en el conjunto A = (x, y, z) R 3 : x
ÁLULO Primer curso de ngeniero de elecomunicación egundo Examen Parcial. de Junio de Ejercicio. Hallar los extremos absolutos de la función f (x, y, z) =x + y + z, en el conjunto A = (x, y, z) R 3 : x
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 19 de Junio de 2004 Primera parte
 CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 9 de Junio de 4 Primera parte Ejercicio. Un depósito subterráneo de gasolina tiene forma de cilindro elíptico con semieje orizontal a
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 9 de Junio de 4 Primera parte Ejercicio. Un depósito subterráneo de gasolina tiene forma de cilindro elíptico con semieje orizontal a
Tema 1 (Resultados).- Cónicas y Cuádricas.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ejercicios Tema 4: INTEGRAL DE SUPERFICIE (incluye ejercicios exámenes cursos anteriores)
 Ejercicios Tema 4: INTEGRAL DE UPERFICIE (incluye ejercicios exámenes cursos anteriores) 1. Hallar el flujo del campo vectorial F x, y, z a través de la superficie total del cilindro x 2 y 2 R 2, 0 z h.
Ejercicios Tema 4: INTEGRAL DE UPERFICIE (incluye ejercicios exámenes cursos anteriores) 1. Hallar el flujo del campo vectorial F x, y, z a través de la superficie total del cilindro x 2 y 2 R 2, 0 z h.
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
Examen Final de Cálculo Vectorial MATE PREGUNTAS ABIERTAS TEMA A Diciembre 6 de Nombre: Código:
 UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
Integrales sobre superficies
 Capítulo 12 Integrales sobre superficies En este capítulo estudiaremos la noción de área de superficies en R 3, y las integrales de campos escalares y vectoriales definidos sobre éstas. Una superficie
Capítulo 12 Integrales sobre superficies En este capítulo estudiaremos la noción de área de superficies en R 3, y las integrales de campos escalares y vectoriales definidos sobre éstas. Una superficie
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS. 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2.
 INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
INTEGRALES INTEGRALES DOBLES E ITERADAS SOBRE RECTANGULOS 1.- Evalué (, ), donde f es la función dada, y = (, ): 1 4, 0 2. 1 1 4, 0 1 a.- (, ) = 2 1 4, 1 2 2 1 < 3, 0 < 1 b.- (, ) = 1 1 < 3, 1 2 3 3 4,
1. Hallar la ecuación del plano que pasa por el punto (3, 1, 2) y satisface la condición dada. a) paralelo al plano xy b) perpendicular al eje y
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 5 1. Hallar la ecuación del plano que
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 5 1. Hallar la ecuación del plano que
Examen final de Cálculo Integral
 Examen final de Cálculo Integral 8 de junio de (Soluciones) Cuestiones C Sí se puede asegurar que es integrable, como consecuencia del teorema 4. de los apuntes: Llamamos W y f : W R a la esfera y a la
Examen final de Cálculo Integral 8 de junio de (Soluciones) Cuestiones C Sí se puede asegurar que es integrable, como consecuencia del teorema 4. de los apuntes: Llamamos W y f : W R a la esfera y a la
G. SERRANO SOTELO. H = e 0 + E
 CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
Ejercicios de Fundamentos Matemáticos I. Rafael Payá Albert. Ingeniería de Telecomunicaciones. Departamento de Análisis Matemático
 Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
a n en las que n=1 s n = n + 1 Solución: a) Utilizando el criterios de D Alembert se obtiene que a n+1 n a n 3 > 1 n=1
 EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
EJERCICIO DE FUNDAMENTO MATEMÁTICO eries. Estudia el carácter de las series (a El término general es a n en las que (b la suma parcial n-sima es a n n n+ 3 n, n,, 3,... s n n, n,, 3,... n + olución: a
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
Guía de Estudio para la Sección de Matemáticas del Examen de Admisión
 1 Guía de Estudio para la Sección de Matemáticas del Examen de Admisión 215-1 El material relativo al temario puede ser consultado en la amplia bibliografía que allí se menciona o en alguno de los muchísimos
1 Guía de Estudio para la Sección de Matemáticas del Examen de Admisión 215-1 El material relativo al temario puede ser consultado en la amplia bibliografía que allí se menciona o en alguno de los muchísimos
Relación de ejercicios del tema 3
 Relación de ejercicios del tema 3 Asignatura: Curvas y Superficies. Grado en Matemáticas. Grupo: 3 0 -B Profesor: Rafael López Camino (Do Carmo, sección 2.2) 1. Demostrar que el cilindro {(x, y, z) R 3
Relación de ejercicios del tema 3 Asignatura: Curvas y Superficies. Grado en Matemáticas. Grupo: 3 0 -B Profesor: Rafael López Camino (Do Carmo, sección 2.2) 1. Demostrar que el cilindro {(x, y, z) R 3
x y z x y z x y z z z z z z z
 . Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
. Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
Clase 4. Campos Vectorialesy OperadoresDiferenciales
 lase 4. ampos Vectorialesy Operadoresiferenciales Un campo vectorial en R n es una función F : R n R n. i F es un campo vectorial, una línea de flujo (línea de corriente o curva integral) para F es una
lase 4. ampos Vectorialesy Operadoresiferenciales Un campo vectorial en R n es una función F : R n R n. i F es un campo vectorial, una línea de flujo (línea de corriente o curva integral) para F es una
y v 0, 0, 1 y v 1, 0, 1 se tiene la ecuación
 SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Comentarios y ejemplos - Práctica 10
 ANÁLII MATEMÁTICO II - Grupo Ciencias 218 Comentarios y ejemplos - Práctica 1 A. Parametrizaciones de superficies El concepto de parametrización de una superficie es análogo al de parametrización de una
ANÁLII MATEMÁTICO II - Grupo Ciencias 218 Comentarios y ejemplos - Práctica 1 A. Parametrizaciones de superficies El concepto de parametrización de una superficie es análogo al de parametrización de una
MATEMÁTICAS 2. Curso 2016/17. Integración en varias variables.
 MATEMÁTICA 2. Curso 2016/17. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles siguientes
MATEMÁTICA 2. Curso 2016/17. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles siguientes
AMPLIACIÓN DE MATEMÁTICAS. Curso 2015/16. Integración en varias variables.
 AMPLIACIÓN DE MATEMÁTICA. Curso 2015/16. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles
AMPLIACIÓN DE MATEMÁTICA. Curso 2015/16. Integración en varias variables. 1. Calcular para = [0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcular las integrales dobles
Lección 4. Integrales múltiples. 4. Superficies parametrizadas.
 GRADO DE INGENIERÍA AEROESPACIAL CURSO 0 MATEMÁTICAS III DPTO DE MATEMÁTICA APLICADA II Lección 4 Integrales múltiples 4 Superficies parametrizadas Representación paramétrica de una superficie La primera
GRADO DE INGENIERÍA AEROESPACIAL CURSO 0 MATEMÁTICAS III DPTO DE MATEMÁTICA APLICADA II Lección 4 Integrales múltiples 4 Superficies parametrizadas Representación paramétrica de una superficie La primera
Vectores. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo equivalente a QP.
 Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables.
 AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables. 1. Calcular para =[0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcularlasintegralesdoblessiguientesenlosrecintosqueseindican:
AMPLIACIÓN DE CÁLCULO. Curso 2008/9. Hoja 1: Integración en varias variables. 1. Calcular para =[0, 1] [0, 3] las integrales (a) xydxdy. (b) xe y dxdy. (c) y 2 sin xdxdy. 2. Calcularlasintegralesdoblessiguientesenlosrecintosqueseindican:
Matemáticas III Tema 5 Integrales de ĺınea
 Matemáticas III Tema 5 Integrales de ĺınea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 2014. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons Attribution- Nonomercial-ShareAlike
Matemáticas III Tema 5 Integrales de ĺınea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 2014. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons Attribution- Nonomercial-ShareAlike
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
Integrales de Superficie.
 CAPÍTULO 9. Integrales de Superficie. Este capítulo cierra los tipos de integrales que estudiamos en el curso. Se practica el concepto de integral de superficie y se dan aplicaciones geométricas y físicas.
CAPÍTULO 9. Integrales de Superficie. Este capítulo cierra los tipos de integrales que estudiamos en el curso. Se practica el concepto de integral de superficie y se dan aplicaciones geométricas y físicas.
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Definir la Integral del campo vectorial F sobre una superficie S como una suma de Riemann.
 .7. Integral de superfície de campos vectoriales. Otra de las aplicaciones importantes de la integral de superficies, es cuando se integra un campo vectorial sobre ella. El significado que adquiere este
.7. Integral de superfície de campos vectoriales. Otra de las aplicaciones importantes de la integral de superficies, es cuando se integra un campo vectorial sobre ella. El significado que adquiere este
Cálculo diferencial e integral 4
 álculo diferencial e integral 4 Guía 4 1. alcular la divergencia y el rotacional de los siguientes campos vectoriales: a) V (x, y, z) = yzi + xzj + xyk. b) V (x, y, z) = x 2 i + (x + y) 2 j + (x + y +
álculo diferencial e integral 4 Guía 4 1. alcular la divergencia y el rotacional de los siguientes campos vectoriales: a) V (x, y, z) = yzi + xzj + xyk. b) V (x, y, z) = x 2 i + (x + y) 2 j + (x + y +
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
OCW-Universidad de Málaga, (2014). Bajo licencia. Creative Commons Attribution- NonComercial-ShareAlike 3.
 OCW-Universidad de Málaga, http://ocw.uma.es 14. Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3. Spain Matemáticas III Relación de ejercicios Tema 3 Ejercicios Ej. 1 Reparametriza
OCW-Universidad de Málaga, http://ocw.uma.es 14. Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3. Spain Matemáticas III Relación de ejercicios Tema 3 Ejercicios Ej. 1 Reparametriza
SUPERFICIES. 2.2 Plano tangente y recta normal. 2.3 Métrica sobre una superficie: Primera forma fundamental y aplicaciones.
 SUPERFICIES. 2.2 Plano tangente y recta normal. 2.3 Métrica sobre una superficie: Primera forma fundamental y aplicaciones. 2.1 Superficie parametrizacida. Ecuaciones implícitas. Curvas paramétricas. 2.2
SUPERFICIES. 2.2 Plano tangente y recta normal. 2.3 Métrica sobre una superficie: Primera forma fundamental y aplicaciones. 2.1 Superficie parametrizacida. Ecuaciones implícitas. Curvas paramétricas. 2.2
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Tema 3. Integrales dobles y triples y sus aplicaciones Septiembre {(x,y)/0 x 2, 0 y } x. I = f(x, y)dydx. 2 4 x. 2 4 x.
 CÁLCULO III (05) Tema. Integrales dobles y triples y sus aplicaciones eptiembre 06. Dibuje la región de integración y calcule las integrales dobles siguientes: d. e. f. g. yda, donde es la región limitada
CÁLCULO III (05) Tema. Integrales dobles y triples y sus aplicaciones eptiembre 06. Dibuje la región de integración y calcule las integrales dobles siguientes: d. e. f. g. yda, donde es la región limitada
PRÁCTICAS DE CÁLCULO PARA I. QUÍMICA
 PRÁCTICS DE CÁLCULO PR I. QUÍMIC Departamento de nálisis Matemático Curso 2005/2006 Práctica 1 Cálculo Diferencial............................... 1 Práctica 2 Cálculo Integral.................................
PRÁCTICS DE CÁLCULO PR I. QUÍMIC Departamento de nálisis Matemático Curso 2005/2006 Práctica 1 Cálculo Diferencial............................... 1 Práctica 2 Cálculo Integral.................................
Tema 4: INTEGRAL DE SUPERFICIE Introducción.
 Profesor: Roque Molina Legaz Tema 4: INTEGRAL DE UPERFICIE Introducción. De la misma forma que la integral de línea extiende el concepto de integral sobre un intervalo del eje real al caso de curvas en
Profesor: Roque Molina Legaz Tema 4: INTEGRAL DE UPERFICIE Introducción. De la misma forma que la integral de línea extiende el concepto de integral sobre un intervalo del eje real al caso de curvas en
PRÁCTICAS DE ANÁLISIS VECTORIAL
 PRÁCTICAS E ANÁLISIS VECTORIAL epartamento de Análisis Matemático Curso 24/25 Profesores responsables Pablo Galindo Aníbal Moltó Práctica 1 Integral de línea. Superficies y áreas de superficie............
PRÁCTICAS E ANÁLISIS VECTORIAL epartamento de Análisis Matemático Curso 24/25 Profesores responsables Pablo Galindo Aníbal Moltó Práctica 1 Integral de línea. Superficies y áreas de superficie............
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Integrales de Superficie.
 CAPÍTULO 10 Integrales de Superficie. Este capítulo cierra los tipos de integrales que estudiamos en el curso. Se practica el concepto de integral de superficie y se dan aplicaciones geométricas y físicas.
CAPÍTULO 10 Integrales de Superficie. Este capítulo cierra los tipos de integrales que estudiamos en el curso. Se practica el concepto de integral de superficie y se dan aplicaciones geométricas y físicas.
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
SERIE # 2 CÁLCULO VECTORIAL
 SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
Problemas resueltos del Boletín 1
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín Problema. Dada la curva r (t) = t [0, π], parametrizarla naturalmente. ( (cos t + t sen t), (sen t t cos t), t ), con En primer
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín Problema. Dada la curva r (t) = t [0, π], parametrizarla naturalmente. ( (cos t + t sen t), (sen t t cos t), t ), con En primer
CÁLCULO INTEGRAL. HOJA 9.
 CÁLCULO INTEGRL. HOJ 9. EL TEOREM DEL CMIO DE VRILES. 1. Teorema (del cambio de variables). Sea g : U V un difeomorfismo de clase C 1 entre dos abiertos de R n, sea f : V R medible. Entonces f g es medible
CÁLCULO INTEGRL. HOJ 9. EL TEOREM DEL CMIO DE VRILES. 1. Teorema (del cambio de variables). Sea g : U V un difeomorfismo de clase C 1 entre dos abiertos de R n, sea f : V R medible. Entonces f g es medible
Certamen 2 - Mate 024 (Pauta)
 Certamen - Mate 4 (Pauta) noviembre 6, 14 1. Calcular γ x 4 + y 4 1 dx + y 3 x 4 + y 4 1 dy en cada uno de los siguientes casos: a) γ es la curva x + y = 1 4 y se recorre en sentido positivo. b) γ es la
Certamen - Mate 4 (Pauta) noviembre 6, 14 1. Calcular γ x 4 + y 4 1 dx + y 3 x 4 + y 4 1 dy en cada uno de los siguientes casos: a) γ es la curva x + y = 1 4 y se recorre en sentido positivo. b) γ es la
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
4 Integrales de línea y de superficie
 a t e a PROBLEMA DE ÁLULO II t i c a s 1 o Ings. Industrial y de Telecomunicación URO 2009 2010 4 Integrales de línea y de superficie 4.1 Integrales sobre curvas y campos conservativos. Problema 4.1 Integra
a t e a PROBLEMA DE ÁLULO II t i c a s 1 o Ings. Industrial y de Telecomunicación URO 2009 2010 4 Integrales de línea y de superficie 4.1 Integrales sobre curvas y campos conservativos. Problema 4.1 Integra
INTEGRALES MÚLTIPLES
 INTEGALES MÚLTIPLES Introducción: Si f es una función definida sobre una región, la integral doble se puede interpretar como el volumen del sólido limitado superiormente por la superficie z = f(,, inferiormente
INTEGALES MÚLTIPLES Introducción: Si f es una función definida sobre una región, la integral doble se puede interpretar como el volumen del sólido limitado superiormente por la superficie z = f(,, inferiormente
CÁLCULO II Funciones de varias variables
 CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen del 14 de Septiembre de 2000 Primera parte
 ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
ÁLULO Primer curso de Ingeniero de Telecomunicación Examen del de Septiembre de Primera parte Ejercicio. Un flan tiene forma de tronco de paraboloide de revolución, siendo r y r losradiosdesusbasesyh su
Relación de ejercicios del tema 3
 Relación de ejercicios del tema 3 Asignatura: Curvas y Superficies. Grado en Matemáticas. Grupo: 2 0 -B Profesor: Rafael López Camino 1. Probar que en un punto hiperbólico, las direcciones principales
Relación de ejercicios del tema 3 Asignatura: Curvas y Superficies. Grado en Matemáticas. Grupo: 2 0 -B Profesor: Rafael López Camino 1. Probar que en un punto hiperbólico, las direcciones principales
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Geometría Diferencial Preguntas de la teoría para el examen
 Geometría Diferencial - 2015 Preguntas de la teoría para el examen Observaciones: Una pregunta del examen puede ser sólo una parte de una de las preguntas siguientes. Si en esta lista una pregunta tiene
Geometría Diferencial - 2015 Preguntas de la teoría para el examen Observaciones: Una pregunta del examen puede ser sólo una parte de una de las preguntas siguientes. Si en esta lista una pregunta tiene
SERIE # 4 CÁLCULO VECTORIAL
 SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Relación de ejercicios del tema 3
 Asignatura: Curvas y Superficies Grado en Matemáticas. Curso 2015/16 Grupo: 2 0 -B Profesor: Rafael López Camino Relación de ejercicios del tema 3 (Ejercicios tomados de los libros de do Carmo y Montiel-Ros)
Asignatura: Curvas y Superficies Grado en Matemáticas. Curso 2015/16 Grupo: 2 0 -B Profesor: Rafael López Camino Relación de ejercicios del tema 3 (Ejercicios tomados de los libros de do Carmo y Montiel-Ros)
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
INTEGRALES MÚLTIPLES. 9 xy c) 4
 de 6 TRABAJO PRÁCTICO Nº A.M. II - INTEGRALES MÚLTIPLES INTEGRALES DOBLES - Calcule las siguientes integrales: a d d d d d b d d sen e 6 d d --. Grafique la región de integración eprese la integral invirtiendo
de 6 TRABAJO PRÁCTICO Nº A.M. II - INTEGRALES MÚLTIPLES INTEGRALES DOBLES - Calcule las siguientes integrales: a d d d d d b d d sen e 6 d d --. Grafique la región de integración eprese la integral invirtiendo
Examen final de Cálculo Integral
 Examen final de Cálculo Integral de junio de 11 (Soluciones) Cuestiones C 1 La respuesta es que la función es integrable, como consecuencia del Teorema 1.1 de los apuntes, o el Teorema del Capítulo 5 del
Examen final de Cálculo Integral de junio de 11 (Soluciones) Cuestiones C 1 La respuesta es que la función es integrable, como consecuencia del Teorema 1.1 de los apuntes, o el Teorema del Capítulo 5 del
Cálculo de Geodésicas en Superficies de Revolución
 Cálculo de Geodésicas en Superficies de Revolución Superficies de Revolución Sea S R 3 la superficie de revolución obtenida al girar una curva regular del plano XZ que no corte al eje Z alrededor del mismo.
Cálculo de Geodésicas en Superficies de Revolución Superficies de Revolución Sea S R 3 la superficie de revolución obtenida al girar una curva regular del plano XZ que no corte al eje Z alrededor del mismo.
Campos Vectoriales y Operadores Diferenciales
 Campos Vectoriales y Operadores Diferenciales 1 Campos Vectoriales y Operadores Diferenciales Opcional Un en R n es una función (continua) F : D R n R n. Una (línea de corriente o también curva integral)
Campos Vectoriales y Operadores Diferenciales 1 Campos Vectoriales y Operadores Diferenciales Opcional Un en R n es una función (continua) F : D R n R n. Una (línea de corriente o también curva integral)
Pauta Auxiliar N 10 Aplicaciones de la Integral I Viernes 1 de Junio de 2012
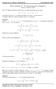 Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
Pauta Auxiliar N Aplicaciones de la Integral I Viernes de Junio de P.- (P Examen Adicional - ) Sea A la región delimitada por las rectas y = x, y = ax, y = ax, a a) Calcule el área de A y el volumen del
UTN FRBA Final de Álgebra y Geometría Analítica 21/05/2013. Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:...
 UTN FRBA Final de Álgebra y Geometría Analítica 1/05/01 Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:... La condición para aprobar esta evaluación es tener bien resueltos como mínimo tres ejercicios.
UTN FRBA Final de Álgebra y Geometría Analítica 1/05/01 Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:... La condición para aprobar esta evaluación es tener bien resueltos como mínimo tres ejercicios.
NOTA: En todos los ejercicios se deberá justificar la respuesta explicando el procedimiento seguido en la resolución del ejercicio.
 Asignatura: álculo II PRUEBAS DE EVALUAIÓN NOTA: En todos los ejercicios se deberá justificar la respuesta eplicando el procedimiento seguido en la resolución del ejercicio. URSO 010 011 JUNIO URSO 10
Asignatura: álculo II PRUEBAS DE EVALUAIÓN NOTA: En todos los ejercicios se deberá justificar la respuesta eplicando el procedimiento seguido en la resolución del ejercicio. URSO 010 011 JUNIO URSO 10
Matemáticas III Tema 5 Integrales de línea
 Matemáticas III Tema 5 Integrales de línea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 14. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons ttribution- Nonomercial-Sharelike
Matemáticas III Tema 5 Integrales de línea Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino órdoba, S. 14. OW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia reative ommons ttribution- Nonomercial-Sharelike
Diferenciación SEGUNDA PARTE
 ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
