Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica
|
|
|
- Purificación Soriano Martínez
- hace 7 años
- Vistas:
Transcripción
1 Capítulo 1: Fundamentos: Lógica y Demostraciones Clase 3: Relaciones, Funciones, y Notación Asintótica Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 1 / 23
2 Relaciones Sean A y B conjuntos. Una relación entre A y B es un subconjunto de A B. O en otros términos, es un conjunto R de pares (a,b) tal que a A y b B. Ejemplo: Sea C el conjunto de ciudades de Chile, y D el conjunto de regiones de Chile. Entonces, la relación está en contiene todos los pares (c,d) C D tal que la ciudad c está en la región d. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 2 / 23
3 Relación sobre un conjunto Si A es un conjunto, entonces una relación en A es una relación entre A y A. Ejemplo: Las siguiente son relaciones en N {(a,b) a b}, {(a,b) a + b 3} Ejercicio: Cuántas relaciones existen en un conjunto con n elementos? P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 3 / 23
4 Propiedades de las relaciones Una relación R en un conjunto A es: refleja: (a,a) R, para todo a A; simétrica: (a,b) R implica (b,a) R, para todo a,b A; antisimétrica: (a,b) R y (b,a) R implica a = b, para todo a,b A; transitiva: (a,b) R y (b,c) R implica (a,c) R, para todo a,b,c A. Ejercicio: Exprese estas propiedades en lógica de predicados. Ejercicio: Estudie algunas relaciones en N con respecto a cuáles de estas propeidades satisfacen. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 4 / 23
5 Operaciones en relaciones Típicas operaciones en relaciones: unión: R R ; intersección: R R ; diferencia: R R ; inverso: R 1 ; composición: R R = {(a,c) (a,b) R,(b,c) R }. Sea R relación en A. Definimos R n, n 1, como sigue: R 1 = R y R n+1 = R n R P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 5 / 23
6 Ejercicios Ejercicio: Demuestre que la relación R en A es transitiva si y sólo si R n R, para cualquier n 1. Ejercicio: Demuestre que R es simétrica si y sólo si R = R 1. Ejercicio: Sea R simétrica. Demuestre que R n es simétrica, para todo n 1. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 6 / 23
7 Ejercicios Ejercicio: Demuestre que la relación R en A es transitiva si y sólo si R n R, para cualquier n 1. Ejercicio: Demuestre que R es simétrica si y sólo si R = R 1. Ejercicio: Sea R simétrica. Demuestre que R n es simétrica, para todo n 1. Pregunta: En qué área de la computación las relaciones son de particular importancia? P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 6 / 23
8 Clausuras La clausura transitiva R de R es la menor relación R que contiene a R y tal que R es transitiva. Equivalentemente podríamos definir las clausuras refleja y simétrica de R. Ejemplo: La clausura transitiva de la relación de sucesor en los números naturales es la relación de orden. La clausura refleja de la relación < en los números naturales es la relación. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 7 / 23
9 Clausura transitiva Intuitivamente, (a,b) R si y sólo si existen elementos a 1,...,a n A, tal que (a,a 1 ),(a 1,a 2 ),...,(a n 1,a n ),(a n,b) es una secuencia de pares en R. Si representamos R como un grafo, entonces R contiene todos aquellos pares (a,b) tal que existe camino desde a hasta b en ese grafo. Ejercicio: Demuestre que si A tiene n elementos, entonces R = 1 i n Ri. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 8 / 23
10 Relaciones de equivalencia Una relación R en A es de equivalencia si es refleja, simétrica, y transitiva. Ejemplo: Sea p 2. Entonces la relación p de congruencia módulo p es una relación de equivalencia. Recuerde que a p b p divides (a b). Ejercicio: Sea R una relación simétrica y transitiva, tal que para cada a A existe b A tal que (a,b) R. Demuestre que R es de equivalencia. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 9 / 23
11 Clases de equivalencia Para a A, denotamos por [a] R a la clase de equivalencia de a con respecto a la relación de equivalencia R. Esta se define como {b (a,b) R}. Ejemplo: [1] p = {1,1 + p,1 + 2p,1 + 3p,... }. Ejercicio: Demuestre que los siguientes enunciados son equivalentes: (a,b) R; [a] R = [b] R ; [a] R [b] R. Ejercicio: Demuestre que a A [a] R = A. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 10 / 23
12 Ordenes parciales Una relación R en A es un orden parcial si es refleja, antisimétrica, y transitiva. Ejemplo: es un orden parcial en N. Ejercicio: Demuestre que la relación de divisibilidad es un orden parcial en N \ 0. Ejercicio: Demuestre que es un orden parcial en 2 S, para cualquier conjunto S. Comúnmente denotamos los ordenes parciales como (A, ). P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 11 / 23
13 Ordenes totales Un orden parcial (A, ) es, además, total si para cada a,b A se tiene que a b o b a. Ejemplo: (Z, ) es un orden total. Sea (A, ) un orden total. Decimos que es un buen orden en A, si cada A A tiene un menor elemento con respecto a. Ejemplo: La relación en (Z, ) no es un buen orden. Ejercicio: Demuestre que la relación en Z + Z + definida por (a 1,a 2 ) (b 1,b 2 ) a 1 < b 1, o a 1 = b 1 y a 2 b 2, es un buen orden en Z + Z +. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 12 / 23
14 Inducción Demuestre el siguiente teorema: Teorema (Inducción bien ordenada): Sea A un conjunto que tiene un buen orden. Entonces la propiedad P es cierta para todo elemento a A, si: Inducción: Para todo b A, si P es cierto para todo a A tal que a b pero a b, entonces P es cierto en b. Este resultado justifica la utilización del método inductivo en los naturales. Y además explica porque no podemos utilizar el mismo método en los enteros. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 13 / 23
15 Funciones Una función entre A y B es una relación R entre A y B, tal que: Para todo a A existe b B tal que (a,b) R; para todo a A, si (a,b) R y (a,b ) R, entonces b = b ; Escribimos f : A B para denotar a una función, y f (a) = b para denotar que el par (a,b) está en la relación que representa a la función. El dominio de f es A, y su codominio es B. Si f (a) = b decimos que b es la imagen de a, y a la preimagen de b. El rango de f es el conjunto {b B f (a) = b,para algún a A}. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 14 / 23
16 Funciones uno-a-uno y sobre Una función f : A B es: Uno-a-uno o inyectiva: si para todo a, b A, a b implica f (a) f (b); Sobre o sobreyectiva: si para todo b B existe a A tal que f (a) = b; Biyectiva: si es uno-a-uno y sobre. Ejemplo: La función f : N N tal que f (n) = 2n es uno-a-uno, pero no es sobre. La función f : N N tal que f (0) = 1 y f (n) = n 1, para todo n > 0, es sobre pero no uno-a-uno. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 15 / 23
17 Funciones inversas Sea f : A B una función biyectiva. Entonces la función inversa f 1 : B A se define como f 1 (b) = a f (a) = b. Pregunta: Por qué pedimos que f sea biyectiva? Sean f : A B y g : B C. La composición de g y f, denotada por g f, es una función de A en C tal que (g f )(a) = g(f (a)). Nota: f 1 f es la función identidad, asumiendo que f es biyectiva. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 16 / 23
18 Ejercicios Ejercicio: Es cierto que si f y f g son uno-a-uno, entonces g es uno-a-uno? Ejercicio: Lo mismo para funciones sobre. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 17 / 23
19 Funciones importantes La función techo asigna a cada número real x el valor x del menor entero y tal que x y. La función piso asigna a cada número real x el valor x del mayor entero y tal que x y. La función factorial asigna a cada número natural n el producto n! de los primeros n enteros positivos (asumimos que 0! = 1). P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 18 / 23
20 Ejercicios Ejercicio: Demuestre que para todo número real x y entero n, x + n = x + n. Ejercicio: Demuestre que para todo número real x, 2x = x + x Ejercicio: Demuestre que para todo número real x, x = x. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 19 / 23
21 Crecimiento de funciones Describimos el crecimiento de funciones utilizando la notación O. Sean f y g definidas desde Z o R en R. Decimos que f (x) es O(g(x)) si existen constantes c y k tal que f (x) c g(x), para todo x > k. Ejercicio: Demuestre que f (x) = x 2 + 2x + 1 es O(x 2 ). Ejercicio: En general, demuestre que todo polinomio de grado n con coeficientes reales es O(x n ). P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 20 / 23
22 Ejercicios Ejercicio: Demuestre que no existe polinomio de grado n > 1 que sea O(x n 1 ). Ejercicio: Utilize la notación O para estimar el tamaño de n i=1 i y de n!. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 21 / 23
23 Crecimiento de funciones combinadas Si tenemos un algoritmo que se compone de dos subprocedimientos, cómo podemos estimar la complejidad de tal algoritmo? Teorema Si f 1 es O(g 1 (x)) y f 2 es O(g 2 (x)), entonces f 1 (x) + f 2 (x) es O(max {g 1 (x),g 2 (x)}). f 1 (x) f 2 (x) es O(g 1 (x) g 2 (x)). Ejercicio: Demuestre el teorema. Ejercicio: Encuentre una (buena) estimación del crecimiento de la función (x + 1)log (x 2 + 1) + 3x 2. P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 22 / 23
24 Otras notaciones Decimos que f (x) es Ω(g(x)) si y sólo si g(x) es O(f (x)). Decimos que f (x) es Θ(g(x)) (o f (x) es de orden g(x)), si y sólo si f (x) es O(g(x)) y g(x) es O(f (x)). Ejercicio: Demuestre que n log n es Θ(log n!). P. Barceló Matemática Discreta - Cap. 1: Fundamentos: Lógica y Demostraciones 23 / 23
Conjuntos, Aplicaciones y Relaciones
 Conjuntos, Aplicaciones y Relaciones Curso 2017-2018 1. Conjuntos Un conjunto será una colección de objetos; a cada uno de estos objetos lo llamaremos elemento del conjunto. Si x es un elemento del conjunto
Conjuntos, Aplicaciones y Relaciones Curso 2017-2018 1. Conjuntos Un conjunto será una colección de objetos; a cada uno de estos objetos lo llamaremos elemento del conjunto. Si x es un elemento del conjunto
Definiciones Un conjunto es una colección de objetos distintos. Notaremos. A = {a, b, c, d, } por extensión
 CONJUNTOS Definiciones Un conjunto es una colección de objetos distintos. Notaremos A = {a, b, c, d, } por extensión A = {x / x tiene la propiedad P} por comprensión El cardinal de un conjunto es el número
CONJUNTOS Definiciones Un conjunto es una colección de objetos distintos. Notaremos A = {a, b, c, d, } por extensión A = {x / x tiene la propiedad P} por comprensión El cardinal de un conjunto es el número
Capítulo 4: Conjuntos
 Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
Capítulo 4: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2014 Olalla (Universidad de Sevilla) Capítulo 4: Conjuntos Septiembre de
2. Estructuras Algebraicas
 2. Estructuras Algebraicas 2.1. Conjuntos Un conjunto es una reunión en un todo de determinados objetos bien definidos y diferentes entre sí. Llamamos elementos a los objetos que lo forman. Requisitos:
2. Estructuras Algebraicas 2.1. Conjuntos Un conjunto es una reunión en un todo de determinados objetos bien definidos y diferentes entre sí. Llamamos elementos a los objetos que lo forman. Requisitos:
Estructuras Discretas. Conjuntos. Conjuntos & Funciones. Especificación de Conjuntos.
 Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos clobos@inf.utfsm.cl niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Matemáticas Discretas Relaciones y funciones
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas y funciones Cursos Propedéuticos 2010 Ciencias Computacionales INAOE y funciones Propiedades de relaciones Clases de equivalencia
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas y funciones Cursos Propedéuticos 2010 Ciencias Computacionales INAOE y funciones Propiedades de relaciones Clases de equivalencia
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 3 Conjuntos, Relaciones y Funciones Conjuntos y Operaciones Los conjuntos se representan con letras mayúsculas,
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 3 Conjuntos, Relaciones y Funciones Conjuntos y Operaciones Los conjuntos se representan con letras mayúsculas,
CLASIFICACIÓN DE FUNCIONES SEGÚN SU CODOMINIO
 CLSIFICCIÓN DE FUNCIONES SEGÚN SU CODOMINIO Ejemplos 1. De acuerdo con la gráfica adjunta correspondiente a la función f x determine cuán debe ser su codominio para que sea una función sobreyectiva. Solución
CLSIFICCIÓN DE FUNCIONES SEGÚN SU CODOMINIO Ejemplos 1. De acuerdo con la gráfica adjunta correspondiente a la función f x determine cuán debe ser su codominio para que sea una función sobreyectiva. Solución
Conjuntos, relaciones de equivalencia y aplicaciones
 CAPíTULO 1 Conjuntos, relaciones de equivalencia y aplicaciones 1. Conjuntos La idea de conjunto es una de las más significativas en Matemáticas. La mayor parte de los conceptos matemáticos están construidos
CAPíTULO 1 Conjuntos, relaciones de equivalencia y aplicaciones 1. Conjuntos La idea de conjunto es una de las más significativas en Matemáticas. La mayor parte de los conceptos matemáticos están construidos
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación. Lecturas en Ciencias de la Computación ISSN
 Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Universidad Central de Venezuela Facultad de Ciencias Escuela de Computación Lecturas en Ciencias de la Computación ISSN 1316-6239 Relaciones Prof. Luis Manuel Hernández R. ND 2006-02 Centro de Cálculo
Álgebra Lineal y Estructuras Matemáticas. J. C. Rosales y P. A. García Sánchez. Departamento de Álgebra, Universidad de Granada
 Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 1 Conjuntos, relaciones y aplicaciones 1. Conjuntos La idea de conjunto
Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 1 Conjuntos, relaciones y aplicaciones 1. Conjuntos La idea de conjunto
1. Conjuntos y funciones
 Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Centro de Matemática Facultad de Ciencias Universidad de la República Introducción a la Topología Curso 2016 PRACTICO 1: CONJUNTOS. 1 1. Conjuntos y funciones Ejercicio 1. Si I es un conjunto y A α es
Relaciones IIC1253. IIC1253 Relaciones 1 / 32
 Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
Relaciones IIC1253 IIC1253 Relaciones 1 / 32 Relaciones binarias Dado: conjunto A R es una relación binaria sobre A si R A A. Para indicar que a,b A están relacionados a través de R usamos las notaciones:
MatemáticaDiscreta&Lógica 1. Funciones. Aylen Ricca. Tecnólogo en Informática San José
 MatemáticaDiscreta&Lógica 1 Funciones Aylen Ricca Tecnólogo en Informática San José 2014 http://www.fing.edu.uy/tecnoinf/sanjose/index.html FUNCIÓN.::. Definición. Sean A y B conjuntos no vacíos, una funciónf
MatemáticaDiscreta&Lógica 1 Funciones Aylen Ricca Tecnólogo en Informática San José 2014 http://www.fing.edu.uy/tecnoinf/sanjose/index.html FUNCIÓN.::. Definición. Sean A y B conjuntos no vacíos, una funciónf
MÉTODOS MATEMÁTICOS DE LA FÍSICA I
 MÉTODOS MATEMÁTICOS DE LA FÍSICA I Ignacio Sánchez Rodríguez Curso 2006-07 TEMA PRELIMINAR ÍNDICE 1. Lenguaje matemático 2 2. Conjuntos 6 3. Aplicaciones 10 4. Relaciones 12 5. Estructuras algebraicas
MÉTODOS MATEMÁTICOS DE LA FÍSICA I Ignacio Sánchez Rodríguez Curso 2006-07 TEMA PRELIMINAR ÍNDICE 1. Lenguaje matemático 2 2. Conjuntos 6 3. Aplicaciones 10 4. Relaciones 12 5. Estructuras algebraicas
CAPÍTULO III RELACIONES Y FUNCIONES
 RELACIONES Y FUNCIONES 41 CAPÍTULO III RELACIONES Y FUNCIONES 3.1 RELACIONES 1 Una relación R de un conjunto A a un conjunto B asigna a cada par (a,b) en A x B exactamente uno de los enunciados siguientes:
RELACIONES Y FUNCIONES 41 CAPÍTULO III RELACIONES Y FUNCIONES 3.1 RELACIONES 1 Una relación R de un conjunto A a un conjunto B asigna a cada par (a,b) en A x B exactamente uno de los enunciados siguientes:
1. Conjuntos y funciones
 PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
PRACTICO 1: CONJUNTOS. 1. Conjuntos y funciones Es útil saber de memoria las siguientes propiedades de conjuntos y funciones. Tanto como saber las tablas. Ejercicio 1. Si I es un conjunto y A α es un conjunto
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2017
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2017 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2017 1
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2016
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2016 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2016 1
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES
 SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
SESIÓN N 07 III UNIDAD RELACIONES Y FUNCIONES RELACIONES BINARIAS PAR ORDENADO Es un arreglo de dos elementos que tienen un orden determinado donde a es llamada al primera componente y b es llamada la
RELACIONES Y FUNCIONES
 ELCIONES Y FUNCIONES INTODUCCION a B b c 3 Cuando manejamos esquemas de este tipo, solemos decir que se estableció una relación o correspondencia entre los conjuntos y B en donde al elemento a le corresponde
ELCIONES Y FUNCIONES INTODUCCION a B b c 3 Cuando manejamos esquemas de este tipo, solemos decir que se estableció una relación o correspondencia entre los conjuntos y B en donde al elemento a le corresponde
Contenido. BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática
 Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
Contenido BLOQUE I: PRELIMINARES Tema 2 ALGUNAS NOCIONES DE TEORÍA DE CONJUNTOS, RELACIONES Y FUNCIONES Lógica Grado en Ingeniería Informática Alessandra Gallinari URJC Nociones de teoría de conjuntos
P(f) : P(B) P(A) (A.2)
 TEMA 2. APLICACIONES 227 Tema 2. Aplicaciones Definición A.2.1. Una correspondencia entre dos conjuntos A y B es un subconjunto del producto cartesiano A B. Una aplicación f entre dos conjuntos A y B es
TEMA 2. APLICACIONES 227 Tema 2. Aplicaciones Definición A.2.1. Una correspondencia entre dos conjuntos A y B es un subconjunto del producto cartesiano A B. Una aplicación f entre dos conjuntos A y B es
Tema 1: Conjuntos. Miguel Ángel Olalla Acosta Departamento de Álgebra Universidad de Sevilla. Septiembre de 2018
 Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Tema 1: Conjuntos Miguel Ángel Olalla Acosta miguelolalla@us.es Departamento de Álgebra Universidad de Sevilla Septiembre de 2018 Olalla (Universidad de Sevilla) Tema 1: Conjuntos Septiembre de 2018 1
Curso Propedéutico de Cálculo Sesión 1: Funciones
 Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Solución del Examen de Matemática I - 19 de setiembre de 2011
 Solución del Examen de Matemática I - 19 de setiembre de 2011 Ejercicio 1 a) Dados los conjuntos y, hallar el mayor conjunto que cumpla simultáneamente con:, y. Justificar. Si consideramos, entonces y
Solución del Examen de Matemática I - 19 de setiembre de 2011 Ejercicio 1 a) Dados los conjuntos y, hallar el mayor conjunto que cumpla simultáneamente con:, y. Justificar. Si consideramos, entonces y
MATEMÁTICAS BÁSICAS. Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano
 MATEMÁTICAS BÁSICAS Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad
MATEMÁTICAS BÁSICAS Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad
Conjuntos. Relaciones. Aplicaciones
 Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
Conjuntos. Relaciones. Aplicaciones Conjuntos 1. Considera el subconjunto A de números naturales formado por los múltiplos de 4 y el conjunto B N de los números que terminan en 4. Comprueba que A B y B
Inducción Matemática Conjuntos Funciones. Matemática Discreta. Agustín G. Bonifacio UNSL. Repaso de Inducción, Conjuntos y Funciones
 UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
UNSL Repaso de Inducción, y Inducción Matemática (Sección 1.7 del libro) Supongamos que queremos demostrar enunciados del siguiente tipo: P(n) : La suma de los primeros n números naturales es n(n+1)
Relaciones Binarias. Matemática Discreta. Agustín G. Bonifacio UNSL. Relaciones Binarias
 UNSL Relaciones Binarias Relaciones Binarias (Sección 3.1 del libro) Definición Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X Y. Si (x,y) R, escribimos
UNSL Relaciones Binarias Relaciones Binarias (Sección 3.1 del libro) Definición Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X Y. Si (x,y) R, escribimos
Ejemplo 66 Sea A = {los alumnos de este curso}, entonces podemos definir la siguiente relación el el conjunto A, dada por:
 Capítulo 3 Relaciones Definición 8 Sea A un conjunto no vacío. Se dice que R es una relación en A si y sólo si R A A. Ejemplo 65 Sea A = {a,b,c}, luego definimos los conjuntos: R 1 = {(a,a),(a,b),(b,c)},r
Capítulo 3 Relaciones Definición 8 Sea A un conjunto no vacío. Se dice que R es una relación en A si y sólo si R A A. Ejemplo 65 Sea A = {a,b,c}, luego definimos los conjuntos: R 1 = {(a,a),(a,b),(b,c)},r
PRELIMINARES. En este capítulo vamos a dar, sin ser muy estrictos, algunas nociones necesarias para la compresión de la asignatura.
 1 PRELIMINARES 1. CONJUNTOS En este capítulo vamos a dar, sin ser muy estrictos, algunas nociones necesarias para la compresión de la asignatura. 1.1 Def:. Se define un conjunto como una colección de objetos.
1 PRELIMINARES 1. CONJUNTOS En este capítulo vamos a dar, sin ser muy estrictos, algunas nociones necesarias para la compresión de la asignatura. 1.1 Def:. Se define un conjunto como una colección de objetos.
Tema 1: Fundamentos.
 Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
Tema 1: Fundamentos. 1. Nociones básicas de la Teoría de Conjuntos. Definición. Un conjunto es una colección de objetos. A los objetos de un conjunto se les llama elementos del conjunto. Se denominará
INSTITUTO TECNOLÓGICO DE NUEVO LAREDO ING. EN SISTEMAS COMPUTACIONALES UNIDAD: 5
 NOMBRE DE LA Ejercicios de Relaciones OBJETIVO: El estudiante desarrollará diversos ejercicios de representación y operaciones con relaciones MATERIAL Y EQUIPO NECESARIO: Papel y lápiz Pág. 270 4.- Dar
NOMBRE DE LA Ejercicios de Relaciones OBJETIVO: El estudiante desarrollará diversos ejercicios de representación y operaciones con relaciones MATERIAL Y EQUIPO NECESARIO: Papel y lápiz Pág. 270 4.- Dar
Una manera de describir un conjunto es por extensión y consiste en enumerar sus elementos entre llaves
 CONJUNTOS: DEFINICIÓN Y CARDINAL DE UN CONJUNTO : Un conjunto es una colección bien definida de objetos en la que el orden es irrelevante. Dichos objetos pueden ser reales o conceptuales y se llaman elementos
CONJUNTOS: DEFINICIÓN Y CARDINAL DE UN CONJUNTO : Un conjunto es una colección bien definida de objetos en la que el orden es irrelevante. Dichos objetos pueden ser reales o conceptuales y se llaman elementos
TEMA 1. Teoría de Conjuntos. Ejercicio 1.1. Decidir si A = B, A B ó A B en los siguientes casos:
 TEMA 1 Teoría de Conjuntos Ejercicio 1.1. Decidir si A = B, A B ó A B en los siguientes casos: i) A = { }, B = {{ }} ii) A = {, { }}, B = {, {, { }}} iii) A = {{ }, {, { }}}, B = {{ }} Ejercicio 1.2. Dar
TEMA 1 Teoría de Conjuntos Ejercicio 1.1. Decidir si A = B, A B ó A B en los siguientes casos: i) A = { }, B = {{ }} ii) A = {, { }}, B = {, {, { }}} iii) A = {{ }, {, { }}}, B = {{ }} Ejercicio 1.2. Dar
ÁLGEBRA I. Curso Grado en Matemáticas
 ÁLGEBRA I. Curso 2012-13 Grado en Matemáticas Relación 1: Lógica Proposicional y Teoría de Conjuntos 1. Establecer las siguientes tautologías: (a) A A A (b) A A A (c) A B B A (d) A B B A (e) (A B) C A
ÁLGEBRA I. Curso 2012-13 Grado en Matemáticas Relación 1: Lógica Proposicional y Teoría de Conjuntos 1. Establecer las siguientes tautologías: (a) A A A (b) A A A (c) A B B A (d) A B B A (e) (A B) C A
7. Seguiría siendo válida la proposición anterior si algunos de los conjuntos A, B, C y D son vacíos?
 UNIVERSIDAD SIMÓN BOLÍVAR DEPARTAMENTO DE COMPUTACIÓN Y TECNOLOGÍA DE LA INFROMACIÓN ESTRUCTURAS DISCRETAS I GUÍA PRÁCTICA Nº 2. Demuestre lo siguiente mediante inducción matemática: a) 3 + 2 4 + 3 5 +...
UNIVERSIDAD SIMÓN BOLÍVAR DEPARTAMENTO DE COMPUTACIÓN Y TECNOLOGÍA DE LA INFROMACIÓN ESTRUCTURAS DISCRETAS I GUÍA PRÁCTICA Nº 2. Demuestre lo siguiente mediante inducción matemática: a) 3 + 2 4 + 3 5 +...
Clase 8 Matrices Álgebra Lineal
 Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Clase 8 Matrices Álgebra Lineal Código Escuela de Matemáticas - Facultad de Ciencias Universidad Nacional de Colombia Matrices Definición Una matriz es un arreglo rectangular de números denominados entradas
Práctica para prueba de bachillerato Funciones
 Práctica para prueba de bachillerato Funciones Resumen Este documento es parte de una publicación del KIOSCO DE INFORMACION, distribuida anteriormente, a través de los CEREDI. Fue preparado para las pruebas
Práctica para prueba de bachillerato Funciones Resumen Este documento es parte de una publicación del KIOSCO DE INFORMACION, distribuida anteriormente, a través de los CEREDI. Fue preparado para las pruebas
UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS
 UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
Relaciones. Estructuras Discretas. Relaciones. Relaciones en un Conjunto. Propiedades de Relaciones en A Reflexividad
 Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
Análisis de Algoritmos
 Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación?
Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación?
Imagenes inversas de funciones. x f 1 (A) f(x) A
 Imagenes inversas de funciones Denición. Sean f : X Y y A una parte del codominio Y. Imagen inversa ó preimagen del subconjunto A Y, es el conjunto de los elementos del dominio cuyas imagenes pertenecen
Imagenes inversas de funciones Denición. Sean f : X Y y A una parte del codominio Y. Imagen inversa ó preimagen del subconjunto A Y, es el conjunto de los elementos del dominio cuyas imagenes pertenecen
1.1. Relaciones de equivalencia
 Capítulo 1 Preliminares. Operaciones 1.1. Relaciones de equivalencia Denición 1.1. El producto cartesiano A B de conjuntos A y B es A B = {(a, b) a A, b B} Los elementos de A B se llaman pares ordenados.
Capítulo 1 Preliminares. Operaciones 1.1. Relaciones de equivalencia Denición 1.1. El producto cartesiano A B de conjuntos A y B es A B = {(a, b) a A, b B} Los elementos de A B se llaman pares ordenados.
Propiedades de números enteros (lista de problemas para examen)
 Propiedades de números enteros (lista de problemas para examen) Denotamos por Z al conjunto de los números enteros y por N al conjunto de los números enteros positivos: N = 1, 2, 3,...}. Valor absoluto
Propiedades de números enteros (lista de problemas para examen) Denotamos por Z al conjunto de los números enteros y por N al conjunto de los números enteros positivos: N = 1, 2, 3,...}. Valor absoluto
Funciones de Variable Real
 Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Tema 1 Funciones de Variable Real 1.1. La Recta Real Los números reales se pueden ordenar como los puntos de una recta. Los enteros positivos {1, 2, 3, 4,...} que surgen al contar, se llaman números naturales
Análisis de Algoritmos
 Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación?
Análisis de Algoritmos IIC1253 IIC1253 Análisis de Algoritmos 1 / 36 Complejidad de un algoritmo Un algoritmo A puede ser pensado como una función A : {0,1} {0,1} Qué tan general es esta representación?
Nociones de Localidad
 Nociones de Localidad IIC3260 IIC3260 Nociones de Localidad 1 / 48 Notación: Grafo de Gaifman Dado: Vocabulario L y L-estructura A Primero suponemos que L sólo contiene símbolos de relación IIC3260 Nociones
Nociones de Localidad IIC3260 IIC3260 Nociones de Localidad 1 / 48 Notación: Grafo de Gaifman Dado: Vocabulario L y L-estructura A Primero suponemos que L sólo contiene símbolos de relación IIC3260 Nociones
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2007 Ciencias Computacionales INAOE Dr. Luis Villaseñor Pineda villasen@inaoep.mx http://ccc.inaoep.mx/~villasen
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2007 Ciencias Computacionales INAOE Dr. Luis Villaseñor Pineda villasen@inaoep.mx http://ccc.inaoep.mx/~villasen
ELEMENTOS DE LA MATEMATICA
 ELEMENTOS DE LA MATEMATICA SEMESTRE: Primero CODIGO ANTERIOR: 22G7 CODIGO: 8101 REQUISITOS: No tiene CREDITOS: 6 HORAS DE TEORIA: 4 HORAS DE PRACTICA : 4 TEMA 1: Lógica simbólica. Las conectivas lógicas.
ELEMENTOS DE LA MATEMATICA SEMESTRE: Primero CODIGO ANTERIOR: 22G7 CODIGO: 8101 REQUISITOS: No tiene CREDITOS: 6 HORAS DE TEORIA: 4 HORAS DE PRACTICA : 4 TEMA 1: Lógica simbólica. Las conectivas lógicas.
Preliminares. 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros.
 CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
CAPíTULO 1 Preliminares 1. Notación simbólica. Conjuntos. También se da en el curso de Conjuntos y Numeros. El método matemático es axiomático y deductivo: a partir de unos principios aceptados inicialmente
Relaciones Binarias. Matemática Discreta. Agustín G. Bonifacio UNSL. Relaciones Binarias
 UNSL Relaciones Binarias Relaciones Binarias (Sección 3.1 del libro) Definición Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X Y. Si (x,y) R, escribimos
UNSL Relaciones Binarias Relaciones Binarias (Sección 3.1 del libro) Definición Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X Y. Si (x,y) R, escribimos
Programa analítico. Cátedra: Matemática Discreta
 Programa analítico Cátedra: Matemática Discreta Código: K951C Carrera: Ingeniería en Sistemas de Información Plan: ORD. No 1150 Régimen de dictado: Cuatrimestral Horas semanales: 6 (seis) Año: 2015 Programa
Programa analítico Cátedra: Matemática Discreta Código: K951C Carrera: Ingeniería en Sistemas de Información Plan: ORD. No 1150 Régimen de dictado: Cuatrimestral Horas semanales: 6 (seis) Año: 2015 Programa
Funciones y relaciones
 Funciones y relaciones Entrenamiento #7 para el nacional 29 de Octubre-1 de Noviembre de 2015 Por: Argel y Fernando Resumen En el presente material se hablará acerca de las funciones y relaciones, probablemente
Funciones y relaciones Entrenamiento #7 para el nacional 29 de Octubre-1 de Noviembre de 2015 Por: Argel y Fernando Resumen En el presente material se hablará acerca de las funciones y relaciones, probablemente
1. Números reales. Análisis de Variable Real
 1. Números reales Análisis de Variable Real 2014 2015 Índice 1. Sistemas numéricos 2 1.1. Números naturales. Principio de Inducción... 2 1.2. Números enteros... 4 1.3. Números racionales... 6 2. Los números
1. Números reales Análisis de Variable Real 2014 2015 Índice 1. Sistemas numéricos 2 1.1. Números naturales. Principio de Inducción... 2 1.2. Números enteros... 4 1.3. Números racionales... 6 2. Los números
Asignaturas antecedentes y subsecuentes Álgebra Elemental
 PROGRAMA DE ESTUDIOS ÁLGEBRA SUPERIOR Área a la que pertenece: ÁREA SUSTANTIVA PROFESIONAL Horas teóricas: 4 Horas prácticas: 0 Créditos: 8 Clave: F0030 Asignaturas antecedentes y subsecuentes Álgebra
PROGRAMA DE ESTUDIOS ÁLGEBRA SUPERIOR Área a la que pertenece: ÁREA SUSTANTIVA PROFESIONAL Horas teóricas: 4 Horas prácticas: 0 Créditos: 8 Clave: F0030 Asignaturas antecedentes y subsecuentes Álgebra
Funciones I. Clasificación de funciones. PREUNIVERSITARIO POPULAR FRAGMENTOS COMUNES MATEMÁTICA Guía Teórico Práctica N 8.
 Funciones I Una función es una regla que relaciona los elementos de dos conjuntos y, es decir a todos los elementos del conjunto, que llamaremos dominio se le asigna por medio de alguna regla, uno y sólo
Funciones I Una función es una regla que relaciona los elementos de dos conjuntos y, es decir a todos los elementos del conjunto, que llamaremos dominio se le asigna por medio de alguna regla, uno y sólo
Conjuntos. 17 {perro, gato, 17, x 2 }
 Conjuntos Qué es un conjunto? Informalmente, es una agrupación de cosas, o una descripción que dice qué elementos están y qué elementos no están. Para describir un conjunto usamos llavecitas y enumeramos
Conjuntos Qué es un conjunto? Informalmente, es una agrupación de cosas, o una descripción que dice qué elementos están y qué elementos no están. Para describir un conjunto usamos llavecitas y enumeramos
Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones
 Conjuntos Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones 1. Dado el conjunto A = {1, 2, 3}, determinar cuáles de las siguientes afirmaciones son verdaderas i) 1 A ii) {1} A iii) {2, 1} A iv)
Conjuntos Álgebra I Práctica 1 - Conjuntos, Relaciones y Funciones 1. Dado el conjunto A = {1, 2, 3}, determinar cuáles de las siguientes afirmaciones son verdaderas i) 1 A ii) {1} A iii) {2, 1} A iv)
14/02/2017. TEMA 3: EL CUERPO DE LOS NUMEROS REALES Esp. Prof. Liliana N. Caputo
 TEMA 3: EL CUERPO DE LOS NUMEROS REALES Esp. Prof. Liliana N. Caputo Así como al estudiar conjuntos hablamos de la existencia de términos primitivos (que no se definen), para definir algunos conjuntos,
TEMA 3: EL CUERPO DE LOS NUMEROS REALES Esp. Prof. Liliana N. Caputo Así como al estudiar conjuntos hablamos de la existencia de términos primitivos (que no se definen), para definir algunos conjuntos,
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio! Conjuntos, Relaciones y Funciones 0.1 Conjuntos
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio! Conjuntos, Relaciones y Funciones 0.1 Conjuntos
FUNCIÓN. La Respuesta correcta es D
 FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
FUNCIONES FUNCIÓN La Respuesta correcta es D FUNCIÓN Función Continua: Es aquella en la que su gráfica se puede recorrer en forma ininterrumpida en toda su extensión. FUNCIÓN Función Discontinua: Es aquella
Capítulo 2. Conjuntos Finitos Funciones
 Capítulo 2 Conjuntos Finitos 2.1. Funciones Definición 2.1. Considere dos conjuntos A y B y suponga que a cada elemento x A es asociado un elemento de B, denotado por f(x). En este caso decimos que f es
Capítulo 2 Conjuntos Finitos 2.1. Funciones Definición 2.1. Considere dos conjuntos A y B y suponga que a cada elemento x A es asociado un elemento de B, denotado por f(x). En este caso decimos que f es
PROGRAMA DE CURSO. Horas de Trabajo Personal ,0 2,0 5,0. Horas de Cátedra
 PROGRAMA DE CURSO Código MA1101 Nombre Introducción al Álgebra Nombre en Inglés Introduction to Algebra SCT Unidades Docentes Horas de Cátedra Horas Docencia Auxiliar Horas de Trabajo Personal 6 10 3,0
PROGRAMA DE CURSO Código MA1101 Nombre Introducción al Álgebra Nombre en Inglés Introduction to Algebra SCT Unidades Docentes Horas de Cátedra Horas Docencia Auxiliar Horas de Trabajo Personal 6 10 3,0
Fecha de elaboración: Agosto de 2004 Fecha de última actualización: Julio de 2010
 Programa elaborado por: PROGRAMA DE ESTUDIO Álgebra Superior Programa Educativo: Licenciatura en Matemáticas Área de Formación : Sustantiva Profesional Horas teóricas: 4 Horas prácticas: 0 Total de Horas:
Programa elaborado por: PROGRAMA DE ESTUDIO Álgebra Superior Programa Educativo: Licenciatura en Matemáticas Área de Formación : Sustantiva Profesional Horas teóricas: 4 Horas prácticas: 0 Total de Horas:
Teorema de Lagrange. En esta sección demostramos algunos hechos básicos sobre grupos, que se pueden deducir de la definición
 Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Teorema de Lagrange Capítulo 3 3.1 Introducción En este capítulo estudiaremos uno de los teoremas más importantes de toda la teoría de grupos como lo es el Teorema de Lagrange. Daremos en primer lugar
Álgebra Básica. Departamento de Álgebra.
 Ejercicios de Álgebra Básica. Curso 2010/11 Ejercicio 1. Construir las tablas de verdad de las siguientes proposiciones: (1). p q (2). [(p q) q] p (3). [(p q) r] p (q r) (4). [(p q) q] p (5). [(p q) p]
Ejercicios de Álgebra Básica. Curso 2010/11 Ejercicio 1. Construir las tablas de verdad de las siguientes proposiciones: (1). p q (2). [(p q) q] p (3). [(p q) r] p (q r) (4). [(p q) q] p (5). [(p q) p]
Uno de los más importantes conceptos en Matemática se refiere a un tipo particular de relación entre elementos de dos conjuntos; las funciones.
 MATEMÁTICA GENERAL 005, HERALDO GONZALEZ S 37 FUNCIONES Uno de los más importantes conceptos en Matemática se reiere a un tipo particular de relación entre elementos de dos conjuntos; las unciones Una
MATEMÁTICA GENERAL 005, HERALDO GONZALEZ S 37 FUNCIONES Uno de los más importantes conceptos en Matemática se reiere a un tipo particular de relación entre elementos de dos conjuntos; las unciones Una
Tema 1: El cuerpo de los números reales
 Una definición axiomática debe ser: tal que: Tema 1: El cuerpo de los números reales - Ningún axioma se debe deducir o demostrar de otro anterior - Han de ser los mínimos para demostrar una teoría Axiomas
Una definición axiomática debe ser: tal que: Tema 1: El cuerpo de los números reales - Ningún axioma se debe deducir o demostrar de otro anterior - Han de ser los mínimos para demostrar una teoría Axiomas
TEMA 1: NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN
 1 TEMA 1: NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN 1. INTRODUCCIÓN Los números naturales aparecen debido a la necesidad que tiene el hombre para contar. Para poder construir este conjunto N, podemos seguir
1 TEMA 1: NÚMEROS NATURALES. SISTEMA DE NUMERACIÓN 1. INTRODUCCIÓN Los números naturales aparecen debido a la necesidad que tiene el hombre para contar. Para poder construir este conjunto N, podemos seguir
Contenido. Contenidos interactivos... xiii Plataforma de contenidos interactivos... xviii Prefacio... xix. Parte I Fundamentos...
 Contenido Contenidos interactivos... xiii Plataforma de contenidos interactivos... xviii Prefacio... xix Parte I Fundamentos... 1 Capítulo I Lógica, conjuntos e inducción... 2 1.1 Introducción... 4 1.2
Contenido Contenidos interactivos... xiii Plataforma de contenidos interactivos... xviii Prefacio... xix Parte I Fundamentos... 1 Capítulo I Lógica, conjuntos e inducción... 2 1.1 Introducción... 4 1.2
Álgebra Lineal y Estructuras Matemáticas. J. C. Rosales y P. A. García Sánchez. Departamento de Álgebra, Universidad de Granada
 Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 2 Aritmética entera y modular 1. Los números enteros Dado un entero
Álgebra Lineal y Estructuras Matemáticas J. C. Rosales y P. A. García Sánchez Departamento de Álgebra, Universidad de Granada Capítulo 2 Aritmética entera y modular 1. Los números enteros Dado un entero
Álgebra Básica. Departamento de Álgebra (2n 1) = n 2,
 Ejercicios de Álgebra Básica. Curso 2012/13 Ejercicio 1. Probar, usando el método de inducción, la fórmula de la suma de n términos de una progresión geométrica de razón r, S n = ra n a 1 r 1. Ejercicio
Ejercicios de Álgebra Básica. Curso 2012/13 Ejercicio 1. Probar, usando el método de inducción, la fórmula de la suma de n términos de una progresión geométrica de razón r, S n = ra n a 1 r 1. Ejercicio
Números Reales. Hermes Pantoja Carhuavilca. Matematica I. Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos
 Introducción Intervalos Valor Absoluto Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Introducción Intervalos Valor Absoluto Contenido 1 Introducción 2 3 Intervalos
Introducción Intervalos Valor Absoluto Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Introducción Intervalos Valor Absoluto Contenido 1 Introducción 2 3 Intervalos
Unidad I Elementos de lógica y de Teoría de Conjuntos
 INSTITUTO SUPERIOR DE FORMACION DOCENTE Nº 813 SEDE LAGO PUELO PROFESORADO EN MATEMÁTICA PROGRAMA DE ALGEBRA I AÑO 2008 Prof. Ricardo J. Tamer Unidad I Elementos de lógica y de Teoría de Conjuntos Introducción
INSTITUTO SUPERIOR DE FORMACION DOCENTE Nº 813 SEDE LAGO PUELO PROFESORADO EN MATEMÁTICA PROGRAMA DE ALGEBRA I AÑO 2008 Prof. Ricardo J. Tamer Unidad I Elementos de lógica y de Teoría de Conjuntos Introducción
Ing. Bruno López Takeyas. Relaciones
 Relaciones Las relaciones son conjuntos, por lo tanto se puede usar la representación de conjuntos para representar relaciones. Una relación n-aria es un conjunto de n-tuplas. Las relaciones binarias con
Relaciones Las relaciones son conjuntos, por lo tanto se puede usar la representación de conjuntos para representar relaciones. Una relación n-aria es un conjunto de n-tuplas. Las relaciones binarias con
Inyectivas, Suprayectivas, Biyectivas, Inversas. Relaciones Funcionales. f : A B se lee f es una función con dominio A y codominio B
 Relaciones Funcionales Sean A, B dos conjuntos no vacíos, que llamaremos dominio y contradominio respectivamente. Entenderemos por función de A en B toda regla que hace corresponder a cada elemento del
Relaciones Funcionales Sean A, B dos conjuntos no vacíos, que llamaremos dominio y contradominio respectivamente. Entenderemos por función de A en B toda regla que hace corresponder a cada elemento del
y exámenes. Temas 3 y 4
 U N I V E R S I D A D D E M U R C I A Ejercicios DEPARTAMENTO DE MATEMÁTICAS CONJUNTOS Y NÚMEROS 2017/2018. de talleres y exámenes. Temas 3 y 4 Se recuerda que la resolución de algunos de estos ejercicios
U N I V E R S I D A D D E M U R C I A Ejercicios DEPARTAMENTO DE MATEMÁTICAS CONJUNTOS Y NÚMEROS 2017/2018. de talleres y exámenes. Temas 3 y 4 Se recuerda que la resolución de algunos de estos ejercicios
PROGRAMA DE CURSO UNIDADES TEMÁTICAS. Unidades Docentes Cátedra Auxiliares Trabajo Personal
 PROGRAMA DE CURSO Código MA1101 Nombre del Curso Introducción al Álgebra Unidades Docentes Cátedra Auxiliares Trabajo Personal 10 3.0 2.0 5.0 Requisitos Requisitos específicos Carácter del curso Ingreso
PROGRAMA DE CURSO Código MA1101 Nombre del Curso Introducción al Álgebra Unidades Docentes Cátedra Auxiliares Trabajo Personal 10 3.0 2.0 5.0 Requisitos Requisitos específicos Carácter del curso Ingreso
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Total de horas: Horas de teoría: semana UNIDAD 1 OBJETIVO
 PROGRAMA DE ESTUDIOS Nombre de la unidad de aprendizaje Seminario de solución de problemas de Matemáticas Discretas Modalidad: Presencial Departamento: Departamento de Ciencias Básicas, Aplicadas e Ingenierías
PROGRAMA DE ESTUDIOS Nombre de la unidad de aprendizaje Seminario de solución de problemas de Matemáticas Discretas Modalidad: Presencial Departamento: Departamento de Ciencias Básicas, Aplicadas e Ingenierías
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Conjuntos Parcialmente Ordenados y Reticulados. Matemática Discreta. Agustín G. Bonifacio UNSL. Conjuntos Parcialmente Ordenados y Reticulados
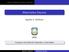 y UNSL y y y Capítulo 4 del libro de B. Kolman, R. Busby y S. Ross. Definición Una relación R sobre un conjunto X es un orden orden parcial si es reflexiva, antisimétrica y transitiva. El conjunto A con
y UNSL y y y Capítulo 4 del libro de B. Kolman, R. Busby y S. Ross. Definición Una relación R sobre un conjunto X es un orden orden parcial si es reflexiva, antisimétrica y transitiva. El conjunto A con
Conjuntos. Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por. a R. se entiende que a pertenece a R.
 Conjuntos Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por se entiende que a pertenece a R. a R Normalmente, podremos definir a un conjunto de dos maneras: Por
Conjuntos Un conjunto es una colección de objetos. Si a es un objeto y R es un conjunto entonces por se entiende que a pertenece a R. a R Normalmente, podremos definir a un conjunto de dos maneras: Por
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES
 MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES RESPUESTA Y DESARROLLO DE EJERCICIOS AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO 6.1.- a) b) S={(4,1),(4,3),(5,1),(5,3)}
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES RESPUESTA Y DESARROLLO DE EJERCICIOS AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO 6.1.- a) b) S={(4,1),(4,3),(5,1),(5,3)}
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 1: Funciones de una variable real. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo
 Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 35 Por qué estudiamos
Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 35 Por qué estudiamos
Conjuntos Finitos e Infinitos
 Araceli Guzmán y Guillermo Garro Facultad de Ciencias UNAM Semestre 2018-1 doyouwantmektalwar.wordpress.com Conjuntos Finitos El segmento inicial de tamaño n, donde n 0, es el conjunto 1 n = {1,..., n}
Araceli Guzmán y Guillermo Garro Facultad de Ciencias UNAM Semestre 2018-1 doyouwantmektalwar.wordpress.com Conjuntos Finitos El segmento inicial de tamaño n, donde n 0, es el conjunto 1 n = {1,..., n}
Semana03[1/17] Funciones. 16 de marzo de Funciones
![Semana03[1/17] Funciones. 16 de marzo de Funciones Semana03[1/17] Funciones. 16 de marzo de Funciones](/thumbs/48/24900626.jpg) Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Semana03[1/17] 16 de marzo de 2007 Introducción Semana03[2/17] Ya que conocemos el producto cartesiano A B entre dos conjuntos A y B, podemos definir entre ellos algún tipo de correspondencia. Es decir,
Matemáticas Discretas
 Matemáticas Discretas Relaciones (1) Curso Propedéutico 2009 Maestría en Ciencias Computacionales, INAOE Relaciones & Funciones (1) Dr Luis Enrique Sucar Succar esucar@inaoep.mx Dra Angélica Muñoz Meléndez
Matemáticas Discretas Relaciones (1) Curso Propedéutico 2009 Maestría en Ciencias Computacionales, INAOE Relaciones & Funciones (1) Dr Luis Enrique Sucar Succar esucar@inaoep.mx Dra Angélica Muñoz Meléndez
TEMA 2. TEORÍA DE CONJUNTOS
 TEMA 2. TEORÍA DE CONJUNTOS 1. Introducciónalalógica de proposiciones 1.1 Definición. Una proposición es una oración declarativa de la cual se puede decir sin ambigüedad si es verdadera o falsa. 1.2 Definición.
TEMA 2. TEORÍA DE CONJUNTOS 1. Introducciónalalógica de proposiciones 1.1 Definición. Una proposición es una oración declarativa de la cual se puede decir sin ambigüedad si es verdadera o falsa. 1.2 Definición.
Modelos de Computación y Complejidad PRELIMINARES
 Modelos de Computación y Complejidad Grado en Ingeniería Informática. Tecnologías Informáticas PRELIMINARES Mario de J. Pérez Jiménez Dpto. Ciencias de la Computación e Inteligencia Artificial E.T.S. Ingeniería
Modelos de Computación y Complejidad Grado en Ingeniería Informática. Tecnologías Informáticas PRELIMINARES Mario de J. Pérez Jiménez Dpto. Ciencias de la Computación e Inteligencia Artificial E.T.S. Ingeniería
UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS
 UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
UNIVERSIDAD DON BOSCO - DEPARTAMENTO DE CIENCIAS BÁSICAS UNIDAD 5 : ESTRUCTURAS ALGEBRAICAS ÁLGEBRA LINEAL - GUIÓN DE CLASE - SEMANA 10 - CICLO 01-2015 Estudiante: Grupo: 1. Aplicaciones 1.1. Aplicaciones.
Polinomios (lista de problemas para examen)
 Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
Polinomios (lista de problemas para examen) En esta lista de problemas el conjunto de los polinomios de una variable con coeficientes complejos se denota por P(C). También se usa la notación C[x], si la
Clase 1: Primalidad. Matemática Discreta - CC3101 Profesor: Pablo Barceló. P. Barceló Matemática Discreta - Cap. 5: Teoría de números 1 / 32
 Capítulo 5: Teoría de Números Clase 1: Primalidad Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 5: Teoría de números 1 / 32 Teoría de números En esta parte
Capítulo 5: Teoría de Números Clase 1: Primalidad Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 5: Teoría de números 1 / 32 Teoría de números En esta parte
Que importancia tienen las funciones matemáticas?
 Funciones Que importancia tienen las funciones matemáticas? Justificación Las funciones son de mucho valor y utilidad para resolver problemas de la vida diaria, problemas de finanzas, de economía, de estadística,
Funciones Que importancia tienen las funciones matemáticas? Justificación Las funciones son de mucho valor y utilidad para resolver problemas de la vida diaria, problemas de finanzas, de economía, de estadística,
