TEMA 1: NÚMEROS REALES 1.1 Numeros racionales Ejemplo:
|
|
|
- Trinidad Sáez Cortés
- hace 7 años
- Vistas:
Transcripción
1 TEMA : NÚMEROS REALES. Numeros racionales Ejemplo: 4... Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible. En nuestro caso Otro ejemplo de número racional es Siendo en este caso la fracción generatriz 8 Volvemos al.0 que es un número decimal exacto pues la división es exacta, es decir el resto es cero. Volvemos al 0.85 que es un número decimal exacto pues la división es exacta, es decir el 8 resto es cero. Cojemos. que es un número decimal periodico puro pues la tiene un bloque de cifras que se repite indefinidamente a continucacion de si mismo justo después de la coma. Cojemos que es un número decimal periodico mixto pues hay cifras entre 4 la coma y el bloque de cifras que se repite indefinidamente a continucacion de si mismo. De igual forma hemos de ser capaces de transformar un número decimal en una fracción. Vamos a hacerlo para un número decimal exacto: Vamos a hacerlo para un número decimal periódico puro: Llamamos N Multiplicamos N por 00, pues tiene dos cifras de periodo: 00N Es decir, hemos obtenido otro número decimal periódico puro con el mism periodo que el dado. Esto hace que cuando restemos el mayor del menor, me desaparezcan los periodos: 00N N lo que nos da 99N N Vamos a hacerlo para un número decimal periódico mixto: Tenemos dos cifras de anteperiodo (5) y una cifra de periodo. Llamamos N.5... Multiplicamos N por 00, pues tiene dos cifras de anteperiodo: 00N 5... También multiplicamos N por 000 pues tenemos dos cifras de anteperiodo y una de periodo. 000N 5... Es decir, hemos obtenido dos números decimales periódicos puros con el mismo periodo. Esto hace que cuando restemos el mayor del menor, me desaparezcan los periodos: 000N N N 00N N 84 Asi, al restar en columna nos da 900N 84 N Tareas 0-09-: todos los ejercicios de la página 0. Números irracionales. Números reales. Ejemplos de números irracionales
2 Da ejemplos de números que sean irracionales: a) es un número irracional pues tiene infinitas cifras decimales sin En general todas las raíces no exactas son números irracionales. b) es un número irracional pues tiene infinitas cifras decimales sin c) es un número irracional pues tiene infinitas cifras decimales sin d) es un número irracional pues tiene infinitas cifras decimales sin e) es un número irracional pues tiene infinitas cifras decimales sin f) es un número irracional pues tiene infinitas cifras decimales sin Ejemplo de valores absolutos. Calcula el valor absoluto de los siguientes números: a) pues o b) pues 0 Comprueba la verdad de las propiedades del valor absoluto: a) Los ejemplos del apartado anterior confirman que el valor absoluto de un número no nulo es mayor que cero. b) Por otro lado tenemos que: Entonces podemos concluir que: c) 8 8 Por otro lado tenemos que: 4 Entonces podemos concluir que: Tareas 0-09-: todos los ejercicios de la página.. Representación de números reales Tareas para casa: -09- todos los ejercicios de la página..4 Aproximaciones de un número real. Errores. Ejemplos de redondeo de números irracionales: Redondea a los siguientes ordenes: a) a las décimas:. b) a las milésimas:.4 c) a las cienmilésimas:. 459 d) a las diezmilésimas:. 46 Ejemplos de errores cometidos al redondear un número irracional: Calcula los errores cometidos en cada uno de los redondeos del apartado anterior: a) a las décimas: E En este caso la aproximación ha sido por defecto pues b) a las milésimas: E En este caso la aproximación ha sido por exceso pues
3 Vamos a calcular a partir de los errores absolutos obtenidos anteriormente los correspondientes errores relativos.. a) a las décimas: E r b) a las milésimas: E r El error relativo es mayor en las décimas. Tareas para casa: -09- todos los ejercicios de la página..5 Suma y producto de números reales Tareas para casa: todos los ejercicios de la página 4..6 Potencias de números reales Ejemplo de las propiedades de las potencias Aplica las propiedades de las potencias en las siguientes expresiones: a) 5 5 b) c) Tareas para casa: todos los ejercicios de la página 5.. Radicales Ejemplo Realiza las siguientes operaciones: a) Tareas para casa: todos los ejercicios de la página..8 Intervalos y entornos Ejemplos de entornos e intervalos, junto con su representación Define y representa los siguientes conjuntos numéricos: a),4 x R/x 4 serían todos los números reales tales que x es menor que 4. Es un semirrecta. b) 0, x R/x 0 serían todos los números reales tales que x es mayor o igual que -0 Es un semirrecta. c) 5, No es nada pues el extremo inferior ha de ser más pequeño que el superior. d), x R/ x serían todos los números reales tales que x es mayor que - pero más pequeño que. Es un intervalo abierto e) 5,6 x R/5 x 6 serían todos los números reales comprendidos entre 5 y 6 incluyendo a estos. Es un intervalo cerrado. f) E,0.5 x R/ 0.5 x 0.5 x R/.5 x.5.5,.5
4 Es el entorno abierto de centro - y radio 0.5 g) E4,0.5 x R/4 0.5 x x R/.5 x 4.5.5,4,5 Es el entorno cerrado de centro 4 y radio 0.5 Tareas todos los ejercicios de la página 8 Tareas todos los ejercicios de la página 9 Ejercicios finales del Tema Di si los siguientes números son naturales, enteros, racionales o reales: a) 8 4 es un número natural, por lo tanto es entero, es racional y por último es real. b) es un número entero, es racional y por último es real. c) es un número decimal exacto por lo tanto es una fracción, es decir, es un número racional y por último es real. d) es un número decimal exacto por lo tanto es una fracción, es decir, 5 es un número racional y por último es real. e) 9 es un número natural, por lo tanto es entero, es racional y por último es real. f) 4 es un número irracional pues la 4 no es una raiz exacta. Por lo tanto sólo es real Tareas para casa -09:, 4 Halla un número fraccionario comprendido entre y Buscamos fracciones equivalentes a las dadas que no tengan numeradores consecutivos. Elegimos el 4 porque me apetece: Ya tenemos dos fracciones que no tienen numeradores consecutivos. Una solución sería: Tareas para casa -09:5, 6, 8 Calcula de forma exacta el resultado de: Tenemos que encontrar la fracción generatriz de todos los números decimales periódicos que aparecen. a) b) c) d) Por lo tanto: Tareas -09-: 9 NOTA: Fracción generatriz de un decimal exacto: en el numerador se escribe el número decimal sin 4
5 coma y, en el denominador, la unidad seguida de tantos ceros como cifras decimales tenga. Fracción generatriz de un decimal periódico puro: en el numerador se escribe el número sin coma hasta el final del periodo y se le resta la parte entera; en el denominador se ponen tantos nueves como cifras tenga el periodo. Fracción generatriz de un decimal periódico mixto: en el numerador se escribe el número sin coma hasta el final del periodo y se le resta la parte entera y el anteperiodo; en el denominador se ponen tantos nueves como cifras tenga el periodo y tantos ceros como cifras tenga el anteperiodo. 40 Desarrolla el valor absoluto de las siguientes expresiones omitiendo los valores absolutos. a) x 4 x Sabemos que x x if x 0 x if x 0 x 4 x x 4 x if x 4 0 x 4 x if x 4 0 x 4 if x 4 x 4 x if x 4 x 4 if x 4 x 4 if x 4 x 4 if x x 4 if x Tareas 8-09-: el resto de los ejercicios del 40, 4 4 Representa los siguientes números reales. e) 5 Buscamos cuadrados que al sumarlos me de Entonces 5 Aplicando el Teorema de Pitágoras, 5 será la hipotenusa de un triángulo rectángulo de cuyos catetos miden y. Tareas 8-09-: el resto de los ejercicios del 4, Escribe aproximaciones por exceso y por defecto con tres cifras decimales de los siguientes números. b) Otra forma de hacerlo sería: 4 Utilizando la calculadora tenemos que: por exceso por defecto Tareas 8-09-: el resto de los ejercicios del 45, 46, 4, 48, Calcula los errores absoluto y relativo que se cometen al tomar.9 como valor de. E E r Tareas 0-0-: 50, 5, 5, 5, Calcula con tres decimales mediante aproximaciones sucesivas. 5
6 Tomo el redondeo de con dos cifras decimales: Tomo el redondeo de con una cifra decimal: aproximaciones de aproximaciones de Halla las siguientes multiplicaciones y divisiones con radicales: d) x x x x x x 4 x x 4 x x x x x 4 x 9 4 x 5 x 5 Tareas 0-0-: todos los ejercicios que faltan del 56 5 Halla las siguientes sumas y restas de radicales: d) Tareas 0-0-: todos los ejercicios que faltan del 5 58 Simplifica el valor de las siguientes expresiones. h) 4 Aplicamos el cuadrado de la diferencia: a b a ab b Tareas 0-0-: todos los ejercicios que faltan del Simplifica las siguientes expresiones: b) Se puede hacer aplicando: el cuadrado de la diferencia suma por diferencia: a ba b a b Vamos a intentarlo de otra manera: Sacaremos factor común,
7 Tareas 0-0-: todos los ejercicios que faltan del Racionaliza los denominadores de las siguientes expresiones f) Tareas 0-0-: todos los ejercicios que faltan del Dados los intervalos A,4 y B,6, calcula: a) A B,6 La unión se define como los elementos que pertenecen a A o a B. Es decir, los que están en A o en B. b) A B,4 La intersección se define como los elementos que pertenecen a A y a B. Es decir, los elementos que están a la vez en A y en B. Tareas 0-0-: 6,6 64 Expresa en forma de intervalo y de entorno los siguientes conjuntos de números reales: d) x x Aqui tenemos el conjunto x R/ x x R/ x x R/ x E,, Tareas 04-0-: todos los ejercicios que faltan del Escribe en notación científica los siguientes números: f) Tareas 04-0-: todos los ejercicios que faltan del Halla los siguientes productos y cocientes dando el resultado en notación científica. d) Tareas 04-0-: todos los ejercicios que faltan del 66, 6, 69, 0 68 Una habitación con forma de ortoedro de base cuadrada y altura la mitad del lado de la base se pinto en tres días. Se pintaron las cuatro paredes y el techo. En el primer día se pintó la tercera parte de la superficie; en el segundo, la mitad de lo que quedada, y en el tercero los 5 m que faltaban para acabar el trabajo. a) Calcula la superficie total de la habitación y la superficie que se hizo cada día. Llamamos x al lado de la base cuadrada. Por lo tanto, la altura del ortoedro será x. En total pintamos cuatro paredes iguales y el techo (que coincide con la base). La superficie de una de las paredes es: x x x La superficie del techo es: x x x La superficie total será: 4 x x 4 x x x x x el primer día se pintó la tercera parte de la superficie: x x
8 el segundo, la mitad de lo que quedada: x x el tercero los 5 m que faltaban para acabar el trabajo (x x x x : 5 x x 5 La solución es que la base vale 5 Entonces la superficie total será: x 5 45 m Cada día se pintaron: 5 m pues todos los días se pintó la misma superficie. b) Calcula las medidas de cada una de las paredes y el volumen con la precisión adecuada. Las paredes tienen de longitudes 5 m y 5 m por lo que la superficie es: 5m Elvolumenesáreadelabaseporlaaltura: m Como trabajamos en el mundo real vamos a tomar m medida de la base. Por lo tanto el volumen será: m Tareas 05-0-:,, 6,, 8, 80, 8, 8, Una empresa elabora latas de conserva con forma cilíndrica de dimensiones 5 cm de radi de la base y 0 cm de altura. Tras un estudio de mercado, decide cambiar la forma de las latas: serán ortoedros de base cuadrada y de altura el doble del lado de la base. Cuáles serán las dimensiones de la nueva forma si la capacidad debe de ser la misma? Establece la solución con la aproximación que consideres oportuna. Volumen de la lata: área de la basealtura cm Volumen del tetrabrik: área de la basealtura x x x (ortoedro) Como los volúmenes han de ser iguales: 50 x x cm Asi trabajaremos en mm. Las dimensiones serán 9.cm para el lado de la base y 8.4 paralaalturadelalata. 4 Una empresa A cobra por el alquiler de una furgoneta 80 euros diarios. Otra empresa B cobra por el mismo alquiler 60 euros al día. Pero a esta cantidad se le deben añadir 00 euros independientemente del tiempo que se contrate. A partir de cuántos días es más económica la segunda empresa? Escribe la solución en forma de desigualdad y de intervalo. fijo diario total x días empresa A x empresa B x Igualamos: 80x 00 60x, Solution is: 0 80x if 0 x 0 Alquiler de la furgoneta 00 60x if 0 x 80x if x 0, x if x 0, 8
TEMA 1: NÚMEROS REALES
 . Numeros racionales Ejemplo: TEMA : NÚMEROS REALES 4.............................................. Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible.
. Numeros racionales Ejemplo: TEMA : NÚMEROS REALES 4.............................................. Entonces puedo expresar el "" de infinitas formas, siendo su fracción generatriz la que es irreducible.
8, ,125 4, ,5 0, , , ,25
 1.- Escribe la fracción irreducible (representante canónico), la expresión decimal y el tipo de número decimal, de los números racionales del cuadro siguiente: número racional fracción irreducible expresión
1.- Escribe la fracción irreducible (representante canónico), la expresión decimal y el tipo de número decimal, de los números racionales del cuadro siguiente: número racional fracción irreducible expresión
TEMA 2 NÚMEROS DECIMALES
 TEMA 2 NÚMEROS DECIMALES 2.2 Fracciones y números decimales de paso de fracción a número decimal. Convierte en número decimal las siguientes fracciones: clasifica también los números decimales obtenidos.
TEMA 2 NÚMEROS DECIMALES 2.2 Fracciones y números decimales de paso de fracción a número decimal. Convierte en número decimal las siguientes fracciones: clasifica también los números decimales obtenidos.
PREPARACIÓN CONTROL TEMA 1 4ºESO
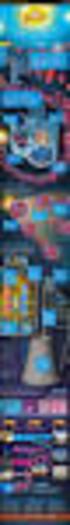 1. (1,5 puntos). Efectúa las operaciones siguientes, expresando el resultado en forma de fracción irreducible: a) 4 2 4 8 13 : 5 3 5 7 14 4 2 b) 3 8 1 2 2 4 : 1 1 1 2 3 2 3 5 2. (1,5 puntos). Realiza las
1. (1,5 puntos). Efectúa las operaciones siguientes, expresando el resultado en forma de fracción irreducible: a) 4 2 4 8 13 : 5 3 5 7 14 4 2 b) 3 8 1 2 2 4 : 1 1 1 2 3 2 3 5 2. (1,5 puntos). Realiza las
CONTROL TEMA 1 4ºESO
 1. (1,5 puntos). Efectúa las operaciones siguientes, expresando el resultado en forma de fracción irreducible: a) 4 2 4 8 1 : 5 5 7 14 4 2 b) 8 1 2 2 4 : 1 1 1 2 2 5 2. (1,5 puntos). Realiza las siguientes
1. (1,5 puntos). Efectúa las operaciones siguientes, expresando el resultado en forma de fracción irreducible: a) 4 2 4 8 1 : 5 5 7 14 4 2 b) 8 1 2 2 4 : 1 1 1 2 2 5 2. (1,5 puntos). Realiza las siguientes
16/11/2015. Tema 1º Números reales 1.0) Conceptos previos. 1.1) Fracciones. Números racionales. 1.2) Operaciones con números racionales.
 Irracionales (I) 16/11/01 1.) Operaciones con números racionales. 1.) Expresiones fraccionarias y decimal de un número racional. Irracional 1.) Representación de números racionales 1.10) Intervalos y semirrectas.
Irracionales (I) 16/11/01 1.) Operaciones con números racionales. 1.) Expresiones fraccionarias y decimal de un número racional. Irracional 1.) Representación de números racionales 1.10) Intervalos y semirrectas.
a) 1,5 1,3:
 1. Dados los siguientes números: 3,2 3 1 81 1,... Sitúa cada uno de ellos en su lugar correspondiente dentro del diagrama. Si alguno es racional indica de qué tipo es. 2. Efectúa las operaciones siguientes,
1. Dados los siguientes números: 3,2 3 1 81 1,... Sitúa cada uno de ellos en su lugar correspondiente dentro del diagrama. Si alguno es racional indica de qué tipo es. 2. Efectúa las operaciones siguientes,
EJERCICIOS PROPUESTOS b) 2 20 x 8 x 5
 EJERCICIOS PROPUESTOS 1.1 Halla el valor de x para que las siguientes fracciones sean equivalentes. a) 1 x 4 b) x 8 a) 1 4 x x 4 b) x 8 x 8 1. Expresa estas fracciones con el mismo denominador. a), 1 1
EJERCICIOS PROPUESTOS 1.1 Halla el valor de x para que las siguientes fracciones sean equivalentes. a) 1 x 4 b) x 8 a) 1 4 x x 4 b) x 8 x 8 1. Expresa estas fracciones con el mismo denominador. a), 1 1
1. Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de: c) 0,175 No es un número periódico
 Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de: 8 9,, 0 9 9 90 9900 Parte entera 9, anteperiodo, periodo Parte entera, anteperiodo, periodo 0, No es
Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de: 8 9,, 0 9 9 90 9900 Parte entera 9, anteperiodo, periodo Parte entera, anteperiodo, periodo 0, No es
1 Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de:
 . NUMEROS REALES Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de:,.. 8 0,... 0 Parte entera, anteperiodo, periodo 00 Parte entera, anteperiodo, periodo
. NUMEROS REALES Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de:,.. 8 0,... 0 Parte entera, anteperiodo, periodo 00 Parte entera, anteperiodo, periodo
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
Cuando se enumeran todos los elementos que componen el conjunto. A = { 1, 2, 3, 4, 5 }
 LOS NÚMEROS REALES TEMA 1 IDEAS SOBRE CONJUNTOS Partiremos de la idea natural de conjunto y del conocimiento de si un elemento pertenece (* ) o no pertenece (* ) a un conjunto. Los conjuntos se pueden
LOS NÚMEROS REALES TEMA 1 IDEAS SOBRE CONJUNTOS Partiremos de la idea natural de conjunto y del conocimiento de si un elemento pertenece (* ) o no pertenece (* ) a un conjunto. Los conjuntos se pueden
TEMA 3: LAS FRACCIONES
 . Fracciones equivalentes TEMA : LAS FRACCIONES Determina si los siguientes pares de fracciones son equivalentes:. y 0 Calculamos como los productos son iguales, si son fracciones equivalentes. 0. 0 y
. Fracciones equivalentes TEMA : LAS FRACCIONES Determina si los siguientes pares de fracciones son equivalentes:. y 0 Calculamos como los productos son iguales, si son fracciones equivalentes. 0. 0 y
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES.-LA RECTA REAL Los NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros:
Actividades iniciales y de recuperación
 Actividades iniciales y de recuperación.- Ordenar de menor a mayor los siguientes decimales: 6 milésimas; décimas; 60 cienmilésimas; 60 diezmilésimas.- Calcula mentalmente el valor exacto de: a) 0, @ 000
Actividades iniciales y de recuperación.- Ordenar de menor a mayor los siguientes decimales: 6 milésimas; décimas; 60 cienmilésimas; 60 diezmilésimas.- Calcula mentalmente el valor exacto de: a) 0, @ 000
Página 3. Página 4. Página 5
 Soluciones de las actividades Página 3. El menor de los conjuntos al que pertenecen estos números son: a) Entero b) Entero c) Racional d) Natural e) Racional. Cualquier fracción irreducible puede expresarse
Soluciones de las actividades Página 3. El menor de los conjuntos al que pertenecen estos números son: a) Entero b) Entero c) Racional d) Natural e) Racional. Cualquier fracción irreducible puede expresarse
UNIDAD 1. NÚMEROS REALES
 UNIDAD 1. NÚMEROS REALES Conocemos y manejamos varios conjuntos numéricos. Todos ellos están bien estructurados: Los números naturales, Ν = { 1,2,3,4,... }. Son los números que sirven para contar. Si a
UNIDAD 1. NÚMEROS REALES Conocemos y manejamos varios conjuntos numéricos. Todos ellos están bien estructurados: Los números naturales, Ν = { 1,2,3,4,... }. Son los números que sirven para contar. Si a
TEMA 1: Los números reales. Tema 1: Los números reales 1
 TEMA 1: Los números reales Tema 1: Los números reales 1 ESQUEMA DE LA UNIDAD 1.- Números naturales y enteros..- Números racionales. 3.- Números irracionales. 4.- Números reales. 5.- Jerarquía en las operaciones
TEMA 1: Los números reales Tema 1: Los números reales 1 ESQUEMA DE LA UNIDAD 1.- Números naturales y enteros..- Números racionales. 3.- Números irracionales. 4.- Números reales. 5.- Jerarquía en las operaciones
NÚMEROS 1º E.S.O. NÚMEROS DECIMALES ÓRDENES DE UNIDADES DECIMALES NÚMEROS DECIMALES. 1 U = 10 d = 100 c = 1000 m =...
 NÚMEROS DECIMALES NÚMEROS DECIMALES 1º E.S.O. NÚMEROS DECIMALES ÓRDENES DE UNIDADES DECIMALES Los números decimales se componen de dos partes separadas por una coma. La parte entera, formada por las cifras
NÚMEROS DECIMALES NÚMEROS DECIMALES 1º E.S.O. NÚMEROS DECIMALES ÓRDENES DE UNIDADES DECIMALES Los números decimales se componen de dos partes separadas por una coma. La parte entera, formada por las cifras
TEMA 3: NÚMEROS REALES
 . Intervalos y semirrectas TEMA : NÚMEROS REALES Ejemplo Dados los siguientes intervalos y semirrectas, exprésalos en forma de conjunto y represéntalos sobre la recta real:. El intervalo abierto de extremos
. Intervalos y semirrectas TEMA : NÚMEROS REALES Ejemplo Dados los siguientes intervalos y semirrectas, exprésalos en forma de conjunto y represéntalos sobre la recta real:. El intervalo abierto de extremos
Los números decimales ilimitados no periódicos se llaman números irracionales, que designaremos
 Unidad Didáctica NÚMEROS REALES. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal
Unidad Didáctica NÚMEROS REALES. NÚMEROS IRRACIONALES: CARACTERIZACIÓN. En el tema correspondiente a números racionales hemos visto que estos números tienen una característica esencial: su expresión decimal
NÚMEROS REALES. a de dos números enteros: a, y b Z con b 0. Con un número entero o con una expresión decimal exacta o no exacta y periódica.
 NÚMEROS REALES NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros: a, y b Z con b 0 Con un número entero o con una expresión
NÚMEROS REALES NÚMEROS RACIONALES: Se caracterizan porque pueden expresarse: En forma de fracción, es decir, como cociente b a de dos números enteros: a, y b Z con b 0 Con un número entero o con una expresión
E J E R C I C I O S P R O P U E S T O S. Indica, sin realizar la división, el tipo de expresión decimal de estos números.
 NÚMEROS REALES E J E R C I C I O S P R O P U E S T O S. Indica, sin realizar la división, el tipo de expresión decimal de estos números. a) b) 9 6 c) 7 d) 7 7 0 a) Periódico mixto c) 7 Periódico mixto
NÚMEROS REALES E J E R C I C I O S P R O P U E S T O S. Indica, sin realizar la división, el tipo de expresión decimal de estos números. a) b) 9 6 c) 7 d) 7 7 0 a) Periódico mixto c) 7 Periódico mixto
1º BACHILLERATO CCSSI - MATEMÁTICAS UNIDAD 1. NÚMEROS REALES. 1. Reduce a común denominador y después ordena de menor a mayor:
 º BACHILLERATO CCSSI - MATEMÁTICAS UNIDAD. NÚMEROS REALES. NÚMEROS RACIONALES (FRACCIONES). Reduce a común denominador y después ordena de menor a mayor: a),, b),, c),,,. Realiza las siguientes operaciones:
º BACHILLERATO CCSSI - MATEMÁTICAS UNIDAD. NÚMEROS REALES. NÚMEROS RACIONALES (FRACCIONES). Reduce a común denominador y después ordena de menor a mayor: a),, b),, c),,,. Realiza las siguientes operaciones:
TEMA 1 CONJUNTOS NUMÉRICOS
 TEMA 1 CONJUNTOS NUMÉRICOS. Objetivos / Criterios de evaluación O.1.1 Realizar correctamente operaciones con fracciones: Suma, resta, producto, cociente, potencia y radicación. O.1.2 Resolver operaciones
TEMA 1 CONJUNTOS NUMÉRICOS. Objetivos / Criterios de evaluación O.1.1 Realizar correctamente operaciones con fracciones: Suma, resta, producto, cociente, potencia y radicación. O.1.2 Resolver operaciones
Se representa conlaletra Q
 1.- FRACCIONES. NÚMEROS RACIONALES 1. Indica cómo se llama el conjunto de los números que se pueden expresar en forma de fracción y con qué letra se representa Es el conjunto de los números racionales
1.- FRACCIONES. NÚMEROS RACIONALES 1. Indica cómo se llama el conjunto de los números que se pueden expresar en forma de fracción y con qué letra se representa Es el conjunto de los números racionales
Indica cuáles de los números son racionales y cuáles son irracionales.
 SOLUCIONARIO ACTIVIDADES 06 0 08 09 040 Razona cuáles de los siguientes números decimales son racionales y cuáles son irracionales. a), e), b), f), c), g), d), h), a) Racional, periódico puro. e) Racional,
SOLUCIONARIO ACTIVIDADES 06 0 08 09 040 Razona cuáles de los siguientes números decimales son racionales y cuáles son irracionales. a), e), b), f), c), g), d), h), a) Racional, periódico puro. e) Racional,
TEMA 2. FRACCIONES Y NÚMEROS DECIMALES
 TEMA 2. FRACCIONES Y NÚMEROS DECIMALES ÍNDICE 1. Operaciones con fracciones 2. Operaciones con números decimales 3. Fracciones y números decimales 4. Fracción generatriz Tema 2. Fracciones y números decimales
TEMA 2. FRACCIONES Y NÚMEROS DECIMALES ÍNDICE 1. Operaciones con fracciones 2. Operaciones con números decimales 3. Fracciones y números decimales 4. Fracción generatriz Tema 2. Fracciones y números decimales
CONJUTOS NÚMERICOS NÚMEROS NATURALES
 CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
CONJUTOS NÚMERICOS NÚMEROS NATURALES El conjunto de números naturales tiene gran importancia en la vida práctica ya que con sus elementos se pueden encontrar elementos u objetos de otros conjuntos. El
Prueba de evaluación. Nombre: Apellidos: Curso: Fecha: Calificación: Sean los números racionales representados por las fracciones,,, y.
 Números racionales Prueba de evaluación Nombre: Apellidos: Curso: Fecha: Calificación: Sean los números racionales representados por las fracciones,,, y. Ordénalos 0 0 de menor a mayor y escribe sus fracciones
Números racionales Prueba de evaluación Nombre: Apellidos: Curso: Fecha: Calificación: Sean los números racionales representados por las fracciones,,, y. Ordénalos 0 0 de menor a mayor y escribe sus fracciones
N Ú M E R O S R E A L E S
 N Ú M E R O S R E A L E S 1. E L C O N J U N T O D E L O S N Ú M E R O S R E A L E S Al conjunto de todos los números que se pueden expresar mediante fracciones se le llama conjunto de los números racionales
N Ú M E R O S R E A L E S 1. E L C O N J U N T O D E L O S N Ú M E R O S R E A L E S Al conjunto de todos los números que se pueden expresar mediante fracciones se le llama conjunto de los números racionales
CONJUNTO DE LOS NÚMEROS REALES
 NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES Al conjunto de todos los números que se pueden expresar mediante fracciones se le llama conjunto de los números racionales y se representa por Q. Tanto
NÚMEROS REALES 1. EL CONJUNTO DE LOS NÚMEROS REALES Al conjunto de todos los números que se pueden expresar mediante fracciones se le llama conjunto de los números racionales y se representa por Q. Tanto
Lección 1 Números Reales
 Lección Números Reales 4º ESO MATEMÁTICAS ACADÉMICAS El número real 2 LECCIÓN. NÚMERO REAL.- CONJUNTOS NUMÉRICOS Números Naturales. Son los números más intuitivos y simples. Sirven, básicamente, para contar:
Lección Números Reales 4º ESO MATEMÁTICAS ACADÉMICAS El número real 2 LECCIÓN. NÚMERO REAL.- CONJUNTOS NUMÉRICOS Números Naturales. Son los números más intuitivos y simples. Sirven, básicamente, para contar:
Pon tres ejemplos de números racionales que tengan la parte decimal de distinto tipo. Hazlo en forma de fracción y da la forma decimal también.
 Numeros Reales 1 Decimal Fracciones 1 Pon tres ejemplos de números racionales que tengan la parte decimal de distinto tipo. Hazlo en forma de fracción y da la forma decimal también. Qué es la parte decimal
Numeros Reales 1 Decimal Fracciones 1 Pon tres ejemplos de números racionales que tengan la parte decimal de distinto tipo. Hazlo en forma de fracción y da la forma decimal también. Qué es la parte decimal
Ejercicios Tema 1. a) b) c) d) e) f) Ejercicio 6. Escribe en forma de intervalo y representa:
 Ejercicios Tema 1 Números Reales Ejercicio 1. Clasifica los siguientes números en el lugar que conjunto que corresponde: a) b) c) Ejercicio 2. Clasifica los siguientes números: Ejercicio 3. a) Cuáles de
Ejercicios Tema 1 Números Reales Ejercicio 1. Clasifica los siguientes números en el lugar que conjunto que corresponde: a) b) c) Ejercicio 2. Clasifica los siguientes números: Ejercicio 3. a) Cuáles de
Bloque 1. Aritmética y Álgebra
 Bloque 1. Aritmética y Álgebra 3. Los números racionales 1. Los números racionales o fraccionarios Fracción es una o varias partes iguales en que dividimos la unidad. Las fracciones representan siempre
Bloque 1. Aritmética y Álgebra 3. Los números racionales 1. Los números racionales o fraccionarios Fracción es una o varias partes iguales en que dividimos la unidad. Las fracciones representan siempre
Una fracción decimal tiene por denominador la unidad. Número decimal. Es aquel que se puede expresar mediante una fracción
 Fracción decimal Una fracción decimal tiene por denominador la unidad seguida de ceros. Número decimal decimal. Es aquel que se puede expresar mediante una fracción Consta de dos partes: entera y decimal.
Fracción decimal Una fracción decimal tiene por denominador la unidad seguida de ceros. Número decimal decimal. Es aquel que se puede expresar mediante una fracción Consta de dos partes: entera y decimal.
IES CUADERNO Nº 3 NOMBRE: FECHA: / / Números decimales
 Números decimales Contenidos 1. Números decimales Elementos de un número decimal Redondeo y truncamiento de un decimal 2. Operaciones con decimales Suma de números decimales Resta de números decimales
Números decimales Contenidos 1. Números decimales Elementos de un número decimal Redondeo y truncamiento de un decimal 2. Operaciones con decimales Suma de números decimales Resta de números decimales
1Soluciones a las actividades de cada epígrafe PÁGINA 20
 Soluciones a las actividades de cada epígrafe PÁGINA 0 RACIONALES Q ENTEROS Z NO RACIONALES 8,, 8,, NATURALES N ENTEROS NEGATIVOS FRACCIONARIOS (racionales no enteros) 8 0, 7,,, 8, 8,, 7 8 8,9;,8; ) 7
Soluciones a las actividades de cada epígrafe PÁGINA 0 RACIONALES Q ENTEROS Z NO RACIONALES 8,, 8,, NATURALES N ENTEROS NEGATIVOS FRACCIONARIOS (racionales no enteros) 8 0, 7,,, 8, 8,, 7 8 8,9;,8; ) 7
Cuaderno de actividades 1º Bachillerato
 Cuaderno de Actividades º Operaciones con reales. Calcula : a. Cuaderno de actividades º Bachillerato Solución.. 0 0 0 0 0. 0 9 8 00 0 00 00 b :. c d.calcula pasando a fracción: a 0, 0, 0, b,0, c 0,,.
Cuaderno de Actividades º Operaciones con reales. Calcula : a. Cuaderno de actividades º Bachillerato Solución.. 0 0 0 0 0. 0 9 8 00 0 00 00 b :. c d.calcula pasando a fracción: a 0, 0, 0, b,0, c 0,,.
Números. Índice del libro. 1. Los números reales. 2. Operaciones con números enteros y racionales. 3. Números decimales
 1. Los números reales 2. Operaciones con números enteros y racionales 3. decimales 4. Potencias de exponente entero 5. Radicales 6. Notación científica y unidades de medida 7. Errores Índice del libro
1. Los números reales 2. Operaciones con números enteros y racionales 3. decimales 4. Potencias de exponente entero 5. Radicales 6. Notación científica y unidades de medida 7. Errores Índice del libro
Intervalos abiertos, cerrados, semiabiertos y semicerrados.
 008 _ 04-000.qxd 9//08 9:06 Página 69 Números reales INTRODUCCIÓN En la unidad anterior se estudiaron los números racionales o fraccionarios y se aprendió a compararlos, operar con ellos y utilizarlos
008 _ 04-000.qxd 9//08 9:06 Página 69 Números reales INTRODUCCIÓN En la unidad anterior se estudiaron los números racionales o fraccionarios y se aprendió a compararlos, operar con ellos y utilizarlos
Introducción histórica. Números irracionales
 Introducción histórica A finales del siglo V a.c., la Escuela de Pitágoras descubrió que no existían dos números naturales m y n, cuyo cociente sea igual a la proporción entre el lado de un cuadrado y
Introducción histórica A finales del siglo V a.c., la Escuela de Pitágoras descubrió que no existían dos números naturales m y n, cuyo cociente sea igual a la proporción entre el lado de un cuadrado y
Números reales ACTIVIDADES
 ACTIVIDADES No pueden representar el mismo número racional, puesto que si una fracción tiene un término negativo, el cociente es negativo; y si sus dos términos son positivos, el cociente es positivo.
ACTIVIDADES No pueden representar el mismo número racional, puesto que si una fracción tiene un término negativo, el cociente es negativo; y si sus dos términos son positivos, el cociente es positivo.
Enteros (Z):..., -3, -2, -1, 0, 1, 2, 3,... Números enteros (positivos o negativos), sin decimales. Incluye a los naturales.
 Tema 1: Números Reales 1.1 Conjunto de los números Naturales (N): 0, 1, 2, 3. Números positivos sin decimales. Sirven para contar. Enteros (Z):..., -3, -2, -1, 0, 1, 2, 3,... Números enteros (positivos
Tema 1: Números Reales 1.1 Conjunto de los números Naturales (N): 0, 1, 2, 3. Números positivos sin decimales. Sirven para contar. Enteros (Z):..., -3, -2, -1, 0, 1, 2, 3,... Números enteros (positivos
1º BACHILLERATO - MATEMÁTICAS CCSS - TEMA 1 NÚMEROS REALES
 1º BACHILLERATO - MATEMÁTICAS CCSS - TEMA 1 NÚMEROS REALES ˆ PÁGINA 4, EJERCICIO 68 Una habitación con forma de ortoedro de base cuadrada y altura la mitad del lado de la base se pintó en tres días. Se
1º BACHILLERATO - MATEMÁTICAS CCSS - TEMA 1 NÚMEROS REALES ˆ PÁGINA 4, EJERCICIO 68 Una habitación con forma de ortoedro de base cuadrada y altura la mitad del lado de la base se pintó en tres días. Se
OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Valor de cada cifra en función de la posición que ocupa. Expresión polinómica de un número.
 8966 _ 049-008.qxd /6/08 09: Página 49 Números reales INTRODUCCIÓN Los conceptos que se estudian en esta unidad ya han sido tratados en cursos anteriores. A pesar de ello, es importante volverlos a repasar,
8966 _ 049-008.qxd /6/08 09: Página 49 Números reales INTRODUCCIÓN Los conceptos que se estudian en esta unidad ya han sido tratados en cursos anteriores. A pesar de ello, es importante volverlos a repasar,
!!! " " # " "!!! $ $ $ % % & % % $ $ $!!! " " # " "!!! $ $ $ % % & % % $ $ $!!! " " # " "!!! $ $ $ % % & % % $ $ $!!! " " # " "!!!!!! " " # " "!!!
 UNIIDAD Nº º NÚMEEROSS REEALLEESS! Resuelve tú ( Pág "# ) Resuelve la ecuación : 9x + 8x 6 ; 9x + 8x 6 ; 9x 8x 8; 9x 8x 8x 8x 8 ; x - 8. Resuelve tú ( Pág "" ) Completa la resolución de 7x 6x + { pasar
UNIIDAD Nº º NÚMEEROSS REEALLEESS! Resuelve tú ( Pág "# ) Resuelve la ecuación : 9x + 8x 6 ; 9x + 8x 6 ; 9x 8x 8; 9x 8x 8x 8x 8 ; x - 8. Resuelve tú ( Pág "" ) Completa la resolución de 7x 6x + { pasar
LOS NÚMEROS DECIMALES
 1 LOS NÚMEROS DECIMALES Al dividir el numerador entre el denominador de una fracción se obtiene un número decimal. 5 5 0,; 1,5;,15 10 4 8 C D U d c m dm, 1 5 Parte entera Parte decimal Tres unidades, ciento
1 LOS NÚMEROS DECIMALES Al dividir el numerador entre el denominador de una fracción se obtiene un número decimal. 5 5 0,; 1,5;,15 10 4 8 C D U d c m dm, 1 5 Parte entera Parte decimal Tres unidades, ciento
Matemática 2 Módulo 1
 Matemática Módulo Contenidos: Números reales. Repaso de racionales. Decimales periódicos, puros y mixtos. Irracionales. Operaciones con radicales. Racionalización. Actividades de inicio, desarrollo y cierre.
Matemática Módulo Contenidos: Números reales. Repaso de racionales. Decimales periódicos, puros y mixtos. Irracionales. Operaciones con radicales. Racionalización. Actividades de inicio, desarrollo y cierre.
Números reales EJERCICIOS. Calcula las siguientes potencias. a) 3 2 d) ( 5) 3 g) (4,25) 4. b) 7 4 e) ( 2,02) 4 h) c) ( 9) 2 f) 5
 Números reales EJERCICIOS 00 Calcula las siguientes potencias. a) d) () g) (,) b) e) (,0) h) c) (9) f) i) (,) 8 8 a) 9 d) g) 6,906 b).0 e) 6,69666 h) c) 8 f). i) 8.6.99,9006.68 00 Calcula (0,8), (0,8)
Números reales EJERCICIOS 00 Calcula las siguientes potencias. a) d) () g) (,) b) e) (,0) h) c) (9) f) i) (,) 8 8 a) 9 d) g) 6,906 b).0 e) 6,69666 h) c) 8 f). i) 8.6.99,9006.68 00 Calcula (0,8), (0,8)
1Soluciones a las actividades de cada epígrafe PÁGINA 20
 Soluciones a las actividades de cada epígrafe PÁGINA 0 RACIONALES Q ENTEROS Z NO RACIONALES 8,, 8,, NATURALES N ENTEROS NEGATIVOS FRACCIONARIOS (racionales no enteros) 8 0,,,, 8, 8,, 8 8,;,8; ) ; 8 ; Pág.
Soluciones a las actividades de cada epígrafe PÁGINA 0 RACIONALES Q ENTEROS Z NO RACIONALES 8,, 8,, NATURALES N ENTEROS NEGATIVOS FRACCIONARIOS (racionales no enteros) 8 0,,,, 8, 8,, 8 8,;,8; ) ; 8 ; Pág.
b) Expresa como fracción aquellos que sea posible. c) Cuáles son irracionales? a) No pueden expresarse como cociente: 3; 3π y 2 5.
 PÁGINA 9 Entrénate 1 a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? 2; 1,7; ; 4, 2; ),75; ) π; 2 5 b) Expresa como fracción aquellos que sea posible. c)
PÁGINA 9 Entrénate 1 a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? 2; 1,7; ; 4, 2; ),75; ) π; 2 5 b) Expresa como fracción aquellos que sea posible. c)
DECIMALES. Ejercicio nº 1.- a Expresa en forma de fracción: a.1) 2,3. a.2) 2, b) Escribe en forma decimal las fracciones: y.
 DECIMALES Ejercicio nº 1.- a Expresa en forma de fracción: a.1) 1,2 a.2) 2,08 1 7 b) Escribe en forma decimal las fracciones: y. 0 Justifica, previamente, si los decimales van a ser exactos o periódicos.
DECIMALES Ejercicio nº 1.- a Expresa en forma de fracción: a.1) 1,2 a.2) 2,08 1 7 b) Escribe en forma decimal las fracciones: y. 0 Justifica, previamente, si los decimales van a ser exactos o periódicos.
Tema 1: Aritmética. Repaso de 3º de ESO. NÚMEROS REALES. POTENCIAS Y RAÍCES. Ejercicios resueltos en video
 Tema : Aritmética. Repaso de º de ESO. NÚMEROS REALES. POTENCIAS Y RAÍCES. EJERCICIOS Los conjuntos numéricos.. (º ESO) Cuáles de los números siguientes son racionales? e irracionales? Pon en forma de
Tema : Aritmética. Repaso de º de ESO. NÚMEROS REALES. POTENCIAS Y RAÍCES. EJERCICIOS Los conjuntos numéricos.. (º ESO) Cuáles de los números siguientes son racionales? e irracionales? Pon en forma de
Colegio Portocarrero. Curso Departamento de matemáticas. Números Reales.
 Números Reales. Lo primero que hemos hecho en este primer curso de bachillerato, es repasar lo visto en cursos anteriores, para resolver cualquier duda que pudiésemos tener, y asentar bien la base, para
Números Reales. Lo primero que hemos hecho en este primer curso de bachillerato, es repasar lo visto en cursos anteriores, para resolver cualquier duda que pudiésemos tener, y asentar bien la base, para
FRACCIONES. Las partes que tomamos ( 3 ó 5 ) se llaman numerador y las partes en que dividimos el queso ( 8 ) denominador.
 FRACCIONES Una fracción, en general, es la expresión de una cantidad dividida por otra, y una fracción propia representa las partes que tomamos de un todo. El ejemplo clásico es el de un queso que partimos
FRACCIONES Una fracción, en general, es la expresión de una cantidad dividida por otra, y una fracción propia representa las partes que tomamos de un todo. El ejemplo clásico es el de un queso que partimos
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 7 PRACTICA Aproximación y errores Expresa con un número adecuado de cifras significativas: a) Audiencia de un programa de televisión: 07 9 espectadores. b) Tamaño de un virus: 0,007 mm. c)
Pág. Página 7 PRACTICA Aproximación y errores Expresa con un número adecuado de cifras significativas: a) Audiencia de un programa de televisión: 07 9 espectadores. b) Tamaño de un virus: 0,007 mm. c)
1.1. Los conjuntos numéricos
 Capítulo NÚMEROS.. Los conjuntos numéricos Usted conoce los números desde su más tierna infancia cuando aprendió a contar. Recuerde que los campos numéricos son los siguientes: Los números naturales N
Capítulo NÚMEROS.. Los conjuntos numéricos Usted conoce los números desde su más tierna infancia cuando aprendió a contar. Recuerde que los campos numéricos son los siguientes: Los números naturales N
Números reales ACTIVIDADES
 ACTIVIDADES No pueden representar el mismo número racional, puesto que si una fracción tiene un término negativo, el cociente es negativo; y si sus dos términos son positivos, el cociente es positivo.
ACTIVIDADES No pueden representar el mismo número racional, puesto que si una fracción tiene un término negativo, el cociente es negativo; y si sus dos términos son positivos, el cociente es positivo.
TEMA 1: NÚMEROS REALES
 TEMA 1: NÚMEROS REALES 1. INTRODUCCIÓN El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por Con los números reales podemos realizar todas las
TEMA 1: NÚMEROS REALES 1. INTRODUCCIÓN El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por Con los números reales podemos realizar todas las
1.- CONJUNTOS NUMÉRICOS
 N 1º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA 1.- NÚMEROS-2 PROFESOR: RAFAEL NÚÑEZ NOGALES Números reales(r) 1.- CONJUNTOS NUMÉRICOS N úm e ros natu :Ejemplo:7 E l n úm e ro 0 rales Números enteros(z)
N 1º BACHILLERATO (LOMCE) MATEMÁTICAS CC SS TEMA 1.- NÚMEROS-2 PROFESOR: RAFAEL NÚÑEZ NOGALES Números reales(r) 1.- CONJUNTOS NUMÉRICOS N úm e ros natu :Ejemplo:7 E l n úm e ro 0 rales Números enteros(z)
SISTEMAS NUMERICOS. Todas las fracciones equivalentes a una fracción dada determinan un mismo número, que se llama número racional.
 . NÚMEROS RACIONALES SISTEMAS NUMERICOS Desde la aparición de las sociedades humanas los números desempeñan un papel fundamental para ordenar y contar los elementos de un conjunto. Así surgen, en primer
. NÚMEROS RACIONALES SISTEMAS NUMERICOS Desde la aparición de las sociedades humanas los números desempeñan un papel fundamental para ordenar y contar los elementos de un conjunto. Así surgen, en primer
Página 29. Página Representa los siguientes conjuntos: a) ( 3, 1) b) [4, c) (3, 9] d) 0)
![Página 29. Página Representa los siguientes conjuntos: a) ( 3, 1) b) [4, c) (3, 9] d) 0) Página 29. Página Representa los siguientes conjuntos: a) ( 3, 1) b) [4, c) (3, 9] d) 0)](/thumbs/82/85250741.jpg) Página. Representa los siguientes conjuntos: a) (, ) b) [, + @) c) (, ] d) ( @, 0) a) 0 b) 0 c) 0 d) 0. Representa los siguientes conjuntos: a) {x / Ì x < } b) [, ) «(, 7] c) ( @, 0) «(, +@) d) ( @, )
Página. Representa los siguientes conjuntos: a) (, ) b) [, + @) c) (, ] d) ( @, 0) a) 0 b) 0 c) 0 d) 0. Representa los siguientes conjuntos: a) {x / Ì x < } b) [, ) «(, 7] c) ( @, 0) «(, +@) d) ( @, )
Conjunto de Números Racionales.
 Conjunto de Números Racionales. El conjunto de los números racionales está formado por: el conjunto de los números enteros (-2, -1, 0, 1, 2, ) y los números fraccionarios y se representan con una Q. Números
Conjunto de Números Racionales. El conjunto de los números racionales está formado por: el conjunto de los números enteros (-2, -1, 0, 1, 2, ) y los números fraccionarios y se representan con una Q. Números
3º ESO PMAR NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa NÚMEROS REALES
 º ESO PMAR NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números racionales son lo que habitualmente conocemos como fracciones. Un número racional o fracción está
º ESO PMAR NÚMEROS REALES DEPARTAMENTO DE MATEMÁTICAS. NÚMEROS REALES.- NÚMEROS RACIONALES Los números racionales son lo que habitualmente conocemos como fracciones. Un número racional o fracción está
ACTIVIDADES DE LOS TEMAS 1, 2, 3, 4, 5, 6, 7 1. Calcula la forma fraccionaria o decimal (identificando cada una de sus partes), según corresponda de:
 ACTIVIDADES DE LOS TEMAS,,, 4,,, 7. Calcula la forma fraccionaria o decimal (identificando cada una de sus partes, según corresponda de 8 9,777.. b b4,777... c 0. Clasifica los siguientes números según
ACTIVIDADES DE LOS TEMAS,,, 4,,, 7. Calcula la forma fraccionaria o decimal (identificando cada una de sus partes, según corresponda de 8 9,777.. b b4,777... c 0. Clasifica los siguientes números según
UNIDAD 6 AULA 360. Números decimales
 UNIDAD 6 Números decimales 1. Números decimales. Ordenación y representación 2. Tipos de números decimales 3. Conversión de decimal a fracción 4. Operaciones con números decimales 1. Números decimales
UNIDAD 6 Números decimales 1. Números decimales. Ordenación y representación 2. Tipos de números decimales 3. Conversión de decimal a fracción 4. Operaciones con números decimales 1. Números decimales
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1. conjunto de todos ellos se les designa con la letra Q.
 Matemáticas B º E.S.O. Tema 1 Los números Reales 1 TEMA 1 LOS NÚMEROS REALES 1.1 CLASIFICACIÓN DE LOS NÚMEROS REALES º 1.1.1 TIPOS DE NÚMEROS º Los números naturales son : 1, 2,,..., 10, 11,..., 102, 10,....
Matemáticas B º E.S.O. Tema 1 Los números Reales 1 TEMA 1 LOS NÚMEROS REALES 1.1 CLASIFICACIÓN DE LOS NÚMEROS REALES º 1.1.1 TIPOS DE NÚMEROS º Los números naturales son : 1, 2,,..., 10, 11,..., 102, 10,....
NÚMEROS DECIMALES PROFESOR: RAFAEL NÚÑEZ NOGALES
 NÚMEROS DECIMALES 1 y 2.- ÓRDENES Y DECIMALES. FRACCIONES Y DECIMALES (A) Lectura de números decimales 241,58 241 unidades y 58 centésimas 3,007 3 unidades y 7 milésimas 4005,6 4005 unidades y 6 décimas
NÚMEROS DECIMALES 1 y 2.- ÓRDENES Y DECIMALES. FRACCIONES Y DECIMALES (A) Lectura de números decimales 241,58 241 unidades y 58 centésimas 3,007 3 unidades y 7 milésimas 4005,6 4005 unidades y 6 décimas
EJERCICIOS REFUERZO MATEMÁTICAS 3 ESO 1º TRIMESTRE
 EJERCICIOS REFUERZO MATEMÁTICAS ESO º TRIMESTRE NÚMEROS RACIONALES º. Amplifica las siguientes fracciones para que todas tengan denominador º. Cuál de las siguientes fracciones es una fracción amplificada
EJERCICIOS REFUERZO MATEMÁTICAS ESO º TRIMESTRE NÚMEROS RACIONALES º. Amplifica las siguientes fracciones para que todas tengan denominador º. Cuál de las siguientes fracciones es una fracción amplificada
TEMA 2. Números racionales. Teoría. Matemáticas
 1 1.- Números racionales Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por Las fracciones también pueden
1 1.- Números racionales Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero. Se representa por Las fracciones también pueden
TEMA 2: POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS
 TEMA : POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. Potenciación Aplica las propiedades de las potencias en las siguientes expresiones: 5 5 5 5 5 8 a 5 a a 5 a n n n n x 9 x 6 x 96 x a a a 6 b b b c c c 9
TEMA : POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. Potenciación Aplica las propiedades de las potencias en las siguientes expresiones: 5 5 5 5 5 8 a 5 a a 5 a n n n n x 9 x 6 x 96 x a a a 6 b b b c c c 9
Ejercicios Tema 1 El número real Matemáticas I 1º Bach. 1
 Ejercicios Tema El número real Matemáticas I º Bach. TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN GRÁFICA DE NÚMEROS REALES EJERCICIO : Clasifica los siguientes números como 0 π ; ;,...; ; 6; ; ;,
Ejercicios Tema El número real Matemáticas I º Bach. TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN GRÁFICA DE NÚMEROS REALES EJERCICIO : Clasifica los siguientes números como 0 π ; ;,...; ; 6; ; ;,
BATERIA DE EJERCICIOS TEMA 1: NÚMEROS RACIONALES. 4º Op A
 BATERIA DE EJERCICIOS TEMA : NÚMEROS RACIONALES. º Op A - Problemas con fracciones. Un ciclista recorre el primer día / de la distancia el segundo día / y el tercero /. Qué fracción de distancia lleva
BATERIA DE EJERCICIOS TEMA : NÚMEROS RACIONALES. º Op A - Problemas con fracciones. Un ciclista recorre el primer día / de la distancia el segundo día / y el tercero /. Qué fracción de distancia lleva
Números fraccionarios y decimales
 Unidad didáctica Números fraccionarios y decimales 1.- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Unidad didáctica Números fraccionarios y decimales 1.- Las fracciones. a Una fracción es un número racional, escrito en la forma, tal que b 0 y representa una parte b de un total. El denominador (el número
Equivalencias entre fracción y decimal
 Equivalencias entre fracción y decimal. Fracción a decimal Para transformar una fracción a número decimal basta dividir el numerador por el denominador. Ejemplos: Ejercicios:. Clasificación de decimales
Equivalencias entre fracción y decimal. Fracción a decimal Para transformar una fracción a número decimal basta dividir el numerador por el denominador. Ejemplos: Ejercicios:. Clasificación de decimales
ACTIVIDADES INICIALES. 23 f) 1 h) 5 3. a) 2 (3 2 6) (10 3) (5 2 3) 2 (3 12) 7 (5 6) 2 ( 9) 7 ( 1) EJERCICIOS PROPUESTOS. b) 2.
 Solucionario Números reales ACTIVIDADES INICIALES.I. Indica a qué conjuntos numéricos pertenecen los números siguientes. a) c), e) g) b) d) f) h) a) Z c) Q e) Q g) Q b) R d) R f) N h) Q.II Realiza las
Solucionario Números reales ACTIVIDADES INICIALES.I. Indica a qué conjuntos numéricos pertenecen los números siguientes. a) c), e) g) b) d) f) h) a) Z c) Q e) Q g) Q b) R d) R f) N h) Q.II Realiza las
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. Página 22 La siguiente lista consta de todos los números escritos en la pizarra y algunos más: 0; ; ; 0,; 2 ; ; ; ; 2 ; 2 ; ; ; ;, ; ) π; Sitúalos, en tu cuaderno, sobre un cuadro como el de abajo.
Pág. Página 22 La siguiente lista consta de todos los números escritos en la pizarra y algunos más: 0; ; ; 0,; 2 ; ; ; ; 2 ; 2 ; ; ; ;, ; ) π; Sitúalos, en tu cuaderno, sobre un cuadro como el de abajo.
Ejercicios Tema 1 El número real Matemáticas CCSSI 1º Bach. 1
 Ejercicios Tema El número real Matemáticas CCSSI º Bach. TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN GRÁFICA DE NÚMEROS REALES EJERCICIO : Clasifica los siguientes números como 0 π ; ;,...; ; 6;
Ejercicios Tema El número real Matemáticas CCSSI º Bach. TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN GRÁFICA DE NÚMEROS REALES EJERCICIO : Clasifica los siguientes números como 0 π ; ;,...; ; 6;
TEMA 1. Números Reales. Teoría. Matemáticas
 1 1.- Los números reales Cuáles son los números reales? Los números reales son todos los números racionales y todos los números irracionales. El conjunto de los números reales se designa con el símbolo
1 1.- Los números reales Cuáles son los números reales? Los números reales son todos los números racionales y todos los números irracionales. El conjunto de los números reales se designa con el símbolo
Potencias y raíces CLAVES PARA EMPEZAR VIDA COTIDIANA RESUELVE EL RETO. a) 125 c) 625 e) 1 b) 125 d) 625 f) 1. a) 4 c) 6 e) 3,46.
 CLAVES PARA EMPEZAR a) 15 c) 65 e) 1 b) 15 d) 65 f) 1 a) 4 c) 6 e) 3,46 b),65 d) 3,16 VIDA COTIDIANA 3, 10 7 m 3, 10 4 mm 1 10 4 mm El científico sí puede diferenciar las dos células con el microscopio.
CLAVES PARA EMPEZAR a) 15 c) 65 e) 1 b) 15 d) 65 f) 1 a) 4 c) 6 e) 3,46 b),65 d) 3,16 VIDA COTIDIANA 3, 10 7 m 3, 10 4 mm 1 10 4 mm El científico sí puede diferenciar las dos células con el microscopio.
4 ; 3. d) 2 y 5 3. a) 2,2 b) c) 2,24 d) 2,236 e) 2,23607
 EL NÚMERO REAL.- LOS NÚMEROS IRRACIONALES. NÚMEROS REALES - Indicar a qué conjuntos ( Ν, Ζ, Q, R ) pertenecen los siguientes números: -2 ; ; -4/ 5; 6/ 4; 4 ; 25 ; Ν ; 6/ 4 Ζ -2 ; 25 Q -4/ 5 ; 6 ; 4 ; 8
EL NÚMERO REAL.- LOS NÚMEROS IRRACIONALES. NÚMEROS REALES - Indicar a qué conjuntos ( Ν, Ζ, Q, R ) pertenecen los siguientes números: -2 ; ; -4/ 5; 6/ 4; 4 ; 25 ; Ν ; 6/ 4 Ζ -2 ; 25 Q -4/ 5 ; 6 ; 4 ; 8
1Soluciones a los ejercicios y problemas PÁGINA 36
 PÁGINA 6 Pág. P RACTICA Números reales a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ;,7; ;, ; ),7; ) π; b)expresa como fracción aquellos que sea posible.
PÁGINA 6 Pág. P RACTICA Números reales a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ;,7; ;, ; ),7; ) π; b)expresa como fracción aquellos que sea posible.
P RACTICA. 1 a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros?
 Pág. 1 P RACTICA Números reales 1 a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ; 1,7; ; 4, ; ),7; ) π; b)expresa como fracción aquellos que sea posible.
Pág. 1 P RACTICA Números reales 1 a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ; 1,7; ; 4, ; ),7; ) π; b)expresa como fracción aquellos que sea posible.
El despeje es directo = = El despeje es directo. = El despeje queda = Son similares a los despejes en N y Z. El despeje es directo 4 +6=11 2
 Estudio del l conjunto de los números racionales Q (Segunda Parte) Ecuaciones en Q Una vez que conocemos bien las operaciones básicas en el conjunto Q (adición, multiplicación y división), podemos utilizar
Estudio del l conjunto de los números racionales Q (Segunda Parte) Ecuaciones en Q Una vez que conocemos bien las operaciones básicas en el conjunto Q (adición, multiplicación y división), podemos utilizar
NÚMEROS REALES. Expresiones decimales infinitas no periódicas que presentan algún tipo de regularidad:
 NÚMEROS REALES NÚMEROS IRRACIONALES: Se caracterizan porque: 1. No pueden expresarse en forma de fracción. 2. Su expresión decimal tiene infinitas cifras y no es periódica. El conjunto de todos los números
NÚMEROS REALES NÚMEROS IRRACIONALES: Se caracterizan porque: 1. No pueden expresarse en forma de fracción. 2. Su expresión decimal tiene infinitas cifras y no es periódica. El conjunto de todos los números
TEMA 3. NÚMEROS RACIONALES.
 TEMA 3. NÚMEROS RACIONALES. Concepto de fracción Una fracción es el cociente de dos números enteros a y b, que representamos de la siguiente forma: b denominador, indica el número de partes en que se ha
TEMA 3. NÚMEROS RACIONALES. Concepto de fracción Una fracción es el cociente de dos números enteros a y b, que representamos de la siguiente forma: b denominador, indica el número de partes en que se ha
CENTRO DE EDUCACIÓN DE PERSONAS ADULTAS.
 C/ Francisco García Pavón, Tomelloso 700 (C. Real) Teléfono Fax: 9 9 9 Números reales a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ;,7; ;, ; ),7; ) π;
C/ Francisco García Pavón, Tomelloso 700 (C. Real) Teléfono Fax: 9 9 9 Números reales a) Cuáles de los siguientes números no pueden expresarse como cociente de dos números enteros? ;,7; ;, ; ),7; ) π;
NÚMEROS RACIONALES Y REPRESENTACIÓN DECIMAL. Mate 3041 Profa. Milena R. Salcedo Villanueva
 NÚMEROS RACIONALES Y REPRESENTACIÓN DECIMAL Mate 3041 Profa. Milena R. Salcedo Villanueva 1 FRACCIONES Una fracción tiene dos términos: numerador y denominador Denominador indica las veces que se divide
NÚMEROS RACIONALES Y REPRESENTACIÓN DECIMAL Mate 3041 Profa. Milena R. Salcedo Villanueva 1 FRACCIONES Una fracción tiene dos términos: numerador y denominador Denominador indica las veces que se divide
CUADERNO DE REPASO DE VERANO
 CUADERNO DE REPASO DE VERANO MATEMÁTICAS ACADÉMICAS º ESO Las actividades deben realizarse en folios, indicando el número de la actividad y el enunciado necesario para el desarrollo. Hay que realizar todo
CUADERNO DE REPASO DE VERANO MATEMÁTICAS ACADÉMICAS º ESO Las actividades deben realizarse en folios, indicando el número de la actividad y el enunciado necesario para el desarrollo. Hay que realizar todo
NÚMEROS RACIONALES. Evaluación A. Ten en cuenta. Recuerda. Recuerda
 NÚMEROS RACIONALES Evaluación A 1. Ordena de menor a mayor estas fracciones: 1 2, 9 20, 18 25, 3 5 Para ordenar fracciones, expresamos la solución mediante las fracciones iniciales, no las equivalentes
NÚMEROS RACIONALES Evaluación A 1. Ordena de menor a mayor estas fracciones: 1 2, 9 20, 18 25, 3 5 Para ordenar fracciones, expresamos la solución mediante las fracciones iniciales, no las equivalentes
TEMA 1: NÚMEROS REALES
 TEMA 1: NÚMEROS REALES 3º ESO Matemáticas Apuntes para trabajo del alumnos en el aula. 1. Fracciones. Números racionales Si se multiplican o dividen el numerador y el denominador de una fracción por un
TEMA 1: NÚMEROS REALES 3º ESO Matemáticas Apuntes para trabajo del alumnos en el aula. 1. Fracciones. Números racionales Si se multiplican o dividen el numerador y el denominador de una fracción por un
MATEMÁTICAS B 4º ESO
 MATEMÁTICAS B 4º ESO Las unidades trabajadas durante el curso han sido: UNIDAD 1: NÚMEROS REALES UNIDAD : POTENCIAS Y RADICALES UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS UNIDAD 4: ECUACIONES E INECUACIONES
MATEMÁTICAS B 4º ESO Las unidades trabajadas durante el curso han sido: UNIDAD 1: NÚMEROS REALES UNIDAD : POTENCIAS Y RADICALES UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS UNIDAD 4: ECUACIONES E INECUACIONES
MATEMÁTICAS Cuaderno de ejercicios NÚMEROS REALES
 MATEMÁTICAS Cuaderno de ejercicios NÚMEROS REALES 1.* Relacionad cada número con su fracción equivalente. a) 0,625 b) c) 3 d) 0,4203821 e) 2.* Indicad si estas parejas están constituidas o no por fracciones
MATEMÁTICAS Cuaderno de ejercicios NÚMEROS REALES 1.* Relacionad cada número con su fracción equivalente. a) 0,625 b) c) 3 d) 0,4203821 e) 2.* Indicad si estas parejas están constituidas o no por fracciones
NUMEROS REALES. Recordemos
 NUMEROS REALES Recordemos El conjunto de los números racionales está constituido por los números enteros y los números fraccionarios. Por tanto, cualquier número que pueda expresarse en forma de fracción
NUMEROS REALES Recordemos El conjunto de los números racionales está constituido por los números enteros y los números fraccionarios. Por tanto, cualquier número que pueda expresarse en forma de fracción
