Nudo Es todo punto de la red en que concurren tres o más conductores.
|
|
|
- Lourdes Padilla Torres
- hace 7 años
- Vistas:
Transcripción
1 ltos Rgls Kirhho Un iruito, n gnrl, stá ormo por un onjunto rsistnis y gnrors..m. ontos un orm ritrri, mnr qu no simpr s posil sustituir los onjuntos rsistnis por sus quivlnts, y qu no suln str onts n sri o n prllo. GUSTAV ROBERT KIRCHHOFF ( , ísio lmán nio n Prusi, nunió ls rgls qu llvn su nomr y qu prmitn lulr ls intnsis qu iruln por los irnts lmntos un r onutors. Es priso stlr, nts plir sts rgls un r, los siguints onptos: Nuo Es too punto l r n qu onurrn trs o más onutors. Mll Es too iruito qu pu sr rorrio prtino un nuo y volvino él sin psr os vs por un mismo onutor. Un ls rgls Kirhho s rir los nuos, y l otr ls mlls. Rgl los nuos Un nuo s l simpl unión vrios onutors y n él no hy ningún lmnto pz lmnr o rtnr rg létri. Por onsiguint, En uni timpo, l nti rg qu llg un nuo s igul l nti rg qu sl él, y pusto qu l rg qu irul por uni timpo s lo qu s in omo intnsi un orrint létri, L sum ls intnsis qu llgn un nuo s igul l sum ls intnsis qu sln él. Si s onsirn positivs ls intnsis qu llgn un nuo, y ngtivs ls qu sln él, l sum lgrái ls intnsis onurrnts n un nuo s nul. ΣI i = 0 [4.12-1] L ly los nuos s un onsuni l prinipio onsrvión l rg. Si n un r hy n nuos, son linlmnt inpnints n 1 nuos. Si s pli ih ly l nuo nésimo, s otin un uión qu s ominión linl ls n 1 uions ntriors y, por tnto, no s váli pr rsolvr l prolm. Rgl ls mlls Si s lul, plino l ly Ohm gnrliz, l irni potnil ntr os nuos onsutivos un mll V V i = Σε i I ΣR i y s sumn ls uions otnis, s nuln ls irnis potnil, on lo qu rsult [4.12-2] Σε = ΣI i R i [4.12-3] L rgl ls mlls, omo onsuni qu s l ly Ohm gnrliz, s l prinipio gnrl onsrvión l nrgí plio un iruito létrio. [Vés, Cpítulo Furz ltromotriz.p, pígr 11.3] Apliión ls rgls Kirhho Ls rgls Kirhho s pun plir un r siguino os métoos: I Métoo nuos y mlls S ominz por signr rm l r, omprni ntr os noos onsutivos, un intnsi orrint létri n l sntio irulión qu rmos oportuno. S pli l ly los nuos n 1 nuos. Ruérs qu si s pli ih ly l nuo nésimo s otin un uión qu s un ominión linl ls n 1 uions ntriors y no s váli pr rsolvr l prolm. A ontinuión s pli l rgl ls mlls un lls pr sriir l primr mimro l uión [4.12-3], rorrino l mll n un sntio ritrrio. En l sum lgrái ls..m. los gnrors qu vmos nontrno n nustro rorrio s onsirn positivs qulls..m. qu tinn prouir orrint n iho sntio, y ngtivs, n so ontrrio. Hy qu tnr n unt qu no onsirmos l sntio n qu irul l orrint qu hymos signo, sino l sntio n qu tin prouir orrint ih..m.., s ir, l sntio n qu prouirí orrint si stuvis ont ll sol n l mll.
2 2 ltos S vulv rorrr ih mll pr sriir l sum lgrái l sguno mimro l uión ], multiplino l intnsi trmo omprnio ntr os nuos onsutivos por l rsistni totl iho trmo, onsirno positivs ls intnsis uyo sntio oini on l rorrio l mll, y ngtivs, n so ontrrio. Los vlors ls rsistnis s onsirn simpr númros positivos. S pli l rgl ls mlls ls rstnts tnino n unt qu no tos son inpnints. Un mll s inpnint ls qu y s hyn utilizo, si n ll intrvin lgún onutor qu no hy ormo prt ls mlls ntriors. D st orm s vn sriino ls uions ls mlls hst ompltr, junto on ls uions los n 1 nuos, tnts uions omo inógnits hy n l r. Si l rsolvr l sistm uions, lgun intnsi rsult sr ngtiv, signii qu su sntio s ontrrio l qu hmos supusto, pro no hy qu volvr plntr l prolm. S h onstr sí n l rspust inl. Y si ih intnsi intrvin n lgún álulo postrior, s sustituy mntnino l signo ngtivo. Ejmplo Vmos lulr ls intnsis n rm l iruito l igur, y l irni potnil ntr los nuos y. Los puntos,, y, no son nuos sino simpls rrnis pr por nominr ls mlls áilmn- Comnzmos por inir, por mio un lh, l intnsi l orrint n rm l r, n l sntio qu rmos onvnint. Aplimos l rgl los nuos, tnino n unt qu los os nuos, y, sólo uno llos s inpnint. Elgimos l nuo : 4 Ω + = [1] S pu ompror qu si plimos l rgl los nuos l nuo, l uión qu s otin s l mism: = + 6 Ω 3 Ω D moo qu tnmos un uión y trs inógnits:,. Es nsrio, por tnto, ompltr l sistm uions plino l rgl ls mlls os lls. En l r hy trs mlls: l ----, l ---- y l Esogmos ls os primrs y vmos rorrrls, prtino un nuo, n l sntio ontrrio l ls gujs l rloj. Est sntio s ritrrio, y no s nsrio rorrr ls os mlls n l mismo sntio. Mll ---- Esriimos n primr lugr, prtino l nuo, l sum lgrái ls urzs ltromotris orrsponint l primr mimro l uión [4.12-3]. L primr..m. qu nontrmos n nustro rorrio s l. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l ontrrio l qu rorrmos l mll, por tnto, s ngtiv. Sguimos rorrino l mll, y ontinuión nontrmos l..m.. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l mismo sntio n qu rorrmos l mll, por tnto, s positiv. Por onsiguint, l sum lgrái ls urzs ltromotris st mll s: =. Σε = = [2] Rorrmos nuvmnt l mll, prtino l nuo, pr sriir l sum lgrái l sguno mimro l uión [4.12-3]. L primr intnsi qu nontrmos n nustro rorrio s, uyo sntio s ontrrio l rorrio l mll, por tnto, s ngtiv, y multipli por to l rsistni qu rorr s hst, rsult (2+4. Sguimos rorrino l mll, y ontinuión nontrmos l intnsi, uyo sntio s l mismo qu l rorrio l mll, por tnto, s positiv, y multipli por to l rsistni qu rorr s, psno por y hst,hst, rsult (1+2. En onsuni, l sum lgrái l sguno mimro l uión [4.12-3] s ΣIR = ( (1+ 2 = Sustituyno [2] y [3] n l uión [4.12-3], s otin pr st mll l uión [3]
3 ltos 3 S rpit l mismo proso pr l siguint mll: Mll = [4] Esriimos n primr lugr, prtino l nuo, l sum lgrái ls urzs ltromotris orrsponint l primr mimro l uión [4.12-3]. L primr..m. qu nontrmos n nustro rorrio s l. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l ontrrio l rorrio l mll, por tnto, s ngtiv. Sguimos rorrino l mll, y ontinuión nontrmos l..m.. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l mismo sntio n qu rorrmos l mll, por tnto, s positiv. Por onsiguint, l sum lgrái ls urzs ltromotris st mll s: 3+15= 12 V. Σε = = 12 V [5] Rorrmos nuvmnt l mll, prtino l nuo, pr sriir l sum lgrái l sguno mimro l uión [4.12-3]. L primr intnsi qu nontrmos n nustro rorrio s, uyo sntio s l mismo qu l rorrio l mll, por tnto, s positiv, y multipli por to l rsistni qu rorr s hst, trvés y, rsult (6+3. Sguimos rorrino l mll, y ontinuión nontrmos l intnsi, uyo sntio s l mismo qu l rorrio l mll, por tnto, s positiv, y multipli por to l rsistni qu rorr s hst, rsult (4+2. En onsuni, l sum lgrái l sguno mimro l uión [4.12-3] pr st mll s ΣIR =( (4 + 2 = Sustituyno [5] y [6] n l uión [4.12-3], s otin pr st mll l uión [6] Ls uions [1], [4] y [7] ormn l sistm uy soluión, un vz simpliio y rsulto, s 12V = = = = 12 = 3 A = 1 A El signo ngtivo l intnsi ini qu irul n sntio ontrrio l qu hmos supusto, s ir hi. S pu sguir otro métoo pr plir ls rgls Kirhho II Métoo ls mlls En st métoo no intrvinn los nuos. S supon qu mll s rorri por un sol intnsi n l sntio irulión qu rmos oportuno. Mll ---- I 1 I 2 4 Ω 6 Ω 3 Ω Vmos suponr qu l mll ---- s rorri por l intnsi I 1 n sntio ontrrio l ls gujs l rloj, Esriimos n primr lugr, prtino l nuo, l sum lgrái ls urzs ltromotris orrsponint l primr mimro l uión [4.12-3]. L primr..m. qu nontrmos n nustro rorrio s l. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l ontrrio l qu rorrmos l mll, por tnto, s ngtiv. Sguimos rorrino l mll, y ontinuión nontrmos l..m.. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l mismo sntio n qu rorrmos l mll, por tnto, s positiv. [7] [8] [9]
4 4 ltos Por onsiguint, l sum lgrái ls urzs ltromotris st mll s: =. Σε = = [10] Hst quí hmos sguio los mismos psos pr sriir l primr mimro l uión [4.12-3], qu n l métoo ntrior, pro l rorrr nuvmnt l mll, prtino l nuo, pr sriir l sum lgrái l sguno mimro l uión [4.12-3], hy un irni importnt: Dmos tnr n unt qu l trmo - s rorrio simultánmnt por ls intnsis I 1 I 2, y omo l intnsi I 1 s positiv, por sr l mismo sntio qu l rorrio l mll, I 2, ngtiv, por sr sntio opusto, l intnsi nt qu rorr st trmo s l irni I 1 I 2 ms intnsis, y multipli por to l rsistni qu rorr s hst, rsult (2+4(I 1 I 2 Sguimos rorrino l mll, y ontinuión nontrmos l trmo --- qu s rorrio solmnt por l intnsi I 1, qu multipli por to l rsistni l trmo --- qu rorr rsult (1+2I 1. En onsuni, l sum lgrái l sguno mimro l uión [4.12-3] s, pr st mll ΣIR =(2 + 4(I 1 I 2 +(1+ 2I 1 = 6(I 1 I 2 + 3I 1 = 9I 1 6I 2 [11] Sustituyno [10] y [11] n l uión [4.12-3], s otin pr st mll ----, l uión Mll = 9I 1 6I 2 [12] Esriimos n primr lugr, prtino l nuo, l sum lgrái ls urzs ltromotris orrsponint l primr mimro l uión [4.12-3]. L primr..m. qu nontrmos n nustro rorrio s l. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l ontrrio l rorrio l mll, por tnto, s ngtiv. Sguimos rorrino l mll, y ontinuión nontrmos l..m.. Est...m.., si stuvir ll sol n l mll prouirí orrint n l sntio hi, s ir, n l mismo sntio n qu rorrmos l mll, por tnto, s positiv. Por onsiguint, l sum lgrái ls urzs ltromotris st mll s: 3+15= 12 V. Σε = = 12 V [13] Siguino un rzonminto nálogo l qu hmos utilizo pr sriir l sum lgrái l sguno mimro l uión [4.12-3], l mll ntrior, l rorrr nuvmnt st mll, prtino l nuo, nontrmos l trmo ---, qu s rorrio solmnt por l intnsi I 2, qu s hor positiv porqu su sntio s l mismo qu l rorrio l mll, y multipli por to l rsistni iho trmo rsult (6+3I 2. A ontinuión nontrmos. l trmo - qu s rorrio simultánmnt por ls intnsis I 1 I 2, pro hor, I 1 s ngtiv por su sr su sntio ontrrio l rorrio l mll y l intnsi nt qu rorr st trmo s l irni I 2 I 1 ms intnsis, y multipli por to l rsistni qu rorr s hst, rsult (2+4(I 2 I 1 En onsuni, l sum lgrái l sguno mimro l uión [4.12-3] s, pr st mll ΣIR =(6 + 3I 2 +(2 + 4(I 2 I 1 = 9I 2 + 6(I 2 I 1 = 15I 2 [14] Sustituyno [13] y [14] n l uión [4.12-3], s otin pr st mll l uión Ls uions [12], [15] ormn l sistm uy soluión, un vz simpliio y rsulto, s 12 = 15I 2 [15] 15 = 9I 1 6I 2 12 = 15I 2 I ' 1 = 3 A I ' 2 Ls intnsis qu iruln por ls irnts rms l iruito son: Rm -: L intnsi s l irni ntr I 2 I 1, y pusto qu s I 2 > I 1, l orrint rsultnt s 1 A y irul hi, rsulto qu onur on l otnio por l primr métoo [16] [17]
5 ltos 5 Rm ---: Por st rm irul solmnt l intnsi I 1 = 3 A, qu s l intnsi qu hmos nomino n l métoo ntrior. Rm ---: Por st rm irul solmnt l intnsi I 2, qu s l intnsi qu hmos nomino n l métoo ntrior. Como pu vrs, s otinn los mismos rsultos on mos métoos. Dirni potnil ntr los nuos y Ahor stmos n oniions lulr ih irni potnil plino l ly gnrl Ohm [Vés, Cpítulo Furz ltromotriz.p, pígr 11.3]: I ΣR i = Σε i (V V i Pr llo, utilizmos l igur y los rsultos otnios on l primr métoo, on ojto prtir l uso ih ly pliánol un ls trs rms l iruito. Rm ---: (1+ 2 = 30 (V 4 Ω Dspjno y sustituyno = 3 A V = = 21 V Rm -: (4 + 2 = 15 (V Dspjno y sustituyno = 1 A [18] 6 Ω 3 Ω V = 15 6 = 15 6( 1 = 21 V [19] Ruérs qu l intnsi irul, n rli, n sntio opusto l inio n l igur. Rm ---: (6 + 3 = 3 (V V Dspjno y sustituyno V = = = 21 V [20] Como s vint, s otin l mismo rsulto pr l irni potnil, ulquir qu s l rm utiliz pr su álulo.
En un grafo se puede recorrer la información de diferentes maneras para llegar de un punto a otro.
CAMINOS Y CIRCUITOS En un grfo s pu rorrr l informión ifrnts mnrs pr llgr un punto otro. Cmino Ciruito (Cilo) Ciruito simpl longitu n Cmino simpl longitu n ulquir suni noos n l qu pr son ynts. Es un mino
MÉTODO INDUCTIVO. Capítulo TRILCE
pítulo É V l É V r lys prtir l osrvión los hhos, mint l gnrlizión l omportminto osrvo; n rli, lo qu rliz s un spi gnrlizión, sin qu por mio l lógi pu onsguir un mostrión ls its lys o onjunto onlusions.
Números Racionales 1. INTRODUCCIÓN
Númros Rionls Título: Númros Rionls Trgt: PROFESORES DE MATEMÁTICAS Asigntur: Mtmátis Autor: Emilin Oliván Clz Lini n Mtmátis Prosor Mtmátis n Euión Sunri 1 INTRODUCCIÓN En l ominio intgri (DI) los númros
FACTORIZACIÓN. Capítulo TRILCE
TRILCE Cpítulo FACTORIZACIÓN Ftorizr un polinomio s somponrlo n os o más polinomios llmos ftors, tl moo qu, l multiplirlos, s otng l polinomio originl. Ejmplo : y ( y)( y) Ants ftorizr y ftorizo ftors
Minimización por el método de QUINE-McCLUSKEY
Minimizión por l métoo QUINE-MCLUSKEY S tinn os forms srrollr l métoo Quin-MClusky: on un ominión inri y un ominión iml. Ams forms s srrollrán mint os jmplos, rsptivmnt. Cominión BINARIA. S l funión: F(A,
SEMEJANZA DE TRIÁNGULOS
IES ÉLAIOS Curso - Ruprión ª Evluión ÁREA: MATEMÁTICAS º ESO OPCIÓN B TEMAS,, 6 y 7 ACTIVIDADES DE RECUPERACIÓN DE LA ª EVALUACIÓN SEMEJANZA DE TRIÁNGULOS. S quir onstruir un prtrr on orm triángulo rtángulo.
(a+1)x+ay=3 (a+1)x+(a+1)y+(a+2)z=1 (a 2 +a)x+(a 2-1)y+(a 2-2a-8)z=2a+5. a 1. a+1. a+2 a 2-2a a+5 ~1 0. a=-1
EXTRAORDINARIO DE 4. PROBLEMA A. Estudi l siguint sistm d uions linls dpndint dl prámtro rl y rsuélvlo n los sos n qu s omptil: Aplimos l método d Guss: ~ + + + + + - 3 + --6 - -+3 (+)+y3 (+)+(+)y+(+)z
DESIGUALDADES E INECUACIONES VALOR ABSOLUTO
TRILCE Cpítulo DESIGUALDADES E INECUACIONES VALOR ABSOLUTO DESIGUALDADES Torms l Dsigul Dfiniión S nomin sigul l omprión qu s stl ntr os prsions rls, mint los signos rlión >,
Reducción de. Estados equivalentes. Reducción de estados equivalentes. Ejemplo. Tabla de estados Mario Medina C. 1
Ruión stos quivlnts Mrio Min. mriomin@u.l Ruión stos quivlnts Proso isño ntrior no sgur l númro mínimo stos Ruión númro stos Ru l númro lip-lops Ru l lógi ominionl Asignión vrils sto tmién pu ruir lógi
Matemáticas II Bloque VI Carlos Tiznado Torres
Mtmátis II loqu VI rlos Tizno Torrs IRUNFERENI El írulo y l irunfrni son os ojtos gométrios qu hn llmo l tnión y hn sio l ojto stuio un grn númro mtmátios s timpos ntiguos, sino más grn utili práti pr
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO 6. RELACIONES
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO. RELACIONES DIAGRAMAS DE HASSE. AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO Digrms Hss Un rlión R:A B s orn pril o prilmnt orn si
FUNCIONES DERIVABLES EN UN INTERVALO
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
B B B B B a) Siguiendo el orden establecido arriba, los subconjuntos se corresponden con los bloques
4 Álgr Bool 4 Álgr Bool 1 Sn B = {0, 1} y f: B 4 B un funión lógi utro vrils,,, y. Si n B 4 sustituimos B por lguno sus suonjuntos no víos {0} o {1} o B s otinn suonjuntos B 4. Así tnmos qu {1} {0} {0}
DEPARTAMENTO DE MATEMÁTICAS Alumno/a 4º ESO Nº TRIGONOMETRIA 1º PARTE
DEPRTMENTO DE MTEMÁTIS lumno/ 4º ESO Nº TRIGONOMETRI 1º PRTE 84 Introuión Un rinto poligonl simpr lo pomos iviir n triángulos. omo por jmplo Lo pomos iviir n triángulos D E F G H I J K L M N Ñ O P Q R
Distribución de corriente
Ensyo tipo sgún DN EN 439-1 Durnt un nsyo tipo sistm s rlizron los siguints nsyos n los sistms rrs RiLin, sí omo n omponnts montj rprsnttivos RiLin: Distriuión orrint Digrms rsistni l ortoiruito sgún EC
MÓDULO Nº5 COMPARADORES Y SUMADORES
MÓULO Nº OMPRORES Y SUMORES UNI: LÓGI OMINTORI TEMS: omprors. Sumors. OJETIVOS: Explir qu s un ompror y sus prinipls rtrístis. Explir qu s un sumor y sus prinipls rtrístis.. omprors: ESRROLLO E TEMS En
EJERCICIOS DE REFUERZO DE ECUACIONES 4º ESO A
Dprtmnto Cinis Mtmátis ºA Euions, sistms inuions Colio Con Espin Prosor Ánl Fuiio Mrtínz EJERCICIOS DE REFUERZO DE ECUACIONES º ESO A Rsolvr ls siuints uions: - = - = + + = = + = + = - = - -=- - = - -
Examen de Introducción a la Investigación de Operaciones Fecha: 14 de Diciembre de 2010
Emn Introuión l Invstigión Oprions Fh: 4 Diimr 00 INDICACIONES Durión l mn: 4 hrs. Esriir ls hojs un solo lo. Numrr ls hojs. Ponr nomr y éul inti n l ángulo suprior rho hoj. Esriir n l primr hoj l totl
Una ecuación tiene dos miembros 3x 2 + 5x = 3 (x-3) + 3
TEMA : ECUACIONES CONCEPTO DE ECUACIÓN Un uión s un igul lgri qu solo s umpl pr irtos vlors trminos. A stos vlors qu hn irt l uión s ls llm soluions. 0 tin omo soluión X.. Un igul lgri qu s váli pr ulquir
TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES
3. LÍMITES COLEGIO RAIMUNDO LULIO Frnciscnos T.O.R. Cód. 8367 TEMA 3 LÍMITES Y CONTINUIDAD DE FUNCIONES Dfinición: S dic qu l límit d l función f s igul L, cundo tind, si cundo s proim, f s proim L, sin
Teoría Problemas Total
Not Prátis: Not Torí+ Pro: NOTA FNA: Funmntos Físios l nformáti º- ngnirí nformáti onvotori xtrorinri spil. TEOÍA 9 iimr 00 Apllios y Nomr: Soluión Grupo: Torí Prolms Totl A NOTA DE TEOÍA ONSTTUYE E 0
Es fácil ver que la criptoaritmética es un procedimiento de cifrar por sustitución y que la clave es una regla matemática.
TILC Cpítulo CIPTOITÉTIC L riptoritméti s un rt qu smpñó un importnt ppl n l snvolviminto l Histori. L riptoritméti no s más qu un jugo. No s s n qué épo s invntó; pro los fiionos ls vris omnzron intrsrs
TEMA 4: MONOMIOS Y POLINOMIOS MONOMIOS Es el producto de un número por una o varias letras. Todo monomio consta de varias partes.
TEM : MONOMIOS Y OLINOMIOS MONOMIOS Es l prouto un númro por un o vris ltrs. Too monomio onst vris prts. El ro un monomio s l númro ltrs qu tin s lul sumno los ponnts ls ltrs. El ro l monomio ntrior srá.
Teoría Problemas Total
Not Prátis: Not orí+ Pro: NO FN: Funmntos Físios l nformáti º- ng. nf. onvotori xtrorinri. EOÍ sptimr 00 pllios y Nomr: Soluión Grupo: orí Prolms otl NO DE EOÍ ONSUYE E 0 % DE NO O DE EXMEN. D PEGUN DE
TRABAJO PRÁCTICO N 5 AÑO 2017 TEORÍA DE GRAFOS Y ÁRBOLES
Pr l grfo l Fig., trmin: TRABAJO PRÁCTICO N 5 AÑO 27 TEORÍA DE GRAFOS Y ÁRBOLES ) un mino - qu no s un rorrio; ) un rorrio qu no s un mino simpl; ) un mino simpl - ; ) un mino rro - qu no s un iruito;
Desarrollado por Ricardo Soto De Giorgis. Desarrollado por Ricardo Soto De Giorgis Representación de Grafos Matriz de Adyacencia
. Grfos Un grfo s un onjunto puntos y un onjunto líns llms rists o ros, un ls uls un un punto llmo noo o vérti on otro. S rprsntn l onjunto vértis un grfo o G por V G V G = {,,,, El onjunto ros por A G
CONTEO DE FIGURAS. Capítulo TRILCE T R I L C E 5 6
TRILCE Cpítulo CONTEO DE FIGURAS INTRODUCCIÓN El srrollo l tnologí n los últimos ños, h sio rlmnt vrtiginoso, ls pizs, y omponnts los prtos mornos s hn ruio notlmnt su tmño y quirio un sin fin forms, puino
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------
IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d
Determinantes D - 1 DETERMINANTES
Determinntes D - DETERMINNTES Determinnte e un mtri ur e oren os Definiión: D un mtri ur e oren os numero rel: Det (), se llm eterminnte e l El eterminnte e un mtri ur e oren os es igul l routo e los elementos
1.- Resolver utilizando el método de Gauss el siguiente sistema. 3.- Resuelve tres de las siguientes ecuaciones exponenciales y logaritmicas
Colo L Conpón EJERCICIOS REPASO PARA SEPTIEMBRE º BACHILLERATO-B 00-0 NOMBRE:.- Rsolvr utlzno l métoo Guss l unt stm. z z z 8.- Rsulv os ls unts uons 7.- Rsulv trs ls unts uons ponnls lortms lo lo 7 8
1ºC i 2ºC i 3ºC. Número de intervalos de tiempo (I) Nº de campanadas Nº de intervalos Tiempo 3 7
TRILCE Cpítulo CRONOETRÍA A. PROBLEAS SOBRE CAPANADAS O AFINES Cuno nos rfrimos un vnto qu impli un ión, omo mpns golps, onttos sguios vloi onstnt, mos onsirr qu l timpo trnsurrio s propimnt l los prioos
A puede expresarse como producto de matrices elementales
TLLER GEOMETRÍ VECTORIL Y NLÍTIC FCULTD DE INGENIERÍ-UNIVERSIDD DE NTIOQUI - Profsor: Jim nrés Jrmillo Gonzálz jimj@onptoomputorsom Prt l mtril s tomo oumntos los profsors lrto Jrmillo Grimlo Ols En los
POTENCIA BASE EXPONENTE VALOR
TEMA POTENCIAS Y RADICALES CONCEPTO DE POTENCIA Un potni s un or rvi sriir un prouto oro por vrios tors iuls. = Los lntos qu onstitun un potni son L s l potni s l núro qu ultiplios por sí iso n st so l.
OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)
IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo
F U T S W W P V F W P V G U T S P V G F P V W P V P V W. nfec. G nfe C. Energía libre y fuerza electromotriz.
nrgí libr y furz lctromotriz. Dsd un punto d vist trmodinámico, sbmos qu tmprtur constnt, l disminución d l nrgí libr d Hlmholtz, F (pr un procso rvrsibl), rprsnt l trbjo totl (W) hcho sobr los lrddors,
Aquauno Video 2 Plus
Cont l progrmor l grifo. Aquuno Vio 2 Plus Pág. 1 Guí uso 3 START STOP RESET CANCEL 3 4 5 6 3 4 5 6 3 4 5 6 Cli! Pr Aquuno Vio 2 (ó.): 8454-8428 Pr Aquuno Vio 2 Plus (ó.): 8412 Ar l móulo progrmión, prsionno
Primer Parcial de Introducción a la Investigación de Operaciones Fecha: 5 de mayo de 2015
Primr Pril Introuión l Invstigión Oprions Fh: 5 myo 2015 INDICACIONES Durión l pril: 3 hrs. Esriir ls hojs un solo lo. No s prmit l uso mtril ni lulor. Numrr ls hojs. Ponr nomr y númro éul n l ángulo suprior
4.3 Cuál es el número máximo de arcos que puede tener un grafo no dirigido sin ciclos? Y cuál será para un grafo dirigido acíclico (GDA)?
Tm. Grfos. Do un árol xpnsión, rsultnt un rorrio sor un grfo no irigio, qué tipo ros (prt los l árol) pun prr si l rorrio s un úsqu n profuni o un úsqu n nhur? Qué ros prrán si l rorrio (n profuni o n
TEMA 5: FRACCIONES. Las fracciones permiten trabajar de manera simbólica con cantidades no enteras.
Alonso Fernánez Glián TEMA FRACCIONES Ls friones permiten trjr e mner simóli on nties no enters.. CONCEPTO DE FRACCIÓN Un frión es un expresión e l form numeror enominor ( 0) Represent el resulto e iviir
Estructuras de Datos. Grafos. Grafos. Grafos. Tema 1. Grafos. Definiciónes básicas: Definiciónes básicas:
Estruturs Dtos m 1. 1. Dfiniions ásis 2. Implmntions 3. Funions mnipulión 4. Rorrios Dfiniións ásis: L torí grfos: rm l mtmáti omintori muy útil n l soluión prolms prátios qu s formuln mnr nturl por mio
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE CASTILLA Y LEÓN JUNIO (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
IES STER BDJOZ RUEB DE ESO (OGSE) UNIVERSIDD DE STI Y EÓN JUNIO - (RESUETOS por ntonio nguino) TEÁTIS II Tipo áio: hors inutos ritrios gnrls vluión l pru: S osrvrán funntlnt los siguints sptos: orrt utiliión
INTEGRAL DEFINIDA ÁREAS Y VOLUMENES
Intgrl indinid. gl d Brrow INTEGA DEFINIDA ÁEAS Y OUMENES siguint rgl, qu s s n l torm undmntl dl cálculo intgrl, rlcion l intgrl dinid con ls intgrls indinids prmit clculr ls intgrls dinids. intgrl dinid
SOLUCIONES DE LOS EJERCICIOS DE CORRIENTE CONTINUA -1 er TRIMESTRE-. problemas:11, 12 y 14
R= SOLUCONES DE LOS PROLEMS DE ELECTRCDD DE C.C. SOLUCONES DE LOS EJERCCOS DE CORRENTE CONTNU - er TRMESTRE-. prolems:, y ª ) Soluionremos este prolem por el método generl de nálisis por lzos ásios, omprondo
3,2. 2) Determina la ecuación ordinaria y el resto de los elementos de las elipses con las siguientes ecuaciones generales:
REPASO EXAMEN SEMESTRAL MATEMATICAS GRUPO 0 TEMA: ELIPSE ) Dtrmin l uión orinri, uión gnrl y l rsto los lmntos ls lipss on los siguints lmntos: *Horizontl C, 7 V ', B, ) Dtrmin l uión orinri y l rsto los
También pueden descomponerse los segmentos en función de los vectores posición lo que da como resultado:
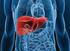EL ÁLGER GEÉTRI EL ESPI Y TIEP 87 6. GEETRÍ EL TETRER Volmn l ttrro El volmn n ttrro s l st prt l volmn l prllpípo q lo ontin (vés igr 5.6). El volmn l prllpípo s igl l proto trior trs rists lsqir no prlls.
ECUACIONES DE PRIMER Y SEGUNDO GRADO
TRILCE Cpítulo 0 ECUACIONES DE PRIMER Y SEGUNDO GRADO Euions Son iguls oniionls, n ls qu l mnos istir un ltr llm inógnit : Ejmplo : - = 7 + Es un uión inógnit "". Soluión un uión Es l vlor o vlors l inógnit
UNIDAD 6 DETERMINANTES. 1. DETERMINANTE DE ORDEN UNO. Dada una matriz cuadrada de orden uno A = ( a DETERMINANTE DE ORDEN DOS.
IES Pr Pov Guix Mtátis II UNIDD DETERMINNTES.. DETERMINNTE DE ORDEN UNO. D un triz ur orn uno sri o in, oo l núro rl:. DETERMINNTE DE ORDEN DOS. D un triz ur orn os oo l núro rl: Ejplos:, s in l rinnt,
Árboles binarios. Árbol: definición. Árbol (del latín arbor oris):
Árol: iniión Árols inrios Árol (l ltín ror oris): Plnt prnn, trono lñoso y lvo, qu s rmii irt ltur l sulo. (otrs, vr Rl Ami Espñol ) Frno Guii Polno Esul Innirí Inustril Pontiii Univrsi Ctóli Vlpríso,
Ejercicios PSU. Guía Función inversa Bloque 32
PROGRAMA EGRESADOS Guí Funión invrs Bloqu 32 Ejriios PSU A ontinuión, s prsntn los siguints jriios, los uls sugrimos rsponr l máimo posil y lugo, junto tu profsor(), rvisr tllmnt ls prgunts más rprsnttivs,
Analógicos ELECTROSÓN INSTRUMENTOS ANALÓGICOS CARACTERÍSTICAS GENERALES CM-04 EN60051, VDE 0410, BS-89, EN50081, EN50082, EN61010
CRCTERÍSTICS GENERLES Norms EN0051, VDE 010, S-89, EN50081, EN5008, EN1010 Crtifiions ISO 9001:008 DER NORSKE VERITS, UREU VERITS Envolvnts IEC 155 x, 9x9, 1x1 MODULR (pr rril DIN) Esls Vlor finl sl DIN
JUEGOS DE INGENIO. Capítulo TRILCE. A. TRANSMISIONES H : Horario ; AH : Antihorario AH H. Como A es más grande que B, Entonces :
TRILCE Cpítulo 2 JUEGOS DE INGENIO. TRNSMISIONES : orrio ; : ntihorrio Como s más grn qu, Entons : mnos vults qu mos rorrn l mism nti ints Ls rus uis n un mismo j girn l mism vloi y n l mismo sntio Ejmplo
3A,,. Prueba que M es un subespacio
.- Dtin os tis us X Y on tls qu: Y X Y X.- Estui l inpnni linl ls tis C.- Pu qu ls siguints tis son un s l spio vtoil ls tis us on.- S onsi l onjunto } R. Pu qu s un suspio vtoil.- Hll os tis us on os
Capítulo TRILCE SUCESIONES NUMÉRICAS
TILCE Cpítulo SUCESIONES Un susión s un onjunto orno lmntos (pun sr númros, ltrs, figurs o un ominión los sos ntriors), moo qu uno oup un lugr stlio, tl qu s pu istinguir l primro, l sguno, l trro y sí
1) Halla La ecuación del lugar geométrico de los puntos del plano cuya distancia a P(1,2) es doble que su distancia a Q(-1,8).
ÓNIS º BHILLERTO ) Hll L uión lugr gométrio los untos lno u istni P(,) s ol qu su istni Q(-,). ( R, P) ( R, Q) ( ) ( ) ( ) ( ) ( ) ) Enuntr l irunfrni irunsrit l triángulo vértis (-,); B(-,); (-,). lul
UNIDAD. Polígonos. Se dedica este tema al conocimiento de los polígonos y al estudio de sus construcciones, y se inicia haciendo tres consideraciones:
UNI Polígonos ÍNIE E ONTENIOS 1. ONEPTOS ÁSIOS SORE TRIÁNGULOS.......................................... 58 2. ONSTRUIONES ELEMENTLES E TRIÁNGULOS................................... 59 2.1. ritrios igul
I.E.S. Mediterráneo de Málaga Junio 2012 Juan Carlos Alonso Gianonatti PROPUESTA A
I.E.S. Mditrráno d Málg Junio Jun Crlos lonso Ginontti PROPUEST.- ( punto) S f() un función positiv n l intrvlo [ ] sí ( ) f pr. Si l ár itd por f() l j d bciss (j O) ls rcts s igul clcul l ár dl rcinto
IES Mediterráneo de Málaga Solución Junio 2004 Juan Carlos Alonso Gianonatti OPCIÓN A
IES Mditrráno d Málg Solución Junio Jun rlos lonso Ginontti OPIÓN - undo l ño 8 Bthovn scrib su Primr Sinoní su dd s di vcs mor qu l dl jovncito Frn Schubrt Ps l timpo s Schubrt quin compon su célbr Sinoní
26 EJERCICIOS de LOGARITMOS
6 EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.
Soluciones a los ejercicios, problemas y cuestiones Unidad 1. El conjunto de los números reales Matemáticas aplicadas a las Ciencias Sociales I
Soluions los jriios prolms ustions Uni. El onjunto los númros rls Mtmátis plis ls inis Soils I NÚMEROS RIONLES E IRRIONLES. Hll l númro iml qu orrspon un ls siguints rions. omnt l rsulto: 0 00 0 0000 00
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE GALICIA SEPTIEMBRE (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos
IES CSTELR DJOZ Mnguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE GLICI SEPTIEMRE - (RESUELTOS por ntonio Mnguino) MTEMÁTICS II Timpo máimo: hors minutos El lumno db rspondr solmnt los jrcicios d un d ls opcions
PROGRESIONES. Capítulo TRILCE. Progresión aritmética (P.A.) 3. Número de términos (n)
TRILCE Cpítulo 7 PROGRESIONES Progrsió ritméti (PA) Es qull susió or l qu térmio, xpto l primro, s igul l térmio trior umto u vlor ostt llmo rzó l progrsió Rprstió u PA r r ( )r Númro térmios () r 4 Térmios
1º ITIS Matemática discreta Relación 5 RETÍCULOS Y ÁLGEBRAS DE BOOLE. ordenado por divisibilidad. Dibujar el diagrama de orden de A.
º ITIS Mtmáti isrt Rlión 5 RETÍCULOS Y ÁLGEBRAS DE BOOLE. S A = {,2,3,4,6,8,9,2,8,24} orno por ivisiili. Diujr l irm orn A. 2. S X {,, } =. Diujr l irm orn (inlusión) ( X ). 3. S S = { 2,4,6,2,2} orno
Algebra I 1er. Cuatrimestre 2013 Práctica 1 - Conjuntos
lr I 1r. utrimstr 013 Práti 1 - onjuntos Si s un suonjunto un onjunto rrnil V, notrmos por l omplmnto rspto V. Por onvnión, si x s un númro rl positivo, x not l únio númro rl positivo uyo uro s x. 1. Do
Bajo petición, se pueden suministrar otros tipos de ganchos. La mayoría de los ganchos vienen suministrados con lengüeta de seguridad.
Gnhos Apliions Los nhos s utilizn n sistms lvión omo un onxión ntr l r y l l o n. Aln Vn Bst or un mpli m nhos, s nhos normls orjos ro l rono hst nhos irtorios ro lo, qu son tmplos y rvnios. Bjo ptiión,
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 7. INTEGRALES DEFINIDAS E IMPROPIAS
FUNDAMENTOS MATEMÁTICOS (Grdo n Ingnirí Informátic) Práctic 7. INTEGRALES DEFINIDAS E IMPROPIAS.- L intgrl dfinid d Rimnn. L intgrl dfinid d Rimnn surg prtir dl prolm dl cálculo d árs d suprficis dlimitds
UNIVERSIDAD DE LA RIOJA JUNIO lim
IES Mditrráno d Málg Emn Junio d Jun Crlos lonso Ginontti UNIVERSIDD DE L RIOJ JUNIO El lumno contstrá los jrcicios d un d ls dos propusts ( o ) qu s l ofrcn. Nunc dbrá contstr jrcicios d un propust jrcicios
Proyecciones ortogonales (diédricas y triédricas)
Proyccions ortogonls (diédrics y triédrics) Pro. Rúl F. ongiorno S dnominn proyccions ortogonls l sistm d rprsntción qu nos prmit diujr n dirnts plnos un ojto situdo n l spcio. undo hlmos d sistms d rprsntción
Hacia la universidad Álgebra lineal
Hi l universi Álger linel OPCIÓN A Soluionrio. Un mtriz ur A se llm ntisimétri uno su trspuest es igul su opuest. Otén l form generl e un mtriz A e oren que se ntisimétri. Clul A, A y A. Consieremos l
Algunos Algoritmos Sobre Gráficas
Arturo Díz Pérz Algunos Algoritmos Sor Gráis Arturo Díz Pérz Sión Computión Dprtmnto Ingnirí Elétri CINVESTAV-IPN A. Instituto Politénio Nionl No. 08 Col. Sn Pro Ztno Méxio, D. F. CP 0700 Tl. ()747 800
Matrices y determinantes
Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net) Mtries eterminntes CTS. Sen ls mtries, C. Hll l mtri ( C). Soluión: Mtemátis CCSS II Mtries José Mrí Mrtíne Meino (SM, www.profes.net)
Cálculo II (0252) TEMA 3 INTEGRAL IMPROPIA. Semestre
Cálulo II (5) Smstr - TEMA 3 INTEGRAL IMPROPIA Smstr - Junio Dprtmnto d Mtmáti Aplid U.C.V. F.I.U.C.V. CÁLCULO II (5) Ls nots prsntds ontinuión tinn omo únio fin, l d prstr poyo l studint y filitr su ntndiminto
Tema 3. Guías de Onda y Líneas de Transmisión
Tm 3. Guís On Líns Trnsmisión 3. Inrouión 3. Soluions gnrls pr ons TM T TM 3.3 L guí plnos prllos 3.4 L guí rngulr 3.5 L guí on irulr 3.6 l bl oil 3.7 Líns plnrs 3.8 Comprión nr isinos ipos líns guís Bibliogrfí
, donde a y b son números cualesquiera.
Mtemátis Mtries José Mrí Mrtínez Meino (SM, www.profes.net) MJ6 D l mtriz enuentr tos ls mtries P tles que P = P. Soluión: Se ese que Por tnto, ee umplirse que: Por tnto, P, one y son números ulesquier.
Problemas y preguntas de tipo test. Integrales indefinidas. 1. Calcula las siguientes integrales: b) dx = dx
Análisis Mmáio. Ingrls Prolms y prguns d ipo s Ingrls indfinids. Clul ls siguins ingrls: ) d ) d ) S sri l ingrndo omo s indi: d = d ) (sin ) d d os d) = d ln ) d = d 7 / 5 / / 7 / = d ) Ajusndo onsns:
0. x = 0. 0. x = b. x Solución:
TEMA : ECUACIONES E INECUACIONES CONCEPTO DE ECUACIÓN Un uión s un igul lgri qu l umpln tn solo un sri númros qu son ls soluions. Es ir, Ls soluions un uión son los vlors qu n tomr ls ltrs pr qu l igul
EJERCICIOS PROPUESTOS
EJERIIOS PROPUESTOS 0. Do l onjunto: = {4; 3; {6}; 8} y ls proposiions: * { 3} * { 4} * { 6} * { 6} * 8 * * * { 3 ; 8} Iniqu l númro proposiions vrrs: ) 7 ) 6 ) 5 ) 4 ) 3 0. Dos los onjuntos iguls: 3 ;
Soluciones a los ejercicios, problemas y cuestiones Unidad 2. Polinomios y fracciones algebraicas Matemáticas aplicadas a las Ciencias Sociales I
Soluios los jriios prolms ustios Ui oliomios rios lgris Mtmátis plis ls Ciis Soils I EJECICIOS SUMA ESTA Y MULTILICACIÓN DE OLINOMIOS Dos los poliomios Dtrmi si stá ruios si so ompltos ii su gro Clul trmi
TEMA 9. DETERMINANTES.
Uni.Determinntes TEM. DETERMINNTES.. Coneptos previos, permutiones. Definiión generl e eterminntes. Determinnte e mtries e oren y oren... Determinnte mtries urs e oren.. Determinnte mtries urs e oren.
Función exponencial y logarítmica:
MATEMÁTICAS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA º DE BACHILLER Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii)
MATRICES: un apunte teórico-práctico
MRICES: un punte teório-prátio Definiión Un mtriz e tmño n x m es un rreglo e números reles oloos en n fils (o renglones) y m olumns, e l siguiente form: [ ].. n Los números se llmn elementos o entrs e
PROBLEMAS DE ÁLGEBRA DE MATRICES
Mtemátis Álger e mtries José Mrí Mrtínez Meino PROLEMS DE ÁLGER DE MTRCES Oservión: L myorí e estos ejeriios proeen e ls prues e Seletivi D l mtriz enuentr tos ls mtries P tles que P P Soluión: Se ese
ÁREAS DE REGIONES SOMBREADAS
TILE pítulo 0 ÁE E EGIE E Ejplo º i s un uro lo y "" s ntro, ntons l ár l rgión sor s: soluión : or trslo rgions sors sí tnos qu l ár l rgión sor s un triángulo, qu s igul l urt prt l uro. so Ejplo º i
Deducción de las reglas de derivación. Partiendo de las derivadas de la función potencial, la función exponencial y la función seno, ( ) ( ) 1
dmttmtics.wordprss.com Btriz d Otto Lópz Dducción d ls rgls d drivción Prtindo d ls drivds d l función potncil, l función ponncil l función sno, = R = f = =, f = sn = cos, f,, d ls rgls d drivción pr l
SOLUCIONES DE LIMITES
SOLUCIONES DE LIMITES.. Ln Sustituyndo por obtnmos: INDETERMINADO Ln Como s trt d un indtrminción d tipo L Hopitl, plicmos dich rgl: Ln Ln Rsolvmos prt l it Ln INDETERMINACIÓN d tipo L Hopitl otr vz: 6Ln
TRANSFORMADORES EN PARALELO
TRNFORMDORE EN PRLELO. Trnsformdors d igul rzón d trnsformción Not: no s tomn n cunt ls pérdids n l firro. q q q llmrmos s cumpl b. Trnsformdors d rzón d trnsformción un poco distints Rfridos l scundrio:
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL
Cpít ulo RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO EN POSICIÓN NORMAL Dfiniions Pvis: I. ÁNGULO EN POSICIÓN NORMAL Llmo tmién n posiión nóni o stán. Es quél ángulo tigonométio uo véti oini on l oign l sistm
ALELUYA. D A Bmi F#mi ALELUYA, ALELU ALELUYA G D A ALELUYA, ALELUYA. D A Bmi F#mi ALELUYA, ALELU ALELUYA, G D A D ALELUYA, ALELUUUYA SANTO
NTR UNTS VS --0 1---3-3-3 1---5-5 1 3 0 --1---3---5-5-5---3---6-6---3---5---1 UNTS VS SINO NIÑO T R ON MIS VRSOS T I QU T MB //POO POO ON L TIMPO mi OLVINOM TI mi POR MINOS QU S LJN M PRI// HOY H VULTO
9 TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO
9 TRSLINES, GIRS SIMETRÍS EN EL PLN EJERIIS PRPUESTS 9. ibuja un parallogramo y razona qué pars d vctors dtrminados por los vértics son quipolnts. Son quipolnts los qu son parallos y dl mismo sntido, y
MATRICES. MATRIZ INVERSA. DETERMINANTES.
DP. - S - 59 7 Mtemátis ISSN: 988-79X 6 MTRICES. MTRIZ INVERS. DETERMINNTES. plino ls propiees e los eterminntes y sin utilizr l regl e Srrus, lulr rzonmente ls ríes e l euión polinómi. Enunir ls propiees
DERIVABILIDAD.. Intuitivamente: cuando no presenta saltos en ese punto. Toda función derivable en un punto, es continua en ese punto.
ERIVABILIA.... inir unción continu n un punto. inir unción drivbl n un punto. s posibl ponr un jmplo d un unción qu n s: ) Continu y drivbl. b) rivbl y no continu. c) Continu y no drivbl. y s continu n
Matemáticas Discretas Tc1003 Teoría de Grafos. Teoría de Grafos
Mtmátis Disrts Torí Gros OBJETIVO Torí Gros Uni Tm utm Ojtivos VIII Torí Gros 7.1 Diniions 7.2 Trytoris y iruitos Eulr 7.3 Trytoris y iruitos Hmilton 7.4 Árols Dinir ronor un ro pr stlr l soluión un prolm.
MATEMÁTICAS MATERIAL DE REFUERZO 1º E.S.O. Soluciones: a) 14 b) 16 c) 2 d) 5 e) 4. Soluciones: a) 10 b) 18 c) 27 d) 29 e) 10 f) 11
MATEMÁTICAS MATERIAL DE REFUERZO º E.S.O Primr vluión. Clul ( 0 7 ( 8 0 ( 7 ( 7 8 [( ( ( ] [( 8 ( ( ] ( [ ( 8 ( ] [( 0 8 ( ] ( 0. Clul ( ( ( ( ( 8 ( ( ( ( ( ( ( 8 ( ( ( ( ( 0 ( 0 ( ( ( 8 ( ( ( 0 8 ( (
ACTIVIDADES FINALES EJERCICIOS. trino grau fernández. x lím. lím. lím. lím. sen x 1. x 1. lím x 0 sen x x. lím. x lím. sen x. x arcsen x lím 11.
L Í M I T E S th ls ACTIVIDADES FINALES EJERCICIOS Ln tg sn sn [ ( )] 5 sn 6 cotg 7 sn sn 8 9 sn rcsn sn b sn sn cotg 5 sn cos 6 sn 7 n 8 Ln 9 Ln trino gru frnándz th ls 5 Clculr pr qu s cumpl: π Ln tg
1 Álgebra de matrices
Álgr d mtrics Págin Vuls intrncinls I = B C B B B B Págin A t 7 = ; B t = ; C t = ; 7 7 7 D t = ; E t = 7 ; F t = 7 Pr jml, X =. Págin E = Págin 7 A C = ; A D = 7 B A = ; C B = D C = ; D D = 7 Págin ridd
= 0 ' = 0 ' Fracciones equivalentes (productos cruzados iguales): c. Fracción generatriz:
Dprtmto Mtmátis http://www.olgiovirggri.org/so/mt.htm Aritméti. ARITMÉTICA... Cojutos umérios. I Númros tros: úmros turls Númros riols: os juto o sus opustos (úmros imls prióios gtivos). Númros turls:
CARRETONES y transbordadores
CARRETONES y trnsorors irionl trí sor ríls trí sor ríls orrint Crrtons irionls trí, sor ríls trí, sor ríls létrios. 2 Los rrtons GH prmitn l moviminto too tipo rgs nivl l sulo n too tipo inustris y pr
INTEGRALES IMPROPIAS
INTEGRALES IMPROPIAS INDICE.- Integrles impropis de primer espeie....- Integrles impropis de segund espeie.- Integrles impropis del tipo C... 8 4.- Criterios de omprión 8.- Biliogrfi 0 DEFINICION DE INTEGRALES
34 EJERCICIOS de LOGARITMOS
EJERCICIOS d LOGARITMOS Función ponncil y rítmic:. Pr cd un d ls funcions qu figurn continución, s pid: i) Tbl d vlors y rprsntción gráfic. ii) Signo d f(). iii) Corts con los js. iv) Intrvlos d crciminto.