np {N q = n N q > 0} = (1 ρ) n=1 = (1 ρ) nρ n 1 = 1 (3.34) P {T q t T q > 0} = P {T q t T q > 0} P {T q
|
|
|
- Francisco Medina López
- hace 8 años
- Vistas:
Transcripción
1 52 CAPÍTULO 3. SISTEMAS DE ESPERA Luego: P {N q = n N q > 0} = P n+1 2 = (1 ) n 1, n = 1, 2, (3.33) Nótesequelaprobabilidadqueexistan N probabilidadgeométricaconparámetro n 1,locualesigualaladistribuciónprobabilidad q entidasenespera,sigueunadistribución N,eliminandolaentidadqueestásiendoatendida.Enefecto: P {N q = n N q > 0}=P n 1, n = 1, 2,. El valor esperado entidas en espera es igual a: E {N q N q > 0} = np {N q = n N q > 0} = (1 ) n n 1 = (1 ) n n 1 = 1 (3.34) 1 n=0 cola, Se dado requiere que terminar la entidad està la distribuciòn efectivamente en la cola. Esto l tiempo se nomina permanencia distribuciòn en la probabilidad l tiempo espera y se termina usando el Teorema Bayes: P {T q t T q > 0} = P {T q t T q > 0} P {T q (3.35) > 0} Como P {T q > 0} =, ver 3.188, y: P {T q t T q > 0} = P {0 < T q t} = P {T q t} P {T q 0} (3.36) Luego, usando la ecuación 3.26: 1 exp ( [µ λ] t) (1 ) P {T q t T q > 0} = = 1 exp ( [µ λ] t) (3.37) Lo que signica que el tiempo espera sigue una distribución exponencial parámetro w = µ λ,don w El valor esperado l senominalatasaespera(tambiénelpermanencia)enelsistema. tiempo espera es: E {T q T q > 0} = 1 µ λ = 1 w Nótese que el valor esperado l tiempo permanencia (3.38), µ > en λ 3.29 es: la cola, ya mostrado en E {T q } = E {T q T q = 0} P {T q = 0} + E {T q T q > 0} P {T q > 0} = 0 P {T q = 0} + E {T q T q > 0} P {T q > 0} = µ λ (3.39) Ejemplo 3.1 Un sistema cómputo procesa trabajos en serie. El tiempo proceso (spacho) cada trabajo está distribuído exponencialmente con un valor esperado 3 minutos. Los trabajos llegan a una tasa 1 trabajo cada 4 minutos. Halle los siguientes parámetros:
2 3.2. EL SISTEMA M/M/1 53 La probabilidad que un trabajo que llegue requiera más 15 minutos para ser procesado. La longitud promedio la cola para los trabajos que ben esperar, es cir, el valor esperado los trabajos que ben esperar en la cola. Se tiene: λ = 1/4 = 0.25 trabajos/minuto. µ = 1/3 = trabajos/minuto. = λ/µ = 0.75 Erlang. La probabilidad que un trabajo que llegue requiera más 15 minutos para ser procesado se calcula con 3.18 P {T > 15} = 1 P {T 15} = exp ( [µ λ] 15) = exp ( 0, ) = 0,287 El valor esperado los trabajos que ben esperar en la cola se calcula con 3.34 E {N q N q > 0} = 1 1 = 4trabajos. Ejemplo 3.2 Un sistema cmputo procesa trabajos en serie. El tiempo proceso (spacho) cada trabajo está distribuído exponencialmente con un valor esperado 3 minutos. El valor esperado l tiempo en que los trabajos permanecen en el sistema es 30 minutos. Halle los siguientes parámetros: La probabilidad que un trabajo que llegue requiera más 15 minutos para ser procesado. La longitud promedio la cola para los trabajos que ben esperar, es cir, el valor esperado los trabajos que ben esperar en la cola. Se tiene: w = µ λ = 1/30 = trabajos/minuto. µ = 1/3 = trabajos/minuto. λ = µ w = 0.3 trabajos/minuto = λ/µ = 0.9 Erlang. La probabilidad que un trabajo que llegue requiera más 15 minutos para ser procesado se calcula con 3.18 P {T > 15} = 1 P {T 15} = exp ( [µ λ] 15) = exp ( 0, ) = 0,606 El valor esperado los trabajos que ben esperar en la cola se calcula con 3.34 E {N q N q > 0} = 1 1 = 10trabajos. Al comparar estos resultados con los l ejemplo anterior, se nota que al aumentar la tasa llegada trabajos λ 0.25 a 0.3 trabajos/minuto, el valor esperado permanencia los trabajos en el sistema 1/w aumenta 12 a 30 minutos.
3 54 CAPÍTULO 3. SISTEMAS DE ESPERA Ejemplo 3.3 El cajero atención un banco atien, en horas ocina (8 horas diarias), 8 usuarios por hora en promedio, y llegan en promedio 56 usuarios por día. Halle los siguientes parámetros: La probabilidad que el cajero esté socupado. La probabilidad que en el banco exista un máximo K usuarios, entre los que hacen la y los que son atendidos La probabilidad que NO existan más dos usuarios en el banco La probabilidad que no exista cola cuando un usuario llegue La probabilidad que en el banco existan más K usuarios, entre los que hacen la y los que son atendidos La probabilidad que existan más dos usuarios en el banco El valor esperado l número usuarios en el banco El valor esperado l número usuarios en la cola El valor esperado l tiempo permanencia un usuario en el banco El valor esperado l tiempo permanencia en la cola (espera). Se tiene: µ = 8 usuarios / hora. λ = 56 usuarios / 8 horas = 7 usuarios / hora. = λ/µ = Erlang. La probabilidad que el cajero esté socupado se calcula con 3.5: p(0) = 0 (1 ) = 0,125 La probabilidad que en el banco exista un máximo K usuarios, entre los que hacen la y los que son atendidos, se calcula con 3.5: P {N K} = p(0) + P P K = (1 ) K n = 1 K+1 La probabilidad que NO existan más K = 2 usuarios en el banco, se calcula con: P {N 2} = 1 3 = 0,33 La probabilidad que no exista cola cuando un usuario llegue, se calcula con: P {N 1} = 1 2 = 0,23 La probabilidad que en el banco existan más K usuarios, entre los que hacen la y los que son atendidos, se calcula con 3.184:
4 3.2. EL SISTEMA M/M/1 55 P {N > K} = P {N K + 1} = K+1 La probabilidad que existan más dos usuarios en el banco, se calcula con: P {N > 2} = 3 = 0,67 El valor esperado l número usuarios en el banco, se calcula con 3.11: E {N} = 1 = 7usuarios El valor esperado l número usuarios en la cola, se calcula con 3.12: E {N q } = 2 1 = 6,125usuarios El valor esperado l tiempo permanencia un usuario en el banco, se calcula con 3.21: E {T } = λ (1 ) = 1hora. El valor esperado l tiempo permanencia en la cola (espera), se calcula con 3.29: E {T q } = = 0,875horas = 52,5minutos (µ λ) Ejemplo 3.4 El cajero atención un banco atien, en horas ocina (8 horas diarias), 8 usuarios por hora en promedio, y llegan en promedio 56 usuarios por día. Al haber realizado una medición la actividad permanencia usuarios en el banco, se terminó que el usuario que espera más media hora se impacienta y siste efectuar sus operaciones en el banco. Halle la probabilidad que el usuario se impaciente, y calcule la tasa spacho, tal que se quiera impacientar hasta el 10 por ciento los usuarios. Se tiene: µ = 8 usuarios / hora. λ = 56 usuarios / 8 horas = 7 usuarios / hora. = λ/µ = Erlang. La probabilidad que el usuario se impaciente, es la probabilidad que el usuario espere más media hora, lo cual se calcula con 3.26: P {T q > 0,5} = 1 P {T q 0,5} = exp ( [µ λ] 0,5) = 0,53 Si se quiere impacientar hasta el 10 por ciento los usuarios: P {T q > 0,5} = exp ( [µ λ] 0,5) 0,1 Luego, con λ = 7 usuarios / hora. 7 exp ( [µ 7] 0,5) 0,1 µ
5 56 CAPÍTULO 3. SISTEMAS DE ESPERA Resolviendo con métodos numéricos, como se ve en la Figura 3.4, la tasa spacho requerida es µ usuarios / hora. Al comparar estos resultados, se nota que al aumentar la tasa spacho µ 8 a trabajos/hora, la probabilidad impaciencia los usuarios P {T q > 0,5} disminuye l 53 al 10 por ciento. Figura 3.4: Probabilidad impaciencia vs tasa spacho en el sistema M/M/1 l ejemplo 3.3. El sistema M/M/c Descripción scrito Se scribe por el proceso a continuación nacimiento la aplicación y muerte la ecuación la gura, 2.38 don y el tiempo Se tiene entre el llegadas sistema sigue una distribución una distribución exponencial, exponencial, el sistema el tiempo tiene spacho también sigue c atención es FCFS (Primero en llegar, primero en ser atendido). servidores, Por lo tanto, y la la disciplina notacin Kendalles al sistema, M M c.deacuerdoconlagura, y λeslatasapromediollegadaentidas µ Como cada entidad es la llega tasa alsistema promedio conla spacho mismatasa cada llegada,las uno los servidores tasas transición l sistema. unestadoalotrosescriben,tomandolagura2.7. λ 1 = λ 2 = λ 3 =... = λ n = tasa spacho pen l estado l sistema, a medida que llegan entidas λ.comola al sistema,
2. Modelo de colas poissoniano con un servidor M/M/1. 3. Modelo con un servidor y capacidad finita M/M/1/K
 CONTENIDOS 1. Introducción a las colas poissonianas. 2. Modelo de colas poissoniano con un servidor M/M/1 3. Modelo con un servidor y capacidad finita M/M/1/K 4. Modelo con varios servidores M/M/c. Fórmula
CONTENIDOS 1. Introducción a las colas poissonianas. 2. Modelo de colas poissoniano con un servidor M/M/1 3. Modelo con un servidor y capacidad finita M/M/1/K 4. Modelo con varios servidores M/M/c. Fórmula
2 Teoría de colas o líneas de espera
 2 Teoría de colas o líneas de espera El tráfico en redes se puede modelar con la ayuda de la teoría de colas, es por ello ue es importante estudiarlas y comprenderlas. Existen varias definiciones sobre
2 Teoría de colas o líneas de espera El tráfico en redes se puede modelar con la ayuda de la teoría de colas, es por ello ue es importante estudiarlas y comprenderlas. Existen varias definiciones sobre
PROBLEMAS RESUELTOS DE TEORÍA DE COLAS. (M/M/1: Un servidor con llegadas de Poisson y tiempos de servicio Exponenciales)
 PROBLEMAS RESUELTOS DE TEORÍA DE COLAS. (M/M/1: Un servidor con llegadas de Poisson y tiempos de servicio Exponenciales) Prof.: MSc. Julio Rito Vargas A. I. Suponga que en una estación con un solo servidor
PROBLEMAS RESUELTOS DE TEORÍA DE COLAS. (M/M/1: Un servidor con llegadas de Poisson y tiempos de servicio Exponenciales) Prof.: MSc. Julio Rito Vargas A. I. Suponga que en una estación con un solo servidor
Teoría de Colas. TC: Parte de la Investigación Operativa que estudia el comportamiento de sistemas cuyos elementos incluyen líneas de espera (colas).
 Teoría de Colas TC: Parte de la Investigación Operativa que estudia el comportamiento de sistemas cuyos elementos incluyen líneas de espera (colas). IO 07/08 - Teoría de Colas 1 Teoría de Colas: ejemplos
Teoría de Colas TC: Parte de la Investigación Operativa que estudia el comportamiento de sistemas cuyos elementos incluyen líneas de espera (colas). IO 07/08 - Teoría de Colas 1 Teoría de Colas: ejemplos
4 Pruebas y análisis del software
 4 Pruebas y análisis del software En este capítulo se presentan una serie de simulaciones donde se analiza el desempeño de ambos sistemas programados en cuanto a exactitud con otros softwares que se encuentran
4 Pruebas y análisis del software En este capítulo se presentan una serie de simulaciones donde se analiza el desempeño de ambos sistemas programados en cuanto a exactitud con otros softwares que se encuentran
Ejercicios de Teoría de Colas
 Ejercicios de Teoría de Colas Investigación Operativa Ingeniería Informática, UC3M Curso 08/09 1. Demuestra que en una cola M/M/1 se tiene: L = ρ Solución. L = = = = = ρ np n nρ n (1 ρ) nρ n n=1 ρ n ρ
Ejercicios de Teoría de Colas Investigación Operativa Ingeniería Informática, UC3M Curso 08/09 1. Demuestra que en una cola M/M/1 se tiene: L = ρ Solución. L = = = = = ρ np n nρ n (1 ρ) nρ n n=1 ρ n ρ
PROBLEMAS RESUELTOS DE TEORÍA DE COLAS. (M/M/1: Un servidor con llegadas de Poisson y tiempos de servicio Exponenciales)
 PROBLEMAS RESUELTOS DE TEORÍA DE COLAS. (M/M/: Un servidor con llegadas de Poisson y tiempos de servicio Exponenciales) Prof.: MSc. Julio Rito Vargas A.. Suponga que en una estación con un solo servidor
PROBLEMAS RESUELTOS DE TEORÍA DE COLAS. (M/M/: Un servidor con llegadas de Poisson y tiempos de servicio Exponenciales) Prof.: MSc. Julio Rito Vargas A.. Suponga que en una estación con un solo servidor
SIMULACION. Formulación de modelos: solución obtenida de manera analítica
 SIMULACION Formulación de modelos: solución obtenida de manera analítica Modelos analíticos: suposiciones simplificatorias, sus soluciones son inadecuadas para ponerlas en práctica. Simulación: Imitar
SIMULACION Formulación de modelos: solución obtenida de manera analítica Modelos analíticos: suposiciones simplificatorias, sus soluciones son inadecuadas para ponerlas en práctica. Simulación: Imitar
Análisis de Decisiones II
 Tema 14 Distribución de llegadas Poisson, distribución de servicio Exponencial, varios servidores, servicio PEPS, población y cola infinita Objetivo de aprendizaje del tema Al finalizar el tema serás capaz
Tema 14 Distribución de llegadas Poisson, distribución de servicio Exponencial, varios servidores, servicio PEPS, población y cola infinita Objetivo de aprendizaje del tema Al finalizar el tema serás capaz
DISEÑO DEL SOFTWARE TRAFFIC ANALYZER. Analyzer. En este capítulo se reporta el desarrollo que se llevó a cabo para realizar el software
 3 Diseño del Software Traffic Analyzer En este capítulo se reporta el desarrollo que se llevó a cabo para realizar el software que analiza el tráfico en redes de telefonía y computadoras, denominado Traffic
3 Diseño del Software Traffic Analyzer En este capítulo se reporta el desarrollo que se llevó a cabo para realizar el software que analiza el tráfico en redes de telefonía y computadoras, denominado Traffic
Líneas de espera. Introducción.
 Líneas de espera. Introducción. En este capítulo se aplica la teoría de colas. Una Cola es una línea de espera y la teoría de colas es una colección de modelos matemáticos que describen sistemas de líneas
Líneas de espera. Introducción. En este capítulo se aplica la teoría de colas. Una Cola es una línea de espera y la teoría de colas es una colección de modelos matemáticos que describen sistemas de líneas
Ambas componentes del sistema tienen costos asociados que deben de considerarse.
 1. Introducción. En este trabajo se aplica la teoría de colas. Una Cola es una línea de espera y la teoría de colas es una colección de modelos matemáticos que describen sistemas de líneas de espera particulares
1. Introducción. En este trabajo se aplica la teoría de colas. Una Cola es una línea de espera y la teoría de colas es una colección de modelos matemáticos que describen sistemas de líneas de espera particulares
Recursos HELP DESK Biblioteca 2012
 Investigación operativa aplicada al Help Desk INTRODUCCION Este artículo está dirigido a aquellas personas que tienen la responsabilidad del diseño de estructuras de soporte, ya sea de empresas de Outsourcing
Investigación operativa aplicada al Help Desk INTRODUCCION Este artículo está dirigido a aquellas personas que tienen la responsabilidad del diseño de estructuras de soporte, ya sea de empresas de Outsourcing
PLAN DE CONVERGENCIA PROYECTO Nº 36-B INTERPRETACIÓN NORMA FINANCIERA (INF) INF-Chile TRANSACCIONES CON ACCIONES PROPIAS Y ACCIONES DEL GRUPO
 PLAN DE CONVERGENCIA PROYECTO Nº 36-B INTERPRETACIÓN NORMA FINANCIERA (INF) INF-Chile TRANSACCIONES CON ACCIONES PROPIAS Y ACCIONES DEL GRUPO (Comité de Interpretaciones de las Normas Internacionales de
PLAN DE CONVERGENCIA PROYECTO Nº 36-B INTERPRETACIÓN NORMA FINANCIERA (INF) INF-Chile TRANSACCIONES CON ACCIONES PROPIAS Y ACCIONES DEL GRUPO (Comité de Interpretaciones de las Normas Internacionales de
Teoría de Colas o Fenómenos de Espera
 Teoría de Colas o Fenómenos de Espera Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Febrero 2011 Introducción 2 Introducción............................................................
Teoría de Colas o Fenómenos de Espera Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Febrero 2011 Introducción 2 Introducción............................................................
DISTRIBUCIÓN DE LA MEDIA MUESTRAL. b) Las medias muestrales de tamaño n se distribuyen según la normal
 1 DISTRIBUCIÓN DE LA MEDIA MUESTRAL La mayoría de estos problemas han sido propuestos en exámenes de selectividad de los distintos distritos universitarios españoles. 1. Considérese una población en la
1 DISTRIBUCIÓN DE LA MEDIA MUESTRAL La mayoría de estos problemas han sido propuestos en exámenes de selectividad de los distintos distritos universitarios españoles. 1. Considérese una población en la
Tema 5: Teoría de colas. Ezequiel López Rubio Departamento de Lenguajes y Ciencias de la Computación Universidad de Málaga
 Tema 5: Teoría de colas Ezequiel López Rubio Departamento de Lenguajes y Ciencias de la Computación Universidad de Málaga Sumario Conceptos básicos Cola M M Cola M M c Cola M M k Redes de colas Redes de
Tema 5: Teoría de colas Ezequiel López Rubio Departamento de Lenguajes y Ciencias de la Computación Universidad de Málaga Sumario Conceptos básicos Cola M M Cola M M c Cola M M k Redes de colas Redes de
UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG)
 PAEG Junio 0 Propuesta A Matemáticas aplicadas a las CCSS II º Bachillerato UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales
PAEG Junio 0 Propuesta A Matemáticas aplicadas a las CCSS II º Bachillerato UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales
A continuación se muestra el programa resumido de la asignatura, el cual se describirá con detalle posteriormente.
 Fecha de impresión: 03/07/2007 13:29:00 2007/2008 Tipo: UNI Curso: 2 Semestre: B CREDITOS Totales TA TS AT AP PA 4,5 1 1 0 0 1 PI 0 PL 1,5 PC 0 OBJETIVOS El objetivo global de la asignatura Teletráfico,
Fecha de impresión: 03/07/2007 13:29:00 2007/2008 Tipo: UNI Curso: 2 Semestre: B CREDITOS Totales TA TS AT AP PA 4,5 1 1 0 0 1 PI 0 PL 1,5 PC 0 OBJETIVOS El objetivo global de la asignatura Teletráfico,
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2
 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2 1. Se eligen tres autos al azar y cada uno es clasificado N si tiene motor naftero o D si tiene motor diesel (por ejemplo, un resultado posible sería NND). a)
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2 1. Se eligen tres autos al azar y cada uno es clasificado N si tiene motor naftero o D si tiene motor diesel (por ejemplo, un resultado posible sería NND). a)
Primera ley de la Termodinámica para un volumen de control
 Primera ley de la Termodinámica para un volumen de control 1. Objetivo Utilizar la primera ley de la termodinámica para el análisis del volumen de control de un caso real. 2. Método Se considerará un volumen
Primera ley de la Termodinámica para un volumen de control 1. Objetivo Utilizar la primera ley de la termodinámica para el análisis del volumen de control de un caso real. 2. Método Se considerará un volumen
TEORIA DE COLAS SIMULACIÓN DE SISTEMAS
 SIMULACIÓN DE SISTEMAS UNIVERSIDAD ALAS PERUANAS FILIAL- ICA Ing. Las LINEAS DE ESPERA, FILAS DE ESPERA o COLAS, son realidades cotidianas: Personas esperando para una caja en un banco, Estudiantes esperando
SIMULACIÓN DE SISTEMAS UNIVERSIDAD ALAS PERUANAS FILIAL- ICA Ing. Las LINEAS DE ESPERA, FILAS DE ESPERA o COLAS, son realidades cotidianas: Personas esperando para una caja en un banco, Estudiantes esperando
Inferencia Estadística
 EYP14 Estadística para Construcción Civil 1 Inferencia Estadística El campo de la inferencia estadística está formado por los métodos utilizados para tomar decisiones o para obtener conclusiones sobre
EYP14 Estadística para Construcción Civil 1 Inferencia Estadística El campo de la inferencia estadística está formado por los métodos utilizados para tomar decisiones o para obtener conclusiones sobre
TEORIA DE COLAS, FENOMENOS DE ESPERA
 Universidad del Bío-Bío Facultad de Ingeniería Depto. Ingeniería Industrial Investigación de Operaciones II: TEORIA DE COLAS, FENOMENOS DE ESPERA Integrantes: Pedro Chávez Cristian Guajardo Victor Pino
Universidad del Bío-Bío Facultad de Ingeniería Depto. Ingeniería Industrial Investigación de Operaciones II: TEORIA DE COLAS, FENOMENOS DE ESPERA Integrantes: Pedro Chávez Cristian Guajardo Victor Pino
SISTEMA DE AMORTIZACION. Tomado de : http://memoriasmatefinanciera.blogspot.com/2013/04/sistemade-amortizacion.html
 SISTEMA DE AMORTIZACION Tomado de : http://memoriasmatefinanciera.blogspot.com/2013/04/sistemade-amortizacion.html DEFINICIÓN: La amortización es, desde el punto de vista financiero, el proceso de pago
SISTEMA DE AMORTIZACION Tomado de : http://memoriasmatefinanciera.blogspot.com/2013/04/sistemade-amortizacion.html DEFINICIÓN: La amortización es, desde el punto de vista financiero, el proceso de pago
MODELOS DE INVENTARIO
 MODELOS DE INVENTARIO Los modelos de inventarios son métodos que ayudan a reducir o minimizar los niveles de inventario requeridos en la producción. Existen varios métodos que nos ayudan a conseguir dicho
MODELOS DE INVENTARIO Los modelos de inventarios son métodos que ayudan a reducir o minimizar los niveles de inventario requeridos en la producción. Existen varios métodos que nos ayudan a conseguir dicho
RECOMENDACIONES Y CONCLUSIONES. al igual que la ley la elaboración de los libros diario y mayor, ya que son la base para la
 RECOMENDACIONES Y CONCLUSIONES RECOMENDACIONES Los principios de contabilidad generalmente aceptados podrían considerar mencionar al igual que la ley la elaboración de los libros diario y mayor, ya que
RECOMENDACIONES Y CONCLUSIONES RECOMENDACIONES Los principios de contabilidad generalmente aceptados podrían considerar mencionar al igual que la ley la elaboración de los libros diario y mayor, ya que
MÉTODOS DE ELIMINACIÓN Son tres los métodos de eliminación más utilizados: Método de igualación, de sustitución y de suma o resta.
 ECUACIONES SIMULTÁNEAS DE PRIMER GRADO CON DOS INCÓGNITAS. Dos o más ecuaciones con dos incógnitas son simultáneas cuando satisfacen iguales valores de las incógnitas. Para resolver ecuaciones de esta
ECUACIONES SIMULTÁNEAS DE PRIMER GRADO CON DOS INCÓGNITAS. Dos o más ecuaciones con dos incógnitas son simultáneas cuando satisfacen iguales valores de las incógnitas. Para resolver ecuaciones de esta
Introducción a la Investigación de Operaciones Facultad de Ingeniería - Universidad de la República Oriental del Uruguay
 Introducción a la Investigación de Operaciones Facultad de Ingeniería - Universidad de la República Oriental del Uruguay Procesos Estocásticos de Tiempo Contínuo Práctico Ejercicio 1 Sean X e Y variables
Introducción a la Investigación de Operaciones Facultad de Ingeniería - Universidad de la República Oriental del Uruguay Procesos Estocásticos de Tiempo Contínuo Práctico Ejercicio 1 Sean X e Y variables
SISTEMAS DE ECUACIONES LINEALES
 SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
SISTEMAS DE ECUACIONES LINEALES INTRODUCCIÓN En el presente documento se explican detalladamente dos importantes temas: 1. Descomposición LU. 2. Método de Gauss-Seidel. Se trata de dos importantes herramientas
APÉNDICE E: MANUAL DE USUARIO PARA EL SISTEMA DE MONITOREO DE REDES LAN.
 APÉNDICE E: MANUAL DE USUARIO PARA EL SISTEMA DE MONITOREO DE REDES LAN. Objetivo: Mostrar al usuario administrador el funcionamiento del sistema, junto con los datos que debe ingresar, además de interactuar
APÉNDICE E: MANUAL DE USUARIO PARA EL SISTEMA DE MONITOREO DE REDES LAN. Objetivo: Mostrar al usuario administrador el funcionamiento del sistema, junto con los datos que debe ingresar, además de interactuar
CAPITULO 4 JUSTIFICACION DEL ESTUDIO. En este capítulo se presenta la justificación del estudio, supuestos y limitaciones de
 CAPITULO 4 JUSTIFICACION DEL ESTUDIO En este capítulo se presenta la justificación del estudio, supuestos y limitaciones de estudios previos y los alcances que justifican el presente estudio. 4.1. Justificación.
CAPITULO 4 JUSTIFICACION DEL ESTUDIO En este capítulo se presenta la justificación del estudio, supuestos y limitaciones de estudios previos y los alcances que justifican el presente estudio. 4.1. Justificación.
SECCIÓN 16 DETERIORO DEL VALOR DE LOS ACTIVOS. Aspectos Conceptuales Básicos SECCIÓN 27
 SECCIÓN 16 SECCIÓN 27 DETERIORO DEL VALOR DE LOS ACTIVOS Aspectos Conceptuales Básicos Objetivo y Alcance (Sec. 27.1) Una pérdida por deterioro se produce cuando el importe en libros de un activo es superior
SECCIÓN 16 SECCIÓN 27 DETERIORO DEL VALOR DE LOS ACTIVOS Aspectos Conceptuales Básicos Objetivo y Alcance (Sec. 27.1) Una pérdida por deterioro se produce cuando el importe en libros de un activo es superior
ESPECIALIZACIÓN GERENCIA DE PROYECTOS Curso: Finanzas del proyecto- Profesor: Carlos Mario Morales C Taller No 2- Solucionado
 1. Cuál será la inversión que debe realizar una empresa en un fondo para tener el dinero necesario para reponer sus equipos de cómputo dentro de 38 meses? Se estima que los equipos tendrán un valor de
1. Cuál será la inversión que debe realizar una empresa en un fondo para tener el dinero necesario para reponer sus equipos de cómputo dentro de 38 meses? Se estima que los equipos tendrán un valor de
Plan de Estudios. Maestría en Matemáticas Aplicadas y Tecnologías Educativas
 Plan de Estudios Maestría en Matemáticas Aplicadas y Tecnologías Educativas CONTENIDOS 1) Presentación 5) Objetivos 2) Requisitos 6) Cursos Obligatorios 3) Plan de Estudios / Duración 7) Cursos Sugeridos
Plan de Estudios Maestría en Matemáticas Aplicadas y Tecnologías Educativas CONTENIDOS 1) Presentación 5) Objetivos 2) Requisitos 6) Cursos Obligatorios 3) Plan de Estudios / Duración 7) Cursos Sugeridos
Selectividad Junio 2008 JUNIO 2008 PRUEBA A
 Selectividad Junio 008 JUNIO 008 PRUEBA A 3 a x + a y =.- Sea el sistema: x + a y = 0 a) En función del número de soluciones, clasifica el sistema para los distintos valores del parámetro a. b) Resuélvelo
Selectividad Junio 008 JUNIO 008 PRUEBA A 3 a x + a y =.- Sea el sistema: x + a y = 0 a) En función del número de soluciones, clasifica el sistema para los distintos valores del parámetro a. b) Resuélvelo
Diseño de la muestra censal 2010
 Diseño la muestra censal 2010 i Obras complementarias publicadas por el INEGI sobre el tema: Clasificaciones l Censo Población y Vivienda 2010. Síntesis metodológica y conceptual l Censo Población y Vivienda
Diseño la muestra censal 2010 i Obras complementarias publicadas por el INEGI sobre el tema: Clasificaciones l Censo Población y Vivienda 2010. Síntesis metodológica y conceptual l Censo Población y Vivienda
PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2
 7 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2 1. Se eligen tres autos al azar y cada uno es clasificado N si tiene motor naftero o D si tiene motor diesel (por ejemplo, un resultado posible sería N N D).
7 PROBABILIDADES Y ESTADÍSTICA (C) Práctica 2 1. Se eligen tres autos al azar y cada uno es clasificado N si tiene motor naftero o D si tiene motor diesel (por ejemplo, un resultado posible sería N N D).
EL INTERÉS SIMPLE. El interés, como precio por el uso del dinero, se puede presentar como interés simple o como interés compuesto.
 EL INTERÉS SIMPLE El concepto de interés tiene que ver con el precio del dinero. Si alguien pide un préstamo debe pagar un cierto interés por ese dinero. Y si alguien deposita dinero en un banco, el banco
EL INTERÉS SIMPLE El concepto de interés tiene que ver con el precio del dinero. Si alguien pide un préstamo debe pagar un cierto interés por ese dinero. Y si alguien deposita dinero en un banco, el banco
Teoría de Líneas de Espera
 Teoría de Colas Teoría de Líneas de Espera COLAS: Líneas de espera que utiliza modelos matemáticos que describen sistemas de líneas particulares o Sistemas de Colas. Modelos presentan las siguientes características:
Teoría de Colas Teoría de Líneas de Espera COLAS: Líneas de espera que utiliza modelos matemáticos que describen sistemas de líneas particulares o Sistemas de Colas. Modelos presentan las siguientes características:
El Éxito del ICFES frente al reto de la Flexibilidad. Ingrid Picón Directora de Tecnología e Información ICFES
 El Éxito del ICFES frente al reto de la Flexibilidad Ingrid Picón Directora de Tecnología e Información ICFES Acerca del ICFES Entidad especializada en ofrecer servicios de evaluación de la educación en
El Éxito del ICFES frente al reto de la Flexibilidad Ingrid Picón Directora de Tecnología e Información ICFES Acerca del ICFES Entidad especializada en ofrecer servicios de evaluación de la educación en
Teoría a de Colas o Filas de Espera. M. En C. Eduardo Bustos Farías
 Teoría a de Colas o Filas de Espera M. En C. Eduardo Bustos Farías as Introducción Una línea de espera es la resultante de un sistema cuando la demanda por un bien o servicio supera la capacidad que puede
Teoría a de Colas o Filas de Espera M. En C. Eduardo Bustos Farías as Introducción Una línea de espera es la resultante de un sistema cuando la demanda por un bien o servicio supera la capacidad que puede
Caso práctico 1: Determinación del coste de capital de REGRESENGER.
 Caso práctico 1: Determinación del coste de capital de REGRESENGER. REGRESENGER, SA, tiene previsto realizar un proyecto, de entre dos posibles, ambos con unas necesidades financieras por importe de 1
Caso práctico 1: Determinación del coste de capital de REGRESENGER. REGRESENGER, SA, tiene previsto realizar un proyecto, de entre dos posibles, ambos con unas necesidades financieras por importe de 1
NIIF 2 Transacciones con Acciones Propias y del Grupo
 CINIIF 11 Interpretación CINIIF 11 NIIF 2 Transacciones con Acciones Propias y del Grupo La CINIIF 11 NIIF 2-Transacciones con Acciones Propias y del Grupo fue desarrollada por el Comité de Interpretaciones
CINIIF 11 Interpretación CINIIF 11 NIIF 2 Transacciones con Acciones Propias y del Grupo La CINIIF 11 NIIF 2-Transacciones con Acciones Propias y del Grupo fue desarrollada por el Comité de Interpretaciones
Circuitos Electrónicos. Septiembre 2005/2006. Problema 1º parcial
 Circuitos Electrónicos. Septiembre 2005/2006. Problema 1º parcial Se pretende realizar el circuito lógico interno de una máquina tragaperras de tres ruletas. El sistema completo tiene un esquema como el
Circuitos Electrónicos. Septiembre 2005/2006. Problema 1º parcial Se pretende realizar el circuito lógico interno de una máquina tragaperras de tres ruletas. El sistema completo tiene un esquema como el
Análisis de Decisiones II. Conceptos básicos de Teoría de Colas. Objetivo de aprendizaje del tema
 Tema 11 Conceptos básicos de Teoría de Colas Objetivo de aprendizaje del tema Al finalizar el tema serás capaz de: Explicar en qué consiste la Teoría de Colas. D.R. Universidad TecMilenio 1 Introducción
Tema 11 Conceptos básicos de Teoría de Colas Objetivo de aprendizaje del tema Al finalizar el tema serás capaz de: Explicar en qué consiste la Teoría de Colas. D.R. Universidad TecMilenio 1 Introducción
NÓMINA Y RECURSOS HUMANOS LIQUIDACIÓN DE CESANTÍAS E INTERESES DE CESANTÍAS
 NÓMINA Y RECURSOS HUMANOS LIQUIDACIÓN DE CESANTÍAS E INTERESES DE CESANTÍAS Qué son cesantías? Las cesantías son en Colombia, una prestación social que todo empleador debe reconocer a sus trabajadores
NÓMINA Y RECURSOS HUMANOS LIQUIDACIÓN DE CESANTÍAS E INTERESES DE CESANTÍAS Qué son cesantías? Las cesantías son en Colombia, una prestación social que todo empleador debe reconocer a sus trabajadores
CAPITULO 2 DISEÑO DE GRAFICAS ESTADISTICO-ECONOMICAS DE CONTROL DE CALIDAD.
 CAPITULO 2 DISEÑO DE GRAFICAS ESTADISTICO-ECONOMICAS DE CONTROL DE CALIDAD. En este capítulo se presenta la definición de diseño estadístico, económico y económico-estadístico para gráficas de control,
CAPITULO 2 DISEÑO DE GRAFICAS ESTADISTICO-ECONOMICAS DE CONTROL DE CALIDAD. En este capítulo se presenta la definición de diseño estadístico, económico y económico-estadístico para gráficas de control,
PENSIONES PENSION DE SOBREVIVIENTES
 BOLETIN 20 PENSION DE SOBREVIVIENTES En la pensión de sobrevivientes los beneficiarios son aquellos individuos que se encuentren en primer grado de consanguinidad y primer grado de afinidad es decir el
BOLETIN 20 PENSION DE SOBREVIVIENTES En la pensión de sobrevivientes los beneficiarios son aquellos individuos que se encuentren en primer grado de consanguinidad y primer grado de afinidad es decir el
SOFTWARE PARA MEDICIÓN Y SUPERVISIÓN DE ENERGÍA SMSE
 SOFTWARE PARA MEDICIÓN Y SUPERVISIÓN DE ENERGÍA SMSE Página 2 de 6 SOFTWARE PARA MONITOREO Y SUPERVISIÓN DE LA ENERGÍA ELÉCTRICA (SMSE) El SMSE en conjunto con un medidor de energía con comunicación es
SOFTWARE PARA MEDICIÓN Y SUPERVISIÓN DE ENERGÍA SMSE Página 2 de 6 SOFTWARE PARA MONITOREO Y SUPERVISIÓN DE LA ENERGÍA ELÉCTRICA (SMSE) El SMSE en conjunto con un medidor de energía con comunicación es
NÓMINA - LIQUIDACIÓN DE CESANTÍAS E INTERESES DE CESANTÍAS
 NÓMINA - LIQUIDACIÓN DE CESANTÍAS E INTERESES DE CESANTÍAS Qué son cesantías? Las cesantías son en Colombia, una prestación social que todo empleador debe reconocer a sus trabajadores con el fin de que
NÓMINA - LIQUIDACIÓN DE CESANTÍAS E INTERESES DE CESANTÍAS Qué son cesantías? Las cesantías son en Colombia, una prestación social que todo empleador debe reconocer a sus trabajadores con el fin de que
V Unidad: Teoría de Colas (Líneas de espera) de Espera: Teoría de Colas
 UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-NORTE INVESTIGACIÓN DE OPERACIONES II INGENIERIA INDUSTRIAL E INGENIERIA DE SISTEMAS V Unidad: Teoría de Colas (Líneas de espera) de Espera: Teoría de Colas Maestro
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-NORTE INVESTIGACIÓN DE OPERACIONES II INGENIERIA INDUSTRIAL E INGENIERIA DE SISTEMAS V Unidad: Teoría de Colas (Líneas de espera) de Espera: Teoría de Colas Maestro
SISTEMAS DE COLAS EXPONENCIALES
 UNIVERSIDAD POLITÉCNICA DE MADRID FACULTAD DE INFORMÁTICA SISTEMAS DE COLAS EXPONENCIALES M a ISABEL RODRÍGUEZ GALIANO Madrid, Junio de 2002 Índice Introducción 2 Sistema de Colas M/M/ 3 3 Sistema de Colas
UNIVERSIDAD POLITÉCNICA DE MADRID FACULTAD DE INFORMÁTICA SISTEMAS DE COLAS EXPONENCIALES M a ISABEL RODRÍGUEZ GALIANO Madrid, Junio de 2002 Índice Introducción 2 Sistema de Colas M/M/ 3 3 Sistema de Colas
Cuentas de Liquidación para Multifondos de AFP
 Cuentas de Liquidación para Multifondos de AFP Versión 3 8, enero 2004 INDICE: 1. Introducción...3 2. Apertura de Cuenta de Liquidación...3 3. Modo de Operación...3 3.1 DEPÓSITOS POR CAJA...3 3.2 COMPRAS
Cuentas de Liquidación para Multifondos de AFP Versión 3 8, enero 2004 INDICE: 1. Introducción...3 2. Apertura de Cuenta de Liquidación...3 3. Modo de Operación...3 3.1 DEPÓSITOS POR CAJA...3 3.2 COMPRAS
PRUEBA ESPECÍFICA PRUEBA 2014
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES DE 5 AÑOS PRUEBA ESPECÍFICA PRUEBA 014 PRUEBA SOLUCIONARIO HAUTAPROBAK 5 URTETIK 014ko MAIATZA DE 5 AÑOS MAYO 014 Aclaraciones previas Tiempo de duración de la
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES DE 5 AÑOS PRUEBA ESPECÍFICA PRUEBA 014 PRUEBA SOLUCIONARIO HAUTAPROBAK 5 URTETIK 014ko MAIATZA DE 5 AÑOS MAYO 014 Aclaraciones previas Tiempo de duración de la
SISTEMA CON UN SERVIDOR
 TALLER 6 : Problemas de Líneas de Espera. 1.SISTEMA CON UN SERVIDOR. Una compañía estatal tiene un numero de estaciones para el pesado de camiones a lo largo de una gran autopista, para verificar que el
TALLER 6 : Problemas de Líneas de Espera. 1.SISTEMA CON UN SERVIDOR. Una compañía estatal tiene un numero de estaciones para el pesado de camiones a lo largo de una gran autopista, para verificar que el
ZOOM. Sistema de temporizador para atención al automóvil con Administración empresarial HME CLOUD
 ZOOM Sistema de temporizador para atención al automóvil con Administración empresarial HME CLOUD Dentro de una semana de haber instalado ZOOM en un local con problemas históricos de velocidad de servicio,
ZOOM Sistema de temporizador para atención al automóvil con Administración empresarial HME CLOUD Dentro de una semana de haber instalado ZOOM en un local con problemas históricos de velocidad de servicio,
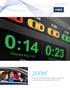
El aeropuerto se puede modelar como un sistema de colas M/G/1 con distribución uniforme de tiempo de servicio E[S] = 60 seg y σ 2 S = 48 seg 2.
![El aeropuerto se puede modelar como un sistema de colas M/G/1 con distribución uniforme de tiempo de servicio E[S] = 60 seg y σ 2 S = 48 seg 2. El aeropuerto se puede modelar como un sistema de colas M/G/1 con distribución uniforme de tiempo de servicio E[S] = 60 seg y σ 2 S = 48 seg 2.](/thumbs/32/15401881.jpg) ESTUDIO DE OPERACIONES URBANAS MATERIAL REUNIDO POR JAMES S. KANG OTOÑO 2001 Soluciones trabajo 4 3/10/2001 1. Problema 4.12 LO (Pinker, 1994; Kang, 2001) El aeropuerto se puede modelar como un sistema
ESTUDIO DE OPERACIONES URBANAS MATERIAL REUNIDO POR JAMES S. KANG OTOÑO 2001 Soluciones trabajo 4 3/10/2001 1. Problema 4.12 LO (Pinker, 1994; Kang, 2001) El aeropuerto se puede modelar como un sistema
Unidad 13. Amortización y Fondos de Amortización
 Unidad 13 Amortización y Fondos de Amortización INTRODUCCION En la sección 6.8 se mencionó que la palabra amortizar proviene del latín y que su significado literal es "dar muerte". En matemática financiera
Unidad 13 Amortización y Fondos de Amortización INTRODUCCION En la sección 6.8 se mencionó que la palabra amortizar proviene del latín y que su significado literal es "dar muerte". En matemática financiera
x 10000 y 8000 x + y 15000 a) La región factible asociada a las restricciones anteriores es la siguiente: Pedro Castro Ortega lasmatematicas.
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Septiembre 2012 - Propuesta A 1. Queremos realizar una inversión en dos tipos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Septiembre 2012 - Propuesta A 1. Queremos realizar una inversión en dos tipos
Administración de Recursos Informáticos Unidad II: El Proceso Administrativo El Proceso Administrativo... Cont.
 El Proceso Administrativo... Cont. Como hemos visto en clases anteriores, el Proceso Administrativo esta formado por cinco funciones que debe realizar el administrador de la organización. Estas funciones
El Proceso Administrativo... Cont. Como hemos visto en clases anteriores, el Proceso Administrativo esta formado por cinco funciones que debe realizar el administrador de la organización. Estas funciones
VIDEOS ONLINE CIFRAS Y TENDENCIAS DEL MERCADO INTERNACIONAL (Varias Fuentes) Marzo 2013
 VIDEOS ONLINE CIFRAS Y TENDENCIAS DEL MERCADO INTERNACIONAL (Varias Fuentes) Marzo 2013 RESUMEN EJECUTIVO El presente reporte es un resumen de varios informes internacionales sobre el mercado de los Videos
VIDEOS ONLINE CIFRAS Y TENDENCIAS DEL MERCADO INTERNACIONAL (Varias Fuentes) Marzo 2013 RESUMEN EJECUTIVO El presente reporte es un resumen de varios informes internacionales sobre el mercado de los Videos
2) Un establecimiento comercial dispone a la venta dos artículos en una de sus secciones, de precios p
 Universidad de Sevilla Facultad de Ciencias Económicas y Empresariales Licenciatura de Economía Universidad de Sevilla ESTADÍSTICA I RELACIÓN 5 MODELOS Y DATOS ESTADÍSTICOS DEPARTAMENTO DE ECONOMÍA APLICADA
Universidad de Sevilla Facultad de Ciencias Económicas y Empresariales Licenciatura de Economía Universidad de Sevilla ESTADÍSTICA I RELACIÓN 5 MODELOS Y DATOS ESTADÍSTICOS DEPARTAMENTO DE ECONOMÍA APLICADA
Convergencia del ingreso per cápita en los países miembros del FLAR
 Convergencia del ingreso per cápita en los países miembros del FLAR La convergencia macroeconómica, en un sentido amplio, puede definirse como el proceso a través del cual disminuyen las diferencias entre
Convergencia del ingreso per cápita en los países miembros del FLAR La convergencia macroeconómica, en un sentido amplio, puede definirse como el proceso a través del cual disminuyen las diferencias entre
VI ESTUDIO SOBRE VELOCIDAD EN INTERNET 2007-2008
 VI ESTUDIO SOBE VELOCIDAD EN INTENET 2007-2008 Introducción Como en años anteriores la Asociación de Internautas continúa realizando sus estudios sobre la velocidad de acceso a Internet, aunque en esta
VI ESTUDIO SOBE VELOCIDAD EN INTENET 2007-2008 Introducción Como en años anteriores la Asociación de Internautas continúa realizando sus estudios sobre la velocidad de acceso a Internet, aunque en esta
SERVIDOR WEB PARA ACCESO EN TIEMPO REAL A INFORMACIÓN METEOROLÓGICA DISTRIBUIDA
 SERVIDOR WEB PARA ACCESO EN TIEMPO REAL A INFORMACIÓN METEOROLÓGICA DISTRIBUIDA E. SÁEZ, M. ORTIZ, F. QUILES, C. MORENO, L. GÓMEZ Área de Arquitectura y Tecnología de Computadores. Departamento de Arquitectura
SERVIDOR WEB PARA ACCESO EN TIEMPO REAL A INFORMACIÓN METEOROLÓGICA DISTRIBUIDA E. SÁEZ, M. ORTIZ, F. QUILES, C. MORENO, L. GÓMEZ Área de Arquitectura y Tecnología de Computadores. Departamento de Arquitectura
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL PROYECTO SEMESTRAL DE CÁLCULO DIFERENCIAL
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL PROYECTO SEMESTRAL DE CÁLCULO DIFERENCIAL I Término Académico 2010-2011 Titulo: Tendencia de variabilidad de la constante de los resortes cónicos Autores: Coordinador:
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL PROYECTO SEMESTRAL DE CÁLCULO DIFERENCIAL I Término Académico 2010-2011 Titulo: Tendencia de variabilidad de la constante de los resortes cónicos Autores: Coordinador:
SÍNTESIS Y PERSPECTIVAS
 SÍNTESIS Y PERSPECTIVAS Los invitamos a observar, a identificar problemas, pero al mismo tiempo a buscar oportunidades de mejoras en sus empresas. REVISIÓN DE CONCEPTOS. Esta es la última clase del curso.
SÍNTESIS Y PERSPECTIVAS Los invitamos a observar, a identificar problemas, pero al mismo tiempo a buscar oportunidades de mejoras en sus empresas. REVISIÓN DE CONCEPTOS. Esta es la última clase del curso.
1 UNIDAD: CONCEPTOS BASICOS. ACTIVIDAD ECONOMICA: Es la serie de actos realizados por el hombre para la obtención de los bienes que le son necesarios.
 1 Instituto Comercial Blas Cañas Carmen Nº 136, F: 6398996 Santiago Inst.blascanas@gmail.com Virtud y Trabajo ESPECIALIDAD : Contabilidad MODULO : Contabilidad Básica Terceros Medios PROFESOR : Sr. Freddy
1 Instituto Comercial Blas Cañas Carmen Nº 136, F: 6398996 Santiago Inst.blascanas@gmail.com Virtud y Trabajo ESPECIALIDAD : Contabilidad MODULO : Contabilidad Básica Terceros Medios PROFESOR : Sr. Freddy
RECOMENDACIONES. HALLAZGOS Objetivos especifico Justificación/Norma ANEXO
 HALLAZGOS HALLAZGOS Objetivos especifico Justificación/Norma 1 No se estiman los presupuestos y calendario l proyecto En el objetivo específico 7 Verificar si se asigna los recursos necesarios para el
HALLAZGOS HALLAZGOS Objetivos especifico Justificación/Norma 1 No se estiman los presupuestos y calendario l proyecto En el objetivo específico 7 Verificar si se asigna los recursos necesarios para el
En la presente investigación, se contrastará el modelo propuesto en la. investigación de Marisa Bucheli y Carlos Casacubierta, Asistencia escolar y
 Capítulo 2.- Metodología En la presente investigación, se contrastará el modelo propuesto en la investigación de Marisa Bucheli y Carlos Casacubierta, Asistencia escolar y Participación en el mercado de
Capítulo 2.- Metodología En la presente investigación, se contrastará el modelo propuesto en la investigación de Marisa Bucheli y Carlos Casacubierta, Asistencia escolar y Participación en el mercado de
RELACIONES DE RECURRENCIA
 Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
Unidad 3 RELACIONES DE RECURRENCIA 60 Capítulo 5 RECURSIÓN Objetivo general Conocer en forma introductoria los conceptos propios de la recurrencia en relación con matemática discreta. Objetivos específicos
guía para LOS PADRES Apoyando a su hijo en segundo grado matemáticas
 TM guía para LOS PADRES Apoyando a su hijo en segundo grado matemáticas 2 Las escuelas de los Estados Unidos de América están trabajando para brindar una enseñanza de mayor calidad nunca antes vista. La
TM guía para LOS PADRES Apoyando a su hijo en segundo grado matemáticas 2 Las escuelas de los Estados Unidos de América están trabajando para brindar una enseñanza de mayor calidad nunca antes vista. La
La NIC 32 acompaña a la NIC 39, instrumentos financieros: reconocimiento y medición.
 Como clausura del Quinto Curso de la Normas Internacionales de Información Financiera a través de fundación CEDDET y el IIMV, se realizó del 30 de octubre al 1 de noviembre de 2012, en Montevideo Uruguay,
Como clausura del Quinto Curso de la Normas Internacionales de Información Financiera a través de fundación CEDDET y el IIMV, se realizó del 30 de octubre al 1 de noviembre de 2012, en Montevideo Uruguay,
PRINCIPALES DEFINICIONES
 USO DEL TIEMPO Y TRABAJO NO REMUNERADO EN URUGUAY 2013 PRINCIPALES DEFINICIONES Carga global de trabajo: Es la suma del total de horas dedicadas al trabajo no remunerado más el total de horas dedicadas
USO DEL TIEMPO Y TRABAJO NO REMUNERADO EN URUGUAY 2013 PRINCIPALES DEFINICIONES Carga global de trabajo: Es la suma del total de horas dedicadas al trabajo no remunerado más el total de horas dedicadas
guía para LOS PADRES APOYANDO A SU HIJO EN CUARTO GRADO MATEMÁTICAS
 TM guía para LOS PADRES APOYANDO A SU HIJO EN CUARTO GRADO MATEMÁTICAS 4 Las escuelas de los Estados Unidos de América están trabajando para brindar una enseñanza de mayor calidad nunca antes vista. La
TM guía para LOS PADRES APOYANDO A SU HIJO EN CUARTO GRADO MATEMÁTICAS 4 Las escuelas de los Estados Unidos de América están trabajando para brindar una enseñanza de mayor calidad nunca antes vista. La
En los últimos años, se ha presentado una enorme demanda por servicios portátiles,
 Capítulo 1 Introducción En los últimos años, se ha presentado una enorme demanda por servicios portátiles, a los que se les ha llamado tecnologías móviles, este repentino crecimiento de tecnologías ha
Capítulo 1 Introducción En los últimos años, se ha presentado una enorme demanda por servicios portátiles, a los que se les ha llamado tecnologías móviles, este repentino crecimiento de tecnologías ha
NIF B-3 Estado de resultado integral 1
 NIF B-3 Estado de resultado integral 1 OBJETIVO El objetivo de esta Norma de Información Financiera (NIF) es establecer las normas generales para la presentación y estructura del estado de resultado integral,
NIF B-3 Estado de resultado integral 1 OBJETIVO El objetivo de esta Norma de Información Financiera (NIF) es establecer las normas generales para la presentación y estructura del estado de resultado integral,
H E R R A M I E N T A S D E A N Á L I S I S D E D A T O S HERRAMIENTAS DE ANÁLISIS DE DATOS
 H E R R A M I E N T A S D E A N Á L I S I S D E D A T O S HERRAMIENTAS DE ANÁLISIS DE DATOS Una situación que se nos plantea algunas veces es la de resolver un problema hacia atrás, esto es, encontrar
H E R R A M I E N T A S D E A N Á L I S I S D E D A T O S HERRAMIENTAS DE ANÁLISIS DE DATOS Una situación que se nos plantea algunas veces es la de resolver un problema hacia atrás, esto es, encontrar
7. Conclusiones. 7.1 Resultados
 7. Conclusiones Una de las preguntas iniciales de este proyecto fue : Cuál es la importancia de resolver problemas NP-Completos?. Puede concluirse que el PAV como problema NP- Completo permite comprobar
7. Conclusiones Una de las preguntas iniciales de este proyecto fue : Cuál es la importancia de resolver problemas NP-Completos?. Puede concluirse que el PAV como problema NP- Completo permite comprobar
Los mayores cambios se dieron en las décadas de los setenta, atribuidos principalmente a dos causas:
 SISTEMAS DISTRIBUIDOS DE REDES 1. SISTEMAS DISTRIBUIDOS Introducción y generalidades La computación desde sus inicios ha sufrido muchos cambios, desde los grandes equipos que permitían realizar tareas
SISTEMAS DISTRIBUIDOS DE REDES 1. SISTEMAS DISTRIBUIDOS Introducción y generalidades La computación desde sus inicios ha sufrido muchos cambios, desde los grandes equipos que permitían realizar tareas
Infraestructura Tecnológica. Sesión 1: Infraestructura de servidores
 Infraestructura Tecnológica Sesión 1: Infraestructura de servidores Contextualización La infraestructura de cualquier servicio o mecanismo es importante, define el funcionamiento de los elementos en que
Infraestructura Tecnológica Sesión 1: Infraestructura de servidores Contextualización La infraestructura de cualquier servicio o mecanismo es importante, define el funcionamiento de los elementos en que
Control de Inventarios y Líneas de Espera. Patricia E. Balderas Cañas empatbal@unam.mx
 TERCER SEMINARIO PENSAMIENTO SISTÉMICO Y ANÁLISIS DE SISTEMAS marzo junio 2014 Control de Inventarios y Líneas de Espera Patricia E. Balderas Cañas empatbal@unam.mx Introducción El análisis cuantitativo
TERCER SEMINARIO PENSAMIENTO SISTÉMICO Y ANÁLISIS DE SISTEMAS marzo junio 2014 Control de Inventarios y Líneas de Espera Patricia E. Balderas Cañas empatbal@unam.mx Introducción El análisis cuantitativo
Circuito RC, Respuesta a la frecuencia.
 Circuito RC, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (13368) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se armó un
Circuito RC, Respuesta a la frecuencia. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (13368) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se armó un
Unidad 1. Fundamentos en Gestión de Riesgos
 1.1 Gestión de Proyectos Unidad 1. Fundamentos en Gestión de Riesgos La gestión de proyectos es una disciplina con la cual se integran los procesos propios de la gerencia o administración de proyectos.
1.1 Gestión de Proyectos Unidad 1. Fundamentos en Gestión de Riesgos La gestión de proyectos es una disciplina con la cual se integran los procesos propios de la gerencia o administración de proyectos.
EANNA 2012 Conocimiento y uso de alcohol y drogas en adolescentes de 12 a 17 años
 Subsecretaría de Evaluación Social EANNA 2012 Conocimiento y uso de alcohol y drogas en adolescentes de 12 a 17 años Noviembre 2013 RESUMEN Comparación entre grupos según tipo de consumo (consumo exploratorio
Subsecretaría de Evaluación Social EANNA 2012 Conocimiento y uso de alcohol y drogas en adolescentes de 12 a 17 años Noviembre 2013 RESUMEN Comparación entre grupos según tipo de consumo (consumo exploratorio
Embarazo Adolescente en el Triángulo Norte Guatemala, Honduras y El Salvador
 Embarazo Adolescente en el Triángulo Norte Guatemala, Honduras y El Salvador Por: Andrely Cisneros IIES-Universidad de San Carlos de Guatemala La Organización de las Naciones Unidas define como adolescente
Embarazo Adolescente en el Triángulo Norte Guatemala, Honduras y El Salvador Por: Andrely Cisneros IIES-Universidad de San Carlos de Guatemala La Organización de las Naciones Unidas define como adolescente
Teoría de Colas Ernesto Ponsot Balaguer Universidad de Los Andes Escuela de Estadística
 Teoría de Colas Ernesto Ponsot Balaguer Universidad de Los Andes Escuela de Estadística El Objetivo La teoría de colas o líneas de espera, procura el estudio riguroso del fenómeno (muy común en estos tiempos)
Teoría de Colas Ernesto Ponsot Balaguer Universidad de Los Andes Escuela de Estadística El Objetivo La teoría de colas o líneas de espera, procura el estudio riguroso del fenómeno (muy común en estos tiempos)
Sistemas operativos avanzados. 1.3 Algoritmos de planificación del procesador
 Sistemas operativos avanzados 1.3 Algoritmos de planificación del procesador Parámetros Cuando tenemos más de un proceso en condiciones de ejecutar, debemos escoger uno de entre ellos. Para escogerlo empleamos
Sistemas operativos avanzados 1.3 Algoritmos de planificación del procesador Parámetros Cuando tenemos más de un proceso en condiciones de ejecutar, debemos escoger uno de entre ellos. Para escogerlo empleamos
NOTA TÉCNICA LA ESPERANZA DE VIDA DE LOS NEGOCIOS EN MÉXICO
 BOLETÍN DE PRENSA NÚM. 087/15 18 DE FEBRERO DE 2015 AGUASCALIENTES, AGS. PÁGINA 1/2 ESPERANZA DE VIDA DE LOS NEGOCIOS El INEGI desarrolló una línea de investigación denominada Demografía Económica, cuyo
BOLETÍN DE PRENSA NÚM. 087/15 18 DE FEBRERO DE 2015 AGUASCALIENTES, AGS. PÁGINA 1/2 ESPERANZA DE VIDA DE LOS NEGOCIOS El INEGI desarrolló una línea de investigación denominada Demografía Económica, cuyo
LICEO BRICEÑO MÉNDEZ S0120D0320 DEPARTAMENTO DE CONTROL Y EVALUACIÓN CATEDRA: FISICA PROF.
 LICEO BRICEÑO MÉNDEZ S0120D0320 CATEDRA: FISICA PROF. _vwéa gxâw á atätá GRUPO # 4to Cs PRACTICA DE LABORATORIO #2 CALCULADORA CIENTIFICA OBJETIVO GENERAL: Comprender la importancia del cálculo haciendo
LICEO BRICEÑO MÉNDEZ S0120D0320 CATEDRA: FISICA PROF. _vwéa gxâw á atätá GRUPO # 4to Cs PRACTICA DE LABORATORIO #2 CALCULADORA CIENTIFICA OBJETIVO GENERAL: Comprender la importancia del cálculo haciendo
Redes de máscara variable.
 1 Redes de máscara variable. Elaborado por: Rebeca Castro Artavia Rolando Moraga Mora 2 Creación de subredes con máscara variable. En este documento se va a explicar paso a paso como crear subredes de
1 Redes de máscara variable. Elaborado por: Rebeca Castro Artavia Rolando Moraga Mora 2 Creación de subredes con máscara variable. En este documento se va a explicar paso a paso como crear subredes de
Todo el potencial de la Minería de Datos para el análisis avanzado del cliente. Por: Willyam L. Alcalá
 Todo el potencial de la Minería de Datos para el análisis avanzado del cliente Por: Willyam L. Alcalá El análisis correcto El paso indicado La mejor decisión» Un solo lugar Todo el potencial de la Minería
Todo el potencial de la Minería de Datos para el análisis avanzado del cliente Por: Willyam L. Alcalá El análisis correcto El paso indicado La mejor decisión» Un solo lugar Todo el potencial de la Minería
SIMULACIÓN VERSUS OPTIMIZACIÓN:
 SIMULACIÓN MONTE CARLO Procesos Químicos II La idea básica de la simulación es la construcción de un dispositivo experimental, o simulador, que actuará como (simulará) el sistema de interés en ciertos
SIMULACIÓN MONTE CARLO Procesos Químicos II La idea básica de la simulación es la construcción de un dispositivo experimental, o simulador, que actuará como (simulará) el sistema de interés en ciertos
Medidas de tendencia central o de posición: situación de los valores alrededor
 Tema 10: Medidas de posición y dispersión Una vez agrupados los datos en distribuciones de frecuencias, se calculan unos valores que sintetizan la información. Estudiaremos dos grandes secciones: Medidas
Tema 10: Medidas de posición y dispersión Una vez agrupados los datos en distribuciones de frecuencias, se calculan unos valores que sintetizan la información. Estudiaremos dos grandes secciones: Medidas
En Evaluaciones y Análisis Financiero, La TASA DE INTERES recibe diferentes
 CLASES DE TASAS DE INTERES En Evaluaciones y Análisis Financiero, La TASA DE INTERES recibe diferentes Nombres según las Condiciones en que esté Operando, y es así como encontramos los siguientes Términos
CLASES DE TASAS DE INTERES En Evaluaciones y Análisis Financiero, La TASA DE INTERES recibe diferentes Nombres según las Condiciones en que esté Operando, y es así como encontramos los siguientes Términos
La cuenta corriente es la parte de la. México, evolución reciente de la cuenta corriente. Comercio Exterior, Vol. 63, Núm. 2, Marzo y abril de 2013
 Comercio Exterior, Vol. 63, Núm. 2, Marzo y abril de 2013 México, evolución reciente de la cuenta corriente Juan Pablo Góngora Pérez* Fuente: http://flickrcc.bluemountains.net/flickrcc/index.php?terms=industry&page=10&edit=yes&com=no#
Comercio Exterior, Vol. 63, Núm. 2, Marzo y abril de 2013 México, evolución reciente de la cuenta corriente Juan Pablo Góngora Pérez* Fuente: http://flickrcc.bluemountains.net/flickrcc/index.php?terms=industry&page=10&edit=yes&com=no#
Guía de Preparación de Muestras para PLASTICOS para el Software de Formulación de Datacolor
 Guía de Preparación de Muestras para PLASTICOS para el Software de Formulación de Datacolor 1. Generalidades 2. Qué se necesita para comenzar? 3. Qué hacer para sistemas opacos y translúcidos? 4. Qué hacer
Guía de Preparación de Muestras para PLASTICOS para el Software de Formulación de Datacolor 1. Generalidades 2. Qué se necesita para comenzar? 3. Qué hacer para sistemas opacos y translúcidos? 4. Qué hacer
Puede dar pérdida un Casino?
 Puede dar pérdida un Casino? por Ernesto Mordecki En esta nota calculamos la probabilidad de que pierda la banca en la ruleta, en un período dado de tiempo. uestro enfoque consiste en determinar cuantas
Puede dar pérdida un Casino? por Ernesto Mordecki En esta nota calculamos la probabilidad de que pierda la banca en la ruleta, en un período dado de tiempo. uestro enfoque consiste en determinar cuantas
