Hacia un Interaprendizaje Holístico de Álgebra y Geometría. Mario Orlando Suárez Ibujes. Colegio Nacional Teodoro Gómez de la Torre
|
|
|
- María Luisa López Valdéz
- hace 7 años
- Vistas:
Transcripción
1
2
3 Hci un Interprendizje Holístico de Álger y Geometrí Mrio Orlndo Suárez Iujes Colegio Ncionl Teodoro Gómez de l Torre Región interior E Fronter Región eterior D F 0 l r A C e B Vértice Circunferenci inscrit Circunferenci circunscrit n( n ) Digonl = Ldo l ( ) 6 =
4 Bjo el uspicio del Colegio Ncionl Teodoro Gómez de l Torre Rector: Dr. Rmiro Terán Acost Vicerrector: Lic. Crlos Verdezoto Núnez Derechos Reservdos del Autor: Instituto Ecutorino de l Propiedd Intelectul Dirección Ncionl de Derecho de Autor y Derechos Coneos Derecho de Autor Nº 00 ISBN Impresión: Gráfics Plnet Primer Edición Est or no puede ser reproducid totl ni prcilmente por ningún medio sin epreso consentimiento del utor. Pedidos l teléfono: 666 Irr-Ecudor 00
5 A MIS PADRES, MIS PRIMEROS MAESTROS
6 ACRÓSTICO M dre, en tu nomre moroso se A cuñ l más snt nolez soñd en D onde el corzón ofrece l roj flor del mor R egd de ternur infinit y sntos E ncntos que tu represents, oh Mdre querid Dedico este Acróstico l más dmirle ser que Dios puso sore l tierr, mi Mdre. El Autor 6
7 PRESENTACIÓN Cundo se mencion l plr Mtemátic, lo primero que piensn l myorí de persons es que es lgo urrido de cálculos difíciles con complicds y strcts operciones. Este criterio erróneo que tienen ls persons se dee quizá que desde temprns eddes escolres no se les enseñ que l Mtemátic es un cienci que tiene un nturlez lógic y precis que rind numerosos eneficios intelectules y formtivos (cretividd, imginción, orden mentl, ectitud, responsilidd, puntulidd, constnci) que contriuyen l desrrollo de ls demás ciencis. Consultdo por un discípulo sore ls fuerzs dominntes de los destinos de los homres, Pitágors, filósofo y mtemático griego respondí: Los números rigen el mundo. L Mtemátic está en l nturlez, en l sociedd, en l poesí, en l músic, en l stronomí y en culquier prte que se usque (en l tryectori de los plnets y comets, en el disco solr, en los edificios, en los dimntes, en l estrell de mr, en l tryectori de un ej que descrie el número 8 pr visr que h descuierto un fuente de miel, en un got de gu, en un grno de ren). Los conocimientos mtemáticos desde siempre hn sido un herrmient estrtégic pr l 7
8 creción de nuevos medios científicos y tecnológicos que hn permitido l humnidd desrrollrse. Por ello es necesrio que l enseñr est cienci se trte prolems mtemáticos sore situciones práctics y concrets, evitndo utilizr el simple cálculo rutinrio sin comprensión de lo que se está hciendo. Esto yudrá mejorr el domino de ls operciones mtemátics y el conocimiento del por qué? de su necesidd o utilidd, generndo un desrrollo mtemático y un misión y visión superior de l vid. En este conteto surge l necesidd de poner considerción de discentes y docentes est propuest, cuyo ojetivo es contriuir mejorr el nivel de interprendizje de l Mtemátic con situciones prolemátics de l vid diri que estimuln en el discente l cpcidd de prender, interpretr y plicr est hermos cienci en su dirio vivir. El Autor 8
9 CONTENIDOS p CONTRAPORTADA DEDICATORIA ACRÓSTICO PRESENTACIÓN CONTENIDOS 7 EVALUACIÓN DIAGNÓSTICA CAPÍTULO I.- REPASO DE LOS NÚMEROS REALES..-Definición..- Relción de orden..- Vlor soluto..- Operciones en los números reles...- Ejemplos ilustrtivos...- Ejercicios de refuerzo CAPÍTULO II.- INTRODUCCIÓN AL UNIVERSO ALGEBRAICO..- Reseñ históric del Álger 7..- Nomencltur lgeric 8..-Clsificción de epresiones lgerics..- Reducción de términos semejntes..- Sum y rest de polinomios Multiplicción lgeric.7.- División lgeric Productos notles Teorem del inomio Cocientes notles 79 CAPÍTULO III.- ECUACIONES E INECUACIONES..- Ecuciones...- Definición 8 9
10 ...- Términos de un ecución...-grdo de un ecución Solución de un ecución Ejemplos ilustrtivos..6.- Ejercicios de refuerzo 9..- Inecuciones...- Definición 0...-Grdo de un ecución...- Solución de un ecución...- Ejemplos ilustrtivos Ejercicios de refuerzo 08 CAPÍTULO IV.- LA REALIDAD OBSERVADA DESDE LOS POLÍGONOS..- Definición de Polígono Elementos de los Polígonos 0..- Clsificción de los Polígonos...- De cuerdo l crácter entrnte o sliente de sus ángulos:...- De cuerdo su regulridd...- De cuerdo l número de ldos..- L Circunferenci...- Definición...- Elementos...- El número..- Ejemplos ilustrtivos 6.6.-Ejercicios de Refuerzo 7 REFERENCIAS BIBLIOGRÁFICAS ANEXOS 0
11 EVALUACIÓN DIAGNÓSTICA Orientciones Didáctics: En cd pregunt usted tiene cutro posiles respuests, de ls cules después de resolver comprorá que un es l correct, en los préntesis escri el literl correspondiente dich respuest. Cd pregunt vle dos puntos. ) El resultdo de l operción 00 es: ) 8 ) 8+ c) d) + ) El áre de l región somred de l figur es? )6, cm ) 6, cm c) 6 cm d) 6, cm ) El Perímetro de l figur somred nterior es: )0,8 cm ) 0 cm c) cm d) 9 cm ) En un clse de 0 estudintes ls tres quints prtes son homres. Cuánts mujeres hy en el curso? ) 8 ) c) d) 6 ) Se tiene 00 liros pr vender, si se h vendido / $ y el resto $6. Cuánto dinero se tiene después de vender todos los liros? ) $60 ) $00 c) $60 d) $60
12 6) Se dese curir con un lfomr el piso de un lco de 8m de lrgo por, m de ncho. Cuánto cuest lfomrrlo si el precio por m es $? ) $ ) $66 c) $6 d) $60 7) L nriz de Pinocho mide cm Su longitud se suplic cd vez que miente. Cuánto medirá l nriz de Pinocho luego de mentirs? ) ) 0 c) d) 8 8) En un corrl hy el mismo número de chnchos, de ptos y gllins. Estos nimles tienen, todos en conjunto, pts. Cuánts gllins hy? ) ) c) d) 8 9) Un ptio rectngulr tiene de lrgo el dole que su ncho, si el perímetro es m. Cuál es el lrgo del ptio? ) ) 8 c) d) 0) Un ptio rectngulr tiene de lrgo 6m más que su ncho, si el perímetro es 0 m. Cuál es el lrgo del ptio? ) ) 8 c) d) 8 Ser Relist es Soñr con lo Imposile
13 CAPÍTULO I REPASO DE LOS NÚMEROS REALES El conjunto formdo por todos los números rcionles (7/, -,) y los irrcionles ( 6,989...,=,...; e =,78...) es el de los números reles. Estos números ocupn l rect numéric punto punto, por lo que se llm rect rel. 7/ -, Recordemos que l epresr un número rcionl, no entero, en form deciml se otiene tres clses de números decimles: -Deciml finito o ecto: 0, -Deciml infinito o periódico puro: 0, Deciml infinito o periódico mito:, CÁLCULO DE UNA FRACCIÓN GENERATRIZ...- Pr clculr l frcción genertriz de un número deciml ecto, el número se escrie en form de entero l numerdor y por denomindor se pone un unidd seguid de
14 tntos ceros como cifrs decimles tiene el deciml. Después se simplific si es posile Ejemplos ilustrtivos: 0, = ;, = Pr clculr l frcción genertriz de un deciml periódico puro, se pone l numerdor un período como entero y l denomindor tntos nueves como cifrs tiene el período. L prte enter del deciml se hce preceder l frcción como entero. Finlmente el número mito se reduce número rcionl. Ejemplos ilustrtivos: ,66... ;, Pr clculr l frcción genertriz de un deciml periódico mito, l prte nteperiódic se pone como deciml ecto y se le sum l frcción que tiene por numerdor un período y por denomindor tntos nueves como cifrs tiene el período y tntos ceros cunts cifrs nteperiódics hy. L prte enter del deciml se l hce preceder ls frcciones como entero. Finlmente el mito se reduce querdo impropio Ejemplos ilustrtivos: 8 6 0, , Repso de los números reles
15 ...- Ejercicios de Refuerzo Clculr l frcción genertriz de los siguientes decimles: ) 0,6 9 S = ), 09 S = 00 ) 0,... 7) 0,... 9) 8,... ) 0,7... ),09... ), ),6... S = 9 S = S = S = 9 7 S = 8 S = 7 S = 9), S = 7 ), S = ), S = ), 09 S = 0 6), 8) 0,6... 0),... ),... ),... 6),... 8) 0, S = 9 7 S = S = 07 S = 7 S = 8 S = 7 S = 0) 0,0707 S = 7 7 ),777 S = Repso de los números reles
16 ..- RELACIÓN DE ORDEN Es indicr si un número es myor o menor con respecto otro número. Se emplen l simologí: > = Myor que y < = Menor que...-ejemplos ilustrtivos:.-ordenr de menor myor los siguientes números: - ;, ; 6 ; 7/ ; - ; -0 ; ; 0. Solución: -0 < - < - < 0 < <, < 6 < 7/.- Ordenr en form descendente los siguientes números: ; -; ; -00; -; 0; 8/;,7 Solución: >,7 > 8/ > > 0 > >- > VALOR ABSOLUTO Se llm vlor soluto de un número, l distnci que eiste desde el cero hst dicho número. Se design con y es igul l propio si es positivo o cero, y - si es negtivo. Es decir: -Si > 0 =. Por ejemplo: 7 = 7 -Si < 0 = -. Por ejemplo: -7 = -(-7) = 7. Not: El vlor soluto de un número es siempre positivo. Ejercicios de refuerzo Repso de los números reles 6
17 ) Escri l relción de orden entre ls siguientes prejs de números: ) )...- ) ) ) 0, ).../7 7) / 8) ) ) )... - e ) - e... - ) Ordenr en form descendente los siguientes números: ; -7; ; -; -,; -0,; /7 ; -/; 8 ; - ; /8 y - c) Ordenr en form scendente los siguientes números: -; ; -; ;,; -0,; - ; -/; /; 7 ; e;; - y d) Represente en l rect numéric los números del ejercicio nterior...- OPERACIONES CON NÚMEROS...- Ejemplos Ilustrtivos. ) Resolver los siguientes ejercicios: ) 0,06 0,, 6 ) 0,,6,7 7, ) (0,...) 0, ,87 Repso de los números reles 7
18 Repso de los números reles 8 Solución: Afirmciones Rzones ), 0, 0,06 6 = n m n m y encontrndo l frcción genertriz de los decimles = 6 6 y Simplificndo = 6 Restndo = - 6 = - = Simplificndo = n n = = (+)(-) = - = Restndo
19 Repso de los números reles 9 = - = - = (-)(-) = + = Trnsformndo el número Q = 6 Sumndo = 9 6+ =9 = Trnsformndo número mito ) 7,,7,6, 0 = Encontrndo l frcción genertriz de los decimles = n n = n m n m
20 Repso de los números reles 0 = 8 9 Etryendo l ríz cudrd = Restndo = = = 8 9 n n = 8 9 = 8 9 Sumndo = 9-8 = = 9 (-)(+) = - = 9 9 Restndo = 9 7 Operndo Escriir ls rzones en el siguiente ejercicio resuelto: ) ,87 (0,...) 0,6
21 Repso de los números reles = =
22 ) Resolver los siguientes prolems: ) Un estudinte h leído dos tercers prtes de 90 liros. Cuántos liros h leído? Solución: Entonces h leído 60 liros Repso de los números reles
23 ) Un deportist h recorrido el 60% de un competenci de Km. Cuántos kilómetros le fltn pr llegr l met? Solución: El 60% trnsformndo número Q es igul: 60 60% 00 El deportist h recorrido: km km km 9km Le fltn por recorrer: km 9km 6km...- Ejercicios de Refuerzo ) Resolver los siguientes ejercicios: ) +(-) +(-) S = ) -(-) -(-) S = -6 ) ( 0 8 )+( 60 8 ) S = ) [() 0 ] [() ] S = Repso de los números reles
24 ) 6 S = 0, 6 6) 0,... 0,, ) 0, 0,.. 0,,,... 0, 8) 0, S = S = 7 0 S = 0,, S = 9) 0) 0, 8, S = 8 0, S = ) 0, 8 9 0, ) 0, 0, S = 7 Repso de los números reles
25 0,666.., ) ) S = 0, 0, 0,... 0, ,... 0, ) 0,8.. 0, ) 7) 0, S = 0,... 0,... S = S = - 0,8, 0,, 0,, S = 0,.. 0, ,666.., 8) 0,, 6 S = 6,, 0, 0,7 9) 6 0,, S = 8 Repso de los números reles
26 0) 8 7 S = 0 ) ,.. 0, , S = 0, 0 ) 0, 0, ,... 6 S = 6 0, 0, , ) 0,,, 6 7 S = 0 0, ,.. 0, 0,.. 0,666.. ) 0,... S = 6 Repso de los números reles 6
27 ) 0, , 8 0, S = ) Resolver los siguientes prolems: ) En un clse de estudintes se reliz un emen de Mtemátic, en el que no otienen un clificción de 0 ls dos quints prtes. Cuántos estudintes otuvieron 0? S = 7 estudintes ) Un deportist h gndo 0 medlls de oro y plt, de ls cuáles tres quints prtes son de oro. Cuánts medlls de plt h gndo? S =6 medlls ) Un utomóvil h recorrido ls dos tercers prtes de 60 km. Un us h recorrido ls tres curts prtes de 60 km. Cuál h recorrido un myor distnci y cuál es es diferenci? S = El us con km más que el utomóvil ) Un person compr un televisor $ 0 y luego le vende gnándose el %. A cuánto vendió el televisor?. S = $00 Repso de los números reles 7
28 ) En cuántos dís se terminn $00, el que dirimente gst el % de ese dinero? S = dís 6) Un deportist recorre cd hor el 0% de 0 km. En cuánts hors recorre 0 km? S= hors 7) Un person compr 0 fruts, de ls cules el 60% son sndís, el 0% pers y el restnte son mnzns. Cuál es el número de cd frut que compró? S = 7 sndís, pers, 6 mnzns 8) Se tiene 00 liros pr vender, si se h vendido / $ 6 y el resto $7. Cuánto dinero se tiene después de vender todos los liros? S = $00 c) Plnter y resolver ejercicios y prolems similres los presentdos nteriormente. Se recomiend desrrollr l cpcidd imgintiv e inventiv. Not: Recuerde que l cretividd es uno de los múltiples eneficios intelectules y formtivos que se desrroll trvés de l Mtemátic, los cules son tn indispensles pr sorevivir en el mundo ctul. Repso de los números reles 8
29 CAPÍTULO II INTRODUCCIÓN AL UNIVERSO ALGEBRAICO..-RESEÑA HISTÓRICA DEL ÁLGEBRA L histori del álger comenzó en el ntiguo Egipto y Biloni, donde fueron cpces de resolver ecuciones lineles y cudrátics, sí como ecuciones indeterminds como con vris incógnits. Est ntigu sidurí sore resolución de ecuciones encontró, su vez, cogid en el mundo islámico, en donde se l llmó cienci de reducción y equilirio. (L plr áre l-ŷr que signific reducción, es el origen de l plr álger). A los áres se dee el desrrollo del Álger (siglo IX). Al-Jurismi, el más grnde mtemático musulmán, escriió uno de los primeros liros áres de álger Kit l-muhtsr fi hisd l-gr w-lmuql, de donde deriv el nomre de est cienci. Al-gr signific ecución o resturción; l-muql son los términos que hy que gregr o quitr pr que l iguldd no se ltere. Por esto, en rigor, el Álger no es más que un teorí de ls ecuciones. (Bldor A., 99). En ls civilizciones ntigus se escriín ls epresiones lgerics utilizndo reviturs sólo ocsionlmente; sin emrgo, en l edd medi, los mtemáticos áres fueron cpces de descriir culquier potenci de l incógnit, y desrrollron el álger fundmentl de los polinomios, unque sin usr los símolos modernos. L trducción l ltín del Álger de Al-Jwrizmi fue pulicd en el siglo XII.
30 Un vnce importnte en el Álger fue l introducción, en el siglo XVI, de símolos pr ls incógnits y pr ls operciones y potencis lgerics. Deido este vnce, el Liro III de l Geometrí (67), escrito por el mtemático y filósofo frncés René Descrtes se prece stnte un teto moderno de Álger. Sin emrgo, l contriución más importnte de Descrtes l Mtemátic fue el descurimiento de l Geometrí Anlític, que reduce l resolución de prolems geométricos l resolución de prolems lgericos. Su liro de Geometrí contiene tmién los fundmentos de un curso de teorí de ecuciones, incluyendo lo que el propio Descrtes llmó l regl de los signos pr contr el número de ríces verdders (positivs) y flss (negtivs) de un ecución. (Biliotec de Consult Microsoft Encrt 00) En l ctulidd los conocimientos del Álger hn encontrdo plicciones en tods ls rms de l Mtemátic y en muchs otrs ciencis llegndo ser empledos hst pr investigciones sore ls leyes del pensmiento..- NOMENCLATURA ALGEBRAICA...- Epresión Algeric.- Es l representción de un símolo lgerico o de un o más operciones lgerics, sí por ejemplo:,, (+c), +y, Término.- Es un epresión lgeric que const de un solo símolo o de vrios símolos no seprdos entre sí por el signo + o -, sí por ejemplo:, y, -c, -yz Introducción l universo lgerico 0
31 ...- Elementos de un término.-son cutro: el signo, el coeficiente, l prte literl y el grdo, sí por ejemplo: Signo Coeficiente Signo Coeficiente Prte literl - c Grdo Prte literl Grdo En el cso de el signo es positivo (cundo un término no v precedido de ningún signo es positivo), el coeficiente es, l prte literl es y el grdo es (segundo grdo). En el cso de - c el signo es negtivo, el coeficiente es (cundo un término no v precedido de ningún coeficiente, el coeficiente es l unidd), l prte literl es c y el grdo de primer grdo con relción l letr porque el eponente de este fctor es l, de segundo grdo con relción l letr, y de tercer grdo con relción l letr c. Not: Pr otener el grdo soluto de un término se sum los eponentes de sus fctores literles. En el cso de -y z el grdo soluto de seto grdo porque l sum de los eponentes de sus fctores es ++=6...- Clses de términos - Término entero.- El que no tiene denomindor literl, sí por ejemplo 7y z. Introducción l universo lgerico
32 - Término frccionrio.- El que tiene denomindor literl, sí por ejemplo - Término rcionl.- El que no tiene rdicl, como los ejemplos nteriores - Término irrcionl.- El que tiene rdicl. Ejemplo y - Términos homogéneos.- Los que tienen el mismo grdo soluto, sí por ejemplo c y y z son homogéneos porque mos son de séptimo grdo soluto - Términos heterogéneos.- Los que no tienen el mismo grdo soluto...- Ejercicios de Refuerzo ) De los términos y, z,,, y llenr l siguiente tl Homogéneos Heterogéneos Introducción l universo lgerico
33 ) Unir con línes el término correspondiente 7 Entero rcionl Entero irrcionl Frccionrio rcionl Frccionrio irrcionl ) Escriir cinco ejemplos de términos que sen enteros y rcionles l vez. Dos positivos y tres negtivos ) Escriir cinco ejemplos de términos que sen frccionrios e irrcionles l vez. Tres positivos y dos negtivos ) Escriir cinco ejemplos de términos homogéneos ) Escriir cinco ejemplos de términos heterogéneos Introducción l universo lgerico
34 7) Escriir un término de cd uno de los grdos solutos pr llenr l siguiente tl: Grdo Primer Segundo Quinto Décimo Vigésimo Ejemplo..-CLASIFICACIÓN DE EXPRESIONES ALGEBRAICAS...- Monomio.- Es un epresión lgeric que const de un solo término, sí por ejemplo: Binomio.- Es un epresión lgeric que const de dos términos, sí por ejemplo:...- Trinomio.- Es un epresión lgeric que const de tres términos, sí por ejemplo: + - c...- Cutrinomio.- Es un epresión lgeric que const de cutro términos, sí por ejemplo: Not: En generl l epresión lgeric que const de más de un término (inomio, trinomio, cutrinomio,...) se llm Polinomio El grdo de un polinomio puede ser soluto y con relción un letr El grdo soluto de un polinomio es el grdo de su término de myor grdo. Ejemplo: El polinomio es de quinto grdo. Introducción l universo lgerico
35 El grdo con relción un letr de un polinomio es el myor eponente de dich letr. Ejemplo: El polinomio + 6 es de seto grdo con relción l letr y de tercer grdo con relción l letr. Un polinomio puede estr ordendo con relción un letr, llmd letr ordentriz, en orden descendente o en orden scendente. Así por ejemplo: El polinomio + y y + y + y - y + está ordendo en form descendente respecto l letr ordentriz y en orden scendente respecto de l letr ordentriz y. El término de un polinomio que no tiene prte literl se llm término independiente (el número del ejemplo) y l ordenr un polinomio se lo uic siempre l finl....- Ejercicios de Refuerzo Escriir un polinomio de cd uno de los grdos solutos pr llenr l siguiente tl: Grdo Curto Quinto Octvo Décimo Vigésimo Trigésimo Ejemplo Orden descendente Orden scendente Introducción l universo lgerico
36 ..- REDUCCIÓN DE TÉRMINOS SEMEJANTES Dos o más términos son semejntes cundo tienen l mism prte literl, o se, cundo tienen letrs igules con eponentes igules. Así por ejemplo: con ; 8 con 7; con ; n+m con n+m L reducción de términos semejntes es un operción trvés de l cul se convierte en l menor cntidd de términos dos o más términos semejntes. Pr l que se sigue los psos: -Se reliz tods ls operciones previs en el cso de eistir (eliminción de signos de grupción, plicción de ls diferentes propieddes de los números,..) -Se sumn todos los coeficientes positivos y todos los coeficientes negtivos conservndo el signo y l prte literl correspondiente. -A los dos resultdos otenidos nteriormente se plic ls leyes de l sum y rest (signos igules se sum y se conserv el signo de los sumndos, y signos diferentes se rest y se conserv el signo del número de myor vlor soluto)....- Ejemplos Ilustrtivos Reducir los siguientes polinomios: ) 7- + Solución: Afirmciones Rzones 7- + Dtos del ejercicio Introducción l universo lgerico 6
37 = 7+- Propiedd Conmuttiv = - Sumndo entre positivos y entre negtivos = 8 Signos diferentes se rest y se conserv el signo del número de myor vlor soluto ) 7 m - m + m - m Solución: Afirmciones Rzones 7 m - m + m - m Dtos del ejercicio =7 m + m - m - m Propiedd Conmuttiv = m - m Sumndo entre positivos y entre negtivos = 6 m Signos diferentes se rest y se conserv el signo del número de myor vlor soluto ) Solución: Afirmciones Rzones Dtos del ejercicio Encontrndo el mcm y operndo Sumndo entre positivos y entre negtivos Signos diferentes se rest y se conserv el signo del número de myor vlor soluto Trnsformndo número mito Introducción l universo lgerico 7
38 Introducción l universo lgerico 8 ) z y z y Solución: Afirmciones Rzones z y z y Dtos del ejercicio 6 Operndo con ls y y y y y y Operndo con ls y z z z z z z 6 Operndo con ls z 9 0 Operndo con los términos independientes = z y Uniendo ls respuests prciles ) Solución: Afirmciones Rzones Dtos del ejercicio = Eliminndo ls llves
39 = 6 0 = Eliminndo los corchetes Operndo con ls Operndo con ls Operndo con los términos independientes Uniendo ls respuests prciles...- Ejercicios de Refuerzo ) Reducir los siguientes polinomios: ) 9 S = ) m m 6m m m 8m S = m mn ) mn mn mn m n S = ) S = ) S = 8 6 6) m m m m m S = m ) S = ) 0,m m,m m S = 0 9) 8 0, S = m Introducción l universo lgerico 9
40 Introducción l universo lgerico 0 0) 0 7, S = ), S = ),, 8 S = 0 9 ), 7 0, m m m m m m S = m m ) 0, 0, n n m m m m S = n m m ) 0, 0, 0, c c S = c 6) 0, 0, m m m m m S = m
41 Introducción l universo lgerico 7) n m n m n m n m n m, 0, 0, 0 S = n m 8) y y y y y m m m m m 0,, (,),9 0 S = y m 60 9) 0,, S = ) 0, 0,) ( S = 0 9 ) Plnter y resolver ejercicios similres los ejercicios nteriores. Not: Recuerde que cundo un estudinte prende plnter y resolver ejercicios ument su nivel de comprensión mtemátic, convirtiéndole en un sujeto cpcitdo pr poder desrrollr ctividdes de cretividd y trnsformción tnto en Mtemátic como en otrs circunstncis de su dirio vivir.
42 ..- SUMA Y RESTA DE POLINOMIOS L sum y rest de polinomios no es otr cos que l reducción de términos semejntes, pr lo cul se sigue los siguientes psos: - Se orden los polinomios en form descendente o decreciente. - Se cmi el signo en los términos del polinomio que se v restr. - Se escrie los monomios semejntes, uno dejo de otro. - Si flt lgún monomio en un de ls columns, se coloc un monomio semejnte con coeficiente cero o se dej el espcio lire. - Se sum lgericmente los polinomios....- Ejemplos Ilustrtivos ) De l sum de - -- con restr Solución: ) Ordenndo los polinomios, escriiendo los monomios semejntes uno dejo del otro y cmindo los signos en el tercer polinomio se otiene: Introducción l universo lgerico
43 ) Finlmente sumndo lgericmente los polinomios: ) Restr 7+ de l sum de con Solución: ) Ordenndo los polinomios, escriiendo los monomios semejntes uno dejo del otro, cmindo los signos en el primer polinomio y dejndo los espcios en los monomios fltntes se otiene: ) Finlmente sumndo lgericmente los polinomios: ) De l sum de 0 restr m m 6 m m m con m m m m Introducción l universo lgerico
44 Solución: ) Relizndo los psos de los ejemplos nteriores se otiene: m m m m m m 0 m m 6 m ) Cálculo del monomio resultnte en l primer column: m m m 9 m m m m m 6 c) Cálculo del monomio resultnte en l segund column: 0 9m 0m 0m m m m m d) Cálculo del monomio resultnte en l tercer column: 6m 6m m 7 m m m m e) Cálculo del monomio resultnte en l curt column: f) Solución finl: m 7 m m 9 0 Introducción l universo lgerico
45 ) Clculr los monomios que fltn pr otener l respuest indicd Solución: ) Cálculo del monomio fltnte en l primer column: Se otiene restndo los monomios sumndos ( y ) de l respuest indicd (0 ), sí: = ) Cálculo del monomio fltnte en l segund column: Se otiene relizndo el procedimiento nterior: = -8 c) Cálculo del monomio fltnte en l tercer column: + - = d) Cálculo del monomio fltnte en l curt column: = -7 e) Cálculo del monomio o término independiente fltnte en l quint column: = -7 f) Escriiendo los monomios clculdos: Introducción l universo lgerico
46 ) Clculr el polinomio que sumdo con 9 y 9 d como respuest 6 Solución: Se otiene restndo los polinomios sumndos de l respuest indicd ) Clculr el perímetro de l siguiente figur en form lgeric, y en form numéric pr = 8 Introducción l universo lgerico 6
47 Solución: ) Form lgeric: Se otiene sumndo los polinomios: ) Form numéric: Se sustituye = 8 8 en el perímetro clculdo en form lgeric: Perímetro = P P = () () 0 7 uniddes...- Ejercicios de Refuerzo ) De l sum de 8 7 con restr 8 S = 6 ) De l sum de con restr S = ) De l sum de y y y y con y y restr S = y y ) De l sum de con restr S = 6 Introducción l universo lgerico 7
48 Introducción l universo lgerico 8 ) Restr de l sum de con S = 6 6) Restr de l sum de con S = 7) De l sum de con restr S = 7 8) De l sum de con 6 restr 7 0 S = 0 9 9) Restr y y y de l sum de y y y con y y y S = 7 y y
49 0) Restr,,,, de l sum de 0, con, 6 S = ) Restr 0, 7 de l sum de 0,8 0, 0, con,, 0, 0, S = 0 0 ) Restr, 7 m m,m 0,m de l sum de m 0,m con, m,m 0,m, S = 7 m 0 6 ) Clculr los monomios que fltn pr otener l respuest indicd S = ; ; ; 6 Introducción l universo lgerico 9
50 ) Clculr los monomios que fltn pr otener l respuest indicd S = ; 7 ; ; ) Clculr el polinomio que sumdo con y d como resultdo S = 6) Clculr el polinomio que sumdo con y d como resultdo S = Introducción l universo lgerico 0
51 7) Clculr el perímetro del siguiente triángulo escleno en form lgeric, y en form numéric pr = 8 S = ; 7 uniddes 8) Clculr el perímetro del siguiente trpecio escleno en form lgeric, y en form numéric pr = S = 6 ; 0 uniddes 9) Clculr el perímetro del siguiente trpecio rectángulo en form lgeric, y en form numéric pr = 6 Introducción l universo lgerico
52 S = ; uniddes 0) Clculr el perímetro del siguiente triángulo escleno en form lgeric, y en form numéric pr = S = ; uniddes Not: Se recomiend que se dee seguir hciendo hincpié en que el estudinte resuelv ejercicios plntedos por el mismo. De est mner se contriuye trnsformr l estudinte en un sujeto cretivo y no repetitivo. Introducción l universo lgerico
53 .6.- MULTIPLICACIÓN ALGEBRAICA L multiplicción lgeric es un operción trvés de l cul prtir de dos cntiddes llmds multiplicndo y multiplicdor se hll un tercer cntidd, llmd producto. El multiplicndo y multiplicdor se llmn fctores del producto. L Multiplicción se fundment en l propiedd distriutiv c c y propieddes de los eponentes de m n mn potencis de igul se Multiplicción de un Monomio por un Polinomio Se multiplic el monomio por cd uno de los términos del polinomio Ejemplos Ilustrtivos Multiplicr: ) 8 Solución: Afirmciones Rzones 8 Dtos del ejercicio = 8 ( c) c m n mn = = Operndo ) Introducción l universo lgerico
54 Introducción l universo lgerico Solución: Afirmciones Rzones Dtos del ejercicio = c c ) ( = 0 8 n m n m = 0 8 Operndo ) Solución: Afirmciones Rzones Dtos del ejercicio = c c ) ( = n m n m = 6 Sumndo los eponentes = 6 7 Términos semejntes en los eponentes = 6 7 Operndo en los eponentes
55 Introducción l universo lgerico ) 9 Solución: Afirmciones Rzones 9 Dtos del ejercicio = 9 c c ) ( = 9 d c d c n m n m = 6 8 Operndo en los eponentes ) 6 6 Solución: Afirmciones Rzones 6 6 Dtos del ejercicio = 6 6 c c ) (
56 = = = = 6 m c d n c d mn Multiplicndo sumndo Términos semejntes y Operndo en los eponentes 6) Clculr el perímetro y el áre del siguiente rectángulo en form lgeric, y en form numéric pr = Solución: ) Cálculo del perímetro Afirmciones Rzones Form lgeric Perímetro = P =se+ltur) Definición de Perímetro P = ( ) ( ) Reemplzndo vlores P = Suprimiendo préntesis P = Términos semejntes P = 6 Multiplicndo Introducción l universo lgerico 6
57 Form numéric P = 6 Reemplzndo = en l form lgeric P = Multiplicndo P = uniddes Términos semejntes ) Cálculo del áre Afirmciones Rzones Form lgeric Áre = A =se ltur Definición de Perímetro A = Reemplzndo vlores A = Multiplicndo Form numéric A = Reemplzndo = en l form lgeric A = = A = 8 Multiplicndo A = uniddes cudrds Términos semejntes Ejercicios de Refuerzo Multiplicr: ) ( ) S = mn m mn n ) ( ) S = 6 9 ) m m m m S = mn 6 mn m m m mn Introducción l universo lgerico 7
58 m m m m 8 ) S = 6 6 ) 9 6 6) 8 0,, 0,8 0,6 7) 0,m, m 0,m m 0,m 0,8m m,m 8), 0,6 0, S = S = S = S = m m m m 7 m 0 6 m 7 m m m Clculr el perímetro y el áre de ls siguientes figurs en form lgeric, y en form numéric pr = 9) R: P = 6 ; P = ; A = 6 ; A = 8 0) R: P = 8 ; P = 8 ; A = 6 6 ; A = 8 Introducción l universo lgerico 8
59 .6..- Multiplicción de Polinomios por Polinomios Se multiplic cd término del multiplicndo por todos y cd uno de los términos del multiplicdor Ejemplos Ilustrtivos Multiplicr: ) por Solución: Se escrie los polinomios ordendos dejndo lire el espcio del término que no eiste ) n y y n n y por n y n n y y Solución: n y - n y + 0 y n - 0 y n + n y + n y n y + n y y n + n y + n y - n y + n y y n + 0 y n - y n - y n n y y n n y Introducción l universo lgerico 9
60 ) 9 n 6 n n por n n n Solución: 8 8 n n n + 9 n + n n + n 9 - n n + n n n n n n n + + n n n n n ) Clculr el perímetro y el áre del siguiente rectángulo en form lgeric, y en form numéric pr = Solución: ) Cálculo del perímetro Introducción l universo lgerico 60
61 Afirmciones Rzones Form lgeric Perímetro = P =se+ltur) Definición de Perímetro P = ( ) ( ) Reemplzndo vlores P = Suprimiendo préntesis P = 6 Términos semejntes P = Multiplicndo Form numéric P = () () Reemplzndo = en l form lgeric P = Operndo P = 8 Multiplicndo P = 6 Términos semejntes ) Cálculo del áre Afirmciones Rzones Form lgeric Áre = A =se ltur Definición de Perímetro A = Reemplzndo vlores A = 8 ( c) c A = 8 Términos semejntes Form numéric A = () 8 Reemplzndo = en l form lgeric A = 8 8 Operndo A = 6 Términos semejntes Introducción l universo lgerico 6
62 Ejercicios de Refuerzo Multiplicr: ) m m por 7 m S = 0m m 0m ) por S = ) 6 por S = 6 ) c por c S = 7 c c c ) por S = 8 6) por S = 6 7) y y por y y S = 9 60 y 7 0 y y 8 y Introducción l universo lgerico 6
63 8) por 7 6 S = ) Clculr el perímetro y el áre del siguiente rectángulo en form lgeric, y en form numéric pr = S: P = 6 6; P=; A = ; A=0 0) Clculr el perímetro y el áre del siguiente rectángulo en form lgeric, y en form numéric pr = S: P = 6 ; P=; A= ; A= Introducción l universo lgerico 6
64 .7.- DIVISIÓN ALGEBRAICA L división lgeric es un operción invers l multiplicción trvés de l cul prtir de dos cntiddes llmds dividendo y divisor se hll un tercer cntidd, llmd cociente. L división se fundment en l propiedd distriutiv c c y propieddes de los eponentes de m n mn potencis de igul se División de Polinomios por Monomios Se divide cd uno de los términos del polinomio (dividendo) por el monomio (divisor) Ejemplos Ilustrtivos Dividir: ) y 6 y 8 y entre y Solución: Antes de comenzr dividir, el polinomio dee estr ordendo en form decreciente y - 6 y + y 8 y - y 0-6 y + 8 y + 6 y y -8 y 0 - y + y Introducción l universo lgerico 6
65 ) m m 6 m entre m Solución: m - m 6-0 m m m + m m m m m ) m m entre m Solución: m - m 0 - m m + 0 m - m - m - m + m 0 m m - 8 m - m Introducción l universo lgerico 6
66 Ejercicios de Refuerzo Dividir: ) m 9mn 6m n entre m S = m mn n ) entre S = 0 ) y y 6 y entre y S = y y ) 9m n mn mn entre mn S = m 8n ) entre S = 6) entre S = 7) y 6y y entre y S = y 6y y 8) m n m n mn entre S = m n mn m m m m 9) m m 6m entre m S = m m m Introducción l universo lgerico 66
67 Introducción l universo lgerico 67 0) 6 entre S = 6 ) 6 n m n m n m entre n m S = 6 n m n m n m ) 8 y y entre S = 8 y y ) 6 entre 6 S = 0 9 y ) n n n entre 6 n S = 9 0 ) 6 y y y n m n m n m entre n m S = y y y n m n m n m
68 .7..- División entre Polinomios Pr dividir un polinomio por otro polinomio, se sugiere el siguiente procedimiento: - Ordenr los polinomios en form decreciente. -Cundo el polinomio dividendo no es completo se reemplzn los correspondientes términos fltntes con vriles que tengn coeficientes cero o se dej los espcios, tnto en el dividendo como en el divisor. - Dividir el primer término del dividendo pr el primer término del divisor. - Cundo los coeficientes del dividendo no son divisiles por los coeficientes del divisor, los cocientes respectivos se escrien en form frccionri - El primer término del cociente se multiplic por cd uno de los términos del divisor y el producto (con signos opuestos) se rest de los términos semejntes del dividendo, oteniendo sí el primer resto prcil. - El primer término del resto prcil se divide por el primer término del divisor y se otiene el segundo término del cociente. - El proceso se repite hst que el residuo se cero o de menor grdo que el divisor. Introducción l universo lgerico 68
69 Ejemplos Ilustrtivos Dividir: ) entre ) 7m m m entre m m - m -m 0 - m + 7 m + m + 6m 0 6m + 7 m - 6m -9 m 0 - m - + m m m - m + m - m + m Ejercicios de Refuerzo Dividir: ) 6 entre S = Introducción l universo lgerico 69
70 ) 9 entre S = ) 0 m m m entre m S = m 6m ) entre S = ) c c entre c S = c n n n n 6) entre n n S = n n 7) n n n n entre n n n n S = n 8) n n n n n n entre n n n n S = 9) entre S = Introducción l universo lgerico 70
71 0) 6 y 6 6 y entre S = ) 8 6 entre S = ) y y y entre y 6 8 S = y y ) El áre del prlelogrmo es. Clculr el polinomio que represent l se. S: = Introducción l universo lgerico 7
72 ) El áre del rectángulo es Clculr el polinomio que represent l ltur h. S: h = ) El áre del trpecio es. 6 8 Clculr el polinomio que represent l ltur h. S: h = Introducción l universo lgerico 7
73 .8.- PRODUCTOS NOTABLES Se llmn productos notles ciertos productos que cumplen regls fijs y cuyo resultdo puede ser escrito por simple inspección, es decir, sin verificr l multiplicción Cudrdo de un Binomio: ( ) Ejemplos ilustrtivos: ) ( ) ( )( ) ( ) ( ) El cudrdo de l sum de dos cntiddes es igul l cudrdo de l primer cntidd, más el dole producto de l primer por l segund cntidd, más el cudrdo de l segund cntidd: ( ) ) ( ) ( )( ) ( ) ( ) El cudrdo de l diferenci de dos cntiddes es igul l cudrdo de l primer cntidd, menos el dole producto de l primer por l segund cntidd, más el cudrdo de l segund cntidd: ( ) Introducción l universo lgerico 7
74 Introducción l universo lgerico Cuo de un Binomio: ) ( Ejemplos ilustrtivos: ) ) )( )( ( ) ( ) )( ( ) ( ) ( ) ( El cuo de l sum de dos cntiddes es igul l cuo de l primer cntidd, más el triple producto del cudrdo de l primer por l segund, más el triple producto de l primer por el cudrdo de l segund, más el cuo de l segund cntidd: ) ( ) ) )( )( ( ) ( ) )( ( ) ( ) ( ) ( El cuo de l diferenci de dos cntiddes es igul l cuo de l primer cntidd, menos el triple producto del cudrdo de l primer por l segund, más el triple producto de l primer por el cudrdo de l segund, menos el cuo de l segund cntidd: ) (
75 .8..- Cudrdo de un Polinomio: Ejemplo ilustrtivo: ( c) ( c)( c) ( c) c c c c c ( c) c c c El cudrdo de un polinomio es igul l sum de los cudrdos de cd un de ls cntiddes, más el dole producto de cd cntidd por cd un de ls demás cntiddes Producto de l Sum por l Diferenci de dos Cntiddes: ( )( ) Ejemplo ilustrtivo: ( )( ) ( )( ) El producto de l sum de dos cntiddes por l diferenci de ls misms es igul l cudrdo de l primer cntidd, menos el cudrdo de l segund cntidd Producto de dos Binomios que tienen un Término Común: Ejemplo ilustrtivo: ( )( ) 6 ( )( ) 6 El producto de dos inomios que tienen un término común es igul l producto de los términos comunes, más l sum lgeric de los términos intermedios y de los términos etremos, más el producto de los términos no comunes. Introducción l universo lgerico 7
76 Ejercicios de Refuerzo ) Unir con línes cd producto notle con su nomre correcto: Producto Notle: Nomre: ( ) -Cudrdo de un inomio ( ) -Cudrdo de un polinomio ( )( ) -Producto de l sum por l diferenci de dos cntiddes ( ) -Producto de dos inomios que tienen un término Común ( )( ) -Cuo de un inomio ) Unir con línes cd ejercicio con su respectiv solución: Ejercicios: ( ) ( ) ( ) Solución: )( ) 6 ( ) ( ( ) 6 8 ( )( ) 6 ( )( ) ( )( ) 6 9 ( ) 6 9 ) Plnter y resolver ejercicios de cd clse de producto notle. Introducción l universo lgerico 76
77 .9.- TEOREMA DEL BINOMIO El producto de un inomio elevdo culquier potenci puede ser otenido directmente medinte l plicción del teorem del inomio, cuy ley de los coeficientes se represent en el Triángulo de Pscl, tmién conocido como triángulo de Trtgli Regl pr elevr un inomio culquier potenci Se sigue el siguiente procedimiento: - El número de términos del producto de l potenci es igul l número que represent el eponente del inomio, umentdo en uno. - Los eponentes del primero y último términos del producto son igules l eponente del inomio. - Los eponentes de l prte literl correspondiente l primer término vn disminuyendo de uno en uno y los eponentes de l prte literl del segundo término vn umentndo de uno en uno. - Cundo los dos términos del inomio son positivos, todos los términos del producto son positivos. Cundo el segundo término del inomio es negtivo, los signos del producto se lternn con más y menos - Los coeficientes de los términos del producto umentn y disminuyen de cuerdo ls relciones que se indicn en el siguiente esquem conocido con el nomre de Triángulo de Pscl. Este triángulo tiene como segund fil dos. Pr ls demás fils, l sum de cd pr de números dycentes de l fil nterior se uic por dejo de ellos. Se ñde un en cd Introducción l universo lgerico 77
78 etremo. Los números que se otienen son los coeficientes que precen l multiplicr ( ) por sí mismo, sí por ejemplo: ( ) 0 = ( ) = ( ) = ( ) = ( ) = ( ) = ( ) 6 = Ejemplo ilustrtivo: Desrrollr ( ) Solución: ) Se form el triángulo de Pscl hst ) Se tom los coeficientes de l últim fil y se plic l regl sugerid nteriormente. (+) 6 = () 6 +6() () +() () +0() () +() () +6() () +() 6 (+) 6 = 6 +6( )() +( )( ) +0( )(8 ) +( )(6 ) +6()( ) +6 6 (+) 6 = Introducción l universo lgerico 78 6
79 .9..- Dtos iográficos de Pscl Blise Pscl (6-66), mtemático filósofo, científico y físico frncés, considerdo un de ls mentes privilegids de l histori intelectul de Occidente. Nció en Clermont-Ferrnd el 9 de junio de 6, y su fmili se estleció en Prís en 69. Pscl fue uno de los más eminentes mtemáticos y físicos de su époc y uno de los más grndes escritores místicos de l litertur cristin. Sus trjos religiosos se crcterizn por su especulción sore mteris que sorepsn l comprensión humn. Pscl rgument que es rzonle tener fe, unque ndie pued demostrr l eistenci o ineistenci de Dios; los eneficios de creer en Dios, si efectivmente eiste, supern con mucho ls desventjs de dich creenci en cso de que se fls. En 6 inventó l primer máquin de clculr mecánic. Pscl creí que el progreso humno se estimul con l cumulción de los descurimientos científicos. (Biliotec de Consult Microsoft Encrt) Actividd: Relizr un comentrio sore los dtos iográficos de Pscl.9..- Ejercicios de Refuerzo Desrrollr: ) ( ) S = 8 6 Introducción l universo lgerico 79
80 Introducción l universo lgerico 80 ) ( ) S = 8 08 ) 6 ( ) S = ) 6 ) ( S = ) S = ) S =
81 Introducción l universo lgerico COCIENTES NOTABLES Se llmn cocientes notles ciertos cocientes de uso frecuente que oedecen regls fijs y que pueden ser escritos por simple inspección, es decir, sin verificr l división Diferenci de Potencis Igules pr l Diferenci de sus ríces:... n n n n n L diferenci de potencis, pres o impres, igules pr l diferenci de sus ríces son positivos todos los términos del cociente. Ejemplos ilustrtivos: ) L diferenci de los cudrdos de dos cntiddes dividid por l diferenci de sus ríces es igul l sum de sus ríces. ) L diferenci de los cuos de dos cntiddes dividid por l diferenci de sus ríces es igul l cudrdo de l primer ríz, más el producto de l primer por l segund ríz, más el cudrdo de l segund ríz.
82 Introducción l universo lgerico 8 ) ) () () () () Diferenci de Potencis Igules Pres pr l Sum de sus ríces:... n n n n n Ejemplo ilustrtivo: ) L diferenci de los cudrdos de dos cntiddes dividid por l sum de sus ríces es igul l diferenci de sus ríces. ) ) ) ( ) ( 9 ) (
83 Introducción l universo lgerico Sum de Potencis Igules Impres pr l Sum de sus ríces:... n n n n n Ejemplos ilustrtivos: ) L sum de los cuos de dos cntiddes dividid por l sum de sus ríces es igul l cudrdo de l primer ríz, menos el producto de l primer por l segund ríz, más el cudrdo de l segund ríz. ) ) () () () () Ejercicios de Refuerzo Hllr, por simple inspección, el cociente de:
84 6 S = 6 ) 6 S = ) S = ) S = ) 6 S = 8 ) 6 S = 6 6 6) 6 S = 7) 6 7 S = 9 8) ( ) S = 9) ( ) ( ) ( ) S = 0) ( ) ( ) S = ) S = ) 7 ( ) ( ) S = ) ( ) ( ) ( ) ( ) S = 7 ) ( ) ( ) 9 Introducción l universo lgerico 8
85 CAPÍTULO III ECUACIONES E INECUACIONES..- ECUACIONES Muchos prolems de l vid diri pueden plnterse trvés de un relción de iguldd, llmd ecución. Ls ecuciones tienen plicción en tods ls rms de l Mtemátic y de ls ciencis en generl, por lo que su estudio es de sum importnci....- Definición.- Ecución es un iguldd entre dos epresiones lgerics, que solo se verific pr ciertos vlores determindos. En el cso de 7, l iguldd se cumple si y sólo si vle, por lo tnto es un ecución. En l cso de ( ) ( ), l iguldd se cumple pr culquier vlor de, por lo tnto no es un ecución. En este cso de trt de un identidd. L identidd tmién es un iguldd entre dos epresiones lgerics l igul que un ecución, pero que se verific pr culquier vlor. Ls igulddes de los productos y cocientes notles, estudids en el cpítulo nterior, son identiddes....- Términos de un Ecución.-Son cd un de ls cntiddes que están conectds por los signos + ó -
86 El primer miemro corresponde tod l epresión que está ntes del signo =. El segundo miemro corresponde tod l epresión que está después del signo = Los términos y 7 que no están compñdos de letrs se llmn términos independientes. L letr o letrs presentes en l ecución se llmn incógnits o vlores desconocidos...- Grdo de un Ecución.- El grdo de un ecución está ddo por el myor eponente de l incógnit. L ecución es un ecución de primer grdo o linel, y que el myor eponente de es l. L ecución 6 0 es un ecución de segundo grdo o cudrátic, y que el myor eponente de es Ecuciones e Inecuciones 86
87 ...- Solución de un Ecución.- Es verigur el vlor o los vlores de l incógnit. Este vlor se llm ríz. Pr encontrr l solución o ríz de un ecución se despej l incógnit medinte l trnsposición de términos con operción contrri (Si está sumndo ps l otro miemro de l ecución restr o vicevers, si está multiplicndo ps l otro miemro dividir o vicevers.) El principio de l trnsposición de términos se fundment en ls siguientes propieddes de ls igulddes: - Si los dos miemros de un ecución se sum o rest un mism cntidd, l iguldd susiste. - Si los dos miemros de un ecución se multiplicn o dividen un mism cntidd, l iguldd susiste. -Si los dos miemros de un ecución se elevn un mism potenci o se etre un mism ríz, l iguldd susiste....- Ejemplos ilustrtivos ) Clculr l solución de ls siguientes ecuciones ) ) Solución: Afirmciones Rzones Ecución inicil Trnsposición de términos 8 Términos semejntes Ecuciones e Inecuciones 87
88 8 Trsponiendo el Operndo ) Comproción: Afirmciones Rzones Ecución inicil () () Reemplzndo el vlor encontrdo ( = ) en l ecución inicil 6 8 Multiplicndo Términos semejntes Como l cntidd que se otuvo en el primer miemro es igul l cntidd que se otuvo en el segundo miemro, qued comprodo que l solución de l ecución es correct. ) 7 ) Solución: Afirmciones Rzones 7 Ecución inicil 7 Trnsposición de términos 0 Términos semejntes 0 Cmindo de signo todos los términos de l ecución. Not: Cundo l incógnit qued con signo negtivo, es consejle cmir de signo todos términos de l ecución. Ecuciones e Inecuciones 88
89 0 Trsponiendo el 0 Operndo ) Comproción: Afirmciones Rzones 7 Ecución inicil ( 0) 7 ( 0) Reemplzndo el vlor encontrdo en l ecución inicil Multiplicndo 7 7 Términos semejntes ) ( 8) 0 ) Solución: Afirmciones ( 8) Rzones Ecución inicil Supresión del préntesis Términos semejntes 8 0 Supresión del corchete 8 0 Trnsposición de términos Términos semejntes Cmindo de signo todos los términos de l ecución. Ecuciones e Inecuciones 89
90 Trsponiendo el Operndo ) Comproción: Afirmciones ( 8) 0 ( 8) 0 Rzones Ecución inicil Reemplzndo el vlor encontrdo en l ecución inicil 9 ( 8) 0 Multiplicndo Términos semejntes Supresión del préntesis 8 8 Operndo ) ( 7) ) Solución: Afirmciones ( )( ) ( ) Rzones ( 7) ( )( ) ( ) Ecución inicil 9 9 ( ) ( ) Productos notles Supresión de préntesis Trnsposición de térm. 0 8 Términos semejntes 0 8 Cmindo de signo Ecuciones e Inecuciones 90
91 8 0 9 Trnsponiendo el 0 Simplificndo Not: L comproción qued como tre pr el estudinte ) 0 Solución: Afirmciones Rzones Ecución inicil Trnsposición de términos Términos semejntes Términos semejntes Trnsponiendo el 0 7 Simplificndo el 0 7 Trnsponiendo el 7 Operndo Ecuciones e Inecuciones 9
92 Ecuciones e Inecuciones 9 6) Solución: Afirmciones Rzones Ecución inicil 7 Supresión de préntesis 7 Trnsposición de términos 6 6 Términos semejntes 6 Trnsponiendo el 0 6 Cmindo de signo Simplificndo Trnsponiendo el Operndo ) Resolver los siguientes prolems ) El duplo de un número es igul l número umentdo en 0. Hllr el número
93 Solución: ) Se trsform el enuncido del prolem l lenguje mtemático, trvés del simolismo lgerico, pr lo cul se requiere lcnzr destrez en el mnejo del siguiente simolismo: Enuncidos Un número culquier El duplo de un número Simolismo El tercio de un número / El cudrdo de un número Un número umentdo en Un número disminuido en El duplo de un número disminuido en El cudrdo de un número menos el número El 7% de un número 7 / 00 Tres números consecutivos,, Tres números pres consecutivos,, Tres números impres consecutivos,, El duplo de un número =, Número umentdo en 0 = +0 ) Se plnte l ecución: 0 Ecuciones e Inecuciones 9
94 c) Se resuelve l ecución d) Se reliz l comproción. Cundo se trt de prolems que se resuelven con ecuciones, l comproción se hce en se los resultdos otenidos. Se evidenci que 0 es el número que cumple ls condiciones del presente prolem. ) L sum de dos números es 0 y su diferenci es. Hllr los números Solución: ) Se trsform el enuncido del prolem l lenguje mtemático = primer número, 0 = segundo número ) Se plnte l ecución: ( 0 ) c) Se resuelve l ecución ( 0 ) (er. número) Como0 = segundo número 0 7 (do. número) Ecuciones e Inecuciones 9
95 ) Hllr tres números impres consecutivos es cuy sum es. Solución: ) Se trsform el enuncido del prolem l lenguje mtemático = er. número, = do. Número, = er. número ) Se plnte l ecución: ( ) ( ) c) Se resuelve l ecución ( ) ( ) 9 9 (er número) do número = do número = er número = er número = 7 ) En un curso de 0 estudintes hy 0 homres más que mujeres. Cuántos homres y cuánts mujeres hy? Solución: ) Se trsform el enuncido del prolem l lenguje mtemático = número de mujeres, 0 = número de homres ) Se plnte l ecución: 0 0 Ecuciones e Inecuciones 9
96 c) Se resuelve l ecución (Nº de mujeres) Nº de homres = 0 Nº de homres = 0 0 =0 ) El lrgo de un terreno rectngulr ecede l ncho en 0 m. Si el lrgo se ument en 0 m y el ncho se disminuye en 6m el áre no vrí. Hllr el áre del terreno. Solución: ) Se trsform el enuncido del prolem l lenguje mtemático Primer condición: = ncho Segund condición: 6m= ncho 0m = lrgo ( 0m) 0m = lrgo ) Se plnte l ecución: ( 0) 6( 0) 0 c) Se resuelve l ecución 6( 0) 0 ( 0) Ecuciones e Inecuciones 96
97 Ancho = Lrgo = 60 m 0m Lrgo = 60m 0m 90m Áre = Lrgo ncho = 90m 60m 00m..6.- Ejercicios de Refuerzo ) Resolver ls siguientes ecuciones y relizr l respectiv comproción ) = 0 ) = ) 7 6 = 7 ) = - ) 6 ( ) ( ) 0 = 6) 8 ( 9) ( ) = 7) 7 ( ) ( ) ( ) = 8) ( ) ( )( ) ( )( ) ( ) = 9) ( ) ( ) 0 ( )( ) S: = Ecuciones e Inecuciones 97
98 Ecuciones e Inecuciones 98 0) ) ( 7) 6( ) ( ) ( = - 7 ) 7 0 = ) 6 = - 9 ) 6 = 7 ) = 0 ) = - 6) = 9 7) = 8) 0 = - 9) = 0) = 9 7
99 ) Resolver los siguientes prolems ) El duplo de un número es igul l número umentdo en 0. Hllr el número S = 0 ) El triple de un número es igul l número umentdo en 8. Hllr el número S = ) El duplo de un número disminuido en uno es igul l número umentdo en. Hllr el número S = ) El triple de un número disminuido en dos es igul l duplo del número umentdo en. Hllr el número S = ) L sum de dos números es 0 y su diferenci es 0. Hllr los números S = y 6) L sum de dos números es y su diferenci es. Hllr los números S = y 7) Hllr dos números consecutivos cuy sum se 7 S = y 8) Hllr dos números pres consecutivos cuy sum se 0 S = y 6 Ecuciones e Inecuciones 99
100 9) Hllr tres números impres consecutivos cuy sum se S =, y 7 0) Hllr tres números pres consecutivos cuy sum se S = 6, 8 y 0 ) En un hotel de dos pisos hy 8 hitciones. Si ls hitciones del segundo piso son l mitd de ls del primero. Cuánts hitciones hy en cd piso? S: er piso = hitciones, do piso = 6 hitciones ) En un competenci tlétic de resistenci en l que prticipn 80 deportists el número que llegn l met es veces el número de los que no llegn. Cuántos llegn y cuántos nos llegn l met? S = Llegn 6; no llegn 6 ) Anit tiene tres veces el número de mnzns que su hermno y entre los dos tienen 8 mnzns. Cuánts mnzns tienen cd uno? S: Anit= 6 mnzns ; hermno = mnzns ) L sum de ls eddes de un pdre y su hijo es 78 ños y l edd del pdre es el dole de l edd del hijo. Cuál es l edd de cd uno? S: Hijo = 6 ños; pdre = ños ) En un curso de 7 estudintes hy 9 homres más que mujeres. Cuántos homres y cuánts mujeres hy? S = 9 mujeres y 8 homres Ecuciones e Inecuciones 00
101 6) En un estcionmiento hy 00 vehículos entre utomóviles y cmiones, si hy 8 utomóviles más que cmiones. Cuántos vehículos de cd clse hy? S = cmiones y 69 utomóviles 7) Un terreno rectngulr tiene de lrgo el dole que su ncho, si el perímetro es m. Cuál es el lrgo del terreno? S = 8 m 8) Un ptio rectngulr tiene de lrgo el triple que su ncho, si el perímetro es 6 m. Cuál es el lrgo del ptio? S = m 9) Un rectángulo tiene de lrgo 6m más que su ncho, si el perímetro es 0m. Cuál es el lrgo del rectángulo? S = m 0) Un terreno rectngulr tiene de ncho m menos que su lrgo, si el perímetro es 70m. Cuál es áre del terreno? S = 00 m ) El perímetro de un triángulo es 6 m. El ldo mide m más que el ldo c y el ldo es el tercio del ldo. Cuánto mide cd ldo del triángulo? S: = m, = m, c = 0 m ) El perímetro de un triángulo es 7 m. El ldo mide m más que el ldo c y el ldo es el 80% del ldo. Cuánto mide cd ldo del triángulo S: = m, = m, c = 0 m Ecuciones e Inecuciones 0
102 ) Un hitción rectngulr tiene dole lrgo que ncho. Si el lrgo se disminuye en 6m y el ncho se ument en m, el áre de l hitción no vrí. Hllr el perímetro de l hitción. S: 7 m ) El lrgo de un rectángulo ecede l ncho en m. Si el lrgo se ument en m y el ncho se disminuye en m el áre no vrí. Hllr el áre del rectángulo. S = 60 m ) Un terreno rectngulr tiene 0 m más de lrgo que de ncho. Si el lrgo tuviese 00 m más y el ncho 0m menos el áre no vrí. Hllr el perímetro del terreno. S: 60 m 6) Un rectángulo y un cudrdo tienen l mism áre. El lrgo del rectángulo ecede en m l ldo del cudrdo y su ncho es m menor que el ldo del cudrdo. Hllr el áre del rectángulo. S: 6 m Ecuciones e Inecuciones 0
103 ..- INECUACIONES Al sustituir l incógnit de dos epresiones lgerics, por culquier vlor numérico, dquieren diferente vlor, se form un desiguldd. Ls desigulddes son epresiones que indicn que un cntidd es myor o menor que otr. Los signos de desiguldd son (myor que), (menor que), (myor o igul que) y (menor o igul que) Así se lee myor que >, se lee myor que...- Definición.- Ls desigulddes en ls que hy un o más incógnits y que sólo se verific pr determindos vlores de ls incógnits se llmn inecuciones....- Solución de un Inecución.- Es verigur los vlores de ls incógnits se stisfgn l inecución. Este vlor se llm ríz. Pr encontrr l solución o ríz de un ecución se despej l incógnit medinte l trnsposición de términos con operción contrri (Si está sumndo ps l otro miemro de l ecución restr o vicevers, si está multiplicndo ps l otro miemro dividir o vicevers.) El principio de l trnsposición de términos se fundment en ls siguientes propieddes de ls desigulddes: - Si los dos miemros de un desiguldd se sum o rest un mism cntidd, el signo de l desiguldd no vrí. Ecuciones e Inecuciones 0
104 - Si los dos miemros de un desiguldd se multiplicn o dividen un mism cntidd positiv, el signo de l desiguldd no vrí. ( ) ( ) - Si los dos miemros de un desiguldd se multiplicn o dividen un mism cntidd negtiv, el signo de l desiguldd cmi. ( )( ) () ( ) ( ) () - Si se cmi el orden de los miemros, l desiguldd cmi de signo. - Si se invierten los miemros, l desiguldd cmi de signo Ecuciones e Inecuciones 0
105 ...- Ejemplos Ilustrtivos ) ( ) 7 Solución: ( ) Afirmciones ( ) 7 Rzones ( ) Inecución inicil 7 Productos notles 7 Trnsposición de términos 0 Términos semejntes 0 Trnsponiendo el 6 Operndo L inecución se cumple pr todos los vlores myores de, es decir, pr = 6, 7, 8, 9 + Not: Pr indicr en el gráfico que no se tom en cuent l (por l respuest es ), se trz un circunferenci sin pintr en el número Cd vlor que sirve como solución pr un inecución se llm solución prticulr (El número 6, 7 o 8,.. del ejemplo) y el conjunto de soluciones se denomin solución generl o conjunto solución (- = 6, 7, 8, 9 + del ejemplo. L solución de un inecución se verific l reemplzr, en l inecución inicil, un de ls soluciones prticulres Ecuciones e Inecuciones 0
106 ) ( ) ( ) ( )( ) Solución: Afirmciones Rzones ( ) ( ) ( )( ) Inecución inicil Eliminndo préntesis Trnsposición de términos Términos semejntes Trnsponiendo el Operndo L inecución se cumple pr todos los vlores menores o igules, es decir, pr = -,- Not: Pr indicr en el gráfico que si se tom en cuent l (por l respuest es ), se trz un circunferenci en el número pintndo su región interior. ) Solución: Ecuciones e Inecuciones 06
107 Afirmciones Rzones Inecución inicil Eliminndo préntesis Trnsposición de términos Términos semejntes Términos semejntes Términos semejntes Trnsponiendo el 6 6 Operndo L inecución se cumple pr todos los vlores myores o igules,, es decir, pr = + Ecuciones e Inecuciones 07
108 ) 8 8 Solución: Afirmciones Rzones Inecución inicil Eliminndo préntesis Trnsposición de términos Términos semejntes 7 6 Términos semejntes Simplificndo Cmindo de signo Trnsponiendo el 6 Multiplicndo Trnsponiendo el 6 6 Operndo Ecuciones e Inecuciones 08
109 L inecución se cumple pr todos los vlores menores, es decir, pr = -, -, ) Cuáles son los números que restdos en 8 son myores que 0? Solución: ) Se trsform el enuncido del prolem l lenguje mtemático emplendo el simolismo lgerico 8 = Números restdos en 8 ) Se plnte l ecución: 8 0 c) Se resuelve l inecución L inecución se cumple pr todos los vlores myores 8, es decir, pr = 9, 0,, + d) Se reliz l comproción. Cundo se trt de prolems que se resuelven con inecuciones, l comproción se hce en se los resultdos otenidos. Se evidenci que 9, 0,, cumplen ls condiciones del prolem. Ecuciones e Inecuciones 09
110 ...- Ejercicios de Refuerzo ) Error! No se pueden crer ojetos modificndo códigos de cmpo. ) 0 ) S: ) ( )( ) Error! No se pueden crer ojetos modificndo códigos de cmpo. ) ( )( ) ( )( ) 8 6) 6( ) ( ) ( )( ) 6 7 7) ( ) ( ) 9 8) ( 7) ( ) ( ) 60 9) Cuáles son los números que restdos en 8 son myores que 0 8 0) Cuáles son los números cuyos cuádruplos disminuidos en son myores que 0 Ecuciones e Inecuciones 0
111 CAPÍTULO IV LA REALIDAD OBSERVADA DESDE LOS POLÍGONOS..- DEFINICIÓN DE POLÍGONO El estudio de los Polígonos (del griego poly = mucho; goni = ángulo) corresponde l Geometrí (del griego geo = tierr; metrein = medir), y su importnci y plicción es ntigu y múltiple que incluso Pltón mndó colocr en l puert de su escuel el siguiente letrero: Ndie entr si no se Geometrí. Est cienci h reciido el porte de grndes sios como Tles de Mileto, Pltón, Pitágors y otros que hn contriuido l conocimiento de l Geometrí y dentro de ell de los polígonos y sus propieddes, que se estudirá en el presente cpítulo. Polígono es un porción de plno limitd por un líne poligonl cerrd. Un polígono qued determindo por sus ldos, que son los segmentos de l poligonl, y por sus ángulos, que son los que formn cd dos ldos consecutivos. El polígono que tiene todos sus ldos y ángulos igules se llm polígono regulr. Un polígono determin en el plno un región interior y un eterior. L unión de un polígono y su región interior recien el nomre de región poligonl. Se nomr los polígonos con ls letrs de sus vértices. Ls letrs en el polígono se ponen en sentido nti horrio
112 ..- ELEMENTOS DE UN POLÍGONO En un polígono como el siguiente ABCDEF se considern tmién estos elementos. Región interior E Fronter Región eterior D F 0 l r A C e B Vértice Circunferenci inscrit Circunferenci circunscrit - Centro = 0. Es el punto que equidist (está igul distnci) de todos los vértices y ldos. - Rdio = r. Es l distnci entre el centro y culquier vértice. En un polígono regulr de ldo l y potem se cumple: r Ldo l - Apotem =. Líne que une el centro con el punto medio de culquier ldo. Es perpendiculr los ldos. - Ángulo interior.- Se llm ángulo interior o, simplemente, ángulo del polígono, l que formn dos ldos consecutivos. Ejemplo: FAB. L sum de los ángulos interiores de un polígono de n ldos es 80º(n ). L relidd oservd desde los polígonos
113 - Ángulo eterior = e. Formdo por l prolongción de un ldo y el ldo siguiente. - Ángulo centrl =. Formdo por dos rdios consecutivos. 60 Un polígono de n ldos tiene: n - Digonl.- Líne rect que une dos vértices no consecutivos. Ejemplo: FD. n( n ) Un polígono de n ldos tiene digonles. En un polígono regulr el perímetro (P) es: P = n.l n = Número de ldos; l = ldo El áre de un polígono regulr es: A = P..- CLASIFICACIÓN DE LOS POLÍGONOS...- De cuerdo l crácter entrnte o sliente de sus ángulos: - Polígono conveo.- Cundo todos sus ángulos son slientes o conveos ( 80 0 ). En este cso un rect culquier sólo cort l polígono en dos puntos C L D B A L relidd oservd desde los polígonos
114 - Polígono cóncvo.- Cundo tiene lgún ángulo entrnte o cóncvo ( 80 0 ). En este cso un rect culquier R puede cortr l polígono en más de dos puntos. C B L D A...- De cuerdo su regulridd: - Polígono regulr.- Aquel que tiene todos los ldos y todos los ángulos igules - Polígono irregulr.- Aquel que no tiene todos sus ldos y ángulos igules...- De cuerdo l número de ldos: Los polígonos se clsificn de l siguiente mner: Triángulo (tres), cudrilátero (cutro), pentágono (cinco), heágono (seis), heptágono (siete), octágono (ocho), nonágono (nueve), decágono (diez), endecágono (once), dodecágono (doce), pentdecágono (quince), icoságono (veinte) y, en generl, se denomin n-ágono l polígono de n ldos. Not: L circunferenci es un polígono de infinitos ldos L relidd oservd desde los polígonos
115 Pr reforzr los contenidos presentdos, con l yud del compás, el grdudor y un regl trzr los siguientes polígonos regulres: triángulo, cudrdo, pentágono, heágono, heptágono, octágono, nonágono y decágono. Pr ello, clculr los ángulos centrles y luego medirlos desde el centro de l circunferenci; unir los puntos donde se cort l circunferenci y se otendrá los polígonos. Finlmente completr l tl que se present continución: Polígono regulr Número de ldos Número de triángulos Sum de los ángulos interiores en todos los triángulos n n (n-) Nº de grdos en el ángulo de cd vértice 80 0 ( n ) n Nº de digonles n( n ) Triángulo Cudrdo 60 0 Pentágono Heágono 0 0 Heptágono Octágono Nonágono Decágono Endecágono Dodecágono Pentdecágono Icoságono L relidd oservd desde los polígonos
116 ..- LA CIRCUNFERENCIA...- Definición.- Es un curv pln cerrd en l que cd uno de sus puntos equidist de un punto fijo, llmdo centro de l circunferenci. No se dee confundir con el círculo (superficie), unque mos conceptos están estrechmente relciondos....- Elementos: - Centro.- Es el punto interior del cul equidistn todos los puntos de l circunferenci - Cuerd.- Es el segmento que une dos puntos de l circunferenci. - Diámetro (D).- Es l cuerd que ps el centro de l circunferenci - Rdio (r).- Es el segmento que une el centro con un punto culquier de l circunferenci. Es l mitd del diámetro. - Tngente.- Es l rect que tom contcto en l circunferenci en un solo punto, llmdo punto de tngenci. L tngente es L relidd oservd desde los polígonos 6
117 perpendiculr con respecto l rdio que ps por el punto de tngenci. - Secnte.- Es l rect que ps cortndo dos puntos de l circunferenci - Sgit o flech.- Segmento comprendid entre el punto medio de un rco y el de su cuerd. Es perpendiculr con respecto l cuerd. - Arco ( ).- Porción de l circunferenci entre dos puntos de l mism. L longitud del rco está dd por l ecución r Sector Circulr.-Porción de círculo comprendid entre un rco y los dos rdios que psn por sus etremiddes. El áre de un sector circulr se clcul con l ecución:...- El número.-l relción entre l longitud de l circunferenci y su diámetro se llmd Pi cuyo símolo es. Est constnte mtemátic es proimdmente igul, , unque considerr,6, o incluso,, es suficiente pr l myorí de los cálculos. Actividd eperimentl: Relizr los siguientes psos pr encontrr el vlor de : ) Emplendo un compás trzr circunferencis de rdios igules cm, cm, cm, cm y cm. Clculr los respectivos diámetros L relidd oservd desde los polígonos 7
118 ) Emplendo un hilo psr lrededor de ls circunferencis trzds nteriormente, hciendo que coincidir el perímetro de l circunferenci con el hilo. ) Medir l longitud del hilo, etensión que representrá el perímetro de ls circunferencis. ) Dividir el perímetro encontrdo pr su respectivo diámetro. Compruee que en todos los csos se otiene un constnte igul ) Los vlores otenidos notr en l siguiente tl. Rdio r (cm) Diámetro D (cm) Perímetro P (cm) PD De quí se deduce que el perímetro de l circunferenci es P = D P = r ) Ddo el Polígono:..- EJEMPLOS ILUSTRATIVOS L relidd oservd desde los polígonos 8
119 ) Llenr l siguiente tl sore el tipo de polígono que se trt l figur nterior: De cuerdo sus ldos De cuerdo su regulridd De cuerdo l crácter entrnte o sliente de sus ángulos Solución: De cuerdo sus ldos De cuerdo su regulridd De cuerdo l crácter entrnte o sliente de sus ángulos Pentágono Irregulr Conveo ) Simolizr los vértices y trzr ls sets (flechs) de los ángulos interiores. Solución: Ls sets se trzn en sentido nti horrio, sí: c) Clculr el número de digonles Solución: n( n ) ( ) () Nº de digonles = d) Trzr ls digonles pr compror que los cálculos nteriores fueron correctos: L relidd oservd desde los polígonos 9
120 Solución: Como se puede oservr, el polígono tiene digonles e) Un pentágono regulr tendrá el mismo número de digonles que un pentágono irregulr? L solución qued como tre pr el discente. ) En l figur se tiene un cudrdo de ldo l = cm. En ls esquins se tiene cudrdos de ldo l/. Clculr el áre de l región somred Solución: ) Cálculo del áre del cudrdo de l = cm : A = l = (cm) = 6 cm ) Cálculo del áre del cudrdo de ldo l/: A= cm 6 cm 9,78 cm c) Cálculo del áre de l región somred Áre Somred = A - A= 6 cm (,78 cm ) Áre Somred = 6 cm 7, cm 8,88 cm L relidd oservd desde los polígonos 0
121 ) Clculr el áre de l región somred Solución: ) Cálculo del áre del círculo A r A ( cm) 6cm,6cm 0, cm ) Cálculo del áre del cudrdo Si el rdio de l circunferenci es cm, entonces el ldo del cudrdo es 8 cm, es decir, Si r = cm l = 8cm Entonces el áre del cudrdo es: A = l = (8cm) = 6 cm c) Cálculo del áre de l región somred Se otiene l restr el áre del círculo de l del cudrdo ) Clculr el áre de l región somred (sector circulr) en donde r cm y el tiene un tercio de Solución: L relidd oservd desde los polígonos
122 ) Cálculo del rdio r: Si r cm r cm 7 ) Cálculo del ángulo c) Cálculo del áre del sector circulr: ) Clculr el áre de l región somred (coron circulr) en donde r cm. Solución: ) Cálculo del rdio sudos: Si r cm r cm cm cm cm ) Cálculo del rdio suuno: L relidd oservd desde los polígonos
123 Si r r r cm r cm c) Cálculo del áre del círculo de rdio sudos: A r A, ( cm), cm,6 cm d) Cálculo del áre del círculo de rdio suuno: e) Cálculo del áre de l coron circulr 6) Clculr el áre de l región somred (trpecio circulr) en donde r 6 cm. Solución: ) Cálculo del rdio suuno: Si r 6 r cm 6 cm r cm = 6 cm = 6 cm ) Cálculo del rdio suuno: r cm Si r r cm c) Cálculo del sector circulr de rdio suuno: L relidd oservd desde los polígonos
124 d) Cálculo del sector circulr de rdio sudos: e) Cálculo del áre del trpecio circulr: 7) De un pizz se h comido 6 como indic l figur: L pizz ce ectmente en un cj cudrd que tiene 60 cm de perímetro. Clculr el áre y l longitud del rco de l prte comid. Solución.- Primer form: ) Cálculo del ldo de l cj cudrd P 60 cm Si el perímetro es P 0 cm ) Cálculo del rdio de l pizz L relidd oservd desde los polígonos
125 Si Si 0 cm Diámetro ( D) 0 cm D 0 cm D 0 cm rdio( r) r 0 cm c) Cálculo del áre totl de l pizz d) Cálculo del áre de l prte comid Como l prte comid es 6 = Entonces: de l pizz, e) Cálculo del perímetro de l pizz P r P, 0cm, 6 cm f) Cálculo de l longitud del rco de l prte comid P,6cm, 7 cm 8 8 Solución.- Segund form: ) Cálculo del ldo de l cj cudrd P 60 cm Si el perímetro es P 0 cm ) Cálculo del rdio de l pizz Si 0 cm Diámetro ( D) 0 cm L relidd oservd desde los polígonos
126 Si D 0 cm D 0 cm rdio( r) r 0 cm c) Cálculo del ángulo n 8 d) Cálculo del áre de l prte comid 0 e) Cálculo de l longitud del rco de l prte comid 0 r, 0 cm ˆ, 7 cm Not: Recuerde que tnto en Mtemátic como en l vid diri el mismo prolem tiene vris forms de solución. En este conteto, l Mtemátic cumple rol estrtégico, y que est cienci permite ver soluciones en donde otros no oservn. 8) Clculr el áre de l región somred en donde d = 00 cm y = 6 cm. Solución: ) Cálculo de l digonl: L relidd oservd desde los polígonos 6
127 Si d = 00 cm d 00 cm 0 cm ) Cálculo de l se: Si = 6 6 cm cm c) Cálculo de l ltur plicndo el Teorem de Pitágors: d d (0 cm) (8 cm) 00 cm 6 cm 6 cm 6 d) Cálculo del áre de l región pintd, l mism que es un triángulo: cm A = 8 cm 6 cm 8 cm cm 9) Si d = 6 cm. Clculr el áre de l región somred Solución: ) Cálculo de l digonl L relidd oservd desde los polígonos 7
128 Si d = 6 cm d 6 cm d 6 cm ) Cálculo del ldo del cudrdo Por Pitágors d d d 6 cm 6 cm 6 cm 6 cm c) Cálculo del áre del cudrdo d) Cálculo del áre del triángulo sin somrer e) Cálculo del áre somred 0) Si l = cm y = 7 cm. Clculr el áre de l región somred Solución: ) Cálculo del perímetro del heágono: P = n.l P = 6 cm = 8 cm L relidd oservd desde los polígonos 8
129 ) Cálculo del áre del heágono: P 8cm 7cm A = A = 9cm 7cm A = 9 9cm 9 cm 7 cm 6,77 cm c) Cálculo del rdio Se se que r r 6 7cm 7cm 9cm 6cm r cm r 6 d) Cálculo del áre del círculo con l ecución: c) Cálculo del áre de l región somred Áre somred = A - A Áre somred =,0 cm 6,77 cm = 66,7 cm Not: Como se puede oservr en los ejemplos ilustrtivos, l Mtemátic no represent complicds operciones, sino ms ien son procesos lógicos que trvés de l práctic se dese que el estudinte piense que pueden llegr ser simples operciones, y sí y no le teng miedo est hermos cienci que por tener un nturlez lógic y precis fvorece el desrrollo de múltiples destrezs y vlores que permiten otener un visión superior de l relidd. L relidd oservd desde los polígonos 9
130 .6.- EJERCICIOS DE REFUERZO ) Relizr los cálculos respectivos pr completr l siguiente tl (epresr ls respuests en términos de ): Rdio (r) Diámetro (D) ) Relizr los cálculos respectivos pr completr l siguiente tl: Rdio (r) ,9 6, L relidd oservd desde los polígonos 0
131 ) El rdio de l rued de un iciclet es cm. Qué distnci recorre l iciclet en cd revolución (vuelt)?. S =,0 m ) Un ro de ásquetol de cm de diámetro está hecho de un rrill. Qué cntidd de mteril se requiere pr construir 0 ros? S =, m ) En l figur se tiene un cudrdo de ldo cm. En ls esquins se tiene cudrdos de ldo cm. Clculr el áre de l región somred S = cm 6) El ldo del cudrdo es 6 cm. Clculr el áre de l región somred S =,86 cm L relidd oservd desde los polígonos
132 7) El rdio de l circunferenci es cm. Clculr el áre de l región somred 8) Si r S =, cm cm. Clculr el áre de l región somred S = 00, cm 9) Clculr el áre de l región somred S = 7, cm L relidd oservd desde los polígonos
133 0) El ldo del cudrdo es 6 cm. Clculr el áre de l región somred ) Clculr el áre de l región somred S = 8 cm ) Clculr el áre de l región somred S = 6 cm S = 00, cm L relidd oservd desde los polígonos
134 ) L siguiente figur muestr ls dimensiones de ls cnchs de ásquetol profesionl. Clculr el áre de l región somred. S = 8,9 m ) L siguiente figur muestr ls dimensiones de un cmpo de fútol. Clculr el áre de l región somred. S = 997, m L relidd oservd desde los polígonos
135 ) Si 6 cm. Clculr el áre de l región somred S =, cm 6) Si 6 cm. Clculr el áre de l región somred S = 9, cm 7) Si cm. Clculr el áre de l región somred S =,6 cm L relidd oservd desde los polígonos
136 8) Si 6 cm. Clculr el áre de l región somred S = 9, cm 9) Si cm. Clculr el áre de l región somred 6 S =,7 cm 0) Clculr el áre de l región somred (Triángulo rectángulo) S = 6 cm L relidd oservd desde los polígonos 6
137 ) Clculr el áre de l región somred (triángulo rectángulo isósceles) S =, cm ) Clculr el áre de l región somred (Trpecio rectángulo) ) Clculr el áre de l región somred S = cm S = cm L relidd oservd desde los polígonos 7
138 ) Clculr el áre de l región somred S = cm ) Clculr el áre de l región somred S = 6 cm 6) Clculr el áre de l región somred S = 9 cm L relidd oservd desde los polígonos 8
139 7) Clculr el áre de l región somred S = 6 cm 8) El diámetro de l circunferenci es cm. Clculr el áre de l región somred S = 8 cm 9) Si el perímetro del cudrdo es cm. Clculr el áre de l región somred S =, cm L relidd oservd desde los polígonos 9
140 0) En l siguiente figur se present un triángulo rectángulo isósceles inscrito en un semicircunferenci de rdio cm. Demostrr que el áre del triángulo es igul l áre somred, es decir, A A A ) En l siguiente figur demostrr que A A A ) El siguiente triángulo está inscrito en un circunferenci de cm de rdio y tiene cm de potem. Clculr el áre de l región somred S = 7,7 cm L relidd oservd desde los polígonos 0
141 ) El siguiente triángulo está inscrito en un circunferenci de cm de diámetro y tiene 6 cm de perímetro. Clculr el áre de l región somred S = 7,7 cm ) El diámetro de l circunferenci es cm. Clculr el áre de l región somred S =,6 cm ) El perímetro del romo equiángulo es 8 cm. Clculr el áre de l región somred S =,6 cm 6) El ldo del siguiente pentágono regulr mide, cm y su opotem,6 cm. Clculr el áre de l región somred S =,96 cm L relidd oservd desde los polígonos
142 7) El ldo del siguiente pentágono regulr mide 9,6 cm y su potem 6, cm. Clculr el áre de l región somred S = 7,6 cm 8) El ldo del siguiente heágono regulr mide cm y su potem cm. Clculr el áre de l región somred S =,7 cm 9) El rdio de l circunferenci es cm y el ldo del heágono regulr mide cm. Clculr el áre de l región somred. S =,7 cm L relidd oservd desde los polígonos
143 0) El rdio de l circunferenci es cm y l potem del heágono regulr mide cm. Clculr el áre de l región somred. S =,7 cm ) El diámetro de l circunferenci es cm y el perímetro del heágono regulr mide cm. Clculr el áre de l región somred. S =,7 cm ) A prtir de un heágono regulr de cm de ldo e inscrito en un circunferenci de cm de diámetro se otiene l siguiente figur. Clculr el áre de l región somred S =, cm L relidd oservd desde los polígonos
1. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN
 http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
http://www.cepmrm.es ACFGS - Mtemátics ESG - /0 Pág. de Polinomios: Teorí ejercicios. EXPRESIONES ALGEBRAICAS. CLASIFICACIÓN Tnto en mtemátics, como en físic, en economí, en químic,... es corriente el
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
el blog de mate de aida: Matemáticas Aplicadas a las Ciencias Sociales I. Ecuaciones. pág. 1
 el de mte de id: Mtemátics Aplicds ls Ciencis Sociles I. Ecuciones. pág. ECUACIONES Un ecución es un propuest de iguldd en l que interviene un letr llmd incógnit. L solución de l ecución es el vlor o vlores
el de mte de id: Mtemátics Aplicds ls Ciencis Sociles I. Ecuciones. pág. ECUACIONES Un ecución es un propuest de iguldd en l que interviene un letr llmd incógnit. L solución de l ecución es el vlor o vlores
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
Unidad 1: Números reales.
 Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
Unidd 1: Números reles. 1 Unidd 1: Números reles. 1.- Números rcionles e irrcionles Números rcionles: Son quellos que se pueden escriir como un frcción. 1. Números enteros 2. Números decimles exctos y
CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS
 CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS ACTIVIDAD ACADEMICA: LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD
CORPORACION UNIFICADA NACIONAL DE EDUCACION SUPERIOR CUN DEPARTAMENTO DE CIENCIAS BASICAS: MATEMATICAS ACTIVIDAD ACADEMICA: LOGICA Y PENSAMIENTO MATEMATICO DOCENTE: LIC- ING: ROSMIRO FUENTES ROCHA UNIDAD
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
CURSO DE NIVELACIÓN 2012 EJERCITARIO TEÓRICO DE MATEMÁTICA I
 CURSO DE NIVELACIÓN 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I. Con relción l potencición, se firm que es un operción: ) Conmuttiv. ) Distriutiv respecto l sum. 3) Distriutiv
CURSO DE NIVELACIÓN 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I 0 EJERCITARIO TEÓRICO DE MATEMÁTICA I. Con relción l potencición, se firm que es un operción: ) Conmuttiv. ) Distriutiv respecto l sum. 3) Distriutiv
GUIA Nº: 7 PRODUCTOS NOTABLES
 CORPORACION UNIFICADA NACIONAL DE EDUCACIÓN SUPERIOR CUN DEPARTAMENTO DE INGENIERIAS Y CIENCIAS BÁSICAS FUNDAMENTOS DE MATEMATICAS PRODUCTOS NOTABLES Y FACTORIZACION GUIA Nº: 7 PRODUCTOS NOTABLES Productos
CORPORACION UNIFICADA NACIONAL DE EDUCACIÓN SUPERIOR CUN DEPARTAMENTO DE INGENIERIAS Y CIENCIAS BÁSICAS FUNDAMENTOS DE MATEMATICAS PRODUCTOS NOTABLES Y FACTORIZACION GUIA Nº: 7 PRODUCTOS NOTABLES Productos
UNIVERSIDAD DE CANTABRIA DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA NÚMEROS COMPLEJOS. Miguel Angel Rodríguez Pozueta
 DEPARTAMENTO DE INGENIERÍA ELÉCTRICA ENERGÉTICA NÚMEROS COMPLEJOS Miguel Angel Rodríguez Pozuet Doctor Ingeniero Industril OBSERVACIONES SOBRE LA NOMENCLATURA En este teto, siguiendo l nomencltur hitul
DEPARTAMENTO DE INGENIERÍA ELÉCTRICA ENERGÉTICA NÚMEROS COMPLEJOS Miguel Angel Rodríguez Pozuet Doctor Ingeniero Industril OBSERVACIONES SOBRE LA NOMENCLATURA En este teto, siguiendo l nomencltur hitul
La hipérbola es el lugar geométrico de todos los puntos cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante e igual a 2a.
 INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
INSTITUTO VALLADOLID PREPARATORIA Págin 11 7 LA HIPÉRBOLA 7.1 DEFINICIONES L hipérol es el lugr geométrico de todos los puntos cuy diferenci de distncis dos puntos fijos, llmdos focos, es constnte e igul.
Inecuaciones con valor absoluto
 Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
Inecuciones con vlor soluto El vlor soluto de un número rel se denot por y está definido por:, si 0 si 0 Propieddes Si y son números reles y n es un número entero, entonces: 1.. 3. n 4. n L noción de vlor
el blog de mate de aida: Matemáticas I. Ecuaciones. pág. 1
 el log de mte de id: Mtemátics I. Ecuciones. pág. ECUACIONES Un ecución es un propuest de iguldd en l que interviene un letr llmd incógnit. L solución de l ecución es el vlor o vlores de l incógnit (o
el log de mte de id: Mtemátics I. Ecuciones. pág. ECUACIONES Un ecución es un propuest de iguldd en l que interviene un letr llmd incógnit. L solución de l ecución es el vlor o vlores de l incógnit (o
Efectuando la división (2x 2 = 1x y 6 2=3) se tiene III. PROBLEMAS QUE SE RESUELVEN UTILIZANDO ECUACIONES DE PRIMER GRADO CON UNA INCOGNITA.
 TEORIA GENERAL DE LAS ECAUCIONES I. IGUALDADES Y ECUACIONES Ls igulddes son epresiones en donde precen el símolo = Ejemplos:. 5 + = 15-7. + 6 = 5 Alguns propieddes de ls igulddes que utilizremos son: Si
TEORIA GENERAL DE LAS ECAUCIONES I. IGUALDADES Y ECUACIONES Ls igulddes son epresiones en donde precen el símolo = Ejemplos:. 5 + = 15-7. + 6 = 5 Alguns propieddes de ls igulddes que utilizremos son: Si
DIVERSIFICACIÓN CURRICULAR
 ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
ECUACIÓN DE PRIMER GRADO Se llmn ecuciones igulddes en ls que precen número y letrs (incógnits) relciondos medinte operciones mtemátics. Por ejemplo: - y = + Son ecuciones con un incógnit cundo prece un
Guía de Trabajo n 1 Octavo año básico Refuerzo Contenido y Aprendizaje N. Cero (restitución de aprendizajes) Números
 Colegio Antil Mwid Deprtmento de Mtemátic Profesor: Nthlie Sepúlved Guí de Trjo n Octvo ño ásico Refuerzo Contenido y Aprendizje N Fech Tiempo 2 Hors Nomre del/l lumno/ Unidd Nº Núcleos temáticos de l
Colegio Antil Mwid Deprtmento de Mtemátic Profesor: Nthlie Sepúlved Guí de Trjo n Octvo ño ásico Refuerzo Contenido y Aprendizje N Fech Tiempo 2 Hors Nomre del/l lumno/ Unidd Nº Núcleos temáticos de l
UNIDAD I FUNDAMENTOS BÁSICOS
 Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
Repúblic Bolivrin de Venezuel Universidd Alonso de Ojed Administrción Mención Gerenci y Mercdeo UNIDAD I FUNDAMENTOS BÁSICOS Ing. Ronny Altuve Ciudd Ojed, Septiembre de 2015 Conjuntos Numéricos ) Los Números
TEMA 1. LOS NÚMEROS REALES.
 TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
TEMA. LOS NÚMEROS REALES... Repso de números enteros y rcionles - Operciones con números enteros - Pso de deciml frcción y de frcción de deciml - Operciones con números rcionles - Potencis. Operciones
CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES
 FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
FUNDAMENTOS DEL ÁLGEBRA CUADERNO DE TRABAJO PARA LA CLASE NÚMEROS REALES NOMBRE ID SECCIÓN SALÓN Prof. Evelyn Dávil Tbl de contenido TEMA A. CONJUNTOS NUMÉRICOS... REGLA PARA LA SUMA DE NÚMEROS REALES...
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
NUMEROS IRRACIONALES Conocemos hst hor distintos conjuntos numéricos: - Los n nturles: (, 8,.978), representdos por l letr N - Los n enteros: ( -, -, 8, 68), representdos por l letr Z - Los n rcionles
DESIGUALDADES < d < En el campo de los números reales tenemos una. Un momento de reflexión muestra que una
 DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
DESIGUALDADES 7 60 < d < 7 70 En el cmpo de los números reles tenemos un propiedd de orden que se costumbr designr con el símbolo (
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Los números enteros y racionales
 Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
Los números enteros y rcionles Objetivos En est quincen prenderás : Representr y ordenr números enteros Operr con números enteros Aplicr los conceptos reltivos los números enteros en problems reles Reconocer
NÚMEROS RACIONALES. Los números racionales son todos aquellos números de la forma b
 NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
NÚMEROS RACIONALES Los números rcionles son todos quellos números de l form b con y b números enteros y b distinto de cero. El conjunto de los números rcionles se represent por l letr Q. IGUALDAD ENTRE
1 Agrupa aquellos monomios de los que siguen que sean semejantes, y halla su suma: , cuando:
 Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
Agrup quellos monomios de los que siguen que sen semejntes, y hll su sum: m, bn y, m, bm, b my, m, n by, mb Son semejntes el º, el º y el º, su sum es: Tmbién lo son el º y el º: bn y 0 Lo mismo ocurre
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Polinomios 3º Año Cód P r of. M a r í a d el L u já n Matemática M a r t í n ez P r of. M ir t a R o s i t o Dpto.
 Polinomios Mtemátic º Año Cód. 0- P r o f. M r í d e l L u j á n M r t í n e z P r o f. M i r t R o s i t o Dpto. de Mtemátic POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrile,
Polinomios Mtemátic º Año Cód. 0- P r o f. M r í d e l L u j á n M r t í n e z P r o f. M i r t R o s i t o Dpto. de Mtemátic POLINOMIOS Polinomios. Generliddes Llmremos polinomios de grdo n en l vrile,
Colegio Diocesano Sagrado Corazón de Jesús EJERCICIOS MATEMÁTICAS 3º ESO VERANO 2015
 Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Colegio Diocesno Sgrdo Corzón de Jesús EJERCICIOS MATEMÁTICAS º ESO VERANO º. Amplific ls siguientes frcciones pr que tods tengn denomindor b c d º. Cuál de ls siguientes frcciones es un frcción mplificd
Números Reales. Los números naturales son {1; 2; 3; }, el conjunto de todos ellos se representa por.
 Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
Se distinguen distints clses de números: Números Reles Los números nturles son {1; 2; 3; }, el conjunto de todos ellos se represent por. El primer elemento es el 1 y no tiene último elemento Todo número
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
A modo de repaso. Preliminares
 UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
UNIDAD I A modo de repso. Preliminres Conjuntos numéricos. Operciones. Intervlos. Conjuntos numéricos Los números se clsificn de cuerdo con los siguientes conjuntos: Números nturles.- Son los elementos
Máximo común divisor. 2. Descomposición en primos Ejemplo. Encontrar mcd 504,300 Se descomponen ambos números en primos 504 2 252 2 126 2 63 3 21 3
 Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
Máximo común divisor El máximo común divisor de dos números nturles y es el número más grnde que divide tnto como. se denot mcd,. Lists: (tl vez, el más intuitivo, pero el menos eficiente) Encontrr mcd
OPERACIONES CON FRACIONES
 LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
LEY DE SIGNOS OPERACIONES CON FRACIONES SUMA Y RESTA: Si se sumn dos números con el mismo signo, se sumn los vlores solutos y se coloc el signo común (+) + (+) = + 8 (-) + (-) = - 8 Si se sumn dos números
OPERACIONES CON RADICALES
 OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
OPERACIONES CON RADICALES RAÍCES Y RADICALES L ríz n-ésim de un número, representd por n, es un operción sore que d como resultdo un número tl que n. Si n es pr, h dos resultdos posiles: positivo negtivo:,
Material Complementario Matemática Básica
 Mteril Complementrio Mtemátic Básic Primer Semestre 006 Autores: M Adl, MC Silv, A Lizn, M Glz & V Fzio DEPARTAMENTO DE CIENCIAS BÁSICAS Mteril Complementrio Mtemátic Básic 006 UNIDAD I: PREPARACIÓN PARA
Mteril Complementrio Mtemátic Básic Primer Semestre 006 Autores: M Adl, MC Silv, A Lizn, M Glz & V Fzio DEPARTAMENTO DE CIENCIAS BÁSICAS Mteril Complementrio Mtemátic Básic 006 UNIDAD I: PREPARACIÓN PARA
Los Números Racionales
 Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
Cpítulo 12 Los Números Rcionles El conjunto de los números rcionles constituyen un extesión de los números enteros, en el sentido de que incluyen frcciones que permiten resolver ecuciones del tipo x =
PROGRESIONES ARITMETICAS
 PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
PROGRESIONES ARITMETICAS. Hllr l sum de los primeros cien enteros positivos múltiplos de 7. L sum de n términos de un progresión ritmétic viene dd por l expresión: + n Sn n Aplicndo pr 00 términos: + 00
Resolver inecuaciones como las siguientes. Expresar la solución en forma gráfica y algebraica. Comparar las soluciones de los ejercicios e), f) y g).
 64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
64 Tercer Año Medio Mtemátic Ministerio de Educción Actividd 3 Resuelven inecuciones y sistems de inecuciones con un incógnit; expresn ls soluciones en form gráfic y en notción de desigulddes; nlizn ls
OBJETIVO 1 DIFERENCIAR ENTRE LENGUAJE NUMÉRICO Y ALGEBRAICO NOMBRE: CURSO: FECHA: Cuadrado: P = a + a + a + a a
 OBJETIVO 1 DIFERENCIAR ENTRE LENGUAJE NUMÉRICO Y ALGEBRAICO NOMBRE: CURSO: FECHA: Potenci es l form brevid de escribir un multiplicción de fctores igules. n = (n veces) = Perímetro de un polígono es l
OBJETIVO 1 DIFERENCIAR ENTRE LENGUAJE NUMÉRICO Y ALGEBRAICO NOMBRE: CURSO: FECHA: Potenci es l form brevid de escribir un multiplicción de fctores igules. n = (n veces) = Perímetro de un polígono es l
TEMA 3: PROPORCIONALIDAD Y PORCENTAJES.
 TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
TEM : PROPORCIONLIDD Y PORCENTJES.. Conceptos de Rzón y Proporción. Se define l RZÓN entre dos números como l frcción que se form con ellos. Es decir l rzón entre y es:, con 0. De quí que ls frcciones
NÚMEROS RACIONALES ABSOLUTOS
 NÚMEROS RACIONALES ABSOLUTOS Frcción: es un pr ordendo de números nturles con l segund componente distint de cero. (, ) pr ordendo frcción es un frcción N N EQUIVALENCIA DE FRACCIONES * Frcciones diferentes,
NÚMEROS RACIONALES ABSOLUTOS Frcción: es un pr ordendo de números nturles con l segund componente distint de cero. (, ) pr ordendo frcción es un frcción N N EQUIVALENCIA DE FRACCIONES * Frcciones diferentes,
Los números racionales:
 El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
El número rel MATEMÁTICAS I 1 1. EL CONJUNTO DE LOS NÚMEROS REALES. LA RECTA REAL 1.1. El conjunto de los números reles. Como y sbes los números nturles surgen de l necesidd de contr, expresr medids, pr
LA FUNCIÓN LOGARÍTMICA
 LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
LA FUNCIÓN LOGARÍTMICA.- Definición.- Se denomin ritmo en bse de un número, l eponente que es preciso elevr pr que resulte. debe ser un número positivo y distinto de l unidd. Pr epresr que y es el ritmo
Taller de Matemáticas I
 Tller de Mtemátics I Semn y Tller de Mtemátics I Universidd CNCI de México Tller de Mtemátics I Semn y Temrio. Los números positivos.. Representción de números positivos... Frcciones... Decimles... Porcentjes..4.
Tller de Mtemátics I Semn y Tller de Mtemátics I Universidd CNCI de México Tller de Mtemátics I Semn y Temrio. Los números positivos.. Representción de números positivos... Frcciones... Decimles... Porcentjes..4.
REPASO DE ECUACIONES (4º ESO)
 TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
TIPOS DE ECUACIONES.- REPASO DE ECUACIONES ( ESO) Eisten diversos tipos de ecuciones, entre ells estudiremos: Polinómics: En ells, l incógnit prece solmente en epresiones polinómics. El grdo de un ecución
Números Naturales. Los números enteros
 Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
Números Nturles Con los números nturles contmos los elementos de un conjunto (número crdinl). O bien expresmos l posición u orden que ocup un elemento en un conjunto (ordinl). El conjunto de los números
1. Cuales son los números naturales?
 Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
Guí de mtemátics. Héctor. de bril de 015 1. Cules son los números nturles? Los números nturles son usdos pr contr (por ejemplo, hy cinco moneds en l mes ) o pr imponer un orden (por ejemplo,. Es t es l
DETERMINANTES. Los menores y los cofactores son de gran utilidad para encontrar determinantes de matrices de orden n>1.
 DETERINNTES DETERINNTE DE UN TRIZ CUDRD socido cd mtri cudrd h un número llmdo determinnte de, denotdo como det. Los determinntes nos proporcionn un método pr el cálculo de l mtri invers (en cso de eistir)
DETERINNTES DETERINNTE DE UN TRIZ CUDRD socido cd mtri cudrd h un número llmdo determinnte de, denotdo como det. Los determinntes nos proporcionn un método pr el cálculo de l mtri invers (en cso de eistir)
Toda ecuación lineal con dos incógnitas tiene un número ilimitado de soluciones de la forma (, y) gráfica determina una recta.
 Fcultd de Contdurí y Administrción. UNAM Sistems de ecuciones Autor: Dr. José Mnuel Becerr Espinos MATEMÁTICAS BÁSICAS SISTEMAS DE ECUACIONES SISTEMAS DE ECUACIONES Un ecución linel con dos incógnits x
Fcultd de Contdurí y Administrción. UNAM Sistems de ecuciones Autor: Dr. José Mnuel Becerr Espinos MATEMÁTICAS BÁSICAS SISTEMAS DE ECUACIONES SISTEMAS DE ECUACIONES Un ecución linel con dos incógnits x
Introducción. Objetivos de aprendizaje. Determinar las propiedades de las operaciones de números racionales
 L rect numéric, un cmino l estudio de los números reles Deducción de propieddes en ls operciones de números rcionles Introducción 0,1 1/ / 0,0 Multiplic por Rest 0, 1/ /7 1/ Figur 1. Rulet Objetivos de
L rect numéric, un cmino l estudio de los números reles Deducción de propieddes en ls operciones de números rcionles Introducción 0,1 1/ / 0,0 Multiplic por Rest 0, 1/ /7 1/ Figur 1. Rulet Objetivos de
INSTITUTO VALLADOLID PREPARATORIA página 1
 INSTITUTO VALLADOLID PREPARATORIA págin 1 págin PRODUCTOS NOTABLES 1.- CONCEPTO Conviene recordr lguns definiciones ásics. Así como cundo Adlerto se dedic jugr, por ejemplo, el futol, se le llm futolist
INSTITUTO VALLADOLID PREPARATORIA págin 1 págin PRODUCTOS NOTABLES 1.- CONCEPTO Conviene recordr lguns definiciones ásics. Así como cundo Adlerto se dedic jugr, por ejemplo, el futol, se le llm futolist
UNIVERSIDAD NACIONAL DE SAN LUIS FACULTAD DE CIENCIAS ECONÓMICAS JURÍDICAS y SOCIALES DEPARTAMENTO DE CIENCIAS BASICAS AREA DE MATEMATICA
 UNIVERSIDAD NACIONAL DE SAN LUIS FACULTAD DE CIENCIAS ECONÓMICAS JURÍDICAS SOCIALES DEPARTAMENTO DE CIENCIAS BASICAS AREA DE MATEMATICA UNIDAD Nº. NÚMEROS REALES. UNIVERSIDAD NACIONAL DE SAN LUIS FACULTAD
UNIVERSIDAD NACIONAL DE SAN LUIS FACULTAD DE CIENCIAS ECONÓMICAS JURÍDICAS SOCIALES DEPARTAMENTO DE CIENCIAS BASICAS AREA DE MATEMATICA UNIDAD Nº. NÚMEROS REALES. UNIVERSIDAD NACIONAL DE SAN LUIS FACULTAD
ÁLGEBRA: NIVEL MEDIO SUPERIOR ECUACIONES
 . LINEALES. Concepto de iguldd. º. Si l seleccionr dos conjuntos se encuentr que tienen los mismos elementos, estos conjuntos son igules. c c A B Pr presentr l iguldd se utiliz el símolo por lo que A B
. LINEALES. Concepto de iguldd. º. Si l seleccionr dos conjuntos se encuentr que tienen los mismos elementos, estos conjuntos son igules. c c A B Pr presentr l iguldd se utiliz el símolo por lo que A B
REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS
 TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
TRIIGONOMETRÍÍA REPASO DE MEDIDAS DE ÁNGULOS Y EQUIVALENCIAS Recuerd que los ángulos los medímos en grdos o en rdines. Además, los grdos podín dividirse en minutos segundos, de form similr como se distribuen
DETERMINANTES. Determinante es la expresión numérica de una matriz. Según el orden de la matriz el determinante se resuelve de distintas formas:
 ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
ÁLGEBR Educgui.com DETERMINNTES Determinnte es l expresión numéric de un mtriz. Según el orden de l mtriz el determinnte se resuelve de distints forms: DETERMINNTE DE SEGUNDO ORDEN Pr poder solucionr un
(lo podemos visualizar como el área de un cuadrado de lado 4) Pues bien, diremos que la base de dicha potencia, 4, es su raíz cuadrada exacta: 16 = 4.
 Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
Deprtmento de Mtemátics http://www.colegiovirgendegrci.org/eso/dmte.htm ARITMÉTICA: Rdicles. RADICALES... Ríz cudrd. Anlicemos los siguientes ejemplos: == es un potenci de se y exponente. El resultdo,,
TEMA 1. NÚMEROS REALES
 TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
TEMA. NÚMEROS REALES. El número que indic los dís del ño es un número muy curioso. Es el único número que es sum de los cudrdos de tres números nturles consecutivos y que demás es sum de los cudrdos de
( ) 4. Colegio Diocesano Sagrado Corazón de Jesús. MATEMÁTICAS I / 1º Bachillerato C y T LOGARTIMOS. log. log. log. 1 log log 3.
 Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
Colegio Diocesno Sgrdo Corzón de Jesús MATEMÁTICAS I / º Bchillerto C y T LOGARTIMOS Logritmos El ritmo de un número, m, positivo, en bse, positiv y distint de uno, es el eponente l que hy que elevr l
IES LA ASUNCIÓN
 IES LA ASUNCIÓN http://www.ieslsuncion.org Bloque II. Álger. Tem 7: Polinomios TEORÍA MATEMÁTICAS º ESO 1. EL ÁLGEBRA: PARA QUÉ SIRVE? Llmmos álger l prte de ls mtemátics en l que se utilizn letrs pr epresr
IES LA ASUNCIÓN http://www.ieslsuncion.org Bloque II. Álger. Tem 7: Polinomios TEORÍA MATEMÁTICAS º ESO 1. EL ÁLGEBRA: PARA QUÉ SIRVE? Llmmos álger l prte de ls mtemátics en l que se utilizn letrs pr epresr
INSTITUTO VALLADOLID PREPARATORIA Página 105 ELIPSE
 INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
INSTITUTO VALLADOLID PREPARATORIA Págin 05 6 LA ELIPSE 6. DEFINICIONES L elipse es el lugr geométrico de todos los puntos cuy sum de distncis dos puntos fijos, llmdos focos, es constnte. En l figur 6.,
LÁMINA No. 1.1 LECTURA Y ESCRITURA DE UN NÚMERO
 6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
6 LÁMINA No. 1.1 REPRESENTACION GRÁFICA DE N N {0, 1,,, 4, 5,...} Propieddes de N: 1. Tiene primer elemento. 0 1 4 5... 1er elemento suc() último elemento. Todo número tiene sucesor. No existe último elemento
CURSO PROPEDÉUTICO 2013 B
 CURSO PROPEDÉUTICO 01 B INSTITUTO TECNOLÓGICO SUPERIOR DE ZAPOPAN Fís. Edgr I. Sánchez Rngel L.P. Alm Luz Rndeles Gómez M en C. Frncisco Jvier Villseñor Pérez Mtr. A. Lizette Gutiérrez Gutiérrez Profs.
CURSO PROPEDÉUTICO 01 B INSTITUTO TECNOLÓGICO SUPERIOR DE ZAPOPAN Fís. Edgr I. Sánchez Rngel L.P. Alm Luz Rndeles Gómez M en C. Frncisco Jvier Villseñor Pérez Mtr. A. Lizette Gutiérrez Gutiérrez Profs.
Actividades que corregiremos los primeros días de clase
 ACTIVIDADES DE MATEMÁTICAS º ESO Actividdes que corregiremos los primeros dís de clse BLOQUE I: NÚMEROS I (Nº NATURAL POTENCIAS Y RAÍCES DIVISIBILIDAD Nº ENTEROS). Oserv ls siguientes plrs: BICICLETA (
ACTIVIDADES DE MATEMÁTICAS º ESO Actividdes que corregiremos los primeros dís de clse BLOQUE I: NÚMEROS I (Nº NATURAL POTENCIAS Y RAÍCES DIVISIBILIDAD Nº ENTEROS). Oserv ls siguientes plrs: BICICLETA (
El conjunto de los números reales se forma mediante la unión del conjunto de los números racionales y el conjunto de los números irracionales.
 El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
El conjunto de los números reles (R) El conjunto de los números reles se form medinte l unión del conjunto de los números rcionles y el conjunto de los números irrcionles. Propieddes del conjunto R R =
PRODUCTOS NOTABLES GUIA CIU NRO:
 Repúlic Bolivrin de Venezuel Ministerio de l Defens Universidd Ncionl Eperimentl Politécnic de l Fuerz Armd Núcleo Crcs Curso de Inducción Universitri CIU Cátedr: Rzonmiento Mtemático PRODUCTOS NOTABLES
Repúlic Bolivrin de Venezuel Ministerio de l Defens Universidd Ncionl Eperimentl Politécnic de l Fuerz Armd Núcleo Crcs Curso de Inducción Universitri CIU Cátedr: Rzonmiento Mtemático PRODUCTOS NOTABLES
Repaso de Matemática Básica
 Addison-Wesley s Repso de Mtemátic Básic Números Propieddes Importntes NÚMEROS NATURALES NÚMEROS ENTEROS NO NEGATIVOS {, 2, 3, 4, 5, } {0,, 2, 3, 4, } NÚMEROS ENTEROS {, 3, 2,, 0,, 2, } Rect Numéric 5
Addison-Wesley s Repso de Mtemátic Básic Números Propieddes Importntes NÚMEROS NATURALES NÚMEROS ENTEROS NO NEGATIVOS {, 2, 3, 4, 5, } {0,, 2, 3, 4, } NÚMEROS ENTEROS {, 3, 2,, 0,, 2, } Rect Numéric 5
Aplicaciones del cálculo integral
 Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
Aplicciones del cálculo integrl Aplicciones del cálculo integrl Cálculo del áre de un función Pr clculr el áre encerrd por un función en un intervlo [,] con el eje X, dee utilizrse l integrl definid. Csos:
3. El logaritmo de una potencia cuya base es igual a la base del logaritmo es igual al exponente de la potencia: Log a a m = m, ya que a m =a m
 LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
LOGARITMOS Ddo un número rel positivo, no nulo y distinto de 1, ( > 0; 0; 1), y un número n positivo y no nulo (n > 0;n 0), se llm ritmo en bse de n l exponente x l que hy que elevr dich bse pr obtener
Taller de Álgebra. 0, 1, 2, 3, 4, 5, los llamamos enteros no negativos o números naturales 0.5, 0.333, 0.75, 0.875, 4.333
 Tller de Álger. Dr. Blnc M. Prr UIA Tijun 0. Números reles rect numéric. Números reles son todos los números que representmos en l rect numéric. A cd punto de l rect corresponde un número rel pr cd número
Tller de Álger. Dr. Blnc M. Prr UIA Tijun 0. Números reles rect numéric. Números reles son todos los números que representmos en l rect numéric. A cd punto de l rect corresponde un número rel pr cd número
Respuesta: Con este resultado Anahí decide contratar a estos pintores.
 Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
Universidd de Concepción Fcultd de Ciencis Veterinris Nivelción de Mtemátics(0) Unidd-I: Conjunto de los Números Rcionles Introducción: Al plnter l necesidd de dividir números enteros, surge un problem:
APUNTES DE MATEMÁTICAS
 APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
APUNTES DE MATEMÁTICAS TEMA 8: FUNCIONES.LÍMITES º BACHILLERATO FUNCIONES.Límites y continuidd ÍNDICE. LíMITES Y CONTINUIDAD DE FUNCIONES...3. Definición límite de un función en un punto...4 3. Definición
Tutorial MT-m3. Matemática Tutorial Nivel Medio. Función cuadrática
 12345678901234567890 M te m átic Tutoril MT-m3 Mtemátic 2006 Tutoril Nivel Medio Función cudrátic Mtemátic 2006 Tutoril Función Cudrátic Mrco Teórico 1. Función cudrátic: Está representd por: y = x 2 +
12345678901234567890 M te m átic Tutoril MT-m3 Mtemátic 2006 Tutoril Nivel Medio Función cudrátic Mtemátic 2006 Tutoril Función Cudrátic Mrco Teórico 1. Función cudrátic: Está representd por: y = x 2 +
REGLAS DE LOS PRODUCTOS NOTABLES
 UNIDAD V.- PRODUCTOS NOTABLES Y FACTORIZACIO N Productos Notbles ( (b ( (d (e ( REGLAS DE LOS PRODUCTOS NOTABLES Un producto notble (multiplicción es quel que se puede obtener su resultdo sin necesidd
UNIDAD V.- PRODUCTOS NOTABLES Y FACTORIZACIO N Productos Notbles ( (b ( (d (e ( REGLAS DE LOS PRODUCTOS NOTABLES Un producto notble (multiplicción es quel que se puede obtener su resultdo sin necesidd
= a 11 a 22 a 12 a 21. = a 11 a 22 a 33 + a 12 a 23 a 31 + a 21 a 32 a 13
 Mtemátics Determntes Resumen DETERMINANTES (Resumen) Defición El determnte de un mtriz cudrd n x n es un número. Se otiene sumndo todos los posiles productos que se pueden formr tomndo n elementos de l
Mtemátics Determntes Resumen DETERMINANTES (Resumen) Defición El determnte de un mtriz cudrd n x n es un número. Se otiene sumndo todos los posiles productos que se pueden formr tomndo n elementos de l
EXPRESIONES ALGEBRAICAS. POLINOMIOS
 EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc
De preferencia aquella que tenga algún 1 como elemento. Mejor aún si conteniendo el 1 también tiene elementos iguales a cero.
 DETERMINANTE DE UNA MATRIZ DE ORDEN O MÁS PREGUNTA Clculr los determinntes siguientes ) ) c) RESOLUCIÓN Pr resolver el determinnte de un mtriz cudrd de orden o más es recomendle plicr el método de Reducción
DETERMINANTE DE UNA MATRIZ DE ORDEN O MÁS PREGUNTA Clculr los determinntes siguientes ) ) c) RESOLUCIÓN Pr resolver el determinnte de un mtriz cudrd de orden o más es recomendle plicr el método de Reducción
XI. LA HIPÉRBOLA LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO
 XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
XI. LA HIPÉRBOLA 11.1. LA HIPÉRBOLA COMO LUGAR GEOMÉTRICO Definición L hipérol es el lugr geométrico descrito por un punto P que se mueve en el plno de tl modo que el vlor soluto de l diferenci de sus
PSU Matemática NM-4 Guía 22: Congruencia de Triángulos
 Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
Centro Educcionl Sn Crlos de Argón. Dpto. Mtemátic. Nivel: NM 4 Prof. Ximen Gllegos H. PSU Mtemátic NM-4 Guí : Congruenci de Triángulos Nombre: Curso: Fech: - Contenido: Congruenci. Aprendizje Esperdo:
IES LA ASUNCIÓN
 MATEMÁTICAS º ESO Tem : ÁLGEBRA: Polinomios frcciones lgerics. TEORÍA. EXPRESIONES ALGEBRAICAS Trjr en álger consiste en mnejr relciones numérics en ls que un o más cntiddes son desconocids. Ests cntiddes
MATEMÁTICAS º ESO Tem : ÁLGEBRA: Polinomios frcciones lgerics. TEORÍA. EXPRESIONES ALGEBRAICAS Trjr en álger consiste en mnejr relciones numérics en ls que un o más cntiddes son desconocids. Ests cntiddes
3. Resuelve y simplifica: 6. Resuelve y simplifica: Nombre y apellidos : Materia: MATEMATICAS (PENDIENTES) Curso: 2º ESO.
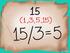 Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
Nombre y pellidos : Mteri: MATEMATICAS PENDIENTES) Curso: º ESO ª entreg Fech: INSTRUCCIONES: Pr est primer entreg deberás trbjr losejercicios del l que quí te djuntmos pr ello debes yudrte de tu cuderno
SOLUCIONARIO Poliedros
 SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
SOLUCIONARIO Poliedros SGUICES06MT-A16V1 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA Poliedros Ítem Alterntiv 1 D A Comprensión E B 5 D 6 C 7 D 8 B 9 D 10 C 11 E 1 D 1 A 1 C 15 E Comprensión 16 B Comprensión 17
 1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
1 VECTORES 1. MAGNITUDES ESCALARES Y VECTORIALES. Un mgnitud es un concepto bstrcto. Se trt de l ide de lgo útil que es necesrio medir. Ncen sí mgnitudes como l longitud, que represent l distnci entre
TEOREMA 1 (Criterio de la segunda derivada para extremos relativos)
 .. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
.. Problems de plicciones de máimos y mínimos En est sección se muestr como usr l primer y segund derivd de un función en l búsqued de vlores etremos en los llmdos: problems de plicciones o problems de
pág. 71 LIMITES 1. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerda del curso pasado los límites de sucesiones.
 LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
LIMITES. LIMITE DE UNA SUCESIÓN. EL NÚMERO e Recuerd del curso psdo los límites de sucesiones. L sucesión 4 4 n 4 n es especilmente interesnte. Empezmos desrrollndol. n,5,7...,44... Se trt de un sucesión
(a + b) 2 = a 2 + 2ab + b 2
 PRODUCTOS NOTABLES. BINOMIO CUADRADO. REPRESENTACIÓN GRÁFICA DEL CUADRADO DE LA SUMA DE DOS CANTIDADES El cudrdo de l sum de dos cntiddes puede representrse geométricmente cundo los vlores son positivos.
PRODUCTOS NOTABLES. BINOMIO CUADRADO. REPRESENTACIÓN GRÁFICA DEL CUADRADO DE LA SUMA DE DOS CANTIDADES El cudrdo de l sum de dos cntiddes puede representrse geométricmente cundo los vlores son positivos.
EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES 2º PARCIAL
 Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
Mtemátics pendientes de 1º (º prcil) 1 EJERCICIOS DE MATEMÁTICAS PARA ALUMNOS CON LAS MATEMÁTICAS DE 1º E.S.O. PENDIENTES º PARCIAL Fech tope pr entregrlos: 17 de bril de 015 Exmen el 3 de bril de 015
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO CALCULO DIFERENCIAL. Integral Indefinida
 Integrl Indefinid Estmos costumrdos decir que el producto el cociente son operciones inverss. Lo mismo sucede con l potencición l rdicción. Vmos estudir hor l operción invers de l diferencición. Dd l función
Integrl Indefinid Estmos costumrdos decir que el producto el cociente son operciones inverss. Lo mismo sucede con l potencición l rdicción. Vmos estudir hor l operción invers de l diferencición. Dd l función
 Wlter Orlndo Gonzles Cicedo POLINOMIOS NOTCIÓN FUNCIONL Se utiliz pr indicr ls vriles en un epresión lgeric. Pr ello empleremos letrs como P, F, G,, etc. P) se lee P de : vrile F;) se lee F de :, vrile,,
Wlter Orlndo Gonzles Cicedo POLINOMIOS NOTCIÓN FUNCIONL Se utiliz pr indicr ls vriles en un epresión lgeric. Pr ello empleremos letrs como P, F, G,, etc. P) se lee P de : vrile F;) se lee F de :, vrile,,
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
Pág Págin 56 PRACTICA Escribe los seis primeros términos de ls siguientes sucesiones: ) Cd término se obtiene sumndo l nterior El primero es 8 b) El primer término es 6 Los demás se obtienen multiplicndo
LÍMITES CONCEPTO INTUITIVO DE LÍMITE
 Mrí Teres Szostk Ingenierí Comercil Mtemátic II Clse Nº, LÍMITES El concepto de ite, es uno de los pilres en que se bs el Análisis Mtemático, se encontrb en 8 en estdo potencil, ern más principios intuitivos
Mrí Teres Szostk Ingenierí Comercil Mtemátic II Clse Nº, LÍMITES El concepto de ite, es uno de los pilres en que se bs el Análisis Mtemático, se encontrb en 8 en estdo potencil, ern más principios intuitivos
CENTRO DE FORMACIÓN PROFESIONAL. REVILLAGIGEDO Jesuitas - Gijón JOSÉ MANUEL FERNÁNDEZ GARCÍA
 CENTRO DE FORACIÓN PROFESIONAL REVILLAGIGEDO Jesuits - Gijón PRONTUARIO DE ATEÁTICAS PARA ELECTRÓNICOS Y ELÉCTRICOS JOSÉ ANUEL FERNÁNDEZ GARCÍA CÁLCULO NUÉRICO. Redondeo. Dependiendo de ls mgnitudes con
CENTRO DE FORACIÓN PROFESIONAL REVILLAGIGEDO Jesuits - Gijón PRONTUARIO DE ATEÁTICAS PARA ELECTRÓNICOS Y ELÉCTRICOS JOSÉ ANUEL FERNÁNDEZ GARCÍA CÁLCULO NUÉRICO. Redondeo. Dependiendo de ls mgnitudes con
lasmatematicas.eu Pedro Castro Ortega materiales de matemáticas Repaso de operaciones con números enteros
 lsmtemtics.eu Pedro Cstro Orteg Repso de operciones con números enteros º ESO Cómo se sumn y se restn números enteros? Es más fácil verlo con lgunos ejemplos que explicrlo con plrs. Ejemplo 1: Ejemplo
lsmtemtics.eu Pedro Cstro Orteg Repso de operciones con números enteros º ESO Cómo se sumn y se restn números enteros? Es más fácil verlo con lgunos ejemplos que explicrlo con plrs. Ejemplo 1: Ejemplo
open green road Guía Matemática FRACCIONES ALGEBRAICAS profesor: Nicolás Melgarejo .co
 Guí Mtemátic FRACCIONES ALGEBRAICAS profesor: Nicolás Melgrejo.co . Introducción El mnejo lgebrico es un herrmient básic que nos permite comunicr ides en el mbiente científico sin importr l lengu que ellos
Guí Mtemátic FRACCIONES ALGEBRAICAS profesor: Nicolás Melgrejo.co . Introducción El mnejo lgebrico es un herrmient básic que nos permite comunicr ides en el mbiente científico sin importr l lengu que ellos
INSTITUTO VALLADOLID PREPARATORIA página 81
 INSTITUTO VALLADOLID PREPARATORIA págin 81 págin 8 Si se divide un curt prte de un pstel l mitd se otiene un octv prte del mismo, lo que escrito en simologí mtemátic es Lo nterior es lo mismo que 1 1 4
INSTITUTO VALLADOLID PREPARATORIA págin 81 págin 8 Si se divide un curt prte de un pstel l mitd se otiene un octv prte del mismo, lo que escrito en simologí mtemátic es Lo nterior es lo mismo que 1 1 4
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES
 71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
71 BAC CNyS VECTORES 1. PRESENTACIÓN DEL TEMA 2. VECTORES Y OPERACIONES 3. COORDENADAS DE UN VECTOR 4. PRODUCTO ESCALAR DE VECTORES 5. APLICACIONES (EN UNA BASE ORTONORMAL) 6. EJERCICIOS Y PROBLEMAS Vectores
Manual de teoría: Álgebra Matemática Bachillerato
 Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
Mnul de teorí: Álgebr Mtemátic Bchillerto Relizdo por José Pblo Flores Zúñig Álgebr: José Pblo Flores Zúñig Págin Contenido: ) Álgebr. Fctorizción. Simplificción de epresiones lgebrics. Ecuciones Álgebr:
TEMA 3 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Matemáticas CCSSII 2º Bachillerato 1
 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Mtemátics CCSSII 2º Bchillerto 1 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES.1 DETERMINANTES DE ORDEN 2.1.1 DEFINICIÓN: El determinnte de un mtriz
TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Mtemátics CCSSII 2º Bchillerto 1 TEMA RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES.1 DETERMINANTES DE ORDEN 2.1.1 DEFINICIÓN: El determinnte de un mtriz
MATRICES. MATRIZ INVERSA. DETERMINANTES.
 DP. - AS - 59 7 Mteátics ISSN: 988-79X 5 6 MATRICES. MATRIZ INVERSA. DETERMINANTES. () Define rngo de un triz. () Un triz de tres fils y tres coluns tiene rngo tres, cóo vrí el rngo si quitos un colun?
DP. - AS - 59 7 Mteátics ISSN: 988-79X 5 6 MATRICES. MATRIZ INVERSA. DETERMINANTES. () Define rngo de un triz. () Un triz de tres fils y tres coluns tiene rngo tres, cóo vrí el rngo si quitos un colun?
MATEMÁTICAS PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 25 AÑOS LOGARITMOS
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS LOGARITMOS Unidd 4 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES 5 AÑOS UNIDAD DIDÁCTICA 4: LOGARITMOS. ÍNDICE. Introducción. Potencis funciones eponenciles.
