Funciones. Rectas y parábolas
|
|
|
- Gregorio Aguilera Sáez
- hace 7 años
- Vistas:
Transcripción
1 0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo de la figura, calcula: el perímetro. el área. P I E N S A C A L C U L A Perímetro = ( + ) = 6 Área = = Indica cuál de las siguientes gráficas es función: y = y = + + Logarítmica. c) Irracional. d) Trigonométrica. e) Racional. f) Eponencial. A P L I C A L A T E O R Í A Sí es función. No es función. Hay valores de para los que eisten dos valores de y. Por ejemplo, para =, y =,y = Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario de los 0 apartados. y = Clasifica las siguientes funciones: y = + y = log ( + ) c) y = + d) y = cos e) y = f) y = + Polinómica.Tipo de función: polinómica.. Dominio: Dom(f) = = Continuidad: es continua.. Periodicidad: no es periódica.. Simetrías: no es simétrica respecto del eje ni respecto del origen O(0, 0) 0 SOLUCIONARIO
2 6. Asíntotas: Verticales: no tiene. Horizontales: no tiene. 7. Corte con los ejes: Eje : O(0, 0),A(, 0) Eje : O(0, 0). Máimos y mínimos relativos: Máimo relativo: no tiene. Mínimo relativo: B(, ) Monotonía: Creciente ( ): (, Decreciente ( ): Puntos de infleión: no tiene. Curvatura: Convea (á): = Cóncava (Ü): Ö 0. Recorrido o imagen: Im(f) = [, Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario de los 0 apartados. y = +. Tipo de función: polinómica.. Dominio: Dom(f) = = Continuidad: es continua.. Periodicidad: no es periódica.. Simetrías: no es simétrica respecto del eje ni respecto del origen O(0, 0) 6. Asíntotas: Verticales: no tiene. Horizontales: no tiene. 7. Corte con los ejes: Eje : A(, 0), B(, 0) Eje : C(0, ). Máimos y mínimos relativos: Máimo relativo: D(, ) Mínimo relativo: no tiene. Monotonía: Creciente ( ): ) Decreciente ( ): (, Puntos de infleión: no tiene. Curvatura: Convea (á): Ö Cóncava (Ü): = 0. Recorrido o imagen: Im(f) = Función lineal y función afín Dada la función f() =, indica si es lineal o afín y calcula la pendiente. Función lineal. Pendiente: m = P I E N S A C A L C U L A TEMA 0. FUNCIONES. RECTAS PARÁBOLAS 0
3 A P L I C A L A T E O R Í A Dadas las funciones lineales siguientes, halla su pendiente e indica si son crecientes o decrecientes. Represéntalas: y = y = c) y = / m = ò y = m = ò Creciente. P(, ) m = ò y = m = ò Decreciente. 7 Dadas las funciones afines siguientes, halla su pendiente y la ordenada en el origen, e indica si son crecientes o decrecientes. Represéntalas: y = / y = / + m = / ò Creciente. b = c) m = / ò Creciente. 6 Halla las ecuaciones de las siguientes rectas: m = / ò Decreciente. b = P(, ) Halla las ecuaciones de las siguientes rectas: 0 SOLUCIONARIO
4 A(0, ) B(, ) A(0, ) B(, ) m = = 0 b = y = + ( ) m = = 0 b = y =. Función cuadrática Dada la función f() =, representada en el margen, indica: la ecuación del eje de simetría. las coordenadas del vértice, y si P I E N S A C A L C U L A = 0 V(0, ) es un mínimo. Halla el eje de simetría y las coordenadas del vértice, e indica si éste es un máimo o un mínimo en las siguientes funciones cuadráticas: y = 6 y = + c) y = d) y = + Eje de simetría: = V(, ) es un mínimo. Eje de simetría: = V(, ) es un máimo. c) Eje de simetría: = 0 V(0, ) es un mínimo. d) Eje de simetría: = V(, ) es un mínimo. 0 Representa las siguientes parábolas: y = y = A P L I C A L A T E O R Í A TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
5 Representa la parábola y = ; a partir de ella, representa la parábola y =. Halla el eje de simetría y las coordenadas del vértice, e indica si Eje de simetría: = V(, 0) es un máimo. Representa la parábola y = ; a partir de ella, representa la parábola y = ( ). Halla el eje de simetría y las coordenadas del vértice, e indica si Eje de simetría: = 0 V(0, ) es un mínimo. Representa la parábola y = ; a partir de ella, representa la parábola y = ( + ). Halla el eje de simetría y las coordenadas del vértice, e indica si Eje de simetría: = V(, ) es un mínimo. =. La parábola Dada la función f() =, representada en el margen, indica: la ecuación del eje de simetría. las coordenadas del vértice y si éste es máimo o mínimo. Eje de simetría: = V(, ) es un mínimo. P I E N S A C A L C U L A SOLUCIONARIO
6 Halla el eje de simetría y las coordenadas del vértice, indicando si éste es un máimo o un mínimo, de las siguientes funciones cuadráticas, y represéntalas: y = y = 6 + c) y = + + d) y = + A P L I C A L A T E O R Í A Halla la ecuación de la siguiente parábola: Eje de simetría: = V(, ) es un mínimo. = = (0, ) Eje de simetría: = V(, ) es un máimo. V(, ) V(, ) a = Eje de simetría: b = ò b = a ò b = a c = y = + = c) Eje de simetría: = V(, ) es un mínimo. 6 Halla la ecuación de la siguiente parábola: d) Eje de simetría: = V(, ) Es un máimo. = V(, ) (0, ) = V(, ) = a = Eje de simetría: b = ò b = a ò b = 6 a TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
7 c = y = = (0, ) 7 Halla la ecuación de la siguiente parábola: a = Eje de simetría: b = ò b = a ò b = a c = y = + + SOLUCIONARIO
8 Ejercicios y problemas. Funciones Indica cuál de las siguientes gráficas es función: Sí es función. No es función. Hay valores de para los que eisten dos valores de y. Por ejemplo, para = 0, y =, y = Clasifica las siguientes funciones: y = + y = log ( ) c) y = d) y = sen ( + π) e) y = f) y = Polinómica. Logarítmica. c) Irracional. d) Trigonométrica. e) Racional. f) Eponencial. y = + 6 y + =. Tipo de función: polinómica.. Dominio: Dom(f) = = Continuidad: es continua.. Periodicidad: no es periódica.. Simetrías: es simétrica respecto del eje 6. Asíntotas: Verticales: no tiene. Horizontales: no tiene. 7. Corte con los ejes: Eje : A(, 0), B(, 0) Eje : C(0, ). Máimos y mínimos relativos: Máimo relativo: no tiene. Mínimo relativo: C(0, ) Monotonía: Creciente ( ): (0, Decreciente ( ): Puntos de infleión: no tiene. Curvatura: Convea (á): = Cóncava (Ü): Ö 0. Recorrido o imagen: Im(f) = [, Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario de los diez apartados. y = + 0 Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario de los diez apartados. y =. Tipo de función: polinómica.. Dominio: Dom(f) = = Continuidad: es continua.. Periodicidad: no es periódica.. Simetrías: no es simétrica respecto del eje ni respecto del origen O(0, 0) TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
9 Ejercicios y problemas 6. Asíntotas: Verticales: no tiene. Horizontales: no tiene. 7. Corte con los ejes: Eje : O(0, 0),A(, 0) Eje : O(0, 0). Máimos y mínimos relativos: Máimo relativo: B(, ) Mínimo relativo: no tiene. Monotonía: Creciente ( ): Decreciente ( ): (, Puntos de infleión: no tiene. Curvatura: Convea (á): Ö Cóncava (Ü): = 0. Recorrido o imagen: Im(f) = Función lineal y función afín Halla mentalmente la pendiente de las siguientes funciones lineales o de proporcionalidad directa, di si son crecientes o decrecientes y represéntalas: y = y = c) y = d) y = c) m = / ò Creciente. d) m = / ò Decreciente. Halla las ecuaciones de las siguientes rectas: m = ò Creciente. m = / ò Decreciente. m = ò y = P(, ) 6 SOLUCIONARIO
10 d) m = / ò Decreciente. b = P(, ) m = ò y = Halla mentalmente la pendiente y la ordenada en el origen de las siguientes funciones afines, di si son crecientes o decrecientes y represéntalas: y = + y = + Halla las ecuaciones de las siguientes rectas: c) y = d) y = + m = ò Creciente. b = A(0, ) B(, ) m = / ò Decreciente. b = ( ) m = = 0 b = y = c) m = / ò Creciente. b = A(0, ) B(, ) m = = 0 b = y = + TEMA 0. FUNCIONES. RECTAS PARÁBOLAS 7
11 Ejercicios y problemas. Función cuadrática 6 Halla el eje de simetría y las coordenadas del vértice, e indica si éste es un máimo o un mínimo en las siguientes funciones cuadráticas: y = 6 + y = + c) y = + d) y = + Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? Eje de simetría: = V(, ) es un mínimo. Eje de simetría: = V(, ) es un máimo. c) Eje de simetría: = 0 V(0, ) es un mínimo. d) Eje de simetría: = V(, ) es un mínimo. = 0 V(0, 0) es un máimo. c) Creciente ( ): Decreciente ( ): (0, d) Es cóncava (Ü) 7 Representa la siguiente parábola: y = Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? Representa la parábola y = A partir de ella, representa la siguiente parábola: y = + Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? = 0 V(0, 0) es un mínimo. c) Creciente ( ): (0, Decreciente ( ): d) Es convea (á) Representa la siguiente parábola: y = = 0 V(0, ) es un máimo. c) Creciente ( ): Decreciente ( ): (0, d) Es cóncava (Ü) 0 Representa la función y = A partir de ella, representa la siguiente parábola: SOLUCIONARIO
12 y = ( ) Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)?. La parábola Representa la siguiente parábola: y = + Halla el eje de simetría. Halla las coordenadas del vértice, e indica si V(, 0) V(, ) = V(, 0) es un mínimo. c) Creciente ( ): (, Decreciente ( ): d) Es convea (á) = = V(, ) es un mínimo. = Representa la función y = A partir de ella, representa la siguiente parábola: y = ( + ) Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? Representa la siguiente parábola: y = 6 Halla el eje de simetría. Halla las coordenadas del vértice, e indica si V(, ) = = V(, ) es un máimo. = = V(, ) es un mínimo. c) Creciente ( ): (, Decreciente ( ) d) Es convea (á) Representa la siguiente parábola: y = + Halla el eje de simetría. Halla las coordenadas del vértice, e indica si TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
13 Ejercicios y problemas V(, ) = V(, ) es un mínimo. = = Representa la siguiente parábola: y = + 6 Halla el eje de simetría. Halla las coordenadas del vértice, e indica si = V(, ) es un máimo. 6 Halla la ecuación de las siguientes parábolas: a = Eje de simetría: b = ò b = a ò b = a c = y = + (0, 6) a = Eje de simetría: b = ò b = a ò b = a c = 6 y = (0, ) = = 0 SOLUCIONARIO
14 Para ampliar 7 Clasifica las siguientes funciones en lineales o afines. Halla mentalmente la pendiente, di si son crecientes o decrecientes y represéntalas: y = y = c) y = d) y = Halla las ecuaciones de las siguientes rectas: Función lineal. m = / ò Decreciente. c) d) Función afín. m = ò Decreciente. y = y = + c) y = + 6 d) y = c) Función afín. m = / ò Creciente. Representa la siguiente parábola: y = A partir de ella, representa la parábola: y = ( ) Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? d) Función lineal. m = / ò Creciente. = V(, 0) es un mínimo. = V(, 0) TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
15 Ejercicios y problemas Representa la siguiente parábola: y = 0 A partir de ella representa la parábola: y = ( ) + Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? c) Creciente ( ): (, Decreciente ( ): d) Es convea (á) = V(, ) = V(, ) es un mínimo. c) Creciente ( ): (, Decreciente ( ): ) d) Es convea (á) Halla la ecuación de las siguientes parábolas: = V(, ) es un máimo. c) Creciente ( ): Decreciente ( ): (, d) Es cóncava (Ü) Representa la siguiente parábola: y = Halla el eje de simetría. Halla las coordenadas del vértice, e indica si c) Dónde es creciente y dónde decreciente? d) Es convea (á) o cóncava (Ü)? (0, ) a = Eje de simetría: b = ò b = a ò b = a c = y = + = V(, ) = a = = (0, 0) SOLUCIONARIO
16 Eje de simetría: b = ò b = a ò b = 6 a c = 0 y = + 6 Halla algebraicamente los puntos de corte de las siguientes parábolas con los ejes de coordenadas, representa las parábolas y comprueba el resultado. y = + + y = c) y = + + d) y = + Eje : + + = 0 ò =, = A(, 0), B(, 0) Eje : C(0, ) Eje : = 0 ò = 0, = O(0, 0), B(, 0) Eje : O(0, 0) d) Eje : + = 0 ò No tiene solución. Eje :A(0, ) Halla algebraicamente los puntos de corte de la recta y la parábola siguientes, representa las gráficas y comprueba el resultado: y = y = Se resuelve el sistema formado por la ecuación de la recta y de la parábola: =, y = ò A(, ) =, y = ò B(, ) B(, ) A(, ) c) Eje : + + = 0 ò = A(, 0) Eje : B(0, ) Halla algebraicamente los puntos de corte de las siguientes parábolas, representa las parábolas y comprueba el resultado: y = y = + TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
17 Ejercicios y problemas Se resuelve el sistema formado por las ecuaciones de las dos parábolas: =,y = ò A(, ) =, y = ò B(, ) A(, ) B(, ) Problemas 6 La parábola y = a + b + c pasa por el origen de coordenadas. Cuánto vale c? Si la parábola pasa además por los puntos A(, ) y B(, ), calcula el valor de los coeficientes a y b c) Escribe la ecuación de la parábola. d) Represéntala gráficamente. c = 0 Se resuelve el sistema: a b = a + b = } a =, b = c) y = + d) B(, ) Se resuelve el sistema: 6 + b + c = + b + c = } b =,c = y = + c) B(, ) A(, ) La distancia de seguridad que deben guardar los coches entre sí, en circulación, se recoge en la tabla siguiente: 7 A(, ) Sea la parábola y = + b + c Calcula los valores de b y c sabiendo que pasa por los puntos A(, ) y B(, ) Escribe la ecuación de la parábola. c) Represéntala gráficamente. Velocidad (km/h) Distancia de seguridad (m) Epresa la distancia de seguridad en función de la velocidad, y representa la gráfica. SOLUCIONARIO
18 y = ( ) 0 Longitud (m) Velocidad (km/h) El perímetro de un rectángulo mide m. Epresa el área del rectángulo, en función del lado de la base. Representa la función e indica el valor del lado de la base para el que el área se hace máima. Dinero ( ) 0, 0, 0, 0, 0, Tiempo (min) El beneficio, en miles de euros, que se obtiene al vender a una unidad de un determinado producto viene dado por la fórmula B() = + 0 Representa la función B() Determina el precio al que hay que vender el producto para obtener el máimo beneficio. Si el perímetro mide m, la base más la altura mide m Dinero ( 000) 7 6 = V(, ) 67 Dinero ( ) y = ( ) y = El máimo se obtiene para =, que forma un cuadrado de área m 0 Un servicio de telefonía cobra 0, por el uso del servicio y 0,06 por cada minuto. Escribe la fórmula de la función que epresa el dinero que se paga en función del tiempo y representa su gráfica. y = 0, + 0,06 y = = V(, ) A la unidad, se obtiene el máimo beneficio, que es de 000 Se depositan 000 a un % de interés simple anual. Epresa el interés en función del tiempo y representa la gráfica. y = 000 0,0 y = 0 Dinero ( ) Tiempo (años) La energía cinética de un móvil de masa m viene dada por la siguiente fórmula: TEMA 0. FUNCIONES. RECTAS PARÁBOLAS
19 Ejercicios y problemas E(v) = mv donde v es la velocidad del móvil en m/s; m, la masa en kilos, y E, la energía en julios. Dibuja la gráfica que epresa la energía cinética en función de la velocidad de un cuerpo de kg de masa. Qué tipo de gráfica es? E = mv Si m = kg E = v Velocidad (m/h) Energía (julios) Es una parábola. Energía (julios) / 67 Velocidad (m/s) Halla el área de un cuadrado en función del lado. Represéntala gráficamente. / Para profundizar 6 Escribe la ecuación de la parábola que tiene el vértice en V(, ) y pasa por P(, ) Si el vértice es V(, ) y pasa por P(, ) ò a = Se resuelve el sistema: + b + c = + b + c = } b =, c = 6 y = + 6 Escribe la función que da el volumen de un cilindro de 0 cm de altura en función del radio de la base. Represéntala. y = 0π Volumen (cm ) cm Longitud (cm) y = Área (m ) 7 67 Longitud (m) 7 La demanda y la oferta de un determinado producto en función del precio son: Oferta: y = Demanda: y = + donde se epresa en euros, e y es la cantidad ofertada o demandada. Halla el punto de equilibrio algebraicamente. Representa las funciones y comprueba el resultado. 6 SOLUCIONARIO
20 Se resuelve el sistema de las dos ecuaciones: =, y = Dos móviles inician su movimiento desde un punto O. El primero se desplaza según la fórmula e = t, y el segundo móvil, según e = t; donde t se mide en segundos, y e, en metros. Representa las gráficas de sus movimientos e interpreta el resultado. Dinero ( ) Oferta Demanda 670 Dinero ( ) Al principio, el móvil recorre un mayor espacio en el mismo tiempo; éste se iguala a los s, y a partir de los s, el er móvil recorre un espacio mayor. Dos móviles inician su movimiento desde un punto O. El primero se desplaza según la fórmula e = t, y el segundo móvil, según e = t; donde t se mide en segundos, y e, en metros. Representa las gráficas de sus movimientos e interpreta el resultado sabiendo que el segundo móvil parte s más tarde que el primero. El móvil alcanza al primero a los s y está por delante hasta los 6 s, cuando se vuelven a encontrar a los m del recorrido.a partir de ese instante, el er móvil va por delante del. Longitud (m) E 0 e = t 7 6 e = t T 670 Tiempo (s) Longitud (m) E 0 e = t 7 6 e = t T 670 Tiempo (s) TEMA 0. FUNCIONES. RECTAS PARÁBOLAS 7
6 Funciones. 1. Estudio gráfico de una función. Piensa y calcula. Aplica la teoría
 6 Funciones 1. Estudio gráfico de una función Piensa y calcula Indica cuál de las siguientes funciones es polinómica y cuál racional: 2 + 5 f() = f() = 3 5 2 + 6 4 2 4 Racional. Polinómica. Aplica la teoría
6 Funciones 1. Estudio gráfico de una función Piensa y calcula Indica cuál de las siguientes funciones es polinómica y cuál racional: 2 + 5 f() = f() = 3 5 2 + 6 4 2 4 Racional. Polinómica. Aplica la teoría
BLOQUE IV. Funciones. 10. Funciones. Rectas y parábolas 11. Funciones racionales, irracionales, exponenciales y logarítmicas 12. Límites y derivadas
 BLOQUE IV Funciones 0. Funciones. Rectas y parábolas. Funciones racionales, irracionales, exponenciales y logarítmicas. Límites y derivadas 0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo
BLOQUE IV Funciones 0. Funciones. Rectas y parábolas. Funciones racionales, irracionales, exponenciales y logarítmicas. Límites y derivadas 0 Funciones. Rectas y parábolas. Funciones Dado el rectángulo
Cálculo de derivadas
 0 Cálculo de derivadas. La derivada Piensa y calcula La gráfica f() representa el espacio que recorre un coche en función del tiempo. Calcula mentalmente: a) la pendiente de la recta secante, r, que pasa
0 Cálculo de derivadas. La derivada Piensa y calcula La gráfica f() representa el espacio que recorre un coche en función del tiempo. Calcula mentalmente: a) la pendiente de la recta secante, r, que pasa
Funciones algebraicas y trascendentes
 7 Funciones algebraicas y trascendentes. Funciones polinómicas Piensa y calcula Dibuja una recta que tenga de pendiente y pase por el punto P(0, ) P(0, ) Aplica la teoría. Analiza de qué grado pueden ser
7 Funciones algebraicas y trascendentes. Funciones polinómicas Piensa y calcula Dibuja una recta que tenga de pendiente y pase por el punto P(0, ) P(0, ) Aplica la teoría. Analiza de qué grado pueden ser
Aplicaciones de las derivadas
 11 Aplicaciones de las derivadas 1. Representación de funciones polinómicas Piensa y calcula Calcula mentalmente: a) lím ( 3 3) b) lím ( 3 3) +@ a) + @ b) @ @ Aplica la teoría Representa las siguientes
11 Aplicaciones de las derivadas 1. Representación de funciones polinómicas Piensa y calcula Calcula mentalmente: a) lím ( 3 3) b) lím ( 3 3) +@ a) + @ b) @ @ Aplica la teoría Representa las siguientes
Alonso Fernández Galián
 Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
Alonso Fernández Galián TEMA 3: ESTUDIO Y REPRESENTACIÓN DE FUNCIONES Para representar gráficamente una función deben estudiarse los siguientes aspectos: i) Dominio. ii) Puntos de corte con los ejes de
BLOQUE III Funciones
 BLOQUE III Funciones 8. Funciones 9. Continuidad, límites y asíntotas 0. Cálculo de derivadas. Aplicaciones de las derivadas. Integrales 8 Funciones. Estudio gráfico de una función Piensa y calcula Indica
BLOQUE III Funciones 8. Funciones 9. Continuidad, límites y asíntotas 0. Cálculo de derivadas. Aplicaciones de las derivadas. Integrales 8 Funciones. Estudio gráfico de una función Piensa y calcula Indica
Funciones racionales, irracionales y exponenciales
 0 Funciones racionales, irracionales y eponenciales. Funciones racionales Despeja y de la epresión y = 6. Qué tipo de función es? P I E N S A C A L C U L A 6 y = Es una función racional que corresponde
0 Funciones racionales, irracionales y eponenciales. Funciones racionales Despeja y de la epresión y = 6. Qué tipo de función es? P I E N S A C A L C U L A 6 y = Es una función racional que corresponde
SOLUCIÓN. BLOQUE DE FUNCIONES.
 SOLUCIÓN. BLOQUE DE FUNCIONES. Análisis de funciones 1. a) y c) son funciones, porque para cada valor de hay un único valor de y. b) no es una función, porque para cada valor de hay dos valores de y. 2.
SOLUCIÓN. BLOQUE DE FUNCIONES. Análisis de funciones 1. a) y c) son funciones, porque para cada valor de hay un único valor de y. b) no es una función, porque para cada valor de hay dos valores de y. 2.
REPRESENTACIÓN DE FUNCIONES
 REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
REPRESENTACIÓN DE FUNCIONES Página 5 REFLEXIONA Y RESUELVE Descripción de una gráfica Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos, y sin mirar la gráfica que aparece al principio,
Página 194 EJERCICIOS Y PROBLEMAS PROPUESTOS. Tasa de variación media PARA PRACTICAR UNIDAD
 UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
UNIDAD Página 9 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Tasa de variación media Calcula la tasa de variación media de esta función en los intervalos: a) [, 0] b) [0, ] c) [, 5] 0 5 f (0) f ( ) a)
Funciones racionales, irracionales y exponenciales
 0 Funciones racionales, irracionales y exponenciales. Funciones racionales Despeja y de la expresión xy = 6. Qué tipo de función es? P I E N S A C A L C U L A 6 y = x Es una función racional que corresponde
0 Funciones racionales, irracionales y exponenciales. Funciones racionales Despeja y de la expresión xy = 6. Qué tipo de función es? P I E N S A C A L C U L A 6 y = x Es una función racional que corresponde
Ficha 1. Formas de expresar una función
 Ficha 1. Formas de expresar una función 1. En unas instalaciones deportivas cobran 5 euros por la entrada, que da derecho a la utilización de todas las dependencias salvo las pistas de tenis, por las que
Ficha 1. Formas de expresar una función 1. En unas instalaciones deportivas cobran 5 euros por la entrada, que da derecho a la utilización de todas las dependencias salvo las pistas de tenis, por las que
x = 1 Asíntota vertical
 EJERCICIO Sea la función f ( ). a) Indique el dominio de definición de f, sus puntos de corte con los ejes, sus máimos mínimos, eisten, sus intervalos de crecimiento decrecimiento. b) Obtenga las ecuaciones
EJERCICIO Sea la función f ( ). a) Indique el dominio de definición de f, sus puntos de corte con los ejes, sus máimos mínimos, eisten, sus intervalos de crecimiento decrecimiento. b) Obtenga las ecuaciones
Página 267 EJERCICIOS Y PROBLEMAS PROPUESTOS. Dominio de definición PARA PRACTICAR UNIDAD. 1 Halla el dominio de definición de estas funciones:
 0 Página 7 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Dominio de definición Halla el dominio de definición de estas funciones: y = y = c) y = + ( ) d) y = e) y = f) y = + + 5 + Á {, 0} Á {} c) Á {
0 Página 7 EJERCICIOS PROBLEMAS PROPUESTOS PARA PRACTICAR Dominio de definición Halla el dominio de definición de estas funciones: y = y = c) y = + ( ) d) y = e) y = f) y = + + 5 + Á {, 0} Á {} c) Á {
BLOQUE III Funciones
 BLOQUE III Funciones 0. Rectas e hipérbolas 0 Rectas e hipérbolas. Las funciones P I E N S A C A L C U L A Representa en unos ejes de coordenadas todos los puntos en que la ordenada sea el doble de la
BLOQUE III Funciones 0. Rectas e hipérbolas 0 Rectas e hipérbolas. Las funciones P I E N S A C A L C U L A Representa en unos ejes de coordenadas todos los puntos en que la ordenada sea el doble de la
FUNCIONES REALES DE VARIABLE REAL
 MatemáticasNM Curso 0- FUNCIONES REALES DE VARIABLE REAL. Determina gráficamente el dominio y recorrido de cada una de las siguientes funciones: a) f() = b) f() = c) f() = d) f() = + d) f() = + e) f()
MatemáticasNM Curso 0- FUNCIONES REALES DE VARIABLE REAL. Determina gráficamente el dominio y recorrido de cada una de las siguientes funciones: a) f() = b) f() = c) f() = d) f() = + d) f() = + e) f()
Completa esta parábola y señala sus elementos y sus propiedades. 1 X. El dominio de la función es todos los números reales:.
 Representa la función que relaciona el área de un triángulo rectángulo isósceles la longitud del cateto. a) Cuál es la variable dependiente? b) la variable independiente? = a) La variable independiente
Representa la función que relaciona el área de un triángulo rectángulo isósceles la longitud del cateto. a) Cuál es la variable dependiente? b) la variable independiente? = a) La variable independiente
TEMA 0 FUNCIONES ***************
 TEMA 0. Definición y terminología.. Funciones conocidas. 3. Operaciones con funciones. 4. Funciones inversas. FUNCIONES ***************. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable
TEMA 0. Definición y terminología.. Funciones conocidas. 3. Operaciones con funciones. 4. Funciones inversas. FUNCIONES ***************. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable
5Soluciones a los ejercicios y problemas PÁGINA 116
 Soluciones a los ejercicios y problemas PÁGINA 6 Pág. P RACTICA Funciones lineales Asocia a cada función su ecuación. Di, en cada caso, cuál es su pendiente. a) y + = 0 b) y = c) y = 6 d) y = b) y = 6
Soluciones a los ejercicios y problemas PÁGINA 6 Pág. P RACTICA Funciones lineales Asocia a cada función su ecuación. Di, en cada caso, cuál es su pendiente. a) y + = 0 b) y = c) y = 6 d) y = b) y = 6
TEMA 4 FUNCIONES ELEMENTALES
 Tema 4 Funciones elementales Matemáticas CCSSI º Bachillerato TEMA 4 FUNCIONES ELEMENTALES FUNCIÓN EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
Tema 4 Funciones elementales Matemáticas CCSSI º Bachillerato TEMA 4 FUNCIONES ELEMENTALES FUNCIÓN EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
6 si x -4 (x+2) 2 si -4 < x -1 4 si x > x+1 si 0 x 1 x si 1 < x < 3 6-x si 3 x 4
 . Calcula la derivada de las siguientes funciones:. y = 2-2 +2 2. y = 2-2 2 +2. y = 2 -ln +e 4. y = 2 e 2 5. y = e 6. y = 2 ln 2 7. y = 2-8. y = e. y = 2 + 4. y = ln 2-5. y = 2 2 2 6. y = 2-9. y = e 2
. Calcula la derivada de las siguientes funciones:. y = 2-2 +2 2. y = 2-2 2 +2. y = 2 -ln +e 4. y = 2 e 2 5. y = e 6. y = 2 ln 2 7. y = 2-8. y = e. y = 2 + 4. y = ln 2-5. y = 2 2 2 6. y = 2-9. y = e 2
Apuntes de Funciones
 Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
1. Función cuadrática y traslación vertical. Completa la siguiente tabla y di qué números se obtienen en la última fila: 36 Diferencia de áreas
 0 Función cuadrática. Función cuadrática y traslación vertical Completa la siguiente tala y di qué números se otienen en la última fila: P I E N S A C A L C U L A Longitud del lado: x 0 4 5 6 Superficie:
0 Función cuadrática. Función cuadrática y traslación vertical Completa la siguiente tala y di qué números se otienen en la última fila: P I E N S A C A L C U L A Longitud del lado: x 0 4 5 6 Superficie:
TEMA 7. FUNCIONES ELEMENTALES
 TEMA 7. FUNCIONES ELEMENTALES 8.1. Funciones cuya gráfica es una recta. - Función constante. - Función de proporcionalidad. - Función lineal. - Pendiente. 8.2. Función cuadrática. - Representación gráfica
TEMA 7. FUNCIONES ELEMENTALES 8.1. Funciones cuya gráfica es una recta. - Función constante. - Función de proporcionalidad. - Función lineal. - Pendiente. 8.2. Función cuadrática. - Representación gráfica
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Página 75 REFLEIONA RESUELVE Tomar un autobús en marca En la gráfica siguiente, la línea roja representa el movimiento de un autobús que arranca de la
7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Página 75 REFLEIONA RESUELVE Tomar un autobús en marca En la gráfica siguiente, la línea roja representa el movimiento de un autobús que arranca de la
Características globales de las funciones
 Características globales de las funciones. Funciones Considera los rectángulos con un lado de doble longitud que el otro. Expresa el perímetro y el área en función del lado menor. P = (x + x) = x A = x
Características globales de las funciones. Funciones Considera los rectángulos con un lado de doble longitud que el otro. Expresa el perímetro y el área en función del lado menor. P = (x + x) = x A = x
8. Características globales de las funciones
 9 SOLUCIONARIO 8. Características globales de las funciones. FUNCIONES PIENSA CALCULA Considera los rectángulos con un lado de doble longitud que el otro. Expresa el perímetro y el área en función del
9 SOLUCIONARIO 8. Características globales de las funciones. FUNCIONES PIENSA CALCULA Considera los rectángulos con un lado de doble longitud que el otro. Expresa el perímetro y el área en función del
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva 1, Ejercicio, Opción A Reserva
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Página 0 REFLEXIONA Y RESUELVE Tomar un autobús en marca En la gráfica siguiente, la línea roja representa el movimiento de un autobús que arranca de la
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Página 0 REFLEXIONA Y RESUELVE Tomar un autobús en marca En la gráfica siguiente, la línea roja representa el movimiento de un autobús que arranca de la
Funciones 1. D = Dom ( f ) = x R / f(x) R. Recuerda como determinabas los dominios de algunas funciones: x x
 Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
IES PADRE SUÁREZ MATEMÁTICAS II DEPARTAMENTO DE MATEMÁTICAS
 Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
Ejercicios de continuidad y derivabilidad. Selectividad de 008, 009, 00 y 0 Anális 008 Ejercicio.- Sean f : R R y g : R R las funciones definidas por f() = + a + b y g() = c e -(+). Se sabe que las gráficas
REPRESENTACIÓN DE FUNCIONES
 8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
8 REPRESENTACIÓN DE FUNCIONES Página 86 Descripción de una gráfica. Copia en tu cuaderno los datos encuadrados en rojo. A partir de ellos y sin mirar la gráfica que aparece al principio, representa esta
que asocia a cada número entero su triple menos dos:
 Dada la función f que asocia a cada número entero su triple menos dos: a) Escribe la epresión que nos proporciona f 0,, b) Calcula la imagen para ) Dada la siguiente función : ), ) y 0) a) Calcula b) Determina
Dada la función f que asocia a cada número entero su triple menos dos: a) Escribe la epresión que nos proporciona f 0,, b) Calcula la imagen para ) Dada la siguiente función : ), ) y 0) a) Calcula b) Determina
Matemáticas II TEMA 9 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Propuestos
 Matemáticas II TEMA 9 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Propuestos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión
Matemáticas II TEMA 9 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Propuestos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión
A) IMÁGENES Y ANTI-IMÁGENES. DOMINIO E IMAGEN DE UNA FUNCIÓN. COMPOSICIÓN DE FUNCIONES Y FUNCIÓN INVERSA. ( (
 A) IMÁGENES Y ANTI-IMÁGENES. DOMINIO E IMAGEN DE UNA FUNCIÓN. COMPOSICIÓN DE FUNCIONES Y FUNCIÓN INVERSA. 1. Calcula el dominio de las siguientes funciones: ( ( ( ( ( ( 2. Calcula la imagen de las siguientes
A) IMÁGENES Y ANTI-IMÁGENES. DOMINIO E IMAGEN DE UNA FUNCIÓN. COMPOSICIÓN DE FUNCIONES Y FUNCIÓN INVERSA. 1. Calcula el dominio de las siguientes funciones: ( ( ( ( ( ( 2. Calcula la imagen de las siguientes
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 5 Pág. Página 5 PRACTICA Funciones cuadráticas Representa las siguientes funciones haciendo, en cada caso, una tabla de valores como esta, y di cuál es el vértice de cada parábola: y a) y = + b) y = c)
5 Pág. Página 5 PRACTICA Funciones cuadráticas Representa las siguientes funciones haciendo, en cada caso, una tabla de valores como esta, y di cuál es el vértice de cada parábola: y a) y = + b) y = c)
Unidad 6: Funciones reales de variable real.
 Funciones reales de variable real 1 Unidad 6: Funciones reales de variable real. 1.- Concepto de función. Expresión analítica de una función. Variables x e y Existe relación entre x e y No hay relación
Funciones reales de variable real 1 Unidad 6: Funciones reales de variable real. 1.- Concepto de función. Expresión analítica de una función. Variables x e y Existe relación entre x e y No hay relación
8 Aplicaciones. de las derivadas. 1. Máximos, mínimos y monotonía. Piensa y calcula. Aplica la teoría
 8 Aplicaciones de las derivadas. Máimos, mínimos y monotonía Piensa y calcula Dada la gráfica de la función f() = representada en el margen, halla los máimos y los mínimos relativos y los intervalos de
8 Aplicaciones de las derivadas. Máimos, mínimos y monotonía Piensa y calcula Dada la gráfica de la función f() = representada en el margen, halla los máimos y los mínimos relativos y los intervalos de
APLICACIONES DE LAS DERIVADAS
 APLICACIONES DE LAS DERIVADAS Apuntes de A. Cabañó. Calcula la tasa de variación media de la función +- en los intervalos: a) [-,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación
APLICACIONES DE LAS DERIVADAS Apuntes de A. Cabañó. Calcula la tasa de variación media de la función +- en los intervalos: a) [-,0], b) [0,], c) [,]. Sol: a) 0; b) ; c) 6. Calcula la tasa de variación
x 2 a) Calcula el valor de k. b) Halla la ecuación de la recta tangente a la gráfica de la función f en el punto de abscisa x = 1.
 . [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
. [0] [SEP-B] Sea la función f definida por f() = e- para. - a) Estudia las asíntotas de la gráfica de f. b) Halla los etremos relativos (abscisas donde se obtienen y valores que se alcanzan) y los intervalos
1. y = 3x 5-4x y = x+ln x 3. y = 2x 2 -e 2 4. y = xe x 5. y = x x 6. y = x+2 x-2
 Colección A.. Calcula la derivada de las siguientes funciones:. y = 5-4 -4. y = +ln. y = -e 4. y = e 5. y =. y = + 7. y = ln 8. y = e + 9. y = (+) 0. y =. y = e -. y = (-)e - e. y = - 4. y = ln 5. y =
Colección A.. Calcula la derivada de las siguientes funciones:. y = 5-4 -4. y = +ln. y = -e 4. y = e 5. y =. y = + 7. y = ln 8. y = e + 9. y = (+) 0. y =. y = e -. y = (-)e - e. y = - 4. y = ln 5. y =
Propiedades de las funciones derivables. Representación gráfica de funciones. Determinar los puntos de inflexión. (Junio 1997)
 Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
Matemáticas II. Curso 008/009 de funciones 1 1. Determinar las asíntotas de f () =. Estudiar la concavidad y conveidad. 1 + Determinar los puntos de infleión. (Junio 1997) 1 Por un lado, lim 1 = 0 y =
EJERCICIOS RESUELTOS TEMA 2: DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. APLICACIONES.
 EJERCICIOS RESUELTOS TEMA : DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. APLICACIONES. Ejercicio 1 Calcula las funciones derivadas de las siguientes funciones y simplifícalas: a) f ( ) sine b)
EJERCICIOS RESUELTOS TEMA : DERIVADA DE UNA FUNCIÓN EN UN PUNTO. FUNCIÓN DERIVADA. APLICACIONES. Ejercicio 1 Calcula las funciones derivadas de las siguientes funciones y simplifícalas: a) f ( ) sine b)
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 Pág. Página 58 PRACTICA Funciones cuadráticas Representa las siguientes funciones haciendo, en cada caso, una tabla de valo- y res como esta, y di cuál es el vértice de cada parábola: a) y = + b) y = c)
Pág. Página 58 PRACTICA Funciones cuadráticas Representa las siguientes funciones haciendo, en cada caso, una tabla de valo- y res como esta, y di cuál es el vértice de cada parábola: a) y = + b) y = c)
PÁGINA Representa: a) y = 2x. b) y = 2 3 x. c) y = 1 4 x. d) y = 7 3 x. 2 Representa: a) y = 3 b) y = 2 c) y = 0. d) y = 5
 Soluciones a las actividades de cada epígrafe PÁGINA 6 Pág. Representa: a) y = x y = x y = x 3 b) y = 3 x c) y = x y = x d) y = 7 3 x 7 y = x 3 Representa: a) y = 3 b) y = c) y = 0 y = 3 y = 0 y = d) y
Soluciones a las actividades de cada epígrafe PÁGINA 6 Pág. Representa: a) y = x y = x y = x 3 b) y = 3 x c) y = x y = x d) y = 7 3 x 7 y = x 3 Representa: a) y = 3 b) y = c) y = 0 y = 3 y = 0 y = d) y
Autoevaluación. Bloque IV. Análisis. BACHILLERATO Matemáticas I. Página Observa la gráfica de la función y = f (x) y a partir de ella responde:
 Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
Autoevaluación Página Observa la gráfica de la función y = f () y a partir de ella responde: a) Cuál es su dominio de definición? su recorrido? b) Representa gráficamente: y = f ( + ); y = f () + ; y =
La variable independiente x es aquella cuyo valor se fija previamente. La variable dependiente y es aquella cuyo valor se deduce a partir de x.
 Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
Bloque 8. FUNCIONES. (En el libro Temas 10, 11 y 12, páginas 179, 197 y 211) 1. Definiciones: función, variables, ecuación, tabla y gráfica. 2. Características o propiedades de una función: 2.1. Dominio
9. Rectas e hipérbolas
 08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
08 SOLUCIONARIO 9. Rectas e hipérbolas Representa gráficamente las siguientes ecuaciones. Di cuáles son funciones y clasifícalas: 8. y =. FUNCIONES CONSTANTES LINEALES PIENSA CALCULA y = Halla mentalmente
FUNCIONES FUNCIONES POLINÓMICAS DE GRADO UNO Y CERO. Funciones de proporcionalidad directa
 Funciones de ecuación: ( ) FUNCIONES = m + n ; m y n son números reales Dom = R. Es continua en su dominio. Gráica: una recta m es la pendiente de la recta La pendiente de una recta es el cociente entre
Funciones de ecuación: ( ) FUNCIONES = m + n ; m y n son números reales Dom = R. Es continua en su dominio. Gráica: una recta m es la pendiente de la recta La pendiente de una recta es el cociente entre
Bloque 3. Funciones. 1. Análisis de funciones
 Bloque 3. Funciones 1. Análisis de funciones 1. Concepto de función Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda,
Bloque 3. Funciones 1. Análisis de funciones 1. Concepto de función Una función es una relación entre dos magnitudes, de tal manera que a cada valor de la primera le corresponde un único valor de la segunda,
Bloque 3. Análisis. 2. Tipos de funciones
 Bloque 3. Análisis 2. Tipos de funciones 1. Función lineal Es una función polinómica de primer grado y tiene una ecuación del tipo: y = mx. Su gráfica es una línea recta que pasa por el origen de coordenadas,
Bloque 3. Análisis 2. Tipos de funciones 1. Función lineal Es una función polinómica de primer grado y tiene una ecuación del tipo: y = mx. Su gráfica es una línea recta que pasa por el origen de coordenadas,
2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.
![2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima. 2. [2014] [EXT-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima.](/thumbs/55/36437401.jpg) cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
cos() - e + a. [04] [ET-A] Sabiendo que lim 0 sen() es finito, calcula a y el valor del límte.. [04] [ET-B] De entre todos los números reales positivos, determina el que sumado con su inverso da suma mínima..
CONTINUIDAD Y DERIVABILIDAD
 . Sea la función f ( ) = 6 CONTINUIDAD Y DERIVABILIDAD a. Determine sus puntos de corte con los ejes. b. Calcule sus etremos relativos y su punto de infleión. c. Represente gráficamente la función.. Sea
. Sea la función f ( ) = 6 CONTINUIDAD Y DERIVABILIDAD a. Determine sus puntos de corte con los ejes. b. Calcule sus etremos relativos y su punto de infleión. c. Represente gráficamente la función.. Sea
Funciones, límites y continuidad
 8/0/016 Funciones, límites y continuidad C U R S O 0 1 5-0 1 6 Funciones, limites y continuidad Los puntos rojos son los que entran en el eamen de º evaluación 1) Concepto de función. Dominio y recorrido.
8/0/016 Funciones, límites y continuidad C U R S O 0 1 5-0 1 6 Funciones, limites y continuidad Los puntos rojos son los que entran en el eamen de º evaluación 1) Concepto de función. Dominio y recorrido.
INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
 UNIDAD 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Página 68. En la gráfica siguiente, la línea roja representa el movimiento de un autobús que arranca de la parada y va, poco a poco, ganando velocidad.
UNIDAD 7 INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES Página 68. En la gráfica siguiente, la línea roja representa el movimiento de un autobús que arranca de la parada y va, poco a poco, ganando velocidad.
1. Estudia la derivabilidad de la función )En qué punto del intervalo (0,ð) la recta tangente a y=tg(x) tiene pendiente 2?.
 ejerciciosyeamenes.com EXAMEN DERIVADAS. Estudia la derivabilidad de la función si f ()= si > 3. )En qué punto del intervalo (0,ð) la recta tangente a y=tg() tiene pendiente?. 4. Ecuación de la recta tangente
ejerciciosyeamenes.com EXAMEN DERIVADAS. Estudia la derivabilidad de la función si f ()= si > 3. )En qué punto del intervalo (0,ð) la recta tangente a y=tg() tiene pendiente?. 4. Ecuación de la recta tangente
1. Calcula la tasa de variación media de las siguientes funciones en los intervalos que se indican. 1
 6 Derivadas CRITERIOS DE EVALUACIÓN ACTIVIDADES DE EVALUACIÓN A. Calcular la tasa de variación media de una función en un intervalo.. Calcula la tasa de variación media de las siguientes funciones en los
6 Derivadas CRITERIOS DE EVALUACIÓN ACTIVIDADES DE EVALUACIÓN A. Calcular la tasa de variación media de una función en un intervalo.. Calcula la tasa de variación media de las siguientes funciones en los
APLICACIONES DE LA DERIVADA. Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente
 APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
APLICACIONES DE LA DERIVADA.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. 1 Crecimiento y decrecimiento. APLICACIONES DE LA DERIVADA Cuando una función es derivable en un punto, podemos conocer si es creciente
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES
 EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
EJERCICIOS DE REPASO DE MATEMÁTICAS I PENDIENTES 1 er PARCIAL 1. Obtén los valores reales que cumplen las siguientes condiciones: x+ x 3 5 x 1/ =1. Opera y expresa el resultado en notación científic (5,
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
Solución: Para calcular la pendiente, despejamos la y: La ordenada en el origen es n. 3 Puntos de corte con los ejes: 1 Eje Y 0, 3
 EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas de la recta 6y 0. Represéntala gráficamente. Para calcular la pendiente, despejamos la y: 6y 0
EJERCICIO. Halla la pendiente, la ordenada en el origen y los puntos de corte con los ejes de coordenadas de la recta 6y 0. Represéntala gráficamente. Para calcular la pendiente, despejamos la y: 6y 0
Análisis de funciones y representación de curvas
 12 Análisis de funciones y representación de curvas 1. Análisis gráfico de una función Aplica la teoría 1. Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario
12 Análisis de funciones y representación de curvas 1. Análisis gráfico de una función Aplica la teoría 1. Dada la siguiente gráfica, analiza todas sus características, es decir, completa el formulario
10 Integral. indefinida y definida. 1. Reglas de integración. Piensa y calcula. Aplica la teoría
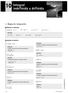 Integral indefinida y definida. Reglas de integración Piensa y calcula Calcula: a y =, y' = b y' =, y = c y = e, y' = d y' = e,y = a y' = b y = c y' = e d y = e Aplica la teoría. 7 d Se aplica la integral
Integral indefinida y definida. Reglas de integración Piensa y calcula Calcula: a y =, y' = b y' =, y = c y = e, y' = d y' = e,y = a y' = b y = c y' = e d y = e Aplica la teoría. 7 d Se aplica la integral
Funciones polinómicas, racionales y exponenciales
 008 _ 06-08.qd 9/7/08 9:07 Página 6 Funciones polinómicas, racionales eponenciales INTRODUCCIÓN Uno de los objetivos de esta unidad es que los alumnos aprendan a hallar la ecuación de una recta dados dos
008 _ 06-08.qd 9/7/08 9:07 Página 6 Funciones polinómicas, racionales eponenciales INTRODUCCIÓN Uno de los objetivos de esta unidad es que los alumnos aprendan a hallar la ecuación de una recta dados dos
TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos
 64 TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión. Dada la función
64 TEMA 9. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Problemas Resueltos Crecimiento y decrecimiento. Máimos y mínimos relativos; puntos de infleión. Dada la función
EJERCICIOS DE REFUERZO FUNCIONES 1) Calcula f(0), f(1), f(-1), f(2) y f(-3) de las siguientes funciones: 1
 EJERCICIOS DE REFUERZO FUNCIONES 1) Calcula f(0), f(1), f(-1), f() y f(-3) de las siguientes funciones: 1 a) f () b)f () 3 c) f () ) Calcula f(3) f(-1) f(4) y f(-4) 4º ESO B d) f () 3) Cuáles de las siguientes
EJERCICIOS DE REFUERZO FUNCIONES 1) Calcula f(0), f(1), f(-1), f() y f(-3) de las siguientes funciones: 1 a) f () b)f () 3 c) f () ) Calcula f(3) f(-1) f(4) y f(-4) 4º ESO B d) f () 3) Cuáles de las siguientes
Funciones y sus gráficas
 y sus gráficas Marzo de 2006 Índice 1 polinómicas función constante función lineal función afín función cuadrática 2 racionales función de proporcionalidad inversa función racional 3 exponenciales 4 Ejemplos
y sus gráficas Marzo de 2006 Índice 1 polinómicas función constante función lineal función afín función cuadrática 2 racionales función de proporcionalidad inversa función racional 3 exponenciales 4 Ejemplos
A partir de la gráfica de las siguientes funciones, indica cuál es su dominio de definición y su recorrido:
 Modelo de eamen Ejercicio nº. Halla el dominio de definición de las siguientes funciones: a) y = ( 3) b) y = S Fecha: b) > 0 > Dominio = (, + ) Ejercicio nº. A partir de la gráfica de las siguientes funciones,
Modelo de eamen Ejercicio nº. Halla el dominio de definición de las siguientes funciones: a) y = ( 3) b) y = S Fecha: b) > 0 > Dominio = (, + ) Ejercicio nº. A partir de la gráfica de las siguientes funciones,
Los números complejos
 7 Los números complejos 1. Forma binómica del número complejo Piensa y calcula Halla mentalmente cuántas soluciones tienen las siguientes ecuaciones en el conjunto de los números reales. a) x 2 25 = 0
7 Los números complejos 1. Forma binómica del número complejo Piensa y calcula Halla mentalmente cuántas soluciones tienen las siguientes ecuaciones en el conjunto de los números reales. a) x 2 25 = 0
RESUMEN PARA HACER EL ANÁLISIS COMPLETO DE UNA FUNCIÓN:
 RESUMEN PARA HACER EL ANÁLISIS COMPLETO DE UNA FUNCIÓN: Ejemplo: 1 Dominio Representación de en el intervalo [,] Los puntos que no pertenecen al dominio de una función racional, son aquellos que anulan
RESUMEN PARA HACER EL ANÁLISIS COMPLETO DE UNA FUNCIÓN: Ejemplo: 1 Dominio Representación de en el intervalo [,] Los puntos que no pertenecen al dominio de una función racional, son aquellos que anulan
, siendo ln(1+x) el logaritmo neperiano de 1+x. x
 Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
Selectividad CCNN 00. [ANDA] [JUN-B] Considera la función f: definida por f() = (+)e -. (a) Halla las asíntotas de la gráfica de f. (b) Determina los etremos de f y los puntos de infleión de su gráfica.
Colegio Portocarrero. Curso Departamento de matemáticas. Análisis. (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas)
 Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Análisis (Límites/Asíntotas/Continuidad/Derivadas/Aplicaciones de las derivadas) Problema 1: Sea la función Determina: a) El dominio de definición. b) Las asíntotas si existen. c) El o los intervalos de
Continuidad, límites y asíntotas
 9 Continuidad, ites y asíntotas. Funciones especiales Piensa y calcula Completa la siguiente tabla: Parte entera de Parte decimal de Valor absoluto de 0,3 0,3,8,8 2,4 2,4 3,9 Ent () Dec () 3,9 0,3 0,3,8,8
9 Continuidad, ites y asíntotas. Funciones especiales Piensa y calcula Completa la siguiente tabla: Parte entera de Parte decimal de Valor absoluto de 0,3 0,3,8,8 2,4 2,4 3,9 Ent () Dec () 3,9 0,3 0,3,8,8
UNIDAD 3: FUNCIONES -PROPIEDADES GLOBALES -OPERACIONES -FUNCIONES ELEMENTALES -INTERPOLACIÓN
 UNIDAD 3: FUNCIONES -PROPIEDADES GLOBALES -OPERACIONES -FUNCIONES ELEMENTALES -INTERPOLACIÓN 46 OBJETIVOS DIDÁCTICOS En esta unidad aprenderás a:. Analizar si una gráfica es o no función.. Analizar las
UNIDAD 3: FUNCIONES -PROPIEDADES GLOBALES -OPERACIONES -FUNCIONES ELEMENTALES -INTERPOLACIÓN 46 OBJETIVOS DIDÁCTICOS En esta unidad aprenderás a:. Analizar si una gráfica es o no función.. Analizar las
MODELO 1 EXAMEN DE CÁLCULO DIFERENCIAL. siendo a un nº real
 MODELO 1 EXAMEN DE CÁLCULO DIFERENCIAL 1. Escribe la ecuación de la recta normal a la curva de ecuación: arcsen abscisa 1. Haz un estudio de todas las asíntotas de la función: 1 e f ( ). Halla los valores
MODELO 1 EXAMEN DE CÁLCULO DIFERENCIAL 1. Escribe la ecuación de la recta normal a la curva de ecuación: arcsen abscisa 1. Haz un estudio de todas las asíntotas de la función: 1 e f ( ). Halla los valores
REPASO MATE3171 Parcial 3
 REPASO MATE3171 Parcial 3 ya estudie jeje!! voy lento, pero seguro!!! aún no he empezado!!! REPASO PARA EL TERCER PARCIAL (MATE3171)ISEM14-15 Profa: Ysela Ochoa Tapia Cap2 Transformaciones 1) La gráfica
REPASO MATE3171 Parcial 3 ya estudie jeje!! voy lento, pero seguro!!! aún no he empezado!!! REPASO PARA EL TERCER PARCIAL (MATE3171)ISEM14-15 Profa: Ysela Ochoa Tapia Cap2 Transformaciones 1) La gráfica
PROBLEMAS DE REPASO. Solución: Si llamamos x e y a las longitudes de cada uno de los catetos, sabemos que: x 2 y 2 1 y 2 1 x 2 El volumen del cono es:
 PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
PROBLEMAS DE REPASO 1. La hipotenusa de un triángulo rectángulo mide 1 dm. Hacemos girar el triángulo alrededor de uno de sus catetos. Determina la longitud de los catetos de forma que el cono engendrado
m = 0 constante m > 0 creciente m < 0 decreciente n es la ordenada en el origen (donde la función corta al eje Y, imagen de x=0)
 1. FUNCIONES POLINÓMICAS. D(f) = R A. FUNCIONES LINEALES: n = 1 Su gráfica es una recta. D (f) = R. Im (f) = R m = 0 constante m es la pendiente (inclinación) m > 0 creciente y = mx + n m < 0 decreciente
1. FUNCIONES POLINÓMICAS. D(f) = R A. FUNCIONES LINEALES: n = 1 Su gráfica es una recta. D (f) = R. Im (f) = R m = 0 constante m es la pendiente (inclinación) m > 0 creciente y = mx + n m < 0 decreciente
F U N C I O N E S R E A L E S D E V A R I A B L E R E A L
 F U N C I O N E S R E A L E S D E V A R I A B L E R E A L 1. C O N C E P T O D E F U N C I Ó N Una función f del conjunto A en el conjunto B es una relación de dependencia entre dos magnitudes A y B, de
F U N C I O N E S R E A L E S D E V A R I A B L E R E A L 1. C O N C E P T O D E F U N C I Ó N Una función f del conjunto A en el conjunto B es una relación de dependencia entre dos magnitudes A y B, de
Unidad 8 Representación gráfica de funciones
 Unidad 8 Representación gráfica de funciones PÁGINA 187 SOLUCIONES 1. Las funciones quedan: a) f( ) = 8 Dominio: Dom f =R Puntos de corte con el eje OX: Puntos de corte con el eje OY Simetrías: f( ) =
Unidad 8 Representación gráfica de funciones PÁGINA 187 SOLUCIONES 1. Las funciones quedan: a) f( ) = 8 Dominio: Dom f =R Puntos de corte con el eje OX: Puntos de corte con el eje OY Simetrías: f( ) =
EJERCICIOS DE REPASO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE 2007 DE MATEMÁTICAS B PARA LOS CURSOS 4º ESO A Y 4º ESO B
 EJERCICIOS DE REPASO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE 007 DE MATEMÁTICAS B PARA LOS CURSOS 4º ESO A Y 4º ESO B ) Clasifica los siguientes números como naturales, enteros, racionales e irracionales,
EJERCICIOS DE REPASO PARA PREPARAR EL EXAMEN DE SEPTIEMBRE 007 DE MATEMÁTICAS B PARA LOS CURSOS 4º ESO A Y 4º ESO B ) Clasifica los siguientes números como naturales, enteros, racionales e irracionales,
FUNCIONES ELEMENTALES
 0 FUNCIONES ELEMENTALES Página PARA EMPEZAR, REFLEIONA RESUELVE Problema Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con
0 FUNCIONES ELEMENTALES Página PARA EMPEZAR, REFLEIONA RESUELVE Problema Las siguientes gráficas corresponden a funciones, algunas de las cuales conoces y otras no. En cualquier caso, vas a trabajar con
2. Calcula las velocidades medias anteriores tomando valores sobre la ecuación del movimiento de dicha partícula: s = 2
 Unidad. Derivadas Resuelve Página 0 Movimiento de una partícula Un investigador, para estudiar el movimiento de una partícula, la a iluminado con destellos de flas cada décima de segundo (0, s) durante
Unidad. Derivadas Resuelve Página 0 Movimiento de una partícula Un investigador, para estudiar el movimiento de una partícula, la a iluminado con destellos de flas cada décima de segundo (0, s) durante
Tema 7. Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización
 Tema 7 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Aplicaciones de la derivada primera para el estudio de la variación de una función El signo de la derivada primera
Tema 7 Aplicaciones de las derivadas: Representación gráfica de funciones y Optimización Aplicaciones de la derivada primera para el estudio de la variación de una función El signo de la derivada primera
FUNCIONES PRÁCTICA N 2
 Capitulo II FUNCIONES PRÁCTICA N. En cada uno de los siguientes casos dar la ley de la función descripta: a) El área de un rectángulo es de 0 cm². Epresar el perímetro del mismo en función de la longitud
Capitulo II FUNCIONES PRÁCTICA N. En cada uno de los siguientes casos dar la ley de la función descripta: a) El área de un rectángulo es de 0 cm². Epresar el perímetro del mismo en función de la longitud
Si se pueden obtener las imágenes de x por simple sustitución.
 TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
UNIDADES 1 y 2: FRACCIONES Y DECIMALES. POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. 1º.- Ordena de menor a mayor las siguientes fracciones:
 UNIDADES y : FRACCIONES Y DECIMALES. POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. º.- Ordena de menor a mayor las siguientes fracciones: ; 6 5 7 4 ; 5 4 ; ; ; 8 6 9 º.- Efectúa las siguientes operaciones y
UNIDADES y : FRACCIONES Y DECIMALES. POTENCIAS Y RAÍCES. NÚMEROS APROXIMADOS. º.- Ordena de menor a mayor las siguientes fracciones: ; 6 5 7 4 ; 5 4 ; ; ; 8 6 9 º.- Efectúa las siguientes operaciones y
EXAMEN GLOBAL. 4. Dada la función y = 1/x. Existe algún punto en el que la recta tangente esté inclinada 45º?, y 135º?. Calcula esa recta tangente.
 ejerciciosyeamenes.com. a) Enunciado y demostración del teorema del seno. b) Dos coches parten al mismo tiempo de un mismo punto. Van por carreteras rectas que forman entre sí un ángulo de 30º. El primer
ejerciciosyeamenes.com. a) Enunciado y demostración del teorema del seno. b) Dos coches parten al mismo tiempo de un mismo punto. Van por carreteras rectas que forman entre sí un ángulo de 30º. El primer
- El coeficiente de x, la m, se llama pendiente de la recta y nos indica la inclinación de la recta.
 º ESO C MATEMÁTICAS ACADÉMICAS UNIDAD.- FUNCIONES LINEALES CUADRÁTICAS..- FUNCIONES CUA GRÁFICA ES UNA RECTA Funciones lineales Son aquellas cuya fórmula es del tipo y = mx, siendo m 0. - El coeficiente
º ESO C MATEMÁTICAS ACADÉMICAS UNIDAD.- FUNCIONES LINEALES CUADRÁTICAS..- FUNCIONES CUA GRÁFICA ES UNA RECTA Funciones lineales Son aquellas cuya fórmula es del tipo y = mx, siendo m 0. - El coeficiente
-, se pide: b) Calcula el área del recinto limitado por dicha gráfica, el eje horizontal y la vertical que pasa por el máximo relativo de la curva.
 EJERCICIOS PARA PREPARAR EL EXAMEN GLOBAL DE ANÁLISIS ln ) Dada la función f ( ) = +, donde ln denota el logaritmo - 4 neperiano, se pide: a) Determinar el dominio de f y sus asíntotas b) Calcular la recta
EJERCICIOS PARA PREPARAR EL EXAMEN GLOBAL DE ANÁLISIS ln ) Dada la función f ( ) = +, donde ln denota el logaritmo - 4 neperiano, se pide: a) Determinar el dominio de f y sus asíntotas b) Calcular la recta
Matemáticas Problemas resueltos de gráficas de funciones (1) PROBLEMAS RESUELTOS DE GRÁFICAS DE FUNCIONES (1)
 PROBLEMAS RESUELTOS DE GRÁFICAS DE FUNCIONES (1) 1) Halle los intervalos de monotonía y los etremos relativos, los intervalos de curvatura y los puntos de infleión de la función g() + +. Represéntela gráficamente.
PROBLEMAS RESUELTOS DE GRÁFICAS DE FUNCIONES (1) 1) Halle los intervalos de monotonía y los etremos relativos, los intervalos de curvatura y los puntos de infleión de la función g() + +. Represéntela gráficamente.
TEMA 4 FUNCIONES ELEMENTALES
 TEMA 4 FUNCIONES ELEMENTALES 4.1. Funciones lineales, cuadráticas y polinómicas 4.1.1. Funciones lineales. Las unciones lineales o aines tienen por epresión analítica ( m n. Si m > 0, la unción aín tiene
TEMA 4 FUNCIONES ELEMENTALES 4.1. Funciones lineales, cuadráticas y polinómicas 4.1.1. Funciones lineales. Las unciones lineales o aines tienen por epresión analítica ( m n. Si m > 0, la unción aín tiene
Función es una relación entre dos variables a las que, en general, se les llama x e y. Viene representado por: y f (x)
 TEMA 9: :.- CONCEPTO DE FUNCIÓN: Función es una relación entre dos variables a las que, en general, se les llama e y. Viene representado por: y (, donde es la variable independiente e y es la variable
TEMA 9: :.- CONCEPTO DE FUNCIÓN: Función es una relación entre dos variables a las que, en general, se les llama e y. Viene representado por: y (, donde es la variable independiente e y es la variable
3º ESO FUNCIONES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa FUNCIONES
 º ESO FUNCIONES DEPARTAMENTO DE MATEMÁTICAS. FUNCIONES.- CARACTERÍSTICAS DE LAS FUNCIONES Definición: Una función es una relación entre dos variables de tal forma que a cada valor de la primera (variable
º ESO FUNCIONES DEPARTAMENTO DE MATEMÁTICAS. FUNCIONES.- CARACTERÍSTICAS DE LAS FUNCIONES Definición: Una función es una relación entre dos variables de tal forma que a cada valor de la primera (variable
f: D IR IR x f(x) v. indep. v. dependiente, imagen de x mediante f.
 TEMA 5: FUNCIONES ELEMENTALES. 5. Función real de variable real. 5. Operaciones con funciones: composición e inversa. 5.3 Construcción de gráficas de funciones elementales y sus transformaciones. 5.4 Interpolación
TEMA 5: FUNCIONES ELEMENTALES. 5. Función real de variable real. 5. Operaciones con funciones: composición e inversa. 5.3 Construcción de gráficas de funciones elementales y sus transformaciones. 5.4 Interpolación
APLICACIONES DE LA DERIVADA
 7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
TEMAS 4 LAS FUNCIONES ELEMENTALES
 TEMA 4 FUNCIONES ELEMENTALES MATEMÁTICAS CCSSI º Bach. TEMAS 4 LAS FUNCIONES ELEMENTALES Son funciones? EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
TEMA 4 FUNCIONES ELEMENTALES MATEMÁTICAS CCSSI º Bach. TEMAS 4 LAS FUNCIONES ELEMENTALES Son funciones? EJERCICIO : Indica cuáles de las siguientes representaciones corresponden a la gráfica de una función.
CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos:
 CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos: a) {x/ -5
CURSO: 1º bachillerato GRUPO: A Nº: FECHA: CALIF. 1. (1 puno) Representa sobre la recta real los siguientes conjuntos: a) {x/ -5
