EJERCICIOS RESUELTOS DE: Ecuaciones Diferenciales
|
|
|
- Alberto Espinoza Segura
- hace 7 años
- Vistas:
Transcripción
1 EJEROS RESUETOS DE: Euaions Difrnials AADEMA DE MATEMÁTAS ESUEA DE NGENERÍA EN OMPUTAÓN Y EETRÓNA UNVERSDAD DE A SAE BAJO
2 EUAONES DERENAES APTUO - Slionar nr las siguins uaions las qu son linals, sablr la variabl dndin rsolvrlas a d d, b ϑ ϑ ρ ρ ρ θ ρ, d d inal s No d d d, d d d sn i i os, sn i - d di f inal s No df d g d d, h inal s No d s ds s os i inal s No d d d
3 j sn rsn sn r d sn g r dr θ θ θ θ θ θ, k d d ln, l inal s No ' m inal s No d d d n d d d d d d, φ φ φ φ φ φ φ φ φ o inal s No d d os o g os os, os ' q, d d r arg arg g ar d g ar d,
4 s 5 d d No s inal sn d [ os s g] d,s g s g - D las uaions qu qudn dl roblma rsolvr las qu rnn al io Brnoulli d d υ f i l o s d df 5 υ d d υ ' υ 5 d 5 d d υ 5 υ 5 os sn os d d - Rsolvr las uaions h m qu son las qu qudan dl roblma s s s ds s os d d d h m sn sn d Rsolvr: on la ondiión ara
5 a ' d d d d d d d d μ uión: b E ERsn Esn X f Ri X d Esn Ri di Ri Esn d di Esn Ri d di d os μ dond,r,e son onsans, on la ondiión i ara uión: R Rsn R E i os Rsolvr a os z,mlando sn os z z dz d z d d z z d d z d d z z d d sn d d
6 d z z d b d z z d d d z ' d dz z z d d v v d d v v d d d d d v v d d d v v d dv v v v d d dv v v v sol a sn 8 sol b sol sol d APTUO 8, mlando mlando z v -Un muhaho s muv n una lina ra d modo qu su vloidad d n a su disania rso d un uno fijo d la ra si r 5 uando hallar la uaión d movimino 5 -halla l imo nsario ara qu una anidad d dinro aumn al dobl al 5% or año inrs omuso oninuo sugrnia: d d} 5 dond s la suma al abo d años años -l radio s dsomon a una vloidad roorional a la anidad rsn Si la ora miad d la anidad original dsaar n años hallar l ornaj d rdida d años %
7 5- n un ulivo d lvadura la anidad d frmno aivo r a una vloidad roorional a la anidad rsn Si s dulia la anidad n hora uanas vs ud srars qu s nga la anidad original dsaar n años hallar l ornaj d rdida n años 7vs -si uando la mraura d air s s nfría una susania dsd hasa n minuos hallar la mraura dus d minuos 5 7- Un anqu onindl d salmura obnida disolvindo kg d sal n agua s inrodu n l anqu a una vloidad d dlmin agua qu onin kg d sal or daliro la mzla onsrvada homogna mdian agiaión sal a una vloidad d dlmin halla la anidad d sal n l anqu al abo d una hora sugrnia d d 7 8- Hallar l imo qu s nsia ara vaiar un anqu d sion uadrada d m dm d rofundidad, a ravz d un agujroirular d dm d radio raiando n l fondo suongas, omo n l roblma, v 8 h dm sol 7 min sg - Una ard d ladrillo k in un ssor d m Si l arámro inrior sa a l rior a, hallar la mraura n la ard omo una funion d la disania dl arámro rior la rdida d alor or dia a ravz d un mro uadrado T al - Un hombr su mbaraión san lb Si la furza jrida rmando n la dirion dl movimino s d lb si la rsisnia n lb al movimino s l dobl d la vloidad issg, hallar la vloidad 5 sg dsués d qu la mbaraión haa mzado a movrs 7, issg msg - Hallar l imo qu s nsia ara vaiar un anqu ilíndrio d radio 8dm alura dm a ravés d un orifiio rdondo d radio dm siuado n l fondo dl anqu, sabindo qu or un orifiio d s io sal l agua a una vloidad aroimada v 8 h dm, dond h s la alura dl agua n l anqu, sg S ud asimilar l volumn d agua qu sal or sgundo a un ilindro d radio alura v Por lo ano, l volumn qu sal al abo d d sgundos s dm Π 8 h d 8 h d Π
8 Dsignando or dh la orrsondin aída d nivl d agua n l anqu, l volumn d agua qu sal ambién s ud dar or Π ugo Π 8 h d Πdh dh dh d dond d 8 h h ngrando Enr, h, h d dh, h 8 h 8 sg hmin 5- Sgún la l d Nwon d nfriamino, la vloidad a qu s nfría una susania al air libr s roorional a la difrnia nr la mraura d la susania la dl air Si la mraura dl air s la susania s nfría d a 7 n 5 minuos uándo srá la mraura d la susania? T s la mraura d la susania a minuos dt d k T dt T kd 7 5 dt k d, T n n 7-5k n 7 5k n 7 5 dt k T d 5n7 n n7 k, 5k 5n7, 5min 5 - Bajo iras ondiions la anidad onsan Q aloríassgundo d alor qu asa a ravés d una ard sá dada or dt Q ka d Dond k s la onduividad dl marial, A m s la surfii d una ara s la ard rndiular a la dirión dl flujo T s la mraura a m d sa ara, d forma qu T disminu uando aumna Hallar l numro d alorías or hora dl alor qu asa a ravés d m d la ard d una habiaión frigorífia d 5 m d ssor k,5, si la mraura d la ara inrior s d -5 Sa la disania a qu sá d la ara rior un uno inrior d la ard 5 5 Q Q 8kA 8,5 al dt d, 8 5, Q ka ka 5 5 sg 75
9 APTUO d d d d d d
10 K K K d d d d d d d d - d d d d d d d d,, - - Y - Y -
11 - Y 5-7 Y 5 u, 7 dvd u dud 7 dvd 5-5, d d d d d d 8 d d
12 d d d d d d d d d d d d ln ln ln - Y Drivando rso P d d -ƒ d - X - -, - - Y ln ln
13 X ln ln, - Y Drivamos rso a, d - d d, d d d ngrando d D ½ - - X -5, -5
14 APTUO nvsigar las soluions singulars los lugars Gomérios raños - a soluión s la siguin: Para saar la rimiiva n s aso s susiu n la Euaión d lairau Por lo qu l rsulado s l siguin: a uión Singular s la siguin: En s aso ara odr saar la rimiiva s hizo l siguin rodimino * k k k k k k v d dv d dv v d dv d dv d dv k d dv d dv v k k
15 a soluión singular s la siguin: d d d d Prim, SS, Rsolvindo d d
16 Prim SS, d d d - d - uion Prim, l rroso, ninguna
17 7- uion Prim, s s, l rroso, l d h, 8-P 8,, P 8
18 f - f - f : X - -
GUÍA Nº 04. son constantes, estamos en presencia de una EDO lineal de segundo orden, que será homogénea si 0 y no homogénea en caso contrario.
 Dirión d Formaión Gnral Programa d Mamáia Cálulo II GUÍA Nº 04 Euaions Difrnials Linals d Sgundo Ordn Rordamos qu una EDO linal d ordn n n gnral pud sribirs omo: n n d d d an a... a a0 g n n n d d d Si
Dirión d Formaión Gnral Programa d Mamáia Cálulo II GUÍA Nº 04 Euaions Difrnials Linals d Sgundo Ordn Rordamos qu una EDO linal d ordn n n gnral pud sribirs omo: n n d d d an a... a a0 g n n n d d d Si
EJERCICIOS DE INTEGRALES EULERIANAS PROPUESTOS EN EXÁMENES. x y = 1. π 2 3. sen x cos xdx (Septiembre Ex. Or.)
 TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mail: imozas@l.und.s hp://lfonica.n/wb/imm EJERCICIOS DE INTEGRALES EULERIANAS PROPUESTOS EN EXÁMENES.- Razon y obnga qu la ingral ulriana (p) (gamma d p) para p
TUTORÍA DE MATEMÁTICAS III (º A.D.E.) -mail: imozas@l.und.s hp://lfonica.n/wb/imm EJERCICIOS DE INTEGRALES EULERIANAS PROPUESTOS EN EXÁMENES.- Razon y obnga qu la ingral ulriana (p) (gamma d p) para p
Unidad 2 : Ecuaciones Diferenciales Lineales de Orden Superior
 Unidad : Euaions Difrnials Linals d Ordn Surior Ta.a : Método d Cofiints Indtrinados En sta sión studiaros uno d los dos étodos ara rsolvr EDL No- Hooénas d ordn aor o iual a dos. Ezaros on las EDLNH d
Unidad : Euaions Difrnials Linals d Ordn Surior Ta.a : Método d Cofiints Indtrinados En sta sión studiaros uno d los dos étodos ara rsolvr EDL No- Hooénas d ordn aor o iual a dos. Ezaros on las EDLNH d
La ecuación diferencial ordinaria lineal de primer y segundo orden
 La uaión ifrnial orinaria linal rimr sguno orn José Graro Dionisio Romro Jiménz Aamia Mamáias l Daramno Ingniría n Comuniaions Elrónia Esula Surior Ingniría Mánia Eléria IPN Méxio Rsumn. En s rabajo s
La uaión ifrnial orinaria linal rimr sguno orn José Graro Dionisio Romro Jiménz Aamia Mamáias l Daramno Ingniría n Comuniaions Elrónia Esula Surior Ingniría Mánia Eléria IPN Méxio Rsumn. En s rabajo s
Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica. Cálculo Vectorial Tarea 5
 Integrales Múltiples álulo Vetorial Tarea 5 1. Evalúe las siguientes integrales: 1.1 0 1 4 ( 1 8 dd 1. 1 0 sin 1. 0 0 (Res. 57 ( 1 dd (Res. 0/ (1 os (Res. dd 1 1 1.4 os( sen( 0 (Res. dd 7 9. Utilie una
Integrales Múltiples álulo Vetorial Tarea 5 1. Evalúe las siguientes integrales: 1.1 0 1 4 ( 1 8 dd 1. 1 0 sin 1. 0 0 (Res. 57 ( 1 dd (Res. 0/ (1 os (Res. dd 1 1 1.4 os( sen( 0 (Res. dd 7 9. Utilie una
Tema 2: Modelos de concentración de contaminantes atmosféricos. 2.1 Modelos de celda fija z. c = Σ c i f. c e = b + q L / u H
 Tma : Modlos d onnraión d onaminans amosférios. Modlos d lda fija saionaria no saionaria. Modlos d disprsión: modlo gaussiano para onaminans qu no raionan.3 Inorporaión d inéia d primr ordn n l modlo gaussiano.
Tma : Modlos d onnraión d onaminans amosférios. Modlos d lda fija saionaria no saionaria. Modlos d disprsión: modlo gaussiano para onaminans qu no raionan.3 Inorporaión d inéia d primr ordn n l modlo gaussiano.
TEMA 3: CÁLCULO INTEGRAL DE UNA VARIABLE.
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Ingniría Indusrial (GITI/GITI+ADE) Ingniría d Tlcomunicación (GITT/GITT+ADE) CÁLCULO Curso -6 TEMA : CÁLCULO INTEGRAL
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA APLICADA TITULACIONES Ingniría Indusrial (GITI/GITI+ADE) Ingniría d Tlcomunicación (GITT/GITT+ADE) CÁLCULO Curso -6 TEMA : CÁLCULO INTEGRAL
2.6 SOLUCION DE SISTEMAS DE ECUACIONES DIFERENCIALES CON COEFICIENTES CONSTANTES MEDIANTE EL METODO DE LOS OPERADORES
 Euaions difrnials Profsor Bogar Ménd /7 6 SOLUCION E SISTEMAS E ECUACIONES IFERENCIALES CON COEFICIENTES CONSTANTES MEIANTE EL METOO E LOS OPERAORES En sa sión aprndrmos a rsolvr sismas d uaions difrnials
Euaions difrnials Profsor Bogar Ménd /7 6 SOLUCION E SISTEMAS E ECUACIONES IFERENCIALES CON COEFICIENTES CONSTANTES MEIANTE EL METOO E LOS OPERAORES En sa sión aprndrmos a rsolvr sismas d uaions difrnials
7.6 SEÑOREAJE E HIPERINFLACIÓN
 Ecuacions qu componn l modlo: a) Equilibrio n l mrcado d dinro: M P aπ () = +, dond π π. b) Expcaivas adapaivas: c M P d + + c) Crcimino monario: i + b + b b i i= 0 () π π = ( π π ) π = ( ) π. M (3) +
Ecuacions qu componn l modlo: a) Equilibrio n l mrcado d dinro: M P aπ () = +, dond π π. b) Expcaivas adapaivas: c M P d + + c) Crcimino monario: i + b + b b i i= 0 () π π = ( π π ) π = ( ) π. M (3) +
Si R=1.00 [kω] y ε=250 [V] en la figura 1, determine la dirección y magnitud de la corriente en el alambre horizontal entre a y e.
![Si R=1.00 [kω] y ε=250 [V] en la figura 1, determine la dirección y magnitud de la corriente en el alambre horizontal entre a y e. Si R=1.00 [kω] y ε=250 [V] en la figura 1, determine la dirección y magnitud de la corriente en el alambre horizontal entre a y e.](/thumbs/63/48813313.jpg) 0.1. Ciruito. Si R=1.00 [kω] y ε=250 [V] en la figura 1, determine la direión y magnitud de la orriente en el alambre horizontal entre a y e. b R 2R d ε 4R 3R 2ε a e Soluión: Dibujemos las orrientes Figura
0.1. Ciruito. Si R=1.00 [kω] y ε=250 [V] en la figura 1, determine la direión y magnitud de la orriente en el alambre horizontal entre a y e. b R 2R d ε 4R 3R 2ε a e Soluión: Dibujemos las orrientes Figura
CALCULO INTEGRAL. Ejercicios. 1 a Parte: Diferenciales. Rumbo al examen de recuperación. Faus2016. x 1
 En los problmas complt la tabla siguint para cada función. d d DIVISION DE INGENIERIA ELECTRONICA.. Rumbo al amn d rcupración a Part: CALCULO INTEGRAL Ejrcicios Difrncials Dfinición. Faus6 Supóngas qu
En los problmas complt la tabla siguint para cada función. d d DIVISION DE INGENIERIA ELECTRONICA.. Rumbo al amn d rcupración a Part: CALCULO INTEGRAL Ejrcicios Difrncials Dfinición. Faus6 Supóngas qu
2. Definición de Cadena de Markov Propiedad Markoviana y estacionariedad. 3. Matriz de Probabilidades de transición y Diagrama de estados.
 SESIÓN a CAENAS E ARKOV INTROUCCIÓN Noción d rocso Esocásico finición E asociados a un sisma finición d Cadna d arov roidad aroviana y sacionaridad 3 ariz d robabilidads d ransición y iagrama d sados 4
SESIÓN a CAENAS E ARKOV INTROUCCIÓN Noción d rocso Esocásico finición E asociados a un sisma finición d Cadna d arov roidad aroviana y sacionaridad 3 ariz d robabilidads d ransición y iagrama d sados 4
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE MEZCLAS
 APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE MEZCLAS 0 Considérs un anqu qu in un volumn inicial V 0 d solución (una mzcla d soluo y solvn). Hay un flujo ano d
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE MEZCLAS 0 Considérs un anqu qu in un volumn inicial V 0 d solución (una mzcla d soluo y solvn). Hay un flujo ano d
GUÍA PARA EL EXAMEN A TÍTULO DE SUFICIENCIA DE ECUACIONES DIFERENCIALES MAYO 2010, ACADEMIA DE MATEMÁTICAS IE, ICA, ISISA
 GUÍA PARA EL EXAMEN A TÍTULO DE SUFICIENCIA DE ECUACIONES DIFERENCIALES MAYO 00, ACADEMIA DE MATEMÁTICAS IE, ICA, ISISA I. ECUACIONES DIFERENCIALES DE PRIMER ORDEN VARIABLES SEPARABLES Para a ión proporiona
GUÍA PARA EL EXAMEN A TÍTULO DE SUFICIENCIA DE ECUACIONES DIFERENCIALES MAYO 00, ACADEMIA DE MATEMÁTICAS IE, ICA, ISISA I. ECUACIONES DIFERENCIALES DE PRIMER ORDEN VARIABLES SEPARABLES Para a ión proporiona
CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS:
 CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS: TEMAS: - Demostrar la euaión de la tensión de torsión, su apliaión y diseño de miembros sometidos a tensiones de torsión 5.1. Teoría de torsión simple 5..
CAP. 5 DISEÑO DE MIEMBROS EN TORSIÓN OBJETIVOS: TEMAS: - Demostrar la euaión de la tensión de torsión, su apliaión y diseño de miembros sometidos a tensiones de torsión 5.1. Teoría de torsión simple 5..
ECUACIONES DIFERENCIALES ORDINARIAS DE SEGUNDO
 ECUACIONES DIFERENCIALES ORDINARIAS DE SEGUNDO ORDEN. RESOLUCIÓN REDUCIÉNDOLA A UNA ECUACIÓN DIFERENCIAL ORDINARIA DE PRIMER ORDEN Miguel Angel Nastri, Osar Sardella miguelangelnastri@ahoo.om.ar, osarsardella@ahoo.om.ar
ECUACIONES DIFERENCIALES ORDINARIAS DE SEGUNDO ORDEN. RESOLUCIÓN REDUCIÉNDOLA A UNA ECUACIÓN DIFERENCIAL ORDINARIA DE PRIMER ORDEN Miguel Angel Nastri, Osar Sardella miguelangelnastri@ahoo.om.ar, osarsardella@ahoo.om.ar
OPCIÓN A. MATEMÁTICAS 2º BACHILLERATO B Lo contrario de vivir es no arriesgarse. Fito y los Fitipaldis
 MATEMÁTICAS º BACHILLERATO B --5 Lo contrario d vivir s no arrisgars Análisis Fito y los Fitipaldis OPCIÓN A.- a) S dsa construir un parallpípdo rctangular d 9 dm d volumn y tal qu un lado d la bas sa
MATEMÁTICAS º BACHILLERATO B --5 Lo contrario d vivir s no arrisgars Análisis Fito y los Fitipaldis OPCIÓN A.- a) S dsa construir un parallpípdo rctangular d 9 dm d volumn y tal qu un lado d la bas sa
Reacciones Reversibles. Reacciones Paralelas o Competitivas. Reacciones Consecutivas. Reacciones en Cadena Ramificada. Explosiones
 Raccions Rrsibls Raccions Parallas o Compiias Raccions Conscuias Raccions n Cadna Ramificada. Explosions Mcanismos d Racción Raccions Rrsibls Para la racción A _ B dond ano la racción dirca como la inrsa
Raccions Rrsibls Raccions Parallas o Compiias Raccions Conscuias Raccions n Cadna Ramificada. Explosions Mcanismos d Racción Raccions Rrsibls Para la racción A _ B dond ano la racción dirca como la inrsa
Vector de Poynting. Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA CAMPOS Y ONDAS
 Vector de Poynting Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA H J E S P µ ε d dv dv t 2 2 2 2 ( E H) S+ ( E J) = H + E SC Vector de Poynting Onda Plana Progresiva,
Vector de Poynting Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA H J E S P µ ε d dv dv t 2 2 2 2 ( E H) S+ ( E J) = H + E SC Vector de Poynting Onda Plana Progresiva,
Universidad Nacional de Ingeniería P.A Facultad de Ingeniería Mecánica 21/07/15 DACIBAHCC EXAMEN SUSTITUTORIO DE METODOS NUMERICOS (MB536)
 Unirsidad aional d Ingniría P.A. 05- Faultad d Ingniría Mánia /07/5 Probla EXAME SUSTITUTORIO DE METODOS UMERICOS (MB536) SOLO SE PERMITE EL USO DE UA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMETE
Unirsidad aional d Ingniría P.A. 05- Faultad d Ingniría Mánia /07/5 Probla EXAME SUSTITUTORIO DE METODOS UMERICOS (MB536) SOLO SE PERMITE EL USO DE UA HOJA DE FORMULARIO Y CALCULADORA ESCRIBA CLARAMETE
Unidad 2 : Ecuaciones Diferenciales Lineales de Orden Superior. Tema 2.1 : Definiciones y Terminología
 7 Unidad : Euaions Dirnials inals d Ordn Surior Tma. : Diniions Trminología a Euaión Dirnial inal d o rdn No Homogéna tin la orma: a d d d d a a g uaión EDN H a Euaión Dirnial inal d o rdn Homogéna Asoiada
7 Unidad : Euaions Dirnials inals d Ordn Surior Tma. : Diniions Trminología a Euaión Dirnial inal d o rdn No Homogéna tin la orma: a d d d d a a g uaión EDN H a Euaión Dirnial inal d o rdn Homogéna Asoiada
DEFINICIONES DEFINICIONES
 DEFINICIONES Líneas de corriente: línea imaginaria, tangente en cada punto al ector elocidad de la partícula que en un instante determinado pasa por dicho punto. Las líneas de corriente son las enolentes
DEFINICIONES Líneas de corriente: línea imaginaria, tangente en cada punto al ector elocidad de la partícula que en un instante determinado pasa por dicho punto. Las líneas de corriente son las enolentes
Integración doble Integrales dobles sobre regiones no rectangulares
 Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
Nuestra intención es extender la definición de integral doble, de funciones continuas, sobre regiones más generales que el rectángulo. Para ello definiremos dos tipos de regiones en el plano, que llamaremos
Definición de derivada
 Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
Dfinición d drivada. Halla, utilizando la dfinición, la drivada d la función f ( ) n l punto =. Compruba aplicando las rglas d drivación qu tu rsultado s corrcto. f ( ) f () La drivada pdida val: f ()
= 1n. + c. x dy. x x. + 2r. y y. Rojas Huachin Miryan. Homogéneas y Reducibles a Homogéneas
 Ecacions difrncials Ejrcicios d Ecacions Difrncials Homogénas Rdcibls a Homogénas. arsolvr: ' r b Drminar para q valors d r in solcions d la forma la cación ''' '' ' 0 Solción a Hacmos l cambio: ' ' Rmplaando
Ecacions difrncials Ejrcicios d Ecacions Difrncials Homogénas Rdcibls a Homogénas. arsolvr: ' r b Drminar para q valors d r in solcions d la forma la cación ''' '' ' 0 Solción a Hacmos l cambio: ' ' Rmplaando
4 M. a) La(s) ecuación(es) diferencial(es) del movimiento del sistema a partir de las ecuaciones de movimiento lineal y angular.
 Un si-disco unifor d radio asa, ruda sin dslizar sor una suprfici orizontal. Una partícula d asa s ncuntra conctada al disco n su iso plano, por dos varillas rígidas, d asa dprcial, coo s ustra n la figura.
Un si-disco unifor d radio asa, ruda sin dslizar sor una suprfici orizontal. Una partícula d asa s ncuntra conctada al disco n su iso plano, por dos varillas rígidas, d asa dprcial, coo s ustra n la figura.
2º Bachillerato: ejercicios modelo para el examen de las lecciones 11, 12 y 13
 º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
º Bachillrato: jrcicios modlo para l amn d las lccions, y 3 Sa la unción F ( ) t dt a) Calcular F (), studiar l crciminto d F() y hallar sus máimos y mínimos. b) Calcular F () y studiar la concavidad y
Aplicaciones de ED de segundo orden
 CAPÍTULO 5 Apliaiones de ED de segundo orden 5.. Vibraiones amoriguadas libres Coninuando el desarrollo del esudio de las vibraiones, supongamos que se agrega ahora un disposiivo meánio (amoriguador) al
CAPÍTULO 5 Apliaiones de ED de segundo orden 5.. Vibraiones amoriguadas libres Coninuando el desarrollo del esudio de las vibraiones, supongamos que se agrega ahora un disposiivo meánio (amoriguador) al
SISTEMAS ABIERTOS. José Agüera Soriano
 SISTEMAS ABIERTOS José Agüera Soriano 0 José Agüera Soriano 0 SISTEMAS ABIERTOS ECUACIONES FUNDAMENTALES DE UN FLUJO VELOCIDAD DEL SONIDO EN UN GAS PROCESOS DE DERRAME ESTRANGULACIÓN DE UN FLUJO TRANSPORTE
SISTEMAS ABIERTOS José Agüera Soriano 0 José Agüera Soriano 0 SISTEMAS ABIERTOS ECUACIONES FUNDAMENTALES DE UN FLUJO VELOCIDAD DEL SONIDO EN UN GAS PROCESOS DE DERRAME ESTRANGULACIÓN DE UN FLUJO TRANSPORTE
PROBLEMAS DEL TEOREMA FUNDAMENTAL DE LAS INTEGRALES DE LÍNEA
 ROBLEMAS DEL TEOREMA UNDAMENTAL DE LAS INTEGRALES DE LÍNEA. Indpndncia dl camino n una ingal d lína. alcula l abajo llvado a cabo po l campo d ua al llva un objo dsd A hasa B siguindo a un camino compuso
ROBLEMAS DEL TEOREMA UNDAMENTAL DE LAS INTEGRALES DE LÍNEA. Indpndncia dl camino n una ingal d lína. alcula l abajo llvado a cabo po l campo d ua al llva un objo dsd A hasa B siguindo a un camino compuso
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω
 ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
ECUACION DINÁMICA DE ROTACIÓN PURA DE UN CUERPO RIGIDO ALREDEDOR DE UN EJE ω Suponiendo un cuerpo rígido que gira con velocidad angular ω alrededor del eje Z que permanece fijo al cuerpo. dl = ( dm R 2
Matemáticas III Andalucía-Tech. Integrales múltiples
 Matemátias III Andaluía-Teh Tema 4 Integrales múltiples Índie. Preliminares. Funión Gamma funión Beta. Integrales dobles.. Integral doble de un ampo esalar sobre un retángulo................ Integral doble
Matemátias III Andaluía-Teh Tema 4 Integrales múltiples Índie. Preliminares. Funión Gamma funión Beta. Integrales dobles.. Integral doble de un ampo esalar sobre un retángulo................ Integral doble
MATEMÁTICAS FINANCIERAS
 MATEMÁTICAS FINANCIERAS TEMA: INTERÉS COMPUESTO CONTINUO. Inrés Compuso Coninuo 2. Mono Compuso a Capialización Coninua 3. Equivalncia nr Tasas d Inrés Compuso Discro y Coninuo 4. Equivalncia nr Tasa d
MATEMÁTICAS FINANCIERAS TEMA: INTERÉS COMPUESTO CONTINUO. Inrés Compuso Coninuo 2. Mono Compuso a Capialización Coninua 3. Equivalncia nr Tasas d Inrés Compuso Discro y Coninuo 4. Equivalncia nr Tasa d
1.- Qué funciones son primitivas de la función cosx: Tachar lo que no proceda
 .- Qué funcions son primitivas d la función cos: Tachar lo qu no procda.- Hallar + sn() si < cos si si > continua d: f() g() f()+g() f() g() -cos si
.- Qué funcions son primitivas d la función cos: Tachar lo qu no procda.- Hallar + sn() si < cos si si > continua d: f() g() f()+g() f() g() -cos si
La relación que existe entre un cambio de elevación h, en un líquido y un cambio en la presión, Δp, p h [Kg/m 2 ]
![La relación que existe entre un cambio de elevación h, en un líquido y un cambio en la presión, Δp, p h [Kg/m 2 ] La relación que existe entre un cambio de elevación h, en un líquido y un cambio en la presión, Δp, p h [Kg/m 2 ]](/thumbs/62/48298239.jpg) II.3. DESRROLLO DE L RELCION PRESION-ELEVCION es: La relaión que existe entre un ambio de elevaión h, en un líquido un ambio en la resión, Δ, h [Kg/m ].3. Donde γ es el eso eseífio del líquido, esta viene
II.3. DESRROLLO DE L RELCION PRESION-ELEVCION es: La relaión que existe entre un ambio de elevaión h, en un líquido un ambio en la resión, Δ, h [Kg/m ].3. Donde γ es el eso eseífio del líquido, esta viene
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL
 APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL 74 Cuando un problma gométrico stá nunciado n términos d la rcta
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS QUE INVOLUCRAN A LA RECTA TANGENTE Y LA RECTA NORMAL 74 Cuando un problma gométrico stá nunciado n términos d la rcta
IES Mediterráneo de Málaga Solución Septiembre 2010 (Específico) Juan Carlos Alonso Gianonatti OPCIÓN A. 2, se pide determinar:
 IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y
flujo irreversible de energía que se aleja de la fuente transportada por dichas ondas.
 Radiación Qué es radiación? ONDAS ELECTROMAGNÉTICAS Se genera una OEM debido a configuraciones de cargas aceleradas y corrientes variables. ONDAS ACÚSTICAS Se genera una onda acústica propagativa debido
Radiación Qué es radiación? ONDAS ELECTROMAGNÉTICAS Se genera una OEM debido a configuraciones de cargas aceleradas y corrientes variables. ONDAS ACÚSTICAS Se genera una onda acústica propagativa debido
1. INTEGRALES MÚLTIPLES
 1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
1. INTEGALES MÚLTIPLES 1. Calcular las siguientes integrales iteradas: 1. x x 7 y dy dx dx 1. x x y y dx dy 1 1 7. (1 + xy) dx dy 1 1 π/. x sen y dy dx 5. (x + y) dx dy 6/ 1 6. (x + y) 8 dx dy 616 5 1
FÍSICA II. Guía De Problemas Nº4:
 Univrsidad Nacional dl Nordst Facultad d Ingniría Dpartanto d Físico-Quíica/Cátdra Física II FÍSIC II Guía D roblas Nº4: rir rincipio d la Trodináica 1 ROBLEMS RESUELTOS 1- S dsa calcular l trabajo ralizado
Univrsidad Nacional dl Nordst Facultad d Ingniría Dpartanto d Físico-Quíica/Cátdra Física II FÍSIC II Guía D roblas Nº4: rir rincipio d la Trodináica 1 ROBLEMS RESUELTOS 1- S dsa calcular l trabajo ralizado
INTEGRALES INDEFINIDAS
 Ingrals Indfinidas@JEMP INTEGRALES INDEFINIDAS MÉTODOS DE INTEGRACIÓN. Ingración inmdiaa.- Tnindo n cuna qu l procso d ingración s l invrso d la drivación, podmos scribir fácilmn las ingrals indfinidas
Ingrals Indfinidas@JEMP INTEGRALES INDEFINIDAS MÉTODOS DE INTEGRACIÓN. Ingración inmdiaa.- Tnindo n cuna qu l procso d ingración s l invrso d la drivación, podmos scribir fácilmn las ingrals indfinidas
7.1. CAMPOS VECTORIALES EN DEFINICIONES
 7 n 7.. AMPO VETOIALE EN 7.. 7.. DEFINIIONE 7.. 7.. POPIEDADE 7.. 7.4. AMPO VETOIALE 7.4. ONEVATIVO 7.5. INTEGALE DE LÍNEA 7.6. TEOEMA DE GEEN 7.7. INTEGAL DE LÍNEA PAA EL ÁEA DE UNA EGIÓN PLANA 7.8. INTEGALE
7 n 7.. AMPO VETOIALE EN 7.. 7.. DEFINIIONE 7.. 7.. POPIEDADE 7.. 7.4. AMPO VETOIALE 7.4. ONEVATIVO 7.5. INTEGALE DE LÍNEA 7.6. TEOEMA DE GEEN 7.7. INTEGAL DE LÍNEA PAA EL ÁEA DE UNA EGIÓN PLANA 7.8. INTEGALE
TOBERAS Y DIFUSORES. José Agüera Soriano
 TOBERAS Y DIFUSORES José Agüera Soriano 0 José Agüera Soriano 0 VELOCIDAD DEL SONIDO EN UN GAS κ s d d s a κ s d d s olumen eseífio κ s oefiiente de omresibilidad isoentróio d d s a K K gas erfeto a R
TOBERAS Y DIFUSORES José Agüera Soriano 0 José Agüera Soriano 0 VELOCIDAD DEL SONIDO EN UN GAS κ s d d s a κ s d d s olumen eseífio κ s oefiiente de omresibilidad isoentróio d d s a K K gas erfeto a R
TEMA 11. La integral definida Problemas Resueltos
 Matmáticas II (Bachillrato d Cincias) Solucions d los problmas propustos Tma 9 Intgrals dfinidas TEMA La intgral dfinida Problmas Rsultos Halla l valor d: 7 a) ( + ) d b) 5 + d c) + d d) Para hallar una
Matmáticas II (Bachillrato d Cincias) Solucions d los problmas propustos Tma 9 Intgrals dfinidas TEMA La intgral dfinida Problmas Rsultos Halla l valor d: 7 a) ( + ) d b) 5 + d c) + d d) Para hallar una
1. (RMJ15) a) (1,5 puntos) Discute el siguiente sistema de ecuaciones en función del parámetro a:
 EXAMEN DE MATEMÁTICAS II (Eamn Final, Rcupración d Análisis Intgrals) BACHILLERATO EXAMEN FINAL (RMJ5) a) (,5 puntos) Discut l siguint sistma d cuacions n función dl parámtro a: + y + az + ay + z a a +
EXAMEN DE MATEMÁTICAS II (Eamn Final, Rcupración d Análisis Intgrals) BACHILLERATO EXAMEN FINAL (RMJ5) a) (,5 puntos) Discut l siguint sistma d cuacions n función dl parámtro a: + y + az + ay + z a a +
I. Fundamentos matemáticos. ticos. Campos Electromagnéticos. ticos. 5. Divergencia y rotacional. Ingeniero de Telecomunicación
 I. Fundamentos matemá 5. Divergencia y rotacional Gabriel Cano Gómez, G 2009/10 Dpto. Física F Aplicada III (U. Sevilla Campos Electromagné Ingeniero de Telecomunicación I. Fundamentos matemá 1. Coordenadas
I. Fundamentos matemá 5. Divergencia y rotacional Gabriel Cano Gómez, G 2009/10 Dpto. Física F Aplicada III (U. Sevilla Campos Electromagné Ingeniero de Telecomunicación I. Fundamentos matemá 1. Coordenadas
Coordenadas Generalizadas en el Espacio
 Capítulo 3 Coordenadas Generalizadas en el Espacio Las coordenadas cartesianas usuales en R 3 pueden verse también como un sistema de tres familias de superficies en el espacio, de modo que cada punto
Capítulo 3 Coordenadas Generalizadas en el Espacio Las coordenadas cartesianas usuales en R 3 pueden verse también como un sistema de tres familias de superficies en el espacio, de modo que cada punto
Matemáticas II TEMA 11 La integral definida Problemas Propuestos y Resueltos
 Análisis Intgral dfinida Matmáticas II TEMA La intgral dfinida Problmas Propustos y Rsultos Intgrals dfinidas Halla l valor d: 7 a) ( + ) d b) 5 + d c) + d d) Para hallar una primitiva d cada función hay
Análisis Intgral dfinida Matmáticas II TEMA La intgral dfinida Problmas Propustos y Rsultos Intgrals dfinidas Halla l valor d: 7 a) ( + ) d b) 5 + d c) + d d) Para hallar una primitiva d cada función hay
PROBLEMAS DE FLUIDOS ( )
 ROBLEMA DE FLUIDO (-) riniio de Arquímedes FLUIDO. Un sólido metálio se susende de un dinamómetro y se mide su eso, que resulta ser de.5 N. eguidamente se somete a las siguientes oeraiones:. El sólido
ROBLEMA DE FLUIDO (-) riniio de Arquímedes FLUIDO. Un sólido metálio se susende de un dinamómetro y se mide su eso, que resulta ser de.5 N. eguidamente se somete a las siguientes oeraiones:. El sólido
Momentos de Inercia de cuerpos sólidos: EJE. Varilla delgada. Disco. Disco. Cilíndro. Esfera. Anillo I = MR
 91 Momentos de Ineria de uerpos sólidos: EJE Varilla delgada 1 I = ML 1 Diso 1 I = M Diso 1 I = M 4 ilíndro 1 I = M Esfera I = M 5 Anillo I = M 9 Observaión: Los momentos de ineria on respeto a ejes paralelos
91 Momentos de Ineria de uerpos sólidos: EJE Varilla delgada 1 I = ML 1 Diso 1 I = M Diso 1 I = M 4 ilíndro 1 I = M Esfera I = M 5 Anillo I = M 9 Observaión: Los momentos de ineria on respeto a ejes paralelos
BI_UII Más ejemplos de construcción de una segunda solución a partir de otra ya conocida (secc ) 469
 BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida (s..6.) 69 Apéndi BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida. (s..6.) Ejmplo BI. Sindo soluión
BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida (s..6.) 69 Apéndi BI_UII Más jmplos d onstruión d una sgunda soluión a partir d otra a onoida. (s..6.) Ejmplo BI. Sindo soluión
1 2 +! $ = # 1$ $ Pensamiento Algebraico GUÍA DE PARA LOS ASPIRANTES A LA MME Temas que debe dominar:
 Pensamiento lgebraio Temas que debe dominar: GUÍ DE PR LOS SPIRNTES L MME-06 Definiión, operaiones y propiedades de: Números Naturales Números Enteros Números raionales Números irraionales Números omplejos
Pensamiento lgebraio Temas que debe dominar: GUÍ DE PR LOS SPIRNTES L MME-06 Definiión, operaiones y propiedades de: Números Naturales Números Enteros Números raionales Números irraionales Números omplejos
MODELADO CON ECUACIONES DIFERENCIALES PROBLEMAS RESUELTOS
 UNIVERSIDAD DE ORIENTE NÚCLEO DE BOLÍVAR UNIDAD DE ESTUDIOS BÁSICOS DEPARTAMENTO DE CIENCIAS ASIGNATURA: MATEMÁTICAS IV Prof. José Gregorio Páez Veraciera Úlima acualización: 0-09-007 MODELADO CON ECUACIONES
UNIVERSIDAD DE ORIENTE NÚCLEO DE BOLÍVAR UNIDAD DE ESTUDIOS BÁSICOS DEPARTAMENTO DE CIENCIAS ASIGNATURA: MATEMÁTICAS IV Prof. José Gregorio Páez Veraciera Úlima acualización: 0-09-007 MODELADO CON ECUACIONES
Ecuaciones de Máxwell y ondas electromagnéticas
 Zero Order of Magnitude ZOoM)-PID 13-28 Euaiones de Máxwell y ondas eletromagnétias 1. Estímese la intensidad y la potenia total de un láser neesario para elevar una pequeña esfera de plástio de 15 µm
Zero Order of Magnitude ZOoM)-PID 13-28 Euaiones de Máxwell y ondas eletromagnétias 1. Estímese la intensidad y la potenia total de un láser neesario para elevar una pequeña esfera de plástio de 15 µm
Contactores TeSys. Referencias 5. Bobinas en corriente alterna para contactores tri o tetrapolares TeSys d
 Referencias 5 537496 Para contactores a LC1 D09...D38 y LC1 DT0 DT40 Llamada (cos ϕ = 0,75) 70 VA. Mantenimiento (cos ϕ = 0,3) 50 Hz: 7 VA, 60 Hz: 7,5 VA. Campo de funcionamiento (θ y 60 C): 50 Hz: 0,8
Referencias 5 537496 Para contactores a LC1 D09...D38 y LC1 DT0 DT40 Llamada (cos ϕ = 0,75) 70 VA. Mantenimiento (cos ϕ = 0,3) 50 Hz: 7 VA, 60 Hz: 7,5 VA. Campo de funcionamiento (θ y 60 C): 50 Hz: 0,8
Tema 5. Geometría de masas 1.
 Tema 5. Geometría de masas. Profesorado Grupo A: María Tirado Miranda Grupo B: Jorge Portí Durán Grupo : Artur cmitt Tema 5. Geometría de masas. Material elaorado por Juan Francisco Gómez opera. Tema 5.
Tema 5. Geometría de masas. Profesorado Grupo A: María Tirado Miranda Grupo B: Jorge Portí Durán Grupo : Artur cmitt Tema 5. Geometría de masas. Material elaorado por Juan Francisco Gómez opera. Tema 5.
El campo magnético de las corrientes estacionarias
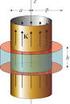 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
ACTIVIDAD DE APRENDIZAJE APRENDIZAJE(S) ESPERADO(S) NOMBRE DE LA ACTIVIDAD
 ACTIVIDAD DE APRENDIZAJE Sila Curso MAT0 Nombr Curso Cálculo I Crédios 0 Hrs. Smsrals Toals 5 Rquisios MAT00 o MAT00 Fcha Acualización Escula o Prorama Transvrsal Prorama d Mamáica Currículum Carrra/s
ACTIVIDAD DE APRENDIZAJE Sila Curso MAT0 Nombr Curso Cálculo I Crédios 0 Hrs. Smsrals Toals 5 Rquisios MAT00 o MAT00 Fcha Acualización Escula o Prorama Transvrsal Prorama d Mamáica Currículum Carrra/s
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DEIVADA Ecucación d la rcta tangnt Ejrcicio nº.- Halla las rctas tangnts a la circunrncia: y y 6 n Ejrcicio nº.- Dada la unción abscisa., scrib la cuación d su rcta tangnt n l punto
APLICACIONES DE LA DEIVADA Ecucación d la rcta tangnt Ejrcicio nº.- Halla las rctas tangnts a la circunrncia: y y 6 n Ejrcicio nº.- Dada la unción abscisa., scrib la cuación d su rcta tangnt n l punto
Tema 9. Modelos de equilibrio de cartera
 Tma 9. Modlos d quilibrio d carra Caracrísicas gnrals En la drminación dl ipo d cambio no sólo incid l mrcado monario: ambién l mrcado d bonos y l mrcado d bins No xis susiuibilidad prca nr los acivos
Tma 9. Modlos d quilibrio d carra Caracrísicas gnrals En la drminación dl ipo d cambio no sólo incid l mrcado monario: ambién l mrcado d bonos y l mrcado d bins No xis susiuibilidad prca nr los acivos
Introducción a la integración de funciones compuestas INTREGRACION POR SUSTITUCION
 Inroducción a la ingración d funcions compusas INTREGRACION POR SUSTITUCION Cuando s raa d funcions compusas, s aplica un méodo qu s llama ingración por susiución, s méodo srá nndido sin dificulad n la
Inroducción a la ingración d funcions compusas INTREGRACION POR SUSTITUCION Cuando s raa d funcions compusas, s aplica un méodo qu s llama ingración por susiución, s méodo srá nndido sin dificulad n la
() t ( )exp( ) 2. La transformada de Fourier
 1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
1 x d La ransormada d ourr x d La ransormada d ourr Sa una uncón localmn ngrabl cuya ngral valor absoluo sa acoada n R. S dn su ransormada d ourr como: 1 d Esas xrsons nos rmn calcular la xrsón domno d
ESTUDIO DE UNA FUNCIÓN CON AYUDA DE LA DERIVADA. 1. a) Halla los valores de los coeficientes b, c y d para que la gráfica de la función
 ESTUDIO DE UNA FUNCIÓN CON AYUDA DE LA DERIVADA CMS05. a) Halla los valors d los coficints b, c y d para qu la gráfica d la función y b c d cort al j OY n l punto (0, ), pas por l punto (, ) y, n s punto,
ESTUDIO DE UNA FUNCIÓN CON AYUDA DE LA DERIVADA CMS05. a) Halla los valors d los coficints b, c y d para qu la gráfica d la función y b c d cort al j OY n l punto (0, ), pas por l punto (, ) y, n s punto,
TEMA 7 APLICACIONES DE LA DERIVADA
 Tma Aplicacions d la drivada Matmáticas CCSSII º Bachillrato 1 TEMA APLICACIONES DE LA DERIVADA RECTA TANGENTE 1 Escrib 0 EJERCICIO 1 : la cuación d la rcta tangnt a la curva f n 0. Ordnada dl punto: f
Tma Aplicacions d la drivada Matmáticas CCSSII º Bachillrato 1 TEMA APLICACIONES DE LA DERIVADA RECTA TANGENTE 1 Escrib 0 EJERCICIO 1 : la cuación d la rcta tangnt a la curva f n 0. Ordnada dl punto: f
Modelo 3 Opción A. , + ) Decreciente: (0, )) = ( , f(
 Modlo Opción A Ejrcicio º Sa f : (, ) R la función dfinida por f() Ln() (Ln dnota la función logarito npriano). (a) [ 5 puntos] Dtrina los intrvalos d crciinto d dcrciinto los tros rlativos d f (puntos
Modlo Opción A Ejrcicio º Sa f : (, ) R la función dfinida por f() Ln() (Ln dnota la función logarito npriano). (a) [ 5 puntos] Dtrina los intrvalos d crciinto d dcrciinto los tros rlativos d f (puntos
PAU Movimiento Vibratorio Ejercicios resueltos
 PU Moviiento Vibratorio jeriios resueltos 99-009 PU CyL S995 ley Hooke alitud y freuenia Colgado de un soorte hay un resorte de onste = 0 N/ del que uelga una asa de kg. n estas irunsias y en equilibrio,
PU Moviiento Vibratorio jeriios resueltos 99-009 PU CyL S995 ley Hooke alitud y freuenia Colgado de un soorte hay un resorte de onste = 0 N/ del que uelga una asa de kg. n estas irunsias y en equilibrio,
Campo de un hilo infinito. Fuerzas magnéticas. Teorema de Ampère. Campo magnético de una espira circular
 El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Problemas Resueltos. 1. La distribución de la temperatura en una placa metálica, viene dada por la función: 70 =
 Problemas Resueltos 1. La distribución de la temperatura en una placa metálica, viene dada por la función: 70 T (, ) =, donde T está medida en grados centígrados,,z en metros. 1+ + + z En qué dirección
Problemas Resueltos 1. La distribución de la temperatura en una placa metálica, viene dada por la función: 70 T (, ) =, donde T está medida en grados centígrados,,z en metros. 1+ + + z En qué dirección
Capítulo 10. Rotación de un Cuerpo Rígido
 Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Capítulo 10 Rotación de un Cuerpo Rígido Contenido Velocidad angular y aceleración angular Cinemática rotacional Relaciones angulares y lineales Energía rotacional Cálculo de los momentos de inercia Teorema
Mecánica estadística de Maxwell-Boltzman. (resumen)
 Mcánica stadística d Maxwll-oltzman (rsumn) Química Física dl stado Sólido U M 2 0 0 4 0 5 Luis Sio Contnidos Mcánica stadística (Maxwll-oltzman) Colctivo canónico Cálculo d las robabilidads Función d
Mcánica stadística d Maxwll-oltzman (rsumn) Química Física dl stado Sólido U M 2 0 0 4 0 5 Luis Sio Contnidos Mcánica stadística (Maxwll-oltzman) Colctivo canónico Cálculo d las robabilidads Función d
f (x)dx = f (x) dx. Si la respuesta es afirmativa justifíquese, si es negativa,
 CALCULO INTEGRAL.(97).- Sa f() una función tal qu, para cualquira qu sa > s cumpl qu = Pruébs qu, ntoncs, s vrifica qu f( ) = f(), para todo >. f f..(97).- Sa la función f() = -. S pid: a) Hacr un dibujo
CALCULO INTEGRAL.(97).- Sa f() una función tal qu, para cualquira qu sa > s cumpl qu = Pruébs qu, ntoncs, s vrifica qu f( ) = f(), para todo >. f f..(97).- Sa la función f() = -. S pid: a) Hacr un dibujo
Simulación de Series Temporales: Una Aplicación al Precio del Petróleo
 1 Simulación de Series Temporales: Una Aplicación al Precio del Petróleo Dr. Ricardo A. Queralt (CUNEF) Lorena Zaragozá (CEPSA) 2 INDICE 1 Introducción 2 Modelos de Series Temporales y @Risk 3 Precios
1 Simulación de Series Temporales: Una Aplicación al Precio del Petróleo Dr. Ricardo A. Queralt (CUNEF) Lorena Zaragozá (CEPSA) 2 INDICE 1 Introducción 2 Modelos de Series Temporales y @Risk 3 Precios
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2013 MATEMÁTICAS II TEMA 5: INTEGRALES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 3 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejrcicio, Opción A Junio, Ejrcicio, Opción B Rsrva, Ejrcicio, Opción A Rsrva, Ejrcicio, Opción B Rsrva, Ejrcicio, Opción
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 3 MATEMÁTICAS II TEMA 5: INTEGRALES Junio, Ejrcicio, Opción A Junio, Ejrcicio, Opción B Rsrva, Ejrcicio, Opción A Rsrva, Ejrcicio, Opción B Rsrva, Ejrcicio, Opción
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATMÁTICA
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATMÁTICA CURSO: Maemáica Inermedia 3 JORNADA: SEMESTRE: Mauina er. Semesre AÑO: 205 TIPO DE EXAMEN: NOMBRE DEL AUXILIAR: NOMBRE
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATMÁTICA CURSO: Maemáica Inermedia 3 JORNADA: SEMESTRE: Mauina er. Semesre AÑO: 205 TIPO DE EXAMEN: NOMBRE DEL AUXILIAR: NOMBRE
FUNCIONES DE DOS VARIABLES DOMINIOS, DERIVADAS PARCIALES Y DIRECCIONALES. Preguntas de dominios y curvas de nivel
 FUNCIONES DE DOS VARIABLES DOMINIOS, DERIVADAS PARCIALES Y DIRECCIONALES Prguntas d dominios curvas d nivl Dtrmina l dominio d las uncions: a) (, ) b) (, sin + + En cada caso indica dos puntos qu no san
FUNCIONES DE DOS VARIABLES DOMINIOS, DERIVADAS PARCIALES Y DIRECCIONALES Prguntas d dominios curvas d nivl Dtrmina l dominio d las uncions: a) (, ) b) (, sin + + En cada caso indica dos puntos qu no san
Electromagnetismo II. Semestre: TAREA 6 Dr. A. Reyes-Coronado
 Electromagnetismo II Semestre: 2015-1 TAREA 6 Dr. A. Reyes-Coronado Por: Pedro Eduardo Roman Taboada 1.- Problema: (10pts) Un modelo primitivo para el átomo consiste en un núcleo puntual con carga +q rodeada
Electromagnetismo II Semestre: 2015-1 TAREA 6 Dr. A. Reyes-Coronado Por: Pedro Eduardo Roman Taboada 1.- Problema: (10pts) Un modelo primitivo para el átomo consiste en un núcleo puntual con carga +q rodeada
Electromagnetismo. Introducción. Líneas de campo magnético. Experimento de Oersted. El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
Recursión y Relaciones de Recurrencia. UCR ECCI CI-1204 Matemáticas Discretas M.Sc. Kryscia Daviana Ramírez Benavides
 Reursión y Relaiones de Reurrenia UCR ECCI CI-04 Matemátias Disretas M.S. Krysia Daviana Ramírez Benavides Algoritmos Reursivos Un algoritmo es reursivo si se soluiona un problema reduiéndolo a una instania
Reursión y Relaiones de Reurrenia UCR ECCI CI-04 Matemátias Disretas M.S. Krysia Daviana Ramírez Benavides Algoritmos Reursivos Un algoritmo es reursivo si se soluiona un problema reduiéndolo a una instania
Solución: Para que sea continua deben coincidir los límites laterales con su valor de definición en dicho punto x = 2. b 1 + b
 Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
Matmáticas Emprsarials I PREGUNTAS DE TIPO TEST DERIVADAS Y APLICACIONES Drivabilidad ( ) b si S09. La función f ( ) s continua y drivabl n = : a( ) si a) Si a = y b = b) Si a = y b = 5 c) Nunca pud sr
Matemáticas Avanzadas para Ingeniería Funciones reales extendidas al Plano Complejo, problemas resueltos
 . Considr los siguints númros compljos: ) z = 3 i 2) z 2 = 2 3 i 3) z 3 = + 3 i ) z = i π Matmáticas Avanzadas para Ingniría Funcions rals xtndidas al Plano Compljo, problmas rsultos Dtrmin la part ral
. Considr los siguints númros compljos: ) z = 3 i 2) z 2 = 2 3 i 3) z 3 = + 3 i ) z = i π Matmáticas Avanzadas para Ingniría Funcions rals xtndidas al Plano Compljo, problmas rsultos Dtrmin la part ral
La integral Indefinida MOISES VILLENA MUÑOZ
 . DEFINIIÓN. TÉNIAS DE INTEGRAIÓN.. FORMULAS.. PROPIEDADES.. INTEGRAIÓN DIRETA.. INTEGRAIÓN POR SUSTITUIÓN.. INTEGRAIÓN POR PARTES..6 INTEGRALES DE FUNIONES TRIGONOMÉTRIAS..7 INTEGRAIÓN POR SUSTITUIÓN
. DEFINIIÓN. TÉNIAS DE INTEGRAIÓN.. FORMULAS.. PROPIEDADES.. INTEGRAIÓN DIRETA.. INTEGRAIÓN POR SUSTITUIÓN.. INTEGRAIÓN POR PARTES..6 INTEGRALES DE FUNIONES TRIGONOMÉTRIAS..7 INTEGRAIÓN POR SUSTITUIÓN
Problemas de AMPLIACIÓN DE MATEMÁTICAS
 Problemas de AMPLIACIÓN DE MATEMÁTICAS Ingeniería Industrial. Curso 3-4. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema : Series. Problema. Halle la representación en serie de McLaurin
Problemas de AMPLIACIÓN DE MATEMÁTICAS Ingeniería Industrial. Curso 3-4. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema : Series. Problema. Halle la representación en serie de McLaurin
PROBLEMAS RESUELTOS. a. La potencia útil. b. El par motor. W t d. P útil P F
 ROBLEMAS RESUELTOS El moor de n aomóvil sminisra na poenia de 90 C a 5000 r.p.m. El vehílo se enenra sbiendo na pendiene, por lo qe iene qe vener na ferza de 1744,5 N en la direión del movimieno. La ransmisión
ROBLEMAS RESUELTOS El moor de n aomóvil sminisra na poenia de 90 C a 5000 r.p.m. El vehílo se enenra sbiendo na pendiene, por lo qe iene qe vener na ferza de 1744,5 N en la direión del movimieno. La ransmisión
RESOLUCIÓN RESOLUCIÓN. RESOLUCIÓN Sea N el número. RESOLUCIÓN Raíz cúbica sabemos: SEMANA 12 POTENCIACIÓN Y RADICACIÓN
 SEMANA 1 POTENCIACIÓN Y RADICACIÓN 1. Si l numral aann s un cuadrado prfcto; Calcul la suma d cifras d su raíz cuadrada? A) 15 B) 1 C) 19 D) 1 E) 1 aann K 11 aann difrncia s cro; ntoncs s múltiplo d 11
SEMANA 1 POTENCIACIÓN Y RADICACIÓN 1. Si l numral aann s un cuadrado prfcto; Calcul la suma d cifras d su raíz cuadrada? A) 15 B) 1 C) 19 D) 1 E) 1 aann K 11 aann difrncia s cro; ntoncs s múltiplo d 11
UNIVERSIDAD DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO
 Seleividad ndaluía. Maemáias pliadas a las ienias Soiales II. JUNIO 5. UNIVERSIDD DE NDLUÍ PRUE DE ESO L UNIVERSIDD URSO 4-5 MTEMÁTIS PLIDS LS IENIS SOILES II Insruiones: EJERIIO a) Duraión: hora y minuos.
Seleividad ndaluía. Maemáias pliadas a las ienias Soiales II. JUNIO 5. UNIVERSIDD DE NDLUÍ PRUE DE ESO L UNIVERSIDD URSO 4-5 MTEMÁTIS PLIDS LS IENIS SOILES II Insruiones: EJERIIO a) Duraión: hora y minuos.
FUNCIONES EXPONENCIAL Y LOGARÍTMICA TRANSFORMACIONES ABACOS Prof : Sergio Weinberger. 2 3x. El número e
 NOMBRE P 6º I 8 FUNCIONES EXPONENCIAL Y LOGARÍTMICA TRANSFORMACIONES ABACOS Pro : Srgio Winbrgr MATEMÁTICA A Lico: Nº NOCT. Rsolvr : a 44 b d 8. 4. 5 5 c 6. 6 Rsolvr : a 5 5 4 b 5 > 4 El númro n "El númro
NOMBRE P 6º I 8 FUNCIONES EXPONENCIAL Y LOGARÍTMICA TRANSFORMACIONES ABACOS Pro : Srgio Winbrgr MATEMÁTICA A Lico: Nº NOCT. Rsolvr : a 44 b d 8. 4. 5 5 c 6. 6 Rsolvr : a 5 5 4 b 5 > 4 El númro n "El númro
Θ(estas fórmulas se usan cuando no se sabe el tiempo)
 FORMULARIO DE FÍSIA INEMÁTIA M.R.U M.R.U.A. e = = 0 ± a e = 0 ± a MOIMIENTO DE AÍDA LIBRE = 0 ± a e Θ Moimieno acelerado g > 0 (posiia) Moimieno decelerado g < 0 (negaia) Θ(esas fórmulas se usan cuando
FORMULARIO DE FÍSIA INEMÁTIA M.R.U M.R.U.A. e = = 0 ± a e = 0 ± a MOIMIENTO DE AÍDA LIBRE = 0 ± a e Θ Moimieno acelerado g > 0 (posiia) Moimieno decelerado g < 0 (negaia) Θ(esas fórmulas se usan cuando
IES Fco Ayala de Granada Junio de 2013 (Modelo 1 Específico 2 ) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala d Granada Junio d 03 (Modlo Espcífico ) Grmán-Jsús Rubio Luna Opción A Ejrcicio opción A, modlo Junio 03, spcífico [ 5 puntos] Halla las dimnsions dl rctángulo d ára máima inscrito n un triangulo
IES Fco Ayala d Granada Junio d 03 (Modlo Espcífico ) Grmán-Jsús Rubio Luna Opción A Ejrcicio opción A, modlo Junio 03, spcífico [ 5 puntos] Halla las dimnsions dl rctángulo d ára máima inscrito n un triangulo
COORDINACION ACADEMICA UNIDAD QUERETARO. Problemas representativos para el examen de ingreso a doctorado. Termodinámica
 UNIDAD QUEREARO roblemas representativos para el examen de ingreso a doctorado ermodinámica Equilibrio térmico, ecuaciones de estado y trabajo 1.- Los sistemas 1 y son sales paramagnéticas con coordenadas
UNIDAD QUEREARO roblemas representativos para el examen de ingreso a doctorado ermodinámica Equilibrio térmico, ecuaciones de estado y trabajo 1.- Los sistemas 1 y son sales paramagnéticas con coordenadas
Fórmula integral de Cauchy
 Fórmula integral de Cauhy Fórmula integral de Cauhy. Si una funión f es analítia en una región que ontiene a urva simple errada y a su interior, entones para ada punto z 0 enerrado por, dz = 2πi f(z 0
Fórmula integral de Cauhy Fórmula integral de Cauhy. Si una funión f es analítia en una región que ontiene a urva simple errada y a su interior, entones para ada punto z 0 enerrado por, dz = 2πi f(z 0
Conductividad en presencia de campo eléctrico
 6. Fenómenos de transporte Fenómenos de transporte Conductividad térmicat Viscosidad Difusión n sedimentación Conductividad en presencia de campo eléctrico UAM 01-13. Química Física. Transporte CT V 1
6. Fenómenos de transporte Fenómenos de transporte Conductividad térmicat Viscosidad Difusión n sedimentación Conductividad en presencia de campo eléctrico UAM 01-13. Química Física. Transporte CT V 1
El mercado de dinero. El mercado de dinero
 El mercado de dinero El mercado de dinero 3.1 Introducción 3.2 El sistema financiero 3.3 Mercado de dinero y de bonos 3.3.1 La demanda de dinero 3.4 Determinación de la oferta monetaria 3.4.1 El multilicador
El mercado de dinero El mercado de dinero 3.1 Introducción 3.2 El sistema financiero 3.3 Mercado de dinero y de bonos 3.3.1 La demanda de dinero 3.4 Determinación de la oferta monetaria 3.4.1 El multilicador
x y x y y x a) Dibujar el conjunto de puntos del plano donde f no está definida. b) Estudiar la continuidad de f en (0,0) y
 ( ) (, ) (,) 1.- Dada la función f(, ) : (, ) (,) a) Dibujar el conjunto de puntos del plano donde f no está definida. b) Estudiar la continuidad de f en (,) c) Calcular (,) (,) (si es necesario prolongar
( ) (, ) (,) 1.- Dada la función f(, ) : (, ) (,) a) Dibujar el conjunto de puntos del plano donde f no está definida. b) Estudiar la continuidad de f en (,) c) Calcular (,) (,) (si es necesario prolongar
Ecuaciones del movimiento de un fluido
 Ecuaciones del movimiento de un fluido 1 Foma fundamental El tenso de tensiones Relación constitutiva paa un fluido Newtoniano La ecuación de Navie-Stokes El tenso de tensiones paa flujos incompesibles
Ecuaciones del movimiento de un fluido 1 Foma fundamental El tenso de tensiones Relación constitutiva paa un fluido Newtoniano La ecuación de Navie-Stokes El tenso de tensiones paa flujos incompesibles
FUNCIONES DERIVABLES EN UN INTERVALO
 DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
DERIVADAS.- BACHILLERATO.- TEORÍA Y EJERCICIOS. Pá. FUNCIONES DERIVABLES EN UN INTERVALO Ls unions qu son ontinus n un intrvlo rrdo [, ] y drivls n un intrvlo irto, tinn propidds importnts. Torm d Roll.
DERIVADAS. Las gráficas A, B y C son las funciones derivadas de las gráficas 1, 2 y 3, pero en otro orden. = 0 utilizando la definición.
 DERIVADAS Dinición d drivada Ejrcicio nº.- Las gráicas A, B y C son las uncions drivadas d las gráicas, y, pro n otro ordn. Cuál s la drivada d cual? Justiica tus rspustas. Ejrcicio nº.- Calcula la drivada
DERIVADAS Dinición d drivada Ejrcicio nº.- Las gráicas A, B y C son las uncions drivadas d las gráicas, y, pro n otro ordn. Cuál s la drivada d cual? Justiica tus rspustas. Ejrcicio nº.- Calcula la drivada
El Teorema de Green. Una curva dada por r(t) = x(t) i + y(t) j, a t b, se dice simple si no se corta consigo misma, es decir, r(c) Curva no simple
 El Teorema de Green Una curva dada por r(t) x(t) i + y(t) j, a t b, se dice simple si no se corta consigo misma, es decir, r(c) r(d) si c d. urva simple urva no simple urva orientada positivamente La curva
El Teorema de Green Una curva dada por r(t) x(t) i + y(t) j, a t b, se dice simple si no se corta consigo misma, es decir, r(c) r(d) si c d. urva simple urva no simple urva orientada positivamente La curva
Radiación de cargas en movimiento
 Radiación de cargas en movimiento 1 Potenciales de Liénard-Wiechert Potenciales Retardados: Φr, t)= v r r Ar, t) = 1 c v ρ r, t r r /c) Jr, t r r /c) r r dv...4) dv...5) 2 Consideremos una carga puntual
Radiación de cargas en movimiento 1 Potenciales de Liénard-Wiechert Potenciales Retardados: Φr, t)= v r r Ar, t) = 1 c v ρ r, t r r /c) Jr, t r r /c) r r dv...4) dv...5) 2 Consideremos una carga puntual
Supercies Regladas. Ejemplo El cilíndro y el cono circular son ejemplos de supercies regladas
 Unidad 1. Superies Cuádrias 1.6 Superies Regladas Superies Regladas Deniión 1. Una superie on la propiedad de que para ada punto en ella hay toda una reta que está ontenida en la superie y que pasa por
Unidad 1. Superies Cuádrias 1.6 Superies Regladas Superies Regladas Deniión 1. Una superie on la propiedad de que para ada punto en ella hay toda una reta que está ontenida en la superie y que pasa por
3dx dx 3. dx 1-4x. 7. 3xdx 4+x x 2
 MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
MsMtscom Intgrls Clculr l intgrl: ++ + (-) (+) - 7 + 8 ln - cos sn - - - + (+) ln ln 7 8 cos ln + + - +- - - + -+ ++ Ls gráfic (i), (ii) y (iii) corrspondn, no ncsrimnt por s ordn, ls d un función drivbl
