ACTIVIDAD 2: La distribución Normal
|
|
|
- Catalina Aguilar Prado
- hace 7 años
- Vistas:
Transcripción
1 Actividad 2: La distribución Normal ACTIVIDAD 2: La distribución Normal CASO 2-1: CLASE DE BIOLOGÍA El Dr. Saigí es profesor de Biología en una prestigiosa universidad. Está preparando una clase en la que pretende mostrar con ejemplos el hecho de que la distribución normal es muy útil a la hora de describir el comportamiento de muchas variables fisiológicas de los seres vivos. Así, p.e., se sospecha que la longitud de una determinada planta sigue un comportamiento aproximadamente normal con media µ = 64 cm y desviación estándar σ = 3,1 cm. El Dr. Saigí pretende comparar los resultados obtenidos en una práctica de campo, en la que sus alumnos midieron 60 plantas de la especie anterior, con una simulación por ordenador realizada a partir de una normal. 1. Simular con Minitab la medición de 60 plantas de la especie anterior. A fin de que todos obtengamos los mismos datos, usar como base para la generación de datos aleatorios provenientes de una normal el número 333. Seleccionamos Calc > Set Base : Ahora usamos la opción Calc > Random Data > Normal : A2-1
2 Estadística Aplicada con Minitab Habremos generado 60 valores aleatorios procedentes de una distribución normal con los parámetros indicados. 2. Mostrar un resumen descriptivo y gráfico (histograma + gráfico de normalidad) de los datos obtenidos en el apartado anterior mediante simulación. Seleccionar Stat > Basic Statistics > Display Descriptive Statistics > Graphs : El programa nos dará el siguiente output: Descriptive Statistics Variable N Mean Median TrMean StDev SE Mean SIMULADO 60 64,584 64,523 64,635 2,931 0,378 Variable Minimum Maximum Q1 Q3 SIMULADO 58,051 70,316 62,734 66,640 Histogram of SIMULADOS, with Normal Curve 10 Frequency SIMULADOS A2-2
3 Actividad 2: La distribución Normal Ahora queremos un gráfico de normalidad: Stat > Basic Statistics > Normality Test: Normal Probability Plot Probability,999,99,95,80,50,20,05,01, Av erage: 64,5844 Anderson-Darling Normality Test StDev : 2,93060 A-Squared: 0,236 N: 60 P-Value: 0, SIMULADOS 70 Observar que los puntos se aproximan bastante a la línea roja, lo cual era de esperar puesto que esto ocurrirá siempre que los datos sean aproximables por una distribución normal (y de hecho estos datos provienen de una normal). A2-3
4 Estadística Aplicada con Minitab 3. Hacer lo mismo que en el apartado 2 pero ahora con los datos obtenidos en el campo, los cuales se encuentran en el archivo campo.mtw. Qué podrían concluir los alumnos del Dr. Saigí?. Repitiendo los pasos anteriores con estos nuevos datos, obtendremos los siguientes resultados: Descriptive Statistics Variable N Mean Median TrMean StDev SE Mean Longitud 60 65,357 66,000 65,402 3,472 0,448 Variable Minimum Maximum Q1 Q3 Longitud 57,200 71,300 62,425 68,225 Histogram of Longitud, with Normal Curve Frequency Longitud Normal Probability Plot,999,99,95 Probability,80,50,20,05,01,001 Av erage: 65,3567 StDev : 3,47155 N: Longitud 70 W-test for Normality R: 0,9853 P-Value (approx): > 0,1000 Si bien ahora los puntos se alejan más que antes de la línea roja, siguen estando lo suficientemente próximos a la misma como para que consideremos que se distribuyen de forma aproximadamente normal. Parece pues que los dos conjuntos de datos son bastante similares. A2-4
5 Actividad 2: La distribución Normal CASO 2-2: SALARIOS MEDIOS Según viene publicado en una prestigiosa revista de economía, el salario semanal medio de los profesores universitarios europeos es de 406,15. Se estima además que la desviación estándar de dichos salarios es de 55,50. Supongamos ahora que pretendemos tomar una muestra aleatoria de 100 profesores para estudiar sus salarios. Calcular las siguientes probabilidades referentes a la media de dicha muestra: 1. La probabilidad de que la media de la muestra sea menor de 400. En primer lugar, observar lo siguiente: como n = 100 >> 30, por el Teorema Central del Límite tendremos que la distribución de las medias muestrales X se podrá aproximar por una normal con media 406,15 y desviación estándar 5,50. Hemos de hallar P ( X < 400) : Seleccionamos: Calc > Probability Distributions > Normal : Cumulative Distribution Function Normal with mean = 406,150 and standard deviation = 5,55000 x P( X <= x) 400,0000 0,1339 A2-5
6 Estadística Aplicada con Minitab 2. La probabilidad de que la media de la muestra esté entre 400 y 410. Sabemos que P ( 400 < X < 410) = P( X < 410) P( X < 400). La segunda de éstas probabilidades ya la hemos calculado en el apartado anterior. Para calcular la primera se razona análogamente, obteniendo que: Cumulative Distribution Function Normal with mean = 406,150 and standard deviation = 5,55000 x P( X <= x) 410,0000 0,7561 Por tanto, tendremos: P ( 400 < X < 410) = P( X < 410) P( X < 400) = 0, La probabilidad de que la media de la muestra sea mayor de 415. En este caso, P ( X > 415) = 1 P( X < 415). Hemos de calcular pues esta última probabilidad, lo cual haremos de forma análoga a los apartados anteriores. Obtendremos lo siguiente: Cumulative Distribution Function Normal with mean = 406,150 and standard deviation = 5,55000 x P( X <= x) 415,0000 0,9446 Por consiguiente, P ( X > 415) = 1 P( X < 415) = 0, Hallar el valor del salario medio c tal que P( X < c) = 0,95. Seleccionamos nuevamente: Calc > Probability Distributions > Normal, pero ahora elegiremos la opción Inverse Cumulative Probability, con lo que obtendremos : Inverse Cumulative Distribution Function Normal with mean = 406,150 and standard deviation = 5,55000 P( X <= x) x 0, ,2789 A2-6
7 Actividad 2: La distribución Normal CASO 2-3: APROXIMACIÓN NORMAL A UNA BINOMIAL Para muchas combinaciones de n y p es posible aproximar bastante bien una distribución binomial B(n,p) mediante una distribución normal de media µ = np y varianza σ 2 = np(1-p). Generalmente, esta aproximación tiende a ser tanto mejor cuanto mayor es el número de pruebas n. 1. Introducir en la columna C1 de una hoja de trabajo los números 0, 1, 2,..., 16. En la columna C2 calcular P(X = 0), P(X = 1),..., P(X = 16), siendo X una binomial de parámetros n = 16 y p = 0,5. Seleccionamos: Calc > Make Patterned Data > Simple Set of Numbers : Ahora hacemos: Calc > Probability Distributions > Binomial : A2-7
8 Estadística Aplicada con Minitab El resultado será el siguiente: Data Display Row C1 C , , , , , , , , , , , , , , , , , Introducir en la columna C3 el valor de la función de densidad de probabilidad (f.d.p.) asociada a los valores de la C1 para una distribución normal que aproxime a la binomial anterior. Observar que: µ = n*p = 8 y σ 2 = n*p*(1-p) = 4 Hacemos: Calc > Probability Distributions > Normal : A2-8
9 Actividad 2: La distribución Normal 3. Dibujar un diagrama de barras con los datos de las columnas C1 (en eje x) y C2 (en eje y). Superpuesto a él, dibujad la función de densidad que se obtiene a partir de las columnas C1 (en eje x) y C3 (en eje y). Qué observas?. A fin de superponer ambos gráficos, elegimos la opción: Graph > Layout : Seleccionamos: Graph > Chart : Finalmente hacemos: Graph > Plot : A2-9
10 Estadística Aplicada con Minitab Para representar los gráficos superpuestos basta con hacer: Graph > End Layout : Aproximación normal a una binomial 0,2 C2 y C3 0,1 0,0 binomial fdp normal C A partir del gráfico anterior se comprende mejor el hecho de que podemos aproximar la probabilidad de que una variable binomial tome un determinado valor mediante la f.d.p. de una distribución normal. Así, p.e., podemos estimar P(X = 7) (área en azul) por P(6,5 < X < 7,5) (área comprendida entre la curva roja y ambos puntos). En el primer caso estamos considerando que la variable X es binomial, mientras que en el segundo consideramos que es normal (y por tanto hacemos uso de la aproximación por continuidad, puesto que para cualquier variable continua la probabilidad puntual es cero). A2-10
LA DISTRIBUCIÓN NORMAL
 LA DISTRIBUCIÓN NORMAL Autores: Ángel A. Juan (ajuanp@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu). ESQUEMA DE CONTENIDOS CARACTERÍSTICAS Y REPRESENTACIÓN DE UNA DISTRIBUCIÓN
LA DISTRIBUCIÓN NORMAL Autores: Ángel A. Juan (ajuanp@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu). ESQUEMA DE CONTENIDOS CARACTERÍSTICAS Y REPRESENTACIÓN DE UNA DISTRIBUCIÓN
DISTRIBUCIONES MUESTRALES
 DISTRIBUCIONES MUESTRALES Distribuciones muestrales Autores: Ángel A. Juan (ajuanp@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu). ESQUEMA DE CONTENIDOS CARACTERÍSTICAS DE LA
DISTRIBUCIONES MUESTRALES Distribuciones muestrales Autores: Ángel A. Juan (ajuanp@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu). ESQUEMA DE CONTENIDOS CARACTERÍSTICAS DE LA
Solución ESTADÍSTICA. Prueba de evaluación continua 1 - PEC1
 Semestre sep04 - feb05 Módulos: 1-11 Prueba de evaluación continua 1 - PEC1 Solución Presentación y objetivos Enunciados: descripción teórica de las prácticas a realizar Materiales Criterios de evaluación
Semestre sep04 - feb05 Módulos: 1-11 Prueba de evaluación continua 1 - PEC1 Solución Presentación y objetivos Enunciados: descripción teórica de las prácticas a realizar Materiales Criterios de evaluación
Tema 4: Probabilidad y Teoría de Muestras
 Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
Teorema Central del Límite (1)
 Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
Teorema Central del Límite (1) Definición. Cualquier cantidad calculada a partir de las observaciones de una muestra se llama estadístico. La distribución de los valores que puede tomar un estadístico
5. DISTRIBUCIONES DE PROBABILIDADES
 5. DISTRIBUCIONES DE PROBABILIDADES Dr. http://academic.uprm.edu/eacunaf UNIVERSIDAD DE PUERTO RICO RECINTO UNIVERSITARIO DE MAYAGUEZ DISTRIBUCIONES DE PROBABILIDADES Se introducirá el concepto de variable
5. DISTRIBUCIONES DE PROBABILIDADES Dr. http://academic.uprm.edu/eacunaf UNIVERSIDAD DE PUERTO RICO RECINTO UNIVERSITARIO DE MAYAGUEZ DISTRIBUCIONES DE PROBABILIDADES Se introducirá el concepto de variable
ACTIVIDAD 5: Correlación y Regresión Lineal
 Actividad 5: Correlación y Regresión Lineal ACTIVIDAD 5: Correlación y Regresión Lineal CASO 5-1: RELACIONES ENTRE VARIABLES A continuación se muestran cuatro variables y seis valores (observaciones) asociados
Actividad 5: Correlación y Regresión Lineal ACTIVIDAD 5: Correlación y Regresión Lineal CASO 5-1: RELACIONES ENTRE VARIABLES A continuación se muestran cuatro variables y seis valores (observaciones) asociados
Distribución muestral de proporciones. Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua
 Distribución muestral de proporciones Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua Distribución muestral de Proporciones Existen ocasiones
Distribución muestral de proporciones Algunas secciones han sido tomadas de: Apuntes de Estadística Inferencial Instituto Tecnológico de Chiuhuahua Distribución muestral de Proporciones Existen ocasiones
JUNIO Bloque A
 Selectividad Junio 009 JUNIO 009 Bloque A 1.- Estudia el siguiente sistema en función del parámetro a. Resuélvelo siempre que sea posible, dejando las soluciones en función de parámetros si fuera necesario.
Selectividad Junio 009 JUNIO 009 Bloque A 1.- Estudia el siguiente sistema en función del parámetro a. Resuélvelo siempre que sea posible, dejando las soluciones en función de parámetros si fuera necesario.
DISTRIBUCIÓN N BINOMIAL
 DISTRIBUCIÓN N BINOMIAL COMBINACIONES En muchos problemas de probabilidad es necesario conocer el número de maneras en que r objetos pueden seleccionarse de un conjunto de n objetos. A esto se le denomina
DISTRIBUCIÓN N BINOMIAL COMBINACIONES En muchos problemas de probabilidad es necesario conocer el número de maneras en que r objetos pueden seleccionarse de un conjunto de n objetos. A esto se le denomina
Variables aleatorias
 Variables aleatorias DEFINICIÓN En temas anteriores, se han estudiado las variables estadísticas, que representaban el conjunto de resultados observados al realizar un experimento aleatorio, presentando
Variables aleatorias DEFINICIÓN En temas anteriores, se han estudiado las variables estadísticas, que representaban el conjunto de resultados observados al realizar un experimento aleatorio, presentando
LECTURA 01: LA DISTRIBUCIÓN NORMAL GENERAL. LA DISTRIBUCIÓN NORMAL ESTÁNDAR (PARTE I). TEMA 1: LA DISTRIBUCION NORMAL GENERAL.
 LECTURA 1: LA DISTRIBUCIÓN NORMAL GENERAL LA DISTRIBUCIÓN NORMAL ESTÁNDAR (PARTE I) TEMA 1: LA DISTRIBUCION NORMAL GENERAL PROPIEDADES 1 INTRODUCCION La distribución de probabilidad continua más importante
LECTURA 1: LA DISTRIBUCIÓN NORMAL GENERAL LA DISTRIBUCIÓN NORMAL ESTÁNDAR (PARTE I) TEMA 1: LA DISTRIBUCION NORMAL GENERAL PROPIEDADES 1 INTRODUCCION La distribución de probabilidad continua más importante
Unidad IV. Una variable aleatoria X es continua si su función de distribución es una función continua.
 Unidad IV Distribuciones de Probabilidad Continuas 4.1. Definición de variable aleatoria continúa. Una variable aleatoria X es continua si su función de distribución es una función continua. En la práctica,
Unidad IV Distribuciones de Probabilidad Continuas 4.1. Definición de variable aleatoria continúa. Una variable aleatoria X es continua si su función de distribución es una función continua. En la práctica,
Distribuciones de probabilidad con R Commander
 Distribuciones de probabilidad con R Commander En el menú Distribuciones podemos seleccionar Distribuciones discretas Distribuciones continuas Las distribuciones discretas que aparecen en R Commander son
Distribuciones de probabilidad con R Commander En el menú Distribuciones podemos seleccionar Distribuciones discretas Distribuciones continuas Las distribuciones discretas que aparecen en R Commander son
ESTADÍSTICA CON EXCEL
 ESTADÍSTICA CON EXCEL 1. INTRODUCCIÓN La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
ESTADÍSTICA CON EXCEL 1. INTRODUCCIÓN La estadística es la rama de las matemáticas que se dedica al análisis e interpretación de series de datos, generando unos resultados que se utilizan básicamente en
RELACIÓN DE EJERCICIOS TEMA 2
 1. Sea una distribución estadística que viene dada por la siguiente tabla: Calcular: x i 61 64 67 70 73 f i 5 18 42 27 8 a) La moda, mediana y media. b) El rango, desviación media, varianza y desviación
1. Sea una distribución estadística que viene dada por la siguiente tabla: Calcular: x i 61 64 67 70 73 f i 5 18 42 27 8 a) La moda, mediana y media. b) El rango, desviación media, varianza y desviación
Habilidades Matemáticas. Alejandro Vera
 Habilidades Matemáticas Alejandro Vera La distribución normal Introducción Una de las herramientas de mayor uso en las empresas es la utilización de la curva normal para describir situaciones donde podemos
Habilidades Matemáticas Alejandro Vera La distribución normal Introducción Una de las herramientas de mayor uso en las empresas es la utilización de la curva normal para describir situaciones donde podemos
CAPÍTULO 5. 5.3 La Distribución Normal
 CAPÍTULO 5 5.3 La Distribución Normal Si una variable aleatoria X tiene una distribución Normal y queremos calcular la probabilidad de que X caiga entre dos valores a y b entonces, debemos hallar el área
CAPÍTULO 5 5.3 La Distribución Normal Si una variable aleatoria X tiene una distribución Normal y queremos calcular la probabilidad de que X caiga entre dos valores a y b entonces, debemos hallar el área
CAPÍTULO 5 DISTRIBUCIONES DE PROBABILIDADES
 CAPÍTULO 5 DISTRIBUCIONES DE PROBABILIDADES En este capítulo se introducirá el concepto de variable aleatoria, cuya importancia radica en introducir modelos matemáticos en el cálculo de probabilidades.
CAPÍTULO 5 DISTRIBUCIONES DE PROBABILIDADES En este capítulo se introducirá el concepto de variable aleatoria, cuya importancia radica en introducir modelos matemáticos en el cálculo de probabilidades.
Matemáticas 2.º Bachillerato. Intervalos de confianza. Contraste de hipótesis
 Matemáticas 2.º Bachillerato Intervalos de confianza. Contraste de hipótesis Depto. Matemáticas IES Elaios Tema: Estadística Inferencial 1. MUESTREO ALEATORIO Presentación elaborada por el profesor José
Matemáticas 2.º Bachillerato Intervalos de confianza. Contraste de hipótesis Depto. Matemáticas IES Elaios Tema: Estadística Inferencial 1. MUESTREO ALEATORIO Presentación elaborada por el profesor José
Distribuciones de Probabilidad Normal [Gaussiana]
![Distribuciones de Probabilidad Normal [Gaussiana] Distribuciones de Probabilidad Normal [Gaussiana]](/thumbs/48/24246416.jpg) Distribuciones de Probabilidad Normal [Gaussiana] Distribución Normal o Gaussiana Una variable aleatoria X es llamada variable aleatoria normal (guassiana) si su pdf está dado por, 1 2 2 x / 2 f X x e
Distribuciones de Probabilidad Normal [Gaussiana] Distribución Normal o Gaussiana Una variable aleatoria X es llamada variable aleatoria normal (guassiana) si su pdf está dado por, 1 2 2 x / 2 f X x e
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E
 PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E CURSO 00-.003 - CONVOCATORIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES - Cada alumno debe elegir sólo una de las pruebas (A o B) y, dentro de ella, sólo
PRUEBAS DE ACCESO A LA UNIVERSIDAD L.O.G.S.E CURSO 00-.003 - CONVOCATORIA: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES - Cada alumno debe elegir sólo una de las pruebas (A o B) y, dentro de ella, sólo
Distribución Chi (o Ji) cuadrada (χ( 2 )
 Distribución Chi (o Ji) cuadrada (χ( 2 ) PEARSON, KARL. On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it Can Reasonably
Distribución Chi (o Ji) cuadrada (χ( 2 ) PEARSON, KARL. On the Criterion that a Given System of Deviations from the Probable in the Case of a Correlated System of Variables is such that it Can Reasonably
MODELOS DE PROBABILIDAD
 MODELOS DE PROBABILIDAD Modelos de probabilidad Autores: Angel Juan (ajuanp@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu), José Francisco Martínez (jmartinezbos@uoc.edu), Anna
MODELOS DE PROBABILIDAD Modelos de probabilidad Autores: Angel Juan (ajuanp@uoc.edu), Máximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu), José Francisco Martínez (jmartinezbos@uoc.edu), Anna
Tema: ESTADÍSTICA DESCRIPTIVA BÁSICA CON SPSS 8.0
 Ignacio Martín Tamayo 11 Tema: ESTADÍSTICA DESCRIPTIVA BÁSICA CON SPSS 8.0 ÍNDICE ------------------------------------------------------------- 1. Introducción 2. Frecuencias 3. Descriptivos 4. Explorar
Ignacio Martín Tamayo 11 Tema: ESTADÍSTICA DESCRIPTIVA BÁSICA CON SPSS 8.0 ÍNDICE ------------------------------------------------------------- 1. Introducción 2. Frecuencias 3. Descriptivos 4. Explorar
Ejemplos y ejercicios de. Estadística Descriptiva. yanálisis de Datos. 2 Descripción estadística de una variable. Ejemplos y ejercicios.
 ESTADÍSTICA DESCRIPTIVA Y ANÁLISIS DE DATOS Ejemplos y ejercicios de Estadística Descriptiva yanálisis de Datos Diplomatura en Estadística Curso 007/08 Descripción estadística de una variable. Ejemplos
ESTADÍSTICA DESCRIPTIVA Y ANÁLISIS DE DATOS Ejemplos y ejercicios de Estadística Descriptiva yanálisis de Datos Diplomatura en Estadística Curso 007/08 Descripción estadística de una variable. Ejemplos
CONTENIDO. Prólogo a la 3. a edición en español ampliada... Prólogo...
 CONTENIDO Prólogo a la 3. a edición en español ampliada.................................. Prólogo.................................................................. vii xvii 1. Métodos descriptivos................................................
CONTENIDO Prólogo a la 3. a edición en español ampliada.................................. Prólogo.................................................................. vii xvii 1. Métodos descriptivos................................................
6. VARIABLES ALEATORIAS
 6. VARIABLES ALEATORIAS Objetivo Introducir la idea de una variable aleatoria y su distribución y características como media, varianza etc. Bibliografía recomendada Peña y Romo (1997), Capítulo 15. Hasta
6. VARIABLES ALEATORIAS Objetivo Introducir la idea de una variable aleatoria y su distribución y características como media, varianza etc. Bibliografía recomendada Peña y Romo (1997), Capítulo 15. Hasta
Conceptos Básicos de Inferencia
 Conceptos Básicos de Inferencia Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Inferencia Estadística Cuando obtenemos una muestra, conocemos
Conceptos Básicos de Inferencia Álvaro José Flórez 1 Escuela de Ingeniería Industrial y Estadística Facultad de Ingenierías Febrero - Junio 2012 Inferencia Estadística Cuando obtenemos una muestra, conocemos
EJERCICIOS RESUELTOS DE ESTADÍSTICA II
 EJERCICIOS RESUELTOS DE ESTADÍSTICA II RESUMEN DE EJERCICIOS DADOS EN CLASES PARTE I POR: EILEEN JOHANA ARAGONES GENEY DISTRIBUCIONES DOCENTE: JUAN CARLOS V ERGARA SCHMALBACH ESTIMACIÓN PRUEBAS DE HIPÓTESIS
EJERCICIOS RESUELTOS DE ESTADÍSTICA II RESUMEN DE EJERCICIOS DADOS EN CLASES PARTE I POR: EILEEN JOHANA ARAGONES GENEY DISTRIBUCIONES DOCENTE: JUAN CARLOS V ERGARA SCHMALBACH ESTIMACIÓN PRUEBAS DE HIPÓTESIS
Polinomios y Estadística
 Funciones polinomiales Universidad de Concepción, Chile Departamento de Geofísica Programación Científica con Software libre Primavera, 2011 Universidad de Concepción Contenidos Funciones polinomiales
Funciones polinomiales Universidad de Concepción, Chile Departamento de Geofísica Programación Científica con Software libre Primavera, 2011 Universidad de Concepción Contenidos Funciones polinomiales
AJUSTE DE DATOS POR UNA DISTRIBUCIÓN TEÓRICA CON MINITAB
 AJUSTE DE DATOS POR UNA DISTRIBUCIÓN TEÓRICA CON MINITAB Autor: Ángel A. Juan (ajuanp@uoc.edu). ESQUEMA DE CONTENIDOS Ajuste mediante una distribución continua conocida (Minitab) Introducción a los tests
AJUSTE DE DATOS POR UNA DISTRIBUCIÓN TEÓRICA CON MINITAB Autor: Ángel A. Juan (ajuanp@uoc.edu). ESQUEMA DE CONTENIDOS Ajuste mediante una distribución continua conocida (Minitab) Introducción a los tests
Tema 5 Algunas distribuciones importantes
 Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Algunas distribuciones importantes 1 Modelo Bernoulli Distribución Bernoulli Se llama experimento de Bernoulli a un experimento con las siguientes características: 1. Se realiza un experimento con dos
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2009) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2009) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Una carpintería vende paneles de contrachapado de dos tipos A y B.
Examen de Matemáticas Aplicadas a las CC. Sociales II (Septiembre 2009) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (3 puntos) Una carpintería vende paneles de contrachapado de dos tipos A y B.
2.- Tablas de frecuencias
 º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II TEMA 3.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------
º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II TEMA 3.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ -----------------------------------------------------------------------------------------------------------------------------------------------------------------
UNIDAD 6. Estadística
 Matemática UNIDAD 6. Estadística 2 Medio GUÍA N 1 MEDIDAS DE DISPERSIÓN PARA DATOS NO AGRUPADOS ACTIVIDAD Consideremos los siguientes conjuntos de valores referidos a las edades de los jugadores de dos
Matemática UNIDAD 6. Estadística 2 Medio GUÍA N 1 MEDIDAS DE DISPERSIÓN PARA DATOS NO AGRUPADOS ACTIVIDAD Consideremos los siguientes conjuntos de valores referidos a las edades de los jugadores de dos
Tema 4: Probabilidad y Teoría de Muestras
 Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
Tema 4: Probabilidad y Teoría de Muestras Estadística. 4 o Curso. Licenciatura en Ciencias Ambientales Licenciatura en Ciencias Ambientales (4 o Curso) Tema 4: Probabilidad y Teoría de Muestras Curso 2008-2009
INTERPRETACIÓN DE LA REGRESIÓN. Interpretación de la regresión
 INTERPRETACIÓN DE LA REGRESIÓN Este gráfico muestra el salario por hora de 570 individuos. 1 Interpretación de la regresión. regresión Salario-Estudios Source SS df MS Number of obs = 570 ---------+------------------------------
INTERPRETACIÓN DE LA REGRESIÓN Este gráfico muestra el salario por hora de 570 individuos. 1 Interpretación de la regresión. regresión Salario-Estudios Source SS df MS Number of obs = 570 ---------+------------------------------
UNIDAD 12.- Estadística. Tablas y gráficos (tema12 del libro)
 UNIDAD 12.- Estadística. Tablas y gráficos (tema12 del libro) 1. ESTADÍSTICA: CLASES Y CONCEPTOS BÁSICOS En sus orígenes históricos, la Estadística estuvo ligada a cuestiones de Estado (recuentos, censos,
UNIDAD 12.- Estadística. Tablas y gráficos (tema12 del libro) 1. ESTADÍSTICA: CLASES Y CONCEPTOS BÁSICOS En sus orígenes históricos, la Estadística estuvo ligada a cuestiones de Estado (recuentos, censos,
La distribución normal o gaussiana es la distribución. Definición 42 Se dice que una variable X se distribuye como normal con parámetros µ y σ si
 La distribución normal La distribución normal o gaussiana es la distribución continua más importante. Definición 42 Se dice que una variable X se distribuye como normal con parámetros µ y σ si f(x) = 1
La distribución normal La distribución normal o gaussiana es la distribución continua más importante. Definición 42 Se dice que una variable X se distribuye como normal con parámetros µ y σ si f(x) = 1
APROXIMACIÓN DE LA DISTRIBUCIÓN BINOMIAL A LA NORMAL, LA CALCULADORA Y LAS TIC
 APROXIMACIÓN DE LA DISTRIBUCIÓN BINOMIAL A LA NORMAL, LA CALCULADORA Y LAS TIC SIGMA 28 Abel Martín (*) y Rosana Álvarez García (**) En dos artículos anteriores ya hemos estudiado la distribución Binomial
APROXIMACIÓN DE LA DISTRIBUCIÓN BINOMIAL A LA NORMAL, LA CALCULADORA Y LAS TIC SIGMA 28 Abel Martín (*) y Rosana Álvarez García (**) En dos artículos anteriores ya hemos estudiado la distribución Binomial
Agro 6998 Conferencia 2. Introducción a los modelos estadísticos mixtos
 Agro 6998 Conferencia Introducción a los modelos estadísticos mixtos Los modelos estadísticos permiten modelar la respuesta de un estudio experimental u observacional en función de factores (tratamientos,
Agro 6998 Conferencia Introducción a los modelos estadísticos mixtos Los modelos estadísticos permiten modelar la respuesta de un estudio experimental u observacional en función de factores (tratamientos,
Variable Aleatoria Continua. Principales Distribuciones
 Variable Aleatoria Continua. Definición de v. a. continua Función de Densidad Función de Distribución Características de las v.a. continuas continuas Ejercicios Definición de v. a. continua Las variables
Variable Aleatoria Continua. Definición de v. a. continua Función de Densidad Función de Distribución Características de las v.a. continuas continuas Ejercicios Definición de v. a. continua Las variables
Histograma del puntaje de vocabulario y la aproximación por una curva gaussiana.
 35 Curvas de densidad Existe alguna manera de describir una distribución completa mediante una única expresión? un diagrama tallo-hoja no es práctico pues se trata de demasiados datos un histograma elimina
35 Curvas de densidad Existe alguna manera de describir una distribución completa mediante una única expresión? un diagrama tallo-hoja no es práctico pues se trata de demasiados datos un histograma elimina
Prácticas de Fiabilidad
 Prácticas de Fiabilidad Práctica : Objetivo: El objetivo de esta práctica es conocer y aprender a manejar las herramientas que nos van a permitir decidir si nuestros datos de supervivencia se comportan
Prácticas de Fiabilidad Práctica : Objetivo: El objetivo de esta práctica es conocer y aprender a manejar las herramientas que nos van a permitir decidir si nuestros datos de supervivencia se comportan
 FACULTAD DE INGENIERÍA UNAM PROBABILIDAD Y ESTADÍSTICA Irene Patricia Valdez y Alfaro irenev@servidor.unam.m T E M A S DEL CURSO. Análisis Estadístico de datos muestrales.. Fundamentos de la Teoría de
FACULTAD DE INGENIERÍA UNAM PROBABILIDAD Y ESTADÍSTICA Irene Patricia Valdez y Alfaro irenev@servidor.unam.m T E M A S DEL CURSO. Análisis Estadístico de datos muestrales.. Fundamentos de la Teoría de
DISTRIBUCIONES DE PROBABILIDAD
 DISTRIBUCIONES DE PROBABILIDAD Se llama variable aleatoria a toda función que asocia a cada elemento del espacio muestral E un número real. Una variable aleatoria discreta es aquella que sólo puede tomar
DISTRIBUCIONES DE PROBABILIDAD Se llama variable aleatoria a toda función que asocia a cada elemento del espacio muestral E un número real. Una variable aleatoria discreta es aquella que sólo puede tomar
8.2.5. Intervalos para la diferencia de medias de dos poblaciones
 8.. INTERVALOS DE CONFIANZA PARA LA DISTRIBUCIÓN NORMAL 89 distribuye de modo gaussiana. Para ello se tomó una muestra de 5 individuos (que podemos considerar piloto), que ofreció los siguientes resultados:
8.. INTERVALOS DE CONFIANZA PARA LA DISTRIBUCIÓN NORMAL 89 distribuye de modo gaussiana. Para ello se tomó una muestra de 5 individuos (que podemos considerar piloto), que ofreció los siguientes resultados:
ESTADÍSTICA. Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal. continua
 ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
ESTADÍSTICA Población Individuo Muestra Muestreo Valor Dato Variable Cualitativa ordinal nominal Cuantitativa discreta continua DISTRIBUCIÓN DE FRECUENCIAS Frecuencia absoluta: fi Frecuencia relativa:
CONTRASTES DE HIPÓTESIS NO PARAMÉTRICOS
 CONTRASTES DE HIPÓTESIS NO PARAMÉTRICOS 1 POR QUÉ SE LLAMAN CONTRASTES NO PARAMÉTRICOS? A diferencia de lo que ocurría en la inferencia paramétrica, ahora, el desconocimiento de la población que vamos
CONTRASTES DE HIPÓTESIS NO PARAMÉTRICOS 1 POR QUÉ SE LLAMAN CONTRASTES NO PARAMÉTRICOS? A diferencia de lo que ocurría en la inferencia paramétrica, ahora, el desconocimiento de la población que vamos
MICROSOFT EXCEL PARA DIRECCIÓN FINANCIERA I. 1. Resolución de problemas de simulación de Montecarlo mediante el uso de la hoja de cálculo.
 MICROSOFT EXCEL PARA DIRECCIÓN FINANCIERA I. 1. Resolución de problemas de simulación de Montecarlo mediante el uso de la hoja de cálculo. Mediante el modelo de Hertz o Simulación de Montecarlo, trataremos
MICROSOFT EXCEL PARA DIRECCIÓN FINANCIERA I. 1. Resolución de problemas de simulación de Montecarlo mediante el uso de la hoja de cálculo. Mediante el modelo de Hertz o Simulación de Montecarlo, trataremos
OPCIÓN A. La empresa A (x) tiene 30 trabajadores, la B (y) 20 trabajadores y la C (z) 13 trabajadores.
 PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA EL ALUMNADO DE BACHILLERATO. 159 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES. JUNIO 16 EXAMEN RESUELTO POR JAVIER SUÁREZ CABALLERO (@javiersc9) OBSERVACIONES IMPORTANTES:
PRUEBAS DE ACCESO A LA UNIVERSIDAD PARA EL ALUMNADO DE BACHILLERATO. 159 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES. JUNIO 16 EXAMEN RESUELTO POR JAVIER SUÁREZ CABALLERO (@javiersc9) OBSERVACIONES IMPORTANTES:
Curso de nivelación Estadística y Matemática
 Curso de nivelación Estadística y Matemática Tercera clase: Introducción al concepto de probabilidad y Distribuciones de probablidad discretas Programa Técnico en Riesgo, 2014 Agenda 1 Concepto de probabilidad
Curso de nivelación Estadística y Matemática Tercera clase: Introducción al concepto de probabilidad y Distribuciones de probablidad discretas Programa Técnico en Riesgo, 2014 Agenda 1 Concepto de probabilidad
Distribuciones de probabilidad
 Distribuciones de probabilidad Prof, Dr. Jose Jacobo Zubcoff Departamento de Ciencias del Mar y Biología Aplicada Inferencia estadística: Parte de la estadística que estudia grandes colectivos a partir
Distribuciones de probabilidad Prof, Dr. Jose Jacobo Zubcoff Departamento de Ciencias del Mar y Biología Aplicada Inferencia estadística: Parte de la estadística que estudia grandes colectivos a partir
ESTADÍSTICA DESCRIPTIVA CON MINITAB
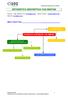 ESTADÍSTICA DESCRIPTIVA CON MINITAB Autores: Angel Alejandro Juan (ajuanp@uoc.edu), Maximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu). MAPA CONCEPTUAL DEFINICIÓN DE POBLACIÓN Y MUESTRA ESTADÍSTICA
ESTADÍSTICA DESCRIPTIVA CON MINITAB Autores: Angel Alejandro Juan (ajuanp@uoc.edu), Maximo Sedano (msedanoh@uoc.edu), Alicia Vila (avilag@uoc.edu). MAPA CONCEPTUAL DEFINICIÓN DE POBLACIÓN Y MUESTRA ESTADÍSTICA
b) dado que es en valor absoluto será el área entre -1,071 y 1,071 luego el resultado será F(1,071)-(1-F(1,071)=0,85-(1-0,85)=0,7
 EJERCICIOS T12-MODELOS MULTIVARIANTES ESPECÍFICOS 1. Un determinado estadístico J se distribuye según un modelo jhi-dos de parámetro (grados de libertad) 14. Deseamos saber la probabilidad con la que dicho
EJERCICIOS T12-MODELOS MULTIVARIANTES ESPECÍFICOS 1. Un determinado estadístico J se distribuye según un modelo jhi-dos de parámetro (grados de libertad) 14. Deseamos saber la probabilidad con la que dicho
Otra característica poblacional de interés es la varianza de la población, 2, y su raíz cuadrada, la desviación estándar de la población,. La varianza
 CARACTERÍSTICAS DE LA POBLACIÓN. Una pregunta práctica en gran parte de la investigación de mercado tiene que ver con el tamaño de la muestra. La encuesta, en principio, no puede ser aplicada sin conocer
CARACTERÍSTICAS DE LA POBLACIÓN. Una pregunta práctica en gran parte de la investigación de mercado tiene que ver con el tamaño de la muestra. La encuesta, en principio, no puede ser aplicada sin conocer
Tema 5: Introducción a la inferencia estadística
 Tema 5: Introducción a la inferencia estadística 1. Planteamiento y objetivos 2. Estadísticos y distribución muestral 3. Estimadores puntuales 4. Estimadores por intervalos 5. Contrastes de hipótesis Lecturas
Tema 5: Introducción a la inferencia estadística 1. Planteamiento y objetivos 2. Estadísticos y distribución muestral 3. Estimadores puntuales 4. Estimadores por intervalos 5. Contrastes de hipótesis Lecturas
PRUEBA ESPECÍFICA PRUEBA 2011
 PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES PRUEBA ESPECÍFICA PRUEBA 011 PRUEBA SOLUCIONARIO Aclaraciones previas Tiempo de duración de la prueba: 1 hora Contesta cinco de los seis ejercicios propuestos.
PRUEBA DE ACCESO A LA UNIVERSIDAD MAYORES PRUEBA ESPECÍFICA PRUEBA 011 PRUEBA SOLUCIONARIO Aclaraciones previas Tiempo de duración de la prueba: 1 hora Contesta cinco de los seis ejercicios propuestos.
EJERCICIOS RESUELTOS TEMA 7
 EJERCICIOS RESUELTOS TEMA 7 7.1. Seleccione la opción correcta: A) Hay toda una familia de distribuciones normales, cada una con su media y su desviación típica ; B) La media y la desviaciones típica de
EJERCICIOS RESUELTOS TEMA 7 7.1. Seleccione la opción correcta: A) Hay toda una familia de distribuciones normales, cada una con su media y su desviación típica ; B) La media y la desviaciones típica de
4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE
 Análisis de funciones de una variable 49 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable: En la parte final hay ejercicios
Análisis de funciones de una variable 49 4. ANÁLISIS DE FUNCIONES DE UNA VARIABLE En esta sección realizaremos algunos ejercicios sobre el estudio de funciones de una variable: En la parte final hay ejercicios
Algunas Distribuciones Continuas de Probabilidad. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Introducción a MINITAB 15. David R. González Barreto. Ofrecido en Wyeth, Carolina, Puerto Rico
 Introducción a MINITAB 15 Ofrecido en Wyeth, Carolina, Puerto Rico INDICE Listado de Archivos...2 Pantalla Principal..3 Texto a Número.4 Estibar (Stack)..6 Split 8 Dotplot Una población.10 Dotplot Dos
Introducción a MINITAB 15 Ofrecido en Wyeth, Carolina, Puerto Rico INDICE Listado de Archivos...2 Pantalla Principal..3 Texto a Número.4 Estibar (Stack)..6 Split 8 Dotplot Una población.10 Dotplot Dos
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL
 DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
DOCUMENTO 3: DISTRIBUCIÓN DE PROBABILIDAD DE V. A. CONTINUA: LA DISTRIBUCIÓN NORMAL 3.1 INTRODUCCIÓN Como ya sabes, una distribución de probabilidad es un modelo matemático que nos ayuda a explicar los
1 - TEORIA DE ERRORES : distribución de frecuencias
 - TEORIA DE ERRORES : distribución de frecuencias CONTENIDOS Distribución de Frecuencias. Histograma. Errores de Apreciación. Propagación de errores. OBJETIVOS Representar una serie de datos mediante un
- TEORIA DE ERRORES : distribución de frecuencias CONTENIDOS Distribución de Frecuencias. Histograma. Errores de Apreciación. Propagación de errores. OBJETIVOS Representar una serie de datos mediante un
ESTADISTICA GENERAL. INFERENCIA ESTADISTICA Profesor: Celso Celso Gonzales
 ESTADISTICA GENERAL INFERENCIA ESTADISTICA Profesor: Celso Celso Gonzales Objetivos Entender los conceptos de estimación puntual y estimación por intervalos. Calcular e interpretar intervalos de confianza
ESTADISTICA GENERAL INFERENCIA ESTADISTICA Profesor: Celso Celso Gonzales Objetivos Entender los conceptos de estimación puntual y estimación por intervalos. Calcular e interpretar intervalos de confianza
III Verano de Probabilidad y Estadística Curso de Procesos de Poisson (Víctor Pérez Abreu) Lista de Ejercicios
 III Verano de Probabilidad y Estadística Curso de Procesos de Poisson (Víctor Pérez Abreu) Lista de Ejercicios Esta lista contiene ejercicios y problemas tanto teóricos como de modelación. El objetivo
III Verano de Probabilidad y Estadística Curso de Procesos de Poisson (Víctor Pérez Abreu) Lista de Ejercicios Esta lista contiene ejercicios y problemas tanto teóricos como de modelación. El objetivo
Hoja 6: Estadística descriptiva
 Hoja : Estadística descriptiva Hoja : Estadística descriptiva May Dada la siguiente distribución de frecuencias, halle: a) la mediana; b) la media. Número (x) Frecuencia (y) May De enero a septiembre la
Hoja : Estadística descriptiva Hoja : Estadística descriptiva May Dada la siguiente distribución de frecuencias, halle: a) la mediana; b) la media. Número (x) Frecuencia (y) May De enero a septiembre la
La distribución de Probabilidad normal, dada por la ecuación:
 La distribución de Probabilidad normal, dada por la ecuación: Donde: x = X -, la distancia entre X y en el eje de las X. = la media de la población o universo ( de las X ) fx= La altura de la ordenada
La distribución de Probabilidad normal, dada por la ecuación: Donde: x = X -, la distancia entre X y en el eje de las X. = la media de la población o universo ( de las X ) fx= La altura de la ordenada
MOOC UJI: La Probabilidad en las PAU
 4. Probabilidad Condicionada: Teoremas de la Probabilidad Total y de Bayes 4.1. Probabilidad Condicionada Vamos a estudiar como cambia la probabilidad de un suceso A cuando sabemos que ha ocurrido otro
4. Probabilidad Condicionada: Teoremas de la Probabilidad Total y de Bayes 4.1. Probabilidad Condicionada Vamos a estudiar como cambia la probabilidad de un suceso A cuando sabemos que ha ocurrido otro
FICHA DE REPASO: ESTADÍSTICA
 FICHA DE REPASO: ESTADÍSTICA 1. Indica la población y la muestra de los siguientes estudios estadísticos: a) El número de móviles de los alumnos de 2º de la E.S.O de nuestro instituto. b) La altura de
FICHA DE REPASO: ESTADÍSTICA 1. Indica la población y la muestra de los siguientes estudios estadísticos: a) El número de móviles de los alumnos de 2º de la E.S.O de nuestro instituto. b) La altura de
Teoría de errores -Hitogramas
 FÍSICA I Teoría de errores -Hitogramas Autores: Pablo Iván ikel - e-mail: pinikel@hotmail.com Ma. Florencia Kronberg - e-mail:sil_simba@hotmail.com Silvina Poncelas - e-mail:flo_kron@hotmail.com Introducción:
FÍSICA I Teoría de errores -Hitogramas Autores: Pablo Iván ikel - e-mail: pinikel@hotmail.com Ma. Florencia Kronberg - e-mail:sil_simba@hotmail.com Silvina Poncelas - e-mail:flo_kron@hotmail.com Introducción:
(L i 1, L i ] x i n i N i f i F i a i h i (20, 50] 35 2 2 (, 60] 10 0.125 (60, ] 0.425 10 (, ] 75 0.225 (, 100] 28 80 1.4
![(L i 1, L i ] x i n i N i f i F i a i h i (20, 50] 35 2 2 (, 60] 10 0.125 (60, ] 0.425 10 (, ] 75 0.225 (, 100] 28 80 1.4 (L i 1, L i ] x i n i N i f i F i a i h i (20, 50] 35 2 2 (, 60] 10 0.125 (60, ] 0.425 10 (, ] 75 0.225 (, 100] 28 80 1.4](/thumbs/39/19126908.jpg) Problemas Tema 1-I 1. Un gabinete de trabajo ha realizado un estudio sobre la distribución de la renta per cápita por municipio, construyéndose una tabla que posteriormente se extravió, quedando sólo la
Problemas Tema 1-I 1. Un gabinete de trabajo ha realizado un estudio sobre la distribución de la renta per cápita por municipio, construyéndose una tabla que posteriormente se extravió, quedando sólo la
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos
 Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema de ecuaciones dependiente del parámetro real a:
Examen de Matemáticas Aplicadas a las CC. Sociales II (Junio 2015) Selectividad-Opción A Tiempo: 90 minutos Problema 1 (2 puntos) Se considera el sistema de ecuaciones dependiente del parámetro real a:
P (X 5) = P (x = 5) + P (X = 6) + P (X = 7) + P (X = 8) = 0.005416467 + 0.051456432 + 0.79334918 + 0.663420431 = 0.999628249
 Hoja 3: robabilidad y variables aleatorias 1. La probabilidad de que un enfermo se recupere tomando un nuevo fármaco es 0.95. Si se les administra a 8 enfermos, hallar: a La probabilidad de que se recuperen
Hoja 3: robabilidad y variables aleatorias 1. La probabilidad de que un enfermo se recupere tomando un nuevo fármaco es 0.95. Si se les administra a 8 enfermos, hallar: a La probabilidad de que se recuperen
Variables aleatorias continuas
 Probabilidades y stadística Computación Facultad de Ciencias actas y Naturales Universidad de uenos ires na M ianco y lena J Martínez 004 Variables aleatorias continuas jemplo: Con el in de realizar un
Probabilidades y stadística Computación Facultad de Ciencias actas y Naturales Universidad de uenos ires na M ianco y lena J Martínez 004 Variables aleatorias continuas jemplo: Con el in de realizar un
Tests de hipótesis estadísticas
 Tests de hipótesis estadísticas Test de hipótesis sobre la media de una población. Introducción con un ejemplo. Los tests de hipótesis estadísticas se emplean para muchos problemas, en particular para
Tests de hipótesis estadísticas Test de hipótesis sobre la media de una población. Introducción con un ejemplo. Los tests de hipótesis estadísticas se emplean para muchos problemas, en particular para
Tema 4 Variables Aleatorias
 Tema 4 Variables Aleatorias 1 Introducción En Estadística Descriptiva, se estudiaron las distribuciones de frecuencias de conjuntos de datos y posteriormente se vimos los fundamentos de la teoría de probabilidades.
Tema 4 Variables Aleatorias 1 Introducción En Estadística Descriptiva, se estudiaron las distribuciones de frecuencias de conjuntos de datos y posteriormente se vimos los fundamentos de la teoría de probabilidades.
Modelos Estadísticos de Crimen
 Universidad de los Andes Modelos Estadísticos de Crimen 27 de Mayo de 2015 Motivacion Conocer la densidad de probabilidad del crimen sobre una ciudad, a distintas horas del día, permite Modelos Estadísticos
Universidad de los Andes Modelos Estadísticos de Crimen 27 de Mayo de 2015 Motivacion Conocer la densidad de probabilidad del crimen sobre una ciudad, a distintas horas del día, permite Modelos Estadísticos
para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua
 Pruebas de hipótesis para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua Las secciones anteriores han mostrado cómo puede estimarse un parámetro de
Pruebas de hipótesis para una muestra Ref: Apuntes de Estadística, Mtra Leticia de la Torre Instituto Tecnológico de Chiuhuahua Las secciones anteriores han mostrado cómo puede estimarse un parámetro de
Tercera práctica de REGRESIÓN.
 Tercera práctica de REGRESIÓN. DATOS: fichero practica regresión 3.sf3 1. Objetivo: El objetivo de esta práctica es aplicar el modelo de regresión con más de una variable explicativa. Es decir regresión
Tercera práctica de REGRESIÓN. DATOS: fichero practica regresión 3.sf3 1. Objetivo: El objetivo de esta práctica es aplicar el modelo de regresión con más de una variable explicativa. Es decir regresión
Distribuciones de probabilidad más usuales
 Tema 5 Distribuciones de probabilidad más usuales En este tema se estudiarán algunas de las distribuciones discretas y continuas más comunes, que se pueden aplicar a una gran diversidad de problemas y
Tema 5 Distribuciones de probabilidad más usuales En este tema se estudiarán algunas de las distribuciones discretas y continuas más comunes, que se pueden aplicar a una gran diversidad de problemas y
Análisis de datos del Aguacate Hass (presentación caja 10 kilogramos)
 Análisis de datos del Aguacate Hass (presentación caja 10 kilogramos) Alberto Contreras Cristán, Miguel Ángel Chong Rodríguez. Departamento de Probabilidad y Estadística Instituto de Investigaciones en
Análisis de datos del Aguacate Hass (presentación caja 10 kilogramos) Alberto Contreras Cristán, Miguel Ángel Chong Rodríguez. Departamento de Probabilidad y Estadística Instituto de Investigaciones en
INTERVALOS DE CONFIANZA. La estadística en cómic (L. Gonick y W. Smith)
 INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
INTERVALOS DE CONFIANZA La estadística en cómic (L. Gonick y W. Smith) EJEMPLO: Será elegido el senador Astuto? 2 tamaño muestral Estimador de p variable aleatoria poblacional? proporción de personas que
VI. CAPACIDAD DE PROCESOS
 V. Capacidad de Procesos V. CAPACDAD DE PROCESOS NTRODUCCÓN Una vez hayamos comprobado que el proceso está bajo control, estaremos interesados en saber si es un proceso capaz, es decir, si cumple con las
V. Capacidad de Procesos V. CAPACDAD DE PROCESOS NTRODUCCÓN Una vez hayamos comprobado que el proceso está bajo control, estaremos interesados en saber si es un proceso capaz, es decir, si cumple con las
Análisis de Decisiones II. Tema 17 Generación de números al azar. Objetivo de aprendizaje del tema
 Tema 17 Generación de números al azar Objetivo de aprendizaje del tema Al finalizar el tema serás capaz de: Obtener números aleatorios a partir de un proceso de generación. Validar las características
Tema 17 Generación de números al azar Objetivo de aprendizaje del tema Al finalizar el tema serás capaz de: Obtener números aleatorios a partir de un proceso de generación. Validar las características
T1. Distribuciones de probabilidad discretas
 Estadística T1. Distribuciones de probabilidad discretas Departamento de Ciencias del Mar y Biología Aplicada Inferencia estadística: Parte de la estadística que estudia grandes colectivos a partir de
Estadística T1. Distribuciones de probabilidad discretas Departamento de Ciencias del Mar y Biología Aplicada Inferencia estadística: Parte de la estadística que estudia grandes colectivos a partir de
Variables aleatorias. Examen Junio La función de distribución de una variable continua X es de la forma:
 TEMA 6: Variables aleatorias Examen Junio 003.- La función de distribución de una variable continua X es de la forma: 3 F ( t) = P( X t) = a + bt ct t, Se sabe que la densidad verifica f(-)=f()=0. [ ]
TEMA 6: Variables aleatorias Examen Junio 003.- La función de distribución de una variable continua X es de la forma: 3 F ( t) = P( X t) = a + bt ct t, Se sabe que la densidad verifica f(-)=f()=0. [ ]
7. Distribución normal
 7. Distribución normal Sin duda, la distribución continua de probabilidad más importante, por la frecuencia con que se encuentra y por sus aplicaciones teóricas, es la distribución normal, gaussiana o
7. Distribución normal Sin duda, la distribución continua de probabilidad más importante, por la frecuencia con que se encuentra y por sus aplicaciones teóricas, es la distribución normal, gaussiana o
Métodos Estadísticos de la Ingeniería Tema 10: Inferencia Estadística, Intervalos de Confianza Grupo B
 Métodos Estadísticos de la Ingeniería Tema 10: Inferencia Estadística, Intervalos de Confianza Grupo B Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Abril 010 Contenidos...............................................................
Métodos Estadísticos de la Ingeniería Tema 10: Inferencia Estadística, Intervalos de Confianza Grupo B Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Abril 010 Contenidos...............................................................
LEAN SIX SIGMA YELLOW BELT
 LEAN SIX SIGMA YELLOW BELT CARACTERISTICAS GENERALES Duración: 32 Horas Son personas que participan activamente en el desarrollo de los proyectos Lean-Six Sigma de su área de trabajo, si son operadores
LEAN SIX SIGMA YELLOW BELT CARACTERISTICAS GENERALES Duración: 32 Horas Son personas que participan activamente en el desarrollo de los proyectos Lean-Six Sigma de su área de trabajo, si son operadores
ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO
 ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO RELACIÓN DE PROBLEMAS PROPUESTOS DE UNA VARIABLE Curso académico 2004-2005 DPTO. ECONOMÍA APLICADA I 1. Obtener las frecuencias acumuladas, las frecuencias relativas
ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO RELACIÓN DE PROBLEMAS PROPUESTOS DE UNA VARIABLE Curso académico 2004-2005 DPTO. ECONOMÍA APLICADA I 1. Obtener las frecuencias acumuladas, las frecuencias relativas
b. Universidad Nacional-Sede Medellín
 Comparación de Intervalos de Confianza para el Coeficiente de Correlación Juan Carlos Correa a, Liliana Vanessa Pacheco b Email: jccorrea@unal.edu.co a. Universidad Nacional-Sede Medellín b. Universidad
Comparación de Intervalos de Confianza para el Coeficiente de Correlación Juan Carlos Correa a, Liliana Vanessa Pacheco b Email: jccorrea@unal.edu.co a. Universidad Nacional-Sede Medellín b. Universidad
ESTRUCTURA DEL EXAMEN DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II PARA ALUMNOS DE BACHILLERATO
 ESTRUCTURA DEL EXAMEN DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II PARA ALUMNOS DE BACHILLERATO El examen presentará dos opciones diferentes entre las que el alumno deberá elegir una y responder
ESTRUCTURA DEL EXAMEN DE MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II PARA ALUMNOS DE BACHILLERATO El examen presentará dos opciones diferentes entre las que el alumno deberá elegir una y responder
UNIVERSIDAD DE MANAGUA Al más alto nivel
 UNIVERSIDAD DE MANAGUA Al más alto nivel SIMULACIÓN DE SISTEMAS Guía práctica #3 Prof.: MSc. Julio Rito Vargas A. Febrero 2013 Objetivos: Obtener muestras a partir de números aleatorios. Usando muestras
UNIVERSIDAD DE MANAGUA Al más alto nivel SIMULACIÓN DE SISTEMAS Guía práctica #3 Prof.: MSc. Julio Rito Vargas A. Febrero 2013 Objetivos: Obtener muestras a partir de números aleatorios. Usando muestras
Práctica de AJUSTE DE DISTRIBUCIONES II (ajuste de datos)
 Práctica de AJUSTE DE DISTRIBUCIONES II (ajuste de datos) 1 1. Objetivos de la práctica En esta práctica vamos a ajustar modelos de distribución a datos reales. Un vez que hayamos hecho esto, podremos
Práctica de AJUSTE DE DISTRIBUCIONES II (ajuste de datos) 1 1. Objetivos de la práctica En esta práctica vamos a ajustar modelos de distribución a datos reales. Un vez que hayamos hecho esto, podremos
JUNIO Opción A
 Junio 010 (Prueba Específica) JUNIO 010 Opción A 1.- Discute y resuelve según los distintos valores del parámetro a el siguiente sistema de ecuaciones: a x + a y + az 1 x + a y + z 0.- Una panadería se
Junio 010 (Prueba Específica) JUNIO 010 Opción A 1.- Discute y resuelve según los distintos valores del parámetro a el siguiente sistema de ecuaciones: a x + a y + az 1 x + a y + z 0.- Una panadería se
Métodos de Investigación en Psicología (10) Dra. Lucy Reidl Martínez Dra. Corina Cuevas Reynaud Dra. Renata López Hernández
 Métodos de Investigación en Psicología (10) Dra. Lucy Reidl Martínez Dra. Corina Cuevas Reynaud Dra. Renata López Hernández El método incluye diferentes elementos Justificación Planteamiento del problema
Métodos de Investigación en Psicología (10) Dra. Lucy Reidl Martínez Dra. Corina Cuevas Reynaud Dra. Renata López Hernández El método incluye diferentes elementos Justificación Planteamiento del problema
TÉCNICAS ESTADÍSTICAS APLICADAS EN NUTRICIÓN Y SALUD
 TÉCNICAS ESTADÍSTICAS APLICADAS EN NUTRICIÓN Y SALUD Contrastes de hipótesis paramétricos para una y varias muestras: contrastes sobre la media, varianza y una proporción. Contrastes sobre la diferencia
TÉCNICAS ESTADÍSTICAS APLICADAS EN NUTRICIÓN Y SALUD Contrastes de hipótesis paramétricos para una y varias muestras: contrastes sobre la media, varianza y una proporción. Contrastes sobre la diferencia
