I.E.S. Mediterráneo de Málaga Junio 2015 Juan Carlos Alonso Gianonatti OPCIÓN A

IES Mediterráneo de Málaga Solución Junio 2010 Juan Carlos Alonso Gianonatti OPCIÓN A

IES Medieáneo de Málg Soluión Junio Jun Clo lono Ginoni OPCIÓN Ejeiio. [ puno] L hipoenu de un iángulo eángulo ide. Si e he gi lededo de uno de u eo el iángulo engend un ono. Qué edid hn de ene lo eo del

IES Mediterráneo de Málaga Solución Septiembre 2010 (Específico) Juan Carlos Alonso Gianonatti OPCIÓN A. 2, se pide determinar:

IES Mdirráno d Málg Soluión Spimr (Espíio) Jun Crlos lonso Ginoni OPCIÓN E.- Dd l unión ( ), s pid drminr: ) El dominio, los punos d or on los js y ls sínos ( puno) ) Los inrvlos d rimino y drimino, y

IES Mediterráneo de Málaga Reserva1.- 2012 Juan Carlos Alonso Gianonatti. Propuesta A

ES Medieáeo Málg Reev.- Ju lo loo Gioi Popue.- ) Eui el eoe vlo edio Lgge d u iepeió geoéi ( puo) ) lul u puo l ievlo [ ] e que l e gee l gái l uió e plel l ued (o egeo) que ue lo puo () e ( puo) ) Teoe

( ) ( ) ( ) ( ) ( ) 2. ( ) t ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) OPCIÓN A. lim. =. Calcular. du I = + ln u = + + + e ln. e ln.

ES diáo d álg Solció Jio J Clo loo Gioi OPCÓN E.- S ) Clcl d ( po) ) S d g. Clcl g ( po) d g ) d d K d d d d B B B B B B d d d d d d d d d ) g Hopil L' plicdo ES diáo d álg Solció Jio J Clo loo Gioi E.-

2. MÉTODO DE COEFICIENTES INDETERMINADOS.

. MÉTODO DE COEFICIENTES INDETERMINADOS. E un étodo r hllr un olución rticulr d l cución linl colt [], u conit fundntlnt n intuir l for d un olución rticulr. No udn dr rgl n l co d cucion linl con coficint

R e a l i z a r p r e g u n t a s y r e s p u e s t a s e n u n e n t o r n o d e c o m p r a s R e c o n o c e r s a l u d o s s e n c i l l o s R e

ACCIÓN FORMATIVA: INGLÉS INTERMEDIO MODALIDAD: Di s t a n c i a DU R AC IÓ N : 2 5 0 h o r a s N º h o r a s t e ó r i c a s : 1 1 6 h o r a s N º h o r a s p r á c t i c a s : 1 3 4 h o r a s DE S T IN

P A R T E I I C r í t i c a r y j u s t i f i c a r s e CAPITULO 5 El imperio de la crítica S o b r e l a s o c i o l ó g i c a d e l r i e s g o y e l d e l i t o t e c n o l ó g i c o s Si el científico,

A C T I N O M IC O S I S Ó r g a n o : M u c o s a b u c a l T é c n i ca : H / E M i c r o s c o p í a: L o s c o r t e s h i s t o l ó g i c oms u e

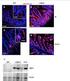T R A B A J O P R Á C T I C O N º 4 I N F L A M A C I Ó N E S P E C Í F I C A. P A T O L O G Í A R E G I O N A L P r e -r e q u i s i t o s : H i s t o l o g ída e l t e j i d oc o n e c t i v o( c é l

IES Mediterráneo de Málaga 2009 Juan Carlos Alonso Gianonatti. DISTRITO UNIVERSITARIO DE Madrid MATEMÁTICAS (Mayores de 25 años).

IES Mditáo d Málg Ju los loso Giotti DISTRITO UNIVERSITRIO DE Mdid MTEMÁTIS (Mos d ños. OPIÓN Ejcicio.- (. tos. S id l cució ticil do ls tics:. tos. Idic ls dios qu d t l ti.. tos. lcul l is -. c. tos.

IES Mediterráneo de Málaga Solución Septiembre 2006 Juan Carlos Alonso Gianonatti PRUEBA A PROBLEMAS

IES Mditáno d Málg Solución Spti 6 Jun Clos lonso Ginontti PRUEB PROBLEMS PR-- - ) Hálls l lo d p l qu l ct l plno sn pllos ) P clcúls l cución dl plno qu contin s ppndicul ) Los ctos dictos d ct plno

I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l. U l a d i s l a o G á m e z S o l a n o

1 A n t o l o g í a : P r o m o c i ó n y A n i m a c i ó n d e l a l e c t u r a M i n i s t e r i o d e E d u c a c i ó n P ú b l i c a I n s t i t u t o d e D e s a r r o l l o P r o f e s i o n a l.

Guía promocional de tarifas

Guía promocional de tarifas P a q u e te s E s p e c ia les P a q u e te D e s c r ip c ión T a r if a p o r p a q u e t e 1 Ocu la r E x p r e s s A p e r tu r a d e l c o n ten e d o r p o r I P M s

Reglamento de D i v er s i ones y E s p ec tá c u los P ú b li c os Ayuntamiento Constitucional de Zapotlanejo 2007-2009 e n t e M u n i c i Z a t n e j o, J a o, a h a t a n t e m u n i c i o h a g o

- S o b r e los m o d e l o s de ge s t i ó n y pri v a t i z a c i o n e s.

ACTO DE SALUD EN VILADECA N S, 4 DE MARZO DE 2010. B u e n a s tar d e s : E s t a m o s aq u í p a r a h a b l a r de sal u d y d e at e n c i ó n sa n i t a r i a pú b l i c a en el B a i x Ll o b r

( x) ( 1) OPCIÓN A Ejercicio 1 : Calificación máxima: 3 puntos. = + 1 ln. x x + x. 4 x = + = + = 0 + = 0. x x. x x. lim lim = + 1 lim. ln 1 1 1.

ES Mdiáno d Málaga Solción Jnio Jan Calos lonso Gianonai OPCÓN Ejcicio : Caliicación áia: pnos. ada la nción ( dond dnoa l logaio npiano s pid: a ( pnos ina l doinio d ss asínoas. b ( pnos Calcla la ca

P R O G R A M A D E G O B I E R N O 2012-2015. C o n g e s t i n, s e g u r i d a d y t r a b a j o

P R O G R A M A D E G O B I E R N O 2012-2015 C o n g e s t i n, s e g u r id a d y t r a b a jo 1 W I L M A N H A R R Y M A R ح N C A S T A ر O H O J A D E V I D A N a c ي e l 1 7 de S e p t ie m b r

IES Mediterráneo de Málaga Solución Junio 2011 Juan Carlos Alonso Gianonatti OPCIÓN A

IES Mediterráneo de Málaga Solución Junio Juan Carlo lono Gianonatti g con OX uncione la de corte de Punto g OPCIÓN E.- Calcular el área de la región inita itada por la gráica de la unción () el eje de

JUNIO 2013. CIRUGIA PLASTICA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

JUIO 2013. JUIO 2013. SSI 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 D. DGDO UÑ x x D. ICDO FLOS x D. COLI BDLS x D. IGOBO IH x D. COLI HYLOCK x D. JOS OLDO DIZ x

PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE NAVARRA JUNIO 2012 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 horas y 30 minutos

IES CSTELR DJOZ nguino PRUE DE CCESO (LOGSE) UNIVERSIDD DE NVRR JUNIO (GENERL) (RESUELTOS por nonio nguino) TEÁTICS II Timpo máimo: hors minuos Rlir un d ls dos opcions propuss ( o ) OPCIÓN º) Esudi l

Ruta Alimentadora Sur

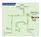Ad Ru Ador Ad Lo Horzo Ad B A-02 ALAEDA UR Ad Lo Cd P PUENTE VILLA E o P Hy J rí E o Ovo L Cv Grd Cv ERVICIO EPECIAL CIRCUITO DE PLAYA L Gvo Hy Tr A-04 VILLA EL ALVADOR Rvou Ro A-07 AÉRICA L Uó Grd A-08

GRAVITACIÓN I: LEY DE LA GRAVITACIÓN UNIVERSAL

8 0 GRVICIÓ I: LEY DE L GRVICIÓ UIVERSL j Sigue pcticndo Indic sobe l tyectoi de un plnet con óbit elíptic lededo del Sol, que ocup uno de los focos, los puntos de áxi y íni elocidd Rzon l espuest b t

OPCIÓN A. Días de lectura Total de páginas Quijote Eva E D ED Marta E 5 D + 14 (E 5).( D + 14) Susana E 11 D + 44 (E 11).( D + 44)

IES Mditrráno d Málg Solución Junio Jun Crlos lonso Ginontti OPCIÓN..- Ev Mrt Susn son trs jóvns migs qu s compromtn lr El Quijot st vrno. Cd un por sprdo n unción dl timpo dl qu dispon dcid lr un mismo

BE FREE. energía creativa. Te presentamos la herramienta de comunicación online más innovadora!

Gnt con nrgí crtiv. BE FREE. EL FREEBIE ONLINE: LA HERRAMIENTA DE INBOUND MARKETING MÁS CREATIVA. EL REGALO INFINITO. El frbi un hrrint d prooción y counicción onlin originl, intrctiv, virl, útil y grtuit.

BLOQUE III: INDICADORES Y RESULTADOS CERTIFICACIÓN N ISO Y OBJETIVOS DEL SEGUIMIENTO ERCA. Dr. Juan Manuel Buades Fuster

BLOQUE III: INDICADORES Y RESULTADOS CERTIFICACIÓN N ISO Y OBJETIVOS DEL SEGUIMIENTO ERCA Dr. Juan Manuel Buades Fuster Servicio de Nefrología del Hospital Son Llàtzer Palma de Mallorca Acudir a una consulta

LOS RECURSOS NATURALES EN EL DESARROLLO ECONOMICO

LOS RECURSOS NATURALES EN EL DESARROLLO ECONOMICO E d i t o r i a l U n i v e r s i t a r i a, S. A., 1 9 7 0 In s c r i p c i ó n N 3 8. 5 3 5 D e r e c h o s e x c lu s iv o s r e s e r v a d o s p a

Buda predicó el S ut ra de la P ro f un da Bo n dad de lo s padres y la D if icult ad en R et rib uirla T r a d u cci ó n a l es p a ñ o l d e l a v er s i ó n ch i n a d e K u m a r a j i v a Plegaria

Logaritmos y exponenciales:

Logrimos ponncils: L rsolución d cucions ponncils s s n l siguin propidd d ls poncis : Dos poncis con un mism s posiiv disin d l unidd son iguls, si sólo si son iguls sus ponns. Es dcir, p. j. Si = noncs

ESTADOS FINANCIEROS INTERMEDIOS

PASUR Forestal, Constructora y Comercial del Pacifico Sur S.A. ESTADOS FINANCIEROS INTERMEDIOS Correspondientes al periodo terminado al 30 de Septiembre de 2015 - Estados Financieros - Notas a los Estados

Introducción a la dinámica Segunda Ley de Newton

noduión l dinái Seund e de Newon Objeio Deeinión de l eleión de un óil io usndo diess énis eeienles on el disosiio indido esqueáiene en l Fiu, que inlue un ooineuo edi el deslzieno en unión del ieo. Esudio

EL CUERPO DE LAS FRACCIONES DE UN DOMINIO DE INTEGRIDAD

EL CUERPO DE L FRCCIONE DE UN DOMINIO DE INTEGRIDD CRLO CHINE EL CUERPO DE L FRCCIONE DE UN DOMINIO DE INTEGRIDD Ddo un nillo intero ; L L donde e un conunto L e l ley ditiv y e L l ley ultiplictiv no

3.5.1 Trasformada de Laplace de la función escalón unitario

.5. Trformd de Lplce de l función eclón unirio 0.5. Trformd de Lplce de l función eclón unirio Función Eclón Unirio Tmbién llmd función lo unidd de Heviide, y con frecuenci e uiliz en pliccione que rn

PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE MURCIA JUNIO 2012 (GENERAL) MATEMÁTICAS II SOLUCIONES Tiempo máximo: 1 horas y 30 minutos ----------

IES ASTELAR BADAJOZ A nguino PRUEBA DE AESO (LOGSE) UNIVERSIDAD DE URIA JUNIO (GENERAL) ATEÁTIAS II SOLUIONES Timpo máimo: hors minutos Osrvcions importnts: El lumno drá rspondr tods ls custions d un d

ENCUESTA BUENAS PRACTICAS EN TIC'S

239 16. ANEXO 1: ENCUESTA BUENAS PRÁCTICAS EN TIC S Facultad de Ciencias Económicas y Administrativas Escuela de Economía y Administración ENCUESTA BUENAS PRACTICAS EN TIC'S El objetivo de la siguiente

JUGAMOS CON LAS LETRAS Y PALABRAS

JUGAMOS CON LAS LETRAS Y PALABRAS Con este material se pretende reforzar el reconocimiento de las letras trabajadas en el aula a través del método letrilandia ; este es un paso posterior al conocimiento

EPÍLOGO Accidente y mentira Aquí no nos ocupamos de la maldad, a la que la religión y la literatura han intentado pasar cuentas, sino del mal; no del pecado y los grandes v illanos, que se conv irtieron

ACCIÓN FORMATIVA: INGLÉS AVANZADO MODALIDAD: DISTANCIA DU R AC IÓ N : 2 5 0 h o r a s Nº h o r a s t e ó r i ca s : 1 1 6 h o r a s Nº h o r a s p r á ct i ca s : 1 3 4 h o r a s DE S T IN AT AR IOS :

EXPRESIONES ALGEBRAICAS. POLINOMIOS

EXPRESIONES ALGEBRAICAS. POLINOMIOS A. EXPRESIONES ALGEBRAICAS. Cundo se quiere indicr un número no conocido, un cntidd o un expresión generl de l medid de un mgnitud (distnci, superficie, volumen, etc

MATERIALES PARA TRABAJAR LECTOESCRITURA

Centro de Recursos de Educación Especial de Navarra C/Tajonar, nº 14 31006 PAMPLONA Tfno.948 19 86 38 FAX 948 19 84 93 http://www.creena.educacion.navarra.es creenaud@educacion.navarra.es MATERIALES PARA

MATERIALES PARA TRABAJAR LECTOESCRITURA

Centro de Recursos de Educación Especial de Navarra C/Tajonar, nº 14 B 31006 PAMPLONA Tfno.948 19 86 38 FAX 948 19 84 93 http://www.creena.educacion.navarra.es creenaud@educacion.navarra.es MATERIALES

glosario de BBVA GLOSARIO -Bolsa-

BBVA GLOSARIO -B- A : Aó: C ó 100 í. V í ó. E. A A : E ó í. S ó í á ó ó. Aó : Aó, ú ó, ó. Aó : S ó. Aó : Aó. S : ) ) ó. Aó : Aó ó. Aó : Tí ó B, ó. Aó : Té,,,, ó. S ó, ó. Aó : (G ):E. C,. E é é ; á. Aó

$/Kg. Vivo por Clasificación Diciembre 2015

S ST EMA NFORMAT VODE PREC OSPORC NOS P RE C OSP ORC NOS D N o d M u yf D C E MBRE2015 CONT ROLAGROPECUAR O M N S T E R ODEAGRO NDUS T R A DEL ANAC ÓN: Co R dobu y S dag u u G d yp : g Ag R dong D N o

Local de. e u o. u s po r. n s. o t. j an. a ba

MINISTERIO DE EDUCACIÓN VICE MINISTERIO DE GESTIÓN INSTITUCIONAL OFICINA DE APOYO A LA ADMINISTRACIÓN DE LA EDUCACIÓN UNIDAD DE ORGANIZACIÓN Y MÉTODOS Local de r T a ba educación de calidad a n u s po

I N F O R M E S O B R E V E R I F I C A C I O N D E L V A L O R D E C L A R A D O N 1 1 8-3 D 1 3 1 0-2014- 000122- S U N A T

S U P E R I N T E N D E N C I A N A C I O N A L D E A D M I N I S T R A C I Ó N T R I B U T A R I A I N T E N D E N C I A D E L A A D U A N A M A R Í T I M A D E L C A L L A O A v e n i d a G u a r d i

MATERIALES PARA TRABAJAR LECTOESCRITURA

Centro de Recursos de Educación Especial de Navarra C/Tajonar, nº 14 31006 PAMPLONA Tfno.948 19 86 38 FAX 948 19 84 93 http://www.creena.educacion.navarra.es creenaud@educacion.navarra.es MATERIALES PARA

Tipo de. beneficiarios o. Dirección y teléfono de la oficina y atención al. usuarios del. dependencia que ofrece el servicio público

A. 7 d l Ly Ogái d Tspi y As l Ifmió úbli - LOTAI d) Ls s qu f y ls fms d d lls, his d ió y dmás idiis sis, p qu l iuddí pud sus dhs y umpli sus Rquisis p l bió dl Cóm d l dimi Dmiió dl (S dsib l dll dl

Definición de un árbol Rojinegro

Definición de un árol Rojinegro Árol inrio esrico (los nodos nulos se ienen en cuen en l definición de ls operciones odo nodo oj es nulo) Cd nodo iene esdo rojo o negro Nodos oj (nulos) son negros L rí

CLA CLE CLI CLO CLU NOMBRE:... CURSO:...

CLE CLO CLU NOMBRE:... CURSO:... RODEA EL SONIDO QUE TENGA EL DIBUJO: CLE CLO CLE CLO CLU CAL CIL COL CAL CLO CAL CLO COL CLO CIL CLE CLO CIL CAL 2 RODEA EL SONIDO QUE TENGA EL DIBUJO: CLE CLO CEL CIL

Sistemas de ecuaciones lineales

Sistems de ecuciones lineles º) L sum de ls tres cifrs de un número es 8, siendo l cifr de ls decens igul l medi de ls otrs dos. Si se cmbi l cifr de ls uniddes por l de ls centens, el número ument en

Lista provisional de becas de comedores, por colegios

1-3601 - 75 % 3 EP 2-3602 - 75 % 3 EI 3-3603 - 100 % 3 EP 4-3604 - 75 % 3 EP 5-3605 - 90 % 3 EP 6-3606 - 100 % 2 EI 7-3607 - 100 % 3 EI 8-3608 - 100 % 4 EP 9-3609 - 100 % 3 EI 10-3610 - 100 % 6 EP 11-3611

Resultados a 31 de marzo de 2016

Resultados a 31 de marzo de 2016 P á g i n a 0 / 9 Presentación de los resultados del primer trimestre de 201 6 via webcast y Conferencia telefónica Ac e r i n o x r e a l iz a r á u n a p r e s e n t

! "#$ % "#$ &'% "($ &% ")$ #*+, % -.+ #%,), ( #,( ).,/ ' 0 ' "-(/$ 1 "+2/$

! "#$ % "#$ &'% "($ &% ")$ #*+, % -.+ #%,), ( #,( ).,/ ' 0 ' "-(/$ 1 "+2/$ 3 &% "4% 45 % 6% 7$% 0 (, 8% 0 69:; & #,%< 8 0 #.2 ) % 3 6% 4% 45 7 0 #. ) (* % #, = 0 % 0 3 % 3 3 & 10 >, 1%?? 1 > 8 ' 3 '% 1%

CAPITULO 2 LA TABLA PERIODICA

1.0079 1 H HIDROGENO 6.941 3 Li LITIO 22.989 11 Na SODIO 30.098 19 K POTASIO CAPITULO 2 LA TABLA PERIODICA ORDENAMIENTO ACTUAL GRUPOS Y PERIODOS PROPIEDADES PERIODICAS TAMAÑO POTENCIAL DE IONIZACION AFINIDAD

Ín d i c e. De c u o ta. Es c r i t u r a. Fo r m u l a r i o... 662. Limitación d e g a r a n t í a. Es c r i t u r a. Fo r m u l a r i o...

Ín d i c e TOMO IV Contrato de Hipoteca Co n t r at o s Hi p o t e c a. Es c r i t u r a. Fo r m u l a r i o 1... 649 Hi p o t e c a. Es c r i t u r a. Fo r m u l a r i o 2... 653 Hi p o t e c a. Es c

Axonometria, calculos y artefactos

, o9 r t di do 2 o d c ln ln i t b li po tiro o r c o 3 d cid n s ri ln io ñ o b ofus C tir r, D s T CIA: 9 Sig TAN DIS C n D ri s Sig tiro b d DIS s T ln cro TA ro c po li NC d IA: fusio o 2 til,3 n tiro

Modelo 4 de sobrantes de 2005 - Opción A

Modelo de onte de - Opción A Ejecicio. 8 Se f : R R l función definid po f () () [ punto] Clcul lo punto de cote de l gáfic de f con lo eje coodendo. () [ punto] Hll l íntot de l gáfic de f. (c) [ punto]

Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:

Deptmento de Físic, UTFSM Físic Genel II / of: A. Bunel. FIS10: FÍSICA GENERAL II GUÍA #3: otencil Eléctico. Objetivos de pendizje Est guí es un hemient que usted debe us p log los siguientes objetivos:

Resolución de circuitos complejos de corriente continua: Leyes de Kirchhoff.

Resolución de circuitos complejos de corriente continu: Leyes de Kirchhoff. Jun P. Cmpillo Nicolás 4 de diciemre de 2013 1. Leyes de Kirchhoff. Algunos circuitos de corriente continu están formdos por

A S E S O R A M I E N T O J U R Í D I C O Y E C O N Ó M I C O E N

P e n a l E c o n ó m i c o y d e l a E m p r e s a A S E S O R A M I E N T O J U R Í D I C O Y E C O N Ó M I C O E N M A T E R I A D E C O R P O R A T E C O M P L I A N C E ( A p o r t a c i o n e s p

ITALY IS BEAUTIFUL. AND SMART.

- C, VON ITLY I BUTIFUL. ND MT. D. 30/01/14 Compra en www.zonzini.it MP CON ITM D CONTOL D L CLIDD 9001 CTIFICDO ZONZINI s.r.l. Carretillas salvaescaleras Via Don Luigi turzo, 8 - z.i. - 37052 Casaleone

diseño gráfico e impresión TARIFAS

diseño gráfico e impresión TARIFAS Copia e impresión B LAN CO Y N E GRO 1-9 10-19 20-99 -499 +500 A4 A3 21x29,7cm 42x29,7cm 0,10 0,20 0,08 0,16 0,06 0,12 0,05 0,10 0,04 0,08 Para cantidades superiores

TEMA 1. ÁLGEBRA LINEAL

Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y

Electromagnetismo. es nula. Encuentre el campo eléctrico en todo el espacio.

Electromgnetismo olución Prueb 1 de Cátedr Profesor: José ogn C. 17 de Abril del 24 Ayudntes: Pmel Men. Felipe Asenjo Z. 1. Un distribución de crg esféricmente simétric de rdio tiene un densidd interior

XIII. La a nube de puntos-variables

XIII. La a nube de punto-vaiable Una vaiable e epeentada con un vecto en R n. El conunto de etemidade de lo vectoe que epeentan la vaiable contituyen la nube de punto N. m im m n i m Pogama PRESTA - 999

ASIGNATURA: INGENIERIA DE PROCESOS III (ITCL 234) PROFESOR: Elton F. Morales Blancas

UNIVESIDD USTL DE CILE INSTITUTO DE CIENCI Y TECNOLOGI DE LOS LIMENTOS (ICYTL) / SIGNTU: INGENIEI DE POCESOS III (ITCL 34) POESO: Elton. Moals Blancas UNIDD : TNSEENCI DE CLO PO CONDUCCION (ESTDO ESTCIONIO)

EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS

EJERCICIOS DE PUNTOS, RECTAS Y PLANOS PUNTOS Ejecicio nº.- Repeent lo punto iguiente: A(, 5, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto iguiente: A(,, ), B(,, ) C(,, ) Ejecicio nº.- Repeent lo punto

Tema 8. Funciones vectoriales de variable real.

Tem 8. Funciones vecoiles de vile el. 8.1 Cuvs ecuciones pméics. Cálculo en pméics. 8. Funciones vecoiles: límie, coninuidd, deivción e inegción. 8.3 Cuvs en coodends poles. Aneo: cónics. E. U. Poliécnic

Los 9 Poderosos Factores Secretos Para Subir de Peso

Los 9 Poderosos Factores Secretos Para Subir de Peso Aquí veras la verdad de cómo engordar Res erv ado s t odo s l os d erechos. Ning un a p art e de est a p ub li cación pu ed e s er rep ro du ci da,

2. REPRESENTACIÓN ANALÍTICA Y GRÁFICA DE UN VECTOR

1. INTRODUCCIÓN CÁLCULO VECTORIAL Mgnitud: Es todo quello que se puede medir eperimentlmente. Ls mgnitudes físics se clsificn en esclres ectoriles. Mgnitud esclr: Es quell que iene perfectmente definid

E S T A D O A C T U A L PROPUESTA PLAZA FACULTAD DE ARQUITECTURA A VESTÍBULO F A

D C L LZ FCLD D QIC VÍBL F D C L FCLD D FILFI Y L INVNCIN N M N CN DICCIDD FCLD D FILFI Y L D INVNCIN N M N CN DICCIDD D C L FCLD D FILFI Y L NCI D ÑLMIN D CC NL FCLD D FILFI Y L D ÑLMIN D CC NL D C L

la integral de línea de B alrededor de un trayecto cerrado

LEY DE AMPERE L ley de Guss de los cmpos elécticos implic el flujo de E tvés de un supeficie ced; estlece que este flujo es igul l cociente de l cg totl enced dento de l supeficie ente l constnte ε. En

REACCIONES QUÍMICAS. Ocurren en la naturaleza. Se expresan por ECUACIONES QUÍMICAS

REACCIONES QUÍMICAS Ocurren en la naturaleza Se expresan por ECUACIONES QUÍMICAS NaCl + AgNO 3 AgCl + NaNO 3 REACTIVOS PRODUCTOS ECUACIÓN QUÍMICA Estequiométrica (ecuación balanceada) Representar una reacción

ESTADÍSTICAS VITALES. Indicadores Generales

ESTADÍSTICAS VITALES Indicadores Generales NACIMIENTOS NATALIDAD REGISTRADA SEGUN CIFRAS ABSOLUTAS POR DEPARTAMENTOS AÑOS 1993 A 2012. PROVINCIA TIERRA DEL FUEGO 3000 2500 2000 1500 1000 500 0 1993 1994

EJERCICIOS DE CINEMÁTICA PARA REPASAR

EJERCICIOS DE CINEMÁTICA PARA REPASAR 1. L poición de un óvil, que igue un tryectori rectilíne, qued deterind por l ecución x = 5 + t, en l que tod l gnitude etán expred en el S.I. ) Arrnc el óvil dede

X obtener las relaciones que deben

odelo. Ejercicio. Clificción áxi puntos ) ( punto) Dd l triz y l triz t z y x X otener ls relciones que deen cuplir x, y, z, t pr que l triz X verifique X X. ) (, puntos) Dr un ejeplo de l triz X distint

Ejercicios de Matemáticas

Ejercicios resuelos de lger Ejercicios de Meáics. Se N M. ) Clcul e pr que MN = NM. ) Clcul M M ) MN ; NM = = = ) M = I M = M M = I M = M... Se ve que si el eponene es pr es igul l ri unidd si es ipr es

$%# ! "#$% &' *& & -& **. *+ #$/0$% % &' &)* (*& &*& ()& +&', . & # *+ &(* & //$ % & 1 &*+ % * & & &* & *2&, +& *3& (* & *& &

!"#! "#$% &' &( )*'*+&,&(*+&& *& & -& **. *+ #$/0$% % &' &)* (*& &*& ()& +&',. *+#$$% '&)*(*&&*& #. & # *+ &(* & * )&(&*&0, %" //$ % & 1 &*+ % * & & &* # % &'&( )*'&)* & *2&, +& *3& (* & *& & -&4 )&(*&&*&

Reconsiderando los fondos sociales: Los canjes de deuda para educación

R f : L j u p uó O Ugh L f Lé é u yu pz y u vó pg yu pí, f h v u pó p f ó v qu p ñ é p gó p pz y pó pí ju pñ zó p pí h ú á g L ó g y f qu é uó, p y u á uy u uv pz qu xp u M y qu pp u pz p L f í u p, g,

TALKINGISTEACHING.ORG

l b T Tlk Wht c o my lo ock? Wht c olo you? Tlk, d, d ig with you child ight fom th tt. It build thi bi d pp thm fo ucc i chool d byod. Fo id, viit TALKINGISTEACHING.ORG Sh you tlk, d, ig momt t th ludomt!

N.º 33 NUEVA ÉPOCA ISSN 1962-6510. Sistemas Operativos Móviles. Introducción TECNOLOGÍA, INNOVACIÓN Y CALIDAD -21- Docente

R alidad y R i ISSN 1962-6510 N.º 33 NUEVA ÉPOCA S a : a l i la i a i Sistemas Operativos Móviles i Fi a Docente Introducción El i l i i al d i i a a id la i a i d i a ad a di a i i i la a d di i i i li

Los acuerdos de reconocimiento de títulos

Los acuerdos de reconocimiento de títulos El Ejercicio profesional en la Globalización Estándares internacionales y Normativa nacional Buenos Aires, Argentina 17 de Septiembre de 2004 De qué títulos hablamos?

TEMA 7. SUCESIONES NUMÉRICAS.

º EO Tem 7 TEMA 7. UCEIONE NUMÉRICA.. UCEIONE NUMÉRICA. Imgiemos el ecoido que efectú u bló que se h lzdo l suelo y midmos ls distcis ete bote y bote: Ls distcis fom u sucesió de úmeos: 0, 5, 0, 5,. U

Proyecto de innovación de la gestión documental aplicada a expedientes de contratación de servicios y obras de infraestructuras de transporte

Proyecto de innovación de la gestión documental aplicada a expedientes de contratación de servicios y obras de infraestructuras de transporte Universidad de Sevilla Tecnocom Aportaciones desde la Archivística

LA TRANSFORMADA DE LAPLACE

LA RANSFORMADA DE LAPLACE (pun crio por Dr. Mnul Prgd). INRODUCCIÓN Enr l rnformcion má uul qu oprn con funcion f(x) cumplindo condicion dcud n I[,b, pr obnr or funcion n I, án por jmplo : L oprción D

I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN. TERCERA EVALUACIÓN. GEOMETRÍA MATERIA: MATEMÁTICAS II OPCIÓN A

Examen de Evaluación. Geometía. Matemática II. Cuo 009-00 I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN. TERCERA EVALUACIÓN. GEOMETRÍA Cuo 009-00 -V-00 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES

Unidad 4 : DERIVADAS PARCIALES. dy dt. d dt. z x. = dt

Unidad DEIVADAS PACIALES Tma. gla d la Cadna (Edia la Scción. n l Sa ª Edición Hac la Taa No. ) gla d la Cadna paa na nción d na aiabl q a dpnd d oa aiabl. d d d d Si g nonc d d d d d d Ejmplo d n co d

APLICACION DE LA TEORIA DE GRAFOS A LA CONTABILIDAD

y APLICACION DE LA TEORIA DE GRAFOS A LA CONTABILIDAD GUILLERMO CUELLAR M. Profmor titu la r Facultad de Ciencias Contables y Adm inistrativas CONCEPTOS BASICOS DE LA TEO RIA DE GRAFOS La teoría de patos

( ) [ ( )] ( ) MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES. a + b se puede obtener multiplicando término a término:

Fult Cotuí Aiitió. UNAM Pouto otl Auto: D. Joé Mul B Eio MATEMÁTICAS BÁSICAS PRODUCTOS NOTABLES CONCEPTO DE PRODUCTO NOTABLE Tto l ultiliió li oo l itéti iu u loito uo o ou l ulto. Si o, it outo lio u

Nombre del documento: Procedimiento para Auditorías de Servicio. Referencia a la Norma ISO 9001:2008 5.2, 8.2.1

Página 1 de 5 1. Propósito Evaluar en forma sistemática, los servicios que ofrece el Instituto Tecnológico en relación con las expectativas del cliente. 2. Alcance Aplica a todas las áreas de servicio

Oficina Económica y Comercial de la Embajada de España en Rusia. Rusia: Pavimentos y Revestimientos Cerámicos

Oficina Económica y Comercial de la Embajada de España en Rusia Estudios de Mercado Rusia: Pavimentos y Revestimientos Cerámicos Estudios de Mercado Rusia: Pavimentos y Revestimientos Cerámicos Este estudio

Tribunal Sentencia Liquidación Total Principal Intereses Fecha de pago

A.P. SANTA CRUZ DE TENERIFE BLOQUE II Compañía Española de Petróleos, S.A. (CEPSA) A.N. P.O. 802/1999 1998/35754 1.170,76 710,91 459,85 19/08/2010 A.N. P.O. 802/1999 1998/35755 216,73 131,60 85,13 19/08/2010

L a p rog r amació n l in eal d a re sp ue s ta a s itua c ione s e n las qu e s e

PROGRAMACION LINEAL L a p rog r amació n l in eal d a re sp ue s ta a s itua c ione s e n las qu e s e e xig e maxi miz ar o min i miz ar f u n cio n es q u e s e e nc u en t ran s u je ta s a d et e rm

La V i r t u al i z ac i ón f r e nt e a l o s d e s af ío s d e l N e g o c i o d e 2 0 0 9 Alfonso Ramír e z D i r e c t or G e ne r al V M w ar e E sp aña y P or t u g al Ab r i l 2 0 0 9 G El Problema

PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE EXTREMADURA JUNIO 2009. (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 hora y 30 minutos

I.E.S. CSTELR BDJOZ PRUEB DE CCESO (LOGSE) UNIVERSIDD DE EXTREMDUR JUNIO 9 (RESUELTOS po ntonio Menguino) MTEMÁTICS II Tiempo máimo: ho minutos El lumno elegiá un de ls dos opciones popuests. Cd un de

ÍNDICE GENeRAL. CAPÍTULO I Teoría general de los contratos atípicos

ÍNDICE GENeRAL Pre s e n ta c i ó n... xix CAPÍTULO I Teoría general de los contratos atípicos 1. In t r o d u c c i ó n... 1 2. El ti p o... 3 3. La tipicidad... 5 4. El ti p o y la tipicidad co n t r

MATRICES Y DETERMINANTES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS. APLICACIONES

Mtrices. Estudio de l comptibilidd de sistems Abel Mrtín & Mrt Mrtín Sierr MATRICES Y DETERMINANTES. ESTUDIO DE LA COMPATIBILIDAD DE SISTEMAS. APLICACIONES. Actividd propuest Escribe un mtri A de dimensión

TEMAS 6 Y 7 GEOMETRÍA EN EL ESPACIO

Tems Geometí en el espcio Mtemátics II º Bchilleto TEMAS Y GEOMETRÍA EN EL ESACIO ECUACIONES DE RECTAS Y LANOS EJERCICIO es plelo plno que contiene l ect Escibe l ecución del. s hll l ecución de un plno,

1) Cal c ul a r el t érm i n o d es c o n oc i do d e l a s si g ui en t es p r o p or ci o n es : x. d) x 12

PRO PO RCIO NALIDADES 1) Cal c ul a r el t érm i n o d es c o n oc i do d e l a s si g ui en t es p r o p or ci o n es : a) 4 x 10 60 b) 9 12 12 x c) 8 2 32 3 x x d) x 12 Sol : a) x= 2 4, b) x= 1 6, c)

NUEVAS PRÁCTICAS MOTIVADORAS PARA LOS ALUMNOS DE ESO. BINGO

NUEVAS PRÁCTICAS MOTIVADORAS PARA LOS ALUMNOS DE ESO. BINGO Teresa Ruano Culla COLEGIO SAN ANTONIO DE PADUA II Catarroja Introducción: La motivación de este proyecto es realizar nuevas actividades en los