MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN
|
|
|
- Victoria Ramírez Alvarado
- hace 7 años
- Vistas:
Transcripción
1 MAQUETERÍA 02: POLIEDROS, CUERPOS REDONDOS Y SU CONSTRUCCIÓN Concepto de Poliedro Definiremos como poliedro a un cuerpo geométrico tridimensional que encierra un espacio limitado. La palabra proviene de la palabra griega polyedron que literalmente significa muchas caras. Los poliedros son en esencia formas 3D que están compuestos de varios polígonos los cuales son las llamadas caras de este. Por definición, las caras de un poliedro son siempre planas. Por esto mismo, los conos o cilindros NO son poliedros sino que son llamados cuerpos redondos. Los componentes de un poliedro son: Donde tenemos lo siguiente: Caras: son los planos de los polígonos que conforman el poliedro. Aristas: son los segmentos que cortan las caras del poliedro. Vértices: son los puntos donde se intersecan o cortan las aristas del poliedro.
2 Al igual que en el caso de los polígonos, los poliedros pueden ser cóncavos o convexos. Serán convexos si todas las caras pueden apoyarse en el plano horizontal (debido a sus ángulos convexos) y si alguna no lo hace, el poliedro será cóncavo. Poliedro Cóncavo Poliedro Convexo Tipos de Poliedros Los tipos de poliedros son los siguientes: Prismas: un prisma es un tipo de poliedro en el cual se cumplen las siguientes relaciones:
3 a) tener dos caras basales paralelas con polígonos iguales. b) tener tantas caras laterales de tipo paralelogramo, como aristas tenga este polígono. A los prismas se les clasifica según el número de lados que tengan las caras basales, por lo tanto podremos clasificarlos según el siguiente criterio: Los prismas pueden ser regulares, si sus polígonos basales están conformados por polígonos de tipo regular (imagen de arriba), o irregulares si sus bases son polígonos irregulares. Otra característica importante de los prismas es que además poseen una altura. Si esta coincide con las aristas laterales del prisma entonces este será un prisma recto, en caso contrario será un prisma oblicuo, de acuerdo a la imagen de abajo:
4 Desarrollo 2D de Prismas Todos los prismas tienen la particularidad de ser desarrollables, es decir, que todas sus caras pueden representarse en un plano bidimensional y mediante plegados puede ser construido de forma tridimensional. El desarrollo de un prisma recto es bastante simple ya que está compuesto por sus caras basales y un rectángulo que tiene por medida la cantidad de divisiones de las caras laterales. La imagen de abajo ilustra el desarrollo de tres tipos de prismas regulares: En el caso del desarrollo de un prisma oblicuo, este dependerá del grado de inclinación y de las caras rectas visibles, aunque en el caso
5 que la inclinación sea hacia un solo lado debemos repetir la cara oblicua mediante un efecto espejo. Prismas Paralelepípedos Un paralelepípedo es un prisma en el cual todas sus caras son paralelógramos (caras opuestas iguales y paralelas). Como todos los prismas, pueden ser rectos u oblicuos y siempre son prismas cuadrangulares. Los paralelepípedos son los siguientes: En el caso del Ortoedro, sus caras son rectángulos. En el caso del Cubo, sus caras son cuadrados. En el caso del Romboedro, sus caras son rombos. En el caso del Romboiedro, sus caras son romboides. Pirámides
6 Una pirámide es un tipo de poliedro en el cual se cumplen las siguientes relaciones: a) tener una base la cual es un polígono. b) tener tantas caras triangulares como lados tenga la base. El punto donde convergen las caras triangulares se denomina cúspide. Las pirámides pueden ser cóncavas o convexas dependiendo del tipo de polígono de su base. Al igual que en el caso de los prismas, las pirámides cual se define desde el vértice a la base. Sin embargo derá del centro de gravedad del polígono base. Si la cide con este la pirámide será oblicua. Si el centro altura la pirámide será recta. poseen altura la la altura depenaltura no coincoincide con la Pirámides regulares Una pirámide es regular si todas las caras laterales son iguales, formadas por triángulos isósceles.
7 La altura de cada una de estas caras es denominada apotema. Podremos calcularla mediante el teorema de Pitágoras, usando la medida del punto medio de la base del triángulo hasta el centro y la altura de la pirámide como catetos, de acuerdo a la siguiente fórmula: C2 = a2 + b2 Desarrollo 2D de Pirámides Al igual que en el caso de los prismas, todas las pirámides tienen la particularidad de ser desarrollables, es decir, que todas sus caras pueden representarse en un plano bidimensional y mediante plegados puede ser construido de forma tridimensional. El desarrollo de una pirámide recta está compuesto por su base y las proyecciones de los triángulos isósceles de las caras laterales, unidas por sus aristas mayores.
8 Desarrollo de una pirámide de bases Hexagonal y Rectangular Poliedros regulares Un Poliedro es regular si todas sus caras son iguales. También son conocidos como sólidos platónicos ya que en la antigua Grecia fueron estudiados por Platón. Sólo existen 5 poliedros regulares los cuales son: Tetraedro, pirámide formada por triángulos equiláteros. Cubo, paralelepípedo formado por cuadrados. Octaedro, formado por ocho triángulos equiláteros.
9 Dodecaedro, formado por doce pentágonos regulares. Icosaedro, formado por veinte triángulos equiláteros. Desarrollo 2D de poliedros regulares al igual que en los casos snteriores, todas los poliedros regulares tienen la particularidad de ser desarrollables, es decir, que todas sus caras pueden representarse en un plano bidimensional y mediante plegados puede ser construido de forma tridimensional. A continuación se muestra el desarrollo de los 5 poliedros ya mencionados. Desarrollo de un Tetraedro: Desarrollo de un Cubo:
10 Desarrollo de un Octaedro:
11 Desarrollo de un Dodecaedro: Desarrollo de un Icosaedro:
12 Cuerpos redondos Definiremos como cuerpo redondo a un cuerpo geométrico tridimensional que posee al menos una cara cuya superficie es curva. Estos cuerpos suelen ser generados mediante las rotaciones de sus caras en torno a un eje determinado. Los cuerpos redondos típicos son los siguientes: El cilindro
13 Un cilindro es un cuerpo redondo que se genera a partir de la rotación de un rectángulo en torno a uno de sus lados el cual es a su vez el eje de revolución. Los tres lados restantes del rectángulo son la generatriz de este. En el cilindro distinguimos la superficie curva como superficie lateral y posee dos bases paralelas formadas por un círculo en la parte superior e inferior. Ambas bases son exactamente iguales. En un cilindro recto podremos distinguir la altura la cual será la distancia entre las dos bases, y que coincide con la Generatriz. Al igual que en el caso de los prismas y las pirámides, los cilindros pueden ser rectos u oblicuos. Desarrollo 2D del cilindro recto Los cilindros tienen la particularidad de ser desarrollables, es decir, que todas sus caras pueden representarse en un plano bidimensional y mediante plegados puede ser construido en el espacio 3D. En el desarrollo 2D del cilindro, la bases serán círculos iguales y la superficie curva será lograda a partir de un rectángulo el cual tendrá por altura la Generatriz y cuyo largo será el perímetro de uno de los círculos de las bases el cual se calcula con la conocida fórmula de cálculo de perímetro: L = 2 x? x R
14 El cono Un cono es un cuerpo redondo que se genera a partir de la rotación de una recta inclinada la cual se intersecta con el eje de revolución y siguiendo a una base redonda como directriz. En el cono distinguimos la superficie curva como superficie lateral y la base, formada por un círculo. El punto donde convergen todas las generatrices se conoce como vértice.
15 En un cono recto podremos distinguir la altura la cual será la distancia entre el vértice y la base, y que coincidirá con el eje de revolución. Al igual que en el caso de los prismas y las pirámides, los cilindros pueden ser rectos u oblicuos. Desarrollo 2D del cono recto Los conos tienen la particularidad de ser desarrollables, es decir, que todas sus caras pueden representarse en un plano bidimensional y mediante plegados puede ser construido de forma tridimensional. En el desarrollo 2D del cono, la base será un círculo y la superficie curva será lograda a partir de un sector circular con el radio de la generatriz, y la sección será determinada por la longitud del arco o perímetro de la directriz mediante la conocida fórmula de cálculo de perímetro: L = 2 x? x R Para calcular el ángulo del sector circular del desarrollo (y así poder dibujarlo) debemos usar la siguiente fórmula: A = Radio de la base / Generatriz x 360
16 La esfera La esfera es un cuerpo redondo que se genera a partir de la rotación de un semicírculo en torno a un eje de revolución el cual es a la vez
17 el diámetro de este. En este caso, el diámetro es el eje y el semicírculo la Generatriz. Este cuerpo redondo es el único que no puede desarrollarse en el plano 2D ya que todo su volumen es curvo. Ejercicios propuestos Construir en cartón forrado los siguientes poliedros, tomando medidas arbitrarias: El cubo. El tetraedro. El Octaedro. El dodecaedro. El Icosaedro. El Cilindro. El Cono. Un prisma de Base Hexagonal. Una pirámide de base Pentagonal. Solución: primero debemos dibujar los polígonos necesarios según las técnicas de dibujo vistas en el apunte sobre polígonos. Luego estos polígonos deberán ser recortados para ser ocupados como molde para dibujar el desarrollo de los poliedros en el cartón.
18 Finalmente recortamos los moldes y plegamos las aristas para pegarlas y construir las formas. NOTA: debemos considerar pestañas extras para poder pegar las aristas. Para el caso de los cuerpos redondos bastará dibujar directamente los desarrollos en el cartón. En el caso del cilindro se deberán dibujar líneas verticales paralelas a la altura de modo que se puedan doblar para formar el cuerpo de este, el cono será ejecutado de manera similar pero las líneas serán radiales a igual distancia y partirán desde la cúspide hasta la base.
19 Debemos recordar que dominar la construcción de poliedros y cuerpos redondos es fundamental para el desarrollo de estructuras y formas 3D en maquetería.
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
Cuerpos geométricos. Objetivos. Antes de empezar. 1. Poliedros...pág. 138 Definición Elementos de un poliedro
 8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Cuerpos geométricos. Volúmenes
 4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
CONOCER Y DIFERENCIAR LOS POLIEDROS REGULARES
 OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
Qué son los cuerpos geométricos?
 Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos
 Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
INSTITUCION EDUCATIVA DIVERSIFICADO DE CHIA TALLER DE VOLUMENES Y POLIEDROS
 Sep. 18 de 2015 Señores Estudiantes grados Novenos El siguiente trabajo ya lo estamos realizando en clase, pero los datos que a continuación aparecen son refuerzo para terminar las figuras geométricas
Sep. 18 de 2015 Señores Estudiantes grados Novenos El siguiente trabajo ya lo estamos realizando en clase, pero los datos que a continuación aparecen son refuerzo para terminar las figuras geométricas
MÓDULO Nº 4. Nivelación. Matemática 2005. Módulo Nº4. Contenidos. Circunferencia y Círculo Volúmenes
 MÓDULO Nº 4 Nivelación Matemática 2005 Módulo Nº4 Contenidos Circunferencia y Círculo Volúmenes Nivelación Circunferencia y Círculo Circunferencia. Es una línea curva cerrada, cuyos puntos tienen la propiedad
MÓDULO Nº 4 Nivelación Matemática 2005 Módulo Nº4 Contenidos Circunferencia y Círculo Volúmenes Nivelación Circunferencia y Círculo Circunferencia. Es una línea curva cerrada, cuyos puntos tienen la propiedad
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
Diferencias entre Figuras y
 10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Programa Entrenamiento MT-22
 Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
5º de E. Primaria LOS CUERPOS GEOMÉTRICOS -TEMA 15
 LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
 ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
UNIDAD 2: ELEMENTOS GEOMÉTRICOS
 UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES
 TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
Recuerda lo fundamental
 12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) TALLER DE REPASO PARA EL BIMESTRAL 3P
 COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
ELEMENTOS Y CLASES DE ÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Geometría en el espacio. Poliedros
 Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Poliedro cóncavo: es aquel que no cumple la propiedad anterior. Una recta puede cortarlo por más de dos puntos.
 El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
Problemas geométricos
 Problemas geométricos Contenidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores y segmentos 2. Cuerpos geométricos Prismas Pirámides Troncos de
Problemas geométricos Contenidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores y segmentos 2. Cuerpos geométricos Prismas Pirámides Troncos de
Poliedros regulares Cuerpos de revolución
 Poliedros regulares Cuerpos de revolución Poliedro. Un poliedro es un cuerpo limitado por caras poligonales. Ángulo diedro. Ángulo poliedro Se llama ángulo diedro de un poliedro el que está formado por
Poliedros regulares Cuerpos de revolución Poliedro. Un poliedro es un cuerpo limitado por caras poligonales. Ángulo diedro. Ángulo poliedro Se llama ángulo diedro de un poliedro el que está formado por
Created with novapdf Printer (www.novapdf.com)
 GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
GEOMETRÍA LONGITUDES Longitud de la circunferencia Es una línea curva cerrada que equidistan todos sus puntos del centro. Radio Centro: punto situado a igual distancia de todos los puntos de la circunferencia.
CUERPOS GEOMÉTRICOS. Clases de cuerpos geométricos. Los poliedros. Los poliedros regulares.
 CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
III: Geometría para maestros. Capitulo 1: Figuras geométricas
 III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
11 POLIEDROS EJERCICIOS. 6 Cuántas caras, vértices y aristas hay en los siguientes poliedros? a) b) c)
 11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
Unidad 8 Áreas y Volúmenes
 Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
open green road Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno .co
 Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno.co 1. Geometría en el espacio Al observar nuestro alrededor podemos notar una infinidad de objetos que ocupan un lugar en el espacio físico en el
Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno.co 1. Geometría en el espacio Al observar nuestro alrededor podemos notar una infinidad de objetos que ocupan un lugar en el espacio físico en el
CENTRO EDUCATIVO PAULO FREIRE TALLER
 CENTRO EDUCATIVO PAULO FREIRE TALLER 1: Una plaza circular está limitada por una circunferencia de longitud 188,4m. Determinar el diámetro y el área de la plaza. 2: Si el área de un círculo es 144 cm 2,
CENTRO EDUCATIVO PAULO FREIRE TALLER 1: Una plaza circular está limitada por una circunferencia de longitud 188,4m. Determinar el diámetro y el área de la plaza. 2: Si el área de un círculo es 144 cm 2,
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
Piden: Dato: Piden: Dato: Piden: Dato:
 SEMANA 1 PRISMAS Y PIRÁMIDE 1. Calcule el número de caras de un prisma donde el número de vértices más el número de aristas es 50. A) 10 B) 0 C) 0 D) 1 E) 18 Sea n el número de lados de la base del prisma:
SEMANA 1 PRISMAS Y PIRÁMIDE 1. Calcule el número de caras de un prisma donde el número de vértices más el número de aristas es 50. A) 10 B) 0 C) 0 D) 1 E) 18 Sea n el número de lados de la base del prisma:
VOLUMENES. Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad
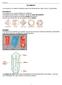 VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad POLIEDROS Un poliedro es un cuerpo limitado por polígonos Los polígonos que limiten el poliedro, se llaman
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS
 RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA.
 GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA. Profesor: Alumno:. Curso: Sección: 1. LAS FIGURAS PLANAS 2. ÁREA DE LAS FIGURAS PLANAS 3. CUERPOS GEOMÉTRICOS . FIGURAS PLANAS 1. Los polígonos y suss elementos
GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA. Profesor: Alumno:. Curso: Sección: 1. LAS FIGURAS PLANAS 2. ÁREA DE LAS FIGURAS PLANAS 3. CUERPOS GEOMÉTRICOS . FIGURAS PLANAS 1. Los polígonos y suss elementos
Los poliedros y sus elementos
 Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia
 geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
Cuerpos geométricos OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Elementos de un poliedro y su desarrollo. Los poliedros regulares y sus características.
 826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
Tema 10: Cuerpos geométricos y transformaciones geométricas
 Tema 10: Cuerpos geométricos y transformaciones geométricas Regla. Escuadra. Cartabón. Compás. Transportador de ángulos. Calculadora Portaminas. Goma 10.1 Polígonos MATERIAL DE CLASE OBLIGATORIO PROBLEMAS
Tema 10: Cuerpos geométricos y transformaciones geométricas Regla. Escuadra. Cartabón. Compás. Transportador de ángulos. Calculadora Portaminas. Goma 10.1 Polígonos MATERIAL DE CLASE OBLIGATORIO PROBLEMAS
LOS CUERPOS GEOMÉTRICOS POLIEDROS Y CUERPOS REDONDOS
 LOS CUERPOS GEOMÉTRICOS POLIEDROS Y CUERPOS REDONDOS Se llaman poliedros todos los cuerpos geométricos que tienen todas sus caras planas. Los cuerpos redondos son aquellos que tienen alguna de sus superficies
LOS CUERPOS GEOMÉTRICOS POLIEDROS Y CUERPOS REDONDOS Se llaman poliedros todos los cuerpos geométricos que tienen todas sus caras planas. Los cuerpos redondos son aquellos que tienen alguna de sus superficies
Problemas geométricos
 8 Problemas geométricos Objetivos En esta quincena aprenderás a: Aplicar las razones trigonométricas para estudiar las relaciones que existen entre los ángulos y los lados de las figuras planas. Calcular
8 Problemas geométricos Objetivos En esta quincena aprenderás a: Aplicar las razones trigonométricas para estudiar las relaciones que existen entre los ángulos y los lados de las figuras planas. Calcular
Uso no comercial 12.4 CUERPOS REDONDOS
 1.4 CUERPOS REDONDOS Designamos en general como cuerpos redondos el conjunto de puntos del espacio obtenido cuando una figura gira alrededor de una recta, de tal forma que cada punto de la figura conserva,
1.4 CUERPOS REDONDOS Designamos en general como cuerpos redondos el conjunto de puntos del espacio obtenido cuando una figura gira alrededor de una recta, de tal forma que cada punto de la figura conserva,
1. ESQUEMA - RESUMEN Página. 2. EJERCICIOS DE INICIACIÓN Página. 3. EJERCICIOS DE DESARROLLO Página. 4. EJERCICIOS DE AMPLIACIÓN Página
 1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
Los Cuerpos Geométricos
 06 Lección Apertura Matemáticas Los Cuerpos Geométricos APRENDO JUGANDO Competencia Describe qué son e identifica las características de los cuerpos geométricos. Diseño instruccional El maestro comenta
06 Lección Apertura Matemáticas Los Cuerpos Geométricos APRENDO JUGANDO Competencia Describe qué son e identifica las características de los cuerpos geométricos. Diseño instruccional El maestro comenta
CLASIFICACIÓN DE LAS FIGURAS Y CUERPOS GEOMÉTRICOS. Según los lados. Triángulos. Según los ángulos. Paralelogramo. Cuadriláteros.
 CLASIFICACIÓN DE LAS FIGURAS Y CUERPOS GEOMÉTRICOS Equilátero Polígonos Según los lados Isósceles Figuras geometrícas Nombre según los lados 3-Triángulo 4-Cuadrilátero 5-Pentágono 6-Hexágono 7-Heptágono
CLASIFICACIÓN DE LAS FIGURAS Y CUERPOS GEOMÉTRICOS Equilátero Polígonos Según los lados Isósceles Figuras geometrícas Nombre según los lados 3-Triángulo 4-Cuadrilátero 5-Pentágono 6-Hexágono 7-Heptágono
FIGURAS PLANAS. Es una figura plana delimitada por una línea poligonal cerrada.
 1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
1.- Qué es un polígono? FIGURAS PLANAS Es una figura plana delimitada por una línea poligonal cerrada. Los elementos de un polígono son: - Lado: Se llama lado a cada segmento que limita un polígono - Vértice:
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10.2 Completa la siguiente tabla. Caras (C ) Vértices (V ) Aristas (A) C V A 2 Tetraedro 4
EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10.2 Completa la siguiente tabla. Caras (C ) Vértices (V ) Aristas (A) C V A 2 Tetraedro 4
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Matemáticas 3º Eso.
 Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Sistemas Ejercicios de a reas y volu menes I 1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho
Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Sistemas Ejercicios de a reas y volu menes I 1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho
CONCEPTO DE POLÍGONO. RECONOCER Y CLASIFICAR POLÍGONOS
 OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
MATEMÁTICAS Y SU DIDÁCTICA
 MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
Soluciones Primer Nivel - 5º Año de Escolaridad
 Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
Primer Nivel - 5º Año de Escolaridad Problema 1. La diagonal del cuadrado mide cm. El cuadrado se descompone en cuatro triángulos rectángulos cuyos catetos miden 1cm. Las áreas de estos triángulos miden
11 Cuerpos geométricos
 89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
GEOMETRIA 8 AÑO 2011 1. Nombre:.Curso:
 GEOMETRIA 8 AÑO 2011 1 GUÍA DE APOYO AL TEMA : GEOMETRÍA Prof. Juan Schuchhardt E. Nombre:.Curso: UNIDAD #4 GEOMETRIA Tema # 2: Cuerpos geométricos En esta unidad aprenderás a: Identificar cuerpos poliédricos,
GEOMETRIA 8 AÑO 2011 1 GUÍA DE APOYO AL TEMA : GEOMETRÍA Prof. Juan Schuchhardt E. Nombre:.Curso: UNIDAD #4 GEOMETRIA Tema # 2: Cuerpos geométricos En esta unidad aprenderás a: Identificar cuerpos poliédricos,
Los cuerpos geométricos
 Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
1 Cuáles de estas figuras son semejantes? Cuál es la razón de semejanza? 2 a) Son semejantes los triángulos interior y exterior?
 Pág. 1 Figuras semejantes 1 uáles de estas figuras son semejantes? uál es la razón de semejanza? F 1 F 2 F 3 2 a) Son semejantes los triángulos interior y eterior? b) uántas unidades medirán los catetos
Pág. 1 Figuras semejantes 1 uáles de estas figuras son semejantes? uál es la razón de semejanza? F 1 F 2 F 3 2 a) Son semejantes los triángulos interior y eterior? b) uántas unidades medirán los catetos
Liceo N 1 Javiera Carrera 8 años 2011
 GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
1. Aplicar el teorema de Pitágoras para responder a las siguientes cuestiones (y hacer un dibujo aproximado,
 FICHA 1: Teorema de Pitágoras 1. Aplicar el teorema de Pitágoras para responder a las siguientes cuestiones (y hacer un dibujo aproximado, cuando proceda): a) Hallar la hipotenusa de un triángulo rectángulo
FICHA 1: Teorema de Pitágoras 1. Aplicar el teorema de Pitágoras para responder a las siguientes cuestiones (y hacer un dibujo aproximado, cuando proceda): a) Hallar la hipotenusa de un triángulo rectángulo
CUERPOS DE REVOLUCIÓN
 PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
Sistemas de Representación y Dibujo Técnico Año 2015. Geometría Básica
 EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
MATEMÁTICAS BÁSICAS. Jeanneth Galeano Peñaloza. 13 de agosto de Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas
 MATEMÁTICAS BÁSICAS Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 13 de agosto de 2012 Parte I Introducción a la geometría elemental Nociones básicas
MATEMÁTICAS BÁSICAS Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 13 de agosto de 2012 Parte I Introducción a la geometría elemental Nociones básicas
Áreas de cuerpos geométricos
 9 Áreas de cuerpos geométricos Objetivos En esta quincena aprenderás a: Calcular el área de prismas rectos de cualquier número de caras. Calcular el área de pirámides de cualquier número de caras. Calcular
9 Áreas de cuerpos geométricos Objetivos En esta quincena aprenderás a: Calcular el área de prismas rectos de cualquier número de caras. Calcular el área de pirámides de cualquier número de caras. Calcular
Nº caras. Nº vértices
 Tipo De Caras (Ángulo Interior) Triángulo Equilátero (60º) Cuadrado (90º) Pentágono (108º) Hexágono (10º) Nº caras por vértice Suma de los ángulos de cada vértice Nº caras Nº vértices Nº aristas C + V
Tipo De Caras (Ángulo Interior) Triángulo Equilátero (60º) Cuadrado (90º) Pentágono (108º) Hexágono (10º) Nº caras por vértice Suma de los ángulos de cada vértice Nº caras Nº vértices Nº aristas C + V
Plan de clase (1/3) Escuela: Fecha: Profr. (a): Curso: Matemáticas 9 Eje temático: F. E. y M.
 Plan de clase (1/3) Escuela: Fecha: Profr. (a): Curso: Matemáticas 9 Eje temático: F. E. y M. Contenido: 9.4.2 Análisis de las características de los cuerpos que se generan al girar sobre un eje, un triángulo
Plan de clase (1/3) Escuela: Fecha: Profr. (a): Curso: Matemáticas 9 Eje temático: F. E. y M. Contenido: 9.4.2 Análisis de las características de los cuerpos que se generan al girar sobre un eje, un triángulo
Clasificación de los triángulos
 Página 213 Clasificación de los triángulos 1. Di cómo son, según sus lados y según sus ángulos, los triángulos siguientes: A B C D A isósceles y obtusángulo. C equilátero y acutángulo. B escaleno y acutángulo.
Página 213 Clasificación de los triángulos 1. Di cómo son, según sus lados y según sus ángulos, los triángulos siguientes: A B C D A isósceles y obtusángulo. C equilátero y acutángulo. B escaleno y acutángulo.
CUERPOS GEOMÉTRICOS. POLIEDROS
 INTRODUCCIÓN CUERPOS GEOMÉTRICOS - POLIEDROS Este texto te servirá para que estudies los contenidos sobre poliedros que fueron desarrollados por los distintos grupos en clases y tiene como objetivos que
INTRODUCCIÓN CUERPOS GEOMÉTRICOS - POLIEDROS Este texto te servirá para que estudies los contenidos sobre poliedros que fueron desarrollados por los distintos grupos en clases y tiene como objetivos que
MATEMÁTICAS 3º ESO PENDIENTES HOJA 1 GEOMETRÍA PLANA. 1.- Calcular el área y el perímetro de los siguientes polígonos:
 MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
MATEMÁTICAS º ESO PENDIENTES HOJA GEOMETRÍA PLANA.- Calcular el área y el perímetro de los siguientes polígonos: a) Un cuadrado de lado 5 cm de lado b) Un cuadrado de diagonal 0 cm. c) Un rectángulo de
PRISMAS Y PIRÁMIDES. Qué es un poliedro? Un poliedro es un cuerpo geométrico que tiene alto, ancho y largo.
 PRISMAS Y PIRÁMIDES. 06 1 Comprende la relación que existe entre el volumen de un prisma con respecto al volumen de una pirámide que tienen la misma base y altura. En Presentación de Contenidos para explicar
PRISMAS Y PIRÁMIDES. 06 1 Comprende la relación que existe entre el volumen de un prisma con respecto al volumen de una pirámide que tienen la misma base y altura. En Presentación de Contenidos para explicar
UNIDAD 11. GEOMETRÍA DEL ESPACIO (I).
 UNIDAD 11. GEOMETRÍA DEL ESPACIO (I). Al final deberás haber aprendido... El examen tratará sobre... Describir los cuerpos geométricos del espacio e identificar sus elementos. Deducir las fórmulas para
UNIDAD 11. GEOMETRÍA DEL ESPACIO (I). Al final deberás haber aprendido... El examen tratará sobre... Describir los cuerpos geométricos del espacio e identificar sus elementos. Deducir las fórmulas para
Cuerpos geométricos. 2.1 Poliedros. El desarrollo del prisma pentagonal está formado por: ' ' "'-^ ^, Dos pentágonos congruentes.
 Cuerpos geométricos Un cuerpo geométrico o sólido es una porción del espacio limitada por superficies planas o curvas llamadas caras. 2.1 Poliedros Los poliedros son cuerpos geométricos limitados por cuatro
Cuerpos geométricos Un cuerpo geométrico o sólido es una porción del espacio limitada por superficies planas o curvas llamadas caras. 2.1 Poliedros Los poliedros son cuerpos geométricos limitados por cuatro
Introducción a la geometría
 Introducción a la geometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares. Plan de estudios (217 temas)
Introducción a la geometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares. Plan de estudios (217 temas)
Los cuerpos geométricos
 Los cuerpos geométricos Los poliedros y sus elementos Clasifica estos cuerpos en poliedros y no poliedros. A B C D E F G poliedros> B, D, E, F A, C, G no poliedros > Cuenta las caras, los vértices y las
Los cuerpos geométricos Los poliedros y sus elementos Clasifica estos cuerpos en poliedros y no poliedros. A B C D E F G poliedros> B, D, E, F A, C, G no poliedros > Cuenta las caras, los vértices y las
