1 Problemas de Optimización
|
|
|
- Fernando Páez Rivero
- hace 7 años
- Vistas:
Transcripción
1 1 Problemas de Optimización Eercise 1.1 Hallar un número positivo ue sumado con su inverso nos dé una suma mínima Si llamamos a dicho número; entonces la epresión ue nos permite calcular la suma de él con su inversa es: S = + 1 Por la naturaleza del problema, el dominio de esta función es el conjunto ]0, + [ Vamos pues a determinar el valor de para el cual S es mínima Calculamos S 0 S 0 =1 1 = 1 (D(f 0 )=]0, + [) Valores ue anulan S 0 (posibles máimos o mínimos locales) ( 1 =1 ]0, + [ =0 1=0 = 1 / ]0, + [ EstudiodelsignodeS 0 Si 0 < < 1; 1 < 0; S 0 = 1 < 0 S es est. decreciente en ]0, 1[ Si 1 < ; 1 > 0; S 0 = 1 > 0 S es est. creciente en ]1, + [ Por lo tanto; por la condición suficiente de mínimo local (criterio de la 1 a derivada) podemos afirmar ue para =1la suma S =es mínima La gráfica de la función S = + 1 en ]0, + [
2 El punto P (1, ) es mínimo local y absoluto de S en]0, + [ Eercise 1. Con un alambre de m de longitud se uiere formar un rectángulo desuperficie máima Si denominamos alaanchuraey alaalturadedichorectángulo;entonces su superficie es S = y (*) Como nos dicen ue el perímetro ha de ser de m entonces = +y 1= + y y =1 sustituyendo la epresión obtenida para y en (*) tendremos: S = (1 ) = El dominio de esta función es ]0, +1[ S 0 =1 (D(S 0 )=]0, +1[ Valores ue anulan S 0 (posibles máimos o mínimos locales) 1 =0 ½ = 1 ]0, 1[ EstudiodelsignodeS 0 Si 0 < < 1 ; S0 =1 >0; S es est. creciente en ]0, 1 [ Si 1 < < 1; S0 =1 <0 S es est. decreciente en ] 1, 1[ Por lo tanto; por la condición suficiente de máimo local (criterio de la 1 a derivada) podemos afirmar ue para = 1 mlasuperficie S = 1 1 = 1 m es máima La gráfica de la función S = en ]0, 1[ es :
3 El punto P ( 1, 1 ) es máimo local y absoluto de S en]0, 1[ Eercise 1. Con una cuerda de 0 m se uiere formar un triángulo isósceles de área máima. Cuál es el valor de dicha área? Figure 1: Si denominamos a los dos lados iguales y y al lado desigual; entonces la altura de dicho triángulo la podemos epresar en función de e y h = y Su superficie es pues: S = y y (**) Por ser el perímetro de 0 m tendremos: 0 = +y =15 y
4 Sustituyendo en (**) la epresión obtenida para y tendremos S = y (15 y) y = y (5 0y) = 5y 0y D(f) ={y < + /5 0y >0} =]0, 15 [ ds dy = S 0 = 5y 5y 5y 0y = 5 5y (5 0y) Valores ue anulan S 0 (posibles máimos o mínimos locales) 5 5y (5 0y) =0;5 5y =0 y =5m EstudiodelsignodeS 0 Si 0 < y < 5; S 0 = Si 5 < < 15 ; S0 = 5 5y (5 0y) > 0; S es est. creciente en ]0, 5[ 5 5y (5 0y) < 0 S es est. decreciente en ]5, 15 [ Por lo tanto; por la condición suficiente de máimo local (criterio de la 1 a derivada) podemos afirmar ue para y =5la superficie S =5 (5 150) = 5 m es máima Fíjate ue si y =5m =10m Luego; para ue la superficie sea máima el triángulo ha de ser euilátero La gráfica de la función S = y (5 0y) en ]0, 7.5[ es
5 y El punto P (5, 5 ) es máimo local y absoluto de S en]0, 7.5[ Eercise 1. De todos los rectángulos de área 16 m. Cuálessonlasdimensiones del ue tiene menor perímetro? Si denominamos alaanchuraey alaalturadedichorectángulo. Como el rectángulo tiene de supeficie 16 m ;entonces:.y =16 y = 16 P = +y P 0 = = Valores ue anulan P 0 EstudiodelsignodeP 0 P = + =0 = 0 con ]0, + [ ( = ]0, + [ = / ]0, + [ Si 0 < < ; P 0 = < 0; P es est. decreciente en ]0, [ Si < ; P 0 = > 0 P es est. decreciente en ], + [ Por lo tanto; por la condición suficiente de mínimo local (criterio de la 1 a derivada) podemos afirmar ue para =melperímetrop =8+ =16 mesmínimo La gráfica de la función P = + en ]0, + [ es : 5
6 El punto P (, 16) es mínimo local y absoluto de la función P = + en ]0, + [ Eercise 1.5 Un jardinero ha de construir un parterre en forma de sector circularyuetengaunperímetrode0m. Quéradiohadetenerpara lograr ue el área sea máima? Cual será entonces la longitud de su arco y su amplitud? Nota1 : Si denominas al ángulo en radianes,r al radio y l alalongitud del arco; has de saber ue = l entonces como el perímetro es de 0 m r resultará ue: 0 r r + l =0 r + r =0 = (a) r Nota : Si el área de un círculo de radio r es πr yadichasuperficie le corresponde una vuelta completa o sea π radianes; entonces la superficie del sector circular de radio r y ángulo en radianes 1 es S = r Y la del sector de ángulo en radianes es: S = r (b) Sustituyendo la epresión para de (a) en la epresión (b) tendremos: S = r 0 r r =10r r 6
7 Observa ue r ha de ser un número positivo ue no puede ser igual o superior a10 cm S 0 =10 r Valores ue anulan S 0 10 r =0 r =5 Como S 00 = ; entonces para r =5la superficie S =50 5 = 5cm es máima Sustituyendo en la epresión a el valor de r obtendremos ue el ángulo en radianes es: = 0 5 =rad 5 Por ultimo, la longitud del arco correspondiente a este sector circular es l =10cm La gráfica de la función S =10r r en el intervalo [0, 10] es: r Eercise 1.6 (Septiembre 00) De todos los cuadrados inscritos en un cuadrado de lado 16 m determina auél cuya superficie sea mínima 7
8 Es evidente, ue la superficie del cuadrado inscrito es: S = L = +(16 ) = +56donde ]0, 16[ El mínimo local y absoluto en ]0, 16[ de la función S = + 56, ha de ser el vértice de la parábola. Si dibujamos su gráfica Vemos ue su mínimo es V (8, 18) Comprobémoslo Valores ue anulan S 0 Estudio del signo de S 0 S 0 = +(16 )( 1) = = 0 =8 8
9 Si 0 <<8; S 0 < 0 S es est. decreciente en ]0, 8[ Si 8 <<16; S 0 > 0 S es est. creciente en ]8, 16[ Por la condición suficiente de mínimo local, podemos afirmar ue para =8m,S(8) = 18 m es mínima. Fíjate ue el lado del cuadrado mide L =8 Eercise 1.7 De todos los rectángulos inscritos en un cuadrado de lado 10 m determina auél cuya superficie sea máima ) Fíjate ue: PQ = + = QR = (10 ) +(10 ) =(10 ) Es evidente; ue la superficie del rectángulo PQRT es: S = PQ QR =(10 ) =0 donde ]0.10[ El máimo local y absoluto en ]0, 10[ de la función S =0, ha de ser el vértice de la parábola. Fíjate en su gráfica, y observarás ue su máimo es el vértice V (5, 50) 9
10 Comprobémoslo Calculemos de esta función su máimo Valores ue anulan S 0 Estudio del signo de S 0 S 0 =0 0 =0 =5 Si 0 <<5; S 0 > 0 S es est. creciente en ]0, 5[ Si 5 <<10; S 0 < 0 S es est. decrecreciente en ]5, 10[ Por la condición suficiente de máimo local, podemos afirmar ue para =5m,S(5) = 50 m es máima. Fíjate ue el rectángulo es un cuadrado cuyo lado mide L =5 m Eercise 1.8 (Junio 00) Desde un punto N de la orilla del mar, un nadadordebealcanzarunaboyaueflota a km de la costa y dista 5 km del punto N. Si recorriendo la orilla (ue se supone recta y plana), su velocidad media es de 5 km h y nadando, de km. Cuánto tiempo deberá h caminar hasta lanzarse al mar, para alcanzar la boya en el menor tiempo posible? ) 10
11 Si te fijas en el dibujo NO = r ³ 5 =6 Si consideramos un punto C y designamos por al segmento NC,es evidente ue CO =6 El segmento NC es el trayecto ue realiza andando el nadador. Como nos dicen ue anda a una velocidad de 5 km h esa distancia es T NC = 5. El tiempo empleado en recorrer El segmento CB = +(6 ) es el trayecto ue realiza nadando. Como nos dicen ue nada a una velocidad de km h El tiempo empleado 11
12 +(6 ) en recorrer esa distancia es T CB = El tiempo total empleado será: T = T NC + T CB = 5 + +(6 ) con [0, 6] Calculemos pues el valor de para ue el tiempo empleado sea mínimo Valores ue anulan T 0 dt d = T 0 = 1 5 (6 ) +(6 ) 1 (6 ) (6 ) =0 5 = +(6 ) +(6 ) 5 Elevando al cuadrado, tendremos: (6 ) +(6 ) = (6 ) =81+9(6 ) Aislando (6 ) (6 ) = = 9 = 15 6 = 9 = > 6 no me sirve El único valor ue anula T 0 es = 15 Km Calculemos ahora la segunda derivada dt 0 d = T 00 1 = 1 (6 ) +(6 ) ³ +(6 ) Vamos a simplificarla dt 0 d = T 00 = 1 +(6 ) h 1 (6 ) +(6 ) i = 1 +(6 ) 9 +(6 ) = ³ +(6 ) Como T 0 ( 15)=0 y T 00 ( 15)= ³ +(6 15 =
13 Por la condición suficiente de mínimo local (criterio de la segunda derivada), podemos afirmar ue: Para = 15 Km el tiempo empleado en llegar de N a B,de la manera 15 descrita en el problema, T = 5 + +(6 15 ) =hes mínimo Eercise 1.9 (Junio 00) Encontrar razonadamente el punto de la curva y = 1 en el ue la recta tangente a la curva tiene pendiente máima y 1+ calcular el valor de esa pendiente. Calculemos y 0 Si y =(1+ ) 1 y 0 = 1(1 + ) = (1 + ) Nos están pidiendo los valores de para los cuales la función H = y 0 es máima, siendo H = y 0 = (1 + (El dominio de H es <) ) Si te fijas en su gráfica (la de H) Observarás, ue eiste un único máimo local y absoluto para esta función. Determinémoslo Obtengamos su derivada H 0 = y 00 = (1+ ) + (1 + ) (1 + ) = (1 + )[ (1 + )+8 ] (1 + ) = 6 (1 + ) 1
14 Calculemos los valores ue anulan H 0 (Posibles máimos y mínimos de H) ( = 6 1 =0 = 1 Estudio del signo de H 0 (El signo de H 0 depende del signo de 6 ) Si < 1 H 0 > 0 H es est. creciente en], 1 [ Si 1 1 < < H 0 < 0 H es est. decreciente en ] 1 1, [ Si 1 < H 0 > 0 H es est. creciente en ] 1, [ Luego; podemos afirmar ue: Para = 1 ( ; H = 1 ) ³ = 8 es máima ) 1+( 1 ) Para = 1 ( ; H = 1 ³ = 8 es mínima ) 1+( 1 Conclusión: 1 El punto de la curva y = en el ue la recta tangente a la curva 1+ tiene pendiente máima es el punto de coordenadas = 1 1 y = 1+ ³ = 1. El valor de la pendiente de la recta tangente a la curva en ese punto es 8 La ecuació de su recta tangente en ese punto es: y = 8 1 ( + ) Nota: Este punto P ( 1, ) es el punto de infleión cóncavo-conveo de la función y = 1. Compruébalo tú, utilizando el criterio de la segunda 1+ derivada Si nos hubiesen pedido también: Cuál es el punto de la curva y = 1 1+ en el ue su recta tangente tiene pendiente mínima? 1
15 Dicho punto es el punto de coordenadas = 1 1 y = 1+ ³ = 1. El valor de la pendiente de la recta tangente a la curva en ese punto es 8 La ecuació de su recta tangente en ese punto es: Nota: Este punto Q( 1 la función y = derivada 1 ( ) y = 8, ) es el punto de infleión conveo-cóncavo de 1.Compruébalo tú, utilizando el criterio de la segunda Eercise 1.10 De todos los triángulos rectángulos de hipotenusa 10 m determina las dimensiones del ue tenga superficie máima 15
16 Como + y =100 S = y S = 100 Nota: S es máima H = S = (100 ) Calculemos H 0 H 0 = 1 (00 ) Puntos singulares de H (Valores ue anulan H 0 ) 00 =0 Estudio del signo de H 0 en ]0, 10[ con ]0, 10[ =0no es del dominio =5 = 5 no es del dominio = 1 (100 ) lo es Si 0 < < 5 H 0 > 0 H es est. creciente en ]0, 5 [ Si 5 < < 10 H 0 < 0 H es est. decreciente en ]5, 10[ Por lo tanto; para =5 H = S = 1 µ100 ³ 5 ³ 5 =65es máima Así pues; el triángulo rectangulo de hipotenusa ( 10 m ycuyasuperficie =5 (S =5m ) es máima es el ue tiene por catetos y = = 5. Se trata de un triángulo rectángulo isósceles. Eercise 1.11 De todos los triángulos rectángulos de superficie 100 m determina las dimensiones del ue tenga perímetro mínimo 16
17 Como 100 = y + y = z y = = z La función a minimizar es el perímetro del triangulo. Como P = + y + z P = + 00 s P 0 = ( ) ( y = 00 s ) = 00 + ( 0000) ( +0000) = z con ]0, + [ Para facilitar los valores ue anulan P 0 vamos a factorizar su epresión: P 0 = ) + ( = 1 ( 00) ) ( ( +0000) ( +0000) Valores ue anulan P 0 ( 00) 1+ ( +00) ( +0000) = 0 ( 00) = 0 = Estudio del signo de P 0 Si 0 <<10 P 0 < 0 P es est. decreciente en ]0, 10 [ Si >10 P 0 > 0 P es est. creciente en ]10, + [ Para =10 m y = =10 m z = 0 m el perímetro P =0 +0es mínimo. Se trata pues de un triángulo rectángulo isósceles. v u t ( no es del dominio ³ ³ = 10 Eercise 1.1 De todos los triángulos rectángulos de perímetro 0 m determina las dimensiones del ue tenga superficie máima. La función a maimizar es la superficie S = y Intentemos encontrar una relación entre las variables e y, apartirde los datos del problema = ( +00) ( +0000) > 0 17
18 Por ser el perímetro de 0 m + y + z =0 (1) Por el teorema de Pitágoras + y = z () De la epresión (1) despejamos z y elevamos al cuadrado, obteniendo: z =(0 y) = y + +y + y () Sustituyendo lo obtenido para z en la epresión (); tendremos: + y = y + +y + y () 0 = y +y (5) Aislando y de la epresión (5) y = = 0( 15) ( 0) (6) Así pues; la función a maimizar es: S = 0( 15) ( 0) =15 ( 15) ( 0) con ]0, 0[ La derivada de S es: S 0 =15 ( 15)( 0) ( 15) = ( 0) ( 0) 18
19 Valores ue anulan S 0 (posibles máimos o mínimos locales) =0 Estudio del signo de S 0 ( =0+15 / ]0, 0[ =0 15 Si 0 < < 0 15 S 0 > 0 S es est. crec. en ]0, 0 15 [ Si 0 15 < < 0 S 0 < 0 S es est. decrec. en ]0 15, 0[ Luego para =0 15 m y = 0( ) (0 15 =0 15 0) ³ 0 15 m la superficie S = = 5 ³ m es máima Se trata pues de un triángulo rectángulo isósceles. Eercise 1.1 Qué dimensiones tiene el rectángulo de área máima inscrito en una circunferencia de radio 8 m de radio? Eercise 1.1 Se necesita construir un marco rectangular para una ventana de 1 m de área. El coste del marco se estima en 500 pts por cada metro de altura y 0 m. de anchura. Cuáles son las dimensiones para ue el coste sea mínimo? Eercise 1.15 Unahojadepapeltiene18cm de teto impreso. Los márgenes superior e inferior han de tener cm cada uno y los laterales 1 cm Dimensiones del papel para ue el gasto sea mínimo? Eercise 1.16 Una hoja de papel debe contener 18 cm de teto impreso. Los márgenes superior e inferio han de tener cm cada uno y los laterales 1 cm Dimensiones del papel para ue el perímetro sea mínimo? Eercise 1.17 Se desea construir un bote cilíndrico de volumen 1 m. Cuáles son las dimensiones del ue tenga superficie mínima? 19
20 Eercise 1.18 (Septiembre 005) El perímetro de un sector circular de radio R vale m. Cuántos radianes α ha de medir su ángulo central para ue su área sea máima? El área de otro sector circular es 1 m. Para ué radio es mínimo su perímetro? Eercise 1.19 Se desea inscribir en un triángulo euilátero, de 10 m de lado, un rectángulo de manera ue su base esté contenida en uno de sus lados. Dimensiones de dicho rectángulo para ue su superficie sea máima? Eercise 1.0 Cuáles son las dimensiones de un cilindro inscrito en una esfera de radio 6 m para ue su volumen sea máimo? Eercise 1.1 Cuáles son las dimensiones de un rectángulo inscrito en una semicircunferencia de radio 6 m para ue su superficie sea máima? Nota: Uno de los lados ha de estar contenido en el diámetro de la semicircunferencia Eercise 1. Cuáles son las dimensiones de un triángulo rectángulo inscrito en una semicircunferencia de radio 6 m para ue su superficie sea máima? Nota:Lahipotenusaeseldiámetrodelasemicircunferencia Eercise 1. De un rectángulo de dimensiones 0 cm de altura por 18 cm de anchura, cortamos en las cuatro esuinas un cuadrado eactamente igual y después construimos una caja rectangular. Cuánto ha de valer el lado del cuadrado para ue el volumen de la caja sea máimo? Eercise 1. De todos los conos circunscritos en la esfera de radio 6 m. Determina las dimensiones del ue tenga volumen mínimo Ayuda:Elvolumendeunconoes V = 1 πr h Eercise 1.5 Cuáles son las dimensiones de un triángulo rectángulo ue está inscrito en una semicircunferencia de radio 6 m para ue su superficie sea máima? Nota:Lahipotenusahadeestarcontenidaeneldiámetrodelasemicircunferencia 0
21 Eercise 1.6 Se uiere construir un recipiente cónico de generatriz g =10 cm y de capacidad máima. Cuál debe ser el radio,r, de la base y la altura h? Ayuda:Elvolumendeunconoes V = 1 πr h g = h + r Eercise 1.7 Calcula la altura y el radio ue debe tener un bote cilíndrico de leche condensada, cuya área total (dos tapas también) es de 150 cm para ue su volumen sea máimo Ayuda: La superficie total de un cilindro y su volumen son respectivamente S =πr +πrh V = πr h Eercise 1.8 De todas las rectas ue pasan por el punto P (1, ) encuentra la ue determina con los ejes coordenadas, y en el primer cuadrante, un triángulo de área mínima Ayuda: la ecuación canónica de una recta en el plano, ue corta a los ejes de coordenadas en los puntos P (a, 0),Q(0,b) es: a + y b =1 1
APLICACIONES DE LA DERIVADA
 APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
APLICACIONES DE LA DERIVADA Ejercicio -Sea f: R R la función definida por f ( ) = + a + b + a) [ 5 puntos] Determina a, b R sabiendo que la gráfica de f pasa por el punto (, ) y tiene un punto de infleión
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS
 ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
ACTIVIDADES SELECTIVIDAD APLICACIONES DERIVADAS Ejercicio 1 De la función se sabe que tiene un máximo en, y que su gráfica corta al eje OX en el punto de abscisa y tiene un punto de inflexión en el punto
APLICACIONES DE LAS DERIVADAS
 UNIDAD APLICACIONES DE LAS DERIVADAS Página 98 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f
UNIDAD APLICACIONES DE LAS DERIVADAS Página 98 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f
APLICACIONES DE LA DERIVADA
 7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
7 APLICACIONES DE LA DERIVADA Página 68 Relación del crecimiento con el signo de la primera derivada Analiza la curva siguiente: f decrece f' < 0 f crece f' > 0 f decrece f' < 0 f crece f' > 0 f decrece
Repaso de Geometría. Ahora formulamos el teorema:
 Repaso de Geometría Preliminares: En esta sección trabajaremos con los siguientes temas: I. El Teorema de Pitágoras. II. Fórmulas básicas de geometría: perímetro, área y volumen. I. El Teorema de Pitágoras.
Repaso de Geometría Preliminares: En esta sección trabajaremos con los siguientes temas: I. El Teorema de Pitágoras. II. Fórmulas básicas de geometría: perímetro, área y volumen. I. El Teorema de Pitágoras.
DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES
 UNIDAD 6 DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES Página 5 Problema y f () 5 5 9 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(). f'() 0; f'(9) ; f'() Di otros tres puntos en
UNIDAD 6 DERIVADAS. TÉCNICAS DE DERIVACIÓN. APLICACIONES Página 5 Problema y f () 5 5 9 Halla, mirando la gráfica y las rectas trazadas, f'(), f'(9) y f'(). f'() 0; f'(9) ; f'() Di otros tres puntos en
1. Estudia la derivabilidad de la función )En qué punto del intervalo (0,ð) la recta tangente a y=tg(x) tiene pendiente 2?.
 ejerciciosyeamenes.com EXAMEN DERIVADAS. Estudia la derivabilidad de la función si f ()= si > 3. )En qué punto del intervalo (0,ð) la recta tangente a y=tg() tiene pendiente?. 4. Ecuación de la recta tangente
ejerciciosyeamenes.com EXAMEN DERIVADAS. Estudia la derivabilidad de la función si f ()= si > 3. )En qué punto del intervalo (0,ð) la recta tangente a y=tg() tiene pendiente?. 4. Ecuación de la recta tangente
Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm.
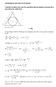 OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
OPTIMIZACION DE FUNCIONES Calcular la altura del cono de superficie lateral mínima circunscrito a una esfera de radio 4cm. S = пrg Si los triángulos DCO y DAB que son semejantes, pues OC AB y poseen un
Programa Entrenamiento MT-22
 Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
Programa Entrenamiento MT- SOLUCIONARIO Guía de ejercitación avanzada SGUICEN0MT-A6V TABLA DE CORRECCIÓN Guía de ejercitación ÍTEM ALTERNATIVA HABILIDAD D E B 4 C 5 C Comprensión 6 B 7 E Comprensión 8
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
f(x) = sen x f(x) = cos x
 www.matemáticagauss.com Trigonometría f(x) = sen x f(x) = cos x Función tangente f(x) = tan x Dominio: Ámbito: Periodo: Siempre crece 1 Prof. Orlando Bucknor Masís tel.: 9 9990 1) Un intervalo en el que
www.matemáticagauss.com Trigonometría f(x) = sen x f(x) = cos x Función tangente f(x) = tan x Dominio: Ámbito: Periodo: Siempre crece 1 Prof. Orlando Bucknor Masís tel.: 9 9990 1) Un intervalo en el que
1 Ángulos en las figuras planas
 Unidad 11. Elementos de geometría plana 1 Ángulos en las figuras planas Página 139 1. Cinco de los ángulos de un heágono irregular miden 147, 101, 93, 1 y 134. Halla la medida del seto ángulo. Los seis
Unidad 11. Elementos de geometría plana 1 Ángulos en las figuras planas Página 139 1. Cinco de los ángulos de un heágono irregular miden 147, 101, 93, 1 y 134. Halla la medida del seto ángulo. Los seis
Matemáticas 2 Agosto 2015
 Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
Laboratorio # 1 Línea recta I.-Determina la ecuación de la recta que satisface las siguientes condiciones y exprésala en la forma general. Pasa por el punto (1,5) y tiene pendiente 2 Pasa por y Pendiente
1 Cuáles de estas figuras son semejantes? Cuál es la razón de semejanza? 2 a) Son semejantes los triángulos interior y exterior?
 Pág. 1 Figuras semejantes 1 uáles de estas figuras son semejantes? uál es la razón de semejanza? F 1 F 2 F 3 2 a) Son semejantes los triángulos interior y eterior? b) uántas unidades medirán los catetos
Pág. 1 Figuras semejantes 1 uáles de estas figuras son semejantes? uál es la razón de semejanza? F 1 F 2 F 3 2 a) Son semejantes los triángulos interior y eterior? b) uántas unidades medirán los catetos
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
Aplicaciones de la derivada 7
 Aplicaciones de la derivada 7 ACTIVIDADES 1. Página 160 a) La pendiente de la recta tangente es 12. b) La pendiente de la recta tangente es 3. 2. Página 160 a) La pendiente de la recta tangente es. b)
Aplicaciones de la derivada 7 ACTIVIDADES 1. Página 160 a) La pendiente de la recta tangente es 12. b) La pendiente de la recta tangente es 3. 2. Página 160 a) La pendiente de la recta tangente es. b)
I. E. S. ATENEA. SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL. PRIMERA EVALUACIÓN. ANÁLISIS
 Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
Eamen Global Análisis Matemáticas II Curso 010-011 I E S ATENEA SAN SEBASTIÁN DE LOS REYES EXAMEN GLOBAL PRIMERA EVALUACIÓN ANÁLISIS Curso 010-011 1-I-011 MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES
La circunferencia y el círculo
 La circunferencia y el círculo 1.- LA CIRCUNFERENCIA Es una línea curva, cerrada y plana en la que todos sus puntos están a la misma distancia de un punto interior llamado centro. 2.- ELEMENTOS DE LA CIRCUNFERENCIA:
La circunferencia y el círculo 1.- LA CIRCUNFERENCIA Es una línea curva, cerrada y plana en la que todos sus puntos están a la misma distancia de un punto interior llamado centro. 2.- ELEMENTOS DE LA CIRCUNFERENCIA:
Ejercicios para aprender a derivar
 Ejercicios para aprender a derivar Derivación de polinomios y series de potencias Reglas de derivación: f ( ) k f '( ) 0 f ( ) a f '( ) a n n f ( ) a f '( ) an f ( ) u( ) + v( ) f '( ) u' + v' Ejemplos:
Ejercicios para aprender a derivar Derivación de polinomios y series de potencias Reglas de derivación: f ( ) k f '( ) 0 f ( ) a f '( ) a n n f ( ) a f '( ) an f ( ) u( ) + v( ) f '( ) u' + v' Ejemplos:
TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS
 IES IGNACIO ALDECOA 19 TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS 4.1 Medida de ángulos. Equivalencias. Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
IES IGNACIO ALDECOA 19 TEMA 4: TRIGONOMETRÍA. RAZONES TRIGONOMÉTRICAS 4.1 Medida de ángulos. Equivalencias. Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas
MATEMÁTICAS BÁSICAS. Jeanneth Galeano Peñaloza. 13 de agosto de Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas
 MATEMÁTICAS BÁSICAS Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 13 de agosto de 2012 Parte I Introducción a la geometría elemental Nociones básicas
MATEMÁTICAS BÁSICAS Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 13 de agosto de 2012 Parte I Introducción a la geometría elemental Nociones básicas
Demuestra que el punto de tangencia, T, es el lugar de la recta r desde el que se ve el segmento AB con ángulo máximo.
 Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 7 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura.
Matemáticas aplicadas a las Ciencias Sociales II Resuelve Página 7 Optimización Una persona se acerca a una estatua de m de altura. Los ojos de la persona están m por debajo de los pies de la escultura.
1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Solución:
 RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
RELACIÓN DE PROBLEMAS DE SELECTIVIDAD DE ANÁLISIS. I Departamento de Matemáticas 1.- Entre todos los triángulos rectángulos de 5 metros de hipotenusa, determina los catetos del de área máxima. Función
MATEMÁTICAS BÁSICAS. Autora: Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano
 MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad Nacional de Colombia
MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad Nacional de Colombia
a1 3 siendo a 1 y a 2 las aristas. 2 a a1
 Semejanza y Trigonometria. 77 Ejercicios para practicar con soluciones Dos rectángulos tienen sus lados proporcionales. Los lados del primero miden 6 y 8 cm respectivamente. Si el perímetro del segundo
Semejanza y Trigonometria. 77 Ejercicios para practicar con soluciones Dos rectángulos tienen sus lados proporcionales. Los lados del primero miden 6 y 8 cm respectivamente. Si el perímetro del segundo
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
Ángulos 1º = 60' = 3600'' 1' = 60''
 Ángulos Definición de ángulo Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. Medida de ángulos Para
Ángulos Definición de ángulo Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice. Medida de ángulos Para
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
Estudio de funciones mediante límites y derivadas
 Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
Estudio de funciones mediante límites y derivadas CVS0. El precio del billete de una línea de autobús se obtiene sumando dos cantidades, una fija y otra proporcional a los kilómetros recorridos. Por un
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
2. Obtener la longitud de la base de un triángulo isósceles cuyos lados iguales miden 17 cm y su altura 8 cm.
 ACTIVIDAD DE APOYO GEOMETRIA GRADO 11 1. Calcular el valor de la altura del triángulo equilátero y de la diagonal del cuadrado (resultado con dos decimales, bien aproimados): h 6 cm (Sol: 3,46 cm) (Sol:
ACTIVIDAD DE APOYO GEOMETRIA GRADO 11 1. Calcular el valor de la altura del triángulo equilátero y de la diagonal del cuadrado (resultado con dos decimales, bien aproimados): h 6 cm (Sol: 3,46 cm) (Sol:
11 Aplicaciones. de las derivadas. 1. Máximos, mínimos y monotonía. Piensa y calcula. Aplica la teoría
 Aplicaciones de las derivadas. Máimos, mínimos y monotonía Piensa y calcula Dada la gráfica de la función f representada en el margen, halla los máimos y los mínimos relativos y los intervalos de crecimiento
Aplicaciones de las derivadas. Máimos, mínimos y monotonía Piensa y calcula Dada la gráfica de la función f representada en el margen, halla los máimos y los mínimos relativos y los intervalos de crecimiento
Unidad 3: Razones trigonométricas.
 Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 3: Razones trigonométricas 1 Unidad 3: Razones trigonométricas. 1.- Medida de ángulos: grados y radianes. Las unidades de medida de ángulos más usuales son el grado sexagesimal y el radián. Se define
Unidad 8 Áreas y Volúmenes
 Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
7 Aplicaciones de las derivadas
 Solucionario 7 Aplicaciones de las derivadas ACTIVIDADES INICIALES 7.I. Calcula el volumen del cilindro que está inscrito en el cono de la figura: cm 8 cm Aplicando el Teorema de Pitágoras, se calcula
Solucionario 7 Aplicaciones de las derivadas ACTIVIDADES INICIALES 7.I. Calcula el volumen del cilindro que está inscrito en el cono de la figura: cm 8 cm Aplicando el Teorema de Pitágoras, se calcula
Ejercicio 1 Relacione convenientemente cada una de las siguientes expresiones: (considere x > 0 ) P Q a b. ax + bxh + h. x bxh
 Módulo 1 DERIVADAS 1.1 Reglas de diferenciación Reconocimiento de saberes Ejercicio 1 Relacione convenientemente cada una de las siguientes epresiones: (considere > 0 ) ln ( e ) ln ln ( e ) ln e ln + ln
Módulo 1 DERIVADAS 1.1 Reglas de diferenciación Reconocimiento de saberes Ejercicio 1 Relacione convenientemente cada una de las siguientes epresiones: (considere > 0 ) ln ( e ) ln ln ( e ) ln e ln + ln
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Universidad de San Carlos de Guatemala
 Clave: 03-2-M-2-00-203 Universidad de San Carlos de Guatemala Facultad de Ingeniería Departamento de matemática Curso: Matemática Básica 2 Código del curso: 03 Semestre: Segundo semestre 203 Tipo de eamen:
Clave: 03-2-M-2-00-203 Universidad de San Carlos de Guatemala Facultad de Ingeniería Departamento de matemática Curso: Matemática Básica 2 Código del curso: 03 Semestre: Segundo semestre 203 Tipo de eamen:
Aplicaciones de la derivada
 0.1 Problemas prácticos de máimos mínimos 1 Aplicaciones de la derivada En esta sección vamos a dedicarnos a calcular los máimos mínimos de funciones con diferentes propósitos. En muchas situaciones de
0.1 Problemas prácticos de máimos mínimos 1 Aplicaciones de la derivada En esta sección vamos a dedicarnos a calcular los máimos mínimos de funciones con diferentes propósitos. En muchas situaciones de
UNIDAD 2: ELEMENTOS GEOMÉTRICOS
 UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
UNIDAD 2: ELEMENTOS GEOMÉTRICOS POLÍGONO Región del plano limitada por una línea poligonal cerrada. 1. Dibuja polígonos y señala los lados, vértices y ángulos. 4 lados Ángulo Vértice Lado 5 lados Este
Geometría
 Geometría Geometría www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2012 Contenido 1. Geometría 2 1.1. Definiciones....................................... 2 1.2. Postulados........................................
Geometría Geometría www.math.com.mx José de Jesús Angel Angel jjaa@math.com.mx MathCon c 2007-2012 Contenido 1. Geometría 2 1.1. Definiciones....................................... 2 1.2. Postulados........................................
Tema 10: Cuerpos geométricos y transformaciones geométricas
 Tema 10: Cuerpos geométricos y transformaciones geométricas Regla. Escuadra. Cartabón. Compás. Transportador de ángulos. Calculadora Portaminas. Goma 10.1 Polígonos MATERIAL DE CLASE OBLIGATORIO PROBLEMAS
Tema 10: Cuerpos geométricos y transformaciones geométricas Regla. Escuadra. Cartabón. Compás. Transportador de ángulos. Calculadora Portaminas. Goma 10.1 Polígonos MATERIAL DE CLASE OBLIGATORIO PROBLEMAS
CIRCUNFERENCIA Y CÍRCULO
 CIRCUNFERENCIA Y CÍRCULO 1. Circunferencia y círculo. Elementos. 2. Posiciones relativas de una recta y una circunferencia. 3. Posiciones relativas de dos circunferencias. 4. Ángulos centrales. 5. Ángulos
CIRCUNFERENCIA Y CÍRCULO 1. Circunferencia y círculo. Elementos. 2. Posiciones relativas de una recta y una circunferencia. 3. Posiciones relativas de dos circunferencias. 4. Ángulos centrales. 5. Ángulos
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Uso no comercial 12.4 CUERPOS REDONDOS
 1.4 CUERPOS REDONDOS Designamos en general como cuerpos redondos el conjunto de puntos del espacio obtenido cuando una figura gira alrededor de una recta, de tal forma que cada punto de la figura conserva,
1.4 CUERPOS REDONDOS Designamos en general como cuerpos redondos el conjunto de puntos del espacio obtenido cuando una figura gira alrededor de una recta, de tal forma que cada punto de la figura conserva,
Problemas de selectividad. Análisis
 Departamento de Matemáticas Página 1 Problemas de selectividad. Anális 14.01.- De entre todos los triángulos rectángulos de área 8 cm, determina las dimenones del que tiene la hipotenusa de menor longitud.
Departamento de Matemáticas Página 1 Problemas de selectividad. Anális 14.01.- De entre todos los triángulos rectángulos de área 8 cm, determina las dimenones del que tiene la hipotenusa de menor longitud.
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES.
 APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
APLICACIÓN DE DERIVADAS: PROBLEMAS DE OPTIMIZACIÓN CON 2 VARIABLES. 001 Hallar 2 números cuya suma es 20, sabiendo que su producto es 002 003 004 005 Halla dos números cuya suma sea 25, tales que el doble
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
250 Si la razón entre las longitudes de la realidad y de la representación es razón entre las áreas es ( 20 )
 Soluciones a las actividades de cada epígrafe PÁGIN Entrénate 1 Una parcela con forma de cuadrilátero irregular tiene 80 m de área y su lado menor mide 40 m. Hacemos un plano de la parcela en el que el
Soluciones a las actividades de cada epígrafe PÁGIN Entrénate 1 Una parcela con forma de cuadrilátero irregular tiene 80 m de área y su lado menor mide 40 m. Hacemos un plano de la parcela en el que el
b) Cuántas asíntotas oblicuas y cuántas asíntotas verticales puede tener una función racional cualquiera?. Razónalo. dx x 2 1 x 1 si x >1 x 1 x < 0
 ANÁLISIS. (Junio 994) a) Encontrar las asíntotas de la curva f () = 2 3 2 4 b) Cuántas asíntotas oblicuas y cuántas asíntotas verticales puede tener una función racional cualquiera?. Razónalo. 2. (Junio
ANÁLISIS. (Junio 994) a) Encontrar las asíntotas de la curva f () = 2 3 2 4 b) Cuántas asíntotas oblicuas y cuántas asíntotas verticales puede tener una función racional cualquiera?. Razónalo. 2. (Junio
CUERPOS DE REVOLUCIÓN
 PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
PROPÓSITOS: Identificar los cuerpos redondos o de revolución. Resolver problemas, donde se aplique el volumen y área de cuerpos de revolución. CUERPOS DE REVOLUCIÓN Existen cuerpos geométricos que no tienen
dada por c(x) = donde x indica el tamaño de los pedidos para renovar existencias
 FUNCIONES +, si
FUNCIONES +, si
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Matemática 3 Colegio N 11 B. Juárez
 Unidad 4: RAZONES Y PROPORCIONES Definición de RAZÓN: Se denomina razón entre dos números racionales a y b, al cociente (división) entre ambos, siendo b distinto de 0. a se denomina antecedente Ejemplo
Unidad 4: RAZONES Y PROPORCIONES Definición de RAZÓN: Se denomina razón entre dos números racionales a y b, al cociente (división) entre ambos, siendo b distinto de 0. a se denomina antecedente Ejemplo
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
5.5 LÍNEAS TRIGONOMÉTRICAS
 5.5 LÍNES TRIGONOMÉTRIS Sea (O, ) una circunferencia con centro en el origen de coordenadas O(0, 0) radio la unidad. Si se construe un ángulo con vértice en el origen sentido positivo podemos obtener las
5.5 LÍNES TRIGONOMÉTRIS Sea (O, ) una circunferencia con centro en el origen de coordenadas O(0, 0) radio la unidad. Si se construe un ángulo con vértice en el origen sentido positivo podemos obtener las
CAPÍTULO 9: LONGITUDES Y ÁREAS 1. PERÍMETROS Y ÁREAS DE POLÍGONOS
 88 CAPÍTULO 9: LONGITUDES Y ÁREAS 1. PERÍMETROS Y ÁREAS DE POLÍGONOS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes de sus lados.
88 CAPÍTULO 9: LONGITUDES Y ÁREAS 1. PERÍMETROS Y ÁREAS DE POLÍGONOS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes de sus lados.
Ejercicios de Análisis propuestos en Selectividad
 Ejercicios de Análisis propuestos en Selectividad.- Dada la parábola y 4, se considera el triángulo rectángulo T( r ) formado por los ejes coordenados y la tangente a la parábola en el punto de abscisa
Ejercicios de Análisis propuestos en Selectividad.- Dada la parábola y 4, se considera el triángulo rectángulo T( r ) formado por los ejes coordenados y la tangente a la parábola en el punto de abscisa
LA CIRCUNFERENCIA. x y r. (x h) (y k) r. d(p; 0) x y r. d(p; C) (x h) (y k) r. Definición. Ecuación de la circunferencia. Geometría Analítica 3
 Definición LA CIRCUNFERENCIA Se llama circunferencia a la sección cónica generada al cortar un cono recto con un plano perpendicular al eje del cono. La circunferencia es el lugar geométrico de todos los
Definición LA CIRCUNFERENCIA Se llama circunferencia a la sección cónica generada al cortar un cono recto con un plano perpendicular al eje del cono. La circunferencia es el lugar geométrico de todos los
SOLUCIONES A LAS ACTIVIDADES DE CADA EPÍGRAFE
 Pág. 1 PÁGIN 212 Recorta en cartulina cada una de estas figuras y sujétalas en palillos de dientes. Sosteniendo el palillo entre los dedos y soplando en el lateral, qué ves en cada caso? Triángulo ono
Pág. 1 PÁGIN 212 Recorta en cartulina cada una de estas figuras y sujétalas en palillos de dientes. Sosteniendo el palillo entre los dedos y soplando en el lateral, qué ves en cada caso? Triángulo ono
APLICACIONES DEL CÁLCULO DIFERENCIAL-II
 APLICACIONES DEL CÁLCULO DIFERENCIAL-II. Estudia si crecen o decrecen las siguientes funciones en los puntos indicados: π a) f() cos en 0 b) f() ln ( arc tg ) en 0 π c) f() arc sen en 0 d) f() ln en 0
APLICACIONES DEL CÁLCULO DIFERENCIAL-II. Estudia si crecen o decrecen las siguientes funciones en los puntos indicados: π a) f() cos en 0 b) f() ln ( arc tg ) en 0 π c) f() arc sen en 0 d) f() ln en 0
UNIDAD DIDÁCTICA 6: Trigonometría
 UNIDAD DIDÁCTICA 6: Trigonometría 1. ÍNDICE 1. Introducción 2. Ángulos 3. Sistemas de medición de ángulos 4. Funciones trigonométricas de un ángulo 5. Teorema de Pitágoras 6. Problemas sobre resolución
UNIDAD DIDÁCTICA 6: Trigonometría 1. ÍNDICE 1. Introducción 2. Ángulos 3. Sistemas de medición de ángulos 4. Funciones trigonométricas de un ángulo 5. Teorema de Pitágoras 6. Problemas sobre resolución
TEMA 12: LONGITUDES Y ÁREAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 009 TEMA 1: LONGITUDES Y ÁREAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/009 TEMA 1: Longitudes y Áreas. TEMA 1: LONGITUDES Y ÁREAS. 1.
009 TEMA 1: LONGITUDES Y ÁREAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/009 TEMA 1: Longitudes y Áreas. TEMA 1: LONGITUDES Y ÁREAS. 1.
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Guía de Estudio Algebra y Trigonometría Para Ciencias Agropecuarias
 Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
Guía de Estudio Para Ciencias Agropecuarias Unidad: Geometría Analítica Los siguientes ejercicios están relacionados con los principales temas de Geometría Analítica e involucra todos los conocimientos
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
EJERCICIOS DE MATEMÁTICAS 2º E.S.O. TEOREMA DE PITÁGORAS Y DISTANCIAS
 Colegio Ntra. Sra. de las Escuelas Pías Dpto. de Matemáticas EJERCICIOS DE MATEMÁTICAS 2º E.S.O. TEOREMA DE PITÁGORAS Y DISTANCIAS 1. Un ángulo agudo de un triángulo rectángulo mide la mitad que el otro.
Colegio Ntra. Sra. de las Escuelas Pías Dpto. de Matemáticas EJERCICIOS DE MATEMÁTICAS 2º E.S.O. TEOREMA DE PITÁGORAS Y DISTANCIAS 1. Un ángulo agudo de un triángulo rectángulo mide la mitad que el otro.
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2015 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 05 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva, Ejercicio,
Contenido Objetivos Recursos Total de hora s Polígono regular. Clasificación, elementos, áreas.
 Contenido Objetivos Recursos Total de hora s Polígono regular. Clasificación, elementos, áreas. Identifica las clasificacione s de los polígonos regulares Power Point: clasificación y elementos de los
Contenido Objetivos Recursos Total de hora s Polígono regular. Clasificación, elementos, áreas. Identifica las clasificacione s de los polígonos regulares Power Point: clasificación y elementos de los
1º BACHILLERATO - MATEMÁTICAS CCSS - TEMA 1 NÚMEROS REALES
 1º BACHILLERATO - MATEMÁTICAS CCSS - TEMA 1 NÚMEROS REALES ˆ PÁGINA 4, EJERCICIO 68 Una habitación con forma de ortoedro de base cuadrada y altura la mitad del lado de la base se pintó en tres días. Se
1º BACHILLERATO - MATEMÁTICAS CCSS - TEMA 1 NÚMEROS REALES ˆ PÁGINA 4, EJERCICIO 68 Una habitación con forma de ortoedro de base cuadrada y altura la mitad del lado de la base se pintó en tres días. Se
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
MATEMÁTICAS 1º DE ESO LOMCE TEMA X: POLÍGONOS Y CIRCUNFERENCIAS Triángulos. Elementos y relaciones. Tipos de triángulos. Rectas y puntos notables: o Mediatrices y circuncentro. o Bisectrices e incentro.
Calcula la tangente de las siguientes curvas en los puntos dados: Calcula la derivada de las siguientes funciones: e) f (x) = x x.
 Derivadas Definición Reglas de derivación jercicio Calcula la tangente de las siguientes curvas en los puntos dados: a) y = en el origen + b) y = cos() en ( c) y = + en (3, 0) π, 0) d) y = en (, ) Solución
Derivadas Definición Reglas de derivación jercicio Calcula la tangente de las siguientes curvas en los puntos dados: a) y = en el origen + b) y = cos() en ( c) y = + en (3, 0) π, 0) d) y = en (, ) Solución
Aplicaciones de la derivada Ecuación de la recta tangente
 Aplicaciones de la derivada Ecuación de la recta tangente La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto. La recta tangente a una curva en un punto
Aplicaciones de la derivada Ecuación de la recta tangente La pendiente de la recta tangente a una curva en un punto es la derivada de la función en dicho punto. La recta tangente a una curva en un punto
DEPARTAMENTO DE MATEMATICAS
 1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
1.- Halla la suma de los ángulos interiores de los siguientes polígonos convexos. a) Cuadrilátero b) Heptágono c) Octógono 2.- Halla la medida de los ángulos interiores de: a) Un octógono regular. b) Un
, calcule el área del triángulo ABN.
 Universidad Peruana de iencias plicadas (UP) Perímetros y Áreas ompuestas 1. alcule el área de un triángulo isósceles si el ángulo desigual mide 30º y los lados iguales miden 8m. 30º 8 m 8 m. alcule el
Universidad Peruana de iencias plicadas (UP) Perímetros y Áreas ompuestas 1. alcule el área de un triángulo isósceles si el ángulo desigual mide 30º y los lados iguales miden 8m. 30º 8 m 8 m. alcule el
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
 ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
Universidad de la Frontera Departamento de Matemática y Estadística. Problemas de Optimización. Cĺınica de Matemática. J. Labrin - G.
 Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Problemas de Optimización J. Labrin - G.Riquelme 1. Una caja con base cuadrada y parte superior abierta debe
Universidad de la Frontera Departamento de Matemática y Estadística Cĺınica de Matemática 1 Problemas de Optimización J. Labrin - G.Riquelme 1. Una caja con base cuadrada y parte superior abierta debe
La circunferencia es una curva plana y cerrada, cuyos puntos equidistan de otro punto interior llamado centro.
 Geometría y Trigonometría Circunferencia 6. CIRCUNFERENCIA 6.1 Definición y notación de una circunferencia La circunferencia es una curva plana y cerrada, cuyos puntos equidistan de otro punto interior
Geometría y Trigonometría Circunferencia 6. CIRCUNFERENCIA 6.1 Definición y notación de una circunferencia La circunferencia es una curva plana y cerrada, cuyos puntos equidistan de otro punto interior
CONCEPTO DE POLÍGONO. RECONOCER Y CLASIFICAR POLÍGONOS
 OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
OBJETIVO 1 CONCEPTO DE POLÍGONO. RECONOCER Y CLASIICAR POLÍGONOS NOMBRE: CURSO: ECHA: POLÍGONOS Varios segmentos unidos entre sí forman una línea poligonal. Una línea poligonal cerrada es un polígono.
Llamamos área o superficie a la medida de la región interior de un polígono. Figura Geométrica Perímetro Área. p = a + b + c 2 2.
 GUÍA GEOMETRÍA PERÍMETRO Y AREA DE FIGURAS PLANAS Llamamos área o superficie a la medida de la región interior de un polígono. El perímetro corresponde a la suma de los lados del polígono. Figura Geométrica
GUÍA GEOMETRÍA PERÍMETRO Y AREA DE FIGURAS PLANAS Llamamos área o superficie a la medida de la región interior de un polígono. El perímetro corresponde a la suma de los lados del polígono. Figura Geométrica
f(x) f(x 0 ) = L IR h 0 = 0 = f (x 0 ); con lo que f (x) = 0 para todo x IR. (x x = lím x + x 0 = 2x 0 = f (x 0 ), y f (x) = 2x en IR.
 Matemáticas I : Cálculo diferencial en IR Tema Funciones derivables. Derivada de una función en un punto Definición 4.- Se dice que f: (a, b IR es derivable en el punto (a, b si f( f( = L IR es decir,
Matemáticas I : Cálculo diferencial en IR Tema Funciones derivables. Derivada de una función en un punto Definición 4.- Se dice que f: (a, b IR es derivable en el punto (a, b si f( f( = L IR es decir,
1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones:
 F. EJERCICIOS PROPUESTOS. 1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones: (a) f(x) =x 3 /3+3x 2 /2 10x. Resp.: Crece en (, 5) y en (2, ); decrece en ( 5, 2). (b) f(x) =x 3
F. EJERCICIOS PROPUESTOS. 1.- Encontrar los intervalos de crecimiento y decrecimiento de las funciones: (a) f(x) =x 3 /3+3x 2 /2 10x. Resp.: Crece en (, 5) y en (2, ); decrece en ( 5, 2). (b) f(x) =x 3
IES Fco Ayala de Granada Septiembre de 2011 (Septiembre Modelo 2) Solución Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
IES Fco Ayala de Granada Septiembre de 0 (Septiembre Modelo ) Germán-Jesús Rubio Luna UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD CURSO 00-0. MATEMÁTICAS II Opción A Ejercicio opción A,
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Funciones reales. Números complejos
 Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones reales. Números complejos Funciones reales 1. Encuentra todos los números reales x que verifican: a) (x 1)(x 3) > 1 b) x + 1 > 1 1 x c) x 1 + x + 1 < 1 d) 5 < x 2 14x + 5 < 26 2. Si la gráfica
Funciones 1. D = Dom ( f ) = x R / f(x) R. Recuerda como determinabas los dominios de algunas funciones: x x
 Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
Funciones. DEFINICIÓN Y TERMINOLOGÍA.. Definición de función real de variable real. "Es toda correspondencia, f, entre un subconjunto D de números reales y R (o una parte de R), con la condición de que
1.- Un jardín rectangular tiene por ancho Xm y largo X+10, encontrar la función que describe el área del jardín y graficar.
 1.- Un jardín rectangular tiene por ancho Xm y largo X+1, encontrar la función que describe el área del jardín y graficar. Largo=X+3 Ancho=X Área=(Largo)(ancho) Area=(X+3)X A x = X 2 + 3X La grafica de
1.- Un jardín rectangular tiene por ancho Xm y largo X+1, encontrar la función que describe el área del jardín y graficar. Largo=X+3 Ancho=X Área=(Largo)(ancho) Area=(X+3)X A x = X 2 + 3X La grafica de
= + = 1+ Cuarta relación fundamental
 1.- Determina las razones trigonométricas de los siguientes ángulos, relacionándolos con algunos ángulos notables (0º, 0º,, 60º, 90º, 180º, 70º, 60º), indicando en qué cuadrante se encuentran: a) 40º b)
1.- Determina las razones trigonométricas de los siguientes ángulos, relacionándolos con algunos ángulos notables (0º, 0º,, 60º, 90º, 180º, 70º, 60º), indicando en qué cuadrante se encuentran: a) 40º b)
Tema 6: Trigonometría.
 Tema 6: Trigonometría. Comenzamos un tema, para mi parecer, muy bonito, en el que estudiaremos algunos aspectos importantes de la geometría, como son los ángulos, las principales razones e identidades
Tema 6: Trigonometría. Comenzamos un tema, para mi parecer, muy bonito, en el que estudiaremos algunos aspectos importantes de la geometría, como son los ángulos, las principales razones e identidades
POLÍGONOS
 POLÍGONOS 8.1.1 8.1.5 Después de estudiar los triángulos y los cuadriláteros, los alumnos ahora amplían su estudio a todos los polígonos. Un polígono es una figura bidimensional, cerrada, formada por tres
POLÍGONOS 8.1.1 8.1.5 Después de estudiar los triángulos y los cuadriláteros, los alumnos ahora amplían su estudio a todos los polígonos. Un polígono es una figura bidimensional, cerrada, formada por tres
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
Abajo está una mezcla de expresiones racionales. Haga la operación indicada y simplifique su solución, si puede.
 Unidad 1 Llendo a campar: D írculos 1 D-8. bajo está una mezcla de epresiones racionales. Haga la operación indicada simplifique su solución, si puede. 6 + 8 + 1 + 6 5 + 10 + 8 + + 5 ( + 1) d) + + 5 10
Unidad 1 Llendo a campar: D írculos 1 D-8. bajo está una mezcla de epresiones racionales. Haga la operación indicada simplifique su solución, si puede. 6 + 8 + 1 + 6 5 + 10 + 8 + + 5 ( + 1) d) + + 5 10
TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
2009 TEMA 10: FORMAS Y FIGURAS PLANAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 10: FORMAS Y FIGURAS PLANAS. 1. Polígonos. 2.
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
ÁREAS DE FIGURAS PLANAS
 6. ÁREAS DE FIGURAS PLANAS EN ESTA UNIDAD VAS A APRENDER ÁREAS POLÍGONOS RECTÁNGULO CUADRADO PARALELOGRAMO TRIÁNGULO TRAPECIO ROMBO POLÍGONO IRREGULAR FÓRMULA RESOLUCIÓN DE PROBLEMAS CÍRCULO FÓRMULA FIGURAS
6. ÁREAS DE FIGURAS PLANAS EN ESTA UNIDAD VAS A APRENDER ÁREAS POLÍGONOS RECTÁNGULO CUADRADO PARALELOGRAMO TRIÁNGULO TRAPECIO ROMBO POLÍGONO IRREGULAR FÓRMULA RESOLUCIÓN DE PROBLEMAS CÍRCULO FÓRMULA FIGURAS
