Tema 0: Repaso de Conceptos
|
|
|
- Lucía Ramos Guzmán
- hace 7 años
- Vistas:
Transcripción
1 Mtemátics 1º Bchillerto Tem 0: Repso de Coceptos 1.- Números Reles Cojutos Numéricos 1..- Itervlos y semirrects. 1..-Vlor Asoluto Propieddes de ls potecis..- Idetiddes Notles..- Rdicles..1.- Propieddes de los rdicles...- Simplificció de Rdicles...- Reducció ídice comú..4.- Rciolizció..5.- Etrcció de fctores de u rdicl..6.- Itroducció de fctores e u rdicl. 4.- Logritmos Propieddes de los logritmos Opercioes co logritmos Logritmos e l clculdor Cmio de Bse. 5.- Epresioes lgerics Opercioes co poliomios Descomposició fctoril Frccioes Algerics. 6.- Ecucioes, iecucioes y sistems Ecucioes de segudo grdo Ecucioes de grdo myor que Ecucioes Rcioles Ecucioes Irrcioles Ecucioes epoeciles Ecucioes Logrítmics Sistems de ecucioes. Método de Guss Iecucioes de 1º grdo co u icógit Iecucioes de º Grdo co u icógit Iecucioes Frccioris Sistems de ecucioes co u icógit Sistems de iecucioes co dos icógits. 7.- Ejercicios Resueltos Rúl Gozález Medi 015 Tem 0: Repso de coceptos de úmeros y álger O-1
2 Mtemátics 1º Bchillerto Tem 0 1. TEMA 0:NÚMEROS REALES 1.1. CONJUNTOS NUMÉRICOS 1.. REPRESENTACIÓN SOBRE LA RECTA L represetció de u úmero rel sore l rect se hrá de u modo u otro segú el tipo de úmero que se: Etero o deciml ecto: ;,47 Deciml periódico: Puede epresrse e form de frcció y, de este modo, se represet dividiedo cd uidd etre ls prtes que teg el deomidor y tomdo tts de ess prtes como idique el umerdor: 5/6, -8/5 Rciol cudrático: Costruyedo triágulos rectágulos y teiedo el cuet el (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-
3 Mtemátics 1º Bchillerto Tem 0 Teorem de Pitágors: 6; INTERVALOS Y SEMIRECTAS INTERVALO ABIERTO DE EXTREMOS A Y B. Es el cojuto de úmeros compredidos etre y, si coger éstos. Se suele represetr de ls siguietes forms: (,) { R / < < } 1... INTERVALO CERRADO DE EXTREMOS A Y B. Es el cojuto de úmeros reles compredidos etre y icluyedo éstos. Se suele represetr de ls siguietes forms: [,] { R / } 1... INTERVALO SEMIABIERTO O SEMICERRADO. So itervlos dode uo de sus etremos es ierto y el otro cerrdo. Se os puede presetr los siguietes csos: (,], itervlo ierto e y cerrdo e. Es el cojuto de úmeros compredidos etre y si coger l y tomdo l. Sus otrs forms de represetció so { R / < } [,), itervlo cerrdo e y ierto e. Es el cojuto de úmeros compredidos etre y, cogiedo l y o l. Sus otrs forms de represetció so { R / < } SEMIRECTAS. So itervlos dode uo de sus etremos es u úmero rel y el otro es Teemos los siguietes csos: ± [, ) { R / } (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-
4 Mtemátics 1º Bchillerto Tem 0 (, ) { R / < } (,] { R / } (,) { R / < } B 1.4. ENTORNOS Se llm etoro de cetro y rdio r, y se deot por Er() o E(,r), l itervlo ierto (-r, +r). Er() (-r, +r) Los etoros se epres co yud del vlor soluto. Er(0) (-r, r) se epres tmié <0, o ie, -r < < r. Er() (-r, +r) se epres tmié - <0, o ie, -r < < +r ENTORNO REDUCIDO Se emple cudo se quiere ser qué ps e ls proimiddes del puto, si que iterese lo que ocurre e dicho puto. E r*() { (-r, +r), } 1.5. VALOR ABSOLUTO. Cosideremos los úmeros 5 y 5, estos dos úmeros tiee el mismo vlor si el sigo, o lo que es lo mismo, tiee el mismo vlor soluto. El vlor soluto de u úmero se desig por y coicide co el úmero si este es positivo o co el opuesto si este es egtivo... si si... < 0 Tomemos por ejemplos - -(-) (-6) 6 Oservd que pr elimir ls rrs del vlor soluto, os teemos que fijr e el sigo de lo que vy detro de ls rrs del vlor soluto. Si es positivo, qued igul y si es egtivo, cmimos el sigo de lo que vy detro. El prolem se os preset cudo o coozcmos el sigo. Por ejemplo, resolver l siguiete ecució co vlor soluto Pr resolverl, lo primero es quitr el vlor soluto. Deemos coocer el sigo de lo de detro (). Como o coocemos el vlor de, o coocemos su sigo, o podemos quitr el vlor soluto. (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-4
5 Mtemátics 1º Bchillerto Tem 0 E estos csos se supoe que lo de detro del vlor soluto puede presetr los dos sigos, luego el prolem tiee dole solució. Supoemos e primer lugr que > 0 ê Supoemos e segudo lugr que < Ejemplo: Hllr l solució (es) de l siguiete ecució: Supoemos - 1< Supoemos hor -1> PROPIEDADES DE LAS POTENCIAS ( ) m.m 5.- m m ( ) m 6.- m. m+ 7.- m : m- 8.- (..c) d d. d.c d 9.- c c Todo úmero etero que ce e ceros, se puede epresr como producto del úmero si los ceros, por u poteci de se 10 y epoete igul l úmero de ceros: (otció cietífic) Todo úmero deciml se puede epresr como producto del úmero si l com por u poteci de se 10 y epoete egtivo igul l úmero de cifrs decimles.. IGUALDADES NOTABLES (+) (-) +.- (+) + ª (-) ª (+).(-) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-5
6 Mtemátics 1º Bchillerto Tem 0 Ejemplos: ( + 5) ( 5) () ( + 1) ( ( )+1) ( ) +1 +(( ))1 ( ) +(-) - (-)+( ) ( ) ( + ) () 9 4. DEFINICIÓN DE RADICAL. Dd l ecució, llmmos ríz -ésim de, u de ls solucioes de dich ecució, y que se simoliz por, dode es el ídice de l ríz y el rdicdo..1. Propieddes de los rdicles m. m m 4.- ( ) m.. Simplificció de rdicles Ddo m, si y m tiee divisores e comú, podemos simplificr el rdicl, por ejemplo:.. Reducció ídice comú Oteer el ídice comú de vrios rdicles cosiste e hllr el m.c.m. de los ídices, dividir este mcm etre cd ídice y el resultdo multiplicrlo por el epoete del rdicdo. Por ejemplo, reducir ídice comú los siguietes rdicles:,, 6 7 El mcm(,,6) 6 ê 6, 6, Rciolizr. Rciolizr u frcció cosiste e elimir ls ríces del deomidor de u frcció multiplicdo el umerdor y el deomidor por u epresió decud. Dich epresió v e fució de l epresió del deomidor. Podemos distiguir dos csos: (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-6
7 Mtemátics 1º Bchillerto Tem m. m. m m. m. m ( + c ) +.- c ( c )(. + c ) c c Ejemplos:Rciolizr ls siguietes epresioes: ( + ) ( )(. + ) Etrcció de fctores de u rdicl. Pr etrer fctores de u rdicl p, p dee ser myor o igul que. Se divide p etre, el cociete os dice cuátos fctores sle y el resto os idic cuátos se qued: Itroducció de fctores e u rdicl. 4 Pr itroducir fctores detro de u rdicl, se elev el fctor l ídice: Ej : SUMA DE RADICALES. 5. Pr sumr o restr rdicles, éstos dee ser semejtes, es decir, h de teer el mismo ídice y el mismo rdicdo: ( )..6.. PRODUCTO Y COCIENTE DE RADICALES Pr multiplicr y dividir rdicles lo primero es reducir ídice comú y, plicdo propieddes de rdicles, reducir u solo rdicl (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-7
8 Mtemátics 1º Bchillerto Tem 0 4. CONCEPTO DE LOGARITMO. Se u úmero rel positivo, o ulo y distito de 1, y A otro úmero positivo o ulo. Se llm logritmo e se del úmero A, l epoete que dee elevrse l se pr oteer el úmero A. Se represet por log A A Ejemplos 1.- Hllr los siguietes logritmos: ) log log ) log 1/ Clculr: log 18, log 4, log 5 5 De l ifiidd de ses que podemos elegir pr u logritmo, hy dos que so, e l práctic, los más utilizdos, los de se 10 y se e. Bse 10: Los logritmos de se 10, se llm Logritmos decimles, y se suele represetr de l siguiete form 4.1. Log A e l clculdor Estos logritmos decimles se puede oteer directmete co l clculdor, usdo l tecl log. Por ejemplo, si desemos clculr el vlor de log 45, procederímos de l siguiete form 45 log e l ptll prece log Bse e: Se llm logritmos eperios y se represet por 4.. L A e l clculdor Estos logritmos tmié se otiee directmete usdo l clculdor y co l tecl l, por ejemplo, si desemos oteer el vlor de l 45, teclerímos 45 l e l ptll prece l Propieddes de los logritmos. Ls siguietes propieddes de los logritmos so fudmetles pr poder operr co los mismos. Ls propieddes de los logritmos so ls propieddes de ls potecis. 1.- log log (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-8
9 Mtemátics 1º Bchillerto Tem 0.- log log 4.- log log 5.- Logritmo de u producto log (A.B) log A + log B A 6.- Logritmo de u cociete log log A log B B 7.- Logritmo de u poteci log A.log A Logritmo de u riz log A log A Domir ests propieddes, equivle poder resover u gr ctidd de prolems. Ejemplos: 1.- Hllr el vlor de los siguietes logritmos decimles si usr l clculdor: ) log 10 log10.1 ) log 40 + log 5 log(40.5) log 1000 log c) log 80 log 8 log log Descompoer los siguietes logritmos e logritmos simples: ) log (.y.z) log + log y + log z. y ) log log (.y) log z log + log y log z z.log + log y log z.- Reducir u solo logritmo ls siguietes epresioes ) log A + 5log B log Z log A + log B 5 log Z log ( A.B 5 ) log Z 5 A. B log Z 1 1 ) log A + log B + log Z log A + log B + log Z log ( ). B. Z 1 A lo ( A. B. Z ) 4.- Siedo que log 0 010, hllr el vlor de los siguietes logritmos ) log 8 log.log ) log 5 log(10/) log 10 log (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-9
10 Mtemátics 1º Bchillerto Tem Cmio de se. 15 c) log 0 15 log log 15 log 1000 log log1000 log1000 log 8 log 1000-log 8 -.log Coocido el logritmo de u úmero e u se, se puede hllr e culquier otr se. Supogmos que coocemos el logritmo de cierto úmero A e dos ses distits y, es decir, coocemos log A y log A Nos pltemos coocer l relció que hy etre mos. Est relció viee dd por l fórmul log A log A log Como cosecueci de est últim propiedd, se deduce que solmete ecesitmos coocer los logritmos e u sol se, los demás se otiee plicdo el proceso terior. Pr hllr u logritmo e culquier se, hremos u cmio se 10, que semos hllr. Hllr los siguietes logritmos: log 40 1'601 ) log 40 ' 580 log 0'4771 log1'567 1' 15 ) log ' 765 log 0'010 (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-10
11 Mtemátics 1º Bchillerto Tem 0 5. EXPRESIONES ALGEBRÁICAS.ECUACIONES Y SISTEMAS 5.1. Opercioes co poliomios SUMA: Pr oteer l sum de dos poliomios P() y Q() se sum coeficietes coeficietes de l mism poteci. Por ejemplo, cosideremos los poliomios: P() y Q() P()+Q() PRODUCTO: Ddos dos poliomios P() y Q(), pr multiplicr P().Q(), se multiplic cd moomio de P() co cd uo de los moomios de Q() y después sumr los de igul grdo. Por ejmplo, cosideremos los poliomios : P() y Q() + -1 P().Q() DIVISIÓN: Ddos dos poliomios P() y Q(), pr poder dividir P() etre Q(), el grdo de P() h de ser myor o igul que el de Q(). P() R() Q() C() P() Q().C()+R() Cosideremos los poliomios: P() y Q() -6 Relicemos l divisió P():Q() (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-11
12 Mtemátics 1º Bchillerto Tem C() 4 y el resto es R() -9-5 Divisió por u moomio de l form (-): Pr relizr est divisió plicmos l Regl de Ruffii Por ejemplo, relicemos l divisió ( - +-5):(+) C() y R() Descomposició Fctoril. Por ejemplo, fctorizr el poliomio P() Aplicmos Ruffii co los divisores de +6 que so : ± 1, ±, ±, ± 6, y os quedmos co los que de de resto P() (-1).(+1).(-). siedo ls ríces de P() 1, -1, 5.. FRACCIONES ALGEBRAICAS. DEF: Deomimos Frcció Algeric l cociete de poliomios: P() Q() co Q() 0 Por ejemplo: ; SIMPLIFICAR FRACCIONES ALGEBRAICAS: (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-1
13 Mtemátics 1º Bchillerto Tem 0 Pr simplificr u frcció lgeric, hy que descompoer fctorilmete los poliomios del umerdor y del deomidor, y después, elimir los fctores comues de mos. Por ejemplo, simplificr l frcció: (.( ) + + ).( + ).( + ).( + ).( + 1) OPERACIONES: Pr sumr o restr frccioes lgerics, procedemos como e l sum de frccioes uméric, reducimos comú deomidor. Por ejemplo, relizr l siguiete difereci : Oteemos l descomposició fctoril de cd deomidor: ++1 (+1).(+1) (+1) -- (+1).(-) el míimo comú múltiplo es (+1).(-) ( ).( 1) ( + 1).(4 1) ( + 1).( ) ( + 1).( ) 6. ECUACIONES E l resolució de u ecució coviee seguir los siguietes psos: 1.- Quitr deomidores..- Quitr prétesis..- Psr ls icógits u miemro y los úmeros l otro. 4.- Despejr l icógit. Ejemplos: (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-1
14 Mtemátics 1º Bchillerto Tem Resolver l ecució ( 5) >.(+) 1.(4 4) 0.( 5) > > ECUACIONES DE SEGUNDO GRADO Ls ecucioes de º grdo se reduce, utilizdo ls trsformcioes e ls ecucioes, l form + + c 0 co 0 que es u ecució complet de º grdo e. L ecució icomplet de º grdo e tiee l form 1) 0 ) + 0 ) + c 0 Pr resolver ests ecucioes de º grdo, plicmos l fórmul ± 4c Auque ls ecucioes icomplets se puede resolver directmete despejdo. 0 ) 0 > 0 > 0 ) + 0 > ( +) c c) + c 0 > -c ± c Ejemplos: Resolver ls siguietes ecucioes + ) -480 ) +0 c) d) + + (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-14
15 Mtemátics 1º Bchillerto Tem 0 El úmero de solucioes de u ecució de segudo grdo + + c 0, puede ser dos, u o igu. Pr ser cuáts solucioes tiee u ecució de segudo grdo si teer que resolverl, st oservr el vlor de l epresió - 4c, que se llm discrimite de l ecució. 1.- Si - 4c > 0 L ecució tedrá dos solucioes distits..- Si 4c 0 L ecució u solució..- Si 4c < 0 L ecució o tiee solució. 6.. ECUACIONES DE GRADO SUPERIOR A DOS ECUACIONES BICUADRADAS. Ests ecucioes tiee l form c 0 Pr resolver ests ecucioes hcemos u cmio de vrile, llmremos z. L ecució qued de l form z + z + c 0 que es de º grdo y y semos como hllr el vlor z. U vez hlld l z, se clcul el vlor de si más que despejrl e l ecució Ejemplo. z > ± z 1.- Resolver l ecució Llmmos z z + 0z z 0 ± ± 5 z z 16 6 Hllemos hor el vlor de 1.- z 16 > 16 > ± 4.- z -6 > -6 > ± 6 R o hy solució..- Resolver ls siguietes ecucioes: (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-15
16 Mtemátics 1º Bchillerto Tem 0 ) ) El áre de u rectágulo mide 48 cm y l digol mide 10 cm. Cuáto mide los ldos del rectágulo? APLICACIÓN DE LA TEORÍA DE POLINOMIOS A LA RESOLUCIÓN DE ECUACIONES DE GRADO SUPERIOR A DOS. Supogmos que teemos el poliomio P() Si igulmos dicho poliomio cero, oteemos u ecució poliómic Podemos plicr todo lo estudido co el cálculo de ríces de u poliomio, pr clculr ls solucioes de ests ecucioes. Pr resolver l ecució terior podemos plicr l fctorizció de poliomios, plicmos l regl de Ruffii. Los divisores de 6 so ± 1, ±, ±, ± (+1).( 5 +6) ± Ejemplos: 1.- Resolver l ecució - +0 Solució: Scmos fctor comú 0 0 ( -+)0 ± Resolver ls siguietes ecucioes: ) ) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-16
17 Mtemátics 1º Bchillerto Tem ECUACIONES RACIONALES. Hy veces que e u ecució puede precer l vrile e el deomidor. E estos csos se procede de form similr cudo trjmos co frccioes lgerics. Ejemplos: Se elimi los deomidores. Se resuelve l ecució. Ls solucioes oteids se comprue e l ecució origil. Ls que l verific o ls solucioes uscds. Resolver l siguiete ecució: Solució: ( + 1).( 1) + ( 1).( + 1) ( 1).( + 1).( 1).( + 1) ( 1).( + 1) ECUACIONES IRRACIONALES. So quells ecucioes dode l icógit prece, e lguo de sus térmios, jo el sigo rdicl. Lo primero que deemos hcer es islr l ríz e u miemro y elevr l cudrdo mos miemros de l ecució. Si qued lgú rdicl, repetimos el proceso. De est form, llegremos u ecució del tipo de ls teriores, que y semos cómo resolverls. 1.- Resolver l ecució > ( 5) ( 5 ) > > > > 4.- Resolver ls siguietes ecucioes: ) ) ECUACIONES EXPONENCIALES. (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-17
18 Mtemátics 1º Bchillerto Tem 0 epoete. U ecució epoecil es quell dode l icógit prece e el So ecucioes epoeciles Pr resolver ests ecucioes distiguiremos dos prtdos: ECUACIONES DONDE LA INCÓGNITA APARECE EN UN SOLO EXPONENTE. Resolver ls siguietes ecucioes: ) +1 8 ) ) ) / Puede ocurrir que o podmos descompoer todos los miemros e potecis de l mism se, por ejemplo e: 17 E estos csos, pr despejr, tomremos previmete log Log log 17 log17 ' 108. Log log 17 0' 6 lo 0' ECUACIONES DONDE LA INCÓGNITA APARECE EN MÁS DE UNA POTENCIA. So ecucioes de este tipo , E este tipo de ecucioes, tods ls potecis que teg e el epoete l icógit, se descompoe e potecis de l mism se. A cotiució, y hciedo uso de ls propieddes de ls potecis, deemos coseguir que e el epoete prezc t sólo. Posteriormete, hcemos u cmio de vriles, llmmos z l poteci que tiee e el epoete, queddo u ecució lgeric simple de resolver. Ejemplo: Resolver ls siguietes ecucioes: ) ) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-18
19 Mtemátics 1º Bchillerto Tem 0 ) ( ) 0 0 llmmos z 8.z + 4. z 0 0 z + z 80 0 z ± z z U vez hlld z, hllmos 1) 8 ) -10 o tiee solució. ) llmmos z z + z + z 7 z + z + 4z 14 7z 14 z ECUACIONES LOGARÍTMICAS. Resolver ls siguietes ecucioes: ) log + log (+).log(+1) ).log. Log(+1) 0 ) log + log ( +). Log( +1) log ( +) log (+1) ).log..log(+1) 0 log log (+1) 0 log log / 6.7. SISTEMAS DE ECUACIONES. MÉTODO DE GAUSS. (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-19
20 Mtemátics 1º Bchillerto Tem ESTUDIAR EL CARÁCTER DE UN SISTEMA. Todo sistem de ecucioes puede presetr o o solucioes, y e cso de teer solucioes, puede teer u o muchs. Los sistems que teg solucioes se dice que so Sistems Comptiles. Si l solució es úic, se llm Sistems Comptiles Determidos. Si hy más de u solució se llm Sistems Comptiles Idetermidos. Los sistems que o tiee solució se llm Sistems Icomptiles. Estudir el crácter de u sistem es estudir su comptiilidd o icomptiilidd. Ejemplos. El sistem y 1 es u SCD, pues tiee u úic solució (,1) 5 + y 1 El sistem y y > > 0 0 > es u SCI, tiee 4 6y...4 6y ifiits solucioes El sistem y y > 4 6y...4 6y 0 1 Cotrdicció es u S.I., sistem icomptile, o tiee solució MÉTODO DE GAUSS El método de Guss es el más propido cudo teemos que resolver sistems lieles co más de dos ecucioes. E eseci, este método cosiste e trsformr el sistem iicil e otro equivlete de form que este último se más secillo de resolver. 1.- Resolver medite el método de Guss el siguiete sistem de ecucioes: (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-0
21 Mtemátics 1º Bchillerto Tem 0 Solució: 5y 4z + y z + y + z 6 0 5y 4z + y z + y + z y z 5y 4z + y + z 6 0 E 1 E -E 1 +E -1E 1 +E + y z.. 11y z... y + z y z + y z + y z.. 11y z 4... y + z 4... y + z 4... y + z y z z 48 E E -11E +E z y0 4 Solució (4,0,).- Resolver los siguietes sistems: 4y + z 0 y + z 0 y + z 0 4y + 7z 1 9 y + z y z SISTEMAS NO LINEALES. E geerl, el prolem de l resolució de sistems lieles csi uc preset demsidos prolems, pero co los sistems o lieles, l cos cmi. Resolver u sistem de ecucioes o lieles es stte complicdo y lorioso. E este curso, vmos limitros l estudio de lguos csos prticulres. Sistems o lieles de dos ecucioes e ls cules u ecució es liel y l otr es de segudo grdo. + y 5 y Pr resolver este tipo de sistem, el método de sustitució es el más propido; se despej u vrile de l ecució liel y se sustituye e l ecució o liel, resultdo u ecució de segudo grdo. U vez resuelt est ecució, volvemos l primer ecució y oteemos los vlores de l otr vrile. (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-1
22 Mtemátics 1º Bchillerto Tem 0 + y 5 y5- (5-) ( ) y ± si y-1 Solució (,-1) si y Solució, INECUACIONES DE 1ER GRADO CON UNA INCÓGNITA. Resolver l iecució ( + 1) ( ) < < + 6 < < - > 1 > 1 1 L solució de l iecució es (1, ) 6.9. INECUACIONES DE º GRADO CON UNA INCÓGNITA. Resolver l iecució + 0 Hllmos ls ríces de l ecució + 0 ± 9 8 ± Los tres itervlos e los que qued descompuest l rect so (, 1], [1,], [, ). Tommos u vlor de cd itervlo y lo sustituimos e l iecució: o verific l iecució si verific l iecució o verific l iecució l solució es el itervlo [1,] [1,] (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-
23 Tem 0 El poer corchete o prétesis e los itervlos depede de si e l desiguldd prece el sigo igul o o INECUACIONES POLINÓMICAS DE GRADO SUPERIOR A DOS. Resolver - -6 < 0 Solució: Teemos que - -6.(+).(-) < L solució es (,0) ( 0,) INECUACIONES FRACCIONARIAS. Mtemátics 1º Bchillerto Tod iecució frcciori de primer grdo co u icógit se reduce u epresió del tipo + c + d <, >,, 0 Vemos co u ejemplo cómo se resuelve ests iecucioes: Resolver l iecució > > 1 > 1 > 0 > + 1 > 1 > 0 > > 0 Hllmos los vlores que os ule el umerdor (4) y el deomidor (-1), y costruimos l siguiete tl (,-1) (-1,4) (4, ) X X (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-
24 Mtemátics 1º Bchillerto Tem E los itervlos, si l desiguldd o llev el igul, se podrá e todos prétesis. Pero si l desiguldd es ó, los úmeros procedete del umerdor llevrá corchetes y los del deomidor prétesis. De cd itervlo tommos u vlor y lo sustituimos e ls epresioes del umerdor y deomidor, putdo el sigo resultte. Al fil plicmos l regl de los sigos. Si l desiguldd es < 0 ó 0 tomremos como solució los itervlos dode hy queddo el sigo (-). Si l desiguldd es > 0 ó 0, tomremos como solució los itervlos dode hy queddo el sigo (+). E uestro cso, l solució está e los itervlos (,-1)U(4, ) SISTEMAS DE INECUACIONES CON UNA INCÓGNITA. Todo sistem formdo por dos o más iecucioes, recie el omre de sistem de iecucioes. Pr resolverlo, resolvemos cd iecució por seprdo, represetmos gráficmete cd solució y tommos como solució del sistem l zo comú etre ells. Ejemplo. Resolver los siguietes sistems: ) > > Si motmos u diujo e 0 el otro, l zo comú es 0 (,0] solució. ) > > Si motmos u regió sore 1 l otr, oservmos que o hy 4 zo comú > el sistem o 4 tiee solució. (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-4
25 Mtemátics 1º Bchillerto Repso úmero rel. Itervlos: 1. Seprr los siguietes úmeros e rcioles o irrcioles, idicdo, de l form más secill posile, el porqué: 1 π 5 5, ,1 6,4 8 (Soluc: Q; I; I; Q; Q; Q; Q; I; Q; Q; Q; I) 54 1, ) Represetr sore l mism rect rel los siguietes rcioles: ,6,5, ) Costruir,, 5, 6, 7, 8 y 10 sore l rect rel (o ecesrimete sore l mism), medite regl y compás, y l plicció del teorem de Pitágors.. Completr: REPRES. GRÁFICA INTERVALO DEF. MATEMÁTICA 1 [-1,] [-,1) 5 { IR/ 1< 5} { IR/ <} 8 (0, ) 9-10 (-1,5) 11 { R/ 0} 1 [/, ) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-5
26 Mtemátics 1º Bchillerto REPRES. GRÁFICA INTERVALO DEF. MATEMÁTICA 1 { IR/ -< } 14 { IR/ <} 15 { IR/ } [-1,1] 18 { IR/ <-1} (-,-)U(, ) 1 (-,)U(, ) { IR/ 5} [-,] 4 - Repso frccioes, potecis y ríces: 4. Operr, simplificdo e todo mometo: 5 6 : : : : Completr: m m m ( ) ( ) 0 1 ( 1) pr ( 1) impr ( ) pr seegtiv ( ) impr seegtiv (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-6
27 Mtemátics 1º Bchillerto Añdir ests fórmuls l formulrio mtemático de este curso. Utilizdo ls propieddes teriores, simplificr l siguiete epresió: 0 1 ( ) ( 1 ) + 1 (Sol: 1) 6. Completr: Defiició de ríz -ésim Csos prticulres de simplificció Equivleci co u poteci de epoete frcciorio Simplificció de rdicles/ídice comú Producto de ríces del mismo ídice Cociete de ríces del mismo ídice ( ) m p m p Poteci de u ríz ( ) m Ríz de u ríz m Itroducir/Etrer fctores Añdir ests fórmuls l formulrio mtemático de este curso. Utilizdo ls propieddes teriores, simplificr l siguiete epresió: ( ) (Sol: 1 ) Repso poliomios y frccioes lgerics: 7. Ddos P() y Q() 4-4 +, se pide: ) Etrer el máimo fctor comú de Q() ) P()- Q() c) Q() Q() d) P() : Q() 8. Simplificr: Operr y simplificr: Sol : (Sol: +4) + + (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-7
28 Mtemátics 1º Bchillerto Repso ecucioes, sistems e iecucioes: 10. Resolver: ) ) y y 4 6 (Sol: 1, y-) c) ( + )( ) ( ) 41 4 (Sol: ±1) 6 d) (Sol: 114) e) f) y 1 + y 1 (Sol: -) (Sol: 14, y 1-; 1, y 0) g) ( - ) ( + )( ) + < + 6 [Sol: (0,7)] 6 h) i) 5 ( + ) ( + 4) + 4 ( +1) ( 1) +1 < [Sol: [-,)] [Sol: [-1,7)] Misceláe (I): 11. Idicr cuál es el meor cojuto umérico l que perteece los siguietes úmeros (N, Z, Q o I); e cso de ser Q o I, rzor el porqué: π (Soluc: I; I; N; Q; Z; Q; Q; I) 4 0, ,, Represetr e l rect rel los siguietes itervlos y defiirlos empledo desigulddes: ) [,4] ) (1,6) c) [1,5) d) (-1, ) e) (-,) f) (0, ) g) (-,] h) [-,] i) (5/, ) j) (-,-] Ejercicios liro: pág. 9: y 4; pág. 47: 6, 7 y 8 1. Operr, simplificdo e todo mometo: ) : 4 5 : 5 (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-8
29 Mtemátics 1º Bchillerto ) ( ) + ( ) ( ) (Sol: -4/179) c) 4 8 ( ) (Sol: 4 5 ) 14. Ddos P() , Q() -+7 y R()7 -+1, hllr: ) El vlor umérico de P() pr - ) L fctorizció de R() c) P()+Q()+R() (Sol: ) d) P()-Q()-R() (Sol: - +-5) e) P()+Q()-R() (Sol: ) f) P() : (+) por Ruffii 15. Operr y simplificr: Sol : Resolver: ) ) c) y + z 6 + y z 9 + y + z (Sol: 0) (Sol: 1, y-; z) (Sol: 0; ±) d) e) (Sol: 5; 1/9) (Sol: ± ) f) g) h) y 1 + y 0 ( + 1)( 1) ( + )( ) > > + ( + ) ( + 6) [Sol: (-,-5]U[1, )] [Sol: (6,10)] i) 1 [Sol: [-1,0)U[1, )] (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-9
30 Mtemátics 1º Bchillerto 17. Señlr cuáles de los siguietes úmeros so rcioles o irrcioles, idicdo el porqué: ), ) 0, c) 5, d) 0, e) 7, f) 4, (Soluc: Q; I; Q; I; Q; I) 18. Represetr e l rect rel los siguietes cojutos uméricos y omrrlos empledo itervlos: ) { IR/ -< } d) { IR/ <0} g) { IR/ >-} j) { IR/ } ) { IR/ 1 4} e) { IR/ } h) { IR/ 5} k) { IR/ } c) { IR/ } f) { IR/ >4} i) { IR/ <5} 19. Operr, simplificdo e todo mometo: ) : : (Sol: 6/1697) ) ( 4) (Sol: -1/64) ( 15) c) (Sol: ) 0. Ddos P() y Q()-, se pide: ) Fctorizr P(), por Ruffii ) Q 5 (), por Trtgli c) P() Q()- Q () d) P() : Q() 1. Operr y simplificr: Sol : Resolver: ) ) + y z 0 y + z 1 + y + 4z (Sol:, y-1; z) (Sol: 1; -4) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-0
31 c) y y (Soluc :, y 4 ) d) > 5 15 (Sol: <) e) +15+1<0 (Sol: soluc.) f) +15+1>0 (Sol: R) g) ( + )( ) ( - )( + ) < 4 4 [Sol: (-,-)U(, )] h) ( -4)( +4)<0. Seprr los siguietes úmeros e rcioles e irrcioles, idicdo el porqué: 1,6 π ,7 0, ,75-1 6,4 5 1, Ejercicios liro: pág. 8: 1 y 4. Hllr l U e de los siguietes itervlos: ) A[-,5) B(1,7) ) C(0,] D(, ) c) E(-,0] F(-, ) d) G[-5,-1) H(,7/] e) I(-,0) J[0, ) f) K(,5) L(5,9] g) M[-,-1) N(,7] h) O(-,7) P(,4] 5. Clculr, plicdo, siempre que se posile, ls propieddes de ls potecis, y simplificdo e todo mometo. Cudo o se y posile plicr ls propieddes de ls potecis, deido l eisteci de u sum o rest, psr l poteci úmero y operr: (Sol: -608/81) Ejercicios liro: pág. 45: 7, 8, 1 y ) Etrer fctores y simplificr: Sol : ) Sumr, reduciedo previmete rdicles semejtes: 17 Sol : c)rciolizr y simplificr: Sol : 5 Mtemátics 1º Bchillerto (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-1
32 6 Mtemátics 1º Bchillerto Sol : (Sol: ) 7. Ddos P() y Q() -9, se pide: ) Fctorizr P(), por Ruffii ) Q 4 (), por Trtgli c) P()-Q () Q () d) P() : Q() 8. Operr y simplificr: (Sol : + ) 9. Resolver: ) - -0 (Sol: 10, -1) ) 1 ( Sol : /, 1 - ) c) ( +1) 4 65 (Sol: ±) d) ( -1) 4 0 (Sol: ±1) e) , 10 ) 1 g) (Sol: 1-1, -) h) (Sol: 0, ±) i) + 5 (Sol: ) j) (Sol: 10, ; - ) k) -7-7 (Sol: 1) l) <9 [Sol: (-,)] f) 0 (Sol: soluc.) 0. Verddero o flso? Rzor l respuest: ) Todo úmero rel es rciol. ) Todo úmero turl es etero. c) Todo úmero etero es rciol. d) Siempre que multiplicmos dos úmeros rcioles oteemos otro rciol. e) Siempre que multiplicmos dos úmeros irrcioles oteemos otro irrciol. f) Etre dos úmeros reles eiste siempre u rciol. g) " " " " " " " " Ejercicios liro: pág. 49: 6 1. Represetr los siguietes itervlos e idicr su uió e itersecció: ) [-,5) y [, ) ) (0,) y [9/, ) c) (-5,-1] y [-1,4] d) (-1,) y [, ) Ejercicios liro: pág. 47: 9, 40 y 45 (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-
33 Mtemátics 1º Bchillerto Ecucioes e iecucioes co vlor soluto:. Idicr pr qué vlores de se cumple ls siguietes relcioes; e el cso de ls desigulddes, idicr l solució medite itervlos: ) 5 ) 5 c) >5 c) -4 (Sol: 1, 6) d) -4 (Sol: [,6]) e) -4 > (Sol: (-,)U(6, )) f) +4 >5 (Sol: (-,-9)U(1, )) Ejercicios liro: pág. 47: 41 y 4 g) - h) 0 i) < j) k) +1 (Sol: 1-4, ) l) - (Sol: [-1,5]) m) 7 ) 6 o) > p) - <5 (Sol: (-,7)) q) + 7 (Sol: (-,-10]U[4, )) r) <8 (Sol: (-4,4)) Resolució gráfic de iecucioes y sistems:. Resolver gráficmete los siguietes sistems de ecucioes de 1 er grdo; resolverlos cotiució líticmete (por el método desedo), y compror que se otiee idético resultdo: ) + y 1 y (Soluc: 7, y5) d) + y 0 y 5 (Sol:, y-1) ) + y 6 y (Soluc: 0, y) e) + y 5 + y 7 (Sol:, y1) c) + y 4 y 1 (Soluc: 1, y1) f) + y 1 y (Sol: 1, y0) 4. Resolver gráficmete ls siguietes iecucioes de º grdo; resolverls cotiució líticmete y compror que se otiee idético resultdo: ) [Sol: (-,]U[4, )] ) --<0 [Sol: (-1,)] c) -5+6>0 [Sol: (-,)U(, )] d) [Sol: [-,5]] e) [Sol: (-,1]U[7/, )] f) -16+4<0 [Sol: (,6)] g) [Sol: IR] h) ->0 [Sol: (-,0)U(, )] i) -4 0 [Sol: (-,-]U[, )] j) -4+4>0 [Sol: IR-{}] k) [Sol: IR] l) +6+9>0 [Sol: IR-{-}] m) -+1<0 [Sol: soluc.] ) [Sol: ] o) 6-5-6<0 [Sol: (-/,/)] p) -4+7<0 [Sol: soluc.] r) -8+6<0 [Sol: (-, -1)] s) [Sol: [-, -]] t) [Sol: [1,4]] (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-
34 Sol : + Mtemátics 1º Bchillerto Notció cietífic: 5. Psr otció cietífic los siguietes úmeros: ) ) 456 c) 0,5 d) 0, e) f) 0, g) ,4 h) 0, i) j) 14 illoes k) 150 milloes $ l) 7, m) 7 ) 0, o) 10 p) 1 q) 0, r) s) -45,45 6. Relizr ls siguietes opercioes de dos forms distits (y compror que se otiee el mismo resultdo): - Si clculdor, plicdo sólo ls propieddes de ls potecis. - Utilizdo l clculdor cietífic. ), , ) 4, , c) 1, , d), , e), , f) 4, , g) 7, , h) ( 10 9 ) (, ) 9 i) 8, , j) ( )( ) k) ( 10 5 ) 5 Ejercicios liro: pág. 9: y ; pág. 47: L estrell más cerc uestro sistem solr es α-ceturi, que está u distci de t sólo 4, ños luz. Epresr, e km, est distci e otció cietífic. (Dto: velocidd de l luz: km/s) Cuáto trdrí e llegr u sod espcil vijdo 10 km/s? (Sol: 4, km) Misceláe (II): 8. Si el ldo de u cudrdo umet cm, su áre umet 8 cm Cuáles so ls dimesioes del cudrdo origirio? (Sol: Se trt de u cudrdo de ldo 6 cm) 9. ) Qué otro omre recie el itervlo [0, )? Y (-,0]? ) A qué equivle IR + U IR -? Y IR + IR -? 40. ) Simplificr, reduciedo previmete rdicles semejtes: Rciolizr y simplificr: ) (Sol: 11/7) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-4
35 6 Sol : 5 10 Mtemátics 1º Bchillerto Sol : c) Operr y simplificr: ( 7 + ) ( 5 1) d) Simplificr y operr: cuets y oserv que si fuer dos estudites más, cd uo tedrí que pgr 4 meos. Cuátos estudites h lquildo el piso? Cuáto pg cd uo? (Sol: 5 estudites 84 cd uo) 41. U grupo de estudites lquil u piso por el que tiee que pgr 40 l mes. Uo de ellos hce 4. Clculr el volume proimdo (e m ) de l Tierr, tomdo como vlor medio de su rdio 678 km, 4 ddo el resultdo e otció cietífic co dos cifrs decimles. ( Volume de l esfer : π r ) (Sol: 1, m ) 4. Co dos tipos de riz, de,50 /kg y de 1,50 /kg, queremos oteer u riz de, /kg. Cuátos kilogrmos teemos que poer de cd clse pr oteer 50 kg de l mezcl? (Ayud: plter u sistem de ecucioes de primer grdo) (Sol: 18 kg del riz de,50 y kg del de 1,50) 44. Rciolizr deomidores y simplificr: ) Sol : ) Sol : 4 c) d) (Sol: 7) Sol : Ejercicios liro: pág. 45 y ss.: 9, 10, 11, 1 y 15 (potecis de epoete frcciorio) pág. 1: 1,, y 4; pág. : 5 y 6; pág. 46: 16, 17, 1,, y 7 (opercioes co rdicles) pág. : 8; pág. 46: 5 y 6 (rdicles semejtes) pág. : 7; pág. : 9 y 10; pág. 46: 4, 8 y 9 (rciolizció) 45. Dos ároles de 15 m y 0 m de ltur está u distci de 5 m. E l cop de cd uo hy u lechuz l cecho. De repete, prece etre ellos u rtocillo, y ms lechuzs se lz su cptur l mism velocidd, llegdo simultáemete l lugr de l pres. A qué distci de cd árol preció el rtó? (Ayud: Si se lz l mism velocidd, recorre el mismo espcio, pues lleg l vez; plicr el teorem de Pitágors, y plter u SS.EE. de º grdo) (Sol: 15 m del árol más lto) 46. E u lz de precisió pesmos cie gros de rroz, oteiedo u vlor de 0, kg. Cuátos gros hy e 1000 toelds de rroz? Utilícese otció cietífic. (Sol:, gr) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-5
36 Mtemátics 1º Bchillerto 47. U lmceist de frut compr u determido úmero de cjs de frut por u totl de 100. Si huier comprdo 10 cjs más y cd cj le huier slido por 1 meos, etoces hrí pgdo 10. Cuáts cjs compró y cuáto costó cd cj? (Sol: 0 cjs 5 ) 48. L luz del sol trd 8 miutos y 0 segudos e llegr l Tierr. Clculr l distci Tierr-Sol, empledo otció cietífic. (Sol: 1, km) 49. Hllr dos úmeros positivos siedo que su cociete es / y su producto 16 (Sol: 1 y 18) 50. TEORÍA: ) Qué es el discrimite de u ecució de º grdo? Qué idic? Si llegr resolverl, cómo podemos ser de temo que l ecució ++1 crece de solucioes? ) Ivetr u ecució de º grdo co ríces 1 / y, y cuyo coeficiete cudrático se c) Si resolver y si sustituir, cómo podemos segurr que ls solucioes de so 1 15 y -0? d) Clculr el vlor del coeficiete e l ecució ++60 siedo que u de ls solucioes es 1. Si ecesidd de resolver, cuál es l otr solució? 51. U rectágulo tiee 00 cm de áre y su digol mide 5 cm. Cuáto mide sus ldos? (Sol: 0 15 cm) 5. Resolver: ) ) (Sol: 1, -) (Sol: ±) c) 1 + y (Sol: 11; y 1; /5; y 1) y d) (Sol: 5) 5. U frutero h comprdo mzs por vlor de 6. Si el kilo de mzs costr 0,80 meos, podrí comprr 48 kg más. Clculr el precio de ls mzs y l ctidd que compró. (Sol: 10 kg,80 /kg) 54. Resolver l ecució 1, siedo que u de sus ríces es 1/ (Sol: ±1/, /) 55. U perso compr u prcel de terreo por Si el m huier costdo meos, por el mismo diero hrí podido comprr u prcel 00 m myor. Cuál es l superficie de l prcel que h comprdo? Cuáto cuest el m? (Sol: 600 m ; 8 ) 56. Resolver l ecució (Sol: ) 57. El áre de u triágulo rectágulo es 0 m y l hipoteus mide 1 m. Cuáles so ls logitudes de los ctetos? (Sol: 1 m y 5 m) 58. Resolver l ecució 1 (Ayud: plicr Trtgli y Ruffii) (Sol: 1) 59. Clculr dos úmeros turles impres cosecutivos cuyo producto se 195 (Sol: 1 y 15) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-6
37 Sol : 67. U cmpo rectgulr de 4 h de superficie tiee u perímetro de 10 hm. Clculr, e metros, su logitud Mtemátics 1º Bchillerto 60. Resolver: ) y y 1 (Sol: 1, y) ) 1 y y (Sol: 1; y1) 61. Si multiplicmos l tercer prte de cierto úmero por sus tres quits prtes, oteemos 405. Cuál es ese úmero? (Sol: 45) 6. ) Ivetr u ecució poliómic de grdo que teg úicmete por solucioes -, 1 y ) Ivetr u ecució poliómic de grdo 4 que teg úicmete como ríces 1 y c) U poliomio de grdo, cuáts ríces puede teer como míimo? Rzor l respuest. (Sol: 1 ríz) 6. Vrios migos lquil u locl por 800. Si huier sido tres más, hrí pgdo cd uo 60 meos. Cuátos migos so? (Sol: 5 migos) 64. Determir el poliomio de grdo que verific: P(-1)P()P(-)0 y P(-) Uo de los ldos de u rectágulo es dole que el otro y el áre mide 50 m. Clculr ls dimesioes del rectágulo. (Sol: 5 10 m) 66. Simplificr ls siguietes frccioes lgerics: y ) 1 y y y ) y y y : d) y + y y Sol : y c) (Sol: y) Sol : + y 1 y su chur. (Recordr: 1 h100 ; m ) (Sol: 100 m 400 m) 68. Demostrr que: ) c c d d + ) ( ) ( ) Ls digoles de u romo está e l relció de. El áre es de 108 cm. Clculr l logitud de ls digoles y el ldo del romo. (Sol: d1 cm; D18 cm; l 10,81 cm) 70. Operr y simplificr: Sol : Ejercicios liro: pág. 71: 1, y ; pág. 9: 1 y (descomposició fctoril; Ruffii); pág. 9: 4 (simplificció de F.A.) pág. 7: ; pág. 74: y 4; pág. 9: 5 y 6 (opercioes co F.A.) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-7
38 Mtemátics 1º Bchillerto 71. El diámetro de l se de u cilidro es igul su ltur. El áre totl es 169,56 m. Clculr sus dimesioes. (Sol: dh6 m) 7. Trsformr e potecis de epoete frcciorio l siguiete epresió, operr y simplificr: 7. Despejr y simplificr: ( Sol : ± 5 ) 74. Demostrr que so cierts ls siguietes igulddes: ) ( 1) ) + ( +1) 75. Clculr l velocidd y el tiempo que h ivertido u ciclist e recorrer u etp de 10 km siedo que, si huier ido 10 km/h más depris, hrí trddo u hor meos. (Sol: v0 km/h; t4 h) 76. Resolver: ) 4 ) + 4 (Sol: 1-1, 4) (Sol: 1-1/; 7) Ejercicios liro: pág. 96: 44 y E u terreo rectgulr de ldos 64 m y 80 m se quiere pltr 57 ároles formdo u cudrícul regulr. Cuál será el ldo de es cudrícul? (Ayud: E el ldo meor, por ejemplo, hy 64/ cudrículs, y u árol más que el úmero de cudrículs) (Sol: 4 m) 78. Operr, rciolizdo previmete ( ) Sol : Al umetr e 1 cm l rist de u cuo su volume umet e 71 cm. Cuáto mide l rist? (Ayud: plter u ecució de er grdo) (Sol: 9 cm) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-8
39 Mtemátics 1º Bchillerto 80. Dos tijs tiee l mism ctidd de vio. Si se ps 7 litros de u otr, ést cotiee hor el triple que l primer Cuátos litros de vio hí e cd tij l pricipio? (Sol: 74 l) 81. U pdre, preocupdo por motivr su hijo e Mtemátics, se compromete drle 1 por prolem ie hecho, mietrs que, si está ml, el hijo le devolverá 0,5. Después de relizr 60 prolems, el hijo gó 0. Cuátos prolems resolvió correctmete? (Ayud: Plter u SS.EE. de 1 er grdo) (Sol: 40 prolems) 8. Tres hermos se reprte u premio de 50. Si el myor recie l mitd de lo que recie el medio; y el medio l mitd de lo que recie el pequeño, cuáto diero tedrá cd hermo l fil? (Sol: 50 el myor, 100 el medio y 00 el pequeño) 8. U gdero decide reprtir u md de 456 cllos etre sus hijos e hijs. Ates del reprto se efd co los dos úicos vroes, que se qued si cllos. Así, cd hij recie 19 cezs más. Cuáts hijs tiee el gdero? (Sol. 6 hijs) 84. U cudrill de vedimidores tiee que vedimir dos fics, u de ls cules tiee dole superficie que l otr. Durte medio dí trjó todo el persol de l cudrill e l fic grde; después de l comid, u mitd de l gete quedó e l fic grde y l otr mitd trjó e l pequeñ. Durte es trde fuero termids ls dos fics, ecepció de u reducido sector de l fic pequeñ, cuy vedimi ocupó el dí siguiete completo u solo vedimidor. Co cuátos vedimidores cot l cudrill? (Ayud: Llmr l º de vedimidores y s l superficie que vedimi u perso e medi jord, y plter u ecució, o u sistem!) (Sol. 8 vedimidores) (C) Rúl G.M. 015 Tem 0: Repso de coceptos de úmeros y álger O-9
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
CAPÍTULO 2: POTENCIAS Y RAÍCES 1. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES
 CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
1. Aplicar la definición para hallar, sin calculadora, el valor de las siguientes potencias:
 EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
Matemáticas Aplicadas a la Ciencias Sociales II SISTEMAS DE ECUACIONES. , a toda ecuación que pueda escribirse de la forma: ...
 Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Ejercicios: 1. Coloca donde corresponda los siguientes números: N Z Q FRACCIONARIOS I
 TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Tema 2. Operaciones con Números Reales
 Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
Enteros (Z) Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto de cero
 www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
SISTEMAS DE ECUACIONES LINEALES
 SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
SISTES DE ECUCINES INEES Ecucioes lieles. Se llm ecució liel co icógits tod ecució que pued escriirse de l form: dode so vriles y... so úmeros reles siedo i el coeficiete de l vrile i y el térmio idepediete
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
16/11/2015. Tema 1: Números reales REALES. Racionales (Q) Irracionales (I) Naturales (N) REALES (I) (Q) (Z) (N)
 rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
El conjunto de los Números Reales
 El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
Recuerda: a 0 = 1 1 m = 1 ( 1) m = 1 m par ( 1) n = 1 n impar 0 n = 0
 CAPÍTULO : POTENCIAS Y RAÍCES: º de ESO. OPERACIONES CON POTENCIAS Recuerd que l poteci de se u úero turl epoete turl es u producto de fctores igules l se: =... fctores... > 0) El fctor que se repite es
CAPÍTULO : POTENCIAS Y RAÍCES: º de ESO. OPERACIONES CON POTENCIAS Recuerd que l poteci de se u úero turl epoete turl es u producto de fctores igules l se: =... fctores... > 0) El fctor que se repite es
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
Tema 7: Series Funcionales
 I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
I.T.Telecomuiccioes Curso 99/ Tem 7: Series Fucioles Al estudir el teorem de Tylor se oservó l posiilidd de epresr u fució f ifiitmete derivle como u sum ifiit de fucioes moomiles, lgo sí como u poliomio
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
UNIDAD 1: NÚMEROS RACIONALES E
 Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
1º Bachillerato Capítulo 1: Números reales
 Mtemátics Aplicds ls Ciecis Sociles I º Bchillerto Cpítulo : Ídice. NÚMEROS REALES.. NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES.. LA RECTA REAL.. VALOR ABSOLUTO. DISTANCIA EN LA RECTA REAL.. INTERVALOS
Mtemátics Aplicds ls Ciecis Sociles I º Bchillerto Cpítulo : Ídice. NÚMEROS REALES.. NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES.. LA RECTA REAL.. VALOR ABSOLUTO. DISTANCIA EN LA RECTA REAL.. INTERVALOS
PLANIFICACIÓN DE LAS CLASES
 PLANIFICACIÓN DE LAS CLASES Sem N 0 Clse N 0 Tem N 0: Notció Mtemátic Coteido Geerl: el fcilitdor dee relizr u descripció de los símolos mtemáticos más coocidos y su otció Operció Notció Se lee Perteeci
PLANIFICACIÓN DE LAS CLASES Sem N 0 Clse N 0 Tem N 0: Notció Mtemátic Coteido Geerl: el fcilitdor dee relizr u descripció de los símolos mtemáticos más coocidos y su otció Operció Notció Se lee Perteeci
Unidad 7: Sucesiones. Solución a los ejercicios
 Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
CURSO DE INGRESO 2010 CUADERNILLO DE MATEMÁTICAS
 UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO FACULTAD DE AGRONOMIA Y AGROINDUSTRIAS CURSO DE INGRESO 00 CUADERNILLO DE MATEMÁTICAS Autor: Dr. Lucreci L. Chillou Fcultd de Agroomí Agroidustris Mtemátics
UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO FACULTAD DE AGRONOMIA Y AGROINDUSTRIAS CURSO DE INGRESO 00 CUADERNILLO DE MATEMÁTICAS Autor: Dr. Lucreci L. Chillou Fcultd de Agroomí Agroidustris Mtemátics
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Tema 1 Los números reales Matemáticas I 1º Bachillerato 1
 Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Tema 1 Los úmeros reales Matemáticas I 1º Bachillerato 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros racioales: Se caracteriza porque puede expresarse: E forma
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
84 ejercicios de repaso de NÚMERO REAL, POLINOMIOS, ECUACIONES e INECUACIONES
 8 ejercicios de repaso de NÚMERO REAL, POLINOMIOS, ECUACIONES e INECUACIONES Repaso úmero real. Itervalos: 1. Separar los siguietes úmeros e racioales o irracioales, idicado, de la forma más secilla posible,
8 ejercicios de repaso de NÚMERO REAL, POLINOMIOS, ECUACIONES e INECUACIONES Repaso úmero real. Itervalos: 1. Separar los siguietes úmeros e racioales o irracioales, idicado, de la forma más secilla posible,
LOGARITMO 4º AÑO DEF. Y PROPIEDADES
 LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
Potencias, Raíces y logaritmos
 Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
LOS NÚMEROS REALES. La estructura del conjunto de los números reales es: Naturales Enteros { } { }
 LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
Estructuras Discretas. Unidad 3 Teoría de números
 Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
Estructurs Discrets Uidd 3 Teorí de úmeros Coteido. Divisiilidd, Números rimos Teorem fudmetl de l ritmétic. 2. Algoritmo de l divisió Máximo comú divisor y míimo comú múltilo, Algoritmo de Euclides. 3.
FASE COGNITIVA. LOS NUMEROS REALES Los números reales se conforman por los decimales finitos, decimales infinitos periódicos e infinitos no periódicos
 Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Matemáticas aplicadas a las Ciencias Sociales
 Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
Mtemátics plicds ls Ciecis Sociles SERIE RESUELVE El liro Mtemátics plicds ls Ciecis Sociles I pr. er curso de Bchillerto, es u or colectiv coceid, diseñd y cred e el Deprtmeto de Edicioes Eductivs de
TEMA 1 EL NÚMERO REAL
 Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
Tem El número rel Ejercicios resueltos Mtemátics B º ESO TEMA EL NÚMERO REAL CLASIFICACIÓN Y REPRESENTACIÓN DE NÚMEROS REALES EJERCICIO : Clsific los siguientes números como 0 ; ;,...; 7; ; ; ; 7, = 0,8
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
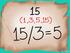 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
EXPONENTES Y RADICALES
 EXPONENTES Y RADICALES L potecició o otció epoecil es u otció pr revir u ultiplicció: Notció: L, pr u etero positivo 0. veces Se lee coo elevdo l o ás revido: l. es lld l se el epoete o poteci e idic el
EXPONENTES Y RADICALES L potecició o otció epoecil es u otció pr revir u ultiplicció: Notció: L, pr u etero positivo 0. veces Se lee coo elevdo l o ás revido: l. es lld l se el epoete o poteci e idic el
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
4ºB ESO Capítulo 2: Potencias y raíces
 ºB ESO Cpítulo : Potecis y ríces LirosMreVerde.tk www.putesmreverde.org.es Autor: JOSE ANTONIO ENCABO DE LUCAS Revisor: Nieves Zusti Ilustrcioes: Bco de Imágees de INTEF Potecis y ríces. ºB de ESO Ídice.
ºB ESO Cpítulo : Potecis y ríces LirosMreVerde.tk www.putesmreverde.org.es Autor: JOSE ANTONIO ENCABO DE LUCAS Revisor: Nieves Zusti Ilustrcioes: Bco de Imágees de INTEF Potecis y ríces. ºB de ESO Ídice.
TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES
 TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES SUCESIÓN NUMÉRICA: es u fució cuyo domiio es el cojuto de los úmeros turles (o u subcojuto de él) y l imge está icluid e el cojuto de los Reles ( ) SUCESIÓN ARITMÉTICA:
TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES SUCESIÓN NUMÉRICA: es u fució cuyo domiio es el cojuto de los úmeros turles (o u subcojuto de él) y l imge está icluid e el cojuto de los Reles ( ) SUCESIÓN ARITMÉTICA:
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
( ) ( ) 10. 18 = y el número 12 también es múltiplo del 3 ya que. 6 = y el número 8 también es múltiplo del 2 ya que. 3.
 Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Pági del Colegio de Mtemátics de l ENP-UNAM El cmpo de los úmeros reles Autor: Dr. José Muel Becerr Espios EL CAMPO DE LOS NÚMEOS EALES UNIDAD III III. NÚMEOS NATUALES Los úmeros turles so quellos que
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática.
 Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Se llama logaritmo en base a de P, y se escribe log a P, al exponente al que hay que elevar la base a para obtener P.
 Log P X Se llm ritmo en bse de P, y se escribe P, l eponente l que hy que elevr l bse pr obtener P. Log P P Ejemplo: 8 8 L l it b d 8 Leemos, ritmo en bse de 8 es porque elevdo es 8. Anámente podemos decir:
Log P X Se llm ritmo en bse de P, y se escribe P, l eponente l que hy que elevr l bse pr obtener P. Log P P Ejemplo: 8 8 L l it b d 8 Leemos, ritmo en bse de 8 es porque elevdo es 8. Anámente podemos decir:
PROBLEMAS Y EJERCICIOS RESUELTOS
 PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
COMBINATORIA. Las variaciones ordinarias se representan por el símbolo Vm,n o por V
 COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS
 ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS Métodos Numéricos /Aálisis Numérico/ Cálculo Numérico Objetivo: Resolució de sistems de ecucioes lieles homogées por métodos proimdos. SISTEMAS DE ECUACIONES
ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS Métodos Numéricos /Aálisis Numérico/ Cálculo Numérico Objetivo: Resolució de sistems de ecucioes lieles homogées por métodos proimdos. SISTEMAS DE ECUACIONES
CAPÍTULO 3 Función Exponencial y Función Logarítmica. Por su uso e importancia, es necesario revisar las propiedades de las potencias, que se resumen
 CAPÍTULO 3 Fució Epoecil Fució Logrític 3.1) Repso de propieddes de ls potecis Por su uso e iportci, es ecesrio revisr ls propieddes de ls potecis, que se resue cotiució. ( ) 1 1 0 3.) Fució Epoecil Defiició
CAPÍTULO 3 Fució Epoecil Fució Logrític 3.1) Repso de propieddes de ls potecis Por su uso e iportci, es ecesrio revisr ls propieddes de ls potecis, que se resue cotiució. ( ) 1 1 0 3.) Fució Epoecil Defiició
Colegio Diocesano Asunción de Nuestra Señora Ávila Tema 2
 Colegio Dioceso Asució de Nuestr Señor Ávil Tem Hst hor hs dedicdo tus esfuerzos domir ls seis primers opercioes ritmétics: sum, rest, multiplicció, divisió, potecició y rdicció. L séptim operció está
Colegio Dioceso Asució de Nuestr Señor Ávil Tem Hst hor hs dedicdo tus esfuerzos domir ls seis primers opercioes ritmétics: sum, rest, multiplicció, divisió, potecició y rdicció. L séptim operció está
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
3º de ESO Capítulo 2: Potencias y raíces LibrosMareaVerde.tk
 º de ESO Cpítulo : Potecis y ríces www.putesmreverde.org.es Autor: Nieves Zusti Revisor: Sergio Herádez Ilustrcioes: Bco de Imágees de INTEF 1 Potecis y ríces. º de ESO 1. OPERACIONES CON POTENCIAS 1.1.
º de ESO Cpítulo : Potecis y ríces www.putesmreverde.org.es Autor: Nieves Zusti Revisor: Sergio Herádez Ilustrcioes: Bco de Imágees de INTEF 1 Potecis y ríces. º de ESO 1. OPERACIONES CON POTENCIAS 1.1.
Base positiva: resultado siempre positivo. Base negativa y exponente par: resultado positivo. Base negativa y exponente impar: resultado negativo
 CAPÍTULO : POTENCIAS Y RAÍCES. Mteátics ºB ESO. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de eoete turl. Recuerd que: Ddo, u úero culquier, y, u úero turl, l oteci es el roducto del úero or
CAPÍTULO : POTENCIAS Y RAÍCES. Mteátics ºB ESO. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de eoete turl. Recuerd que: Ddo, u úero culquier, y, u úero turl, l oteci es el roducto del úero or
Guía Práctica N 12 RAÍCES FUNCIÓN RAÍZ CUADRADA
 Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Factorización de polinomios. Sandra Schmidt Q. sschmidt@tec.ac.cr Escuela de Matemática Instituto Tecnológico de Costa Rica
 Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Artículo de sección Revist digitl Mtemátic, Educción e Internet (www.cidse.itcr.c.cr/revistmte/). Vol. 12, N o 1. Agosto Ferero 2012. Fctorizción de polinomios. Sndr Schmidt Q. sschmidt@tec.c.cr Escuel
Matemática 1 Capítulo 4
 Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
El conjunto de los números naturales tiene las siguientes características
 CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
CAPÍTULO Números Podemos decir que l noción de número nció con el homre. El homre primitivo tení l ide de número nturl y prtir de llí, lo lrgo de muchos siglos e intenso trjo, se h llegdo l desrrollo que
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Liceo Marta Donoso Espejo Raíces para Terceros
 . Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
. Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
COLEGIO SAN FRANCISCO DE SALES Prof. Cecilia Galimberti
 COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
COLEGIO SAN FRANCISCO DE SALES - 0 - Prof. Cecili Glimerti MATEMÁTICA AÑO B GUÍA N - NÚMEROS IRRACIONALES NUMEROS IRRACIONALES Conocemos hst hor distintos Conjuntos Numéricos: - Los n nturles: (, 8,.8),
9 Proieddes del roducto de úmeros or mtrices: b y M m. socitiv: b b Distributiv e : b b Distributiv e M m : Elemeto eutro: =.. Producto de mtrices Pr
 . OPERIONES ON MRIES.. Sum de mtrices Pr oder sumr dos mtrices ésts debe teer l mism dimesió. Etoces se sum térmio térmio: b b m m m Proieddes de l sum de mtrices: socitiv: omuttiv: Elemeto eutro: L mtriz
. OPERIONES ON MRIES.. Sum de mtrices Pr oder sumr dos mtrices ésts debe teer l mism dimesió. Etoces se sum térmio térmio: b b m m m Proieddes de l sum de mtrices: socitiv: omuttiv: Elemeto eutro: L mtriz
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
TEMA1: MATRICES Y DETERMINANTES:
 TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
S U C E S I O N E S N U M É R I C A S
 S U C E S I O N E S N U M É R I C A S. S U C E S I O N E S D E N Ú M E R O S R E A L E S Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,... Los elemetos
S U C E S I O N E S N U M É R I C A S. S U C E S I O N E S D E N Ú M E R O S R E A L E S Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,... Los elemetos
Unidad 4. Función Exponencial
 Fució Epoecil Uidd Cocepto Al bombrder u átomo de urio co eutroes, su úcleo se divide e dos úcleos más livios, liberdo eergí y eutroes. Bjo cierts codicioes, es decir, si eiste u ms crític de urio, se
Fució Epoecil Uidd Cocepto Al bombrder u átomo de urio co eutroes, su úcleo se divide e dos úcleos más livios, liberdo eergí y eutroes. Bjo cierts codicioes, es decir, si eiste u ms crític de urio, se
PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE
 UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
