Objetivos de la Unidad:
|
|
|
- Nicolás Naranjo Flores
- hace 7 años
- Vistas:
Transcripción
1 MATEMÁTICA Uidd Utilicemos Rdicles Objetivos de l Uidd: Aplicrás co seguridd ls lees de los rdicles pr l resolució de problems relciodos co el etoro
2 Rdicció idetificció de Elemetos de u rdicl Regls de los rdicles uso de regls proceso de simplificció ( ) Epresió co rdicl. Epoetes frcciorios. covertir simplificr Operció co rdicles Sum rest operr co rdicles semejtes b Producto b Divisió m Rciolizció m Descripció del proecto Al fil de est uidd ivestigrás ls fórmuls de volúmees áres de lguos poliedros sólidos geométricos tles como: l esfer, el coo, l pirámide, el cilidro, etc. Mtemátic - Noveo Grdo
3 Quit Uidd Lecció Rdicció Algebric Motivció E est uidd estudirás de mer itereste todo lo reltivo este elemeto lgebrico su operció llmd Rdicció. Hgmos de cso que os iicimos e el tem cosider l siguiete situció: Se quiere costruir u trim rectgulr cu superficie teg 7 m de áre, cuo lrgo se tres veces su cho. Cuáles so ls dimesioes de l trim? Idicdores de logro: Idetificrás co seguridd tods ls prtes de u rdicl. Eplicrás etrerás co cofiz l ríz -ésim. Simplificrás co seguridd epresioes que coteg rdicles hciedo uso de sus propieddes. Comiez por lo más importte: defie : cho de l trim,, lrgo de l trim. E cosecueci u ecució lgebric pr el áre es: ( ) = A (Lrgo por cho igul áre); l cul, l reuirl co l iformció 7 m, te coduce : = 7. Y est epresió o es más que u ecució cudrátic icomplet; cu solució trbjste e l uidd. = 7, =, = 0 Fctorizs tiees: ( ) ( + )= 0 Por lo tto ls ríces de l ecució so: = = Como o puede hber trims que teg cho egtivo, te decides por l ríz pricipl = Co u cho de m u lrgo de m, obtiees 7 m de áre. Mu bie!, Hz resuelto el problem! Pero cuádo prece los rdicles? Aprece cudo e u ecució, u vrible rel está elevd u poteci (o epoete) se quiere coocer el vlor que tom es vrible. Noveo Grdo - Mtemátic 7
4 UNIDAD L ríz cudrd de u úmero E el problem que viees resolviedo tiees: ( )= = Qué úmero multiplicdo por si mismo es igul? Obvimete se te ocurre que =. Dirás que es l ríz cudrd del úmero. El símbolo, llmdo sigo de rdicl, se us pr deotr l ríz cudrd o egtiv (o ríz pricipl) de u úmero. Pr el cso = se lee ríz cudrd de es igul. Ejemplo Ecuetr l ríz cudrd pricipl de los siguietes úmeros: ) 8 c) 0. b) d) 9 Del ejemplo, puedes etrer los siguietes resultdos, mu importtes: L ríz cudrd pricipl de u úmero positivo es positiv. Los úmeros egtivos o tiee ríces cudrds e el sistem de los úmeros reles. De mer geerl puedes referirte l ríz cudrd de u úmero de l siguiete form: Cosider que b so dos úmeros reles positivos. Dices que l ríz cudrd pricipl del úmero, es igul b, si: = b sigific que = b Se emple pr l ríz cudrd. Deot l ríz cudrd egtiv. L pregut que debes hcerte es l siguiete: Qué úmero multiplicdo por si mismo (o elevdo l cudrdo) d por resultdo l cifr que está detro del sigo rdicl? ) 8= 9, que 9 = 8 b) =, que = = c) 0. = 0., que ( 0. )( 0. )=( 0. ) = 0. d) 9 o es u úmero rel, que o eiste u úmero rel que l ser elevdo l cudrdo se igul 9. 8 Mtemátic - Noveo Grdo
5 UNIDAD Ejemplo Ecuetr: ) b) 9 ) = 8 Ríz cudrd egtiv. b) = 9 7 ( ) = c) ( 8) d) ( 9) c) 8 8 Culquier úmero rel elevdo l cudrdo siempre es positivo. ( ) =( ) = d) L ríz cúbic de u úmero Cuáto mide l rist de u cubo cuo volume es uiddes cúbics? Volume =( b)( b)( b)= b b Si b =, etoces el úico vlor que puede tomr b es el, que ( )( )( )= b b Etoces, es l ríz cúbic de. E otció mtemátic escribes: =, que se lee ríz cúbic de es. E geerl, te refieres l ríz cúbic señldo: = b sigific que = b dode b so culesquier úmero rel. Ejemplo Ecuetr: ( ) ) 000 b) 8 c) d) ) 000 = 0 Y que 0 = 000 ; (ot que 000 = 0 ) b) 8 = Y que ( ) = 8 ; (Así 8 = ( ) ) c) = = = Y que: = ( ) =( ) = d) Del ejemplo puedes etrer el siguiete resultdo importte: Pr culquier úmero rel, siempre eiste u ríz cúbic, que es úic. Noveo Grdo - Mtemátic 9
6 UNIDAD Ríz -ésim de u úmero: Cosider u úmero etero, te refieres l ríz -ésim del úmero rel, señldo: = b Sigific que = b ( ) Si es pr, los úmeros b debe ser positivos 0, b 0. Si es impr, los úmeros b puede ser culquier úmero rel. Los elemetos de l epresió rdicl se idetific sí: A l operció de etrer l ríz de u úmero que est detro del sigo rdicl, se le llm rdicció. Ejemplo Ídice Ctidd subrdicl o rdicdo Sigo de rdicl = b Idetific los elemetos de ls siguietes epresioes rdicles: ) = b) = ) Ídice: b) Ídice: Rdicdo: Rdicdo: Ríz: Ríz: Es costumbre omitir el ídice e l ríz cudrd. Ríz -ésim Actividd ) 7 c) e) 0. ( ) g) 8 7 i) b) d) f) 8 h) 8 j) Mtemátic - Noveo Grdo
7 UNIDAD Regls de los rdicles H cierts regls o propieddes que te será útiles pr simplificr epresioes lgebrics que coteg rdicles. U primer regl, mu simple l puedes deducir si emis el literl d) de los ejemplos. E el ejemplo, hiciste lo siguiete: ( ) =( ) = E el ejemplo, hiciste: ( ) =( ) = Qué observs e comú e los dos ejemplos? Escribe quí tu observció: Ejemplo Ecuetr: ( ) ( ) ) 8 b) ( ) =( ) = ) 8 8 b) ( ) = ( ) = Puedes deducir l regl? Por supuesto que sí! L poteci -ésim de l ríz -ésim de u úmero, es igul. ( ) =, ( ) = Ejemplos: 80 ( ) = 80, 7 7 U segud regl es deducible de l mism defiició. Hemos señldo por ejemplo que: Si 000 = 0 etoces 000 = 0 Si 8= etoces 8= Si = etoces = ( ) Pero esto sigific que puedes epresr el rdicdo, e cd cso como u poteci, luego etrer l ríz; es decir: 000 = 0 = 0 8= = = ( ) = Regl Si, es u úmero rel ( el rdicl represet u úmero rel);, es u etero Se tiee: ( ) = Puedes señlr cómo es l regl? Noveo Grdo - Mtemátic
8 UNIDAD Regl Si, es u úmero rel ( el rdicl represet u úmero rel);, es u etero. Se tiee : = L ríz -ésim de l poteci -ésim de, es igul U cso especil se preset cudo se tiee u úmero rel egtivo elevdo u poteci pr. El resultdo de ( ) debe tomrse como ( o como ) que culquier úmero elevdo u poteci pr, debe ser positivo. Ejemplo Utiliz l regl pr comprobr que: ) 8( 7) = 8 7 b) Llevdo u comprobció de igulció: L ríz -ésim de u producto de úmeros, es igul l producto de ls ríces -ésims de tles úmeros. 8 7 = 8 7 ) 8( 7) = 8 7 b) Te ivito que e tu cudero desrrolles ( ) = l comprobció de ( ) = este literl. Sólo hz lo mismo que e ) = = Vs empler el ejemplo pr itroducir ls dos últims regls de est lecció. Regl = ( ) Si e so úmeros reles : Si e so úmeros reles Regl ( 0 ) : = L ríz -ésim de u cociete de úmeros es igul l ríz -ésim del umerdor etre l ríz -ésim del deomidor. Mtemátic - Noveo Grdo
9 UNIDAD Ejemplo 7 Simplific ls epresioes co rdicl. Supó que ls vribles e so positivs. 8 9 ) b) c) 8 Simplificr el rdicl sigific etrer tods ls ríces hst que el rdicdo sólo teg vribles co epoetes meores que el ídice del rdicl. = ( ) ( ) = ( ) 9 ) ( ) = = b) = = = ( ) = ( ) = c) 8 = 7 Le cceltiv = = Resume E est lecció hz predido etrer l ríz -ésim de epresioes co rdicles recoocer sus elemetos. Tmbié te hz fmilirizdo co cutro de ls priciples regls que se emple pr simplificr rdicles. ( ) = = ( ) = = Noveo Grdo - Mtemátic
10 UNIDAD Simplific ls epresioes co rdicles seleccio e cd cso l respuest correct: 8 8 ) 9 b) 9 c) d) 7 Autocomprobció El resultdo de. es igul : ) b) c) d) 0 ) b) 8 7 c) d) Seleccioe el eucido que NO es verddero: ) = b) ( ) = c) 8 = d) 9 = Solucioes. c.. d.... b. RAPIDEZ DE UN AUTO AL FRENAR L policí utiliz l rdicció cudo clcul l velocidd l que ib u vehículo cudo se le orde prr l coductor. E l fórmul S =. fd l letr d represet l distci e metros desde que plic el freo hst dode pró. L f es u coeficiete de fricció que es igul, cudo l crreter está sec 0. cudo está mojd. De tl mer que: si u uto derrp metros co f = A qué rpidez vei el uto e crreter sec? A qué rpidez vei si l crreter estb mojd? Utiliz f = Mtemátic - Noveo Grdo
11 Quit Uidd Lecció Idetificció de epresioes rdicles Motivció Qué so los epoetes rcioles? E l uidd estudiste l potecició co epoetes eteros te fmilirizste co lgus regls. Recuerds ésts? 0 = = = = Mu bie! Ls misms regls te sirviero pr deducir otrs regls: = 0 =, por lo tto tuviste que ceptr que: =, = Observ ( se puede escribi r ) E geerl = co, úmero etero. Pero Qué sucede si el epoete es u úmero rciol l epresió dopt l form? Verás que pr obteer u epresió equivlete debes hcer uso de rdicles. Idicdores de logro: Covertirás co iterés esmero epresioes co rdicles potecis co epoetes frcciorios vicevers. Recuerds l siguiete defiició de ríz cúbic? Si = b etoces = b, pero tmbié si = b etoces = b Vs emplerl e u ejemplo cocreto, verigudo qué es igul l epresió frcciori. Cosider que es igul u úmero rel b. = b, = b Elevs l cubo mbos ldos de l ecució. = b Lees de los epoetes. = b Pero etoces de cuerdo uestr defiició Si = b etoces = b Es decir que: =. Este es u ejemplo que relcio ls epresioes co epoete co ls epresioes co rdicl. L regl geerl qued sí: = Noveo Grdo - Mtemátic
12 UNIDAD Ejemplo Hciedo uso de l regl de epoetes rcioles, clcul: ) 9 d) 8 b) e) c) ) 9 = 9 = = b) = = = c) = = = d) 8 = = = = 8 8 e) : ot que este ejercicio se sle de uestr regl, que el umerdor de l frcció o es, sio que es. Si embrgo, si respets ls lees de los epoetes, puedes hcer lo siguiete: = = ( ) =( ) = Tmbié se lleg l mism respuest si hces: = = = ( ) = = L discusió de este literl te sirve pr orgizr l siguiete regl de los epoetes rcioles. m U epoete rciol de l form, dode m, so eteros co > 0, es equivlete l siguiete epresió co rdicl: m m =( ) Tmbié es equivlete: m Por ejemplo: = ; = m =( ) Mtemátic - Noveo Grdo
13 UNIDAD Ejemplo Coversió de u epresió rdicl poteci co epoete frcciorio Covierte ls epresioes co rdicl, epresioes co epoetes frcciorios simplific: ) 8 b) c) d) 9 ) 8 8 b) = ( ) e) f) = =( ) = Tmbié pudiste hberlo hecho sí: 8 = = c) = ( ) = ( ) = d) ( )= ( ) = ( ) = = e) = = = 8 8 ( ) f) = = = ( ) ( ) = 8 Actividd Covierte ls epresioes co rdicl, epresioes co epoetes frcciorios. Simplific si es posible. ) 9 = d) 7 = b) 7 = e) = ( ) c) ( ) = f) =, ( ) Segurmete e el ejercicio f) procediste sí: = ( ) =( ) =( ) = Tmbié pudiste hber hecho lo siguiete: = = = Puedes otr que ls lees de los epoetes so ls que más se emple. Si ls utilizs correctmete, puedes poco poco ir desrrolldo ejercicios más complejos. Noveo Grdo - Mtemátic 7
14 UNIDAD Ejemplo Supoiedo que ls vribles so positivs, simplific cd epresió. Epres l respuest de mer que sólo h epoetes positivos. ) b) ( ) ( ) ( ) c) d) ( ) + + ) = = ( ) ( ) b) 7 ( ) ( ) = =( )( )= 0 ( ) c) = = = = ( ) d) ( ) = = = 8 = Ejemplo Escribe los rdicles como epoetes rcioles simplific. ( ) b) ( )( ) c) ) b ( ) =( ) =( ) ( ) = ) b b b b b) ( )( )= = + = c) = ( ) = = = Itet resolver los siguietes ejercicios: 9 = b =( ) ( ) Actividd Trsld ls epresioes co rdicl su equivlete co epoete frcciorio simplific. ) ( )( ) d) b) c) ( ) ( ) e) Evlú el producto 0 Aboemos u poco más l compresió de uestr regl. Supote que e el ejercicio ) hubiers teido u epresió como: ( )( )( )=..., Hubiers procedido: = + + = = O bie: = = ( )( )( )( )= 8 Mtemátic - Noveo Grdo
15 UNIDAD Resumiedo tiees que: ( ) = ( ) = ( ) = Est secueci de resultdos justific u poco más l defiició de epresió co rdicles: l poteci de u rdicdo, co ídice rdicl, tiee como resultdo el rdicdo Epréslo quí: Mu bie! Ahor prcticrás co los epoetes rcioles e el setido cotrrio, es decir: covertir e rdicl, u epresió rciol. Coversió de potecis e epoetes frcciorios epresioes co rdicles Se trt de utilizr uestrs defiicioes: = = E csos como los siguietes: = = Reliz lguos ejercicios e este setido. Ejemplo m Epres e form de rdicl ls potecis frccioris simplific: ) c) b) ( ) d) z ) ( )( ) = = m + = = ( ) = = ( ) ( ) = = ( ) ( ) = ( ) ( ) = ( ) b) c) = = = d) = z z = = = z = z = z Puedes observr e ls respuests de los ejercicios resueltos, que los epoetes de ls vribles del rdicdo, so siempre meores que el ídice del rdicl. Por ejemplo l respuest del literl ) es ; es clro que es mor que. Cudo este se cumple es que puedes decir que l simplificció h termido. No puedes cosiderr que hs termido, si tiees por ejemplo ; tmbié si h u producto o cociete de rdicles que tiee el mismo ídice debe reuirse e u solo rdicl. Noveo Grdo - Mtemátic 9
16 UNIDAD Actividd Epres e form de rdicl ls potecis frccioris simplific. ) ( ) 8b d) b b) e) z c) z f) Ejemplo Clcul el vlor de ls epresioes: 0 ) + + pr = 8 b) 0 + b + b pr =, b =. ) = + + = + + = Sustitues = 8 8 = + ( )+ = + + = 9 b) 0 + b + b = + + b b = + + b Sustitues = b = b = + + = + + = 7 70 Mtemátic - Noveo Grdo
17 UNIDAD E est lecció hs cotiudo eriqueciedo tus coocimietos sobre los rdicles. Auque quizás lo más importte que hs obteido h sido l etesió de l potecició co epoetes frcciorios su equivlete como epresió co rdicl. Ahor sbes que 9 o puede ser otr cos más que 9 cos más que 9. ; su vez 9 De igul form cooces hor que es igul vicevers. Not que de cuerdo esto se puede dr otrs equivlecis, por ejemplo: o puede ser otr = =, que es coforme co ls lees usules de los epoetes, que: =( ) = E muchs simplificcioes de epresioes lgebrics, result mu útil el empleo de ests equivlecis. A veces u epresió co epoetes frcciorios, se desrroll mejor si l pss su equivlete co rdicles, e otrs l epresió co rdicl se trbj mejor si l pss epresió rciol. Observ los siguietes ejemplos: ( ) = ( ) = ( ) = ( ) = = = = =( ) = = 8 Ls regls más importtes de est lecció: Resume = ; m =( ) m Noveo Grdo - Mtemátic 7
18 UNIDAD Al simplificr l epresió obtiees: ) b) ( ) c) d) Autocomprobció Señl cuál de ls igulddes es icorrect: ) 9 = 7 c) 9 b) 7 ( )= d) = 8 = Al simplificr, obtiees: ) b) c) d) Al sustituir = 8 e l ecució + + obtiees: ) 0 b) c) d) 0 0 Solucioes... b.. d.. c. RADICALES EN LA GEOMETRIA U plicció de los rdicles e l geometrí, cosiste e ecotrr uo de los ldos de u triágulo, sí: Si se cooce el ldo de u triágulo equilátero su ltur h se clcul medite h = E efecto utilizdo el teorem de Pitágors se tiee: h + =, h = h =, luego h = = U ejemplo es el Triágulo de ls Bermuds. 7 Mtemátic - Noveo Grdo
19 Quit Uidd Lecció Opercioes co rdicles Motivció Se puede sumr restr los rdicles? Ivestiguemos si puede hcerse. Supote que por lgu suerte de sortilegio l ríz cúbic de es igul u sdí = sdí. Obvimete esto te oblig ceptr que si tiees, etoces eres el orgulloso dueño de sdís. Por lo tto u operció tl como =, es u operció correct. De igul mer + = Idicdores de logro: Idetificrás, reducirás efecturás opercioes co rdicles semejtes co seguridd. Etrerás co seguridd fctores de u rdicl. Rdicles semejtes E l situció terior observste que si es posible operr co sdís; es decir co ; pero, se podrá relizr ls siguietes opercioes? ) + 7 =... b) =... c) 0 =... Verás que sólo u es posible. E el literl ), 7 so úmeros primos mu diferetes, por lo tto 7 o puede ser u sdí. No se puede sumr e el literl b); el álisis es más fácil l ríz cudrd de, o puede ser igul l ríz cúbic de. No se puede restr. De cuerdo lo que se h dicho, es el literl c) el que se puede operr, observ: 0 = 8 = 8 = = 0 Puedes decir que 0 es u térmio que tiee u rdicl semejte co L siguiete defiició es l que utilizrás pr idetificr rdicles semejtes.. Los rdicles so semejtes si tiee igules sus ídices tmbié igules sus ctiddes subrdicles. Noveo Grdo - Mtemátic 7
20 UNIDAD Ejemplo So semejtes los rdicles: ) 8 7 b) 8 8 Si los rdicles tiee el mismo ídice lo que debes hcer es trbjr co l ctidd subrdicl. U mecismo cosiste e descompoer los rdicdos e sus fctores primos. ) = 8 9 So semejtes. 8 b) 8 = ( ) = 8 8 So semejtes. Etoces, cuádo es que se puede sumr restr rdicles? Cudo los térmios que vs sumr o restr tiee rdicles semejtes. Por supuesto que, l morí de ls veces tiees que utilizr ls regls de rdicles pr simplificr totlmete el rdicl ddo, hst que se coviert e u térmio co u rdicl semejte l térmio que quieres operr del rdicdo. L descomposició e fctores primos, debe ser el primer pso. Por ejemplo: = = = = Ejemplo Efectú ls siguietes opercioes, si es posible. ) b) 7 8 c) + 9 ) Como trbjste los rdicles 8 7 e el ejemplo, tiees que 8 = 7 =. Como so rdicles semejtes puedes sumrlos sí: = + = ( + ) = 9 ( )( ) = ( ) = 7 Mtemátic - Noveo Grdo
21 UNIDAD b) De l mism form: 7 8 = 8 = ( 8) = c) Primero tiees que utilizr ls regls de rdicles pr ver si éstos so semejtes. = = que l = Actividd Sum, rest simplific ls siguietes epresioes. ) 9 + d) = = utilizste l propiedd = ; demás que = Luego los rdicles so semejtes puedes sumrlos ( ) + 9 = + = + Ejemplo Sum, rest simplific ls siguietes epresioes co rdicles. ) c) b) 8 + e) 8c d 7c d c) + 00 f) 8 + b) d) + + ) = ( + ) 7 = 7 b) Ecuetrs todos los fctores de los rdicdos: ( ) + ( ) ( ) = = 0 c) = = = ( ) = d) + + = + + = + + = ( + )+ = ( + ) + ( ) = ( ) Noveo Grdo - Mtemátic 7
22 UNIDAD Actividd Reliz ls sums del térmio de fil co el térmio de colum complet l tbl. Sólo lle los recudros de quellos resultdos que proviee de rdicles semejtes. E los dos primeros cudros de l segud colum tiees u ejemplo: + 8 = + ( ) = + = + 8 : Blco. No h rdicles semejtes El siguiete ejercicio tiee u poco de dificultd pero te servirá pr observr como se puede combir los coocimietos dquiridos trsceder e el mejo del álgebr. Digmos que se trt del uso de los rdicles semejtes e l solució de u ecució, que termi siedo cudrátic. Ejemplo Resuelve l ecució: = 0 = 0 ( ) = 0 Regl de epoetes frcciorios. ( ) = 0 Equivleci de epoete frcciorio co rdicl. Ahor le podremos u podo. Covegmos que = Sustituedo e l ecució tiees: = 0, que se h covertido e u ecució cudrátic. El cmio que sigue lo cooces: ( ) + ( )= 0 = ; = so ls solucioes. 7 Mtemátic - Noveo Grdo
23 UNIDAD Pero recuerd que =. Por lo tto: = = = = = ( ) = L solució pr es de l ecució origil es S = {, } Es mu recomedble dquirir como costumbre, que siempre que resuelvs u ecució debes comprobr si el cojuto solució que hs ecotrdo stisfce l ecució dd. E el presete cso: Si teemos: ( ) =( ) = ( ) Si = ( ) = ( ) ( ) = + = 0 = 0 = 0 Observ que e efecto los dos vlores stisfce l ecució. E l opertori de rdicles tú puedes tmbié echr mo de otros coocimietos que tiees, por ejemplo, l le distributiv de los úmeros: b + c = ( b + c ) Ejemplo Ecuetr l respuest de l siguiete epresió co rdicles ( + )+ ( + )+ = ( + )+ Le del producto de rdicles = ( + )+ Ríz de u poteci = ( + )+ Aplics Fctor Comú = + + Reduces térmios semejtes = 7 + = [ 7 + ] Noveo Grdo - Mtemátic 77
24 UNIDAD Etrcció de fctores de u rdicl De hecho est operció l hs veido hciedo, l relizr ls simplificcioes e los ejercicios. Te hs mprdo e l defiició =, que e plbrs puedes trducir: E l rdicció, si el ídice del rdicl es igul l epoete que está elevd u ctidd o vrible e el rdicdo, etoces es ctidd o vrible sle del rdicdo. 7 ( ) = 7 = 7 ; = ; = ; 7 Hs visto que tmbié es válid si vrios fctores tiee potecis igules l ídice, es decir: π = π Lo que os rest pr hcer más práctico el proceso de simplificció es que, si los fctores tiee epoetes m que so múltiplos del ídice, etoces el fctor sle del rdicl co epoete m Esto es: Ejemplo Simplific ) π = π = π c) 8 b) 00 7 d) 9 b 0 ) 0 = = = 7 b) 00 = ( ) ( ) = ( ) = 0 c) 8 8 = ( ) = d) 9 b = b = b = = = b = b 78 Mtemátic - Noveo Grdo
25 UNIDAD Simplific hst que el epoete del fctor se meor que el ídice del rdicl. Actividd ) 7 b = d) = b) 0 7 = e) 7c d c 8 d = c) b b = f) 7 7 = E est lecció hs predido idetificr rdicles semejtes utilizr tus coocimietos pr reducir o simplificr epresioes co rdicles. Tmbié hs dquirido mejores herrmiets pr etrer fctores de u rdicl. H lgus coss importtes remrcr: Los fctores detro del rdicl debes descompoerlos e fctores co epoetes que se múltiplos del ídice del rdicl. De es mer podrás etrerlos del rdicl. Detro del rdicl o debe quedr fctores co epoete mor que el ídice del rdicl. Simplific el rdicdo tes del proceso de etrcció de fctores: = = = = = = = = Debes recordr que pr logrr mor cofiz seguridd e tus procedimietos de solució tiees, ecesrimete, que prcticr relizr suficietes ejercicios. Resume Noveo Grdo - Mtemátic 79
26 UNIDAD Autocomprobció 7 Al simplificr obtiees: ) c) Seleccio l iguldd que o se cumple: ( ) = ) b) d) b) ( b ) = b c) 8 = d) = es igul : ) b) c) d) El resultdo de simplificr b 8b es: ) b b) b b c) b d) b b Solucioes. b.... d.. b. DISTANCIA AL HORIZONTE L curvtur de l Tierr limit l distci que se puede ver desde u edificio. U fórmul que clcul l distci máim es d = rh + h dode h: es l ltur del edificio r es el rdio de l Tierr. (r = 7 km) Si tto d, r h se mide e km, qué distci máim se observrí desde l zote de u edificio de 00 m? d = ( 7)( 0. )+( 0. ) = 798. km Cuál es l distci máim que se puede observr desde l zote de u edificio de 00 m? Verific d =.7 km. 80 Mtemátic - Noveo Grdo
27 Quit Uidd Lecció Fctores de los rdicles Motivció Cómo se itroduce fctores detro de u rdicl? U úmero rel, se ecotrb de pseo por u crreter cudo de proto se topó co u túel, dode hbí u eorme ríz quit. Si o te coviertes e u poteci cico, o te dejo psr le dijo l ríz quit. El úmero rel vio que l cos ib e serio, sí que o tuvo más remedio que hcer: ( )( )( )( )( )= etrr l rdicl, ivocr l le de etrccioes de fctores de u rdicl slir como si d del otro ldo del túel. Idicdores de logro: Itroducirás fctores bjo el sigo del rdicl, co cofiz. Trsformrás co seguridd los rdicles empledo cmbio de ídices. Rciolizrás co orde epresioes rdicles. Itroducció de fctores e u rdicl L operció cotrri de etrer fctores es itroducir fctores. De cuerdo l lecció terior, pr etrer los fctores de l epresió 8 procedís sí: 8 = = = Si hor deses hcer l operció cotrri, es decir regresr los fctores detro del rdicl, (l se h queddo mu sol) bstrí co elevr cd fctor l poteci. Noveo Grdo - Mtemátic 8
28 UNIDAD Ejemplo Itroduce los fctores e el rdicl simplific el rdicdo. ) b b) c) d) ) b = ( ) b = ( ) b = b ( ) = ( ) = b) = 7 c) = ( ) = ( ) = d) = = = 8 E geerl puedes justificr este procedimieto empledo ls regls coocids: b = b = b Defiició ríz, de u poteci Regl del producto Actividd Itroduce los fctores e el rdicl simplific el rdicdo. ) = c) + = b) b c c = d) = Cmbio de ídice e u rdicl De cuerdo ls lees cceltivs de los úmeros reles, sbes que: = = = =... 9 Luego si, es u úmero rel, teemos que: 9 = = = =... Y hor, de cuerdo ls lees de los epoetes frcciorios su equivlete e form de rdicl se tiee que: 9 = = = =... 8 Mtemátic - Noveo Grdo
29 UNIDAD Hs epresdo u rdicl de ídice, e rdicl de ídice, ídice 9, ídice, etc. Es mu importte dvertir que, 9,,, so múltiplos de. Sólo puedes umetr el ídice del rdicl e múltiplos del ídice del rdicl ddo. No se puede umetr, que o es múltiplo de. Los siguietes so umetos válidos: = = 8 = =... 0 b b 0 = = b = b =... Crees que puedes deducir u regl? Por ejemplo: Puedes epresr e rdicl ídice? Mu bie! Sé que lo hs hecho! Itetdo ser prácticos puedes proceder tmbié sí: = ( ) = Puedes escribir u regl hor? Not lo siguiete: = = ( ) = Se puede regresr l epresió iicil. Ejemplo Icremet el ídice del rdicl ddo, l ídice señldo. Simplific el rdicdo. ) ídice 8 b) ídice c) b ídice 8 ) Pr umetr ídice 8, debes multiplicr el ídice por = = ( ) = ( ) = b) 8 8 = ( ) = ( ) = = c) b = ( b ) = ( b ) = 8 b Noveo Grdo - Mtemátic 8
30 UNIDAD Actividd Icremet el ídice del rdicl ddo, l ídice señldo. Simplific el rdicdo. ) b ríz de : c) z ríz de 9: b) b ríz de 0: d) b z ríz de 7: Reducir el ídice de u rdicl Se trt de relizr, si es posible, l operció cotrri. Por ejemplo, ddo u rdicl e ídice epréslo como rdicl ídice. Lo que es importte señlr hor, es que el ídice l cul se quiere reducir el rdicl debe ser submúltiplo del ídice del rdicl iicil. U ídice se puede reducir ídice,,. El proceso es ectmete l revés. Si quieres reducir 8 ídice, procedes sí: Ejemplo 8 = 8 = 8 = ( ) = Reducir el ídice del rdicl ddo, l ídice meor posible. Simplific el rdicdo. ) 9 b b) 8 8 b 8 c) b c ) Los múltiplos de so el el. Al observr el rdicdo puedes dvertir que se puede etrer fctores si el rdicdo se ecotrr detro de. Por lo tto puedes hcer: 9 b = b = b 9 b) b = b = b c) 8 b c b c = = b c = bc Hs visto que puedes icremetr reducir el ídice de u rdicl. L regl geerl que puedes precisr que e l práctic hs veido utilizdo l puedes deducir sí: De los ejemplos prticulres de l form: = m m m m Puedes estblecer: = ; m, eteros 8 Mtemátic - Noveo Grdo
31 UNIDAD Reduce el ídice del rdicl ddo, l ídice meor posible. Simplific el rdicdo. Actividd ) = d) 7 = b) 8 = e) = c) 9 b = Rciolizció de rdicles A meudo el deomidor de u frcció cotiee u rdicl. Por ejemplo: Rciolizr el deomidor de u frcció sigific de mer simple, hcer desprecer el rdicl del deomidor. E el cso de, h que hcer desprecer del deomidor. L clve pr hcer está e multiplicr por u coveiete úmero ( Por ejemplo = ), ( ) = +, + = Pr el cso de, l rciolizció se cosigue hciedo = = ( ) Noveo Grdo - Mtemátic 8
32 UNIDAD Ejemplo Rcioliz el deomidor de l epresió simplific ) b) c) d) e) ) = = = ( ) ( ) ( ) b) = ( ) = = = = ( ) c) H u form lter más rápid de resolver este ejercicio. Not que sólo flt u e el rdicdo pr completr que l puede slir del rdicl. d) = = = = = = = e) Este ejercicio es u poco diferete los demás. Se debe multiplicr por pr que el rdicl pued desprecer. + = ( + ) ( ) = El producto e el deomidor es: ( + ) ( )= + =( ) = Revisemos u poco más uestros procedimietos de rciolizció Si el deomidor tiee Debemos multiplicr rrib bjo por ( ) Pr obteer e el deomidor b + b b + b b b + 8 Mtemátic - Noveo Grdo
33 UNIDAD Actividd Rcioliz el deomidor de l epresió simplific: ) = c) = e) = b) 0 = d) = f) 7 = Resume E est lecció hs predido itroducir fctores detro del sigo rdicl, idetificádol como l operció ivers de etrcció de fctores. Si el fctor itroducir es Y el rdicl es El rdicdo qued sí: ( ) = b b = 0 b Hs revisdo tmbié vridos ejemplos desrrolldo ejercicios relciodos co umetr o bie reducir el ídice de u rdicl. Debes recordr quí que solo puedes umetr el ídice e múltiplos del ídice del rdicl ddo. = = Y e el proceso cotrrio solo puedes reducir u ídice e sub-múltiplos del ídice ddo. = = 9 = Filmete hs desrrolldo, co seguridd cofiz, vrios ejercicios de rciolizció del deomidor de u frcció. Noveo Grdo - Mtemátic 87
34 UNIDAD Al rciolizr el deomidor de obtiees: ) c) b) d) 9 Autocomprobció Al reducir el ídice del rdicl l meor ídice posible simplificr l epresió 9 obtiees: ) c) b) d) Al itroducir detro del rdicl los fctores de l epresió obtiees: ) c) b) d) Al icremetr el ídice de ) tiees: 7 7 c) b) d) Solucioes. c.. b.... d. RADICALES EN EL CALCULO DE VOLUMEN Alguos tques subterráeos e ls gsoliers tiee l form de u cilidro circulr recto está colocdos horizotlmete co l superficie. El volume V de gsoli e el tque está clculdo medite l fórmul 9 V = 0h, dode h es l ltur de l h gsoli e pulgds. Si l itroducir u vrill de profudidd e el tque l ltur es h = 8 pulgds Cuát gsoli h e el tque? 88 Mtemátic - Noveo Grdo
35 Quit Uidd Lecció Opercioes co rdicles Motivció A Mrcelo le h dejdo l tre de sumr los rdicles siguietes: ; ; 7 ; 8 9 Él solo recuerd que h que simplificr los rdicles. Puedes tú udrle Mrcelo sumr estos rdicles? Idicdores de logro: Efecturás sums rests de rdicles co seguridd Efecturás multipliccioes divisioes de rdicles co destrez seguridd. Resolverás problems utilizdo rdicles sus opercioes co orde esmero. Co u clculdor de bolsillo tu puedes hcer +,.,, obteer u respuest rápid., Si embrgo, si o dispoes de clculdor o el profesor o te lo permite e est etp de tu estudio, debes coocer como proceder pr relizr culquier operció co rdicles. Es lo que vmos revisr e est últim lecció. Sum rest de rdicles E l lecció de est uidd tú trbjste co rdicles semejtes. Si recuerds: dos rdicles so semejtes si tiee igul ídice e igul ctidd sub-rdicl o rdicdo So rdicles semejtes los siguietes? Respode flso (f) o verddero (v) ) 8 d) b) 7 e) 8 8 c) 8 f) Noveo Grdo - Mtemátic 89
36 UNIDAD Pr relizr sums rests co los rdicles solo debemos lizr ls situcioes. Los ídices los rdicdos so ectmete igules 8 se puede sumr restr directmete. Sum : + ( 8 ) = ( 8) = Rest : + ( 8 ) = + 8 ( ) = + 8 = 0 Los ídices so igules pero los rdicdo o lo so, uque posiblemete lo se si se simplific. se puede sumr restr pero debemos simplificr. = Sum: + ( )= = ( ) = Rest: ( )= ( + ) = 7 Puede suceder que l simplificció del rdicdo o coduzc u rdicl semejte. E ese cso o se puede relizr l operció. + = + = + o so semejtes. Ejemplo Sum, rest simplific ls siguietes epresioes. ) 0 + c) ( 0) b) 9 + d) 8 + ) 0 + = 0. + ( 0)( ) ( 0 + ) 8 b) 9 + = + =( )( ) + ( ) = = ( 9 + 0) c) =... = = ( ). ( ) d) 8 + = + = = ( ) 90 Mtemátic - Noveo Grdo
37 UNIDAD Efectú simplific ls siguietes epresioes Actividd ) + d) 8 0 ( 0) b) 7 e) c) Producto de rdicles El procedimieto e l multiplicció de rdicles puede ser mucho más fácil que e ls sums rests que o se ecesite que los rdicles se semejtes. Vmos cosiderr el siguiete esquem pr desrrollr uestro tem. Los ídices de los rdicles so igules so igules. E este cso o h problem pues bst que utilicemos uestr regl de l ríz e-ésim de u producto. ( )( ) = ( )( ) = Es mu fácil, o es cierto? = Los ídices de los rdicles o so igules, quí si h u pequeño problem, pero teemos dos cmios que podemos seguir. El primero cosiste e icremetr los rdicles su míimo comú múltiplo. Por ejemplo si desemos hcer el producto debemos epresr los dos ( )( ) rdicles como, el míimo comú múltiplo de es, esto lo hicimos e l lecció. Y hor podemos hcer el producto cudo se tiee ríces igules. ( )( )=( )( )= El otro cmio cosiste e hcer uso de los epoetes rcioles su form equivlete como rdicl: = m Retomdo uestro producto de rrib hcemos. ( )( )=( ) ( ) = m los deomidores de los epoetes frcciorios debe ser igules (míimo comú múltiplo de es ) = =( ) ( ) =( ) = X Puedes otr que hemos llegdo l mismo resultdo. Co u poco de práctic tú podrás utilizr culquier de los dos recursos pr efretr los productos. = = = = Noveo Grdo - Mtemátic 9
38 UNIDAD Ejemplo Multiplicr los rdicles simplificr. ( )( ) d) ( ) e) ( )( 9) ) b) c) f) ) ( )( )= = ( ) = = ( ) = =( )( )= ( ) b) =( )( )= = = c) d) ( )= ( )( )= = = = = = = e) f) = ( ) ( ) = = = Actividd Multiplic los rdicles simplific. ) ( 8) ( )= d) ( )( )= ( )( )= b) 0 = e) c) ( )( )= f) + ( ) = 9 Mtemátic - Noveo Grdo
39 UNIDAD Ejemplo Clcul el vlor de ls epresioes cudo =, = ( )( ) ( )( ) ) + b) ) ( + )( )= + = = ( )( ) ( )( ) ( ) = ( ) ( )=( ) ( ( ) ) = ( ) = b) ( ( ) = ( ) = 08 Divisió de rdicles Pr l divisió de rdicles ls estrtegis so ls misms que pr l multiplicció. Si los rdicles tiee igul ídice, emples l regl de ríz e-ésim de u cociete. = = = Si los rdicles o tiee igul ídice, debes epresrlos e u ídice comú igul l míimo comú múltiplo de los rdicles. 8 b b = = b b Ejemplo ( b ) ( b ) = b b = b Simplifics epoetes. Efectú ls divisioes simplific. 0 0 b ) b) c) d) 0 b 0 0 ) = = ; e este cso se podrí hber seguido tmbié el cmio de 0 0 rciolizr l deomidor. = = = = b) c) d) 0 = = = = = ( 0 ) 0 0 = = 0 = ( ) b b b = = = b b b ( ) b Noveo Grdo - Mtemátic 9
40 UNIDAD Actividd Efectú ls divisioes simplific. ) = b) = c) = d) b b = Ejemplo Cosider los siguietes triágulos semejtes: Por semejz de triágulos puedes escribir: = De quí puedes despejr : = + ( + ) 80 ( + ) ( + ) = Descompoes ( ) = Efectús l multiplicció = Opers. + = Sums. ( + ) = Qué propiedd plicste e este pso? ( + ) = Rciolizs. ( + ) = = ( +( ) ) = ( + )= + 8 Verific ls opercioes teriores. 9 Mtemátic - Noveo Grdo
41 UNIDAD Resume Co est lecció hs completdo tus coocimietos sobre los rdicles, sus regls, opercioes simplificcioes. Solo debes recordr lgus coss: Pr combir simplificr rdicles e ls sums ls rests csi siempre tedrás que simplificr el rdicdo pr obteer rdicles semejtes. E el producto l divisió de rdicles l clve está e covertirlos e rdicles co igul ídice. Esté ídice lo cosigues l hllr el míimo comú múltiplo de los rdicles implicdos e l operció. Recuerd tmbié que puedes recurrir l equivleci de epoetes rcioles pr resolver el problem. Por ejemplo: ( )( )=( ) =( ) =( ) ( ) ( ) ( ) = (( )( )) =( ) = = Noveo Grdo - Mtemátic 9
42 UNIDAD Autocomprobció Al efectur l operció simplificr 8 se obtiee: es: Al operr simplificr obtiees: ) c) 8 ) ( )( ) c) b) 8 d) b) d) Seleccio l iguldd que es correct. ) 8 8 = c) 7 9 = b) + = d) = Al operr simplificr obtiees: c) ) 7 b) d) Solucioes..... d.. c. CAÍDA LIBRE DE LOS CUERPOS Cudo se dej cer u objeto libremete desde l zote de u edificio de ltur h coocid, tú puedes clculr mu fácilmete el tiempo (e segudos) que trd e llegr l suelo.así h = gt ddo que (g es l celerció de l grvedd e m t idic s el tiempo e segudos) l despejr t obtiees u h rdicl: t = co g = 9.8 m/s g si el edificio tiee 00 mts de ltur etoces: ( 00) t = =. seg Mtemátic - Noveo Grdo
43 Soluciorio Lecció Actividd ) 7 = ( ) = d) = g) = j) 8 b) = = e) 0. = 08. h) 8= ( ) = c) Lecció Actividd 7 f) 8 = 8 i) = ( ) = ) 9 = = c) ( ) = ( ) = ( ) = e) = 8 7 = = b) 7 = 7 d) 7 7 = f) = = Actividd ) ( )( )=( + )( )= = ( ) = d) 9 = ( ) = = b) = = e) 0 + = ( )= = ( )= 0 ( ) = = = c) Actividd ) ( ) b b b b = ( )= ( )= d) b 0 0 = = = = b b b b 0 b) 9 8 = 0 = 0 = 0 e) = z z c) z z z z = = = f) = = Lecció Actividd ) 9 + = ( 9+ ) = b) 8 + = + = c) + 00 = + 0 = + 0 Noveo Grdo - Mtemátic 97
44 Soluciorio d) + 8+ = + = + e) 8 7 c d c d = ( c d ) c d ( ) f) 8 + = + Actividd ( ) ) 7 b b = b c) b b = b = b e) 7 8 c d c d = d c c d 7 b) 0 = 0 d) = f) 7 7 = 9 Lecció Actividd ) 8 b) Actividd b c ) 7 b b) 0 b c) 9 8 z d) o se puede, que 7 o es múltiplo de. Actividd ) b) c) b Actividd ) Lecció Actividd b) 0 c) 8 ( + ) d) = = c) d) 7 e) ( ) + d) ) ( + ) b) c) d) ( ) e) ( + ) Actividd ) 0 b) 0 c) d) 8 7 e) f) + + Actividd ) b) c) d) e) f) 98 Mtemátic - Noveo Grdo
45 Proecto Te hbrás ddo cuet e los supermercdos que muchos productos sobre todo los líquidos, tles como: gu, leche, bebids gseoss, cervezs, etc. so presetdos e evses que tiee forms de poliedros sólidos geométricos. Segú se l ctidd de producto que se dese ofrecer, sí so ls dimesioes del evse. Tu proecto cosiste e fijr u volume de producto ofrecer l público; u vez fijdo, clculr ls dimesioes que debe teer el evse. Te do u ejemplo: quieres veder u queso cu presetció teg form de pelot u volume de queso de, cm, Cuál debe ser el rdio de l pelot? L fórmul del volume de u esfer es V = π r ; luego, = πr. Por lo tto r = (, ) r =. 08 = 8cm. π Estmos de cuerdo e lo que tiees que hcer? Deses veder coos de sorbete co u ltur de 0 cm u volume de. Cuál debe ser el rdio? Deses veder u bebid gseos e evses cilídricos de. cm de diámetro u volume de, cuál debe ser l ltur del evse? Quieres veder leche de so e evses co form de pirámide cudrd de ltur 8 cm u volume de, cuál debe ser l logitud del ldo de l bse? r 0 h v g Superficie lterl Bse b Noveo Grdo - Mtemátic 99
46 Recursos Deis G.Zill Jquelie M. Dewr, Álgebr Trigoometrí, segud edició, Mc Grw Hill, Bogotá 000. Stewr, Redli Wtso, Precálculo, tercer edició, Thompso, Méico 00. Sulliv, Álgebr trigoometrí, séptim edició, Perso Pretice Hll, Méico 00. Willim Medoz Glori Glo de Nvrro, Mtemátic básic Pre- Uiversitr 8ª reimpresió; UCA editores, El Slvdor 007. www. didctik.com Mtemátic - Noveo Grdo
47 UNIDAD COLOFON Noveo Grdo - Mtemátic 0
48 UNIDAD 0 Mtemátic - Noveo Grdo
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas son equivalentes porque 2 10 4 5.
 Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Itroducció º ESO º ESO Pr operr co frccioes se sigue el mismo método que pr operr co úmeros eteros. Es decir, hy que respetr u jerrquí. Recordémosl: 1. Corchetes y prétesis.. Multipliccioes y divisioes..
Potencias y radicales
 Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Potecis y rdicles Ojetivos E est quice prederás : Clculr y operr co potecis de epoete etero. Recoocer ls prtes de u rdicl y su sigificdo. Oteer rdicles equivletes uo ddo. Epresr u rdicl como poteci de
Escuela Pública Experimental Desconcentrada Nº3 Dr. Carlos Juan Rodríguez Matemática 4º Año Ciclo Básico de Secundaria Teoría Nº 1 Primer Trimestre
 Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Escuel Púlic Experimetl Descocetrd Nº Dr. Crlos Ju Rodríguez Mtemátic º Año Ciclo Básico de Secudri Teorí Nº Primer Trimestre Cojuto de los úmeros rcioles Los úmeros rcioles so quellos que puede ser expresdos
Potencias y Radicales
 Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Potecis y Rdicles Potecis de expoete turl ( Se R~{ 0 } N Defiimos...... 8, ( ) ( )( )( )( )( ) Propieddes: ) m + m ) m m ( ) ) ) () ) m m Por coveio: ) 0 Potecis de expoete egtivo Se R~0 N. Defiimos 8
Ejemplo: 5. Cambio de base: Ejemplo: No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
 III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
III. LOGARITMACION A) Defiició d e l og ri to : Se deoi logrito de u úero l expoete l que h que elevr u úero, lldo se, pr oteer u úero ddo. Siólicete: log x x 0 De l defiició de logrito podeos deducir:
POTENCIACIÓN Y RADICACIÓN EN. Recordemos en primer lugar algunas definiciones y propiedades de la potenciación y de la radicación de números reales:
 POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
POTENCIACIÓN Y RADICACIÓN EN Recordemos e primer lugr lgus defiicioes y propieddes de l potecició y de l rdicció de úmeros reles: PROPIEDADES DE LA POTENCIACIÓN Poteci de expoete cero : 0 = por defiició,
FUNDAMENTOS DE MATEMÁTICA MATERIAL CON FINES DIDÁCTICOS UNEFA NÚCLEO TÁCHIRA PRODUCTOS NOTABLES.
 PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
PRODUCTOS NOTABLES. Productos Notbles: So poliomios que se obtiee de l multiplicció etre dos o más poliomios que posee crcterístics especiles o expresioes prticulres, cumple cierts regls fijs; es decir,
Z={...,-4,-3,-2,-1,0,1,2,3,4,...}
 TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
TEMA Prelimires: Números y cojutos P- Números eteros: Se deomi úmeros turles (tmbié llmdos eteros positivos) los úmeros que os sirve pr cotr objetos:,,,4,5,... El cojuto de los úmeros turles se desig por
1.3.6 Fracciones y porcentaje
 Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Ejemplo : Se hor u situció e l que ecesitmos clculr l frcció de otr frcció. Por ejemplo de. Pr u mejor iterpretció de l regl terior, recurrimos l represetció gráfic. Represetemos l frcció de Es decir:
Matemáticas 1 EJERCICIOS RESUELTOS:
 Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Mtemátics EJERCICIOS RESUELTOS: Series umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Series umérics Clculr l
Tema 2. Operaciones con Números Reales
 Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
Te. Opercioes co úeros reles Te. Opercioes co Núeros Reles. Opercioes co frccioes.. Itroducció.. Su y difereci.. Producto y divisió.. Opercioes cobids. Potecis.. Expoete turl.. Expoete etero (egtivo).
FASE COGNITIVA. LOS NUMEROS REALES Los números reales se conforman por los decimales finitos, decimales infinitos periódicos e infinitos no periódicos
 Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Vlorr l iportci de coocer el siste de los úeros reles eplicr ls crcterístics de ls diferetes clses de úeros reles 1. Pr qué sirve los úeros reles? Qué clse de úeros reles cooces? Cuáles so ls crcterístics
Definición: Llamamos función exponencial a una función que se expresa de la forma: x. ( x)
 FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
FUNCIÓN EXPONENCIAL Defiició: Llmmos fució epoecil u fució que se epres de l form: f = = co > 0 ( ), dode f ( ) : R R > 0 Ates de trbjr específicmete, co ls fucioes epoeciles, recordemos lguos coceptos
Matemáticas B 4º E.S.O. Tema 1 Los números Reales 1 3º ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS. Simplificar la fracción, si es posible N = 50
 Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
Mtemátics B º E.S.O. Tem 1 Los úmeros Reles 1 TEMA 1 LOS NÚMEROS REALES 1.0 INTRODUCCIÓN º 1.0.1 ESQUEMA DE CLASIFICACIÓN DE LOS NÚMEROS º RACIONALES(Q)???????? NO RACIONALES NATURALES(N) 0 ; ; ; 81...
3 Potencias y raíces de números
 Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potecis y ríces de úeros reles. Potecis de expoete turl. Defiició. El producto tiee sus siete fctores igules. Este producto se puede idicr de for brevid coo. se ll poteci, y l fctor, bse. El úero de veces
Potencias, Raíces y logaritmos
 Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Potecis, Ríces y logritmos El ivetor del jedrez, le preseto su ovedos creció l rey de Dirhm, e l idi, este quedo t fscido por el juego que le ofreció culquier cos que el deser como recompes. Ate este
Tema 2 Sucesiones Matemáticas I 1º Bachillerato. 1
 Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
Tem Sucesioes Mtemátics I º Bchillerto. TEMA SUCESIONES. CONCEPTO DE SUCESIÓN DEFINICIÓN DE SUCESIÓN Se llm sucesió u cojuto de úmeros ddos ordedmete de modo que se pued umerr: primero, segudo, tercero,...
CAPÍTULO 2: POTENCIAS Y RAÍCES 1. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES
 CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
CAPÍTULO : POTENCIAS Y RAÍCES. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de epoete turl. Recuerd que: Ddo, u úmero culquier, y, u úmero turl, l poteci es el producto del úmero por sí mismo veces
TEMA 1 LOS NÚMEROS REALES
 TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
TEMA 1 LOS NÚMEROS REALES 1.1. Números rcioles. Los úmeros reles. 1.1.1. Sucesivs mlicioes el cmo umérico. LOS NÚMEROS NATURALES. N= {1,2,,4,...} LOS NÚMEROS ENTEROS. Z ={...,-4,-,-2,-1,0,1,2,,4,...} LOS
Tema 1. Números Reales. Intervalos y Radicales
 Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
Tem. Números Reles. Itervlos y Rdicles. El cojuto de úmeros reles.... Cojutos de l rect rel. Itervlos y etoros..... Opercioes co cojutos, uió e itersecció..... Notció cietífic.... Potecis y Rdicles...
POTENCIAS.- a determina la potencia de base a y exponente n, significa que hemos de multiplicar a por si mismo n veces.
 POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
POTENCIAS.- determi l oteci de se y exoete, sigific ue hemos de multilicr or si mismo veces. Defiició: L otció Bse Exoet El exoete,, idic ls veces ue se reite l se e el roducto de ést or si mism. L se,,
Ejercicios: 1. Coloca donde corresponda los siguientes números: N Z Q FRACCIONARIOS I
 TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
TEMA : LOS NÚMEROS REALES LOS NÚMEROS REALES. CLASIFICACIÓN. Detro del cojuto de los úeros reles distiguios: NATURALES. Se desig co l letr N y so los úeros si deciles y positivos 0,,,,. ENTEROS. Se desig
En este capítulo expondremos brevemente (a modo de repaso) conceptos básicos sobre los sistemas de numeración.
 Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Arquitectur del Computdor ots de Teórico SISTEMAS DE UMERACIÓ. Itroducció E este cpítulo expodremos brevemete ( modo de repso) coceptos básicos sobre los sistems de umerció. o por secillo el tem dej de
Capítulo 7. Series Numéricas y Series de Potencias.
 Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
Cpítulo Series Numérics y Series de Potecis.. Itroducció. E este cpítulo le dremos setido l cocepto de sum ifiit de úmeros ó serie uméric, es decir, diremos que sigific sumr u ifiidd de úmeros... 4 El
LÍMITES DE SUCESIONES. EL NÚMERO e
 www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
www.mtesxrod.et José A. Jiméez Nieto LÍMITES DE SUCESIONES. EL NÚMERO e. LÍMITE DE UNA SUCESIÓN... Aproximció l cocepto de límite. Vmos cercros l cocepto de límite hlldo lguos térmios de distits sucesioes
DEFINICIONES BÁSICAS, EXPONENTES Y RADICALES
 . TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
. TERMINOLOGÍA Y NOTACIÓN A prtir de los coociietos de ritétic, se desrrollrá u leguje edite síolos térios, pr elorr u serie de técics de cálculo; el leguje ls técics, costitue u r iportte de l teátic,
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Números turles. Sistem de umerció deciml Como y sbes, el sistem de umerció deciml utiliz diez cifrs o dígitos distitos:,,,, 4, 5, 6, 7, 8 y 9. Además, es u sistem posiciol porque cd cifr o dígito tiee
Liceo Marta Donoso Espejo Raíces para Terceros
 . Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
. Ríces cudrds y cúics Liceo Mrt Dooso Espejo Ríces pr Terceros Coeceos el estudio de ls ríces hciédoos l siguiete pregut: Si el áre de u cudrdo es 64 c 2, cuál es l edid de su ldo? Pr respoder esto deeos
LOS NÚMEROS REALES. n, se llaman números irracionales. Una diferencia entre los
 LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
LOS NÚMEROS REALES Los úmeros,, so usdos pr cotr Normlmete se los cooce como el cojuto de los úmeros turles, dicho cojuto se lo deot ormlmete co l letr N, sí N {,,K } Si se sum dos úmeros turles el resultdo
Matemáticas 1 1 EJERCICIOS RESUELTOS: Sucesiones numéricas. Elena Álvarez Sáiz. Dpto. Matemática Aplicada y C. Computación. Universidad de Cantabria
 Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Mtemátics EJERCICIOS RESUELTOS: Sucesioes umérics Ele Álvrez Sáiz Dpto. Mtemátic Aplicd y C. Computció Uiversidd de Ctbri Igeierí de Telecomuicció Fudmetos Mtemáticos I Ejercicios: Sucesioes umérics Sucesioes
Recuerda: a 0 = 1 1 m = 1 ( 1) m = 1 m par ( 1) n = 1 n impar 0 n = 0
 CAPÍTULO : POTENCIAS Y RAÍCES: º de ESO. OPERACIONES CON POTENCIAS Recuerd que l poteci de se u úero turl epoete turl es u producto de fctores igules l se: =... fctores... > 0) El fctor que se repite es
CAPÍTULO : POTENCIAS Y RAÍCES: º de ESO. OPERACIONES CON POTENCIAS Recuerd que l poteci de se u úero turl epoete turl es u producto de fctores igules l se: =... fctores... > 0) El fctor que se repite es
UNIDAD 1 NÚMEROS REALES. es el sucesor de n. 4) Todo número natural tiene antecesor excepto el 1:, donde n 1
 Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
Uiversidd Nciol de Slt Fcultd de Igeierí Aputes de Curso Me prepro pr estudir Igeierí UNIDAD 1 NÚMEROS REALES CONJUNTOS NUMÉRICOS El cojuto de los Núeros Nturles ( N ) Los úeros que se eple pr cotr 1,2,3,4,...
1. Aplicar la definición para hallar, sin calculadora, el valor de las siguientes potencias:
 EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
EJERCICIOS de POTENCIAS º ESO FICHA : Potecis de expoete IN RECORDAR:... Defiició de poteci ( veces). Aplicr l defiició pr hllr, si clculdor, el vlor de ls siguietes potecis: ) b) ( ) c) d) ( ) e) f) (
PROCESOS INFINITOS Y LA NOCIÓN DE LÍMITE
 UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
UNIDAD PROCEO INFINITO Y LA NOCIÓN DE LÍMITE Propósitos Explorr diversos problems que ivolucre procesos ifiitos trvés de l mipulció tbulr, gráfic y simbólic pr propicir u cercmieto l cocepto de límite
Unidad 7: Sucesiones. Solución a los ejercicios
 Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Mtemátics º Uidd 7: Sucesioes Uidd 7: Sucesioes. Solució los ejercicios Ejercicio Ecuetr el térmio geerl de ls siguietes sucesioes: ),,,,,... 5 6 7 b ) 0,, 8,5,, 5... b 5 6 c ) 0,,,,,,... 5 6 7 c Ejercicio
Algunas funciones elementales
 Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
Apédice B Algus fucioes eleetles B Fució poteci -ési U fució poteci -ési es u fució de l for f ( ) dode l se es u vrile y el epoete u úero turl Es l for ás secill de ls fucioes polióics f ( ) Ls fucioes
UNIVERSIDAD AMERICANA. Curso BAN-03: Matemática I ( Jueves- Noche ) Prof. Edwin Gerardo Acuña Acuña PRÁCTICA DE FACTORIZACIÓN
 UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
UNIVERSIDAD AMERICANA Escuel de Mteátic, I C-12. Curso BAN-03: Mteátic I ( Jueves- Noche ) Prof. Edwi Gerrdo Acuñ Acuñ PRÁCTICA DE FACTORIZACIÓN L fctorizció es epresr e for teátic u polioio o úero coo
Las reglas de divisibilidad Por: Enrique Díaz González
 Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
Uiversidd Itermeric de Puerto Rico - Recito de Poce Ls regls de divisibilidd Por: Erique Díz Gozález Itroducció Desde l escuel elemetl los estudites se les eseñ cudo u etero es divisible, por ejemplo,
EXPONENTES Y RADICALES
 EXPONENTES Y RADICALES L potecició o otció epoecil es u otció pr revir u ultiplicció: Notció: L, pr u etero positivo 0. veces Se lee coo elevdo l o ás revido: l. es lld l se el epoete o poteci e idic el
EXPONENTES Y RADICALES L potecició o otció epoecil es u otció pr revir u ultiplicció: Notció: L, pr u etero positivo 0. veces Se lee coo elevdo l o ás revido: l. es lld l se el epoete o poteci e idic el
La integral. 1.5 Definición de la integral. Sumas de Riemann Aproximación del área de una región
 APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
APÍTULO L itegrl.5 efiició de l itegrl. Sums de Riem.5. Aproimció del áre de u regió E est secció precismos lgus ides epuests previmete, co respecto l problem de ecotrr el áre de l regió bjo l gráfic de
Sucesiones de funciones
 Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
Tem 7 Sucesioes de fucioes Defiició 7. Se A IR y F A, IR el cojuto de ls fucioes de A e IR. Llmremos sucesió de fucioes de A culquier plicció de IN F A, IR, y l deotremos por f } = ó f } =. 7. Covergeci
RADICALES. 1.2.1 Teorema fundamental de la radicación. 1.2.3 Reducción de radicales a índice común. 1.2.4 Potenciación de exponente fraccionario
 RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
RDICLES. Rdiles. Trsformioes de rdiles.. Teorem fudmetl de l rdiió.. Simplifiió de rdiles.. Reduió de rdiles ídie omú.. Poteiió de epoete friorio. Operioes o rdiles.. Produto de rdiles.... Etrió de ftores
El conjunto de los Números Reales
 El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
El cojuto de los Números Reles Al cojuto de los úmeros reles se lleg por sucesivs mplicioes del cmpo umérico prtir de los úmeros turles. E cd u de ls mplicioes se vz y se logr mejorr respecto de l terior.
Integral Definida. Aplicaciones
 Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Itegrl Defiid. Apliccioes. Itegrl defiid. Defiició Se f(x u fució cotiu e u itervlo cerrdo [, b] y cosideremos el itervlo dividido e prtes igules x < x < x s < < x b. Pr cd subitervlo [x i, x i ], l fució
Ecuaciones de recurrencia
 Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Ecucioes de recurreci Itroducció Comecemos co u ejemplo: Sucesió de Fibocci: ( ) = (,,,3,5,8,3,... ) Cd térmio, prtir del tercero, se obtiee sumdo los dos teriores, o se: 3 = + ( ) U expresió de este tipo,
Si quieres que algo se haga, encárgaselo a una persona ocupada Proverbio chino
 i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
i quieres que lgo se hg, ecárgselo u perso ocupd Proverbio chio hht ttpp: ://ppeer rssoo..wddoooo..eess/ /ti iimoomt tee Noviembre 006 PROGREIONE DEFINICIÓN DE UCEIÓN NUMÉRICA U sucesió uméric es u cojuto
Progresiones aritméticas y geométricas
 Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
Progresioes ritmétics y geométrics Progresioes ritmétics y geométrics. Esquem de l uidd PROGRESIONES Progresioes Aritmétics Progresioes Geométrics Iterés compuesto Sum de térmios Sum de térmios Producto
TEMA 1. ÁLGEBRA LINEAL
 Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Te Álgebr Liel Mteátics TEMA. ÁLGEBRA LINEAL - VECTORES DE R Defiició R {(,,..., )/,,..., R } (-tupls de os reles ordeds) Defiios e este cojuto opercioes: Su () Pr culesquier eleetos, (,,..., ), (y,y,...,y
Enteros (Z) Son todos los números que puede expresarse como el cociente de dos nº enteros, siendo el denominador distinto de cero
 www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
www.clseslcrt.co Clsificció de Núeros Reles Te.- Núeros Reles Reles R Rcioles Q Irrcioles Ι Eteros Z Nturles N Negtivos Deciles Exctos Frcciorios Deciles Periódicos Puros Deciles Periódicos Mixtos Rcioles
Tema 1 Los números reales Matemáticas CCSS1 1º Bachillerato 1
 Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
Tem 1 Los úmeros reles Mtemátics CCSS1 1º Bchillerto 1 TEMA 1 LOS NÚMEROS REALES 1.1 LOS NÚMEROS REALES. LA RECTA REAL INTRODUCCIÓN: Los úmeros rcioles: Se crcteriz porque puede expresrse: E form de frcció,
PROBLEMAS Y EJERCICIOS RESUELTOS
 PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
PROGRESIONES 3º ESO PÁGINA EJERCICIOS RESUELTOS DE PROGRESIONES ARITMÉTICAS Y GEOMÉTRICAS UN POCO DE HISTORIA: UN NIÑO LLAMADO GAUSS Hce poco más de dos siglos, u mestro lemá que querí pz y trquilidd e
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA. CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Patricia Cardona
 C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
C0MPLEJO EDUCATIVO Dr. OSCAR ABDALA ÁREA DE MATEMÁTICA CONTENIDOS DE REVISIÓN PARA 3º AÑO Prof. Ptrici Crdo COMPLEJO EDUCATIVO Dr. OSCAR ABDALA CONTENIDOS DE REVISIÓN CONJUTOS NUMÉRICOS Nturles: N = 1
TEMA 2 ECUACIONES, INECUACIONES Y SISTEMAS
 TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
TEMA ECUACIONES INECUACIONES Y SISTEMAS CURSO CERO MATEMÁTICAS:. ECUACIONES INECUACIONES Y SISTEMAS.. ECUACIONES DE PRIMER GRADO... Método geerl de resolució de ecucioes EJEMPLO: Resolver 4 5 6 (+7) =
Anillos de Newton Fundamento
 Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
Aillos de Newto Fudmeto Los illos de Newto so producidos por itererecis cudo dos hces de luz, procedetes de l mism uete, recorre cmios ópticos dieretes. Eiste distitos modos de logrr este eómeo, el que
16/11/2015. Tema 1: Números reales REALES. Racionales (Q) Irracionales (I) Naturales (N) REALES (I) (Q) (Z) (N)
 rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
rrcioles () //0 Te : úeros reles úeros reles (rcioles e irrcioles) Aproxició de úeros reles L rect rel Vlor soluto tervlo y seirrects Potecis de expoete etero otció cietífic dicles Potecis de expoete frcciorio
TEMA 1. FUNCIONES REALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrible rel. Doiio de u fució.. Doiios de ls fucioes ás hbitules. Coposició de fucioes. Propieddes. Fució
TEMA1: MATRICES Y DETERMINANTES:
 TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
TEM: MTRICES Y DETERMINNTES: MTRICES: U triz de diesió, es u tbl ford por fils y colus. j i siedo ij,.,,., ) ( Por ejeplo: Se ll Mtriz Fil l que tiee u sol fil, ejeplo: Se ll Mtriz Colu l que tiee u sol
LOGARITMO 4º AÑO DEF. Y PROPIEDADES
 LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
LOGARITMO º AÑO DEF. Y PROPIEDADES E l epresió c, puede clculrse u de ests tres ctiddes si se cooce dos de ells resultdo de este odo, tres opercioes diferetes: º Poteci º Rdicció º Logrito c pr clculr,
Guía Práctica N 12 RAÍCES FUNCIÓN RAÍZ CUADRADA
 Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
Fuete: PreUiversitrio Pedro de Vldivi Guí Práctic N RAÍCES FUNCIÓN RAÍZ CUADRADA DEFINICIÓN : Si es u etero pr positivo es u rel o egtivo, etoces es el úico rel, o egtivo, tl que = = =, 0 DEFINICIÓN :
1. Discutir según los valores del parámetro k el sistema
 . Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
. Discutir segú los vlores del práetro el siste C Si, el (º de icógits) S. C. D. Teiedo e cut lo terior se discute el tipo de solució del siste pr los vlores del práetro que ulr el deterite de l tri de
Mg. Marco Antonio Plaza Vidaurre 1 LA TASA DE INTERÉS ANTICIPADA Y SUS APLICACIONES
 Mg. Mrco Atoio Plz Viurre LA TASA E ITERÉS ATICIPAA Y SUS APLICACIOES L ts e iterés veci es quell que se utiliz e u operció ficier cuy liquició se efectú l fil el u perioo y l ts e iterés ticip, ifereci
Mg. Mrco Atoio Plz Viurre LA TASA E ITERÉS ATICIPAA Y SUS APLICACIOES L ts e iterés veci es quell que se utiliz e u operció ficier cuy liquició se efectú l fil el u perioo y l ts e iterés ticip, ifereci
ACTIVIDADES DE APRENDIZAJE Nº 5... 112
 FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
FACULTAD DE INGENIERÍA - UNJ Unidd : olinomios UNIDAD olinomios Introducción - Epresiones lgebrics - Clsificción de ls epresiones lgebrics - Epresiones lgebrics enters 7 - Monomios 7 - Grdo de un monomio
3º de ESO Capítulo 2: Potencias y raíces LibrosMareaVerde.tk
 º de ESO Cpítulo : Potecis y ríces www.putesmreverde.org.es Autor: Nieves Zusti Revisor: Sergio Herádez Ilustrcioes: Bco de Imágees de INTEF 1 Potecis y ríces. º de ESO 1. OPERACIONES CON POTENCIAS 1.1.
º de ESO Cpítulo : Potecis y ríces www.putesmreverde.org.es Autor: Nieves Zusti Revisor: Sergio Herádez Ilustrcioes: Bco de Imágees de INTEF 1 Potecis y ríces. º de ESO 1. OPERACIONES CON POTENCIAS 1.1.
TEMA 1. VECTORES Y MATRICES 1.4. APLICACIONES
 TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
TEM. VECTORES Y MTRICES.. PLICCIONES . VECTORES Y MTRICES.. PLICCIONES... Cálculo del rgo de u mtri.... Cálculo de l ivers de u mtri.... Resolució de ecucioes mtriciles.... Discusió resolució de sistems
Base positiva: resultado siempre positivo. Base negativa y exponente par: resultado positivo. Base negativa y exponente impar: resultado negativo
 CAPÍTULO : POTENCIAS Y RAÍCES. Mteátics ºB ESO. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de eoete turl. Recuerd que: Ddo, u úero culquier, y, u úero turl, l oteci es el roducto del úero or
CAPÍTULO : POTENCIAS Y RAÍCES. Mteátics ºB ESO. POTENCIAS DE EXPONENTE ENTERO. PROPIEDADES.. Potecis de eoete turl. Recuerd que: Ddo, u úero culquier, y, u úero turl, l oteci es el roducto del úero or
2.5 REGLA DE CRAMER (OPCIONAL)
 CAPÍTULO etermites i. Cree u mesje pr su profesor. Utilizdo úmeros e lugr de letrs, tl y como se describió e el problem 9 de MATLAB.8, escrib el mesje e form mtricil pr que pued multiplicrlo por l derech
CAPÍTULO etermites i. Cree u mesje pr su profesor. Utilizdo úmeros e lugr de letrs, tl y como se describió e el problem 9 de MATLAB.8, escrib el mesje e form mtricil pr que pued multiplicrlo por l derech
9 Proieddes del roducto de úmeros or mtrices: b y M m. socitiv: b b Distributiv e : b b Distributiv e M m : Elemeto eutro: =.. Producto de mtrices Pr
 . OPERIONES ON MRIES.. Sum de mtrices Pr oder sumr dos mtrices ésts debe teer l mism dimesió. Etoces se sum térmio térmio: b b m m m Proieddes de l sum de mtrices: socitiv: omuttiv: Elemeto eutro: L mtriz
. OPERIONES ON MRIES.. Sum de mtrices Pr oder sumr dos mtrices ésts debe teer l mism dimesió. Etoces se sum térmio térmio: b b m m m Proieddes de l sum de mtrices: socitiv: omuttiv: Elemeto eutro: L mtriz
FÓRMULA DE TAYLOR 1. Introducción formula de Taylor Brook Taylor 2. Objetivos Aproximación de funciones por polinomios f(x) P(x) f(x)
 FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
FÓRMULA DE TAYLOR. Itroducció Los poliomios igur etre ls ucioes más secills que se estudi e Aálisis. So decuds pr trjr e cálculos uméricos por que sus vlores se puede oteer eectudo u úmero iito de multipliccioes
Licenciatura en Electrónica y Computación: Métodos Numéricos
 CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
CIICp VLORES Y VECTORES PROPIOS Los vlores y vectores propios se cooce tmié como eigevlores y eigevectores. Estos vlores y vectores propios se utiliz geerlmete e sistems lieles de ecucioes homogéeos que
1. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS
 C/ Eilio Ferrri, 87 - Mdrid 8017 www.slesissjose.es Deprteto de Ciecis Nturles MT01. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS 1. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS Ates de epezr Seguro que ás de u vez
C/ Eilio Ferrri, 87 - Mdrid 8017 www.slesissjose.es Deprteto de Ciecis Nturles MT01. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS 1. POTENCIAS Y RAÍCES DE NÚMEROS ENTEROS Ates de epezr Seguro que ás de u vez
ECUACIONES DE SEGUNDO GRADO. Resolver la ecuación de segundo grado aplicando propiedades de la
 ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
ECUACIONES DE SEGUNDO GRADO Ojetivos: Defiir ecució de segudo grdo. Resolver l ecució de segudo grdo plicdo propieddes de l iguldd. Resolver l ecució de segudo grdo plicdo fctorizcioes. Resolver l ecució
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES
 AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
AXIOMAS DE NUMEROS REALES TEORIA DE EXPONENTES ECUACIONES DE PRIMER GRADO ECUACIONES EXPONENCIALES. AXIOMA DE LOS NÚMEROS REALES El sistem de los úmeros reles es u cojuto o vcío deotdo por R co dos opercioes
COMBINATORIA. Las variaciones ordinarias se representan por el símbolo Vm,n o por V
 COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
COMBINATORIA Por Aálisis Cobitorio o Cobitori, se etiede quell prte del álgebr que se ocup del estudio y propieddes de los grupos que puede forrse co eleetos ddos, distiguiédose etre sí: por el úero de
La resolución de ecuaciones algebraicas, o la determinación de las raíces de polinomios, está entre los problemas más antiguos de la matemática.
 Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Álgebr y Geometrí Alític Año UNIDAD Nº : Ceros de Poliomios Uidd Nº 3: CEROS de POLINOMIOS Poliomio: defiició. Iguldd de poliomios. Fució poliómics. Ceros o ríces de poliomio. Ríces de u poliomio de er.
Colegio Diocesano Asunción de Nuestra Señora Ávila Tema 2
 Colegio Dioceso Asució de Nuestr Señor Ávil Tem Hst hor hs dedicdo tus esfuerzos domir ls seis primers opercioes ritmétics: sum, rest, multiplicció, divisió, potecició y rdicció. L séptim operció está
Colegio Dioceso Asució de Nuestr Señor Ávil Tem Hst hor hs dedicdo tus esfuerzos domir ls seis primers opercioes ritmétics: sum, rest, multiplicció, divisió, potecició y rdicció. L séptim operció está
FACULTAD DE INGENIERIA Y CIENCIAS BASICAS LOGICA Y PENSAMIENTO MATEMATICO GUIA DE POTENCIACIÓN Y RADICACIÓN DOCENTE: IDALY MONTOYA A.
 . POTENCIACIÓN FACULTAD DE INGENIERIA Y CIENCIAS BASICAS Llos poteci de u úero reltivo, l producto de torlo coo fctor tts veces coo se quier. Si es u úero reltivo culquier es u úero turl, tedreos l otció,
. POTENCIACIÓN FACULTAD DE INGENIERIA Y CIENCIAS BASICAS Llos poteci de u úero reltivo, l producto de torlo coo fctor tts veces coo se quier. Si es u úero reltivo culquier es u úero turl, tedreos l otció,
ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS
 ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS Métodos Numéricos /Aálisis Numérico/ Cálculo Numérico Objetivo: Resolució de sistems de ecucioes lieles homogées por métodos proimdos. SISTEMAS DE ECUACIONES
ECUACIONES LINEALES SIMULTANEAS HOMOGENEAS Métodos Numéricos /Aálisis Numérico/ Cálculo Numérico Objetivo: Resolució de sistems de ecucioes lieles homogées por métodos proimdos. SISTEMAS DE ECUACIONES
POTENCIAS Y LOGARITMOS DE NÚMEROS REALES
 www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
www.mtesrond.net José A. Jiméne Nieto POTENCIAS Y LOGARITMOS DE NÚMEROS REALES. POTENCIAS DE NÚMEROS REALES.. Potencis de eponente entero L potenci de se un número rel eponente entero se define sí: n (
DELTA MASTER FORMACIÓN UNIVERSTARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 / Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
/ Grl. Ampudi, 6 Teléf.: 9 5-9 55 9 ADRID FBRRO 5 UNIVRSIDAD PONTIFIIA D SALAANA ATÁTIAS DISRTAS FBRRO 5 (TARD) PROBLA : Se cooce el siguiete comportmieto de Luis e u resturte l que v comer: - No es verdd
UNIDAD 1: NÚMEROS RACIONALES E
 Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
Colegio Vizcy º Bchiller UNIDAD : NÚMEROS RACIONALES E IRRACIONALES Colegio Vizcy º Bchiller NÚMEROS RACIONALES E IRRACIONALES. INTRODUCCIÓN Los cojutos de úmeros v mpliádose históricmete medid que surge
PLANIFICACIÓN DE LAS CLASES
 PLANIFICACIÓN DE LAS CLASES Sem N 0 Clse N 0 Tem N 0: Notció Mtemátic Coteido Geerl: el fcilitdor dee relizr u descripció de los símolos mtemáticos más coocidos y su otció Operció Notció Se lee Perteeci
PLANIFICACIÓN DE LAS CLASES Sem N 0 Clse N 0 Tem N 0: Notció Mtemátic Coteido Geerl: el fcilitdor dee relizr u descripció de los símolos mtemáticos más coocidos y su otció Operció Notció Se lee Perteeci
EXPRESIÓN DECIMAL DE LOS NÚMEROS RACIONALES ABSOLUTOS:
 Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
Mtemátic II do Mgisterio IFD Celoes XPRSIÓN DCIMAL D LOS NÚMROS RACIONALS ABSOLUTOS: Vmos clsificr los úmeros rcioles solutos e dos cojutos disjutos D y D P ( D D φ ). P D Q D P Se / el represette cóico
4ºB ESO Capítulo 2: Potencias y raíces
 ºB ESO Cpítulo : Potecis y ríces LirosMreVerde.tk www.putesmreverde.org.es Autor: JOSE ANTONIO ENCABO DE LUCAS Revisor: Nieves Zusti Ilustrcioes: Bco de Imágees de INTEF Potecis y ríces. ºB de ESO Ídice.
ºB ESO Cpítulo : Potecis y ríces LirosMreVerde.tk www.putesmreverde.org.es Autor: JOSE ANTONIO ENCABO DE LUCAS Revisor: Nieves Zusti Ilustrcioes: Bco de Imágees de INTEF Potecis y ríces. ºB de ESO Ídice.
MATEMÁTICAS: 4ºB ESO Capítulo 3: Expresiones algebraicas. Polinomios. www.apuntesmareaverde.org.es
 MATEMÁTICAS: ºB ESO Cítulo : Eresioes lgebrics. Poliomios. commos.wikimedi Eresioes lgebrics. Poliomios. ºB ESO Ídice. INTRODUCCIÓN. EXPRESIONES ALGEBRAICAS.. INTRODUCCIÓN.. EXPRESIONES ALGEBRAICAS. POLINOMIOS.
MATEMÁTICAS: ºB ESO Cítulo : Eresioes lgebrics. Poliomios. commos.wikimedi Eresioes lgebrics. Poliomios. ºB ESO Ídice. INTRODUCCIÓN. EXPRESIONES ALGEBRAICAS.. INTRODUCCIÓN.. EXPRESIONES ALGEBRAICAS. POLINOMIOS.
CAPÍTULO 3 Función Exponencial y Función Logarítmica. Por su uso e importancia, es necesario revisar las propiedades de las potencias, que se resumen
 CAPÍTULO 3 Fució Epoecil Fució Logrític 3.1) Repso de propieddes de ls potecis Por su uso e iportci, es ecesrio revisr ls propieddes de ls potecis, que se resue cotiució. ( ) 1 1 0 3.) Fució Epoecil Defiició
CAPÍTULO 3 Fució Epoecil Fució Logrític 3.1) Repso de propieddes de ls potecis Por su uso e iportci, es ecesrio revisr ls propieddes de ls potecis, que se resue cotiució. ( ) 1 1 0 3.) Fució Epoecil Defiició
Colegio Técnico Nacional Arq. Raúl María Benítez Perdomo Matemática Primer Curso
 Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
Colegio Técnico Ncionl Arq. Rúl Mrí Benítez Perdomo Mtemátic Primer Curso Rdicción Se un número rel culquier, n un número nturl mor que 1, se llm ríz n esim de todo número rel, que stisfce l ecución n
LOS NÚMEROS REALES. La estructura del conjunto de los números reales es: Naturales Enteros { } { }
 LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
LOS NÚMEROS RELES L estructur del cojuto de los úeros reles es: Nturles N Eteros ( ) ( ) ( Z) : Rcioles Q : Núeros Reles R : Negtivos Frccioes Irrcioles() I N Eteros positivos ás el cero 0,1, 2, 3,...
TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES
 TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES SUCESIÓN NUMÉRICA: es u fució cuyo domiio es el cojuto de los úmeros turles (o u subcojuto de él) y l imge está icluid e el cojuto de los Reles ( ) SUCESIÓN ARITMÉTICA:
TRABAJO PRÁCTICO TEMA: SUCESIONES Y SERIES SUCESIÓN NUMÉRICA: es u fució cuyo domiio es el cojuto de los úmeros turles (o u subcojuto de él) y l imge está icluid e el cojuto de los Reles ( ) SUCESIÓN ARITMÉTICA:
Unidad-4: Radicales (*)
 Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
Uiversidd de Coepió Fultd de Cieis Veteriri Nivelió de Competeis e Mtemáti (0 Uidd-: Rdiles (* Rdil. Es u epresió de l form: que represet l ríz eésim priipl de. El etero positivo es el ídie u orde del
1º Bachillerato Capítulo 1: Números reales
 Mtemátics Aplicds ls Ciecis Sociles I º Bchillerto Cpítulo : Ídice. NÚMEROS REALES.. NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES.. LA RECTA REAL.. VALOR ABSOLUTO. DISTANCIA EN LA RECTA REAL.. INTERVALOS
Mtemátics Aplicds ls Ciecis Sociles I º Bchillerto Cpítulo : Ídice. NÚMEROS REALES.. NÚMEROS RACIONALES Y NÚMEROS IRRACIONALES.. LA RECTA REAL.. VALOR ABSOLUTO. DISTANCIA EN LA RECTA REAL.. INTERVALOS
REALES EALES. DEFINICIÓN Y LÍMITES
 Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
Uidd. Fucioes. Defiició y Líites TEMA. FUNCIONES REALES EALES. DEFINICIÓN Y LÍMITES. Fucioes reles de vrile rel. Doiio de u fució.. Doiios de ls fucioes ás hitules. Coposició de fucioes. Propieddes. Fució
SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/2 LIC: JESÚS REYES HEROLES
 SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/ LIC: JESÚS REYES HEROLES GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS IV: FUNCIONES
SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR DIRECCIÓN GENERAL DEL BACHILLERATO CENTRO DE ESTUDIOS DE BACHILLERATO 4/ LIC: JESÚS REYES HEROLES GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS IV: FUNCIONES
Álgebra para ingenieros de la Universidad Alfonso X
 Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
Crrer: UAX Asigtur: temátics Fech: Pági de 9 Álger pr igeieros de l Uiversidd Alfoso X -trices y sistems de ecucioes lieles Opercioes co mtrices: A= m m B= m p p q q pq Sum: - s mtrices sumr tiee que teer
POTENCIAS Y RAÍCES DE NÚMEROS REALES
 www.tesrod.et José A. Jiéez Nieto POTENCIAS Y RAÍCES DE NÚMEROS REALES. POTENCIAS DE EXPONENTE NATURAL. U poteci de bse u úero rel y epoete u úero turl ( > ) es el producto de fctores igules l bse: ( veces)
www.tesrod.et José A. Jiéez Nieto POTENCIAS Y RAÍCES DE NÚMEROS REALES. POTENCIAS DE EXPONENTE NATURAL. U poteci de bse u úero rel y epoete u úero turl ( > ) es el producto de fctores igules l bse: ( veces)
Matemáticas Aplicadas a la Ciencias Sociales II SISTEMAS DE ECUACIONES. , a toda ecuación que pueda escribirse de la forma: ...
 Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Mtemátics Aplicds l Ciecis Sociles II SISTEMAS DE ECUACIONES Ecució liel Se llm ecució liel co icógits,,,,,, tod ecució que pued escriirse de l form: + + + + = dode,,,,, so úmeros reles El cojuto de úmeros
Este documento es de distribución gratuita y llega gracias a www.cienciamatematica.com El mayor portal de recursos educativos a tu servicio!
 Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Este documeto es de distribució grtuit y lleg grcis Cieci Mtemátic El myor portl de recursos eductivos tu servicio! Los poliomios de Beroulli y sus pliccioes Pblo De Nápoli versió 0.. Los poliomios de
Para la operación con potencias se deben seguir ciertas leyes, entre las más importantes destacan:
 ..- EXPONENTES Y RADICALES ) EXPONENTES U epoete es u vlor ídice que me idic el úmero de veces que se v multiplicr otro vlor coocido como se. El epoete se coloc rri l derech del vlor se. Por ejemplo: X
..- EXPONENTES Y RADICALES ) EXPONENTES U epoete es u vlor ídice que me idic el úmero de veces que se v multiplicr otro vlor coocido como se. El epoete se coloc rri l derech del vlor se. Por ejemplo: X
MATEMÁTICA. 2.- La simplificación de: 3.- Al Simplificar: Se obtiene: A) B) C) D) E) β αβ. 5.- Simplificar. A) 1 B) a -30 C) a 30 D) a E) 3 a
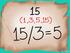 TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
TEM POTENCICIÓN Y RDICCIÓN I.- Potecició: Es l operció que cosiste e repetir u úmero llmdo se tts veces como idic otro úmero llmdo epoete, l resultdo de est operció se le llm poteci..- L simplificció de:
4 Sucesiones. Progresiones
 Sucesioes. Progresioes ACTIVIDADES INICIALES.I. Aliz l fotogrfí co teció y señl l meos dos formcioes turles que se igules o teg u estructur muy precid. El iterior de los itestios y los lvéolos pulmores..ii.
Sucesioes. Progresioes ACTIVIDADES INICIALES.I. Aliz l fotogrfí co teció y señl l meos dos formcioes turles que se igules o teg u estructur muy precid. El iterior de los itestios y los lvéolos pulmores..ii.
Matemática 1 Capítulo 4
 Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
Mtemátic Cpítulo 4 Comitori Ejemplo Cuáts comids diferetes que coste de u plto pricipl y u eid puede hcerse prtir del siguiete meú? Etrds Sop Esld Pltos priciples Pst Miles de pollo Filete de pescdo Beids
