UNIVERSIDAD POLITÉCNICA DE MADRID FACULTAD DE INFORMÁTICA GENERACIÓN DE TESELACIONES PERIÓDICAS: GRUPOS DE FRISO Y DE ROSETA.
|
|
|
- Agustín Peralta Rivero
- hace 7 años
- Vistas:
Transcripción
1 UNIVERSIDAD POLITÉCNICA DE MADRID FACULTAD DE INFORMÁTICA TRABAJO FIN DE CARRERA GENERACIÓN DE TESELACIONES PERIÓDICAS: GRUPOS DE FRISO Y DE ROSETA. AUTOR: Javier Pina Chavero TUTOR: Manuel Abellanas Oar
2 Para mis padres, mi hermana y Marina, por ser mi apoyo y mi base en todo momento a lo largo de toda la carrera, sobre todo en los momentos duros.
3 AGRADECIMIENTOS A D. Manuel Abellanas por su ayuda, interés e implicación en el proyecto. A mis amigos de la facultad por sus ayudas y continuos apoyos. A mis amigos y compañeros de trabajo de la FNMT-RCM con los que sin su ayuda esto no hubiese sido posible. A mis amigos de toda la vida por tener que aguantar mis tertulias informáticas. Y a todas las personas a las que he preguntado y que han aportado alguna idea a este proyecto. Muchas gracias.
4
5 ÍNDICE AGRADECIMIENTOS I INTRODUCCIÓN 1 CAPÍTULO 1 DESARROLLO TEÓRICO INTRODUCCIÓN MATEMÁTICA Geometría vs. geometría computacional Transformaciones geométricas Isometrías o movimientos Simetría central Simetría axial Simetría con deslizamiento Traslación Rotación o giro Homotecia Grupos de simetría de una figura plana GRUPOS DE FRISO Introducción y definiciones Clasificación de frisos Grupo de Friso F Grupo de Friso F Grupo de Friso F 3 (F 1 1 ) Grupo de Friso F 4 (F 2 1 ) Grupo de Friso F 5 (F 3 1 ) Grupo de Friso F 6 (F 1 2 ) Grupo de Friso F 7 (F 2 ) Tabla Resumen de Características de los Frisos GRUPOS PUNTUALES DE SIMETRÍA O DE LEONARDO Grupos cíclicos C n Grupos diédricos D n GRUPOS CRISTALOGRÁFICOS PLANOS 26 CAPÍTULO 2 DESARROLLO PRÁCTICO INTRODUCCIÓN DESARROLLO Algoritmo general de los frisos Algoritmo de generación del Friso 1 (F 1 ). 32 iii
6 Algoritmo de generación del Friso 2 (F 2 ) Algoritmo de generación del Friso 3 (F 1 1 ) Algoritmo de generación del Friso 4 (F 2 1 ) Algoritmo de generación del Friso 5 (F 3 1 ) Algoritmo de generación del Friso 6 (F 1 2 ) Algoritmo de generación del Friso 7 (F 2 2 ) Algoritmo general de las rosetas o rosetones Algoritmo de generación de las rosetas de tipo C n (grupos cíclicos) Calculo del triángulo fundamental de las rosetas de tipo C n Algoritmo de generación de la roseta C Algoritmo de generación de la roseta C Algoritmo de generación de la roseta C Algoritmo de generación de la roseta C Algoritmo de generación de la roseta C Algoritmo de generación de la roseta C n Algoritmo de generación de las rosetas de tipo D n (grupos diédricos) Cálculo del triángulo fundamental de las rosetas de tipo D n Algoritmo de generación de la roseta D Algoritmo de generación de la roseta D Algoritmo de generación de la roseta D Algoritmo de generación de la roseta D Algoritmo de generación de la roseta D Algoritmo de generación de la roseta D Algoritmo de generación de la roseta D n. 58 CAPÍTULO 3 MANUAL DE USUARIO INTRODUCCIÓN INTERFAZ DE USUARIO Área de dibujado Cuadro de selección de transformaciones Cuadro de funciones básicas Barra de menú Barra de estado MODO DE EJECUCIÓN. 66 CAPÍTULO 4 TECNOLOGÍAS EMPLEADAS LENGUAJE DE PROGRAMACIÓN Applets ventajas e inconvenientes ENTORNO DE DESARROLLO USADO 72 CAPÍTULO 5 RESULTADOS Y CONCLUSIONES RESULTADOS OBTENIDOS CONCLUSIONES PERSONALES 74 iv
7 BIBLIOGRAFÍA Y REFERENCIAS 76 v
8 Generación de teselaciones periódicas: frisos y rosetas INTRODUCCIÓN A lo largo de la historia se han utilizado motivos geométricos con fines decorativos. Aunque han sido muchos los objetos que han sido embellecidos con diseños geométricos regulares, tales como vasijas, tejidos, puertas, ventanas y otros elementos arquitectónicos, nos vamos a limitar a la ornamentación de muros y suelos. El arte de los recubrimientos o teselaciones del plano mediante figuras poligonales tiene una historia tan antigua como la propia civilización. Diversos e imaginativos patrones han decorado las construcciones y objetos más diversos (muros, alfombras, ventanales, etc.). En tiempos recientes el interés por las teselaciones ha ido más allá de su interés puramente decorativo. Por ejemplo, en metalurgia y cristalografía interesa saber cómo se disponen de manera natural de una forma periódica. En arquitectura interesa conocer cómo se pueden combinar componentes estructurales simples para crear complejos constructivos más grandes, y los fabricantes de ordenadores esperan poder integrar los patrones de circuitos electrónicos simples para formar potentes procesadores, como son las redes neuronales. El análisis matemático de los patrones de recubrimientos es una respuesta a estas necesidades contemporáneas. Al mismo tiempo la creación y exploración de las teselaciones o recubrimientos del plano proporciona un contexto interesante para la investigación geométrica y la resolución de problemas en las clases de matemáticas. El diccionario de la Real Academia Española de la Lengua indica que la palabra tesela (del latín, tessella) significa "Cada una de las piezas cúbicas de mármol, piedra, barro cocido o cualquier otro material, con que los antiguos formaban los pavimentos de mosaico" Desde un punto de vista matemático más general consideramos que una tesela es cualquier curva cerrada simple, con su interior. Un conjunto de teselas forma una teselación de una figura si dicha figura está completamente cubierta por las teselas sin solapamientos de puntos interiores de dichas figuras. El caso particular de recubrimientos del plano que nos interesa son los formados por polígonos; la figura que se recubre suele ser el plano completo [3]. Llamamos cubrimiento regular del plano al resultado de someter a una figura dada a repeticiones (isometrías planas) de forma que el plano quede recubierto de dichas figuras sin dejar huecos y sin que haya solapamientos. Si a una figura la sometemos a traslaciones en una sola dirección obtenemos los frisos, si la sometemos a dos traslaciones de direcciones distintas se obtienen los mosaicos y si la sometemos a rotaciones con un punto fijo obtenemos las rosetas o rosetones. Tanto los frisos como los mosaicos como las rosetas constituyen patrones geométricos, es decir, formas que se obtienen mediante una figura generadora (figura mínima) a la que se le aplica un grupo de transformaciones. 2
9 Generación de teselaciones periódicas: frisos y rosetas Los patrones geométricos son usados frecuentemente en motivos decorativos de paredes, alfombras, etc. Es necesario mostrar un fragmento de tamaño suficiente para mostrar el motivo que se repite indefinidamente. Un patrón puede tener otras simetrías además de la simetría por traslación. Sin embargo, las posibilidades son limitadas. Por ejemplo, la única simetría rotacional de un friso es media vuelta. El hecho de que sólo ciertas simetrías pueden coexistir en un patrón hace posible clasificar los tipos de simetrías de los patrones. En particular, se ha demostrado que hay sólo siete tipos de frisos, diecisiete tipos de mosaicos y dos tipos de roseta con un orden finito (dependiendo del ángulo de rotación) [3]. Este proyecto surge como respuesta a las inquietudes y curiosidades de cómo puede afectar la geometría a la vida cotidiana. Cabe reconocer que los grupos de simetría que se van a exponer a lo largo de este proyecto están presentes en el día a día de cada persona: en el pavimento de nuestras ciudades, los edificios tanto civiles como religiosos y el embaldosado y azulejado de muchos hogares, en diferentes manifestaciones culturales, como en la Alambra de Granada. Y no solo en arte y en matemáticas sino en muchas otras ciencias. Así, la simetría aparece en física, química, biología, geología, etc. El objetivo de este proyecto es la construcción de una aplicación que sea capaz de generar cualquiera de los grupos de simetría que existen en las matemáticas, en la que, partiendo de una fotografía como patrón geométrico, se rellene una figura finita (rosetas), una banda (frisos) o un mural (cristalográficos). El proyecto en su totalidad es de gran envergadura y puesto que es un proyecto ambicioso la propuesta se distribuyó entre dos personas, presentando así un valor añadido al Trabajo Fin de Carrera: el trabajo en equipo. Con ello se plantearon dos Trabajos de Fin de Carrera centrados en distintas partes del desarrollo. El presente documento junto con el correspondiente al Trabajo Fin de Carrera Generación de Teselaciones periódicas: grupos cristalográficos planos [9] describen por completo el sistema desarrollado, complementándose el uno al otro. Este documento se centra en los grupos que cubren figuras finitas y bandas o cintas (grupos de roseta y grupos de friso), mientras que el otro documento anteriormente mencionado detalla los grupos que cubren todo el plano: los grupos cristalográficos. 2
10
11 Generación de teselaciones periódicas: frisos y rosetas CAPÍTULO 1 DESARROLLO TEÓRICO 1.1 Introducción matemática Antes de adentrarnos en la teoría de frisos y rosetas se expondrá en este punto una breve explicación matemática de las funciones y términos geométricos, necesarios en la generación de dichos elementos Geometría vs. geometría computacional La geometría es la parte de las matemáticas que se encarga de estudiar el espacio en que vivimos a través de su medida y sus relaciones. La geometría computacional es una disciplina que se ocupa del diseño y análisis de algoritmos que resuelven problemas geométricos. En ella concurren elementos puramente matemáticos con cuestiones y herramientas propias de la informática. Se desprende por tanto, que es un campo bastante reciente (20 o 30 años). Sin embargo, sus antecedentes pueden encontrarse en la Grecia Clásica, hace 2600 años, donde los problemas geométricos que se planteaban los matemáticos de la época eran abordados desde el punto de vista constructivo, es decir, algorítmico. La palabra geometría (del griego geo, "tierra"; metrein, "medir") alude a "medir la tierra". Una antigua opinión, transmitida por Herodoto, atribuía el origen de la geometría a la necesidad de medir las tierras de labranza después de cada crecida del río Nilo, que podía modificar su extensión, con el objeto de fijar equitativamente el impuesto a pagar al rey. Del mismo modo, la necesidad de comparar las áreas y volúmenes de figuras simples, la construcción de canales y edificios, las figuras decorativas, los movimientos de los astros, contribuyeron también al nacimiento de esas reglas y propiedades geométricas que se encuentran en los documentos de las antiguas civilizaciones egipcia y mesopotámica. Evidentemente, el paso de herramientas de cálculo tales como la regla y el compás utilizadas por los griegos al ordenador electrónico digital, supone grandes cambios en el carácter y en el planteamiento de los problemas geométricos que se estudian. El ordenador aporta la capacidad de manejar un número grande de datos (elementos geométricos) y la rapidez en el cálculo. De hecho, son características habituales en los problemas que se abordan en Geometría Computacional el tratamiento de objetos geométricos relativamente simples: puntos, polígonos, segmentos, rectas, etc. pero en un gran número de ellos. 2
12 Por lo que hoy dichas reglas de geometría se utilizan en un sinfín de aplicaciones (gráficas por ordenador, modelación industrial, esterolitografía, etc. ), incluida la que se expone en este proyecto, y que en un primer vistazo uno no es consciente de que la fundamentación básica de su funcionamiento radica en reglas geométricas básicas. Pasaremos sin más a la descripción de algunas de esas reglas Transformaciones geométricas Una transformación geométrica, o simplemente una transformación, es una aplicación que hace corresponder a cada punto del plano otro punto del plano. Como consecuencia, las figuras se transforman en otras figuras. A estos transformados obtenidos también se les llama homólogos [17]. Las transformaciones más usuales son las traslaciones, rotaciones, simetrías y las homotecias. Todas ellas mantienen la forma de las figuras, pero pueden disminuir el tamaño y cambiar la figura de posición. 1. Una primera clasificación de las transformaciones sería: Directa: cuando conservan el sentido en el plano orientado. Inversa: cuando los sentidos del original y el homólogo son contrarios. 2. Otra clasificación sería en función del aspecto de la figura homologa respecto a la original: Isométricas: cuando conservan las dimensiones y ángulos; se denominan también movimientos: simetrías, traslaciones y giros. Isomórficas: cuando conservan la forma de la figura original (los ángulos). Existe proporcionalidad entre las dimensiones de la figura original y homóloga como la homotecia. Anamórficas: cuando cambia la forma de la figura original, por ejemplo la inversión. En este caso nos centramos en las isometrías y en la transformación isomórfica de la homotecia Isometrías o movimientos Como se ha mencionado anteriormente un movimiento o isometría es una transformación que preserva todas las distancias y por ello preserva el tamaño y la forma. (Nota: iso significa "igual" y metría significa "medida"). La imagen de una figura bajo esta transformación siempre es congruente con la figura original. Una definición más formal de movimiento sería: Sea A un espacio afín euclídeo de dimensión n, un movimiento g de A, es una aplicación afín tal que la aplicación lineal asociada f (del espacio R n ), es una isometría, es decir conserva las distancias. El conjunto de movimientos de A forma un grupo. Este grupo de los movimientos se puede clasificar de manera sencilla en: 4
13 Movimientos Directos (Det. (f)=1): Estos movimientos no cambian la orientación de una figura. Constituyen el subgrupo formado por las traslaciones y los giros o rotaciones. Movimientos Inversos (Det (f) = -1): Estos movimientos invierten la orientación de la figura. Pueden clasificarse en simetría central, simetría axial y simetría con deslizamiento Simetría central Una simetría central de centro O es una transformación que hace corresponder a cada punto P otro punto P tal que O es el punto medio del segmento PP. Figura 1.1: Imagen de simetría central. Una simetría de este tipo coincide con un giro del mismo centro y ángulo 180º. Es, por tanto, un movimiento directo. Algunas propiedades: El elemento característico de esta transformación es el Centro de Simetría (O). Es involutivo: la aplicación sucesiva de dos simetrías con el mismo centro de simetría obtiene el elemento original. La simetría central transforma rectas en rectas paralelas. Los elementos dobles son: el propio Centro de simetría, las rectas que pasan por él, y las circunferencias que tienen como centro el Centro de simetría (en este último caso es doble la entidad, pero no los puntos de la misma). 5
14 Simetría axial Una simetría axial de eje e es una transformación que hace corresponder a cada punto P otro punto P tal que la recta e es mediatriz del segmento PP. Figura 1.2: Imagen de simetría axial. Las simetrías axiales son movimientos inversos porque para hacer coincidir una figura con su simétrica es necesario sacarla del plano y abatirla de nuevo sobre la otra cara. Algunas propiedades: El elemento característico de esta transformación es el eje de simetría. Es involutivo y es inverso (como se ha explicado antes no conserva la relación de ordenación del plano, como puede verse en la figura del ejemplo). Los elementos dobles son: el propio eje de simetría e, las rectas perpendiculares al eje, y las circunferencias cuyo centro están situadas en el eje de simetría (en este último caso es doble la entidad, pero no los puntos de que esta compuesta) Simetría con deslizamiento Se trata de una combinación de dos movimientos: una traslación y una simetría axial, da igual el orden en que se apliquen, pues el resultado final es el mismo. Se denota por T a os r, si se aplica primero la simetría y después la traslación, y por S r ot a en caso contrario. (El símbolo o es el de la composición de dos movimientos). 6
15 Traslación Dado un vector t, una traslación es una transformación geométrica que hace corresponder a cada punto P otro punto P tal que PP = t Las traslaciones son movimientos directos, es decir, mantienen la forma y el tamaño de las figuras, a las cuales deslizan según el vector t. Figura 1.3: Imagen de una traslación. Algunas propiedades: Su elemento característico es un vector que nos define una dirección, un módulo y un sentido ( ). Es una transformación directa como se observa en la figura, pero no involutiva. Si existe, por el contrario, la traslación recíproca definida por el vector opuesto. Solo podemos considerar como elementos dobles las rectas cuya dirección sea la traslación, teniendo en cuenta que no son dobles los puntos de que están compuestas. 7
16 Rotación o giro Dado un centro O y ángulo α, un giro es una transformación geométrica que hace corresponder a cada punto P otro punto P tal que: y. Figura 1.4: Imagen de una rotación. Las Rotaciones son movimientos directos, es decir, mantienen la forma y el tamaño de las figuras. Algunas propiedades: Sus elementos característicos son el Centro de Giro y el Ángulo de Giro. Es una transformación directa. Los elementos dobles serían el Centro de Giro y las circunferencias cuyo centro es el Centro de Giro (en este último caso es doble la entidad, aunque no los puntos de que esta compuesta). 8
17 Homotecia La homotecia consiste en la formación de figuras semejantes en las que los puntos correspondientes están alineados dos a dos con respecto a otro punto fijo. Una homotecia de centro O y de razón k, lleva a toda recta que pasa por O a sí misma, y a una recta L que no pasa por O, a una recta L, paralela a L. Hemos de tener en cuenta que los lados aumentan si k>1, disminuyen si k<1 y se mantienen si k =1. Además, si k=1 decimos que los triángulos son congruentes, es decir, si los lados correspondientes son iguales y sus ángulos correspondientes son iguales. Figura 1.5: Imagen de una homotecia de centro O y razón 2. Algunas propiedades: A la vista del ejemplo anterior, podemos comprobar que los elementos característicos de la Homotecia serán su Centro de Homotecia (0) y la Razón de la Homotecia, que cumplirá: k = 0C /0C Para aquellos valores de k > 0, los elementos homotéticos estarán a un mismo lado del Centro de Homotecia, mientras que para valores inferiores a 0 estarán a distinto lado. Si k > 1 la figura homóloga será mayor, mientras que si es inferior a 1 será de menor tamaño. Como se vio en la definición de Transformación Isomórfica, se conservan los ángulos y las distancias serán proporcionales a k. Es una transformación directa Los elementos dobles serán el Centro de la Homotecia y las rectas que pasen por él teniendo en cuenta en este último caso que nos son dobles los puntos de dichas rectas Grupos de simetría de una figura plana Una definición formal de grupo de simetría sería: 9
18 Llamaremos grupo de simetría de la figura F al conjunto de movimientos del plano que dejan invariante la figura F. Por lo tanto, un movimiento f está en el grupo de simetría de F si y sólo si f(f) = F. De forma general, si H es cualquier figura del plano, el conjunto de movimientos que fijan a H es un subgrupo de O(R 2 ), el grupo de los movimientos en el plano. Este grupo asociado a H, que denotaremos por G H, se llama grupo de simetrías de H. Dicho grupo nos da una gran cantidad de información sobre los aspectos geométricos, y en especial las simetrías, de H. Se puede afirmar que mientras más simetrías posea la figura H, mayor será el grupo de simetrías asociado a ella. Toda figura simétrica está compuesta por una baldosa o forma básica K que se repite, mediante rotaciones, traslaciones y reflexiones de la figura básica. Entonces, al hacer actuar el grupo de simetrías de H sobre K, obtendremos toda la figura H. Usando el lenguaje de la teoría de grupos, podemos decir que H es la órbita de K bajo GH. Estos grupos GH, serán llamados grupos ornamentales del plano y se dividen en tres categorías [5], de acuerdo al tipo de traslaciones que se encuentren en G H : 1 Categoría Grupos de Frisos: El primer tipo de grupos, que admiten simetrías por traslación sólo en una dirección, corresponde a las decoraciones que vemos en los frisos de la fachada de los templos o en las paredes de nuestras viejas casas coloniales, para embellecer los zaguanes y las salas. Este tipo de grupo se les llama Grupo de Frisos. Figura 1.6: Imagen de un friso. 2 Categoría Grupos de Leonardo o Rosetas: Este segundo tipo de grupos, en donde no hay traslaciones, fue estudiado por Leonardo da Vinci, quien los utilizó en el diseño de las capillas dentro de las iglesias. Por esta razón se les denomina Grupos de Leonardo. Leonardo demostró que los únicos grupos posibles eran los Cíclicos C n y los Diédricos D n.en arquitectura es habitual ver el grupo D 2, en las pirámides el grupo D 4 y en algunas torres el D 6. El grupos D 5 es bastante inusual (una excepción es el Pentágono de Washington) pese a ser habitual en la naturaleza, por ejemplo en las flores. 10
19 Figura 1.7: Imagen de una roseta. 3 Categoría Mosaicos o Grupos Cristalográficos: El último grupo admite simetría por traslación en dos direcciones, la figura básica se repite en todo el plano infinitamente generando una celosía, embaldosado o mosaico. Estos son los llamados Grupos Cristalográficos Planos. Figura 1.8: Imagen de un mosaico. En 1891, el cristalógrafo E. S. Feodorov, demostró que sólo existen básicamente 17 grupos cristalográficos, al hacer una clasificación exhaustiva de ellos. Más tarde en 1897 F. Klein y R. Fricke redescubrieron este resultado. Es de hacer notar que los árabes en plena edad media, conocían ya éstos 17 grupos y los empleaban en la decoración de sus mezquitas, castillos y fortalezas. 1.2 Grupos de friso Introducción y definiciones Las figuras con este tipo de simetría consisten en la repetición de un mismo motivo a lo largo de una recta, dicho de forma matemática se trata de embaldosados periódicos. Para poder decir que el embaldosado es periódico, en comparación con simplemente una repetición, la repetición sucede de una manera regular. Este tipo de simetría se encuentra en numerosos motivos ornamentales. Un ejemplo sencillo se encuentra en los balcones de las casas, como los de la figura siguiente: F 11
20 F F Figura 1.9: Frisos en balcones. Es fácil observar que en cada uno de los frisos de la figura (Figura1.9) hay un motivo que se repite en la dirección del friso. Si se considera los grupos de simetría de los frisos F, F y F de la figura (Figura1.9) y se les denota respectivamente por G, G y G. Al considerar cada friso, se supone que no está limitado, es decir que continua indefinidamente tanto hacia a la izquierda como a la derecha [16]. Por lo tanto en los tres grupos de simetría hay traslaciones. Se observa que, además de las traslaciones mencionadas, pueden aparecer otros movimientos en cada grupo de simetría considerado, por ejemplo en el caso que se esta tratando aparecen: En G hay simetrías respecto de rectas verticales. El grupo G no contiene ningún tipo de simetrías, los únicos movimientos que contiene son traslaciones. El grupo G contiene simetrías respecto de rectas verticales, al igual que en G, pero además contiene la simetría respecto de la recta horizontal que divide el friso en dos partes iguales. Se observa que G también contiene giros. Interesa por tanto el estudio de cuántos tipos posibles de grupos de simetría pueden aparecer. Este número queda establecido en la clasificación que se verá más adelante. Se procede a exponer a continuación una serie de definiciones interesantes dentro de este grupo y por las que esta caracterizado: Si u es un vector del plano R 2, el grupo generado por la traslación de vector u, t u, está formado por todos los múltiplos enteros de dicha traslación: { t u } = { t n u n Z} Este grupo se denomina grupo cíclico infinito y se suele denotar por C. 12
21 Si se considera un motivo que se repita en un friso. La traslación que lleva dicho motivo sobre una de sus repeticiones deja invariante el friso y por lo tanto también cualquier múltiplo entero de la mencionada traslación. Es decir, todas esas traslaciones son movimientos de su grupo de simetría. Se observa también, en los ejemplos, que hay una recta horizontal que queda invariante por los movimientos de cada uno de los grupos de simetría G, G y G. De hecho estas dos condiciones anteriores caracterizan a los frisos y dan lugar a la siguiente definición: Se denota por T el grupo formado por todas las traslaciones del plano. Un grupo de simetría G de una figura plana, se dice que es el grupo de un friso si las traslaciones que contiene G son un grupo cíclico infinito, es decir, están generadas por una traslación. G T = { t u } = { t n u n Z} Donde u es un vector fijo. Además G ha de dejar invariante una recta, que se denomina recta centro del friso. Se observa que la recta centro ha de tener la dirección del vector u. Además el vector u es el vector no nulo de norma mínima tal que la traslación t u pertenece a G. Es claro de la definición y de la observación anterior, que los grupos G, G y G son grupos de un friso. Se observa también que G es un grupo que conserva la orientación mientras que G y G no conservan la orientación porque contienen simetrías. El grupo de un friso ha de dejar invariante a la recta centro del friso, por lo tanto los únicos movimientos que puede contener son de los tipos siguientes: La identidad (este movimiento siempre está en un grupo de simetría). Traslaciones en la dirección de la recta centro. Giros con centro un punto de la recta centro y ángulo Π. La simetría respecto de la recta centro. Simetrías respecto de rectas perpendiculares a la recta centro. Simetría con deslizamiento con eje la recta centro y deslizamiento en la dirección de dicha recta. De hecho los movimientos listados arriba forman el grupo de simetría de una recta del plano. Dada una figura cuyo grupo de simetría es un friso, llamamos vector fundamental u al vector no nulo y de norma mínima tal que la traslación t u pertenece al grupo de simetría. Llamamos rectángulo fundamental a cualquier rectángulo que contenga al motivo del friso y uno de cuyos lados coincide con el vector fundamental. 13
22 Figura 1.10: Rectángulos fundamentales. Es fácil deducir, que si se tiene un rectángulo fundamental, cualquier traslación suya en la dirección de la recta centro del friso es también un rectángulo fundamental Clasificación de frisos A continuación se propone una clasificación de todos los grupos de frisos posibles. Esta clasificación esta basada en el siguiente teorema: Sólo hay siete grupos de frisos esencialmente distintos, que denotamos por la letra F seguida de un subíndice, que denota el orden de los giros que aparecen, y añadimos un superíndice si el grupo no conserva la orientación. Giros de orden 2 Conserva la orientación No conserva la orientación NO F 1 F 1 1, F 1 2, F 1 3 SI F 2 F 2 1, F 2 2 Visto de una forma más gráfica sería: 14
23 Figura 1.11: Clasificación de Frisos Grupo de Friso F 1 El grupo de friso más sencillo es el que denotamos por F 1 y no es otro que el grupo cíclico infinito. Recordemos que este grupo no contiene más que traslaciones, de hecho está generado por una traslación[16]. La imagen de la siguiente figura es un friso cuyo grupo de simetría es F 1, donde hemos marcado unos rectángulos fundamentales. Figura 1.12: Friso F1. Figura 1.13: Paralelogramos fundamentales de F1. 15
24 El grupo de simetría de este friso sólo contiene las traslaciones múltiplo de la traslación t u, donde u es el vector fundamental que recordemos corresponde al lado horizontal del rectángulo fundamental marcado en azul. El grupo F 1 está generado por tanto por dicha traslación F 1 = {t u } = {t n u n Z} Grupo de Friso F 2 Este grupo de friso conserva la orientación por tanto sólo puede contener traslaciones y giros con centro en la recta centro del friso y ángulo Π. Figura 1.14: Friso 2. Figura 1.15: Paralelogramos fundamentales de F2. Figura 1.16: Centros de giro de F2. Los elementos de F 2 son las traslaciones múltiplos de t u y los giros con ángulo Π y los centros marcados en la figura. Observemos que los centros de los giros están en la recta centro del friso y distan entre sí ½ u. El grupo F 2 está generado por la traslación t u y uno de los giros g P0, Π con centro en un punto P 0 de la recta centro. F 2 = { t u, g P0, Π } = { t n u n Z} { g Pi Pi = P0 + i/2 u, n Z} El subíndice en la notación de los grupos de frisos, denota por tanto el orden máximo de los giros que aparecen en el grupo de simetría. Es decir, el subíndice 2 indica que aparecen giros de ese orden, que recordemos tienen ángulo Π. El subíndice 1 denota que 16
25 no hay giros propios en el grupo de simetría, salvo el giro de ángulo cero, que es la identidad Grupo de Friso F 3 (F 1 1 ) En este grupo de friso no aparecen giros de orden dos pero si existe una simetría respecto de la recta centro. Este nuevo grupo se denota con un superíndice 1, F 1 1. La siguiente figura es un ejemplo de un friso con grupo de simetría F 1 1. Figura 1.17: Friso 3. Figura 1.18: Paralelogramos de F3. Figura 1.19: Eje de simetría de F3. En la figura están señalados rectángulos fundamentales y el eje de simetría, que en este caso es la recta centro del friso. Observemos que F 1 1 está generado por la traslación t u y la simetría s respecto de la recta centro del friso. F 1 1 = { t u, s} Se puede dar una lista completa de todos los movimientos del grupo F 1 1., que se obtienen componiendo de todas las formas posibles la traslación t u y la simetría s: La identidad. La simetría s respecto de la recta centro. Las traslaciones de la forma t n u, donde n es un número entero. Las simetrías con deslizamiento con eje la recta centro del friso y deslizamiento n u, donde n es un número entero, t n u ο s 17
26 Grupo de Friso F 4 (F 1 2 ) Si no hay simetría respecto de la recta centro pero sí aparece alguna otra simetría, forzosamente su eje ha de ser perpendicular a la recta centro. De esta manera obtenemos el grupo de friso que denotamos F 1 2. Un ejemplo de un friso con este grupo de simetría aparece en la siguiente figura: Figura 1.20: Friso F 1 2. Figura 1.21: Paralelogramos Fundamentales de F 2 1. Figura 1.22: ejes de Simetría de F 1 2. Se observa que ahora aparecen infinitos ejes de simetría, separados entre sí una distancia igual a la mitad de la longitud del vector u. El grupo de simetría F 1 2 está generado por la traslación t u y una de las simetrías mencionadas, digamos s. F 1 2 = { t u, s } Los movimientos que contiene este grupo de simetría son: La identidad. Las traslaciones de la forma t n u, donde n es un número entero. Las simetrías con eje perpendicular a la recta centro del friso, que se obtienen componiendo s y la traslación t n u, es decir s n = t n u ο s Grupo de Friso F 5 (F 1 3 ) Puede ocurrir que no aparezca ningún eje de simetría, pero sí haya simetrías con deslizamiento. Este es el caso del grupo F 1 3. Un ejemplo de un friso con este grupo de simetría aparece en la siguiente figura. 18
27 Figura 1.23: Friso F 1 3. Figura 1.24: Paralelogramos fundamentales de F 1 3. Figura 1.25: Ejes de Simetría de F 1 3. Se Observa que aparece la simetría con deslizamiento s que se obtiene componiendo la simetría s respecto de la recta centro y la traslación t 1/2u, s = t 1/2u ο s. En este caso la recta centro es un eje de simetría con deslizamiento. El grupo F 1 3 está generado por la traslación t u y la simetría con deslizamiento s. F 1 3 = { t u, s } Los movimientos de este grupo de simetría son: La identidad. Las traslaciones de la forma t n u, donde n es un número entero. Las simetrías con deslizamiento de eje la recta centro del friso y deslizamiento n u + 1/2u, donde n es un número entero, s i = t n u ο s Grupo de Friso F 6 (F 2 1 ) Si aparece la simetría s respecto de la recta centro obtenemos el grupo F 2 1. Es fácil concluir que en este caso también obtenemos ejes de simetría perpendiculares a la recta centro, ya que el giro de ángulo Π y centro en un punto P 0 de la recta centro del friso g P0, Π puede expresarse como producto de la simetría s y una simetría s de eje perpendicular a la recta centro del friso, g P0, Π = s ο s. De donde s = s ο g P0, Π teniendo que s, g P0, Π F
28 Todos los centros de los giros de orden dos pertenecen a un eje de simetría. De hecho, los centros de orden dos son la intersección de dos ejes de simetría. Un ejemplo de un friso con este grupo de simetría aparece en la figura siguiente. Figura 1.26: Friso F 2 1. Figura 1.27: Paralelogramos Fundamentales de F 2 1 Figura 1.28: Ejes de Simetría y centros de Giro de F 2 1. Donde, como en los casos anteriores, señalamos un rectángulo fundamental y los ejes de simetría. Este grupo de simetría está generado por la traslación t u, un giro g P0, Π de ángulo Π y centro en P 0 que pertenece a la recta centro del friso, y la simetría s respecto de la recta centro. Pero también puede ser generado por la traslación t u, el giro g P0, Π y una simetría s respecto de un eje vertical, ya que g P0, Π = s ο s. F 2 1 = { t u, g P0, Π, s} = { t u, g P0, Π, s } = { t u, s, s } Los movimientos que contiene este grupo de simetría son La identidad. Las traslaciones de la forma t n u, donde n es un número entero. La simetría de eje la recta centro, s. Los giros con ángulo Π y centro en los puntos P n intersección de dos ejes de simetría, g Pn, Π = t n u ο g Pn, Π. Las simetrías de ejes perpendiculares a la recta centro que se obtienen componiendo los giros anteriores y la simetría respecto de la recta centro, 20
29 s n = g P0, Π ο s. Las simetrías con deslizamiento de eje la recta centro y deslizamiento n u, donde n es un número entero, t n u ο s. Este grupo de simetría contiene a F Grupo de Friso F 7 (F 2 2 ) Si el grupo de simetría que consideramos contiene a F 2 y no aparece simetría respecto de la recta centro, pero sí aparecen otras simetrías, entonces obtenemos el grupo F 2 2. Un ejemplo de un friso con este grupo de simetría aparece en la figura siguiente: Figura 1.29: Friso F 2 2. Figura 1.30: Paralelogramos Fundamentales de F 2 2. Figura 1.31: Ejes de Simetría y Centros de Giro de F 2 2. En este caso se observa que no hay ningún centro de giro de orden dos que esté en un eje de simetría. Los ejes de simetría son todos perpendiculares a la recta centro y pasan por el punto medio de los centros de dos giros. Este grupo de simetría está generado por la traslación t u, un giro g P0,Π de ángulo Π con centro en un punto P 0 de la recta centro y una simetría s respecto de un eje perpendicular a la recta centro. F 2 2 = { t u, g P0, Π, s } Los movimientos que contiene este grupo de simetría son 21
30 La identidad. Las traslaciones de la forma t n u, donde n es un número entero. Los giros g Pn, Π con ángulo Π y centros P n los puntos de la recta centro que equidistan de dos ejes de simetría, g Pn, Π = t n u ο g P0, Π. Las simetrías s n de ejes perpendiculares a la recta centro, s n = t n u ο s. Las simetrías con deslizamiento de eje la recta centro y deslizamiento n u + 1/2 u, donde n es un número entero, t n u ο g P0, Π ο s Tabla Resumen de Características de los Frisos Las características que aparecen para cada grupo de friso determinan dicho grupo [16]. Es decir, que un friso cuyo grupo de simetría cumpla las características que aparecen descritas en la siguiente tabla se puede asegurar que es del tipo señalado en ella. F 1 1 F 1 2 F 1 3 F 1 F 2 No hay giros de orden 2. No hay ejes de simetría ni ejes de simetrías con deslizamiento No hay giros de orden 2. La recta centro del friso es un eje de simetría. De hecho es el único eje de simetría que hay. No hay giros de orden 2. La recta centro no es eje de simetría, pero sí hay otros ejes de simetría perpendiculares a la recta centro. No hay giros de orden 2. No hay ningún eje de simetría. La recta centro es un eje de una simetría con deslizamiento. Hay giros de orden 2. No hay ejes de simetría. F 2 1 F 2 2 Hay giros de orden 2. La recta centro del friso es un eje de simetría. También aparecen ejes de simetría perpendiculares. Todos los centros de orden 2 están en la intersección de dos ejes de simetría. Hay giros de orden 2. La recta centro del friso no es un eje de simetría, pero hay ejes de simetría perpendiculares a la recta centro. Todos los centros de orden 2 están fuera de los ejes de simetría. 22
31 1.3 Grupos puntuales de simetría o de Leonardo. Un tipo especial de grupo de simetría es el llamado grupo puntual o de Leonardo, en honor a Leonardo da Vinci, quien utilizó tales grupos en algunos de sus diseños arquitectónicos de capillas. Un grupo de simetría S F de una figura plana F, se llama puntual o de Leonardo si S F es un grupo finito y existe un punto θ de F, fijo por todos los elementos de S F. A dicho punto se le denomina un centro de simetría de F [4]. Tales grupos no poseen traslaciones. Un polígono o una imagen tienen simetría rotacional si pueden ser rotados α grados y aparecen como si no hubiesen cambiado. Si el ángulo es α y n = 360 / α es un número entero, entonces se dice que la rotación es una rotación de orden n. Un grupo de simetría se dice que es de Leonardo si sólo contiene un número finito de movimientos. Si G es un grupo de simetría de Leonardo entonces existe un punto P del plano fijo por dicho grupo. Además, o bien G es el grupo generado por un giro de centro P (grupo cíclico), o bien G está generado por un giro de centro P y una simetría respecto de una recta que pasa por P (grupo diédrico). Según el Teorema de Leonardo, los únicos grupos puntuales de simetría de Leonardo son los grupos cíclicos C n o los grupos diédricos D n, para n = 1,2,... Una de las propiedades que cumplen los grupos diédricos es que para todo n 3, el grupo diédrico D n es exactamente el grupo de simetría del n-polígono regular. Estas son las simetrías que se cumplen en la aplicación de la que posteriormente hablamos. Figura 1.32: D 4 es el grupo de simetría del cuadrado 23
32 1.3.1 Grupos cíclicos C n. Los grupos cíclicos C n tienen simetría rotacional de orden n y no tienen simetría horizontal. Están generados por un giro g de orden n tal que: C n = g = { Id, g, g 2, g 3,..., g n-1 }. Para n = 1, el grupo consta de la identidad. Algunos ejemplos son: C 1 C 2 C 3 C 4 C 5 Figura 1.33: ejemplos de grupos cíclicos. 24
33 1.3.2 Grupos diédricos D n. Los grupos diédricos D n tienen simetría rotacional de orden n y simetría horizontal. Están generados por un giro g de orden n y una simetría s respecto de una recta que pasa por el centro de giro tal que: D n = g, s = { Id, g, g 2, g 3,..., g n-1, s, g o s, g 2 o s,..., g n-1 o s}. Para n = 1, el grupo D1 consta de la identidad y la simetría. Algunos ejemplos son: D 1 D 2 D 3 D 4 D 5 Figura 1.34: ejemplos de grupos diédricos. 25
34 1.4 Grupos cristalográficos planos 1 Cuando el grupo admite simetría por traslación en dos direcciones, la figura básica se repite en todo el plano infinitamente generando un mosaico. Fedorov demostró en 1891 que no hay más de 17 estructuras básicas para las infinitas decoraciones posibles del plano formado mosaicos periódicos. Son los 17 grupos cristalográficos planos. Cada uno de ellos recibe una denominación que procede de la cristalografía, y se pueden clasificar según la naturaleza de sus giros. Los 17 grupos de simetría del plano se pueden agrupar en cinco apartados, según el orden máximo de los giros: Grupos de simetría sin giros: 4 grupos de simetría. Grupos de simetría con giros de 180º: 5 grupos de simetrías Grupos de simetría con giros de 120º: 3 grupos de simetrías. Grupos de simetría con giros de 90º: 3 grupos de simetrías. Grupos de simetría con giros de 60º: 2 grupos de simetrías. Los árabes fueron unos excelentes creadores de mosaicos geométricos. Dado que su religión les impedía dibujar personas o animales, su creatividad se decantó hacia la caligrafía y los dibujos geométricos, en los que alcanzaron cotas de belleza y complejidad difícilmente superables. Los creadores de los mosaicos de la Alhambra no podían conocer el teorema de clasificación de Fedorov, y por lo tanto no conocían cuántos grupos de simetrías podían usarse para rellenar el plano con losetas (teselación del plano), por eso resulta impactante que conocieran todos y cada uno de los 17 existentes. Efectivamente, todos ellos están representados en los variados y bellísimos mosaicos de la Alhambra. Abundan los que tienen giros de 90º mientras que algunos grupos aparecen escasamente, pero absolutamente todos están representados. La lista completa de los grupos es la siguiente: p1: Dos traslaciones p2: Tres simetrías centrales (o giros de 180º) p3: Dos giros de 120º p4: Una simetría central (o giro de 180º) y un giro de 90º p6: Una simetría central y un giro de 120º pm: Dos simetrías axiales y una traslación pmm: Cuatro simetrías axiales en los lados de un rectángulo pmg: Una simetría axial y dos simetrías centrales cmm: Dos simetrías axiales perpendiculares y una simetría central 1 De este grupo de simetría se verá a continuación una breve descripción, puesto que serán desarrollados en profundidad en el proyecto de fin de carrera de título: Generación de Teselaciones periódicas: grupos cristalográficos planos [9] (cuya autora es Marina Rodríguez Silvestre) y que complementa la aplicación aquí presentada. 26
35 p31m: Una simetría axial y un giro de 120º p3m1: Tres simetrías axiales en los lados de un triángulo equilátero (ángulos ) p4g: Una simetría axial y un giro de 90º p4m: Tres simetrías axiales en los lados de un triángulo de ángulos p6m: Tres simetrías axiales en los lados de un triángulo de ángulos cm: Una simetría axial y una simetría con deslizamiento perpendicular pg: Dos simetrías con deslizamiento paralelas pgg: Dos simetrías con deslizamiento perpendiculares 27
36 CAPÍTULO 2 DESARROLLO PRÁCTICO 2.1 Introducción En este apartado se describirán los algoritmos utilizados para la generación, a partir de una imagen, tanto de los grupos de frisos como de los grupos de rosetas. La generación de los grupos cristalográficos queda pendiente en la otra parte del proyecto de fin de carrera de título: Generación de teselaciones periódicas: Grupos Cristalográficos Planos [9] (cuya autora es Marina Rodríguez Silvestre) y que complementa la aplicación aquí presentada. Los frisos, elementos sustanciales de la ornamentación clásica, tienen como denominador común la repetición de un determinado modulo, figura o motivo a lo largo de una banda rectangular, mientras que en las rosetas el motivo se repite a lo largo de una superficie circular, dándose siempre una periodicidad sistemática en la repetición del modulo, lo que constituye, precisamente, la base del ritmo que el friso o la roseta comunica. Por eso, en el diseño de frisos o rosetas existen de entrada dos grados de libertad: la elección del motivo generador y la elección de aquellas transformaciones que aplicadas al motivo inicial permiten llenar la banda rectangular que contiene el friso o la superficie circular que contiene la roseta o rosetón. Con la realización de este programa se han abordado todas las posibles transformaciones para ambos grupos, y el motivo generador va a correr a cargo de la imagen que el usuario cargue por pantalla. Esto quiere decir que se requiere un polígono (rectángulo en el caso de los frisos y triángulo en el caso de las rosetas) como figura generadora al que aplicar las transformaciones. A partir de un fichero grafico (.jpg,.gif, etc.) que contiene uno de estos polígonos, bien interno a la aplicación o bien creado por el usuario (como ocurre con las rosetas, en las que el polígono sobre el que se realizan las transformaciones tiene que ser un triángulo), se realizará la creación de un mosaico lineal (frisos periódicos) o uno radial (rosetones o rosetas) mediante el tipo de simetría seleccionada (7 tipos para los frisos y 13 tipos en las rosetas para este caso). El resultado de la transformación se mostrará por pantalla. 2.2 Desarrollo Algoritmo general de los frisos. 28
37 La generación de los frisos a partir de una imagen dada no resultó una tarea muy complicada debido en gran medida a que las únicas isometrías permitidas para estos grupos son cualquier grupo de isometrías del plano que dejan fija una recta r y que contienen como únicas Traslaciones al grupo generado por las Traslaciones de vector a, siendo éste el vector director de r. Las isometrías que pueden formar parte de un Grupo de Simetría con recta fija r son: Traslaciones Ta de vector, el vector a, vector director de r. Simetría axial Sr, cuyo eje es la recta r. Simetría axial Sr', cuyo eje r' es perpendicular a r. Giro G A 180º, siendo A un punto de la recta r. Las composiciones de las isometrías anteriores. Cualquier otro tipo de isometría violaría la condición de la invariabilidad de r Se han realizado 7 algoritmos para la generación de frisos periódicos, es decir, uno por cada grupo de simetría. Sin embargo todos parten de la misma base. Todos los algoritmos comienzan con la obtención de un fichero tipo grafico o de imágenes (ficheros con extensión jpg, gif, etc.). Este fichero contiene un polígono regular de partida. Cada uno de los 7 grupos de friso parte de un polígono regular específico, que en el caso de los frisos es un rectángulo, contenido en el fichero grafico: Los grupos de frisos utilizan todos el fichero grafico sin transformar, es decir, usan un rectángulo cuya longitud de los lados coincide con el alto y ancho del fichero grafico de partida. ancho Imagen alto Figura 2.1: dimensiones de la imagen original Cada una de las simulaciones requiere 2 fases: A partir del fichero grafico de partida se construye la transformación principal, aplicando diferentes giros, simetrías y desplazamientos según el tipo de simetría. Una vez que se ha generado la transformación principal, se construye el grupo de simetría, bien aplicando sucesivas traslaciones en el caso de los frisos, bien aplicando sucesivas rotaciones como en el caso de las rosetas. 29
38 El organigrama general podría ser el siguiente: Leer polígono de partida Generar transformación principal Generar friso Figura 2.2: organigrama general del algoritmo de la generación de los frisos Una vez leído el fichero gráfico, la fase del algoritmo que genera la transformación principal es distinta para cada grupo de simetría. Por otra parte, en la fase de generación del grupo a partir de la transformación principal se aplica reiteradamente a la transformación traslaciones de un vector. Para dibujar el friso en pantalla se ha tomado como origen de coordenadas el punto superior izquierdo de la superficie de dibujado, por lo que las coordenadas del eje x crecen hacia la derecha y las coordenadas del eje y crecen hacia abajo. Esto se ha realizado así para facilitar el manejo de las transformaciones y posicionamientos en la superficie de dibujado, que cuenta con el mismo sistema de coordenadas, ya que si no fuese así, para cualquier transformación habría que añadir una conversión de un sistema a otro. (0,0) X Y Figura 2.3: sistema de coordenadas de la superficie de dibujado. 30
39 También cabe destacar que el posicionamiento del friso en la superficie de dibujado no se ha situado en la esquina superior izquierda como se podría suponer, sino que, por cuestiones de estética, se ha centrado en la pantalla. friso Superficie de dibujado Figura 2.4: posicionamiento del friso en la superficie de dibujado 31
40 Algoritmo de generación del Friso 1 (F 1 ). La generación de este friso es la mas sencilla de todas, pues el grupo esta formado solo por traslaciones. El dominio fundamental es un rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. D C A B Figura 2.5: rectángulo fundamental ABCD Para generar el friso se parte del rectángulo ABCD y a partir de él se generan las correspondientes traslaciones según el vector AB cuya longitud es igual al ancho de la imagen de partida. El grupo de simetría de este friso sólo contiene las traslaciones múltiplo de la traslación t AB. Mediante la traslación del rectángulo ABCD se genera la banda que origina el friso. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: traslación de la imagen una distancia igual a su ancho (vector AB ). Paso 3: repetir el paso 2 incrementando la longitud de dicha traslación en múltiplos del vector AB hasta que la imagen llegue al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado. 32
41 Algoritmo de generación del Friso 2 (F 2 ). Este friso esta formado por giros con centro en la recta horizontal que pasa por el centro de la imagen y ángulo 180º. Como en la generación del friso anterior y en la generación de los frisos posteriores partimos de rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. A partir de él, realizamos un giro de 180º sobre el punto de la recta centro perteneciente a la imagen situado a la derecha. A partir de este giro generamos las correspondientes traslaciones cuya longitud del vector de traslación es múltiplo del doble del ancho del rectángulo inicial (rectángulo inicial + rectángulo rotado). D C Centro de giro Recta centro A B Figura 2.6: triángulo fundamental ABCD D C F Recta centro A B E Figura 2.7: rotación del rectángulo ABCD sobre el centro de giro El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: Hacemos una rotación del rectángulo ABCD con centro de giro el punto de la recta centro mas a la derecha que pertenece también a la imagen. Paso 3: traslación del rectángulo AEFD una distancia igual al vector AE. Paso 4: repetir el paso 3 incrementando la longitud de dicha traslación en múltiplos del vector de traslación AE hasta que la imagen llegue al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado. 33
42 Algoritmo de generación del Friso 3 (F 1 1 ). Este friso esta formado por una simetría vertical respecto de la recta centro del friso combinado con las consiguientes traslaciones. Como en la generación de todos los frisos partimos de rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. A partir de él, realizamos una simetría vertical de dicho rectángulo tomando como eje de simetría la recta centro. A partir de esta simetría generamos las correspondientes traslaciones cuya longitud del vector de traslación es el ancho del rectángulo inicial ABCD. D C Recta centro = Eje de simetría A B E F Figura 2.8: simetría vertical del rectángulo ABCD sobre el eje de simetría El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: Hacemos una simetría vertical del rectángulo ABCD con eje de simetría la recta centro. Paso 3: traslación de los rectángulos una distancia igual a su ancho (vector AB ). Paso 4: repetir el paso 3 incrementando la longitud de dicha traslación en múltiplos del vector de traslación del paso 3 (vector AB ) hasta que los rectángulos lleguen al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado Algoritmo de generación del Friso 4 (F 1 2 ). Este friso esta formado por una simetría horizontal seguido de las consiguientes traslaciones. Como en la generación de todos los frisos partimos de rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. A partir de él, realizamos una simetría horizontal de dicho rectángulo tomando como eje de simetría la recta vertical perpendicular a la 34
43 recta centro y que es coincidente con el lado derecho del rectángulo (lado BC). A partir de esta simetría generamos las correspondientes traslaciones cuya longitud del vector de traslación es el doble del ancho del rectángulo inicial (rectángulo inicial + rectángulo de la simetría). Eje de simetría D C F Recta centro A B E Figura 2.9: simetría horizontal del rectángulo ABCD sobre el eje de simetría El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: Hacemos una simetría horizontal del rectángulo con eje de simetría la recta perpendicular a la recta centro y que pasa por el lado derecho del rectángulo. Paso 3: traslación de los rectángulos una distancia igual a dos veces su ancho (vector AE ). Paso 4: repetir el paso 3 incrementando la longitud de dicha traslación en múltiplos del vector de traslación del paso 3 (vector AE ) hasta que los rectángulos lleguen al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado Algoritmo de generación del Friso 5 (F 1 3 ). Friso formado por una simetría con deslizamiento seguido de las consiguientes traslaciones. Como en la generación de todos los frisos partimos de rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. A partir de él, realizamos una simetría con deslizamiento (que se obtiene componiendo la simetría respecto de la recta horizontal que pasa por el centro del rectángulo y la traslación de longitud el ancho del rectángulo (vector AB )). A partir de esta simetría generamos las correspondientes traslaciones cuya longitud del vector de traslación es el doble del ancho del rectángulo inicial (rectángulo inicial + rectángulo de la simetría). 35
44 D C F Recta centro = Eje de simetría A B E Figura 2.10: simetría con reflexión del rectángulo ABCD respecto del eje de simetría. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: Hacemos una simetría con deslizamiento del rectángulo. Paso 3: traslación de los rectángulos una distancia igual a dos veces su ancho (vector AE ). Paso 4: repetir el paso 3 incrementando la longitud de dicha traslación en múltiplos del vector de traslación del paso 3 (vector AE ) hasta que los rectángulos lleguen al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado Algoritmo de generación del Friso 6 (F 2 1 ). Este friso esta formado por una simetría vertical seguido de un giro de ángulo 180º con centro en la recta centro del friso y seguido de unas traslaciones. Como en la generación de todos los frisos partimos de rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. A partir de él, realizamos una simetría vertical de dicho rectángulo tomando como eje de simetría la recta centro. A partir de ella, realizamos un giro de 180º sobre el punto de la recta centro perteneciente al rectángulo situado a la derecha (vértice B). A partir de este giro generamos las correspondientes traslaciones cuya longitud del vector de traslación es el doble del ancho del rectángulo inicial (vector EG ). D C A B Recta centro = Eje de simetría E F Figura 2.11: simetría vertical del rectángulo ABCD sobre el eje de simetría. 36
45 D C I Centro de giro A B H Recta centro E F G Figura 2.12: rotación de 180º del rectángulo EFCD con centro de giro el punto B El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: Hacemos una simetría vertical del rectángulo con eje de simetría la recta centro (generando el rectángulo EFCD). Paso 3: Hacemos una rotación de dicho rectángulo EFCD con centro de giro el punto de la recta centro mas a la derecha que pertenece también al rectángulo FECD (punto B), generando el rectángulo EGID. Paso 4: traslación del rectángulo EGID una distancia igual a su ancho (vector EG ). Paso 5: repetir el paso 4 hasta que los rectángulos lleguen al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado Algoritmo de generación del Friso 7 (F 2 2 ). Este friso esta formado por una simetría horizontal seguido de un giro de ángulo 180º con centro en la recta centro del friso y seguido de unas traslaciones. Como en la generación de todos los frisos partimos del rectángulo ABCD que coincide con las dimensiones de la imagen inicial, por lo que no hay que hacer ningún tipo de transformación inicial. A partir de él, realizamos una simetría horizontal de dicho rectángulo tomando como eje de simetría la recta vertical perpendicular a la recta centro y que es coincidente con el lado derecho del rectángulo (lado BC). A partir de ella, realizamos un giro de 180º sobre el punto de la recta centro perteneciente al rectángulo situado a la derecha. A partir de este giro generamos las correspondientes traslaciones cuya longitud del vector de traslación es cuatro veces el ancho del rectángulo inicial. 37
46 Eje de simetría D C F Recta centro A B E Figura 2.13: simetría horizontal del rectángulo ABCD respecto del eje de simetría. D C Recta centro F Centro de giro H A B E G Figura 2.14: rotación de 180º del rectángulo AEFD respecto del centro de giro. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado derecho de la superficie de dibujado. Paso 2: Hacemos una simetría horizontal del rectángulo ABCD con eje de simetría la recta perpendicular a la recta centro y que pasa por el lado derecho del rectángulo (lado BC). Paso 3: Hacemos una rotación del rectángulo resultante AEFD con centro de giro el punto de la recta centro mas a la derecha que pertenece también al nuevo rectángulo. Paso 4: traslación del rectángulo AGHD una distancia igual a su ancho (vector AG ). Paso 5: repetir el paso 4 hasta que los rectángulos lleguen al final de la superficie de dibujo (hasta completar la fila). Si se ha llegado, el algoritmo ha terminado. 38
47 2.2.2 Algoritmo general de las rosetas o rosetones. El teorema de Leonardo dice que hay dos tipos de patrones de rosetas: C n, el cual tiene simetría rotacional de orden n y no tiene simetría horizontal (grupo cíclico). D n, el cual tiene simetría rotacional de orden n y simetría horizontal (grupo diédrico). La generación de las rosetas a partir de una imagen dada tampoco resultó una tarea muy complicada debido en gran medida a que las únicas isometrías permitidas para estos grupos son las simetrías rotacionales que dependen del orden del grupo de roseta que se quiera representar y, en todo caso, una simetría horizontal para representar las rosetas de tipo D n. Las rosetas representadas en esta aplicación para ambos tipos han variado hasta llegar al orden 6. También se ha creado una roseta para cada modelo en el que el orden es relativamente infinito. Se ha obviado el algoritmo del grupo C 1 por ser trivial. Se han realizado 13 algoritmos para la generación de rosetas, es decir, uno por cada grupo de simetría. Sin embargo todos parten de la misma base. Todos los algoritmos comienzan con la obtención de un fichero tipo grafico o de imágenes (ficheros con extensión jpg, gif, etc.). Este fichero contiene un polígono regular de partida. Cada uno de los 13 grupos de roseta parte de un polígono regular específico. Los grupos de roseta necesitan un triángulo como polígono de partida. El tipo de triángulo es distinto para cada grupo: Los grupos cíclicos C n necesitan un triángulo isósceles cuyo vértice superior tenga un ángulo determinado dependiendo del grupo del que se trate. Figura 2.15: triángulo inicial de los grupos cíclicos Los grupos diédricos D n necesitan un triángulo rectángulo. Figura 2.16: triángulo inicial de los grupos diédricos 39
48 Cada una de las simulaciones requiere 2 fases: A partir del fichero gráfico de partida se construye la transformación principal, aplicando diferentes giros, simetrías y desplazamientos según el tipo de simetría. Una vez que se ha generado la transformación principal, se construye el grupo de simetría, aplicando sucesivas rotaciones en el caso de las rosetas. El organigrama general podría ser el siguiente: Leer polígono de partida Generar transformación principal Generar roseta Figura 2.17: organigrama general del algoritmo de la generación de las rosetas Una vez leído el fichero gráfico, la fase del algoritmo que genera la transformación principal es distinta para cada grupo de simetría. Por otra parte, en la fase de generación del grupo a partir de la transformación principal se aplica reiteradamente a la transformación rotaciones sobre un punto fijo. Para dibujar la roseta en pantalla se ha tomado como origen de coordenadas el punto superior izquierdo de la superficie de dibujado, por lo que las coordenadas del eje x crecen hacia la derecha y las coordenadas del eje y crecen hacia abajo. Esto se ha realizado así para facilitar el manejo de las transformaciones y posicionamientos en la superficie de dibujado, que cuenta con el mismo sistema de coordenadas, ya que si no fuese así, para cualquier transformación habría que añadir una conversión de un sistema a otro. 40
49 (0,0) X Y Figura 2.18: sistema de coordenadas de la superficie de dibujo. También cabe destacar que el posicionamiento de la roseta en la superficie de dibujado no se ha situado en la esquina superior izquierda como se podría suponer, sino que, por cuestiones de estética, se ha centrado en la pantalla. roseta Superficie de dibujado Figura 2.19: posicionamiento de la roseta en la superficie de dibujado Algoritmo de generación de las rosetas de tipo C n (grupos cíclicos). La generación de las rosetas de tipo C n son más sencillas que las rosetas de tipo D n como ya hemos anunciado anteriormente, al solo disponer de simetría rotacional. El subíndice nos indica el número de rotaciones que se hacen al dar una vuelta completa. Se ha obviado la representación del grupo de roseta C 1 ya que es inmediato. Representa ciclos con giros de 360º. El dominio fundamental de este grupo es el triángulo. Si se supone que las dimensiones de la imagen es el rectángulo ABCD, se necesita coger un triángulo como el que aparece en la siguiente figura. D E C A F G B Figura 2.20: dominio fundamental de los grupos cíclicos 41
50 Este triángulo es el que contiene la imagen original. Un fichero gráfico que contenga una imagen siempre tiene dimensiones rectangulares, por lo que el triángulo esta incluido en el rectángulo. La parte del rectángulo que no pertenece al triángulo tiene que ser transparente a la aplicación. La forma que tiene que adoptar el triángulo para poder generar los grupos cíclicos depende de cual de ellos se quiera representar. Lo único que varia de un grupo a otro es el ángulo del vértice E del triángulo. Entonces, para poder generar una roseta de un grupo C n solamente hay que hacer la sencilla operación de dividir el ángulo que tiene la circunferencia completa entre el orden del grupo cíclico (360 / n) para hallar el ángulo que tiene que tener el vértice E. Es decir, si se quiere hallar las dimensiones del triángulo que se necesita para generar el grupo C 6 a partir de la imagen inicial, solamente debemos saber que el ángulo del vértice superior del triángulo debe valer 360 / 6 = 60º Cálculo del triángulo fundamental de las rosetas de tipo C n. Una vez que ya conocemos el valor del ángulo del vértice superior del triángulo, calcular las longitudes de los lados a partir del rectángulo que forma la imagen es simplemente aplicar las formulas del triángulo y de la trigonometría circular. D E C A F G B Figura 2.21: triángulo fundamental Si se conocen los valores tanto del ancho como del alto del rectángulo que contiene a la imagen, se puede saber que la altura del triángulo es igual al alto del rectángulo. Si se corta ese triángulo por la mitad, se obtiene otro triángulo del que ahora se saben los valores de dos de los ángulos y uno de los lados. Es más, se sabe que uno de los ángulos es un ángulo recto (90º), por lo que se pueden aplicar las formulas del seno y coseno. F a b P h E Figura 2.22: lados y vértices de un triángulo rectángulo. 42
51 Se sabe que el ángulo del vértice P es un ángulo recto (90º), también se sabe cuanto mide el ángulo del vértice E, que es la mitad que el ángulo del triángulo de arriba (triángulo FGE), es decir, 360/2n. Por ultimo, se sabe cual es la medida del lado PE, que es igual al largo de la foto, es decir, h. Por lo tanto: tan(α) = a/h a = tan(α) * h, siendo α= 360/2n Una vez que se sabe el valor de a y de h, se puede adivinar el valor de b por medio del teorema de Pitágoras: b 2 = a 2 + h 2 Por lo tanto, ya se tienen los valores de los tres lados del triángulo, ya se puede recortar sobre la imagen original el triángulo que se necesita en cada grupo. Cabe tener en cuenta que dependiendo del ancho de la imagen, si se aplicara lo que previamente se ha explicado, la figura que saliese no fuera un triángulo, sino un pentágono irregular. Figura 2.23: pentágono irregular En este caso, se recortaría el triángulo quitando el rectángulo de la base. Lo quitamos Figura 2.24: triángulo resultante de quitar la base al pentágono irregular 43
52 Algoritmo de generación de la roseta C 2. En el caso que nos ocupa, para la generación de la roseta de tipo C2 se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/n 360/2 = 180º. Como eso es imposible debido a que la suma de los tres ángulos de un triángulo debe ser de 180º, para este caso se hace una excepción y se coge como figura inicial transformada la propia figura inicial, es decir, el rectángulo ABCD. D C A B Figura 2.25: polígono fundamental de la roseta C 2 Para generar la roseta se parte del rectángulo ABCD y a partir de él se generan las correspondientes rotaciones de 180º, obteniendo una roseta rectangular. Obsérvese que una vez que se ha hecho la primera rotación la roseta ya se encuentra completa, por lo que el nº de rotaciones que se tienen que hacer es de (n-1). El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen a partir del borde centrado de la superficie de dibujado. Paso 2: se gira el rectángulo un ángulo de 180º. Paso 3: como si se vuelve a repetir el paso se vuelve a pintar el rectángulo original, hemos terminado. El resultado es un rectángulo Algoritmo de generación de la roseta C 3. Esta roseta esta formada por rotaciones múltiplo de ángulo 360/n como n = 3 360/3 = 120º. Para la generación de la roseta de tipo C 3 necesitamos coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/n 360/3 = 120º. D E C A F G B Figura 2.26: polígono fundamental de la roseta C 3 44
53 Una vez que se obtiene el triángulo y que dicho vértice superior se encuentra situado en el centro de la superficie de pintado, se comienzan a generar las rotaciones. Para generar la roseta se parte del triángulo EFG y a partir de él se generan las correspondientes rotaciones de 120º. El nº de rotaciones que necesitamos es (n-1) = 2 y el numero de imágenes es n = 3. La roseta generada es un triángulo equilátero. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el triángulo EFG que contiene la imagen con el vértice E en el centro de la superficie de dibujado. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 2: giramos la imagen un ángulo de (120º * contador) e incrementamos el valor del contador en 1. Paso 3: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta C 4. Esta roseta esta formada por rotaciones múltiplo de ángulo 360/n como n = 4 360/4 = 90º. Para la generación de la roseta de tipo C 4 necesitamos coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/n 360/4 = 90º. D E C A F G B Figura 2.27: polígono fundamental de la roseta C 4 Una vez que se obtiene el triángulo y que dicho vértice superior se encuentra situado en el centro de la superficie de pintado, se comienzan a generar las rotaciones. Para generar la roseta se parte del triángulo EFG y a partir de él se generan las correspondientes rotaciones de 90º. El nº de rotaciones que necesitamos es (n-1) = 3 y el numero de imágenes es n = 4. La roseta generada es un cuadrado. 45
54 El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el triángulo EFG que contiene la imagen con el vértice E en el centro de la superficie de dibujado. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 2: giramos la imagen un ángulo de (90º * contador) e incrementamos el valor del contador en 1. Paso 3: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta C 5. Esta roseta esta formada por rotaciones múltiplo de ángulo 360/n como n = 5 360/5 = 72º. Para la generación de la roseta de tipo C 5 necesitamos coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/n 360/5 = 72º. D E C A F G B Una vez que se obtiene el triángulo y que dicho vértice superior se encuentra situado en el centro de la superficie de pintado, se comienzan a generar las rotaciones. Para generar la roseta se parte del triángulo EFG y a partir de él se generan las correspondientes rotaciones de 72º. El nº de rotaciones que necesitamos es (n-1) = 4 y el numero de imágenes es n = 5. La roseta generada es un pentágono regular. El algoritmo es el siguiente: Figura 2.28: polígono fundamental de la roseta C 5 Paso 1: carga de la imagen original. Se dibuja el triángulo EFG que contiene la imagen con el vértice E en el centro de la superficie de dibujado. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 2: giramos la imagen un ángulo de (72º * contador) e incrementamos el valor del contador en 1. 46
55 Paso 3: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta C 6. Esta roseta esta formada por rotaciones múltiplo de ángulo 360/n como n = 6 360/6 = 60º. Para la generación de la roseta de tipo C 6 necesitamos coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/n 360/6 = 60º. D E C A F G B Una vez que se obtiene el triángulo y que dicho vértice superior se encuentra situado en el centro de la superficie de pintado, se comienzan a generar las rotaciones. Para generar la roseta se parte del triángulo EFG y a partir de él se generan las correspondientes rotaciones de 60º. El nº de rotaciones que necesitamos es (n-1) = 5 y el numero de imágenes es n = 6. La roseta generada es un hexágono regular. El algoritmo es el siguiente: Figura 2.29: polígono fundamental de la roseta C 6 Paso 1: carga de la imagen original. Se dibuja el triángulo EFG que contiene la imagen con el vértice E en el centro de la superficie de dibujado. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 2: giramos la imagen un ángulo de (60º * contador) e incrementamos el valor del contador en 1. Paso 3: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta C n. Esta roseta, al igual que el grupo de roseta D n, es un poco especial. Se trata de un grupo cíclico que representa a todos los grupos cíclicos previamente descritos e incluso, como 47
56 la cardinalidad de estos grupos es infinita, también a grupos cíclicos cuyo orden es mayor (C 7, C 8, C 10, C 12,...). Parte de la roseta C 2 y en cada paso va originando una roseta de orden mayor. Cuanto mayor sea el orden de la roseta, el polígono generado va tendiendo a parecerse a un círculo, ya que los lados de dicho polígono se van haciendo más pequeños. En el programa se ha puesto un limite al orden calculado en 30 (grupo cíclico C 30 ), ya que a partir de ahí la diferencia entre los polígonos generados es casi despreciable. El algoritmo es el siguiente: Se parte de la imagen original. Paso 1: Se realiza el grupo de roseta C 2. Paso 2: Se realiza el grupo de roseta C Paso n: Se realiza el grupo de roseta C n Algoritmo de generación de las rosetas de tipo D n (grupos diédricos). La generación de las rosetas de tipo D n son algo mas complejas que las rosetas de tipo D n ya que, además de disponer de simetría rotacional tienen simetría horizontal. El subíndice nos indica el número de rotaciones que se hacen al dar una vuelta completa. Cada roseta esta compuesta por n simetrías rotacionales y n simetrías horizontales o de espejo. El dominio fundamental de este grupo es el triángulo. Si se supone que las dimensiones de la imagen es el rectángulo ABCD, se necesita coger un triángulo como el que aparece en la siguiente figura. D C A E B Figura 2.30: polígono fundamental de los grupos diédricos El triángulo EBC es el que contiene la imagen original. Un fichero gráfico que contenga una imagen siempre tiene dimensiones rectangulares, por lo que el triángulo esta incluido en el rectángulo. La parte del rectángulo que no pertenece al triángulo tiene que ser transparente a la aplicación. La forma que tiene que adoptar el triángulo para poder generar los grupos cíclicos depende de cual de ellos se quiera representar. Lo único que varia de un grupo a otro es el ángulo del vértice C del triángulo. 48
57 Entonces, para poder generar una roseta de un grupo D n solamente hay que hacer la sencilla operación de dividir el ángulo que tiene la circunferencia completa entre el doble del orden del grupo cíclico (360 / 2n) para hallar el ángulo que tiene que tener el vértice C. Es decir, si se quiere hallar las dimensiones del triángulo que se necesita para generar el grupo D 6 a partir de la imagen inicial, solamente debemos saber que el ángulo del vértice superior del triángulo debe valer 360 / 2*6 = 30º. Cabe destacar que esta vez se divide la circunferencia entre dos veces su orden ya que en este tipo de grupos de roseta previa a las sucesivas rotaciones hay una simetría horizontal, encargada de duplicar el triángulo sobre el que se van a realizar las sucesivas rotaciones Cálculo del triángulo fundamental de las rosetas de tipo D n. Una vez que ya conocemos el valor del ángulo del vértice superior del triángulo, calcular las longitudes de los lados a partir del rectángulo que forma la imagen es simplemente aplicar las formulas del triángulo y de la trigonometría circular. D C A E B Figura 2.31: polígono fundamental Si se conocen los valores tanto del ancho como del alto del rectángulo que contiene a la imagen, se puede saber que la altura del triángulo es igual al alto del rectángulo. Al ser un triángulo rectángulo, la altura es igual a uno de sus lados. Es más, se sabe que uno de los ángulos es un ángulo recto (90º), por lo que se pueden aplicar las fórmulas del seno y coseno. b C h E a B Figura 2.32: lados y vértices de un triángulo rectángulo 49
58 Se sabe que el ángulo del vértice B es un ángulo recto (90º), también se sabe cuanto mide el ángulo del vértice C, es decir, 360/2n. Por ultimo, se sabe cual es la medida del lado BC, que es igual al largo de la foto, es decir, h. Por lo tanto: tan(α) = h/a a = h/ tan(α), siendo α= 360/2n Una vez que se sabe el valor de a y de h, se puede adivinar el valor de b por medio del teorema de Pitágoras: b 2 = a 2 + h 2 Por lo tanto, ya se tienen los valores de los tres lados del triángulo, ya se puede recortar sobre la imagen original el triángulo que se necesita en cada grupo. Cabe tener en cuenta que dependiendo del ancho de la imagen, si se aplicara lo que previamente se ha explicado, la figura que saliese no fuera un triángulo, sino un cuadrilátero irregular. En este caso, se recortaría Figura el triángulo 2.33: cuadrilátero quitando irregular el rectángulo de la base. Lo quitamos Figura 2.34: triángulo resultante de quitar la base al cuadrilátero irregular 50
59 Algoritmo de generación de la roseta D 1. En el caso que nos ocupa, para la generación de la roseta de tipo D 1 se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/2n 360/2 = 180º. Como eso es imposible debido a que la suma de los tres ángulos de un triángulo debe ser de 180º y en este caso, al tener ya uno de ellos 90º tampoco poder ser mayor o igual a 90º, para este caso se hace una excepción y se coge como figura inicial transformada la propia figura inicial, es decir, el rectángulo ABCD. D C A B Figura 2.35: polígono fundamental de la roseta D 1 Para generar la roseta se parte del rectángulo ABCD y a partir de el se genera su simetría horizontal respecto del eje de simetría que contiene al segmento BC. Eje de simetría D C F A B E Figura 2.36: simetría horizontal del rectángulo ABCD sobre el eje de simetría Posteriormente se generan las correspondientes rotaciones de 360º/n = 360, obteniendo una roseta rectangular. Como generar una rotación de 360º es dar una vuelta completa, este grupo no dispone de ninguna rotación. El nº de imágenes con sus correspondientes simetrías es n = 1 y el nº de rotaciones es (n 1) = 0. 51
60 El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen con el vértice C en el centro de la superficie de dibujado. Paso 2: se realiza una simetría horizontal respecto al eje de simetría que contiene al segmento BC. Paso 3: como si se vuelve a repetir el paso se vuelve a pintar el rectángulo original, hemos terminado. El resultado es un rectángulo Algoritmo de generación de la roseta D 2. Para este caso, la generación de la roseta de tipo D 2, se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/2n 360/4 = 90º. Como eso no es posible debido a que el triángulo es un triángulo rectángulo, y por lo tanto, al tener ya uno de ellos 90º no puede ser mayor o igual a 90º, para este caso se hace una excepción y se coge como figura inicial transformada la propia figura inicial, es decir, el rectángulo ABCD. D C A B Figura 2.37: polígono fundamental de la roseta D 2 Para generar la roseta se parte del rectángulo ABCD y a partir de él se genera su simetría horizontal respecto del eje de simetría que contiene al segmento BC. Eje de simetría D C F A B E Figura 2.38: simetría horizontal del rectángulo ABCD respecto del eje de simetría 52
61 Posteriormente se generan las correspondientes rotaciones de 360º/n = 360/2 = 180, obteniendo una roseta rectangular. El nº de imágenes con sus correspondientes simetrías es n = 2 y el nº de rotaciones es (n 1) = 1. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el rectángulo ABCD que contiene la imagen con el vértice C en el centro de la superficie de dibujado. Paso 2: se realiza una simetría horizontal respecto al eje de simetría que contiene al segmento BC. Paso 3: se realiza una rotación de 180º de los dos rectángulos (el rectángulo inicial y su rectángulo simétrico) Paso 4: como si se vuelve a repetir el paso 3 se vuelve a pintar el rectángulo original junto con su simétrico, hemos terminado. El resultado es un rectángulo Algoritmo de generación de la roseta D 3. Para este caso, la generación de la roseta de tipo D 3, se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/2n 360/6 = 60º. Por lo tanto, nuestra figura inicial transformada es el triángulo EBC. C E B Figura 2.39: polígono fundamental de la roseta D 3 Para generar la roseta se parte del triángulo EBC y a partir de él se genera su simetría horizontal respecto del eje de simetría que contiene al segmento BC. C Eje de simetría E B D Figura 2.40: simetría horizontal del triángulo EBC respecto del eje de simetría 53
62 Posteriormente se generan las correspondientes rotaciones de 360º/n = 360/3 = 120, obteniendo una roseta rectangular. El nº de imágenes con sus correspondientes simetrías es n = 3 y el nº de rotaciones es (n 1) = 2. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el triángulo EBC que contiene la imagen con el vértice C en el centro de la superficie de dibujado. Paso 2: se realiza una simetría horizontal respecto al eje de simetría que contiene al segmento BC. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 3: se realiza una rotación de (120º *contador) de los dos triángulos (el triángulo inicial y su triángulo simétrico) e incrementamos el valor del contador en 1 Paso 4: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta D 4. Para este caso, la generación de la roseta de tipo D 4, se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/2n 360/8 = 45º. Por lo tanto, nuestra figura inicial transformada es el triángulo EBC. C E B Figura 2.41: polígono fundamental de la roseta D 4 Para generar la roseta se parte del triángulo EBC y a partir de él se genera su simetría horizontal respecto del eje de simetría que contiene al segmento BC. C Eje de simetría E B D Figura 2.42: simetría horizontal del triángulo EBC respecto del eje de simetría 54
63 Posteriormente se generan las correspondientes rotaciones de 360º/n = 360/4 = 90, obteniendo una roseta rectangular. El nº de imágenes con sus correspondientes simetrías es n = 4 y el nº de rotaciones es (n 1) = 3. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el triángulo EBC que contiene la imagen con el vértice C en el centro de la superficie de dibujado. Paso 2: se realiza una simetría horizontal respecto al eje de simetría que contiene al segmento BC. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 3: se realiza una rotación de (90º *contador) de los dos triángulos (el triángulo inicial y su triángulo simétrico) e incrementamos el valor del contador en 1 Paso 4: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso 3. 55
64 Algoritmo de generación de la roseta D 5. Para este caso, la generación de la roseta de tipo D 5, se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/2n 360/10 = 36º. Por lo tanto, nuestra figura inicial transformada es el triángulo EBC. C E B Figura 2.43: polígono fundamental de la roseta D 5 Para generar la roseta se parte del triángulo EBC y a partir de él se genera su simetría horizontal respecto del eje de simetría que contiene al segmento BC. C Eje de simetría E B D Figura 2.44: simetría horizontal del triángulo EBC respecto del eje de simetría Posteriormente se generan las correspondientes rotaciones de 360º/n = 360/5 = 72º, obteniendo una roseta rectangular. El nº de imágenes con sus correspondientes simetrías es n = 5 y el nº de rotaciones es (n 1) = 4. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el triángulo EBC que contiene la imagen con el vértice C en el centro de la superficie de dibujado. Paso 2: se realiza una simetría horizontal respecto al eje de simetría que contiene al segmento BC. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. Paso 3: se realiza una rotación de (72º *contador) de los dos triángulos (el triángulo inicial y su triángulo simétrico) e incrementamos el valor del contador en 1 56
65 Paso 4: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta D 6. Para este caso, la generación de la roseta de tipo D 6, se necesita coger como dominio fundamental un triángulo isósceles cuyo ángulo que forma el vértice superior sea de 360/2n 360/12 = 30º. Por lo tanto, nuestra figura inicial transformada es el triángulo EBC. C E B Figura 2.45: polígono fundamental de la roseta D 6 Para generar la roseta se parte del triángulo EBC y a partir de él se genera su simetría horizontal respecto del eje de simetría que contiene al segmento BC. C Eje de simetría E B D Figura 2.46: simetría horizontal del triángulo EBC respecto del eje de simetría Posteriormente se generan las correspondientes rotaciones de 360º/n = 360/6 = 60º, obteniendo una roseta rectangular. El nº de imágenes con sus correspondientes simetrías es n = 6 y el nº de rotaciones es (n 1) = 5. El algoritmo es el siguiente: Paso 1: carga de la imagen original. Se dibuja el triángulo EBC que contiene la imagen con el vértice C en el centro de la superficie de dibujado. Paso 2: se realiza una simetría horizontal respecto al eje de simetría que contiene al segmento BC. Inicializamos un contador a 1 para saber el nº de imágenes triangulares que vamos pintando. 57
66 Paso 3: se realiza una rotación de (60º *contador) de los dos triángulos (el triángulo inicial y su triángulo simétrico) e incrementamos el valor del contador en 1 Paso 4: si el contador es igual a n hemos terminado. Si no es así, volvemos al paso Algoritmo de generación de la roseta D n. Esta roseta, al igual que el grupo de roseta C n, es un poco especial. Se trata de un grupo diédrico que representa a todos los grupos diédricos previamente descritos e incluso, como la cardinalidad de estos grupos es infinita, también a grupos diédricos cuyo orden es mayor (D 7, D 8, D 10, D 12,...). Parte de la roseta D 1 y en cada paso va originando una roseta de orden mayor. Cuanto mayor sea el orden de la roseta, el polígono generado va tendiendo a parecerse a un círculo, ya que los lados del polígono se van haciendo más pequeños. En el programa se ha puesto un limite al orden calculado en 30 (grupo diédrico D 30 ), ya que a partir de ahí la diferencia entre los polígonos generados es casi despreciable. El algoritmo es el siguiente: Se parte de la imagen original. Paso 1: Se realiza el grupo de roseta D 1. Paso 2: Se realiza el grupo de roseta D Paso n: Se realiza el grupo de roseta D n. 58
67 CAPÍTULO 3 MANUAL DE USUARIO 3.1 Introducción En esta sección se va a intentar explicar el funcionamiento de la aplicación. Esta aplicación genera teselaciones periódicas del plano a partir de un motivo inicial o dominio fundamental incluido en un fichero de imagen (archivo con extensión.jpg,.gif,.tif, etc) seleccionado por el usuario. El usuario será el encargado de seleccionar arbitrariamente el motivo generador y aquella transformación que, aplicada al motivo generador, permite la realización de la teselación periódica del plano. Esto es, el usuario selecciona una imagen y un grupo de simetría (hay trece grupos de rosetas, siete grupos de frisos y diecisiete grupos cristalográficos) y la aplicación se encarga de generar las teselaciones aplicando ese grupo de simetría a la imagen original. 3.2 Interfaz de usuario. La interfaz de la aplicación es bastante sencilla e intuitiva. En ella podemos destacar cinco regiones bien diferenciadas: Área de dibujado: es la superficie sobre la que se representan gráficamente el motivo inicial y las teselaciones generadas por la aplicación. Cuadro de selección de transformaciones: es el área en la que el usuario puede seleccionar la transformación con la que quiere realizar la teselación del plano. Cuadro de funciones básicas: es donde se encuentran los botones que ejecutan las funciones básicas de la aplicación (abrir imagen, guardar imagen, imprimir, salir, ejecutar,...) Barra de Menú: es un elemento de tipo menú donde se encuentran las mismas funcionalidades que en el cuadro de funciones básicas. Barra de estado: es una barra que se encuentra en la superficie inferior de la aplicación y es la encargada de sacar mensajes de información o de aviso al usuario sobre el estado de la aplicación. 59
68 Figura 3.1: pantalla principal de la aplicación 60
69 3.2.1 Área de dibujado. En este área es donde se van a representar gráficamente el motivo inicial y las correspondientes transformaciones que se vayan realizando sobre ese motivo. Es una superficie inicial con el fondo blanco (aunque ese color puede ser variado por el usuario en función de sus preferencias) y dos líneas perpendiculares que se cortan en el centro y que dividen dicha superficie en cuatro partes iguales. La función de estas líneas es meramente informativa para saber donde se situan correctamente las imágenes transformadas de nuestra aplicación. El área de esta superficie es de (800 x 600). Área de dibujado Figura 3.2: Área de dibujado de la interfaz del programa Cuadro de selección de transformaciones. Aquí es donde el usuario selecciona el tipo de transformación que quiere aplicar a la imagen original. Esta compuesto por tres pestañas seleccionables dependiendo de que tipo de decoración quiera efectuar el usuario sobre su imagen inicial: Pestaña de los grupos de Friso: pestaña compuesta por 7 botones de selección que agrupan a todos y cada uno de los grupos de friso existentes. Si el usuario quiere generar uno de esos grupos a partir de la imagen inicial, tendrá que seleccionar uno de estos botones. Estos botones de selección son los siguientes: o Botón de Friso 1 (o F 1 en notación matemática) o Botón de Friso 2 (o F 2 en notación matemática) 61
70 o Botón de Friso 3 (o F 1 1 en notación matemática) o Botón de Friso 4 (o F 1 2 en notación matemática) o Botón de Friso 5 (o F 1 3 en notación matemática) o Botón de Friso 6 (o F 2 1 en notación matemática) o Botón de Friso 7 (o F 2 2 en notación matemática) Pestaña de los grupos de Roseta o rosetones: pestaña compuesta por 13 botones de selección que agrupan a algunos de los grupos de roseta existentes. Si el usuario quiere generar uno de esos grupos a partir de la imagen inicial, tendrá que seleccionar uno de estos botones. Estos botones de selección son los que se enumeran a continuación: o Botón de Roseta C 2 (grupo cíclico de orden 2) o Botón de Roseta C 3 (grupo cíclico de orden 3) o Botón de Roseta C 4 (grupo cíclico de orden 4) o Botón de Roseta C 5 (grupo cíclico de orden 5) o Botón de Roseta C 6 (grupo cíclico de orden 6) o Botón de Roseta D 1 (grupo diédrico de orden 1) o Botón de Roseta D 2 (grupo diédrico de orden 2) o Botón de Roseta D 3 (grupo diédrico de orden 3) o Botón de Roseta D 4 (grupo diédrico de orden 4) o Botón de Roseta D 5 (grupo diédrico de orden 5) o Botón de Roseta D 6 (grupo diédrico de orden 6) o Botón de Roseta C n (grupo cíclico de orden n) o Botón de Roseta D n (grupo diédrico de orden n) Pestaña de los grupos Cristalográficos: pestaña compuesta por 17 botones de selección que agrupa a todos los grupos cristalográficos que existen y que no se van a enumerar por no formar parte de este proyecto, sino ser particular del otro proyecto conjunto que se realiza a la par de éste. Cuadro de selección de transformaciones Figura 3.3: cuadro de selección de transformaciones de la interfaz del programa. 62
71 3.2.3 Cuadro de funciones básicas. Este es el cuadro que agrupa a los botones que realizan las funciones generales de la aplicación. Estos botones también están incluidos en la barra de menú. Simplemente se ha decidido sacarlos también fuera del menú por darle facilidad de uso al usuario. Está formado por los siguientes botones: Botón de abrir: como su nombre bien indica, si el usuario pulsa sobre ese botón, aparece un cuadro de diálogo mediante el cual puede elegir el fichero de imágenes que quiere cargar en la aplicación como motivo inicial y sobre el cual se van a aplicar las transformaciones y simetrías. Si al pulsar el botón hubiera una imagen ya cargada y mostrada en la superficie de dibujado, esta se borraría y el usuario podría continuar con la acción de abrir normalmente. Botón de guardar: este botón tiene la capacidad de guardar con un formato de imagen (.jpg ) las transformaciones y simetrías que se le han aplicado a la imagen inicial y que ya están dibujadas en la superficie de dibujo. Es decir, guarda como una imagen lo que el usuario ve dibujado en la superficie de dibujo. Botón de imprimir: este botón realiza las tareas de impresión de la aplicación. Se encarga de imprimir por la impresora el dibujo generado por la ejecución de la aplicación y que esta visualizado por pantalla en la superficie de dibujado. Al pulsar el usuario sobre este botón aparece un cuadro de dialogo en el que se pueden elegir las opciones de impresión. Botón de salir: este botón, como bien indica su nombre, sirve para que el usuario se pueda salir del programa. Botón de generar: si el usuario pulsa sobre este botón, se generarán las transformaciones y simetrías que el usuario ha seleccionado sobre la imagen inicial. Botón de zoom + : la finalidad de este botón es la de ampliar tanto la imagen original como las imágenes que se hayan podido transformar tantas veces como quiera el usuario. No tiene ninguna limitación. El ampliar una imagen lleva como consecuencia la perdida de definición dentro de esa imagen. Botón de zoom - : este botón es inverso al anterior. Reduce tanto la imagen original como las imágenes que se hayan podido transformar tantas veces como quiera el usuario. No tiene ninguna limitación. Botón de limpiar: la utilidad de este botón es la de limpiar la superficie de dibujado de toda imagen o transformación que haya sobre ella. Deja la superficie 63
72 vacía, incluso borra la imagen de partida a partir de la cual se generan las simetrías. Botón de baldosa: este botón es análogo al anterior pero dejando en el dibujo la imagen original para poder empezar de nuevo el proceso de generación de alguno de los grupos de simetría que elija el usuario. Es decir, limpia la superficie de dibujado dejando solo la imagen inicial. Cuadro de funciones básicas Figura 3.4: cuadro de funciones básicas de la interfaz del programa Barra de menú. Esta barra presenta un menú en el que seleccionar las funciones que puede realizar el programa. Como previamente se ha comentado, muchas de estas funciones se han llevado al cuadro de funciones básicas para una mayor facilidad de uso para el usuario. El menú se compone de los siguientes submenús: Archivo: submenú compuesto de las siguientes opciones: o Nuevo: limpia la superficie de dibujado, dejando solamente la imagen inicial. o Abrir: muestra un dialogo para que el usuario elija la imagen inicial. o Guardar: muestra un dialogo para que el usuario pueda guardar las transformaciones hechas sobre la imagen original en un formato de imagen. o Imprimir: imprime la superficie de dibujado. o Salir: efectúa la salida de la aplicación. 64
73 Edición: submenú con todas las opciones de la superficie de dibujado: o Color de fondo: esta opción muestra un dialogo para que el usuario pueda seleccionar el color de fondo que desea fijar a la superficie de dibujado. Por defecto, esta superficie es de color blanco. o Aumentar: aumenta el tamaño de las imágenes dibujadas en la superficie de dibujado. o Reducir: reduce el tamaño de las imágenes dibujadas en la superficie de dibujado. Opciones: submenú con las opciones de ejecución de la aplicación: o Paso a paso: si esta opción esta activada, la aplicación ejecutará las transformaciones sobre la imagen inicial de una en una en vez de ejecutarlas todas juntas. Ayuda: submenú de ayuda: o Acerca de: muestra un cuadro de diálogo con el nombre de la aplicación y los autores de la misma Barra de estado. Es una barra que se encuentra en la parte inferior de la aplicación. Esta dividida en dos secciones, en la cuales se muestran mensajes que indican el estado de la aplicación. Mensajes como la ruta y el nombre de la imagen que se ha cargado o si la forma de ejecución que ha elegido el usuario es paso a paso o completa son algunos de los mensajes que proporciona dicha aplicación. Barra de menú Barra de estado Figura 3.5: barra de menú y barra de estado. 65
74 3.3 Modo de ejecución. El funcionamiento del programa es bastante sencillo e intuitivo. Una vez que se ejecuta la aplicación aparece una ventana pequeña en la que se puede leer un pequeño mensaje de introducción e información junto con tres botones: uno de entrar, otro de salir y otro de ayuda. Los botones de salir y de ayuda ejecutan las acciones que su nombre indica, mientras que si se pulsa sobre el botón de entrar, la aplicación muestra la ventana principal del programa. Una vez que se ha llegado a la pantalla principal, aparece mostrada en la superficie de dibujado una imagen por defecto. Con esta imagen el usuario ya puede trabajar de una manera normal, aunque si prefiere cargar otra imagen lo único que tiene que hacer pulsar sobre el botón de abrir o ir al menú Archivo/Abrir. Con esta acción se desplegará un cuadro de dialogo en la que el usuario se podrá mover por todos los directorios y subdirectorios del ordenador en el que esté ejecutando la aplicación para abrir la imagen que desee. Si el usuario decide cancelar la operación, la aplicación mostrará la anterior imagen que hubiese cargada o la superficie de dibujado en blanco en el caso de que no hubiese ninguna imagen previa en la pantalla. Figura 3.6: ventana de dialogo de abrir imagen. Si el tamaño de la imagen fuese demasiado grande en relación con la superficie de dibujado, la aplicación mostraría por pantalla una ventana de aviso indicando al usuario este hecho y dándole a elegir entre dos opciones: bien continuar con ese tamaño de imagen o bien poder reducir su tamaño para poder trabajar mejor con ella. Una vez que el usuario ha elegido la opción oportuna, la imagen se dibuja en la superficie de dibujado con el tamaño optado. Figura 3.7: ventana de aviso de que la imagen es grande. 66
75 De todas formas, cabe la posibilidad de ajustar posteriormente el tamaño de la imagen inicial y de las transformaciones con los botones de zoom, tanto de aumentar como de reducir, de los que dispone la aplicación. Una vez que la imagen este cargada en la superficie de dibujado, el siguiente paso seria pulsar sobre el grupo de simetría que el usuario desee aplicar sobre la imagen inicial. La pestaña del cuadro de selección de transformaciones que aparece en primer plano es la del grupo de frisos. Si el usuario decidiese ejecutar una transformación de los grupos de los frisos solamente tendría que pulsar sobre uno de los botones. En el caso de que lo que quiera sea ejecutar un grupo de roseta debería pulsar con el ratón sobre la pestaña titulada con el nombre de grupos de roseta. Con esto el usuario ya tendría en primer plano la pestaña con los botones de dicho grupo y solamente tendría que pulsar sobre el botón correspondiente. Figura 3.8: pantalla general de la aplicación con la imagen inicial ya generada y el grupo de friso ya elegido (friso 6) A continuación, una vez que la imagen inicial ya está cargada y se ha elegido el tipo de transformación que se le quiere aplicar, el usuario deberá pulsar sobre el botón de generar para poder ver las transformaciones hechas sobre la imagen en pantalla. Aquí existen dos opciones: si el usuario quiere ver una a una las transformaciones que se van haciendo sobre la imagen entonces previamente a la pulsación del botón de 67
76 generar deberá activar la opción de ejecutar paso a paso mediante la opción de menú Opciones/Paso a paso. Una vez que el usuario ha activado esta opción, cada vez que quiera ver una a una las transformaciones que se van generando debe pulsar sobre el botón de generar. Por otro lado, si lo que el usuario quiere ver es el resultado final de las transformaciones, solo debe pulsar sobre el botón de generar sin tener activada la opción de paso a paso. Una vez que el usuario ha pulsado sobre ese botón, en la superficie de dibujado se puede observar el resultado de aplicar todas las transformaciones. En todo momento el usuario puede saber si tiene activada la opción de ejecutar paso a paso o de ejecución completa observando el campo derecho de la barra de estado. En este campo se muestra un mensaje diciendo en que tipo de ejecución se encuentra la aplicación. Figura 3.9: generación de una de las simetrías una vez pulsado el botón de generar con tipo de ejecución completa Si se diese el caso de que se pincha sobre el botón de ejecutar sin previamente haber abierto la imagen o sin haber seleccionado uno de los grupos de simetría, la aplicación mostraría una ventana de aviso avisando del error que ha cometido el usuario. 68
77 Figura 3.11: mensaje de aviso al usuario si se pulsa el botón generar sin haber elegido un tipo de simetría. Otra de las funcionalidades del programa es que se puede generar automáticamente las transformaciones sobre una imagen inicial de un grupo de simetría pulsando sobre el botón de ese grupo si previamente ya se había generado otro grupo. Si el grupo anterior había sido generado paso a paso y solo se había desarrollado hasta un cierto paso sin completarse las transformaciones, en el nuevo grupo de simetría seleccionado solo se va a generar hasta ese mismo paso. Esto se puede hacer con todos los botones de un mismo grupo (frisos o rosetas) e incluso con los botones de grupos distintos (cambiar entre frisos y rosetas o viceversa). Si el usuario quiere comenzar la ejecución de un grupo desde el principio, pulsando sobre el botón de baldosa, la superficie de dibujo se borra dejando solamente el motivo inicial, es decir la imagen de partida. Si lo que el usuario quiere es limpiar completamente la pantalla solo tendrá que pulsar el botón de limpiar. Si una vez ejecutado el proceso de transformaciones el usuario quiere guardar la imagen resultante, simplemente tendrá que pulsar el botón guardar. Este botón almacena en la ruta que el usuario elija la imagen formada por las transformaciones con extensión.jpg. 69
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 5: Transformaciones geométricas planas. Orientación espacial
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 5: Transformaciones geométricas planas. Orientación espacial 1 Transformaciones geométricas 2 ISOMETRÍAS EN LIBROS DE PRIMARIA Cuáles de
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 5: Transformaciones geométricas planas. Orientación espacial 1 Transformaciones geométricas 2 ISOMETRÍAS EN LIBROS DE PRIMARIA Cuáles de
Movimientos en el plano y mosaicos
 Matemáticas de Nivel II de ESPA: Movimientos en el plano - 1 Movimientos en el plano y mosaicos En esta unidad se presenta la utilidad de la geometría para ornamentar objetos y espacios en las actividades
Matemáticas de Nivel II de ESPA: Movimientos en el plano - 1 Movimientos en el plano y mosaicos En esta unidad se presenta la utilidad de la geometría para ornamentar objetos y espacios en las actividades
SABEN LAS ABEJAS MATEMÁTICAS?
 SABEN LAS ABEJAS MATEMÁTICAS? A lo largo de los años se ha utilizado la geometría con fines decorativos. Vasijas, tejidos, suelos, muros, puertas, ventanales han sido decorados con diseños geométricos
SABEN LAS ABEJAS MATEMÁTICAS? A lo largo de los años se ha utilizado la geometría con fines decorativos. Vasijas, tejidos, suelos, muros, puertas, ventanales han sido decorados con diseños geométricos
[MATEMÁTICAS DE LA VIDA COTIDIANA]
![[MATEMÁTICAS DE LA VIDA COTIDIANA] [MATEMÁTICAS DE LA VIDA COTIDIANA]](/thumbs/54/33156181.jpg) MOSAICOS, FRISOS Y ROSETONES Una tesela es una pieza que en unión de otras idénticas es capaz de rellenar el plano, de tal manera que no se solapen, y que no existan fisuras entre ellas. El dibujo que
MOSAICOS, FRISOS Y ROSETONES Una tesela es una pieza que en unión de otras idénticas es capaz de rellenar el plano, de tal manera que no se solapen, y que no existan fisuras entre ellas. El dibujo que
TEMA 9.- TRANSFORMACIONES EN EL PLANO.
 GEOMETRÍ: 5.- TRNSFORMIONES EN EL PLNO TEM 9.- TRNSFORMIONES EN EL PLNO. Definición 9.1.- Llamaremos transformación geométrica en el plano a una operación u operaciones geométricas que permiten deducir
GEOMETRÍ: 5.- TRNSFORMIONES EN EL PLNO TEM 9.- TRNSFORMIONES EN EL PLNO. Definición 9.1.- Llamaremos transformación geométrica en el plano a una operación u operaciones geométricas que permiten deducir
TRANSFORMACIONES EN EL PLANO
 ACADEMIA SABATINA TRANSFORMACIONES EN EL PLANO Llamaremos transformación geométrica a una operación que permite producir una nueva figura (imagen) de la dada originalmente. Las podemos clasificar en directas,
ACADEMIA SABATINA TRANSFORMACIONES EN EL PLANO Llamaremos transformación geométrica a una operación que permite producir una nueva figura (imagen) de la dada originalmente. Las podemos clasificar en directas,
MOVIMIENTOS EN EL PLANO
 MOVIMIENTOS EN EL PLANO MOVIMIENTOS EN EL PLANO. ÍNDICE Movimientos en el plano. Definición. Traslación. Rotación. Simetría central. Simetría axial. Los siete tipos de frisos. Ejemplos de movimientos en
MOVIMIENTOS EN EL PLANO MOVIMIENTOS EN EL PLANO. ÍNDICE Movimientos en el plano. Definición. Traslación. Rotación. Simetría central. Simetría axial. Los siete tipos de frisos. Ejemplos de movimientos en
NIVELACIÓN MATEMÁTICA 2 AÑO Contenidos: Transformaciones Isométricas Prof. Juan Schuchhardt
 1 Contenidos: Transformaciones Isométricas Prof. Juan Schuchhardt Introducción: Una transformación de una figura geométrica indica que, de alguna manera, ella es alterada o sometida a algún cambio. En
1 Contenidos: Transformaciones Isométricas Prof. Juan Schuchhardt Introducción: Una transformación de una figura geométrica indica que, de alguna manera, ella es alterada o sometida a algún cambio. En
TEMA 4 TRANSFORMACIONES EN EL PLANO
 TEMA 4 TRANSFORMACIONES EN EL PLANO Introducción. Bloque de herramientas Transformar. Mosaicos. Mosaicos regulares. Mosaicos irregulares. Actividades propuestas. INTRODUCCIÓN En este tema expondremos las
TEMA 4 TRANSFORMACIONES EN EL PLANO Introducción. Bloque de herramientas Transformar. Mosaicos. Mosaicos regulares. Mosaicos irregulares. Actividades propuestas. INTRODUCCIÓN En este tema expondremos las
Resumen de Transformaciones Isométricas. Traslaciones
 Resumen de Transformaciones Isométricas Una transformación es un procedimiento geométrico o movimiento que produce cambios en una figura. La palabra isometría proviene del griego y significa igual medida
Resumen de Transformaciones Isométricas Una transformación es un procedimiento geométrico o movimiento que produce cambios en una figura. La palabra isometría proviene del griego y significa igual medida
ISOMETRÍA ( MOVIMIENTO): transformación que conserva la forma y el tamaño de las figuras.
 ISOMETRÍAS EN EL PLANO ISOMETRÍA ( MOVIMIENTO): transformación que conserva la forma y el tamaño de las figuras. Hay dos tipos de isometrías: Isometría directa: mantiene el sentido de giro de las agujas
ISOMETRÍAS EN EL PLANO ISOMETRÍA ( MOVIMIENTO): transformación que conserva la forma y el tamaño de las figuras. Hay dos tipos de isometrías: Isometría directa: mantiene el sentido de giro de las agujas
Mosaicos y frisos. Adela Salvador
 Mosaicos y frisos Adela Salvador Isometrías en el plano Traslación Giro Simetría Simetría con deslizamiento Traslaciones La traslación queda definida al conocer el vector de traslación Busca dos vectores
Mosaicos y frisos Adela Salvador Isometrías en el plano Traslación Giro Simetría Simetría con deslizamiento Traslaciones La traslación queda definida al conocer el vector de traslación Busca dos vectores
TEMA 6: GEOMETRÍA EN EL PLANO
 TEMA 6: GEOMETRÍA EN EL PLANO Definiciones/Clasificaciones Fórmulas y teoremas Dem. Def. y Clasificación de polígonos: Regular o irregular Cóncavo o convexo Por número de lados: o Triángulos: clasificación
TEMA 6: GEOMETRÍA EN EL PLANO Definiciones/Clasificaciones Fórmulas y teoremas Dem. Def. y Clasificación de polígonos: Regular o irregular Cóncavo o convexo Por número de lados: o Triángulos: clasificación
TALLER TRANSFORMACIONES ISOMÉTRICAS. Transformaciones Isométricas
 TALLER TRANSFORMACIONES ISOMÉTRICAS Introducción étricas Actividad: En los siguientes pares de transformaciones, reconoce aquellas en las que se mantiene la forma y el tamaño. Una transformación de una
TALLER TRANSFORMACIONES ISOMÉTRICAS Introducción étricas Actividad: En los siguientes pares de transformaciones, reconoce aquellas en las que se mantiene la forma y el tamaño. Una transformación de una
MOVIMIENTOS Y TRANSFORMACIONES EN EL PLANO
 MOVIMIENTOS Y TRANSFORMACIONES EN EL PLANO Traslación: Traslación (sin deslizadores) Traslación de un objeto: Traslación de una imagen: Actividad con geogebra: Construye un pentágono regular y trasládalo
MOVIMIENTOS Y TRANSFORMACIONES EN EL PLANO Traslación: Traslación (sin deslizadores) Traslación de un objeto: Traslación de una imagen: Actividad con geogebra: Construye un pentágono regular y trasládalo
Cuaderno I: MOVIMIENTOS EN EL PLANO
 á Cuaderno I: MOVIMIENTOS EN EL PLANO á MOVIMIENTOS EN EL PLANO Las transformaciones geométricas ha sido una de las constantes de la mayoría de las culturas, presentándose en los elementos decorativos
á Cuaderno I: MOVIMIENTOS EN EL PLANO á MOVIMIENTOS EN EL PLANO Las transformaciones geométricas ha sido una de las constantes de la mayoría de las culturas, presentándose en los elementos decorativos
TEMA 4. TRANSFORMACIONES EN EL PLANO
 TEMA 4. TRANSFORMACIONES EN EL PLANO HERRAMIENTAS PARA TRANSFORMACIONES En este bloque encontramos las siguientes herramientas: Simetría axial La herramienta Refleja objeto en recta dibuja la figura simétrica
TEMA 4. TRANSFORMACIONES EN EL PLANO HERRAMIENTAS PARA TRANSFORMACIONES En este bloque encontramos las siguientes herramientas: Simetría axial La herramienta Refleja objeto en recta dibuja la figura simétrica
Traslación: ABCDEF se ha transformado a la figura A B C D E F, en la dirección y longitud del vector d
 PROFESOR SANDRO JAVIER VELASQUEZ LUNA 1 TRANSFORMACIONES ISOMETRICAS Si a una figura geométrica se le aplica una transformación, y esta no produce un cambio en la medida de los lados y ángulos se llama
PROFESOR SANDRO JAVIER VELASQUEZ LUNA 1 TRANSFORMACIONES ISOMETRICAS Si a una figura geométrica se le aplica una transformación, y esta no produce un cambio en la medida de los lados y ángulos se llama
Si el motivo se repite en dos direcciones, se trata de un mosaico, también llamado grupo cristalográfico.
 Este programa, diseñado por Martin on Gagern, permite generar ornamentos de forma sencilla, partiendo de modelos originales realizados a mano alzada los cuales se completan según alguno de los grupos de
Este programa, diseñado por Martin on Gagern, permite generar ornamentos de forma sencilla, partiendo de modelos originales realizados a mano alzada los cuales se completan según alguno de los grupos de
20. TRANSFORMACIONES Y MOVIMIENTOS
 20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
20. TRANSFORMACIONES Y MOVIMIENTOS Los movimientos y las transformaciones son modificaciones aplicadas a los elementos del plano puntos, rectas, figuras_ con el fin de cambiar su posición o para convertirlos
TRANSF0RMACIONES GEOMÉTRICAS
 DIBUJO TÉNCICO 2º BACH TRANSF0RMACIONES GEOMÉTRICAS Nos referimos a Transformaciones Geométricas cuando hablamos de la operación u operaciones necesarias para convertir una figura F en otra figura F portadora
DIBUJO TÉNCICO 2º BACH TRANSF0RMACIONES GEOMÉTRICAS Nos referimos a Transformaciones Geométricas cuando hablamos de la operación u operaciones necesarias para convertir una figura F en otra figura F portadora
Tema 5 Proporcionalidad y escalas
 Tema 5 Proporcionalidad y escalas Tema 5 Proporcionalidad y escalas...1 Proporcionalidad... 2 Razón...2 Proporción...2 Proporcionalidad directa...2 Proporcionalidad inversa...3 Construcción de la media
Tema 5 Proporcionalidad y escalas Tema 5 Proporcionalidad y escalas...1 Proporcionalidad... 2 Razón...2 Proporción...2 Proporcionalidad directa...2 Proporcionalidad inversa...3 Construcción de la media
TRANSFORMACIONES ISOMETRICAS
 PreUnAB Clase # 22 Octubre 2014 TRANSFORMACONES ISOMÉTRICAS Concepto de Isometrías: Las transformaciones isométricas son movimientos que se aplican a figuras geométricas, produciendo cambios de posición,
PreUnAB Clase # 22 Octubre 2014 TRANSFORMACONES ISOMÉTRICAS Concepto de Isometrías: Las transformaciones isométricas son movimientos que se aplican a figuras geométricas, produciendo cambios de posición,
3º ESO - UNIDAD 12.- TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO
 3º ESO - UNIDAD 12.- TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO OBJETIVOS MÍNIMOS DE LA UNIDAD 12 1.- Reconocer los diferentes tipos de movimientos 2.- En cuanto a las traslaciones, saber construir la
3º ESO - UNIDAD 12.- TRASLACIONES, GIROS Y SIMETRÍAS EN EL PLANO OBJETIVOS MÍNIMOS DE LA UNIDAD 12 1.- Reconocer los diferentes tipos de movimientos 2.- En cuanto a las traslaciones, saber construir la
Club GeoGebra Iberoamericano 7 MOSAICOS E ISOMETRÍAS
 7 MOSAICOS E ISOMETRÍAS MOSAICOS E ISOMETRÍAS ISOMETRÍAS. LOS MOVIMIENTOS EN EL PLANO QUE MANTIENEN LAS DISTANCIAS Presentación Encontramos simetría en el rostro humano y en muchos seres vivos. También
7 MOSAICOS E ISOMETRÍAS MOSAICOS E ISOMETRÍAS ISOMETRÍAS. LOS MOVIMIENTOS EN EL PLANO QUE MANTIENEN LAS DISTANCIAS Presentación Encontramos simetría en el rostro humano y en muchos seres vivos. También
MOSAICOS CON GEOGEBRA
 MOSAICOS CON GEOGEBRA FRANCISCO FERNÁNDEZ IES Padre Manjón (Granada) Este taller pone en acción las competencias básicas (digital, cultural y artística) y coadyuva a que el alumnado las vaya alcanzando.
MOSAICOS CON GEOGEBRA FRANCISCO FERNÁNDEZ IES Padre Manjón (Granada) Este taller pone en acción las competencias básicas (digital, cultural y artística) y coadyuva a que el alumnado las vaya alcanzando.
1.3 PROPORCIÓN Y RELACIONES GEOMÉTRICAS (transformaciones geométricas)
 TEMA 1: Dibujo geométrico 1.3 PROPORCIÓN Y RELACIONES GEOMÉTRICAS (transformaciones geométricas) El tamaño es una cualidad de toda figura que percibimos comparándolo con el entorno donde se sitúa. La proporción
TEMA 1: Dibujo geométrico 1.3 PROPORCIÓN Y RELACIONES GEOMÉTRICAS (transformaciones geométricas) El tamaño es una cualidad de toda figura que percibimos comparándolo con el entorno donde se sitúa. La proporción
Transformaciones Isométricas
 19 Transformaciones Isométricas Introducción. Al término de esta lección podrás: Interpretar las transformaciones isométricas de figuras planas como cambios en la posición de una figura. Clasificar las
19 Transformaciones Isométricas Introducción. Al término de esta lección podrás: Interpretar las transformaciones isométricas de figuras planas como cambios en la posición de una figura. Clasificar las
LOS ESGRAFIADOS SEGOVIANOS
 Seminario Estalmat 11 de diciembre de 2010 LOS ESGRAFIADOS SEGOVIANOS Sonia González Pascual TESELACIONES Una teselación es una forma de llenar un plano repitiendo una figura sin que se superpongan ni
Seminario Estalmat 11 de diciembre de 2010 LOS ESGRAFIADOS SEGOVIANOS Sonia González Pascual TESELACIONES Una teselación es una forma de llenar un plano repitiendo una figura sin que se superpongan ni
TRANSFORMACIONES ISOMÉTRICAS EN EL PLANO CARTESIANO
 Matemáticas Aplicadas Tema: Movimiento de los cuerpos geométricos. TRANSFORMACIONES ISOMÉTRICAS EN EL PLANO CARTESIANO Transformación isométrica Isometría proviene del griego iso, prefijo que significa
Matemáticas Aplicadas Tema: Movimiento de los cuerpos geométricos. TRANSFORMACIONES ISOMÉTRICAS EN EL PLANO CARTESIANO Transformación isométrica Isometría proviene del griego iso, prefijo que significa
Translaciones, giros, simetrías.
 Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Geometría Prof. L. Solorza Curso: 1 medio. Guía de isometrías
 Guía de isometrías A) Simetrías a) Reflexiones o Simetrías axiales Concepto: Una reflexión o simetría axial, con eje la recta L, es un movimiento del plano tal que a cada punto P del plano le hace corresponder
Guía de isometrías A) Simetrías a) Reflexiones o Simetrías axiales Concepto: Una reflexión o simetría axial, con eje la recta L, es un movimiento del plano tal que a cada punto P del plano le hace corresponder
Polígonos regulares, el triángulo de Sierpinski y teselados
 Sesión 3 Polígonos regulares, el triángulo de Sierpinski y teselados PROPÓSITOS Plantear y resolver problemas que involucren el análisis de características y propiedades de diversas figuras planas. MATERIALES
Sesión 3 Polígonos regulares, el triángulo de Sierpinski y teselados PROPÓSITOS Plantear y resolver problemas que involucren el análisis de características y propiedades de diversas figuras planas. MATERIALES
a 2 = = 1600 ; a = 40 A = = 80. Iguales A = 361 1:150
 uno es agudo y el otro es obtuso. Á = (48. 5 ) / 2 = 120 D 2 = 20 2 + 10 2 + 6 2 = 536 ; D = 23 15 V = V S + V c = 2 / 3. π 125 + 1 / 3. π 25. 3 = 325/3. π Área = lado x lado = l 2 Los paralelepípedos
uno es agudo y el otro es obtuso. Á = (48. 5 ) / 2 = 120 D 2 = 20 2 + 10 2 + 6 2 = 536 ; D = 23 15 V = V S + V c = 2 / 3. π 125 + 1 / 3. π 25. 3 = 325/3. π Área = lado x lado = l 2 Los paralelepípedos
ROTACIONES. R P,. Si la rotación es negativa se representa por EJEMPLOS
 1. TRASLACIONES CAPÍTULO XII TRANSFORMACIONES ISOMETRICAS ISOMETRIAS I Las traslaciones, son aquellas isometrías que permiten desplazar en línea recta todos los puntos del plano. Este desplazamiento se
1. TRASLACIONES CAPÍTULO XII TRANSFORMACIONES ISOMETRICAS ISOMETRIAS I Las traslaciones, son aquellas isometrías que permiten desplazar en línea recta todos los puntos del plano. Este desplazamiento se
REPRESENTAR FIGURAS Y BUSCAR SIMILITUDES. DOS TRIÁNGULOS ESTÁN UNIDOS POR UN LADO COMPLETO
 REPRESENTAR FIGURAS Y BUSCAR SIMILITUDES. ACTIVIDAD Nº 1 1. Recorta 6 triángulos equiláteros de 6 cm de lado. 2. Combina 2 triángulos, para encontrar nuevas formas geométricas, de acuerdo a la siguiente
REPRESENTAR FIGURAS Y BUSCAR SIMILITUDES. ACTIVIDAD Nº 1 1. Recorta 6 triángulos equiláteros de 6 cm de lado. 2. Combina 2 triángulos, para encontrar nuevas formas geométricas, de acuerdo a la siguiente
unidad 11 Transformaciones geométricas
 unidad 11 Transformaciones geométricas Cómo dibujar ángulos de 60 con regla y compás Página 1 La cuerda de un arco de 60 (apertura del compás) es igual al radio con que se ha trazado. Veamos el proceso:
unidad 11 Transformaciones geométricas Cómo dibujar ángulos de 60 con regla y compás Página 1 La cuerda de un arco de 60 (apertura del compás) es igual al radio con que se ha trazado. Veamos el proceso:
Tema 2: Figuras geométricas
 Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
7 Geometría del plano. Movimientos
 Qué tienes que saber? 7 QUÉ tienes que saber? Lugares geométricos ctividades Finales 7 Teorema de Pitágoras. plicaciones Ten en cuenta Dos rectas secantes forman dos ángulos adyacentes si son consecutivos
Qué tienes que saber? 7 QUÉ tienes que saber? Lugares geométricos ctividades Finales 7 Teorema de Pitágoras. plicaciones Ten en cuenta Dos rectas secantes forman dos ángulos adyacentes si son consecutivos
TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO
 Recopilación Teórica 1 Transformaciones Geométricas TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO Acerca de la temática de esta unidad. La composición arquitectónica tiene como finalidad, la organización de
Recopilación Teórica 1 Transformaciones Geométricas TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO Acerca de la temática de esta unidad. La composición arquitectónica tiene como finalidad, la organización de
Mosaicos regulares del plano
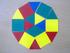 Mosaicos regulares del plano Máster Universitario de formación de Profesorado Especialidad Matemáticas Begoña Hernández Gómez 1 Begoña Soler de Dios 2 Beatriz Carbonell Pascual 3 1 behego@alumni.uv.es
Mosaicos regulares del plano Máster Universitario de formación de Profesorado Especialidad Matemáticas Begoña Hernández Gómez 1 Begoña Soler de Dios 2 Beatriz Carbonell Pascual 3 1 behego@alumni.uv.es
Transformaciones Isométricas
 Transformaciones Isométricas I o Medio Profesor: Alberto Alvaradejo Ojeda Índice 1. Transformación Isométrica 3 1.1. Traslación..................................... 3 1.2. Ejercicios.....................................
Transformaciones Isométricas I o Medio Profesor: Alberto Alvaradejo Ojeda Índice 1. Transformación Isométrica 3 1.1. Traslación..................................... 3 1.2. Ejercicios.....................................
PSU Matemática NM-4 Guía 23: Isometrías. Nombre: Curso: Fecha: -
 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM- Guía : Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza traslaciones
Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM- Guía : Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza traslaciones
GUÍA NÚMERO 22 TRANSFORMACIONES ISOMÉTRICAS
 Saint Gaspar College MISIONEROS DE LA PRECIOSA SANGRE Formando Personas Íntegras Departamento de Matemática RESUMEN PSU MATEMATICA GUÍA NÚMERO 22 TRANSFORMACIONES ISOMÉTRICAS Definición: Se llaman transformaciones
Saint Gaspar College MISIONEROS DE LA PRECIOSA SANGRE Formando Personas Íntegras Departamento de Matemática RESUMEN PSU MATEMATICA GUÍA NÚMERO 22 TRANSFORMACIONES ISOMÉTRICAS Definición: Se llaman transformaciones
Seminario de problemas-eso. Curso Hoja 10
 Seminario de problemas-eso. Curso 011-1. Hoja 10 5. Dado un triángulo cualquiera, demuestra que es posible recubrir el plano con infinitos triángulos iguales al dado, de forma que estos triángulos no se
Seminario de problemas-eso. Curso 011-1. Hoja 10 5. Dado un triángulo cualquiera, demuestra que es posible recubrir el plano con infinitos triángulos iguales al dado, de forma que estos triángulos no se
MATEMÁTICA MÓDULO 1 Eje temático: Geometría
 MATEMÁTICA MÓDULO 1 Eje temático: Geometría 1. CRITERIOS DE CONGRUENCIA Dos triángulos son congruentes cuando sus lados y ángulos correspondientes son congruentes entre sí. Como los elementos primarios
MATEMÁTICA MÓDULO 1 Eje temático: Geometría 1. CRITERIOS DE CONGRUENCIA Dos triángulos son congruentes cuando sus lados y ángulos correspondientes son congruentes entre sí. Como los elementos primarios
ESTALMAT-Andalucía Actividades 06/07
 ACTIVIDAD 1: La proporción de un rectángulo. Qué tienen en común estos rectángulos?, Qué ocurre con sus diagonales? (Usa los instrumentos de dibujo para conseguir respuestas) La proporción de un rectángulo
ACTIVIDAD 1: La proporción de un rectángulo. Qué tienen en común estos rectángulos?, Qué ocurre con sus diagonales? (Usa los instrumentos de dibujo para conseguir respuestas) La proporción de un rectángulo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
Transformaciones isométricas
 Tema 4: Geometría Contenido: Criterios de congruencia de triángulos Nivel: 1 Medio Transformaciones isométricas 1. Transformaciones isométricas Una transformación isométrica es un movimiento en que se
Tema 4: Geometría Contenido: Criterios de congruencia de triángulos Nivel: 1 Medio Transformaciones isométricas 1. Transformaciones isométricas Una transformación isométrica es un movimiento en que se
Club GeoGebra Iberoamericano. 7 MOSAICOS E ISOMETRÍAS 2ª Parte
 7 MOSAICOS E ISOMETRÍAS 2ª Parte MOSAICOS E ISOMETRÍAS MOSAICOS. RELLENAR EL PLANO SIN HUECOS NI SOLAPAMIENTOS Una forma de diferenciar un palacio de los edificios de alrededor consiste en utilizar materiales
7 MOSAICOS E ISOMETRÍAS 2ª Parte MOSAICOS E ISOMETRÍAS MOSAICOS. RELLENAR EL PLANO SIN HUECOS NI SOLAPAMIENTOS Una forma de diferenciar un palacio de los edificios de alrededor consiste en utilizar materiales
Simetrías I. Estímulo del Talento Matemático. Real Academia de Ciencias
 s I Estímulo del Talento Matemático Real Academia de Ciencias 11 de febrero de 2006 1. Simetría... eres tú? La simetría es uno de esos conceptos que resultan más fáciles de intuir que de definir con rigor.
s I Estímulo del Talento Matemático Real Academia de Ciencias 11 de febrero de 2006 1. Simetría... eres tú? La simetría es uno de esos conceptos que resultan más fáciles de intuir que de definir con rigor.
6. Mosaicos y movimientos. en el plano
 6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
Cuáles son las imágenes de los puntos M,N,O,P respecto eje x?
 Guía N 3 Nombre: Curso: 1 Medio A-B-C-D Unidad Geometría Fecha: Profesora: Odette Castro M. Contenidos: Transformaciones isométricas en el plano cartesiano Simetría Axial 1. Dibuja la figura simétrica,
Guía N 3 Nombre: Curso: 1 Medio A-B-C-D Unidad Geometría Fecha: Profesora: Odette Castro M. Contenidos: Transformaciones isométricas en el plano cartesiano Simetría Axial 1. Dibuja la figura simétrica,
PSU Matemática NM-4 Guía 24: Isometrías. Transformaciones isométricas en el plano
 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM-4 Guía 4: Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza diferentes
Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM-4 Guía 4: Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza diferentes
TORNEOS GEOMÉTRICOS Primera Ronda Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
DESARROLLO DE HABILIDADES ISOMETRIAS 8
 DESARROLLO DE HABILIDADES ISOMETRIAS 8 NOMBRE:.. CURSO: Resolver los siguientes ejercicios y problemas relacionados con Transformaciones isométricas, realizando los procedimientos necesarios para marcar
DESARROLLO DE HABILIDADES ISOMETRIAS 8 NOMBRE:.. CURSO: Resolver los siguientes ejercicios y problemas relacionados con Transformaciones isométricas, realizando los procedimientos necesarios para marcar
FIGURAS Y SIMETRIAS EN EL PLANO Y EN EL ESPACIO
 FIGURAS Y SIMETRIAS EN EL PLANO Y EN EL ESPACIO Ana María Redolfi Gandulfo (*), Universidad de Brasilia, Brasil gandulfo@uol.com.br Márcia Helena Resende (*), Secretaría de Educación del Distrito Federal,
FIGURAS Y SIMETRIAS EN EL PLANO Y EN EL ESPACIO Ana María Redolfi Gandulfo (*), Universidad de Brasilia, Brasil gandulfo@uol.com.br Márcia Helena Resende (*), Secretaría de Educación del Distrito Federal,
Guía Práctica Segundos medios
 Fuente: Pre Universitario Pedro de Valdivia Guía Práctica Segundos medios ISMETRÍS Y TESELINES TRSLINES Las traslaciones, son aquellas isometrías que permiten desplazar en línea recta todos los puntos
Fuente: Pre Universitario Pedro de Valdivia Guía Práctica Segundos medios ISMETRÍS Y TESELINES TRSLINES Las traslaciones, son aquellas isometrías que permiten desplazar en línea recta todos los puntos
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos
 Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
Cuerpos Geométricos. Volúmenes de Cuerpos Geométricos Un cuerpo geométrico es un elemento que existe en la realidad o que somos capaces de concebir, llamado sólido, el cual ocupa un volumen en el espacio,
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
Departamento de Matemática
 Departamento de Matemática Isometría, origen griego Igual Medida (ISO = misma METRÍA A = medir) Una trasformación Isométrica produce cambios en una figura que no alteran su tamaño Traslación Rotación Simetría
Departamento de Matemática Isometría, origen griego Igual Medida (ISO = misma METRÍA A = medir) Una trasformación Isométrica produce cambios en una figura que no alteran su tamaño Traslación Rotación Simetría
A. Simetría axial. l, entonces, M es el punto medio de PP y, P sobre el eje de simetría l es el punto P tal que l
 Un eje de simetría es una recta que divide a una figura en dos partes donde cada punto de una parte es la reflexión sobre la recta de un punto en la otra parte de la figura. A. Simetría axial En el ejercicio
Un eje de simetría es una recta que divide a una figura en dos partes donde cada punto de una parte es la reflexión sobre la recta de un punto en la otra parte de la figura. A. Simetría axial En el ejercicio
Unidad 5: Geometría analítica del plano.
 Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
FRISOS Y REJAS UNIDOS POR LAS MATEMÁTICAS
 FRISOS Y REJAS UNIDOS POR LAS MATEMÁTICAS Pilar Lorente Lorente Paloma Plumed Martín Alumnas de 2º Bachillerato 2003/2004 IES Salvador Victoria. Monreal del Campo, Teruel Trabajo presentado en el Congreso
FRISOS Y REJAS UNIDOS POR LAS MATEMÁTICAS Pilar Lorente Lorente Paloma Plumed Martín Alumnas de 2º Bachillerato 2003/2004 IES Salvador Victoria. Monreal del Campo, Teruel Trabajo presentado en el Congreso
SIMETRÍA INFINITA. nt = kt
 SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos
SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA
 EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
MOVIMIENTOS EN EL PLANO
 Ejercicio nº 1.- MOVIMIENTOS EN EL PLANO a) Aplica una traslación de vector t 3, 2 a las figuras y F. F1 2 b Qué habríamos obtenido en cada caso si, en lugar de aplicar la traslación, hubiéramos aplicado
Ejercicio nº 1.- MOVIMIENTOS EN EL PLANO a) Aplica una traslación de vector t 3, 2 a las figuras y F. F1 2 b Qué habríamos obtenido en cada caso si, en lugar de aplicar la traslación, hubiéramos aplicado
TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO
 Alonso Fernández Galián Tema 6: Geometría analítica en el plano TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO La geometría analítica es el estudio de objetos geométricos (rectas, circunferencias, ) por medio
Alonso Fernández Galián Tema 6: Geometría analítica en el plano TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO La geometría analítica es el estudio de objetos geométricos (rectas, circunferencias, ) por medio
CUERPOS EN EL ESPACIO
 CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
CUERPOS EN EL ESPACIO 1. Poliedros. 2. Fórmula de Euler. 3. Prismas. 4. Paralelepípedos. Ortoedros. 5. Pirámides. 6. Cuerpos de revolución. 6.1. Cilindros. 6.2. Conos. 6.3. Esferas. 6.4. Coordenadas geográficas.
Transformaciones Isométricas
 Capítulo 11 Transformaciones Isométricas E l estudio de los movimientos en el plano y el espacio han sido muy importantes en nuestra historia, ya que gracias a ellos hemos aprendido a comprender como se
Capítulo 11 Transformaciones Isométricas E l estudio de los movimientos en el plano y el espacio han sido muy importantes en nuestra historia, ya que gracias a ellos hemos aprendido a comprender como se
TEORÍA TEMA 6 CENTRO DE FUERZAS PARALELAS. A- Centro de fuerzas paralelas caso dos fuerzas- caso n fuerzas. Definición centro de fuerzas paralelas.
 TEORÍA TEMA 6 CENTRO DE FUERZAS PARALELAS A- Centro de fuerzas paralelas caso dos fuerzas- caso n fuerzas. Definición centro de fuerzas paralelas. B- Caso de fuerzas paralelas de igual sentido (gráfico)
TEORÍA TEMA 6 CENTRO DE FUERZAS PARALELAS A- Centro de fuerzas paralelas caso dos fuerzas- caso n fuerzas. Definición centro de fuerzas paralelas. B- Caso de fuerzas paralelas de igual sentido (gráfico)
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Elementos de geometría analítica
 UNIDAD 7: APLIQUEMOS ELEMENTOS DE GEOMETRIA ANALITICA. Introducción Elementos de geometría analítica En esta unidad última nos ocuparemos del estudio de los conceptos más fundamentales de la geometría
UNIDAD 7: APLIQUEMOS ELEMENTOS DE GEOMETRIA ANALITICA. Introducción Elementos de geometría analítica En esta unidad última nos ocuparemos del estudio de los conceptos más fundamentales de la geometría
3º ESO PMAR FUNCIONES DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa FUNCIONES
 FUNCIONES.- CARACTERÍSTICAS DE LAS FUNCIONES Definición: Una función es una relación entre dos variables de tal forma que a cada valor de la primera (variable independiente, ) le corresponde un valor o
FUNCIONES.- CARACTERÍSTICAS DE LAS FUNCIONES Definición: Una función es una relación entre dos variables de tal forma que a cada valor de la primera (variable independiente, ) le corresponde un valor o
Guía del docente. 1. Descripción curricular:
 Guía del docente. 1. Descripción curricular: - Nivel: NM1, Iº medio. - Subsector: Matemática. - Unidad temática: Transformaciones isométricas. - Palabras claves: Geometría; Área; Figuras geométricas; Mosaicos;
Guía del docente. 1. Descripción curricular: - Nivel: NM1, Iº medio. - Subsector: Matemática. - Unidad temática: Transformaciones isométricas. - Palabras claves: Geometría; Área; Figuras geométricas; Mosaicos;
Ámbito Científico-Tecnológico Módulo III Bloque 4 Unidad 6 Eres mi semejante?
 Ámbito Científico-Tecnológico Módulo III Bloque 4 Unidad 6 Eres mi semejante? Cuántas veces nos hemos parado a pensar, esas dos personas mira que se parecen, casi son igualitas! De igual manera, cuando
Ámbito Científico-Tecnológico Módulo III Bloque 4 Unidad 6 Eres mi semejante? Cuántas veces nos hemos parado a pensar, esas dos personas mira que se parecen, casi son igualitas! De igual manera, cuando
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución- CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución- CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α
TEMA 4. Geometría. Teoría. Matemáticas
 1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
1 1.- Rectas y ángulos La geometría se basa en tres conceptos fundamentales que forman parte del espacio geométrico, es decir, el conjunto formado por todos los puntos: El punto La recta El plano Partiendo
Con punto fijo Rotaciones Simetría Axial Sin punto fijo Traslaciones Reflexión Deslizante
 Eje: Geometría, FASCÍCULO 12 Transformaciones Rígidas y Homotecias En el Fascículo 11 vimos que podemos pensar que hay 4 clases de transformaciones rígidas clasificadas de la siguiente manera (pensamos
Eje: Geometría, FASCÍCULO 12 Transformaciones Rígidas y Homotecias En el Fascículo 11 vimos que podemos pensar que hay 4 clases de transformaciones rígidas clasificadas de la siguiente manera (pensamos
Se denomina mosaico a un recubrimiento del plano mediante piezas llamadas teselas sin dejar huecos y sin solapamiento.
 Qué entendemos por Mosaico? Se denomina mosaico a un recubrimiento del plano mediante piezas llamadas teselas sin dejar huecos y sin solapamiento. En otro lenguaje, formar un mosaico es embaldosar una
Qué entendemos por Mosaico? Se denomina mosaico a un recubrimiento del plano mediante piezas llamadas teselas sin dejar huecos y sin solapamiento. En otro lenguaje, formar un mosaico es embaldosar una
WEBS RECOMENDADAS. s1.htm
 WEBS RECOMENDADAS NÚMEROS RACIONALES E IRRACIONALES http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero s1. Presenta los números racionales http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero
WEBS RECOMENDADAS NÚMEROS RACIONALES E IRRACIONALES http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero s1. Presenta los números racionales http://descartes.cnice.mec.es/3_eso/numeros_reales_aproximaciones/numero
Grupos espaciales de simetría
 Grupos espaciales de simetría La simetría de los átomos que constituyen el cristal se describe con un grupo de simetría espacial constituido por un subgrupo de traslación (el retículo) y determinados elementos
Grupos espaciales de simetría La simetría de los átomos que constituyen el cristal se describe con un grupo de simetría espacial constituido por un subgrupo de traslación (el retículo) y determinados elementos
Nombre: Curso: Fecha: -
 1 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM-4 Guía 4: Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza
1 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM-4 Guía 4: Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza
Guía College Board 2012 Rev 28 Página 48 de 120. NOTA: La figura no está dibujada a escala.
 Conceptos de geometría Las figuras que acompañan a los ejercicios en la prueba tienen el propósito de proveerle información útil para resolver los problemas. Las figuras están dibujadas con la mayor precisión
Conceptos de geometría Las figuras que acompañan a los ejercicios en la prueba tienen el propósito de proveerle información útil para resolver los problemas. Las figuras están dibujadas con la mayor precisión
16 PROPORCIONALIDAD INVERSA.-POTENCIA
 16 PROPORCIONALIDAD INVERSA.-POTENCIA 16.1 Características generales. Consideramos que una variable x puede adquirir los valores a, b, c, d,.. y otra variable y los valores a, b, c, d, x e y son inversamente
16 PROPORCIONALIDAD INVERSA.-POTENCIA 16.1 Características generales. Consideramos que una variable x puede adquirir los valores a, b, c, d,.. y otra variable y los valores a, b, c, d, x e y son inversamente
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos:
 ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
Unidad 1. Trazados fundamentales en el plano.
 MATERIA: CURSO: DIBUJO TÉCNICO 2º BACHILLERATO CONTENIDOS MÍNIMOS Unidad 1. Trazados fundamentales en el plano. Suma de segmentos. Diferencia de segmentos. Trazado de la mediatriz de un segmento. Trazado
MATERIA: CURSO: DIBUJO TÉCNICO 2º BACHILLERATO CONTENIDOS MÍNIMOS Unidad 1. Trazados fundamentales en el plano. Suma de segmentos. Diferencia de segmentos. Trazado de la mediatriz de un segmento. Trazado
7. UNIDAD DIDACTICA 7: TRANSFORMACIONES GEOMÉTRICAS
 7. UNIDAD DIDACTICA 7: TRANSFORMACIONES GEOMÉTRICAS Las transformaciones geométricas pueden tener diferentes características y finalidades, todas ellas muy importantes dentro del dibujo técnico. Se llama
7. UNIDAD DIDACTICA 7: TRANSFORMACIONES GEOMÉTRICAS Las transformaciones geométricas pueden tener diferentes características y finalidades, todas ellas muy importantes dentro del dibujo técnico. Se llama
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
12Direcciones de internet
 12Direcciones de internet En la dirección http://www.nucleogestion.8m.com/hall.htm se puede pasear libremente por el museo virtual de Escher. Se puede entrar en la sala que se desee haciendo clic sobre
12Direcciones de internet En la dirección http://www.nucleogestion.8m.com/hall.htm se puede pasear libremente por el museo virtual de Escher. Se puede entrar en la sala que se desee haciendo clic sobre
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
G E O M E T R I A I D I E O M A L E N G U A J E D E L D I S E Ñ O
 G E O M E T R I A I D I E O M A L E N G U A J E D E L D I S E Ñ O Las PALABRAS para el LENGUAJE Las NOTAS para la MUSICA Los NUMEROS para las MATEMATICAS . Un lenguaje estructurado. D G E S T R U C T U
G E O M E T R I A I D I E O M A L E N G U A J E D E L D I S E Ñ O Las PALABRAS para el LENGUAJE Las NOTAS para la MUSICA Los NUMEROS para las MATEMATICAS . Un lenguaje estructurado. D G E S T R U C T U
Estructuras algebraicas. Departamento de Álgebra. Apuntes de teoría
 ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
ESTRUCTURAS ALGEBRAICAS GRADO EN MATEMÁTICAS. CURSO 2015/2016 Apuntes de teoría Tema 1: Grupos y subgrupos. 1.1. Introducción Definición 1.1. Un grupo es un par (G, ), donde G es un conjunto no vacío,
PLANIFICACIÓN DE MATEMÁTICA PRIMERO MEDIO
 Liceo Pedro de Valdivia La Calera PLANIFICACIÓN DE MATEMÁTICA PRIMERO MEDIO - 2015 Nombre del Profesor: Eduardo Hernán Guerra Cuevas Título: Geometría euclidiana Tiempo estimado: 65 horas pedagógicas UNIDAD
Liceo Pedro de Valdivia La Calera PLANIFICACIÓN DE MATEMÁTICA PRIMERO MEDIO - 2015 Nombre del Profesor: Eduardo Hernán Guerra Cuevas Título: Geometría euclidiana Tiempo estimado: 65 horas pedagógicas UNIDAD
REVISIÓN DE ALGUNOS CONCEPTOS DE GEOMETRÍA MÉTRICA
 MAT B Repartido Nº I REVISIÓN DE ALGUNOS CONCEPTOS DE GEOMETRÍA MÉTRICA Conceptos primitivos Partiremos de un conjunto que llamaremos espacio, E, a cuyos elementos llamamos puntos, (a los cuales escribiremos
MAT B Repartido Nº I REVISIÓN DE ALGUNOS CONCEPTOS DE GEOMETRÍA MÉTRICA Conceptos primitivos Partiremos de un conjunto que llamaremos espacio, E, a cuyos elementos llamamos puntos, (a los cuales escribiremos
Objetivos: Trasladar figuras en el plano cartesiano. Reconocer o identificar una traslación.
 Guía N 19 Nombre: Fecha: Contenido: Transformaciones isométricas. Objetivos: Trasladar figuras en el plano cartesiano Reconocer o identificar una traslación. Las transformaciones geométricas están presentes
Guía N 19 Nombre: Fecha: Contenido: Transformaciones isométricas. Objetivos: Trasladar figuras en el plano cartesiano Reconocer o identificar una traslación. Las transformaciones geométricas están presentes
Geometría 3. Ejercicio 2. Dados los puntos = ( 1, 0, 0 ),
 Geometría 3 Ejercicio. Sean los puntos P (,, ), Q (,, 3) R (,3,). ) Calcula el punto P que es la proección del punto P sobre la recta que determinan Q R ) Halla la ecuación del lugar geométrico de los
Geometría 3 Ejercicio. Sean los puntos P (,, ), Q (,, 3) R (,3,). ) Calcula el punto P que es la proección del punto P sobre la recta que determinan Q R ) Halla la ecuación del lugar geométrico de los
Clase N 05 MODULO COMPLEMENTARIO. Ángulos y polígonos
 Pre-universitario Manuel Guerrero Ceballos Clase N 05 MODULO COMPLEMENTARIO Ángulos y polígonos Resumen de la clase anterior Tipos de gráficos Probabilidades Histograma Barras De gráfico a tabla Polígono
Pre-universitario Manuel Guerrero Ceballos Clase N 05 MODULO COMPLEMENTARIO Ángulos y polígonos Resumen de la clase anterior Tipos de gráficos Probabilidades Histograma Barras De gráfico a tabla Polígono

 ᒬ 01) En el triángulo ABC de la figura AD = BD;
ᒬ 01) En el triángulo ABC de la figura AD = BD;